Đề cuối học kì 2 Toán 11 năm 2022 – 2023 trường THPT Giao Thủy – Nam Định

TRƯỜNG THPT GIAO THUỶ
ĐỀ KIỂM TRA CUỐI HỌC KÌ II TỔ TOÁN TIN NĂM HỌC 2022 - 2023
Môn: Toán – Lớp: 11 Mã đề: 101
Thời gian làm bài: 90 Phút. Đề thi gồm: 03 trang.
I. PHẦN TRẮC NGHIỆM (4 ĐIỂM)
Câu 1: Cho hàm số f (x) = 2x + 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hàm số liên tục tại x = 4
− . B. Hàm số gián đoạn tại x = 5 − .
C. Hàm số gián đoạn tại x = 3. D. Hàm số gián đoạn tại x =10.
Câu 2: Đạo hàm của hàm số y = 4 x − 2
3x + 2x − 1 là A. 3
y' = 4x − 3x + 2. B. y = x3 ' 4 − 2x + 2.
C. y' = x3 4 − 6x + . 3 D. y = x3 ' 4 − 6x + 2.
Câu 3: Cho hàm số y = f (x) xác định trên tập D, . x ∈ D 0
Hàm số y = f (x) gọi là liên tục
tại x = x nếu: 0
A. f (x = lim f x . B. f (x = lim f x . 0 ) ( ) 0 ) ( ) x + → → 0 x x 0 x
C. lim f (x) = lim f (x) . D. f (x = lim f x . 0 ) ( ) x + − → − 0 x x→ 0 x x→ 0 x
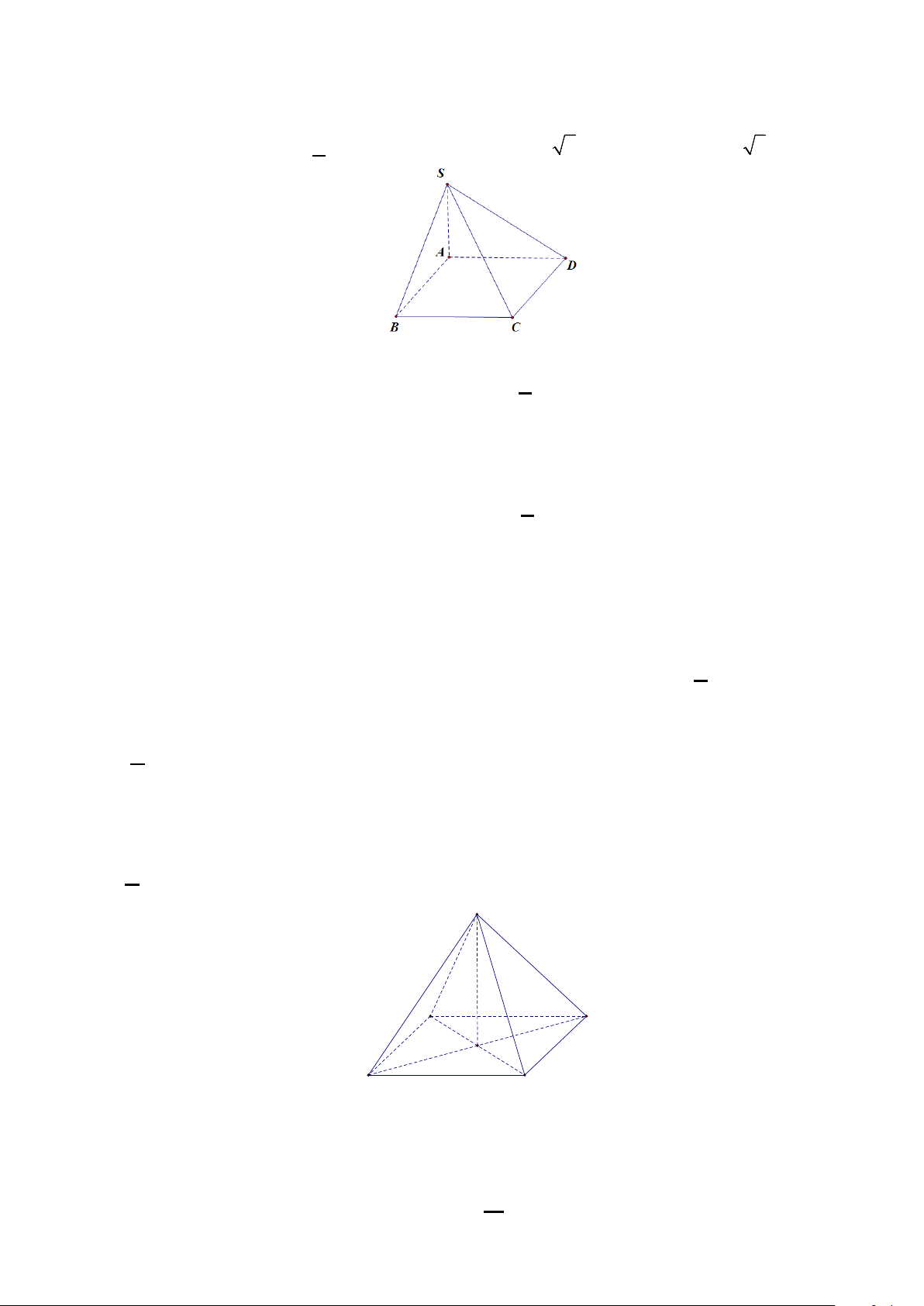
Câu 4: Cho hình chóp S.ABC có đáy là tam giác vuông tại B, SA vuông góc với mặt
phẳng ( ABC). Góc giữa SB và mặt phẳng ( ABC) là A.  SBA. B.  BSA. C.  SAB . D.  ABC . S C A B
Câu 5: Cho hàm số y = f (x) liên tục trên đoạn [ 2 − ; ] 1 f ( , 2 − ) = 3 f ( ) , 1 = 2 − . Trong các
mệnh đề sau, mệnh đề nào đúng?
A. Phương trình f (x) = 0 có nghiệm x = 2. −
B. Phương trình f (x) = 0 có nghiệm x =1.
C. Phương trình f (x) = 0 không có nghiệm thuộc khoảng ( 2; − ) 1 .
D. Phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng ( 2; − ) 1 .
Câu 6: Đạo hàm của hàm số y = 2023x + cos x là
A. y' = 2023x − sin x. B. y' = 2023+ sin .x
C. y' = 2023− sin .x
D. y' = −sin x . Trang 1/3 - Mã đề 101
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = a, SA
vuông góc với mặt phẳng đáy, SA = 2a . Khoảng cách từ S đến mặt phẳng ( ABCD) bằng
A. a . B. 2a . C. a 2 . D. a 5 .
Câu 8: Đạo hàm của hàm số y = xsin x là
A. y' = cos x .
B. y' = sin x + xcos .x
C. y' = sin x − xcos .x D. y' = −sin x + xcos x . 2  + ≠ Câu 9: Cho hàm số x 1 khi x 2 f (x) = 
. Trong các mệnh đề sau, mệnh đề nào đúng? 5  khi x = 2
A. Hàm số không liên tục tại x =1. B. Hàm số liên tục tại điểm x = 2.
C. Hàm số không liên tục tại x = 0. D. Hàm số không liên tục tại x = 1. −
Câu 10: Một chất điểm chuyển động với phương trình 3 2
s = 2t − 3t + 4t, trong đó t được
tính bằng giây và s được tính bằng mét (m).Vận tốc của chất điểm tại thời điểm t = 2(s) bằng
A. 12 (m/s).
B. 6 (m/s).
C. 2 (m/s).
D. 16 (m/s).
Câu 11: Đạo hàm của hàm số y = ( x − )6 3 5 là A. ( x − )5 18. 3 5 . B. ( x − )6 18. 3 5 . C. ( x − )5 3. 3
5 . D. ( x − )5 6. 3 5 .
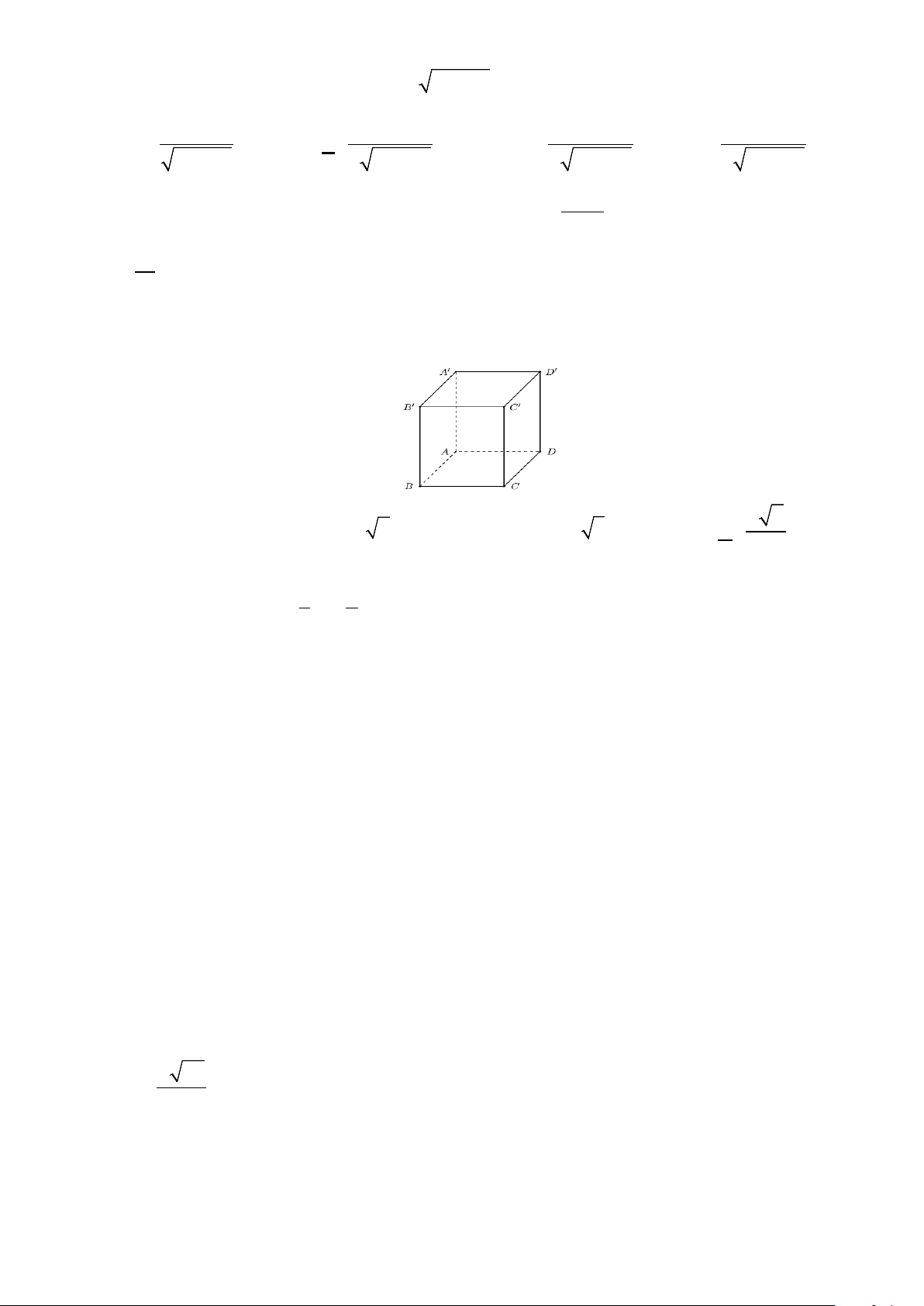
Câu 12: Cho hình chóp đều S.ABCD có O là tâm của đáy. Trong các mệnh đề sau, mệnh đề nào sai?
A. SO ⊥ ( ABCD) .
B. AC ⊥ (SBD).
C. SA ⊥ ( ABCD) .
D. BD ⊥ (SAC). S A D O B C 2 Câu 13:  Cho hàm số ≥ f (x) 2x khi x 1 = 
Trong các mệnh đề sau, mệnh đề nào sai?
x+2 khi x < 1.
A. Hàm số liên tục tại x = 10. −
B. Hàm số liên tục tại điểm x = 3. −
C. Hàm số liên tục tại x = 4. D. Hàm số liên tục tại x =1. Trang 2/3 - Mã đề 101
Câu 14: Đạo hàm của hàm số 2
f (x) = x − 5x là
A. 2x − 5 .
B. 2x − 5 . C. 2x − 5 − . D. 1 . 2 x − 5x 2 2 x − 5x 2 2 x − 5x 2 2 x − 5x
Câu 15: Phương trình tiếp tuyến của đồ thị hàm số x + 2 y = tại điểm (0; ) 1 − là x − 2
A. y = −x −1. B. y = −x + 2 . C. y = −x +1. D. y = x + 2.
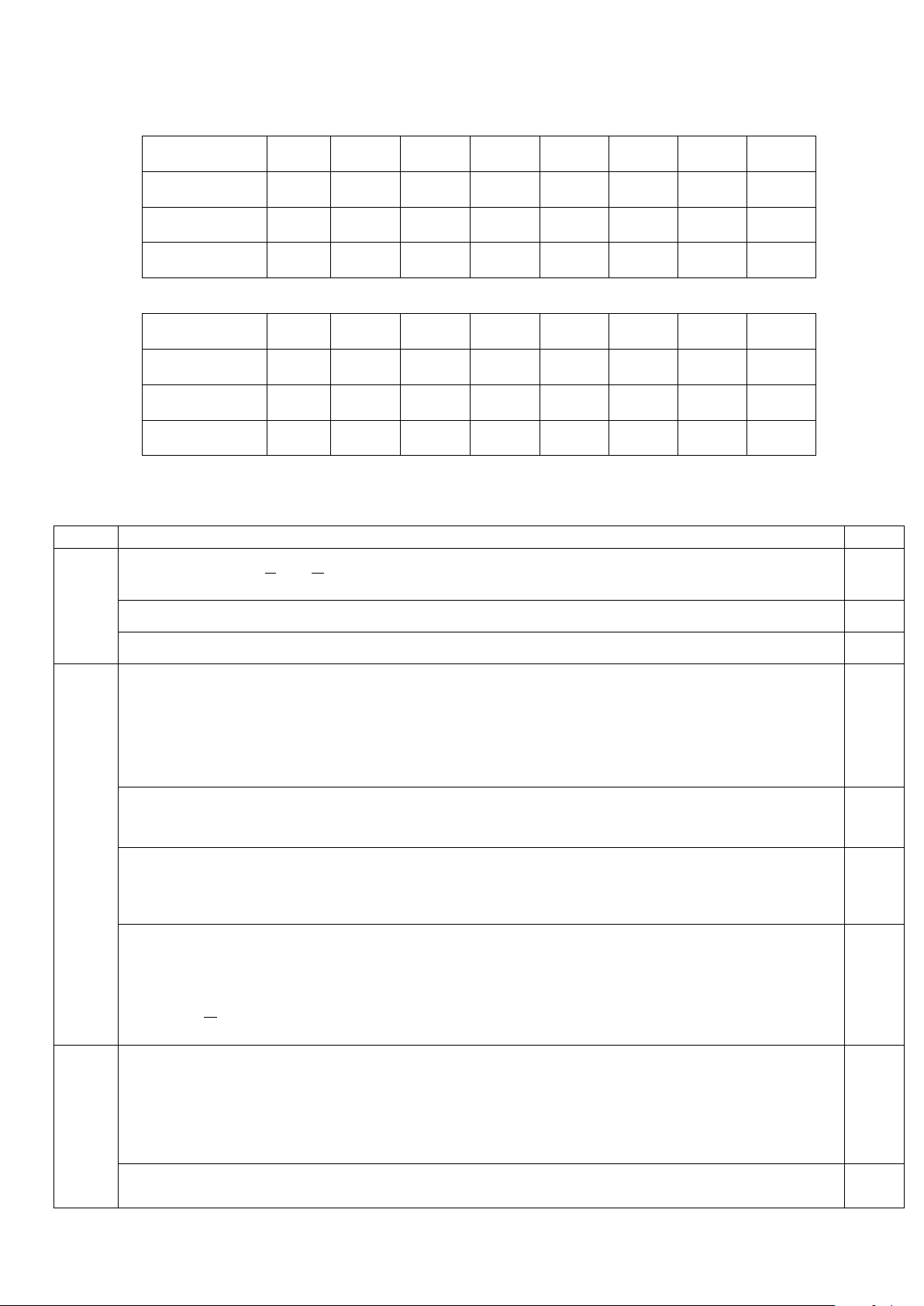
Câu 16: Cho hình lập phương ABC . D A′B C ′ D
′ ′ có cạnh a . Khoảng cách giữa đường
thẳng BB' và mặt phẳng ( ACC ' A') bằng
A. a . B. a 2 .
C. a 3 . D. a 2 . 2
II. PHẦN TỰ LUẬN (6 ĐIỂM) Bài 1: Cho hàm số 1 3 1 2
y = x − x − 2x + 2 . Giải bất phương trình y ' ≤ 0. 3 2
Bài 2: Tìm tất cả các giá trị của tham số m để hàm số 3  + ≥ f (x) x 2mx khi x 1 = 1−3x khi x <1.
liên tục tại x =1.
Bài 3: Cho đồ thị hàm số (C) 3 2
: y = x − 3x + mx +1 ( m là tham số). Tìm tất cả các giá trị
của m để tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 1 cắt các trục Ox,Oy lần
lượt tại hai điểm phân biệt ,
A B sao cho diện tích tam giác OAB bằng 2.
Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B ,
AB = BC = a . Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a .
a. Chứng minh AD ⊥ (SAB) .
b. Tính khoảng cách từ A đến mặt phẳng (SBC) .
c. Cho M là trung điểm cạnh SB, N thuộc cạnh SD thỏa mãn SD = 4SN . Gọi α là góc
giữa hai mặt phẳng ( AMN ) và ( ABCD) . Tính cosα biết khoảng cách giữa BD và SC bằng a 26 . 26
------------Hết------------
Họ và tên thí sinh:........................................... ............. .Số báo danh:.....................................
Họ, tên và chữ ký của GT 1:............................Họ, tên và chữ ký của GT 2:.......... ................ Trang 3/3 - Mã đề 101
ĐÁP ÁN ĐỀ THI CUỐI NĂM LỚP 11 Mã 101 CÂU 1 2 3 4 5 6 7 8 ĐÁP ÁN A D B A D C B B CÂU 9 10 11 12 13 14 15 16 ĐÁP ÁN B D A C D B A D Mã 102 CÂU 1 2 3 4 5 6 7 8 ĐÁP ÁN A D D C A B B D CÂU 9 10 11 12 13 14 15 16 ĐÁP ÁN B A B B C D A D TỰ LUẬN Bài Nội dung Điểm Bài 1 1 1 (1,0 Cho hàm số 3 2
y = x − x − 2x + 2 . Giải bất phương trình y ' ≤ 0. 3 2 điểm) 2
y ' = x − x − 2 0.5
y ' ≤ 0 ⇔ x ∈[ 1; − 2] 0.5
Bài 2 Tìm tất cả các giá trị của tham số m để hàm số (1,0 3
x + 2mx khi x ≥1 điểm)
f (x) = 1−3x khi x <1.
liên tục tại x =1. TXĐ:  lim f (x) = lim + = + 0.25 + + ( 3
x 2mx) 2m 1 x 1 → x 1 →
lim f (x) = lim(1− 3x) = 2 − x 1− x 1− → → 0.25 f ( ) 1 = 2m +1
Hàm số liên tục tại x = 1 ⇔ lim f (x) = lim f (x) = f ( ) 1 0.25 x 1+ x 1− → → ⇔ 2m +1 = 2 − 3 ⇔ m = − 2 0.25
Bài 3 Cho đồ thị hàm số (C) 3 2
: y = x − 3x + mx +1 ( m là tham số). Tìm tất cả các giá trị (1,0
điểm) của m để tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 1 cắt các trục
Ox,Oy lần lượt tại hai điểm phân biệt ,
A B sao cho diện tích tam giác OAB bằng 2. 2
y ' = 3x − 6x + m Trang 4/3 - Mã đề 101 y '( )
1 = m − 3, y( ) 1 = m −1 0.25
PT tiếp tuyến tại điểm có hoành độ bằng 1 là: y = (m − 3) x + 2 (d )
Điều kiện: m ≠ 3  2 Khi đó A ;0 −  , B(0;2) 0.25  m − 3  1 2 S = = OAB . .2 2 2 0.25 m − 3 m = 4 ⇔  (tm) 0.25 m = 2
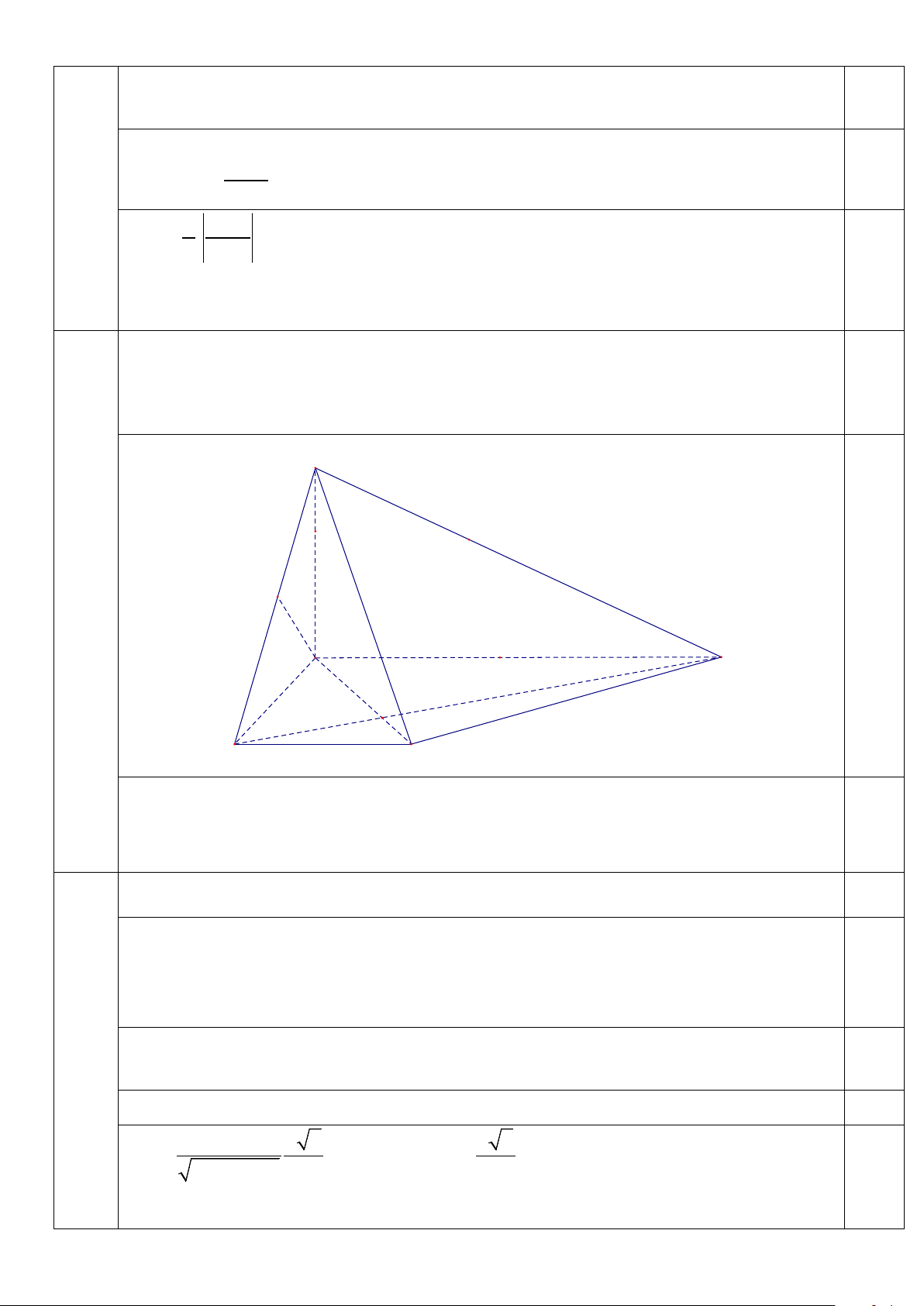
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B ,
AB = BC = a . Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a .
a. Chứng minh AD ⊥ (SAB) . S Bài 4a E (1,0 điểm) A D B C AD ⊥ AB 0.25 AD SA  ⊥  0.25 ⇒ AD ⊥ (SAB) 0.5
Bài b. Tính khoảng cách từ A đến mặt phẳng (SBC). 4b
(1,0 Hạ AE ⊥ SB tại E
điểm) BC ⊥ AB⇒ BC ⊥(SAB) BC ⊥ SA  0.25 ⇒ BC ⊥ AE
AE ⊥ BC⇒ AE ⊥(SBC) AE ⊥ SB 0.25  d ( ,
A (SBC)) = AE 0.25 AS.AB a 2 AE =
⇒ d ( A (SBC)) a 2 , = 2 2 AS + AB 2 2 0.25 Trang 5/3 - Mã đề 101
Bài c. Cho M là trung điểm cạnh SB, N thuộc cạnh SD thỏa mãn SD = 4SN . Gọi α 4c
(1,0 là góc giữa hai mặt phẳng ( AMN ) và ( ABCD) . Tính cosα biết khoảng cách giữa điểm) a
BD và SC bằng 26 . 26 S I N G M≡E K F A D H O B C
O = AC ∩ BD, /
OI /SC với I ∈ SA, M ≡ E ⇒ SC / /(IBD)
⇒ d (SC BD) = d (SC (IBD)) = d (S (IBD)) a 26 , , , = 0.25 26
Đặt AD = x, x > 0 d ( ,
A (IBD)) AI AO AD x x 26 = = = = ⇒ = d ( d ( , A IBD ) S,(IBD)) ( ) SI OC BC a 26 AI x ax = ⇒ AI = SA x + a x + a 0.25
Hạ AH ⊥ BD tại H, AK ⊥ IH tại K
Chứng minh AK ⊥ (IBD) ⇒ d ( ,
A (IBD)) = AK 1 1 1 1 1 1 26 (x + a)2 1 1 x = 3a = + = + + ⇔ = + + ⇔ 2 2 2 2 2 2 AK AI AH AI AB AD 2 2 2 2 2 x x a a x x = 4 − a  (ktm)
Lấy F thuộc cạnh AD thỏa mãn AF = a, G = SF ∩ AN
Chứng minh CF ⊥ (SAD) ⇒ CF ⊥ AG
SG . AF .ND =1 SG ⇒
= 1⇒ G là trung điểm SF ⇒ AG ⊥ SF GF AD NS GF 0.25
⇒ AG ⊥ (SFC) ⇒ AG ⊥ SC
AM ⊥ (SBC) ⇒ AM ⊥ SC
⇒ SC ⊥ ( AMN )
SA ⊥ ( ABCD) ⇒ α = (SA SC)  , =ASC 3 0.25 ⇒ cosα = 3 Trang 6/3 - Mã đề 101 Trang 7/3 - Mã đề 101
Document Outline

• ĐỀ KIỂM TRA CUỐI HỌC KÌ II
• TRƯỜNG THPT GIAO THUỶ
• NĂM HỌC 2022 - 2023
• Môn: Toán – Lớp: 11
• Thời gian làm bài: 90 Phút.