Đề cuối học kỳ 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Kim Thành – Hải Dương
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra cuối học kỳ 1 môn Toán 9 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Kim Thành, tỉnh Hải Dương; đề thi có đáp án trắc nghiệm và hướng dẫn chấm điểm tự luận. Mời bạn đọc đón xem.
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ I HUYỆN KIM THÀNH MÔN: TOÁN 9 NĂM HỌC 2023-2024
Thời gian làm bài: 90 phút
(Không tính thời gian giao đề)
Đề bài gồm: 02 trang
I . Phần trắc nghiệm (3,0 điểm):
Hãy chọn chữ cái đứng trước đáp án đúng?
Câu 1. Với những giá trị nào của x thì x − 2023 có nghĩa? A. x > 2023 B. x > -2023 C. x ≥ 2023 D. x ≤ 2023
Câu 2. Kết quả của phép tính 3− 5. 3+ 5 là: A.3 B. 5 C. 4 D. 2
Câu 3. Đồ thị hàm số y = 2x -3 đi qua điểm nào? A. (1; -3) B. (1; -5) C. (-1; -5) D. (-1; -1)
Câu 4.Hàm số y= (m - 6)x + 7- m là hàm số đồng biến khi nào? A. m < 6 B. m > 6 C. m < - 6 D. m > - 6
Câu 5. Để hàm số y = (2m +4)x -3 là hàm số bậc nhất thì: A. m≠-2 B. m ≤ -2 C. m = -2 D. m ≥-2
Câu 6. Cho hàm số bậc nhất y=(m-5)x+2 và y=2x. Giá trị của m đề đồ thị của hai hàm số cắt nhau là: A. m≠5 B. m≠7 C. m≠5;m≠7 D. m=5;m=7
Câu 7. Cho tam giác ABC vuông tại A. Khi đó SinC bằng: A. AB B. AC C. BC D. AB AC AB AC BC
Câu 8. Đường thẳng và đường tròn cắt nhau thì số điểm chung là: A. 0 B. 1 C. 2 D. 3
Câu 9. ∆ABC vuông tại A có BC = 6cm và 0
B = 60 . Độ dài cạnh AB là: A. 3cm B. 6cm C. 3 3 cm D. 2 cm
Câu 10. Nếu AB là một dây bất kì của đường tròn (O; R) thì: A. AB≤R B.AB<2R C. AB>2R D. AB≤2R
Câu 11. Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường nào? A. Đường cao B. Phân giác C.Trung tuyến D. Trung trực
Câu 12. Cho tam giác ABC vuông tại A, đường cao AH. Hệ thức nào sau đây là sai: A. 2
AB = BC.BH B. 2 AH = . HB HC C. 2
BC = AB + AC D. .
AB AC = BC.AH
II. Tự Luận (7,0 điểm) Câu 13. (1,5 điểm).
1. Thực hiện phép tính : 2 50 −3 72 + 5 32 2. Rút gọn biểu thức : x x 2 x 3 M : với x 0; 9 x
x 3 9 x x 3
Câu 14. (1,0 điểm). Giải phương trình a) 2 (2x −1) = 3 b) 1 9x −18 − 4x −8 = 4 2 Câu 15 (1,5 điểm).
a) Cho hàm số y = 3x + (3− m) Tìm m để đồ thị hàm số đi qua điểm ( A ; 1 ) 2 .
b)Với những giá trị nào của m thì đồ thị các hàm số y = 3x + (3− m) và
y = 2x + (7 + m) cắt nhau tại một điểm trên trục tung? Câu 16 (2,5 điểm).
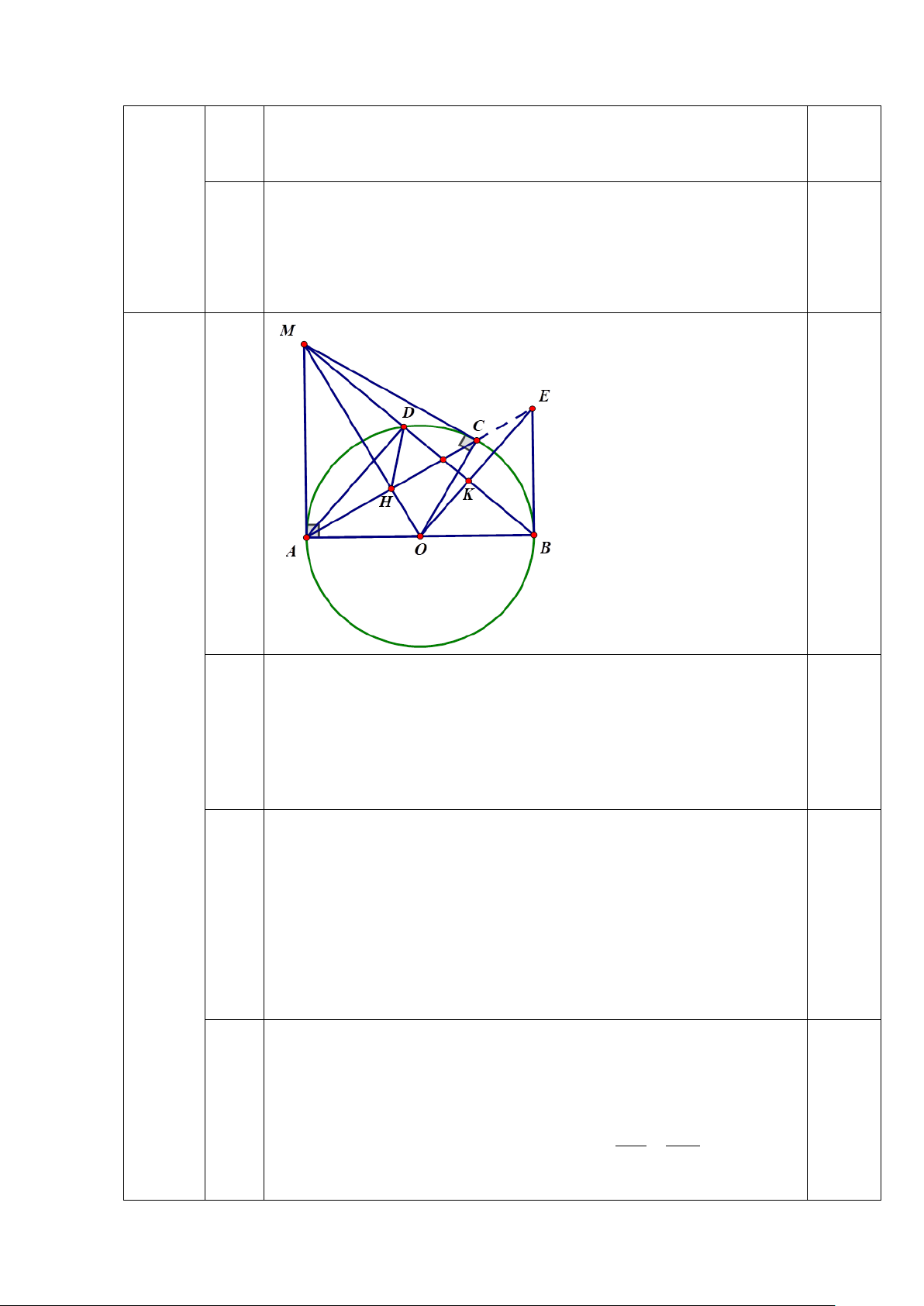
Cho (O) là đường tròn tâm O đường kính AB=2R. Qua A vẽ tiếp tuyến Ax của
(O), trên tia Ax lấy điểm M (M khác A), từ M vẽ tiếp tuyến MC của (O) (C là
tiếp điểm). Gọi H là giao điểm của OM và AC. Đường thẳng MB cắt (O) tại D (D nằm giữa M và B).
a) Chứng minh: OM ⊥ AC tại H và tính OH.OM theo R.
b) Chứng minh: 4 điểm M, D, H, A cùng thuộc 1 đường tròn..
c) Gọi K là trung điểm đoạn thẳng BD. Tiếp tuyến tại B của (O) cắt tia OK
tại E. Chứng minh: Ba điểm A, C, E thẳng hàng. Câu 17. (0,5 điểm)
Cho các số dương a, b, c thỏa mãn điều kiện a + b + c = 3. Chứng minh rằng: 2 2 a + ab + 2 2 b + 2 2 b + bc + 2 2 c + 2 2 c + ca + 2 2 a ≥ 3 5
------------HẾT------------
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN KIM THÀNH
ĐỀ KIỂM TRA CUỐI HỌC KỲ I MÔN: TOÁN 9 NĂM HỌC 2023-2024
Hướng dẫn chấm gồm: 02 trang
I.Phần trắc nghiệm (3 điểm) Mỗi câu chọn đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C D C B A C D C A D B C
II.Phần tự luận (7 điểm ) Câu ý Đáp án Điểm
1 2 50 −3 72 +5 32 =10 2 −18 2 + 20 2 0.25 = 12 2 0.25 x x 2 x 3 M :
x 3 9 x x 3 0,25 x x 2 x 3 M :
x 3 ( x 3)( x 3) x 3 Câu 13.
x( x 3) x x 3 M . 0,25 (1,5
( x 3)( x 3) 2 x 3 điểm). 2x 3 x x 3 M . 0,25 2
( x 3)( x 3) 2 x 3 M x x 3 0,25 Vậy M x với với x 0; 9 x x 3 2
(2x −1) = 3 ⇔ 2x −1 = 3 0,25 a 2x −1 = 3 x = 2 0,25 ⇔ ⇔ Câu 2x −1 = 3 − x = 1 − 14.
Vậy phương trình có nghiệm x = 2; x = -1 (1,0 1 9x −18 −
4x −8 = 4 ⇔ 3 x − 2 − x − 2 = 4 0,25 điểm). 2 ⇔ x − 2 = 2 ĐK: x ≥ 2 0,25
b ⇔ x − 2 = 4 ⇔ x = 6 (t / m)
Vậy phương trình có nghiệm x = 6
a Đồ thị hàm số đi qua điểm A(1;2) nên thay x=1; y=2 vào
hàm số ta được 2= 3.1+ 3-m 0,25 m=4 0,5
b Hai đồ thị hàm số cắt nhau tại 1 điểm nằm trên trục tung 15 khi: 0,25 2 ≠ 3 0,5 3
− m = 7 + m Từ đó tìm được m=-2 a 0,25
Chứng minh: OM ⊥ AC tại H
Ta có: MA = MC (T/c 2 tiếp tuyến cắt nhau) 0,25 OA = OC ( Bán kính (O)) 16
⇒ OM là đường trung trực của đoạn thẳng AC ⇒ OM ⊥ AC tại H 0,25 Khi đó OH.OM= OA2=R2 0,25
b Ta có ∆DAB nội tiếp đường tròn đường kính AB 0,25 ⇒ ∆ DAB vuông tại D ⇒ AD ⊥ MB tại D nên 0
MDA = 90 nên D thuộc đường tròn đường kính MA( 1) 0,25 Mặt khác 0
MHA = 90 nên H thuộc đường tròn đường kính MA(2) 0,25
Từ (1) và (2) suy ra 4 điểm M, D, H, A cùng thuộc 1 đường tròn.
c Ta có OK ⊥ BD tại K ( quan hệ giữa đường kính và dây)
Nên OK.OE = OB2 (3) (Hệ thức lượng trong tam giác)
Mà OH.OM = OA2 (4) (Hệ thức)
Ta có OB = OA (5) (Bán kính (O)) 0,25 Từ (3) (4) và (5) ⇒ . = OK.OE ⇒ OH OH OM = OE OK OM
Suy ra ∆OHE ഗ ∆OKM (c-g-c) ⇒ OHE = OKM 0,25 Mà 0
OKM = 90 ( OK ⊥ BD tại K) ⇒ 0 OHE = 90 ⇒ HE ⊥ OM tại H Mà AC ⊥ OM tại H (cmt)
⇒ Ba điểm A, C, E thẳng hàng. 0,25 Câu Ta có: 4(2a2 + ab + 2b2) 17. (0,5
= 5(a2 + 2ab + b2) + 3(a2 – 2ab + b2) điểm)
= 5(a + b)2 + 3(a - b)2 ≥5(a + b)2, vì (a - b)2 ≥ 0. Vì a, b dương nên: 2 2 2 2 5
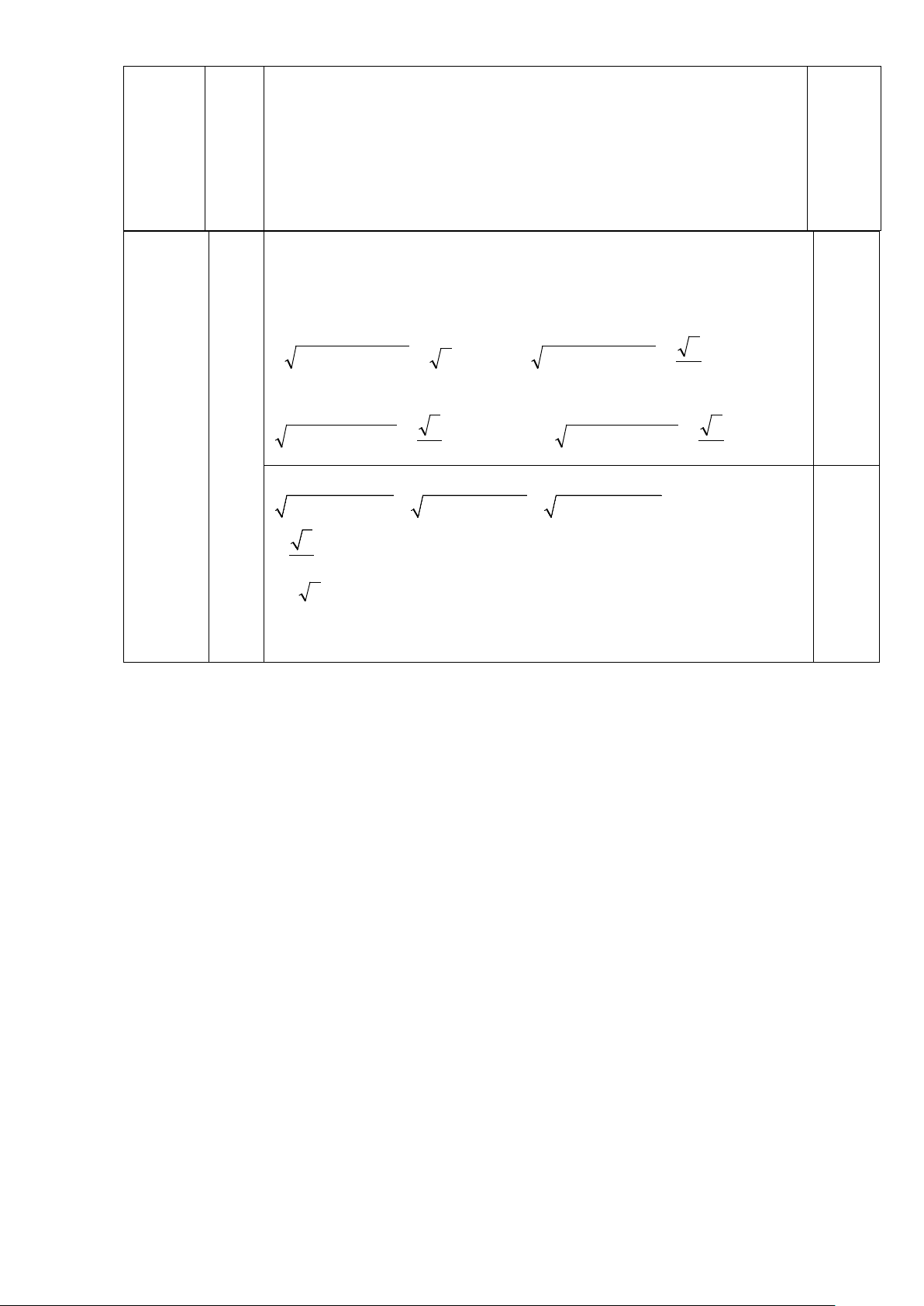
2 2a + ab + 2b ≥ 5(a + b) ⇔ 2a + ab + 2b ≥ (a + b) (1) 0,25 2
Học sinh chứng minh tương tự để có: 2 2 5
2b + bc + 2c ≥ (b + c) (2) và 2 2 5
2c + ca + 2a ≥ (c + a) (3) 2 2
Cộng theo vế các bất đẳng thức (1), (2) và (3) ta được 2 2 2 2 2 2
2a + ab + 2b + 2b + bc + 2c + 2c + ca + 2a 5 ≥
⋅ 2(a + b + c) 2 0,25 = 3 5
Dấu “=” xảy ra a = b = c ⇔
⇔ a = b = c = 1
a + b + c = 3
------------HẾT------------
Document Outline
- ĐỀ KIỂM TRA CUỐI HỌC KỲ I
- HƯỚNG DẪN CHẤM
- ĐỀ KIỂM TRA CUỐI HỌC KỲ I