






Preview text:
TRƯỜNG THPT HOÀNG VĂN THỤ
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ II TỔ TOÁN
MÔN TOÁN – KHỐI 12
NĂM HỌC 2024 – 2025 1. MỤC TIÊU
1.1. Kiến thức: Học sinh ôn tập các kiến thức về:
- Nguyên hàm: khái niệm nguyên hàm của một hàm số, một số tính chất của nguyên hàm, nguyên hàm
của một số hàm số thường gặp
- Tích phân: định nghĩa, tính chất của tích phân, tính tích phân trong những trường hợp đơn giản, vận
dụng tích phân giải quyết một số bài toán liên quan đến thực tiễn
- Ứng dụng hình học của tích phân để tính diện tích hình phẳng, thể tích của một số vật thể
- Phương trình mặt phẳng: Véc tơ pháp tuyến, cặp véc tơ chỉ phương của mặt phẳng, viết phương trình
mặt phẳng, điều kiện hai mặt phẳng vuông góc, hai mặt phẳng song song, tính khoảng cách từ một
điểm đến một mặt phẳng, vận dụng giải quyết một số bài toán liên quan đến thực tiễn.
1.2. Kĩ năng: Học sinh rèn được các kĩ năng
- Trình bày bài, kĩ năng tư duy, tính toán và lập luận toán học,
- Năng lực mô hình hoá toán học và năng lực giải quyết vấn đề toán học thông qua một số bài toán liên quan đến thực tiễn. 2. NỘI DUNG
2.1. MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ II
MÔN: TOÁN, LỚP 12 – THỜI GIAN LÀM BÀI: 90 phút HÌNH THỨC TN TN STT NỘI DUNG 4 lựa Đúng – Tự luận TL ngắn chọn (mức độ Sai (mức độ (mức 2,3) 2,3) độ (mức độ 1, 1, 2, 3) 2) 1 Nguyên hàm 3 1 1 2 Tích phân 3 1 1 2 3
Ứng dụng hình học của tích phân 2 1 1 4 Phương trình mặt phẳng 4 1 1 2 Tổng số câu 12 2 4 6 Tổng số điểm 3 2 2 3 Tỉ lệ % 30 20 20 30
2.2. Câu hỏi và bài tập minh họa NGUYÊN HÀM
PHẦN I. Trắc nghiệm với nhiều phương án lựa chọn
Câu 1. Trong các mệnh đề dưới đây, mệnh đề nào sai? A. f
(x)− g(x) dx = f
(x) dx− g
(x) dx . B. f
(x)+ g(x) dx = f
(x) dx + g (x) dx . C. f
(x) dx = f (x)+C . D. kf
(x) dx = k f
(x) dx, k .
Câu 2. Trong các khẳng định sau, khẳng định nào sai? 1 1 A.
dx = ln x + C . B. cos 2 d x x = sin 2x + C . x 2 x 1 e + e 1 x + C. x e dx = + C . D. e x dx = + C . x +1 e +1
Câu 3. Khẳng định nào dưới đây đúng?
A. sin x x = cos x + d C.
B. cos x x = −sin x + d C. 1 1 C.
dx = cot x + C. D.
dx = tan x + C. 2 sin x 2 cos x
Câu 4. Khẳng định nào dưới đây sai? n+1 A. n x x dx = + C,n 1 − . B. x = x e x e + d C. n + 1 x+1 x 7 C. 7 dx = + C.
D. cos x x = sin x + d C. x + 1
Câu 5. Hàm số nào dưới đây không là nguyên hàm của hàm số f (x) 2 = 3x ? A. 3 y = x . B. 3
y = x + 1. C. 3
y = x − 1. D. y = 6 . x
Câu 6. Hàm số y = sin 2x là một nguyên hàm của hàm số nào dưới đây? cos 2x cos 2x A. y = cos 2 . x B. y = − . C. y = . D. y = 2cos 2 . x 2 2
Câu 7. Họ nguyên hàm của hàm số f (x) 2 = x + 2 là
A. F (x) = 2 . x B. F (x) 3
= x + 2x + C. x x C. F (x) 3 =
+ 2x + C. D. F (x) 3 = + 2 + C. 3 3
Câu 8. Họ nguyên hàm của hàm số f (x) = x( 2 4x + 2) là x x A. F (x) 2 3 4 =
+ 2x + C. B. F (x) 4 2
= x + 2x + C. 2 3 C. F (x) 4 2
= 4x + x + C. D. F (x) 4 2
= x + x + C.
Câu 9. Cho hàm số ( ) 2 x f x = e
+ sin 3x . Khẳng định nào dưới đây đúng? x 1 A. f (x) 2 dx = e
− cos3x + C . B. ( ) 2 d x f x x = e − cos3x + C . 3 x e x x e x C. f (x) 2 sin 3 dx = + + C . D. f (x) 2 cos 3 dx = − + C . 2 3 2 3
Câu 10. Họ nguyên hàm của hàm số ( ) 5x f x = là x+1 5 A. f (x)dx = + C. B. ( ) = x f x x + d 5 C. x + 1 5x C. f (x)dx = + C. D. ( ) = x f x x + d 5 ln 5 C. ln 5
Câu 11. Họ nguyên hàm của hàm số ( ) x = ( 2 2 x f x e e − 3) là 3 2 x e 3 2 x e A. f (x)dx = − 3 x e + C. B. f (x)dx = + 3 x e + C. 3 3 3x e C. ( )d x = ( 2x
f x x e e − 3) + C. D. f
(x)dx = + 3 xe +C. 3
Câu 12. Họ nguyên hàm của hàm số f (x) 2 = 4sin x là 3 4 sin x A. f (x)dx = + C. B. f
(x)dx = 2x−sin2x+C. 3 cos 2x C. f (x)dx = + C. D. f
(x)dx = 2x−2sin2x+C. 2
Câu 13. Họ nguyên hàm của hàm số f (x) 2 2
= cos x − sin x là sin 2x sin 2x A. f (x)dx = + C. B. f (x)dx = − + C. 2 2 cos 2x cos 2x C. f (x)dx = + C. D. f (x)dx = − + C. 2 2
Câu 14. Họ nguyên hàm của hàm số f (x) = 4sinxcos3x là cos 4x cos 4x A. f (x)dx = −
+ cos2x + C. B. f (x)dx = −
− cos2x + C. 2 2 cos 4x cos 4x C. f (x)dx =
− cos2x + C. D. f (x)dx =
+ cos2x + C. 2 2 Câu 15. x + x +
Họ nguyên hàm của hàm số f (x) 3 2 3 2 5 = , x 0 là x A. F (x) 3 2
= x + 2x + 5ln x + C. B. F (x) 3 2
= x + x + 5ln x + C. C. F (x) 3 2
= x + x + 5ln x + C. D. 3 2
x + 2x + 5ln x + C. Câu 16. 1
Họ các nguyên hàm là ( x 2x − ) d 2 1 1 − 1 1 − 1 A. + C . B. + C . C. + C . D. + C . 4x − 2 2x −1 2x −1 4x − 2 + Câu 17. 1 Biết d x x = . a ln x −1 + .
b ln x − 2 + C . Tính a + b . 2 −x + 3x − 2
A. a + b =1.
B. a + b = 5 .
C. a + b = 5 − .
D. a + b = 1 − .
Câu 18. Biết F(x) = 2
ax + bx + 1,(a;b ) là nguyên hàm của hàm số f (x) = 2x + 1. Tổng a + b bằng A. 2. B. 1. C. 3. D. 0.
Câu 19. Biết F ( x) là một nguyên hàm của hàm số ( ) 2 x
f x = e và F (0) = 0 . Giá trị của F (ln 3) bằng A. 2. B. 6 . C. 8 . D. 4 .
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn) Câu 1:
Cho f (x) là hàm số liên tục trên . Khẳng định Đúng Sai a) f
(x)dx = f '(x)+ C. b) f ' x d = +
( ) x f (x) C. c) f '
(x)dx = f (x) . d) f '
(x)dx = f '(x)+ C. Câu 2:
Cho hàm số f (x) = 4 − x + 3 . Khẳng định Đúng Sai a)
Nếu F (x) là một nguyên hàm của f (x) thì F'(2) = 5 − . b) F (x) 2 = 2
− x + 3x là một nguyên hàm của f (x) . c)
Nếu G(x) là một nguyên hàm của f (x) và G( ) 1 = 2 thì G(2) = 1 − . d)
Nếu F (x) là một nguyên hàm của f (x) thì F (−x) là một
nguyên hàm của f (−x) . x Câu 3:
Cho hàm số f (x) = 2cos x và g(x) 2 = 2sin . 2 Khẳng định Đúng Sai a) = + f
(x)dx 2sinx C. b) = − + g
(x)dx cosx C. c) + f
(x) g(x) dx = x + sinx +C. d) f (x)
x = x + C (biết thoả mãn g x ). x ( ) 1 g(x) d 2 − 1 Câu 4:
Tại một khu di tích vào ngày lễ hội hằng năm, tốc độ thay đổi lượng khách tham quan được biểu diễn
bằng hàm số Q(t) 3 2
= 4t − 72t + 288t , trong đó t tính bằng giờ ( 0 t 13 ) , Q(t) tính bằng khách/giờ
. Nguồn: R.Larson and B. Eawads, Calculus 10e, Cengage). Sau 2 giờ đã có 500 người có mặt. Khẳng định Đúng Sai a)
Lượng khách tham quan được biểu diễn bởi hàm số Q(t) 4 3 2
= t − 24t + 144t . b)
Sau 5 giờ lượng khách tham quan là 1325 người. c)
Lượng khách tham quan lớn nhất là 1296 người. d)
Tốc độ thay đổi lượng khách tham quan lớn nhất tại thời điểm t = 6 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. 2 +1 Câu 1: Cho
d = ax + b ln x − 2 + C với a,b
. Tính giá trị a + . b x x x − 2 Câu 2:
Cho hàm số y = f (x) có f
(x)dx = xsinx +C . Tính f . 2 3 x − Câu 3:
Cho F ( x) là một nguyên hàm của hàm số ( ) 12 = x f x e ( 4 2
x − 4x ) . Biết hàm số F ( x) đồng biến trên khoảng ( ;
a +), giá trị nhỏ nhất của a bằng bao nhiêu?
2x + 5 khi x 1 Câu 4:
Cho hàm số f ( x) =
. Giả sử F là nguyên hàm của f trên
thỏa mãn F (0) = 2 . 2 3
x + 4 khi x 1
Tính giá trị của F (− ) 1 + 2F (2). PHẦN IV. Tự luận
Câu 1. Tìm họ nguyên hàm của hàm số f ( x) , biết: 3 a) f ( x) 2 = x + − 2 x
b) f ( x) = x( 3 2 1 + 3x )
c) f ( x) = ( x − )2 3 2 x d) x x f ( x) x 1 − 2 x 1 2 .5 + = e) f (x) 2 cos = g) f (x) 2 =1+ 3sin 1− sin x 2 +
Câu 2. Biết F ( x) là một nguyên hàm của hàm số ( ) 2 1 2x f x = thỏa mãn F (− )
1 = 3 . Tìm F ( x) . x
Câu 3. Biết (3sin2x + 2cos3x)dx = acos2x + bsin3x +C; ;ab ;C . Tính giá trị 2a +3b.
Câu 4. Một quần thể vi sinh vật có tốc độ tăng số lượng cá thể được ước lượng bởi P '(t) =150 t ( cá thể/ngày)
với 0 t 10 . Trong đó P(t) là số lượng cá thể vi sinh vật tại thời điểm t ngày kể từ thời điểm ban đầu. Biết
rằng ban đầu quần thể có 1000 cá thể.
a) Xác định hàm số P (t ) .
b) Ước lượng số cá thể của quần thể sau 5 ngày kể từ thời điểm ban đầu (kết quả làm tròn đến hàng trăm) TÍCH PHÂN
PHẦN I. Trắc nghiệm với nhiều phương án lựa chọn
Câu 1: Xét f (x) là một hàm số tùy ý, F (x) là một nguyên hàm của hàm số f (x) trên đoạn a;b. Mệnh đề nào dưới đây đúng? b b A. f
(x)dx = F(b)−F(a). B. f
(x)dx = F(a)− F(b). a a b b C. f
(x)dx = F(a)+ F(b). D. f
(x)dx = −F(a)− F(b). a a 2 2 2 Câu 1: Biết f
(x)dx = 2 và g
(x)dx = 6. Khi đó, f
(x)− g(x)dx bằng 1 1 1 A. 4. − B. 8. C. 4. D. 8. − 2
Câu 2: Cho hàm số f (x) có đạo hàm trên đoạn 1
;2 , f 1 = 1 và f
(x)dx = 5. Giá trị f (2) bằng ( ) 1 A. 6. B. 4. C. 3. D. 7.
Câu 3: Cho hàm số f ( x) liên tục trên . Gọi F ( x) là một nguyên hàm của hàm số f ( x) trên thỏa mãn 2
F (2) − F (0) = 10 . Khi đó 3 f
(x) dx bằng 0 A. 6 . B. 9 . C. 5 . D. 30 . 3 Câu 4: Biết 3
F(x) = x là một nguyên hàm của hàm số f (x) trên
. Giá trị của (1+ f (x))dx bằng 1 A. 20. B. 22. C. 26. D. 28. 2 5 5
Câu 5: Cho f (x) d x = 5 và f (x) d x = 3
− , khi đó f (x)d x bằng 0 0 2 A. 8 . B. 15 . C. 8 − . D. 15 − . 3 3
Câu 6: Cho hàm số f ( x) liên tục trên 0;
3 . Nếu f (x)dx = 2 thì
x − 3 f (x) dx bằng 0 0 3 A. 3. − 3 B. 3. C. . D. − . 2 2
Câu 7: Cho hàm số f ( x) liên tục trên
và có một nguyên hàm là F ( x) . Biết F ( )
1 = 8 , giá trị F (9) được
tính bằng công thức nào dưới đây?
A. F (9) = f (9) .
B. F (9) = 8 + f ( ) 1 . 9 9 C. F (9) = 8 + f
(x)dx.
D. F (9) = 8 + f
(x)dx . 1 1 3 2 Câu 8: Biết x +
dx = a + 2 ln b
, với a,b . Tổng a + b bằng x 1 A. 3 . B. 5 . C. 7 . D. 6 . b
Câu 9: Có bao nhiêu số thực b thuộc khoảng ( ;3 ) sao cho 4 cos 2 d x x = 1 ? A. 4 . B. 6 . C. 8 . D. 2 . 6 Câu 10: Biết 2
4sin xdx = a + b 3, (a;b ). Tính . ab 0 1 2 3 1 A. . B. . C. . D. − . 3 7 4 6 2 +
Câu 11: Gọi là các số nguyên sao cho x 2 2 e
dx = 2ae + be,(a;b ). Giá trị của 2 2
a + b bằng 0 A. 3 . B. 8 . C. 4 . D. 5 . 3 d Câu 12: Biết = 3 +
2 + với a , b , c là các số hữu tỷ. Tính P = a + b + c . x a b c x +1 − x 1 A. P = 2 5. B. P = 13 . C. P = 16 . D. P = . 3 2 3 1 6x + 3 Câu 13: Biết
dx = a + bln 2 + c ln 5,
(a; ;bc ). Tính a+2b+3 .c 3x + 5 0 A. 3. B. 5. − C. 0. D. 1. 1 2x + 1 Câu 14: Biết
dx = aln 2 + bln 3, a;b . . ab 2 ( ) Tính x − 4 0 3 3 3 3 A. . B. . C. . D. − . 5 8 7 2 5 x Câu 15: Cho
x = a + bln 2 + c ln 3 với a, b, c là các số hữu tỷ. Giá trị của abc bằng (x− ) d2 4 1 1 A. − 2 . B. 3. C. . D. 2. 6 3 4
Câu 16: Cho hàm số f ( x) có đạo hàm trên
là f ( x) = sin c
x osx và f (0) =1. Tính tích phân I = f (x)dx 0 . − 4 − + − A. I = 3 4 . B. I = 3 2 . C. I = 5 2 . D. I = . 2 8 16 16 4
Câu 17: Cho hàm số f (x) . Biết f (0) = 4 và f (x) 2 = 2sin x + 1, x . Khi đó, f
(x)dx bằng 0 2 + 15 2 + 16 − 16 2 + 16 − 4 2 − 4 A. . B. . C. . D. . 16 16 16 16 3
Câu 18: Cho hàm số f ( x) có f (0) = 2
− và đạo hàm f (x) 1 = , x 1 − . Tích phân f
(x)dx bằng x +1 0 64 10 13 A. . B. . C. − 8 . D. − . 3 3 3 3
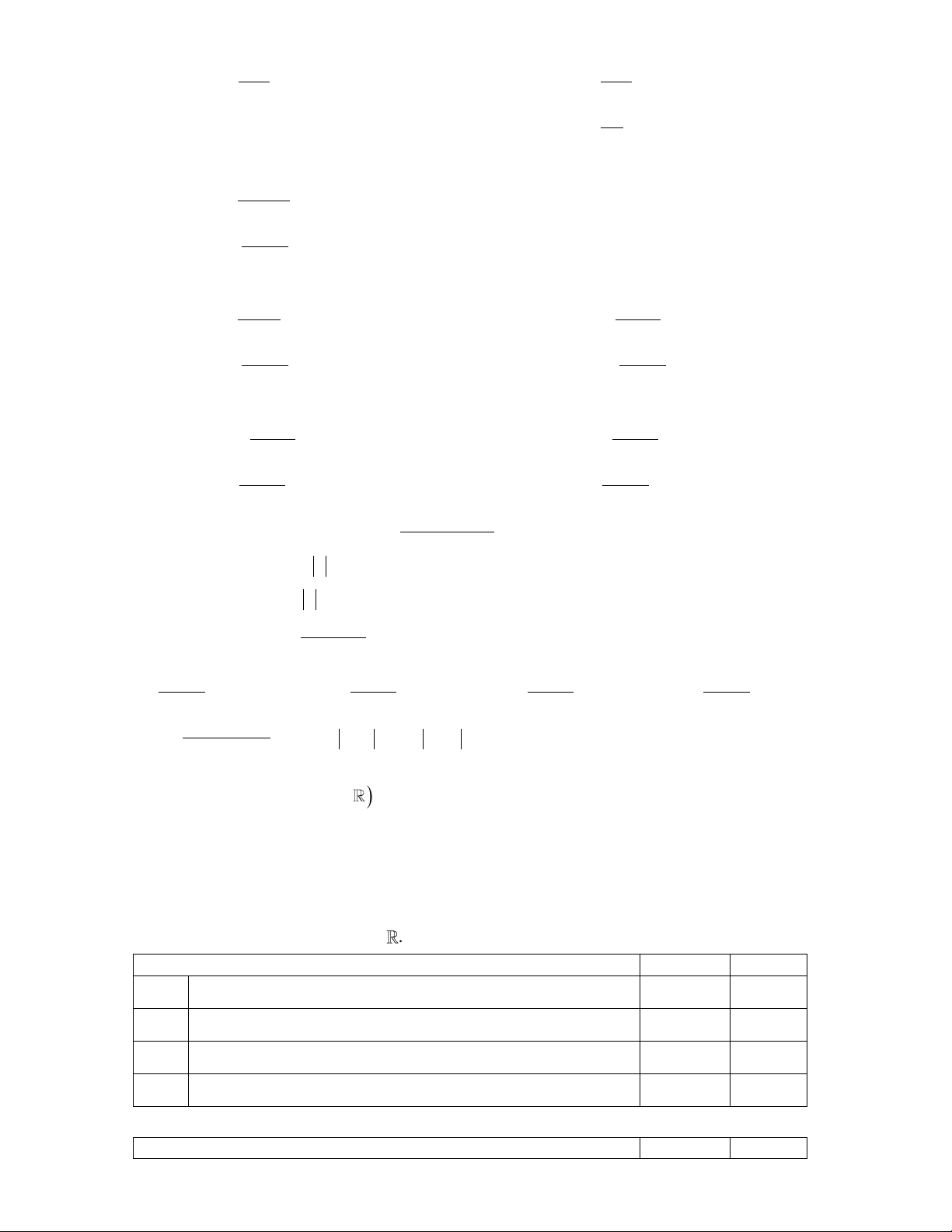
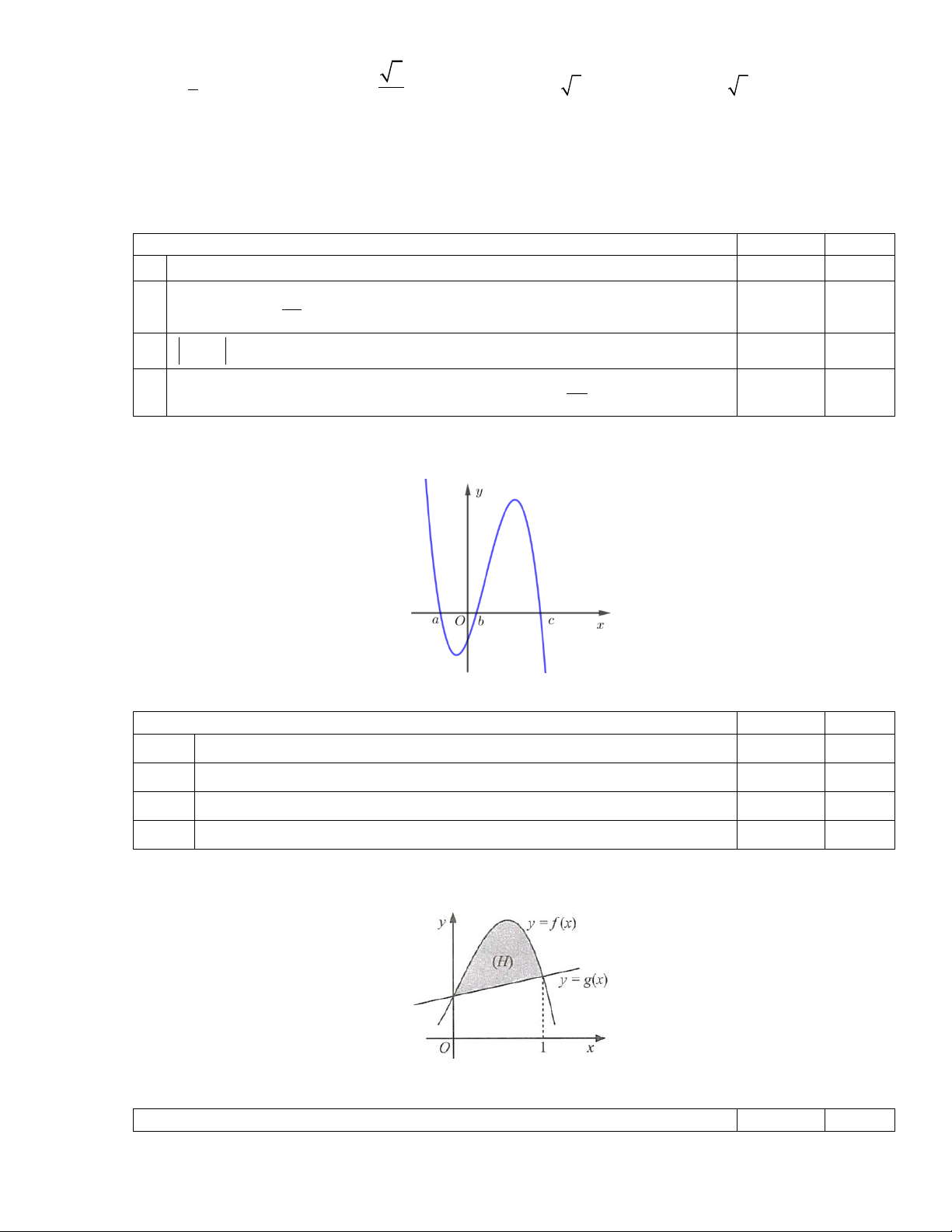
Câu 19: Cho hàm đa thức bậc ba y = f (x) có đồ thị hàm số y = f (
x) được cho bởi hình vẽ sau:
Giá trị biểu thức f (3) − f (2) bằng A. 20 . B. 51 . C. 64 . D. 45 .
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn) Câu 1:
Cho hàm số y = f ( x) liên tục trên đoạn ;
a b . Giả sử F ( x) và G ( x) là các nguyên hàm của f ( x) trên đoạn ; a b . Khẳng định Đúng Sai a) b
f ( x) dx = F (a) − F (b). a b) b f
(x)dx = G(b)−G(a). a c) a
f (x)dx = 0. a d)
G (b) − F (b) = G (a) − F (a). Câu 2:
Cho hàm số f ( x) 2
= 3x − 2x −1 có đạo hàm f (x) . Khẳng định Đúng Sai a) 2
f (x)dx = 3. 1 − b) 1
f (x)dx = 7. 0 c) 3 3
f (x)dx = 42. 0 d) 1 31
xf (x)dx = . 12 0 2
x − 2x khi x 2 Câu 3:
Cho hàm số f (x) = . x − 2 khi x 2 Khẳng định Đúng Sai a) 2 2 f (x)dx = (x−2)d .x 1 1 b) 3 3 f (x)dx =
( 2x −2x)d .x 2 2 c) 2 3 3 2 2 f (x) x x dx =
− 2x + − 2x . 2 2 1 1 2 d) 3 f (x) 5 dx = . 6 1 Câu 4:
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v t = 2t m / s t 1 ( ) (
), trong đó thời gian tính
bằng giây. Sau khi chuyển động được 12 giây thì ô tô gặp chướng ngại vật và người tài xế phanh gấp,
ô tô tiếp tục chuyển động chậm dần đều với vận tốc v t a = − ( 2 8 m / s ) 2 ( ) và gia tốc là cho đến khi dừng hẳn. Khẳng định Đúng Sai a)
Quãng đường ô tô chuyển động nhanh dần đều là 144 m . b)
Vận tốc của ô tô tại thời điểm người tài xế phanh gấp là 24 m / s . c)
Thời gian từ lúc ô tô giảm tốc độ cho đến khi dừng hẳn là 3 giây. d)
Tổng quãng đường ô tô chuyển động từ lúc xuất phát đến khi dừng hẳn là 168 m .
PHẦN III. Câu trắc nghiệm trả lời ngắn. 1 1 1 Câu 1: Cho −
dx = aln 2 + bln 3 + c,( ; a ;
b c ). Tính a + b + . c
x +1 x + 2 0 Câu 2:
Cho hàm số f ( x) . Biết f (0) = 4 và f ( x) 2 '
= 2sin x +1, x . Biết 4 ( ) 2 + + d = ;( ; a b f x x a b
), tính a+ .b 16 0 Câu 3:
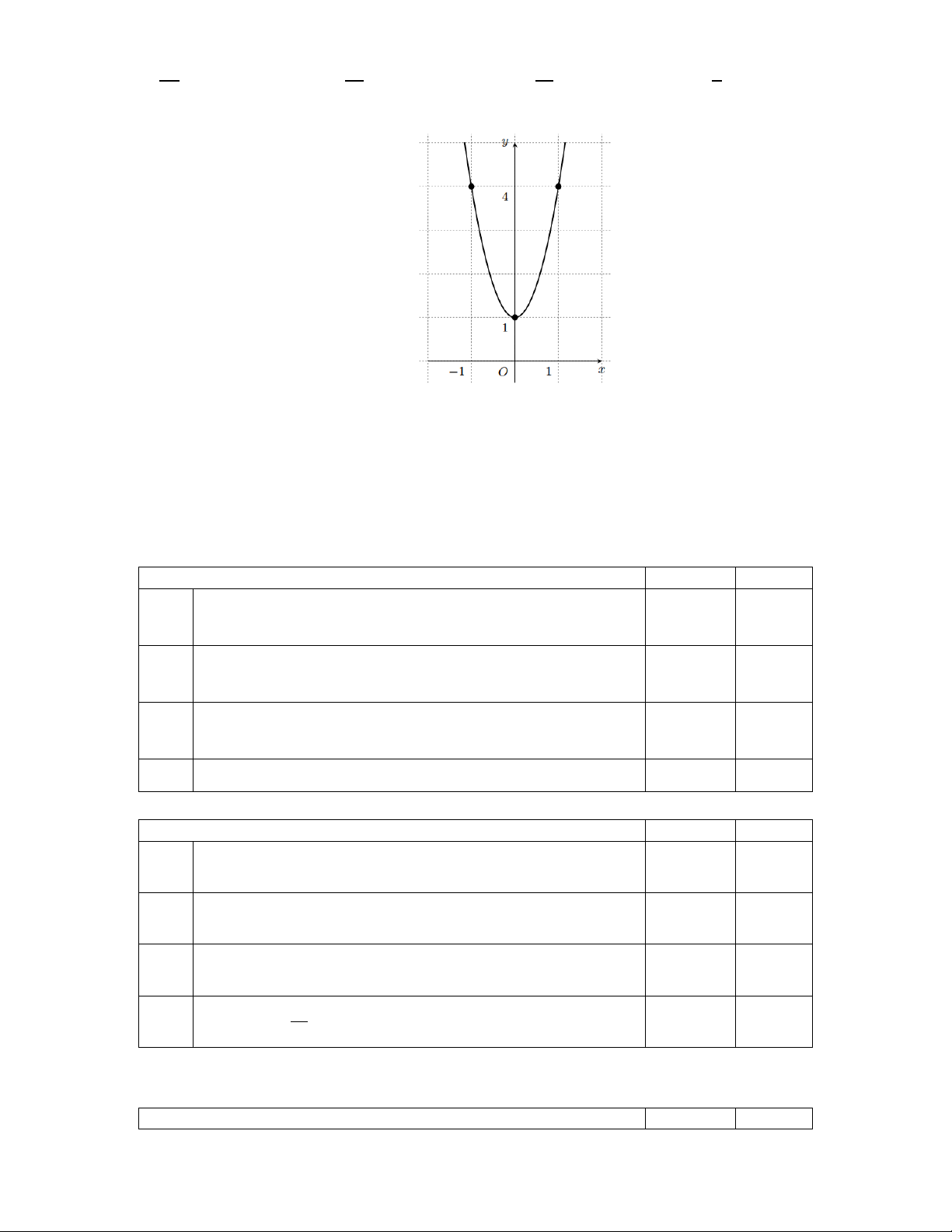
Đường gấp khúc ABC trong hình vẽ bên dưới là đồ thị của hàm số y = f ( x) trên đoạn 2 − ; 3 . 3
Tính f ( x)d . x 2 − 1 d Câu 4: Biết
= a + bln 2 + c ln 3 với a, ,
b c . Tính 3a + b + . c x x (x + 2)2 0 Câu 5:
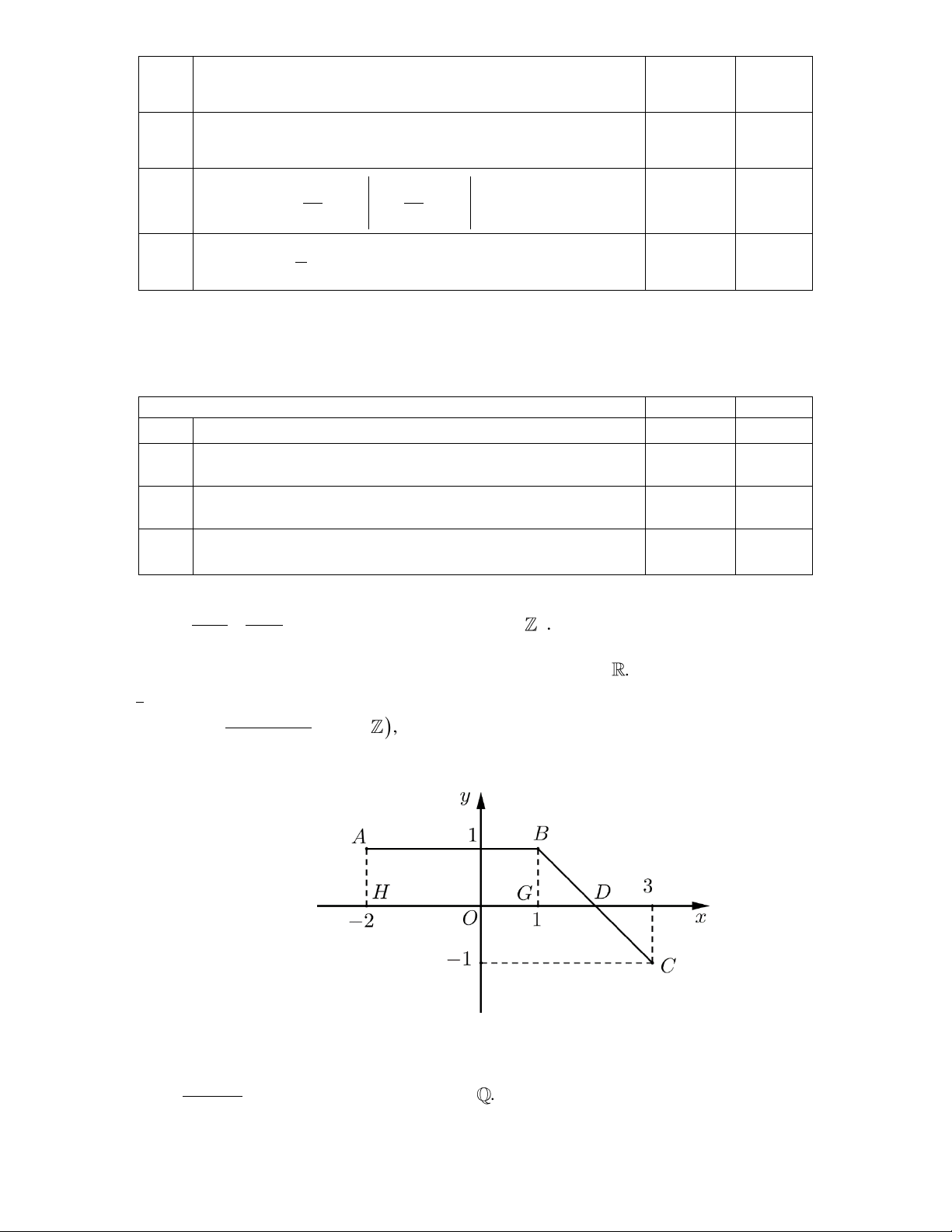
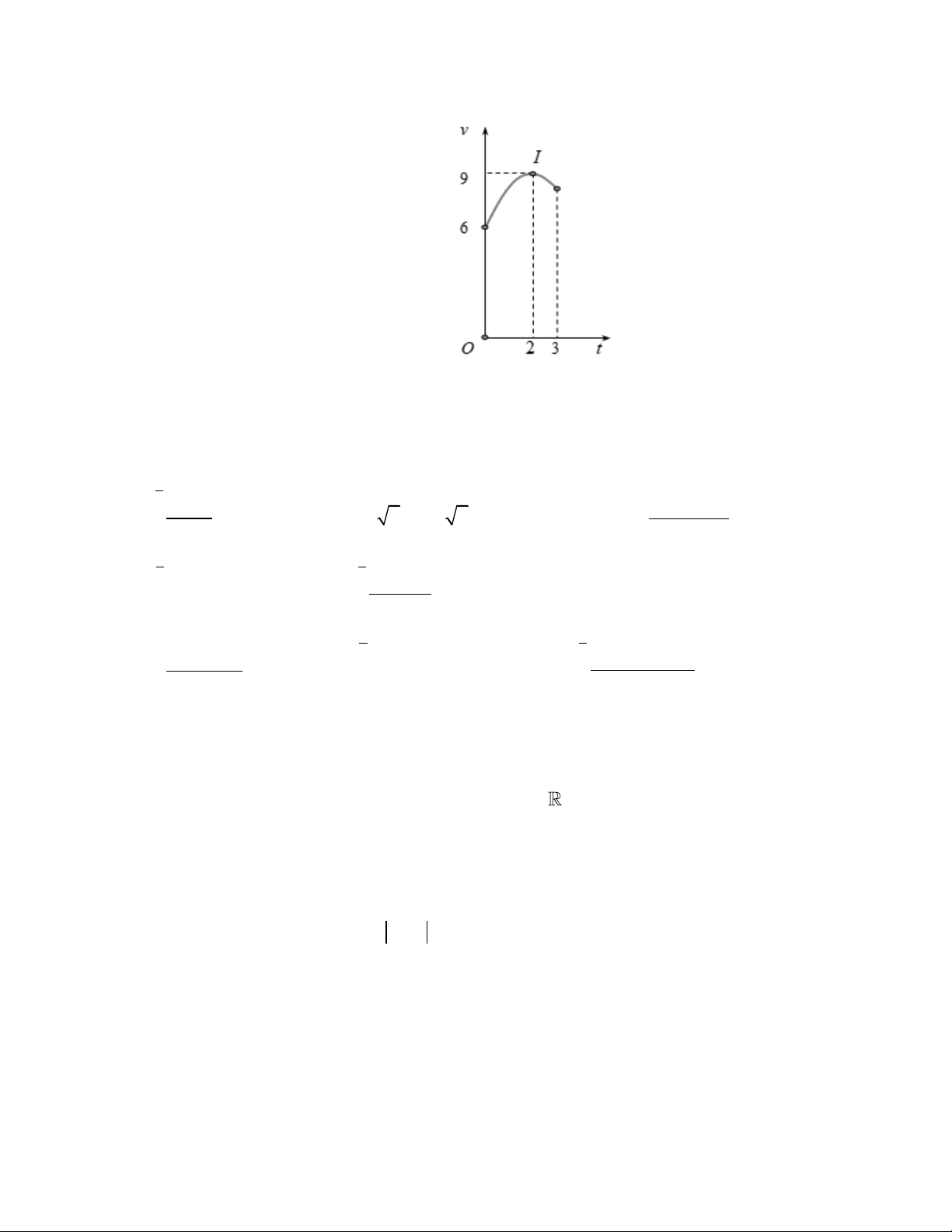
Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần
của đường parabol có đỉnh I (2;9) và trục đối xứng song song với trục tung như hình bên dưới:
Tính gần đúng đến hàng phần chục quãng đường s mà vật di chuyển được trong 3 giờ đó. PHẦN IV. Tự luận Câu 1:
Tính các tích phân sau đây: 4 1 4 2 2 − + a) x 2x 1 dx
b) ( x + 2)( x − 2)dx c) dx 2 cos x x 0 1 1 2 2 2 sin x 1
d) (3s ni x − 2) d x e) dx f) ( 2 1 2 3 . x x − )dx 1 + cos x 0 0 0 3 2 − + 2 4 cos x + cos3x g) x 3x 1dx h) ( 2 2sin x + 3)dx i) dx x −1 cos x 2 0 0
x +1 khi x 0 2 Câu 2:
Cho hàm số f ( x) = . Tính tích phân I = f
(x)dx . 2 x e khi x 0 1 − Câu 3:
Cho hàm số y = f ( x) xác định và liên tục trên , thỏa mãn f
(x) + sin xdx =10. Tính 0 I = f (x)dx. 0 m Câu 4:
Cho 0 m 2 và tích phân I = x − 2 dx = 2 . Khi đó giá trị của tham số bằng bao nhiêu? m 0 Câu 5:
Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm
dần đều với vận tốc v (t ) = 5
− t +10 (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN
PHẦN I. Trắc nghiệm với nhiều phương án lựa chọn
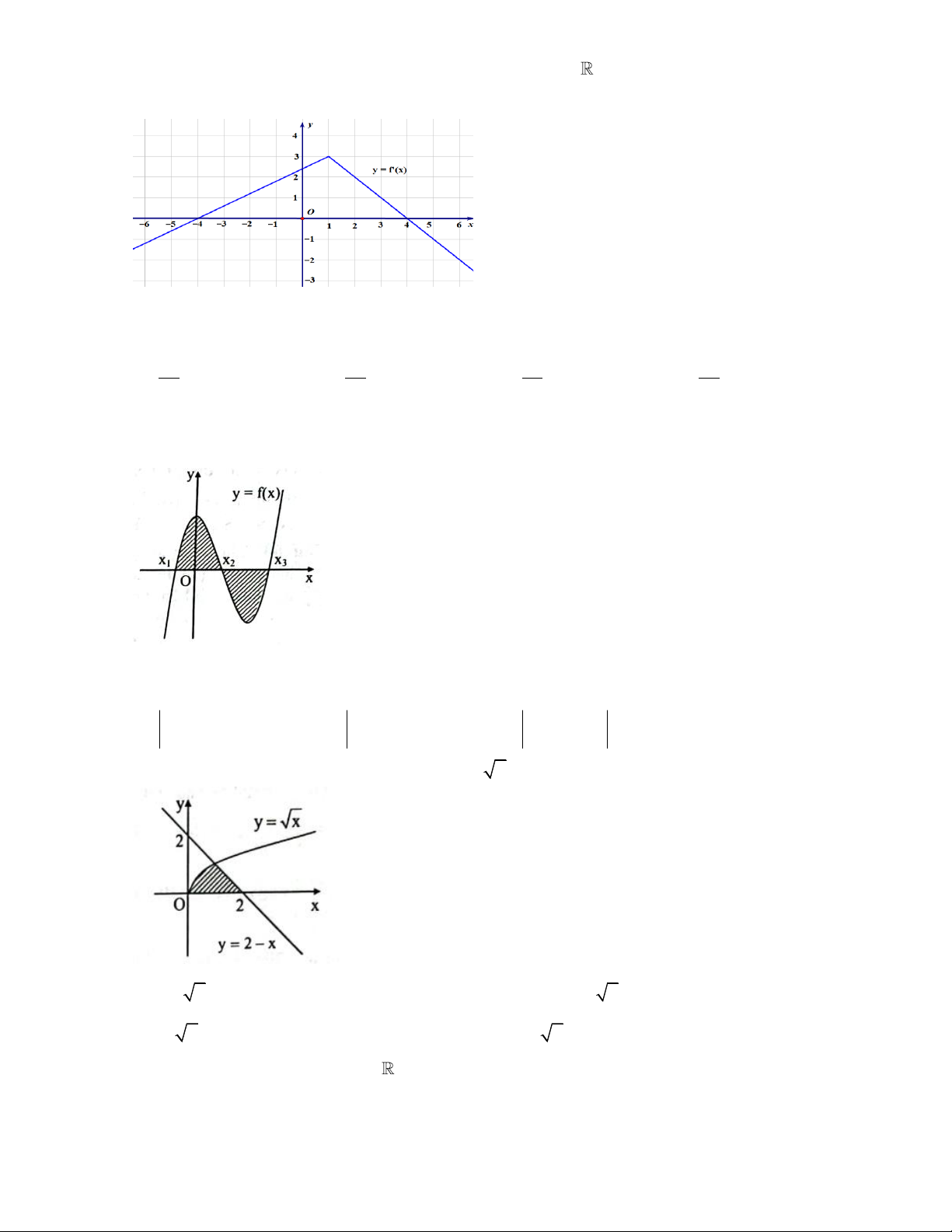
Câu 1. Cho hàm số y = f ( x) thoả mãn hàm y = f ( x) liên tục trên và có đồ thị như hình bên. Giá trị của
biểu thức f (4) − f ( 4 − ) bằng A. 12. B. 3 . C. 24 . D. 6 .
Câu 2. Hình phẳng giới hạn bởi đồ thị hàm số 2
y = x và đường thẳng y = 2x + 3 có diện tích là 49 29 22 32 A. . B. . C. . D. . 3 3 3 3
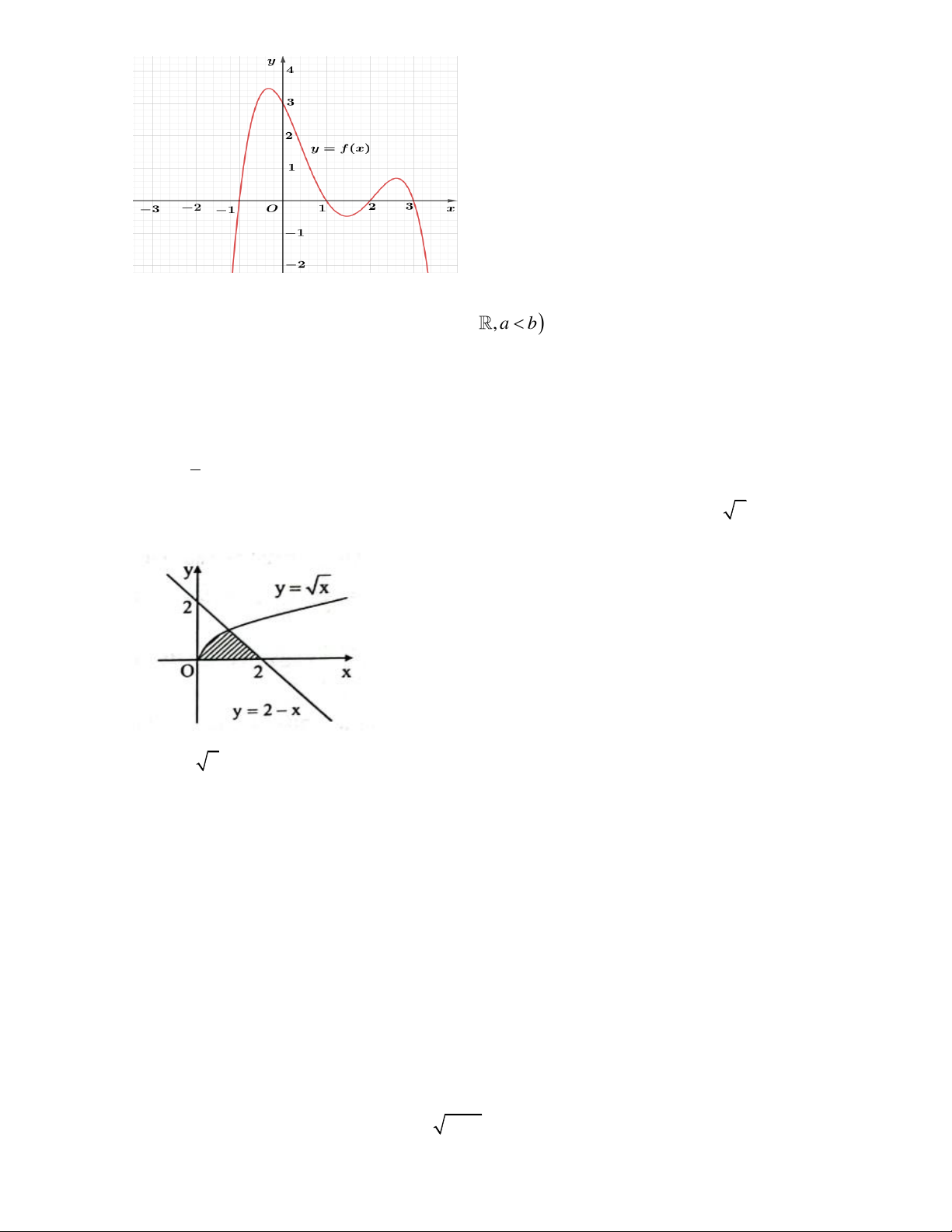
Câu 3. Hình vẽ bên biểu diễn trục hoành cắt đồ thị hàm số y = f ( x) tại ba điểm có hoành độ x , x , x 1 2 3
(x x x . Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số y = f (x) và trục hoành là 1 2 3 ) x x x x 2 1 2 2 A. f
(x)dx+ f
(x)dx. B. f
(x)dx− f
(x)dx. x x x x 1 2 1 2 x x x 2 2 2 C. f
(x)dx+ f
(x)dx . D. f ( x) dx . x x x 1 2 1
Câu 4. Diện tích hình phẳng giới hạn bởi các đường y =
x, y = 2 − x và trục Ox được tính bởi công thức 2 2 A.
x − 2 + x dx . B. 2 − x − x dx . 0 ( ) 0 ( ) 1 2 2 2 C. xdx +
(2− x)dx. D. xdx +
(2− x)dx. 0 1 0 0
Câu 5. Cho hàm số y = f ( x) liên tục trên có đồ thị cắt trục Ox tại đúng 4 điểm phân biệt (hình bên). Biết 1 2 3 rằng f
(x)dx = 21, f (x)dx = 2 − , f
(x)dx = 3. Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số 1 − 1 2
y = f ( x) và trục Ox bằng A. 22 . B. 20 . C. 16 . D. 26 .
Câu 6. Cho hàm số y = f ( x) liên tục trên ;
a b,(a,b , a b) . Gọi D là hình phẳng giới hạn bởi các đường
y = f ( x), x = a, x = b và trục hoành. Quay hình phẳng D quanh trục Ox ta được một khối tròn xoay có thể tích
được tính bởi công thức b a A. = ( f (x))2 V dx .
B. V = ( f (x))2 dx . a b 1 b b
C. V = ( f (x))2 dx .
D. V = ( f (x))2 dx . 3 a a
Câu 7. Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bời các đường y =
x, y = 2 − x và trục
hoành quay xung quanh Ox được tính bời công thức 2 1 2 2 A. x − 2 + x dx . B. d x x +
(2− x) dx . 0 ( )2 0 1 1 2 2 1 2 2 C. d x x +
(2− x) dx. D. d x x +
(2− x) dx 0 1 0 0
Câu 8. Một vật chuyĉ̉n động với vận tốc thay đổi theo thời gian v = f (t ) (với f (t ) 0 t
) Quãng đường vật đi
được trong khoảng thời gian từ thời điểm a đến thời điếm b là: A. b a
f (b) − f (a) . B. f (t ) dt . C. f (t ) dt .
D. f (a) − f (b) . a b
Câu 9. Một chất điểm đang chuyển động với vận tốc v = 15 m / s thì tăng vận tốc với gia tốc 0 a (t ) 2 = t + t ( 2
4 m / s ) . Quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng vận tốc là A. 67, 25 m . B. 68, 25 m . C. 69,75 m . D. 70, 25 m .
Câu 10. Cho phần vật thể (T ) giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2 . Cắt phần vật thể
(T ) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 x 2) , ta được thiết diện là
một tam giác đều có độ dài cạnh bằng x 2 − x . Tính thể tích V của phần vật thể (T ) . 4 3 A. V = . B. V = .
C. V = 4 3 . D. V = 3 . 3 3
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 1. Trong mặt phẳng tọa độ Oxy, xét parabol 2
(P) : y = x − 4 . Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hoành độ giao điểm của (P) và Ox là 2 − và 2 . b) ( x − ) 3 x 2 4 dx =
+ 4x + C 3 c) 2 2
x − 4 = x − 4 x [−2;2] d) 32
Diện tích hình phẳng giới hạn bởi (P) và Ox bằng . 3 Câu 2.
Cho hàm số y = f ( x) có đồ thị hàm số y = f ( x) cắt trục Ox tại ba điểm có hoành độ a b c như hình vẽ
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai a)
f (c) f (a) f (b) b)
f (c) f (b) f (a) c)
f (a) f (b) f (c) d)
f (a) f (b) Câu 3.
Cho các hàm số y = f (x), y = g(x) liên tục trên đoạn [0;1] và có đồ thị như hình bên. Hình
phẳng (H ) giới hạn bởi đồ thị các hàm số y = f (x), y = g(x) và hai đường thẳng x = 0, x = 1 .
Xác định tính đúng, sai của các khẳng định sau: Mệnh đề Đúng Sai a)
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục 1
hoành và hai đường thẳng x = 0, x = 1 là S = f (x)dx 0 b)
Thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng
giới hạn bởi đồ thị hàm số y = f (x) , trục hoành và hai đường 1
thẳng x = 0, x = 1 quanh trục hoành là 2 V = f (x)dx 0 c) 1
Diện tích hình phẳng (H ) là S = f
(x)− g(x) d x . 0 d)
Thể tích vật thể tròn xoay được tạo thành khi quay (H ) quanh trục Ox là 1 2 2
V = f (x) − g (x) d . x 0 2 x Câu 4.
Xét hình phẳng giới hạn bởi các đường y = x, y =
, x = 0, x = 4 . 8
Xác định tính đúng, sai của các khẳng định sau: Mệnh đề Đúng Sai a) 8
Diện tích hình phẳng là . 3 b)
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi
các đường y = x, y = 0, x = 0, x = 4 quanh trục Ox là V = 8 1 c)
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi 2 các đườ x 16 ng y =
, y = 0, x = 0, x = 2 quanh trục Ox là V = 2 8 5 d)
Thể tích khối tròn xoay sinh ra khi quay hình phẳng xung quanh 24
trục Ox là V = 5
PHẦN III. Câu trắc nghiệm trả lời ngắn. Câu 1.
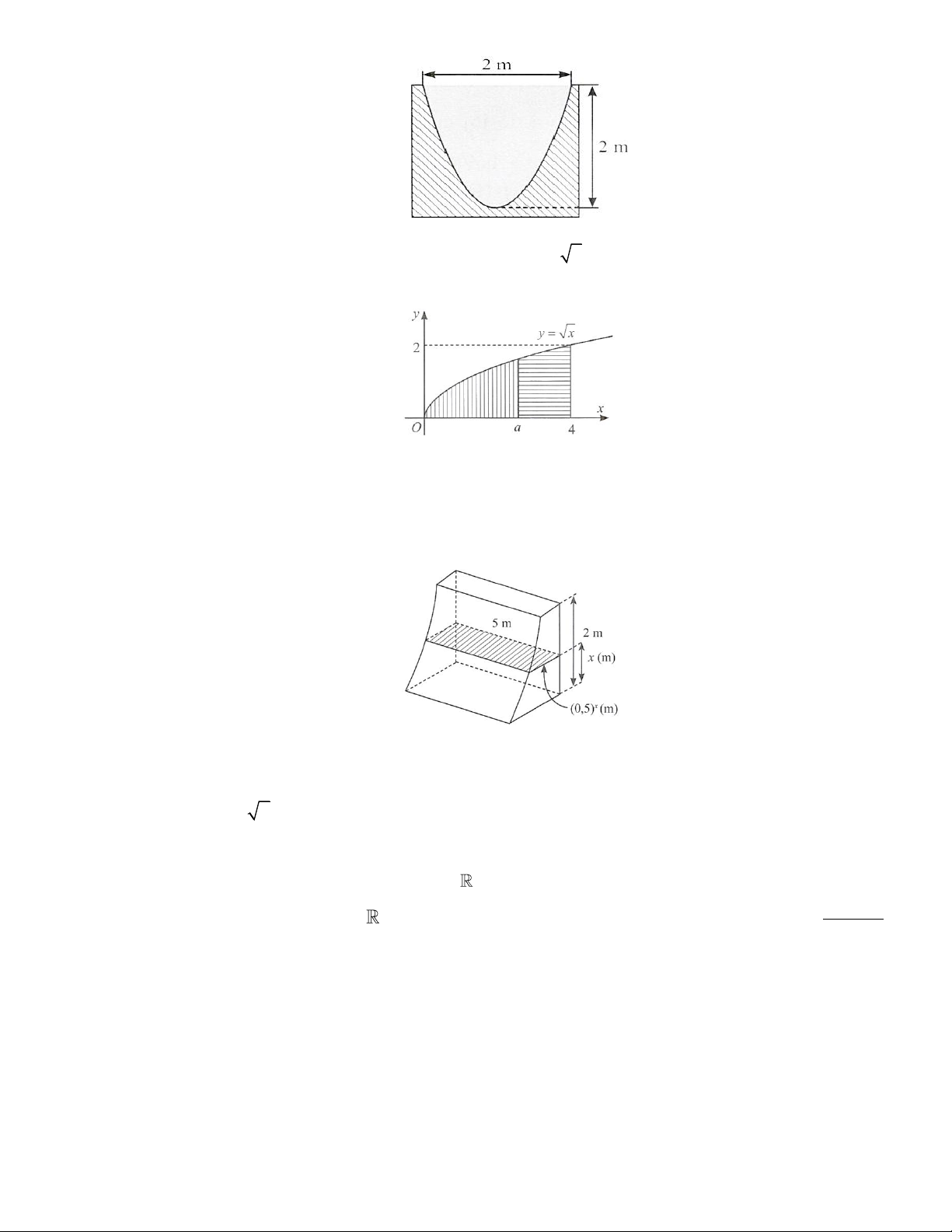
Mặt cắt ngang của lòng máng dẫn nước là hình phẳng giới hạn bởi một parabol và đường thẳng nằm
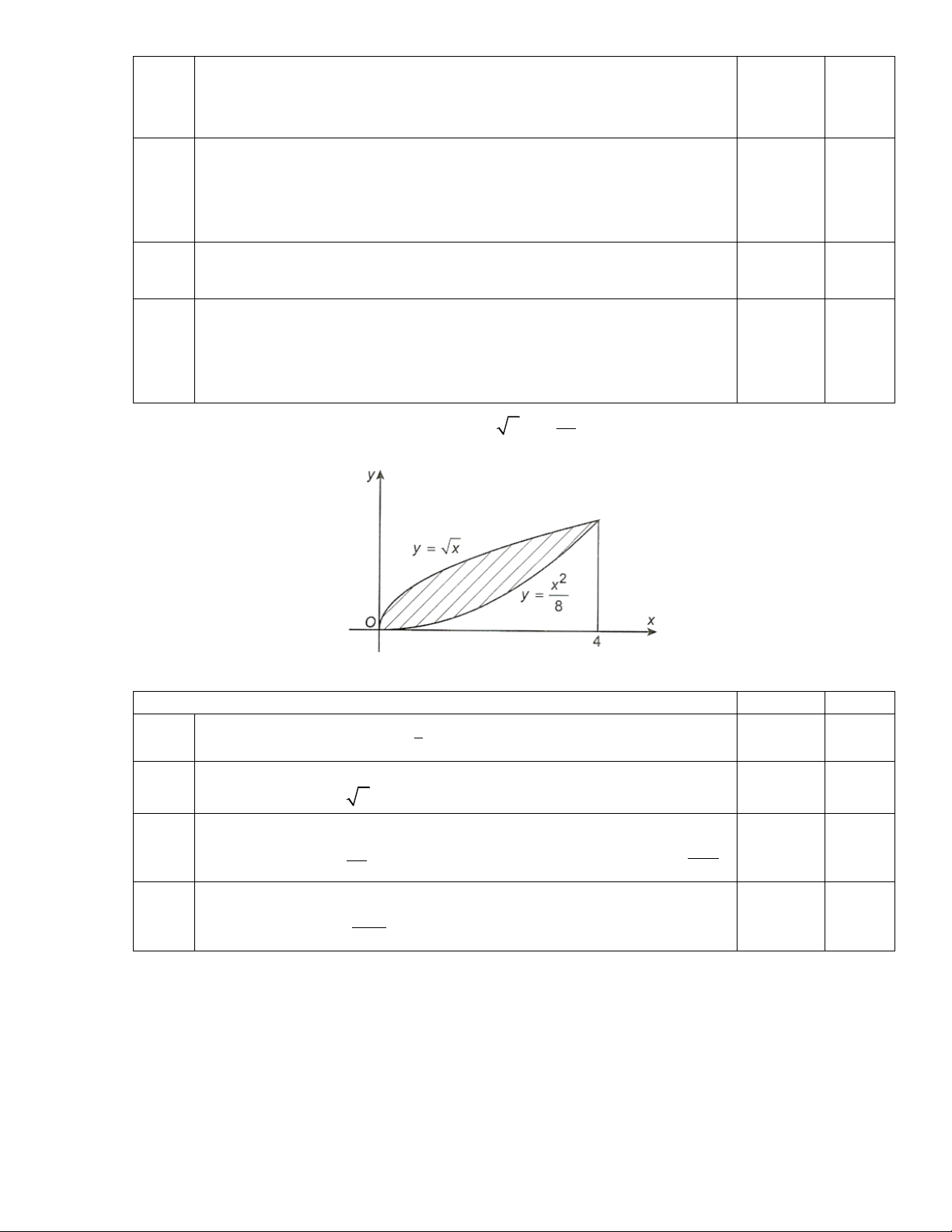
ngang như Hình (phần được tô màu xám). Tính diện tích của mặt cắt ngang đó. Câu 2.
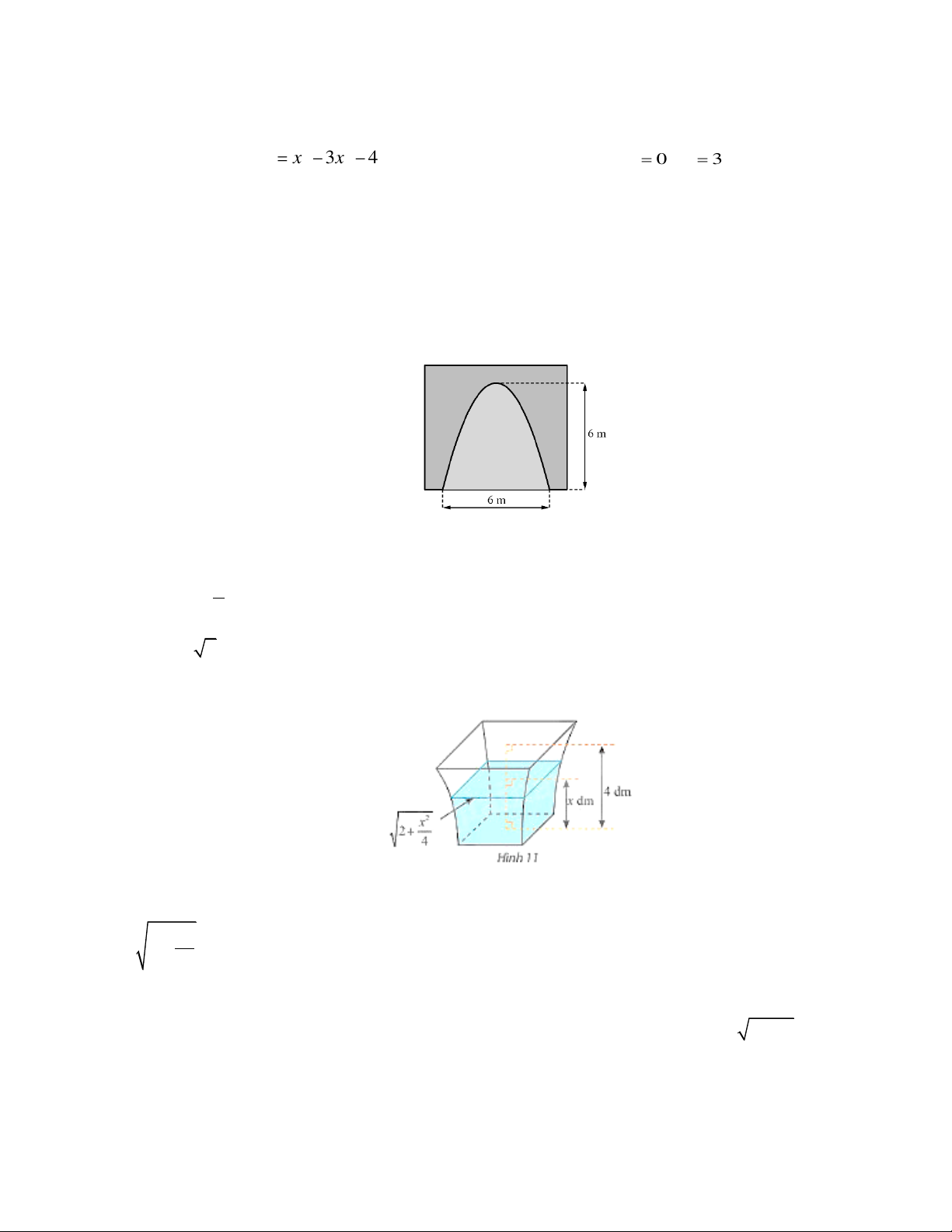
Cho D là hình phẳng giới hạn bởi đồ thị của hàm số y = x , trục hoành và đường thẳng x = 4 .
Đường thẳng x = a(0 a 4) chia D thành hai phần có diện tích bằng nhau (hình)
Tính giá trị của a . Câu 3.
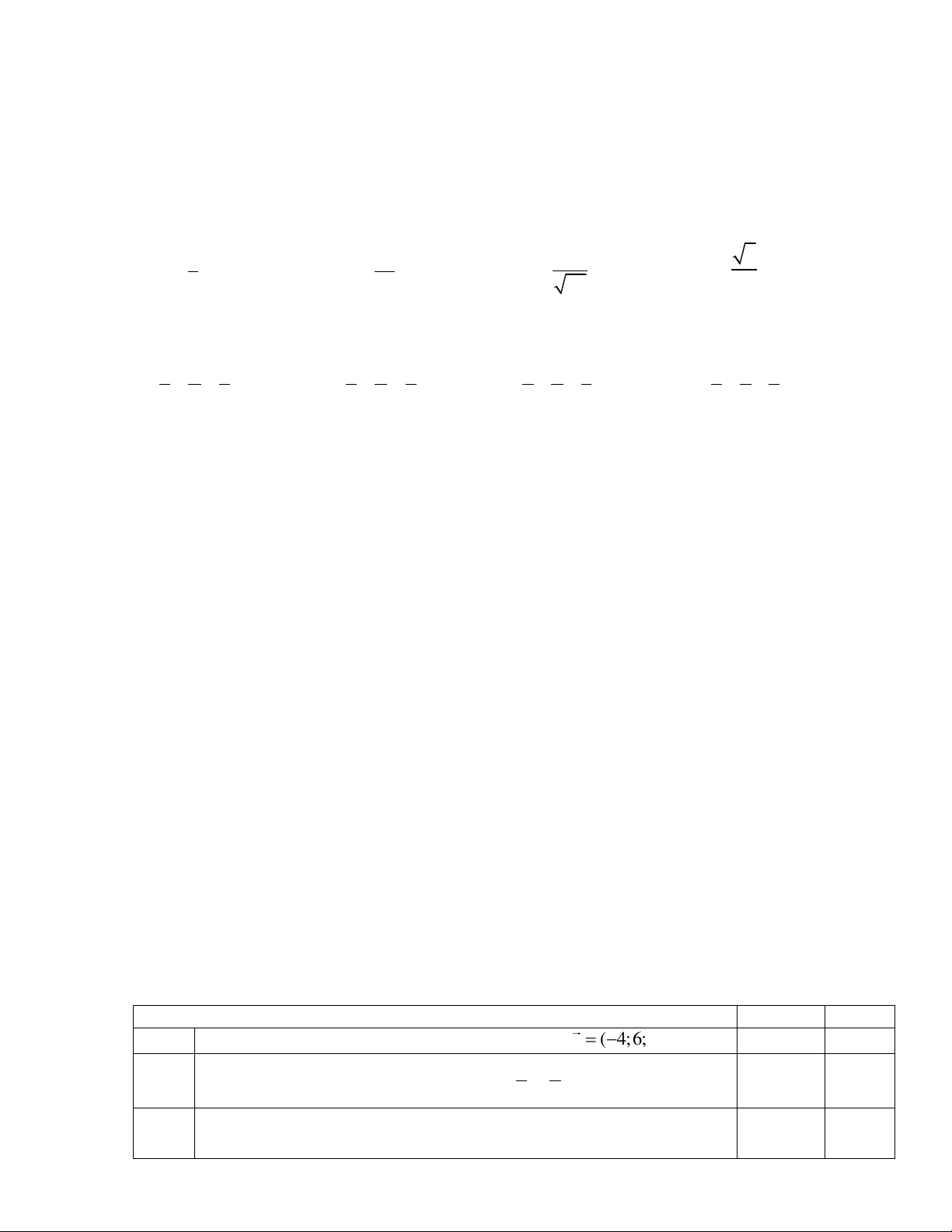
Một khối bê tông cao 2 m được đặt trên mặt đất phẳng. Nếu cắt khối bê tông này bằng mặt phẳng
nằm ngang, cách mặt đất x( m)(0 x 2) thì được mặt cắt là hình chữ nhật có chiều dài 5 m, chiều rộng (0,5)x ( ) m (Hình).
Tính thể tích của khối bê tông (kết quả làm tròn đến hàng phần trăm của mét khối). Câu 4.
Khi sử dụng phần mềm mô phỏng để thiết kế một chậu cây, người ta quay hình phẳng giới hạn bởi đồ thị hàm số y =
x + 2 , trục hoành và hai đường thẳng x = 0, x = 4 quanh trục hoành. Biết đơn vị trên
các trục toạ độ là đềximét. Thể tích của chậu cây (kết quả làm tròn đến hàng phần mười) bằng bao nhiêu đềximét khối? Câu 5.
Cho hàm số f (x) có đạo hàm liên tục trên
và thỏa mãn các điều kiện f (0) = 2 − ,
( 2x + )1 f x΄)+ xf (x) = −x, x
. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số 1 g(x) = , 1+ f (x)
hai trục toạ độ và đường thẳng x = 3 . Quay (H ) quanh trục Ox ta được khối tròn xoay có thể tích
bằng V (đơn vị thể tích). Tính V . (làm tròn kết quả đến hàng đơn vị) PHẦN IV. Tự luận
Câu 1: Tính diện tích hình phẳng giới hạn bởi: a) Đồ thị hàm số 2
y = x , trục hoành và hai đường thẳng x = 0 , x = 2 . b) Đồ thị hàm số ex y =
, trục hoành và hai đường thẳng x = 0 , x = 2 . c) Đồ thị hàm số 3
y = x +1, trục hoành và hai đường thẳng x = 0 , x = 1. d) Đồ thị hàm số 2
y = x + x − 2 và trục hoành. e) Đồ thị hàm số 2
y = x −1, trục hoành và đường thẳng x = 3 . f) Đồ thị hàm số 4 2 y x 3x
4 , trục hoành và hai đường thẳng x 0 , x 3 .
g) Đồ thị của các hàm số 3
y = x , y = 2x −1 và hai đường thẳng x = 1, x = 2 .
h) Đồ thị hàm số y = cos x − 2 , trục hoành và hai đường thẳng x = 0 và x = .
i) Đồ thị của hai hàm số 2
y = x , y = 2 − x và hai đường thẳng x = 0, x = 2.
Câu 2: Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang
như hình sau. Tính diện tích của cửa hầm. Câu 3:
Tính thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường sau quanh trục hoành: x
a) y = cos , y = 0, x = 0, x = ; b) 2 y = x − 2 ,
x y = 0, x = 0, x = 2 . 2
c) y = 2 x, y = 0, x = 1, x = 4 ; d) 3 y = 4 ,
x y = x , x = 0, x = 2 . Câu 4.
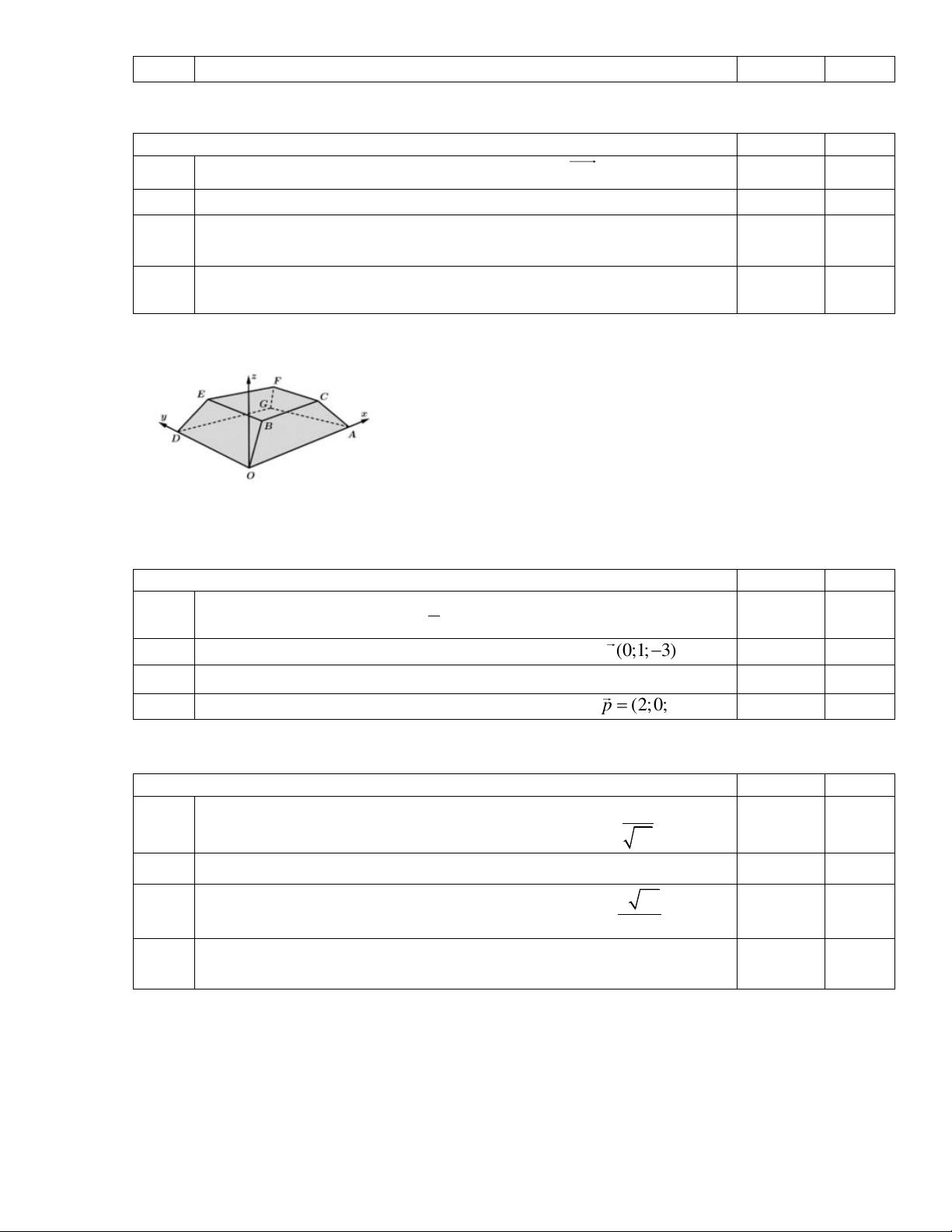
a) Một bình chứa nước có hình dạng như Hình.
Biết rằng khi nước trong bình có chiều cao x(dm)(0 x 4) thì mặt nước là hình vuông có cạnh 2 x 2 +
(dm) . Tính thể tích nước tối đa mà bình chứa được.. 4
b) Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x( 2
− x 2) , mặt cắt là tam giác vuông có một góc 45 và độ dài một cạnh góc vuông là 2
4 − x (dm) . Tính
thể tích của vật thể.
PHƯƠNG TRÌNH MẶT PHẲNG
PHẦN I. Trắc nghiệm với nhiều phương án lựa chọn Câu 1:
Trong không gian Oxyz , mặt phẳng nào dưới đây nhận n = (3;1; 7
− ) là một vectơ pháp tuyến?
A. 3x + z + 7 = 0 .
B. 3x − y − 7z +1 = 0 .
C. 3x + y − 7 = 0 .
D. 3x + y − 7z − 3 = 0 . Câu 2:
Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng ( P) : x + 2y + 3z −1 = 0 và
(Q): x + 2y +3z +6 = 0 là A. 7 . B. 8 . C. 14. D. 5 . 14 14 14 Câu 3:
Trong không gian Oxyz , cho mặt phẳng ( P) : 3x − 2z + 2 = 0 đi qua điểm nào sau đây? A. B (4; 2 ) ;1 .
B. A(1; 2; 4) .
C. D (2;1;4) . D. C (2;4; − ) 1 . Câu 4:
Trong không gian Oxyz , cho điểm A(1; 2;3) . Mặt phẳng chứa điểm A và trục Oz có phương trình là
A. 2x − y = 0 .
B. x + y − z = 0 .
C. 3y − 2z = 0.
D. 3x − z = 0 Câu 5:
Trong không gian Oxyz , cho điểm A(2; 1 − ; 3
− ) và mặt phẳng (P) :3x − 2y + 4z − 5 = 0 . Gọi (Q) là
mặt phẳng đi qua A và song song với mặt phẳng ( P) . Mặt phẳng (Q) có phương trình là:
A. 3x − 2 y + 4z − 4 = 0
B. 3x − 2 y + 4z + 4 = 0 .
C. 3x − 2 y + 4z + 5 = 0 .
D. 3x + 2 y + 4z + 8 = 0 . Câu 6:
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(4;0 ) ;1 và B ( 2
− ;2;3) . Phương trình nào dưới
đây là phương trình mặt phẳng trung trực của đoạn thẳng AB ?
A. 3x + y + z − 6 = 0 . B. 6x − 2y − 2z −1 = 0 . C. 3x − y − z +1 = 0 . D. 3x − y − z = 0 . Câu 7:
Trong không gian với hệ tọa độ Oxyz , cho điểm A(1;1 )
;1 và hai mặt phẳng ( P) : 2x − y + 3z −1 = 0 ,
(Q) : y = 0. Viết phương trình mặt phẳng (R) chứa A, vuông góc với cả hai mặt phẳng (P) và(Q) .
A. 3x − y + 2z − 4 = 0 . B. 3x + y − 2z − 2 = 0 . C. 3x − 2z = 0 .
D. 3x − 2z −1 = 0 . Câu 8:
Trong không gian với hệ tọa độ Oxyz , mặt phẳng đi qua ba điểm A(2;3;5) , B (3;2;4) và C (4;1; 2) có phương trình là
A. 3x − y + 2z − 4 = 0 . B. x + y − 5 = 0 .
C. y − z + 2 = 0.
D. 2x + y − 7 = 0 . Câu 9:
Trong không gian Oxyz mặt phẳng (P) : 2x + y + z − 2 = 0 song song với mặt phẳng nào dưới đây? 1 1 A. x + y −
z −1 = 0 . B. x − y − z − 2 = 0 . C. 4x + 2 y + 2z + 4 = 0 .
D. 2x + y + z − 2 = 0 . 2 2
Câu 10: Trong không gian với hệ tọa độ Oxyz cho mặt phẳng ( P) có phương trình:
mx + (m −1) y + z −10 = 0 và mặt phẳng (Q) : 2x + y − 2z + 3 = 0 . Với giá trị nào của dưới đây của m
thì ( P) và (Q) vuông góc với nhau A. m = 2 − . B. m = 2 . C. m =1. D. m = 1 − .
Câu 11: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) có phương trình: 3x + 4y + 2z + 4 = 0 và điểm A(1; 2
− ;3) . Tính khoảng cách d từ A đến (P) . 5 5 5 5 A. d = . B. d = . C. d = . D. d = . 9 29 29 3
Câu 12. Trong không gian với hệ trục tọa độ Oxyz , cho điểm M (1;2;3) . Gọi ,
A B,C lần lượt là hình chiếu
vuông góc của M trên các trục Ox,Oy,Oz . Viết phương trình mặt phẳng ( ABC) . x y z x y z x y z x y z A. + + =1. B. − + =1. C. + + = 0. D. − + + =1. 1 2 3 1 2 3 1 2 3 1 2 3
Câu 13. Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng ( P) đi qua A(1;1 ) ;1 và
B (0; 2; 2) đồng thời cắt các tia Ox , Oy lần lượt tại hai điểm M , N ( không trùng với gốc tọa độ O ) sao cho
OM = 2ON
A. ( P) : 3x + y + 2z − 6 = 0
B. ( P) : 2x + 3y − z − 4 = 0
C. (P) : 2x + y + z − 4 = 0
D. ( P) : x + 2y − z − 2 = 0
Câu 14. Trong không gian với hệ trục tọa độ Oxyz , cho bốn điểm S ( 1
− ;6;2) , A(0;0;6) , B(0;3;0) , C ( 2
− ;0;0) . Gọi H là chân đường cao vẽ từ S của tứ diện S.ABC . Phương trình mặt phẳng đi qua ba điểm S ,
B , H là
A. x + y − z − 3 = 0 .
B. x + y − z − 3 = 0 .
C. x + 5y − 7z −15 = 0 .
D. 7x + 5y − 4z −15 = 0 .
Câu 15. Trong không gian Oxyz , cho A(2;0;0) , B (0; 4;0) , C (0;0;6) , D (2; 4;6) . Gọi ( P) là mặt phẳng
song song với mp ( ABC) , ( P) cách đều D và mặt phẳng ( ABC ) . Phương trình của ( P) là
A. 6x + 3y + 2z − 24 = 0 .
B. 6x + 3y + 2z −12 = 0 .
C. 6x + 3y + 2z = 0 .
D. 6x + 3y + 2z − 36 = 0 .
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn) Câu 1.
Trong không gian Oxyz , gọi là mặt phẳng đi qua hai điểm (
A 1;3; 4), B(2; 1
− ;5) và vuông góc với mặt
phẳng (Q) : 2x − 3y + z +1 = 0 . Xét tính đúng sai của các mệnh đề sau: Mệnh đề Đúng Sai a)
Một vectơ pháp tuyến của mặt phẳng (Q) là n = ( 4 − ;6; 2 − ) . b)
Trung điểm của đoạn thẳng 3 9 AB là I ;1; . 2 2 c)
Mặt phẳng qua A và song song với (Q) có phương trình là 2
− x + 3y − z + 3 = 0 . d)
Phương trình mặt phẳng (P) là −x + y + 5z − 22 = 0 . Câu 2.
Trong không gian tọa độ Oxyz , cho điểm ( A 1
− ;2;3) và hai mặt phẳng (P) : x − 2 = 0 và
(Q) : y − z −1 = 0 . Xét tính đúng sai của các mệnh đề sau: Mệnh đề Đúng Sai a)
Một vectơ pháp tuyến của mặt phẳng (P) là n (1; 2 − ;0) . ( P) b)
Hai mặt phẳng (P) và (Q) vuông góc với nhau. c)
Phương trình mặt phẳng qua A và song song với (Q) là
y − z +1 = 0 . d)
Phương trình mặt phẳng đi qua điểm A và vuông góc với cả hai
mặt phẳng (P) và (Q) là: y + z − 5 = 0 . Câu 3.
Hình vẽ minh hoạ hình ảnh một toà nhà trong không gian với hệ toạ độ Oxyz (đơn vị trên mỗi trục toạ độ là mét). Biết (
A 50; 0; 0), D(0; 20; 0), B(4k;3k; 2k) với k 0 và mặt phẳng (CBEF ) có phương trình là
z − 3 = 0 . Các mệnh đề sau đúng hay sai Mệnh đề Đúng Sai a) Toạ độ của điểm 9 B là (6; ;3) . 2 b)
Một vectơ pháp tuyến của mặt phẳng (CBEF) là n(0;1; 3 − ) . c)
Phương trình mặt phẳng (AOBC) là 2y − 3z = 0. d)
Mặt phẳng (DOBE) có một vectơ pháp tuyến là p = (2;0; 1 − ) . Câu 4.
Trong không gian Oxyz , cho điểm M (1;3; 2
− ) và hai mặt phẳng (P) : 2x − y + 3z + 4 = 0 ,
(Q): 4x − 2y + 6z −1= 0 . Xét tính đúng sai của các mệnh đề sau: Mệnh đề Đúng Sai a) 15
Khoảng cách từ điểm M đến mặt phẳng (P) bằng . 56 b)
Mặt phẳng (P) vuông góc với mặt phẳng (Q) . c)
Khoảng cách giữa hai mặt phẳng ( 9 56
P) và (Q) bằng . 56 d)
Mặt phẳng qua điểm M và song song với mặt phẳng (P) có
phương trình tổng quát là 2x − y + 3z −10 = 0 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Câu 1:
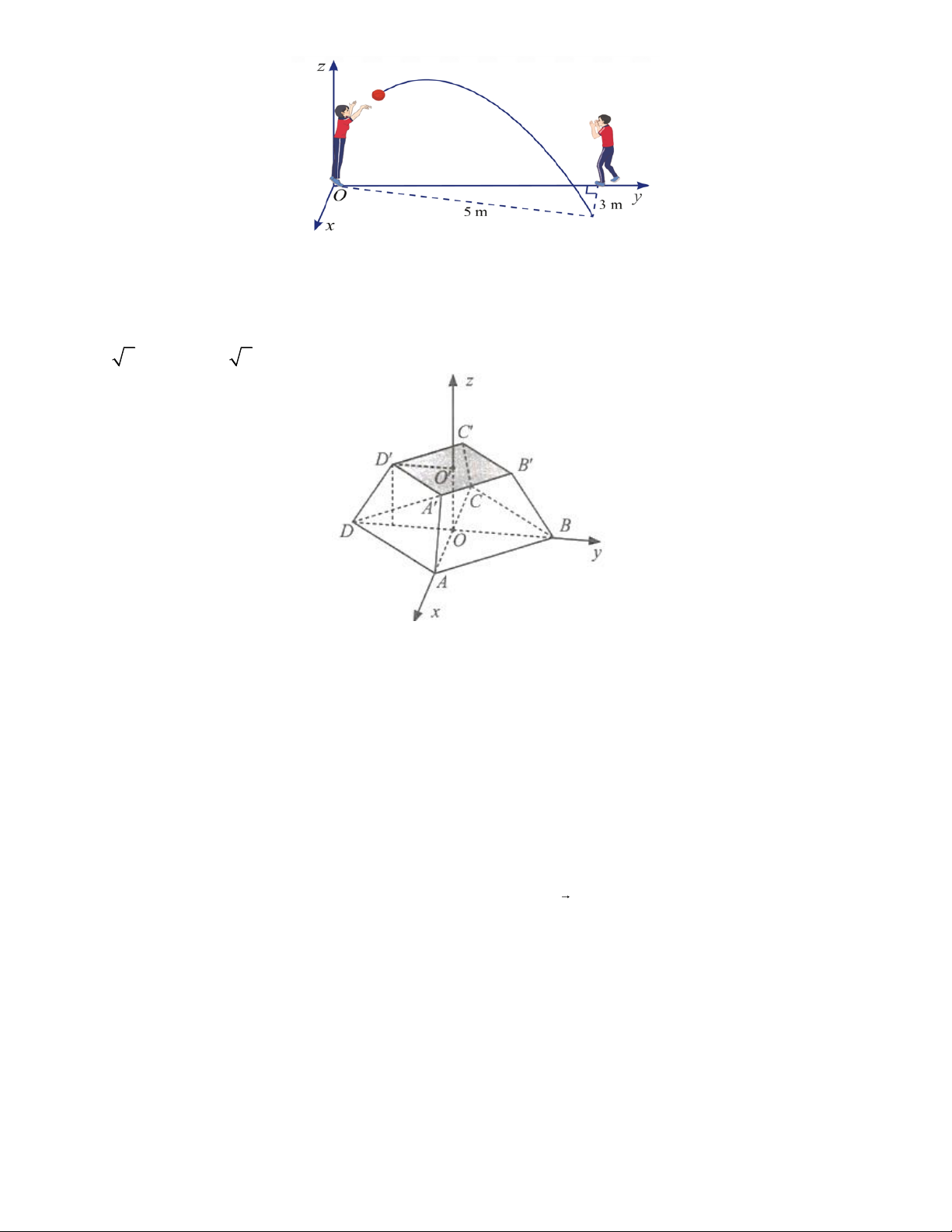
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang
phải và rơi xuống tại vị trí cách bạn nam 3 m , cách bạn nữ 5 m (Hình). Cho biết quỹ đạo của quả bóng nằm
trong mặt phẳng (P) vuông góc với mặt đất. Phương trình của (P) trong không gian (P) được mô tả như trong
hình vẽ có dạng ax + 3y = 0 . Tìm a
Câu 2. Trong không gian Oxyz , tính hoảng cách giữa hai mặt phẳng ( P) : x + 2y + 2z −10 = 0 và
(Q): x + 2y + 2z −3 = 0 (làm tròn kết quả đến hàng phần mười) Câu 3.
Một vật trang trí có đế dạng khối chóp cụt đều ABC .
D A B C D có chiều cao 3 cm , AB 8 2 c , m AB = = 6 2 cm (Hình). Gọi
O là giao điểm của AC và B ,
D O là giao điểm của A C và B D .
Với hệ trục toạ độ như Hình, mặt phẳng (CDD C ) cắt tia Oz tại điểm M (0;0;m) . Tìm giá trị của m .
Câu 4. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A(1;2; ) 3 , B (5; − 4; − )
1 và mặt phẳng (P)
qua Ox sao cho d ( ;
B ( P)) = 2d ( ;
A ( P)) , (P) cắt AB tại I (a; ;
b c) nằm giữa AB . Tính a + b + c . PHẦN IV. Tự luận Câu 1.
Trong không gian Oxyz , viết phương trình mặt phẳng:
1) đi qua điểm M (3; 1
− ;4) đồng thời vuông góc với giá của vectơ a = (1; 1 − ;2)
2) đi qua ba điểm A(2;1;− ) 1 , B ( 1 − ;0;4), C (0; 2 − ; − ) 1 .
3) đi qua điểm A(2; 1
− ;2) và song song với mặt phẳng (P) : 2x − y + 3z + 2 = 0
4) đi qua 3 điểm A(0; 1
− ;0) , B(2;0;0) , C (0;0;3) Câu 2.
Trong không gian Oxyz , viết phương trình mặt phẳng:
1) trung trực của đoạn thẳng AB với A(4;0 ) ;1 và B ( 2 − ;2;3) .
2) đi qua hai điểm A(0;1;0) , B (2;3; )
1 và vuông góc với mặt phẳng (Q) :x + 2 y − z = 0
3) đi qua O đồng thời vuông góc với cả () và ( ) với ( ) : 3x − 2y + 2z + 7 = 0 và ( ) : 5x − 4y + 3z +1 = 0
4) đi qua điểm M (1;2;5) cắt các trục tọa độ Ox,Oy,Oz tại ,
A B, C sao cho M là trực tâm tam giác ABC .
5) đi qua điểm M (1;2;5) cắt các trục tọa độ Ox,Oy,Oz tại ,
A B, C sao cho M là trọng tâm tam giác ABC .
Câu 3. Trong không gian với hệ tọa độ Oxyz , Tính khoảng cách d từ điểm A đến mặt phẳng ( P) biết:
1) mặt phẳng ( P) có phương trình: 3x + 4y + 2z + 4 = 0 và điểm A(1; 2 − ;3) .
2) mặt phẳng ( P) có phương trình: 2x − 2y + z + 4 = 0 và điểm A(1;2 ) ;1 .
3) mặt phẳng ( P) có phương trình: 2x + 2y − z +15 = 0 và điểm A( 1 − ;2; 3 − ) .
Câu 4. Trong không gian với hệ tọa độ Oxyz , Hãy:
1) Tính khoảng cách giữa hai mặt phẳng ( P) : x + 2y + 2z − 8 = 0 và (Q) : x + 2y + 2z − 4 = 0
2) Viết phương trình mặt phẳng Q sao cho Q song song với P và khoảng cách giữa hai mặt phẳng P và 7 Q bằng
, biết phương trình mặt phẳng P : x 2 y 2z 10 0 . 3 2
3) Viết phương trình mặt phẳng ( P) chứa ,
A B sao cho khoảng cách từ C tới ( P) bằng . Biết 3 ( A 1;0;0), B(0; 2 − ;3),C(1;1;1) 2.3.ĐỀ MINH HỌA
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi, học sinh chỉ chọn một phương án.
Học sinh trả lời từ câu 1 đến câu 12.
Câu 1: Khẳng định nào sau đây là SAI? A. sin xdx = os c x + C
B. cos xdx = sin x + C 1 1 C.
dx = tan x + C D. dx = − ot c x + C . 2 cos x 2 sin x Câu 2: 2xdx bằng x x 1 + A. 2 2 .
x ln 2 + C B. 2x + C C. 2 + C D. + C . ln 2 x +1 Câu 3: Hàm số 5
F(x) = x − 2x là một nguyên hàm của hàm số nào sau đây? 6 A. x 1 4 5x − 2 B. 4
5x + C C. + C D. 6 2
x − x + C . 6 6
Câu 4: Cho hàm số y = f ( x) liên tục trên và có một nguyên hàm là F ( x). Biết rằng F ( ) 1 = 9, F (2) = 5. Giá 2 trị của biểu thức f ( x)dx bằng: 1 A. 4. − B. 14. C. 4. D. 45.




