





Preview text:
TRƯỜNG THPT XUÂN ĐỈNH NĂM HỌC 2024 – 2025 MÔN: TOÁN - KHỐI: 12 A. KIẾN THỨC ÔN TẬP
Chương 1 : ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Chương 2 : VECTƠ VÀ HỆ TRỤC TOẠ ĐỘ TRONG KHÔNG GIAN
Chương 4 : NGUYÊN HÀM VÀ TÍCH PHÂN
Chương 5 : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
Bài 14. Phương trình mặt phẳng B. NỘI DUNG
I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số (Trong đề cương giữa HK1)
II. Vectơ và hệ trục toạ độ trong không gian (Trong đề cương HK1)
III. Nguyên hàm và tích phân 1. Nguyên hàm
Phần 1: Trắc nghiệm 4 phương án lựa chọn. Mỗi câu hỏi chỉ chọn một phương án
Câu 1: Tìm nguyên hàm của hàm số f x 3x cos3x 2 3x sin 3x 2 3x sin 3x A. 31 sin 3x C . B. C . C. C . D. 2 3x sin 3x C . 2 3 2 3
Câu 2: Nguyên hàm của hàm số có f x 2 2 tan x cot x là: 1 1
A. 2 tan x 2cot x C . B. 3 3
tan x cot x C . C. tan x cot x 2x C . D. tan x cot x 2x C . 3 3
Câu 3: Tìm nguyên hàm của hàm số 2x x f x e 2x x 1 x 1 2 e A. 2x ln 2 x e C . B. x e C . C. 1 1 2x x e C . D. C . ln 2 x 1 1
Câu 4: Tìm nguyên hàm của hàm số f x 2 x . x
trên khoảng 0; 3 2 x 2 7 1 2 5 1 A. 7 3 x 3 x C . B. 7 3 x x C . C. 5 3 x 3 x C . D. 5 3 x x C . 7 2 3 5 2 3
Câu 5: Tìm nguyên hàm của hàm số f x 1 5x 2 1 1 A. ln 5x 2 C .
B. ln 5x 2 C . C. 5ln 5x 2 C . D. ln 5x 2 C . 5 2
Câu 6: Kí hiệu F x là một nguyên hàm của hàm số f xx 2 2 1 và F 18 1
Khẳng định nào sau đây là 15 đúng? 5 3 x 2x 5 3 x 2x A. F x x. B. F x x . C 5 3 5 3 5 3 x 2x 2 C. F x x 2 4 x 1 . D. F x x 5 3 3 1 TRƯỜNG THPT XUÂN ĐỈNH 3
Câu 7: Cho hàm số f x xác định trên \ 1
và thỏa mãn f x
, f 0 1 và f 1 f 2 2 . x 1 Giá trị f 3 bằng: A. 1 2 ln 2 . B. 1 ln 2 . C. 1. D. 2 ln 2 .
Câu 8: Biết rằng F x 3 ax ab 2 x 2abcx 1
là một nguyên hàm của f x 2 3x 6x 2. Tính tổng S a b c. A. S 2. B. S 3. C. S 4. D. S 5.
Câu 9: Một ô tô đang chạy với vận tốc 20 m/s thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển động
chậm dần đều với vận tốc v t 4
t 20 (m/s) trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu
hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét? A. 25 m. B. 50 m. C. 10 m. D. 30 m.
Câu 10: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia tốc
phụ thuộc thời gian t s là a t t 2 2
7 m / s . Biết vận tốc ban đầu bằng 10 m / s, hỏi trong 6 giây đầu
tiên, thời điểm nào chất điểm ở xa nhất về phía bên phải? A. 5 s. B. 6 s. C. 1 s. D. 2 s.
Phần 2: Trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai 2 x 5x 7
Câu 11: Hàm số f x xác định trên \ 0 thỏa mãn f x
. Xét tính đúng sai của các khẳng x định sau: a) f x 7 x 5 . x 2 x b) f
xdx 5x7ln x C. 2
c) Gọi F x là một nguyên hàm của hàm số f x và thỏa mãn F 1 5 . Khi đó ta tìm được hàm 2 x 1 số F x 5x 7ln x . 2 2
d) Gọi G x là một nguyên hàm của hàm số f x . Biết G 1 4 và G 3 G 9 20 . Khi đó tìm 2 được G 6
aln2 bln3 c , với , a ,
b c là các số hữu tỉ. Vậy a b c . 3 x m , x 0
Câu 12: Cho hàm số f x liên tục trên thỏa mãn f x
(m là hằng số). Giả sử F x 2 x e , x 0
lànguyên hàm của hàm số f x và F x liên tục trên . Các khẳng định sau đúng hay sai? a) m 1. 1 1 x 1 b) Biết F 1
. Khi đó, với x 0 thì F x 2 e . 2 2e 2 2 e 2 4e 1 c) F 1 2 2e
d) Đồ thị hàm số F x có một điểm chung duy nhất với trục hoành. sin x 2 khi x 0
Câu 13: Cho hàm số f x x
. Giả sử F là nguyên hàm của f liên tục trên 2 2 cos khi x 0 2 thỏa mãn F
. Các khẳng định sau đúng hay sai? 3 2 TRƯỜNG THPT XUÂN ĐỈNH
a) sin x 2dx cos x 2x C x 4 3 b) F x 2 2cos dx sin x x 2 3 2
c) Với x 0 thì F x 4 3 2 2x cosx 3 2 2 d) F F F 5 3 3 2
Câu 14: Một bác thợ xây bơm nước vào bể chứa nước. Gọi ht là thể tích nước bơm được sau t giây. Cho h t 2 at bt 3 ' 3
m / s và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là 3
150m . Sau 10 giây thì thể tích nước trong bể là 3
1100m . Các khẳng định sau đúng hay sai? 2 t a) h t 3 ' dt at b C . 2 2 t b) h t 3 at b 1 2 c) a.b 2 .
c) Thể tích nước trong bể sau khi bơm được 20 giây là 3 8040m .
Câu 15: Trong thí nghiệm nuôi cấy một loại vi sinh vật, kí hiệu f t là tổng số lượng vi sinh vật sau t giờ.
Biết rằng sau 3 giờ đầu tiên thì tổng số lượng vi sinh vật là 50 con. Trong 7 giờ tiếp theo, số lượng vi
sinh vật thay đổi với tốc độ f t 2
t 8t (con/giờ). Xét tính đúng sai của các khẳng đính sau: 3 t
a) Họ nguyên hàm của f t là 2
8t C C . 3
b) Số lượng vi khuẩn tăng liên tục trong khoảng từ 3 giờ đến 10 giờ sau thời điểm làm thí nghiệm.
c) Số lượng vi khuẩn là nhỏ nhất sau 8 giờ tính từ lúc bắt đầu làm thí nghiệm.
d) Sau 6 giờ thì số lượng vi khuẩn là 5 con.
Phần 3. Trả lời ngắn. Ở mỗi câu, chỉ điền đáp án
Câu 16: Cho hàm số f x sin .
x cos2x liên tục trên . Giả sử F x là nguyên hàm của hàm số f x thoả 3 5 a b mãn F
. Tính giá trị của T a b c a,b,c & c 0 biết F . 6 2 3 c
Câu 17: Khi được thả từ độ cao 20 m, một vật rơi với gia tốc không đổi 2
a 10m / s . Sau khi rơi được t giây
thì vật có tốc độ bao nhiêu?
Câu 18: Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm t giây (coi t 0 là thời
điểm viên đạn được bắn lên), vận tốc của nó được cho bởi vt 160 9,8t m/s . Tìm độ cao lớn
nhất của viên đạn (tính từ mặt đất). (làm tròn kết quả đến chữ số thập phân thứ nhất). 2. Tích phân
Phần 1: Trắc nghiệm 4 phương án lựa chọn. Mỗi câu hỏi chỉ chọn một phương án
Câu 19: Cho hàm số y f x liên tục trên đoạn ;
a b . Gọi F x là một nguyên hàm của hàm số f x trên đoạn ;
a b . Chọn mệnh đề đúng. b b A. f
xdx F b F a. B. f
xdx F a F b. a a b b C. f
xdx F b F a. D. f x 2 x F b 2 d F a . a a 3 TRƯỜNG THPT XUÂN ĐỈNH 2 Câu 20: Tính tích phân cos t dt . 2 A. 2 . B. 0 . C. 2 . D. 1. 3 3 Câu 21: Nếu f xdx 2 thì f x2xdx bằng 1 1 A. 20 . B. 18 . C. 12 . D. 10 .
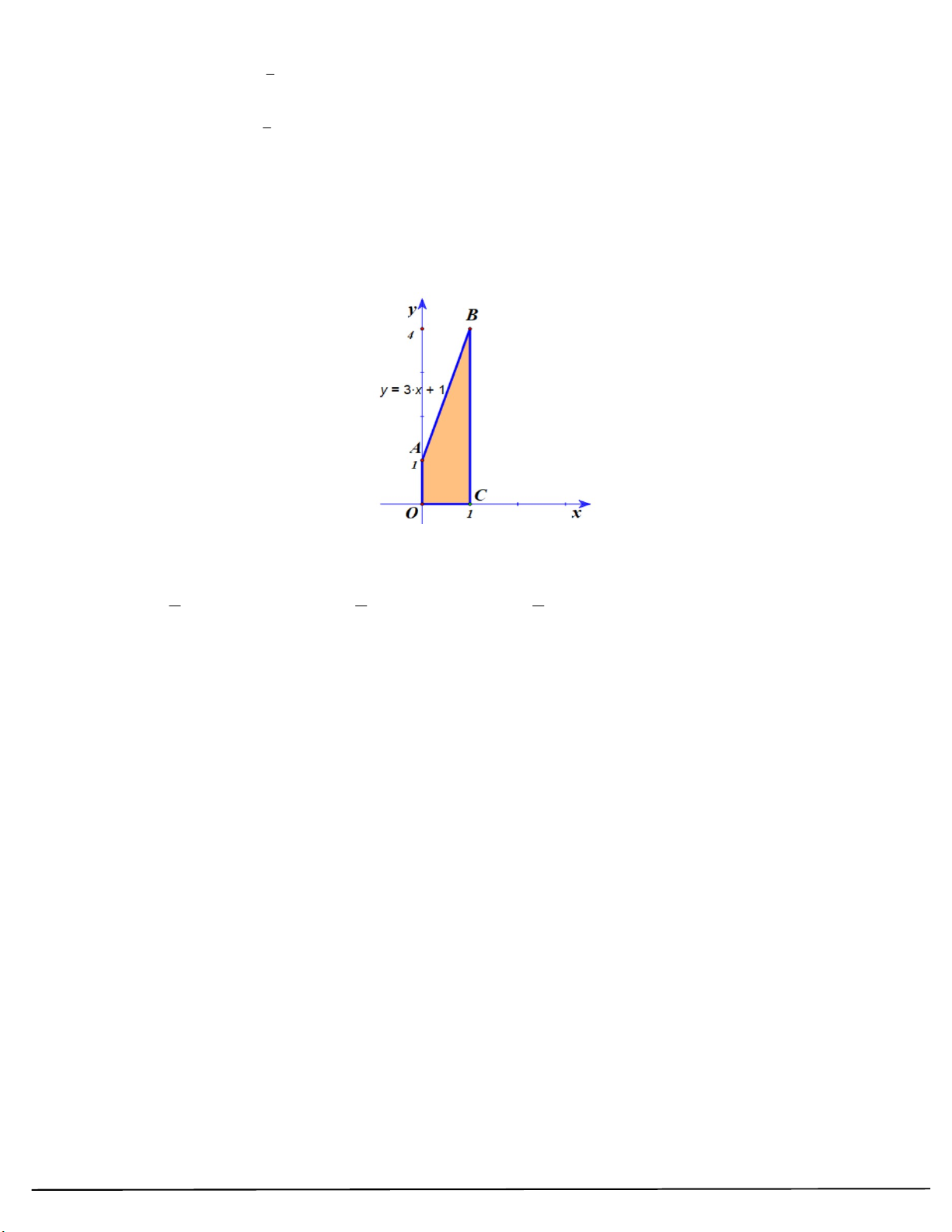
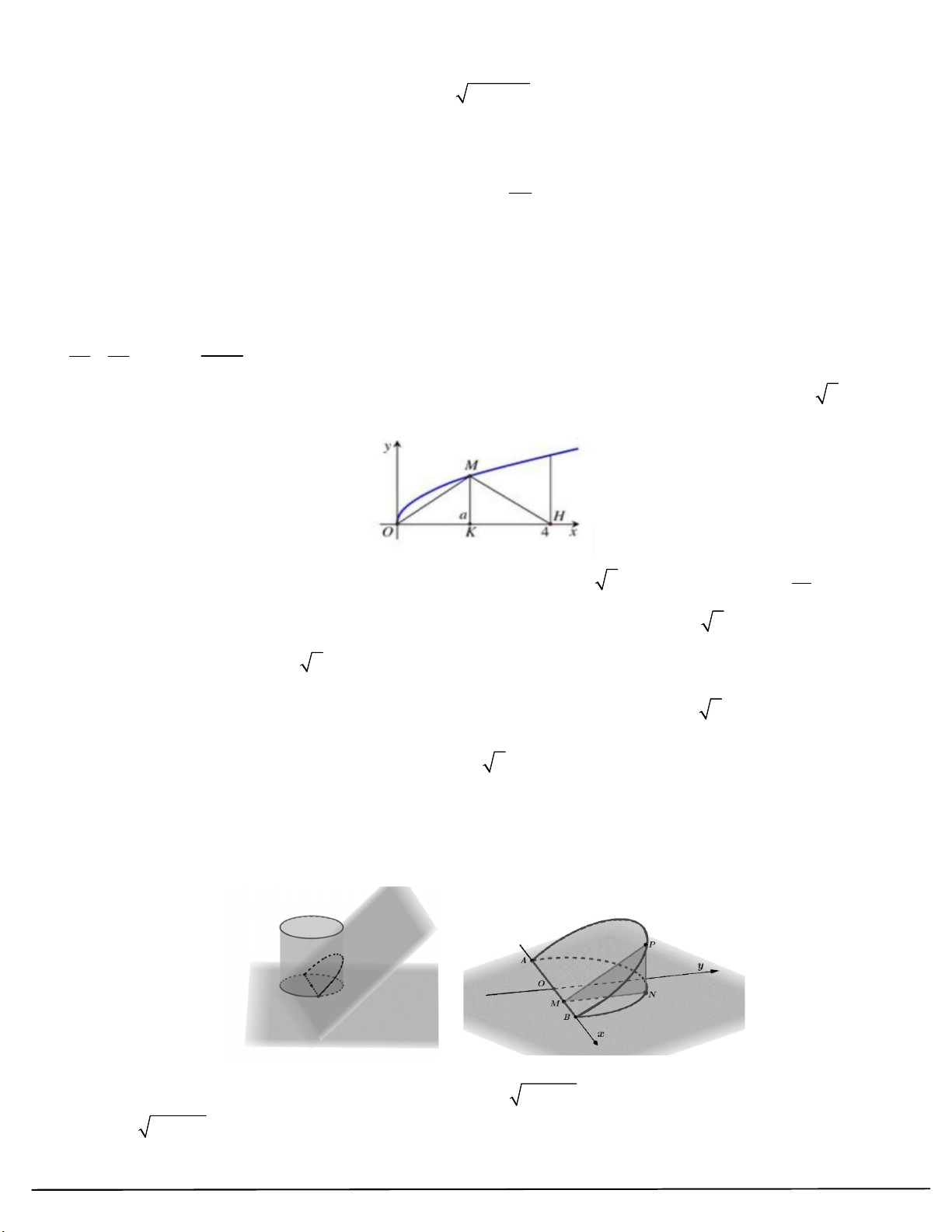
Câu 22: Trong mặt phẳng tọa độ Oxy , cho hình thang OABC giới hạn bởi y 3x 1, trục Ox và hai đường
thẳng x 0, x 1 như hình vẽ). 1 Khi đó 3x 1 dx bằng bao nhiêu? 0 2 5 3 A. . B. . C. . D. 2 . 5 2 2 2 2
Câu 23: Cho f xdx 1 và g
xdx 3. Mệnh đề nào say đây là đúng? 2 2 2 2 A. f
x gxdx 8 . B. f
x gxdx 4 . 2 2 2 2 C. 5 f xdx 5. D. 3 f
x4gxdx 1 5 . 2 2 1 3 3 Câu 24: Cho f xdx 1; f
xdx 5. Tính f xdx 0 0 1 A. 3 . B. 6 . C. 5 . D. 4 . m Câu 25: Cho 2 3x 2x
1 dx 6 . Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. 1;2 . B. ;0 . C. 0;4 . D. 3; 1 .
Câu 26: Vận tốc của một vật chuyển động là v t 2
3t 5 m/s . Quãng đường vật đó đi được từ giây thứ 4 đến giây thứ 10 là A. 669 m. B. 696 m. C. 699 m. D. 966 m.
Câu 27: Giả sử lợi nhuận biên tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức
P x 0,0004x 9,3. Ở đây P x là lợi nhuận tính bằng triệu đồng) khi bán được x đơn vị sản
phẩm. Khi đó sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 125 đơn vị sản phẩm là A. 232,325 triệu đồng. B. 230,315 triệu đồng. C. 321,385 triệu đồng D. 231,375 triệu đồng. 4 TRƯỜNG THPT XUÂN ĐỈNH khi x 2 Câu 28: Cho f x 1 1 . Tính J f xdx 2x 1 khi x 1 1 1 A. 1 B. C. 4 D. 5 2
Phần 2: Trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai 0 0
Câu 29: Cho f xdx 4 và g xdx 3. 3 3 Mệnh đề Đúng Sai 0 a) f
x gxdx 7 3 0 b) f
x gxdx 1 3 0 c) 3 f xdx 12 3 0 d) 2 f
x3gxdx 5 1 3
Câu 30: Cho hàm số f x liên tục và không âm trên đoạn 0;
3 . F x là một nguyên hàm của f x trên đoạn 0;
3 thỏa F 3 2 và F 0 1. Mệnh đề Đúng Sai
a) Hiệu số F 3 F 0 gọi là tích phân từ 3 đến 0 của hàm số f x . 3 0 b) f xdx f
xdx F 3 F 0 0 3 3 c) f tdt 1 0
Hình thang cong giới hạn bởi đồ thị hàm số y f x , trục hoành và hai
d) đường thẳng x 0,x 3 có diện tích bằng 1. 3 Câu 31: Cho 2 I x 2x dx . 0 Mệnh đề Đúng Sai 2 x 2x, 0 x 2 a) Ta có 2 x 2x 2 x 2x, 2 x 3 3 2 3 b) 2 2 2
I x 2x dx x 2x dx x 2x dx 0 0 2 3 2 3 c) 2 I x 2x dx
2x 2xdx 2x 2xdx 0 0 2 2 3 3 3 x x d) 2 2 I x x 3 3 0 2
Câu 32: Giả sử lợi nhuận biên tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức P x 0
,0008x 10,4 . Ở đây P x là lợi nhuận tính bằng triệu đồng) khi bán được x đơn vị sản phẩm. 5 TRƯỜNG THPT XUÂN ĐỈNH Mệnh đề Đúng Sai
Lợi nhuận khi bán được x đơn vị sản phẩm được tính bằng công thức a) Px 2 0 ,0008x 10,4x .
b) Lợi nhuận khi bán được 50 sản phẩm đầu tiên là 519 triệu đồng.
Sự thay đổi của lợi nhuận khi doanh số tăng từ 50 lên 55 đơn vị sản phẩm
c) là 49,79 triệu đồng.
Biết sự thay đổi của lợi nhuận khi doanh số tăng từ 50 lên a đơn vị sản
d) phẩm lớn hơn 517 triệu đồng, khi đó giá trị nhỏ nhất của a là 100.
Câu 33: Ở nhiệt độ 37 C
, một phản ứng hóa học từ chất đầu A , chuyển hóa thành chất sản phẩm B theo
phương trình: A B . Giả sử y x là nồng độ chất A đơn vị mol 1
L ) tại thời điểm x giây),
y x 0 với x 0 , thỏa mãn hệ thức: y x 4 7.10
y x với x 0 . Biết rằng tại x 0 , nồng độ
đầu) của A là 0, 05 mol 1
L . Xét hàm số f x ln y x với x 0 . Khi đó, ta có Mệnh đề Đúng Sai a) f x 4 7.10 b) f x 4 7.10 x ln 0,05 c) y y 4 30 15 6.10
Nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây d) gần bằng 0,05.
Phần 3. Trả lời ngắn. Ở mỗi câu, chỉ điền đáp án
Câu 34: Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t giây) là vt 2
t t 6 mét/giây). Quãng đường mét) vật đi được trong khoảng thời gian 1 t 4 bằng
làm tròn tới hàng phần trăm)
Câu 35: Hiệu suất của tim là lưu lượng máu được bơm bởi tim trên một
đơn vị thời gian lưu lượng máu chảy vào động mạch chủ). Để
đo hiệu suất của tim, người ta bơm Amg chất chỉ thị màu
vào tâm nhĩ phải, chảy qua tim rồi vào động mạch chủ và đo
nồng độ chất chỉ thị màu còn lại ở tim đến thời điểm T s khi
chất chỉ thị màu tan sạch. Gọi c t là nồng độ mg / l chất
chỉ thị màu tại thời điểm t s thì hiệu suất của tim được xác A định bởi F
. Tính hiệu suất của tim khi bơm 8 T l / s c tdt 0 1
mg chất chỉ thị màu vào tâm nhĩ phải, biết c t t 12 t với 0 t 12 kết quả làm tròn đến chữ 4
số thập phân thứ hai). (Nguồn: James Stewart, Calculus, Cengage Learning) ax 1 khi x 1
Câu 36: Cho hàm số f x
với a, b là các tham số thực. Biết rằng f x liên tục và có 2 x b khi x 1 2 m đạo hàm trên .
Biết I f xdx
với a,b là các số nguyên tố cùng nhau. Tính S m n . n 1
3. Ứng dụng hình học tích phân để tính diện tích hình phẳng
Phần 1: Trắc nghiệm 4 phương án lựa chọn. Mỗi câu hỏi chỉ chọn một phương án
Câu 37: Diện tích hình phẳng giới hạn bởi các đường x a , x b , y f x và trục hoành là 6 TRƯỜNG THPT XUÂN ĐỈNH b b b b A. S f xdx . B. S f x dx . C. S f xdx . D. S f x 2 dx . a a a a
Câu 38: Cho hai hàm số f (x) và g(x) liên tục trên a;b. Diện tích hình phẳng giới hạn bởi đồ thị của các
hàm số y f (x) , y g(x) và các đường thẳng x a , x b bằng b b b b
A. f (x) g(x)dx . B. f (x) g(x) dx . C. f (x) g(x) dx
. D. f (x) g(x)dx . a a a a
Câu 39: Gọi S là diện tích hình phẳng giới hạn bởi các đường 3
y x 3x , y 0 , x 0 , x 2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2
S 3x 3xdx . B. S 3x 3x dx . C. 3 S x 3x dx
. D. S 3x 3xdx . 0 0 0 0
Câu 40: Tính diện tích S của hình phẳng giới hạn bởi các đường ex y , y 2 , x 0 , x 1. A. S 4ln 2 e 5. B. S 4ln 2 e 6 . C. 2 S e 7. D. S e 3.
Câu 41: Gọi S là diện tích hình phẳng giới hạn bởi các đường y f x , y g x , x a , x b . Biết rằng
f x g x 8 Mệnh đề nào dưới đây đúng? b b b b A. S 8dx . B. S 8dx . C. S 64dx . D. S 64dx . a a a a
Câu 42: Gọi S là diện tích hình phẳng giới hạn bởi các đường x 0 , x 1 , đồ thị hàm số 3 2 y x 3x và tiếp
tuyến của nó tại điểm x 2 . Mệnh đề nào dưới đây đúng? 1 1 A. S 3 2 x 3x 4dx . B. 3 2 S x 3x 4 dx . 0 0 1 1 C. S 3 2 x 3x 4dx .
D. S x 3x 42 3 2 dx . 0 0 2 x 2x
Câu 43: Tìm a để diện tích S của hình phẳng giới hạn bởi P : y
, đường thẳng d : y x 1 và x 1
x a, x 2a (a 1) bằng ln 3 ? A. a 1. B. a 4. C. a 3. D. a 2.
Câu 44: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng giới
hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng x 1; x 3 . Mệnh đề nào sau đây đúng? 3 3 A. S f xdx . B. S f xdx . 1 1 3 3 2 3 2 3 C. S f xdx f xdx. D. S f xdx f xdx . 1 3 1 3 2 2
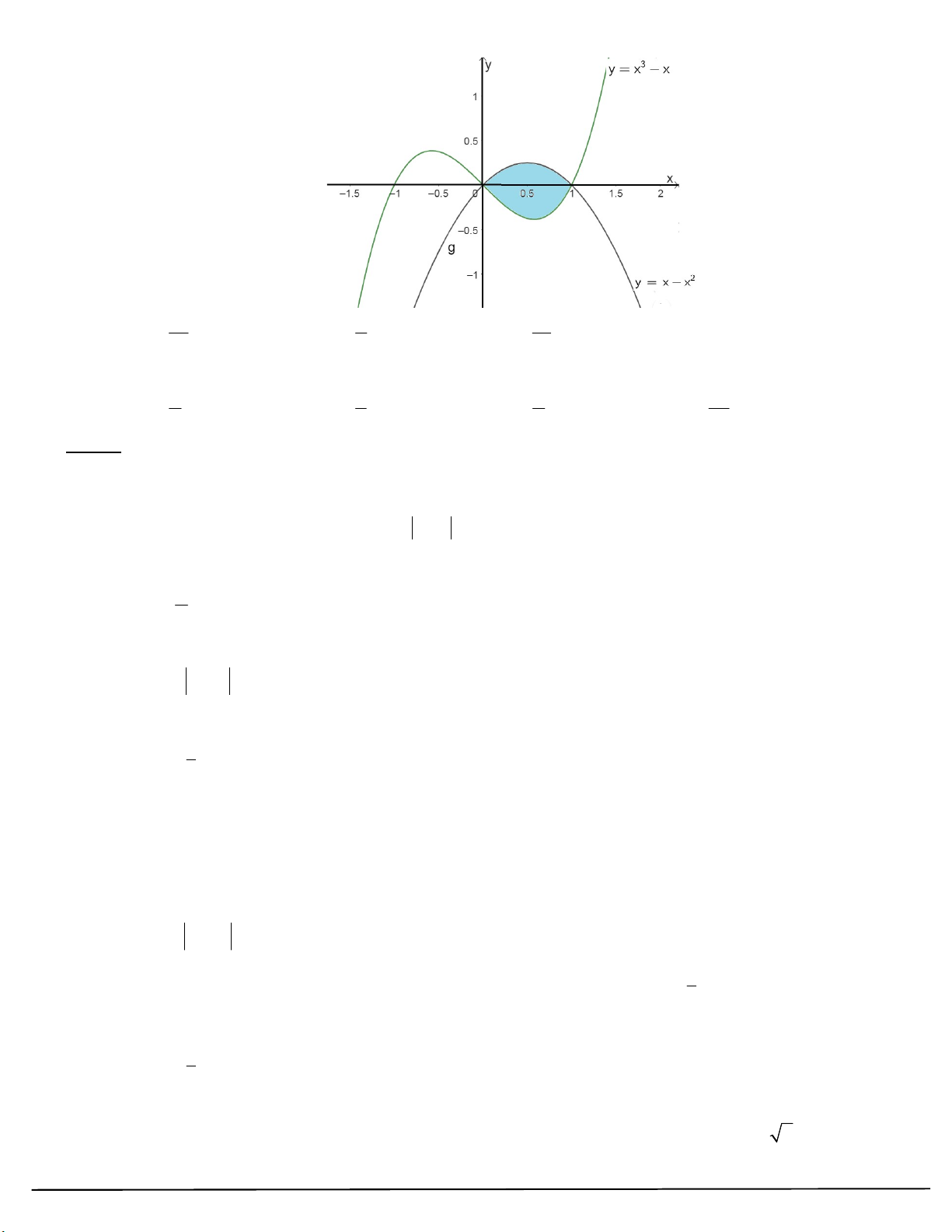
Câu 45: Tính diện tích phần hình phẳng ( Phần tô đậm) trong hình vẽ bên. 7 TRƯỜNG THPT XUÂN ĐỈNH 5 9 81 A. B. C. D. 13 12 4 12
Câu 46: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y 2x là : 4 5 3 23 A. B. C. D. 3 3 2 15
Phần 2: Trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai
Câu 47: Trong mặt phẳng tọa độ Oxy . Các khẳng định sau đúng hay sai?
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y cos x , trục Ox và hai đường thẳng x 0 , π
x π được tính bởi công thức S cos x dx . 0
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y cos x , trục Ox và hai đường thẳng x 0, π x bằng 1. 2
c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y x 1
và trục Ox , được tính bởi công thức 1 2 S x 1 dx . 0
d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y x 1
, trục Ox ; O y và đường thẳng x 1, 4 bằng . 3
Câu 48: Trong mặt phẳng tọa độ Oxy . Các khẳng định sau đúng hay sai?
a) Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y f (x) , y g(x) và hai đường thẳng x a b
, x b được tính bằng công thức S f (x) g(x)dx . a
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x , và y x được tính bằng công thức 1 2 S x x dx . 0 4
c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y x và y 1 bằng . 3
d) Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số 2 y x 1
, và y 1 và đường thẳng x 1 4 bằng . 3
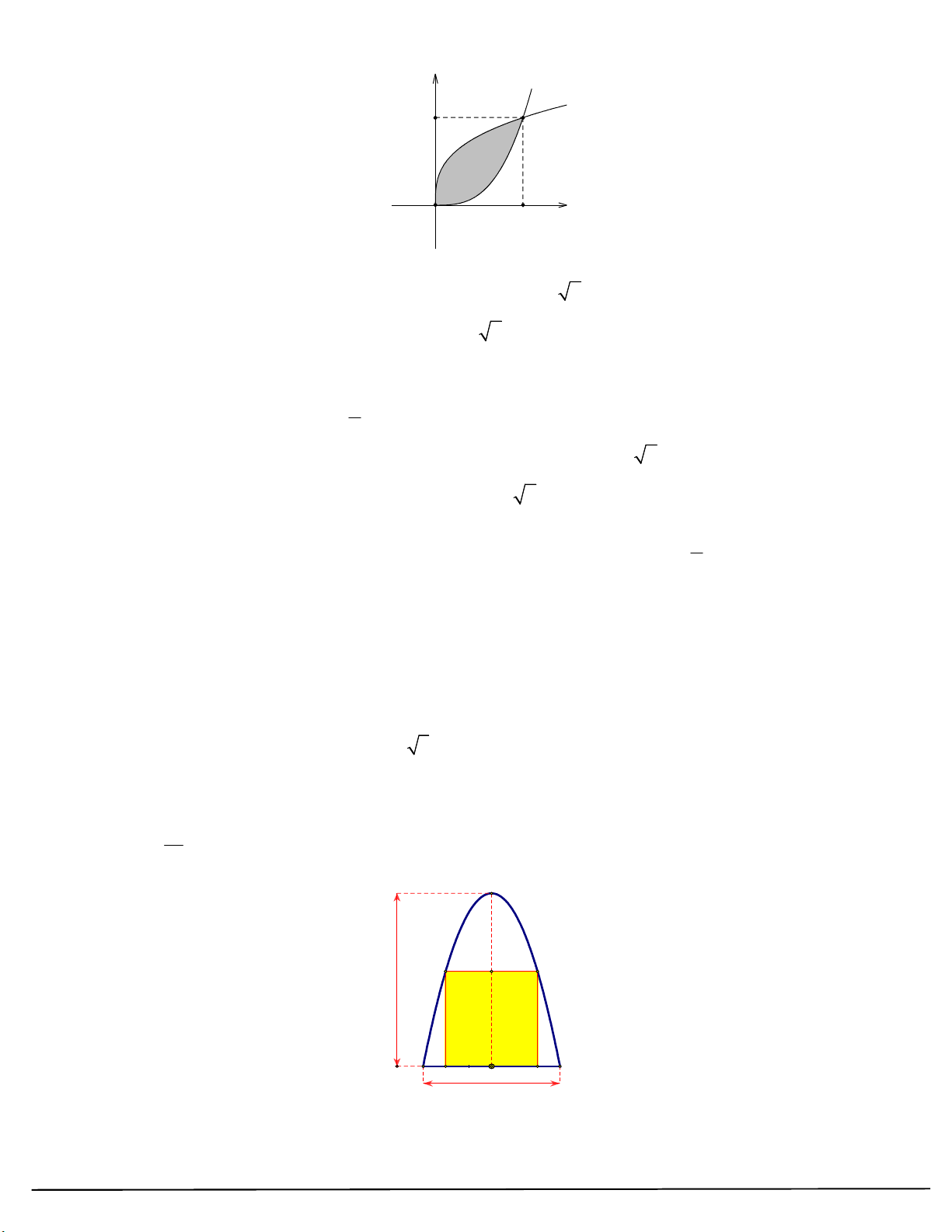
Câu 49: Cho một viên gạch men có dạng hình vuông OABC như hình vẽ. Sau khi tọa độ hóa, ta có O 0;0 , A0; 1 , B 1;
1 , C 1;0 và hai đường cong lần lượt là đồ thị hàm số 3 y x và 3 y x . 8 TRƯỜNG THPT XUÂN ĐỈNH y A B x O C
Các khẳng định sau đúng hay sai?
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục Ox , đường thẳng x 0 và đường 1
thẳng x 1 được tính bằng công thức 3 S | x | dx . 0
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục Ox ,đường thẳng x 0 và đường 3
thẳng x 1 có giá trị bằng (đvdt). 4
c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 y x và 3
y x , đường thẳng x 0 và đường 1
thẳng x 1 được tính bằng công thức S 3 3 x x dx . 0 1
d) Diện tích phần không được tô đậm trên viên gạch men có giá trị bằng (đvdt). 2
Câu 50: Một cánh cổng của tòa nhà có dạng parabol gồm hai phần: Phần làm cửa lối vào là hình chữ nhật
ABCD , còn lại là phần tường trang trí. Biết rằng chiều cao cổng là IO 9 , m EF 6m, AB 4m . S 1
là diện tích phần cánh cửa của lối vào hình chữ nhật, S là diện tích phần tường trang trí. Các khẳng 2 định sau đúng hay sai? 3
a) Giả sử parabol có phương trình là y f x thì diện tích cánh cổng là S f xdx. 3
b) Diện tích phần cửa vào là S 4 5 2 m . 1
c) Diện tích phần tường trang trí là S 16 2 m . 2
d) Giả sử phần tường trang trí hai bên cửa vào cần ốp kính cường lực. Khi đó diện tích kính cần dùng 16 là 2 m . 3 I D C 9 m E A O B F 6 m Câu 51: Cho parabol 2
(P) : y x 2 , đường thẳng d : y x 2 và d ': x a , a là tham số dương. 9 TRƯỜNG THPT XUÂN ĐỈNH 4 2 O 1 2 5 2 2 4 2
a) Diện tích hình phẳng (H ) giới hạn bởi các đường (P) và trục Ox là S . 1 1 3 1
b) Diện tích của hình phẳng (H ) giới hạn bởi các đường (P) và d là S . 2 2 6
c) Diện tích hình phẳng (H ) giới hạn bởi các đường (P) , đường d’ và hai trục tọa độ là 3 a 2 S (x 2)dx 3 . 0
d) Diện tích hình phẳng (H ) giới hạn bởi các đường (P) , đường thẳng d và trục Ox là 4 4 2 5 S . 4 3
Phần 3. Trả lời ngắn. Ở mỗi câu, chỉ điền đáp án
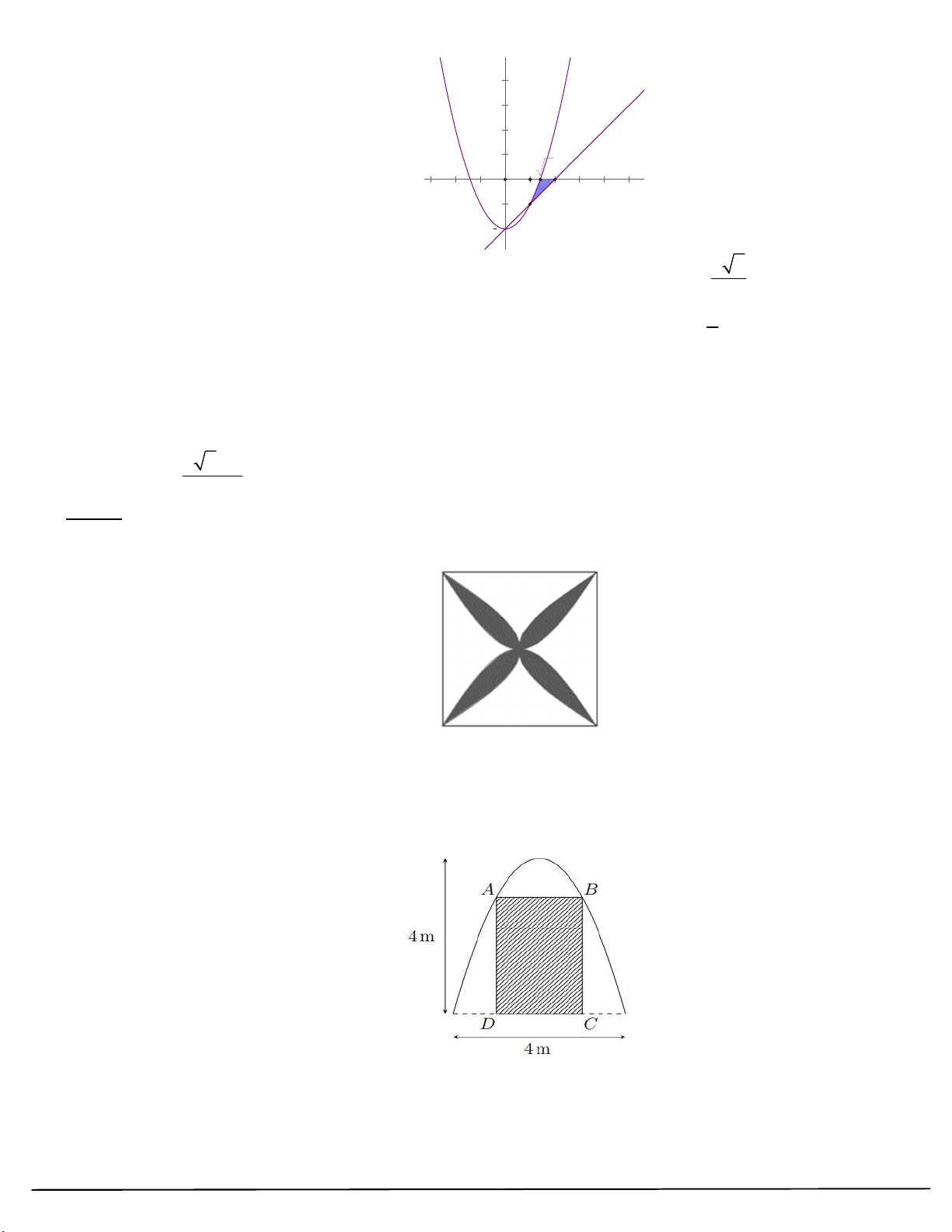
Câu 52: Một viên gạch hoa hình vuông cạnh 60 ( cm ). Người thiết kế đã sử dụng bốn đường parabol có chung
đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô mầu sẫm như hình vẽ bên).
Diện tích phần cánh hoa của viên gạch bằng bao nhiêu?
Câu 53: Cổng của một trại du lịch sinh thái có dạng parabol, lối ra vào cổng là hình chữ nhật như hình vẽ.
Biết rằng, lối đi hình chữ nhật ABCD có kích thước CD 2 m , phía ngoài lối đi hình chữ nhật được
trang trí hoa văn cho phù hợp. Chi phí trang trí hoa văn là 240.000 đồng cho một mét vuông. Hỏi số
tiền để trang trí hoa văn của cổng trại du lịch sinh thái là bao nhiêu triệu đồng?
Câu 54: Sân trường có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa,
nhóm này định chia bồn hoa thành bốn phần, bởi hai đường parabol có cùng đỉnh O và đối xứng nhau
qua O. Hai đường parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có
cạnh bằng 4m (như hình vẽ). Phần diện tích S , S dùng để trồng hoa, phần diện tích S , S dùng để 1 2 3 4
trồng cỏ (Diện tích làm tròn đến chữ số thập phân thứ hai). Biết kinh phí để trồng hoa là 150.000 10 TRƯỜNG THPT XUÂN ĐỈNH đồng/ 2
1m , kinh phí để trồng cỏ là 100.000 đồng/ 2
1m . Hỏi nhà trường cần bao nhiêu tiền để trồng bồn
hoa đó? (Số tiền làm tròn đến hàng chục nghìn).
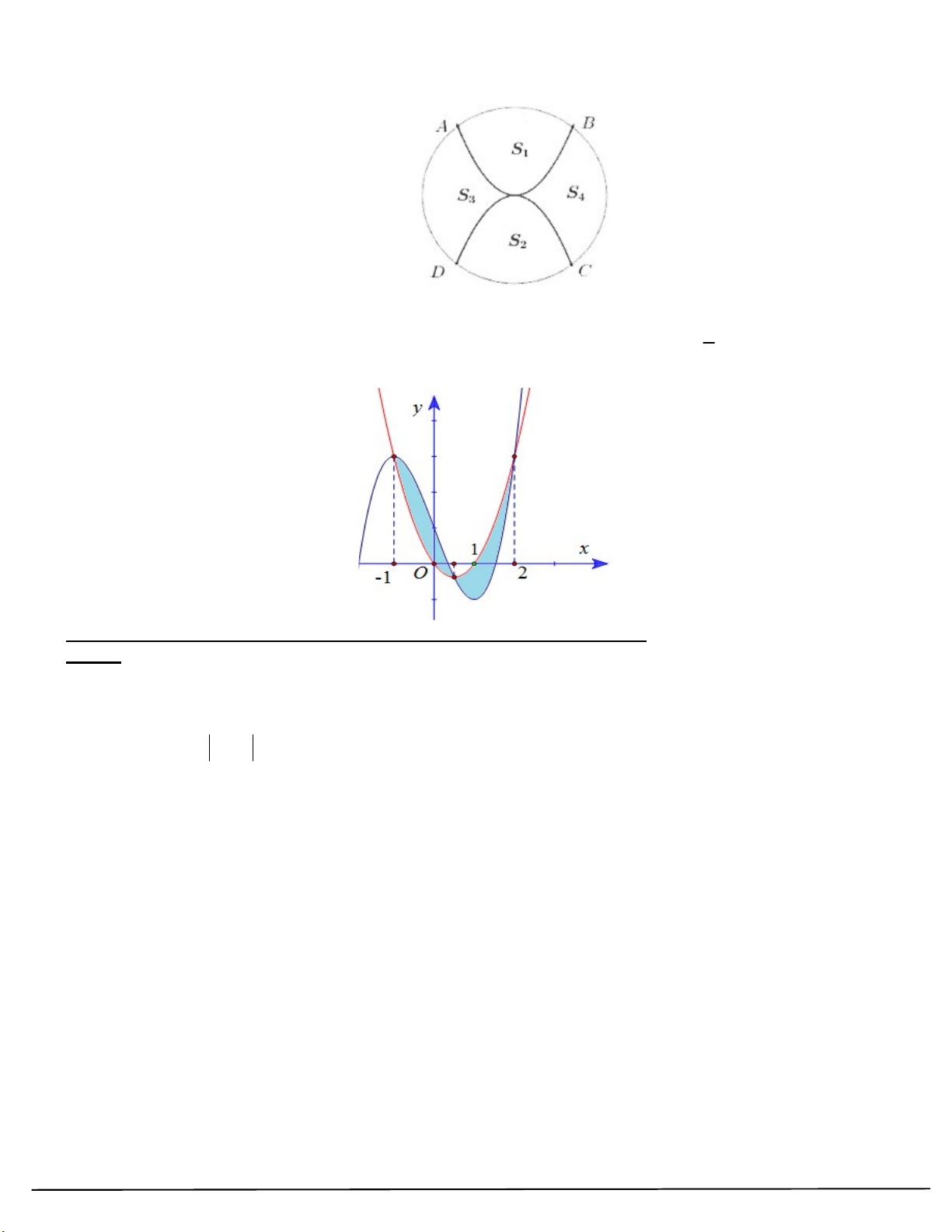
Câu 55: Cho hai hàm số f x 3 2
ax bx cx 1 và 2 g x dx ex a, ,
b c, d,e . Biết rằng đồ thị hàm 1
số y f x và y g x cắt nhau tại 3 điểm có hoành độ lần lượt là 1
; ; 2 (tham khảo hình vẽ). 2
Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng bao nhiêu?
4. Ứng dụng hình học tích phân để tính thể tích vật thể và vật thể tròn xoay
Phần 1: Trắc nghiệm 4 phương án lựa chọn. Mỗi câu hỏi chỉ chọn một phương án
Câu 56: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi
đồ thị hàm số y f x , trục Ox và hai đường thẳng x a, x ba b , xung quanh trục Ox . b b b b A. V f xdx B. 2 V f xdx C. 2 V f xdx D. V f xdx a a a a
Câu 57: Cắt một vật thể bởi hai mặt phẳng vuông góc với trục Ox tại x 1 và x 2 . Một mặt phẳng tùy ý
vuông góc với trục Ox tại điểm có hoành độ x (1 x 2 ) cắt vật thể đó có diện tích S x 2024x .
Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên. A. V 3036 B. V 3036 C. V 1518 D. V 1518
Câu 58: Cắt một vật thể bởi hai mặt phẳng vuông góc với trục Ox tại x 1 và x 3. Một mặt phẳng tùy ý
vuông góc với trục Ox tại điểm có hoành độ x (1 x 3 ) cắt vật thể đó theo thiết diện là một hình
chữ nhật có độ dài hai cạnh là 3x và 2
3x 2 . Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên. A. V 156 B. V 156 C. V 312 D. V 312
Câu 59: Gọi D là hình phẳng giới hạn bởi các đường 3 e x y
, y 0 , x 0 và x 1. Thể tích của khối tròn
xoay tạo thành khi quay D quanh trục Ox bằng: 1 1 1 1 A. 3 e xdx . B. 6 e xdx . C. 6 e xdx . D. 3 e xdx . 0 0 0 0
Câu 60: Gọi D là hình phẳng giới hạn bởi các đường 4x
y e , y 0, x 0 và x 1 . Thể tích của khối tròn
xoay tạo thành khi quay D quanh trục Ox bằng 11 TRƯỜNG THPT XUÂN ĐỈNH 1 1 1 1 A. 4 x e dx . B. 8 x e dx . C. 4 x e dx . D. 8 x e dx . 0 0 0 0
Câu 61: Cho hình phẳng H giới hạn bởi các đường 2
y x 3 , y 0 , x 0 , x 2 . Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay H xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2 A. V 2x 3dx
B. V 2x 3dx C. V 2x 3 dx D. V 2x 3 dx 0 0 0 0
Câu 62: Cho hình phẳng D giới hạn bởi đường cong x
y e , trục hoành và các đường thẳng x 0 , x 1.
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2e 1 2 e 1 2 e 2e 1 A. V B. V C. V D. V 2 2 3 2
Câu 63: Cho hình phẳng D giới hạn với đường cong 2
y x 1 , trục hoành và các đường thẳng
x 0, x 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 4 A. V 2 B. V C. V 2 D. V 3 3
Câu 64: Cho hình phẳng D giới hạn bởi đường cong y 2 cos x , trục hoành và các đường thẳng
x 0, x . Khối tròn xoay tạo thành khi D quay quanh trục hoành có thể tích V bằng bao nhiêu? 2 A. V ( 1) B. V 1 C. V 1 D. V ( 1)
Câu 65: Cho hình phẳng D giới hạn bởi đường cong y 2 sin x , trục hoành và các đường thẳng x 0 ,
x . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu? A. V 2 1 B. V 2 C. V 2 1 D. 2 V 2
Phần 2: Trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai
Câu 66. Các khẳng định sau là đúng hay-sai
a) Công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol P 2 : y x , đường 2 2
thẳng d : y 2x và đường thẳng x 0, x 2 quay xung quanh trục Ox là 2 4 V 4x dx x dx 0 0
b) Cho hình phẳng H giới hạn bởi các đường 2
y x 3, y 0, x 0, x 2 . Gọi V là thể tích khối tròn 2 2
xoay được tạo thành khi quay H xung quanh trục Ox . Khi đó V 2x 3 d .x 0
c) Cho hình phẳng giới hạn bởi các đường y x 2 , y 0 và x 4, x 9 quay xung quanh trục Ox . Thể
tích khối tròn xoay tạo thành bằng 11
d) Cho tam giác vuông OAB có cạnh OA a nằm trên tục Ox và AOB 0
. Gọi (H) là khối tròn 4
xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox . Thể tích V của (H) bằng 3 a 12 TRƯỜNG THPT XUÂN ĐỈNH
Câu 67. Các khẳng định sau là đúng hay sai?
a) Cho hình phẳng D giới hạn bởi đường cong y 2 sin x , trục hoành và các đường thẳng x 0 , x .
Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích bằng 2 1
b) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị của hàm số 2 y x 2x , trục 8
hoành, đường thẳng x 0 và x 1quanh trục hoành bằng 25
c) Cho hình phẳng H giới hạn bởi các đường thẳng 2
y x 2, y 0, x 1, x 2. Gọi V là thể tích của khối 2 2
tròn xoay được tạo thành khi quay H xung quanh trục Ox . Khi đó V 2 x 2 dx 1
d) Gọi V là thể tích khối tròn xoay tạo thành do quay xung quanh trục hoành một elip có phương trình 2 2 x y 320 1. V 25 16 3
Câu 68. Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y x, y 0 và x 4 quanh trục Ox . 16
a. Diện tích hình phẳng tạo thành khi được giới hạn bởi các đường y x, y 0 và x 4 là S . 3
b. Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y x, y 0 và x 4 quanh 4 2
trục Ox có công thức là V x dx . 0
c. Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y x, y 0 và x 4 quanh trục Ox là 8 .
d. Đường thẳng x a 0 a 4 cắt đồ thị hàm số y x tại M ( hình vẽ). Gọi V là thể tích khối tròn xoay 1
tạo thành khi quay tam giác OMH quanh trục Ox .Với V 2V ta có giá trị a 3. 1
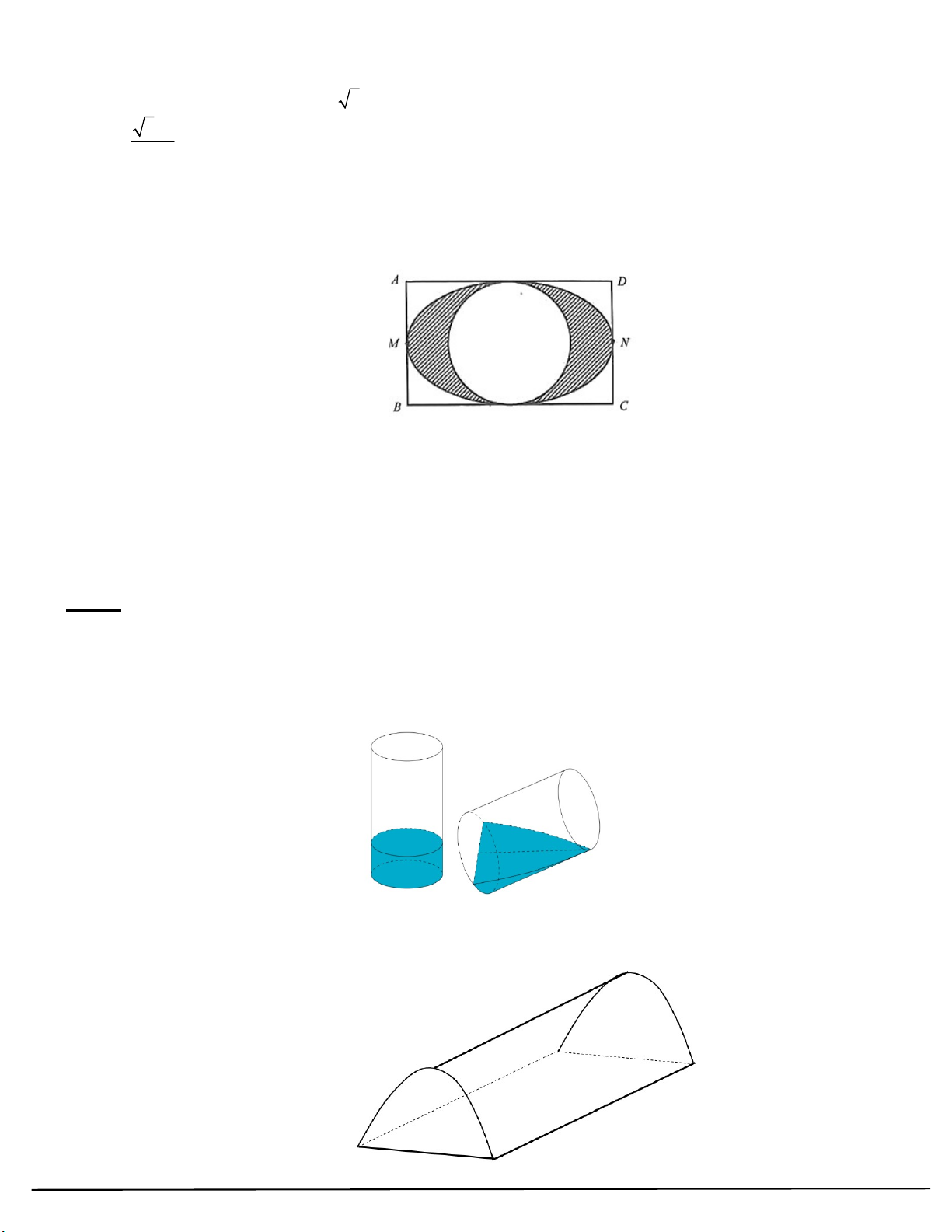
Câu 69. Cho một vật thể có dạng hình trụ với chiều cao và bán kính cùng bằng R . Cắt khối gỗ đó bởi một mặt
phẳng đi qua đường kính của một đáy của khối gỗ và tạo với đáy của khối gỗ đó một góc o 30 ta thu được hai
khối gỗ có thể tích là V ,V với V V . Gắn khối gỗ có dạng hình nêm vào hệ trục toạ độ như hình vẽ dưới đây 1 2 1 2
Xét tính đúng sai của các khẳng định sau:
a) Nửa đường tròn đường kính AB có phương trình là 2 2
y R x với R x R b) 2 2 MN R x 13 TRƯỜNG THPT XUÂN ĐỈNH 2 2 R x
c) Diện tích tam giác MNP bằng 2 3 3 3R d) V 1 9
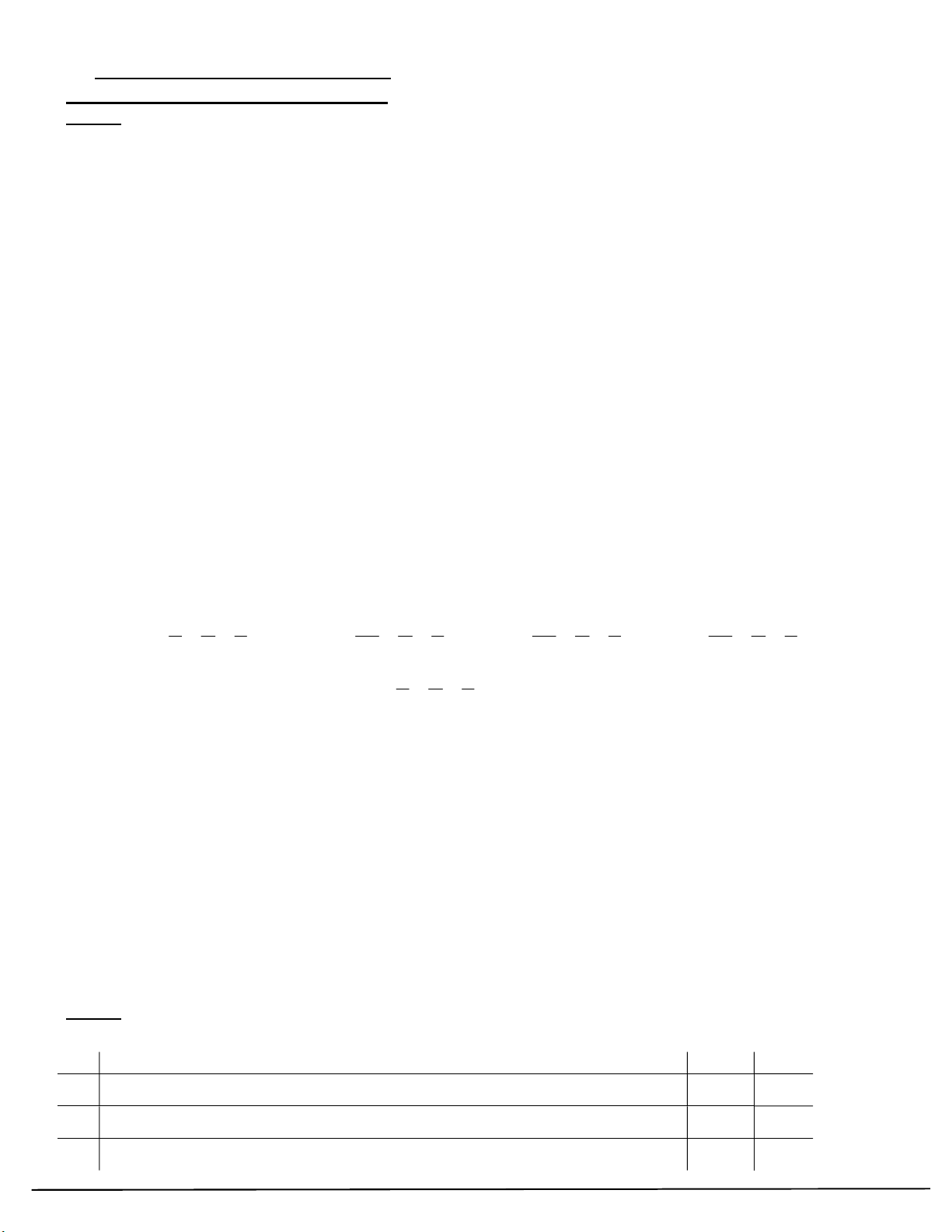
Câu 70. Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền R (phần gạch chéo
trong hình vẽ) quanh trục MN . Biết rằng ABCD là hình chữ nhật với AB 6cm , AD 10cm , M , N lần lượt là
trung điểm của AB , CD , hai đường cong là đường elip có hình chữ nhật cơ sở là ABCD và đường tròn tiếp xúc
với hai cạnh AD và BC (tham khảo hình vẽ).
Xét tính đúng sai của các khẳng định sau: b) C 2 2 : x y 9 2 2 x y
a) Phương trình của elíp là: 1 100 36
b) Phương trình đường tròn là 2 2 x y 9
c) Quay đường elip quanh trục MN tạo ra khối tròn xoay có thể tích là 3 60 cm
d) Thể tích của vật trang trí là: 3 V 75, 4cm .
Phần 3. Trả lời ngắn. Ở mỗi câu, chỉ điền đáp án
Câu 71. Cho hình thang ABCD có AB song song CD và AB AD BC ,
a CD 2a .Tính thể tích
khối tròn xoay khi quay hình thang ABCD quanh trục là đường thẳng AB .
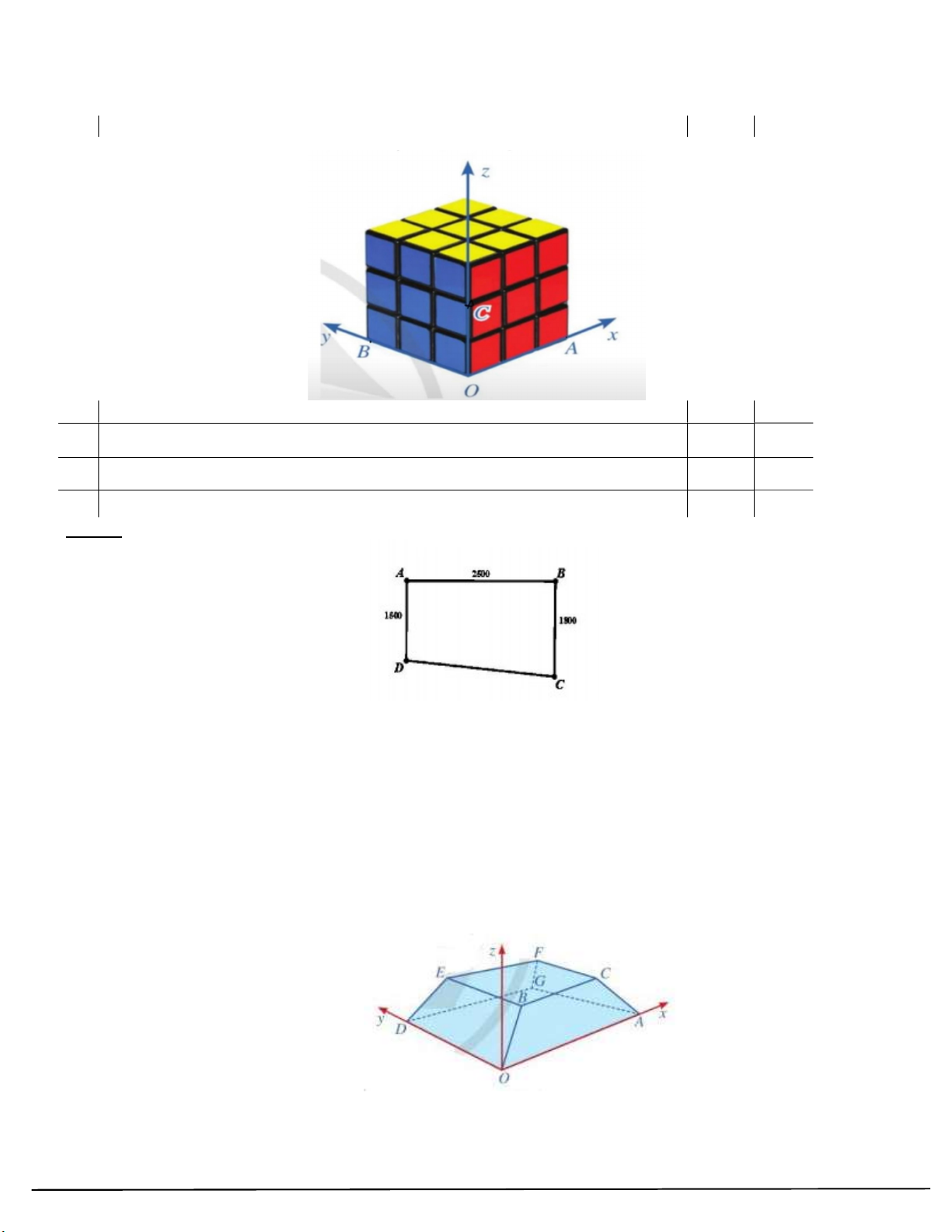
Câu 72. Một cốc thủy tinh hình trụ, bán kính trong lòng đáy cốc là 6 cm, chiều cao trong lòng cốc là 10 cm
đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiêng cốc nước vừa lúc nước chạm
miệng cốc thì đáy của mực nước trùng với đường kính đáy (tham khảo hình vẽ)
Câu 73. Để chuẩn bị hội trại do Đoàn trường tổ chức, lớp 12A dựng một cái lều trại có dạng hình
parabol như hình vẽ. Nền của lều tại là một hình chữ nhật có chiều rộng bằng 3 mét và chiều dài
bằng 6 mét, đỉnh trại cách nền 2 mét. Tính thể tích phần bên trong lều trại. 14 TRƯỜNG THPT XUÂN ĐỈNH
IV. Phương pháp toạ độ trong không gian
1. Phương trình tổng quát của mặt phẳng
Phần 1: Trắc nghiệm 4 phương án lựa chọn. Mỗi câu hỏi chỉ chọn một phương án
Câu 74: Cho hình lập phương ABC . D A B C D
. Vectơ nào là vectơ pháp tuyến của mặt phẳng ABCD ? A. AC . B. AC . C. AA . D. AD .
Câu 75: Trong không gian Oxyz , mặt phẳng P : x y z 3 0 đi qua điểm nào dưới đây: A. M 1 ; 1 ; 1 . B. N 1;1; 1 . C. P 3 ;0;0 . D. Q0;0; 3 .
Câu 76: Trong không gian Oxyz cho mặt phẳng :3x 2y 4z 1 0. Vectơ nào dưới đây là một vectơ
pháp tuyến của ? A. n (3;2;4) . B. n (2; 4 ;1) . C. n (3; 4 ;1) . D. n (3;2; 4 ) . 2 3 1 4
Câu 77: Trong không gian Oxyz , cho mặt phẳng (P) đi qua điểm ( A 0; 1
;4) và có một vectơ pháp tuyến
n 2;2; 1. Phương trình của Plà
A. 2x 2y z 6 0 . B. 2x 2y z 6.
C. 2x 2y z 6 0 .
D. 2x 2y z 6 0 .
Câu 78: Trong không gian Oxyz , cho ba điểm A3;2; 1 , B 1 ;4;
1 ,C 3; 2;5 . Tọa độ nào sau đây là tọa
độ vectơ pháp tuyến của của mặt phẳng ABC ? A. 1;2;2 . B. 8;16;16 . C. 1 ;2; 2 . D. 1;4;4 .
Câu 79: Trong không gian Oxyz , phương trình mặt phẳng đi qua ba điểm A 2 ;0;0, B(0;3;0) C(0;0;1) là x y z x y z x y z x y z A. 1. B. 1. C. 0 . D. 1. 2 3 1 2 3 1 2 3 1 2 3 1 x y z
Câu 80: Vectơ pháp tuyến của mặt phẳng 1 là: 1 2 3 A. n (6;3;2) . B. n (6;2;3) . C. n (3;6;2) . D. n (2;3;6) . 1 2 3 4
Câu 81: Trong không gian Oxyz , phương trình của mặt phẳng Oxz là A. x z 0 . B. y 0 . C. z 0 . D. x 0 .
Câu 82: Trong không gian Oxyz , hình chiếu vuông góc của điểm M (3;4; 2) lên mặt phẳng Oxz có tọa độ là: A. Q(3;0;0) . B. G(3;4;0) . C. E(0;4; 2) . D. F (3; 0; 2) .
Câu 83: Trong không gian Oxyz , cho ba điểm A3; 2 ; 2
, B3;2;0,C 0;2;
1 . Phương trình mặt phẳng ABC là:
A. 2x 3y 6z 12 0 .
B. 2x 3y 6z 12 0 . C. 2x 3y 6z 0 .
D. 2x 3y 6z 12 0 .
Phần 2: Trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai
Câu 84: Trong không gian Oxyz , cho mặt phẳng P : 3x y z 12 0 . Mệnh đề Đúng Sai
(a) Mặt phẳng P có một vectơ pháp tuyến là n 3;1; 1 .
(b) Mặt phẳng P đi qua điểm A5;3; 6 . (c) Cho điểm M ; a ; b
1 thuộc mặt phẳng (P) . Khi đó 3a b 1 3 15 TRƯỜNG THPT XUÂN ĐỈNH
(d) P cắt trục Ox tại A, cắt trục Oz tại B . Chu vi tam giác OAB bằng 12.
Câu 85: Trong không gian Oxyz , cho ba điểm A 1 ;0; 1 , B3;2; 1 ,C 5;3;7 . Mệnh đề Đúng Sai (a) AB 4;2;0 .
(b) Nếu I là trung điểm đoạn thẳng AB thì I 2;1;0
(c) Mặt phẳng trung trực của AB là 2x y 3 0 (d) M (a, ,
b c) thỏa mãn MA MB . Khi đó min MB MC BC Câu 86: Trong không gian Oxyz , cho ba điểm A1;6;0, B 2 ;2; 1 ,C 5; 1 ;3 và
P: x y z 6 0 Mệnh đề Đúng Sai
(a) Một vectơ pháp tuyến của P là n 1;1; 1
Phương trình mặt phẳng Q qua A và vuông góc với BC có phương trình
(b) 3x 3y 4z 15 0
(c) Phương trình mặt phẳng ABC có phương trình 19x 5y 37z 11 0 M (a, ,
b c) thuộc P : x y z 6 0 và cách đều các điểm , A B,C . (d) Tích abc 6
Câu 87: Hình vẽ một khu nhà đang xây dựng được gắn hệ trục tọa độ Oxyz . Mỗi cột bê tông có dạng hình
lăng trụ tứ giác đều và tâm của mặt đáy trên lần lượt là các điểm A B 5 14 2;1;3 , 4;3;3 ,C 6;3; ; D 4;0; . Khi đó 2 5 Mệnh đề Đúng Sai
(a) Mặt phẳng ABC có một vectơ pháp tuyến là n 1;1;4 .
(b) Phương trình ABC : x y 4z 13 0 (c) D ABC
(d) ( ABC) cắt Ox, Oy tại điểm M , N khi đó MN 13 16 TRƯỜNG THPT XUÂN ĐỈNH
Câu 88: Khối rubik được gắn với hệ tọa độ Oxyz có đơn vị bằng độ dài cạnh của hình lập phương nhỏ. Xét
bốn điểm A3;0;0, B0;3;0, C 0;0;2, D3k;3k;2k với k 0 đồng phẳng. Mệnh đề Đúng Sai
(a) Thể tích của khối Rubik là 27 (đơn vị thể tích)
(b) Vectơ AC 3;0;2
(c) Phương trình mặt phẳng ABC có phương trình 3x 3y 2z 6 0 (d) Với D(a, ,
b c) thì a 2b 3c 5
Phần 3. Trả lời ngắn. Ở mỗi câu, chỉ điền đáp án
Câu 89: Một phần sân trường được định vị bởi các điểm , A B,C, D như hình vẽ
Bước đầu chúng được lấy “thăng bằng” để có cùng độ cao, biết ABCD là hình thang vuông ở Avà B với độ dài AB 25 , m AD 15 ,
m BC 18m . Do yêu cầu kĩ thuật, khi lát phẳng sân trường phải
thoát nước ở góc sân ở C nên người ta lấy độ cao ở các điểm B,C, D xuống thấp hơn so với độ cao ở Alà 10c , m a c ,
m 6cm tương ứng. Tính giá trị của a .
Câu 90: Một sân vận động được xây dựng theo mô hình là hình chóp cụt OAGD.BCFE có hai đáy song song
với nhau. Mặt sân OAGD là hình chữ nhật và được gắn hệ trục Oxyz như hình vẽ dưới (đơn vị trên
mỗi trục tọa độ là mét). Mặt sân OAGD có chiều dài OA 100m , chiều rộng OD 60m và tọa độ
điểm B 10;10;8 . Lập phương trình mặt phẳng OACB .
Câu 91: Trong không gian với hệ trục tọa độ Oxyz . Cho điểm M (1;2;3) . Mặt phẳng P đi qua M cắt
các tia Ox,Oy, Oz lần lượt tại các điểm , A B,C ,
A B,C 0 sao cho thể tích tự diện OABC nhỏ
nhất. Viết phương trình của mặt phẳng P. 17 TRƯỜNG THPT XUÂN ĐỈNH
2. Vị trí tương đối của hai mặt phẳng. Khoảng cách từ một điểm đến một mặt phẳng
Phần 1: Trắc nghiệm 4 phương án lựa chọn. Mỗi câu hỏi chỉ chọn một phương án
Câu 92: Trong không gian Oxyz , cho điểm A 2; 1;3 và mặt phẳng P : 3x 2y 4z 5 0 . Gọi Q là
mặt phẳng đi qua A và song song với mặt phẳng P . Mặt phẳng Q có phương trình là:
A. 3x 2y 4z 4 0 B. 3x 2y 4z 4 0 . C. 3x 2y 4z 5 0 . D. 3x 2 y 4z 8 0 .
Câu 93: Trong không gian Oxyz, mặt phẳng (P) : 2x y z 2 0 song song với mặt phẳng nào dưới đây? 1 1
A. x y z 1 0 . B. x y z 2 0 . C. 4x 2 y 2z 4 0 . D. 2x y z 2 0 . 2 2
Câu 94: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P có phương trình:
mx (m 1) y z 10 0 và mặt phẳng (Q) : 2x y 2z 3 0 . Với giá trị nào của dưới đây của m
thì P và Q vuông góc với nhau A. m 2 . B. m 2 . C. m 1. D. m 1 .
Câu 95: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P có phương trình: 3x 4y 2z 4 0 và điểm A1; 2
;3 . Tính khoảng cách d từ A đến P . 5 5 5 5 A. d . B. d . C. d . D. d . 9 29 29 3
Câu 96: Trong không gian Oxyz khoảng cách giữa hai mặt phẳng P : x 2y 3z 1 0 và
Q: x 2y 3z 6 0 là 7 8 5 A. . B. . C. 14 . D. . 14 14 14
Câu 97: Trong không gian Oxyz , điểm M thuộc trục Oy và cách đều hai mặt phẳng: P : x y z 1 0 và
Q: x y z 5 0 có tọa độ là A. M 0;3;0 . B. M 0;3;0 . C. M 0;2;0 . D. M 0;1;0 .
Câu 98: Trong không gian hệ toạ độ Oxyz , lập phương trình các mặt phẳng song song với mặt phẳng
: x y z 3 0 và cách một khoảng bằng 3 .
A. x y z 6 0; x y z 0 .
B. x y z 6 0 .
C. x y z 6 0 ; x y z 0 .
D. x y z 6 0 ; x y z 0 . Câu 99: Trong không gian Oxyz , cho hai mặt phẳng
P: A x B y C z D 0 , 1 1 1 1
Q : A x B y C z D 0 lần lượt có vectơ pháp tuyến n A ; B ;C và n A ; B ;C . 2 2 2 2 1 1 1 1 2 2 2 2
Mặt phẳng P vuông góc với mặt phẳng Q khi và chỉ khi A. n n . B. n k.n . C. n n . D. n k.n . 1 2 1 2 1 2 1 2 Câu 100: Trong không gian Oxyz , cho hai mặt phẳng
P: A x B y C z D 0 , 1 1 1 1
Q : A x B y C z D 0 lần lượt có vectơ pháp tuyến n A ; B ;C và n A ; B ;C . 2 2 2 2 1 1 1 1 2 2 2 2
Mặt phẳng P song song với mặt phẳng Q khi và chỉ khi n k.n A. n n . B. n k.n . C. 1 2 . D. n k.n . 1 2 1 2 D k.D 1 2 1 2
Câu 101: Trong không gian với hệ trục tọa độ Oxyz , cho (
A 1; 2;3) , B 3;4;4 . Tìm tất cả các giá trị của
tham số m sao cho khoảng cách từ điểm A đến mặt phẳng 2x y mz 1 0 bằng độ dài đoạn thẳng AB . 18 TRƯỜNG THPT XUÂN ĐỈNH A. m 2 . B. m 2 . C. m 3 . D. m 2 .
Phần 2: Trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai
Câu 102: Trong không gian Oxyz , cho điểm M 1;3; 2
và mặt phẳng : 2x y z 5 0 . Chọn Đúng
hoặc Sai trong mỗi ý sau:
a) Mặt phẳng có phương trình 2x y z 3 0 đi qua điểm M và song song mặt phẳng .
b) Mặt phẳng có phương trình x 3y z 2024 0 vuông góc với mặt phẳng .
c) Mặt phẳng P đi qua điểm M , song song trục Ox và vuông góc với mặt phẳng có phương
trình là y z 1 0 .
d) Có hai mặt phẳng song song mặt phẳng và cách điểm M một khoảng bằng 2 6 .
Câu 103: Trong không gian Oxyz , cho mặt phẳng P : 4 a x a 3 y z 1 0 và mặt phẳng
Q:3x 4y z 3 0.
a) Mặt phẳng P và mặt phẳng Q song song với nhau khi a 1.
b) Mặt phẳng P và mặt phẳng Q vuông góc với nhau khi a 2 .
c) Không có giá trị nào của a để hai mặt phẳng trên trùng nhau.
d) Mặt phẳng vuông góc với cả hai mặt phẳng trên có vectơ pháp tuyến là n 1; 1 ; 7 .
Câu 104: Trong hệ trục tọa độ Oxyz , cho hai mặt phẳng P : 2x 2y z 1 0 , Q :2 x 2y z 5 0 và các điểm A0;1; 1 , B 2;0; 1 .
Xét tính Đúng, Sai của các mệnh đề sau:
a) Hai mặt phẳng P và Q song song nhau. b) Khoảng cách d , A Q 4 . c) Khoảng cách d , P Q 6 .
d) Cho biết điểm C P và đường thẳng BC tạo với mặt phẳng P góc 0 30 . Khi đó ta có 4 3 khoảng cách BC . 3
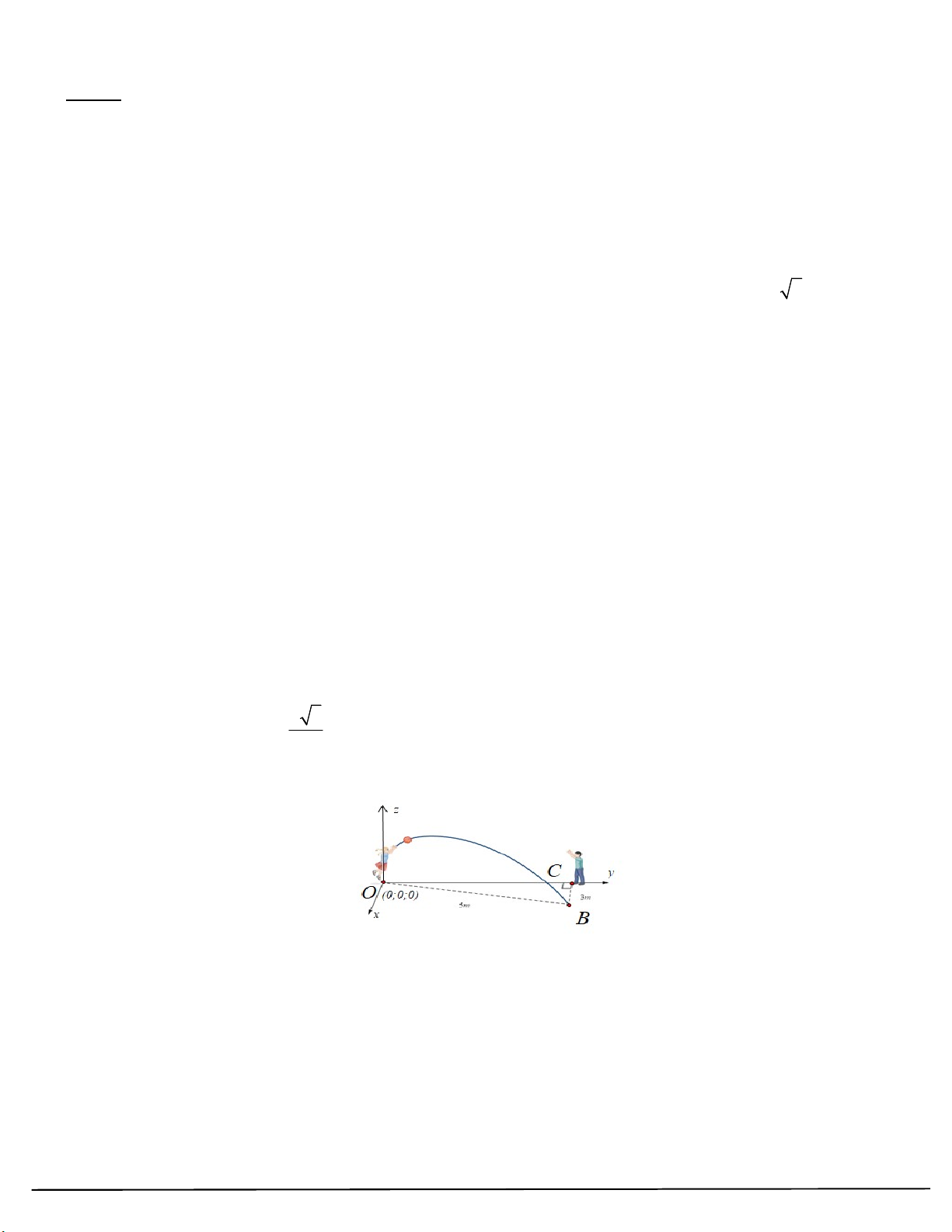
Câu 105: Hai đứa trẻ đang chơi với một quả bóng. Bé gái ném quả bóng cho bé trai. Quả bóng di chuyển trong
không khí, uốn cong 3m về bên phải và rơi cách bé gái 5m (xem hình sau).
Biết mặt phẳng chứa quỹ đạo của quả bóng vuông góc với mặt đất và phương trình tổng quát của nó
có dạng ax by c 0 .
Xét tính Đúng, Sai của các mệnh đề sau:
a) Tọa độ của điểm C 0;4;0 .
b) Tọa độ của điểm B 4;3;0 .
c) Phương trình mặt phẳng chứa quỹ đạo của quả bóng là 4x 3y z 0 .
b) Giá trị a b c 1.
Câu 106: Hình bên dưới minh họa hình ảnh hai mái nhà của một nhà kho trong không gian với hệ tọa độ Oxyz
(đơn vị trên mỗi trục tọa độ là mét). Các bức tường của nhà kho đều được xây vuông góc với mặt đất. 19 TRƯỜNG THPT XUÂN ĐỈNH
Biết rằng tọa độ của điểm P(a;b;c) .
Xét tính Đúng, Sai của các mệnh đề sau:
a) Phương trình mặt phẳng ABQ có dạng: 60x 5y 100z 300 0 .
b) Phương trình mặt phẳng CD
Q có dạng: 60x 5y 100z 900 0 .
c) Tọa độ của điểm P5; 0; 6 .
b) Giá trị a b c 11.
Phần 3. Trả lời ngắn. Ở mỗi câu, chỉ điền đáp án
Câu 107: Biết góc quan sát ngang của một camera là 116 . Trong không gian Oxyz , camera được đặt tại điểm
A2;1;5 và chiếu thẳng về phía mặt phẳng P : 2x y 2z 13 0 . Hỏi vùng quan sát được trên
mặt phẳng P của camera là hình tròn có đường kính bằng bao nhiêu? (làm tròn kết quả đến chữ số hàng chục)
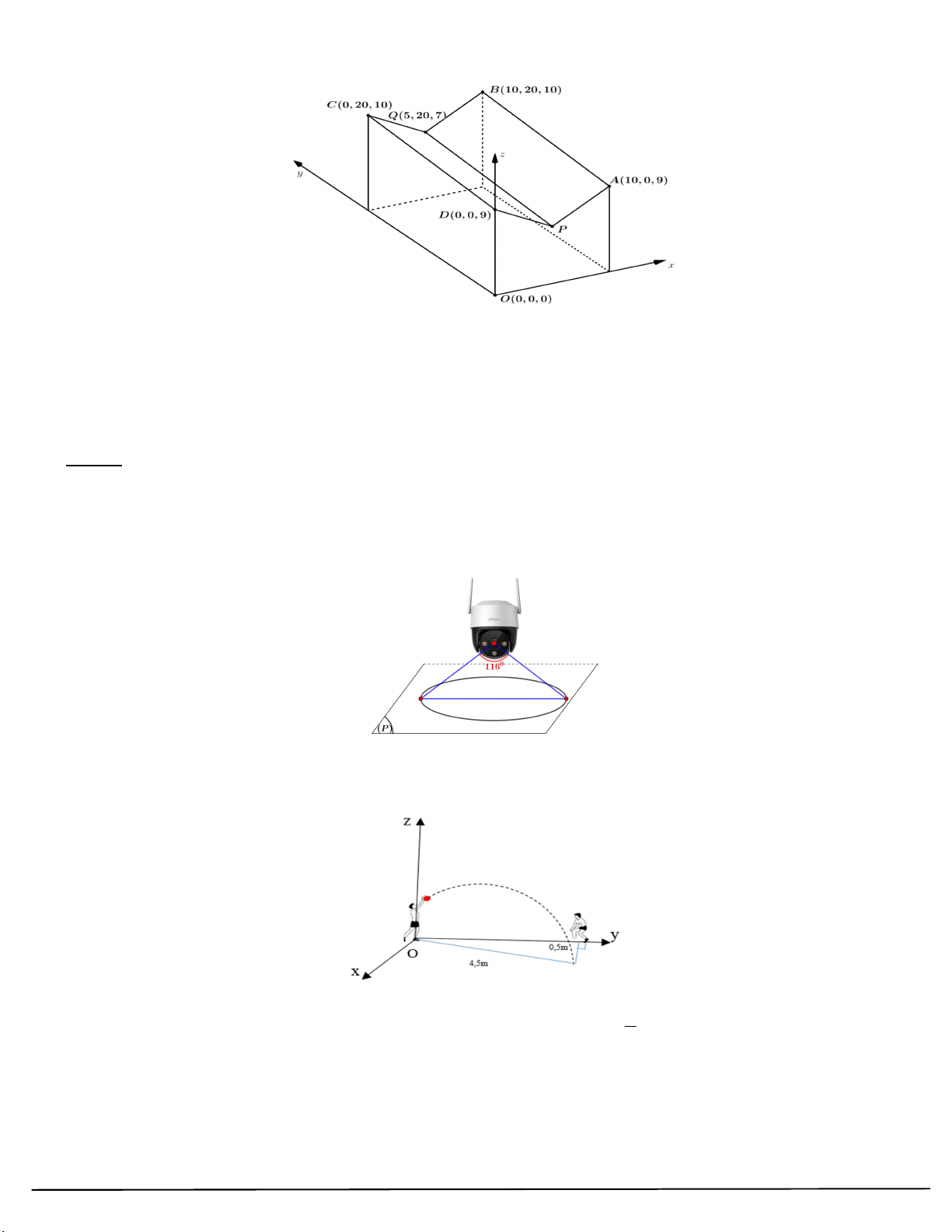
Câu 108: Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Nam và An đang tập chuyền bóng cho nhau, Nam
ném bóng cho An đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Nam và rơi xuống vị trí
cách An 0,5m và cách Nam 4,5m được mô tả bằng hình vẽ bên dưới
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng 1
: ax y cx d 0 và vuông góc với 2
mặt đất. Khi đó giá trị của a c d bằng (kết quả làm tròn đến hàng phần chục).
Câu 109: Trong không gian Oxyz cho các điểm A2;0;0, B0;4;0,C 0;0;6, D2;4;6 . Gọi P là mặt
phẳng song song với mặt phẳng ABC ,P cách đều D và mặt phẳng ABC . Phương trình của
mặt phẳng P là ax by 2z d 0 với a,b,d . Giá trị của d bằng bao nhiêu? 20




