Đề cương giữa kì 2 Toán 12 năm 2022 – 2023 trường chuyên Bảo Lộc – Lâm Đồng

Đề cương giữa kì 2 Toán 12 năm 2022 – 2023 trường chuyên Bảo Lộc – Lâm Đồng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

79 40 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

19 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
TRƢỜNG THPT CHUYÊN BẢO LỘC
TỔ TOÁN
ĐỀ CƢƠNG ÔN TẬP GIỮA HỌC KÌ II MÔN TOÁN KHỐI 12
NĂM HỌC 2022
-2023
PHẦN I – GIẢI TÍCH
A.LÍ THUYẾT
1.Nguyên hàm
- Định nghĩa nguyên hàm, bảng các nguyên hàm cơ bản
.
- Một số tính chất cơ bản của nguyên hàm, vận dụng tính chất của nguyên hàm tìm được nguyên hàm của một
hàm số.
-Công thức tính nguyên hàm bằng phương pháp đổi biến số hoặc phương pháp tính nguyên hàm từng phần. Vận
dụng phương pháp đổi biến số hoặc phương pháp tính nguyên hàm từng phần để tìm nguyên hàm của hàm số.
2.Tích phân
-Khái niệm về diện tích hình thang cong, định nghĩa tích phân của hàm số liên tục bằng công thức Niu- tơn Lai-
bơ – nit. Vận dụng định nghĩa để tính tích phân của hàm số.
- Một số tính chất cơ bản của tích phân. Vận dụng tính chất của tích phân tính được tích phân của một hàm số.
-Vận dụng phương pháp đổi biến số và dụng phương pháp tính tích phân từng phần để tính tích phân của hàm
số
- Ứng dụng của tích phân trong hình học
B. – BÀI TẬP
I – BÀI TẬP TỰ LUẬN
Bài 1: Tìm nguyên hàm của các hàm số sau đây:
a)
1
53
3
( ) 4 2f x x x x
b)
( ) 3 2f x x x
c)
2
1
()
1
x
fx
e
d)

3
2
26
()
23
x
fx
xx
e)
( ) sin3 cos5f x x x
f)

2
( ) (1 2sin )f x x
Bài 2: Cho hàm số
()fx
. Tìm nguyên hàm
()Fx
của hàm số
thỏa điều kiện.
a)
2
( ) s in ; ( ) cos ; ( ) 0g x x x x f x x x F
b)
2
( ) ln ; ( ) ln ; (2) 2g x x x x f x x F
Bài 3. Tìm các họ nguyên hàm sau đây:
a)
3
2
1
x
dx
x
b)
2
.
x
x e dx
c)
3
ln x
dx
x
Bài 4: Tìm các họ nguyên hàm sau.
a)
2
( 2)
x
x e dx
b)
(2 1)cosx xdx
c)
2
(3 1)lnx xdx
d)

(4 1)ln( 1)x x dx
Bài 5: Tính các tích phân sau
a)
1
3
0
32x dx
b)
4
2
)1(xx
dx
c)
2
1
1x dx
d)
4
4
0
cos x dx
e)

0
21
1
x
e dx
f)
2
0
2
dxxx
g)
2
0
2cos1 dxx
(đs: a)
5
.
4
b)
3
ln .
2
c)
42
2 3 .
3
d)
31
.
32 4
e)
3
.
22
ee

f) 1. g)
4 2.
)
Bài 6: Tính các tích phân sau
a)
1
9
34
0
5x x dx
b)
1
15 8
0
13x x dx
c)
2
0
2
1
1
xx
x e dx
d)
e
dx
x
xx
1
lnln31
e)
2
0
3
sin
xdx
f)
4
0
tan
xdx
g)
2
1
22
4 dxxx
h)
1
0
24
1xx
xdx
(đs: a)
10 10
54
.
40
b)
29
.
270
c)
11
.
22e
d)
116
.
135
e)
2
.
3
f)
2
ln .
2
g)
23
.
34
)
Bài 7: Tính các tích phân sau
a)
4
0
2sin
xdxx
b)
dxxe
x
2ln
0
c)
dxxx
e
1
ln
d)
3
2
ln(ln )
e
e
x
dx
x
e)
2
0
3
5sin
xdxe
x
(a)
1
.
4
b)
2ln2 1.
c)
2
1
.
4
e
d)
27
ln 1.
4
e)
3
2
5 3.
.
34
e
)
Bài 8: Tính diện tích hình phẳng giới hạn bởi các đường sau
a)
2
5 6, 0, 2, 4y x x y x x
b)
1
, , 0,y x y y x e
x
c)
2
4 5, 2 4, 4 11y x x y x y x
d)
sin 2cos , 3, 0,y x x y x x
e)
22
11
,3
42
y x y x
f)
2
4 3 , 3y x x y x
g)
2
.ln ; 0; 1; .y x x y x x e
h)
2
5 0, 3 0y x x y
Bài 9: Tính diện tích hình phẳng giới hạn bởi các đường
3
( ): 3 2, 1C y x x x
và tiếp tuyến với (C) tại
điểm có hoành độ x = –2.
Bài 10: Tính thể tích vật thể tròn xoay sinh ra bởi hình (H) giới hạn bởi các đường sau quay quanh trục Ox:
a)
2
2 ; 0; 0; 1y x x y x x
b)
ln , 0, 2y x y x
c)
2
3 ; 0; 0; 1y x x y x x
Bài 11. Tính thể tích vật thể tròn xoay sinh ra bởi hình (H) giới hạn bởi các đường sau quay quanh trục Oy:
a)
2
,4y x y
b)
2
, 1, 4x y y
y
c)
ln ; 0; 0; 1y x x y y
II – BÀI TẬP TRẮC NGHIỆM
Câu 1: Trong các khẳng định dưới đây, có bao nhiêu khẳng định đúng?
(a).Mọi hàm số liên tục trên
[ ; ]ab
đều có đạo hàm trên
[ ; ]ab
.
(b). Mọi hàm số liên tục trên
[ ; ]ab
đều có nguyên hàm trên
[ ; ]ab
.
(c).Mọi hàm số có đạo hàm trên
[ ; ]ab
đều có nguyên hàm trên
[ ; ]ab
.
(d). Mọi hàm số liên tục trên
[ ; ]ab
đều có giá trị lớn nhất và giá trị nhỏ nhất trên
[ ; ]ab
.
A.2 B.3 C.1 D.4
Câu 2: Cho hàm số
( ), ( )f x g x
liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai?
A.
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
. B.
( ). ( ) ( ) . ( )f x g x dx f x dx g x dx
.
C.
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
D.
( ) ( ) 0;kf x dx k f x dx k k

Câu 3: Khẳng định nào sau đây là khẳng định sai?
A.
( ) ( ) kf x dx k f x dx k

B.
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
với
( ); ( )f x g x
liên tục trên
.
C.
1
1
1
x dx x

với
1

.
D.
'
( ) ( )f x dx f x
Câu 4: Cho hàm số
()fx
xác định trên
K
. Khẳng định nào sau đây là sai?
A.Nếu hàm số
()Fx
là một nguyên hàm của
()fx
trên
K
thì với mỗi hằng số
C
, hàm số
( ) ( )G x F x C
cũng là một nguyên hàm của
()fx
trên
K
.
B.Nếu
()fx
liên tục trên
K
thì nó có nguyên hàm trên
K
.
C.Hàm số
()Fx
được gọi là một nguyên hàn của
()fx
trên
K
nếu
'( ) ( )F x f x
với mọi
xK
.
D.Nếu hàm số
()Fx
là một nguyên hàm của
()fx
trên
K
thì hàm số
()Fx
là một nguyên hàm của
()fx
trên
K
.
Câu 5: Hàm số
()Fx
là một nguyên hàm của hàm số
()fx
trên khoảng K nếu:
A.
'( ) ( ),F x f x x K
B.
'( ) ( ),f x F x x K
C.
'( ) ( ),F x f x x K
D.
'( ) ( ),f x F x x K
Câu6: Tìm nguyên hàm của hàm số
2
2
2
()f x x
x

.
A.
3
1
()
3
x
f x dx C
x
B.
3
2
()
3
x
f x dx C
x
C.
3
1
()
3
x
f x dx C
x
D.
3
2
()
3
x
f x dx C
x
Câu 7: Tìm nguyên hàm của hàm số
()fx
thỏa mãn điều kiện
( ) 2 3cos , 3
2
f x x x F



.
A.
2
2
( ) 3sin 6
4
F x x x
B.
2
2
( ) 3sin
4
F x x x
C.
2
2
( ) 3sin
4
F x x x
D.
2
2
( ) 3sin 6
4
F x x x
Câu 8: Tính nguyên hàm sau:
9
( 2)x x dx
.
A.
11
( 2)
22
x
C
B.
11 10
( 2) 2( 2)
11 10
xx
C


C.
10
2( 2)
10
x
C
D.
11 10
( 2) 2( 2)
11 10
xx
C


Câu 9: Tìm nguyên hàm
2
1
4
I dx
x
A.
12
ln
22
x
C
x
B.
12
ln
22
x
C
x
C.
12
ln
42
x
C
x
D.
12
ln
42
x
C
x
Câu 10: Tìm
( 1) 1
dx
I
x x x x
.
A.
21x x C
B.
2 2 1x x C
C.
2 2 1x x C
D.
1x x C
Câu 11: Họ nguyên hàm của hàm số
2
( ) cos 2f x x
là:
A.
1 sin4
28
x
C
B.
sin4
22
xx
C
C.
1 sin4
22
x
C
D.
sin4
28
xx
C
Câu 12: Tìm
sin4 .cosI x xdx
A.
11
cos5 cos3
10 6
x x C
B.
11
cos5 cos3
10 6
x x C
C.
1
cos5 cos3
6
x x C
D.
1
cos5 cos3
10
x x C
Câu 13:
()Fx
là một nguyên hàm của hàm số
2
.
x
y x e
. Hàm số nào sau đây không phải là
()Fx
?
A.
2
( ) 2
2
x
e
Fx
B.
2
1
( ) 5
2
x
F x e
C.
2
1
()
2
x
F x e C
D.
2
1
( ) 2
2
x
F x e
Câu 14: Tìm
tan
2
cos
x
e
dx
x
?
A.
tanx
x e C
B.
tan
tan
x
x e C
C.
tanx
eC
D.
tan
1
2
x
eC
Câu 15: Nguyên hàm của
1 ln
()
ln
x
fx
xx
là:
A.
1 ln
ln ln
ln
x
dx x C
xx

B.
2
1 ln
ln ln
ln
x
dx x x C
xx

C.
1 ln
ln ln
ln
x
dx x x C
xx
D.
1 ln
ln .ln
ln
x
dx x x C
xx

Câu 16: Tìm nguyên hàm của
(2 1)
x
I x e dx

A.
(2 1)
x
I x e C
B.
(2 1)
x
I x e C
C.
(2 3)
x
I x e C
D.
(2 3)
x
I x e C
Câu 17: Kết quả nguyên hàm
2
sin5I x xdx
là:
A.
2
1 2 2
cos5 sin5 cos5
5 25 125
x x x x x C
B.
2
1 2 2
cos5 sin5 cos5
5 25 125
x x x x x C
C.
2
1 2 2
cos5 sin5 cos5
5 25 125
x x x x x C
D.
2
1 2 2
cos5 sin5 cos5
5 25 125
x x x x x C
Câu 18. Khẳng định nào sau đây sai?
A.
(( ) ( d) ( )d )d
aa
b b b
a
x f x x g x xf x g x 
B.
d ( )d ( d( ))
b
ca
bc
a
x f x x f x xfx 
C.
(( d)d)
ba
ba
f xx f xx

D.
d ( )dt()
b
a
b
a
f x f tx

Câu 19: Cho hai số thực
,ab
tùy ý,
()Fx
là một nguyên hàm của hàm số
()fx
trên tập
. Mệnh đề nào dưới
đây là đúng?
A.
( )d ( ) ( )
b
a
f x x f b f a
B.
( )d ( ) ( )
b
a
f x x F b F a
C.
( )d ( ) ( )
b
a
f x x F b F a
D.
( )d ( ) ( )
b
a
f x x F b F a
Câu 20: Cho hàm số
()y f x
liên tục trên đoạn
[ ; ]ab
. Mệnh đề nào dưới đây sai?
A.
( )d ( )dt
bb
aa
f x x f t

B.
( )d ( )
ba
a b
f x x f x dx

C.
( ),
a
b
akdx k b k
D.
( ) ( ) ( ) , ( ; )
b c b
aca
f x dx f x dx f x dx c a b
Câu 21: Cho
1
2
( ) 3f x dx
. Tính tích phân
1
2
2 ( ) 1I f x dx

A.
9
B.
3
C. 3 D. 5
Câu 22: Cho giá trị tích phân
11
4 3 2
12
12
2 , 3I x x dx a I x x dx b


. Tính giá trị
a
b
là:
A.
4
65
P
B.
12
65
P
C.
12
65
P
D.
4
65
P
Câu 23: Giả sử
2
2
0
1
ln5 ln3; ,
43
x
dx a b a b
xx

. Tính
P ab
.
A.
8P
B.
6P 
C.
4P 
D.
5P 
Câu 24: Tích phân
3
2
4
sin
dx
I
x
bằng?
A.
cot cot
34

B.
cot cot
34

C.
cot cot
34


D.
cot cot
34


Câu 25: Cho
2
2
0
()
x
t
F x e dt
. Tính
'(2)F
.
A.
4
'(2) 4Fe
B.
16
'(2) 8Fe
C.
16
'(2) 4Fe
D.
4
'(2)Fe
Câu 26: Cho hàm số
()y f x
liên tục trên
[ ; ]ab
. Giả sử hàm số
()u u x
có đạo hàm liên tục trên
[ ; ]ab
và
( ) [ , ], [ , ],u x x a b

hơn nữa
()fu
liên tục trên đoạn
[ , ]

. Mệnh đề nào sau đây là đúng?
A.
[ ( )] ( )d ( )d
bb
aa
f u x u x x f u u

. B.
()
()
[ ( )] ( )d ( )d
n b b
u a a
f u x u x x f u u

.
C.
()
()
[ ( )] ( )d ( )d
b u b
a u a
f u x u x x f u u

. D.
[ ( )] ( )d ( )d
bb
aa
f u x u x x f x u

Câu 27: Tích phân
2
2
0
3
x
dx
x
bằng:
A.
17
log
23
B.
7
ln
3
C.
17
ln
23
D.
13
ln
27
Câu 28: Biết
4
0
2 1 5
ln2 ln , ,
3
2 3 2 1 3
x
dx a b c a b c
xx
. Tính
2T a b c
.
A.
4T
B.
2T
C.
1T
D.
3T
Câu 29: Tính tích phân
3
3
0
sin
cos
x
I dx
x
.
A.
5
2
I
B.
3
2
I
C.
9
3 20
I

D.
9
4
I
Câu 30: Cho
2
1
1
0
.
x
I x e dx
. Biết rằng
2
ae b
I
. Khi đó
ab
bằng:
A.1 B.0 C.2 D.4
Câu 31: Biết
1
ln 3
ln , ,
ln 2 2
e
x
dx a b a b
xx
. Mệnh đề nào sau đây đúng?
A.
1ab
B.
21ab
C.
22
4ab
D.
20ab
Câu 32: Tích phân
1
2
0
1
1
I dx
x
có giá trị là:
A.
2
I
B.
3
I
C.
4
I
D.
6
I
Câu 33: Tính tích phân
2
0
cos2I x xdx
bằng cách đặt
2
cos2
ux
dv xdx
. Mệnh đề nào dưới đây đúng?
A.
2
0
0
1
sin2 sin2
2
I x x x xdx

B.
2
0
0
1
sin2 2 sin2
2
I x x x xdx

C.
2
0
0
1
sin2 2 sin2
2
I x x x xdx

D.
2
0
0
1
sin2 sin 2
2
I x x x xdx

Câu 34: Cho
2
4
2
0
tan ln
32
I x xdx b
a

, khi đó tổng
ab
bằng
A. 4 B. 8 C. 10 D. 6
Câu 35: Cho
1
22
0
x
I xe dx ae b
(
,ab
là các số hữu tỷ). Khi đó tổng
ab
là
A. 0 B.
1
4
C.1 D.
1
2
Câu 36: Biết
3
2
1
3 ln ln ln
( 1) 4
x a b c
dx
x
với
,,abc
là các số nguyên dương. Giá trị của biểu thức
P a b c
bằng?
A. 46 B. 35 C. 11 D. 48
Câu 37: Biết
1
2
0
4 4 1 , ,
aa
S x x dx a b
bb
là phân số tối giản. Giá trị
4ab
bằng:
A.1 B.
3
C.35 D.3
Câu 38. Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
( ),y f x
trục Ox và các
đường thẳng
, ( )x a x b a b
.
A.
()
b
a
f x dx
B.
2
()
b
a
f x dx
C. ( )
b
a
f x dx
D. ( )
b
a
f x dx
Câu 39: Cho hàm số
()y f x
liên tục trên
và có đồ thị (C) là đường cong như
hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường
thẳng
0, 2xx
(phần tô đậm) là:
A.
2
0
()f x dx
B.
12
01
( ) ( )f x dx f x dx

C.
12
01
( ) ( )f x dx f x dx

D.
2
0
()f x dx
Câu 40: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số
cos2yx
, trục hoành và hai đường thẳng
0,
2
xx

là:
A.2 B. 1 C. 3 D. 4
Câu 41: Cho hàm số
( ), ( )y f x y g x
liên tục trên [a; b]. Gọi
()H
là hình giới hạn bởi hai đồ thị
( ),y f x
()y g x
và các đường thẳng
,x a x b
. Diện tích hình
()H
được tính theo công thức:
A.
| ( )| d | ( ) | d
bb
H
aa
S f x x g x x

B. | ( ) ( )| d
b
H
a
S f x g x x
C.
( ) ( )
b
H
a
S f x g x dx
D.
( ) ( )
b
H
a
S f x g x dx
Câu 42: Hình phẳng (H) giới hạn bởi đồ thị hai hàm số
2
2, 2y x x y x
và hai đường thẳng
2; 3xx
. Diện tích của (H) bằng:
A.
87
5
B.
87
4
C.
87
3
D.
13
Câu 43: Diện tích hình phẳng giới hạn bởi
2
( ): 3P y x
, tiếp tuyến của (P) tại điểm có hoành độ
2x
và
trục tung bằng
A.
8
3
B.
4
3
C. 2 D.
7
3
Câu 44: Trong không gian Oxyz , cho vật thể được giới hạn bởi
hai mặt phẳng
( ),( )PQ
vuông góc với trục Ox lần lượt tại
, ( )x a x b a b
. Một mặt phẳng tùy ý vuông góc với Ox tại
điểm có hoành độ
,( )x a x b
cắt vật thể theo thiết diện có diện
tích là
()Sx
với
()y S x
là hàm số liên tục trên [a ; b]. Thể tích
V
của thể tích đó được tính theo công thức:
A.
2
( )d .
b
a
V S x x
B.
2
( )d
b
a
V S x x
. C.
( )d
b
a
V S x x
.
D. ( )d
b
a
V S x x
Câu 45. Cho hàm số
()y f x
liên tục trên đoạn [a; b]. Gọi
D
là hình phẳng giới hạn bởi đồ thị hàm số
()y f x
, trục hoành và hai đường thẳng
, ( )x a x b a b
. Thể tích khối tròn xoay tạo thành khi quay
D
quanh trục hoành được tính theo công thức.
2
A. ( )d .
b
a
V f x x
B.
2
2 ( )d .
b
a
V f x x
C.
22
( )d .
b
a
V f x x
D.
2
( )d
b
a
V f x x
Câu 46: Cho hình phẳng
()H
giới hạn bởi các đường
2
; 0; 2y x y x
. Tính thể tích
V
của khối tròn xoay
thu được khi quay
H
quanh trục
Ox
.
A.
8
3
V
B.
32
5
V
C.
8
3
V
D.
32
5
V
Câu 47: Thể tích khối tròn xoay thu được khi quay quanh trục
Ox
hình phẳng giới hạn bởi đồ thị hàm số
x
y xe
, trục hoành và đường thẳng
1x
là
A.
2
1
4
e
B.
2
1
1
4
e
C.
4
1
4
e
D.
4
1
1
4
e
PHẦN II - HÌNH HỌC
A-LÍ THUYẾT
1. Hệ tọa độ trong không gian
- Khái niệm tọa độ của vec tơ và tọa độ của điểm thông qua định nghĩa, biểu thức tọa độ của các phép toán
vectơ.
- Tính cùng phương của hai vec tơ, chứng minh 3 điểm thẳng hàng, xác định tọa độ của điểm thỏa mãn điều
kiện nào đó,…
2. Phƣơng trình mặt cầu
- Xác định được tọa độ tâm và tìm được độ dài bán kính mặt cầu có phương trình cho trước.
- Tìm được phương trình mặt cầu nếu biết tâm và bán kính mặt cầu.
3. Phƣơng trình mặt phẳng
- Khái niệm véc tơ pháp tuyến của mặt phẳng, xác định được vec tơ pháp tuyến của mặt phẳng khi biết phương
trình của mặt phẳng đó ; biết dạng phương trình mặt phẳng, nhận biết được điểm thuộc mặt phẳng.
- Vị trí tương đối của hai mặt phẳng
- Bài toán liên quan đến góc, khoảng cách.
B-BÀI TẬP
I-BÀI TẬP TỰ LUẬN
Bài 1: Cho:
2 5 3 0 2 1 1 7 2a b c; ; ; ; ; ;,,

. Tìm tọa độ của vectơ
32
43
u a b c
(đs:
4 67 29
;;
3 6 12



)
Bài 2: Tính góc giữa hai vec tơ
2 5 4 6 0 3ab; ; , ; ;
. (đs:
90
o
)
Bài 3: Tìm m để 3 vectơ
a b c,,

đồng phẳng với
1 2 1 2 1 2 2 a m m m b m m m c; ; , ; ; , ; ;

Bài 4: Cho ba điểm A, B, C.
Chứng tỏ ba điểm A, B, C tạo thành một tam giác.
Tìm toạ độ trọng tâm G của ABC.
Xác định điểm D sao cho ABCD là hình bình hành.
Tính số đo các góc trong ABC.
Tính diện tích ABC. Từ đó suy ra độ dài đường cao AH của ABC.
a)
3 1 2 1 2 1 11 3A B C( ; ; ), ( ; ; ), ( ; ; )
b)
4 1 4 0 7 4 31 2A B C( ; ; ), ( ; ; ), ( ; ; )
(đs: a)
22 50', B=119 50', C=37 20'
o o o
A
,
149 149
, AH= .
23
S
)
Bài 5: Cho bốn điểm A, B, C, D.
Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
Tìm tọa độ trọng tâm G của tứ diện ABCD.
Tính thể tích của khối tứ diện ABCD.
Tính diện tích tam giác BCD, từ đó suy ra độ dài đường cao của tứ diện vẽ từ A.
a)
2 4 1 1 0 1 1 4 2 1 2 1A B C D( ; ; ), ( ; ; ), ( ; ; ), ( ; ; )
b)
3 2 4 2 5 2 1 2 2 4 2 3A B C D( ; ; ), ( ; ; ), ( ; ; ), ( ; ; )
(đs: a)
15
;2;
33
G



7
.
3
V
32
BCD
S
72
.
6
AH
)
Bài 6: Cho hình hộp ABCD.A'B'C'D'.
Tìm toạ độ các đỉnh còn lại.
Tính thể tích khối hộp.
a)
0 2 1 1 11 0 0 0 11 0A B D A( ; ; ), ( ; ; ), ( ; ; ;) , '( ; ; )
b)
0 2 2 0 1 2 111 1 2 1A B C C( ; ; ), ( ; ; ), ( ; ; ), '( ; ; )
Bài7: Tìm tâm và bán kính của các mặt cầu sau:
a)
2 2 2
3 3 3 6 3 15 2 0x y z x y z
b)
2 2 2
6 2 2 10 0x y z x y z
Bài 8: Viết phương trình mặt cầu (S) thỏa mãn điều kiện
a)Có tâm
(1;2; 3)I
và bán kính
2R
b) Có tâm
(2;2; 3)I
và đi qua điểm
( 1;2;5)A
c) Có đường kính AB với
( 2;1;5), (4;7;3)AB
d) Đi qua 4 điểm
2 3 1 4 1 2 6 3 7 5 4 8A B C D( ; ; ), ( ; ; ), ( ; ; ), ( ; ; )
e) Có tâm I và tiếp xúc với mặt phẳng (P) biết
1;2; 1 ;( ): 2 2 8 0I P x y z
Bài 9: Viết phương trình mặt phẳng (P) đi qua
M 4; 1; 2
và có vectơ pháp tuyến
n 0;1;3
.
(đs:
3 7 0yz
)
Bài 10: Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với
2 3 4 4 1 0AB( ; ; ), ( ; ; )
(đs:
2 2 3 0x y z
)
Bài 11: Viết phương trình mặt phẳng đi qua điểm M(1;-2;3) và song song với mặt phẳng
2 3 2 1 0
x y z:
(đs: D=10)
Bài 12:Viết phương trình mặt phẳng đi qua ba điểm
1 2 3 2 4 1 5 1 4A B C; ; , ( ; ; ), ( ; ; )
(đs:
50yz
)
Bài 13: Viết phương trình mặt phẳng () đi qua điểm A và vuông góc với đường thẳng đi qua hai điểm B, C
cho trước, với
0 0 0 2 1 3 4 2 1A B C( ; ; ), ( ; ; ), ( ; ; )
(đs:
6 2 0.x y z
)
Bài 14: Viết phương trình mặt phẳng () đi qua hai điểm A, B và vuông góc với mặt phẳng () cho trước, với:
2 1 3 4 2 1
2 3 2 5 0
AB
x y z
( ; ; ), ( ; ; )
:
(đs:
2 2 5 9 0x y z
)
Bài 15:Viết phương trình mặt phẳng () đi qua điểm M và vuông góc với hai mặt phẳng (), () cho trước, với:
1 2 5 2 3 1 0 2 3 1 0M x y z x y z( ; ; ), : , :

(đs:
20x y z
)
Bài 16:Xét vị trí tương đối của các cặp mặt phẳng sau:
3 2 6 23 0
3 2 6 33 0
x y z
x y z
Bài 17: Tính khoảng cách giữa hai mặt phẳng
2 4 5 0
3 5 1 0
x y z
x y z
Bài 18: Tính góc giữa hai mặt phẳng
2 2 1 0
2 2 5 0
x y z
x y z
(đs:
4
cos
9
)
II – BÀI TẬP TRẮC NGHIỆM
Câu 1: Trong không gian với hê tọa độ
Oxyz
, cho hai điểm
1 2 0A( ; ; )
và
3 0 4B( ; ; )
. Tọa độ của vectơ
AB
là:
A.
424( ; ; )
B.
424( ; ; )
C.
1 1 2( ; ; )
D.
2 2 4( ; ; )
Câu 2: Trong không gian
Oxyz
cho ba điểm
111 5 1 2 3 2 4A B C( ; ; ), ( ; ; ), ( ; ; )
. Tìm tọa độ điểm M thỏa
20 MA MB MC
.
A.
39
4
22




M ;;
B.
39
4
22




M ;;
C.
39
4
22



M ;;
D.
39
4
22



M ;;
Câu 3: Trong không gian
Oxyz
, cho điểm
1 2 3M( ; ; )
. Hình chiếu của
M
lên trục
Oy
là điểm
A.
1 0 0R( ; ; )
B.
0 0 3S( ; ; )
C.
1 0 3P( ; ; )
D.
0 2 0Q( ; ; )
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, cho
3 4 0 0 2 4 4 2 1A B C( ; ; ), ( ; ; ), ( ; ; )
. Tọa độ điểm
D
trên trục
Ox
sao cho
AD BC
.
A.
12
0 0 0 6 0 0DD( ; ; ), ( ; ; )
B.
12
2 0 0 8 0 0DD( ; ; ), ( ; ; )
C.
12
3 0 0 3 0 0DD( ; ; ), ( ; ; )
D.
12
0 0 0 6 0 0DD( ; ; ), ( ; ; )
Câu 5: Trong không gian
Oxyz
, cho các vectơ
5 3 1 1 2 1 3 1 a b c m( ; ; ), ( ; ; ), ( ; ; )
. Giá trị của
m
sao cho


a b c,
là:
A.
2m
B.
2m
C.
1m
D.
1m
Câu 6: Trong không gian với hệ trục tọa độ
Oxyz
, cho hình bình hành
ABCD
. Biết
2 1 3 0 2 5AB( ; ; ), ( ; ; ),
11 3C( ; ; )
. Diện tích hình bình hành
ABCD
là:
A.
2 87
B.
349
2
C.
349
D.
87
Câu 7: Trong không gian với hệ tọa độ
Oxyz
, măt cầu
2 2 2
( ):( 2) ( 1) 4S x y z
có tâm I và bán kính
R
lần lượt là:
A.
( 2;1;0), 4IR
B.
(2; 1;0), 4IR
C.
(2; 1;0), 2IR
D.
( 2;1;0), 2IR
Câu 8: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu (S) có phương trình
2 2 2
2 4 6 5 0x y z x y z
. Diện tích mặt cầu (S) là?
A.
36
B.
36
C.
12
D.
9
Câu 9: Trong không gian với hệ tọa độ
Oxyz
, trong các phương trình sau, phương trình nào không phải là
phương trình của một mặt cầu?
A.
2 2 2
2 2 2 4 6 8 4 0x y z x y z
B.
2 2 2
2 2 6 7 0x y z x y z
C.
2 2 2
2 2 2 2 0x y z x y z
D.
2 2 2
2 2 2 2 0x y z x y
Câu 10: Trong hệ tọa độ
Oxyz
,phương trình nào sau đây là phương trình mặt cầu tâm
(1;2;3)I
bán kính
1?r
A.
2 2 2
( 1) ( 2) ( 3) 1x y z
. B.
2 2 2
( 1) ( 2) ( 3) 1x y z
.
C.
2 2 3
( 1) ( 2) ( 3) 1x y z
. D.
2 2 2
2 4 6 13 0x y z x y z
.
Câu 11: Trong không gian với hệ trục tọa độ Oxyz, cho hai điềm
(1; 2;3)A
và
(5;4;7)B
. Phương trình mặt cầu
nhận AB làm đường kính là.
A.
2 2 2
( 3) ( 1) ( 5) 17x y z
. B.
2 2 2
( 6) ( 2) ( 10) 17x y z
.
C.
2 2 2
( 1) ( 2) ( 3) 17x y z
D.
2 2 2
( 5) ( 4) ( 7) 17x y z
.
Câu 12: Trong không gian với hệ trục tọa độ
Oxyz
, cho bốn điểm
(0;0;1), (0;1;0), (1;0;0), (1;1;1)A B C D
. Bán
kính mặt cầu đi qua bốn điểm
, , ,A B C D
là:
A.
1
2
B.
3
4
C.
3
2
D.
3
Câu 13: Trong không gian tọa độ
Oxyz
, cho điềm
(1;1; 2)M
và mặt phẳng
( ): 2 3.x y z
Viết phương
trình mặt cầu (
S
) có tâm
M
tiếp xúc với mặt phằng
()
.
A.
2 2 2
35
( ): 2 2 4 0
6
S x y z x y z
. B.
2 2 2
14
( ): 2 2 4 0
3
S x y z x y z
C.
2 2 2
35
( ): 2 2 4 0
6
S x y z x y z
D.
2 2 2
16
( ): 2 2 4 0
3
S x y z x y z
Câu 14: Mặt cầu (S) có tâm
( 1;2; 5)I 
cắt
( ):2 2 10 0P x y z
theo thiết diện là hình tròn có diện tích
3
có phương trình (S) là:
A.
2 2 2
( 1) ( 2) ( 5) 16x y z
B.
2 2 2
2 4 10 18 0x y z x y z
C.
2 2 2
( 1) ( 2) ( 5) 25x y z
D.
2 2 2
2 4 10 12 0x y z x y z
Câu 15: Chọn khẳng định sai:
A. Nếu
n
là một vectơ pháp tuyến của mặt phẳng (P) thì
.kn
cũng là một vectơ pháp tuyến của mặt phẳng (P).
B. Một mặt phẳng hoàn toàn được xác định nếu biết một điểm nó đi qua và một vectơ pháp tuyến của nó.
C. Mọi mặt phẳng trong không gian
Oxyz
đều có phương trình dạng:
2 2 2
00Ax By Cz D A B C
D. Trong không gian Oxyz mỗi phương trình dạng:
2 2 2
00Ax By Cz D A B C
đều là phương trình
của một mặt phằng nào đó.
Câu 16: Trong không gian với hệ toạ độ Oxyz, cho
( ;0;0), (0; ;0), (0;0; ),( 0).A a B b C c abc
Khi đó phưong
trình mặt phẳng
()ABC
là:
A.
1
x y z
a b c
. B.
1
x y z
bac
. C.
1
x y z
a c b
D.
1
x y z
c b a
Câu 17: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ):3 2 1 0P x y z
. Mặt phẳng
()P
có
vectơ pháp tuyến là:
A.
(2;3; 1)n 
B.
(3;2; 1)n 
C.
( 1;3;2)n 
D.
(3; 1;2)n 
Câu 18: Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng
( ): 2 2 10 0P x y z
và
( ): 2 2 3 0Q x y z
bằng:
A.
4
3
B.
8
3
C.
7
3
D. 3
Câu 19: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
()P
có phương trình
3 1 0x y z
. Trong
các điểm sau đây, điểm nào thuộc
()P
.
A.
(1; 2; 4)A 
B.
(1;2; 4)C
C.
( 1; 2; 4)D
D.
(1; 2;4)B
Câu 20: Trong không gian với hệ tọa độ
Oxyz
, phương trình mặt phẳng
đi qua điểm
(0; 1;4)M
, nhận
(3;2; 1)n 
là vectơ pháp tuyến là:
A.
3 3 0x y z
B.
2 3 1 0x y z
C.
2 3 6 0x y z
D.
3 2 6 0x y z
Câu 21: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(1; 2;4), (2;1;2)AB
. Viết phương trình mặt phẳng
(P) vuông góc với đường thẳng AB tại điểm
A
.
A.
( ): 3 2 1 0P x y z
B.
( ): 3 2 1 0P x y z
C.
( ): 3 2 13 0P x y z
D.
( ): 3 2 13 0P x y z
Câu 22: Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng đi qua ba điểm
(1;1;4), (2;7;9),AB
(0;9;13)C
.
A.
7 2 9 0x y z
B.
2 2 0x y z
C.
2 1 0x y z
D.
40x y z
Câu 23: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(3; 1; 2)M 
và mặt phẳng
( ):3 2 4 0P x y z
.
Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với (P)?
A.
( ):3 2 14 0Q x y z
B.
( ):3 2 6 0Q x y z
C.
( ):3 2 6 0Q x y z
D.
( ):3 2 6 0Q x y z
Câu 24: Trong không gian với hệ tọa độ
Oxyz
, mặt phẳng đi qua hai điểm
(2; 1;4), (3;2; 1)AB
và vuông góc
với mặt phẳng
: 2 3 0x y z
có phương trình là:
A.
11 7 2 7 0x y z
B.
11 7 2 21 0x y z
C.
11 7 2 7 0x y z
D.
11 7 2 21 0x y z
Câu 25: Trong không gian với hệ trục toa độ Oxyz, cho hai mặt phẳng
( ):3 ( 1) 4 2 0x m y z
,
( ): ( 2) 2 4 0nx m y z
. Với giá trị thực của m, n bằng bao nhiêu để
()
song song
()
A.
3; 6mn
. B.
3; 6mn
. C.
3; 6mn
D.
3; 6mn
.
SỞ GDĐT LÂM ĐỒNG
TRƢỜNG THPT CHUYÊN BẢO LỘC
KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2020 – 2021
Môn: TOÁN 12 (chương trình Cơ bản)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
I- TRẮC NGHIỆM (7đ)
Câu 1: Mệnh đề nào sau đây sai?
A. Nếu
Fx
và
Gx
đều là nguyên hàm của hàm số
fx
thì
F x G x
.
B. Nếu
df x x F x C
thì
df u u F u C
.
C.
1 2 1 2
dddf x f x x f x x f x x


.
D.
ddkf x x k f x x

(
k
là hằng số và
0k
).
Câu 2: Cho
df x x F x C
. Khi đó với
0a
,
a
,
b
là hằng số ta có
df ax b x
bằng.
A.
df ax b x F ax b C
. B.
df ax b x aF ax b C
.
C.
1
df ax b x F ax b C
ab
. D.
1
df ax b x F ax b C
a
.
Câu 3: Tích phân
1
0
d
x
ex
bằng
A.
1
e
B.
1
1
e
C.
1e
e
D.
1e
Câu 4: Nếu
2
d
xfx xx C
thì
fx
là
A.
2fx xC
. B.
32
32
f
xx
x C
.
C.
22fx x
. D.
21fx x
.
Câu 5: Tích phân
2
2
0
d
3
x
x
x
bằng
A.
17
log
23
. B.
7
ln
3
. C.
13
ln
27
. D.
17
ln
23
.
Câu 6: Phương trình mặt phẳng
P
đi qua điểm
1;2;0M
và có vectơ pháp tuyến
4;0; 5n 
là
A.
4 5 4 0xy
. B.
4 5 4 0xz
. C.
4 5 4 0xy
. D.
4 5 4 0xz
.
Câu 7: Cho
fx
là hàm số liên tục trên đoạn
;ab
và
;c a b
. Tìm mệnh đề đúng trong các mệnh đề sau.
A.
d d d
b c b
a a c
f x x f x x f x x
. B.
d d d
b c c
a a c
f x x f x x f x x
.
C.
d d d
c b a
a c b
f x x f x x f x x
. D.
d d d
b a b
a c c
f x x f x x f x x
.
Câu 8: Tính tích phân
0
sin3 dxx
A.
2
3
B.
2
3
C.
1
3
D.
1
3
Câu 9: Cho hàm số
y f x
liên tục trên
[ ; ].ab
Diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
,y f x
trục hoành, các đường thẳng
,x a x b
được xác định bằng công thức nào?
A.
b
a
S f x dx
B.
a
b
S f x dx
C.
b
a
S f x dx
D.
b
a
S f x dx
Câu 10: Cho hàm số
fx
liên tục trên
;ab
và
Fx
là một nguyên hàm của
fx
. Tìm khẳng định sai.
A.
d
b
a
f x x F a F b
. B.
d0
a
a
f x x
.
C.
dd
ba
ab
f x x f x x

. D.
d
b
a
f x x F b F a
.
Câu 11: Cho
2
1
d3f x x
,
3
2
d1f x x 
. Tính
3
1
df x x
.
A.
4
. B.
4
. C.
2
. D.
2
.
Câu 12: Giả sử
9
0
d 37f x x
và
0
9
d 16g x x
. Khi đó,
9
0
2 3 ( ) dI f x g x x


bằng:
A.
26I
. B.
58I
. C.
143I
. D.
122I
.
Câu 13: Với mọi hàm số
,f x g x
liên tục và có đạo hàm trên
. Mệnh đề nào sau đây sai?
A.
kf x dx k f x dx

với mọi hằng số
k
.
B.
f x dx f x C

.
C.
f x g x dx f x dx g x dx



.
D.
f x g x dx f x dx g x dx



.
Câu 14: Mệnh đề nào sau đây đúng?
A.
1
d ln 1 4
14
x x C
x
B.
11
d 4.ln
1 4 1 4
xC
xx

C.
11
d .ln 8 2
1 4 4
x x C
x
D.
11
d .ln 1 4
1 4 4
x x C
x
Câu 15: Nguyên hàm của hàm số
2021
f x x
,
()x
là hàm số nào trong các hàm số dưới đây?
A.
2022
()
2022

x
F x C
,
()C
. B.
2021
( ) 2020.F x x C
,
()C
.
C.
2022
()F x x C
,
()C
. D.
2020
( ) 2021.F x x C
,
()C
Câu 16: Cho tích phân
e
1
3ln 1
d
x
Ix
x
. Nếu đặt
lntx
thì
A.
e
1
3 1 dI t t
B.
1
0
3 1 dI t t
C.
1
0
31
d
e
t
t
It
D.
e
1
31
d
t
It
t
Câu 17: Cho
,fg
là hai hàm số liên tục trên
1;3
thỏa mãn:
3
1
10
f x dx
,
3
1
6
g x dx
. Tính
3
1
f x g x dx


A.
8
. B.
16
. C.
7
. D.
9
.
Câu 18: Trong không gian với hệ trục tọa độ
Oxyz
, mặt cầu
2 2 2
: 8 4 2 4 0S x y z x y z
có bán
kính
R
là
A.
5R
. B.
25R
. C.
2R
. D.
5R
.
Câu 19: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
4;0;1A
và
2;2;3B
. Phương trình nào dưới
đây là phương trình mặt phẳng trung trực của đoạn thẳng
AB
?
A.
3 1 0x y z
. B.
6 2 2 1 0x y z
. C.
30x y z
. D.
3 6 0x y z
.
Câu 20: Nếu
ux
và
vx
là hai hàm số có đạo hàm liên tục trên đoạn
;ab
. Mệnh đề nào sau đây đúng
A.
dv d
bb
b
a
aa
u uv v u

. B.
d d d
b b b
a a a
u v x u x v x
.
C.
dd
bb
b
a
aa
u v uv v v

. D.
d d . d
b b b
a a a
uv x u x v x
.
Câu 21: Tích phân
2
0
2 1 dxI x
có giá trị bằng:
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 22: Trong các hàm số sau, hàm số nào có một nguyên hàm là hàm số
lnF x x
?
A.
3
.
2
x
fx
B.
.f x x
C.
.f x x
D.
1
.fx
x
Câu 23: Một nguyên hàm
Fx
của hàm số
sinf x x
thỏa mãn
2
2
F



là:
A.
cosF x x
B.
cosF x x
C.
cos 2 F x x
D.
cos 2F x x
Câu 24: Cho hai hàm số
fx
,
gx
liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai?
A.
d d df x g x x f x x g x x


. B.
. d d . df x g x x f x x g x x


.
C.
ddkf x x k f x x

0;kk
. D.
d d df x g x x f x x g x x


.
Câu 25: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
3; 2;3A
và
1;2;5B
. Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
.
A.
2;2;1I
. B.
1;0;4I
. C.
2;0;8I
. D.
2; 2; 1I
.
Câu 26: Trong không gian , điểm nào sau đây thuộc trục Oz?
A.
1 0 0M ; ;
. B.
0 2 0M ; ;
. C.
0 0 3M ; ;
. D.
1 0 0M ; ;
.
Câu 27: Cho
Fx
là một nguyên hàm của hàm số
fx
. Khi đó hiệu số
01FF
bằng
A.
1
0
dF x x
. B.
1
0
df x x
. C.
1
0
dF x x
. D.
1
0
df x x
.
Câu 28: Trong không gian
Oxyz
, mặt cầu
2 2 2
1 2 3 4x y z
có tâm và bán kính lần lượt là
A.
1; 2;3I 
;
2R
. B.
1;2; 3I
;
2R
. C.
1;2; 3I
;
4R
. D.
1; 2;3I 
;
4R
.
Câu 29: Họ các nguyên hàm của hàm số
( ) 3
x
fx
.
A.
1
3
3d
1
x
x
xC
x

. B.
3 d 3 ln3
xx
xC
. C.
1
3 d 3
xx
xC

. D.
3
3d
ln3
x
x
xC
.
Câu 30: Tính tích phân
2021
1
d
x
I
x
.
A.
2021I
. B.
2021.ln2 1I
. C.
ln2021I
. D.
ln2020I
.
Câu 31: Cho hàm số
fx
có đạo hàm liên tục trên đoạn
1;3
thỏa mãn
12f
và
39f
. Tính
3
1
dI f x x
.
A.
7I
. B.
2I
. C.
18I
. D.
11I
.
Câu 32: Mặt phẳng
:2 5 1 0x y z
có một vectơ pháp tuyến là:
Oxyz
A.
2;5; 1n 
. B.
2;5;1m

. C.
2; 5; 1
b
. D.
2;5; 1a
.
Câu 33: Trong không gian hệ tọa độ
Oxyz
, phương trình nào sau đây là phương trình của mặt phẳng
Oxz
?
A.
0y
. B.
0x
. C.
0z
. D.
10y 
.
Câu 34: Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
1;2; 4A
và
3;2;2B
. Toạ độ của
AB
là
A.
4;0; 6
. B.
1;2; 1
. C.
4;0;6
. D.
2;4; 2
.
Câu 35: Trong không gian
Oxyz
, điểm
3;4; 2M
thuộc mặt phẳng nào trong các mặt phẳng sau?
A.
: 7 0R x y
. B.
: 5 0S x y z
.
C.
: 1 0Qx
. D.
: 2 0Pz
.
II – TỰ LUẬN (3đ)
Câu 1 (1,0 điểm): Tính giá trị của tích phân sau:
2
cos
0
e .sin d
x
I x x
.
Câu 2 (1,0 điểm): Một cái bồn gồm hai nửa hình cầu đường kính
18
dm
, và một hình trụ có chiều cao
36
dm
.
Tính thể tích
V
của cái bồn đó.
Câu 3 (0,5 điểm): Biết hàm số
y f x
có
2
3 2 1f x x x m
,
21f
và đồ thị của hàm số
y f x
cắt trục tung tại điểm có tung độ bằng
5
. Tìm hàm số
fx
.
Câu 4 (0,5 điểm):
Cho hàm số
fx
liên tục trên R và
1
2 3 .f x f x
x




Tính tích phân
2
1
2
d
fx
Ix
x
----------- HẾT ----------
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƢỜNG THPT CHUYÊN BẢO LỘC TỔ TOÁN
ĐỀ CƢƠNG ÔN TẬP GIỮA HỌC KÌ II MÔN TOÁN KHỐI 12 NĂM HỌC 2022-2023
PHẦN I – GIẢI TÍCH A.LÍ THUYẾT 1.Nguyên hàm
- Định nghĩa nguyên hàm, bảng các nguyên hàm cơ bản.
- Một số tính chất cơ bản của nguyên hàm, vận dụng tính chất của nguyên hàm tìm được nguyên hàm của một hàm số.
-Công thức tính nguyên hàm bằng phương pháp đổi biến số hoặc phương pháp tính nguyên hàm từng phần. Vận
dụng phương pháp đổi biến số hoặc phương pháp tính nguyên hàm từng phần để tìm nguyên hàm của hàm số. 2.Tích phân
-Khái niệm về diện tích hình thang cong, định nghĩa tích phân của hàm số liên tục bằng công thức Niu- tơn Lai-
bơ – nit. Vận dụng định nghĩa để tính tích phân của hàm số.
- Một số tính chất cơ bản của tích phân. Vận dụng tính chất của tích phân tính được tích phân của một hàm số.
-Vận dụng phương pháp đổi biến số và dụng phương pháp tính tích phân từng phần để tính tích phân của hàm số
- Ứng dụng của tích phân trong hình học B. – BÀI TẬP
I – BÀI TẬP TỰ LUẬN
Bài 1: Tìm nguyên hàm của các hàm số sau đây: 1 5 3 1
a) f x x x  3 ( ) 4 2 x
b) f (x)  x 3 x  2
c) f (x)  2x e 1 3 2x  6 d) f (x) 
f (x) sin3x cos5x f x x 2 e)  f)   2 ( ) (1 2sin ) x  2x  3
Bài 2: Cho hàm số f (x) . Tìm nguyên hàm F(x) của hàm số f (x) thỏa điều kiện. 2 2 a) (
g x)  xsin x x ; f (x)  x cos ; x F()  0 b) (
g x)  x ln x x ; f (x)  ln ; x F(2)  2 
Bài 3. Tìm các họ nguyên hàm sau đây: 3 x 3 ln x a)  dx b)  2 . x x e dx c) dx   2 1 x x
Bài 4: Tìm các họ nguyên hàm sau. a)   2 ( 2) x x e dx b) x  (2 1)cosxdx c) x   2 (3 1)ln xdx d) x x  (4 1)ln( 1)dx
Bài 5: Tính các tích phân sau  1 4 2 4 3 dx 4
a) 3x  2 dx b)  c) x 1dx  d) cos x dxx(x  ) 1 0 2 1 0 0 2 2 2x1 e)  e dx f)  2 x x dx g)  1 cos 2xdx 1 0 0  3 (đs: a) 5  3 4 2 3 1 e e . b) ln . c) 2 3  . d)  . e)   . f) 1. g) 4 2. ) 4 2 3 32 4 2 2
Bài 6: Tính các tích phân sau 1 9 1 0 e 3 4 1 3ln x ln x a) x 5  x dx b) 15 8  x 1 3x dx  c)     2 2 1 x x x e dx d)   dx 0 x 0 1  1   2 4 2 1 xdx e)  3 sin xdx f)  tan xdx g)  2 x 4  2 x dx h)  4 x  2 x  1 0 0 1 0 10 10   (đs: a) 5 4 29 1 1 116 2 2 2 3 . b) . c)  . d) . e) . f)  ln . g)  . ) 40 270 2 2e 135 3 2 3 4
Bài 7: Tính các tích phân sau   3 4 ln 2 e e ln(ln x) 2
a)  xsin 2xdx b) xe x dx  c) x ln dx x  d) dx  3 x
e)  e x sin 5xdx 0 0 1 2 e 0 3 1 2 e  1 27 2 5  3.e (a) . b) 2ln 2 1. c) . d) ln 1. e) . ) 4 4 4 34
Bài 8: Tính diện tích hình phẳng giới hạn bởi các đường sau 2 1
a) y x  5x  6, y  0, x  2, x  4
b) y x, y
, y  0, x e x 2
c) y x  4x  5, y  2
x  4, y  4x 11
d) y  sin x  2 cos ,
x y  3, x  0, x   1 2 1 2 2 e) y
x ,y   x  3
y x  4x  3 , y x  3 4 2 f) 2 2 g) y x.ln ;
x y  0; x 1; x  . e
h) y x  5  0, x y  3  0
Bài 9: Tính diện tích hình phẳng giới hạn bởi các đường 3
(C): y x 3x  2, x  1
 và tiếp tuyến với (C) tại
điểm có hoành độ x = –2.
Bài 10: Tính thể tích vật thể tròn xoay sinh ra bởi hình (H) giới hạn bởi các đường sau quay quanh trục Ox: a) 2 y x  2 ;
x y  0; x  0; x  1
b) y  ln x, y  0, x  2 c) 2 y
x  3x; y  0; x  0; x  1
Bài 11. Tính thể tích vật thể tròn xoay sinh ra bởi hình (H) giới hạn bởi các đường sau quay quanh trục Oy: 2 2
a) y x , y  4 b) x  ,y  1,y  4     y c) y ln ; x x 0; y 0; y 1
II – BÀI TẬP TRẮC NGHIỆM
Câu 1: Trong các khẳng định dưới đây, có bao nhiêu khẳng định đúng?
(a).Mọi hàm số liên tục trên [ ;
a b] đều có đạo hàm trên [ ; a b] .
(b). Mọi hàm số liên tục trên [ ;
a b] đều có nguyên hàm trên [ ; a b] .
(c).Mọi hàm số có đạo hàm trên [ ;
a b] đều có nguyên hàm trên [ ; a b] .
(d). Mọi hàm số liên tục trên [ ;
a b] đều có giá trị lớn nhất và giá trị nhỏ nhất trên [ ; a b] . A.2 B.3 C.1 D.4
Câu 2: Cho hàm số f (x), g(x) liên tục trên  . Trong các mệnh đề sau, mệnh đề nào sai?
A.  f (x)  g(x)dx f (x)dx g(x)dx   .
B.  f (x).g(x)dx f (x)d . x g(x)dx   .
C.  f (x)  g(x)dx f (x)dx g(x)dx  
D. kf (x)dx k f (x)dxk  0;k    
Câu 3: Khẳng định nào sau đây là khẳng định sai?
A. kf (x)dx k f (x)dxk    
B.  f (x)  g(x)dx f (x)dx g(x)dx  
với f (x); g(x) liên tục trên  .  1 C.  1 x dx x        với 1. 1 D.  f x dx  ' ( )  f (x)
Câu 4: Cho hàm số f (x) xác định trên K . Khẳng định nào sau đây là sai?
A.Nếu hàm số F (x) là một nguyên hàm của f (x) trên K thì với mỗi hằng số C , hàm số G(x)  F(x)  C
cũng là một nguyên hàm của f (x) trên K .
B.Nếu f (x) liên tục trên K thì nó có nguyên hàm trên K .
C.Hàm số F (x) được gọi là một nguyên hàn của f (x) trên K nếu F '(x)  f (x) với mọi x K .
D.Nếu hàm số F (x) là một nguyên hàm của f (x) trên K thì hàm số F(x) là một nguyên hàm của f (x) trên K .
Câu 5: Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu: A. F '( ) x   f ( ) x , x   K
B. f '(x)  F(x), x  K
C. F '(x)  f (x), x   K D. f '( ) x  F( ) x , x   K 2
Câu6: Tìm nguyên hàm của hàm số 2
f (x)  x  . 2 x 3 x 1 3 x 2 A.
f (x)dx    C  B.
f (x)dx    C  3 x 3 x 3 x 1 3 x 2 C.
f (x)dx    C  D.
f (x)dx    C  3 x 3 x   
Câu 7: Tìm nguyên hàm của hàm số f (x) thỏa mãn điều kiện f (x)  2x  3cos , x F  3   .  2  2  2  A. 2
F (x)  x  3sin x  6  B. 2
F (x)  x  3sin x  4 4 2  2  C. 2
F (x)  x  3sin x  D. 2
F (x)  x  3sin x  6  4 4
Câu 8: Tính nguyên hàm sau: 9
x(x  2) dx  . 11 (x  2) 11 10 (x  2) 2(x  2) 10 2(x  2) 11 10 (x  2) 2(x  2) A.  C B.   C C.  C D.   C 22 11 10 10 11 10 1
Câu 9: Tìm nguyên hàm I dx  2 4  x 1 x  2 1 x  2 1 x  2 1 x  2 A. ln  C B. ln  C C. ln  C D. ln  C 2 x  2 2 x  2 4 x  2 4 x  2 dx
Câu 10: Tìm I   .
(x 1) x x x 1
A. x  2 x 1  C B. 2 x  2 x 1  C
C. 2 x  2 x 1  C
D. x x 1  C
Câu 11: Họ nguyên hàm của hàm số 2
f (x)  cos 2x là: 1 sin 4x x sin 4x 1 sin 4x x sin 4x A.   C B.   C C.   C D.   C 2 8 2 2 2 2 2 8
Câu 12: Tìm I  sin 4 . x cos xdx  1 1 1 1 A.  cos 5x  cos 3x C B. cos 5x  cos 3x C 10 6 10 6 1 1
C. cos 5x  cos 3x C D. 
cos 5x  cos 3x C 6 10 2
Câu 13: F (x) là một nguyên hàm của hàm số  . x y
x e . Hàm số nào sau đây không phải là F (x) ? 2 x e 2 1 2 1 2 1 A. F (x)   2 B. ( )   x F x e  5 C. ( ) x
F x   e C D. ( )   2 x F xe  2 2 2 2 tan x e Câu 14: Tìm dx  ? 2 cos x 1 A. tan x x eC B. tan tan x x eC C. tan x eC D. tan xeC 2 1 ln x
Câu 15: Nguyên hàm của f (x)  là: x ln x 1 ln x 1 ln x A.
dx  ln ln x C  B. 2
dx  ln x ln x Cx ln x x ln x 1 ln x 1 ln x C.
dx  ln x  ln x C  D. dx  ln .
x ln x Cx ln x x ln x
Câu 16: Tìm nguyên hàm của  (2 1) x I x e dx  A.  (  2 1) x I x eC B.  (  2 1) x I x eC C.  (  2  3) x I x eC D.  (  2 3) x I x eC
Câu 17: Kết quả nguyên hàm 2
I x sin 5xdx  là: 1 2 2 1 2 2 A. 2  x cos5x x sin 5x  cos 5x C B. 2  x cos5x x sin 5x  cos 5x C 5 25 125 5 25 125 1 2 2 1 2 2 C. 2 x cos 5x x sin 5x  cos 5x C D. 2  x cos5x x sin 5x  cos 5x C 5 25 125 5 25 125
Câu 18. Khẳng định nào sau đây sai? b b b b b c
A.   f (x)  g(x)dx f (x)dx g(x)dx   B. f (x d ) x
f (x)dx f (x d ) x    a a a a c a b a b b C.
f (x)dx f (x d ) x   D. f (x d ) x f (t)dt   a b a a
Câu 19: Cho hai số thực a, b tùy ý, F (x) là một nguyên hàm của hàm số f (x) trên tập  . Mệnh đề nào dưới đây là đúng? b b A.
f (x)dx f ( )
b f (a)  B.
f (x)dx F( )
b F(a)  a a b b C.
f (x)dx F( )
b F(a)  D.
f (x)dx F( )
b F(a)  a a
Câu 20: Cho hàm số y f (x) liên tục trên đoạn [ ;
a b] . Mệnh đề nào dưới đây sai? b b b a A.
f (x)dx f (t)dt   B.
f (x)dx   f (x)dx   a a a b b b c b C.
kdx k(a  ) b , k     D.
f (x)dx
f (x)dx f (x)d , x c  ( ; a b)    a a a c 1 1 Câu 21: Cho
f (x)dx  3 
. Tính tích phân I  2 f (x)  1dx 2  2  A. 9  B. 3  C. 3 D. 5 1 1  a
Câu 22: Cho giá trị tích phân I    4 3
x  2x dx a, I    2
x  3x dx b . Tính giá trị là: 1 2  b 1  2  4  12 12  4 A. P  B. P  C. P  D. P  65 65 65 65 2 x 1 Câu 23: Giả sử
dx a ln 5  b ln 3; a, b  
 . Tính P ab . 2 x  4x  3 0 A. P  8 B. P  6  C. P  4  D. P  5   3 dx
Câu 24: Tích phân I   bằng? 2  sin x 4         A. cot  cot B. cot  cot C.  cot  cot D.  cot  cot 3 4 3 4 3 4 3 4 2 x 2 Câu 25: Cho ( ) t F x e dt  . Tính F '(2) . 0 A. 4 F '(2)  4e B. 16 F '(2)  8e C. 16 F '(2)  4e D. 4 F '(2)  e
Câu 26: Cho hàm số y f (x) liên tục trên [ ;
a b] . Giả sử hàm số u u(x) có đạo hàm liên tục trên [ ;
a b] và u(x) [,  ], x  [ , a ]
b , hơn nữa f (u) liên tục trên đoạn [,  ]. Mệnh đề nào sau đây là đúng? b bn(b) b A.
f [u(x)]u (x)dx f (u)du   . B.
f [u(x)]u (x)dx f (u)du   . a a u (a) a b u(b) b b  C.
f [u(x)]u (x)dx f (u)du   . D.
f [u(x)]u (x)dx f (x)du   a u (a) a a 2 x Câu 27: Tích phân dx  bằng: 2 x  3 0 1 7 7 1 7 1 3 A. log B. ln C. ln D. ln 2 3 3 2 3 2 7 4 2x 1 5 Câu 28: Biết
dx a b ln 2  c ln 
a, ,bc. Tính T  2abc.
2x  3 2x 1  3 3 0 A. T  4 B. T  2 C. T  1 D. T  3  3 sin x
Câu 29: Tính tích phân I dx  . 3 cos x 0 5 3  9 9 A. I  B. I  C. I   D. I  2 2 3 20 4 1 2  ae b Câu 30: Cho 1  . x I x e dx  . Biết rằng I
. Khi đó a b bằng: 2 0 A.1 B.0 C.2 D.4 e ln x 3 Câu 31: Biết   dx a
b a b . Mệnh đề nào sau đây đúng? x ln x  2 ln ,  ,  2 1
A. a b  1
B. 2a b  1 C. 2 2 a b  4
D. a  2b  0 1 1
Câu 32: Tích phân I dx  có giá trị là: 2 x 1 0     A. I  B. I  C. I  D. I  2 3 4 6  2 u   x
Câu 33: Tính tích phân 2
I x cos 2xdx  bằng cách đặt 
. Mệnh đề nào dưới đây đúng?
dv  cos 2xdx 0   1  1  A. 2 I
x sin 2x x sin 2xdx  B. 2 I
x sin 2x  2 x sin 2xdx  0 2 0 2 0 0   1  1  C. 2 I
x sin 2x  2 x sin 2xdx  D. 2 I
x sin 2x x sin 2xdx  0 2 0 2 0 0  4 2   Câu 34: Cho 2
I x tan xdx   ln b  
, khi đó tổng a b bằng a 32 0 A. 4 B. 8 C. 10 D. 6 1 Câu 35: Cho 2 x 2
I xe dx ae b
( a, b là các số hữu tỷ). Khi đó tổng a b là 0 1 1 A. 0 B. C.1 D. 4 2 3 3  ln x
a  ln b  ln c Câu 36: Biết dx   với a, ,
b c là các số nguyên dương. Giá trị của biểu thức 2 (x 1) 4 1
P a b c bằng? A. 46 B. 35 C. 11 D. 48 1 aa Câu 37: Biết 2 S
4x  4x 1dx  a,b 
 , là phân số tối giản. Giá trị a  4b bằng: b b 0 A.1 B. 3  C.35 D.3
Câu 38. Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y f (x), trục Ox và các
đường thẳng x  , a x  ( b a  ) b . b b b b A. f (x) dx  B. 2 f (x)dx  C. f (x)dx  D.  f (x)dxa a a a
Câu 39: Cho hàm số y f (x) liên tục trên  và có đồ thị (C) là đường cong như
hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường
thẳng x  0, x  2 (phần tô đậm) là: 2 1 2 A. f (x)dx
B.  f (x)dx f (x)dx   0 0 1 1 2 2 C.
f (x)dx f (x)dx   D. f (x)dx  0 1 0
Câu 40: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y  cos 2x , trục hoành và hai đường thẳng  x  0, x  là: 2 A.2 B. 1 C. 3 D. 4
Câu 41: Cho hàm số y f (x), y g( )
x liên tục trên [a; b]. Gọi (H ) là hình giới hạn bởi hai đồ thị y f (x),
y g(x) và các đường thẳng x  ,
a x b . Diện tích hình (H ) được tính theo công thức: b b b A. S
|f (x) | dx
|g(x) | dx   B. S
|f (x)  g(x) | dxH H a a a b b C. S f x g x dx  D. S f x g x dxH  ( ) ( ) H  ( ) ( ) a a
Câu 42: Hình phẳng (H) giới hạn bởi đồ thị hai hàm số 2
y x x  2, y x  2 và hai đường thẳng x  2
 ; x  3. Diện tích của (H) bằng: 87 87 87 A. B. C. D. 13 5 4 3
Câu 43: Diện tích hình phẳng giới hạn bởi 2
(P) : y x  3, tiếp tuyến của (P) tại điểm có hoành độ x  2 và trục tung bằng 8 4 7 A. B. C. 2 D. 3 3 3
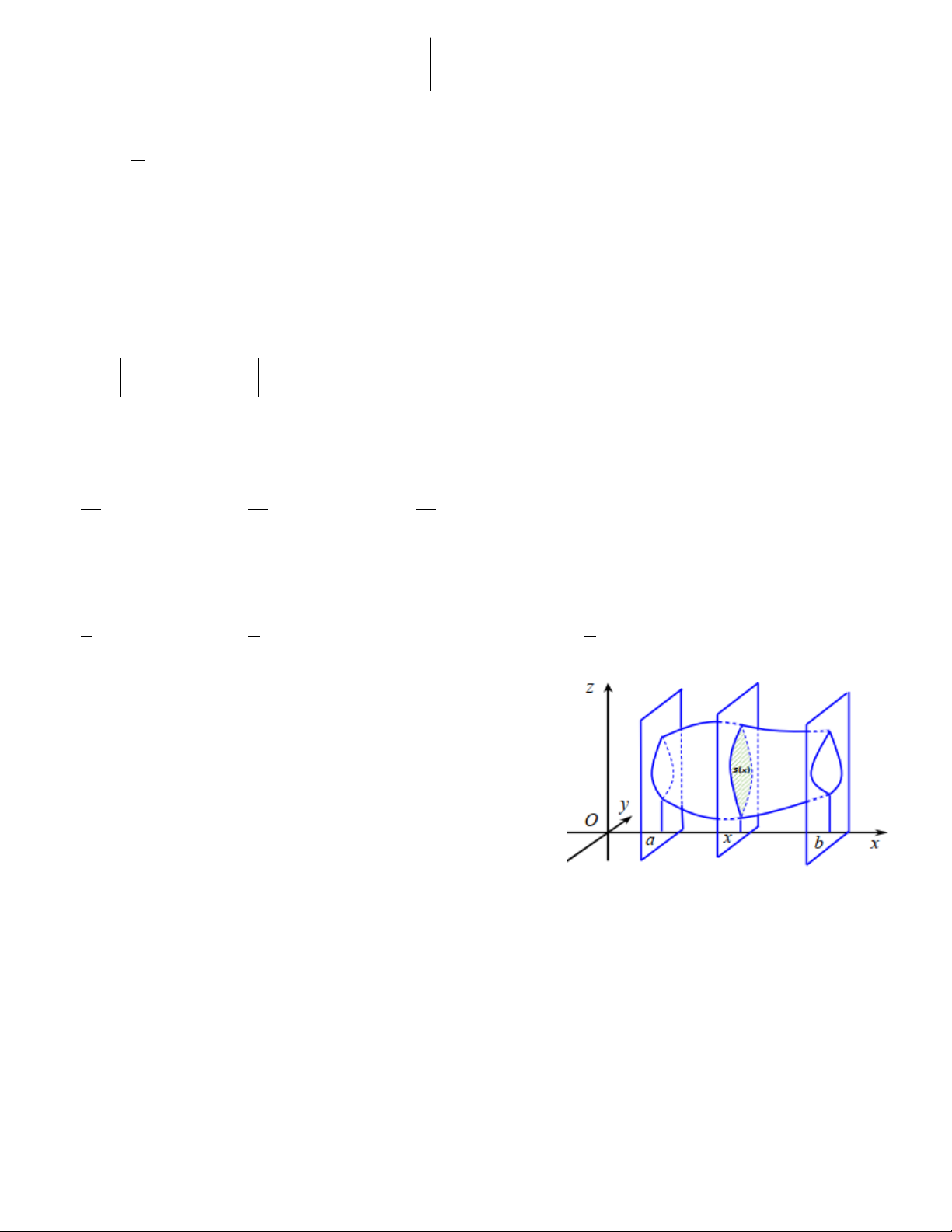
Câu 44: Trong không gian Oxyz , cho vật thể được giới hạn bởi
hai mặt phẳng (P), ( )
Q vuông góc với trục Ox lần lượt tại x  , a x  ( b a  )
b . Một mặt phẳng tùy ý vuông góc với Ox tại điểm có hoành độ ,
x (a x  )
b cắt vật thể theo thiết diện có diện
tích là S(x) với y S(x) là hàm số liên tục trên [a ; b]. Thể tích
V của thể tích đó được tính theo công thức: b b b b A. 2 V S (x)d . x  B. 2 V   S (x)dx  . C. V   S(x)dx  . D.V S(x)dxa a a a
Câu 45. Cho hàm số y f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y f (x) , trục hoành và hai đường thẳng x  , a x  ( b a  )
b . Thể tích khối tròn xoay tạo thành khi quay D
quanh trục hoành được tính theo công thức. b b b b 2 A. V   f (x)d . x  B. 2 V  2 f (x)d . x  C. 2 2 V   f (x)d . x  D. 2 V   f (x)dxa a a a
Câu 46: Cho hình phẳng (H ) giới hạn bởi các đường 2
y x ; y  0; x  2 . Tính thể tích V của khối tròn xoay
thu được khi quay H  quanh trục Ox . 8 32 8 32 A. V  B. V  C. V  D. V  3 5 3 5
Câu 47: Thể tích khối tròn xoay thu được khi quay quanh trục Ox hình phẳng giới hạn bởi đồ thị hàm số x y
xe , trục hoành và đường thẳng x  1 là  1  1 A.  2e  1 B.  2e  1 C.  4e  1 D.  4e  1 4 4 4 4
PHẦN II - HÌNH HỌC A-LÍ THUYẾT
1. Hệ tọa độ trong không gian
- Khái niệm tọa độ của vec tơ và tọa độ của điểm thông qua định nghĩa, biểu thức tọa độ của các phép toán vectơ.
- Tính cùng phương của hai vec tơ, chứng minh 3 điểm thẳng hàng, xác định tọa độ của điểm thỏa mãn điều kiện nào đó,…
2. Phƣơng trình mặt cầu
- Xác định được tọa độ tâm và tìm được độ dài bán kính mặt cầu có phương trình cho trước.
- Tìm được phương trình mặt cầu nếu biết tâm và bán kính mặt cầu.
3. Phƣơng trình mặt phẳng
- Khái niệm véc tơ pháp tuyến của mặt phẳng, xác định được vec tơ pháp tuyến của mặt phẳng khi biết phương
trình của mặt phẳng đó ; biết dạng phương trình mặt phẳng, nhận biết được điểm thuộc mặt phẳng.
- Vị trí tương đối của hai mặt phẳng
- Bài toán liên quan đến góc, khoảng cách. B-BÀI TẬP
I-BÀI TẬP TỰ LUẬN       
Bài 1: Cho: a  2; 5  ; 
3 , b  0; 2;  
1 , c  1;7;2 . Tìm tọa độ của vectơ 3 2
u a b c 4 3   (đs: 4 67 29 ;  ;   )  3 6 12   
Bài 2: Tính góc giữa hai vec tơ a  2;5; 4, b  6;0; 3   . (đs: 90o )      
Bài 3: Tìm m để 3 vectơ a, b,c đồng phẳng với a  m 1; m; m  2, b  m 1; m  2; m, c  1; 2; 2  
Bài 4: Cho ba điểm A, B, C.
 Chứng tỏ ba điểm A, B, C tạo thành một tam giác.
 Tìm toạ độ trọng tâm G của ABC.
 Xác định điểm D sao cho ABCD là hình bình hành.
 Tính số đo các góc trong ABC.
 Tính diện tích ABC. Từ đó suy ra độ dài đường cao AH của ABC. a) A 3 ( ; 1  ;2),B 1 ( ;2; 1  ),C( 1  1 ; ; 3  ) b) A 4 ( 1 ; ;4),B 0 ( ;7; 4  ),C 3 ( 1 ; ; 2  ) (đs: a) 149 149
22o50', B=119o 50', C=37o A  20' , S  , AH= . ) 2 3
Bài 5: Cho bốn điểm A, B, C, D.
 Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
Tìm tọa độ trọng tâm G của tứ diện ABCD.
Tính thể tích của khối tứ diện ABCD.
 Tính diện tích tam giác BCD, từ đó suy ra độ dài đường cao của tứ diện vẽ từ A. a) A 2 ( ;4 1 ; ),B( 1  ;0 1 ; ),C( 1  ;4;2),D 1 ( ; 2  1 ; ) b) A( 3  ;2;4),B 2 ( ;5; 2  ),C 1 ( ; 2  ;2),D(4;2;3)   (đs: a) 1 5 7 7 2 G ; 2;   V  . S  3 2 AH  . )  3 3  3 BCD 6
Bài 6: Cho hình hộp ABCD.A'B'C'D'.
 Tìm toạ độ các đỉnh còn lại.
 Tính thể tích khối hộp. a) A 0 ( ;2 1 ; ),B 1 ( ; 1  1 ; ), D 0 ( ;0;0;), A'( 1  ;1;0) b) A 0 ( ;2;2),B 0 ( 1 ; ;2),C( 1  ;1;1),C' 1 ( ; 2  ; 1  )
Bài7: Tìm tâm và bán kính của các mặt cầu sau: a) 2 2 2
3x  3y  3z  6x  3y 15z  2  0 b) 2 2 2
x y z  6x  2y  2z 10  0
Bài 8: Viết phương trình mặt cầu (S) thỏa mãn điều kiện a)Có tâm I (1; 2; 3
 ) và bán kính R  2 b) Có tâm I (2; 2; 3  ) và đi qua điểm ( A 1  ;2;5)
c) Có đường kính AB với ( A 2  ;1;5), B(4;7;3)
d) Đi qua 4 điểm A 2 ( ;3 1 ; ),B 4 ( 1 ; ; 2  ),C 6 ( ;3;7),D( 5  ; 4  ;8)
e) Có tâm I và tiếp xúc với mặt phẳng (P) biết I 1;2; 
1 ;(P) : x  2y  2z  8  0 
Bài 9: Viết phương trình mặt phẳng (P) đi qua M 4;1;2 và có vectơ pháp tuyến n  0;1;3 .
(đs: y  3z  7  0 )
Bài 10: Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A 2 ( ;3; 4  ), B(4; 1  ;0)
(đs: x  2y  2z  3  0 )
Bài 11: Viết phương trình mặt phẳng đi qua điểm M(1;-2;3) và song song với mặt phẳng
:2x3y2z1 0 (đs: D=10)
Bài 12:Viết phương trình mặt phẳng đi qua ba điểm A1;2;  3 , B( 2  ;4 1 ; ),C 5 ( 1 ; ;4)
(đs: y z  5  0 )
Bài 13: Viết phương trình mặt phẳng () đi qua điểm A và vuông góc với đường thẳng đi qua hai điểm B, C cho trước, với A 0 ( ;0;0), B( 2  ; 1  ;3), C(4; 2  1 ; )
(đs: 6x y  2z  0. )
Bài 14: Viết phương trình mặt phẳng () đi qua hai điểm A, B và vuông góc với mặt phẳng () cho trước, với: A( 2  ; 1  ;3), B(4; 2  1 ; ) 
  : 2x  3y  2z  5  0
(đs: 2x  2y  5z  9  0 )
Bài 15:Viết phương trình mặt phẳng () đi qua điểm M và vuông góc với hai mặt phẳng (), () cho trước, với: M( 1  ; 2
 ;5),  : x  2y 3z 1 0,  : 2x 3y z 1 0
(đs: x y z  2  0 )
x y z  
Bài 16:Xét vị trí tương đối của các cặp mặt phẳng sau: 3 2 6 23 0  3
x  2y  6z  33  0
2x y  4z  5  0
Bài 17: Tính khoảng cách giữa hai mặt phẳng  3
x  5y z 1  0
x  2y  2z 1  0
Bài 18: Tính góc giữa hai mặt phẳng 
2x  2y z  5  0 (đs: 4 cos  ) 9
II – BÀI TẬP TRẮC NGHIỆM 
Câu 1: Trong không gian với hê tọa độ Oxyz , cho hai điểm A 1 ( ; 2  ;0)và B( 3
 ;0;4) . Tọa độ của vectơ AB là: A. (4; 2  ; 4  ) B. ( 4  ;2;4) C. ( 1  ; 1  ;2) D. ( 2  ; 2  ;4)
Câu 2: Trong không gian Oxyz cho ba điểm A 1 ( 1 ; 1 ; ),B 5 ( ; 1  ;2),C 3 ( ;2; 4
 ) . Tìm tọa độ điểm M thỏa    
MA  2MB MC  0.  3 9   3 9   3 9   3 9  A. M 4  ;  ;  B. M 4; ;   C. M 4  ; ;  D. M 4;   ;   2 2   2 2   2 2   2 2 
Câu 3: Trong không gian Oxyz , cho điểm M 1
( ;2;3). Hình chiếu của M lên trục Oy là điểm A. R 1 ( ;0;0) B. S 0 ( ;0;3) C. P 1 ( ;0;3) D. Q 0 ( ;2;0)
Câu 4: Trong không gian với hệ tọa độ Oxyz , cho A 3 ( ; 4  ;0),B 0 ( ;2;4),C(4;2 1
; ) . Tọa độ điểm D trên trục Ox
sao cho AD BC . A. D 0 ( ;0;0),D ( 6  ;0;0)
B. D (2;0;0), D 8 ( ;0;0) 1 2 1 2 C. D ( 3  ;0;0),D 3 ( ;0;0) D. D 0 ( ;0;0),D 6 ( ;0;0) 1 2 1 2   
Câu 5: Trong không gian Oxyz , cho các vectơ a  ( 5  ;3; 1  ),b  1 ( ;2 1
; ),c  (m;3; 1
 ) . Giá trị của m sao cho   
a  b,c   là: A. m  2 B. m  2  C. m  1 D. m  1 
Câu 6: Trong không gian với hệ trục tọa độ Oxyz , cho hình bình hành ABCD . Biết A 2 ( 1 ; ; 3  ),B 0 ( ; 2  ;5), C 1 ( 1
; ;3). Diện tích hình bình hành ABCD là: 349 A. 2 87 B. C. 349 D. 87 2
Câu 7: Trong không gian với hệ tọa độ Oxyz , măt cầu 2 2 2
(S) : (x  2)  ( y 1)  z  4 có tâm I và bán kính R lần lượt là: A. I ( 2  ;1;0), R 4 B. I (2; 1  ;0), R 4 C. I (2; 1
 ;0), R 2 D. I( 2  ;1;0), R 2
Câu 8: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có phương trình 2 2 2
x y z  2x  4y  6z  5  0 . Diện tích mặt cầu (S) là? A. 36 B. 36 C. 12 D. 9
Câu 9: Trong không gian với hệ tọa độ Oxyz , trong các phương trình sau, phương trình nào không phải là
phương trình của một mặt cầu? A. 2 2 2
2x  2y  2z  4x  6y  8z  4  0 B. 2 2 2
x y z  2x  2y  6z  7  0 C. 2 2 2
x y z  2x  2y  2z  2  0 D. 2 2 2
2x y z  2x  2y  2  0
Câu 10: Trong hệ tọa độ Oxyz ,phương trình nào sau đây là phương trình mặt cầu tâm I (1; 2;3) bán kính r  1? A. 2 2 2
(x 1)  ( y  2)  (z  3)  1. B. 2 2 2
(x 1)  ( y  2)  (z  3)  1. C. 2 2 3
(x 1)  ( y  2)  (z  3)  1. D. 2 2 2
x y z  2x  4y  6z 13  0 .
Câu 11: Trong không gian với hệ trục tọa độ Oxyz, cho hai điềm ( A 1; 2
 ;3) và B(5;4;7) . Phương trình mặt cầu
nhận AB làm đường kính là. A. 2 2 2
(x  3)  ( y 1)  (z  5)  17 . B. 2 2 2
(x  6)  ( y  2)  (z 10)  17 . C. 2 2 2
(x 1)  ( y  2)  (z  3)  17 D. 2 2 2
(x  5)  ( y  4)  (z  7)  17 .
Câu 12: Trong không gian với hệ trục tọa độ Oxyz , cho bốn điểm (
A 0;0;1), B(0;1;0),C(1;0;0), D(1;1;1). Bán
kính mặt cầu đi qua bốn điểm , A , B C, D là: 1 3 3 A. B. C. D. 3 2 4 2
Câu 13: Trong không gian tọa độ Oxyz , cho điềm M (1;1; 2
 ) và mặt phẳng () : x y  2z  3. Viết phương
trình mặt cầu ( S ) có tâm M tiếp xúc với mặt phằng ( ) . 35 14 A. 2 2 2
(S) : x y z  2x  2 y  4z   0 . B. 2 2 2
(S) : x y z  2x  2 y  4z   0 6 3 35 16 C. 2 2 2
(S) : x y z  2x  2 y  4z   0 D. 2 2 2
(S) : x y z  2x  2 y  4z   0 6 3
Câu 14: Mặt cầu (S) có tâm I ( 1  ;2; 5  ) cắt ( )
P : 2x  2y z 10  0 theo thiết diện là hình tròn có diện tích 3
có phương trình (S) là: A. 2 2 2
(x 1)  ( y  2)  (z  5)  16 B. 2 2 2
x y z  2x  4y 10z 18  0 C. 2 2 2
(x 1)  ( y  2)  (z  5)  25 D. 2 2 2
x y z  2x  4y 10z 12  0
Câu 15: Chọn khẳng định sai:  
A. Nếu n là một vectơ pháp tuyến của mặt phẳng (P) thì k.n cũng là một vectơ pháp tuyến của mặt phẳng (P).
B. Một mặt phẳng hoàn toàn được xác định nếu biết một điểm nó đi qua và một vectơ pháp tuyến của nó.
C. Mọi mặt phẳng trong không gian Oxyz đều có phương trình dạng: Ax By Cz D   2 2 2
0 A B C  0
D. Trong không gian Oxyz mỗi phương trình dạng: Ax By Cz D   2 2 2
0 A B C  0 đều là phương trình
của một mặt phằng nào đó.
Câu 16: Trong không gian với hệ toạ độ Oxyz, cho ( A ; a 0;0), ( B 0; ; b 0),C(0;0; )
c , (abc  0). Khi đó phưong
trình mặt phẳng ( ABC) là: x y z x y z x y z x y z A.   1. B.   1. C.   1 D.   1 a b c b a c a c b c b a
Câu 17: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( )
P : 3x  2y z 1  0 . Mặt phẳng (P) có vectơ pháp tuyến là:     A. n  (2;3; 1  ) B. n  (3; 2; 1  ) C. n  ( 1  ;3;2) D. n  (3; 1  ;2)
Câu 18: Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng ( )
P : x  2y  2z 10  0 và ( )
Q : x  2y  2z  3  0 bằng: 4 8 7 A. B. C. D. 3 3 3 3
Câu 19: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) có phương trình 3x y z 1  0 . Trong
các điểm sau đây, điểm nào thuộc (P) . A. ( A 1; 2  ; 4  ) B. C(1; 2; 4  ) C. ( D 1  ; 2  ; 4  ) D. B(1; 2  ;4)
Câu 20: Trong không gian với hệ tọa độ Oxyz , phương trình mặt phẳng   đi qua điểm M (0; 1  ;4), nhận  n  (3; 2; 1
 ) là vectơ pháp tuyến là:
A. 3x  3y z  0
B. 2x y  3z 1  0
C. x  2y  3z  6  0
D. 3x  2y z  6  0
Câu 21: Trong không gian với hệ tọa độ Oxyz , cho hai điểm ( A 1; 2
 ;4), B(2;1;2). Viết phương trình mặt phẳng
(P) vuông góc với đường thẳng AB tại điểm A . A. ( )
P : x  3y  2z 1  0 B. ( )
P : x  3y  2z 1  0 C. ( )
P : x  3y  2z 13  0 D. ( )
P : x  3y  2z 13  0
Câu 22: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi qua ba điểm (
A 1;1; 4), B(2;7;9), C(0;9;13) .
A. 7x  2y z  9  0
B. 2x y z  2  0
C. 2x y z 1  0
D. x y z  4  0
Câu 23: Trong không gian với hệ tọa độ Oxyz , cho điểm M (3; 1  ; 2  ) và mặt phẳng ( )
P : 3x y  2z  4  0 .
Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với (P)? A. ( )
Q : 3x y  2z 14  0 B. ( )
Q : 3x y  2z  6  0 C. ( )
Q : 3x y  2z  6  0 D. ( )
Q : 3x y  2z  6  0
Câu 24: Trong không gian với hệ tọa độ Oxyz , mặt phẳng đi qua hai điểm ( A 2; 1  ;4), B(3;2; 1  ) và vuông góc
với mặt phẳng   : x y  2z  3  0 có phương trình là:
A. 11x  7 y  2z  7  0
B. 11x  7 y  2z  21  0
C. 11x  7 y  2z  7  0
D. 11x  7 y  2z  21  0
Câu 25: Trong không gian với hệ trục toa độ Oxyz, cho hai mặt phẳng () : 3x  (m 1) y  4z  2  0 ,
( ) : nx  (m  2) y  2z  4  0 . Với giá trị thực của m, n bằng bao nhiêu để ( ) song song ( )
A. m  3; n  6  .
B. m  3; n  6 . C. m  3  ;n  6 D. m  3  ;n  6  . SỞ GDĐT LÂM ĐỒNG
KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2020 – 2021
TRƢỜNG THPT CHUYÊN BẢO LỘC
Môn: TOÁN 12 (chương trình Cơ bản)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
I- TRẮC NGHIỆM (7đ)
Câu 1: Mệnh đề nào sau đây sai?
A. Nếu F x và G x đều là nguyên hàm của hàm số f x thì F x  G x . B. Nếu f
 xdx FxC thì f
 udu FuC .
C. f x f x  dx f x dx f x dx    . 1   2   1   2   D. kf
 xdx k f
 xdx (k là hằng số và k  0). Câu 2: Cho f
 xdx FxC . Khi đó với a  0 , a , b là hằng số ta có f
 axbdx bằng. A. f
 axbdx F axbC . B. f
 axbdx aFaxbC . 1 1 C. f
 axbdx
F ax b  C . D. f
 axbdx F axbC . a b a 1  Câu 3: Tích phân x e dx  bằng 0 1 1 e  1 A. B. 1 C. D. e 1 e e e Câu 4: Nếu f x 2 dx   x   x
C thì f x là x x
A. f x  2x C .
B. f x 3 2    C . 3 2
C. f x  2x  2 .
D. f x  2x 1. 2 x Câu 5: Tích phân dx  bằng 2 x  3 0 1 7 7 1 3 1 7 A. log . B. ln . C. ln . D. ln . 2 3 3 2 7 2 3 
Câu 6: Phương trình mặt phẳng  P đi qua điểm M  1
 ;2;0 và có vectơ pháp tuyến n  4;0; 5   là
A. 4x  5y  4  0 .
B. 4x  5z  4  0 .
C. 4x  5y  4  0 .
D. 4x  5z  4  0.
Câu 7: Cho f x là hàm số liên tục trên đoạn  ;
a b và c  ;
a b . Tìm mệnh đề đúng trong các mệnh đề sau. b c b b c c A. f
 xdxf
 xdx f  xdx. B. f
 xdxf
 xdx f  xdx. a a c a a c c b a b a b C. f
 xdxf
 xdx f  xdx. D. f
 xdxf
 xdx f  xdx. a c b a c c
Câu 8: Tính tích phân sin 3 d x x  0 2 2 1 1 A. B. C. D.  3 3 3 3
Câu 9: Cho hàm số y f x liên tục trên [ ; a ]
b . Diện tích hình phẳng S giới hạn bởi đồ thị hàm số
y f x, trục hoành, các đường thẳng x  ,
a x b được xác định bằng công thức nào? b a b b
A. S   f  xdx B. S f  xdx C. S f  xdx D. S f  xdx a b a a
Câu 10: Cho hàm số f x liên tục trên  ;
a b và F x là một nguyên hàm của f x . Tìm khẳng định sai. b a A. f
 xdx F a F b. B. f
 xdx  0 . a a b a b C. f
 xdx   f  xdx. D. f
 xdx F b F a. a b a 2 3 3 Câu 11: Cho f
 xdx  3, f xdx  1   . Tính
f x dx  . 1 2 1 A. 4 . B. 4  . C. 2 . D. 2  . 9 0 9 Câu 12: Giả sử f
 xdx 37 và g
 xdx 16. Khi đó, I  2 f
 x3g(x)dx  bằng: 0 9 0 A. I  26 . B. I  58 . C. I  143 . D. I  122 .
Câu 13: Với mọi hàm số f x , g x  liên tục và có đạo hàm trên  . Mệnh đề nào sau đây sai? A. kf
 xdx k f
 xdx với mọi hằng số k . B. f
 xdx f xC .   C. f
  xgxdx f  
 xdx g  xdx  .   D. f
  xgxdx f  
 xdx g  xdx  .
Câu 14: Mệnh đề nào sau đây đúng? 1 1 1 A.
dx  ln 1 4x CB. dx   4.ln  C  1 4x 1 4x 1 4x 1 1 1 1 C.
dx   .ln 8x  2  CD.
dx   .ln 1 4x C  1 4x 4 1 4x 4
Câu 15: Nguyên hàm của hàm số f x 2021  x
, (x  ) là hàm số nào trong các hàm số dưới đây? 2022 x
A. F (x) 
C , (C ) . B. 2021
F(x)  2020.x
C , (C ) . 2022 C. 2022
F(x)  x
C , (C ) . D. 2020
F(x)  2021.x
C , (C ) e 3ln x 1
Câu 16: Cho tích phân I  dx
. Nếu đặt t  ln x thì x 1 e 1 1 3t 1 e 3t 1
A. I  3t    1 dt
B. I  3t    1 dt C. I  dtD. I  dt  et t 1 0 0 1 3 3
Câu 17: Cho f , g là hai hàm số liên tục trên 1; 
3 thỏa mãn:  f xdx 10 ,  g xdx  6 . Tính 1 1 3  f
 x gxdx 1 A. 8 . B. 16 . C. 7 . D. 9 .
Câu 18: Trong không gian với hệ trục tọa độ Oxyz , mặt cầu S  2 2 2
: x y z  8x  4y  2z  4  0 có bán kính R là A. R  5 . B. R  25 . C. R  2 . D. R  5 .
Câu 19: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A4;0;  1 và B  2
 ;2;3 . Phương trình nào dưới
đây là phương trình mặt phẳng trung trực của đoạn thẳng AB ?
A. 3x y z 1  0 .
B. 6x  2y  2z 1  0 . C. 3x y z  0 .
D. 3x y z  6  0 .
Câu 20: Nếu u x và vx là hai hàm số có đạo hàm liên tục trên đoạn  ;
a b . Mệnh đề nào sau đây đúng b b b b b b A. d u v  uv  d v u   .
B. u vdx  d u x  d v x   . a a a a a a b b b b b     b C. d u v uv  d v v   . D. u d v x    d u x  . d v x  . a a a aa   a  2
Câu 21: Tích phân I  2x  1 dx
có giá trị bằng: 0 A. 1 . B. 2 . C. 3 . D. 0 .
Câu 22: Trong các hàm số sau, hàm số nào có một nguyên hàm là hàm số F x  ln x ? x
A. f x 3  .
B. f x  . x
C. f x  x .
D. f x 1  . 2 x   
Câu 23: Một nguyên hàm F x của hàm số f x  sin x thỏa mãn F  2   là:  2 
A. F x  cos x
B. F x  cos x
C. F x  cos x  2
D. F x  cos x  2
Câu 24: Cho hai hàm số f x , g x liên tục trên  . Trong các mệnh đề sau, mệnh đề nào sai? A. f
 x gx dx f
 xdxg  xdx. B. f
 x.gx dx f
 xd .x g  xdx . C. kf
 xdx k f
 xdx k  0;k. D. f
 x gx dx f
 xdxg  xdx.
Câu 25: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3; 2  ;3 và B 1
 ;2;5 . Tìm tọa độ trung điểm
I của đoạn thẳng AB .
A. I 2; 2;  1 .
B. I 1; 0; 4.
C. I 2; 0;8 . D. I 2; 2  ;  1 .
Câu 26: Trong không gian Oxyz , điểm nào sau đây thuộc trục Oz? A. M  1  ;0;0 .
B. M 0; 2  ;0 .
C. M 0;0;3 .
D. M 1;0;0 .
Câu 27: Cho F x là một nguyên hàm của hàm số f x . Khi đó hiệu số F 0  F   1 bằng 1 1 1 1 A. F  xdx . B. f  xdx. C. F  xdx . D.
f x dx  . 0 0 0 0 2 2 2
Câu 28: Trong không gian Oxyz , mặt cầu  x  
1   y  2   z  3  4 có tâm và bán kính lần lượt là A. I  1  ; 2
 ;3 ; R  2. B. I 1;2; 3
  ; R  2. C. I 1;2; 3
  ; R  4. D. I  1  ; 2  ;3 ; R  4 .
Câu 29: Họ các nguyên hàm của hàm số ( ) 3x f x  . x 1  x x 3  x 3 A. 3 dx   C  .
B. 3xd  3x x ln 3  C  . C. x x 1 3 dx  3  C  . D. 3 dx   C  . x 1 ln 3 2021 d
Câu 30: Tính tích phân   x I . x 1 A. I  2021.
B. I  2021.ln 2 1.
C. I  ln 2021.
D. I  ln 2020 .
Câu 31: Cho hàm số f x có đạo hàm liên tục trên đoạn 1;  3 thỏa mãn f  
1  2 và f 3  9 . Tính 3 I f   xdx. 1 A. I  7 . B. I  2 . C. I 18 . D. I 11.
Câu 32: Mặt phẳng   : 2x  5y z 1  0 có một vectơ pháp tuyến là:    
A. n  2;5;  1 .
B. m  2;5;  1 . C. b  2; 5  ;  1 . D. a   2  ;5;  1 .
Câu 33: Trong không gian hệ tọa độ Oxyz , phương trình nào sau đây là phương trình của mặt phẳng Oxz ? A. y  0 . B. x  0 . C. z  0 .
D. y 1  0 . 
Câu 34: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A1; 2; 4 và B  3
 ;2;2 . Toạ độ của AB là A. 4;0; 6   . B.  1  ;2;  1 . C.  4  ;0;6 . D. 2; 4; 2   .
Câu 35: Trong không gian Oxyz , điểm M 3;4; 2
  thuộc mặt phẳng nào trong các mặt phẳng sau?
A. R : x y  7  0 .
B. S  : x y z  5  0.
C. Q : x 1  0 .
D. P : z  2  0 .
II – TỰ LUẬN (3đ)  2
Câu 1 (1,0 điểm): Tính giá trị của tích phân sau: cos  e .sin d  x I x x . 0
Câu 2 (1,0 điểm): Một cái bồn gồm hai nửa hình cầu đường kính 18 dm , và một hình trụ có chiều cao 36 dm .
Tính thể tích V của cái bồn đó.
Câu 3 (0,5 điểm): Biết hàm số y f x có f  x 2
 3x  2x m 1, f 2 1 và đồ thị của hàm số y f x
cắt trục tung tại điểm có tung độ bằng 5
 . Tìm hàm số f x . Câu 4 (0,5 điểm):   2 f x
Cho hàm số f x liên tục trên R và f x 1  2 f  3 . x  
Tính tích phân I  dx   x x 1 2 ----------- HẾT ----------