Đề cương giữa kỳ 2 Toán 12 năm 2022 – 2023 trường Hoàng Văn Thụ – Hà Nội

Đề cương giữa kỳ 2 Toán 12 năm 2022 – 2023 trường Hoàng Văn Thụ – Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

91 46 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
TRƯỜNG THPT HOÀNG VĂN THỤ
MÔN TOÁN
ĐỀ CƯƠNG ÔN TẬP GIA HC K II
MÔN TOÁN - LỚP 12
NĂM HC 2022- 2023
1. MỤC TIÊU
1.1. Kiến thức : Học sinh ôn tập các kiến thức về:
- Nguyên hàm.
- Tích phân.
- Ứng dụng của tích phân trong hình học.
- Hệ tọa độ trong không gian.
- Phương trình mặt phẳng.
- Phương trình mặt cầu.
1.2. Kĩ năng: Học sinh rèn luyện các kĩ năng:
+ Rèn luyện tính cẩn thận chính xác trong tính toán.
+ Biết vận dụng các kiến thức đã học vào giải bài tập.
+Phát triển tư duy logic, khả năng linh hoạt.
+ Sử dụng thành thạo máy tính.
2. NỘI DUNG:
2.1. Các câu hỏi định tính v:
+ Đnh nghĩa, các tính cht, công thức nguyên hm, phương pháp tìm nguyên hm.
+ Đnh nghĩa, các tính cht của tích phân, phương pháp tính tích phân v ứng dụng của tích phân trong
hình học.
+ Hệ trục tọa độ, tọa độ của điểm v vecto; các php toán cộng, tr, nhân vecto vi một s, tích vô hưng
của hai vecto, tích c hưng hai vecto.
+ Phương trình mặt phẳng, phương trình mặt cầu.
2.2. Các câu hỏi định lượng v:
+ Tìm họ nguyên hm của hm s.
+ Tìm nguyên hm tha mãn điều kiện cho trưc.
+ Tính tích phân.
+ Tính diện tích hình phẳng, thể tích vật thể, thể tích khi trn xoay.
+ Tìm tọa độ điểm, vecto tha mãn điều kiện cho trưc.
+ Tính s đo gc gia hai vecto, gc gia hai mặt phẳng.
+ Tính khoảng cách gia hai điểm, khoảng cách t 1 điểm đến 1 mặt phẳng, khoảng cách gia hai mặt
phẳng song song.
+ Tính chu vi tam giác, diện tích tam giác, thể tích khi chp, khi hộp,…
+ Viết phương trình mặt phẳng, mặt cầu.
2
2.3. MA TRẬN ĐỀ (THỜI GIAN LÀM BÀI: 90’)
2. 4. Câu hỏi và bài tập minh họa
Câu 1. Cho
( ) ( )
,f x g x
là các hàm s xác đnh và liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x− = −


. B.
.
C.
( ) ( )
2 d 2 df x x f x x=

. D.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x+ = +


.
Câu 2. Cho hàm s
( )
Fx
là một nguyên hàm của hàm
( )
fx
trên khoảng
K
nếu
A.
( ) ( )
F x f x
=
. B.
( ) ( )
F x f x
=
. C.
( ) ( )
F x f x

=
. D.
( ) ( )
F x f x

=
.
Câu 3. Hàm s no dưi đây không phải là nguyên hàm của hàm s
( )
3
f x x=
?
A.
4
2
4
x
y =+
. B.
4
4
x
y =
. C.
2
3yx=
. D.
4
2019
2
4
x
y =−
.
Câu 4. Họ nguyên hm của hàm s
( )
3cos 3
x
f x x=−
là:
A.
( )
3
3sin
ln3
x
f x dx x C= − +
. B.
( )
3
3sin
ln3
x
f x dx x C= − + +
.
C.
( )
3
3sin
ln3
x
f x dx x C= + +
. D.
( )
3
3sin
ln3
x
f x dx x C= − − +
.
Câu 5. Nguyên hàm
( )
Fx
của hàm s
( )
2
1
2
sin
f x x
x
=+
tha mãn
1
4
F

=−


là
A.
( )
2
2
cot
16
F x x x
= − −
. B.
( )
2
2
cot
16
F x x x
= − + −
. C.
( )
2
cotF x x x= − +
. D.
( )
2
2
cot
16
F x x x
= − +
.
Câu 6. Trong các khẳng đnh sau, khẳng đnh no sai?
A.
2 d 2 ln 2
xx
xC=+
. B.
1
cos2 d sin2
2
x x x C=+
.
MA TRẬN ĐỀ KIM TRA GIA HC K 2 MÔN TON LỚP 12
Kiến thức
Nhận biết
Thông hiu
Vận dng
Vận dng cao
Nguyên hm
4
4
1
Tích phân
5
4
2
3
Ứng dụng của tích phân
4
4
1
Hệ tọa độ trong không gian
2
2
1
Phương trình mặt phẳng
2
3
1
2
Phương trình mặt cầu
1
3
1
Tng
18
20
7
5
3
C.
2
2
d
2
x
x
e
e x C=+
. D.
( )
1
d ln 1 1
1
x x C x
x
= + + −
+
.
Câu 7. Tìm nguyên hàm
( )
Fx
của hàm s
( )
2
21
fx
x
=
−
tha mãn
( )
57F =
.
A.
( )
2 2 1F x x=−
. B.
( )
2 2 1 1F x x= − +
. C.
( )
2 1 4F x x= − +
. D.
( )
2 1 10F x x= − −
.
Câu 8. Gọi
( )
Fx
là một nguyên hàm của hàm s
2
ln
ln 1.
x
yx
x
=+
mà
( )
1
1
3
F =
. Giá tr của
( )
2
Fe
bằng:
A.
8
9
. B.
1
9
. C.
8
3
. D.
1
3
.
Câu 9. Biết
( )
( ) ( )
52 51
50
1 2 1 2
1 2 d ; ,
xx
x x x C a b
ab
−−
− = − +
. Tính giá tr của
ab−
.
A.
0
. B.
4
. C.
1
. D.
4−
.
Câu 10. Xét nguyên hàm
d
1
x
x
e
x
e +
, nếu đặt
1=+
x
te
thì
d
1
x
x
e
x
e +
bằng
A.
2dt
. B.
2
2dtt
. C.
2
dtt
. D.
d
2
t
.
Câu 11. Nguyên hàm của
( )
1 ln
ln
x
fx
xx
+
=
là:
A.
( )
ln lnF x x C=+
. B.
( )
2
ln lnF x x x C=+
.C.
( )
ln lnF x x x C= + +
. D.
( )
ln lnF x x x C=+
.
Câu 12. Tìm họ nguyên hàm:
3
4
()
1
x
F x dx
x
=
−
A.
4
( ) ln 1F x x C= − +
. B.
4
1
( ) ln 1
4
F x x C= − +
.C.
4
1
( ) ln 1
2
F x x C= − +
. D.
4
1
( ) ln 1
3
F x x C= − +
.
Câu 13. Cho
()Fx
là một nguyên hàm của hàm s
( ) ( )
5 1 e
x
f x x=+
và
( )
03F =
. Tính
( )
1F
.
A.
( )
1 11e 3F =−
. B.
( )
1 e 3F =+
. C.
( )
1 e 7F =+
. D.
( )
1 e 2F =+
.
Câu 14. Họ nguyên hàm
( )
Fx
của hàm s
( )
2
cos
1 cos
x
fx
x
=
−
là
A.
( )
cos
sin
x
F x C
x
= − +
. B.
( )
1
sin
F x C
x
= − +
. C.
( )
1
sin
F x C
x
=+
. D.
( )
2
1
sin
F x C
x
=+
.
Câu 15.
2
23
d
1
xx
x
x
++
+
bằng
A.
2
2ln | 1|
2
x
x x C+ + + +
. B.
2
ln | 1|
2
x
x x C+ + + +
.
C.
2
2ln | 1|
2
x
x x C+ + − +
. D.
2ln | 1|x x C+ + +
4
Câu 16. Cho hàm s
( )
fx
tha mãn
( )
2
2
45
x
fx
xx
+
=
++
và
( )
22f −=
. Giá tr
( )
1f
bằng
A.
ln10 2+
. B.
1
ln10 2
2
−
. C.
ln10 2−
. D.
1
ln10 2
2
+
.
Câu 17. Họ nguyên hàm của hàm s
( )
2
lnf x x=
là
A.
2
ln 2 ln 2x x x x x c− + +
. B.
2
ln 2x x x c++
.
C.
2
ln 2 ln 2x x x x x c+ + +
. D.
2
ln 2x x x c−+
.
Câu 18. Cho
( )
Fx
là một nguyên hàm của hàm s
( )
21
23
x
fx
x
+
=
−
tha mãn
(2) 3F =
. Tìm
( )
Fx
:
A.
( ) 4ln 2 3 1F x x x= + − +
. B.
( ) 2ln(2 3) 1F x x x= + − +
.
C.
( ) 2ln 2 3 1F x x x= + − +
. D.
( ) 2ln | 2 3| 1F x x x= + − −
.
Câu 19. Cho
( )
Fx
là một nguyên hàm của hàm s
( )
fx
. Khi đ hiệu s
( ) ( )
10FF−
bằng
A.
( )
1
0
F x dx−
. B.
( )
1
0
f x dx
. C.
( )
1
0
F x dx
. D.
( )
1
0
f x dx−
.
Câu 20. Cho
( )
4
2
d 10f x x =
và
( )
2
4
d5g x x =−
. Tính
( ) ( )
4
2
3 5 df x g x x−


.
A.
5I =
. B.
10I =
. C.
5I =−
. D.
15I =
.
Câu 21. Tính tích phân
4
0
2cos x dx
bằng A.
1
. B.
1
2
. C.
2
. D.
Câu 22. Tính giá tr của tích phân
2
4
1
1
dI x x
x

=+


A.
111
4
I =
. B.
305
16
I =
. C.
196
15
I =
. D.
208
17
I =
.
Câu 23. Cho
( )( )
3
1
d
ln2 ln5 ln7 ( , , )
14
x
a b c a b c
xx
= + +
++
. Tính giá tr
4S a b c= + −
A.
2S =
. B.
3S =
. C.
4S =
. D.
5S =
.
Câu 24. Cho
( ) ( )
,f x g x
là các hàm s liên tục trên
1;3
và tha
mãn
( ) ( )
3
1
3 d 10f x g x x+=


( ) ( )
3
1
2 d 6f x g x x−=


. Tính
( ) ( )
3
1
dI f x g x x=+


bằng
A.
7I =
. B.
6I =
. C.
8I =
. D.
9I =
.
Câu 25. Biết
( )
1
0
2f x dx =−
và
( )
1
2
3,f x dx =
khi đ
( )
2
0
f x dx
bằng
A.
5−
. B.
5
. C.
1−
. D.
1
.
5
Câu 26. Cho
( )
1
0
d2f x x =
. Khi đ
( )
1
0
2d
x
f x e x

+

bằng
A.
3e+
. B.
5 e+
. C.
3 e−
. D.
5 e−
.
Câu 27. Kết quả của tích phân
( )
2
0
2 1 sin dx x x
−−
được viết ở dạng
1
1
ab

−−


a
,
b
. Khẳng đnh
no sau đây l sai?
A.
28ab+=
. B.
5ab+=
. C.
2 3 2ab−=
. D.
2ab−=
.
Câu 28. Biết
( )
6
2
0
3
3 4sin d
6
ac
xx
b
+ = −
, trong đ
a
,
b
nguyên dương v
a
b
ti giản. Tính
abc++
.
A.
8
. B.
16
. C.
12
. D.
14
.
Câu 29. Cho hàm s
( )
fx
c đạo hàm liên tục trên đoạn
2;4
và tha mãn
( ) ( )
2 2, 4 2020ff==
. Tính
tích phân
( )
2
1
2dI f x x
=
.
A.
1009I =
. B.
2022I =
. C.
2018I =
. D.
1011I =
.
Câu 30. Nếu đặt
21ux=+
thì
( )
1
4
0
2 1 dxx+
bằng
A.
3
4
1
1
d
2
uu
. B.
3
4
1
duu
. C.
1
4
0
1
d
2
uu
. D.
1
4
0
duu
.
Câu 31. Tích phân
3
2
0
ln2; ,
cos
3
x
dx a b a b
x
= +
. Khi đ giá tr
ab
thuộc khoảng no sau đây?
A.
2; 1
. B.
1
0;
3
. C.
11
;
22
. D.
1;2
.
Câu 32. Biết
( )
4
2
0
ln 9 d ln5 ln3x x x a b c+ = + +
, trong đ
a
,
b
,
c
là các s nguyên. Giá tr của biểu thức
T a b c= + +
là A.
10T =
. B.
9T =
. C.
8T =
. D.
11T =
.
Câu 33. Cho tích phân
0
(2 )sinI x xdx
=−
. Đặt
2 , sinu x dv xdx= − =
thì
I
bằng
A.
( )
0
0
2 cos cosx x xdx
− − −
B.
( )
0
0
2 cos cosx x xdx
−+
.
C.
( )
0
0
2 cosx xdx
−+
. D.
( )
0
0
2 cos cosx x xdx
− − +
.
6
Câu 34. Cho hàm s
( )
y f x=
c đạo hàm trên
0;1
. Biết
( )
1
1f
e
=
và
( )
1
0
1
d
e
f x x
e
−
=
.
Tính
( )
1
0
dI xf x x
=
.
A.
1I =
. B.
2e
I
e
−
=
. C.
2 e
I
e
−
=
. D.
1I =−
.
Câu 35. Tính tích phân
( )
4
0
1 sin dI x x x
=+
.
A.
82
8
I
−
=
. B.
2
12
8
I
= − −
. C.
2
12
8
I
= − +
. D.
82
8
I
+
=
.
Câu 36. Cho hàm s
( )
fx
liên tục trong đoạn
1;e
, biết
( )
e
1
d1
fx
x
x
=
,
( )
e1f =
. Khi đ
( )
e
1
.ln dI f x x x
=
bằng
A.
4I =
. B.
3I =
. C.
1I =
. D.
0I =
.
Câu 37. Cho
2
1
()
2
Fx
x
=
là một nguyên hàm của hàm s
()fx
x
. Tính
1
'( )ln d
e
f x x x
bằng:
A.
2
2
3
2
e
I
e
−
=
. B.
2
2
2 e
I
e
−
=
. C.
2
2
2e
I
e
−
=
. D.
2
2
3
2
e
I
e
−
=
.
Câu 38. Biết
4
2
0
ln 1 d ln5
a
x x x c
b
, trong đ
,,abc
là các s nguyên. Giá tr của biểu
thức
T a b c
là
A.
5T =
. B.
4T =
. C.
9T =
. D.
1T =
.
Câu 39. Cho hàm s
( )
fx
c đạo hàm trên và tha mãn
( )
3
0
2 4 d 8x f x x
− =
;
( )
22f =
. Tính
( )
1
2
2dI f x x
−
=
.
A.
5I =−
. B.
10I =−
C.
5I =
. D.
10I =
.
Câu 40. Kí hiệu
S
là diện tích hình phẳng gii hạn bởi đồ th hàm s
( )
y f x=
, trục honh, đường thẳng
, x a x b==
(như hình bên).
Hi
khẳng đnh no dưi đây l khẳng đnh đúng?
A.
( ) ( )
dd
cb
ac
S f x x f x x=+

. B.
( ) ( )
dd
cb
ac
S f x x f x x=+

.
7
C.
( ) ( )
dd
cb
ac
S f x x f x x= − +

. D.
( )
d
b
a
S f x x=
.
Câu 41. Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ dưi đây. Công thức tính S là
A.
( ) ( )
12
11
ddS f x x f x x
−
=+

. B.
( )
2
1
dS f x x
−
=
.
C.
( ) ( )
12
11
ddS f x x f x x
−
=−

. D.
( )
2
1
dS f x x
−
=−
.
Câu 42. Diện tích hình phẳng được gii hạn bởi đồ th hàm s
3
1yx
, trục honh v hai đường thẳng
0x
,
2x
là A.
5
.
2
B.
7
.
2
C.
2.
D.
7
.
3
Câu 43. Diện tích hình phẳng gii hạn bởi hai đường thẳng
0x =
,
x
=
, đồ th hàm s
cosyx=
và trục
Ox
là A.
0
cos dS x x
=
. B.
2
0
cos dS x x
=
. C.
0
cos dS x x
=
. D.
0
cos dS x x
=
.
Câu 44. Diện tích hình phẳng được gạch cho như hình vẽ bằng
A.
( )
3
2
1
2 3 .x x dx
−
− + +
B.
( )
3
2
1
2 3 .x x dx
−
−−
C.
( )
3
2
1
2 3 .x x dx
−
+−
D.
( )
3
2
1
2 3 .x x dx
−
− + −
Câu 45. Tính diện tích
S
của hình phẳng
()H
gii hạn bởi các đường cong
3
12y x x= − +
và
2
yx=−
.
A.
937
12
S =
. B.
343
12
S =
. C.
793
4
S =
. D.
397
4
S =
.
Câu 46. Diện tích của hình phẳng gii hạn bởi các đường
2
4yx=−
,
2
2y x x= − −
,
2x =−
và
3x =−
được tính bằng công thức
A.
( )
2
2
3
2 2 dxS x x
−
−
= + −
. B.
( )
1
2
2
2 2 dxS x x
−
= + −
.
C.
( )
2
2
3
2 dxS x x
−
−
= + −
. D.
( )
1
2
2
2 dxS x x
−
= + −
.
Câu 47.
Cho hình phẳng
( )
H
gii hạn bởi các đường
; 1; 4y x y x= = =
. Khi đ cho hình phẳng
( )
H
8
quay quanh trục
Ox
thì thể tích khi trn xoay thu được có thể tích tương ứng bằng:
A.
7
6
. B.
11
3
. C.
9
2
. D.
13
4
.
Câu 48. Cho hình phẳng
( )
H
gii hạn bởi các đường cong
2
; 4 3y x y x= = −
.Thể tích khi tròn xoay khi
cho hình
( )
H
quay quanh trục tung
Oy
tương ứng là:
A.
16
3
. B.
11
3
. C.
184
15
. D.
5
6
.
Câu 49. Tính thể tích vật thể gii hạn bởi hai mặt phẳng
0x =
,
x
=
. Biết rằng thiết diện của vật thể cắt
bởi mặt phẳng vuông góc vi
Ox
tại điểm c honh độ
x
( )
0 x

là một tam giác vuông cân có cạnh huyền
bằng
sin 2x +
.
A.
7
1
6
+
. B.
9
1
8
+
. C.
7
2
6
+
. D.
9
2
8
+
.
Câu 50. Trong không gian vi hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:3 2 0P y z− + =
. Vectơ no dưi đây l
vectơ pháp tuyến của
( )
P
?
A.
( )
1; 1;2n = − −
. B.
( )
3;0;2n =
. C.
( )
3; 1;2n =−
. D.
( )
0; 3;1n =−
.
Câu 51. Trong không gian vi hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:1
3 2 1
x y z
P + + =
. Vectơ no dưi đây l
một vectơ pháp tuyến của
( )
P
?
A.
( )
1
6;3;2n =
. B.
( )
2
2;3;6n =
. C.
3
11
1; ;
23
n
=


. D.
( )
4
3;2;1n =
.
Câu 52. Trong không gian
,Oxyz
cho hai điểm
(1; 1;2)A
và
(2;1;3).B
Gọi
P
là mặt phẳng qua
A
và
vuông góc vi đường thẳng
,AB
điểm no dưi đây thuộc
?P
A.
2; 1;1 .
B.
2; 1; 1 .
C.
2;1; 1 .
D.
1; 2;1 .
Câu 53. Trong không gian vi hệ trục tọa độ
Oxyz
,
cho ba điểm
( ) ( )
1;2;0 , 2;1;1AB= = −
,
( )
3;0; 2C =−
. Phương trình mặt phẳng đi qua
A
, vuông góc vi đường thẳng
BC
là:
A.
5 3 3 0x y z− − − =
. B.
30x y z+ − − =
. C.
20x y z− − =
. D.
4 3 3 2 0x y z− − + =
.
Câu 54. Trong không gian vi hệ tọa độ
Oxyz
, viết phương trình của mặt phẳng
( )
P
đi qua các điểm
( )
1;0;0A
;
( )
0;2;0B
;
( )
0;0; 3C −
.
A.
1
1 2 3
x y z
+ − =
. B.
1
1 2 3
x y z
+ + =
. C.
6 3 2 1x y z+ + =
. D.
6 3 2 0x y z+ + =
.
Câu 55. Trong không gian
Oxyz
, cho hai điểm
( )
4;0;1A
,
( )
2;2;3B −
. Mặt phẳng trung trực của đoạn
thẳng
AB
c phương trình l:
A.
6 2 2 1 0x y z− − − =
. B.
30x y z− − =
. C.
2 6 0x y z+ + − =
. D.
3 6 0x y z+ + − =
.
9
Câu 56. Trong không gian vi hệ tọa độ
Oxyz
, phương trình no dưi đây l phương trình của mặt
phẳng chứa trục
Ox
v đi qua điểm
(2;1; 1)K −
?
A.
20xz+=
. B.
20xz−=
. C.
20yz− − =
. D.
Câu 57. Trong không gian vi hệ trục tọa độ
,Oxyz
cho hai mặt phẳng là
( )
:2 2 2 0P x y z− + + =
và
( )
2
:0Q a x by z a+ + + =
, trong đ
,ab
là các s thực. Để
( )
P
song song vi
( )
Q
thì giá tr của biểu thức
2T a b=+
bằng:
A.
1−
. B. 0. C.
2−
. D. 3.
Câu 58. Trong không gian
( )
Oxyz
, cho hai điểm
( ) ( )
2;1; 3 , 1;2;1AB−−
. Toạ độ của vctơ
AB
là :
A.
( )
3; 1;4 .−−
B.
( )
3;1; 4 .−
C.
( )
3;1;4 .−
D.
( )
3; 1; 4−−
.
Câu 59. Trong không gian
Oxyz
, cho điểm
( )
2;5;0M −
. Tìm hình chiếu vuông góc của điểm
M
lên trục
Oy
.
A.
( )
2;0;0M
−
. B.
( )
2;5;0M
. C.
( )
0; 5;0M
−
. D.
( )
0;5;0M
.
Câu 60. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
1;3; 5 , 3;1; 1AB− − −
. Tìm toạ độ trọng tâm
G
của
tam giác
OAB
.
A.
24
; ; 2
33
G

−−


. B.
24
; ; 2
33
G

− − −


. C.
24
; ; 2
33
G

−−


. D.
24
; ; 2
33
G

−−


.
Câu 61. Trong không gian vi hệ trục tọa độ
Oxyz
, cho hình bình hành
ABCD
. Biết
( )
2;1; 3A −
,
( )
0; 2;5B −
và
( )
1;1;3C
. Diện tích hình bình hành
ABCD
là
A.
2 87
. B.
349
2
. C.
349
. D.
87
.
Câu 62. Trong không gian
Oxyz
, cho hình chóp
.A BCD
có
(0;1; 1), (1;1;2), (1; 1;0)A B C−−
và
(0;0;1)D
.
Tính độ di đường cao của hình chóp
.A BCD
.
A.
22
. B.
32
2
. C.
32
. D.
2
2
.
Câu 63. Trong không gian vi hệ trục tọa độ
Oxyz
, cho
2 2 2OA i j k= + +
,
( 2;2;0)−B
và
(4;1; 1)−C
.
Trên mặt phẳng
()Oxz
, điểm no dưi đây cách đều ba điểm
,,A B C
.
A.
31
;0;
42
N

−−


. B.
31
;0;
42
P

−


. C.
31
;0;
42
Q

−


. D.
31
;0;
42
M



.
Câu 64. Trong không gian vi hệ tọa độ
Oxyz
, cho tam giác
ABC
có
( )
0;1;4A
,
( )
3; 1;1B −
,
( )
2;3;2C −
.
Tính diện tích
S
tam giác
ABC
.
A.
2 62S =
. B.
12S =
. C.
6S =
. D.
62S =
.
Câu 65. Trong không gian tọa độ Oxyz, cho tứ diện
ABCD
vi
( ) ( ) ( )
1; 2;4 , 4; 2;0 , 3; 2;1A B C− − − − −
và
( )
1;1;1D
. Độ cao của tứ diện kẻ t
D
bằng
10
A. 3. B. 1. C. 2. D.
1
2
Câu 66. Trong không gian vi hệ trục tọa độ
,Oxyz
cho tam giác
ABC
biết
( 5;7; 9), (7;9; 5),AB− − −
( 9; 7;5).C −−
Gọi điểm
( ; ; )H a b c
là trực tâm của tam giác
.ABC
Tính
2 2 2
.S a b c= + +
A. Đáp án khác. B.
155.S =
C.
211
.
9
S =
D.
211.S =
Câu 67. Trong không gian
Oxyz
, có tt cả bao nhiêu giá tr nguyên của
m
để
( ) ( )
2 2 2 2
2 1 2 2 2 6 5 0x y z m y m z m+ + + − − − + + =
l phương trình của một mặt cầu?
A.
6
B.
5
C.
7
D.
4
Câu 68. Trong không gian vi hệ tọa độ
Oxyz
, cho tam giác
ABC
vi
(1;0;0)A
,
(3;2;4)B
,
(0;5;4)C
.
Tìm tọa độ điểm
M
thuộc mặt phẳng
()Oxy
sao cho
2MA MB MC++
nh nht.
A.
(1;3;0)M
. B.
(1; 3;0)M −
. C.
(3;1;0)M
. D.
(2;6;0)M
.
2.5. Đ minh họa
Câu 1. Cho
( ) ( )
,f x g x
là các hàm s xác đnh và liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x− = −


. B.
( ) ( )
d dtf x x f t=

.
C.
( ) ( )
ddxf x x x f x x=

. D.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x+ = +


.
Câu 2. Họ nguyên hm của hàm s
( )
32
f x x x=+
lơp;
A.
2
32x x C++
. B.
43
11
43
x x C++
. C.
43
x x C++
. D.
43
43x x C++
.
Câu 3. Họ các nguyên hàm của hàm s
( )
3
e1
x
fx=+
là
A.
3
3e
x
C+
. B.
3
1
e
3
x
C+
. C.
3
3e
x
xC++
. D.
3
1
e
3
x
xC++
.
Câu 4. Tìm nguyên hàm
( )
Fx
của hàm s
( )
6 sin3f x x x=+
, biết
( )
2
0
3
F =
.
A.
( )
2
cos3 2
3
33
x
F x x= − +
. B.
( )
2
cos3
31
3
x
F x x= − −
.
C.
( )
2
cos3
31
3
x
F x x= + +
. D.
( )
2
cos3
31
3
x
F x x= − +
.
Câu 5. Hàm s
( ) ( )
5
12f x x=−
có một nguyên hàm là
( )
Fx
tha
12
23
F

−=


. Tính
( )
1F
.
A.
( )
1 10F =−
. B.
( )
15F =−
. C.
( )
59
1
12
F =
. D.
( )
71
1
12
F =
.
Câu 6. Xét
( )
5
34
4 3 dI x x x=−
. Bằng cách đặt:
4
43ux=−
, khẳng đnh no sau đây đúng?
11
A.
5
1
d
16
I u u=
B.
5
1
d
12
I u u=
. C.
5
dI u u=
. D.
5
1
d
4
I u u=
.
Câu 7. Tìm nguyên hàm của hàm s
( ) ( )
1e
x
f x x=+
A.
2e
x
xC+
. B.
( )
2e
x
xC++
. C.
( )
1e
x
xC−+
. D.
e
x
xC+
.
Câu 8.
cos dx x x
bằng
A.
2
sin
2
x
xC+
. B.
sin cosx x x C++
. C.
sin sinx x x C−+
. D.
2
cos
2
x
xC+
Câu 9. Tìm họ nguyên hàm
d
()
2ln 1
x
Fx
xx
=
+
.
A.
( ) 2 2ln 1F x x C= + +
. B.
( ) 2ln 1F x x C= + +
.
C.
1
( ) 2ln 1
4
F x x C= + +
. D.
1
( ) 2ln 1
2
F x x C= + +
Câu 10. Cho hàm s
( )
fx
và
( )
gx
liên tục trên
0;2
và
( )
2
0
2f x dx =
,
( )
2
0
2g x dx =−
. Tính
( ) ( )
2
0
3 f x g x dx+


. A. 4. B. 8. C. 12. D. 6
Câu 11. Tính tích phân I =
2
2
4
dx
sin x
bằng A. 1. B. 3. C. 4. D. 2.
Câu 12. Cho
( )
fx
và
( )
gx
là hai hàm s liên tục trên . Biết
( ) ( )
5
1
2 3 d 16f x g x x
−
+=


và
( ) ( )
5
1
3 d 1f x g x x
−
− = −


. Tính
( )
2
1
2 1 df x x
−
+
.
A.
1
. B.
5
2
. C.
1
2
. D.
5
.
Câu 13. Cho
( )
4
0
16
d.
3
f x x =
Tính
( )
( )
4
2
0
5
3 d .
1
I f x x
x

=−

+


A.
12I =−
. B.
0I =
. C.
20I =−
. D.
1I =
.
Câu 14. Biết
0
2
1
3 5 1 3
d ln
22
xx
x a b
x
−
+−
=+
−
, vi
,ab
. Tính
2ab+
.
A.
2−
. B.
10
. C.
20
. D.
40
.
Câu 15. Tích phân
( )
2
2
2
1
1
d
x
x
x
−
bằng
12
A.
2
3ln 2
3
+
. B.
1
ln2
2
−
. C.
3
ln2
4
+
. D.
4
2ln2
3
−
Câu 16. Tính tích phân
2
4
0
cos sinI x xdx
=
, bằng cách đặt
costx=
, mệnh đề no đưi đây đúng?
A.
1
4
0
I t dt=
. B.
1
4
0
I t dt=−
. C.
2
4
0
I t dt
=
. D.
2
4
0
I t dt
=−
.
Câu 17. Biết hàm s
()fx
là hàm liên tục trên và
9
0
( ) 9f x dx =
khi đ giá tr của
4
1
(3 3)f x dx−
là?
A.
27
. B.
24
. C.
3
. D.
0
.
Câu 18. Cho tích phân
( )
ln2
0
ln2 ln3
1
d
ee
xx
xa
I c d
b
= = − +
+
, trong đ
, , ,a b c d
là nhng s nguyên dương
và phân s
a
b
ti giản. Giá tr của biểu thức
( )
T a b c d= + + +
bằng A. 4. B. 9. C. 6. D. 8.
Câu 19. Cho
( )
fx
l hm s liên tục trên tha
( )
11f =
và
( )
1
0
1
d
3
f t t =
. Tính
( )
2
0
sin 2 . sin dI x f x x
=
A.
4
3
I =
. B.
2
3
I =
. C.
2
3
I =−
D.
1
3
I =
.
Câu 20. Biết
( )
2
2
0
3 1 e d e
x
x x a b− = +
vi
a
,
b
là các s nguyên. Giá tr
ab+
bằng
A.
12
. B.
16
. C.
6
. D.
10
.
Câu 21. Kết quả của tích phân
2
1
(2 1)ln dK x x x=−
bằng
A.
2ln2K =
. B.
1
2
K =
. C.
1
2ln2
2
K =−
. D.
1
2ln2
2
K =+
.
Câu 22. Cho
,,abc
là các s nguyên tha mãn
2
3
4
cos 2sin cos 3cos
sin
x x x x x
dx a b c
x
+−
=+
. Tính
( )
2
P a b c= + +
A.
13
. B.
49
. C.
1
. D.
9
.
13
Câu 23. Cho hai hàm s
( )
y f x=
và
( )
y g x=
liên tục trên đoạn
;ab
. Diện tích của hình phẳng gii
hạn bởi đồ th các hàm s
( )
y f x=
và
( )
y g x=
v hai đường thẳng
xa=
,
xb=
( )
ab
được tính theo công
thức là:
A.
( )
( ) ( ) d
b
a
S f x g x x=−
. B.
( )
( ) ( ) d
b
a
S f x g x x
=−
.
C.
( ) ( ) d
b
a
S f x g x x=−
. D.
( )
( ) ( ) d
b
a
S f x g x x=−
.
Câu 24. Diện tích của hình phẳng
( )
H
được gii hạn bởi đồ th hàm s
( )
y f x=
, trục hoành và hai
đường thẳng
xa=
,
xb=
( )
ab
(phần tô đậm trong hình
vẽ) tính theo công thức
A.
( )
d
b
a
S f x x=
. B.
( ) ( )
dd
cb
ac
S f x x f x x= − +

.
C.
( )
d
b
a
S f x x=
. D.
( ) ( )
dd
cb
ac
S f x x f x x=+

.
Câu 25. Cho phần hình phẳng
( )
H
được gạch chéo
như hình vẽ. Diện tích của
( )
H
được tính theo công thức no dưi đây?
A.
( )
3
1
dS f x x
−
=
. B.
( ) ( )
35
13
ddS f x x f x x
−
=+

.
C.
( ) ( )
35
13
ddS f x x f x x
−
=−

. D.
( ) ( )
35
13
ddS f x x f x x
−
= − +

.
Câu 26. Diện tích
S
của hình phẳng gii hạn bởi các đường
3
4y x x=−
và
0y =
được tính bởi công thức
no dưi đây.
A.
2
3
2
4S x x dx
−
=−
. B.
2
3
0
4S x x dx=−
. C.
( )
2
3
2
4S x x dx
−
=−
. D.
( )
2
3
2
4S x x dx
−
=−
.
Câu 27. Phần hình phẳng
( )
H
được gạch chéo trong hình vẽ dưi đây được gii hạn bởi đồ th hàm s
( )
y f x=
,
2
4y x x=+
v hai đường thẳng
2; 0xx= − =
14
Biết
( )
0
2
4
d
3
f x x
−
=
, diện tích hình phẳng
( )
H
bằng
A.
16
3
. B.
4
3
.
C.
20
3
. D.
7
3
.
Câu 28. Cho hình phẳng
( )
H
gii hạn bởi các đường
3
1y x x= − +
,
0y =
,
0x =
,
2x =
. Gọi
V
là thể
tích khi trn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề no sau đây đúng?
A.
( )
2
3
0
1dV x x x
= − +
. B.
( )
2
2
3
0
1dV x x x= − +
. C.
( )
2
2
3
0
1dV x x x
= − +
. D.
( )
2
32
0
1dV x x x
= − +
.
Câu 29. Cho hàm s
( )
fx
c đồ th trên đoạn
3;3−
là
đường gp khúc
ABCD
như hình vẽ.
Tính
( )
3
3
df x x
−
.
A.
5
2
. B.
35
6
. C.
5
2
−
. D.
35
6
−
.
Câu 30. Cho hình phẳng
D
gii hạn bởi đường cong
e
x
y =
, trục honh v các đường thẳng
0x =
,
1x =
.
Khi tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
2
e1
2
V
−
=
. B.
( )
2
e1
2
V
+
=
. C.
( )
2
e1
2
V
−
=
. D.
2
e
2
.
Câu 31. Tính thể tích khi trn xoay được tạo thành khi quay hình phẳng gii hạn bởi đồ th hàm s
2
3–y x x=
và trục hoành, quanh trục hoành.
A.
81
10
. B.
85
10
. C.
41
7
. D.
8
7
.
Câu 32. Cho hàm s
()fx
c đạo hàm liên tục trên
R
và tha mãn
(0) 3f =
và
2
( ) (2 ) 2 2f x f x x x+ − = − +
,
xR
. Tích phân
2
0
. '( )x f x dx
bằng
A.
10
3
−
. B.
5
3
−
. C.
11
3
−
. D.
7
3
−
.
Câu 33. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 3 0P x y z+ − + =
. Điểm no sau đây không thuộc
( )
P
?
x
y
D
3
-2
C
1
B
-2
1
A
15
A.
( )
0; 2;1V −
. B.
( )
2; 3;4Q −
. C.
( )
1; 1;1T −
. D.
( )
5; 7;6I −
.
Câu 34. Trong không gian vi hệ trục
Oxyz
, cho mặt phẳng
( )
:3 2 0P x z− + =
. Vc tơ no dưi đây l
một vc tơ pháp tuyến của
( )
P
?
A.
( )
3;0; 1 .n −
B.
( )
3;0; 1 .n −−
C.
( )
3; 1;2 .n −
D.
( )
3; 1;0 .n −
Câu 35. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
(2;1; 1)M −
trên mặt phẳng
()Ozx
có tọa
độ là
A.
( )
0;1;0
. B.
( )
2;1;0
. C.
( )
0;1; 1−
. D.
( )
2;0; 1−
.
Câu 36. Trong không gian
Oxyz
cho mặt cầu
( )
2 2 2
:( 1) ( 2) ( 3) 4S x y z− + + + + =
. Tâm của
( )
S
có tọa độ
là
A.
( )
1;2;3−
B.
( )
1; 2; 3−−
C.
( )
1; 2; 3− − −
D.
( )
1;2;3
Câu 37. Trong không gian
Oxyz
, cho hai điểm
( )
1; 1;2A −
và
( )
1;3;0B −
. Trung điểm của đoạn thẳng
AB
có tọa độ là
A.
( )
0;2;2
. B.
( )
2;4; 2−−
. C.
( )
1;2; 1−−
. D.
( )
0;1;1
.
Câu 38. Trong không gian vi hệ tọa độ
Oxyz
; cho điểm
( )
1;3; 2A −
và
( )
:2 2 3 0P x y z+ − − =
. Khoảng
cách t điểm
A
đến mặt phẳng
( )
P
bằng: A.
1
. B.
2
. C.
2
3
.
D.
3
.
Câu 39. Trong không gian vi hệ trục toạ độ
Oxyz
. Phương trình mặt phẳng qua
( )
2;5;1A
và song song
vi mặt phẳng
( )
Oxy
là:
A.
20x −=
B.
2 5 0x y z+ + =
C.
10z −=
D.
50y −=
Câu 40. Trong không gian
Oxyz
cho
( )
1;4;3A −
và
( )
3;2; 5B −
. Mặt phẳng trung trực của đoạn thẳng
AB
c phương trình l
A.
2 4 4 1 0x y z− − + =
. B.
2 4 3 0x y z− − + =
. C.
2 4 6 0x y z− + − =
. D.
2 4 3 0x y z− − − =
.
Câu 41. Trong không gian vi hệ trục tọa độ
Oxyz
, cho điểm
( )
2; 1;3M −−
. Phương trình mặt phẳng đi
qua các điểm lần lượt là hình chiếu của điểm
M
lên các trục tọa độ
, , Ox Oy Oz
là:
A.
1
2 1 3
x y z
+ + =
−−
. B.
0
2 1 3
x y z
+ + =
−−
. C.
1
2 1 3
x y z
+ + =
−
. D.
0
2 1 3
x y z
+ + =
−
.
Câu 42. Trong không gian vi hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 2 2 0P x y z− + − =
v điểm
( )
1;2; 1I −−
. Viết phương trình mặt cầu
( )
S
có tâm
I
và cắt mặt phẳng
( )
P
theo giao tuyến l đường tròn có
bán kính bằng
5
.
A.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 25.S x y z+ + − + + =
B.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 16.S x y z+ + − + + =
C.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 34.S x y z− + + + − =
D.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 34.S x y z+ + − + + =
16
Câu 43. Trong không gian
Oxyz
, mặt cầu
( )
S
có tâm
(2;1; 2)I −
v đi qua điểm
(1;2;3)A
. Phương trình
của mặt cầu l
A.
2 2 2
4 2 4 18 0x y z x y z+ + + − + − =
. B.
2 2 2
2 4 6 13 0x y z x y z+ + − − − − =
C.
2 2 2
4 2 4 18 0x y z x y z+ + − − + − =
. D.
2 2 2
2 4 6 13 0x y z x y z+ + + + + − =
Câu 44. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6z 2 0+ + − + − − =S x y z x y
. Tìm tọa độ tâm
I
và bán kính
R
của mặt cầu
( )
S
.
A.
( )
1; 2;3−I
và
12=R
. B.
( )
1; 2;3−I
và
4=R
. C.
( )
1;2; 3−−I
và
16=R
. D.
( )
1;2; 3−−I
và
4=R
.
Câu 45. Trong không gian vi hệ tọa độ Oxyz, cho ba điểm
( ) ( )
3;2;8 , 0;1;3MN
và
( )
2; ;4Pm
. Tìm m để
tam giác MNP vuông tại N.
A.
25m =
. B.
4m =
. C.
1m =−
. D.
10m =−
.
Câu 46. Trong không gian vi hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
( ) ( )
: 1 – 2 0P x m y z m+ + + =
và
( )
: 2 – 3 0Q x y +=
vi
m
là tham s thực. Để mặt phẳng
( )
P
và
( )
Q
vuông góc thì giá tr của
m
bằng bao
nhiêu?
A.
5m =−
. B.
1m =
. C.
3m =
. D.
1m =−
.
Câu 47. Trong không gian
Oxyz
, tính khoảng cách gia hai mặt phẳng
( )
:2 2 4 0x y z
− − − =
và
( )
:2 2 2 0x y z
− − + =
. A.
2
. B.
6
. C.
10
3
. D.
4
3
.
Câu 48. Trong không gian Oxyz, cho ba điểm A(1;0;0), B(0;0;1) và C(2;1;1). Diện tích của tam giác
ABC là.
A.
6
2
. B.
5
2
. C.
10
2
. D.
15
2
.
Câu 49. Trong không gian vi hệ trục tọa độ
Oxyz
, cho điểm
( )
1; 1;2A −
và mặt cầu
( )
2 2 2
:9S x y z+ + =
. Mặt phẳng đi qua
A
cắt
( )
S
theo giao tuyến là một đường tròn có bán kính nh nht có
phương trình l:
A.
2 2 0x y z− + − =
. B.
2 6 0x y z− + − =
. C.
20x y z− + =
. D.
2 4 0x y z− + − =
.
Câu 50. Trong không gian vi hệ tọa độ
Oxyz
, cho ba điểm
( ) ( ) ( )
1;0;0 , 2;3;0 , 0;0;3A B C
. Tập hợp các
điểm
( )
;;M x y z
tha mãn
2 2 2
23MA MB MC+ + =
là mặt cầu có bán kính bằng:
A.
3
. B.
5
. C.
3
. D.
23
.
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

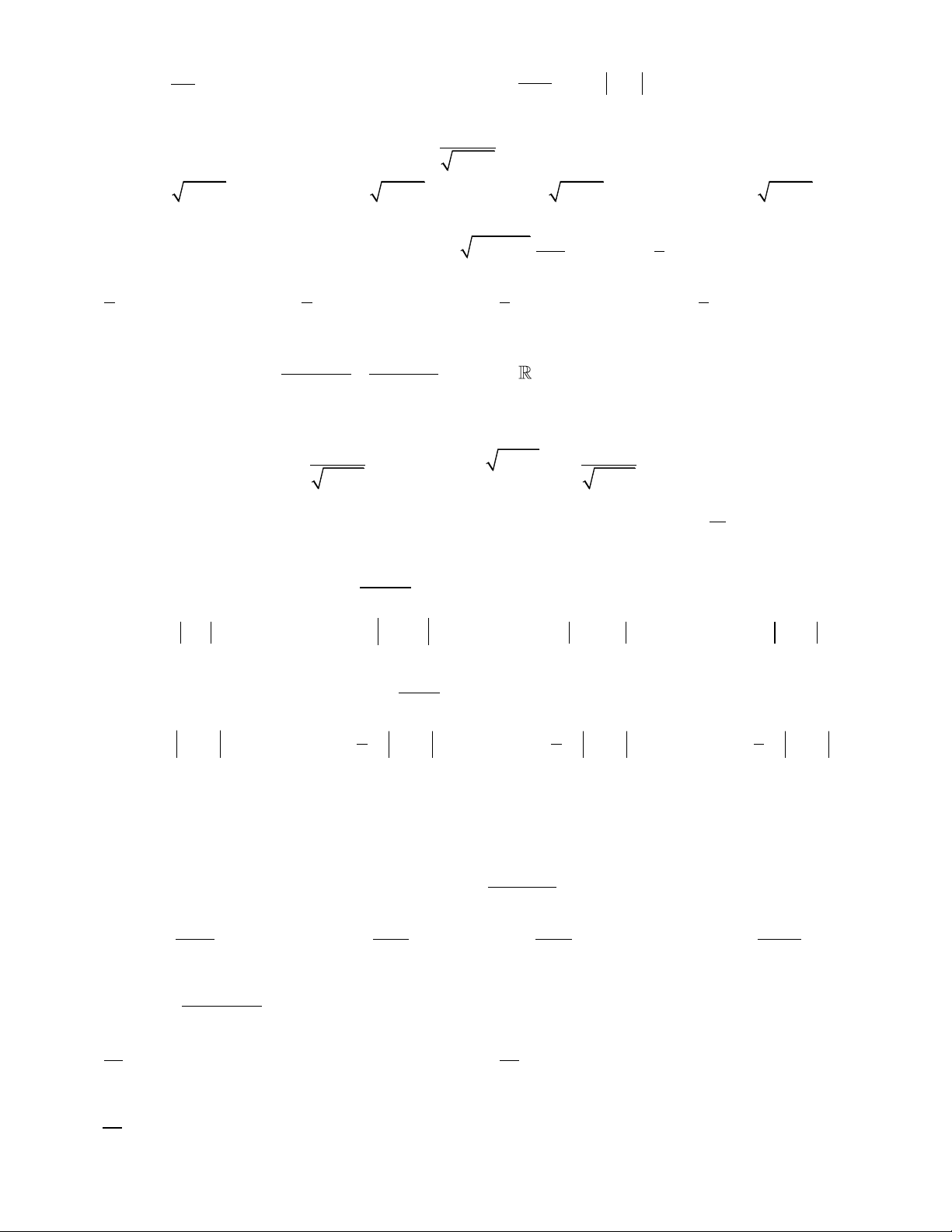
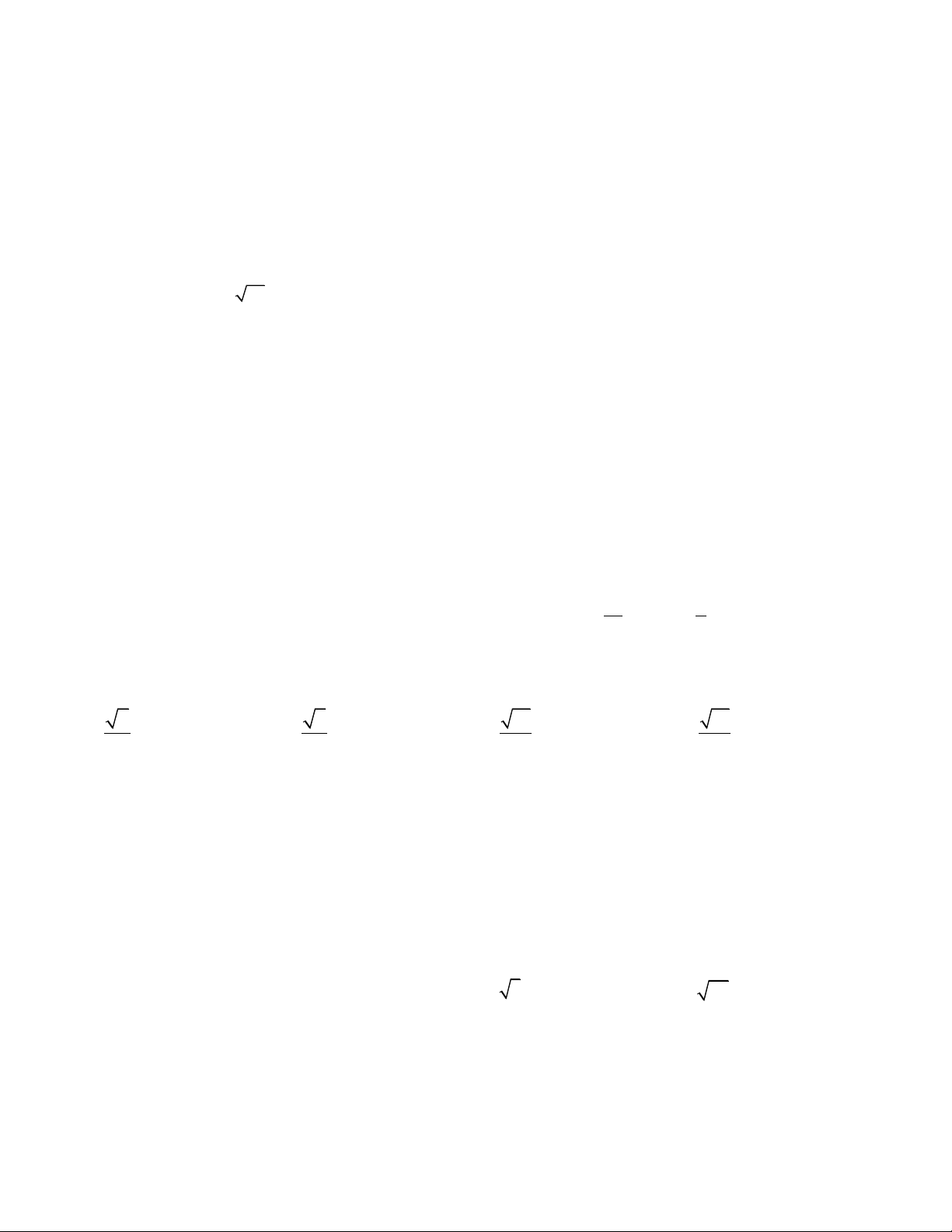
Preview text:

TRƯỜNG THPT HOÀNG VĂN THỤ
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ II MÔN TOÁN MÔN TOÁN - LỚP 12 NĂM HỌC 2022- 2023 1. MỤC TIÊU
1.1. Kiến thức : Học sinh ôn tập các kiến thức về: - Nguyên hàm. - Tích phân.
- Ứng dụng của tích phân trong hình học.
- Hệ tọa độ trong không gian.
- Phương trình mặt phẳng.
- Phương trình mặt cầu.
1.2. Kĩ năng: Học sinh rèn luyện các kĩ năng:
+ Rèn luyện tính cẩn thận chính xác trong tính toán.
+ Biết vận dụng các kiến thức đã học vào giải bài tập.
+Phát triển tư duy logic, khả năng linh hoạt.
+ Sử dụng thành thạo máy tính. 2. NỘI DUNG:
2.1. Các câu hỏi định tính về:
+ Định nghĩa, các tính chất, công thức nguyên hàm, phương pháp tìm nguyên hàm.
+ Định nghĩa, các tính chất của tích phân, phương pháp tính tích phân và ứng dụng của tích phân trong hình học.
+ Hệ trục tọa độ, tọa độ của điểm và vecto; các phép toán cộng, trừ, nhân vecto với một số, tích vô hướng
của hai vecto, tích có hướng hai vecto.
+ Phương trình mặt phẳng, phương trình mặt cầu.
2.2. Các câu hỏi định lượng về:
+ Tìm họ nguyên hàm của hàm số.
+ Tìm nguyên hàm thỏa mãn điều kiện cho trước. + Tính tích phân.
+ Tính diện tích hình phẳng, thể tích vật thể, thể tích khối tròn xoay.
+ Tìm tọa độ điểm, vecto thỏa mãn điều kiện cho trước.
+ Tính số đo góc giữa hai vecto, góc giữa hai mặt phẳng.
+ Tính khoảng cách giữa hai điểm, khoảng cách từ 1 điểm đến 1 mặt phẳng, khoảng cách giữa hai mặt phẳng song song.
+ Tính chu vi tam giác, diện tích tam giác, thể tích khối chóp, khối hộp,…
+ Viết phương trình mặt phẳng, mặt cầu. 1
2.3. MA TRẬN ĐỀ (THỜI GIAN LÀM BÀI: 90’)
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ 2 MÔN TOÁN LỚP 12 Kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao Nguyên hàm 4 4 1 Tích phân 5 4 2 3
Ứng dụng của tích phân 4 4 1
Hệ tọa độ trong không gian 2 2 1 Phương trình mặt phẳng 2 3 1 2 Phương trình mặt cầu 1 3 1 Tổng 18 20 7 5
2. 4. Câu hỏi và bài tập minh họa
Câu 1. Cho f ( x), g ( x) là các hàm số xác định và liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A.  f
 (x)− g(x)dx = f
 (x)dx− g
 (x)dx. B. f
 (x)g(x)dx = f
 (x)dx. g  (x)dx. C. 2 f
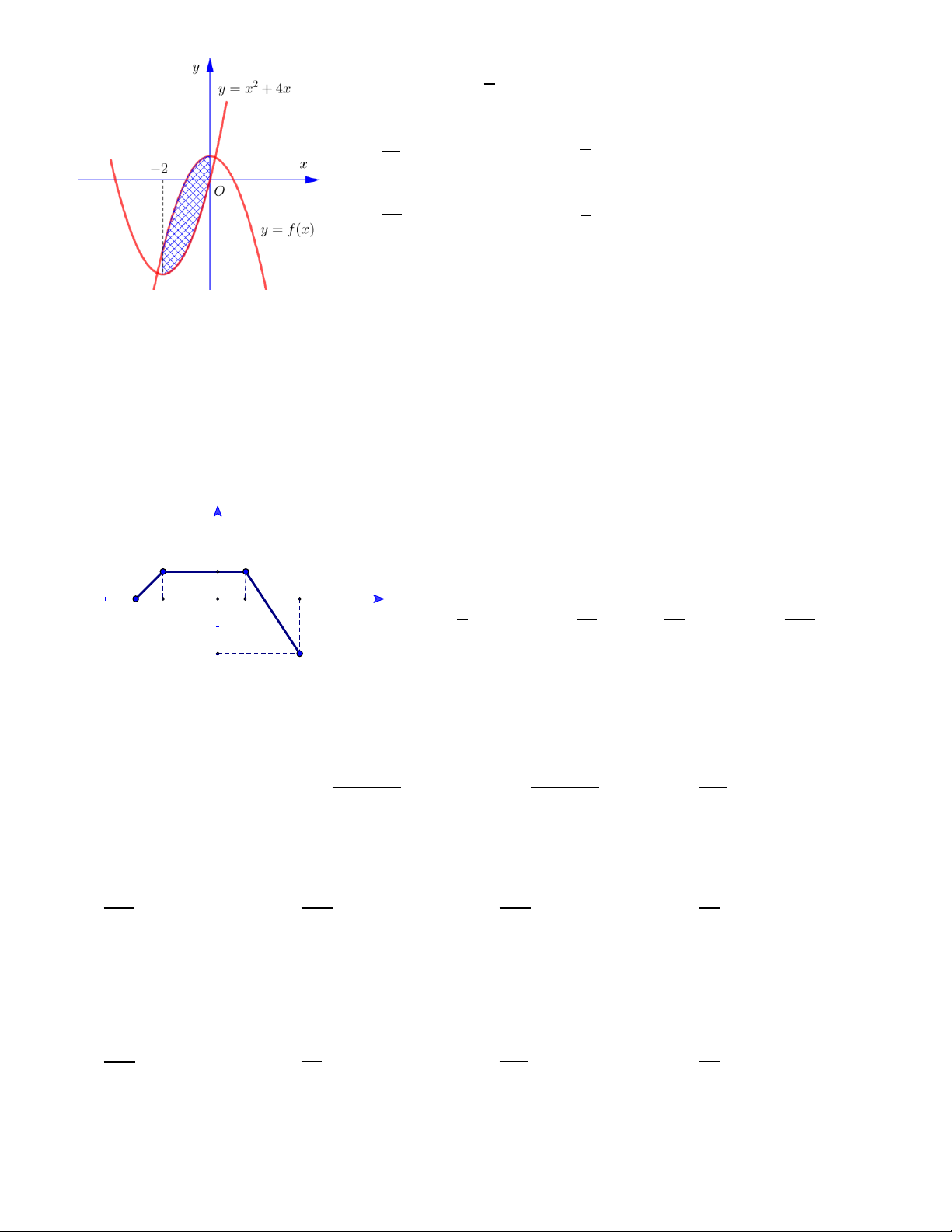
 (x)dx = 2 f
 (x)dx. D.  f
 (x)+ g(x)dx = f
 (x)dx+ g  (x)dx.
Câu 2. Cho hàm số F ( x) là một nguyên hàm của hàm f ( x) trên khoảng K nếu
A. F( x) = f ( x) .
B. F ( x) = f ( x) .
C. F ( x) = f ( x) .
D. F ( x) = f  ( x) .
Câu 3. Hàm số nào dưới đây không phải là nguyên hàm của hàm số ( ) 3 f x = x ? 4 x 4 x 4 x A. y = + 2 . B. y = . C. 2 y = 3x . D. 2019 y = − 2 . 4 4 4
Câu 4. Họ nguyên hàm của hàm số ( ) = 3cos −3x f x x là: x x A. f  (x) 3 dx = 3sin x − + C . B. f  (x) 3 dx = 3 − sin x + + C . ln 3 ln 3 x x C. f  (x) 3 dx = 3sin x + + C . D. f  (x) 3 dx = 3 − sin x − + C . ln 3 ln 3 1   
Câu 5. Nguyên hàm F ( x) của hàm số f ( x) = 2x + thỏa mãn F = 1 −   là 2 sin x  4     A. F ( x) 2 2
= cot x − x − . B. F ( x) 2 2
= −cot x + x − . C. F ( x) 2
= −cot x + x . D. F (x) 2 2 = cot x − x + . 16 16 16
Câu 6. Trong các khẳng định sau, khẳng định nào sai? 1 A. 2xd = 2x x ln 2 + C  . B. cos 2 d x x = sin 2x + C  . 2 2 2 x e 1 C. 2 x e dx = + C  . D.
dx = ln x +1 + C  ( x   − ) 1 . 2 x +1
Câu 7. Tìm nguyên hàm F ( x) của hàm số f ( x) 2 =
thỏa mãn F (5) = 7 . 2x −1
A. F ( x) = 2 2x −1 .
B. F ( x) = 2 2x −1 +1. C. F ( x) = 2x −1 + 4 .
D. F ( x) = 2x −1 −10 . ln x
Câu 8. Gọi F ( x) là một nguyên hàm của hàm số 2 y = ln x +1. mà F ( ) 1 1 = . Giá trị của 2 F (e) bằng: x 3 8 1 8 1 A. . B. . C. . D. . 9 9 3 3 52 51 − − 50 1 2x 1 2x
Câu 9. Biết x (1− 2x) ( ) ( ) dx = −
+ C;a,b 
. Tính giá trị của a − b . a b A. 0 . B. 4 . C. 1. D. 4 − . x e x e Câu 10. Xét nguyên hàm dx  , nếu đặt = x t e +1 thì dx  bằng x e +1 x e +1 2 2 dt A. 2dt  . B. 2t dt  . C. t dt  . D.  . 2 + x Câu 11.
Nguyên hàm của f ( x) 1 ln = là: x ln x
A. F ( x) = ln ln x + C . B. F ( x) 2
= ln x ln x + C .C. F (x) = ln x + ln x +C . D. F (x) = ln xln x +C . 3 x Câu 12.
Tìm họ nguyên hàm: F (x) = dx  4 x −1 1 1 1 A. 4
F (x) = ln x −1 + C . B. 4 F (x) =
ln x −1 + C .C. 4 F (x) =
ln x −1 + C . D. 4 F (x) = ln x −1 + C . 4 2 3 Câu 13.
Cho F (x) là một nguyên hàm của hàm số ( ) = (5 + )1ex f x x
và F (0) = 3. Tính F ( ) 1 . A. F ( ) 1 = 11e − 3 . B. F ( ) 1 = e + 3 . C. F ( ) 1 = e + 7 . D. F ( ) 1 = e + 2 . cos x Câu 14.
Họ nguyên hàm F ( x) của hàm số f ( x) = 2 1− là cos x x 1 A. F ( x) cos = −
+ C . B. F (x) 1 = −
+ C . C. F (x) 1 = + C . D. F ( x) = + C . sin x sin x sin x 2 sin x 2 x + 2x + 3 Câu 15. dx  bằng x +1 2 x 2 x A.
+ x + 2ln | x +1| C + . B.
+ x + ln | x +1| +C . 2 2 2 x C.
+ x + 2ln | x −1| +C .
D. x + 2 ln | x +1| +C 2 3 x + 2 Câu 16.
Cho hàm số f ( x) thỏa mãn f ( x) = f 2
− = 2 . Giá trị f ( ) 1 bằng 2 x + 4x + và ( ) 5 1 1 A. ln10 + 2 . B. ln10 − 2 . C. ln10 − 2 . D. ln10 + 2 . 2 2 Câu 17.
Họ nguyên hàm của hàm số f ( x) 2 = ln x là A. 2
x ln x − 2x ln x + 2x + c . B. 2
x ln x + 2x + c . C. 2
x ln x + 2x ln x + 2x + c . D. 2
x ln x − 2x + c . x + Câu 18.
Cho F ( x) là một nguyên hàm của hàm số f ( x) 2 1 = F
= . Tìm F (x) : 2x − thỏa mãn (2) 3 3
A. F (x) = x + 4 ln 2x − 3 + 1.
B. F (x) = x + 2 ln(2x − 3) + 1 .
C. F (x) = x + 2 ln 2x − 3 + 1 .
D. F (x) = x + 2 ln | 2x − 3 | 1 − . Câu 19.
Cho F ( x) là một nguyên hàm của hàm số f ( x) . Khi đó hiệu số F ( ) 1 − F (0) bằng 1 1 1 1 A. −F  (x)dx . B. f ( x) dx  .
C. F ( x) dx  . D. − f  (x)dx. 0 0 0 0 4 2 4 Câu 20. Cho f
 (x)dx =10và g(x)dx = 5 −  . Tính 3 f
  (x)−5g(x)dx  . 2 4 2 A. I = 5 . B. I = 10 . C. I = 5 − . D. I = 15 .  4 1 Câu 21.
Tính tích phân cos2x dx  bằng A. 1. B. . C. 2 . D. 2 0 4 2  1  Câu 22.
Tính giá trị của tích phân I = x + dx    x  1 111 305 196 208 A. I = . B. I = . C. I = . D. I = . 4 16 15 17 3 dx Câu 23. Cho
= a ln 2 + b ln 5 + c ln 7 ( a, , b c  ) 
. Tính giá trị S = a + 4b − c x +1 x + 4 1 ( )( ) A. S = 2 . B. S = 3. C. S = 4 . D. S = 5 . Câu 24.
Cho f ( x), g ( x) là các hàm số liên tục trên 1;  3 và thỏa 3 3 3 mãn  f
 (x)+3g(x)dx =10  2 f
 (x)− g(x)dx = 6 
. Tính I =  f
 (x)+ g(x)dx  bằng 1 1 1 A. I = 7 . B. I = 6 . C. I = 8 . D. I = 9 . 1 1 2 Câu 25. Biết
f ( x) dx = 2 −  và f
 (x)dx = 3,khi đó f (x)dx  bằng 0 2 0 A. 5 − . B. 5 . C. 1 − . D. 1. 4 1 1 Câu 26. Cho f
 (x)dx = 2. Khi đó 2  ( ) x
f x + e  dx   bằng 0 0
A. e + 3 . B. 5 + e . C. 3 − e . D. 5 − e .  2  1 Câu 27.
Kết quả của tích phân  (2x −1− sin x)dx được viết ở dạng    − −1  
a , b  . Khẳng định  a b  0 nào sau đây là sai? A. a + 2b = 8 . B. a + b = 5 .
C. 2a − 3b = 2 .
D. a − b = 2 .  6 ac 3 Câu 28. Biết ( 2 3 + 4 sin x)dx = − 
, trong đó a , b nguyên dương và a tối giản. Tính a + b + c . b 6 b 0 A. 8 . B. 16 . C. 12 . D. 14 . Câu 29.
Cho hàm số f ( x) có đạo hàm liên tục trên đoạn 2;4 và thỏa mãn f (2) = 2, f (4) = 2020 . Tính 2 tích phân I = f   (2x)dx . 1 A. I = 1009 . B. I = 2022 . C. I = 2018. D. I = 1011. 1 4 Câu 30.
Nếu đặt u = 2x +1thì (2x +  ) 1 dx bằng 0 3 1 3 1 1 1 A. 4 u du  . B. 4 u du  . C. 4 u du  . D. 4 u du  . 2 2 1 1 0 0  3 xCâu 31. Tích phân dx = a
+ b ln 2; a,b  
. Khi đó giá trị a b thuộc khoảng nào sau đây? 2 cos x 3 0 1 1 1 A. 2; 1 . B. 0; . C. ; . D. 1; 2 . 3 2 2 4 Câu 32. Biết x ln
 ( 2x +9)dx = aln5+bln3+c , trong đó a , b , clà các số nguyên. Giá trị của biểu thức 0
T = a + b + c là A. T = 10 . B. T = 9 .
C. T = 8 . D. T =11.  Câu 33.
Cho tích phân I = (2 − x) sin xdx
. Đặt u = 2 − x, dv = sin xdx thì I bằng 0    
A. − (2 − x) cos x − cos xdx
B. (2 − x) cos x + cos xdx  . 0 0 0 0    
C. (2 − x) + cos xdx  .
D. − (2 − x) cos x + cos xdx  . 0 0 0 0 5 1 e −1 Câu 34.
Cho hàm số y = f ( x) có đạo hàm trên 0  ;1 . Biết f ( ) 1 1 = và
f ( x)dx =  . e 0 e 1 Tính I = xf   (x)dx. 0 e − 2 2 − e A. I = 1. B. I = . C. I = . D. I = 1 − . e e  4 Câu 35.
Tính tích phân I =  (1+ x)sin d x x . 0 8 −  2  2  2 8 +  2 A. I = . B. I = 1− 2 − . C. I = 1− 2 + . D. I = . 8 8 8 8 e f ( x) Câu 36.
Cho hàm số f ( x) liên tục trong đoạn 1;e , biết dx = 1  , f (e) = 1. Khi đó x 1 e I = f   (x).ln d x x bằng 1 A. I = 4 . B. I = 3 . C. I = 1. D. I = 0 . 1 f (x) e Câu 37. Cho F (x) =
là một nguyên hàm của hàm số . Tính f '(x) ln d x x  bằng: 2 2x x 1 2 e − 3 2 2 − e 2 e − 2 2 3 − e A. I = . B. I = . C. I = . D. I = . 2 2e 2 e 2 e 2 2e 4 a Câu 38. Biết 2 x ln x 1 dx ln 5
c , trong đó a, b, c là các số nguyên. Giá trị của biểu b 0 thức T a b c là A. T = 5 . B. T = 4 . C. T = 9 . D. T =1. 3 Câu 39.
Cho hàm số f ( x) có đạo hàm trên
và thỏa mãn x f  
(2x − 4)dx = 8 ; f (2) = 2 . Tính 0 1 I = f  (2x)dx . 2 − A. I = 5 − . B. I = 10 −
C. I = 5 . D. I = 10 . Câu 40.
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành, đường thẳng
x = a, x = b (như hình bên). Hỏi
khẳng định nào dưới đây là khẳng định đúng? c b c b A. S = f
 (x)dx+ f
 (x)dx . B.S = f
 (x)dx+ f  (x)dx . a c a c 6 c b b C. S = − f
 (x)dx+ f
 (x)dx . D. S = f  (x)dx. a c a Câu 41.
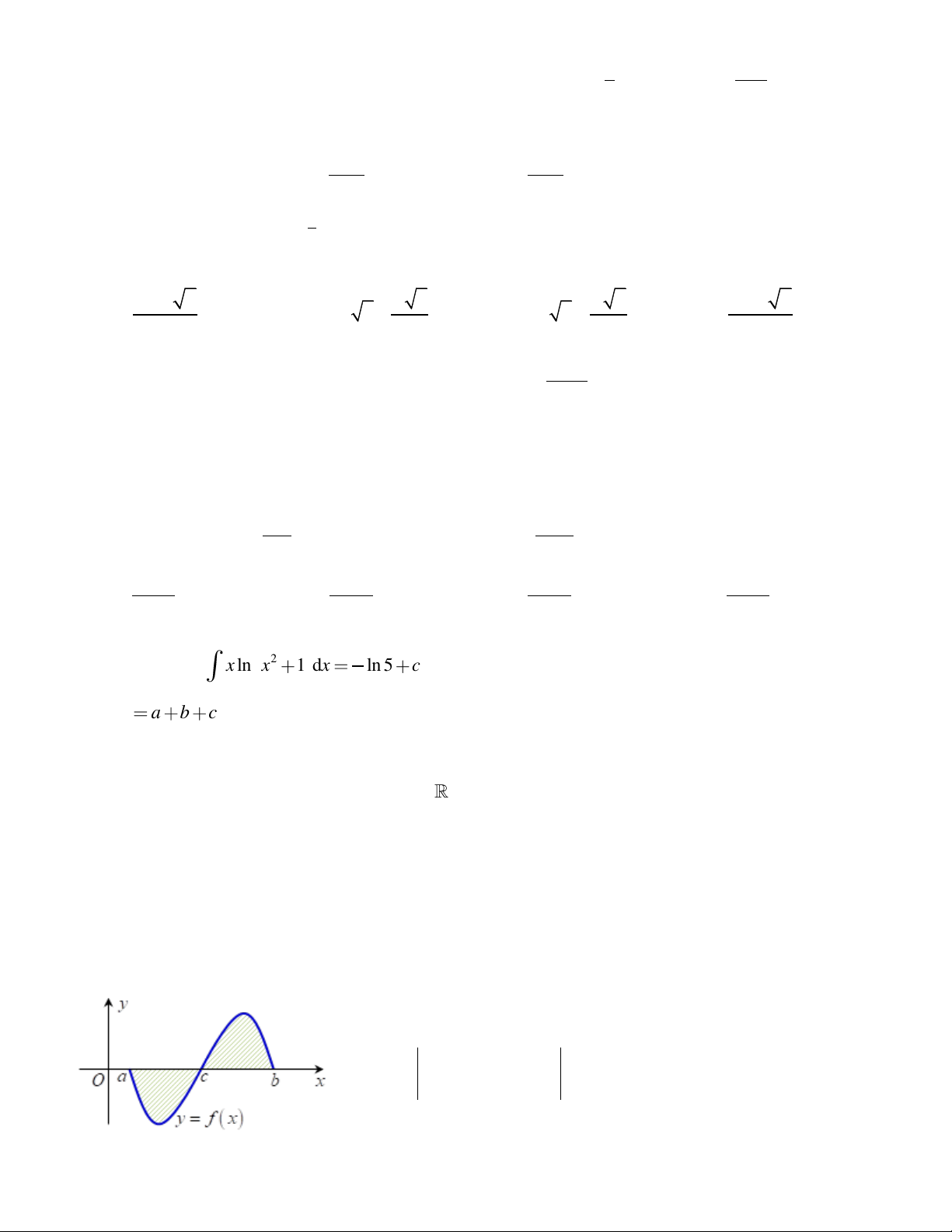
Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ dưới đây. Công thức tính S là 1 2 2 A. S = f
 (x)dx+ f
 (x)dx. B. S = f  (x)dx . 1 − 1 1 − 1 2 2 C. S = f
 (x)dx− f
 (x)dx . D. S = − f  (x)dx . 1 − 1 1 − Câu 42.
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 3 y x
1, trục hoành và hai đường thẳng 5 7 7 x 0 , x 2 là A. . B. . C. 2. D. . 2 2 3 Câu 43.
Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0 , x =  , đồ thị hàm số y = cos x và trục    
Ox là A. S = cos x dx  . B. 2
S = cos x dx  .
C. S =  cos x dx  . D. S = cos x dx  . 0 0 0 0 Câu 44.
Diện tích hình phẳng được gạch chéo như hình vẽ bằng 3 3 A.  ( 2 −x + 2x + 3) . dx B.  ( 2
x − 2x − 3) d . x 1 − 1 − 3 3 C.  ( 2
x + 2x − 3) d . x D.  ( 2
−x + 2x − 3) . dx 1 − 1 − Câu 45.
Tính diện tích S của hình phẳng (H ) giới hạn bởi các đường cong 3
y = −x +12x và 2 y = −x . 937 343 793 397 A. S = . B. S = . C. S = . D. S = . 12 12 4 4 Câu 46.
Diện tích của hình phẳng giới hạn bởi các đường 2 y = x − 4 , 2
y = −x − 2x , x = 2 − và x = 3 −
được tính bằng công thức 2 − 1 A. S = 2  ( 2
x + x − 2)dx . B. S = 2 ( 2
x + x − 2)dx . 3 − 2 − 2 − 1 C. S =  ( 2
x + x − 2)dx . D. S =  ( 2
x + x − 2)dx . 3 − 2 − Câu 47.
Cho hình phẳng ( H ) giới hạn bởi các đường y = x; y = 1; x = 4. Khi đó cho hình phẳng ( H ) 7
quay quanh trục Ox thì thể tích khối tròn xoay thu được có thể tích tương ứng bằng: 7 11 9 13 A. . B. . C. . D. . 6 3 2 4 Câu 48.
Cho hình phẳng ( H ) giới hạn bởi các đường cong 2
y = x ; y = 4x − 3 .Thể tích khối tròn xoay khi
cho hình ( H ) quay quanh trục tung Oy tương ứng là: 16 11 184 5 A. . B. . C. . D. . 3 3 15 6 Câu 49.
Tính thể tích vật thể giới hạn bởi hai mặt phẳng x = 0 , x =  . Biết rằng thiết diện của vật thể cắt
bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x (0  x   ) là một tam giác vuông cân có cạnh huyền bằng s inx + 2 . 7 9 7 9 A. +1. B. +1. C. + 2 . D. + 2 . 6 8 6 8 Câu 50.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : 3y − z + 2 = 0 . Vectơ nào dưới đây là
vectơ pháp tuyến của (P) ? A. n = ( 1 − ; 1 − ;2) . B. n = (3;0; 2) . C. n = (3; 1 − ;2) . D. n = (0; 3 − ) ;1 . x y z Câu 51.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : +
+ =1. Vectơ nào dưới đây là 3 2 1
một vectơ pháp tuyến của ( P) ?  1 1  A. n = 6;3; 2 . B. n = 2;3;6 . C. n = 1; ;   . D. n = 3; 2;1 . 4 ( ) 2 ( ) 1 ( ) 3  2 3  Câu 52.
Trong không gian Oxyz, cho hai điểm (
A 1; 1;2) và B(2;1;3). Gọi P là mặt phẳng qua A và
vuông góc với đường thẳng AB, điểm nào dưới đây thuộc P ? A. 2; 1;1 . B. 2; 1; 1 . C. 2;1; 1 . D. 1; 2;1 . Câu 53.
Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A = (1;2;0), B = ( 2 − ;1; ) 1 ,
C = (3;0; − 2) . Phương trình mặt phẳng đi qua A , vuông góc với đường thẳng BC là:
A. 5x − y − 3z − 3 = 0 .
B. x + y − z − 3 = 0 .
C. 2x − y − z = 0 .
D. 4x − 3y − 3z + 2 = 0 . Câu 54.
Trong không gian với hệ tọa độ Oxyz , viết phương trình của mặt phẳng ( P) đi qua các điểm
A(1;0;0) ; B (0; 2;0) ; C (0;0; 3 − ) . x y z x y z A. + − =1. B. + + =1.
C. 6x + 3y + 2z = 1.
D. 6x + 3y + 2z = 0 . 1 2 3 1 2 3 Câu 55.
Trong không gian Oxyz , cho hai điểm A(4;0 ) ;1 , B ( 2
− ;2;3) . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là:
A. 6x − 2 y − 2z −1 = 0 .
B. 3x − y − z = 0 .
C. x + y + 2z − 6 = 0 .
D. 3x + y + z − 6 = 0 . 8 Câu 56.
Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình của mặt
phẳng chứa trục Ox và đi qua điểm K (2;1; 1 − ) ? A. x + 2z = 0 .
B. x − 2z = 0 .
C. y − z − 2 = 0 . D. Câu 57.
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng là ( P) : 2x − y + 2z + 2 = 0 và (Q) 2
: a x + by + z + a = 0 , trong đó a, b là các số thực. Để ( P) song song với (Q) thì giá trị của biểu thức
T = a + 2b bằng: A. 1 − . B. 0. C. 2 − . D. 3. Câu 58.
Trong không gian (Oxyz) , cho hai điểm A(2;1; 3 − ), B( 1 − ;2; )
1 . Toạ độ của véctơ AB là : A. ( 3 − ; 1 − ;4). B. (3;1; 4 − ). C. ( 3 − ;1;4). D. (3; 1 − ; 4 − ) . Câu 59.
Trong không gian Oxyz , cho điểm M ( 2
− ;5;0) . Tìm hình chiếu vuông góc của điểm M lên trục Oy . A. M ( 2 − ;0;0) . B. M (2;5;0) . C. M (0; 5 − ;0) . D. M (0;5;0) . Câu 60.
Trong không gian Oxyz , cho hai điểm A(1; 3; − 5), B ( 3 − ;1; − )
1 . Tìm toạ độ trọng tâm G của tam giác OAB .  2 4   2 4   2 4   2 4  A. G ; − ; − 2 
 . B. G − ; − ; − 2 . C. G − ; ; − 2 
 . D. G − ; − ; 2   .    3 3   3 3   3 3   3 3  Câu 61.
Trong không gian với hệ trục tọa độ Oxyz , cho hình bình hành ABCD . Biết A(2;1; − 3) ,
B (0; − 2;5) và C (1;1;3) . Diện tích hình bình hành ABCD là 349 A. 2 87 . B. . C. 349 . D. 87 . 2 Câu 62.
Trong không gian Oxyz , cho hình chóp . A BCD có ( A 0;1; 1
− ), B(1;1;2),C(1; 1 − ;0) và D(0;0;1) .
Tính độ dài đường cao của hình chóp . A BCD . 3 2 2 A. 2 2 . B. . C. 3 2 . D. . 2 2 Câu 63.
Trong không gian với hệ trục tọa độ Oxyz , cho OA = 2i + 2 j + 2k , B( 2 − ;2;0) và C(4;1; 1 − ) .
Trên mặt phẳng (Oxz) , điểm nào dưới đây cách đều ba điểm , A B,C .  3 1   3 1   3 1   3 1  A. N − ;0; −   . B. P ;0; −   . C. Q − ;0;   . D. M ; 0;   .  4 2   4 2   4 2   4 2  Câu 64.
Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(0;1; 4) , B (3; 1 − ) ;1 , C ( 2 − ;3;2).
Tính diện tích S tam giác ABC . A. S = 2 62 . B. S = 12 . C. S = 6 . D. S = 62 . Câu 65.
Trong không gian tọa độ Oxyz, cho tứ diện ABCD với A( 1 − ; 2 − ;4), B( 4 − ; 2 − ;0),C (3; 2 − ; ) 1 và D (1;1; )
1 . Độ cao của tứ diện kẻ từ D bằng 9 1 A. 3. B. 1. C. 2. D. 2 Câu 66.
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết ( A 5 − ;7; 9 − ), B(7;9; 5 − ), C( 9 − ; 7 − ;5). = + + Gọi điểm H ( ; a ;
b c) là trực tâm của tam giác ABC. Tính 2 2 2 S a b c . 211 A. Đáp án khác. B. S = 155. C. S = . D. S = 211. 9 Câu 67.
Trong không gian Oxyz , có tất cả bao nhiêu giá trị nguyên của m để 2 2 2
x + y + z + ( − m) y − (m − ) 2 2 1 2 2
2 z + 6m + 5 = 0 là phương trình của một mặt cầu? A. 6 B. 5 C. 7 D. 4 Câu 68.
Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với (
A 1; 0; 0) , B(3; 2; 4) , C(0;5; 4) .
Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho MA + MB + 2MC nhỏ nhất. A. M (1;3; 0) . B. M (1; − 3; 0) . C. M (3;1; 0) . D. M (2; 6; 0) . 2.5. Đề minh họa
Câu 1. Cho f ( x), g ( x) là các hàm số xác định và liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A.  f
 (x)− g(x)dx = f
 (x)dx− g
 (x)dx. B. f
 (x)dx = f  (t)dt . C. xf
 (x)dx = x f
 (x)dx . D.  f
 (x)+ g(x)dx = f
 (x)dx+ g  (x)dx.
Câu 2. Họ nguyên hàm của hàm số ( ) 3 2
f x = x + x làơp; 1 1 A. 2
3x + 2x + C . B. 4 3 x + x + C . C. 4 3
x + x + C . D. 4 3
4x + 3x + C . 4 3
Câu 3. Họ các nguyên hàm của hàm số ( ) 3ex f x = +1là 1 1 A. 3 3e x + C . B. 3 e x + C . C. 3
3e x + x + C . D. 3
e x + x + C . 3 3
Câu 4. Tìm nguyên hàm F ( x) của hàm số f ( x) = 6x + sin 3x , biết F ( ) 2 0 = . 3 cos 3x 2 cos 3x A. F ( x) 2 = 3x − + . B. F ( x) 2 = 3x − −1. 3 3 3 cos 3x cos 3x C. F ( x) 2 = 3x + +1. D. F ( x) 2 = 3x − +1. 3 3  1  2
Câu 5. Hàm số f ( x) = ( − x)5 1 2
có một nguyên hàm là F ( x) thỏa F − =   . Tính F ( ) 1 .  2  3 A. F ( ) 1 = 1 − 0 . B. F ( ) 1 = 5 − . C. F ( ) 59 1 = . D. F ( ) 71 1 = . 12 12
Câu 6. Xét I = x ( x −  )5 3 4 4
3 dx . Bằng cách đặt: 4
u = 4x − 3 , khẳng định nào sau đây đúng? 10 1 1 1 A. 5 I = u du  B. 5 I = u du  . C. 5 I = u du  . D. 5 I = u du  . 16 12 4
Câu 7. Tìm nguyên hàm của hàm số ( ) = ( + ) 1 ex f x x A. 2 ex x + C . B. ( + 2) ex x + C . C. ( − ) 1 ex x + C . D. ex x + C . Câu 8. x cos d x x  bằng 2 x 2 x A. sin x + C .
B. x sin x + cos x + C . C. x sin x − sin x + C . D. cos x + C 2 2 dx
Câu 9. Tìm họ nguyên hàm F (x) =  . x 2 ln x +1
A. F(x) = 2 2 ln x +1 + C .
B. F(x) = 2ln x +1 + C . 1 1 C. F (x) = 2 ln x +1 + C . D. F (x) = 2 ln x +1 + C 4 2 2 2 Câu 10.
Cho hàm số f ( x) và g ( x) liên tục trên 0; 2 và f
 (x)dx = 2, g(x)dx = 2 −  . Tính 0 0 2 3 f
 (x)+ g(x)dx  . A. 4. B. 8. C. 12. D. 6 0  2 dx Câu 11. Tính tích phân I =  bằng A. 1. B. 3. C. 4. D. 2. 2  sin x 4 5 Câu 12.
Cho f ( x) và g ( x) là hai hàm số liên tục trên . Biết 2 f
  (x)+3g(x)dx =16  và 1 − 5 2  f
  (x)−3g(x)dx = 1 −  . Tính f (2x +  ) 1 dx . 1 − 1 − 5 1 A. 1. B. . C. . D. 5 . 2 2 4   16 4 5 Câu 13. Cho f
 (x)dx = .Tính I =  − 3 f x  d . x  2 ( ) 3  x +1  0  ( ) 0  A. I = 12 − . B. I = 0 . C. I = 20 − . D. I = 1. 0 2 3x + 5x −1 3 Câu 14. Biết dx = a ln + b
, với a, b
. Tính a + 2b . x − 2 2 1 − A. 2 − . B. 10 . C. 20 . D. 40 . (x − )2 2 2 1 Câu 15. Tích phân dx  bằng x 1 11 2 1 3 4 A. + 3ln 2 . B. − ln 2 . C. + ln 2 . D. − 2ln 2 3 2 4 3  2 Câu 16. Tính tích phân 4
I = cos x sin xdx
, bằng cách đặt t = cos x , mệnh đề nào đưới đây đúng? 0   1 1 2 2 A. 4 I = t dt  . B. 4 I = − t dt  . C. 4 I = t dt  . D. 4 I = − t dt  . 0 0 0 0 9 4 Câu 17.
Biết hàm số f (x) là hàm liên tục trên và
f (x)dx = 9 
khi đó giá trị của f (3x − 3)dx  là? 0 1 A. 27 . B. 24 . C. 3 . D. 0 . ln 2 dx a Câu 18. Cho tích phân I =
= − c ln 2 + d ln 3  , trong đó a, ,
b c, d là những số nguyên dương ex ex +1 b 0 ( ) a và phân số
tối giản. Giá trị của biểu thức T = (a + b + c + d ) bằng A. 4. B. 9. C. 6. D. 8. b 1 1 Câu 19.
Cho f ( x) là hàm số liên tục trên thỏa f ( ) 1 = 1và
f (t ) dt =  . Tính 3 0  2 I = sin 2 . x f   (sin x)dx 0 4 2 2 1 A. I = . B. I = . C. I = − D. I = . 3 3 3 3 2 x Câu 20. Biết (3x − ) 2 1 e dx = a + e
b với a , b là các số nguyên. Giá trị a + b bằng 0 A. 12 . B. 16 . C. 6 . D. 10 . 2 Câu 21.
Kết quả của tích phân K = (2x −1) ln d x x  bằng 1 1 1 1 A. K = 2ln 2 . B. K = . C. K = 2 ln 2 − . D. K = 2 ln 2 + . 2 2 2
xcos x + 2sin xcos x −3cos x Câu 22.
Cho a , b , c là các số nguyên thỏa mãn 2
dx = a b + c   . Tính 3 sin x 4 = ( + + )2 P a b c A. 13 . B. 49 . C. 1. D. 9 . 12 Câu 23.
Cho hai hàm số y = f ( x) và y = g ( x) liên tục trên đoạn  ;
a b . Diện tích của hình phẳng giới
hạn bởi đồ thị các hàm số y = f ( x) và y = g ( x) và hai đường thẳng x = a , x = b (a b) được tính theo công thức là: b b
A. S = ( f (x) − g(x))dx . B. S =  ( f (x) − g(x))dx . a a b b C. S =
f (x) − g(x) dx
. D. S = ( f (x) − g(x))dx . a a Câu 24.
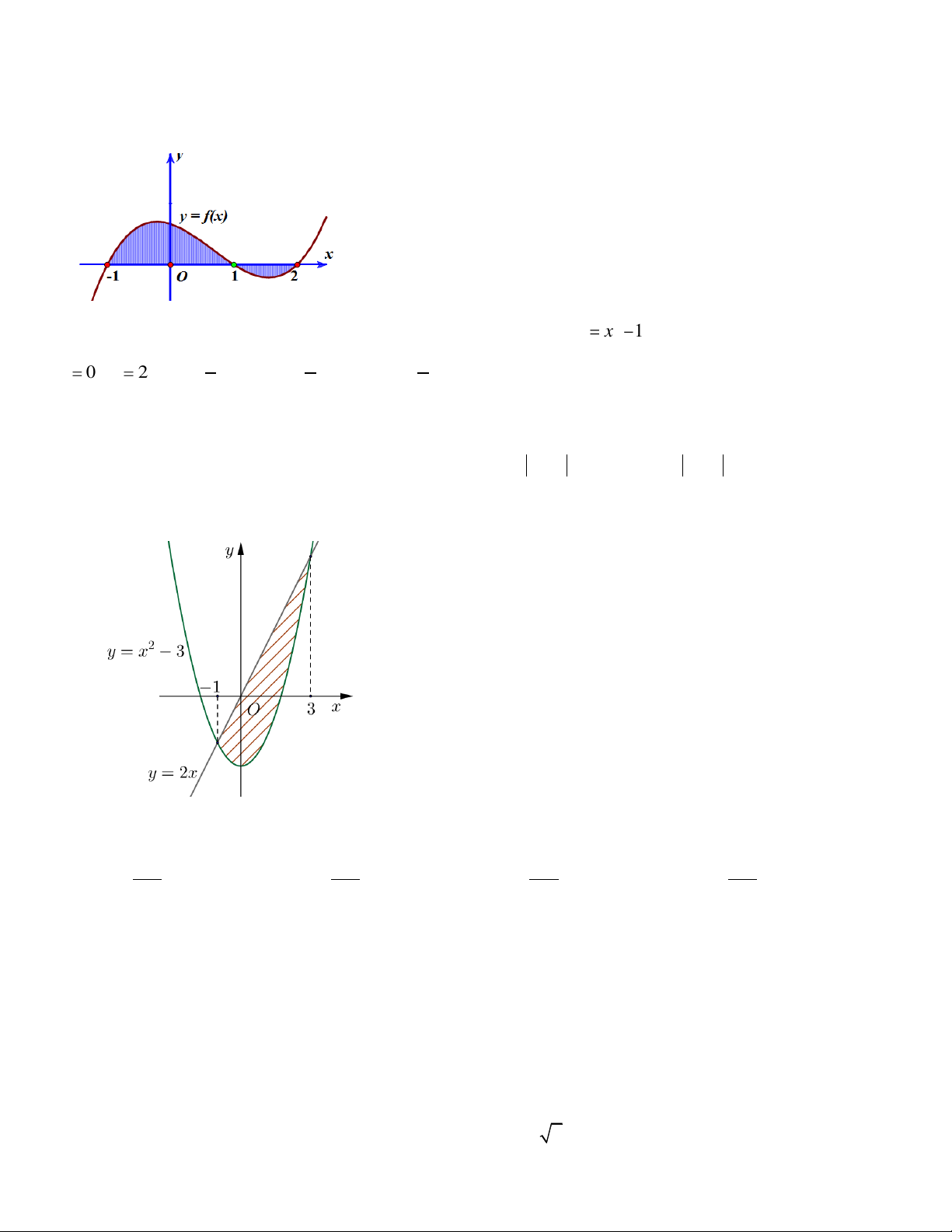
Diện tích của hình phẳng ( H ) được giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành và hai
đường thẳng x = a , x = b (a b) (phần tô đậm trong hình vẽ) tính theo công thức b c b A. S = f  (x)dx. B. S = − f
 (x)dx+ f  (x)dx. a a c b c b C. S = f  (x)dx . D. S = f
 (x)dx+ f  (x)dx. a a c Câu 25.
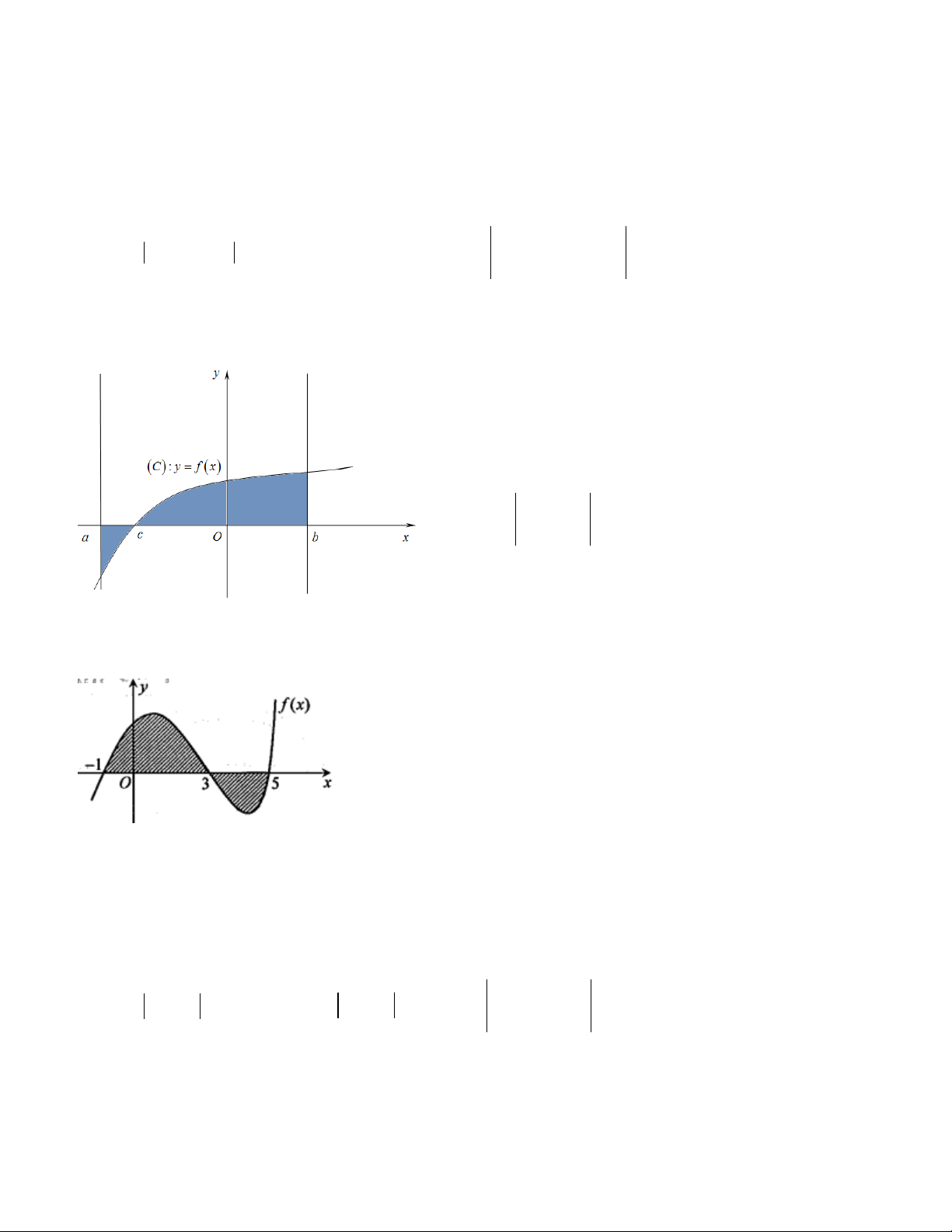
Cho phần hình phẳng ( H ) được gạch chéo
như hình vẽ. Diện tích của (H ) được tính theo công thức nào dưới đây? 3 A. S = f  (x)dx . B. 1 − 3 5 S = f
 (x)dx+ f  (x)dx . 1 − 3 3 5 3 5 C. S = f
 (x)dx− f
 (x)dx . D. S = − f
 (x)dx+ f  (x)dx . 1 − 3 1 − 3 Câu 26.
Diện tích S của hình phẳng giới hạn bởi các đường 3
y = x − 4x và y = 0 được tính bởi công thức nào dưới đây. 2 2 2 2 A. 3 S = x − 4x dx  . B. 3 S = x − 4x dx  . C. S =  ( 3
x − 4x)dx . D. S =  ( 3
x − 4x) dx . 2 − 0 2 − 2 − Câu 27.
Phần hình phẳng ( H ) được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm số
y = f ( x) , 2
y = x + 4x và hai đường thẳng x = 2 − ; x = 0 13 0 4 Biết
f ( x) dx = 
, diện tích hình phẳng ( H ) bằng 3 2 − 16 4 A. . B. . 3 3 20 7 C. . D. . 3 3 Câu 28.
Cho hình phẳng ( H ) giới hạn bởi các đường 3
y = x − x +1 , y = 0 , x = 0 , x = 2 . Gọi V là thể
tích khối tròn xoay được tạo thành khi quay ( H ) xung quanh trục Ox . Mệnh đề nào sau đây đúng? 2 2 2 2 2 2 A. V =  ( 3 x − x + 
)1dx . B. V = ( 3x − x+ 
)1 dx . C. V = ( 3x − x+ 
)1 dx . D. V = ( 3 2 x − x +  )1dx . 0 0 0 0 Câu 29.
Cho hàm số f ( x) có đồ thị trên đoạn  3 − ;  3 là
đường gấp khúc ABCD như hình vẽ. y 3 Tính f  (x)dx . B 1 C −3 3 A x 5 35 5 − −35 -2 1 A. . B. . C. . D. . 2 6 2 6 -2 D Câu 30.
Cho hình phẳng D giới hạn bởi đường cong ex y =
, trục hoành và các đường thẳng x = 0 , x = 1 .
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2 2 2 e −1  (e + ) 1  (e − ) 1 2 e A. V = . B. V = . C. V = . D. . 2 2 2 2 Câu 31.
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số 2
y = 3x – x và trục hoành, quanh trục hoành. 81 85 41 8 A. . B. . C. . D. . 10 10 7 7 Câu 32.
Cho hàm số f (x) có đạo hàm liên tục trên R và thỏa mãn f (0) = 3 và 2 2
f (x) + f (2 − x) = x − 2x + 2 , x
  R . Tích phân .
x f '(x)dx  bằng 0 −10 5 − 11 − 7 − A. . B. . C. . D. . 3 3 3 3 Câu 33.
Trong không gian Oxyz , cho mặt phẳng ( P) : 2x + y − z + 3 = 0 . Điểm nào sau đây không thuộc (P)? 14 A.V (0; 2 − ; ) 1 . B. Q (2; 3 − ;4) . C. T (1; 1 − ) ;1 . D. I (5; 7 − ;6) . Câu 34.
Trong không gian với hệ trục Oxyz , cho mặt phẳng ( P) : 3x − z + 2 = 0 . Véc tơ nào dưới đây là
một véc tơ pháp tuyến của ( P) ? A. n (3;0; − ) 1 . B. n ( 3 − ;0;− ) 1 . C. n (3; 1 − ;2). D. n (3; 1 − ;0). Câu 35.
Trong không gian Oxyz , hình chiếu vuông góc của điểm M (2;1; 1
− ) trên mặt phẳng (Ozx) có tọa độ là A. (0;1;0) . B. (2;1;0) . C. (0;1; − ) 1 . D. (2;0; − ) 1 . Câu 36.
Trong không gian Oxyz cho mặt cầu (S ) 2 2 2
: (x −1) + ( y + 2) + (z + 3) = 4 . Tâm của (S ) có tọa độ là A. ( 1 − ;2;3) B. (1; 2 − ; 3 − ) C. ( 1 − ; 2 − ; 3 − ) D. (1; 2;3) Câu 37.
Trong không gian Oxyz , cho hai điểm A(1; 1 − ;2) và B( 1
− ;3;0) . Trung điểm của đoạn thẳng
AB có tọa độ là A. (0;2;2) . B. ( 2 − ;4; 2 − ). C. ( 1 − ;2;− ) 1 . D. (0;1; ) 1 . Câu 38.
Trong không gian với hệ tọa độ Oxyz ; cho điểm A(1;3; 2
− ) và (P): 2x + y − 2z −3 = 0 . Khoảng 2
cách từ điểm A đến mặt phẳng ( P) bằng: A. 1. B. 2 . C. . D. 3 . 3 Câu 39.
Trong không gian với hệ trục toạ độ Oxyz . Phương trình mặt phẳng qua A(2;5 ) ;1 và song song
với mặt phẳng (Oxy) là: A. x − 2 = 0
B. 2x + 5y + z = 0 C. z −1 = 0 D. y − 5 = 0 Câu 40.
Trong không gian Oxyz cho A( 1
− ;4;3) và B(3;2;−5) . Mặt phẳng trung trực của đoạn thẳng
AB có phương trình là
A. 2x − 4 y − 4z +1 = 0 .
B. 2x − y − 4z + 3 = 0 .
C. 2x − y + 4z − 6 = 0 .
D. 2x − y − 4z − 3 = 0 . Câu 41.
Trong không gian với hệ trục tọa độ Oxyz , cho điểm M ( 2 − ; 1
− ;3) . Phương trình mặt phẳng đi
qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là: x y z x y z x y z x y z A. + + = 1 + + = + + = + + = 2 − 1 − . B. 0 3 2 − 1 − . C. 1 3 2 1 3 − . D. 0 2 1 3 − . Câu 42.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : x − 2y + 2z − 2 = 0 và điểm I ( 1 − ;2;− )
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng ( P) theo giao tuyến là đường tròn có bán kính bằng 5 . 2 2 2 2 2 2
A. (S ) : ( x + )
1 + ( y − 2) + ( z + ) 1 = 25.
B. (S ) : ( x + )
1 + ( y − 2) + ( z + ) 1 =16. 2 2 2 2 2 2
C. (S ) : ( x − )
1 + ( y + 2) + ( z − ) 1 = 34.
D. (S ) : ( x + )
1 + ( y − 2) + ( z + ) 1 = 34. 15 Câu 43.
Trong không gian Oxyz , mặt cầu ( S ) có tâm I (2;1; 2 − ) và đi qua điểm (
A 1; 2;3) . Phương trình của mặt cầu là A. 2 2 2
x + y + z + 4x − 2y + 4z −18 = 0 . B. 2 2 2
x + y + z − 2x − 4y − 6z −13 = 0 C. 2 2 2
x + y + z − 4x − 2y + 4z −18 = 0 . D. 2 2 2
x + y + z + 2x + 4y + 6z −13 = 0 Câu 44.
Trong không gian Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z − 2x + 4 y − 6z − 2 = 0 . Tìm tọa độ tâm
I và bán kính R của mặt cầu ( S ) . A. I (1; 2
− ;3)và R = 12 . B. I (1; 2
− ;3)và R = 4. C. I ( 1 − ;2; 3
− ) và R =16. D. I ( 1 − ;2; 3 − ) và R = 4. Câu 45.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M (3;2;8), N (0;1;3) và P (2; ; m 4) . Tìm m để tam giác MNP vuông tại N. A. m = 25. B. m = 4 . C. m = 1 − . D. m = 10 − . Câu 46.
Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng ( P) : x + (m + )
1 y – 2z + m = 0 và
(Q): 2x – y +3 = 0với m là tham số thực. Để mặt phẳng (P)và (Q) vuông góc thì giá trị của m bằng bao nhiêu? A. m = 5 − . B. m = 1. C. m = 3 . D. m = 1 − . Câu 47.
Trong không gian Oxyz , tính khoảng cách giữa hai mặt phẳng ( ) : 2x − y − 2z − 4 = 0 và ( ) 10 4
: 2x − y − 2z + 2 = 0 . A. 2 . B. 6 . C. . D. . 3 3 Câu 48.
Trong không gian Oxyz, cho ba điểm A(1;0;0), B(0;0;1) và C(2;1;1). Diện tích của tam giác ABC là. 6 5 10 15 A. . B. . C. . D. . 2 2 2 2 Câu 49.
Trong không gian với hệ trục tọa độ Oxyz , cho điểm A(1; 1 − ;2) và mặt cầu (S) 2 2 2
: x + y + z = 9 . Mặt phẳng đi qua A cắt (S ) theo giao tuyến là một đường tròn có bán kính nhỏ nhất có phương trình là:
A. x − y + 2z − 2 = 0 .
B. x − y + 2z − 6 = 0 .
C. x − y + 2z = 0 .
D. x − y + 2z − 4 = 0 . Câu 50.
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;0;0), B (2;3;0), C (0;0;3) . Tập hợp các điểm M ( ; x ; y z ) thỏa mãn 2 2 2
MA + MB + MC = 23 là mặt cầu có bán kính bằng: A. 3 . B. 5 . C. 3 . D. 23 . 16