Đề cương giữa kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Hoàng Văn Thụ – Hà Nội

Đề cương giữa kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Hoàng Văn Thụ – Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

48 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
TRƯỜNG THPT HOÀNG VĂN THỤ
MÔN TOÁN
ĐỀ CƯƠNG ÔN TẬP GIA HC K II
MÔN TOÁN - LỚP 12
NĂM HC 2023- 2024
1. MỤC TIÊU
1.1. Kiến thức : Học sinh ôn tập các kiến thức về:
- Nguyên hàm.
- Tích phân.
- Ứng dụng của tích phân trong hình học.
- Hệ tọa độ trong không gian.
- Phương trình mặt phẳng.
- Phương trình mặt cầu.
1.2. Kĩ năng: Học sinh rèn luyện các kĩ năng:
+ Rèn luyện tính cẩn thận chính xác trong tính toán.
+ Biết vận dụng các kiến thức đã học vào giải bài tập.
+Phát triển tư duy logic, khả năng linh hoạt.
+ Sử dụng thành thạo máy tính.
2. NỘI DUNG:
2.1. Các câu hỏi định tính v:
+ Đnh nghĩa, các tính cht, công thức nguyên hm, phương pháp tìm nguyên hm.
+ Đnh nghĩa, các tính cht của tích phân, phương pháp tính tích phân v ứng dụng của tích phân trong
hình học.
+ Hệ trục tọa độ, tọa độ của điểm v vecto; các php toán cộng, tr, nhân vecto vi một s, tích vô hưng
của hai vecto, tích c hưng hai vecto.
+ Phương trình mặt phẳng, phương trình mặt cầu.
2.2. Các câu hỏi định lượng v:
+ Tìm họ nguyên hm của hm s.
+ Tìm nguyên hm tha mãn điều kiện cho trưc.
+ Tính tích phân.
+ Tính diện tích hình phẳng, thể tích vật thể, thể tích khi trn xoay.
+ Tìm tọa độ điểm, vecto tha mãn điều kiện cho trưc.
+ Tính s đo gc gia hai vecto, gc gia hai mặt phẳng.
+ Tính khoảng cách gia hai điểm, khoảng cách t 1 điểm đến 1 mặt phẳng, khoảng cách gia hai mặt
phẳng song song.
+ Tính chu vi tam giác, diện tích tam giác, thể tích khi chp, khi hộp,…
+ Viết phương trình mặt phẳng, mặt cầu.
2. 3. Câu hỏi và bài tập minh họa
Câu 1. Cho
( ) ( )
,f x g x
là các hàm s xác đnh và liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x− = −


. B.
.
2
C.
( ) ( )
2 d 2 df x x f x x=

. D.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x+ = +


.
Câu 2. Cho hàm s
( )
Fx
là một nguyên hàm của hàm
( )
fx
trên khoảng
K
nếu
A.
( ) ( )
F x f x
=
. B.
( ) ( )
F x f x
=
. C.
( ) ( )
F x f x

=
. D.
( ) ( )
F x f x

=
.
Câu 3. Hàm s no dưi đây không phải là nguyên hàm của hàm s
( )
3
f x x=
?
A.
4
2
4
x
y =+
. B.
4
4
x
y =
. C.
2
3yx=
. D.
4
2019
2
4
x
y =−
.
Câu 4. Họ nguyên hm của hàm s
( )
3cos 3
x
f x x=−
là:
A.
( )
3
3sin
ln3
x
f x dx x C= − +
. B.
( )
3
3sin
ln3
x
f x dx x C= − + +
.
C.
( )
3
3sin
ln3
x
f x dx x C= + +
. D.
( )
3
3sin
ln3
x
f x dx x C= − − +
.
Câu 5. Nguyên hàm
( )
Fx
của hàm s
( )
2
1
2
sin
f x x
x
=+
tha mãn
1
4
F

=−


là
A.
( )
2
2
cot
16
F x x x
= − −
. B.
( )
2
2
cot
16
F x x x
= − + −
. C.
( )
2
cotF x x x= − +
. D.
( )
2
2
cot
16
F x x x
= − +
.
Câu 6. Trong các khẳng đnh sau, khẳng đnh nào sai?
A.
2 d 2 ln 2
xx
xC=+
. B.
1
cos2 d sin2
2
x x x C=+
.
C.
2
2
d
2
x
x
e
e x C=+
. D.
( )
1
d ln 1 1
1
x x C x
x
= + + −
+
.
Câu 7. Tìm nguyên hàm
( )
Fx
của hàm s
( )
2
21
fx
x
=
−
tha mãn
( )
57F =
.
A.
( )
2 2 1F x x=−
. B.
( )
2 2 1 1F x x= − +
. C.
( )
2 1 4F x x= − +
. D.
( )
2 1 10F x x= − −
.
Câu 8. Gọi
( )
Fx
là một nguyên hàm của hàm s
2
ln
ln 1.
x
yx
x
=+
mà
( )
1
1
3
F =
. Giá tr của
( )
2
Fe
bằng:
A.
8
9
. B.
1
9
. C.
8
3
. D.
1
3
.
Câu 9. Biết
( )
( ) ( )
52 51
50
1 2 1 2
1 2 d ; ,
xx
x x x C a b
ab
−−
− = − +
. Tính giá tr của
ab−
.
A.
0
. B.
4
. C.
1
. D.
4−
.
Câu 10. Xét nguyên hàm
d
1
x
x
e
x
e +
, nếu đặt
1=+
x
te
thì
d
1
x
x
e
x
e +
bằng
A.
2dt
. B.
2
2dtt
. C.
2
dtt
. D.
d
2
t
.
3
Câu 11. Nguyên hàm của
( )
1 ln
ln
x
fx
xx
+
=
là:
A.
( )
ln lnF x x C=+
. B.
( )
2
ln lnF x x x C=+
.C.
( )
ln lnF x x x C= + +
. D.
( )
ln lnF x x x C=+
.
Câu 12. Tìm họ nguyên hàm:
3
4
()
1
x
F x dx
x
=
−
A.
4
( ) ln 1F x x C= − +
. B.
4
1
( ) ln 1
4
F x x C= − +
.C.
4
1
( ) ln 1
2
F x x C= − +
. D.
4
1
( ) ln 1
3
F x x C= − +
.
Câu 13. Cho
()Fx
là một nguyên hàm của hàm s
( ) ( )
5 1 e
x
f x x=+
và
( )
03F =
. Tính
( )
1F
.
A.
( )
1 11e 3F =−
. B.
( )
1 e 3F =+
. C.
( )
1 e 7F =+
. D.
( )
1 e 2F =+
.
Câu 14. Họ nguyên hàm
( )
Fx
của hàm s
( )
2
cos
1 cos
x
fx
x
=
−
là
A.
( )
cos
sin
x
F x C
x
= − +
. B.
( )
1
sin
F x C
x
= − +
. C.
( )
1
sin
F x C
x
=+
. D.
( )
2
1
sin
F x C
x
=+
.
Câu 15.
2
23
d
1
xx
x
x
++
+
bằng
A.
2
2ln | 1|
2
x
x x C+ + + +
. B.
2
ln | 1|
2
x
x x C+ + + +
.
C.
2
2ln | 1|
2
x
x x C+ + − +
. D.
2ln | 1|x x C+ + +
Câu 16. Cho hàm s
( )
fx
tha mãn
( )
2
2
45
x
fx
xx
+
=
++
và
( )
22f −=
. Giá tr
( )
1f
bằng
A.
ln10 2+
. B.
1
ln10 2
2
−
. C.
ln10 2−
. D.
1
ln10 2
2
+
.
Câu 17. Họ nguyên hàm của hàm s
( )
2
lnf x x=
là
A.
2
ln 2 ln 2x x x x x c− + +
. B.
2
ln 2x x x c++
.
C.
2
ln 2 ln 2x x x x x c+ + +
. D.
2
ln 2x x x c−+
.
Câu 18. Cho
( )
Fx
là một nguyên hàm của hàm s
( )
21
23
x
fx
x
+
=
−
tha mãn
(2) 3F =
. Tìm
( )
Fx
:
A.
( ) 4ln 2 3 1F x x x= + − +
. B.
( ) 2ln(2 3) 1F x x x= + − +
.
C.
( ) 2ln 2 3 1F x x x= + − +
. D.
( ) 2ln | 2 3| 1F x x x= + − −
.
Câu 19. Cho
( )
Fx
là một nguyên hàm của hàm s
( )
fx
. Khi đ hiệu s
( ) ( )
10FF−
bằng
A.
( )
1
0
F x dx−
. B.
( )
1
0
f x dx
. C.
( )
1
0
F x dx
. D.
( )
1
0
f x dx−
.
4
Câu 20. Cho
( )
4
2
d 10f x x =
và
( )
2
4
d5g x x =−
. Tính
( ) ( )
4
2
3 5 df x g x x−


.
A.
5I =
. B.
10I =
. C.
5I =−
. D.
15I =
.
Câu 21. Tính tích phân
4
0
2cos x dx
bằng A.
1
. B.
1
2
. C.
2
. D.
Câu 22. Tính giá tr của tích phân
2
4
1
1
dI x x
x

=+


A.
111
4
I =
. B.
305
16
I =
. C.
196
15
I =
. D.
208
17
I =
.
Câu 23. Cho
( )( )
3
1
d
ln2 ln5 ln7 ( , , )
14
x
a b c a b c
xx
= + +
++
. Tính giá tr
4S a b c= + −
A.
2S =
. B.
3S =
. C.
4S =
. D.
5S =
.
Câu 24. Cho
( ) ( )
,f x g x
là các hàm s liên tục trên
1;3
và tha
mãn
( ) ( )
3
1
3 d 10f x g x x+=


( ) ( )
3
1
2 d 6f x g x x−=


. Tính
( ) ( )
3
1
dI f x g x x=+


bằng
A.
7I =
. B.
6I =
. C.
8I =
. D.
9I =
.
Câu 25. Biết
( )
1
0
2f x dx =−
và
( )
1
2
3,f x dx =
khi đ
( )
2
0
f x dx
bằng
A.
5−
. B.
5
. C.
1−
. D.
1
.
Câu 26. Cho
( )
1
0
d2f x x =
. Khi đ
( )
1
0
2d
x
f x e x

+

bằng
A.
3e+
. B.
5 e+
. C.
3 e−
. D.
5 e−
.
Câu 27. Kết quả của tích phân
( )
2
0
2 1 sin dx x x
−−
được viết ở dạng
1
1
ab

−−


a
,
b
. Khẳng đnh
no sau đây l sai?
A.
28ab+=
. B.
5ab+=
. C.
2 3 2ab−=
. D.
2ab−=
.
Câu 28. Biết
( )
6
2
0
3
3 4sin d
6
ac
xx
b
+ = −
, trong đ
a
,
b
nguyên dương v
a
b
ti giản. Tính
abc++
.
A.
8
. B.
16
. C.
12
. D.
14
.
Câu 29. Cho hàm s
( )
fx
c đạo hàm liên tục trên đoạn
2;4
và tha mãn
( ) ( )
2 2, 4 2020ff==
. Tính
tích phân
( )
2
1
2dI f x x
=
.
A.
1009I =
. B.
2022I =
. C.
2018I =
. D.
1011I =
.
5
Câu 30. Nếu đặt
21ux=+
thì
( )
1
4
0
2 1 dxx+
bằng
A.
3
4
1
1
d
2
uu
. B.
3
4
1
duu
. C.
1
4
0
1
d
2
uu
. D.
1
4
0
duu
.
Câu 31. Tích phân
3
2
0
ln2; ,
cos
3
x
dx a b a b
x
= +
. Khi đ giá tr
ab
thuộc khoảng no sau đây?
A.
2; 1
. B.
1
0;
3
. C.
11
;
22
. D.
1;2
.
Câu 32. Biết
( )
4
2
0
ln 9 d ln5 ln3x x x a b c+ = + +
, trong đ
a
,
b
,
c
là các s nguyên. Giá tr của biểu thức
T a b c= + +
là A.
10T =
. B.
9T =
. C.
8T =
. D.
11T =
.
Câu 33. Cho tích phân
0
(2 )sinI x xdx
=−
. Đặt
2 , sinu x dv xdx= − =
thì
I
bằng
A.
( )
0
0
2 cos cosx x xdx
− − −
B.
( )
0
0
2 cos cosx x xdx
−+
.
C.
( )
0
0
2 cosx xdx
−+
. D.
( )
0
0
2 cos cosx x xdx
− − +
.
Câu 34. Cho hàm s
( )
y f x=
c đạo hàm trên
0;1
. Biết
( )
1
1f
e
=
và
( )
1
0
1
d
e
f x x
e
−
=
.
Tính
( )
1
0
dI xf x x
=
.
A.
1I =
. B.
2e
I
e
−
=
. C.
2 e
I
e
−
=
. D.
1I =−
.
Câu 35. Tính tích phân
( )
4
0
1 sin dI x x x
=+
.
A.
82
8
I
−
=
. B.
2
12
8
I
= − −
. C.
2
12
8
I
= − +
. D.
82
8
I
+
=
.
Câu 36. Cho hàm s
( )
fx
liên tục trong đoạn
1;e
, biết
( )
e
1
d1
fx
x
x
=
,
( )
e1f =
. Khi đ
( )
e
1
.ln dI f x x x
=
bằng
A.
4I =
. B.
3I =
. C.
1I =
. D.
0I =
.
Câu 37. Cho
2
1
()
2
Fx
x
=
là một nguyên hàm của hàm s
()fx
x
. Tính
1
'( )ln d
e
f x x x
bằng:
6
A.
2
2
3
2
e
I
e
−
=
. B.
2
2
2 e
I
e
−
=
. C.
2
2
2e
I
e
−
=
. D.
2
2
3
2
e
I
e
−
=
.
Câu 38. Biết
4
2
0
ln 1 d ln5
a
x x x c
b
, trong đ
,,abc
là các s nguyên. Giá tr của biểu
thức
T a b c
là
A.
5T =
. B.
4T =
. C.
9T =
. D.
1T =
.
Câu 39. Cho hàm s
( )
fx
c đạo hàm trên và tha mãn
( )
3
0
2 4 d 8x f x x
− =
;
( )
22f =
. Tính
( )
1
2
2dI f x x
−
=
.
A.
5I =−
. B.
10I =−
C.
5I =
. D.
10I =
.
Câu 40. Kí hiệu
S
là diện tích hình phẳng gii hạn bởi đồ th hàm s
( )
y f x=
, trục honh, đường thẳng
, x a x b==
(như hình bên).
Hi
khẳng đnh no dưi đây l khẳng đnh đúng?
A.
( ) ( )
dd
cb
ac
S f x x f x x=+

. B.
( ) ( )
dd
cb
ac
S f x x f x x=+

.
C.
( ) ( )
dd
cb
ac
S f x x f x x= − +

. D.
( )
d
b
a
S f x x=
.
Câu 41. Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ dưi đây. Công thức tính S là
A.
( ) ( )
12
11
ddS f x x f x x
−
=+

. B.
( )
2
1
dS f x x
−
=
.
C.
( ) ( )
12
11
ddS f x x f x x
−
=−

. D.
( )
2
1
dS f x x
−
=−
.
Câu 42. Diện tích hình phẳng được gii hạn bởi đồ th hàm s
3
1yx
, trục honh v hai đường thẳng
0x
,
2x
là A.
5
.
2
B.
7
.
2
C.
2.
D.
7
.
3
Câu 43. Diện tích hình phẳng gii hạn bởi hai đường thẳng
0x =
,
x
=
, đồ th hàm s
cosyx=
và trục
Ox
là A.
0
cos dS x x
=
. B.
2
0
cos dS x x
=
. C.
0
cos dS x x
=
. D.
0
cos dS x x
=
.
Câu 44. Diện tích hình phẳng được gạch cho như hình vẽ bằng
7
A.
( )
3
2
1
2 3 .x x dx
−
− + +
B.
( )
3
2
1
2 3 .x x dx
−
−−
C.
( )
3
2
1
2 3 .x x dx
−
+−
D.
( )
3
2
1
2 3 .x x dx
−
− + −
Câu 45. Tính diện tích
S
của hình phẳng
()H
gii hạn bởi các đường cong
3
12y x x= − +
và
2
yx=−
.
A.
937
12
S =
. B.
343
12
S =
. C.
793
4
S =
. D.
397
4
S =
.
Câu 46. Diện tích của hình phẳng gii hạn bởi các đường
2
4yx=−
,
2
2y x x= − −
,
2x =−
và
3x =−
được tính bằng công thức
A.
( )
2
2
3
2 2 dxS x x
−
−
= + −
. B.
( )
1
2
2
2 2 dxS x x
−
= + −
.
C.
( )
2
2
3
2 dxS x x
−
−
= + −
. D.
( )
1
2
2
2 dxS x x
−
= + −
.
Câu 47.
Cho hình phẳng
( )
H
gii hạn bởi các đường
; 1; 4y x y x= = =
. Khi đ cho hình phẳng
( )
H
quay quanh trục
Ox
thì thể tích khi trn xoay thu được có thể tích tương ứng bằng:
A.
7
6
. B.
11
3
. C.
9
2
. D.
13
4
.
Câu 48. Cho hình phẳng
( )
H
gii hạn bởi các đường cong
2
; 4 3y x y x= = −
.Thể tích khi tròn xoay khi
cho hình
( )
H
quay quanh trục tung
Oy
tương ứng là:
A.
16
3
. B.
11
3
. C.
184
15
. D.
5
6
.
Câu 49. Tính thể tích vật thể gii hạn bởi hai mặt phẳng
0x =
,
x
=
. Biết rằng thiết diện của vật thể cắt
bởi mặt phẳng vuông góc vi
Ox
tại điểm c honh độ
x
( )
0 x

là một tam giác vuông cân có cạnh huyền
bằng
sin 2x +
.
A.
7
1
6
+
. B.
9
1
8
+
. C.
7
2
6
+
. D.
9
2
8
+
.
Câu 50. Trong không gian vi hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:3 2 0P y z− + =
. Vectơ no dưi đây l
vectơ pháp tuyến của
( )
P
?
A.
( )
1; 1;2n = − −
. B.
( )
3;0;2n =
. C.
( )
3; 1;2n =−
. D.
( )
0; 3;1n =−
.
8
Câu 51. Trong không gian vi hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:1
3 2 1
x y z
P + + =
. Vectơ no dưi đây l
một vectơ pháp tuyến của
( )
P
?
A.
( )
1
6;3;2n =
. B.
( )
2
2;3;6n =
. C.
3
11
1; ;
23
n
=


. D.
( )
4
3;2;1n =
.
Câu 52. Trong không gian
,Oxyz
cho hai điểm
(1; 1;2)A
và
(2;1;3).B
Gọi
P
là mặt phẳng qua
A
và
vuông góc vi đường thẳng
,AB
điểm no dưi đây thuộc
?P
A.
2; 1;1 .
B.
2; 1; 1 .
C.
2;1; 1 .
D.
1; 2;1 .
Câu 53. Trong không gian vi hệ trục tọa độ
Oxyz
,
cho ba điểm
( ) ( )
1;2;0 , 2;1;1AB= = −
,
( )
3;0; 2C =−
. Phương trình mặt phẳng đi qua
A
, vuông góc vi đường thẳng
BC
là:
A.
5 3 3 0x y z− − − =
. B.
30x y z+ − − =
. C.
20x y z− − =
. D.
4 3 3 2 0x y z− − + =
.
Câu 54. Trong không gian vi hệ tọa độ
Oxyz
, viết phương trình của mặt phẳng
( )
P
đi qua các điểm
( )
1;0;0A
;
( )
0;2;0B
;
( )
0;0; 3C −
.
A.
1
1 2 3
x y z
+ − =
. B.
1
1 2 3
x y z
+ + =
. C.
6 3 2 1x y z+ + =
. D.
6 3 2 0x y z+ + =
.
Câu 55. Trong không gian
Oxyz
, cho hai điểm
( )
4;0;1A
,
( )
2;2;3B −
. Mặt phẳng trung trực của đoạn
thẳng
AB
c phương trình l:
A.
6 2 2 1 0x y z− − − =
. B.
30x y z− − =
. C.
2 6 0x y z+ + − =
. D.
3 6 0x y z+ + − =
.
Câu 56. Trong không gian vi hệ tọa độ
Oxyz
, phương trình no dưi đây l phương trình của mặt
phẳng chứa trục
Ox
v đi qua điểm
(2;1; 1)K −
?
A.
20xz+=
. B.
20xz−=
. C.
20yz− − =
. D.
Câu 57. Trong không gian vi hệ trục tọa độ
,Oxyz
cho hai mặt phẳng là
( )
:2 2 2 0P x y z− + + =
và
( )
2
:0Q a x by z a+ + + =
, trong đ
,ab
là các s thực. Để
( )
P
song song vi
( )
Q
thì giá tr của biểu thức
2T a b=+
bằng:
A.
1−
. B. 0. C.
2−
. D. 3.
Câu 58. Trong không gian
( )
Oxyz
, cho hai điểm
( ) ( )
2;1; 3 , 1;2;1AB−−
. Toạ độ của vctơ
AB
là :
A.
( )
3; 1;4 .−−
B.
( )
3;1; 4 .−
C.
( )
3;1;4 .−
D.
( )
3; 1; 4−−
.
Câu 59. Trong không gian
Oxyz
, cho điểm
( )
2;5;0M −
. Tìm hình chiếu vuông góc của điểm
M
lên trục
Oy
.
A.
( )
2;0;0M
−
. B.
( )
2;5;0M
. C.
( )
0; 5;0M
−
. D.
( )
0;5;0M
.
Câu 60. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
1;3; 5 , 3;1; 1AB− − −
. Tìm toạ độ trọng tâm
G
của
tam giác
OAB
.
9
A.
24
; ; 2
33
G

−−


. B.
24
; ; 2
33
G

− − −


. C.
24
; ; 2
33
G

−−


. D.
24
; ; 2
33
G

−−


.
Câu 61. Trong không gian vi hệ trục tọa độ
Oxyz
, cho hình bình hành
ABCD
. Biết
( )
2;1; 3A −
,
( )
0; 2;5B −
và
( )
1;1;3C
. Diện tích hình bình hành
ABCD
là
A.
2 87
. B.
349
2
. C.
349
. D.
87
.
Câu 62. Trong không gian
Oxyz
, cho hình chóp
.A BCD
có
(0;1; 1), (1;1;2), (1; 1;0)A B C−−
và
(0;0;1)D
.
Tính độ di đường cao của hình chóp
.A BCD
.
A.
22
. B.
32
2
. C.
32
. D.
2
2
.
Câu 63. Trong không gian vi hệ trục tọa độ
Oxyz
, cho
2 2 2OA i j k= + +
,
( 2;2;0)−B
và
(4;1; 1)−C
.
Trên mặt phẳng
()Oxz
, điểm no dưi đây cách đều ba điểm
,,A B C
.
A.
31
;0;
42
N

−−


. B.
31
;0;
42
P

−


. C.
31
;0;
42
Q

−


. D.
31
;0;
42
M



.
Câu 64. Trong không gian vi hệ tọa độ
Oxyz
, cho tam giác
ABC
có
( )
0;1;4A
,
( )
3; 1;1B −
,
( )
2;3;2C −
.
Tính diện tích
S
tam giác
ABC
.
A.
2 62S =
. B.
12S =
. C.
6S =
. D.
62S =
.
Câu 65. Trong không gian tọa độ Oxyz, cho tứ diện
ABCD
vi
( ) ( ) ( )
1; 2;4 , 4; 2;0 , 3; 2;1A B C− − − − −
và
( )
1;1;1D
. Độ cao của tứ diện kẻ t
D
bằng
A. 3. B. 1. C. 2. D.
1
2
Câu 66. Trong không gian vi hệ trục tọa độ
,Oxyz
cho tam giác
ABC
biết
( 5;7; 9), (7;9; 5),AB− − −
( 9; 7;5).C −−
Gọi điểm
( ; ; )H a b c
là trực tâm của tam giác
.ABC
Tính
2 2 2
.S a b c= + +
A. Đáp án khác. B.
155.S =
C.
211
.
9
S =
D.
211.S =
Câu 67. Trong không gian
Oxyz
, có tt cả bao nhiêu giá tr nguyên của
m
để
( ) ( )
2 2 2 2
2 1 2 2 2 6 5 0x y z m y m z m+ + + − − − + + =
l phương trình của một mặt cầu?
A.
6
B.
5
C.
7
D.
4
Câu 68. Trong không gian vi hệ tọa độ
Oxyz
, cho tam giác
ABC
vi
(1;0;0)A
,
(3;2;4)B
,
(0;5;4)C
.
Tìm tọa độ điểm
M
thuộc mặt phẳng
()Oxy
sao cho
2MA MB MC++
nh nht.
A.
(1;3;0)M
. B.
(1; 3;0)M −
. C.
(3;1;0)M
. D.
(2;6;0)M
.
2.4. 1. MA TRẬN ĐỀ KIỂM TRA GIA HC K II
MA TRẬN ĐỀ KIỂM TRA GIA HC K II
MÔN: TOÁN, LỚP 12 – THỜI GIAN LÀM BÀI: 90 phút
10
2.4.2 . ĐỀ MINH HA
Câu 1. Cho
( )
Fx
là một nguyên hàm của hàm s
( )
2
23f x x x= − +
tha mãn
( )
02F =
, giá tr của
( )
1F
bằng
A.
2
. B.
11
3
. C.
4
. D.
13
3
.
Câu 2. Cho
( )
1
2
0
1 d 10f x x x+=
. Khi đ
( )
2
1
dI f x x=
bằng:
A.
5
. B.
20
. C.
2
. D.
10
.
Câu 3. Tích phân
2023
2
0
d
x
I xe x=
bằng:
A.
( )
4046
1
4045 1
2
Ie=+
. B.
( )
4046
1
4045 1
4
Ie=+
.
C.
( )
4044
1
4043 1
2
Ie=+
. D.
( )
4046
1
4045 1
4
Ie=−
.
Câu 4. Trong không gian
Oxyz
, cho mặt cầu
( )
S
c phương trình
2 2 2
( 2) ( 1) ( 3) 25x y z− + + + + =
. Tọa độ tâm
I
và bán kính
R
của mặt cầu
( )
S
là
A.
( )
2; 1; 3 ; 5IR− − =
B.
( )
2;1;3 ; 5IR−=
C.
( )
2; 1; 3 ; 25IR− − =
D.
( )
2;1;3 ; 25IR−=
Câu 5. Họ nguyên hàm của hàm s
()
x
f x x e=+
là:
A.
2
()
2
x
x
F x e C= + +
. B.
2
()
2
x
xe
F x C
+
=+
.
C.
2
( ) ln2
2
x
x
F x e C= + +
. D.
( ) 1
x
F x e C= + +
.
Câu 6. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 0S x y z x y z+ + + + + =
, mặt phẳng
( )
Oxz
cắt mặt cầu
()S
theo giao tuyến là một đường tròn. Đường tròn giao tuyến này có tâm là
A.
( 1; 2; 3)I − − −
B.
( 1;0; 3)I −−
C.
(1;0;3)I
D.
( 1;2; 3)I −−
Câu 7. Cho hàm s
( )
=y f x
c đạo hàm liên tục trên và tha mãn
( )
45=f
;
( )
0
2
2 4 d 16f x x
−
+=
. Tính
( )
4
0
dI xf x x
=
.
MA TRẬN ĐỀ KIỂM TRA GIA HC K 2 MÔN TON LỚP 12
Kiến thức
Nhận biết
Thông hiu
Vận dng
Vận dng cao
Nguyên hm
4
4
1
Tích phân
5
4
2
3
Ứng dụng của tích phân
4
4
1
Hệ tọa độ trong không gian
2
2
1
Phương trình mặt phẳng
2
3
1
2
Phương trình mặt cầu
1
3
1
Tng
18
20
7
5
11
A.
14I =−
. B.
8=−I
. C.
4=I
. D.
12I =−
.
Câu 8. Cho
( )
2
d
1
x
Ix
x
=
+
và
1tx=+
. Mệnh đề no sau đây đúng?
A.
2
d
1
t
It
t
=
+
. B.
2
1
d
t
It
t
−
=
. C.
( )
2
d
1
t
It
t
=
+
. D.
2
1
d
t
It
t
+
=
.
Câu 9. Cho hàm s bậc ba
( )
32
f x ax bx cx d= + + +
v đường thẳng
( )
:d g x mx n=+
c đồ th như hình vẽ.
Gọi
1 2 3
,,S S S
lần lượt là diện tích của các phần hình phẳng gii hạn như hình bên. Nếu
1
4S =
thì tỷ s
3
21
2
3
S
SS+
bằng.
A.
2
. B.
1
2
. C.
13
14
. D.
1
.
Câu 10. Diện tích hình phẳng gii hạn bởi đồ th hàm s
2
; 2 1y x y x= = −
và
21yx= − −
là
A.
16
3
B.
4
3
C.
2
3
D.
8
3
Câu 11. Cho tích phân
( )
ln2
0
d
ln3 ln2
e e 1
xx
x
I a b c= = + +
+
(vi a,b,c là các s hu tỉ) . Giá tr của biểu thức
22
2T a b c= + +
bằng
A. 0. B. 6. C. 4. D. 9.
Câu 12. Cho
()y f x=
là một hàm s bt kỳ cđạo hàm trên
,R
đặt
1
0
()I x f x dx
=
. Khẳng đnh no dưi đây
đúng:
A.
1
0
( )d (1).I f x x f=−
B.
1
0
(1) ( )d .I f f x x=−
C.
1
0
(1) ( )d .I f f x x=+
D.
0
1
( )d (1).I f x x f=−
Câu 13. Cho
( )
Fx
là một nguyên hàm của hàm s
( )
.lnf x x x=
tha mãn
( )
3
1
4
F =
. Tìm
( )
Fx
.
A.
( )
22
1
ln
2 4 2
xx
F x x= + +
. B.
( )
2
2
1
ln
24
x
F x x x= − +
.
12
C.
( )
22
1
ln
2 4 2
xx
F x x= − +
. D.
( )
22
ln 1
24
xx
F x x= − +
.
Câu 14. Hàm s
3
()
3
x
Fx=
là một nguyên hàm của hàm s nào trong các hàm s sau đây ?
A.
2
()f x x C=+
. B.
2
( ) 3f x x=
. C.
4
()
12
x
fx=
. D.
2
()f x x=
.
Câu 15. Trong không gian
Oxyz
, cho hai điểm
( )
2;0;3A −
và
( )
1;4;5B
. Khoảng cách gia hai điểm
A
và
B
là
A.
21
. B.
29
. C.
89
. D.
3
.
Câu 16. Cho hình phẳng
( )
H
được gii hạn bởi đồ th hàm s
( )
y f x=
, trục honh v hai đường thẳng
2, 1xx= − =
như hình vẽ bên.
Diện tích của hình phẳng
( )
H
bằng
A.
( )
2
2
df x x
−
. B.
( ) ( )
01
20
ddf x x f x x
−
−+

.
C.
( ) ( )
01
20
ddf x x f x x
−
−

. D.
( ) ( )
01
20
ddf x x f x x
−
+

.
Câu 17. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 2 2 0S x y z x y z+ + + − − − =
và mặt
phẳng
( )
:2 2 3 1 0P x y z m+ − + − =
, có bao nhiêu giá tr nguyên dương của tham s m để mặt phẳng
()P
cắt mặt
cầu
()S
theo giao tuyến là một đường tròn có bán kính
1
2
r =
A.
1.
B.
2.
C.
3
D.
4
Câu 18. Một ô tô bắt đầu chuyển động nhanh dần đều vi vận tc
( )
5 4 ( / )v t t m s=+
. Đi được 6 (s) người lái
xe phát hiện chưng ngại vật và phanh gp, ô tô tiếp tục chuyển động chậm dần đều vi gia tc
2
34 ( / )a m s=−
. Tính quãng đường
()Sm
đi được của ô tô t lúc bắt đầu chuyển bánh cho đến khi dng hẳn.
A.
150,5( ).Sm=
B.
17( ).Sm=
C.
131( ).Sm=
D.
114( ).Sm=
Câu 19. Trong không gian
Oxyz
, cho mặt cầu
( )
S
tâm
( )
3;2; 5I −
v đi qua điểm
( )
1;4;7A −
, phương trình
mặt cầu
( )
S
là
13
A.
2 2 2
( 3) ( 2) ( 5) 152x y z+ + + + − =
. B.
2 2 2
( 3) ( 2) ( 5) 164x y z− + − + + =
.
C.
2 2 2
( 3) ( 2) ( 5) 36x y z+ + + + − =
. D.
2 2 2
( 3) ( 2) ( 5) 10x y z− + − + + =
.
Câu 20. Cho hàm s
( )
fx
tha mãn
( ) ( )
23
12
d 3; d 4f x x f x x= − =

. Khi đ giá tr của
( )
3
1
df x x
bằng
A.
7−
. B. 7. C. 1. D.
12−
.
Câu 21. Cho hàm s
( )
=y f x
c đạo hàm liên tục trên đoạn
2;5
, biết
( ) ( )
5 3; 2 1ff==
. Tính
( )
5
2
df x x
A.
3
. B.
2
. C.
5
. D.
4
.
Câu 22. Trong không gian
Oxyz
, cho hai vc tơ
( )
3;2; 1u =−
;
( )
1; 1;2vm=−
. Có bao nhiêu giá tr nguyên của
m
để
( 2 ) 4u u v+=
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 23. Trong không gian
Oxyz
, cho
( )
1;4;3A −
và
( )
3;2; 5B −
. Mặt cầu đường kính
AB
c phương trình l
A.
2 2 2
( 1) ( 3) ( 1) 21x y z− + − + + =
. B.
2 2 2
( 1) ( 3) ( 1) 84x y z− + − + + =
.
C.
2 2 2
( 1) ( 3) ( 1) 21x y z+ + + + − =
. D.
2 2 2
( 4) ( 2) ( 8) 21x y z− + − + + =
.
Câu 24. Giả sử hm s
( )
y f x=
liên tục nhận giá tr dương trên
( )
0;+
v tha mãn
( )
1fe=
,
( ) ( )
. 3 1f x f x x
=+
, vi mọi
0x
. Mệnh đề no sau đây đúng?
A.
( )
10 5 11f
. B.
( )
9 5 10f
. C.
( )
4 5 5f
. D.
( )
2 5 3f
.
Câu 25. Tích phân
3
1
1
d
3
Ix
x
−
=
+
bằng:
A.
ln12
. B.
4ln2
. C.
ln3
. D.
ln4
.
Câu 26. Trong không gian
,Oxyz
cho hai điểm
( ) ( )
2;0; 1 ; 2;1; 2AB−−
và mặt cầu
( )
2 2 2
: 2 4 2 3 0S x y z x y z+ + + + − + =
. Xét khi nón
( )
N
c đỉnh là tâm
I
của mặt cầu v đường trn đáy nằm
trên mặt cầu
( )
S
. Khi
( )
N
có thể tích ln nht thì mặt phẳng chứa đường trn đáy của
( )
N
v đi qua hai điểm
,AB
c phương trình dạng
20ax y cz+ + =
và
0x my nz p+ + + =
. Giá tr của
2 2 2 2 2
a c m n p+ + + +
bằng
A.
93.
B.
12
. C.
24
. D.
29
.
Câu 27. Trong các khẳng đnh sau, khẳng đnh no sai?
A.
2
2d
ln2
x
x
xC=+
. B.
cos d sinx x x C=+
.
C.
d
xx
e x e C=+
. D.
2 d 2 ln 2
xx
xC=+
.
Câu 28. Cho hàm s
( )
y f x=
liên tục, không âm trên
;ab
. Hình phẳng
( )
H
gii hạn bởi đồ th hàm s
( )
y f x=
, trục honh v hai đường thẳng
, x a x b==
. Khi
( )
H
quay quanh trục
Ox
tạo nên một khi tròn
xoay. Thể tích
V
của khi trn xoay được tính theo công thức no sau đây?
A.
( )
2
d
b
a
V f x x=
B.
( )
d
b
a
V f x x
=
C.
( )
d
b
a
V f x x=
D.
( )
2
d
b
a
V f x x
=
.
14
Câu 29. Cho hm s
3
4 - 5 0 1
()
1 2 1 2
x khi x
y f x
x khi x

==
−
. Tính
2
0
( )df x x
A.
6−
. B.
5
. C.
7
. D.
1
.
Câu 30. Cho hình phẳng
( )
H
gii hạn bởi đồ th hàm s
( )
2
f x ax b=+
(vi
a
,
b
là các s thực dương), trục
hoành, trục tung v đường thẳng
1x =
. Biết vật thể trn xoay được tạo thành khi quay
( )
H
quanh trục
Ox
có
thể tích bằng
8
15
và
( )
12f
=
. Khi đ giá tr
3ab−
bằng
A.
0
. B.
2
. C.
4
. D.
3
.
Câu 31. Trong không gian
Oxyz
, cho điểm
M
tha mãn hệ thức
3OM j k=−
. Tọa độ điểm
M
là
A.
( )
0; 3;1M −
. B.
( )
3;1;0M
. C.
( )
0;3; 1M −
. D.
( )
3;0; 1M −
.
Câu 32. Diện tích hình phẳng gii hạn bởi đồ th hàm s
3
yx=
, trục honh v hai đường thẳng
3; 4xx= − =
là
A.
52
B.
175
4
C.
337
4
D.
146
3
Câu 33. Vi php đổi biến:
2sinxt=
thì tích phân
1
2
0
d
4
x
x−
trở thành
A.
6
0
dtt
. B.
3
0
dtt
. C.
3
0
dt
t
. D.
6
0
dt
.
Câu 34. Trong không gian
Oxyz
, cho hai mặt phẳng
( )
:2 3 0;P x y z+ − + =
( )
:4 2 2 23 0Q x y z+ − + =
. V trí
tương đi của
()P
và
()Q
là
A. Song song B. Cắt nhau nhưng không vuông gc
C. Trùng nhau D. Vuông góc
Câu 35. Diện tích hình phẳng gii hạn bởi đồ th hàm s
x
y xe=
, trục honh, hai đường thẳng
1; 1xx= − =
có
công thức tính là
A.
1
1
d
x
S xe x
−
=
. B.
1
1
d
x
S xe x
−
=
. C.
1
1
d
x
S xe x
−
=
. D.
1
1
d
x
S xe x
−
=
.
Câu 36. Trong không gian
Oxyz
, cho ba điểm
( )
2;0;0 ; (0;5;0); (0;0; 1)A B C −
. Phương trình mặt phẳng
( )
ABC
là:
A.
0
5 2 1
x y z
+ + =
−
B.
1
2 5 1
x y z
+ + =
−
C.
0
2 5 1
x y z
+ + =
−
D.
1
5 2 1
x y z
+ + =
−
Câu 37. Cho hai hm s
()fx
và
()gx
liên tụctrên đoạn
[ ; ]ab
, s thực
k
tùy ý. Trong các khẳng đnh sau,
khẳng đnh nào sai?
A.
( )d ( )d
ba
ab
f x x f x x=

. B.
( )d ( )d
bb
aa
kf x x k f x x=

.
C.
( )d ( )d
ba
ab
f x x f x x=−

. D.
( ) ( ) d ( ) ( )d
b b b
a a a
f x g x x f x dx g x x+ = +
.
15
Câu 38. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
2; 2; 3 , 2; 0; 1AB−
. Điểm
M
tha mãn
.4M MBA =
và
điểm
N
thuộc mặt phẳng
( )
:2 2 17 0P x y z− − + =
. Giá tr nh nht của độ di đoạn thẳng
MN
là
A.
5
3
. B.
2
. C.
4
3
. D.
3
.
Câu 39. Trong không gian
Oxyz
, mặt phẳng
( )
P
chứa trục
Oy
v điểm
(4; 1;2)A −
. Phương trình mặt phẳng
( )
P
là
A.
20xy−=
B.
2 2 0xz− + =
. C.
20xz−=
. D.
20xz+=
.
Câu 40. Trong không gian
Oxyz
, cho các điểm
( )
2;0;3 ; (1; 1;5)MN−
;
( )
3;2; 5P −
. Mặt phẳng
( )
vuông góc
vi đường thẳng
MN
v đi qua điểm
P
c phương trình l
A.
2 11 0x y z+ − − =
. B.
2 15 0x y z+ − + =
.
C.
2 15 0x y z− − − =
. D.
2 15 0x y z+ − − =
.
Câu 41. Họ nguyên hàm
2
5
2 5 3
x
dx
xx
+
−+
là:
A.
13
6ln 1 ln 2 3
2
x x C− + − +
. B.
1 2 3
ln
21
x
C
x
−
+
−
.
C.
13
6ln 1 ln 2 3
2
x x C− − + − +
. D.
13
6ln 1 ln 2 3
2
x x C− − − +
.
Câu 42. Trong không gian
Oxyz
, cho điểm
( )
1;3; 2M −
và
( )
:2 2 3 0P x y z+ − − =
. Khoảng cách t điểm
M
đến mặt phẳng
( )
P
bằng:
A.
7
. B.
7
3
. C.
3
. D.
1
3
.
Câu 43. Họ nguyên hàm của hàm s
( )
4
fx
x
=
là:
A.
( )
4lnf x dx x C=+
. B.
( )
4lnf x dx x=
.
C.
( )
4lnf x dx x C=+
D.
4
()
ln
f x dx C
x
=+
.
Câu 44. Họ nguyên hàm
1
dx
x−
là
A.
2
1
C
x
+
−
. B.
1Cx−
. C.
1
C
x−
. D.
21 xC− − +
.
Câu 45. Cho hai hàm s
( )
; ( )y f x y g x==
liên tục trên
;ab
. Hình phẳng
( )
H
gii hạn bởi đồ th hàm s
( )
; ( )y f x y g x==
và hai đường thẳng
, x a x b==
. Diện tích
S
của hình phẳng
( )
H
là
A.
( ( ) ( ))
b
a
S f x g x dx=−
B.
( ) d ( ) d
bb
aa
S f x x g x x=−

C.
( ) ( ) d
b
a
S f x g x x=−
. D.
( )
( ) ( ) d
b
a
S f x g x x=−
16
Câu 46. Trong không gian
Oxyz
, cho điểm
( )
1;2; 3A −
. Tọa độ điểm
A
đi xứng vi điểm
A
qua mặt phẳng
( )
Oxy
là
A.
( )
1;2; 3A
−
B.
( )
1; 2; 3A
− − −
C.
( )
1;2;3A
D.
( )
1;2;0A
Câu 47. Trong không gian
Oxyz
, cho ba điểm
( )
(2;1; 1), 3;0;1 , (2; 1,3)A B C−−
. Gọi
( )
;;H m n p
là trực tâm của
tam giác
ABC
. Tổng
2 2 2
m n p++
A.
134
169
. B.
35
4
. C.
50
. D.
82
.
Câu 48. Một vật thể
V
nằm gia hai mặt phẳng
0x =
và
2x =
, biết rằng thiết diện của vật thể
V
b cắt bởi
mặt phẳng vuông góc vi trục
Ox
tại điểm c honh độ
x
( )
02x
là một nửa hình trn đường kính
2
5dx=
. Thể tích vật thể
V
đ l
A.
8V =
B.
16V
=
C.
8V
=
D.
4V
=
Câu 49. Biết giá tr của tích phân
1
0
( )d 2f x x =
. Giá tr của tích phân
1
0
( ) 2 df x x x−
bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 50. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 3 0P x y z+ − + =
. Vc tơ no dưi đây l một vc tơ
pháp tuyến của
( )
P
?
A.
( )
1
2;1; 1n −
. B.
( )
2
2;1;1n
C.
( )
3
2;1;3n
. D.
( )
4
1; 1;3n −
.
------------- HẾT -------------
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

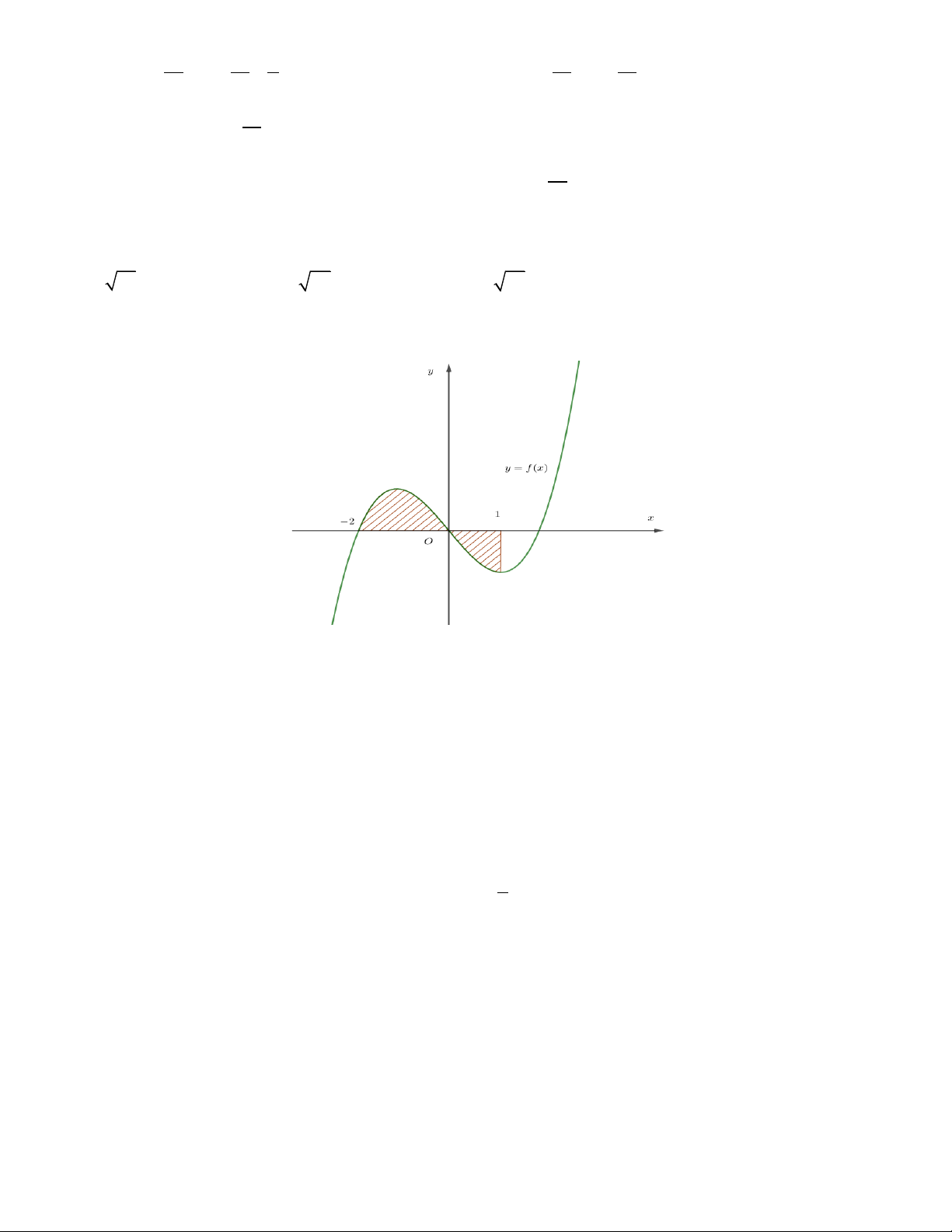
Preview text:

TRƯỜNG THPT HOÀNG VĂN THỤ
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ II MÔN TOÁN MÔN TOÁN - LỚP 12 NĂM HỌC 2023- 2024 1. MỤC TIÊU
1.1. Kiến thức : Học sinh ôn tập các kiến thức về: - Nguyên hàm. - Tích phân.
- Ứng dụng của tích phân trong hình học.
- Hệ tọa độ trong không gian.
- Phương trình mặt phẳng.
- Phương trình mặt cầu.
1.2. Kĩ năng: Học sinh rèn luyện các kĩ năng:
+ Rèn luyện tính cẩn thận chính xác trong tính toán.
+ Biết vận dụng các kiến thức đã học vào giải bài tập.
+Phát triển tư duy logic, khả năng linh hoạt.
+ Sử dụng thành thạo máy tính. 2. NỘI DUNG:
2.1. Các câu hỏi định tính về:
+ Định nghĩa, các tính chất, công thức nguyên hàm, phương pháp tìm nguyên hàm.
+ Định nghĩa, các tính chất của tích phân, phương pháp tính tích phân và ứng dụng của tích phân trong hình học.
+ Hệ trục tọa độ, tọa độ của điểm và vecto; các phép toán cộng, trừ, nhân vecto với một số, tích vô hướng
của hai vecto, tích có hướng hai vecto.
+ Phương trình mặt phẳng, phương trình mặt cầu.
2.2. Các câu hỏi định lượng về:
+ Tìm họ nguyên hàm của hàm số.
+ Tìm nguyên hàm thỏa mãn điều kiện cho trước. + Tính tích phân.
+ Tính diện tích hình phẳng, thể tích vật thể, thể tích khối tròn xoay.
+ Tìm tọa độ điểm, vecto thỏa mãn điều kiện cho trước.
+ Tính số đo góc giữa hai vecto, góc giữa hai mặt phẳng.
+ Tính khoảng cách giữa hai điểm, khoảng cách từ 1 điểm đến 1 mặt phẳng, khoảng cách giữa hai mặt phẳng song song.
+ Tính chu vi tam giác, diện tích tam giác, thể tích khối chóp, khối hộp,…
+ Viết phương trình mặt phẳng, mặt cầu.
2. 3. Câu hỏi và bài tập minh họa
Câu 1. Cho f ( x), g ( x) là các hàm số xác định và liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A.  f
 (x)− g(x)dx = f
 (x)dx− g
 (x)dx. B. f
 (x)g(x)dx = f
 (x)dx. g  (x)dx. 1 C. 2 f
 (x)dx = 2 f
 (x)dx. D.  f
 (x)+ g(x)dx = f
 (x)dx+ g  (x)dx.
Câu 2. Cho hàm số F ( x) là một nguyên hàm của hàm f ( x) trên khoảng K nếu
A. F( x) = f ( x) .
B. F ( x) = f ( x) .
C. F ( x) = f ( x) .
D. F ( x) = f  ( x) .
Câu 3. Hàm số nào dưới đây không phải là nguyên hàm của hàm số ( ) 3 f x = x ? 4 x 4 x 4 x A. y = + 2 . B. y = . C. 2 y = 3x . D. 2019 y = − 2 . 4 4 4
Câu 4. Họ nguyên hàm của hàm số ( ) = 3cos −3x f x x là: x x A. f  (x) 3 dx = 3sin x − + C . B. f  (x) 3 dx = 3 − sin x + + C . ln 3 ln 3 x x C. f  (x) 3 dx = 3sin x + + C . D. f  (x) 3 dx = 3 − sin x − + C . ln 3 ln 3 1   
Câu 5. Nguyên hàm F ( x) của hàm số f ( x) = 2x + thỏa mãn F = 1 −   là 2 sin x  4     A. F ( x) 2 2
= cot x − x − . B. F ( x) 2 2
= −cot x + x − . C. F ( x) 2
= −cot x + x . D. F (x) 2 2 = cot x − x + . 16 16 16
Câu 6. Trong các khẳng định sau, khẳng định nào sai? 1 A. 2xd = 2x x ln 2 + C  . B. cos 2 d x x = sin 2x + C  . 2 2 x e 1 C. 2 x e dx = + C  . D.
dx = ln x +1 + C  ( x   − ) 1 . 2 x +1
Câu 7. Tìm nguyên hàm F ( x) của hàm số f ( x) 2 =
thỏa mãn F (5) = 7 . 2x −1
A. F ( x) = 2 2x −1 .
B. F ( x) = 2 2x −1 +1. C. F ( x) = 2x −1 + 4 .
D. F ( x) = 2x −1 −10 . ln x
Câu 8. Gọi F ( x) là một nguyên hàm của hàm số 2 y = ln x +1. mà F ( ) 1 1 = . Giá trị của 2 F (e) bằng: x 3 8 1 8 1 A. . B. . C. . D. . 9 9 3 3 52 51 − − 50 1 2x 1 2x
Câu 9. Biết x (1− 2x) ( ) ( ) dx = −
+ C;a,b 
. Tính giá trị của a − b . a b A. 0 . B. 4 . C. 1. D. 4 − . x e x e Câu 10. Xét nguyên hàm dx  , nếu đặt = x t e +1 thì dx  bằng x e +1 x e +1 2 2 dt A. 2dt  . B. 2t dt  . C. t dt  . D.  . 2 2 + x Câu 11.
Nguyên hàm của f ( x) 1 ln = là: x ln x
A. F ( x) = ln ln x + C . B. F ( x) 2
= ln x ln x + C .C. F (x) = ln x + ln x +C . D. F (x) = ln xln x +C . 3 x Câu 12.
Tìm họ nguyên hàm: F (x) = dx  4 x −1 1 1 1 A. 4
F (x) = ln x −1 + C . B. 4 F (x) =
ln x −1 + C .C. 4 F (x) =
ln x −1 + C . D. 4 F (x) = ln x −1 + C . 4 2 3 Câu 13.
Cho F (x) là một nguyên hàm của hàm số ( ) = (5 + )1ex f x x
và F (0) = 3. Tính F ( ) 1 . A. F ( ) 1 = 11e − 3 . B. F ( ) 1 = e + 3 . C. F ( ) 1 = e + 7 . D. F ( ) 1 = e + 2 . cos x Câu 14.
Họ nguyên hàm F ( x) của hàm số f ( x) = 2 1− là cos x x 1 A. F ( x) cos = −
+ C . B. F (x) 1 = −
+ C . C. F (x) 1 = + C . D. F ( x) = + C . sin x sin x sin x 2 sin x 2 x + 2x + 3 Câu 15. dx  bằng x +1 2 x 2 x A.
+ x + 2ln | x +1| C + . B.
+ x + ln | x +1| +C . 2 2 2 x C.
+ x + 2ln | x −1| +C .
D. x + 2 ln | x +1| +C 2 x + 2 Câu 16.
Cho hàm số f ( x) thỏa mãn f ( x) = f 2
− = 2 . Giá trị f ( ) 1 bằng 2 x + 4x + và ( ) 5 1 1 A. ln10 + 2 . B. ln10 − 2 . C. ln10 − 2 . D. ln10 + 2 . 2 2 Câu 17.
Họ nguyên hàm của hàm số f ( x) 2 = ln x là A. 2
x ln x − 2x ln x + 2x + c . B. 2
x ln x + 2x + c . C. 2
x ln x + 2x ln x + 2x + c . D. 2
x ln x − 2x + c . x + Câu 18.
Cho F ( x) là một nguyên hàm của hàm số f ( x) 2 1 = F
= . Tìm F (x) : 2x − thỏa mãn (2) 3 3
A. F (x) = x + 4 ln 2x − 3 + 1.
B. F (x) = x + 2 ln(2x − 3) + 1 .
C. F (x) = x + 2 ln 2x − 3 + 1 .
D. F (x) = x + 2 ln | 2x − 3 | 1 − . Câu 19.
Cho F ( x) là một nguyên hàm của hàm số f ( x) . Khi đó hiệu số F ( ) 1 − F (0) bằng 1 1 1 1 A. −F  (x)dx . B. f ( x) dx  .
C. F ( x) dx  . D. − f  (x)dx. 0 0 0 0 3 4 2 4 Câu 20. Cho f
 (x)dx =10và g(x)dx = 5 −  . Tính 3 f
  (x)−5g(x)dx  . 2 4 2 A. I = 5 . B. I = 10 . C. I = 5 − . D. I = 15 .  4 1 Câu 21.
Tính tích phân cos2x dx  bằng A. 1. B. . C. 2 . D. 2 0 4 2  1  Câu 22.
Tính giá trị của tích phân I = x + dx    x  1 111 305 196 208 A. I = . B. I = . C. I = . D. I = . 4 16 15 17 3 dx Câu 23. Cho
= a ln 2 + b ln 5 + c ln 7 ( a, , b c  ) 
. Tính giá trị S = a + 4b − c x +1 x + 4 1 ( )( ) A. S = 2 . B. S = 3. C. S = 4 . D. S = 5 . Câu 24.
Cho f ( x), g ( x) là các hàm số liên tục trên 1;  3 và thỏa 3 3 3 mãn  f
 (x)+3g(x)dx =10  2 f
 (x)− g(x)dx = 6 
. Tính I =  f
 (x)+ g(x)dx  bằng 1 1 1 A. I = 7 . B. I = 6 . C. I = 8 . D. I = 9 . 1 1 2 Câu 25. Biết
f ( x) dx = 2 −  và f
 (x)dx = 3,khi đó f (x)dx  bằng 0 2 0 A. 5 − . B. 5 . C. 1 − . D. 1. 1 1 Câu 26. Cho f
 (x)dx = 2. Khi đó 2  ( ) x
f x + e  dx   bằng 0 0
A. e + 3 . B. 5 + e . C. 3 − e . D. 5 − e .  2  1 Câu 27.
Kết quả của tích phân  (2x −1− sin x)dx được viết ở dạng    − −1  
a , b  . Khẳng định  a b  0 nào sau đây là sai? A. a + 2b = 8 . B. a + b = 5 .
C. 2a − 3b = 2 .
D. a − b = 2 .  6 ac 3 Câu 28. Biết ( 2 3 + 4 sin x)dx = − 
, trong đó a , b nguyên dương và a tối giản. Tính a + b + c . b 6 b 0 A. 8 . B. 16 . C. 12 . D. 14 . Câu 29.
Cho hàm số f ( x) có đạo hàm liên tục trên đoạn 2;4 và thỏa mãn f (2) = 2, f (4) = 2020 . Tính 2 tích phân I = f   (2x)dx . 1 A. I = 1009 . B. I = 2022 . C. I = 2018. D. I = 1011. 4 1 4 Câu 30.
Nếu đặt u = 2x +1thì (2x +  ) 1 dx bằng 0 3 1 3 1 1 1 A. 4 u du  . B. 4 u du  . C. 4 u du  . D. 4 u du  . 2 2 1 1 0 0  3 xCâu 31. Tích phân dx = a
+ b ln 2; a,b  
. Khi đó giá trị a b thuộc khoảng nào sau đây? 2 cos x 3 0 1 1 1 A. 2; 1 . B. 0; . C. ; . D. 1; 2 . 3 2 2 4 Câu 32. Biết x ln
 ( 2x +9)dx = aln5+bln3+c , trong đó a , b , c là các số nguyên. Giá trị của biểu thức 0
T = a + b + c là A. T = 10 . B. T = 9 .
C. T = 8 . D. T =11.  Câu 33.
Cho tích phân I = (2 − x) sin xdx
. Đặt u = 2 − x, dv = sin xdx thì I bằng 0    
A. − (2 − x) cos x − cos xdx
B. (2 − x) cos x + cos xdx  . 0 0 0 0    
C. (2 − x) + cos xdx  .
D. − (2 − x) cos x + cos xdx  . 0 0 0 0 1 e −1 Câu 34.
Cho hàm số y = f ( x) có đạo hàm trên 0  ;1 . Biết f ( ) 1 1 = và
f ( x)dx =  . e 0 e 1 Tính I = xf   (x)dx . 0 e − 2 2 − e A. I = 1. B. I = . C. I = . D. I = 1 − . e e  4 Câu 35.
Tính tích phân I =  (1+ x)sin d x x . 0 8 −  2  2  2 8 +  2 A. I = . B. I = 1− 2 − . C. I = 1− 2 + . D. I = . 8 8 8 8 e f ( x) Câu 36.
Cho hàm số f ( x) liên tục trong đoạn 1;e , biết dx = 1  , f (e) = 1. Khi đó x 1 e I = f   (x).ln d x x bằng 1 A. I = 4 . B. I = 3 . C. I = 1. D. I = 0 . 1 f (x) e Câu 37. Cho F (x) =
là một nguyên hàm của hàm số . Tính f '(x) ln d x x  bằng: 2 2x x 1 5 2 e − 3 2 2 − e 2 e − 2 2 3 − e A. I = . B. I = . C. I = . D. I = . 2 2e 2 e 2 e 2 2e 4 a Câu 38. Biết 2 x ln x 1 dx ln 5
c , trong đó a, b, c là các số nguyên. Giá trị của biểu b 0 thức T a b c là A. T = 5 . B. T = 4 . C. T = 9 . D. T =1. 3 Câu 39.
Cho hàm số f ( x) có đạo hàm trên
và thỏa mãn x f  
(2x − 4)dx = 8 ; f (2) = 2 . Tính 0 1 I = f  (2x)dx . 2 − A. I = 5 − . B. I = 10 −
C. I = 5 . D. I = 10 . Câu 40.
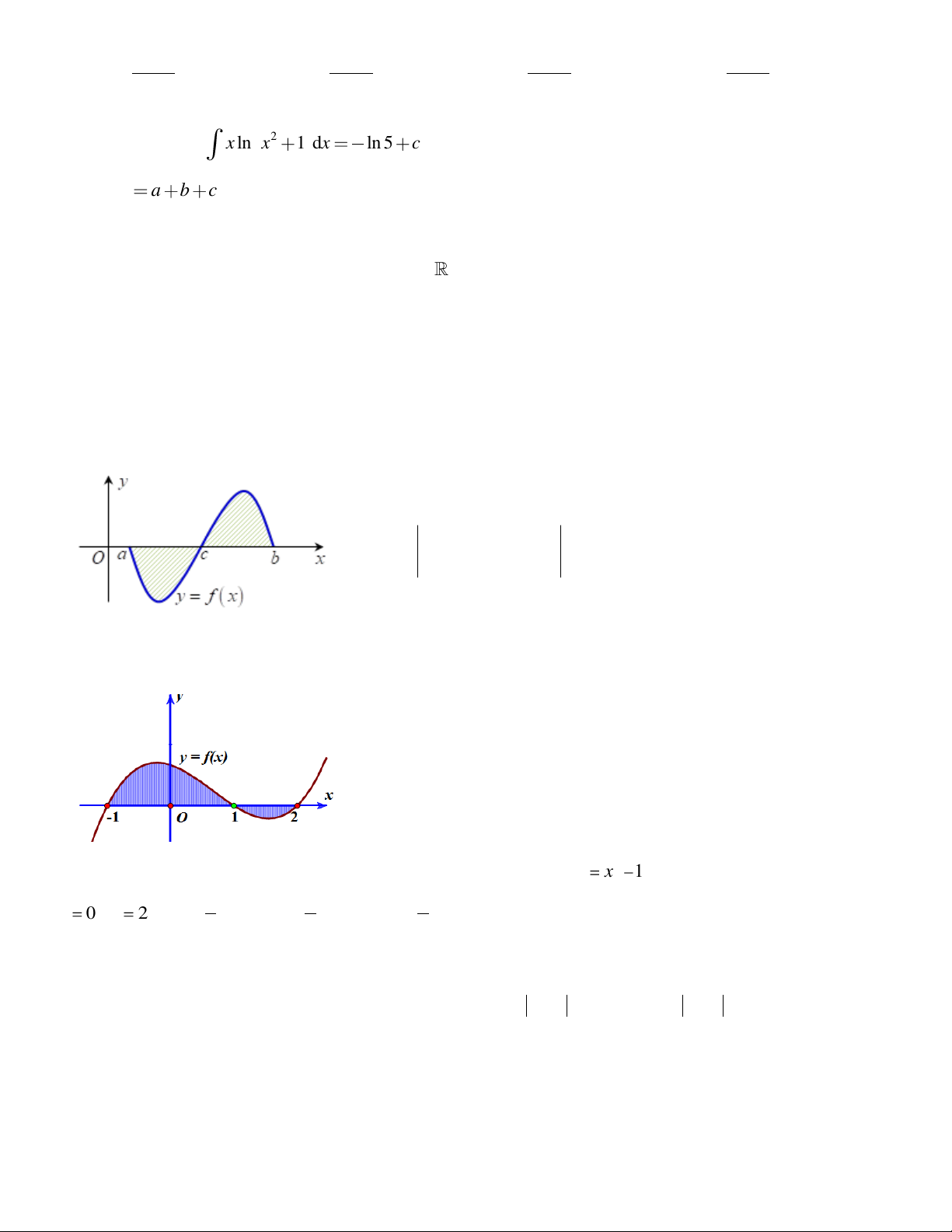
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành, đường thẳng
x = a, x = b (như hình bên). Hỏi
khẳng định nào dưới đây là khẳng định đúng? c b c b A. S = f
 (x)dx+ f
 (x)dx . B.S = f
 (x)dx+ f  (x)dx . a c a c c b b C. S = − f
 (x)dx+ f
 (x)dx . D. S = f  (x)dx. a c a Câu 41.
Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ dưới đây. Công thức tính S là 1 2 2 A. S = f
 (x)dx+ f
 (x)dx. B. S = f  (x)dx . 1 − 1 1 − 1 2 2 C. S = f
 (x)dx− f
 (x)dx . D. S = − f  (x)dx . 1 − 1 1 − Câu 42.
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 3 y x
1, trục hoành và hai đường thẳng 5 7 7 x 0 , x 2 là A. . B. . C. 2. D. . 2 2 3 Câu 43.
Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0 , x =  , đồ thị hàm số y = cos x và trục    
Ox là A. S = cos x dx  . B. 2
S = cos x dx  .
C. S =  cos x dx  . D. S = cos x dx  . 0 0 0 0 Câu 44.
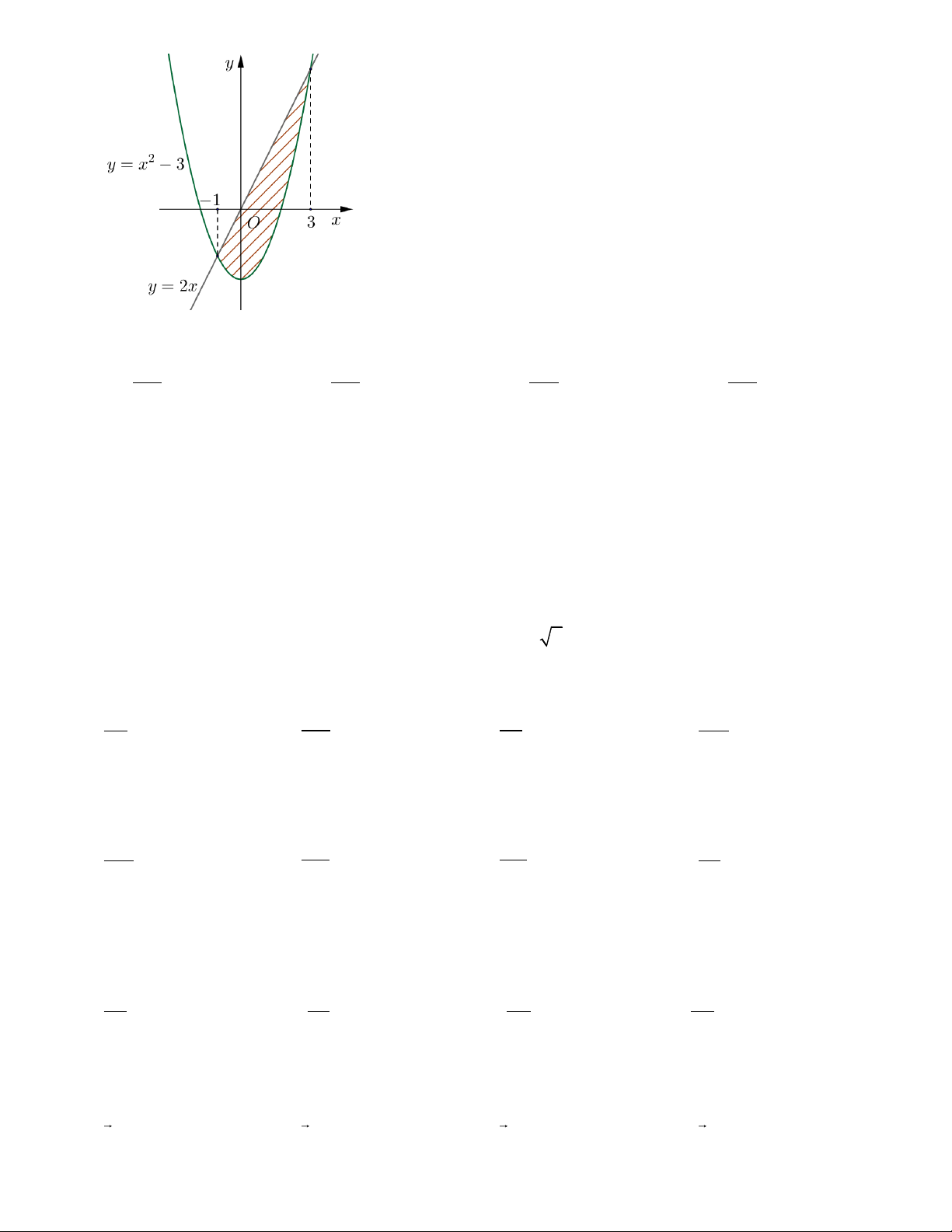
Diện tích hình phẳng được gạch chéo như hình vẽ bằng 6 3 3 A.  ( 2 −x + 2x + 3) . dx B.  ( 2
x − 2x − 3) d . x 1 − 1 − 3 3 C.  ( 2
x + 2x − 3) d . x D.  ( 2
−x + 2x − 3) . dx 1 − 1 − Câu 45.
Tính diện tích S của hình phẳng (H ) giới hạn bởi các đường cong 3
y = −x +12x và 2 y = −x . 937 343 793 397 A. S = . B. S = . C. S = . D. S = . 12 12 4 4 Câu 46.
Diện tích của hình phẳng giới hạn bởi các đường 2 y = x − 4 , 2
y = −x − 2x , x = 2 − và x = 3 −
được tính bằng công thức 2 − 1 A. S = 2  ( 2
x + x − 2)dx . B. S = 2 ( 2
x + x − 2)dx . 3 − 2 − 2 − 1 C. S =  ( 2
x + x − 2)dx . D. S =  ( 2
x + x − 2)dx . 3 − 2 − Câu 47.
Cho hình phẳng ( H ) giới hạn bởi các đường y = x; y = 1; x = 4. Khi đó cho hình phẳng ( H )
quay quanh trục Ox thì thể tích khối tròn xoay thu được có thể tích tương ứng bằng: 7 11 9 13 A. . B. . C. . D. . 6 3 2 4 Câu 48.
Cho hình phẳng ( H ) giới hạn bởi các đường cong 2
y = x ; y = 4x − 3 .Thể tích khối tròn xoay khi
cho hình ( H ) quay quanh trục tung Oy tương ứng là: 16 11 184 5 A. . B. . C. . D. . 3 3 15 6 Câu 49.
Tính thể tích vật thể giới hạn bởi hai mặt phẳng x = 0 , x =  . Biết rằng thiết diện của vật thể cắt
bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x (0  x   ) là một tam giác vuông cân có cạnh huyền bằng s inx + 2 . 7 9 7 9 A. +1. B. +1. C. + 2 . D. + 2 . 6 8 6 8 Câu 50.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : 3y − z + 2 = 0 . Vectơ nào dưới đây là
vectơ pháp tuyến của (P) ? A. n = ( 1 − ; 1 − ;2) . B. n = (3;0; 2) . C. n = (3; 1 − ;2) . D. n = (0; 3 − ) ;1 . 7 x y z Câu 51.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : +
+ =1. Vectơ nào dưới đây là 3 2 1
một vectơ pháp tuyến của ( P) ?  1 1  A. n = 6;3; 2 . B. n = 2;3;6 . C. n = 1; ;   . D. n = 3; 2;1 . 4 ( ) 2 ( ) 1 ( ) 3  2 3  Câu 52.
Trong không gian Oxyz, cho hai điểm (
A 1; 1;2) và B(2;1;3). Gọi P là mặt phẳng qua A và
vuông góc với đường thẳng AB, điểm nào dưới đây thuộc P ? A. 2; 1;1 . B. 2; 1; 1 . C. 2;1; 1 . D. 1; 2;1 . Câu 53.
Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A = (1;2;0), B = ( 2 − ;1; ) 1 ,
C = (3;0; − 2) . Phương trình mặt phẳng đi qua A , vuông góc với đường thẳng BC là:
A. 5x − y − 3z − 3 = 0 .
B. x + y − z − 3 = 0 .
C. 2x − y − z = 0 .
D. 4x − 3y − 3z + 2 = 0 . Câu 54.
Trong không gian với hệ tọa độ Oxyz , viết phương trình của mặt phẳng ( P) đi qua các điểm
A(1;0;0) ; B (0; 2;0) ; C (0;0; 3 − ) . x y z x y z A. + − =1. B. + + =1.
C. 6x + 3y + 2z = 1.
D. 6x + 3y + 2z = 0 . 1 2 3 1 2 3 Câu 55.
Trong không gian Oxyz , cho hai điểm A(4;0 ) ;1 , B ( 2
− ;2;3) . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là:
A. 6x − 2 y − 2z −1 = 0 .
B. 3x − y − z = 0 .
C. x + y + 2z − 6 = 0 .
D. 3x + y + z − 6 = 0 . Câu 56.
Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình của mặt
phẳng chứa trục Ox và đi qua điểm K (2;1; 1 − ) ? A. x + 2z = 0 .
B. x − 2z = 0 .
C. y − z − 2 = 0 . D. Câu 57.
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng là ( P) : 2x − y + 2z + 2 = 0 và (Q) 2
: a x + by + z + a = 0 , trong đó a, b là các số thực. Để ( P) song song với (Q) thì giá trị của biểu thức
T = a + 2b bằng: A. 1 − . B. 0. C. 2 − . D. 3. Câu 58.
Trong không gian (Oxyz) , cho hai điểm A(2;1; 3 − ), B( 1 − ;2; )
1 . Toạ độ của véctơ AB là : A. ( 3 − ; 1 − ;4). B. (3;1; 4 − ). C. ( 3 − ;1;4). D. (3; 1 − ; 4 − ) . Câu 59.
Trong không gian Oxyz , cho điểm M ( 2
− ;5;0) . Tìm hình chiếu vuông góc của điểm M lên trục Oy . A. M ( 2 − ;0;0) . B. M (2;5;0) . C. M (0; 5 − ;0) . D. M (0;5;0) . Câu 60.
Trong không gian Oxyz , cho hai điểm A(1; 3; − 5), B ( 3 − ;1; − )
1 . Tìm toạ độ trọng tâm G của tam giác OAB . 8  2 4   2 4   2 4   2 4  A. G ; − ; − 2 
 . B. G − ; − ; − 2 . C. G − ; ; − 2 
 . D. G − ; − ; 2   .    3 3   3 3   3 3   3 3  Câu 61.
Trong không gian với hệ trục tọa độ Oxyz , cho hình bình hành ABCD . Biết A(2;1; − 3) ,
B (0; − 2;5) và C (1;1;3) . Diện tích hình bình hành ABCD là 349 A. 2 87 . B. . C. 349 . D. 87 . 2 Câu 62.
Trong không gian Oxyz , cho hình chóp . A BCD có ( A 0;1; 1
− ), B(1;1;2),C(1; 1 − ;0) và D(0;0;1) .
Tính độ dài đường cao của hình chóp . A BCD . 3 2 2 A. 2 2 . B. . C. 3 2 . D. . 2 2 Câu 63.
Trong không gian với hệ trục tọa độ Oxyz , cho OA = 2i + 2 j + 2k , B( 2 − ;2;0) và C(4;1; 1 − ) .
Trên mặt phẳng (Oxz) , điểm nào dưới đây cách đều ba điểm , A B,C .  3 1   3 1   3 1   3 1  A. N − ;0; −   . B. P ;0; −   . C. Q − ;0;   . D. M ; 0;   .  4 2   4 2   4 2   4 2  Câu 64.
Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(0;1; 4) , B (3; 1 − ) ;1 , C ( 2 − ;3;2).
Tính diện tích S tam giác ABC . A. S = 2 62 . B. S = 12 . C. S = 6 . D. S = 62 . Câu 65.
Trong không gian tọa độ Oxyz, cho tứ diện ABCD với A( 1 − ; 2 − ;4), B( 4 − ; 2 − ;0),C (3; 2 − ; ) 1 và D (1;1; )
1 . Độ cao của tứ diện kẻ từ D bằng 1 A. 3. B. 1. C. 2. D. 2 Câu 66.
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết ( A 5 − ;7; 9 − ), B(7;9; 5 − ), C( 9 − ; 7 − ;5). = + + Gọi điểm H ( ; a ;
b c) là trực tâm của tam giác ABC. Tính 2 2 2 S a b c . 211 A. Đáp án khác. B. S = 155. C. S = . D. S = 211. 9 Câu 67.
Trong không gian Oxyz , có tất cả bao nhiêu giá trị nguyên của m để 2 2 2
x + y + z + ( − m) y − (m − ) 2 2 1 2 2
2 z + 6m + 5 = 0 là phương trình của một mặt cầu? A. 6 B. 5 C. 7 D. 4 Câu 68.
Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với (
A 1; 0; 0) , B(3; 2; 4) , C(0;5; 4) .
Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho MA + MB + 2MC nhỏ nhất. A. M (1;3; 0) . B. M (1; − 3; 0) . C. M (3;1; 0) . D. M (2; 6; 0) .
2.4. 1. MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ II
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ II
MÔN: TOÁN, LỚP 12 – THỜI GIAN LÀM BÀI: 90 phút 9
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ 2 MÔN TOÁN LỚP 12 Kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao Nguyên hàm 4 4 1 Tích phân 5 4 2 3
Ứng dụng của tích phân 4 4 1
Hệ tọa độ trong không gian 2 2 1 Phương trình mặt phẳng 2 3 1 2 Phương trình mặt cầu 1 3 1 Tổng 18 20 7 5
2.4.2 . ĐỀ MINH HỌA
Câu 1. Cho F ( x) là một nguyên hàm của hàm số f ( x) 2
= x − 2x + 3thỏa mãn F (0) = 2, giá trị của F ( ) 1 bằng 11 13 A. 2 . B. . C. 4 . D. . 3 3 1 2 Câu 2. Cho f  ( 2x + )1 d
x x = 10 . Khi đó I = f
 (x)dx bằng: 0 1 A. 5 . B. 20 . C. 2 . D. 10 . 2023 Câu 3. Tích phân 2 x I = xe dx  bằng: 0 1 1 A. I = ( 4046 4045e + ) 1 . B. I = ( 4046 4045e + ) 1 . 2 4 1 1 C. I = ( 4044 4043e + ) 1 . D. I = ( 4046 4045e − ) 1 . 2 4
Câu 4. Trong không gian Oxyz , cho mặt cầu ( S ) có phương trình 2 2 2
(x − 2) + ( y +1) + (z + 3) = 25 . Tọa độ tâm
I và bán kính R của mặt cầu ( S ) là A. I (2; 1 − ; 3 − );R = 5 B. I ( 2
− ;1;3); R = 5 C. I (2; 1 − ; 3 − ); R = 25 D. I ( 2
− ;1;3); R = 25
Câu 5. Họ nguyên hàm của hàm số ( ) x
f x = x + e là: 2 x 2 x x + e A. F (x) x =
+ e + C .
B. F (x) = + C . 2 2 2 x C. F (x) x =
+ e ln 2 + C . D. ( ) = 1 x F x
+ e + C . 2
Câu 6. Trong không gian Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z + 2x + 4 y + 6z = 0 , mặt phẳng (Oxz) cắt mặt cầu
(S ) theo giao tuyến là một đường tròn. Đường tròn giao tuyến này có tâm là A. I ( 1 − ; 2 − ; 3 − ) B. I ( 1 − ;0; 3 − )
C. I (1; 0;3) D. I ( 1 − ;2; 3 − ) 0
Câu 7. Cho hàm số y = f ( x) có đạo hàm liên tục trên
và thỏa mãn f (4) = 5 ; f
 (2x + 4)dx =16 . Tính 2 − 4 I = xf
 (x)dx . 0 10 A. I = 14 − . B. I = 8 − .
C. I = 4 . D. I = 12 − . x
Câu 8. Cho I =  = + ( và t
x 1. Mệnh đề nào sau đây đúng? x + ) dx 2 1 t t −1 t t +1 A. I = dt  . B. I = dt  . C. I = dt  . D. I = dt  . 2 t +1 2 t ( 2 t + )2 1 t
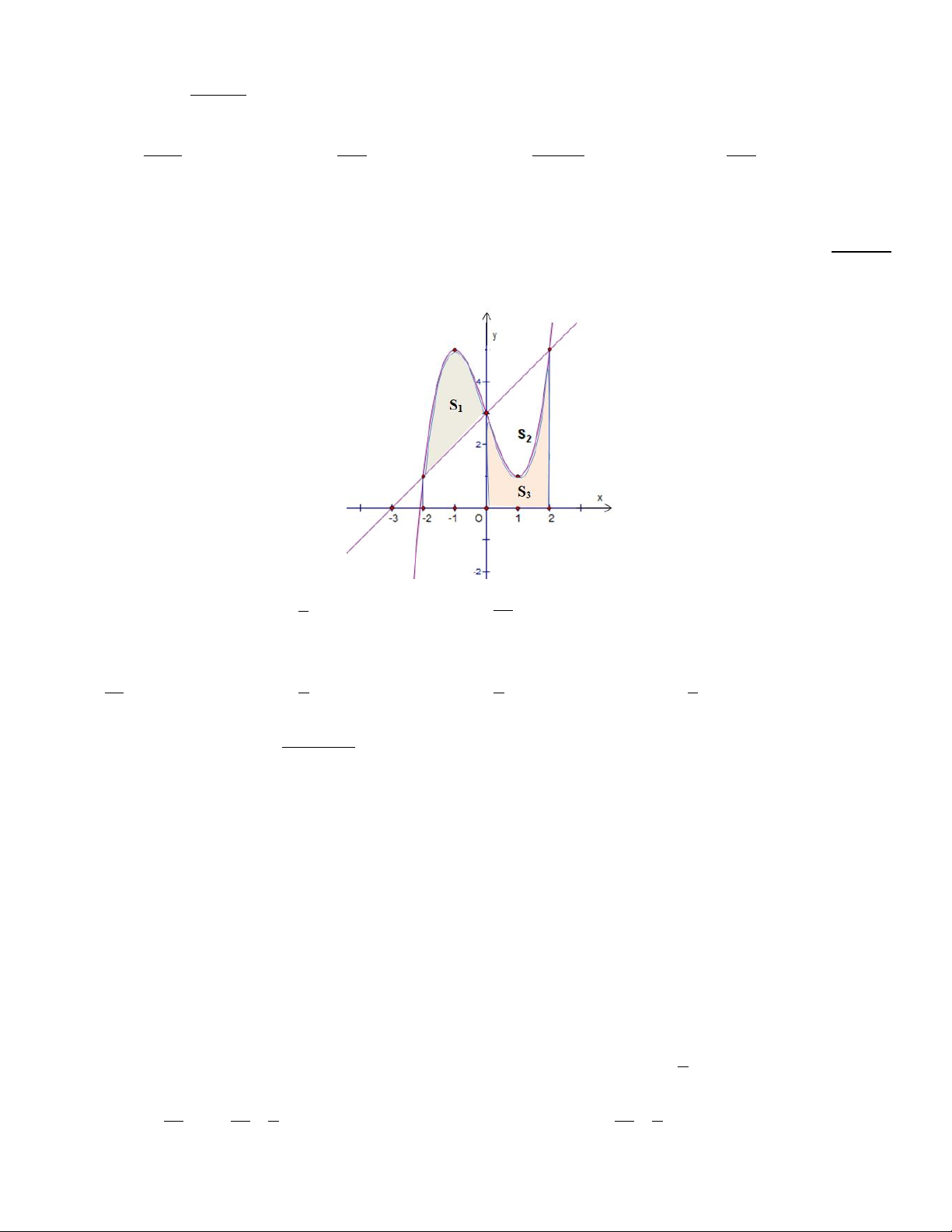
Câu 9. Cho hàm số bậc ba ( ) 3 2
f x = ax + bx + cx + d và đường thẳng d : g ( x) = mx + n có đồ thị như hình vẽ. 2S
Gọi S , S , S lần lượt là diện tích của các phần hình phẳng giới hạn như hình bên. Nếu S = 4 thì tỷ số 3 1 2 3 1 S + 3S 2 1 bằng. 1 13 A. 2 . B. . C. . D. 1. 2 14
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x ; y = 2x −1 và y = 2 − x −1 là 16 4 2 8 A. B. C. D. 3 3 3 3 ln 2 dx
Câu 11. Cho tích phân I =
= a ln 3+ bln 2 + c
(với a,b,c là các số hữu tỉ) . Giá trị của biểu thức ex ex +1 0 ( ) 2 2
T = a + b + 2c bằng A. 0. B. 6. C. 4. D. 9. 1
Câu 12. Cho y = f (x) là một hàm số bất kỳ có đạo hàm trên ,
R đặt I = x f (x) dx
. Khẳng định nào dưới đây 0 đúng: 1 1 A. I =
f (x) dx − f (1). 
B. I = f (1) − f (x) d . x 0 0 1 0
C. I = f (1) + f (x) d . x D. I =
f (x) dx − f (1).  0 1
Câu 13. Cho F ( x) là một nguyên hàm của hàm số f ( x) = .
x ln x thỏa mãn F ( ) 3 1 =
. Tìm F ( x) . 4 x x x 1 A. F ( x) 2 2 1 = ln x + + . B. F ( x) 2 2 = x ln x − + . 2 4 2 2 4 11 x x x x C. F ( x) 2 2 1 = ln x − + . D. F ( x) 2 2 = ln x − +1. 2 4 2 2 4 3 x
Câu 14. Hàm số F (x) =
là một nguyên hàm của hàm số nào trong các hàm số sau đây ? 3 4 x A. 2
f (x) = x + C . B. 2
f (x) = 3x .
C. f (x) = . D. 2
f (x) = x . 12
Câu 15. Trong không gian Oxyz , cho hai điểm A( 2
− ;0;3) và B(1;4;5). Khoảng cách giữa hai điểm A và B là A. 21 . B. 29 . C. 89 . D. 3 .
Câu 16. Cho hình phẳng ( H ) được giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành và hai đường thẳng x = 2
− , x = 1như hình vẽ bên.
Diện tích của hình phẳng ( H ) bằng 2 0 1 A. f
 (x)dx . B. − f
 (x)dx + f
 (x)dx . 2 − 2 − 0 0 1 0 1 C. f
 (x)dx− f
 (x)dx. D. f
 (x)dx + f
 (x)dx . 2 − 0 2 − 0
Câu 17. Trong không gian Oxyz , cho mặt cầu (S) 2 2 2
: x + y + z + 2x − 2 y − z − 2 = 0 và mặt
phẳng ( P) : 2x + y − 2z + 3m −1 = 0 , có bao nhiêu giá trị nguyên dương của tham số m để mặt phẳng (P) cắt mặt 1
cầu (S ) theo giao tuyến là một đường tròn có bán kính r = 2 A. 1. B. 2. C. 3 D. 4
Câu 18. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v (t ) = 5t + 4 (m / s) . Đi được 6 (s) người lái
xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc 2 a = 3
− 4 (m / s ) . Tính quãng đường S (m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn. A. S = 150,5( ) m . B. S = 17 ( ) m . C. S = 131( ) m .
D. S = 114 (m).
Câu 19. Trong không gian Oxyz , cho mặt cầu ( S ) tâm I (3; 2; − 5) và đi qua điểm A( 1 − ;4;7), phương trình
mặt cầu ( S ) là 12 A. 2 2 2
(x + 3) + ( y + 2) + (z − 5) = 152 . B. 2 2 2
(x − 3) + ( y − 2) + (z + 5) = 164 . C. 2 2 2
(x + 3) + ( y + 2) + (z − 5) = 36 . D. 2 2 2
(x − 3) + ( y − 2) + (z + 5) = 10 . 2 3 3
Câu 20. Cho hàm số f ( x) thỏa mãn f  (x)dx = 3 − ; f
 (x)dx = 4. Khi đó giá trị của f (x)dx  bằng 1 2 1 A. 7 − . B. 7. C. 1. D. 12 − . 5
Câu 21. Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn 2; 
5 , biết f (5) = 3; f (2) = 1 . Tính f
 (x)dx 2 A. 3 . B. 2 . C. 5 . D. 4 .
Câu 22. Trong không gian Oxyz , cho hai véc tơ u = (3; 2; − )
1 ; v = (1; m −1; 2) . Có bao nhiêu giá trị nguyên của
m để u(u + 2v) = 4 A. 2 . B. 1. C. 0 . D. 3 .
Câu 23. Trong không gian Oxyz , cho A( 1
− ;4;3) và B(3;2;−5) . Mặt cầu đường kính AB có phương trình là A. 2 2 2
(x −1) + ( y − 3) + (z +1) = 21 . B. 2 2 2
(x −1) + ( y − 3) + (z +1) = 84 . C. 2 2 2
(x +1) + ( y + 3) + (z −1) = 21. D. 2 2 2
(x − 4) + ( y − 2) + (z + 8) = 21.
Câu 24. Giả sử hàm số y = f ( x) liên tục nhận giá trị dương trên (0; +) và thỏa mãn f ( ) 1 = e ,
f ( x) = f ( x). 3x +1 , với mọi x  0 . Mệnh đề nào sau đây đúng?
A. 10  f (5)  11.
B. 9  f (5)  10 .
C. 4  f (5)  5 .
D. 2  f (5)  3 . 3 1
Câu 25. Tích phân I = dx  bằng: x + 3 1 − A. ln12. B. 4ln 2 . C. ln 3 . D. ln 4 . Câu 26. Trong không gian Oxyz, cho hai điểm A(2;0; − ) 1 ; B (2;1; 2 − ) và mặt cầu (S) 2 2 2
: x + y + z + 2x + 4 y − 2z + 3 = 0 . Xét khối nón ( N ) có đỉnh là tâm I của mặt cầu và đường tròn đáy nằm
trên mặt cầu ( S ) . Khi ( N ) có thể tích lớn nhất thì mặt phẳng chứa đường tròn đáy của ( N ) và đi qua hai điểm ,
A B có phương trình dạng ax + 2 y + cz = 0 và x + my + nz + p = 0 . Giá trị của 2 2 2 2 2
a + c + m + n + p bằng A. 93. B. 12 . C. 24 . D. 29 .
Câu 27. Trong các khẳng định sau, khẳng định nào sai? x 2x A. 2 dx = + C  . B. cos d
x x = sin x + C  . ln 2 C. x d x e x = e + C  .
D. 2xd = 2x x ln 2 + C  .
Câu 28. Cho hàm số y = f ( x) liên tục, không âm trên  ;
a b . Hình phẳng ( H ) giới hạn bởi đồ thị hàm số
y = f ( x) , trục hoành và hai đường thẳng x = a, x = b . Khi ( H ) quay quanh trục Ox tạo nên một khối tròn
xoay. Thể tích V của khối tròn xoay được tính theo công thức nào sau đây? b b b b A. 2 V = f
 (x)dx B. V =  f
 (x)dx C. V = f
 (x) dx D. 2 V =  f
 (x)dx. a a a a 13 3
4x - 5 khi 0  x 1 2
Câu 29. Cho hàm số y = f (x) =  . Tính f (x)dx 1
 − 2x khi 1 x  2 0 A. 6 − . B. 5 . C. 7 . D. 1.
Câu 30. Cho hình phẳng ( H ) giới hạn bởi đồ thị hàm số ( ) 2
f x = ax + b (với a , b là các số thực dương), trục
hoành, trục tung và đường thẳng x = 1. Biết vật thể tròn xoay được tạo thành khi quay ( H ) quanh trục Ox có 8 thể tích bằng và f ( )
1 = 2 . Khi đó giá trị a − 3b bằng 15 A. 0 . B. 2 . C. 4 . D. 3 .
Câu 31. Trong không gian Oxyz , cho điểm M thỏa mãn hệ thức OM = 3 j − k . Tọa độ điểm M là
A. M (0; − 3; ) 1 .
B. M (3;1;0) . C. M (0;3; − ) 1 . D. M (3;0; − ) 1 .
Câu 32. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x , trục hoành và hai đường thẳng x = 3 − ; x = 4 là 175 337 146 A. 52 B. C. D. 4 4 3 1 dx
Câu 33. Với phép đổi biến: x = 2sin t thì tích phân  trở thành 2 − 0 4 x     6 3 3 dt 6 A. tdt  . B. tdt  . C.  . D. dt  . t 0 0 0 0
Câu 34. Trong không gian Oxyz , cho hai mặt phẳng ( P) : 2x + y − z + 3 = 0; (Q) : 4x + 2y − 2z + 23 = 0 . Vị trí
tương đối của (P) và (Q) là A. Song song
B. Cắt nhau nhưng không vuông góc C. Trùng nhau D. Vuông góc
Câu 35. Diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y = xe , trục hoành, hai đường thẳng x = 1 − ; x = 1có công thức tính là 1 1 1 − 1 A. x S = xe dx  . B. x S = xe dx  . C. x S = xe dx  . D. x S =  xe dx  . 1 − 1 − 1 1 −
Câu 36. Trong không gian Oxyz , cho ba điểm A(2;0;0); B(0;5;0);C(0;0; 1
− ) . Phương trình mặt phẳng (ABC)là: x y z x y z x y z x y z A. + + = 0 B. + + = 1 C. + + = 0 D. + + = 1 5 2 1 − 2 5 1 − 2 5 1 − 5 2 1 −
Câu 37. Cho hai hàm số f (x) và g(x) liên tụctrên đoạn [ ;
a b] , số thực k tùy ý. Trong các khẳng định sau,
khẳng định nào sai? b a b b A. f (x)dx = f (x)dx   .
B. kf (x)dx = k f (x)dx   . a b a a b a b b b C.
f (x)dx = − f (x)dx   .
D.  f (x) + g(x)dx = f (x)dx + g(x)dx   . a b a a a 14
Câu 38. Trong không gian Oxyz , cho hai điểm A(2; 2; 3), B (2; 0; − )
1 . Điểm M thỏa mãn M . A MB = 4 và
điểm N thuộc mặt phẳng (P) : 2x − y − 2z +17 = 0 . Giá trị nhỏ nhất của độ dài đoạn thẳng MN là 5 4 A. . B. 2 . C. . D. 3 . 3 3
Câu 39. Trong không gian Oxyz , mặt phẳng ( P) chứa trục Oy và điểm ( A 4; 1
− ;2) . Phương trình mặt phẳng (P) là
A. x − 2 y = 0
B. x − 2z + 2 = 0 .
C. x − 2z = 0 .
D. x + 2z = 0 .
Câu 40. Trong không gian Oxyz , cho các điểm M (2;0;3); N(1; 1
− ;5) ; P(3;2;−5) . Mặt phẳng ( ) vuông góc
với đường thẳng MN và đi qua điểm P có phương trình là
A. x + y − 2z −11 = 0 .
B. x + y − 2z +15 = 0 .
C. x − y − 2z −15 = 0 .
D. x + y − 2z −15 = 0 . x + 5
Câu 41. Họ nguyên hàm dx  là: 2 2x − 5x + 3 13 1 2x − 3 A. 6 ln 1− x +
ln 2x − 3 + C . B. ln + C . 2 2 x −1 13 13 C. 6 − ln x −1 +
ln 2x − 3 + C .
D. 6 ln x −1 −
ln 2x − 3 + C . 2 2
Câu 42. Trong không gian Oxyz , cho điểm M (1;3; 2
− ) và (P) : 2x + 2y − z −3 = 0 . Khoảng cách từ điểm M
đến mặt phẳng (P) bằng: 7 1 A. 7 . B. . C. 3 . D. . 3 3
Câu 43. Họ nguyên hàm của hàm số ( ) 4 f x = là: x A. f
 (x)dx = 4ln x +C . B. f
 (x)dx = 4ln x . 4 C. f
 (x)dx = 4ln x+C D. f (x)dx = + C  . ln x dx
Câu 44. Họ nguyên hàm  là 1− x 2 C A. + C .
B. C 1− x . C. . D. 2
− 1− x + C . 1− x 1− x
Câu 45. Cho hai hàm số y = f ( x); y = g(x) liên tục trên  ;
a b . Hình phẳng ( H ) giới hạn bởi đồ thị hàm số
y = f ( x); y = g(x) và hai đường thẳng x = a, x = b . Diện tích S của hình phẳng ( H ) là b b b A. S =
( f (x) − g(x))dx B. S =
f (x) dx − g(x) dx   a a a b b C. S =
f (x) − g(x) dx  .
D. S = ( f (x) − g(x))dx a a 15
Câu 46. Trong không gian Oxyz , cho điểm A(1; 2; 3
− ) . Tọa độ điểm A đối xứng với điểm A qua mặt phẳng (Oxy)là A. A(1; 2; 3 − ) B. A( 1 − ; 2 − ; 3 − )
C. A(1; 2;3)
D. A(1; 2;0)
Câu 47. Trong không gian Oxyz , cho ba điểm ( A 2;1; 1 − ), B(3; 0; ) 1 , C(2; 1 − ,3) . Gọi H ( ; m ;
n p) là trực tâm của
tam giác ABC . Tổng 2 2 2
m + n + p 134 35 A. . B. . C. 50 . D. 82 . 169 4
Câu 48. Một vật thể V nằm giữa hai mặt phẳng x = 0 và x = 2 , biết rằng thiết diện của vật thể V bị cắt bởi
mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0  x  2) là một nửa hình tròn đường kính 2
d = 5x . Thể tích vật thể V đó là
A. V = 8
B. V = 16
C. V = 8
D. V = 4 1 1
Câu 49. Biết giá trị của tích phân
f (x)dx = 2 
. Giá trị của tích phân  f (x) − 2xdx bằng 0 0 A. 1. B. 0 . C. 2 . D. 3 .
Câu 50. Trong không gian Oxyz , cho mặt phẳng ( P) : 2x + y − z + 3 = 0 . Véc tơ nào dưới đây là một véc tơ
pháp tuyến của ( P) ? A. n 2;1; 1 − . B. n 2;1;1
C. n 2;1;3 . D. n 1; 1 − ;3 . 4 ( ) 3 ( ) 2 ( ) 1 ( )
------------- HẾT ------------- 16