Đề cương học kỳ 2 Toán 12 năm 2020 – 2021 trường THPT Yên Hòa – Hà Nội

Đề cương học kỳ 2 Toán 12 năm 2020 – 2021 trường THPT Yên Hòa – Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

78 39 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

66 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT YÊN HÒA
------
o0o
-----
ĐỀ CƯƠNG ÔN TẬP HỌC KỲ 2
NĂM HỌC 2020 – 2021
MÔN: TOÁN
PHẦN I. GIẢI TÍCH
A. NGUYÊN HÀM.
Vấn đề 1. Các câu hỏi lý thuyết.
Câu 1.Giả sử hàm số
F x
là một nguyên hàm của hàm số
f x
trên
K
. Khẳng định nào sau đây đúng.
A. Chỉ có duy nhất một hằng số
C
sao cho hàm số
( )
y F x C
là một nguyên hàm của hàm
f
trên
.
K
B. Với mỗi nguyên hàm
G
của
f
trên
K
thì tồn tại một hằng số
C
sao cho
( ) ( )
G x F x C
với
x
thuộc
K
.
C. Chỉ có duy nhất hàm số
( )
y F x
là nguyên hàm của
f
trên
.
K
D. Với mỗi nguyên hàm
G
của
f
trên
K
thì
( ) ( )
G x F x C
với mọi
x
thuộc
K
và
C
bất kỳ.
Câu 2.Cho hàm số
( )
F x
là một nguyên hàm của hàm số
( )
f x
trên
K
. Các mệnh đề sau, mệnh đề nào sai.
A.
( ) ( ) .
f x dx F x C
B.
( ) ( ).
f x dx f x
C.
( ) ( ).
f x dx f x
D.
( ) ( ).
f x dx F x
Câu 3.Cho hai hàm số
( ), ( )
f x g x
là hàm số liên tục, có
( ), ( )
F x G x
lần lượt là nguyên hàm của
( ), ( )
f x g x
. Xét các mệnh đề sau:
(I).
( ) ( )
F x G x
là một nguyên hàm của
( ) ( ).
f x g x
(II).
. ( )
k F x
là một nguyên hàm của
( )
kf x
với
k

.
(III).
( ). ( )
F x G x
là một nguyên hàm của
( ). ( ).
f x g x
Các mệnh đúng là
A. (I). B. (I) và (II). C. Cả 3 mệnh đề. D. (II).
Câu 4.Trong các khẳng định sau, khẳng định nào sai.
A.
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx
.
B. Nếu
( )
F x
và
( )
G x
đều là nguyên hàm của hàm số
( )
f x
thì
( ) ( )
F x G x C
là hằng số.
C.
( )
F x x
là một nguyên hàm của
( ) 2 .
f x x
D.
2
( )
F x x
là một nguyên hàm của
( ) 2 .
f x x
Câu 5.Trong các khẳng định sau khẳng định nào đúng.
A.
2
2
1 1
2 1 2 1 .
x dx x dx
x x
B.
2
1 1
2 1 2 2 1 .
x dx x dx
x x
C.
2
1 1 1
2 1 2 1 . 2 1 .
x dx x dx x dx
x x x
D.
2
2
2
1 1 2
2 1 4 4 4 .
x dx x dx dx dx xdx dx dx
x x
x
Câu 6.Cho hàm số
f x
có đạo hàm liên tục trên khoảng
0;

. Khi đó
'f x
dx
x
bằng:
A.
1
2
f x C
B.
f x C
C.
2
f x C
D.
2
f x C
Câu 7.Biết
d 3 cos 2 5
f x x x x C
. Tìm khẳng định đúng trong các khẳng định sau.
A.
3 d 3 cos 6 5
f x x x x C
B.
3 d 9 cos 6 5
f x x x x C
C.
3 d 9 cos 2 5
f x x x x C
D.
3 d 3 cos 2 5
f x x x x C
Câu 8.Biết
2
2 d sin ln
f x x x x
. Tìm nguyên hàm
d
f x x
.
A.
2
d sin ln
2
x
f x x x C
. B.
2
d 2 sin 2 ln
2
x
f x x x C
.
C.
2
d 2 sin 2 ln ln 2
f x x x x C
. D.
2
d 2 sin 2 2 ln ln 2
f x x x x C
.
Vấn đề 2. Nguyên hàm của hàm số đa thức.
Câu 9.Nguyên hàm của hàm số
4 2
f x x x
là
A.
5 3
1 1
5 3
x x C
B.
4 2
x x C
C.
5 3
x x C
. D.
3
4 2
x x C
Câu 10.Nguyên hàm của hàm số
3 2
f x x x
là
A.
4 3
1 1
4 3
x x C
B.
2
3 2
x x C
C.
3 2
x x C
D.
4 3
x x C
Câu 11.Tìm nguyên hàm
15
2
7 dx
x x
?
A.
16
2
1
7
2
x C
B.
16
2
1
7
32
x C
C.
16
2
1
7
16
x C
D.
16
2
1
7
32
x C
Câu 12.Nếu
3 2
d 4
f x x x x C
thì hàm số
f x
bằng
A.
3
4
3
x
f x x Cx
. B.
2
12 2
f x x x C
.
C.
2
12 2
f x x x
. D.
3
4
3
x
f x x .
Câu 13.Nguyên hàm của hàm số
3 2
x x
?
A.
2
3 2
x x C
. B.
4 3
1 1
4 3
x x C
. C.
4 3
x x C
. D.
4 3
4 3
x x C
.
Câu 14.Nguyên hàm của hàm số
( )
f x
3 2
1
2 2019
3
x x x
là
A.
2
4 3
1 2
12 3 2
x
x x C
. B.
2
4 3
1 2
2019
9 3 2
x
x x x C
.
C.
2
4 3
1 2
2019
12 3 2
x
x x x C
. D.
2
4 3
1 2
2019
9 3 2
x
x x x C
.
Câu 15.Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số
2019
y x
?
A.
2020
1
2020
x
. B.
2020
2020
x
. C.
2018
2019
y x
. D.
2020
1
2020
x
.
Câu 16.Tìm nguyên
F x
của hàm số
1 2 3 ?
f x x x x
A.
4
3 2
11
6 6
4 2
x
F x x x x C
. B.
4 3 2
6 11 6
F x x x x x C
.
C.
4
3 2
11
2 6
4 2
x
F x x x x C
. D.
3 2 2
6 11 6
F x x x x x C
.
Câu 17.Họ các nguyên hàm của hàm số
5
2 3
f x x
là
A.
6
2 3
12
x
F x C
. B.
6
2 3
6
x
F x C
.
C.
4
10 2 3
F x x C
. D.
4
5 2 3
F x x C
.
Câu 18.Họ nguyên hàm của hàm số
2019
3 2
1f x x x
là
A.
2021 2020
2 2
1 1
1
2 2021 2020
x x
. B.
2021 2020
2 2
1 1
2021 2020
x x
.
C.
2021 2020
2 2
1 1
2021 2020
x x
C
. D.
2021 2020
2 2
1 1
1
2 2021 2020
x x
C
.
Câu 19.Biết rằng hàm số
3 2
3 4 3
F x mx m n x x
là một nguyên hàm của hàm số
2
3 10 4
f x x x
. Tính
mn
.
A.
1
mn
. B.
2
mn
. C.
0
mn
. D.
3
mn
.
Vấn đề 3. Nguyên hàm của hàm số hữu tỉ.
Câu 20.Tìm nguyên hàm của hàm số
2
2
2
f x x
x
.
A.
3
1
d
3
x
f x x C
x
. B.
3
2
d
3
x
f x x C
x
.
C.
3
1
d
3
x
f x x C
x
. D.
3
2
d
3
x
f x x C
x
.
Câu 21.Tìm nguyên hàm của hàm số
1
5 2
f x
x
.
A.
d 1
ln 5 2
5 2 5
x
x C
x
B.
d
ln 5 2
5 2
x
x C
x
C.
d 1
ln 5 2
5 2 2
x
x C
x
D.
d
5 ln 5 2
5 2
x
x C
x
Câu 22.Tìm nguyên hàm của hàm số
4
2
2
x
f x
x
.
A.
3
1
d
3
x
f x x C
x
. B.
3
2
d
3
x
f x x C
x
.
C.
3
1
d
3
x
f x x C
x
. D.
3
2
d
3
x
f x x C
x
.
Câu 23.Tìm nguyên hàm của hàm số
1
1 2
f x
x
trên
1
;
2

.
A.
1
ln 2 1
2
x C
. B.
1
ln 1 2
2
x C
. C.
1
ln 2 1
2
x C
. D.
ln 2 1
x C
.
Câu 24.Cho hàm số
4
2
2 3
( )
x
f x
x
. Khẳng định nào sau đây là đúng?
A.
3
2 3
( )
3 2
x
f x dx C
x
. B.
3
2 3
( )
3
x
f x dx C
x
.
C.
3
2 3
( )
3
x
f x dx C
x
. D.
3
3
( ) 2
f x dx x C
x
.
Câu 25.Họ tất cả các nguyên hàm của hàm số
2
3 2
2
x
f x
x
trên khoảng
2;

là
A.
2
3 ln 2
2
x C
x
B.
2
3 ln 2
2
x C
x
C.
4
3 ln 2
2
x C
x
D.
4
3 ln 2
2
x C
x
.
Câu 26.Cho
F x
là một nguyên hàm của
1
1
f x
x
trên khoảng
1;

thỏa mãn
1 4
F e
Tìm
F x
.
A.
2 ln 1 2
x
B.
ln 1 3
x
C.
4 ln 1
x
D.
ln 1 3
x
Câu 27.Cho biết
2 13
ln 1 ln 2
1 2
x
dx a x b x C
x x
.
Mệnh đề nào sau đây đúng?
A.
2 8
a b
. B.
8
a b
. C.
2 8
a b
. D.
8
a b
.
Câu 28.Cho biết
3
1
ln 1 1 ln
dx a x x b x C
x x
. Tính giá trị biểu thức:
2
P a b
.
A. 0. B. -1. C.
1
2
. D. 1.
Câu 29.Cho biết
2
4 11
dx ln 2 ln 3
5 6
x
a x b x C
x x
. Tính giá trị biểu thức:
2 2
P a ab b
.
A. 12. B. 13. C. 14. D. 15.
Câu 30.Tìm tất cả các họ nguyên hàm của hàm số
9 5
1
3x
f x
x
A.
4
4 4
1 1
x ln
36
3x 3
x
f x d C
x
B.
4
4 4
1 1
x ln
36
12x 3
x
f x d C
x
C.
4
4 4
1 1
x ln
36
3x 3
x
f x d C
x
D.
4
4 4
1 1
x ln
36
12x 3
x
f x d C
x
Câu 31.Tìm hàm số
F x
biết
3
4
d
1
x
F x x
x
và
0 1
F
.
A.
4
ln 1 1
F x x
. B.
4
1 3
ln 1
4 4
F x x
.
C.
4
1
ln 1 1
4
F x x
. D.
4
4 ln 1 1
F x x
.
Câu 32.Biết
2017
2019
1
1 1
. , 1
1
1
b
x
x
dx C x
a x
x
với
,a b
. Mệnh đề nào sau đây đúng?
A.
2
a b
. B.
2
b a
. C.
2018
a b
. D.
2018
b a
.
Câu 33.Đổi biến
1
t x
thì
4
d
( 1)
x
x
x
trở thành
A.
4
1
d .
t
t
t
B.
4
( 1)
d .
t
t
t
C.
4
1
d .
t
t
t
D.
1
d .
t
t
t
Câu 34.Cho
3 2
1
1
I dx
x x
2
2
ln 2 ln 1
a
b x c x C
x
. Khi đó
S a b c
bằng
A.
1
4
. B.
3
4
. C.
7
4
. D.
2
.
Vấn đề 4. Nguyên hàm của hàm số chứa căn.
Câu 35.Tìm nguyên hàm của hàm số
2 1.
f x x
A.
2
2 1 2 1 .
3
f x dx x x C
B.
1
2 1 2 1 .
3
f x dx x x C
C.
1
2 1 .
3
f x dx x C
D.
1
2 1 .
2
f x dx x C
Câu 36.Nguyên hàm của hàm số
1
2 2 1
f x
x
có dạng:
A.
1
d 2 1
2
f x x x C
. B.
d 2 1
f x x x C
.
C.
d 2 2 1
f x x x C
. D.
1
d
2 1 2 1
f x x C
x x
.
Câu 37.Nguyên hàm của hàm số
3
3 1
f x x
là
A.
3
d 3 1 3 1
f x x x x C
. B.
3
d 3 1
f x x x C
.
C.
3
1
d 3 1
3
f x x x C
. D.
3
1
d 3 1 3 1
4
f x x x x C
.
Câu 38.Nguyên hàm của hàm số
3 2
f x x
là
A.
2
(3 2) 3 2
3
x x C
B.
1
(3 2) 3 2
3
x x C
C.
2
(3 2) 3 2
9
x x C
D.
3 1
2
3 2
C
x
Câu 39.Họ nguyên hàm của hàm số
2 1
f x x
là
A.
1
2 1 2 1
3
x x C
. B.
1
2 1
2
x C
.
C.
2
2 1 2 1
3
x x C
. D.
1
2 1 2 1
3
x x C
.
Câu 40.Khi tính nguyên hàm
3
d
1
x
x
x
, bằng cách đặt
1
u x
ta được nguyên hàm nào?
A.
2
2 4 d
u u
. B.
2
4 d
u u
. C.
2
3 d
u u
. D.
2
2 4 d
u u u
.
Câu 41.Biết
2
2 2
dx
a x b x C
x x x x
với a, b là các số nguyên dương và C là
hằng số thực. Giá trị của biểu thức
P a b
là:
A.
2
P
B.
8
P
C.
46
P
D.
22
P
Câu 42.Nguyên hàm
2
3
. 1
P x x dx
là:
A.
2 23
3
1 1
8
P x x C
B.
2 2
3
1 1
8
P x x C
C.
23
3
1
8
P x C
D.
2 23
3
1 1
4
P x x C
Câu 43.Nguyên hàm
1
1
R dx
x x
là:
A.
1 1 1
ln
2
1 1
x
R C
x
B.
1 1 1
ln
2
1 1
x
R C
x
C.
1 1
ln
1 1
x
R C
x
D.
1 1
ln
1 1
x
R C
x
Câu 44.Nguyên hàm
3 2
9
S x x dx
là:
A.
2
2 2
2 2
9 9
3 9 9
5
x x
S x x C
B.
4
2 2
2 2
9 9
3 9 9
5
x x
S x x C
C.
2 2
2
2 2
9 9
3 9 9
5
x x
S x x C
D.
2
2 2
2
9 9
3 9
5
x x
S x C
Câu 45.Nguyên hàm
3
2
1
1
I dx
x
là:
A.
2
2
3
1
x C
B.
2
1
x
C
x
C.
3
2
1
x
C
x
D.
2
1 x
C
x
Câu 46.Cho
3
2
1
x
I dx
x
. Bằng phép đổi biến
2
1
u x
, khẳng định nào sau đây sai?
A.
2 2
1
x u
B.
xdx udu
C.
2
1 .
I u udu
D.
3
3
u
I u C
Câu 47.Cho
2
2
2 1 5
1
x
f x x
x
, biết
F x
là một nguyên hàm của hàm số
f x
thỏa mãn
0 6
F
. Giá trị của
3
4
F
là:
A.
125
16
B.
126
16
C.
123
16
D.
127
16
Câu 48.Nguyên hàm
2 2
9
dx
I
x x
là:
A.
2
9
9
x
I C
x
B.
2
9
9
x
I C
x
C.
2
2
9
9
x
I C
x
D.
2
2
9
9
x
I C
x
Câu 49.Nguyên hàm
3
2
1
x
I dx
x
là:
A.
2 2
1
2 1
3
I x x C
B.
2 2
1
2 1
3
I x x C
C.
2 2
1
2 1
3
I x x C
D.
2 2
1
2 1
3
I x x C
Vấn đề 5. Nguyên hàm của hàm số lượng giác.
Câu 50.Tìm nguyên hàm của hàm số
2 sin
f x x
.
A.
2 sin 2 cos
xdx x C
B.
2 sin 2 cos
xdx x C
C.
2
2 sin sin
xdx x C
D.
2 sin sin 2
xdx x C
Câu 51.Tìm nguyên hàm của hàm số
cos 3
f x x
A.
cos 3 3 sin 3
xdx x C
B.
sin 3
cos 3
3
x
xdx C
C.
cos 3 sin 3
xdx x C
D.
sin 3
cos 3
3
x
xdx C
Câu 52.Họ nguyên hàm của hàm số
cos 3
6
y x
là:
A.
1
sin 3
3 6
f x dx x C
B.
1
sin 3
3 6
f x dx x C
C.
1
sin 3
6 6
f x dx x C
D.
sin 3
6
f x dx x C
Câu 53.Phát biểu nào sau đây đúng?
A.
cos 2
sin 2 ,
2
x
xdx C C
B.
sin 2 cos 2 ,xdx x C C
C.
sin 2 2 cos 2 ,xdx x C C
D.
cos 2
sin 2 ,
2
x
xdx C C
Câu 54.Biết
2
sin 2 cos 2 cos 4
a
x x dx x x C
b
, với a, b là các số nguyên dương,
a
b
là phân số
tối giản và
C
. Giá trị của
a b
bằng:
A. 5. B. 4. C. 2. D. 3.
Câu 55.Nguyên hàm
F x
của hàm số
cos 3 cos
f x x x
, biết đồ thị
y F x
đi qua gốc tọa độ là:
A.
sin 4 sin 2
4 2
x x
F x B.
sin 4 sin 2
8 2
x x
F x
C.
cos 4 cos 2
8 4
x x
F x
D.
sin 8 sin 4
8 4
x x
F x
Câu 56.Biết
5
2 2
cos
cos sin sin 4
m
nx
x x xdx C
p
, với
, ,
m n p
và C là hằng số thực. Giá
trị của biểu thức
T m n p
là:
A.
9
T
B.
14
T
C.
16
T
D.
18
T
Câu 57.Nguyên hàm
2 sin
1 3 cos
x
M dx
x
là:
A.
1
ln 1 3 cos
3
M x C
B.
2
ln 1 3 cos
3
M x C
C.
2
ln 1 3 cos
3
M x C
D.
1
ln 1 3 cos
3
M x C
Câu 58.Gọi
F x
là nguyên hàm của hàm số
2 3
sin 2 . cos 2
f x x x
thỏa
0
4
F
. Giá trị
2019
F
là:
A.
1
2019
15
F
B.
2019 0
F
C.
2
2019
15
F
D.
1
2019
15
F
Câu 59.Tìm nguyên hàm
F x
của hàm số
sin cos
f x x x
thoả mãn
2
2
F
.
A.
cos sin 3
F x x x
B.
cos sin 1
F x x x
C.
cos sin 1
F x x x
D.
cos sin 3
F x x x
Câu 60.Cho hàm số thỏa mãn và
(0) 2020
f
. Mệnh đề nào dưới đây đúng?
A.
( ) sin 2020
f x x
B.
( ) cos 2020
f x x
C.
( ) sin 2020
f x x
. D.
( ) 2020 cos
f x x
Câu 61.Nguyên hàm của hàm số
2
( ) 3 sin cos
f x x x
là
A.
3
sin
x C
. B.
3
sin
x C
. C.
3
cos
x C
. D.
3
cos
x C
.
Câu 62.Tìm nguyên hàm của hàm số
sin
( )
1 3 cos
x
f x
x
.
A.
1
( )d ln 1 3 cos
3
f x x x C
. B.
( ) d ln 1 3 cos
f x x x C
.
C.
( ) d 3 ln 1 3 cos
f x x x C
. D.
1
( ) d ln 1 3 cos
3
f x x x C
.
Câu 63.Tìm các hàm số
( )
f x
biết
'
2
cos
( )
(2 sin )
x
f x
x
.
A.
2
sin
( )
(2 sin )
x
f x C
x
. B.
1
( )
(2 cos )
f x C
x
.
C.
1
( )
2 sin
f x C
x
. D.
sin
( )
2 sin
x
f x C
x
.
Câu 64.Tìm họ nguyên hàm của hàm số
5
tan
f x x
.
A.
4 2
1 1
d tan tan ln cos
4 2
f x x x x x C
.
B.
4 2
1 1
d tan tan ln cos
4 2
f x x x x x C
.
C.
4 2
1 1
d tan tan ln cos
4 2
f x x x x x C
.
D.
4 2
1 1
d tan tan ln cos
4 2
f x x x x x C
.
Câu 65.Biết
F x
là một nguyên hàm của hàm số
sin 2 cos
1 sin
x x
f x
x
và
0 2
F
. Giá trị của
2
F
là:
A.
2 2 8
3
B.
2 2 8
3
C.
4 2 8
3
D.
4 2 8
3
Câu 66.Cho nguyên hàm
4 4
sin 2
cos sin
x
I dx
x x
. Nếu
cos 2
u x
đặt thì mệnh đề nào sau đây đúng?
A.
2
1
1
I du
u
B.
2
1
2 1
I du
u
C.
2
1 1
2
1
I du
u
D.
2
2
1
I du
u
f x
cos
f x x
Câu 67.Cho
3
sin cos 1
cos 2
sin cos 2 sin cos 2
m
n
x x
x
dx C
x x x x
, với
,
m n
và C là hằng số
thực. Giá trị của biểu thức
A m n
là:
A.
5
A
B.
2
A
C.
3
A
D.
4
A
Vấn đề 6. Nguyên hàm của hàm số mũ, logarit.
Câu 68.Tìm nguyên hàm của hàm số
7
x
f x
.
A.
7
7 d
ln 7
x
x
x C
B.
1
7 d 7
x x
x C
C.
1
7
7 d
1
x
x
x C
x
D.
7 d 7 ln 7
x x
x C
Câu 69.Họ nguyên hàm của hàm số
3
( )
x
f x e
là hàm số nào sau đây?
A.
3
x
e C
. B.
3
1
3
x
e C
. C.
1
3
x
e C
. D.
3
3
x
e C
.
Câu 70.Nguyên hàm của hàm số
2 1
e
x
y
là
A.
2 1
2e
x
C
. B.
2 1
e
x
C
. C.
2 1
1
e
2
x
C
. D.
1
e
2
x
C
.
Câu 71.Tính
2
( )
F x e dx
, trong đó
e
là hằng số và
2, 718
e
.
A.
2 2
( )
2
e x
F x C
. B.
3
( )
3
e
F x C
. C.
2
( )
F x e x C
. D.
( ) 2
F x ex C
.
Câu 72.Hàm số
2
x
F x e
là nguyên hàm của hàm số nào trong các hàm số sau:
A.
2
( ) 2
x
f x xe
. B.
2
2
( ) 1
x
f x x e
. C.
2
( )
x
f x e
. D.
2
( )
2
x
e
f x
x
.
Câu 73.Nguyên hàm của hàm số
2 2 5
x x
f x
là
A.
2
5
ln 2
x
x C
. B.
5.2 ln 2
x
x C
.
C.
2 2
5
ln 2 ln 2
x x
x x C
. D.
2
1 5
ln 2
x
C
.
Câu 74.Cho
F x
là một nguyên hàm của hàm số
1
2 3
x
f x
e
thỏa mãn
0 10
F
. Hàm số
F x
là:
A.
1 ln 5
ln 2 3 10
3 3
x
x e
B.
1
10 ln 2 3
3
x
x e
C.
1 3
ln 2 ln 5 ln 2
3 2
x
x e
D.
1 ln 5 ln 2
ln 2 3 10
3 3
x
x e
Câu 75.Hàm số
f x
có đạo hàm liên tục trên
và:
2
2e 1,
x
f x
, 0 2
x f
. Hàm
f x
là
A.
2e 2
x
y x
. B.
2e 2
x
y
. C.
2
e 2
x
y x
. D.
2
e 1
x
y x
.
Câu 76.Nguyên hàm của hàm số
ln
x
f x
x
là:
A.
2
ln
2
x
C
B.
2
1 ln
x
C
x
C.
ln
2
x
C
D.
2
ln
x C
Câu 77.Nguyên hàm
1
ln 1
T dx
x x
là:
A.
1
2 ln 1
T C
x
B.
2 ln 1
T x C
C.
2
ln 1 ln 1
3
T x x C
D.
ln 1
T x C
Câu 78.Tìm họ nguyên hàm của hàm số
3
2 1
.e
x
f x x
.
A.
3
3
1
d .e
3
x
x
f x x C
. B.
3
1
d 3e
x
f x x C
.
C.
3
1
d e
x
f x x C
. D.
3
1
1
d e
3
x
f x x C
.
Câu 79.
Nguyên hàm của
2
sin
sin 2 .
x
f x x e
là
A.
2
2 sin 1
sin .
x
x e C
. B.
2
sin 1
2
sin 1
x
e
C
x
. C.
2
sin x
e C
. D.
2
sin 1
2
sin 1
x
e
C
x
.
Câu 80.Nguyên hàm của hàm số
2
ln 1
f x x x
là
A.
2 2
ln 1 1
F x x x x x C
. B.
2 2
ln 1 1
F x x x x x C
.
C.
2
ln 1
F x x x x C
. D.
2 2
ln 1
F x x x x C
.
Câu 81.Xét nguyên hàm
2
ln
1 ln 1
x
V dx
x x
. Đặt
1 1 ln
u x
, khẳng định nào sau đây
sai?
A.
2 2
dx
u du
x
B.
2
2
2
. 2 2
u u
V u du
u
C.
5 4 3 2
2 5 16
4
5 2 3
V u u u u C
D.
5 4
3 2
16
4
5 2 3
u u
V u u C
Câu 82.Cho hàm số
3
2 2 2
2 2
x x
f x x e xe
, ta có
3
2 2 2
d
x x x
f x x me nxe pe C
. Giá trị của
biểu thức
m n p
bằng
A.
1
3
B.
2
C.
13
6
D.
7
6
Vấn đề 7. Nguyên hàm tổng hợp.
Câu 83.Họ nguyên hàm của hàm số
x
f x e x
là
A.
1
x
e C
B.
2x
e x C
C.
2
1
2
x
e x C
D.
2
1 1
1 2
x
e x C
x
Câu 84.Tính
sin 2 d
x x x
.
A.
2
sin
2
x
x C
. B.
2
cos 2
2
x
x C
. C.
2
cos 2
2
x
x C
. D.
2
cos 2
2 2
x x
C
.
Câu 85.Tìm họ nguyên hàm của hàm số
2
1
3
x
y x
x
.
A.
3
2
3 1
,
3 ln 3
x
x
C C
x
. B.
3
2
1
3 ,
3
x
x
C C
x
.
C.
3
3
ln ,
3 ln 3
x
x
x C C
. D.
3
3
ln ,
3 ln 3
x
x
x C C
.
Câu 86.Họ nguyên hàm của hàm số
2
3 sin
f x x x
là
A.
3
cos
x x C
. B.
6 cos
x x C
. C.
3
cos
x x C
. D.
6 cos
x x C
.
Câu 87.Công thức nào sau đây là sai?
A.
1
ln d
x x C
x
. B.
2
1
d tan
cos
x x C
x
.
C.
sin d cos
x x x C
. D.
e d e
x x
x C
.
Câu 88.Trong các khẳng định sau, khẳng định nào sai?
A.
1
cos 2 sin 2
2
d
x x x C
. B.
e
e
1
1
d
e
x
x x C
.
C.
1
lnd
x x C
x
. D.
1
1
e
e d
x
x
x C
x
.
Câu 89.Họ nguyên hàm của hàm số
1
sin
f x x
x
là
A.
ln cos
x x C
. B.
2
1
cos
x C
x
. C.
ln cos
x x C
. D.
ln cos
x x C
.
Câu 90.Tìm nguyên hàm của hàm số
5
2018
2017
x
x
e
f x e
x
.
A.
4
2018
d 2017
x
f x x e C
x
. B.
4
2018
d 2017
x
f x x e C
x
.
C.
4
504, 5
d 2017
x
f x x e C
x
. D.
4
504, 5
d 2017
x
f x x e C
x
.
Câu 91.Họ nguyên hàm của hàm số
2
2
cos
x
x
e
y e
x
là
A.
2 tan
x
e x C
B.
2 tan
x
e x C
C.
1
2
cos
x
e C
x
D.
1
2
cos
x
e C
x
Câu 92.Hàm số
2
ln sin cos
F x x x x
là nguyên hàm của hàm số nào dưới đây?
A.
2
.
sin cos
x
f x
x x
B.
2
cos sin
2 ln sin cos
sin cos
x x x
f x x x x
x x
.
C.
2
sin cos
sin cos
x x x
f x
x x
.
D.
2
2 ln sin cos
sin cos
x
f x x x x
x x
.
Câu 93.Cho hàm số
ln 2
2 .
x
f x
x
. Hàm số nào dưới đây không là nguyên hàm của hàm số
f x
?
A.
2
x
F x C
B.
2 2 1
x
F x C
C.
2 2 1
x
F x C
D.
1
2
x
F x C
Câu 94.Tìm họ nguyên hàm của hàm số
3
2 1
x
f x x e
A.
5 3 4 2
1 1
2 d ln
4
t t t t t t C
t
.
B.
3
1
d 3
x
f x x e C
.
C.
3
1
1
d
3
x
f x x e C
.
D.
3
3
1
d
3
x
x
f x x e C
.
Câu 95.Biết
cos 2 d sin 2 cos 2
x x x ax x b x C
với
a
,
b
là các số hữu tỉ. Tính tích
ab
?
A.
1
8
ab
. B.
1
4
ab
. C.
1
8
ab
. D.
1
4
ab
.
Câu 96.Họ nguyên hàm của hàm số
4 1 ln
f x x x
là:
A.
2 2
2 ln 3
x x x
. B.
2 2
2 ln
x x x
.
C.
2 2
2 ln 3
x x x C
. D.
2 2
2 ln
x x x C
.
Câu 97.Họ nguyên hàm của hàm số
2
( ) .
x
f x x e
là :
A.
2
1 1
( )
2 2
x
F x e x C
B.
2
1
( ) 2
2
x
F x e x C
C.
2
( ) 2 2
x
F x e x C
D.
2
1
( ) 2
2
x
F x e x C
Câu 98.Họ nguyên hàm của hàm số
( ) 2 (1 )
x
f x x e
là
A.
2
2 1
x
x e x
. B.
2
2 1
x
x e x
. C.
2
2 2
x
x e x
. D.
2
2 2
x
x e x
.
Câu 99.Họ nguyên hàm của
ln
f x x x
là kết quả nào sau đây?
A.
2 2
1 1
ln
2 2
F x x x x C
. B.
2 2
1 1
ln
2 4
F x x x x C
.
C.
2 2
1 1
ln
2 4
F x x x x C
. D.
2
1 1
ln
2 4
F x x x x C
.
Câu 100.Tất cả các nguyên hàm của hàm số
2
s in
x
f x
x
trên khoảng
0;
là
A.
cot ln s in
x x x C
. B.
cot ln s in
x x x C
.
C.
cot ln s in
x x x C
. D.
cot ln s in
x x x C
.
Câu 101.Họ nguyên hàm của hàm số
4
e
x
f x x x
là
A.
5
1
1 e
5
x
x x C
. B.
5
1
1 e
5
x
x x C
.
C.
5
1
e
5
x
x x C
. D.
3
4 1 e
x
x x C
.
Câu 102.Họ nguyên hàm của hàm số
2
l 1
2 n
x
xx
y
x
là
A.
2
2
1 ln
2
x
x x x C
x
. B.
2
2
1 ln
2
x
x x x C
x
.
C.
2
2
1 ln
2
x
x x x C
x
. D.
2
2
1 ln
2
x
x x x C
x
.
Câu 103.Cho hàm số
f x
thỏa mãn
x
f x xe
và
0 2
f
.Tính
1
f
.
A.
1 3
f
. B.
1
f e
. C.
1 5
f e
. D.
1 8 2
f e
.
Câu 104.Gọi
F x
là một nguyên hàm của hàm số
e
x
f x x
. Tính
F x
biết
0 1
F
.
A.
1 e 2
x
F x x
. B.
1 e 1
x
F x x
.
C.
1 e 2
x
F x x
. D.
1 e 1
x
F x x
.
Câu 105.Biết
cos 2 d sin 2 cos 2
x x x ax x b x C
với
a
,
b
là các số hữu tỉ. Tính tích
ab
?
A.
1
8
ab
. B.
1
4
ab
. C.
1
8
ab
. D.
1
4
ab
.
Câu 106.Biết
cos 3
1
sin 3 2019
x a x
F x x
b c
là một nguyên hàm của hàm số
2 sin 3
f x x x
, (với
a
,
b
,
c
). Giá trị của
ab c
bằng
A.
14
. B.
15
. C.
10
. D.
18
.
Câu 107.Cho hàm số
3
2 2 2
2 2
x x
f x x e xe
, ta có
3
2 2 2
d
x x x
f x x me nxe pe C
. Giá trị
của biểu thức
m n p
bằng
A.
1
3
B.
2
C.
13
6
D.
7
6
Câu 108. Cho hàm số
( )
F x
là một nguyên hàm của
2 2
( ) 2019 4 3 2 .
x
f x x x x
Khi đó số điểm
cực trị của hàm số
( )
F x
là
A.
5.
B.
4.
C.
3.
D.
2.
Câu 109.Cho
F x
là một nguyên hàm của hàm số
2
3
4
x
f x e x x
. Hàm số
2
F x x
có bao
nhiêu điểm cực trị?
A.
6
. B.
5
. C.
3
. D.
4
.
Vấn đề 8. Nguyên hàm của hàm ẩn
Câu 110.Hàm số
F x
nào sau đây là một nguyên hàm của hàm số
.
f x g x
, biết
1 3
F
,
1
d
f x x x C
và
2
2
d
g x x x C
.
A.
2
1
F x x
B.
2
3
F x x
C.
2
2
F x x
D.
2
4
F x x
Câu 111.Cho
3
0
d 4 2
f x x x x C
. Tính
2
d
xf x
I x
.
A.
6 2
2
I x x C
. B.
10 6
10 6
x x
I C
. C.
6 2
4
2
I x x C
. D.
2
12 2
I x
.
Câu 112.Cho hàm số
y f x
thỏa mãn
4 2
' .
f x f x x x
. Biết
0 2
f
. Tính
2
2
f .
A.
2
313
2
15
f
. B.
2
332
2
15
f
. C.
2
324
2
15
f
. D.
2
323
2
15
f
.
Câu 113.Cho hai hàm số
,
F x G x
xác định và có đạo hàm lần lượt là
,
f x g x
trên
. Biết rằng
2 2
. ln 1
F x G x x x
và
3
2
2
. .
1
x
F x g x
x
Họ nguyên hàm của
.
f x G x
là
A.
2 2 2
1 ln 1 2 .
x x x C
B.
2 2 2
1 ln 1 2 .
x x x C
C.
2 2 2
1 ln 1 .
x x x C
D.
2 2 2
1 ln 1 .
x x x C
Câu 114.Cho hàm số
f
liên tục và có đạo hàm trên
,
1 , 0 0
f x x f
và thoả mãn
2
1 2 1
f x x x f x
. Tính
3
f
.
A. 9. B. 7. C. 3. D. 0.
Câu 115.Cho hàm số
( )
f x
xác định trên đoạn
1; 2
thỏa mãn
(0) 1
f
và
2 2
( ). ( ) 1 2 3
f x f x x x
.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( )
f x
trên
1; 2
là
A.
3 3
1;2 1; 2
min ( ) 2 ; max ( ) 43
f x f x
. B.
3 3
1;2 1; 2
min ( ) 2 ; max ( ) 40
f x f x
C.
3 3
1;2 1;2
min ( ) 2 ; max ( ) 43
f x f x
. D.
3 3
1;2 1;2
min ( ) 2 ; max ( ) 40
f x f x
.
Câu 116.Cho hàm số
f x
liên tục trên
R
thỏa mãn các điều kiện:
0 2 2,
f
0,
f x
x
và
2
. 2 1 1 ,
f x f x x f x
x
. Khi đó giá trị
1
f
bằng
A.
26
. B.
24
. C.
15
. D.
23
.
Câu 117.Cho h/s
y f x
liên tục trên
0;

thỏa mãn
2
2 ' 3
xf x f x x x
;
1
1
2
f
. Tính
4
f
?
A.
24
. B.
14
. C.
4
. D.
16
.
Câu 118.Cho hàm số
f x
thỏa mãn
2
3
' . '' 2
f x f x f x x x
,
x
và
0 ' 0 1
f f
.
Tính giá trị của
2
2
T f
.
A.
43
30
. B.
16
15
. C.
43
15
. D.
26
15
.
Vấn đề 9. Các bài toán nguyên hàm có điều kiện.
Câu 119.Cho hàm số
( )
f x
xác định trên
1
\
2
thỏa mãn
2
, 0 1, 1 2
2 1
f x f f
x
. Giá trị
của biểu thức
1 3
f f
bằng
A.
2 ln 15
B.
3 ln 15
C.
ln 15
D.
4 ln 15
Câu 120.Biết
F x
là một nguyên hàm của hàm số
2
x
f x e
và
0 0
F
. Giá trị của
ln 3
F bằng
A. 2. B. 6. C. 8. D. 4.
Câu 121.Biết
F x
là một nguyên hàm của hàm
cos 3
f x x
và
2
2 3
F
. Tính
9
F
.
A.
3 2
9 6
F
B.
3 2
9 6
F
C.
3 6
9 6
F
D.
3 6
9 6
F
Câu 122.Cho hàm số
f x
xác định trên
\ 1
R
thỏa mãn
1
1
f x
x
,
0 2017
f
,
2 2018
f
.
Tính
3 1
S f f
.
A.
ln 4035
S
. B.
4
S
. C.
ln 2
S
. D.
1
S
.
Câu 123.Cho hàm số
f x
thỏa mãn
2
3
b
f x ax
x
,
1 3
f
,
1 2
f
,
1 1
2 12
f
. Khi đó
2
a b
bằng
A.
3
2
. B.
0
. C.
5
. D.
3
2
.
Câu 124.Gọi
F x
là một nguyên hàm của hàm số
2
x
f x
, thỏa mãn
1
0
ln 2
F
. Tính giá trị biểu
thức
0 1 ... 2018 2019
T F F F F
.
A.
2019
2 1
1009.
ln 2
T
. B.
2019.2020
2
T
.
C.
2019
2 1
ln 2
T
. D.
2020
2 1
ln 2
T
.
Câu 125.Cho
F x
là một nguyên hàm của hàm số
2
1
cos
f x
x
. Biết
4
F k k
với mọi
k
. Tính
0 ... 10
F F F F
.
A. 55. B. 44. C. 45. D. 0.
Câu 126.Biết
F x
là một nguyên hàm của hàm số
3
sin . cos
f x x x
và
0F
. Tính
2
F
.
A.
2
F
. B.
2
F
. C.
1
2 4
F
. D.
1
2 4
F
.
Câu 127.Cho
( )
F x
là một nguyên hàm của hàm số
4 3 2
2 1
2
x
f x
x x x
trên khoảng
0;

thỏa
mãn
1
1
2
F
. Giá trị của biểu thức
1 2 3 2019
S F F F F
bằng
A.
2019
2020
. B.
2019.2021
2020
. C.
1
2018
2020
. D.
2019
2020
.
Câu 128.Giả sử
F x
là một nguyên hàm của
2
ln 3
x
f x
x
sao cho
2 1 0
F F
. Giá trị của
1 2
F F
bằng
A.
10 5
ln 2 ln 5
3 6
. B.
0
. C.
7
ln 2
3
. D.
2 3
ln 2 ln 5
3 6
.
Câu 129.Gọi
g x
là một nguyên hàm của hàm số
ln 1
f x x
. Cho biết
2 1
g
và
3 ln
g a b
trong đó
,
a b
là các số nguyên dương phân biệt. Hãy tính giá trị của
2 2
3
T a b
A.
8
T
. B.
17
T
. C.
2
T
. D.
13
T
.
Câu 130.Cho hàm số
f x
liên tục trên
,
0
f x
với mọi
x
và thỏa mãn
1
1
2
f
,
2
2 1
x f x
f x
.Biết
1 2 ... 2019 1
a
f f f
b
với
, , , 1
a b a b
.Khẳng định
nào sau đây sai?
A.
2019
a b
. B.
2019
ab
. C.
2 2022
a b
. D.
2020
b
.
Vấn đề 10. Một số bài toán ứng dụng của nguyên hàm.
Câu 131.Một chất điểm chuyển động với phương trình
2
1
2
S t
, trong đó
t
là thời gian tính bằng giây
( )
s
và
S
là quãng đường tính bằng mét
( ).
m
Vận tốc của chất điểm tại thời điểm
0
5
t s
là:
A.
5( / )
m s
B.
25( / )
m s
C.
2,5 ( / ).
m s
D.
10 ( / ).
m s
Câu 132.Một ô tô đang chạy với vận tốc
10( / )
m s
thì người lái xe đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc
10 2 /
v t t m s
, trong đó
t
là khoảng thời gian tính bằng
giây kể từ lúc đạp phanh. Tính quãng đường ô tô di chuyển được trong
8
giây cuối cùng.
A.
50 .
m
B.
25 .
m
C.
55 .
m
D.
10 .
m
Câu 133.Một vận động viên điền kinh chạy với gia tốc
3 2 2
1 5
/
24 16
a t t t m s
, trong đó
t
là
khoảng thời gian tính từ lúc xuất phát. Hỏi vào thời điểm
5( / )
m s
sau khi xuất phát thì vận tốc của vận
động viên là bao nhiêu?
A.
5, 6 /
m s
B.
6, 51 ( / ).
m s
C.
7, 72 ( / )
m s
D.
6, 8 ( / )
m s
Câu 134.Số lượng của một loại vi khuẩn được tính theo công thức
N x
, trong đó x là số ngày kể từ thời
điểm ban đầu. Biết rằng
2000
'
1
N x
x
và lúc đầu số lượng vi khuẩn là 5000 con. Hỏi ngày thứ 12 số
lượng vi khuẩn gần nhất với kết quả nào sau đây?
A. 10130. B. 10120. C. 5154. D. 10132.
Câu 135.Cho
F x
là một nguyên hàm của hàm số
1
1
x
f x
e
thỏa mãn
0 ln 2
F
. Tập nghiệm
S của phương trình
ln 1 3
x
F x e
là:
A.
3
S
B.
3
S
C.
S
D.
3
S
Câu 136.Biết rằng
F x
là một nguyên hàm trên
của hàm số
2018
2
2017
1
x
f x
x
thỏa mãn
1 0
F
. Tìm giá trị nhỏ nhất
m
của
F x
.
A.
1
2
m
. B.
2017
2018
1 2
2
m
. C.
2017
2018
1 2
2
m
. D.
1
2
m
.
Câu 137.Giả sử
2 3 d
1
1 2 3 1
x x
C
x x x x g x
(
C
là hằng số).
Tính tổng các nghiệm của phương trình
0
g x
.
A.
1
. B.
1
. C.
3
. D.
3
.
Câu 138.Cho hàm số
F x
là một nguyên hàm của hàm số
2
2 cos 1
sin
x
f x
x
trên khoảng
0;
. Biết
rằng giá trị lớn nhất của
F x
trên khoảng
0;
là
3
. Chọn mệnh đề đúng trong các mệnh đề sau.
A.
3 3 4
6
F
B.
2 3
3 2
F
C.
3
3
F
D.
5
3 3
6
F
B. TÍCH PHÂN.
Vấn đề 1. Tích phân hàm đa thức
Câu 1. Tính tích phân
0
1
2 1
I x dx
.
A.
0
I
. B.
1
I
. C.
2
I
. D.
1
2
I
.
Câu 2. Tích phân
1
0
3 1 3 d
x x x
bằng
A.
12
. B.
9
. C.
5
. D.
6
.
Câu 3. Tính tích phân
2
0
(2 1)
I x dx
A.
5
I
. B.
6
I
. C.
2
I
. D.
4
I
.
Câu 4. Với
,
a b
là các tham số thực. Giá trị tích phân
2
0
3 2 1 d
b
x ax x
bằng
A.
3 2
b b a b
. B.
3 2
b b a b
. C.
3 2
b ba b
. D.
2
3 2 1
b ab
.
Câu 5. Biết rằng hàm số
f x mx n
thỏa mãn
1
0
d 3
f x x
,
2
0
d 8
f x x
. Khẳng định nào
dưới đây là đúng?
A.
4
m n
. B.
4
m n
. C.
2
m n
. D.
2
m n
.
Câu 6. Cho
2
0
3 2 1 d 6
m
x x x
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
1;2
. B.
; 0

. C.
0;4
. D.
3;1
.
Câu 7. Cho
n
là số nguyên dương khác
0
, hãy tính tích phân
1
2
0
1 d
n
I x x x
theo
n
.
A.
1
2 2
I
n
. B.
1
2
I
n
. C.
1
2 1
I
n
. D.
1
2 1
I
n
.
Vấn đề 2. Tích phân hàm số hữu tỉ.
Câu 8.
2
1
2 3
dx
x
bằng
A.
1
ln 35
2
B.
7
ln
5
C.
1 7
ln
2 5
D.
7
2 ln
5
Câu 9. Cho
1
0
1 1
d ln 2 ln 3
1 2
x a b
x x
với
,
a b
là các số nguyên. Mệnh đề nào dưới đây
đúng?
A.
2 0
a b
B.
2
a b
C.
2 0
a b
D.
2
a b
Câu 10. Tính tích phân
2
1
1 1
e
I dx
x
x
A.
1
I
e
B.
1
1
I
e
C.
1
I
D.
I e
Câu 11. Tính tích phân
2
1
1
d
x
I x
x
.
A.
1 ln 2
I
. B.
7
4
I
. C.
1 ln 2
I
. D.
2 ln 2
I
.
Câu 12. Biết
2
1
d
ln 2 ln 3 ln 5
1 2 1
x
a b c
x x
. Khi đó giá trị
a b c
bằng
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 13. Biết
3
1
2
ln ,
x
dx a b c
x
với
, , , 9.
a b c c
Tính tổng
.
S a b c
A.
7
S
. B.
5
S
. C.
8
S
. D.
6
S
.
Câu 14. Biết
0
2
1
3 5 1 2
ln , ,
2 3
x x
I dx a b a b
x
. Khi đó giá trị của
4
a b
bằng
A.
50
B.
60
C.
59
D.
40
Câu 15. Biết
5
2
3
1
d ln
1 2
x x b
x a
x
với
a
,
b
là các số nguyên. Tính
2
S a b
.
A.
2
S
. B.
2
S
. C.
5
S
. D.
10
S
.
Câu 16. Biết
2
2
2
0
5 2
d ln 3 ln 5
4 3
x x
x a b c
x x
,
, ,a b c
. Giá trị của
abc
bằng
A.
8
. B.
10
. C.
12
. D.
16
.
Câu 17. Tích phân
1
0
1
d
1
I x
x
có giá trị bằng
A.
ln 2 1
. B.
ln 2
. C.
ln 2
. D.
1 ln 2
.
Câu 18. Tính
3
2
2
d
1
x
K x
x
.
A.
ln 2
K
. B.
1 8
ln
2 3
K
. C.
2 ln 2
K
. D.
8
ln .
3
K
Câu 19. Cho tích phân
1
7
5
2
0
d
1
x
I x
x
, giả sử đặt
2
1
t x
. Tìm mệnh đề đúng.
A.
3
2
5
1
1
1
d
2
t
I t
t
. B.
3
3
5
1
1
d
t
I t
t
.
C.
3
2
4
1
1
1
d
2
t
I t
t
. D.
3
4
4
1
1
3
d
2
t
I t
t
.
Câu 20. Có bao nhiêu số thực
a
để
1
2
0
1
x
dx
a x
.
A.
2
B.
1
C.
0
D.
3
Câu 21. Biết
1
2
2
0
2 3 3
ln
2 1
x x
dx a b
x x
với
,
a b
là các số nguyên dương. Tính
2 2
P a b
.
A.
13
. B.
5
. C.
4
. D.
10
.
Vấn đề 3. Tích phân hàm vô tỉ.
Câu 22. Cho
21
5
ln 3 ln 5 ln 7
4
dx
a b c
x x
, với
, ,
a b c
là các số hữu tỉ. Mệnh đề nào sau đây
đúng?
A.
2
a b c
B.
2
a b c
C.
a b c
D.
a b c
Câu 23. Tính tích phân
2
2
1
2 1
I x x dx
bằng cách đặt
2
1
u x
, mệnh đề nào dưới đây đúng?
A.
3
0
I udu
B.
2
1
1
2
I udu
C.
3
0
2
I udu
D.
2
1
I udu
Câu 24. Tích phân
1
0
d
3 1
x
x
bằng
A.
4
3
. B.
3
2
. C.
1
3
. D.
2
3
.
Câu 25. Biết
2
1
( 1) 1
dx
dx a b c
x x x x
với
, ,
a b c
là các số nguyên dương. Tính
P a b c
A.
18
P
B.
46
P
C.
24
P
D.
12
P
Câu 26. Cho tích phân
2 2
2
0
16 d
I x x
và
4 sin
x t
. Mệnh đề nào sau đây đúng?
A.
4
0
8 1 cos 2 d
I t t
. B.
4
2
0
16 sin d
I t t
.
C.
4
0
8 1 cos 2 d
I t t
. D.
4
2
0
16 cos d
I t t
.
Câu 27. Biết
5
1
1
ln 3 ln 5
1 3 1
dx a b c
x
( , , )
a b c Q
. Giá trị của
a b c
bằng
A.
7
3
. B.
5
3
. C.
8
3
. D.
4
3
.
Câu 28. Cho biết
7
3
23
0
d
1
x m
x
n
x
với
m
n
là một phân số tối giản. Tính
7
m n
A.
0
. B.
1
. C.
2
. D.
91
.
Câu 29. Cho
3
0
ln 2 ln 3
3
4 2 1
x a
dx b c
x
với
, ,
a b c
là các số nguyên. Giá trị
a b c
bằng:
A.
9
B.
2
C.
1
D.
7
Câu 30. Tính
3
2
0
d
1
a
x x
I x
x
.
A.
2 2
1 1 1
I a a
. B.
2 2
1
1 1 1
3
I a a
.
C.
2 2
1
1 1 1
3
I a a
. D.
2 2
1 1 1
I a a
.
Câu 31. Giá trị của tích phân
1
2
0
d
1
x
x
x
bằng tích phân nào dưới đây?
A.
4
2
0
2 sin dy
y
. B.
1
2
2
0
sin
d
cos
x
x
x
. C.
4
2
0
sin
dy
cosy
y
. D.
2
2
0
2 sin dy
y
.
Câu 32. Cho tích phân
1
2
0
d
4
x
I
x
nếu đổi biến số
2 sin , ;
2 2
x t t
thì ta được.
A.
3
0
d
I t
. B.
6
0
d
I t
. C.
4
0
d
I t t
. D.
6
0
d
t
I
t
.
Câu 33. Biết
1
3
2
0
15
1
x a b c
dx
x x
với
, ,
a b c
là các số nguyên và
0
b
. Tính
2
P a b c
.
A.
3
P
. B.
7
P
. C.
7
P
. D.
5
P
.
Câu 34. Giả sử
64
3
1
d 2
ln
3
x
I a b
x x
với
,
a b
là số nguyên. Khi đó giá trị
a b
là
A.
17
. B. 5. C.
5
. D.
17
.
Câu 35. Biết
2
2
1
d 2 35
3 9 1
x
x a b c
x x
với
a
,
b
,
c
là các số hữu tỷ, tính
2 7
P a b c
.
A.
1
9
. B.
86
27
. C.
2
. D.
67
27
.
Câu 36. Biết
4
0
2 1d 5
ln 2 ln , ,
3
2 3 2 1 3
x x
a b c a b c
x x
. Tính
2
T a b c
.
A.
4
T
. B.
2
T
. C.
1
T
. D.
3
T
.
Vấn đề 4. Tích phân hàm lượng giác.
Câu 37. Cho hàm số
f x
. Biết
0 4
f
và
2
' 2 sin 1, f x x x
, khi đó
4
0
d
f x x
bằng
A.
2
16 4
.
16
B.
2
4
.
16
C.
2
15
.
16
D.
2
16 16
.
16
Câu 38. Cho hàm số
( )
f x
.Biết
(0) 4
f
và
2
( ) 2 cos 3,f x x x
, khi đó
4
0
( )
f x dx
bằng?
A.
2
8 8
8
. B.
2
8 2
8
. C.
2
6 8
8
. D.
2
2
8
.
Câu 39. Giá trị của
2
0
sin
xdx
bằng
A. 0. B. 1. C. -1. D.
2
.
Câu 40. Giả sử
4
0
2
sin 3
2
I xdx a b
,a b
. Khi đó giá trị của
a b
là
A.
1
6
B.
1
6
C.
3
10
D.
1
5
Câu 41. Biết
2
0
3 sin cos 11
ln 2 ln 3 ,
2 sin 3 cos 3
x x
dx b c b c Q
x x
. Tính
b
c
?
A.
22
3
. B.
22
3
. C.
22
3
. D.
22
13
.
Câu 42. Tính tích phân
3
0
cos . sin d
I x x x
.
A.
1
4
I
B.
4
1
4
I
C.
4
I
D.
0
I
Câu 43. Cho tích phân
2
0
2 cos . sin d
I x x x
. Nếu đặt
2 cos
t x
thì kết quả nào sau đây đúng?
A.
2
3
d
I t t
. B.
3
2
d
I t t
. C.
2
3
2 d
I t t
. D.
2
0
d
I t t
.
Câu 44. Tính tích phân
4
2
4
0
sin
d
cos
x
I x
x
bằng cách đặt
tan
u x
, mệnh đề nào dưới đây đúng?
A.
4
2
0
d
I u u
. B.
2
2
0
1
d
I u
u
. C.
1
2
0
d
I u u
. D.
1
2
0
d
I u u
.
Câu 45. Cho tích phân
2
3
sin
d ln 5 ln 2
cos 2
x
x a b
x
với
, .
a b
Mệnh đề nào dưới đây đúng?
A.
2 0.
a b
B.
2 0.
a b
C.
2 0.
a b
D.
2 0.
a b
Câu 46. Có bao nhiêu số
0;20
a
sao cho
5
0
2
sin sin 2 d
7
a
x x x
.
A. 10.
B.
9.
C.
20.
D.
19.
Câu 47. Biết
6
0
d 3
1 sin
x a b
x c
, với
, ,a b c
và
, ,
a b c
là các số nguyên tố cùng nhau. Giá
trị của tổng
a b c
bằng
A.
5
. B.
12
. C.
7
. D.
1
.
Câu 48. Cho tích phân số
2
3
s in
d ln 5 ln 2
cos 2
x
x a b
x
với
,
a b
. Mệnh đề nào dưới đây đúng?
A.
2 0.
a b
B.
2 0.
a b
C.
2 0.
a b
. D.
2 0.
a b
.
Câu 49. Cho
2
2
0
sin 4
d ln
cos 5 cos 6
x
x a b
c
x x
, với
a
,
b
là các số hữu tỉ,
0
c
. Tính tổng
m
.
A.
3
S
. B.
0
S
. C.
1
S
. D.
4
S
.
Vấn đề 5. Tích phân hàm mũ và logarit.
Câu 50. Cho
F x
là một nguyên hàm của hàm số
ln
x
f x
x
. Tính:
1
I F e F
?
A.
1
2
I
B.
1
I
e
C.
1
I
D.
I e
Câu 51.
1
3 1
0
d
x
e x
bằng
A.
4
1
3
e e
B.
3
e e
C.
4
1
3
e e
D.
4
e e
Câu 52. Cho
2
3 1
1
d
x p q
e x m e e
với
m
,
p
,
q
và là các phân số tối giản. Giá trị
m p q
bằng
A.
10
. B.
6
. C.
22
3
. D.
8
.
Câu 53. Biết tích phân
ln 6
0
e
d ln 2 ln 3
1 e 3
x
x
x a b c
, với
a
,
b
,
c
là các số nguyên. Tính
T a b c
.
A.
1
T
. B.
0
T
. C.
2
T
. D.
1
T
.
Câu 54. Biết
1
ln
2
1 ln
e
x
dx a b
x x
với
,
a b
là các số hữu tỷ. Tính
S a b
.
A.
1
S
. B.
1
2
S
. C.
3
4
S
. D.
2
3
S
.
Câu 55. Cho
1
0
d 1
ln
2
1
x
x e
a b
e
, với
,
a
b
là các số hữu tỉ. Tính
3 3
S a b
.
A.
2
S
. B.
0
S
. C.
1
S
. D.
2
S
.
Câu 56. Cho tích phân
e
1
3 ln 1
d
x
I x
x
. Nếu đặt
ln
t x
thì
A.
1
0
3 1
d
e
t
t
I t
. B.
e
1
3 1
d
t
I t
t
. C.
e
1
3 1 d
I t t
. D.
1
0
3 1 d
I t t
.
Câu 57. Cho
2
1
ln
ln 3 ln 2
3
ln 2
e
x c
I dx a b
x x
, với
, ,
a b c
. Khẳng định nào sau đâu đúng.
A.
2 2 2
1
a b c
. B.
2 2 2
11
a b c
. C.
2 2 2
9
a b c
. D.
2 2 2
3
a b c
.
Câu 58. Biết
n2
0
l
d 1
ln ln ln
e
4
3e
x x
x
I a b c
c
với
a
,
b
,
c
là các số nguyên dương.
Tính
2
P a b c
.
A.
3
P
. B.
1
P
. C.
4
P
. D.
3
P
Vấn đề 6. Tích phân tổng hợp.
Câu 59. Biết rằng
2
1
2
0
d
2
x b c
a
xe x e e
với
, ,
a b c
. Giá trị của
a b c
bằng
A.
4
. B.
7
. C.
5
. D.
6
.
Câu 60. Biết
2
1
1
ln
ln
e
x
dx ae b
x x x
với
,
a b
là các số nguyên dương. Tính giá trị của biểu thức
2 2
.
T a ab b
A. 3. B. 1. C. 0. D. 8.
Câu 61. Biết
2
1
1
2
1
p
x
q
x
x e dx me n
, trong đó
, , ,
m n p q
là các số nguyên dương và
p
q
là phân số
tối giản. Tính
T m n p q
.
A.
11
T
. B.
10
T
. C.
7
T
. D.
8
T
.
Câu 62. Cho hàm số
y f x
có đạo hàm trên
đồng thời thỏa mãn
0 1 5
f f
. Tính tích phân
1
0
d
f x
I f x e x
.
A.
10
I
B.
5
I
C.
0
I
D.
5
I
Câu 63. Biết
4
2
0
ln 9 d ln 5 ln 3
I x x x a b c
trong đó
, ,
a b c
là các số thực. Giá trị của biểu
thức
T a b c
là:
A.
11.
T
B.
9.
T
C.
10.
T
D.
8.
T
Câu 64. Cho
3
3
1
e
2
3 1 ln 3 1
d . .l 1
e en
1 ln
x x x
x a b c
x x
với
, ,
a b c
là các số nguyên và
ln
e
1
. Tính
2 2 2
P a b c
.
A.
9
P
. B.
14
P
. C.
10
P
. D.
3
P
.
Câu 65. Biết
2
2
1
1
d ln ln
ln
x
x a b
x x x
với
a
,
b
là các số nguyên dương. Tính
2 2
P a b ab
.
A.
10
. B.
8
. C.
12
. D.
6
.
Câu 66. Cho
2
1
0
e
d .e ln e
e
x
x
x x
x a b c
x
với
a
,
b
,
c
. Tính
2
P a b c
.
A.
1
P
. B.
1
P
. C.
0
P
. D.
2
P
.
Vấn đề 7. Tích phân dùng tính chất.
Câu 67. Biết
2
1
d 2
f x x
và
2
1
d 6
g x x
, khi đó
2
1
d
f x g x x
bằng
A.
8
. B.
4
. C.
4
. D.
8
.
Câu 68. Biết tích phân
1
0
3
f x dx
và
1
0
4
g x dx
. Khi đó
1
0
f x g x dx
bằng
A.
7
. B.
7
. C.
1
. D.
1
.
Câu 69. Biết
1
0
( )d 2
f x x
và
1
0
( )d 4
g x x
, khi đó
1
0
( ) ( ) d
f x g x x
bằng
A.
6
. B.
6
. C.
2
. D.
2
.
Câu 70. Cho
1
0
d 2
f x x
và
1
0
d 5
g x x
, khi S bằng
A.
8
B.
1
C.
3
D.
12
Câu 71. Khẳng định nào trong các khẳng định sau đúng với mọi hàm
f
,
g
liên tục trên
K
và
a
,
b
là
các số bất kỳ thuộc
K
?
A.
( ) 2 ( ) d ( )d +2 ( )d
b b b
a a a
f x g x x f x x g x x
. B.
( )d
( )
d
( )
( )d
b
b
a
b
a
a
f x x
f x
x
g x
g x x
.
C.
( ). ( ) d ( )d . ( )d
b b b
a a a
f x g x x f x x g x x
. D.
2
2
( )d = ( )d
b b
a a
f x x f x x
.
Câu 72. Cho.
2
2
d 1
f x x
.,
4
2
d 4
f t t
. Tính
4
2
d
f y y
.
A.
5
I
. B.
3
I
. C.
3
I
. D.
5
I
.
Câu 73. Cho
2
0
3
f x dx
và
2
0
7
xg dx
, khi đó
2
0
3
f x g x dx
bằng
A.
16
. B.
18
. C.
24
. D.
10
.
Câu 74. Cho
1
0
( ) 1
f x dx
,
3
0
( ) 5
f x dx
. Tính
3
1
( )
f x
dx
A. 1. B. 4. C. 6. D. 5.
Câu 75. Cho
2
1
d 3
f x x
và
3
2
d 4
f x x
. Khi đó
3
1
d
f x x
bằng
A. 12. B. 7. C. 1. D.
12
.
Câu 76. Cho hàm số
f x
liên tục, có đạo hàm trên
1; 2 , 1 8; 2 1
f f
. Tích phân
2
1
'
f x dx
bằng
A.
1.
B.
7.
C.
9.
D.
9.
Câu 77. Cho hàm số
f x
liên tục trên
R
và có
2 4
0 2
( )d 9; ( )d 4.
f x x f x x
Tính
4
0
( )d .
I f x x
A.
5
I
. B.
36
I
. C.
9
4
I
. D.
13
I
.
Câu 78. Cho
0 3
1 0
3 3.
f x dx f x dx
Tích phân
3
1
f x dx
bằng
A.
6
B.
4
C.
2
D.
0
Câu 79. Cho hàm số
f x
liên tục trên
và
4
0
d 10
f x x
,
4
3
d 4
f x x
. Tích phân
3
0
d
f x x
bằng
A.
4
. B.
7
. C.
3
. D.
6
.
Câu 80. Nếu
1
2 1
F x
x
và
1 1
F
thì giá trị của
4
F bằng
A.
ln 7.
B.
1
1 ln 7.
2
C.
ln 3.
D.
1 ln 7.
Câu 81. Cho hàm số
f x
liên tục trên
thoả mãn
8
1
d 9
f x x
,
12
4
d 3
f x x
,
8
4
d 5
f x x
.
Tính
12
1
d
I f x x
.
A.
17
I
. B.
1
I
. C.
11
I
. D.
7
I
.
Câu 82. Cho hàm số
f x
liên tục trên
0;10
thỏa mãn
10
0
7
f x dx
,
6
2
3
f x dx
. Tính
2 10
0 6
P f x dx f x dx
.
A.
10
P
. B.
4
P
. C.
7
P
. D.
6
P
.
Câu 83. Cho
f
,
g
là hai hàm liên tục trên đoạn
1; 3
thoả mãn:
3
1
3 d 10
f x g x x
,
3
1
2 d 6
f x g x x
. Tính
3
1
d
f x g x x
.
A. 7. B. 6. C. 8. D. 9.
Câu 84. Cho hàm số
f x
liên tục trên đoạn
0;10
và
10
0
7
f x dx
;
6
2
3
f x dx
. Tính
2 10
0 6
P f x dx f x dx
.
A.
4
P
B.
10
P
C.
7
P
D.
4
P
Câu 85. Cho
2
0
d 5
f x x
. Tính
2
0
2 sin d 5
I f x x x
.
A.
7
I
B.
5
2
I
C.
3
I
D.
5
I
Câu 86. Cho
2
1
d 2
f x x
và
2
1
d 1
g x x
. Tính
2
1
2 3 d
I x f x g x x
.
A.
17
2
I
B.
5
2
I
C.
7
2
I
D.
11
2
I
Câu 87. Cho hai tích phân
5
2
d 8
f x x
và
2
5
d 3
g x x
. Tính
5
2
4 1 d
I f x g x x
A.
13
. B.
27
. C.
11
. D.
3
.
Câu 88. Cho
2
0
d 3
f x x
,
2
0
d 1
g x x
thì
2
0
5 d
f x g x x x
bằng:
A.
12
. B.
0
. C.
8
. D.
10
Câu 89. Cho
5
0
d 2
f x x
. Tích phân
5
2
0
4 3 d
f x x x
bằng
A.
140
. B.
130
. C.
120
. D.
133
.
Câu 90. Cho hàm số
f x
liên tục trên
và
2
2
0
3 d 10
f x x x
. Tính
2
0
d
f x x
.
A.
2
. B.
2
. C.
18
. D.
18
.
Câu 91. Cho
6
0
( ) 12
f x dx
. Tính
2
0
(3 ) .
I f x dx
A.
5
I
B.
36
I
C.
4
I
D.
6
I
Câu 92. Số điểm cực trị của hàm số
2
2
2
2 d
1
x
x
t t
f x
t
là
A.
0
B.
1
C.
2
D.
3
Câu 93. Cho biết
5
1
d 15
f x x
. Tính giá trị của
2
0
5 3 7 d
P f x x
.
A.
15
P
. B.
37
P
. C.
27
P
. D.
19
P
.
Câu 94. Cho
4
0
0
d
2 18
f x x
. Tính tích phân
2
0
d
2 4 2
I f x f x x
.
A.
0
I
. B.
2018
I
. C.
4036
I
. D.
1009
I
.
Câu 95. Cho
y f x
là hàm số chẵn, liên tục trên
6;6
. Biết rằng
2
1
d 8
f x x
;
3
1
2 d 3
f x x
. Giá trị của
6
1
d
I f x x
là
A.
5
I
. B.
2
I
. C.
14
I
. D.
11
I
.
Câu 96. Cho hàm số
f x
liên tục trên
và
2
0
d 2018
f x x
, tính
2
0
d .
I xf x x
A.
1008
I
. B.
2019
I
. C.
2017
I
. D.
1009
I
.
Câu 97. Cho
2
1
d 2
f x x
. Khi đó
4
1
d
f x
x
x
bằng
A.
1
. B.
4
. C.
2
. D.
8
.
Câu 98. Cho
2
2
1
1 d 2
f x x x
. Khi đó
5
2
d
I f x x
bằng
A.
2
. B.
1
. C.
4
. D.
1
o
x
.
Câu 99. Cho.
f x
. liên tục trên
thỏa mãn
10
f x f x
và
7
3
d 4
f x x
. Tính
7
3
d
I xf x x
.
A.
80
. B.
60
. C.
40
. D.
20
.
Câu 100. Cho
1
0
d 9
f x x
. Tính
6
0
sin 3 cos 3 d
I f x x x
.
A.
5
I
. B.
9
I
. C.
3
I
. D.
2
I
.
Câu 101. Cho hàm
f x
thỏa mãn
2017
0
d 1
f x x
. Tính tích phân
1
0
2017 d
I f x x
.
A.
1
2017
I . B.
0
I
. C.
2017
I
. D.
1
I
.
Câu 102. Cho hàm số
2 2
3 ; 1
5 ; 1
x x x
y f x
x x
. Tính
1
2
0 0
2 sin cos 3
d d
3 2
I f x x x f x x
.
A.
71
6
I
. B.
31
I
. C.
32
I
. D.
32
3
I
.
Câu 103. Cho
2
1
d 2
I f x x
. Giá trị của
2
0
sin 3 cos 1
d
3 cos 1
xf x
x
x
bằng
A.
2
. B.
4
3
. C.
4
3
. D.
2
.
Câu 104. Biết
4
1
5
f x dx
và
5
4
20
f x dx
. Tính
2 ln 2
2 2
1 0
4 3
x x
f x dx f e e dx
.
A.
15
4
I
. B.
15
I
. C.
5
2
I
. D.
25
I
.
Câu 105. Cho
( )
f x
là hàm số liên tục trên
thỏa mãn
2
( ) (2 ) . ,
x
f x f x x e x
. Tính tích
phân
2
0
( )
I f x dx
.
A.
4
1
4
e
I
. B.
2 1
2
e
I
. C.
4
2
I e
. D.
4
1
I e
.
Câu 106. Cho hàm số
f x
liên tục trên
thỏa mãn
2 3
f x f x
,
x
. Biết rằng
1
0
d 1
f x x
. Tính tích phân
2
1
d
I f x x
.
A.
5
I
B.
6
I
C.
3
I
D.
2
I
Câu 107. Cho hàm số
f x
liên tục trên
thỏa
2018
0
d 2
f x x
. Khi đó tích phân
2018
e 1
2
2
0
ln 1 d
1
x
f x x
x
bằng
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 108. Cho hàm số
f x
liên tục trên
thỏa mãn
4
0
tan d 3
f x x
và
2
1
2
0
d 1.
1
x f x
x
x
Tính
1
0
d .
I f x x
s
A.
2
I
. B.
6
I
. C.
3
I
. D.
4
I
.
Câu 109. Cho hàm số
f x
liên tục trên
và thỏa mãn
16
2
2
1
4
cot . sin d d 1
f x
x f x x x
x
.
Tính tích phân
1
1
8
4
d
f x
x
x
.
A.
3
I
. B.
3
2
I
. C.
2
I
. D.
5
2
I
.
Câu 110. Cho hàm số
f x
liên tục trên đoạn
1; 4
và thỏa mãn
2 1
ln
f x
x
f x
x
x
. Tính tích
phân
4
3
d
I f x x
.
A.
2
3 2 ln 2
I
. B.
2
2 ln 2
I
. C.
2
ln 2
I
. D.
2 ln 2
I
.
Câu 111. Cho hàm số
f x
liên tục trên
thảo mãn:
2
7 4 4 2018 9
f x f x x x
,
x
. Tính
4
0
d
I f x x
.
A.
2018
11
. B.
7063
3
. C.
98
3
. D.
197764
33
.
C. ỨNG DỤNG CỦA TÍCH PHÂN.
Câu 1. Diện tích phần hình phẳng tô đen trong hình vẽ bên dưới được tính theo công thức nào dưới đây?
A.
3
2
( ) ( ) d
f x g x x
. B.
3
2
( ) ( )
g x f x dx
.
C.
0 3
2 0
( ) ( ) d g( ) ( ) d
f x g x x x f x x
. D.
0 3
2 0
( ) ( ) ( ) ( )
g x f x dx f x g x dx
.
Câu 2. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A.
3
2
1
4 3 d
x x x
. B.
3
2
1
2 11 d
x x x
. C.
3
2
1
2 11 d
x x x
. D.
3
2
1
4 3 d
x x x
.
Câu 3. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A.
1
3 2
1
2
2 3 1 d
x x x
. B.
1
3 2
1
2
2 2 3 d
x x x x
.C.
1
3 2
1
2
2 3 1 d
x x x
.D.
1
3 2
1
2
2 2 3 d
x x x x
.
Câu 4. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A.
3
3 2
1
5 9 7 d
x x x x
.B.
3
3 2
1
5 9 7 d
x x x x
.C.
3
3 2
1
9 9 d
x x x x
.D.
3
3 2
1
9 9 d
x x x x
.
Câu 5. Tính diện tích
S
của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
; 2
f x x g x x
và trục hoành là:
A.
7
3
S
. B.
10
3
S
. C.
11
3
S
. D.
13
3
S
.
Câu 6. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số , trục
,Ox Oy
và đường thẳng
2x
.
Tính
S
hình phẳng trên.
A. . B. . C. . D. .
Câu 7. Gọi
S
là diện tích của hình phẳng giới hạn bởi các đường
2
ln
x
y
x
,
0y
,
1x
,
ex
. Mệnh đề
nào dưới đây đúng?
A.
e
2
1
ln
d
x
S x
x
. B.
e
2
1
ln
d
x
S x
x
. C.
2
e
2
1
ln
d
x
S x
x
. D.
2
e
2
1
ln
d
x
S x
x
.
Câu 8. Diện tích hình phẳng được giới hạn bởi các đường
sin 2 ; cos y x y x
và
0;
2
x x
là
A.
B.
C.
D.
Câu 9. Diện tích hình phẳng giới hạn bởi các đường ; ; là:
A. B. C. D.
Câu 10. Diện tích hình phẳng giới hạn bởi các đường ; và là:
A. B. C. D.
Câu 11. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
4 y x x
và trục
Ox
A.
11
. B.
34
3
. C.
31
3
. D.
32
3
.
Câu 12. Diện tích hình phẳng giới hạn bởi hai đường
3
11 6 y x x
và
2
6y x
là
A.
52
. B.
14
. C.
1
4
. D.
1
2
.
Câu 13. Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
:
1
x
H y
x
và các trục tọa độ. Khi đó
giá trị của
S
bằng
A.
2 ln 2 1 S
. B.
ln 2 1 S
. C.
ln 2 1 S
. D.
2 ln 2 1 S
.
Câu 14. Tính diện tích hình phẳng giới hạn bởi hai đồ thị
2
1
: y 8 7
3
P x x
,
7
:
3
x
H y
x
.
A.
3, 455
. B.
9 8 ln 2
. C.
3 ln 4
. D.
161
4 ln 3 8 ln 2
9
.
Câu 15. Diện tích hình phẳng giới hạn bởi các đồ thị và là:
2
x
y e
4
1
e
4
1
1
2
e
4
1
2
e
4
1
1
2
e
1
4
.
1
6
.
3
2
.
1
2
.
2 1
y x
6
y
x
3
x
4 6ln6.
2
4 6 ln .
3
443
.
24
25
.
6
x
y e
1
y
1
x
2.
e
.
e
1.
e
1 .
e
2
4 3
y x x
3
y x
O
x
4
2
2
y
A. B. C. D.
Câu 16. Biết rằng parabol
2
: 2
P y x
chia đường tròn
2 2
: 8
C x y thành hai phần lần lượt có diện tích
là
1
S
,
2
S
(như hình vẽ). Khi đó
2 1
b
S S a
c
với
, ,
a b c
nguyên dương và
b
c
là phân số tối giản. Tính
S a b c
.
A.
13
S
. B.
16
S
. C.
15
S
D.
14
S
.
Câu 17. Cho
H
là hình phẳng giới hạn bởi parabol
2
3
y x
và nửa đường tròn tâm
H
bán kính bằng
2 nằm phía trên trục hoành (phần tô đậm trong hình vẽ bên). Diện tích của
H
được tính theo công thức
nào dưới đây?
A.
1
2 2
0
2 3
S x x dx
. B.
1
2 2
0
2. 4 3
S x x dx
.
C.
1
2 2
0
3 4
S x x dx
. D.
1
2 2
0
4 3
S x x dx
.
Câu 18. Bạn An xây một bể cá hình tròn tâm
O
bán kính
10 m
và chia nó thành 2 phần như hình vẽ sau.
Bạn An sẽ thả cá cảnh với mật độ 4 con cá cảnh trên
2
1m
ở phần bể giới hạn bởi đường tròn tâm O và
Parabol có trục đối xứng đi qua O và chứa O. Gọi S là phần nguyên của diện tích phần thả cá. Hỏi bạn An
thả được bao nhiêu con cá cảnh trên phần bể có diện tích S, biết
,
A B O
và
12
AB m
?
A. 560. B. 650. C. 460. D. 640.
Câu 19. Lương giáo viên thấp nên thầy Nam chăn nuôi thêm 2 con bò. Do diện tích đất của nhà thầy hẹp
nên thầy xây chuồng bò như hình vẽ bên dưới và chia thành 2 phần bằng nhau để nhốt 2 con bò. Biết
ABCD là hình vuông cạnh
4 m
và I là đỉnh của một Parabol có trục đối xứng là trung trực của BC và
parabol đi qua hai điểm A, D. Tiền xây chuồng bò hết
350000
đồng/
2
1 m
. Biết I cách BC một khoảng
5 m
,
hãy tính số tiền chi phí thầy Nam bỏ ra để xây dựng chuồng bò (Làm tròn đến hàng nghìn)?
55
.
6
205
.
6
109
.
6
126
.
5
S
1
x
y
S
2
O
Câu 20. Một cái cổng hình parabol như hình vẽ. Chiều cao
4
GH m
, chiều rộng
4
AB m
,
0,9
AC BD m
. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm giá là
1200000
đồng/m
2
, còn các
phần để trắng làm xiên hoa có giá là
900000
đồng/m
2
.
Hỏi tổng chi phí để là hai phần nói trên gần nhất với số tiền nào dưới đây?
A.
11445000
(đồng). B.
7368000
(đồng). C.
4077000
(đồng). D.
11370000
(đồng)
Câu 21. Một gia đình có khu vườn hình chữ nhật có chiều dài và chiều rộng lần lượt là 9 m và 4 m. Chủ
nhà muốn đào một chiếc ao hình Elip, hỏi diện tích lớn nhất của mặt ao bằng
A.
9
m
2
. B.
10
m
2
. C.
81
4
m
2
.. D.
4
m
2
.
Câu 22. Một vật chuyển động trong 6 giờ với vận tốc
/
v km h
phụ thuộc vào thời gian
t h
có đồ thị như
hình dưới. Trong khoảng thời gian 2 giờ từ khi bắt đầu chuyển động, đồ thị là một phần đường Parabol có
đỉnh
3;9
I và có trục đối xứng song song với trục tung. Khoảng thời gian còn lại, đồ thị vận tốc là một
đường thẳng có hệ số góc bằng
1
4
. Tính quãng đường
s
mà vật di chuyển được trong 6 giờ?
A.
130
3
km
. B.
9
km
. C.
40
km
. D.
134
3
km
.
Câu 23. Cho hàm số
4 3 2
( )
f x ax bx cx dx e
. Hàm số
( )
y f x
có đồ thị như hình vẽ. Trong
các khẳng định sau, khẳng định nào đúng?
A.
0
a c
. B.
0
a b c d
. C.
a c b d
. D.
0
b d c
.
Câu 24. Diện tích hình phẳng giới hạn bởi các đường ; ; bằng . Khi đó
là:
A. B. C. D.
Câu 25. Cho Parabol
2
: 1
P y x
và đường thẳng
: 2
d y mx
với
m
là tham số. Gọi
0
m
là giá trị của
m
để diện tích hình phẳng giới hạn bởi
P
và
d
là nhỏ nhất. Hỏi
0
m
nằm trong khoảng nào?
cos
y mx x
Ox
0;x x
3
m
3.
m
3.
m
4.
m
3.
m
A.
1
( 2; )
2
. B. (0;1). C.
1
( 1; )
2
. D.
1
( ;3)
2
.
Câu 26. Gọi
( )
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
4
y x x
và trục hoành. Hai đường thẳng
y m
và
y n
chia
( )
H
thành 3 phần có diện tích bằng nhau( tham khảo hình vẽ). Giá trị của biểu thức
3 3
(4 ) (4 )
T m n
bằng
A.
320
9
T
. B.
512
15
T
. C. . D. .
Câu 27. Gọi là hình phẳng giới hạn bởi các đường: ; ; ; . Quay xung
quanh trục ta được khối tròn xoay có thể tích là.
A. . B. . C. . D. .
Câu 28. Gọi
( )
H
là hình phẳng giới hạn bởi các đường
.ln ,
y x x
trục
, 1, .
Ox x x e
Tính thể
tích khối tròn xoay được tạo thành khi quay hình phẳng
( )
H
quanh trục
.
Ox
A. . B. . C. . D. .
Câu 29. Thể tích của khối tròn xuay được giới hạn bởi
2
cos sin ; 0; 0; ,
2
y x x x y x x
là:
A.
(3 4
4
B.
(5 4)
4
C.
(3 4)
4
D.
(3 4)
5
Câu 30. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi , trục và đường thẳng
quay xung quanh trục .
A. . B. . C. . D. .
Câu 31. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol và đường thẳng
quay quanh trục bằng
A. . B. . C. . D. .
Câu 32. Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường
có giá trị bằng trong đó a, b là hai số thực nào dưới đây?
A. B. C. D.
Câu 33. Cho đồ thị . Gọi là hình phẳng giới hạn bởi , đường thẳng ,
trục . Cho là điểm thuộc , . Gọi là thể tích khối tròn xoay khi cho quay
405
T
75
2
T
H
sin
y x
O x
0
x
x
H
Ox
2
2
2
2
2
1
4
e
1
3
e
1
3
e
2
1
4
e
ln
y x
Ox
2
x
Ox
2ln 2 1
2 ln 2
2 ln 2
2ln2 1
2
:
P y x
: 2
d y x
Ox
2 2
2 4
0 0
4
x dx x dx
2
2
2
0
2
x x dx
2 2
2 4
0 0
4
x dx x dx
2
2
0
2
x x dx
exyxxy
,0,ln
3
b.e 2
a
a 27,b 5.
a 24,b 6.
a 27,b 6.
a 24,b 5.
; ( )
C y f x x
H
C
9
x
O x
M
C
9;0
A
1
V
H
quanh , là thể tích khối tròn xoay khi cho tam giác quay quanh . Biết . Tính
diện tích phần hình phẳng giới hạn bởi và . (Hình vẽ không thể thiện chính xác điểm ).
A. . B. . C. . D. .
Câu 34. Thể tích khối tròn xoay khi cho Elip quay quanh trục Ox:
A. B. C. D.
Câu 35. Thầy Nam dự định xây một bể bơi hình elip có độ dài trục lớn gấp hai lần trục bé và có diện tích
hình chữ nhật cơ sở bằng . Mỗi khối nước đổ vào bể có giá là đồng/ . Biết bể bơi sâu
. Hỏi thầy Nam cần bao nhiêu tiền để đổ nước vào bể? (Số tiền được làm tròn đến hàng nghìn).
A. 1 126 000 đồng. B. 1 367 000 đồng. C. 1 224 000 đồng. D. 1 046 000 đồng.
Câu 36. Thầy Nam mở trung tâm luyện thi Đại học và làm biển hiệu trung tâm hình chữ nhật có kích
thước như hình vẽ bên. Ở phần bên trái thầy đặt một hình elip tiếp xúc với 3 cạnh hình chữ
nhật và khoảng cách từ tâm hình elip cách chiều rộng biển trung tâm . Kinh phí làm biển hiệu là
đồng. Biết tiền công trang trí phần bên trong hình elip là đồng . Hỏi phần còn lại
làm bao nhiêu tiền trên (Làm tròn đến hàng nghìn)?
A. 260 000 đồng. B. 186 000 đồng. C. 168 000 đồng. D. 206 000 đồng.
Câu 37. Một tàu lửa đang chạy với vận tốc m/s thì người lái tàu đạp phanh; từ thời điểm đó, tàu
chuyển động chậm dần đều với vận tốc m/s. Trong đó khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, tàu còn di chuyển được:
A. . B. . C. . D.
Câu 38. Một ô tô đang chạy với vận tốc thì người lái xe đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc , trong đó là khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Tính quãng đường ô tô đi được trong giây cuối cùng.
A. . B. . C. . D. .
Ox
2
V
AOM
Ox
1 2
9
4
V V
S
C
OM
M
x
y
I
y=
x
A
M
O
1
4 5
3
S
3 3
2
S
27 3
16
S
6
S
2 2
2 2
1
x y
a b
2
4
.
3
a b
2
4
.
3
ab
2
2
.
3
a b
2
2
.
3
ab
2
128m
8500
3
1m
2 m
80%
3 m x 2 m
0,5 m
900.000
100.000
2
/1m
2
1m
200
200 20
v t t
t
1000 m.
500 m.
1500 m.
2000 m.
10 (m/s)
2 10 (m/s)
v t t
t
8
55 (m)
25 (m)
50 (m)
16 (m)
Câu 39. Hai người , đang chạy xe ngược chiều nhau thì xảy ra va chạm, hai xe tiếp tục di chuyển
theo chiều của mình thêm một quãng đường nữa thì dừng hẳn. Biết rằng sau khi va chạm, một người di
chuyển tiếp với vận tốc
1
( ) 6 3v t t
mét trên giây, người còn lại di chuyển với vận tốc
2
( ) 12 4v t t
mét trên giây. Tính khoảng cách hai xe khi đã dừng hẳn.
A. mét. B. mét. C. mét. D. mét.
Câu 40. Một vật chuyển động trong giờ với vận tốc phụ thuộc vào thời gian có đồ thị
vận tốc như hình bên. Trong khoảng thời gian giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần
của đường parabol có đỉnh và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ
thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong giờ đó.
A. . B. . C. . D. .
D. SỐ PHỨC.
Vấn đề 1. Câu hỏi lý thuyết.
Câu 1. Cho hai số phức
,z a bi a b
và
,z a b i a b
. Điều kiện giữa
, , ,a b a b
để
z z
là một số ảo là
A.
0b b
. B.
' 0
' 0
a a
b b
. C.
' 0
' 0
a a
b b
. D.
0a a
.
Câu 2. Cho số phức
z a bi
,a b
tùy ý. Mệnh đề nào sau đây đúng?
A. Mô đun của
z
là một số thực dương.
B.
2
2
z z
.
C. Số phức liên hợp của
z
có mô đun bằng mô đun của số phức
iz
.
D. Điểm
;M a b
là điểm biểu diễn của
z
.
Câu 3. Cho số phức
z a bi
với
,a b
là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
A. Phần ảo của
z
là
bi
. B. Môđun của
2
z bằng
2 2
a b
.
C.
z z
không phải là số thực. D. Số
z
và
z
có môđun khác nhau.
Câu 4. Cho số phức
z a bi
, , , 0a b a b
. Mệnh đề nào sau đây đúng?
A.
z z
. B.
2
2
z z
. C.
1
. 1z z
. D.
2
.z z z
.
Câu 5. Cho hai số phức
z
và
z
. Trong các mệnh đề sai, mệnh đề nào sai?
A.
z z z z
. B.
. .z z z z
. C.
. .z z z z
. D.
z z z z
.
A
B
25
22
20
24
3
v
km/ h
t
h
1
2;5
I
3
15
km
32
3
km
12
km
35
3
km
Câu 6. Cho số phức
z a bi
,a b
. Khẳng định nào sau đây sai?
A.
2 2
z a b
. B.
z a bi
. C.
2
z
là số thực. D.
.
z z
là số thực.
Vấn đề 2. Các phép toán số phức.
Câu 7. Xác định phần ảo của số phức
18 12
z i
.
A.
12
. B.
18
. C.
12
. D.
12
i
.
Câu 8. Số phức liên hợp của số phức
1 2
z i
là
A.
1 2
i
B.
1 2
i
C.
2
i
D.
1 2
i
Câu 9. Tính môđun của số phức
4 3
z i
.
A.
7
z
. B.
7
z . C.
5
z
. D.
25
z
.
Câu 10. Cho số phức
1
1
z i
và
2
2 3
z i
. Tìm số phức liên hợp của số phức
1 2
w z z
?
A.
3 2
w i
. B.
1 4
w i
. C.
1 4
w i
. D.
3 2
w i
.
Câu 11. Tính môđun của số phức
1 2 2 3 2
z i i i i
.
A.
4 10
z
. B.
4 5
z
. C.
160
z . D.
2 10
z
.
Câu 12. Biết
1
3 4
a bi
i
,
,a b
. Tính
ab
.
A.
12
625
. B.
12
625
. C.
12
25
. D.
12
25
.
Câu 13. Cho số phức
1
z i
. Khi đó
3
z
bằng
A.
2
. B.
2 2
. C.
4
. D.
1
.
Câu 14. Tính môđun của số phức là nghịch đảo của số phức
2
1 2
z i
.
A.
1
5
. B.
5
. C.
1
25
. D.
1
5
.
Câu 15. Cho số phức
1 3
2 2
z i
. Tìm số phức
2
1
w z z
.
A.
2 3
i
. B.
1
. C.
0
. D.
1 3
2 2
i
.
Câu 16. Tính
2018 2018
1 3 1 3
P i i
.
A.
2
P
B.
1010
2
P
C.
2019
2
P
D.
4
P
Câu 17. Tính
2 2017 2018
1 ...
S i i i i
A.
S i
. B.
1
S i
. C.
1
S i
. D.
S i
.
Câu 18. Tính
2 3 2017
1009 2 3 ... 2017
S i i i i
.
A.
S 2017 1009 i.
B.
1009 2017 .
i
C.
2017 1009 .
i
D.
1008 1009 .
i
Câu 19. Cho các số phức
1
z
,
2
z
,
3
z
thỏa mãn:
1
4
z
,
2
3
z
,
3
2
z
và
1 2 2 3 1 3
4 16 9 48
z z z z z z
.
Giá trị của biểu thức
1 2 3
P z z z
bằng:
A.
1
B.
8
. C.
2
D.
6
Câu 20. Cho các số phức
1
z
,
2
z
,
3
z
thỏa mãn 2 điều kiện
1 2 3
2017
z z z
và
1 2 3
0.
z z z
Tính
1 2 2 3 3 1
1 2 3
.
z z z z z z
P
z z z
A.
2017.
P
B.
1008,5.
P
C.
2
2017 .
P
D.
6051.
P
Câu 21. Cho số phức
z
thỏa mãn
1
z
. Tìm giá trị lớn nhất của biểu thức
5
1
i
A
z
.
A.
5
. B.
4
. C.
6
. D.
8
.
Câu 22. Cho số phức
z
thỏa mãn
1
z
. Tìm giá trị lớn nhất của biểu thức
1 3 1 .
P z z
A.
3 15
. B.
6 5
. C.
20
. D.
2 20
.
Câu 23. Trong các số phức
z
thỏa mãn
2 3
z i z i
. Tìm số phức
z
có môđun nhỏ nhất.
A.
27 6
5 5
z i
. B.
6 27
5 5
z i
. C.
6 27
5 5
z i
. D.
3 6
5 5
z i
.
Câu 24. Cho số phức
z
thoả mãn đồng thời hai điều kiện
3 4 5
z i và biểu thức
2 2
2
M z z i
đạt giá trị lớn nhất. Môđun của số phức
2
z i
bằng
A.
5
. B.
9
. C.
25
. D.
5
.
Vấn đề 3. Phương trình bậc nhất - bậc hai trong tập số phức
Câu 25. Trên tập số phức, cho phương trình:
2
0
az bz c
, , a b c
. Chọn kết luận sai.
A. Nếu
0
b
thì phương trình có hai nghiệm mà tổng bằng
0
.
B. Nếu
2
4 0
b ac
thì phương trình có hai nghiệm mà môđun bằng nhau.
C. Phương trình luôn có hai nghiệm phức là liên hợp của nhau.
D. Phương trình luôn có nghiệm.
Câu 26. Cho số phức
z
thỏa mãn
2 2 2 3
i z i
. Môđun của
z
là:
A.
5
z
. B.
5 3
3
z
. C.
5 5
3
z
. D.
5
z .
Câu 27. Tìm mô đun của số phức
z
thoả
3 (3 i)(1 i) 2
iz
.
A.
2 2
3
z
. B.
3 2
2
z
. C.
3 3
2
z
. D.
2 3
3
z
.
Câu 28. Tính mô đun của số phức
z
biết
2
1 2 3 4
i z i
.
A.
5
z . B.
4
5
z . C.
2 5
z . D.
5
z
.
Câu 29. Phương trình
2
3 9 0
z z
có hai nghiệm phức
1
z
,
2
z
. Tính
1 2 1 2
S z z z z
.
A.
6
S
. B.
6
S
. C.
12
S
. D.
12
S
.
Câu 30. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
6 11 0
z z
. Giá trị của biểu thức
1 2
3
z z
bằng
A.
22
. B.
11
. C.
2 11
. D.
11
.
Câu 31. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 2 0
z z
. Tính
2018 2018
1 2
T z z
A.
0
T
. B.
2019
2
T
. C.
1
T
. D.
1010
2
T
.
Câu 32. Cho
m
là số thực, biết phương trình
2
5 0
z mz
có hai nghiệm phức trong đó có một nghiệm
có phần ảo là
1
. Tính tổng môđun của hai nghiệm.
A.
3
B.
5
C.
2 5
D.
4
Câu 33. Tìm tổng các giá trị của tham số thực
a
sao cho phương trình
2 2
3 2 0
z z a a
có nghiệm
phức
0
z
thỏa
0
2
z
.
A.
0
. B.
2
. C.
6
. D.
4
.
Vấn đề 4. Điều kiện của bài toán có chứa modul, số phức liên hợp…
Câu 34. Nếu
2
số thực
x
,
y
thỏa:
3 2 1 4 1 24
x i y i i
thì
x y
bằng
A.
4
. B.
3
. C.
2
. D.
3
.
Câu 35. Tìm số thực
m
sao cho
2
1 1
m m i
là số ảo.
A.
0
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 36. Có bao nhiêu số phức
z
thỏa mãn
1 2 13 2
i z i z i
?
A.
4
. B.
3
. C.
2
. D.
1.
Câu 37. Có bao nhiêu số phức
z
thỏa mãn
1
z z z ?
A.
0
. B.
1
. C.
4
. D.
3
.
Câu 38. Tìm số phức
z
thỏa mãn
3 1
z z
và
2
z z i
là số thực
A.
2
z
B.
2 2
z i
C.
2 2
z i
D. không có
z
Câu 39. Cho số phức
,z a bi a b
thỏa mãn
2 5 5
z i
và
. 82
z z
. Tính giá trị của
P a b
.
A.
10
B.
8
C.
35
D.
7
Câu 40. Cho số phức
z a bi
, a b
thỏa mãn
1 3 0
z i z i
. Tính
3
S a b
.
A.
7
3
S
. B.
5
S
. C.
5
S
. D.
7
3
S
.
Câu 41. Cho hai số phức
1
z
,
2
z
thỏa mãn
1
1
z
,
2
2
z
và
1 2
3
z z
. Giá trị của
1 2
z z
là
A.
0
. B.
1
. C.
2
. D. 3.
Câu 42. Tìm môđun của số phức
z
biết
4 1 i 4 3 i
z z z
.
A.
1
2
z
. B.
2
z
. C.
4
z
. D.
1
z
.
Câu 43. Tính môđun của số phức
z
thỏa mãn:
3 . 2017 48 2016 .
z z z z i
A.
4
z
. B.
2016
z . C.
2017
z . D.
2
z
.
Câu 44. Cho số phức
z
thoả mãn
1
i
z
là số thực và
2
z m
với
m
. Gọi
0
m
là một giá trị của
m
để có đúng một số phức thoả mãn bài toán. Khi đó:
A.
0
1
0;
2
m
. B.
0
1
;1
2
m
. C.
0
3
;2
2
m
. D.
0
3
1;
2
m
.
Vấn đề 5. Điểm biểu diễn của số phức
Câu 45. Giả sử
,A B
theo thứ tự là điểm biểu diễn của số phức
1
z
,
2
z
. Khi đó độ dài đoạn
AB
bằng
A.
2 1
z z
. B.
2 1
z z
. C.
1 2
z z
. D.
1 2
z z
.
Câu 46. Trong mặt phẳng phức, gọi
M
là điểm biểu diễn cho số phức
2
z z
với
z a bi
, , 0a b b
. Chọn kết luận đúng.
A.
M
thuộc tia
Ox
. B.
M
thuộc tia
Oy
.
C.
M
thuộc tia đối của tia
Ox
. D.
M
thuộc tia đối của tia
Oy
.
Câu 47. Điểm
3; 1M
là điểm biểu diễn của số phức nào sau đây?
A.
1 3z i
B.
1 3z i
C.
3z i
D.
3z i
Câu 48. Điểm M trong hình vẽ dưới đây biểu thị cho số phức nào?
A.
3 2i
. B.
2 3i
. C.
2 3i
. D.
3 2i
.
Câu 49. Trong hình vẽ dưới đây,
M
là điểm biểu diễn của số phức
z
.
Số phức
z
là
A.
2 i
. B.
1 2i
. C.
1 2i
. D.
2 i
.
Câu 50. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức
1 2z i i
?
A.
P
. B.
M
. C.
N
. D.
Q
.
Câu 51. Cho số phức
z
thoả mãn
2 10 5 i z i
. Hỏi điểm biểu diễn số phức
z
là điểm nào trong các
điểm
M
,
N
,
P
,
Q
trong hình vẽ sau ?
A. Điểm
Q
. B. Điểm
M
. C. Điểm
P
. D. Điểm
N
.
Câu 52. Cho số phức . Trên mặt phẳng tọa độ , tìm điểm biểu diễn số phức .
A. . B. . C. . D. .
Câu 53. Cho số phức
z
thỏa mãn
2 0iz i
. Khoảng cách từ điểm biểu diễn của
z
trên mặt phẳng tọa
độ
Oxy
đến điểm
3; 4M
là
A.
2 5
. B.
13
. C.
2 10
. D.
2 2
.
Câu 54. Cho số phức
z
thỏa mãn điều kiện
2 3 1 9z i z i
. Số phức
5
w
iz
có điểm biểu diễn là
điểm nào trong các điểm
, , , A B C D
ở hình vẽ sau?
A. Điểm
D
. B. Điểm
C
. C. Điểm
B
. D. Điểm
A
.
Câu 55. Số phức
z
được biểu diễn bởi một điểm trên mặt phẳng tọa độ Oxy như hình vẽ:
Trong các hình dưới đây, hình nào có thể là điểm biểu diễn của số phức
i
z
?
2
z i
Oxy
w iz
1;2
M
2; 1
M
2;1
M
1;2
M
x
O
1
1
y
z
A. B.
C. D.
Vấn đề 6. Vận dụng các tính chất hình học để giải toán về số phức
Câu 56. Cho
A
,
B
,
C
tương ứng là các điểm trong mặt phẳng Oxy biểu diễn các số
1
1 2
z i
,
2
2 5
z i
,
3
2 4
z i
. Số phức
z
biểu diễn bởi điểm
D
sao cho tứ giác
ABCD
là hình bình hành là
A.
1 7
i
. B.
5
i
. C.
1 5
i
. D.
3 5
i
.
Câu 57. Trong mặt phẳng tọa độ
Oxy
, gọi
M
là điểm biểu diễn số phức
3 4
z i
;
'
M
là điểm biểu diễn
cho số phức
1
'
2
i
z z
. Tính diện tích tam giác
'
OMM
.
A.
'
25
4
OMM
S
. B.
'
25
2
OMM
S
. C.
'
15
4
OMM
S
. D.
'
15
2
OMM
S
.
Câu 58. Cho các số phức
1
z
,
2
z
thỏa mãn
1
3
z
,
2
4
z
,
1 2
5
z z
. Gọi
A
,
B
lần lượt là các điểm
biểu diễn số phức
1
z
,
2
z
trên mặt phẳng tọa độ. Tính diện tích
S
của
OAB
với
O
là gốc tọa độ.
A.
5 2
S
. B.
6
S
. C.
25
2
S . D.
12
S
.
Câu 59. Cho hai số phức
1
z
,
2
z
thỏa mãn
1 2
1
z z
. Khi đó
2 2
1 2 1 2
z z z z
bằng
A.
2
. B.
4
. C.
1
. D.
0
.
Câu 60. Cho
A
,
B
là hai điểm biểu diễn hình học số phức theo thứ tự
0
z
,
1
z
khác
0
và thỏa mãn đẳng
thức
2 2
0 1 0 1
z z z z
. Tam giác OAB là tam giác gì? Chọn phương án đúng nhất.
A. Đều B. Cân tại
O
C. Vuông tại
O
D. Vuông cân tại
O
Câu 61. Cho hai số phức
1 2
,
z z
thoả mãn
1 2
6, 2
z z
. Gọi
,
M N
là các điểm biểu diễn cho
1
z
và
2
iz
.
Biết
60
MON
. Tính
2 2
1 2
9
T z z
.
A.
18
T
. B.
24 3
T . C.
36 2
T
. D.
36 3
T .
Câu 62. Trên mặt phẳng Oxy, tập hợp các điểm biểu diễn các số phức
z x yi
thỏa mãn
2 3
z i z i
là đường thẳng có phương trình là
A.
1
y x
. B.
1
y x
. C.
1
y x
. D.
1
y x
.
x
O
1
1
y
x
O
1
1
y
x
O
1
1
y
x
y
1
1
O
Câu 63. Cho số phức
z x yi
,x y
thỏa mãn
2 1 0
z i z i
. Trong mặt phẳng tọa độ
Oxy
, điểm
M
là điểm biểu diễn của số phức
z
. Hỏi
M
thuộc đường thẳng có phương trình nào sau
đây?
A.
5 0
x y
. B.
2 0
x y
. C.
2 0
x y
. D.
1 0
x y
.
Câu 64. Trên mặt phẳng
Oxy
, tập hợp điểm biểu diễn số phức
z
thỏa mãn
z i iz
là
A. Đường thẳng
2
y
. B. Đường thẳng
1
2
y
.
C. Đường thẳng
1
2
y
. D. Đường tròn tâm
0; 1
I .
Câu 65. Tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa mãn:
2 4
z i
là đường tròn có tâm
I
và bán kính
R
lần lượt là
A.
2; 1
I
;
4
R
. B.
2; 1
I
;
2
R
. C.
2; 1
I
;
4
R
. D.
2; 1
I
;
2
R
.
Câu 66. Cho số phức
z
thỏa mãn điều kiện
3 4 2.
z i
Trong mặt phẳng
Oxy
tập hợp điểm biểu diễn
số phức
2 1
w z i
là hình tròn có diện tích là
A.
9
S
. B.
12
S
. C.
16
S
. D.
25
S
.
Câu 67. Trong mặt phẳng
Oxy
, tập hợp các điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3
1
z
z
là
A. Đường tròn
2 2
9 9
0
4 8
x y x
. B. Đường tròn
2 2
9 9
0
4 8
x y x
.
C. Đường tròn
2 2
9 9
0
4 8
x y x
. D. Đường tròn tâm
9
0;
8
I
và
1
8
R
.
Câu 68. Cho các số phức
z
thoả mãn
5
z i
. Biết rằng tập hợp điểm biểu diễn số phức
1
w iz i
là
đường tròn. Tính bán kính của đường tròn đó.
A.
20
r
. B.
22
r
. C.
4
r
. D.
5
r
.
Câu 69.
Cho số phức
z
thỏa mãn
2 2 25
z i z i
. Biết tập hợp các điểm
M
biểu diễn số phức
2 2 3
w z i
là đường tròn tâm
;
I a b
và bán kính
c
. Giá trị của
a b c
bằng
A.
17
. B.
20
. C.
10
. D.
18
.
Câu 70. Tìm tập hợp các điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 2 10
z z
.
A. Đường tròn
2 2
2 2 100
x y
. B. Elip
2 2
1
25 4
x y
.
C. Đường tròn
2 2
2 2 10
x y
. D. Elip
2 2
1
25 21
x y
.
Câu 71. Có bao nhiêu số phức
z
thỏa mãn điều kiện
1 2
1 2
iz i
z z i
?
A. 2. B. 0. C. Có vô số số. D. 1.
Câu 72. Cho số phức
z
thỏa mãn
21 z
. Gọi
M
và
m
là giá trị lớn nhất, nhỏ nhất của
z
. Tính
M m
.
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 73. Cho số phức
z
thỏa mãn
1 2 3
z i
. Tìm môđun nhỏ nhất của số phức
1 .
z i
A.
4.
B.
2 2.
C.
2.
D.
2.
Câu 74. Cho các số phức
z
thoả mãn
2
z
. Đặt
1 2 1 2
w i z i
. Tìm giá trị nhỏ nhất của
w
.
A.
2
. B.
3 5
. C.
2 5
. D.
5
.
Câu 75. Cho số phức
z
thỏa mãn: 2 1
z i z i
. Trong mặt phẳng
Oxy
,
z
được biểu diễn bởi điểm
M
. Tìm
z
sao cho độ dài đoạn
MA
ngắn nhất với
1,3
A .
A.
3
i
. B.
1 3
i
. C.
2 3
i
. D.
2 3
i
.
Câu 76. Nếu
z
là số phức thỏa
2
z z i
thì giá trị nhỏ nhất của biểu thức
4
z i z
là
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 77. Cho số phức
z
thỏa mãn
5 1 3 3 1
z i z i z i
. Tìm giá trị lớn nhất
M
của
2 3
z i
?
A.
10
3
M
B.
1 13
M C.
4 5
M D.
9
M
Câu 78. Cho số phức
1
z
,
2
z
thỏa mãn
1
12
z
và
2
3 4i 5
z
. Giá trị nhỏ nhất của
1 2
z z
là
A.
0
. B.
2
C.
7
D.
17
Câu 79. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của
z i
P
z
, với
z
là số phức khác
0
và
thỏa mãn
2
z
. Tính tỷ số
M
m
.
A.
5
M
m
B.
3
M
m
C.
3
4
M
m
D.
1
3
M
m
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT YÊN HÒA
------
o0o
-----
ĐỀ CƯƠNG ÔN TẬP HỌC KỲ 2
NĂM HỌC 2020 – 2021
MÔN: TOÁN
PHẦN II. HÌNH HỌC
Vấn đề 1. Hệ tọa độ trong không gian.
Câu 1. Cho
2 4 6
OA i j k
và
9 7 4
OB i j k

. Vectơ
AB
có tọa độ là
A.
7;3;10
. B.
7; 3; 10
. C.
11;11; 2
. D.
7; 3;10
.
Câu 2. Cho đoạn thẳng
AB
có trung điểm
I
. Biết
2;1; 1
A
,
1;2;0
I
. Khi đó điểm
B
có tọa độ là
A.
1; 1; 1
. B.
3;0; 2
. C.
0;3;1
. D.
1;1;1
.
Câu 3. Cho hình bình hành
ABCD
, biết
1;1;1
A
,
2;2;3
B
,
5; 2;2
C
. Tọa độ điểm
D
là
A.
2; 3;0
. B.
2;3;4
. C.
2;3;0
. D.
8; 1;4
.
Câu 4. Cho điểm
3; 1;1
A
. Hình chiếu của điểm
A
trên mặt phẳng
Oyz
là điểm
A.
3;0;0
M
. B.
0; 1;1
N
. C.
0; 1;0
P
. D.
0;0;1
P
.
Câu 5. Cho điểm
1;2;3
M
. Gọi
H
là hình chiếu vuông góc của
M
trên trục
Oz
. Điểm đối xứng với
M
qua
H
có tọa độ:
A.
0;0;3
. B.
1;2; 3
. C.
1; 2; 3
. D.
1; 2;3
.
Câu 6. Cho hai điểm
(0;3;1)
B ,
( 3;6;4)
C
. Gọi
M
là điểm nằm trên đoạn
BC
sao cho 2
MC MB
.
Tính tọa độ điểm
M
.
A.
( 1;4; 2)
M
. B.
( 1;4;2)
M
. C.
(1; 4; 2)
M
. D.
( 1; 4;2)
M
.
Câu 7. Cho
1;2
A m
,
2;5 2
B m
và
3;4
C m
. Tìm giá trị
m
để
A
,
B
,
C
thẳng hàng?
A.
2
m
. B.
2
m
. C.
1
m
. D.
3
m
.
Câu 8. Cho ba điểm
2; 1;1 ; 3; 2; 1
A B
. Tìm tọa độ giao điểm của đường thẳng AB và mặt phẳng
(yOz)?
#A.
5 3
; ;0
2 2
B.
0; 3; 1
C.
0;1;5
D.
0; 1; 3
Câu 9. Cho véc tơ
2; 2; 4 , 1; 1;1 .
a b
Mệnh đề nào dưới đây là mệnh đề sai?
A.
3; 3; 3 .
a b
B.
a
và
b
cùng phương. C.
3.
b
D.
.
a b
.
Câu 10. Cho sáu điểm
1;2;3 , 2; 1;1 , 3;3; 3 , , ,
A B C A B C
thỏa mãn
0
A A B B C C

. Gọi
; ;
G a b c
là trọng tâm tam giác
A B C
. Giá trị
3
a b c
bằng
A.
6
. B.
1
. C.
11
. D.
3
.
Câu 11. Cho
1; 1;0
A
,
3;1; 1
B
. Điểm
M
thuộc trục
Oy
và cách đều hai điểm
A
,
B
có tọa độ là:
A.
9
0; ;0
4
M
. B.
9
0; ;0
2
M
. C.
9
0; ;0
2
M
. D.
9
0; ;0
4
M
.
Câu 12. Cho ba điểm
1;1;1 , 1;1;0 , 3;1; 1
A B C
. Điểm
; ;
M a b c
trên mặt phẳng
Oxz
cách đều 3
điểm
, ,
A B C
. Giá trị
3
a b c
bằng
A.
6
. B.
1
. C.
3
. D.
1
.
Câu 13. Cho hai điểm
(2;2;1)
M ,
8 4 8
; ;
3 3 3
N
. Tìm tọa độ tâm đường tròn nội tiếp tam giác
OMN
.
A.
(1;1;1)
I
. B.
(0;1;1)
I
. C.
(0; 1; 1)
I
. D.
(1;0;1)
I
.
Câu 14. Cho tam giác
ABC
có
1;2; 1
A
,
2; 1;3
B
,
4;7;5
C
. Gọi
; ;
D a b c
là chân đường phân
giác trong góc
B
của tam giác
ABC
. Giá trị của
2
a b c
bằng
A.
5
. B.
4
. C.
14
. D.
15
.
Câu 15. Cho hình hộp .
ABCD A B C D
có
0;0;0
A
,
;0;0
B a
;
0;2 ;0
D a
,
0;0;2
A a
với
0
a
. Độ
dài đoạn thẳng
AC
là:
A.
a
. B.
2
a
. C.
3
a
. D.
3
2
a
.
Câu 16. Góc giữa hai vectơ
i
và
3;0;1
u
là
A.
120
. B.
30
. C.
60
. D.
150
.
Câu 17. Cho ba điểm
1; 2;3 , 0;3;1 , 4;2;2
A B
. Côsin của góc
BAC
bằng
A.
9
35
. B.
9
2 35
. C.
9
35
. D.
9
2 35
.
Câu 18. Cho
1;2;0
A
,
2; 1;1
B
. Tìm
C
có hoành độ dương trên
Ox
sao cho tam giác
ABC
vuông
tại
C
.
A.
3;0;0
C
. B.
2;0;0
C
. C.
1;0;0
C
. D.
5;0;0
C
.
Câu 19. Cho ba điểm không thẳng hàng
1;2;4
A ,
1;1;4
B ,
0;0;4
C . Tam giác
ABC
là tam giác
gì?
A. Tam giác tù. B. Tam giác vuông. C. Tam giác đều. D. Tam giác nhọn.
Câu 20. Cho ba điểm
2;3; 1
M
,
1;1;1
N ,
1; 1;3
P m . Tìm
m
thì tam giác
MNP
vuông tại
N
A.
3
m
. B.
1
m
. C.
2
m
. D.
0
m
.
Câu 21. Cho hai vecto
,
a b
khác
0
. Kết luận nào sau đây sai?
A.
,3 3 ,
a b a b
. B.
2 , 2 ,
a b a b
. C.
3 ,3 3 ,
a b a b
. D.
, . .sin ,
a b a b a b
.
Câu 22. Cho
1;1;2
u
,
1; ; 2
v m m
. Khi đó
, 14
u v
thì
A.
11
1,
5
m m
. B.
11
1,
3
m m
. C.
1, 3
m m
. D.
1
m
.
Câu 23. Cho
(1; 2;0), (1;0; 1), (0; 1;2), ( 2; ; ).
A B C D m n
Trong các hệ thức liên hệ giữa
,
m n
dưới đây,
hệ thức nào để bốn điểm
, , ,
A B C D
đồng phẳng?
A.
2 13.
m n
B.
2 13.
m n
C.
2 13.
m n
D.
2 3 10.
m n
Câu 24. Trong không gian
Oxyz
cho tứ diện
ABCD
có
0;1;1
A
,
1;0;2
B
,
1;1;0
C
và
2;1; 2
D
. Tính thể tích khối tứ diện
ABCD
.
A.
5
6
. B.
5
. C.
5
2
. D.
5
3
.
Câu 25. Cho tứ diện
ABCD
có
0;1; 1 ; 1;1;2 ; 1; 1;0 ; 0;0;1
A B C D
. Tính độ dài đường cao
AH
của hình chóp
.
A BCD
.
A.
3 2
. B.
2 2
. C.
2
2
. D.
3 2
2
.
Câu 26. Cho tứ diện
ABCD
có
2; 1;1
A
,
3;0; 1
B
,
2; 1;3
C
,
D Oy
và có thể tích bằng
5
.
Tính tổng tung độ của các điểm
D
.
A.
6
. B.
2
. C.
7
. D.
4
.
Câu 27. Cho hai điểm
9; 3;4 , ; ;
A B a b c
. Gọi
, ,
M N P
lần lượt là giao điểm của đường thẳng
AB
với các mặt phẳng
, ,
Oxy Oxz Oyz
. Biết các điểm
, ,
M N P
đều nằm trên đoạn AB sao cho
AM MN NP PB
. Giá trị của
ab bc ca
bằng
A.
17
. B.
17
. C.
9
. D.
12
.
Câu 28. Cho
1; 2;3 ; 2;2;4 ; 3; 3;2
A B C
. Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho:
MA MB MC
ngắn nhất?
A.
2;1;0
M
B.
2; 1;0
M
C.
0; 1;3
M
D.
2;0;3
M
Câu 29. Cho ba điểm
1;2;2 , 3; 1; 2 , 4;0;3
A B C
. Tọa độ điểm
I
trên mặt phẳng
Oxz
sao
cho biểu thức
2 3
IA IB IC
đạt giá trị nhỏ nhất là
A.
19 15
;0;
2 2
I
. B.
19 15
;0;
2 2
I
. C.
19 15
;0;
2 2
I
. D.
19 15
;0;
2 2
I
.
Câu 30. Cho
0;0; 1
A
,
1;1;0
B
,
1;0;1
C
. Tìm điểm
M
sao cho
2 2 2
3 2
MA MB MC
đạt giá trị
nhỏ nhất.
A.
3 1
; ; 1
4 2
M
. B.
3 3
; ; 1
4 2
M
. C.
3 1
; ; 1
4 2
M
. D.
3 1
; ; 2
4 2
M
.
Câu 31. Cho
1; 1;1
A
,
0;1; 2
B
và điểm
M
thay đổi trên
Oxy
. Tìm giá trị lớn nhất của
MA MB
.
A.
14
. B.
14
. C.
6
. D.
6
.
Câu 32. Cho các điểm
1; 2;3
A
,
6; 5;8
B
và
OM ai bk
với
a
,
b
là các số thực luôn thay
đổi. Nếu
2
MA MB
 
đạt giá trị nhỏ nhất thì giá trị của
a b
bằng
A.
25
. B.
13
. C.
0
. D.
26
.
Vấn đề 2. Phương trình mặt phẳng trong hệ trục tọa độ
Oxyz
.
Câu 33. Cho mặt phẳng
: 2 1 0
P x z
. Chọn câu đúng nhất trong các nhận xét sau:
A.
P
đi qua gốc tọa độ
O
. B.
P
song song với
Oxy
.
C.
P
vuông góc với trục
Oz
. D.
P
song song với trục
Oy
.
Câu 34. Ba mặt phẳng
2 6 0
x y z
,
2 3 13 0
x y z
,
3 2 3 16 0
x y z
cắt nhau tại điểm
M
.
Tọa độ của
M
là:
A.
1;2; 3
M
. B.
1; 2;3
M
. C.
1; 2;3
M
. D.
1;2;3
M
.
Câu 35. Gọi
,
m n
là hai giá trị thực thỏa mãn: giao tuyến của hai mặt phẳng
: 2 1 0
m
P mx y nz
và
: 2 0
m
Q x my nz
vuông góc với mặt phẳng
: 4 6 3 0
x y z
.
A.
0
m n
. B.
2
m n
. C.
1
m n
. D.
3
m n
.
Câu 36. Cho điểm
2;1;2
H
,
H
là hình chiếu vuông góc của gốc toạ độ
O
lên mặt phẳng
P
, số đo
góc của mặt phẳng
P
và mặt phẳng
: 11 0
Q x y
.
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
90
Câu 37. Cho các điểm
2;0;0
A
,
0;3;0
B
,
0;0;6
C
,
1;1;1
D
. Có bao nhiêu mặt phẳng phân biệt
đi qua 3 trong 5 điểm
O
,
A
,
B
,
C
,
D
?
A.
10
. B.
5
. C.
7
. D.
6
.
Câu 38. Mặt phẳng
Oxy
có phương trình là
A.
0
z
. B.
0
x
. C.
0
y
. D.
0
x y
.
Câu 39. Mặt phẳng song song với mặt phẳng
Oxz
và đi qua điểm
(1;1;1)
A
có phương trình là
A.
1 0
y
. B.
1 0
x y z
. C.
1 0
x
. D.
1 0.
z
Câu 40. Cho
1; 1;5
A ,
0;0;1
B . Mặt phẳng
P
chứa
,
A B
và song song với trục
Oy
có phương
trình là
A.
4 1 0
x z
. B.
4 1 0
x y z
. C.
2 5 0
x z
. D.
4 1 0
x z
.
Câu 41. Cho hai điểm
1;3; 4
A
,
1;2;2
B
. Phương trình mặt phẳng trung trực của đoạn thẳng AB là
A.
4 2 12 17 0
x y z
. B.
4 2 12 17 0
x y z
. C.
4 2 12 17 0
x y z
. D.
4 2 12 17 0
x y z
.
Câu 42. Cho điểm
2;4;1 ; 1;1;3
A B
và mặt phẳng
: 3 2 5 0
P x y z
. Một mặt phẳng
Q
đi
qua hai điểm
,
A B
và vuông góc với mặt phẳng
P
có dạng
11 0
ax by cz
. Khẳng định nào sau là
đúng?
A.
5
a b c
. B.
15
a b c
. C.
5
a b c
. D.
15
a b c
.
Câu 43. Cho điểm
2;0; 2
A
,
0;3; 3
B
. Gọi
P
là mặt phẳng đi qua
A
sao cho khoảng cách từ
B
đến mặt phẳng
P
là lớn nhất. Khoảng cách từ gốc tọa độ đến mặt phẳng
P
bằng
A.
1
14
. B.
4
14
. C.
2
14
. D.
3
14
.
Câu 44. Mặt phẳng
đi qua gốc tọa độ O và vuông góc với 2 mặt phẳng
: 7 0
P x y z
,
: 3 2 12 5 0
Q x y z
có phương trình là
A.
: 2 3 0
x y z
. B.
:10x 15y 5z 2 0
.
C.
:10 15 5 2 0
x y z
. D.
: 2 3 0
x y z
.
Câu 45. Cho 2 mặt phẳng
( ) : 3 0;( ) : 2 1 0
x y z x y z
. Viết phương trình mặt phẳng (P)
vuông góc với
( )
và
( )
và khoảng cách từ
2; 3;1
M
đến mặt phẳng (P) bằng
14
. Có hai mặt phẳng
thỏa mãn là:
A.
1
2 3 16 0
P x y z
và
2
2 3 12 0
P x y z
B.
1
2 3 16 0
P x y z
và
2
2 3 12 0
P x y z
C.
1
2 3 16 0
P x y z
và
2
2 3 12 0
P x y z
D.
1
2 3 16 0
P x y z
và
2
2 3 12 0
P x y z
Câu 46. Cho mặt phẳng (P):
2 2 10 0
x y z
. Phương trình mặt phẳng (Q) với (Q) song song với (P)
và khoảng cách giữa hai mặt phẳng (P) và (Q) bằng
7
3
là
A.
2 2 3 0; 2 2 17 0
x y z x y z
. B.
2 2 3 0; 2 2 17 0
x y z x y z
.
C.
2 2 3 0; 2 2 17 0
x y z x y z
. D.
2 2 3 0; 2 2 17 0
x y z x y z
.
Câu 47. Phương trình của mp đi qua ba điểm
(1;0;0)
A
,
(0; 1;0)
B
,
1
0;0;
2
C
là
A.
2 1 0.
x y z
B.
2 0
x y z
. C.
2 1 0.
x y z
D.
1 0.
2
z
x y
Câu 48. Viết phương trình mặt phẳng
P
đi qua điểm
1;2;3
G
và cắt ba trục
, ,
Ox Oy Oz
lần lượt tại
, ,
A B C
sao cho G là trọng tâm tam giác
ABC
.
A.
2 3 14 0.
x y z
B.
1
3 6 9
x y z
C.
1.
1 2 3
x y z
D.
1
6 3 9
x y z
Câu 49. Cho điểm
1;2;5
M
. Mặt phẳng
P
đi qua điểm
M
cắt trục tọa độ
, ,
Ox Oy Oz
tại
, ,
A B C
sao
cho
M
là trực tâm tam giác
ABC
. Phương trình mặt phẳng
P
là
A.
8 0
x y z
. B.
2 5 30 0
x y z
. C.
0
5 2 1
x y z
. D.
1
5 2 1
x y z
.
Câu 50. Cho điểm
(1; 2; 3)
A
. Gọi
1 2 3
A , A , A
lần lượt là hình chiếu vuông góc của
A
lên các mặt phẳng
(Oyz), ( ), (O )
Ozx xy
. Phương trình của mặt phẳng
1 2 3
( )
A A A
là:
A.
1
3 6 9
x y z
. B.
1
2 4 6
x y z
. C.
1
1 2 3
x y z
. D.
0
1 2 3
x y z
.
Câu 51. Cho điểm
' 4; 7; 5 , 3; 9; 10
M N
và các đường thẳng
1 2 3
, ,
d d d
cùng đi qua điểm
N
và
lần lượt song song với
, ,
Ox Oy Oz
. Mặt phẳng
'
P
đi qua
'
M
cắt
1 2 3
, ,
d d d
lần lượt tại
', ', '
A B C
sao
cho
'
M
là trực tâm
' ' '
A B C
. Phương trình mặt phẳng
'
P
là
A.
2 5 35 0
x y z
. B.
2 5 35 0
x y z
. C.
0
4 7 5
x y z
. D.
1
4 7 5
x y z
.
Câu 52. Cho điiểm
(3; 1;1)
A
. Tính khoảng cách từ
A
đến mặt phẳng
Oxy
.
A.
1.
B.
3.
C.
0.
D.
2.
Câu 53. Cho mặt phẳng
:16 12 15 4 0
P x y z
và điểm
2 ; 1; 1
A
. Gọi
H
là hình chiếu của
điểm
A
lên mặt phẳng
P
. Tính độ dài đoạn thẳng
AH
.
A.
5
. B.
11
5
. C.
11
25
. D.
22
5
.
Câu 54. Cho điểm
1;2;3
M
gọi
, ,
A B C
lần lượt là hình chiếu vuông góc của điểm
M
lên các trục
, ,
Ox Oy Oz
. Khi đó khoảng cách từ điểm
0;0;0
O
đến mặt phẳng
ABC
có giá trị bằng
A.
1
2
. B.
6
. C.
6
7
. D.
1
14
.
Câu 55. Cho tứ diện
ABCD
với
1;2;3 , 3;0;0 , 0; 3;0 , 0;0;6 .
A B C D Tính độ dài đường cao hạ
từ đỉnh
A
của tứ diện
ABCD
.
A.
9
. B.
1
. C.
6
. D.
3
.
Câu 56. Cho hai mặt phẳng
: 5 5 5 1 0
P x y z
và
: 1 0
Q x y z
. Khoảng cách giữa hai mặt
phẳng
P
và
Q
bằng
A.
2 3
15
. B.
2
5
. C.
2
15
. D.
2 3
5
.
Câu 57. Cho
1;0;0
A
,
0; ;0
B b
,
0;0;
C c
,
0, 0
b c
và mặt phẳng
: 1 0
P y z
. Tính
S b c
biết mặt phẳng
ABC
vuông góc với mặt phẳng
P
và khoảng cách từ
O
đến
ABC
bằng
1
3
.
A.
1
S
. B.
2
S . C.
0
S
. D.
3
2
S
.
Câu 58. Xác định tọa độ điểm
M
là hình chiếu vuông góc của điểm
2;3;1
M
lên mặt phẳng
: 2 0
x y z
A.
5
2; ;3
2
M
. B.
1;3;5
M
. C.
5 3
;2;
2 2
M
. D.
3;1;2
M
.
Câu 59. Trong không gian Oxyz, cho điểm
3; 2;5
A
và mặt phẳng
: 2x 3 5z 13 0
P y
. Tìm tọa
độ điểm A’ đối xứng với điểm A qua mặt phẳng (P).
A.
' 1;8; 5
A
B.
' 2; 4;3
A
C.
' 7;6; 4
A
D.
' 0;1; 3
A
Câu 60. Trong không gian , cho . Trực tâm tam giác có tọa độ
là
A. B. C. D.
Câu 61. Cho
0;1;2
A
,
0;1;0
B
,
3;1;1
C
và mặt phẳng
: 5 0
Q x y z
. Xét điểm
M
thay đổi
thuộc
Q
. Giá trị nhỏ nhất của biểu thức
2 2 2
MA MB MC
bằng
A.
12
. B.
0
. C.
8
. D.
10
.
Câu 62. Cho mặt phẳng
: 4 0
x y z
và ba điểm
1;2;1
A ,
0;1;2
B và
0;0;3
C . Điểm
; ;
M x y z
thuộc
sao cho
3 4
MA MB MC

đạt giá trị nhỏ nhất. Tính giá trị biểu thức
P x y z
.
A.
3
. B.
1
3
. C.
5
3
. D.
4
.
Câu 63. Cho hai điểm
2; 2;4 , 3;3; 1
A B
và mặt phẳng
: 2 2 8 0
P x y z
. Xét
M
là điểm
thay đổi thuộc
P
, giá trị nhỏ nhất của
2 2
2 3
MA MB
bằng:
A.
135
. B.
105
. C.
108
. D.
145
.
Câu 64. Cho tứ diện có điểm , , , . Trên các cạnh ,
, lần lượt lấy các điểm , , thỏa: . Viết phương trình mặt phẳng
biết tứ diện có thể tích nhỏ nhất.
A. . B. .
C. . D. .
Oxyz
1;0;0 , 0;2;0 , 0;0;1
A B C
ABC
4 2 4
; ; .
9 9 9
2;1;2 .
4;2;4 .
4 2 4
; ; .
9 9 9
ABCD
1;1;1
A
2;0;2
B
1; 1;0
C
0;3;4
D
AB
AC
AD
B
C
D
4
AB AC AD
AB AC AD
B C D
AB C D
16 40 44 39 0
x y z
16 40 44 39 0
x y z
16 40 44 39 0
x y z
16 40 44 39 0
x y z
Câu 65. Trong không gian với hệ tọa độ
Ox
yz
, cho mặt phẳng
: 2 0
P x y z
và hai điểm
3;4;1 ; 7; 4; 3
A B
. Điểm
; ; 2
M a b c a
thuộc
P
sao cho tam giác
ABM
vuông tại
M
và có
diện tích nhỏ nhất. Khi đó giá trị biểu thức
T a b c
bằng:
A.
6
T
. B.
8
T
. C.
4
T
. D.
0
T
.
Câu 66. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;0;0), B(0;m;0),C(0;0;n) với m,n là các số
thực dương thoả mãn
2 2
3 4
mn m n
. Mặt phẳng qua A vuông góc với OA cắt đường thẳng qua O
vuông góc với mặt phẳng ( ABC) tại điểm H. Tính OH ?
A.
5
4
B.
4
5
C.
3
4
D.
4
3
Vấn đề 3. Phương trình mặt cầu
Câu 67. Cho tam giác
ABC
. Tập hợp các điểm
M
trong không gian thỏa mãn hệ thức
0
MA MB MC a a
là
A.Mặt cầu bán kính
.
3
a
R
B. Đường tròn bán kính
3
a
R
C. Mặt cầu bán kính
.
R a
D. Đoạn thẳng có độ dài bằng
.
a
Câu 68. Cho hai điểm
2;1;0
A
,
2; 1;2
B
. Phương trình của mặt cầu có đường kính
AB
là
A.
2
2 2
1 24
x y z . B.
2
2 2
1 6
x y z .
C.
2
2 2
1 24
x y z
. D.
2
2 2
1 6
x y z
.
Câu 69. Phương trình mặt cầu tâm
1;2;0
I
và đi qua điểm
2; 2;0
A
là
A.
2 2
2
1 2 100.
x y z B.
2 2
2
1 2 5.
x y z
C.
2 2
2
1 2 10.
x y z D.
2 2
2
1 2 25.
x y z
Câu 70. Gọi
S
là mặt cầu đi qua
4
điểm
2;0;0
A ,
1;3;0
B ,
1;0;3
C ,
1;2;3
D . Tính bán kính
R
của
S
A.
2 2
R . B.
3
R
. C.
6
R
. D.
6
R
.
Câu 71. Cho mặt cầu
2 2 2
: 2 4 6 0
S x y z x y z
cắt các trục
, ,
Ox Oy Oz
lần lượt tại các điểm
, ,
A B C
(
khác
)
O
. Phương trình mặt phẳng
ABC
là
A.
1
2 4 6
x y z
. B.
1
2 4 6
x y z
. C.
0
2 4 6
x y z
. D.
1
2 4 6
x y z
.
Câu 72. Cho điểm
1;2;3
I
và mp
: 4 1 0
P x y z
. Viết ptrình mặt cầu tâm
I
và tiếp xúc với
P
.
A.
2 2 2
( 1) ( 2) ( 3) 2
x y z
. B.
2 2 2
( 1) ( 2) ( 3) 2
x y z .
C.
2 2 2
( 1) ( 2) ( 3) 2
x y z
. D.
2 2 2
( 1) ( 2) ( 3) 1
x y z
.
Câu 73. Cho mặt cầu
S
:
2 2
2 2
3 2 4
x y z m
. Tập các giá trị của
m
để mặt cầu
S
tiếp
xúc với mặt phẳng
Oyz
là:
A.
5
. B.
5
. C.
0
. D.
.
Câu 74. Cho mặt cầu
2 2 2
( ) : 2 6 8 1 0
S x y z x y z
. Xác định bán kính R của mặt cầu
( )
S
và
viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu tại
1;1;1
M
?
A.
5
R
,
( ) : 4 3 7 0
P y z
B.
5
R
,
( ) : 4 3 7 0
P x z
C.
5
R
,
( ) : 4 3 7 0
P y z
D.
3
R
,
( ) : 4 3 7 0
P x y
Câu 75. Cho mặt cầu
S
tâm
1;2;3
I bán kính
3
R
và hai điểm
2;0;0
M ,
0;1;0
N .
: 0
X x by cz d
là mặt phẳng qua MN và cắt
S
theo giao tuyến là đường tròn có bán kính r lớn
nhất. Tính
T b c d
.
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 76. Cho mặt cầu
2
2 2
: 2 1
S x y z
và mặt phẳng
:3 4 12 0
x z
. Khẳng định nào sau
đúng?
A. Mặt phẳng
đi qua tâm mặt cầu
S
.
B. Mặt phẳng
tiếp xúc mặt cầu
S
.
C. Mặt phẳng
cắt mặt cầu
S
theo một đường tròn.
D. Mặt phẳng
không cắt mặt cầu
S
.
Câu 77. Tìm tất cả các giá trị của m để phương trình
2 2 2
2 4 2 6 0
x y z mx y z m
là phương
trình của một mặt cầu trong không gian với hệ tọa độ Oxzy.
A.
1;5
m
B.
C.
5; 1
m
D.
; 5 1;m
 
Câu 78. Cho mặt cầu
2 2 2
: 1 2 3 25.
S x y z Mặt phẳng
Oxy
cắt mặt cầu
S
theo một
thiết diện là đường tròn
.
C
Diện tích của đường tròn
C
là
A.
8
B.
12
C.
16
D.
4
Câu 79. Cho
1;1;1
I và mặt phẳng
: 2 2 4 0
P x y z
. Mặt cầu
S
tâm
I
cắt
P
theo một
đường tròn bán kính
4
r
. Phương trình của
S
là
A.
2 2 2
1 1 1 16
x y z
. B.
2 2 2
1 1 1 5
x y z
.
C.
2 2 2
1 1 1 9
x y z
. D.
2 2 2
1 1 1 25
x y z
.
Câu 80. Cho mặt phẳng
: 2 5 0
Q x y z
và mặt cầu
2 2
2
: 1 2 15.
S x y z
P
song
song với
Q
và cắt mặt cầu
S
theo giao tuyến là đường tròn có chu vi
6
đi qua điểm nào sau đây?
m ;1 5;
 
A.
0; 1; 5
A
B.
1; 2; 0
B
C.
2; 2; 1
C
D.
2; 2; 1
D
Câu 81. Cho mặt cầu
2 2 2
: 6 4 2 5 0
S x y z x y z
. Phương trình mặt phẳng
Q
chứa trục
Ox
và cắt
S
theo giao tuyến là một đường tròn bán kính bằng
2
là
A.
: 2 0
Q y z
. B.
: 2 0
Q x z
. C.
: 2 0
Q y z
. D.
: 2 0
Q y z
.
Câu 82. Cho hai mặt phẳng song song
1
: 2 2 1 0
x y z
,
2
: 2 2 5 0
x y z
và một điểm
1;1;1
A
nằm trong khoảng giữa của hai mặt phẳng đó. Gọi
S
là mặt cầu đi qua A và tiếp xúc với
1 2
,
. Biết rằng khi
S
thay đổi thì tâm I của nó nằm trên một đường tròn cố định
. Tính diện
tích hình tròn giới hạn bởi
.
A.
2
3
. B.
4
9
. C.
8
9
. D.
16
9
.
Câu 83. Cho
2;0;0 , 0;2;0 , 0;0;2
A B C
. Có tất cả bao nhiêu điểm
M
trong không gian thỏa mãn
M
không trùng với các điểm
, ,
A B C
và
90
AMB BMC CMA
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 84. Cho hình chóp .
S ABCD
với
1; 1;6
S
,
1;2;3
A
,
3;1;2
B
,
4;2;3
C
,
2;3;4
D
. Gọi
I
là tâm mặt cầu
S
ngoại tiếp hình chóp. Tính khoảng cách
d
từ
I
đến mặt phẳng
SAD
.
A.
3 3
2
d
. B.
6
2
d
. C.
21
2
d
. D.
3
2
d
.
Câu 85. Cho mặt cầu
2 2 2
: 2 2 2 0
S x y z x y z
và điểm
2;2;0
A . Viết phương trình mặt
phẳng
OAB
, biết rằng điểm
B
thuộc mặt cầu
S
, có hoành độ dương và tam giác
OAB
đều.
A.
0
x y z
. B.
0
x y z
. C.
2 0
x y z
. D.
2 0
x y z
.
Câu 86. Cho hai điểm
3;1; 3
A
,
0; 2;3
B
và mặt cầu
2 2
2
: 1 3 1
S x y z
. Xét điểm
M
thay đổi thuộc mặt cầu
S
, giá trị lớn nhất của
2 2
2
MA MB
bằng
A.
102
. B.
78
. C.
84
. D.
52
.
Câu 87. Cho mặt phẳng
: 2 2 3 0
P x y z
và mặt cầu
S
tâm
5; 3;5
I , bán kính
2 5
R
. Từ
một điểm
A
thuộc
P
kẻ một đường thẳng tiếp xúc với mặt cầu
S
tại
B
. Tính
OA
biết
4
AB
.
A.
11
OA . B.
5
OA
. C.
3
OA
. D.
6
OA
.
Câu 88. Cho mặt phẳng
P
có phương trình
2
x y z
và mặt cầu
S
có phương trình
2 2 2
2
x y z
. Gọi điểm
; ;
M a b c
thuộc giao tuyến giữa
P
và
S
. Khẳng định nào sau đây là
khẳng định đúng?
A.
min 1;1
c . B.
min 1;2
b . C.
max min
a b
. D.
max 2; 2
c
.
Câu 89. Cho mặt cầu
1
S
có tâm
1
3;2;2
I
bán kính
1
2
R
, mặt cầu
2
S
có tâm
2
1;0;1
I
bán kính
2
1
R . Phương trình mặt phẳng
P
đồng thời tiếp xúc với
1
S
và
2
S
và cắt đoạn
1 2
I I
có dạng
2 0
x by cz d
. Tính
T b c d
.
A.
5
. B.
1
. C.
3
. D.
2
.
Câu 90. Cho mặt cầu
2 2
2
: 1 1 1
S x y z
và đường thẳng
2
: .
x t
d y t
z t
Hai m phẳng
,
P Q
chứa
d
tiếp xúc với mặt cầu tại
T
và
T
. Điểm
; ;
H a b c
là trung điểm đoạn
TT
, giá trị
T a b c
là
A.
0
. B.
1
3
. C.
2
3
. D.
1
.
Vấn đề 4. Phương trình đường thẳng trong hệ tọa độ
Oxyz
.
Câu 91. Trong không gian với hệ trục Oxyz, cho hai điểm
7; 2;1
A
và
5; 4; 3
B
,
mặt phẳng (P):
3 2 6 3 0
x y z
. Chọn đáp án đúng?
A. AB không đi qua điểm
1, 1, 1
B. AB vuông góc với mặt phẳng:
6 3 2 10 0
x y z
C. AB song song với đthẳng
1 12
1 6
1 4
x t
y t
z t
D. AB vuông góc với đường thẳng
5
1 2
3
x
y t
z t
Câu 92. Điểm nào dưới đây thuộc đường thẳng
1 1 2
2 1 3
x y z
?
A.
2;1; 3
Q
. B.
2; 1;3
P
. C.
1;1; 2
M
. D.
1; 1;2
N
.
Câu 93. đường thẳng
1 2
: 2 3 ,
3
x t
d y t t
z t
không đi qua điểm nào dưới đây?
A.
(1;2;3)
Q . B.
(3; 1;2)
M
. C.
(2; 2;3)
P
. D.
( 1;5;4)
N
.
Câu 94. Cho mặt phẳng
: 2 3 0
x y z
và đường thẳng
3 1 4
:
4 1 2
x y z
d
. Mmệnh đề nào
đúng?
A.
d
song song với
. B.
d
vuông góc với
. C.
d
nằm trên
. D.
d
cắt
Câu 95. Trong không gian hệ tọa độ Oxyz, hai đường thẳng
1
1 1
:
2 3 1
x y z
d
;
2
1 2 7
:
1 2 3
x y z
d
có vị trí tương đối là:
A. song song B. trùng nhau C. cắt nhau D. chéo nhau
Câu 96. Cho ba điểm
3; 1;2 , 4; 1; 1 , 2;0;2
A B C
và đường thẳng . Gọi M
là giao điểm của và mp . Độ dài đoạn OM bằng
A. B. C. D.
Câu 97. Cho ba điểm
1;2;1
A ,
2; 1;4
B và
1;1; 4
C .Đường thẳng nào dưới đây vuông góc với mp
ABC
A.
1 1 2
x y z
. B.
2 1 1
x y z
. C.
1 1 2
x y z
. D.
2 1 1
x y z
.
Câu 98. Viết phương trình tham số của đường thẳng đi qua hai điểm
1; 2; 3 , 2; 3;1
A B
.
A.
1
2 5
3 2
x t
y t
z t
. B.
2
3 5
1 4
x t
y t
z t
. C.
3
8 5
5 4
x t
y t
z t
. D.
1
2 5
3 4
x t
y t
z t
.
Câu 99. Viết phương trình tham số của đường thẳng (D) qua
1;5; 2
I
và song song với trục Ox.
A.
1
5 ;
2
x t
y t
z
B.
5 ;
2
x m
y m m
z m
C.
2
10 ;
4
x t
y t t
z t
D. Hai câu A và C đều
đúng
Câu 100. Phương trình chính tắc của đường thẳng
d
đi qua điểm
(1; 2;5)
M
và vuông góc với mặt
phẳng
( ) : 4 3 2 5 0
x y z
là
A.
1 2 5
4 3 2
x y z
. B.
1 2 5
4 3 2
x y z
.
C.
1 2 5
4 3 2
x y z
. D.
1 2 5
4 3 2
x y z
.
Câu 101. Cho đường thẳng
1 1 2
:
2 1 3
x y z
d
và mặt phẳng
:
P
1 0
x y z
. Viết phương
trình đường thẳng đi qua
(1;1; 2)
A
, song song với mặt phẳng
( )
P
và vuông góc với đường thẳng
d
.
A.
1 1 2
:
2 5 3
x y z
B.
1 1 2
:
2 5 3
x y z
C.
1 1 2
:
2 5 3
x y z
D.
1 1 2
:
2 5 3
x y z
Câu 102. Gọi
d
là giao tuyến của hai mặt phẳng
: 2 3 7 0
x y z
và
: 2 2 0
x y z
.
Đường thẳng
d
đi qua điểm nào dưới đây?
A.
(2; 1;3)
Q
. B.
(1;0; 3)
M
. C.
( 1;0;3)
P
. D.
(1; 2;1)
N
.
2 3
:
1 3 1
x y z
d
d
ABC
2 2
3
6
3
Câu 103. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
2 1 1
:
1 1 2
x y z
d
và điểm
2;1;0
A
. Viết phương trình mặt phẳng (P) đi qua A và chứa d?
A.
7 4 9 0
x y z
B.
7 4 8 0
x y z
C.
6 4 9 0
x y z
D.
4 3 0
x y z
Câu 104. Trong không gian Oxyz, cho điểm
3; 2; 3
A
và hai đường thẳng
1
1 2 3
:
1 1 1
x y z
d
và
2
3 1 5
:
1 2 3
x y z
d
. Phương trình mặt phẳng chứa d
1
và d
2
có dạng:
A.
5 4 16 0
x y z
B.
5 4 16 0
x y z
C.
5 4 16 0
x y z
D.
5 4 16 0
x y z
Câu 105. Cho hai đường thẳng
1 2
3 2 3
: 1 ; : 2 2
2 1 4
x t x m
d y t d y m
z t z m
. Phương trình tổng quát của mặt
phẳng (P) chứa
1
d
và song song với
2
d
là:
A.
7 5 20 0
x y z
B.
2 9 5 5 0
x y z
C.
7 5 0
x y z
D.
7 5 20 0
x y z
Câu 106. Cho đường thẳng ∆ có phương trình
1 1
2 1 1
x y z
và mặt phẳng (P):
2 2 1 0
x y z
.
Phương trình mặt phẳng (Q) chứa ∆ và tạo với (P) một góc nhỏ nhất là:
A.
2 2 1 0
x y z
B.
10 7 13 3 0
x y z
C.
2 0
x y z
D.
6 4 5 0
x y z
Câu 107. Cho mặt cầu
2 2 2
( ): ( 1) ( 2) ( 3) 9
S x y z
và đường thẳng
6 2 2
:
3 2 2
x y z
.
Phương trình mặt phẳng (P) đi qua M(4;3;4), song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) là:
A.
2 2 19 0
x y z
B.
2 2 1 0
x y z
C.
2 2 18 0
x y z
D.
2 2 10 0
x y z
Câu 108. Cho đường thẳng . Gọi là hình chiếu vuông góc của trên mặt
phẳng tọa độ . Viết phương trình đường thẳng .
A. . B. . C. . D.
Câu 109. Cho đường thẳng . Phương trình nào dưới đây là phương trình hình
chiếu vuông góc của lên mặt phẳng .
A. . B. . C. . D. .
2
: 3 2
1 3
x t
d y t t
z t
d
d
Oxz
d
2
0
1 3
x t
y t
z t
2
3 2
1 3
x t
y t t
z t
0
3 2
1 3
x
y t t
z t
2
3 2
0
x t
y t t
z
1 5 3
:
2 1 4
x y z
d
d
: 5 0
P x
5
7
11 4
x
y t
z t
5
7
11 4
x
y t
z t
1
5 2
3
x
y t
z t
1
5
3 4
x
y t
z t
Câu 110. Phương trình đường thẳng
d
là hình chiếu vuông góc của đường thẳng
d
trên mặt phẳng
P
, biết
12 4
: 9 3
1
x t
d y t
z t
và
:3 5 2 0
P x y z
. Đường thẳng
d
là giao tuyến của hai mphẳng
nào?
A.
3 5 2 0
x y z
và
8 7 11 22 0
x y z
. B.
3 5 2 0
x y z
và
4 7 22 0
x y z
.
C.
3 5 2 0
x y z
và
11 22 0
x y z
. D.
3 5 2 0
x y z
và
8 3 2 0
x y z
.
Câu 111. Cho mặt phẳng và đường thẳng . Đường thẳng
đối xứng với qua mặt phẳng có phương trình là
A. . B. .C. .D. .
Câu 112. Trong không gian với hệ tọa độ , cho điểm và mặt phẳng
. Đường thẳng đi qua và có vectơ chỉ phương cắt tại
điểm . Điểm thay đổi trong sao cho luôn nhìn đoạn dưới góc . Khi độ dài
lớn nhất, đường thẳng đi qua điểm nào trong các điểm sau?
A. . B. . C. . D. .
Câu 113. Viết phương trình đường thẳng đi qua , vuông góc và cắt đường thẳng
.
A. . B. .C. . D. .
Câu 114. Cho mặt phẳng và đường thẳng Viết phương
trình đường thẳng nằm trong mặt phẳng đồng thời cắt và vuông góc với đường thẳng
A. B. C. D.
Câu 115. Cho 2 đường thẳng ; và mp
. Đường thẳng vuông góc với , cắt và lần lượt tại . Độ dài đoạn
là
A. . B. . C. . D. .
Câu 116. Cho đường thẳng
1
d
có vectơ chỉ phương
(1;0; 2)
u
và đi qua điểm
2
3 1 4
(1; 3;2), d : .
1 2 3
x y z
M
Phương trình mặt phẳng
( )
P
cách đều hai đường thẳng
1
d
và
2
d
có
dạng
ax 11 0.
by cz
Giá trị
a 2 3
b c
bằng
: 3 0
P x y z
1 2
:
1 2 1
x y z
d
'
d
d
P
1 1 1
1 2 7
x y z
1 1 1
1 2 7
x y z
1 1 1
1 2 7
x y z
1 1 1
1 2 7
x y z
Oxyz
1; 2; 3
A
: 2 2 9 0
P x y z
d
A
3; 4; 4
u
P
B
M
P
M
AB
0
90
MB
MB
2; 19;3
3;0;15
18; 2;41
3;20;7
1; 1;1
A
4 2 5
:
1 1 1
x y z
d
1 1 1
5 1 8
x y z
1 1 1
1 5 4
x y z
1 1 1
5 5 4
x y z
1 1 1
5 1 8
x y z
: 2 4 0
P x y z
1 2
: .
2 1 3
x y z
d
P
.
d
1 1 1
5 1 3
x y z
1 1 1
5 1 3
x y z
1 1 1
5 1 2
x y z
1 1 1
5 1 3
x y z
1
3 3 2
:
1 2 1
x y z
d
2
5 1 2
:
3 2 1
x y z
d
: 2 3 5 0
P x y z
P
1
d
2
d
,
A B
AB
2 3
14
5
15
A.
42
. B.
32
. C.
11
. D.
20
.
Câu 117. Cho điểm , đường thẳng và mặt phẳng
. Điểm
thuộc thỏa mãn đường thẳng
vừa cắt vừa vuông góc với .
Tọa độ điểm là:
A. . B. . C. . D. .
Câu 118. Cho đường thẳng và mặt phẳng lần lượt có phương trình và
2 8 0
x y z
, điểm
(2; 1; 3)
A
. Phương trình đường thẳng
cắt
d
và
( )
P
lần lượt tại
M
và
N
sao cho
A
là trung điểm của đoạn thẳng
MN
là
A. . B. .
C. . D. .
Câu 119. Cho mặt phẳng và hai điểm , . Viết phương
trình đường thẳng đi qua và song song với sao cho khoảng cách từ đến đường thẳng đó là
nhỏ nhất.
A. . B. . C. . D. .
Câu 120. Trong không gian Oxyz cho 2 điểm
1;3;0
A
và
2;1;1
B
và đường thẳng
1 1
:
2 1 2
x y z
. Viết phương trình mặt cầu đi qua A, B có tâm I thuộc đường thẳng
?
A.
2 2 2
2 13 3 521
5 10 5 100
x y z
B.
2 2 2
2 13 3 25
5 10 5 3
x y z
C.
2 2 2
2 13 3 521
5 10 5 100
x y z
D.
2 2 2
2 13 3 25
5 10 5 3
x y z
Câu 121. Trong mặt phẳng Oxyz, cho đường thẳng
: 1
x t
d y
z t
và 2 mặt phẳng (P) và (Q) lần lượt có
phương trình
2 2 3 0
x y z
;
2 2 7 0
x y z
. Mặt cầu (S) có tâm I thuộc đường thẳng (d), tiếp
xúc với hai mặt phẳng (P) và (Q) có phương trình
A.
2 2 2
4
3 1 3
9
x y z
B.
2 2 2
4
3 1 3
9
x y z
C.
2 2 2
4
3 1 3
9
x y z
D.
2 2 2
4
3 1 3
9
x y z
1;2; 1
A
1 1 2
:
2 1 1
x y z
d
: 2 1 0
P x y z
B
P
AB
d
B
6; 7;0
3; 2; 1
3;8; 3
0;3; 2
d
P
1 2
2 1 1
x y z
1 5 5
3 4 2
x y z
2 1 3
6 1 2
x y z
5 3 5
6 1 2
x y z
5 3 5
3 4 2
x y z
: 2 2 5 0
P x y z
3;0;1
A
0; 1;3
B
d
A
P
B
3 2
1
x t
y t
z
3 2
1
x t
y t
z
3 2
1
x t
y t
z
3 2
1
x t
y t
z
Câu 122. Trong không gian Oxyz, cho điểm
1;3; 2
I
và đường thẳng
4 4 3
:
1 2 1
x y z
.
Phương trình mặt cầu (S) có tâm là điểm I và cắt
tại hai điểm phân biệt A, B sao cho đoạn thẳng AB có
độ dài bằng 4 là:
A.
2 2
2
: 1 3 9
S x y z
B.
2 2 2
: 1 3 2 9
S x y z
C.
2 2 2
: 1 3 2 9
S x y z
D.
2 2 2
: 1 3 2 9
S x y z
Câu 123. Cho , mp và mặt cầu .
Gọi là đt đi qua , nằm trong và cắt tại hai điểm có khoảng cách lớn nhất. Phương trình của
là
A. . B. . C. . D. .
Câu 124. Cho mặt cầu
2 2 2
: 2 4 6 3 0
S x y z x y z m
. Tìm
m
để
1
: 1
2
x t
d y t
z
cắt
S
tại
hai điểm phân biệt
A.
31
2
m
. B.
31
2
m
. C.
31
2
m
. D.
31
2
m
.
Câu 125. Góc giữa hai đường thẳng
1
1 1
:
1 1 2
x y z
d
và
2
1 3
:
1 1 1
x y z
d
bằng:
A. 45
o
B. 90
o
C. 60
o
D. 30
o
Câu 126. Góc giữa đường thẳng
5
: 6
2
x t
d y
z t
và mp
: 1 0
P y z
là:
A.30
0
B.60
0
C.90
0
D.45
0
Câu 127. Trong không gian với hệ tọa độ Oxyz cho
3;0;1 , 6; 2;1
A B
. Viết phương trình mặt phẳng
(P) đi qua A, B và (P) tạo với
mp Oyz
góc
thỏa mãn
2
cos
7
?
A.
2 3 6 12 0
2 3 6 0
x y z
x y z
B.
2 3 6 12 0
2 3 6 1 0
x y z
x y z
C.
2 3 6 12 0
2 3 6 0
x y z
x y z
D.
2 3 6 12 0
2 3 6 1 0
x y z
x y z
Câu 128. Cho điểm A(1;1;1) và hai đường thẳng
1
2 2
: 1
2
x t
d y
z t
;
2
5 3
: 1
3
x s
d y
z s
.
Gọi B,C là các điểm lần lượt di động trên
1 2
;
d d
. Giá trị nhỏ nhất của biểu thức P =AB +BC +CA là:
0; 1; 5
E
: 2 2 3 0
P x y z
2 2
2
: 4 1 25
S x y z
E
P
S
11
1 2
5 26
x t
y t
z t
50
1 23
5 7
x t
y t
z t
11
1 2
5 26
x t
y t
z t
50
1 23
5 7
x t
y t
z t
A.
2 29
B.
2 985
C.
5 10 29
D.
5 10
Câu 129. Cho điểm và mặt cầu Gọi là đường tròn
giao tuyến của với ; điểm và di chuyển trên sao cho . Khi tứ diện
có thể tích lớn nhất thì đường thẳng có phương trình là
A. . B. . C. . D. .
Câu 130. Cho điểm , mp và mặt cầu
. Gọi là đường thẳng đi qua , nằm trong và cắt tại
hai điểm có khoảng cách nhỏ nhất. Biết có một vec-tơ chỉ phương . Tính
A. . B. . C. . D. .
Câu 131. Cho điểm , mặt phẳng và mặt cầu
Gọi là đường thẳng đi qua nằm trong mặt phẳng và cắt mặt
cầu tại hai điểm sao cho tam giác có diện tích lớn nhất với là tâm của mặt cầu .
Phương trình của là
A. . B. . C. . D. .
Câu 132. Cho điểm và mặt cầu Đường thẳng thay đổi, đi qua
điểm cắt mặt cầu tại hai điểm phân biệt Tính diện tích lớn nhất của tam giác
A. . B. . C. . D. .
Câu 133. Cho điểm , và mặt cầu . Gọi
là mặt phẳng đi qua và cắt theo một thiết diện là đường tròn . Đường thẳng cắt
tại hai điểm . Điểm thuộc đường tròn sao cho tam giác cân tại , là đường cao
ứng với cạnh . Khi thiết diện có diện tích nhỏ nhất thì phương trình của là
A. . B. . C. . D. .
0;1;9
A
2 2 2
: 3 4 4 25.
S x y z
C
S
mp Oxy
B
C
C
2 5
BC
OABC
BC
21
4
5
28
3
5
0
x t
y t
z
21 4
28 3
0
x t
y t
z
21
3
5
28
4
5
0
x t
y t
z
21
4
5
28
3
5
0
x t
y t
z
2;1;3
E
: 2 2 3 0
P x y z
2 2 2
: 3 2 5 36
S x y z
E
P
S
0 0
2018; ;
u y z
0 0
.
T z y
0
T
2018
T
2018
T
1009
T
0;1; 2
A
: 1 0
P x y z
2 2 2
: 2 4 7 0.
S x y z x y
A
P
S
,
B C
IB C
I
S
: 1
2
x t
y
z t
: 1
2
x t
y t
z
: 1
2
x t
y t
z
: 1
2
x t
y
z t
1 3
; ;0
2 2
M
2 2 2
: 8.
S x y z
d
,
M
S
, .
A B
S
.
OAB
7
S
4
S
2 7
S
2 2
S
1;1;1
A
2;2;2
B
2 2 2
: 2 2 4 10 0
S x y z x y z
P
,
A B
S
C
AB
C
,
E F
C
C
CEF
C
CH
EF
CH
1
: 1
1
x t
y
z t
1
: 1
1
x t
y t
z
1
: 1
0
x t
y t
z
1
: 1
2
x t
y
z t
Câu 134. Cho đường thẳng
1 2
:
1 2 1
x y z
d
. Gọi
P
là mặt phẳng chứa đường thẳng
d
và tạo với
mặt phẳng
: 2 2 2 0
Q x y z
một góc có số đo nhỏ nhất. Điểm
1;2;3
A
cách
P
một khoảng
bằng:
A.
3
. B.
5 3
3
. C.
7 11
11
. D.
4 3
3
.
Câu 135. Cho đường thẳng và hai điểm , . Tìm điểm M thuộc
đường thẳng
d
sao cho
MA MB
nhỏ nhất.
A. . B. . C. . D. .
Câu 136. Cho hai đường thẳng và . Xét điểm thay đổi. Gọi
lần lượt là khoảng cách từ đến và . Biểu thức đạt nhỏ nhất khi và chỉ khi
. Khi đó bằng
A. . B. . C. . D. .
Câu 137. Cho ba điểm không thẳng hàng Hai mặt cầu có phương trình
và cắt nhau theo đường tròn
Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa và tiếp xúc với ba đường thẳng
A. vô số B. C. D. Không có
Câu 138. Cho mặt cầu và đường thẳng . Hai mặt phẳng
chứa , tiếp xúc với tại và . Điểm là trung điểm của đoạn , giá trị
của biểu thức là
A. . B. . C. . D. .
Câu 139. Cho mặt cầu và đường thẳng .
Điểm nằm trên đường thẳng sao cho từ kẻ được ba tiếp tuyến
đến mặt cầu ( là các tiếp điểm) và , , . Tính
A. . B. . C. . D. .
1 2
: 1
x t
d y t
z t
1;0; 1
A
2;1;1
B
1;1;0
M
3 1
; ;0
2 2
M
5 1 1
; ;
2 2 2
M
5 2 1
; ;
3 3 3
M
1
:
1 1 1
x y z
1
:
1 2 1
x y z
M
,
a b
M
2 2
2
a b
0 0 0 0
; ;
M M x y z
0 0
x y
2
3
0
4
3
2
3;0;0 , 0;3;0 ,
A B
0;0;3 .
C
2 2 2
1
: 2 4 6 9 0
S x y z x y z
2 2 2
2
: 8 4 8 0
S x y z x z
.
C
C
, , ?
AB BC CA
1
3
2 2
2
: 1 1 1
S x y z
2
:
x t
d y t
z t
,
P Q
d
S
T
'
T
; ;
H a b c
'
TT
T a b c
0
1
3
2
3
1
2 2 2
: 2 4 6 13 0
S x y z x y z
1 2 1
:
1 1 1
x y z
d
; ; , 0
M a b c a
d
M
, ,
MA MB MC
S
, ,
A B C
0
60
AMB
0
60
BMC
0
120
CMA
3 3 3
a b c
3 3 3
173
9
a b c
3 3 3
112
9
a b c
3 3 3
8
a b c
3 3 3
23
9
a b c
Vấn đề 5. Tọa độ hóa bài toán hình trong Không gian
Câu 140. Cho hình chóp có đáy là hình chữ nhật, và
vuông góc với đáy . Tính với là góc tạo bởi đường thẳng và mặt phẳng .
A. . B. . C. . D. .
Câu 141. . Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên vuông góc với đáy.
Gọi M là trung điểm cạnh SD. Tính của góc tạo bởi hai mặt phẳng (AMC) và (SBC).
A. . B. . C. . D. .
Câu 142. Cho hình chóp có đáy là hình vuông cạnh bằng , biết và
vuông góc với mặt đáy . Gọi là trung điểm của . Gọi là góc giữa đường thẳng
và mặt phẳng . Tính .
A. . B. . C. . D. .
Câu 143. Cho hình chóp có đáy là hình vuông cạnh , và vuông góc với
đáy. Gọi là trung điểm và là điểm thuộc cạnh sao cho . Tính thể tích khối tứ
diện .
A. . B. . C. . D. .
.
S ABCD
ABCD
,
AB a
3,
BC a
SA a
SA
ABCD
sin
BD
( )
SBC
2
sin
4
7
sin
8
3
sin
5
3
sin
2
2
SA a
cos
5
5
5
3
3
2
2
3
.
S ABCD
ABCD
a
SO a
SO
ABCD
,
M N
,
SA BC
MN
SBD
cos
2
7
21
7
5
10
2
5
.
S ABCD
ABCD
a
SA a
SA
M
SB
N
SD
2
SN ND
ACMN
3
1
12
V a
3
1
8
V a
3
1
6
V a
3
1
36
V a
| 1/66
| | Tải xuống

Có thể bạn quan tâm:

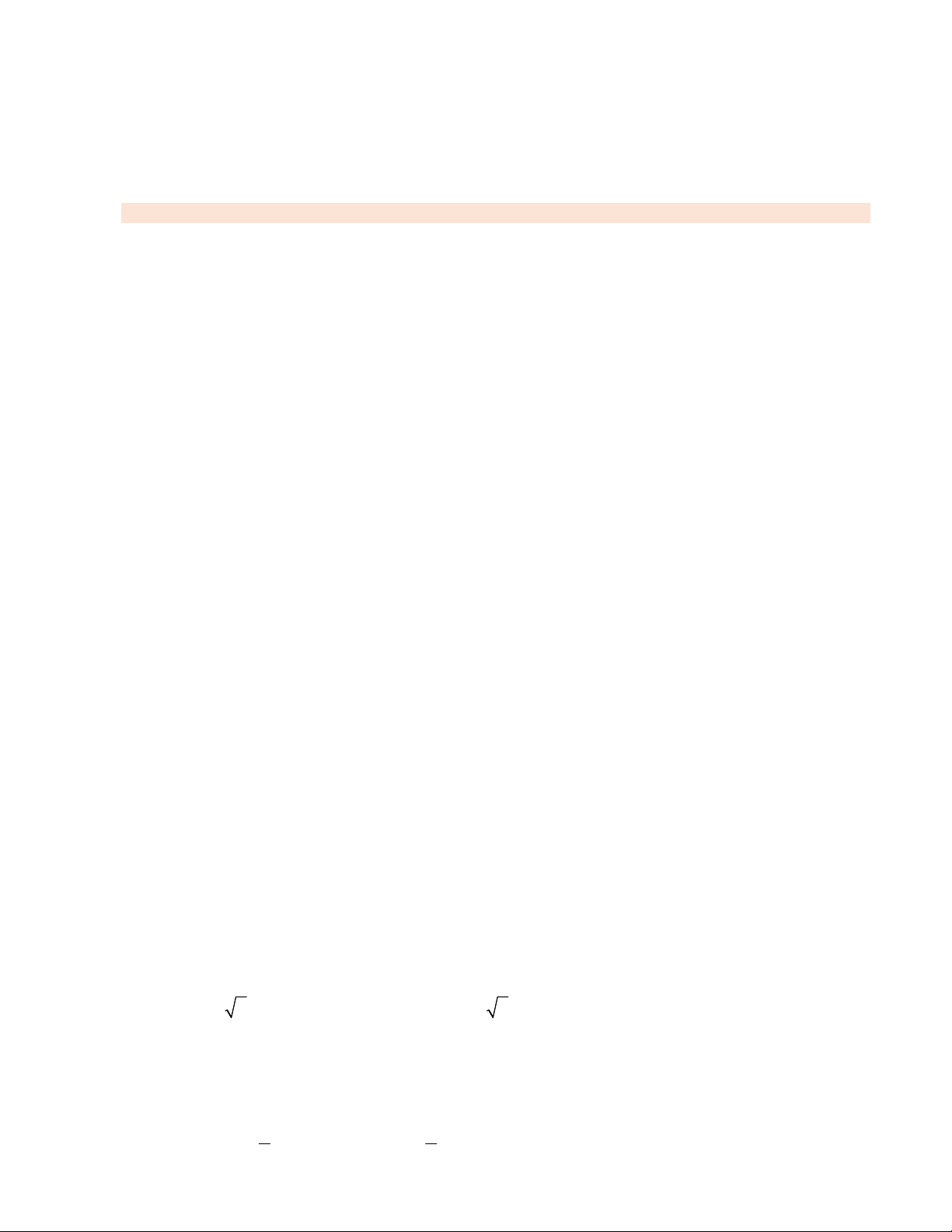
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ CƯƠNG ÔN TẬP HỌC KỲ 2 TRƯỜNG THPT YÊN HÒA NĂM HỌC 2020 – 2021 ------o0o----- MÔN: TOÁN PHẦN I. GIẢI TÍCH A. NGUYÊN HÀM.
Vấn đề 1. Các câu hỏi lý thuyết.
Câu 1.Giả sử hàm số F x là một nguyên hàm của hàm số f x trên K . Khẳng định nào sau đây đúng.
A. Chỉ có duy nhất một hằng số C sao cho hàm số y  F(x) C là một nguyên hàm của hàm f trên K.
B. Với mỗi nguyên hàm G của f trên K thì tồn tại một hằng số C sao cho G(x)  F(x) C với x thuộc K .
C. Chỉ có duy nhất hàm số y  F(x) là nguyên hàm của f trên K.
D. Với mỗi nguyên hàm G của f trên K thì G(x)  F(x) C với mọi x thuộc K và C bất kỳ.
Câu 2.Cho hàm số F(x) là một nguyên hàm của hàm số f (x) trên K . Các mệnh đề sau, mệnh đề nào sai.  A. f(x)dx F  (x) C.  B.  f(x)dx    f(x).   C.  f(x)dx    f (x).  f(x)dx   F (x). D.
Câu 3.Cho hai hàm số f (x), g(x) là hàm số liên tục, có F(x),G(x) lần lượt là nguyên hàm của f (x), g(x) . Xét các mệnh đề sau:
(I). F(x) G(x) là một nguyên hàm của f (x)  g(x).
(II). k.F(x) là một nguyên hàm của kf (x) với k   .
(III). F(x).G(x) là một nguyên hàm của f (x).g(x). Các mệnh đúng là A. (I). B. (I) và (II). C. Cả 3 mệnh đề. D. (II).
Câu 4.Trong các khẳng định sau, khẳng định nào sai.
A.  f(x) g(x )dx  f(x)dx  g(x)dx   .
B. Nếu F(x) và G(x) đều là nguyên hàm của hàm số f (x) thì F(x) G(x)  C là hằng số.
C. F(x)  x là một nguyên hàm của f(x)  2 x. D. 2
F(x)  x là một nguyên hàm của f(x)  2x.
Câu 5.Trong các khẳng định sau khẳng định nào đúng. 2 2  1          1  A. 2x 1 dx   2     x 1   dx           . x   x   2  1    1 B. 2  x 1   dx  2 2      x 1   dx .   x      x  2  1        1            1 C. 2x 1 dx 2x 1 dx. 2        x 1  dx . x   x      x  2  1   1 2 D. 2 2
 x 1   dx  4 x dx  dx  dx  4 xdx  dx  4 dx.       2  x  x   x  f ' x
Câu 6.Cho hàm số f x có đạo hàm liên tục trên khoảng 0;. Khi đó dx  bằng: x 1 A. f x C B. f  x C C. 2f  x C D. 2f  x C 2   Câu 7.Biết f
 xdx  3x cos2x 5C . Tìm khẳng định đúng trong các khẳng định sau. A. f
 3xdx  3x cos6x 5C B. f
 3xdx  9x cos6x 5C C. f
 3xdx  9x cos2x  5C D. f
 3xdx  3x cos2x 5C Câu 8.Biết f   x 2
2 dx  sin x  ln x . Tìm nguyên hàm f xdx  . x x A. f  x 2 dx  sin  ln x C . B. f  x 2 dx  2 sin  2 ln x C . 2 2 C. f  x 2
dx  2 sin x  2 ln x  ln 2 C . D. f  x 2
dx  2 sin 2x  2 ln x  ln 2 C .
Vấn đề 2. Nguyên hàm của hàm số đa thức.
Câu 9.Nguyên hàm của hàm số   4 2 f x  x  x là 1 1 A. 5 3 x  x C B. 4 2 x  x C C. 5 3 x  x C . D. 3 4x  2x C 5 3
Câu 10.Nguyên hàm của hàm số   3 2 f x  x  x là 1 1 A. 4 3 x  x C B. 2 3x  2x C C. 3 2 x  x C D. 4 3 x  x C 4 3 Câu 11.Tìm nguyên hàm x x   15 2 7 dx ? 1 1 1 1 A. x  716 2 C B.  x 716 2 C C. x  716 2 C D. x 716 2 C 2 32 16 32 Câu 12.Nếu f  x 3 2
dx  4x  x C thì hàm số f x bằng x A. f x 3 4  x  Cx . B. f x 2  12x  2x C . 3 x C. f x 2  12x  2x . D. f x 3 4  x  . 3
Câu 13.Nguyên hàm của hàm số 3 2 x  x ? 1 1 A. 2 3x  2x C . B. 4 3 x  x C . C. 4 3 x  x C . D. 4 3 4x  3x C . 4 3 1
Câu 14.Nguyên hàm của hàm số f (x)  3 2 x  2x  x  2019 là 3 2 1 2 x 2 1 2 x A. 4 3 x  x  C . B. 4 3 x  x   2019x C . 12 3 2 9 3 2 2 1 2 x 2 1 2 x C. 4 3 x  x   2019x C . D. 4 3 x  x   2019x C . 12 3 2 9 3 2
Câu 15.Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số 2019 y  x ? 2020 x 2020 x 2020 x A.  1. B. . C. 2018 y  2019x . D. 1. 2020 2020 2020
Câu 16.Tìm nguyên F x của hàm số f xx   1 x  2x  3? x 11 A. F x 4 3 2  6x  x 6x C . B. F x 4 3 2
x 6x 11x  6x C . 4 2 x 11 C. F x 4 3 2   2x  x 6x C . D. F x 3 2 2
x  6x 11x  6x C . 4 2
Câu 17.Họ các nguyên hàm của hàm số f x   x  5 2 3 là x  x  A. F x  6 2 3  C . B. F x  6 2 3  C . 12 6
C. F x   x  4 10 2 3 C .
D. F x   x  4 5 2 3 C .
Câu 18.Họ nguyên hàm của hàm số f x  x x  2019 3 2 1 là
x  2021 x  2020 2 2 1 1  2021 2020 1   2x    2 1 x  1 A.    . B.  . 2  2021 2020    2021 2020  
x  2021 x  2020 2 2 1 1
x  2021 x  2020 2 2 1 1  1  C.   C . D.     C . 2021 2020 2  2021 2020     
Câu 19.Biết rằng hàm số F x 3  mx   m n 2 3
x  4x  3 là một nguyên hàm của hàm số f x 2
 3x  10x  4 . Tính mn . A. mn  1. B. mn  2 . C. mn  0. D. mn  3.
Vấn đề 3. Nguyên hàm của hàm số hữu tỉ. 2
Câu 20.Tìm nguyên hàm của hàm số f x 2  x  . 2 x x x A. f  x 3 1 dx   C . B. f  x 3 2 dx   C . 3 x 3 x x x C. f  x 3 1 dx   C . D. f  x 3 2 dx   C . 3 x 3 x
Câu 21.Tìm nguyên hàm của hàm số f x 1  . 5x  2 dx 1 dx A.  ln 5x  2 C  B.  ln 5x  2 C 5x  2 5  5x  2 dx 1 dx C.   ln 5x  2 C  D.  5 ln 5x  2 C 5x  2 2  5x  2 x  2
Câu 22.Tìm nguyên hàm của hàm số f x 4  . 2 x x x A. f  x 3 1 dx   C . B. f  x 3 2 dx   C . 3 x 3 x x x C. f  x 3 1 dx   C . D. f  x 3 2 dx   C . 3 x 3 x  1
Câu 23.Tìm nguyên hàm của hàm số f x 1  trên   ; . 1  2x  2 1 1 1 A. ln 2x 1 C . B. ln 12xC .
C.  ln 2x  1 C . D. ln 2x 1 C . 2 2 2 4 2  3 Câu 24.Cho hàm số ( ) x f x 
. Khẳng định nào sau đây là đúng? 2 x 3 2x 3 3 2x 3 A. f(x)dx   C  . B. f(x)dx   C 3 2x  . 3 x 3 2x 3 C. f(x)dx   C  . D. 3 3 f(x)dx  2x  C 3 x  . x 3x  2
Câu 25.Họ tất cả các nguyên hàm của hàm số f x 
trên khoảng 2; là x 22 A. x   2 3 ln 2  C B. x   2 3 ln 2  C x  2 x  2 C. x   4 3 ln 2  C D. x   4 3 ln 2  C . x  2 x  2
Câu 26.Cho F x là một nguyên hàm của f x 1 
trên khoảng 1; thỏa mãn F e   1  4 x 1 Tìm F x. A. 2 ln x   1  2 B. ln x   1  3 C. 4 ln x   1 D. ln x   1  3 2x 13
Câu 27.Cho biết         .
 x  dx a ln x 1 b ln x 2 C x 1 2
Mệnh đề nào sau đây đúng? A. a  2b  8 . B. a b  8 . C. 2a b  8 . D. a b  8 . 1 Câu 28.Cho biết
dx  a ln x 1 x  1 b ln x C 
. Tính giá trị biểu thức: P  2a  b . 3    x  x 1 A. 0. B. -1. C. . D. 1. 2 4x  11 Câu 29.Cho biết
dx  a ln x  2 b ln x  3 C 
. Tính giá trị biểu thức: 2 x  5x  6 2 2 P  a ab b . A. 12. B. 13. C. 14. D. 15. 1
Câu 30.Tìm tất cả các họ nguyên hàm của hàm số f x  9 5 x  3x 1 1 x 1 1 x A. f  x 4 dx    ln C B. f  x 4 dx    ln C 4 4 3x 36 x  3 4 4 12x 36 x  3 1 1 x 1 1 x C. f  x 4 dx    ln C D. f  x 4 dx    ln C 4 4 3x 36 x  3 4 4 12x 36 x  3 x
Câu 31.Tìm hàm số F x biết F x 3  dx  và F 0  1. 4 x  1 1 3 A. F x   4 ln x  11. B. F x  ln 4 x  1 . 4 4 1 C. F x  ln 4 x  11. D. F x   4 4 ln x  11. 4   2017 1 1  1 b x x  Câu 32.Biết dx  .    C , x  1  với a , b 
  . Mệnh đề nào sau đây đúng?    x 2019 a x  1 1   A. a  2b . B. b  2a . C. a  2018b . D. b  2018a . x
Câu 33.Đổi biến t  x 1 thì dx  trở thành 4 (x 1) t 1 4 (t  1) t  1 t  1 A. dt.  B. dt. dt. dt. 4 t  C. t  D. 4 t  t 1 a  Câu 34.Cho 2 I  dx  
b ln x  2c ln 1  x C . Khi đó S  a b  c bằng 3 2   x  2 1  x  x 1  3 7 A. . B. . C. . D. 2. 4 4 4
Vấn đề 4. Nguyên hàm của hàm số chứa căn.
Câu 35.Tìm nguyên hàm của hàm số f x  2x 1. 2 1 A. f
 xdx  2x  1 2x 1 C. B. f
 xdx  2x  1 2x 1 C. 3 3 C. f  x 1 dx   2x 1 C. D. f  x 1 dx  2x 1 C. 3 2
Câu 36.Nguyên hàm của hàm số f x 1  có dạng: 2 2x 1 A. f  x 1 dx  2x  1 C . B. f
 xdx  2x 1 C . 2 1 C. f
 xdx  2 2x 1 C . D. f  xdx   C . 2x  1 2x 1
Câu 37.Nguyên hàm của hàm số f x 3  3x  1 là A. f
 x x   x  3 d 3 1 3x  1 C . B. f  x 3 dx  3x  1 C . 1 1 C. f  x 3 dx  3x  1 C . D. f
 xdx  3x  3 1 3x  1 C . 3 4
Câu 38.Nguyên hàm của hàm số f x  3x  2 là 2 1 A. (3x  2) 3x  2 C B. (3x  2) 3x  2 C 3 3 2 3 1 C. (3x  2) 3x  2 C D. C 9 2 3x  2
Câu 39.Họ nguyên hàm của hàm số f x  2x  1 là 1 1 A.  2x   1 2x  1 C . B. 2x  1 C . 3 2 2 1 C. 2x   1 2x  1 C . D. 2x   1 2x  1 C . 3 3 x  3
Câu 40.Khi tính nguyên hàm dx 
, bằng cách đặt u  x  1 ta được nguyên hàm nào? x  1 A.  2 2 u  
4du . B.   2u 4du. C.  2u   3du . D. u   2 2 u  4du . dx Câu 41.Biết    
  với a, b là các số nguyên dương và C là   x   a x b x 2 C x x 2 2 x
hằng số thực. Giá trị của biểu thức P  a b là: A. P  2 B. P  8 C. P  46 D. P  22 Câu 42.Nguyên hàm 3 2 P  x. x  1dx  là: 3 3 A. P   2 x   3 2 1 x  1 C B. P   2 x   2 1 x  1 C 8 8 3 3 C. 3 2 P  x  1 C D. P   2 x   3 2 1 x  1 C 8 4 1 Câu 43.Nguyên hàm R  dx  là: x x  1 1 x  1  1 1 x  1 1 A. R  ln C B. R  ln C 2 x  1 1 2 x  1  1 x  1  1 x  1 1 C. R  ln C D. R  ln C x  1 1 x  1  1 Câu 44.Nguyên hàm 3 2 S  x x  9dx  là: x  2 2 2 9 x  9 A. S   3 2x   2 9 x  9 C 5 x  4 2 2 9 x  9 B. S   3 2x   2 9 x  9 C 5  2x   2 9 x  9 2 C. S   3 2x   2 9 x  9 C 5 x  2 2 2 9 x  9 D. 2 S   3 x  9 C 5 1 Câu 45.Nguyên hàm I  dx  là: 1x 32 x x 2 1 x A. 3 1x 2 2 C B. C C. C D. C 2 1 x  x 32 1 x 3 x Câu 46.Cho I  dx  . Bằng phép đổi biến 2
u  x  1 , khẳng định nào sau đây sai? 2 x  1 3 u A. 2 2 x  u 1 B. xdx  udu C. I   2 u   1.udu D. I  u C 3 x Câu 47.Cho f x   2
2 x  1  5 , biết F x là một nguyên hàm của hàm số f x thỏa mãn 2  x  1   F 0  6 3 . Giá trị của F      là: 4 125 126 123 127 A. B. C. D. 16 16 16 16 dx Câu 48.Nguyên hàm I   là: 2 2 x 9  x 2 9  x 2 9  x A. I   C B. I  C 9x 9x 2 9  x 2 9  x C. I  C D. I   C 2 9x 2 9x 3 x Câu 49.Nguyên hàm I  dx  là: 2 1  x 1 1 A. I    2 x   2 2 1  x C B. I   2 x   2 2 1  x C 3 3 1 1 C. I    2 x   2 2 1  x C D. I   2 x   2 2 1  x C 3 3
Vấn đề 5. Nguyên hàm của hàm số lượng giác.
Câu 50.Tìm nguyên hàm của hàm số f x  2 sinx . A. 2 sin xdx  2 cos x C  B. 2 sin xdx  2 cos x C  C. 2 2 sin xdx  sin x C  D. 2 sin xdx  sin 2x C 
Câu 51.Tìm nguyên hàm của hàm số f x  cos 3x sin 3x A. cos 3xdx  3 sin 3x C  B. cos 3xdx  C  3 sin 3x C. cos 3xdx  sin 3x C  D. cos 3xdx   C  3  
Câu 52.Họ nguyên hàm của hàm số y  cos 3x     là:  6     A. f  x 1 dx  sin3x    C B. f  x 1 dx   sin3x    C 3  6 3  6     C. f  x 1 dx  sin3x    C D. f
 xdx  sin3x    C 6  6  6
Câu 53.Phát biểu nào sau đây đúng? cos 2x A. sin 2xdx  C,C    B. sin 2xdx  cos 2x C,C  2   cos 2x C.
sin 2xdx  2 cos 2x C,C    D. sin 2xdx  C,C    2 a a Câu 54.Biết   x  x2 sin 2
cos 2 dx  x  cos 4x C , với a, b là các số nguyên dương, là phân số b b
tối giản và C   . Giá trị của a b bằng: A. 5. B. 4. C. 2. D. 3.
Câu 55.Nguyên hàm F x của hàm số f x  cos 3x cosx , biết đồ thị y  F x đi qua gốc tọa độ là: x x x x A. F x sin 4 sin 2   B. F x sin 4 sin 2   4 2 8 2 x x x x C. F x cos 4 cos 2   D. F x sin 8 sin 4   8 4 8 4 m nx Câu 56.Biết   x  x5 2 2 cos cos sin sin 4xdx  
C , với m,n, p   và C là hằng số thực. Giá p
trị của biểu thức T  m  n  p là: A. T  9 B. T  14 C. T  16 D. T  18 2 sin x Câu 57.Nguyên hàm M  dx  là: 1  3 cos x 1 2
A. M  ln 1  3 cosxC
B. M  ln 1  3 cos x C 3 3 2 1
C. M   ln 1  3 cos x C
D. M   ln 1  3 cos x C 3 3  
Câu 58.Gọi F x là nguyên hàm của hàm số f x 2 3  sin 2x.cos 2x thỏa F       0  . Giá trị F 2019 4 là: A. F   1
2019   B. F 2019  0 C. F   2 2019   D. F   1 2019  15 15 15  
Câu 59.Tìm nguyên hàm F x của hàm số f x  sin x  cosx thoả mãn F       2  . 2
A. F x  cosx  sin x  3
B. F x  cos x  sin x 1
C. F x  cos x  sin x 1
D. F x  cosx  sin x  3
Câu 60.Cho hàm số f  x thỏa mãn f  x  cos x và f (0)  2020 . Mệnh đề nào dưới đây đúng?
A. f (x)  sin x  2020 B. f (x)  cos x  2020 C. f(x)  sin x  2020 . D. f(x)  2020  cos x
Câu 61.Nguyên hàm của hàm số 2 f(x)  3 sin x cos x là A. 3 sin x C . B. 3 sin x C . C. 3 cos x C . D. 3 cos x C . sin x
Câu 62.Tìm nguyên hàm của hàm số f (x)  . 1  3 cos x 1 A.
f(x)dx  ln 1  3 cos x C  . B.
f(x)dx  ln 1  3 cos x C 3  . 1 C.
f(x)dx  3 ln 1  3 cos x C  . D.
f(x)dx   ln 1  3 cos x C  . 3 cos x
Câu 63.Tìm các hàm số f (x) biết 'f(x)  . 2 (2  sin x) sin x 1 A. f (x)  C . B. f(x)  C . 2 (2  sin x) (2  cos x) 1 sin x C. f (x)   C . D. f (x)  C . 2  sin x 2  sin x
Câu 64.Tìm họ nguyên hàm của hàm số f x 5  tan x . 1 1 A. f  x 4 2
dx  tan x  tan x  ln cosx C . 4 2 1 1 B. f  x 4 2
dx  tan x  tan x  ln cosx C . 4 2 1 1 C. f  x 4 2
dx  tan x  tan x  ln cosx C . 4 2 1 1 D. f  x 4 2
dx  tan x  tan x  ln cosx C . 4 2 x  x  
Câu 65.Biết F x là một nguyên hàm của hàm số f x sin2 cos 
và F 0  2. Giá trị của F        1  sin x 2 là: 2 2  8 2 2  8 4 2  8 4 2  8 A. B. C. D. 3 3 3 3 sin 2x Câu 66.Cho nguyên hàm I  dx 
. Nếu u  cos 2x đặt thì mệnh đề nào sau đây đúng? 4 4 cos x  sin x 1 1 1 1 2 A. I  du  B. I  du I  du I  du 2 u  1  C. 2 2u  1  D. 2 2 u  1  2 u  1 m cos 2x sinx  cosx  1 Câu 67.Cho dx   C 
, với m,n   và C là hằng số sinx  cosx 23 sinx  cosx 2n
thực. Giá trị của biểu thức A  m  n là: A. A  5 B. A  2 C. A  3 D. A  4
Vấn đề 6. Nguyên hàm của hàm số mũ, logarit.
Câu 68.Tìm nguyên hàm của hàm số   7x f x  . x 7x A. 7 dx  C  B. x x 1 7 dx 7   C ln 7  x 1  x 7 C. 7 dx  C  D. 7x d  7x x ln 7 C x  1 
Câu 69.Họ nguyên hàm của hàm số 3 ( ) x
f x  e là hàm số nào sau đây? 1 1 A. 3 x e C . B. 3x e C . C. x e C . D. 3 3 x e C . 3 3
Câu 70.Nguyên hàm của hàm số 2 1 e x y   là 1 1 A. 2 1 2e x C . B. 2 1 e x C . C. 2x 1 e  C . D. ex C . 2 2 Câu 71.Tính 2 F(x)  e dx 
, trong đó e là hằng số và e  2, 718 . 2 2 e x 3 e A. F(x)  C . B. F(x)  C . C. 2 F(x)  e x C . D. F(x)  2ex C . 2 3 Câu 72.Hàm số   2 x
F x  e là nguyên hàm của hàm số nào trong các hàm số sau: 2 x e A. 2 ( )  2 x f x xe . B. 2 2 ( ) x f x  x e 1. C. 2 ( ) x f x  e . D. f(x)  . 2x
Câu 73.Nguyên hàm của hàm số   2x 2 x f x    5 là  2x  A. x  5    x   C . B. x  5.2 ln 2 C . ln2 2x  2x   2x  C.   x  5x    C . D. 1  5    C . ln 2  ln 2  ln2
Câu 74.Cho F x là một nguyên hàm của hàm số f x 1 
thỏa mãn F 0  10 . Hàm số F x 2 x e  3 là: 1 x ln 5 1
A. x  ln2e  3 10  B.  10  ln2 x x e  3 3 3 3 1      x 3 1 x ln 5  ln 2 C. x   ln 2  e    
D. x  ln2e  3 10      ln 5  ln 2 3   2 3 3
Câu 75.Hàm số f x có đạo hàm liên tục trên  và:   2  2e x f x  1, x, f   0  2. Hàm f x là A.  2ex y  2x . B. 2ex y   2 . C. 2  e x y  x  2 . D. 2  e x y  x  1.
Câu 76.Nguyên hàm của hàm số   lnx f x  là: x 2 ln x 1 ln x ln x A. C B. C C. C D. 2 ln x C 2 2 x 2 1 Câu 77.Nguyên hàm T  dx  là: x ln x  1 1 A. T  C B. T  2 ln x  1 C 2 ln x  1 2 C. T  ln x   1 ln x  1 C D. T  ln x  1 C 3
Câu 78.Tìm họ nguyên hàm của hàm số   3 2 1 .ex f x x   . 3 x A. f  x 3 x 1 dx .e   C . B.    3 1 d 3ex f x x   C . 3 1 C.    3 1 d ex f x x   C . D. f  x 3 x 1 dx e   C . 3
Câu 79.Nguyên hàm của   2 sin  sin 2 . x f x x e là 2 sin x 1 e  2 sin x 1 e  A. 2 2 sin 1 sin . x x e  C . B. C . C. 2 sin x e C . D. C . 2 sin x  1 2 sin x 1
Câu 80.Nguyên hàm của hàm số f x   2 ln x  x  1 là A. F x  x  2 x  x   2 ln 1  x  1 C . B. F x  x  2 x  x   2 ln 1  x  1 C . C. F x  x  2 ln x  x  1C . D. F x 2  x  2 ln x  x  1C . 2 ln x
Câu 81.Xét nguyên hàm V   
dx . Đặt u  1  1  ln x , khẳng định nào sau đây x 1  ln x  1 sai? 2 dx  2u 2u A.  2u 2du B. V  .  2u 2du x u 2 5 16 5 4 u u 16 C. 5 4 3 2 V  u  u  u  4u C D. 3 2 V    u  4u C 5 2 3 5 2 3 Câu 82.Cho hàm số   3 2 x 2  2  2  2 x f x x e xe , ta có    3 2  2 2 d x x x f x x  me
 nxe  pe C . Giá trị của
biểu thức m  n  p bằng 1 13 7 A. B. 2 C. D. 3 6 6
Vấn đề 7. Nguyên hàm tổng hợp.
Câu 83.Họ nguyên hàm của hàm số   x f x  e  x là x 1 1 x 1 A. x e  1 C B. x 2 e  x C C. 2 e  x C D. 2 e  x C 2 x  1 2
Câu 84.Tính  x  sin2xdx . 2 x 2 x x 2 x cos 2x A.  sin x C . B.  cos 2x C . C. 2 cos 2 x  C . D.  C . 2 2 2 2 2
Câu 85.Tìm họ nguyên hàm của hàm số 2 1   3x y x  . x 3 3x x 1 3 x x 1 A.   C, C   . B.  3  C, C   . 2 3 ln 3 x 2 3 x 3 3x x 3 3x x C.   ln x C, C   . D.   ln x C, C   . 3 ln 3 3 ln 3
Câu 86.Họ nguyên hàm của hàm số f x 2  3x  sin x là A. 3 x  cos x C . B. 6x  cos x C . C. 3 x  cos x C . D. 6x  cos x C .
Câu 87.Công thức nào sau đây là sai? 1 1 A. ln x dx  C  . B. dx  tan x C x  . 2 cos x C. sin x dx  cos x C  . D. ex d  ex x C  .
Câu 88.Trong các khẳng định sau, khẳng định nào sai? 1 e 1 x  A. cos 2xdx  sin 2x C  . B. e x dx  C 2  . e  1 1 x 1  x e C. dx  ln x C  . D. e dx  C x  . x  1
Câu 89.Họ nguyên hàm của hàm số f x 1   sin x là x 1 A. ln x  cos x C . B.   cos x C . C. ln x  cos x C . D. ln x  cos x C . 2 x    x  2018 x e
Câu 90.Tìm nguyên hàm của hàm số f x  e 2  017     . 5  x  2018 2018 A.   d  2017 x f x x e  C . B.   d  2017 x f x x e  C . 4 x 4 x 504, 5 504, 5 C.   d  2017 x f x x e  C . D.   d  2017 x f x x e  C . 4 x 4 x x  e  
Câu 91.Họ nguyên hàm của hàm số x y  e 2      là 2  cos x  x 1 x 1 A. 2 x e  tan x C B. 2 x e  tan x C C. 2e  C D. 2e  C cos x cos x Câu 92.Hàm số F x 2
 x lnsinx  cosx là nguyên hàm của hàm số nào dưới đây? x A. f x 2  . sin x  cos x 2 x cos x  sin x
B. f x  2x lnsin x  cosx    . sin x  cos x 2 x sin x  cos x C. f x    . sin x  cos x x D. f x  x  x  x 2 2 ln sin cos  . sin x  cos x
Câu 93.Cho hàm số f x x ln 2  2 .
. Hàm số nào dưới đây không là nguyên hàm của hàm số f x? x A.    2 x F x C B.    22 x F x  1C C.    22 x F x  1C D.   1 2 x F x   C
Câu 94.Tìm họ nguyên hàm của hàm số f x 3 2 x 1 x e        1 1 A. 5 3 4  2  t
  2t  dt  t t  ln t C   .  t  4 B.    3 1 d 3 x f x x e   C . 1 C. f  x 3 x 1 dx e   C . 3 3 x D. f  x 3 x 1 dx e   C . 3 Câu 95.Biết
x cos 2xdx  ax sin 2x b cos 2x C 
với a , b là các số hữu tỉ. Tính tích ab ? 1 1 1 1 A. ab  . B. ab  . C. ab   . D. ab   . 8 4 8 4
Câu 96.Họ nguyên hàm của hàm số f x  4x 1  lnx là: A. 2 2 2x ln x  3x . B. 2 2 2x ln x  x . C. 2 2 2x ln x  3x C . D. 2 2 2x ln x  x C .
Câu 97.Họ nguyên hàm của hàm số 2 ( )  . x f x x e là : 1   x 1 1 A. 2 F(x)  e x      C B. 2 ( ) x F x  e x 2C 2  2 2   C. 2 ( )  2 x F x e x 2C D. 2x 1 F(x)  2e x      C   2
Câu 98.Họ nguyên hàm của hàm số ( )  2 (1 x f x x e )là A.    2 2 1 x x e  x . B.    2 2 1 x x e  x . C.    2 2 2 x x e  x . D.    2 2 2 x x e  x .
Câu 99.Họ nguyên hàm của f x  x ln x là kết quả nào sau đây? 1 1 1 1 A. F x 2 2  x ln x  x C . B. F x 2 2  x ln x  x C . 2 2 2 4 1 1 1 1 C. F x 2 2  x ln x  x C . D. F x 2  x ln x  x C . 2 4 2 4 x
Câu 100.Tất cả các nguyên hàm của hàm số f x 
trên khoảng 0; là 2 s in x A. x
 cotx  lns inxC .
B. x cot x  ln s inx C .
C. x cot x  ln s inx C . D. x
 cotx  lnsinxC .
Câu 101.Họ nguyên hàm của hàm số   4   ex f x x x là 1 1 A. 5    1ex x x C . B. 5    1ex x x C . 5 5 1 C. 5  ex x x C . D. 3 4    1ex x x C . 5  2 2x  xlnx 1
Câu 102.Họ nguyên hàm của hàm số y  là x x x A. x  x   2 2 1 ln x   x C . B. x  x   2 2 1 ln x   x C . 2 2 x x C. x  x   2 2 1 ln x   x C . D. x  x   2 2 1 ln x   x C . 2 2
Câu 103.Cho hàm số f xthỏa mãn   x
f x  xe và f 0  2 .Tính f  1. A. f   1  3 . B. f   1  e . C. f   1  5 e . D. f   1  8  2e .
Câu 104.Gọi F x là một nguyên hàm của hàm số   e x f x x  
. Tính F x biết F 0  1. A.    1e x F x x      2 . B.    1e x F x x     1. C.    1e x F x x     2 . D.    1e x F x x      1. Câu 105.Biết
x cos 2xdx  ax sin 2x b cos 2x C 
với a , b là các số hữu tỉ. Tính tích ab ? 1 1 1 1 A. ab  . B. ab  . C. ab   . D. ab   . 8 4 8 4 x a x Câu 106.Biết F x  cos3 1  
 sin 3x  2019 là một nguyên hàm của hàm số b c f x  x  
2 sin 3x , (với a , b , c   ). Giá trị của ab  c bằng A. 14 . B. 15 . C. 10 . D. 18 . Câu 107.Cho hàm số   3 2 x 2  2  2  2 x f x x e xe , ta có    3 2  2 2 d x x x f x x  me
 nxe  pe C . Giá trị
của biểu thức m  n  p bằng 1 13 7 A. B. 2 C. D. 3 6 6
Câu 108. Cho hàm số F(x) là một nguyên hàm của x f x   2x   2 ( ) 2019
4 x  3x  2. Khi đó số điểm
cực trị của hàm số F(x) là A. 5. B. 4. C. 3. D. 2.
Câu 109.Cho F x là một nguyên hàm của hàm số   2 x
f x  e  3x  4x. Hàm số  2 F x  x có bao nhiêu điểm cực trị? A. 6 . B. 5. C. 3 . D. 4 .
Vấn đề 8. Nguyên hàm của hàm ẩn
Câu 110.Hàm số F x nào sau đây là một nguyên hàm của hàm số f x.g x, biết F   1  3, f  xdx  x C và g  x 2 dx  x C . 1 2 A. F x 2  x  1 B. F x 2  x  3 C. F x 2  x  2 D. F x 2  x  4 Câu 111.Cho f  x 3
dx  4x  2x C . Tính I  xf   2xdx . 0 10 6 x x A. 6 2 I  2x  x C . B. I   C . C. 6 2 I  4x  2x C . D. 2 I  12x  2. 10 6
Câu 112.Cho hàm số y  f x thỏa mãn f x f x 4 2 ' .
 x  x . Biết f 0  2. Tính 2f 2. 313 332 324 323 A. 2 f 2  . B. 2 f 2  . C. 2 f 2  . D. 2 f 2  . 15 15 15 15
Câu 113.Cho hai hàm số F x,G x xác định và có đạo hàm lần lượt là f x,g x trên  . Biết rằng F xG x 2  x  2 . ln x  1 2x và F x.g x 3 
. Họ nguyên hàm của f x.G x là 2 x  1 A.  2 x    2x   2 1 ln 1  2x C. B.  2 x    2x   2 1 ln 1  2x C. C.  2 x    2x   2 1 ln 1  x C. D.  2 x    2x   2 1 ln 1  x C.
Câu 114.Cho hàm số f liên tục và có đạo hàm trên  , f x  1 x  ,
 f 0  0 và thoả mãn
f x 2x 1  2x f x1. Tính f  3. A. 9. B. 7. C. 3. D. 0.
Câu 115.Cho hàm số f (x) xác định trên đoạn  1;2  
 thỏa mãn f(0)  1 và 2 2
f (x).f (x)  1  2x  3x .
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số f (x) trên  1;2    là A. 3 3
min f(x)  2 ;max f(x)  43 . B. 3 3
min f(x)  2 ;max f(x)  40  1;2  1;2            1  ;2 1  ;2     C. 3 3
min f(x)  2 ; max f(x)  43 . D. 3 3
min f(x)  2 ; max f(x)  40 .  1;2  1;2            1  ;2 1  ;2    
Câu 116.Cho hàm số f x liên tục trên R thỏa mãn các điều kiện: f 0  2 2, f x  0, x   và
f x f x   x   2 . 2
1 1  f x, x   . Khi đó giá trị f  1 bằng A. 26 . B. 24 . C. 15 . D. 23 .
Câu 117.Cho h/s y  f x liên tục trên 0; thỏa mãn xf x f x 2 2 '  3x x ; f   1 1  . Tính 2 f 4? A. 24 . B. 14 . C. 4 . D. 16 . 2
Câu 118.Cho hàm số f x thỏa mãnf x  f x f x 3 ' . '
 x  2x , x   và f 0  f '  0  1. Tính giá trị của 2 T  f 2. 43 16 43 26 A. . B. . C. . D. . 30 15 15 15
Vấn đề 9. Các bài toán nguyên hàm có điều kiện. 1 2
Câu 119.Cho hàm số f (x) xác định trên  \ 
 thỏa mãn f x  , f  
0  1, f  1  2. Giá trị 2     2x 1
của biểu thức f   1  f   3 bằng A. 2  ln15 B. 3  ln15 C. ln 15 D. 4  ln 15
Câu 120.Biết F x là một nguyên hàm của hàm số   2x
f x  e và F 0  0 . Giá trị của F ln 3 bằng A. 2. B. 6. C. 8. D. 4.     2  
Câu 121.Biết F x là một nguyên hàm của hàm f x  cos 3x và F        . Tính F   . 2 3 9     3  2     3  2     3  6     3  6 A. F             B. F   C. F   D. F   9 6 9 6 9 6 9 6
Câu 122.Cho hàm số f x xác định trên R \   1 thỏa mãn f x 1 
, f 0  2017 , f 2  2018 . x 1
Tính S  f 3 f   1 . A. S  ln 4035 . B. S  4 . C. S  ln 2 . D. S  1. b 1   1
Câu 123.Cho hàm số f x thỏa mãn f x 2  ax  , f  
1  3 , f  1  2, f     . Khi đó 2a b 3 x 2 12 bằng 3 3 A.  . B. 0 . C. 5. D. . 2 2
Câu 124.Gọi F x là một nguyên hàm của hàm số   2x
f x  , thỏa mãn F   1 0  . Tính giá trị biểu ln 2
thức T  F 0 F  
1  ..  F 2018 F 2019. 2019 2  1 A. T  1009. . B. 2019.2020 T  2 . ln 2 2019 2 1 2020 2 1 C. T   . D. T   . ln 2 ln 2 1  
Câu 125.Cho F x là một nguyên hàm của hàm số f x 
. Biết F   k  k với mọi k   2 cos x 4 
. Tính F 0  F   F  . .  F 10. A. 55. B. 44. C. 45. D. 0.  
Câu 126.Biết F x là một nguyên hàm của hàm số f x 3
 sin x.cos x và F 0   . Tính F       . 2         1     1 A. F            . B. F      . C. F        . D. F       . 2 2 2 4 2 4 2x  1
Câu 127.Cho F(x) là một nguyên hàm của hàm số f x 
trên khoảng 0; thỏa 4 3 2 x  2x  x mãn F   1
1  . Giá trị của biểu thức S  F  1 F 2 F  
3  F 2019 bằng 2 2019 2019.2021 1 2019 A. . B. . C. 2018 . D.  . 2020 2020 2020 2020 ln x  3
Câu 128.Giả sử F x là một nguyên hàm của f x   
sao cho F 2  F   1  0 . Giá trị của 2 x
F  1 F 2 bằng 10 5 7 2 3 A. ln 2  ln 5 . B. 0 . C. ln 2 . D. ln 2  ln 5. 3 6 3 3 6
Câu 129.Gọi g x là một nguyên hàm của hàm số f x  lnx  
1 . Cho biết g 2  1 và g 3  a lnb
trong đó a,b là các số nguyên dương phân biệt. Hãy tính giá trị của 2 2 T  3a b A. T  8 . B. T  1  7 . C. T  2 . D. T  13 .
Câu 130.Cho hàm số f x liên tục trên  , f x  0 với mọi x và thỏa mãn f   1 1   , 2
f x   x   2 2 1 f x a .Biết f  
1  f 2. . f 2019  1 với a,b  ,
 a,b  1 .Khẳng định b nào sau đây sai? A. a b  2  019. B. ab  2019 . C. 2a b  2022 . D. b  2020 .
Vấn đề 10. Một số bài toán ứng dụng của nguyên hàm. 1
Câu 131.Một chất điểm chuyển động với phương trình 2
S  t , trong đó t là thời gian tính bằng giây 2
(s) và S là quãng đường tính bằng mét (m). Vận tốc của chất điểm tại thời điểm t  5 s là: 0   A. 5(m / s) B. 25(m / s) C. 2, 5 (m / s). D. 10 (m / s).
Câu 132.Một ô tô đang chạy với vận tốc 10(m / s) thì người lái xe đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc v t  10 2t m / s, trong đó t là khoảng thời gian tính bằng
giây kể từ lúc đạp phanh. Tính quãng đường ô tô di chuyển được trong 8 giây cuối cùng. A. 50m. B. 25m. C. 55m. D. 10m. 1 5
Câu 133.Một vận động viên điền kinh chạy với gia tốc a t 3 2   t  t  2 m / s , trong đó t là 24 16
khoảng thời gian tính từ lúc xuất phát. Hỏi vào thời điểm 5(m / s)sau khi xuất phát thì vận tốc của vận động viên là bao nhiêu? A. 5, 6m / s B. 6, 51 (m / s). C. 7, 72 (m / s) D. 6, 8 (m / s)
Câu 134.Số lượng của một loại vi khuẩn được tính theo công thức N x, trong đó x là số ngày kể từ thời
điểm ban đầu. Biết rằng N x 2000 ' 
và lúc đầu số lượng vi khuẩn là 5000 con. Hỏi ngày thứ 12 số 1  x
lượng vi khuẩn gần nhất với kết quả nào sau đây? A. 10130. B. 10120. C. 5154. D. 10132.
Câu 135.Cho F x là một nguyên hàm của hàm số f x 1 
thỏa mãn F 0  ln 2. Tập nghiệm x e  1
S của phương trình   ln x F x e  1  3 là: A. S    3 B. S    3 C. S   D. S    3 2017x
Câu 136.Biết rằng F x là một nguyên hàm trên  của hàm số f x  thỏa mãn F   1  0 x  2018 2 1
. Tìm giá trị nhỏ nhất m của F x. 1 2017 1 2 2017 1 2 1 A. m   . B. m   . C. m   . D. m  . 2 2018 2 2018 2 2 2x  3dx 1 Câu 137.Giả sử   (C là hằng số).     C
x x 1 x  2x  31 g x
Tính tổng các nghiệm của phương trình g x  0. A. 1. B. 1. C. 3 . D. 3. 2 cos x 1
Câu 138.Cho hàm số F x là một nguyên hàm của hàm số f x 
trên khoảng 0;. Biết 2 sin x
rằng giá trị lớn nhất của F x trên khoảng 0; là 3 . Chọn mệnh đề đúng trong các mệnh đề sau.   2    3   5  A. F       3 3  4      B. F     C. F      3 D. F     3  3 6  3  2 3  6  B. TÍCH PHÂN.
Vấn đề 1. Tích phân hàm đa thức 0
Câu 1. Tính tích phân I  2x   1dx . 1 1 A. I  0 . B. I  1. C. I  2 . D. I   . 2 1
Câu 2. Tích phân  3x  1x  3dx bằng 0 A. 12 . B. 9 . C. 5. D. 6. 2
Câu 3. Tính tích phân I  (2x  1)dx  0 A. I  5. B. I  6. C. I  2. D. I  4 . b
Câu 4. Với a,b là các tham số thực. Giá trị tích phân  2 3x  2ax   1dx bằng 0 A. 3 2 b b a b . B. 3 2 b b a b . C. 3 2 b ba b . D. 2 3b  2ab  1. 1 2
Câu 5. Biết rằng hàm số f x  mx n thỏa mãn f  xdx  3, f
 xdx  8. Khẳng định nào 0 0 dưới đây là đúng? A. m  n  4 . B. m  n  4  . C. m  n  2 . D. m  n  2  . m Câu 6. Cho   2
3x  2x  1dx  6. Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. 1;  2 . B.  ;  0. C. 0;4. D.  3  ; 1. 1 n
Câu 7. Cho n là số nguyên dương khác 0 , hãy tính tích phân I    2 1 x  xdx theo n . 0 1 1 1 1 A. I  . B. I  . C. I  . D. I  . 2n  2 2n 2n 1 2n  1
Vấn đề 2. Tích phân hàm số hữu tỉ. 2 dx Câu 8.  bằng 2x  3 1 1 7 1 7 7 A. ln 35 B. ln C. ln D. 2 ln 2 5 2 5 5 1  1 1  Câu 9. Cho     dx  a ln 2 b ln 3   với 
a,b là các số nguyên. Mệnh đề nào dưới đây x  1 x  2 0 đúng? A. a  2b  0 B. a b  2 C. a  2b  0 D. a  b  2 e 1 1  Câu 10. Tính tích phân I     dx   2 x x  1 1 1 A. I  B. I   1 C. I  1 D. I  e e e 2 x 1
Câu 11. Tính tích phân I  dx  . x 1 7 A. I  1  ln 2. B. I  . C. I  1  ln 2 . D. I  2 ln 2. 4 2 dx Câu 12. Biết
 a ln 2 b ln 3  c ln 5 
. Khi đó giá trị a b  c bằng 1 x   1 2x  1 A. 3. B. 2 . C. 1. D. 0 . 3 x  2 Câu 13. Biết dx  a b ln ,c  với a, , b c  ,
 c  9. Tính tổng S  a b  . c x 1 A. S  7 . B. S  5 . C. S  8 . D. S  6 . 0 2 3x  5x 1 2 Câu 14. Biết I  dx  a ln  ,b 
a,b  . Khi đó giá trị của a  4b bằng x  2 3 1 A. 50 B. 60 C. 59 D. 40 5 2 x  x  1 b Câu 15. Biết dx  a  ln 
với a , b là các số nguyên. Tính S  a  2b . x  1 2 3 A. S  2 . B. S  2 . C. S  5 . D. S  10. 2 2 x  5x  2 Câu 16. Biết dx  a b ln 3  c ln 5 
, a, ,bc  . Giá trị của abc bằng 2 x  4x  3 0 A. 8  . B. 10. C. 12. D. 16 . 1 1 Câu 17. Tích phân I  dx  có giá trị bằng x  1 0 A. ln 2  1. B.  ln 2 . C. ln 2 . D. 1  ln 2 . 3 x Câu 18. Tính K  dx  . 2 x 1 2 1 8 8 A. K  ln 2 . B. K  ln . C. K  2 ln 2 . D. K  ln . 2 3 3 1 7 x Câu 19. Cho tích phân I  dx  , giả sử đặt 2
t  1  x . Tìm mệnh đề đúng. 1x 52 0 1 t  3 2 1 t  3 3 1 A. I  dt  . B. I  dt 5 2 t  . 5 t 1 1 1 t  3 2 1 3 t  3 4 1 C. I  dt  . D. I  dt 4 2 t  . 4 2 t 1 1 1 x
Câu 20. Có bao nhiêu số thực a để dx  1  . 2 a  x 0 A. 2 B. 1 C. 0 D. 3 1 2 2x  3x  3 Câu 21. Biết dx  a  lnb 
với a,b là các số nguyên dương. Tính 2 2 P  a  b . 2 x  2x  1 0 A. 13 . B. 5. C. 4 . D. 10 .
Vấn đề 3. Tích phân hàm vô tỉ. 21 dx Câu 22. Cho  a ln 3 b ln 5 c ln 7  , với a, ,
b c là các số hữu tỉ. Mệnh đề nào sau đây 5 x x  4 đúng? A. a b  2  c B. a b  2  c C. a b  c D. a b  c  2 Câu 23. Tính tích phân 2 I  2x x 1dx  bằng cách đặt 2
u  x  1 , mệnh đề nào dưới đây đúng? 1 3 2 1 3 2 A. I  udu  B. I  udu I  2 udu I  udu 2  C.  D.  0 1 0 1 1 dx Câu 24. Tích phân  bằng 0 3x  1 4 3 1 2 A. . B. . C. . D. . 3 2 3 3 2 dx Câu 25. Biết dx  a  b c 
với a,b,c là các số nguyên dương. Tính 1 (x  1) x  x x  1 P  a b c A. P  18 B. P  46 C. P  24 D. P  12 2 2 Câu 26. Cho tích phân 2 I  16  x dx 
và x  4 sin t . Mệnh đề nào sau đây đúng? 0   4 4
A. I  8 1 cos2tdt . B. 2 I  16 sin d t t  . 0 0   4 4
C. I  8 1 cos2tdt . D. 2 I  16 cos d t t  . 0 0 5 1 Câu 27. Biết dx  a b ln 3  c ln 5 
(a,b,c  Q). Giá trị của a b  c bằng 1 1  3x  1 7 5 8 4 A. . B. . C. . D. . 3 3 3 3 7 3 x m m Câu 28. Cho biết dx   với
là một phân số tối giản. Tính m  7n 3 2  x n n 0 1 A. 0 . B. 1. C. 2 . D. 91. 3 x a Câu 29. Cho dx  b ln 2  c ln 3 
với a,b,c là các số nguyên. Giá trị a b  c 4  2 x  1 3 0 bằng: A. 9 B. 2 C. 1 D. 7 a 3 x  x Câu 30. Tính I  dx  . 2 0 x  1 1 A. I   2 a   2 1 a  1 1 . B. I  2  a  2 1 a 1 1     . 3    1 C. I  2  a  2 1 a 1 1     . D. I   2 a   2 1 a  1  1. 3    1 2 x
Câu 31. Giá trị của tích phân dx 
bằng tích phân nào dưới đây? 1 x 0  1   4 2 2 sin x 4 2 sin y 2 A. 2 2 sin ydy  . B. dx  . C. dy 2 2 sin d y y cos x  . D. cosy  . 0 0 0 0 1 dx  
Câu 32. Cho tích phân I  
nếu đổi biến số x  2 sin t,t      ;    thì ta được. 2  2 2 0 4  x     3 6 4 6 dt A. I  dt  . B. I  dt  . C. I  d t t  . D. I   . t 0 0 0 0 1 3 x a b c Câu 33. Biết dx   với a, ,
b c là các số nguyên và b  0 . Tính 2 x  1  x 15 0 2 P  a b c . A. P  3. B. P  7 . C. P  7  . D. P  5. 64 dx 2 Câu 34. Giả sử I   a ln b 
với a, b là số nguyên. Khi đó giá trị a b là 3 x  x 3 1 A. 1  7 . B. 5. C. 5  . D. 17 . 2 x Câu 35. Biết dx  a b 2  c 35 
với a , b , c là các số hữu tỷ, tính 2 1 3x  9x  1 P  a  2b  c  7 . 1 86 67 A.  . B. . C. 2. D. . 9 27 27 4 2x  1dx 5 Câu 36. Biết  a b ln 2  c ln 
a, ,bc  . Tính T  2a b c. 2x  3 2x  1  3 3 0 A. T  4 . B. T  2 . C. T  1. D. T  3 .
Vấn đề 4. Tích phân hàm lượng giác.  4
Câu 37. Cho hàm số f x. Biết f 0  4 và f x 2 '
 2 sin x  1, x   , khi đó f  xdx bằng 0 2   16  4 2   4 2   15 2   16 16 A. . B. . C. . D. . 16 16 16 16  4
Câu 38. Cho hàm số f (x).Biết f (0)  4 và 2
f (x)  2 cos x  3, x   , khi đó f(x)dx  bằng? 0 2   8  8 2   8  2 2   6  8 2   2 A. . B. . C. . D. . 8 8 8 8  2 Câu 39. Giá trị của sin xdx  bằng 0  A. 0. B. 1. C. -1. D. . 2  4 2 Câu 40. Giả sử I  sin 3xdx  a b   ,ab  
 . Khi đó giá trị của a b là 2 0 1 1 3 1 A.  B.  C.  D. 6 6 10 5  2 3 sin x  cos x 11 b Câu 41. Biết dx  ln 2 b ln 3  c   ,bc Q. Tính ? 2 sin x  3 cos x 3 c 0 22 22 22 22 A. . B. . C. . D. . 3 3 3 13  Câu 42. Tính tích phân 3 I  cos x.sin d x x  . 0 1 1 A. I   B. 4 I    C. 4 I    D. I  0 4 4  2 Câu 43. Cho tích phân I  2  cos x .sin xdx 
. Nếu đặt t  2  cos x thì kết quả nào sau đây đúng? 0  2 3 2 2 A. I  tdt  . B. I  tdt  . C. I  2 tdt  . D. I  tdt  . 3 2 3 0  4 2 sin x
Câu 44. Tính tích phân I  dx 
bằng cách đặt u  tanx , mệnh đề nào dưới đây đúng? 4 cos x 0  4 2 1 1 1 A. 2 I  u du  . B. I  du  . C. 2 I   u du 2 I  u du 2 u  . D.  . 0 0 0 0  2 sin x Câu 45. Cho tích phân dx  a ln 5 b ln 2  với a, b  .
 Mệnh đề nào dưới đây đúng? cos x  2  3 A. 2a  b  0. B. a  2b  0. C. 2a b  0. D. a  2b  0. a 2
Câu 46. Có bao nhiêu số a  0;20sao cho 5 sin x sin 2xdx   . 7 0 A. 10. B. 9. C. 20. D. 19.  6 dx a 3  b Câu 47. Biết   , với a,b ,  c     và a, ,
b c là các số nguyên tố cùng nhau. Giá 1  sin x c 0
trị của tổng a b  c bằng A. 5. B. 12 . C. 7 . D. 1.  2 s inx Câu 48. Cho tích phân số dx  a ln 5 b ln 2 
với a,b   . Mệnh đề nào dưới đây đúng? cos x  2  3 A. 2a  b  0. B. a  2b  0. C. 2a b  0.. D. a  2b  0. .  2 sin x 4 Câu 49. Cho dx  a ln b 
, với a , b là các số hữu tỉ, c  0 . Tính tổng m . cosx2 c 0  5 cosx  6 A. S  3 . B. S  0 . C. S  1. D. S  4 .
Vấn đề 5. Tích phân hàm mũ và logarit.
Câu 50. Cho F x là một nguyên hàm của hàm số   ln x f x 
. Tính: I  F eF   1 ? x 1 1 A. I  B. I  C. I  1 D. I  e 2 e 1 Câu 51. 3x 1 e  dx  bằng 0 1 1 A.  4 e e B. 3 e e C.  4 e e D. 4 e e 3 3 2 Câu 52. Cho 3x 1  d    p q e
x m e e  với m , p, q   và là các phân số tối giản. Giá trị m  p q 1 bằng 22 A. 10 . B. 6 . C. . D. 8 . 3 ln 6 ex Câu 53. Biết tích phân dx  a b ln 2  c ln 3 
, với a , b , c là các số nguyên. Tính x 0 1  e  3 T  a b c . A. T  1. B. T  0 . C. T  2 . D. T  1. e ln x Câu 54. Biết dx  a b 2 
với a,b là các số hữu tỷ. Tính S  a b . 1 x 1  ln x 1 3 2 A. S  1. B. S  . C. S  . D. S  . 2 4 3 1 dx 1 e Câu 55. Cho  a b ln 
, với a, b là các số hữu tỉ. Tính 3 3 S  a b . x e  1 2 0 A. S  2 . B. S  0 . C. S  1 . D. S  2 . e 3 lnx 1 Câu 56. Cho tích phân I  dx 
. Nếu đặt t  ln x thì x 1 1 3t  1 e 3t  1 e 1 A. I  dt  . B. I  dt I 
3t  1 dt . D. I  3t   1dt . et  . C.    t 0 1 1 0 e ln x c Câu 57. Cho I  dx  a ln 3 b ln 2   , với a, ,
b c   . Khẳng định nào sau đâu đúng. x lnx  2 3 1 2 A. 2 2 2 a b  c  1. B. 2 2 2 a b  c  11. C. 2 2 2 a b  c  9 . D. 2 2 2 a b c  3 . n l 2 dx 1 Câu 58. Biết I   lna  lnb  lnc 
với a , b , c là các số nguyên dương. 0 x x    e  3e  4 c Tính P  2a b  c . A. P  3 . B. P  1 . C. P  4 . D. P  3
Vấn đề 6. Tích phân tổng hợp. 1  a Câu 59. Biết rằng 2 x 2 xe dx    b c
e e  với a, ,bc  . Giá trị của a b c bằng 2 0 A. 4 . B. 7 . C. 5. D. 6. e x  1 Câu 60. Biết dx  ln ae b 
với a,b là các số nguyên dương. Tính giá trị của biểu thức 2   x  x ln x 1 2 2 T  a ab b . A. 3. B. 1. C. 0. D. 8. 2 1 p 2 x p
Câu 61. Biết  x  1 x q
e dx  me n , trong đó m,n, ,
p q là các số nguyên dương và là phân số q 1
tối giản. Tính T  m  n  p  q . A. T  11. B. T  10. C. T  7 . D. T  8 .
Câu 62. Cho hàm số y  f x có đạo hàm trên  đồng thời thỏa mãn f 0  f   1  5 . Tính tích phân 1 I  f   x fx e dx . 0 A. I  10 B. I  5 C. I  0 D. I  5 4 Câu 63. Biết I  x ln
  2x  9dx a ln5 b ln3c trong đó a, ,bc là các số thực. Giá trị của biểu 0
thức T  a  b  c là: A. T  11. B. T  9. C. T  10. D. T  8. e  3 x   2 3 1 ln x  3x 1 Câu 64. Cho 3 dx  a.e b c.ln 
e  1 với a, ,bc là các số nguyên và 1  x ln x 1 ln e  1. Tính 2 2 2 P  a  b  c . A. P  9. B. P  14 . C. P  10 . D. P  3. 2 x  1 Câu 65. Biết dx  ln lna b 
với a , b là các số nguyên dương. Tính 2   x  x ln x 1 2 2 P  a  b  ab . A. 10 . B. 8 . C. 12 . D. 6.  2 1 x  xex Câu 66. Cho dx  a.e b ln c 
với a , b , c   . Tính P  a  2b c . x  e  x  e 0 A. P  1. B. P  1. C. P  0. D. P  2  .
Vấn đề 7. Tích phân dùng tính chất. 2 2 2 Câu 67. Biết f  xdx  2 và g
 xdx  6, khi đó f   x gx  dx  bằng 1 1 1 A. 8 . B. 4 . C. 4 . D. 8  . 1 1 1 Câu 68. Biết tích phân f  xdx  3 và g
 xdx  4. Khi đó f   x gx  dx  bằng 0 0 0 A. 7  . B. 7 . C. 1 . D. 1. 1 1 1 Câu 69. Biết f(x)dx  2  và g(x)dx  4  , khi đó f(x) g(x) dx    bằng 0 0 0  A. 6. B. 6. C. 2. D. 2. 1 1 Câu 70. Cho f  xdx  2 và g
 xdx  5 , khi S bằng 0 0 A. 8 B. 1 C. 3 D. 12
Câu 71. Khẳng định nào trong các khẳng định sau đúng với mọi hàm f , g liên tục trên K và a , b là
các số bất kỳ thuộc K ? b f(x)dx b b b b  f(x) A.
f(x) 2g(x)dx  f(x)dx +2 g(x)dx   a     . B. dx   . g(x) b a a a a g(x)dx a b b b 2 b b   C.
f(x).g(x)dx  f(x)dx . g(x)dx   2       . D. f (x)dx= f(x)dx    . a a a a  a   2 4 4 Câu 72. Cho. f  xdx  1., f
 tdt  4. Tính f ydy  . 2  2  2 A. I  5. B. I  3. C. I  3 . D. I  5. 2 2 2 Câu 73. Cho f x dx  3  và g x dx  7  , khi đó f x 3g x d  x  bằng 0      0   0    A. 16 . B. 18 . C. 24 . D. 10 . 1 3 3 Câu 74. Cho f(x)dx  1   , f(x)dx  5  . Tính f(x)  dx 0 0 1 A. 1. B. 4. C. 6. D. 5. 2 3 3 Câu 75. Cho f  xdx  3 và f
 xdx  4. Khi đó f xdx  bằng 1 2 1 A. 12. B. 7. C. 1. D. 12.
Câu 76. Cho hàm số f x liên tục, có đạo hàm trên  1  ;2 , f     1  8; f 2  1    . Tích phân 2 f '  xdx bằng 1 A. 1. B. 7. C. 9. D. 9. 2 4 4
Câu 77. Cho hàm số f x liên tục trên R và có f(x)dx  9; f(x)dx  4.   Tính I  f(x)dx.  0 2 0 9 A. I  5. B. I  36 . C. I  . D. I  13 . 4 0 3 3 Câu 78. Cho f  xdx  3 f
 xdx  3. Tích phân f xdx  bằng 1  0 1 A. 6 B. 4 C. 2 D. 0 4 4 3
Câu 79. Cho hàm số f x liên tục trên  và f  xdx  10, f
 xdx  4. Tích phân f xdx  0 3 0 bằng A. 4 . B. 7 . C. 3 . D. 6. Câu 80. Nếu F x 1  và F  
1  1 thì giá trị của F 4 bằng 2x 1 1 A. ln 7. B. 1  ln 7. C. ln 3. D. 1  ln 7. 2 8 12 8
Câu 81. Cho hàm số f x liên tục trên  thoả mãn f  xdx  9, f  xdx  3, f  xdx  5. 1 4 4 12 Tính I  f  xdx . 1 A. I  17 . B. I  1. C. I  11. D. I  7 . 10 6
Câu 82. Cho hàm số f x liên tục trên 0;10   thỏa mãn f  xdx  7, f  xdx  3. Tính 0 2 2 P  f  x 10 dx  f  xdx . 0 6 A. P  10 . B. P  4 . C. P  7 . D. P  6  .
Câu 83. Cho f , g là hai hàm liên tục trên đoạn 1; 3   thoả mãn: 3 3 3 f        x 3g xd  x  10  , 2f
  xgxdx  6  . Tính f
  xgxdx  . 1 1 1 A. 7. B. 6. C. 8. D. 9. 10 6
Câu 84. Cho hàm số f x liên tục trên đoạn 0;10   và f  xdx  7; f  xdx  3. Tính 0 2 2 P  f  x 10 dx  f  xdx . 0 6 A. P  4 B. P  10 C. P  7 D. P  4    2 2 Câu 85. Cho f  xdx  5. Tính I f   x 2sinx   dx  5  . 0 0  A. I  7 B. I  5  C. I  3 D. I  5   2 2 2 2 Câu 86. Cho f
 xdx  2 và gxdx  1   . Tính I x 2f   x 3gx    dx  . 1  1  1 17 5 7 11 A. I  B. I  C. I  D. I  2 2 2 2 5 2  5 Câu 87. Cho hai tích phân f  xdx  8 và g  xdx  3. Tính I f
  x 4gx 1    dx  2  5 2  A. 13 . B. 27 . C. 11. D. 3 . 2 2 2 Câu 88. Cho f
 xdx  3, gxdx  1   thì f
  x 5gx x   dx  bằng: 0 0 0 A. 12 . B. 0 . C. 8 . D. 10 5 5 Câu 89. Cho f
 xdx  2. Tích phân 4f   x 2 3x   dx  bằng 0 0 A. 140. B. 130. C. 120. D. 133. 2 2
Câu 90. Cho hàm số f x liên tục trên  và  f x 2
 3x dx  10. Tính f xdx  . 0 0 A. 2 . B. 2 . C. 18 . D. 18 . 6 2 Câu 91. Cho f(x)dx  12  . Tính I  f(3x)dx.  0 0 A. I  5 B. I  36 C. I  4 D. I  6 2 x 2tdt
Câu 92. Số điểm cực trị của hàm số f x   là 2  t x 1 2 A. 0 B. 1 C. 2 D. 3 5 2 Câu 93. Cho biết f
 xdx  15. Tính giá trị của P f   5 3x 7    dx  . 1  0 A. P  15 . B. P  37 . C. P  27 . D. P  19 . 4 2 Câu 94. Cho f
 xdx  2018. Tính tích phân I f
  2x f 4 2x    dx  . 0 0 A. I  0 . B. I  2018. C. I  4036 . D. I  1009 . 2
Câu 95. Cho y  f x là hàm số chẵn, liên tục trên 6;6   . Biết rằng f  xdx  8; 1  3 6 f
 2xdx  3. Giá trị của I  f  xdx là 1 1 A. I  5. B. I  2. C. I  14 . D. I  11. 2  
Câu 96. Cho hàm số f x liên tục trên  và f
 xdx  2018, tính I  xf   2xdx. 0 0 A. I  1008 . B. I  2019. C. I  2017 . D. I  1009 . 2 4 f  x  Câu 97. Cho f  xdx  2. Khi đó dx  bằng 1 1 x A. 1. B. 4 . C. 2 . D. 8 . 2 5 Câu 98. Cho f
  2x  1xdx  2 . Khi đó I  f  xdx bằng 1 2 A. 2 . B. 1. C. 4 . D. x  1. o 7
Câu 99. Cho. f x. liên tục trên  thỏa mãn f x  f 10 xvà f  xdx  4. Tính 3 7 I  xf  xdx . 3 A. 80 . B. 60. C. 40 . D. 20.  1 6 Câu 100. Cho f
 xdx  9. Tính I  f  sin3xcos3xdx . 0 0 A. I  5. B. I  9. C. I  3 . D. I  2. 2017 1
Câu 101. Cho hàm f x thỏa mãn f
 xdx 1. Tính tích phân I  f  2017xdx . 0 0 1 A. I  . B. I  0 . C. I  2017 . D. I  1. 2017 x   x x  Câu 102. Cho hàm số y f x 2 2 3 ; 1    . Tính 5  x ;x 1   2 I  2 f  sinx 1 cos xdx  3 f  32xdx . 0 0 71 32 A. I  . B. I  31. C. I  32 . D. I  . 6 3  2 2 sin xf  3 cos x  1 Câu 103. Cho I  f
 xdx  2. Giá trị của dx  bằng 1 0 3 cos x  1 4 4 A. 2 . B.  . C. . D. 2. 3 3 4 5 2 ln2 Câu 104. Biết f  xdx  5 và f
 xdx  20. Tính 4  3     2x 2x f x dx f e e dx . 1 4 1 0 15 5 A. I  . B. I  15 . C. I  . D. I  25. 4 2
Câu 105. Cho f (x)là hàm số liên tục trên  thỏa mãn 2 ( )  (2  )  . x f x f x
x e , x   . Tính tích 2 phân I  f(x)dx  . 0 4 e 1 2e 1 A. I   . B. I   . C. 4 I  e  2 . D. 4 I  e 1. 4 2
Câu 106. Cho hàm số f x liên tục trên  thỏa mãn f 2x  3f x, x   . Biết rằng 1 2 f
 xdx  1. Tính tích phân I  f  xdx . 0 1 A. I  5 B. I  6 C. I  3 D. I  2 2018
Câu 107. Cho hàm số f x liên tục trên  thỏa f
 xdx  2. Khi đó tích phân 0 2018 e 1  x f  ln 2x 1 dx bằng 2  x  1 0 A. 4 . B. 1. C. 2 . D. 3 .  4 1 2 x f x
Câu 108. Cho hàm số f x liên tục trên  thỏa mãn f  tanxdx  3 và dx  1.  Tính 2 x  1 0 0 1 I  f  xdx.s 0 A. I  2 . B. I  6. C. I  3 . D. I  4 .  2 16 f x
Câu 109. Cho hàm số f x liên tục trên  và thỏa mãn cotx.f   2 sin x   dx  dx  1  . x  1 4 1 f 4x Tính tích phân dx  . x 1 8 3 5 A. I  3 . B. I  . C. I  2. D. I  . 2 2 f 2 x  1 lnx
Câu 110. Cho hàm số f x liên tục trên đoạn 1;4
  và thỏa mãn f x   . Tính tích x x 4 phân I  f  xdx . 3 A. 2 I  3  2 ln 2 . B. 2 I  2 ln 2 . C. 2 I  ln 2 . D. I  2 ln 2.
Câu 111. Cho hàm số f x liên tục trên  thảo mãn: f x  f   x 2 7 4 4
 2018x x  9 ,  x   4 . Tính I  f  xdx . 0 2018 7063 98 197764 A. . B. . C. . D. . 11 3 3 33
C. ỨNG DỤNG CỦA TÍCH PHÂN.
Câu 1. Diện tích phần hình phẳng tô đen trong hình vẽ bên dưới được tính theo công thức nào dưới đây? 3 3
A.   f (x)  g(x)dx .
B.  g(x) f (x)dx . 2 2 0 3 0 3
C.   f (x)  g(x)dx  g(x)  f (x)dx .
D.  g(x)  f (x)dx   f (x) g(x)dx . 2 0 2 0
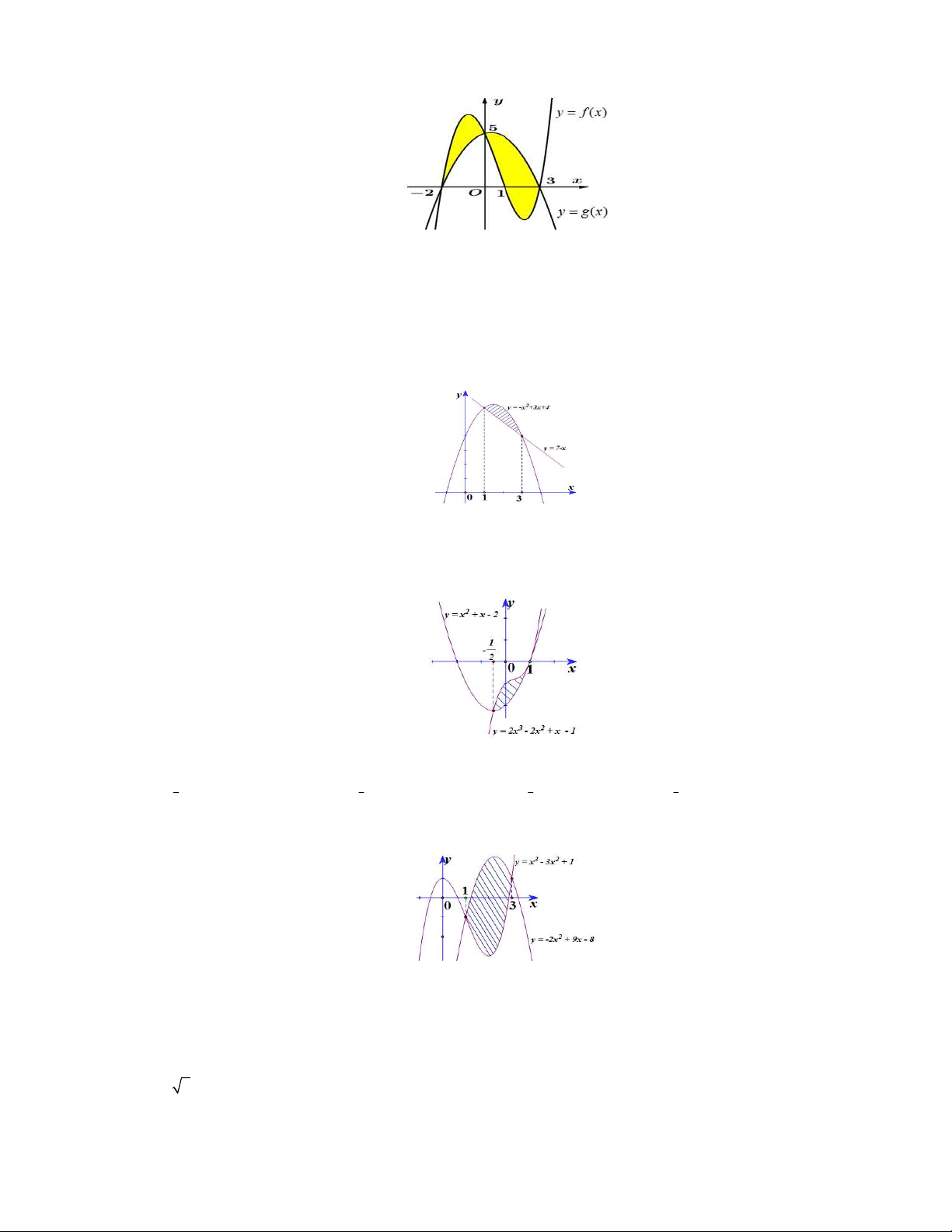
Câu 2. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 3 3 3 3 A.  2 x  4x  3 dx . B.  2 x  2x 1  1 dx .
C.  2x  2x 1 1dx .
D.  2x  4x 3dx. 1 1 1 1
Câu 3. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 1 1 1 1 A.  3 2 2  3   x x 1dx . B.   3 2
2x  x  2x  3 dx .C.  3 2 2  3   x x 1dx.D.   3 2
2x  x  2x  3dx . 1  1  1  1  2 2 2 2
Câu 4. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 3 3 3 3 A.  3 2
x  5x  9x  7 dx .B.   3 2
x  5x  9x  7 dx .C.  3 2
x  x  9x  9dx .D.  3 2 x  x  9x  9 dx . 1 1 1 1
Câu 5. Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
f  x  x; g  x  x  2 và trục hoành là: y 2 O 2 4 x A. 7 S  . B. 10 S  . C. 11 S  . D. 13 S  . 3 3 3 3
Câu 6. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số 2 x
y  e , trục Ox, Oy và đường thẳng x  2 . Tính S hình phẳng trên. 1 1 1 A. 4 e 1 . B.  4 e   1 . C. 4 e . D.  4 e   1 . 2 2 2 Câu 7. Gọi ln
S là diện tích của hình phẳng giới hạn bởi các đường  x y
, y  0 , x  1 , x  e . Mệnh đề 2 x nào dưới đây đúng? e e e 2 e 2 A. ln   ln  ln   ln  d  x S x . B.  d  x S x . C.  d  x S x . D.   d  x S x . 2     x 2 x 2  x  2  x  1 1 1 1
Câu 8. Diện tích hình phẳng được giới hạn bởi các đường  y  sin 2 ;
x y  cos x và x  0; x  là 2 1 1 A. B. C. D. . 1 . 3 . . 4 6 2 2
Câu 9. Diện tích hình phẳng giới hạn bởi các đường y  2x  6 1; y  ; x  3 là: x 25 A. 4  2 6ln 6. B. 4  443 6 ln . C. . D. . 3 24 6
Câu 10. Diện tích hình phẳng giới hạn bởi các đường x
y  e ; y  1 và x 1 là: A. e  2. B. . e C. e 1. D. 1 . e
Câu 11. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y  4x  x và trục Ox A. 11. B. 34 . C. 31 . D. 32 . 3 3 3
Câu 12. Diện tích hình phẳng giới hạn bởi hai đường 3 y  x 11x  6 và 2 y  6x là A. 52 . B. 14 . C. 1 . D. 1 . 4 2 Câu 13. Gọi x 
S là diện tích hình phẳng giới hạn bởi đồ thị hàm số H  1 : y 
và các trục tọa độ. Khi đó x 1 giá trị của S bằng A. S  2 ln 2 1 . B. S  ln 2 1. C. S  ln 2 1 . D. S  2 ln 2 1 .
Câu 14. Tính diện tích hình phẳng giới hạn bởi hai đồ thị  x  P 1 : y    2 x  8x  7 , H  7 : y  . 3 3  x A. 3, 455 . B. 9  8 ln 2 . C. 3  ln 4 . D. 161  4 ln 3 8 ln 2 . 9
Câu 15. Diện tích hình phẳng giới hạn bởi các đồ thị 2
y  x  4x  3 và y  x  3 là: 55 205 109 126 A. . B. . C. . D. . 6 6 6 5
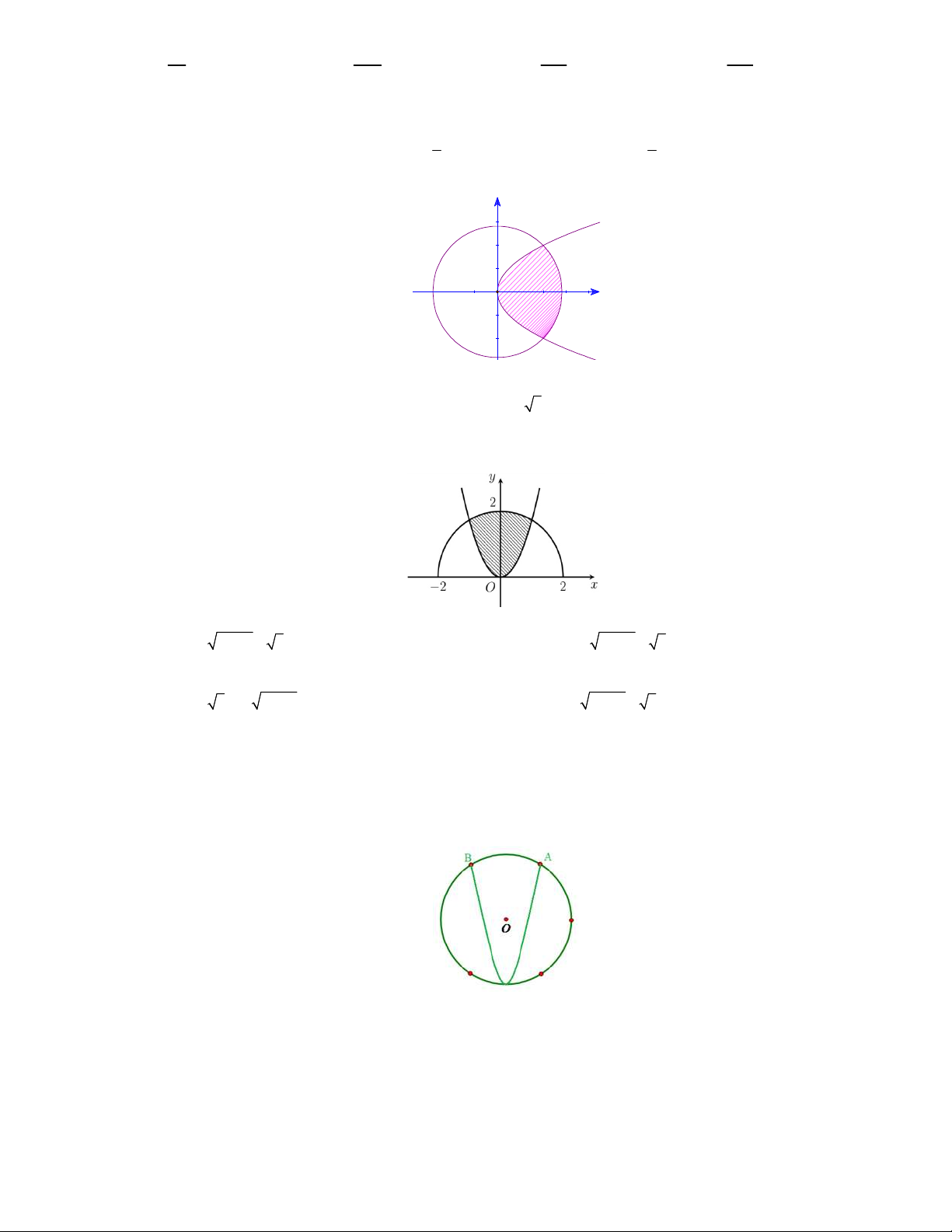
Câu 16. Biết rằng parabol P 2
: y  2x chia đường tròn C 2 2
: x  y  8 thành hai phần lần lượt có diện tích
là S , S (như hình vẽ). Khi đó     b S S a với a, ,
b c nguyên dương và b là phân số tối giản. Tính 1 2 2 1 c c S  a  b  c . y S S 2 1 x O A. S  13 . B. S  16 . C. S  15 D. S  14 .
Câu 17. Cho H  là hình phẳng giới hạn bởi parabol 2
y  3x và nửa đường tròn tâm H  bán kính bằng
2 nằm phía trên trục hoành (phần tô đậm trong hình vẽ bên). Diện tích của H  được tính theo công thức nào dưới đây? 1 1 A. 2 2  S 2 x 3     x  2 2   S   x    dx . B. 2. 4 3x    dx . 0 0 1 1 C. 2 2  S 3x 4     x  2 2   S   x    dx . D. 4 3x    dx . 0 0
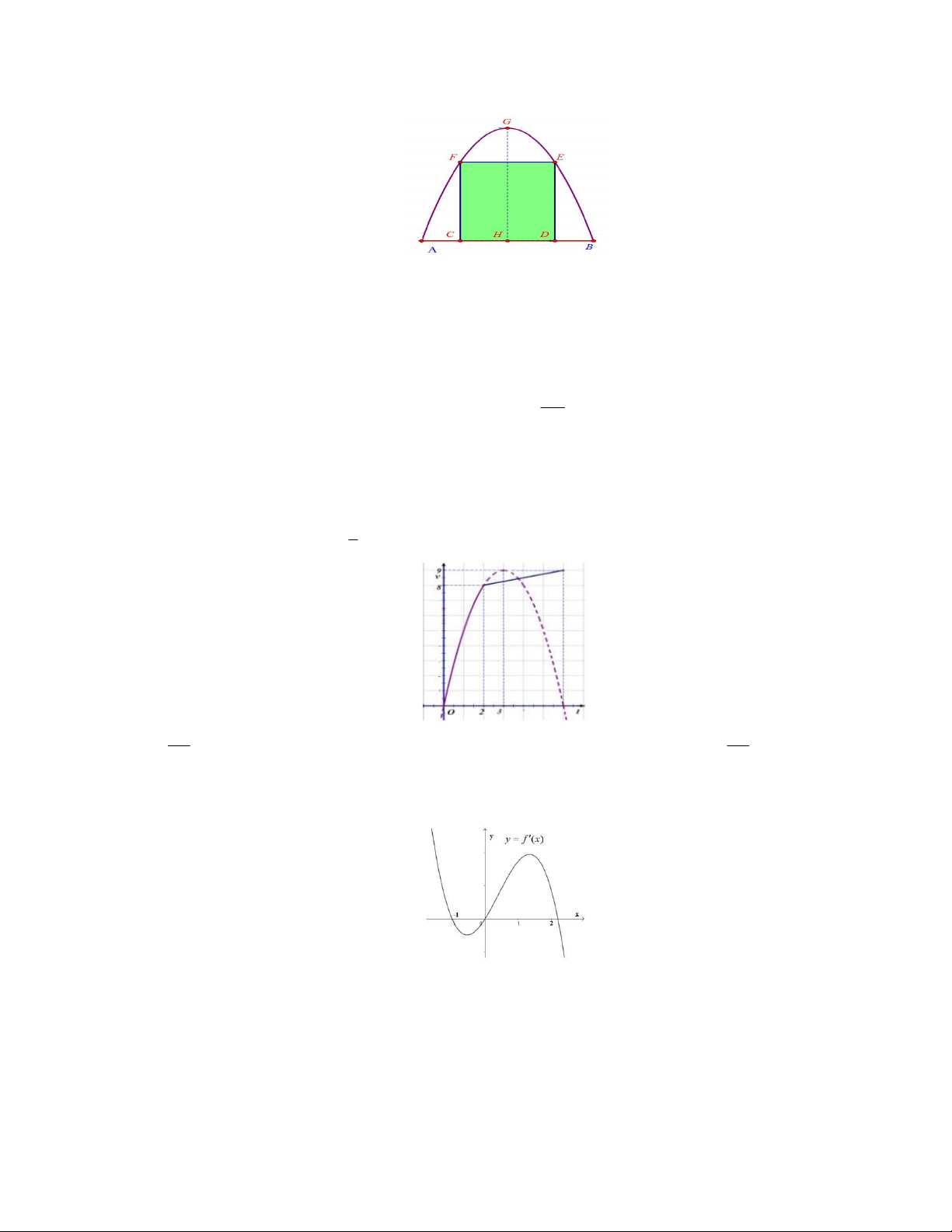
Câu 18. Bạn An xây một bể cá hình tròn tâm O bán kính 10 m và chia nó thành 2 phần như hình vẽ sau.
Bạn An sẽ thả cá cảnh với mật độ 4 con cá cảnh trên 2
1m ở phần bể giới hạn bởi đường tròn tâm O và
Parabol có trục đối xứng đi qua O và chứa O. Gọi S là phần nguyên của diện tích phần thả cá. Hỏi bạn An
thả được bao nhiêu con cá cảnh trên phần bể có diện tích S, biết ,
A B  O và AB  12m ? A. 560. B. 650. C. 460. D. 640.
Câu 19. Lương giáo viên thấp nên thầy Nam chăn nuôi thêm 2 con bò. Do diện tích đất của nhà thầy hẹp
nên thầy xây chuồng bò như hình vẽ bên dưới và chia thành 2 phần bằng nhau để nhốt 2 con bò. Biết
ABCD là hình vuông cạnh 4 m và I là đỉnh của một Parabol có trục đối xứng là trung trực của BC và
parabol đi qua hai điểm A, D. Tiền xây chuồng bò hết 350000 đồng/ 2
1 m . Biết I cách BC một khoảng 5 m ,
hãy tính số tiền chi phí thầy Nam bỏ ra để xây dựng chuồng bò (Làm tròn đến hàng nghìn)?
Câu 20. Một cái cổng hình parabol như hình vẽ. Chiều cao GH  4m , chiều rộng AB  4m , AC  BD  0,9m
. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm giá là 1200000 đồng/m2, còn các
phần để trắng làm xiên hoa có giá là 900000 đồng/m2.
Hỏi tổng chi phí để là hai phần nói trên gần nhất với số tiền nào dưới đây? A. 11445000 (đồng). B. 7368000 (đồng). C. 4077000 (đồng). D. 11370000 (đồng)
Câu 21. Một gia đình có khu vườn hình chữ nhật có chiều dài và chiều rộng lần lượt là 9 m và 4 m. Chủ
nhà muốn đào một chiếc ao hình Elip, hỏi diện tích lớn nhất của mặt ao bằng A.  9 m2. B. 10 m2. C. 81 m2.. D. 4 m2. 4
Câu 22. Một vật chuyển động trong 6 giờ với vận tốc v km / h phụ thuộc vào thời gian t h có đồ thị như
hình dưới. Trong khoảng thời gian 2 giờ từ khi bắt đầu chuyển động, đồ thị là một phần đường Parabol có
đỉnh I 3;9 và có trục đối xứng song song với trục tung. Khoảng thời gian còn lại, đồ thị vận tốc là một
đường thẳng có hệ số góc bằng 1 . Tính quãng đường s mà vật di chuyển được trong 6 giờ? 4 A. 130  134 km . B. 9km . C. 40km . D. km. 3 3 Câu 23. Cho hàm số 4 3 2
f (x)  ax  bx  cx  dx  e . Hàm số y  f (
 x) có đồ thị như hình vẽ. Trong
các khẳng định sau, khẳng định nào đúng? A. a  c  0 .
B. a  b  c  d  0 . C. a  c  b  d . D. b  d  c  0 .
Câu 24. Diện tích hình phẳng giới hạn bởi các đường y  mx cos x; Ox ; x  0; x   bằng 3 . Khi đó m là: A. m  3  . B. m  3. C. m  4  . D. m  3  . Câu 25. Cho Parabol P 2
: y  x 1 và đường thẳng d : y  mx  2 với m là tham số. Gọi m là giá trị của m 0
để diện tích hình phẳng giới hạn bởi P và d là nhỏ nhất. Hỏi m nằm trong khoảng nào? 0 A. 1 ( 2;  ) . B. (0;1). C. 1 ( 1  ; ) . D. 1 ( ; 3) . 2 2 2
Câu 26. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  4x và trục hoành. Hai đường thẳng
y  m và y  n chia (H ) thành 3 phần có diện tích bằng nhau( tham khảo hình vẽ). Giá trị của biểu thức 3 3
T  (4  m)  (4  n) bằng A. 320 T  . B. 512 T  . C. T  75 405 . D. T  . 9 15 2
Câu 27. Gọi H là hình phẳng giới hạn bởi các đường: y  sin x ; O x ; x  0 ; x   . Quay H xung
quanh trục O x ta được khối tròn xoay có thể tích là. 2  A. . B.  . C. .  D. 2  . 2 2
Câu 28. Gọi (H ) là hình phẳng giới hạn bởi các đường y  x.ln x, trục Ox,x  1,x  . e Tính thể
tích khối tròn xoay được tạo thành khi quay hình phẳng (H ) quanh trục Ox.   2 e   1  e  1  e  1   2 e   1 A. . B. . C. . D. . 4 3 3 4
Câu 29. Thể tích của khối tròn xuay được giới hạn bởi 2 y x cos x sin x;y 0;x 0;x       , là: 2 (  3  4 (  5  4) (  3  4) (  3  4) A. B. C. D. 4 4 4 5
Câu 30. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi y  ln x , trục O x và đường thẳng
x 2 quay xung quanh trục Ox . A. 2ln 2 1  . B. 2 ln 2  . C. 2 ln 2 . D. 2ln 2 1  .
Câu 31. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol  P 2
: y  x và đường thẳng
d : y  2 x quay quanh trục O x bằng 2 2 2 2 2 2 A. 2 4  2 4x dx   x dx . B. 2  x  2x dx . C. 2 4  4x dx   x dx . D. 2  x  2x dx .         0 0 0 0 0 0
Câu 32. Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường  y  xln x, y  ,
0 x  e có giá trị bằng  3
b.e  2 trong đó a, b là hai số thực nào dưới đây? a A. a  27, b  5. B. a  24, b  6. C. a  27, b  6. D. a  24, b  5.
Câu 33. Cho đồ thị C; y  f (x)  x . Gọi H là hình phẳng giới hạn bởi C, đường thẳng x  9,
trục O x . Cho M là điểm thuộc C ,  A 9;  0 . Gọi V H
1 là thể tích khối tròn xoay khi cho quay quanh O x , V 9
2 là thể tích khối tròn xoay khi cho tam giác AOM quay quanh O x . Biết V  V . Tính 1 2 4
diện tích S phần hình phẳng giới hạn bởi C và OM . (Hình vẽ không thể thiện chính xác điểm M). y y= x M O 1 A x I 4 5 A. S  3 3 . B. S  27 3 . C. S  . D. S  6 . 3 2 16 2 2 x y
Câu 34. Thể tích khối tròn xoay khi cho Elip   1 quay quanh trục Ox: 2 2 a b 4 4 2 2 A. 2  a . b B. 2  ab . C. 2  a . b D. 2   ab . 3 3 3 3
Câu 35. Thầy Nam dự định xây một bể bơi hình elip có độ dài trục lớn gấp hai lần trục bé và có diện tích
hình chữ nhật cơ sở bằng 2
128m . Mỗi khối nước đổ vào bể có giá là 8500 đồng/ 3 1m . Biết bể bơi sâu
2 m . Hỏi thầy Nam cần bao nhiêu tiền để đổ nước vào 80% bể? (Số tiền được làm tròn đến hàng nghìn). A. 1 126 000 đồng. B. 1 367 000 đồng. C. 1 224 000 đồng. D. 1 046 000 đồng.
Câu 36. Thầy Nam mở trung tâm luyện thi Đại học và làm biển hiệu trung tâm hình chữ nhật có kích
thước 3 m x 2 m như hình vẽ bên. Ở phần bên trái thầy đặt một hình elip tiếp xúc với 3 cạnh hình chữ
nhật và khoảng cách từ tâm hình elip cách chiều rộng biển trung tâm 0,5 m . Kinh phí làm biển hiệu là
900.000 đồng. Biết tiền công trang trí phần bên trong hình elip là 100.000đồng 2 /1m . Hỏi phần còn lại làm bao nhiêu tiền trên 2
1m (Làm tròn đến hàng nghìn)? A. 260 000 đồng. B. 186 000 đồng. C. 168 000 đồng. D. 206 000 đồng.
Câu 37. Một tàu lửa đang chạy với vận tốc 200 m/s thì người lái tàu đạp phanh; từ thời điểm đó, tàu
chuyển động chậm dần đều với vận tốc vt  20020t m/s. Trong đó t khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, tàu còn di chuyển được: A. 1000 m.. B. 500 m.. C. 1500 m.. D. 2000 m.
Câu 38. Một ô tô đang chạy với vận tốc 10 (m/s) thì người lái xe đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc vt  2
 t 10 (m/s), trong đó t là khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Tính quãng đường ô tô đi được trong 8 giây cuối cùng. A. 55 (m) . B. 25 (m) . C. 50 (m) . D. 16 (m) .
Câu 39. Hai người A , B đang chạy xe ngược chiều nhau thì xảy ra va chạm, hai xe tiếp tục di chuyển
theo chiều của mình thêm một quãng đường nữa thì dừng hẳn. Biết rằng sau khi va chạm, một người di
chuyển tiếp với vận tốc v (t)  6  3t mét trên giây, người còn lại di chuyển với vận tốc v (t)  12  4t 1 2
mét trên giây. Tính khoảng cách hai xe khi đã dừng hẳn. A. 25 mét. B. 22 mét. C. 20 mét. D. 24 mét.
Câu 40. Một vật chuyển động trong 3 giờ với vận tốc vkm / h phụ thuộc vào thời gian t h  có đồ thị
vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần
của đường parabol có đỉnh I 2; 
5 và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ
thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong 3 giờ đó. A. 15 km. B. 32 km. C. 12 km. D. 35 km. 3 3 D. SỐ PHỨC.
Vấn đề 1. Câu hỏi lý thuyết.
Câu 1. Cho hai số phức z  a  bi a, b  và z  a  b i a, b . Điều kiện giữa a, b, a, b để
z  z là một số ảo là a  a '  0 a  a '  0 A. b  b  0. B.  . C.  . D. a  a  0 . b   b '  0 b   b'  0
Câu 2. Cho số phức z  a  bi a,b tùy ý. Mệnh đề nào sau đây đúng?
A. Mô đun của z là một số thực dương. B. 2 2 z  z .
C. Số phức liên hợp của z có mô đun bằng mô đun của số phức iz . D. Điểm M  ;
a b là điểm biểu diễn của z .
Câu 3. Cho số phức z  a  bi với a, b là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
A. Phần ảo của z là bi . B. Môđun của 2 z bằng 2 2 a  b .
C. z  z không phải là số thực.
D. Số z và z có môđun khác nhau.
Câu 4. Cho số phức z  a  bi  , a b  ,
 a,b  0 . Mệnh đề nào sau đây đúng? A. z  z . B. 2 2 z  z . C. 1 z.z  1 . D. 2 z.z  z .
Câu 5. Cho hai số phức z và z . Trong các mệnh đề sai, mệnh đề nào sai?
A. z  z  z  z . B. z.z  z . z . C. . z z  z.z .
D. z  z  z  z .
Câu 6. Cho số phức z  a  bi a,b  . Khẳng định nào sau đây sai? A. 2 2 z  a  b . B. z  a  bi . C. 2 z là số thực. D. . z z là số thực.
Vấn đề 2. Các phép toán số phức.
Câu 7. Xác định phần ảo của số phức z  18 12i . A. 12 . B. 18 . C. 12 . D. 12i .
Câu 8. Số phức liên hợp của số phức z  1  2i là A.1 2i B. 1 2i C. 2  i D. 1 2i
Câu 9. Tính môđun của số phức z  4  3i . A. z  7 . B. z  7 . C. z  5 . D. z  25 .
Câu 10. Cho số phức z 1 i và z  2  3i . Tìm số phức liên hợp của số phức w  z  z ? 1 2 1 2 A. w  3  2i . B. w  1 4i . C. w  1   4i . D. w  3  2i .
Câu 11. Tính môđun của số phức z  1 2i2  i  i3  2i   . A. z  4 10 . B. z  4 5 . C. z 160 . D. z  2 10 . 1 Câu 12. Biết
 a  bi , a,b . Tính ab . 3  4i 12 12 12 12 A. . B.  . C.  . D. . 625 625 25 25
Câu 13. Cho số phức z 1 i . Khi đó 3 z bằng A. 2 . B. 2 2 . C. 4 . D. 1.
Câu 14. Tính môđun của số phức là nghịch đảo của số phức z    i2 1 2 . 1 1 1 A. . B. 5 . C. . D. . 5 25 5 1 3
Câu 15. Cho số phức z    i . Tìm số phức 2 w  1 z  z . 2 2 1 3 A. 2  3i . B. 1. C. 0 . D.   i . 2 2 2018 2018 P  1 3i  1 3i Câu 16. Tính . A. P  2 B. 1010 P  2 C. 2019 P  2 D. P  4 Câu 17. Tính 2 2017 2018
S  1 i  i  ...  i  i A. S  i  . B. S  1 i . C. S  1 i . D. S  i . Câu 18. Tính 2 3 2017
S  1009  i  2i  3i  ...  2017i . A. S  2017 1009 i. B. 1009  2017i. C. 2017 1009i. D. 1008 1009i.
Câu 19. Cho các số phức z , z , z thỏa mãn: z  4 , z  3, z  2 và 4z z 16z z  9z z  48. 1 2 3 1 2 3 1 2 2 3 1 3
Giá trị của biểu thức P  z  z  z bằng: 1 2 3 A. 1 B. 8 . C. 2 D. 6
Câu 20. Cho các số phức z , z , z thỏa mãn 2 điều kiện z  z  z  2017 và z  z  z  0. 1 2 3 1 2 3 1 2 3 z z  z z  z z Tính 1 2 2 3 3 1 P  . z  z  z 1 2 3 A. P  2017. B. P  1008, 5. C. 2 P  2017 . D. P  6051. 5i
Câu 21. Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức A  1 . z A. 5 . B. 4 . C. 6 . D. 8 .
Câu 22. Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  1 z  3 1 z . A. 3 15 . B. 6 5 . C. 20 . D. 2 20 .
Câu 23. Trong các số phức z thỏa mãn z  i  z  2  3i . Tìm số phức z có môđun nhỏ nhất. 27 6 6 27 6 27 3 6 A. z   i . B. z    i . C. z    i . D. z   i . 5 5 5 5 5 5 5 5
Câu 24. Cho số phức z thoả mãn đồng thời hai điều kiện z  3  4i  5 và biểu thức 2 2
M  z  2  z  i đạt giá trị lớn nhất. Môđun của số phức z  2  i bằng A. 5 . B. 9 . C. 25 . D. 5 .
Vấn đề 3. Phương trình bậc nhất - bậc hai trong tập số phức
Câu 25. Trên tập số phức, cho phương trình: 2
az  bz  c  0 a, b, c   . Chọn kết luận sai.
A. Nếu b  0 thì phương trình có hai nghiệm mà tổng bằng 0 . B. Nếu 2
  b  4ac  0 thì phương trình có hai nghiệm mà môđun bằng nhau.
C. Phương trình luôn có hai nghiệm phức là liên hợp của nhau.
D. Phương trình luôn có nghiệm.
Câu 26. Cho số phức z thỏa mãn 2  i z  2  2  3i . Môđun của z là: 5 3 5 5 A. z  5 . B. z  . C. z  . D. z  5 . 3 3
Câu 27. Tìm mô đun của số phức z thoả 3iz  (3  i)(1  i)  2 . 2 2 3 2 3 3 2 3 A. z  . B. z  . C. z  . D. z  . 3 2 2 3
Câu 28. Tính mô đun của số phức z biết   i 2 1 2 z  3 4i . A. z  5 . B. 4 z  5 . C. z  2 5 . D. z  5 . Câu 29. Phương trình 2
z  3z  9  0 có hai nghiệm phức z , z . Tính S  z z  z  z . 1 2 1 2 1 2 A. S  6  . B. S  6 . C. S  12 . D. S  1  2 .
Câu 30. Gọi z và z là hai nghiệm phức của phương trình 2
z  6z 11  0 . Giá trị của biểu thức 1 2 3z  z bằng 1 2 A. 22 . B. 11. C. 2 11 . D. 11 .
Câu 31. Gọi z , z là hai nghiệm phức của phương trình 2 z  2z  2  0 . Tính 2018 2018 T  z  z 1 2 1 2 A. T  0 . B. 2019 T  2 . C. T  1. D. 1010 T  2 .
Câu 32. Cho m là số thực, biết phương trình 2
z  mz  5  0 có hai nghiệm phức trong đó có một nghiệm
có phần ảo là 1. Tính tổng môđun của hai nghiệm. A. 3 B. 5 C. 2 5 D. 4
Câu 33. Tìm tổng các giá trị của tham số thực a sao cho phương trình 2 2
z  3z  a  2a  0 có nghiệm phức z thỏa z  2 . 0 0 A. 0 . B. 2 . C. 6 . D. 4 .
Vấn đề 4. Điều kiện của bài toán có chứa modul, số phức liên hợp…
Câu 34. Nếu 2 số thực x , y thỏa: x3  2i  y1 4i  1 24i thì x  y bằng A. 4 . B. 3 . C. 2 . D. 3  .
Câu 35. Tìm số thực m sao cho  2 m   1  m   1 i là số ảo. A. m  0 . B. m  1. C. m  1. D. m  1.
Câu 36. Có bao nhiêu số phức z thỏa mãn 1 i z  2  i z  13 2i ? A. 4 . B. 3 . C. 2 . D. 1.
Câu 37. Có bao nhiêu số phức z thỏa mãn z  z  z  1? A. 0 . B. 1. C. 4 . D. 3 .
Câu 38. Tìm số phức z thỏa mãn z  3  z 1 và  z  2 z  i là số thực A. z  2 B. z  2  2i C. z  2  2i D. không có z
Câu 39. Cho số phức z  a  bi a,b  thỏa mãn z  2  5i  5 và .zz  82 . Tính giá trị của P  a  b . A. 10 B. 8  C. 35 D. 7 
Câu 40. Cho số phức z  a  bi a, b   thỏa mãn z 1 3i  z i  0. Tính S  a  3b . 7 7 A. S  . B. S  5. C. S  5. D. S   . 3 3 z  1 z  2 z  z  3 z  z
Câu 41. Cho hai số phức z , z thỏa mãn 1 , 2 và 1 2 . Giá trị của 1 2 là 1 2 A. 0 . B. 1. C. 2 . D. 3.
Câu 42. Tìm môđun của số phức z biết z  4  1 i z  4  3zi . 1 A. z  . B. z  2. C. z  4 . D. z  1. 2
Câu 43. Tính môđun của số phức z thỏa mãn: 3z.z  2017  z  z   48  2016 .i A. z  4 . B. z  2016 . C. z  2017 . D. z  2 . 1 i
Câu 44. Cho số phức z thoả mãn
là số thực và z  2  m với m   . Gọi m là một giá trị của m z 0
để có đúng một số phức thoả mãn bài toán. Khi đó:  1   1   3   3  A. m  0; . B. m  ;1 . C. m  ;2 . D. m  1; . 0          2  0  2  0  2  0  2 
Vấn đề 5. Điểm biểu diễn của số phức
Câu 45. Giả sử A, B theo thứ tự là điểm biểu diễn của số phức z z
1 , 2 . Khi đó độ dài đoạn AB bằng A. z  z . B. z  z . C. z  z . D. z  z . 2 1 2 1 1 2 1 2
Câu 46. Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức   2 z z với z  a  bi
a, b,b  0 . Chọn kết luận đúng. A. M thuộc tia Ox . B. M thuộc tia Oy .
C. M thuộc tia đối của tia Ox .
D. M thuộc tia đối của tia Oy .
Câu 47. Điểm M 3; 
1 là điểm biểu diễn của số phức nào sau đây? A. z  1   3i B. z  1 3i C. z  3  i D. z  3   i
Câu 48. Điểm M trong hình vẽ dưới đây biểu thị cho số phức nào? A. 3 2i . B. 2   3i . C. 2  3i . D. 3 2i .
Câu 49. Trong hình vẽ dưới đây, M là điểm biểu diễn của số phức z . Số phức z là A. 2  i . B. 1 2i . C. 1 2i . D. 2  i .
Câu 50. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z  1 i2  i ? A. P . B. M . C. N . D. Q .
Câu 51. Cho số phức z thoả mãn 2  i z 10  5i . Hỏi điểm biểu diễn số phức z là điểm nào trong các
điểm M , N , P , Q trong hình vẽ sau ? A. Điểm Q . B. Điểm M . C. Điểm P . D. Điểm N .
Câu 52. Cho số phức z  2  i . Trên mặt phẳng tọa độ Oxy , tìm điểm biểu diễn số phức w  iz . A. M  1  ; 2 . B. M 2;  1 . C. M 2;  1 . D. M 1;2 .
Câu 53. Cho số phức z thỏa mãn iz  2  i  0 . Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa
độ Oxy đến điểm M 3; 4 là A. 2 5 . B. 13 . C. 2 10 . D. 2 2 . 5
Câu 54. Cho số phức z thỏa mãn điều kiện z  2  3i z 1 9i . Số phức w 
có điểm biểu diễn là iz
điểm nào trong các điểm , A B, C, D ở hình vẽ sau? A. Điểm D . B. Điểm C . C. Điểm B . D. Điểm A .
Câu 55. Số phức z được biểu diễn bởi một điểm trên mặt phẳng tọa độ Oxy như hình vẽ: y 1 z 1 x O i
Trong các hình dưới đây, hình nào có thể là điểm biểu diễn của số phức   ? z y 1 y  1 x O 1 x O 1  A. B. y y 1 1  O x O 1 x 1  C. D.
Vấn đề 6. Vận dụng các tính chất hình học để giải toán về số phức
Câu 56. Cho A , B , C tương ứng là các điểm trong mặt phẳng Oxy biểu diễn các số z  1 2i , 1
z  2  5i , z  2  4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là 2 3 A. 1   7i . B. 5  i . C. 1 5i . D. 3  5i .
Câu 57. Trong mặt phẳng tọa độ Oxy , gọi M là điểm biểu diễn số phức z  3 4i ; M ' là điểm biểu diễn 1 i cho số phức z ' 
z . Tính diện tích tam giác OMM '. 2 25 25 15 15 A. S  . B. S  . C. S  . D. S  . O  MM ' 4 O  MM ' 2 OMM ' 4 O  MM ' 2
Câu 58. Cho các số phức z , z thỏa mãn z  3 , z  4 , z  z  5 . Gọi A , B lần lượt là các điểm 1 2 1 2 1 2
biểu diễn số phức z , z trên mặt phẳng tọa độ. Tính diện tích S của O
 AB với O là gốc tọa độ. 1 2 25 A. S  5 2 . B. S  6 . C. S  . D. S  12 . 2
Câu 59. Cho hai số phức z , z thỏa mãn z  z 1. Khi đó 2 2 z  z  z  z bằng 1 2 1 2 1 2 1 2 A. 2 . B. 4 . C. 1. D. 0 .
Câu 60. Cho A , B là hai điểm biểu diễn hình học số phức theo thứ tự z , z khác 0 và thỏa mãn đẳng 0 1 thức 2 2
z  z  z z . Tam giác OAB là tam giác gì? Chọn phương án đúng nhất. 0 1 0 1 A. Đều B. Cân tại O C. Vuông tại O D. Vuông cân tại O
Câu 61. Cho hai số phức z , z thoả mãn z  6, z  2 . Gọi M , N là các điểm biểu diễn cho z và iz . 1 2 1 2 1 2 Biết  MON  60. Tính 2 2 T  z  9z . 1 2 A. T  18 . B. T  24 3 . C. T  36 2 . D. T  36 3 .
Câu 62. Trên mặt phẳng Oxy, tập hợp các điểm biểu diễn các số phức z  x  yi thỏa mãn
z  2  i  z  3i là đường thẳng có phương trình là A. y  x 1. B. y  x 1. C. y  x 1. D. y  x 1.
Câu 63. Cho số phức z  x  yi  x, y  thỏa mãn z  2 i  z 1i  0. Trong mặt phẳng tọa độ
Oxy , điểm M là điểm biểu diễn của số phức z . Hỏi M thuộc đường thẳng có phương trình nào sau đây? A. x  y  5  0 . B. x  y  2  0 . C. x  y  2  0 . D. x  y 1  0 .
Câu 64. Trên mặt phẳng Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn z  i  iz là 1
A. Đường thẳng y  2 .
B. Đường thẳng y   . 2 1 C. Đường thẳng y  .
D. Đường tròn tâm I 0;  1 . 2
Câu 65. Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: z  2  i  4 là đường tròn có tâm I
và bán kính R lần lượt là A. I 2;  1 ; R  4 . B. I  2  ;  1 ; R  2 . C. I 2;  1 ; R  4 . D. I 2;  1 ; R  2 .
Câu 66. Cho số phức z thỏa mãn điều kiện z  3  4i  2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn
số phức w  2z 1 i là hình tròn có diện tích là A. S  9 . B. S  12 . C. S  16 . D. S  25 . z
Câu 67. Trong mặt phẳng Oxy , tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện  3 z 1 là 9 9 9 9 A. Đường tròn 2 2 x  y  x   0 . B. Đường tròn 2 2 x  y  x   0 . 4 8 4 8 9 9  9  1 C. Đường tròn 2 2 x  y  x   0 . D. Đường tròn tâm I 0;   và R  . 4 8  8  8
Câu 68. Cho các số phức z thoả mãn z  i  5 . Biết rằng tập hợp điểm biểu diễn số phức w  iz 1 i là
đường tròn. Tính bán kính của đường tròn đó. A. r  20 . B. r  22 . C. r  4 . D. r  5 .
Câu 69. Cho số phức z thỏa mãn  z  2  i z  2  i  25 . Biết tập hợp các điểm M biểu diễn số phức
w  2z  2  3i là đường tròn tâm I  ;
a b và bán kính c . Giá trị của a  b  c bằng A. 17 . B. 20 . C. 10 . D. 18 .
Câu 70. Tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện z  2  z  2  10 . 2 2 x y
A. Đường tròn  x  2   y  2 2 2  100 . B. Elip  1. 25 4 2 2 x y
C. Đường tròn  x  2   y  2 2 2  10 . D. Elip  1. 25 21  iz  i 1  2
Câu 71. Có bao nhiêu số phức z thỏa mãn điều kiện  ? z 1  z  2  i A. 2. B. 0. C. Có vô số số. D. 1.
Câu 72. Cho số phức z thỏa mãn z 1  2 . Gọi M và m là giá trị lớn nhất, nhỏ nhất của z . Tính M  m . A. 3 . B. 2 . C. 4 . D. 5 .
Câu 73. Cho số phức z thỏa mãn z 1 2i  3. Tìm môđun nhỏ nhất của số phức z 1 .i A. 4. B. 2 2. C. 2. D. 2.
Câu 74. Cho các số phức z thoả mãn z  2. Đặt w  1 2i z 1 2i . Tìm giá trị nhỏ nhất của w . A. 2 . B. 3 5 . C. 2 5 . D. 5 .
Câu 75. Cho số phức z thỏa mãn: z  2i 1  z  i . Trong mặt phẳng Oxy , z được biểu diễn bởi điểm
M . Tìm z sao cho độ dài đoạn MA ngắn nhất với A1,3 . A. 3  i . B. 1 3i . C. 2 3i . D. 2   3i .
Câu 76. Nếu z là số phức thỏa z  z  2i thì giá trị nhỏ nhất của biểu thức z  i  z  4 là A. 2 . B. 3 . C. 4 . D. 5 .
Câu 77. Cho số phức z thỏa mãn 5 z  i  z 1 3i  3 z 1 i . Tìm giá trị lớn nhất M của z  2  3i ? 10 A. M  B. M  1 13 C. M  4 5 D. M  9 3
Câu 78. Cho số phức z , z thỏa mãn z  12 và z  3  4i  5 . Giá trị nhỏ nhất của z  z là 1 2 1 2 1 2 A. 0 . B. 2 C. 7 D. 17 z  i
Câu 79. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của P 
, với z là số phức khác 0 và z M
thỏa mãn z  2 . Tính tỷ số . m M M M 3 M 1 A.  5 B.  3 C.  D.  m m m 4 m 3
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ CƯƠNG ÔN TẬP HỌC KỲ 2 TRƯỜNG THPT YÊN HÒA NĂM HỌC 2020 – 2021 ------o0o----- MÔN: TOÁN PHẦN II. HÌNH HỌC
Vấn đề 1. Hệ tọa độ trong không gian.         
Câu 1. Cho OA  2i  4 j  6k và OB  9i  7 j  4k . Vectơ AB có tọa độ là A. 7;3;10 . B.  7  ; 3;10 . C. 11;11; 2 . D. 7; 3;10 .
Câu 2. Cho đoạn thẳng AB có trung điểm I . Biết A2;1; 
1 , I 1;2;0. Khi đó điểm B có tọa độ là A. 1; 1  ;  1 . B. 3;0; 2  . C. 0;3;  1 . D.  1  ;1;  1 .
Câu 3. Cho hình bình hành ABCD , biết A1;1;  1 , B 2  ;2;  3 , C  5  ; 2  ;  2 . Tọa độ điểm D là A.  2  ; 3  ;  0 . B. 2;3;4. C.  2  ;3;  0 . D.  8  ; 1  ;  4 . Câu 4. Cho điểm A3; 1  ; 
1 . Hình chiếu của điểm A trên mặt phẳng Oyz là điểm A. M 3;0;0 . B. N 0; 1  ;  1 . C. P0; 1  ;0. D. P0;0;  1 .
Câu 5. Cho điểm M 1;2;3 . Gọi H là hình chiếu vuông góc của M trên trục Oz . Điểm đối xứng với M qua H có tọa độ: A. 0;0;3. B. 1;2; 3  . C.  1  ; 2  ; 3   . D.  1  ; 2  ;3 .
Câu 6. Cho hai điểm B(0;3;1) , C( 3
 ;6;4) . Gọi M là điểm nằm trên đoạn BC sao cho MC  2MB . Tính tọa độ điểm M . A. M ( 1  ;4;2). B. M ( 1  ;4;2). C. M (1;4;2) . D. M ( 1  ;4;2).
Câu 7. Cho Am 1;2 , B2;5  2m và C m  3;4 . Tìm giá trị m để A , B , C thẳng hàng? A. m  2  . B. m  2 . C. m 1. D. m  3 .
Câu 8. Cho ba điểm A2;1;  1 ; B 3;2;  
1 . Tìm tọa độ giao điểm của đường thẳng AB và mặt phẳng (yOz)?  5 3  #A. ;  ;0   B. 0; 3; 1 C. 0;1;5 D. 0; 1; 3  2 2   
Câu 9. Cho véc tơ a 2; 2  ;  4 ,b 1; 1  ; 
1 . Mệnh đề nào dưới đây là mệnh đề sai?       
A. a  b  3;3;  3 .
B. a và b cùng phương. C. b  3. D. a  . b .
   
Câu 10. Cho sáu điểm A1;2;  3 , B2; 1  ;  1 ,C3;3; 
3 , A , B ,C thỏa mãn AA B B  C C   0 . Gọi G ; a ;
b c là trọng tâm tam giác AB C
  . Giá trị 3abc bằng A. 6 . B. 1. C. 11. D. 3  . Câu 11. Cho A 1  ; 1  ;0 , B3;1; 
1 . Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:  9   9   9   9  A. M 0; ;0   . B. M 0; ;0   . C. M 0;  ;0   . D. M 0; ;0   .  4   2   2   4 
Câu 12. Cho ba điểm A1;1; 
1 , B1;1;0,C3;1;  1 . Điểm M a; ;
b ctrên mặt phẳng Oxzcách đều 3 điểm , A ,
B C . Giá trị 3a b  cbằng A. 6 . B. 1. C. 3  . D. 1.  8 4 8
Câu 13. Cho hai điểm M (2;2;1) , N  ; ;    
. Tìm tọa độ tâm đường tròn nội tiếp tam giác OMN .  3 3 3 A. I (1;1;1) . B. I (0;1;1) . C. I (0; 1  ; 1  ) . D. I (1;0;1) .
Câu 14. Cho tam giác ABC có A1;2;  1 , B2; 1  ;  3 , C  4  ;7;  5 . Gọi D ; a ;
b c là chân đường phân
giác trong góc B của tam giác ABC . Giá trị của a b2c bằng A. 5. B. 4 . C. 14 . D. 15 . Câu 15. Cho hình hộp ABC . D AB C  D
  có A0;0;0 , B ; a 0;0 ; D0;2 ;
a 0 , A0;0;2a với a  0. Độ
dài đoạn thẳng AC là: 3 A. a . B. 2 a . C. 3 a . D. a . 2  
Câu 16. Góc giữa hai vectơ i và u   3;0;  1 là A. 120 . B. 30 . C. 60 . D. 150 .
Câu 17. Cho ba điểm A1; 2  ;3, B 0;3; 
1 , 4;2; 2 . Côsin của góc  BAC bằng 9  9 9 9  A. . B. . C. . D. . 35 2 35 35 2 35
Câu 18. Cho A1;2;0 , B2; 1  ; 
1 . Tìm C có hoành độ dương trên Ox sao cho tam giác ABC vuông tại C . A. C 3;0;0. B. C 2;0;0 . C. C 1;0;0 . D. C 5;0;0 .
Câu 19. Cho ba điểm không thẳng hàng A 1  ;2;4 , B 1
 ;1;4, C 0;0;4 . Tam giác ABC là tam giác gì? A. Tam giác tù. B. Tam giác vuông. C. Tam giác đều. D. Tam giác nhọn.
Câu 20. Cho ba điểm M 2;3;  1 , N  1  ;1; 
1 , P1;m 1;3 . Tìm m thì tam giác MNP vuông tại N A. m  3 . B. m  1. C. m  2 . D. m  0 .   
Câu 21. Cho hai vecto a,b khác 0 . Kết luận nào sau đây sai?             A. a,3b  3a,b     . B. 2a,b  2 a,b     . C. 3a,3b  3 a,b     . D.       a,b  a . b .sin   a,b.    
Câu 22. Cho u 1;1;2, v 1; ;
m m2. Khi đó u,v  14   thì 11 11 A. m 1,m   . B. m  1  ,m  . C. m 1,m  3  . D. m  1  . 5 3 Câu 23. Cho ( A 1; 2  ;0), B(1;0; 1  ), C(0; 1  ; 2), D( 2  ; ;
m n). Trong các hệ thức liên hệ giữa , m n dưới đây,
hệ thức nào để bốn điểm , A B, C, D đồng phẳng? A. 2m  n  13. B. 2m  n  13. C. m  2n  13. D. 2m  3n  10.
Câu 24. Trong không gian Oxyz cho tứ diện ABCD có A0;1;  1 , B 1  ;0;  2 , C 1  ;1;  0 và D2;1; 
2 . Tính thể tích khối tứ diện ABCD . 5 5 5 A. . B. 5. C. . D. . 6 2 3
Câu 25. Cho tứ diện ABCD có A0;1;  1 ; B1;1;2;C 1; 1  ;0;D0;0; 
1 . Tính độ dài đường cao AH của hình chóp . A BCD . 2 3 2 A. 3 2 . B. 2 2 . C. . D. . 2 2
Câu 26. Cho tứ diện ABCD có A2; 1
 ; 1, B3;0; 1, C2; 1  ; 
3 , D Oy và có thể tích bằng 5 .
Tính tổng tung độ của các điểm D . A. 6 . B. 2 . C. 7 . D. 4  .
Câu 27. Cho hai điểm A9; 3  ;4, B ; a ;
b c . Gọi M , N, P lần lượt là giao điểm của đường thẳng AB
với các mặt phẳng Oxy,Oxz,Oyz . Biết các điểm M , N, P đều nằm trên đoạn AB sao cho
AM  MN  NP  PB . Giá trị của ab  bc  ca bằng A. 17 . B. 17 . C. 9  . D. 12 . Câu 28. Cho A1; 2
 ;3;B2;2;4;C 3; 3
 ;2. Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho:
  
MA  MB  MC ngắn nhất? A. M 2;1;0 B. M 2; 1  ;0 C. M 0; 1  ;3 D. M 2;0;3 Câu 29. Cho ba điểm A 1
 ;2;2, B3;1; 2, C  4
 ;0;3. Tọa độ điểm I trên mặt phẳng Oxz sao   
cho biểu thức IA  2IB  3IC đạt giá trị nhỏ nhất là  19 15   19 15  19 15  19 15  A. I  ;0;   . B. I  ;0;   . C. I ;0;  . D. I ;0;   .  2 2   2 2   2 2   2 2  Câu 30. Cho A0;0;  1 , B 1  ;1;0, C1;0;  1 . Tìm điểm M sao cho 2 2 2
3MA  2MB  MC đạt giá trị nhỏ nhất. A.  3 1        M ; ; 1   . B. 3 3 M  ; ; 1   . C. 3 1 M  ; ; 1   . D. 3 1 M  ; ; 2   .  4 2   4 2   4 2   4 2  A1; 1  ;  1 B 0;1;2 Oxy MA  MB Câu 31. Cho ,
và điểm M thay đổi trên
. Tìm giá trị lớn nhất của . A. 14 . B. 14 . C. 6 . D. 6 .   
Câu 32. Cho các điểm A1;2; 
3 , B6;5;8 và OM  ai bk với a , b là các số thực luôn thay  
đổi. Nếu MA2MB đạt giá trị nhỏ nhất thì giá trị của a b bằng A. 25 . B. 13 . C. 0 . D. 26 .
Vấn đề 2. Phương trình mặt phẳng trong hệ trục tọa độ Oxyz .
Câu 33. Cho mặt phẳng  P : x  2z 1  0 . Chọn câu đúng nhất trong các nhận xét sau:
A. P đi qua gốc tọa độ O.
B. P song song với Oxy .
C. P vuông góc với trục Oz .
D. P song song với trục Oy .
Câu 34. Ba mặt phẳng x  2 y  z  6  0 , 2x  y  3z 13  0 , 3x  2 y  3z 16  0 cắt nhau tại điểm M . Tọa độ của M là: A. M  1  ;2;  3 . B. M 1; 2  ;  3 . C. M  1  ; 2  ;  3 . D. M 1;2;  3 . Câu 35. Gọi ,
m n là hai giá trị thực thỏa mãn: giao tuyến của hai mặt phẳng P  : mx  2y  nz 1  0 và m
Q : x  my  nz  2  0 vuông góc với mặt phẳng  : 4x  y  6z  3  0 . m A. m  n  0 . B. m  n  2 . C. m  n  1. D. m  n  3 .
Câu 36. Cho điểm H 2;1; 
2 , H là hình chiếu vuông góc của gốc toạ độ O lên mặt phẳng P, số đo
góc của mặt phẳng P và mặt phẳng Q: x y 1  10. A. 0 60 . B. 0 30 . C. 0 45 . D. 0 90
Câu 37. Cho các điểm A2;0;0 , B0;3;0 , C0;0;6 , D1;1; 
1 . Có bao nhiêu mặt phẳng phân biệt
đi qua 3 trong 5 điểm O , A, B , C , D ? A. 10 . B. 5. C. 7 . D. 6 .
Câu 38. Mặt phẳng Oxy có phương trình là A. z  0 . B. x  0 . C. y  0. D. x  y  0.
Câu 39. Mặt phẳng song song với mặt phẳng Oxz và đi qua điểm (
A 1;1;1) có phương trình là A. y 1  0 . B. x  y  z 1  0 . C. x 1  0 . D. z 1  0.
Câu 40. Cho A1;1;5 , B0;0; 
1 . Mặt phẳng P chứa ,
A B và song song với trục Oy có phương trình là A. 4x  z 1  0 .
B. 4x  y  z 1  0 . C. 2x  z  5  0 . D. x  4z 1  0 .
Câu 41. Cho hai điểm A1;3; 4   , B 1
 ;2;2 . Phương trình mặt phẳng trung trực của đoạn thẳng AB là
A. 4x  2y 12z 17  0. B. 4x  2y 12z 17  0. C. 4x  2y 12z 17  0 . D. 4x  2y 12z 17  0.
Câu 42. Cho điểm A2;4;  1 ; B  1
 ;1;3 và mặt phẳng P: x 3y  2z 5  0. Một mặt phẳng Q đi qua hai điểm ,
A B và vuông góc với mặt phẳng P có dạng ax  by  cz 11  0 . Khẳng định nào sau là đúng? A. a  b  c  5. B. a  b  c 15. C. a  b  c  5  . D. a b  c  1  5. Câu 43. Cho điểm A 2
 ;0; 2, B0;3; 3 . Gọi P là mặt phẳng đi qua A sao cho khoảng cách từ
B đến mặt phẳng P là lớn nhất. Khoảng cách từ gốc tọa độ đến mặt phẳng P bằng 1 4 2 3 A. . B. . C. . D. . 14 14 14 14
Câu 44. Mặt phẳng   đi qua gốc tọa độ O và vuông góc với 2 mặt phẳng P : x  y  z  7  0 ,
Q : 3x  2 y 12z  5  0 có phương trình là
A.   : 2x  3y  z  0 . B. 
 :10x 15y 5z 2  0.
C.   : 10x  15y  5z  2  0 .
D.   : 2x  3y  z  0 .
Câu 45. Cho 2 mặt phẳng ( ) : x  y  z  3  0;( ) : 2x  y  z 1  0 . Viết phương trình mặt phẳng (P)
vuông góc với () và () và khoảng cách từ M 2;3;1 đến mặt phẳng (P) bằng 14 . Có hai mặt phẳng thỏa mãn là:
A. P x  2 y  3z 16  0 và P x  2 y  3z 12  0 2  1 
B. P 2x  y  3z 16  0 vàP 2x  y  3z 12  0 2  1 
C. P 2x  y  3z 16  0 và P 2x  y  3z 12  0 2  1 
D. P x  2 y  3z 16  0 và P 2x  y  3z 12  0 2  1 
Câu 46. Cho mặt phẳng (P): x  2 y  2z 10  0 . Phương trình mặt phẳng (Q) với (Q) song song với (P) 7
và khoảng cách giữa hai mặt phẳng (P) và (Q) bằng là 3
A. x  2 y  2z  3  0; x  2y  2z 17  0 .
B. x  2y  2z  3  0; x  2y  2z 17  0 .
C. x  2 y  2z  3  0; x  2 y  2z 17  0 .
D. x  2 y  2z  3  0; x  2y  2z 17  0 .  1 
Câu 47. Phương trình của mp đi qua ba điểm (
A 1; 0;0) , B(0;1;0) , C 0;0;   là  2  z A. x  y  2z 1  0. B. x  y  2z  0 . C. x  y  2z 1  0. D. x  y  1  0. 2
Câu 48. Viết phương trình mặt phẳng P đi qua điểm G1;2; 
3 và cắt ba trục Ox,Oy,Oz lần lượt tại ,
A B,C sao cho G là trọng tâm tam giác ABC . x y z x y z x y z
A. x  2 y  3z 14  0. B.    1 C.   1. D.   1 3 6 9 1 2 3 6 3 9
Câu 49. Cho điểm M 1;2;5. Mặt phẳng P đi qua điểm M cắt trục tọa độ O , x Oy,Oz tại , A , B C sao
cho M là trực tâm tam giác ABC . Phương trình mặt phẳng P là x y z x y z
A. x  y  z  8  0 .
B. x  2y  5z  30  0 . C.    0. D.    1. 5 2 1 5 2 1 Câu 50. Cho điểm (
A 1; 2; 3) . Gọi A , A , A lần lượt là hình chiếu vuông góc của A lên các mặt phẳng 1 2 3
(Oyz), (Ozx), (O xy) . Phương trình của mặt phẳng (A A A ) là: 1 2 3 x y z x y z x y z x y z A.    1. B.    1. C.    1. D.    0 . 3 6 9 2 4 6 1 2 3 1 2 3
Câu 51. Cho điểm M '4; 7  ;  5 , N 3; 9  ; 1  
0 và các đường thẳng d , d , d cùng đi qua điểm N và 1 2 3
lần lượt song song với Ox,Oy,Oz . Mặt phẳng P ' đi qua M ' cắt d , d , d lần lượt tại A', B ', C ' sao 1 2 3 cho M ' là trực tâm A
 'B'C'. Phương trình mặt phẳng P ' là x y z x y z
A. x  2y  5z 35  0 . B. x  2y  5z  35  0 . C.    0 . D.   1. 4 7 5 4 7 5 Câu 52. Cho điiểm ( A 3; 1
 ;1) . Tính khoảng cách từ A đến mặt phẳng Oxy . A. 1. B. 3. C. 0. D. 2.
Câu 53. Cho mặt phẳng  P :16x 12y 15z  4  0 và điểm A2 ; 1;  
1 . Gọi H là hình chiếu của
điểm A lên mặt phẳng P . Tính độ dài đoạn thẳng AH . 11 11 22 A. 5. B. . C. . D. . 5 25 5
Câu 54. Cho điểm M 1;2;3 gọi ,
A B,C lần lượt là hình chiếu vuông góc của điểm M lên các trục
Ox, Oy, Oz . Khi đó khoảng cách từ điểm O0;0;0 đến mặt phẳng  ABC có giá trị bằng 1 6 1 A. . B. 6 . C. . D. . 2 7 14
Câu 55. Cho tứ diện ABCD với A1;2;3, B 3  ;0;0,C 0; 3
 ;0, D0;0;6. Tính độ dài đường cao hạ
từ đỉnh A của tứ diện ABCD . A. 9 . B. 1. C. 6 . D. 3 .
Câu 56. Cho hai mặt phẳng P : 5x  5y  5z 1  0 vàQ : x  y  z 1  0 . Khoảng cách giữa hai mặt
phẳng P và Q bằng 2 3 2 2 2 3 A. . B. . C. . D. . 15 5 15 5
Câu 57. Cho A1;0;0, B0; ;
b 0 , C 0;0;c , b  0,c  0 và mặt phẳng P : y  z 1  0. Tính
S  b  c biết mặt phẳng  ABC vuông góc với mặt phẳng P và khoảng cách từ O đến  ABC bằng 1 . 3 3 A. S 1. B. S  2 . C. S  0 . D. S  . 2
Câu 58. Xác định tọa độ điểm M  là hình chiếu vuông góc của điểm M 2;3;  1 lên mặt phẳng
: x 2y  z  0  5   5 3  A. M  2; ;3   . B. M 1;3;5 . C. M  ; 2;  . D. M 3;1;2 .  2   2 2 
Câu 59. Trong không gian Oxyz, cho điểm A3;2;5 và mặt phẳng P : 2x  3y  5z 13  0 . Tìm tọa
độ điểm A’ đối xứng với điểm A qua mặt phẳng (P). A. A '1;8;5 B. A'2;4;3 C. A '7;6;4 D. A'0;1;3
Câu 60. Trong không gian Oxyz , cho A1;0;0, B 0;2;0,C 0;0; 
1 . Trực tâm tam giác ABC có tọa độ là  4 2 4   4 2 4  A. ; ; . B. 2;1;2. C. 4; 2; 4. D.   ; ; .    9 9 9   9 9 9 
Câu 61. Cho A0;1;2 , B 0;1;0 , C 3;1; 
1 và mặt phẳng Q :x  y  z  5  0 . Xét điểm M thay đổi
thuộc Q . Giá trị nhỏ nhất của biểu thức 2 2 2 MA  MB  MC bằng A.12 . B. 0 . C.8 . D.10 .
Câu 62. Cho mặt phẳng   : x  y  z  4  0 và ba điểm A1;2; 
1 , B 0;1;2 và C 0;0;3 . Điểm   
M  x; y; z thuộc   sao cho MA  3MB  4MC đạt giá trị nhỏ nhất. Tính giá trị biểu thức P  x  y  z . 1 5 A. 3 . B.  . C. . D. 4 . 3 3
Câu 63. Cho hai điểm A2; 2;4, B 3  ;3; 
1 và mặt phẳng P : 2x  y  2z 8  0 . Xét M là điểm
thay đổi thuộc P , giá trị nhỏ nhất của 2 2 2MA  3MB bằng: A. 135 . B. 105 . C. 108 . D. 145 .
Câu 64. Cho tứ diện ABCD có điểm A1;1;  1 , B2;0;2 , C  1  ; 1
 ;0 , D0;3;4 . Trên các cạnh AB , AB AC AD
AC , AD lần lượt lấy các điểm B , C , D thỏa:  
 4 . Viết phương trình mặt phẳng AB AC AD B C  D
  biết tứ diện AB C  D
  có thể tích nhỏ nhất.
A. 16x  40 y  44z  39  0 .
B. 16x  40 y  44z  39  0 .
C. 16x  40 y  44z  39  0 .
D. 16x  40 y  44z  39  0 .
Câu 65. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P :x  y  z  2  0 và hai điểm A3;4;  1 ; B 7; 4  ; 3   . Điểm M  ; a ;
b ca  2 thuộc P sao cho tam giác ABM vuông tại M và có
diện tích nhỏ nhất. Khi đó giá trị biểu thức T  a  b  c bằng: A.T  6 . B.T  8. C. T  4 . D.T  0 .
Câu 66. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;0;0), B(0;m;0),C(0;0;n) với m,n là các số thực dương thoả mãn 2 2
3mn  4 m  n . Mặt phẳng qua A vuông góc với OA cắt đường thẳng qua O
vuông góc với mặt phẳng ( ABC) tại điểm H. Tính OH ? 5 4 3 4 A. B. C. D. 4 5 4 3
Vấn đề 3. Phương trình mặt cầu
Câu 67. Cho tam giác ABC . Tập hợp các điểm M trong không gian thỏa mãn hệ thức
  
MA  MB  MC  aa  0 là a a
A.Mặt cầu bán kính R  .
B. Đường tròn bán kính R  3 3
C. Mặt cầu bán kính R  . a
D. Đoạn thẳng có độ dài bằng . a
Câu 68. Cho hai điểm A 2  ;1;0 , B2; 1
 ;2 . Phương trình của mặt cầu có đường kính AB là A. x  y   z  2 2 2 1  24 . B. x  y  z  2 2 2 1  6 . C. x  y   z  2 2 2
1  24 . D. x  y   z  2 2 2 1  6 .
Câu 69. Phương trình mặt cầu tâm I  1
 ;2;0 và đi qua điểm A2; 2;0 là
A.  x  2   y  2 2 1 2  z  100.
B.  x  2   y  2 2 1 2  z  5.
C.  x  2   y  2 2 1 2  z  10.
D.  x  2   y  2 2 1 2  z  25.
Câu 70. Gọi S  là mặt cầu đi qua 4 điểm A2;0;0 , B1;3;0 , C  1
 ;0;3 , D1;2;3. Tính bán kính R S của A. R  2 2 . B. R  3 . C. R  6 . D. R  6 .
Câu 71. Cho mặt cầu S  2 2 2
:x  y  z  2x  4y  6z  0 cắt các trục O ,
x Oy,Oz lần lượt tại các điểm , A ,
B C ( khác O) . Phương trình mặt phẳng  ABC là x y z x y z x y z x y z A.    1. B.    1. C.    0. D.    1. 2 4 6 2 4 6 2 4 6 2 4 6 Câu 72. Cho điểm I  1
 ;2;3 và mpP : 4x  y  z 1 0. Viết ptrình mặt cầu tâm I và tiếp xúc với P. A. 2 2 2
(x 1)  ( y  2)  (z  3)  2 . B. 2 2 2
(x 1)  (y  2)  (z  3)  2 . C. 2 2 2
(x 1)  ( y  2)  (z  3)  2 . D. 2 2 2
(x 1)  ( y  2)  (z  3)  1 .
Câu 73. Cho mặt cầu S: x  2  y z  2 2 2 3
2  m  4 . Tập các giá trị của m để mặt cầu S tiếp
xúc với mặt phẳng Oyz là: A.  5. B.  5. C.   0 . D. . Câu 74. Cho mặt cầu 2 2 2
(S) : x  y  z  2x  6y 8z 1 0. Xác định bán kính R của mặt cầu (S) và
viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu tại M 1;1;1?
A. R  5 , (P) : 4y  3z  7  0
B. R  5, (P) : 4x  3z  7  0
C. R  5 , (P) : 4 y  3z  7  0
D. R  3, (P) : 4x  3y  7  0
Câu 75. Cho mặt cầu S  tâm I 1;2;3 bán kính R  3 và hai điểm M 2;0;0 , N 0;1;0.
 X  : x  by  cz  d  0 là mặt phẳng qua MN và cắt Stheo giao tuyến là đường tròn có bán kính r lớn
nhất. Tính T  b  c  d . A. 1. B. 4. C. 2. D. 3 .
Câu 76. Cho mặt cầu S  x  y   z  2 2 2 :
2  1 và mặt phẳng   : 3x  4z 12  0 . Khẳng định nào sau đúng?
A. Mặt phẳng   đi qua tâm mặt cầu S  .
B. Mặt phẳng   tiếp xúc mặt cầu S  .
C. Mặt phẳng   cắt mặt cầu S  theo một đường tròn.
D. Mặt phẳng   không cắt mặt cầu S  .
Câu 77. Tìm tất cả các giá trị của m để phương trình 2 2 2
x  y  z  2mx  4 y  2z  6m  0 là phương
trình của một mặt cầu trong không gian với hệ tọa độ Oxzy. A. m 1;5 B. m  ;   1  5; C. m  5;  1
D. m  ; 5  1;
Câu 78. Cho mặt cầu S   x  2   y  2   z  2 : 1 2
3  25. Mặt phẳng Oxy cắt mặt cầu S  theo một
thiết diện là đường tròn C. Diện tích của đường tròn C là A. 8 B. 12 C. 16 D. 4 Câu 79. Cho I 1;1; 
1 và mặt phẳng P : 2x  y  2z  4  0 . Mặt cầu S  tâm I cắt P theo một
đường tròn bán kính r  4 . Phương trình của S  là
A.  x  2   y  2   z  2 1 1 1  16 .
B.  x  2   y  2   z  2 1 1 1  5 .
C.  x  2   y  2   z  2 1 1 1  9 .
D.  x  2   y  2   z  2 1 1 1  25.
Câu 80. Cho mặt phẳng Q : x  2y  z 5  0 và mặt cầu S   x  2  y   z  2 2 : 1 2 15. P  song
song với Q và cắt mặt cầu S  theo giao tuyến là đường tròn có chu vi 6 đi qua điểm nào sau đây? A. A0; 1; 5 B. B1;  2; 0 C. C 2;  2;  1 D. D 2  ; 2;   1
Câu 81. Cho mặt cầu S  2 2 2
: x  y  z  6x  4y  2z  5  0 . Phương trình mặt phẳng Q chứa trục Ox
và cắt S  theo giao tuyến là một đường tròn bán kính bằng 2 là
A. Q  : 2 y  z  0 .
B. Q  : 2 x  z  0 . C. Q : y  2z  0 .
D. Q  : 2 y  z  0 .
Câu 82. Cho hai mặt phẳng song song  : 2x  y  2z 1  0,  : 2x  y  2z  5  0 và một điểm 2  1  A 1  ;1; 
1 nằm trong khoảng giữa của hai mặt phẳng đó. Gọi S  là mặt cầu đi qua A và tiếp xúc với
 ,  . Biết rằng khi S thay đổi thì tâm I của nó nằm trên một đường tròn cố định . Tính diện 1   2 
tích hình tròn giới hạn bởi  . 2 4 8 16 A.  . B.  . C.  . D.  . 3 9 9 9
Câu 83. Cho A2;0;0, B0;2;0,C 0;0;2 . Có tất cả bao nhiêu điểm M trong không gian thỏa mãn
M không trùng với các điểm , A , B C và  AMB   BMC   CMA  90 ? A. 0 . B. 1. C. 2 . D. 3 .
S 1;1;6 A1;2;3 B3;1;2 C 4;2;3 D2;3;4
Câu 84. Cho hình chóp S.ABCD với , , , , . Gọi I S SAD là tâm mặt cầu
ngoại tiếp hình chóp. Tính khoảng cách d từ I đến mặt phẳng . 3 3 6 21 3 A. d  . B. d  . C. d  . D. d  . 2 2 2 2
Câu 85. Cho mặt cầu S 2 2 2
: x  y  z  2x  2y  2z  0 và điểm A2;2;0 . Viết phương trình mặt
phẳng OAB , biết rằng điểm B thuộc mặt cầu S  , có hoành độ dương và tam giác OAB đều. A. x  y  z  0 . B. x  y  z  0 . C. x  y  2z  0 . D. x  y  2z  0 . Câu 86. Cho hai điểm 2 2 A3;1;3 , B0; 2
 ;3 và mặt cầu S x   2 : 1  y   z   3 1. Xét điểm M
thay đổi thuộc mặt cầu S  , giá trị lớn nhất của 2 2 MA  2MB bằng A. 102. B. 78. C. 84 . D. 52 .
Câu 87. Cho mặt phẳng  P : x  2y  2z  3  0 và mặt cầu S  tâm I 5; 3
 ;5 , bán kính R  2 5 . Từ
một điểm A thuộc P kẻ một đường thẳng tiếp xúc với mặt cầu S  tại B . Tính OA biết AB  4 . A. OA  11 . B. OA  5 . C. OA  3 . D. OA  6 .
Câu 88. Cho mặt phẳng P có phương trình x  y  z  2 và mặt cầu S có phương trình 2 2 2
x  y  z  2 . Gọi điểm M  ;a ;bc thuộc giao tuyến giữa P và S. Khẳng định nào sau đây là khẳng định đúng? A. min c  1  ;  1 . B. min b1;  2 . C. max a  min b . D. max c   2; 2   .
Câu 89. Cho mặt cầu S có tâm I 3;2;2 bán kính R  2 , mặt cầu S có tâm I 1;0;1 bán kính 2   2  1   1  1
R  1 . Phương trình mặt phẳng P đồng thời tiếp xúc với S và S và cắt đoạn I I có dạng 2  1  2 1 2
2x  by  cz  d  0 . Tính T  b  c  d . A. 5  . B. 1. C. 3  . D. 2 . x  2  t 
Câu 90. Cho mặt cầu S  x   y  2   z  2 2 : 1
1  1 và đường thẳng d : y  t . Hai m phẳng z  t  
P,Q chứa d tiếp xúc với mặt cầu tại T và T. Điểm H  ;a ;bc là trung điểm đoạn TT , giá trị T  a  b  c là 1 2 A. 0 . B. . C. . D. 1. 3 3
Vấn đề 4. Phương trình đường thẳng trong hệ tọa độ Oxyz .
Câu 91. Trong không gian với hệ trục Oxyz, cho hai điểm A7; 2;1 và B 5; 4; 3 ,
mặt phẳng (P): 3x  2 y  6z  3  0 . Chọn đáp án đúng?
A. AB không đi qua điểm 1, 1,   1 B. AB vuông góc với mặt phẳng: 6x  3y  2z 10  0 x 112t x  5  
C. AB song song với đthẳng y  1   6t
D. AB vuông góc với đường thẳng y  1   2t z  1   4t   z  3t  x 1 y 1 z  2
Câu 92. Điểm nào dưới đây thuộc đường thẳng   ? 2 1  3 A. Q 2;1;3 . B. P 2;1;3. C. M 1;1;2 . D. N 1;1;2 . x  1 2t 
Câu 93. đường thẳng d :  y  2  3t , t   không đi qua điểm nào dưới đây? z  3t  A. ( Q 1;2;3) . B. M (3; 1  ;2). C. P(2; 2  ;3) . D. N( 1  ;5;4). x  3 y 1 z  4
Câu 94. Cho mặt phẳng   : x  2y  z  3  0 và đường thẳng d :   . Mmệnh đề nào 4 1  2 đúng?
A. d song song với   . B. d vuông góc với   . C. d nằm trên   . D. d cắt   x 1 y z 1
Câu 95. Trong không gian hệ tọa độ Oxyz, hai đường thẳng d :   ; 1 2 3 1 x 1 y  2 z  7 d :  
có vị trí tương đối là: 2 1 2 3 A. song song B. trùng nhau C. cắt nhau D. chéo nhau x y  z 
Câu 96. Cho ba điểm A3; 1  ;2, B4; 1  ; 
1 , C 2;0;2 và đường thẳng d  2 3 :   . Gọi M 1 3 1  d  ABC là giao điểm của và mp
. Độ dài đoạn OM bằng A. 2 2 B. 3 C. 6 D. 3
Câu 97. Cho ba điểm A1;2;  1 , B 2; 1
 ;4 và C 1;1;4 .Đường thẳng nào dưới đây vuông góc với mp  ABC x y z x y z x y z x y z A.   . B.   . C.   . D.   . 1 1 2 2 1 1 1 1 2 2 1 1 
Câu 98. Viết phương trình tham số của đường thẳng đi qua hai điểm A 1; 2; 3, B 2;  3;1 . x  1 t x  2  t x  3  t x  1 t     A.  y  2  5t . B.  y  3   5t . C.  y  8   5t . D.  y  2  5t . z  3   2t     z  1 4t  z  5  4t  z  3  4t 
Câu 99. Viết phương trình tham số của đường thẳng (D) qua I 1;5; 2 và song song với trục Ox. x  t 1 x  m x  2  t    A. y  5 ;t  B. y  5m;m  C. y 10t ;t  D. Hai câu A và C đều z  2    z  2m  z  4t  đúng
Câu 100. Phương trình chính tắc của đường thẳng d đi qua điểm M (1; 2
 ;5) và vuông góc với mặt
phẳng ( ) : 4x  3y  2z  5  0 là x 1 y  2 z  5 x 1 y  2 z  5 A.   . B.   . 4 3 2 4 3  2 x 1 y  2 z  5 x 1 y  2 z  5 C.   . D.   . 4  3  2  4  3  2 x 1 y 1 z  2
Câu 101. Cho đường thẳng d :  
và mặt phẳng P : x  y  z 1  0 . Viết phương 2 1 3
trình đường thẳng  đi qua ( A 1;1; 2
 ) , song song với mặt phẳng (P) và vuông góc với đường thẳng d . x 1 y 1 z  2 x 1 y 1 z  2 A.  :   B.  :   2 5 3 2 5 3  x 1 y 1 z  2 x 1 y 1 z  2 C.  :   D.  :   2  5 3 2 5  3
Câu 102. Gọi d là giao tuyến của hai mặt phẳng   : 2x  y  3z  7  0 và   : x  2y  z  2  0 .
Đường thẳng d đi qua điểm nào dưới đây? A. Q(2; 1  ;3) . B. M (1;0; 3  ). C. P( 1  ;0;3) . D. N(1; 2  ;1). x  2 y 1 z 1
Câu 103. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và điểm 1 1 2
A 2;1;0 . Viết phương trình mặt phẳng (P) đi qua A và chứa d?
A. x  7 y  4z  9  0
B. x  7 y  4z  8  0
C. x  6 y  4z  9  0 D. x  y  4z  3  0 x 1 y  2 z  3
Câu 104. Trong không gian Oxyz, cho điểm A3; 2; 3 và hai đường thẳng d :   1 1 1 1  x  3 y 1 z  5 và d :  
. Phương trình mặt phẳng chứa d 2 1 và d2 có dạng: 1 2 3
A. 5x  4 y  z 16  0
B. 5x  4 y  z 16  0
C. 5x  4 y  z 16  0
D. 5x  4 y  z 16  0 x  3 2t x  m  3  
Câu 105. Cho hai đường thẳng d : y 1 t ; d : y  2  2m . Phương trình tổng quát của mặt 1   2 z 2 t     z  1 4m  
phẳng (P) chứa d và song song với d là: 1 2
A. x  7 y  5z  20  0
B. 2x  9 y  5z  5  0 C. x  7 y  5z  0
D. x  7 y  5z  20  0 x 1 y z 1
Câu 106. Cho đường thẳng ∆ có phương trình  
và mặt phẳng (P): 2x  y  2z 1  0 . 2 1 1 
Phương trình mặt phẳng (Q) chứa ∆ và tạo với (P) một góc nhỏ nhất là: A. 2x  y  2z 1  0
B. 10x  7 y 13z  3  0 C. 2x  y  z  0
D. x  6 y  4z  5  0 x  6 y  2 z  2 Câu 107. Cho mặt cầu 2 2 2
(S) : (x 1)  (y  2)  (z 3)  9 và đường thẳng  :   . 3 2 2
Phương trình mặt phẳng (P) đi qua M(4;3;4), song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) là:
A. 2x  y  2z 19  0
B. x  2 y  2z 1  0
C. 2x  2 y  z 18  0
D. 2x  y  2z 10  0 x  2  t 
Câu 108. Cho đường thẳng d : y  3
  2t t  . Gọi d là hình chiếu vuông góc của d trên mặt z 13t 
phẳng tọa độ Oxz . Viết phương trình đường thẳng d . x  2  t x  2  t x  0 x  2  t     A.  y  0
t  . B. y  3 2t t  . C. y  3
  2t t  . D. y  3   2t t  z 1 3t     z  1 3t  z  1 3t  z  0  x 1 y  5 z  3
Câu 109. Cho đường thẳng d :  
. Phương trình nào dưới đây là phương trình hình 2 1  4
chiếu vuông góc của d lên mặt phẳng P : x  5  0 . x  5 x  5 x  1 x  1     A.  y  7  t . B.  y  7  t . C. y  5   2t . D. y  5   t . z 11 4t     z  11 4t  z  3  t  z  3  4t 
Câu 110. Phương trình đường thẳng d là hình chiếu vuông góc của đường thẳng d trên mặt phẳng x 12  4t  
P , biết d : y  9  3t và P :3x  5y  z  2  0. Đường thẳng d là giao tuyến của hai mphẳng z 1t  nào?
A. 3x  5y  z  2  0 và 8x  7 y 11z  22  0 .
B. 3x  5y  z  2  0 và 4x  7 y  z  22  0 .
C. 3x  5y  z  2  0 và x  y 11z  22  0 .
D. 3x  5y  z  2  0 và 8x  3y  z  2  0 . x y  z 
Câu 111. Cho mặt phẳng P : x  y  z  3  1 2
0 và đường thẳng d :   . Đường thẳng d ' 1 2 1 
đối xứng với d qua mặt phẳng  P có phương trình là x 1 y 1 z 1 x 1 y 1 z 1 x 1 y 1 z 1 x  y  z  A.   . B.   .C.   1 1 1 .D.   . 1 2 7 1 2 7 1 2 7 1 2 7
Câu 112. Trong không gian với hệ tọa độ Oxyz , cho điểm A1; 2;  3 và mặt phẳng  
P : 2x  2y  z  9  0 . Đường thẳng d đi qua A và có vectơ chỉ phương u  3; 4;  4 cắt P tại
điểm B . Điểm M thay đổi trong P sao cho M luôn nhìn đoạn AB dưới góc 0 90 . Khi độ dài MB
lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau? A.  2  ; 1  9;3 . B. 3;0;15 . C. 18; 2  ;4  1 . D.  3  ;20;7 .
Câu 113. Viết phương trình đường thẳng đi qua A1; 1  ; 
1 , vuông góc và cắt đường thẳng x  4 y  2 z  5 d :   . 1  1 1 x 1 y 1 z 1 x 1 y 1 z 1 x 1 y 1 z 1 x 1 y 1 z 1 A.   . B.   .C.   . D.   . 5 1 8  1 5 4 5 5 4 5 1 8 x  y z 
Câu 114. Cho mặt phẳng  P : x  2y  z  4  1 2 0 và đường thẳng d :   . Viết phương 2 1 3
trình đường thẳng  nằm trong mặt phẳng  P đồng thời cắt và vuông góc với đường thẳng d. x 1 y 1 z 1 x 1 y 1 z 1 x 1 y 1 z 1 x 1 y 1 z 1 A.   B.   C.   D.   5 1 3 5 1 3 5 1  2 5 1 3 x  3 y  3 z  2 x  5 y 1 z  2
Câu 115. Cho 2 đường thẳng d :   d :   1 ; 2 và mp 1 2 1 3  2 1
P: x  2y 3z 5  0 . Đường thẳng vuông góc với P, cắt d và d lần lượt tại , A B . Độ dài đoạn 1 2 AB là A. 2 3 . B. 14 . C. 5. D. 15 . 
Câu 116. Cho đường thẳng d có vectơ chỉ phương u  (1;0; 2  ) và đi qua điểm 1 x  3 y 1 z  4 M (1; 3; 2), d :  
. Phương trình mặt phẳng (P) cách đều hai đường thẳng d và d có 2 1 2  3 1 2
dạng ax  by  cz 11  0. Giá trị a  2b 3c bằng A. 42 . B. 3  2. C. 11. D. 20 . x 1  y 1 z 2
Câu 117. Cho điểm A1;2;  1 , đường thẳng d :   và mặt phẳng 2 1 1  P: x y2z 1
 0. Điểm B thuộc P thỏa mãn đường thẳng AB vừa cắt vừa vuông góc với d . Tọa độ điểm B là: A. 6; 7  ;  0 . B. 3; 2  ; 1. C.  3  ;8;  3 . D. 0;3;  2  . x 1 y z  2
Câu 118. Cho đường thẳng d và mặt phẳng P lần lượt có phương trình   và 2 1 1
x  y  2z  8  0 , điểm (
A 2;1; 3). Phương trình đường thẳng  cắt d và (P) lần lượt tại M và N
sao cho A là trung điểm của đoạn thẳng MN là x 1 y  5 z  5 x  y  z  A.   2 1 3 . B.   . 3 4 2 6 1 2 x  5 y  3 z  5 x  y  z  C.   5 3 5 . D.   . 6 1 2 3 4 2
Câu 119. Cho mặt phẳng P : x  2y  2z  5  0 và hai điểm A 3  ;0; 
1 , B 0;1;3 . Viết phương
trình đường thẳng d đi qua A và song song với  P sao cho khoảng cách từ B đến đường thẳng đó là nhỏ nhất. x  3   2t x  3 2t x  3 2t x  3   2t     A.  y  t  . B.  y  t . C.  y  t  . D.  y  t . z 1     z  1  z  1  z  1 
Câu 120. Trong không gian Oxyz cho 2 điểm A1;3;0 và B 2;1;  1 và đường thẳng  x 1 y 1 z :  
. Viết phương trình mặt cầu đi qua A, B có tâm I thuộc đường thẳng  ? 2 1 2 2 2 2  2   13   3  521 2 2 2  2   13   3  25 A. x   y   z         B. x   y   z          5   10   5  100  5   10   5  3 2 2 2  2   13   3  521 2 2 2  2   13   3  25 C. x   y   z         D. x   y   z          5   10   5  100  5   10   5  3 x  t 
Câu 121. Trong mặt phẳng Oxyz, cho đường thẳng d :  y  1 và 2 mặt phẳng (P) và (Q) lần lượt có  z  t  
phương trình x  2y  2z  3  0 ; x  2y  2z  7  0 . Mặt cầu (S) có tâm I thuộc đường thẳng (d), tiếp
xúc với hai mặt phẳng (P) và (Q) có phương trình
A.  x  2   y  2   z  2 4 3 1 3 
B.  x  2   y  2  z  2 4 3 1 3  9 9
C.  x  2   y  2   z  2 4 3 1 3 
D.  x  2   y  2   z  2 4 3 1 3  9 9 x  4 y  4 z  3
Câu 122. Trong không gian Oxyz, cho điểm I 1;3;2 và đường thẳng  :   . 1 2 1
Phương trình mặt cầu (S) có tâm là điểm I và cắt  tại hai điểm phân biệt A, B sao cho đoạn thẳng AB có độ dài bằng 4 là:
A. S  x  2   y  2 2 : 1 3  z  9
B. S   x  2   y  2   z  2 : 1 3 2  9
C. S  x  2   y  2   z  2 : 1 3 2  9
D. S   x  2   y  2   z  2 : 1 3 2  9 Câu 123. Cho E 0; 1  ; 5
  , mp P : 2x  2y  z 3  0 và mặt cầu S  x  2   y  2 2 : 4 1  z  25 .
Gọi  là đt đi qua E , nằm trong P và cắt S  tại hai điểm có khoảng cách lớn nhất. Phương trình của  là x  11t x  50t x  11t x  50t     A. y  1 2t . B. y  1   23t . C. y  1 2t . D. y  1 23t . z  5  26     t z  5  7  t z  5  26t  z  5  7  t x  1 t 
Câu 124. Cho mặt cầu S  2 2 2
: x  y  z  2x  4y  6z  m  3  0 . Tìm m để d : y 1 t cắt S  tại z  2  hai điểm phân biệt 31 31 31 31 A. m  . B. m  . C. m  . D. m  . 2 2 2 2 x y 1 z 1 x 1 y z  3
Câu 125. Góc giữa hai đường thẳng d :   và d :   bằng: 1 1 1  2 2 1  1 1 A. 45o B. 90o C. 60o D. 30o x  5  t 
Câu 126. Góc giữa đường thẳng d :  y  6 và mp P : y  z 1  0 là: z  2t  A.300 B.600 C.900 D.450
Câu 127. Trong không gian với hệ tọa độ Oxyz cho A3;0;  1 , B 6; 2; 
1 . Viết phương trình mặt phẳng 2
(P) đi qua A, B và (P) tạo với mp Oyz góc  thỏa mãn cos  ? 7
2x  3y  6z 12  0
2x  3y  6z 12  0 A.  B.  2x  3y  6z  0 2x  3y  6z 1  0
2x  3y  6z 12  0 2x 3y  6z 12  0 C.  D.  2x  3y  6z  0 2x 3y  6z 1 0 x  2  2t x  5  3s   d : y  1 d : y  1 1 2 z  2   t z  3  s
Câu 128. Cho điểm A(1;1;1) và hai đường thẳng  ;  .
Gọi B,C là các điểm lần lượt di động trên d ; d . Giá trị nhỏ nhất của biểu thức P =AB +BC +CA là: 1 2 A. 2 29 B.    2 985 C. 5 10 29 D. 5 10
Câu 129. Cho điểm A0;1;9 và mặt cầu S   x  2   y  2   z  2 : 3 4
4  25. Gọi C là đường tròn
giao tuyến của S  với mp Oxy ; điểm B và C di chuyển trên C  sao cho BC  2 5 . Khi tứ diện
OABC có thể tích lớn nhất thì đường thẳng BC có phương trình là  21  21  21 x   4  t x   3t x   4t 5    x  21 4t 5  5   28   28  28 A.  y   3t . B.  y  28  3t . C.  y   4t . D.  y   3t . 5   5  5  z  0 z  0  z  0 z  0   
Câu 130. Cho điểm E 2;1;3 , mp  P : 2x  2y  z  3  0 và mặt cầu
S x  2   y  2 z  2 : 3 2
5  36 . Gọi  là đường thẳng đi qua E , nằm trong P và cắt S  tại 
hai điểm có khoảng cách nhỏ nhất. Biết  có một vec-tơ chỉ phương u  2018; y ; z T  z  y . 0 0  . Tính 0 0 A. T  0 . B. T  2018 . C. T  2018 . D. T  1009 .
Câu 131. Cho điểm A0;1; 2
  , mặt phẳng P : x  y  z 1  0 và mặt cầu S 2 2 2
: x  y  z  2x  4y  7  0. Gọi  là đường thẳng đi qua A nằm trong mặt phẳng P và cắt mặt
cầu S  tại hai điểm B,C sao cho tam giác IB C có diện tích lớn nhất với I là tâm của mặt cầu S  . Phương trình của  là x  t x  t x  t x  t     A.  :y 1 . B.  : y 1 t . C.  :y 1 t . D.  : y 1 . z  2   t     z  2   z  2   z  2  t   1 3  Câu 132. Cho điểm M  ;
;0 và mặt cầu S  2 2 2
: x  y  z  8. Đường thẳng d thay đổi, đi qua  2 2   
điểm M , cắt mặt cầu S  tại hai điểm phân biệt , A .
B Tính diện tích lớn nhất S của tam giác OA . B A. S  7 . B. S  4 . C. S  2 7 . D. S  2 2 .
Câu 133. Cho điểm A1;1; 
1 , B2;2;2 và mặt cầu S  2 2 2
: x  y  z  2x  2y  4z 10  0 . Gọi P là mặt phẳng đi qua ,
A B và cắt S  theo một thiết diện là đường tròn C. Đường thẳng AB cắt C
tại hai điểm E, F . Điểm C thuộc đường tròn C  sao cho tam giác CEF cân tại C , CH là đường cao
ứng với cạnh EF . Khi thiết diện có diện tích nhỏ nhất thì phương trình của CH là x  1 t x  1 t x  1   t x  1 t     A.  :y 1 . B.  :y 1 t . C.  : y 1 t . D.  : y  1 . z 1t     z  1  z  0  z  2  t  x y 1 2  z
Câu 134. Cho đường thẳng d :  
. Gọi P là mặt phẳng chứa đường thẳng d và tạo với 1 2  1
mặt phẳng Q : 2x  y  2z  2  0 một góc có số đo nhỏ nhất. Điểm A1;2;3 cách P một khoảng bằng: 5 3 7 11 4 3 A. 3 . B. . C. . D. . 3 11 3 x  1 2t 
Câu 135. Cho đường thẳng d : y  1 t và hai điểm A 1;0;  1 , B 2;1;  1 . Tìm điểm M thuộc z  t 
đường thẳng d sao cho MA  MB nhỏ nhất.  3 1   5 1 1   5 2 1  A. M 1;1;0 . B. M ; ;0   . C. M ; ;   . D. M ; ;   .  2 2   2 2 2   3 3 3  x y z 1 x  y z
Câu 136. Cho hai đường thẳng  :   1 và  :
  . Xét điểm M thay đổi. Gọi a, b 1 1 1 1 2 1
lần lượt là khoảng cách từ M đến  và  . Biểu thức 2 2
a  2b đạt nhỏ nhất khi và chỉ khi M  M x ; y ; z x  y 0  0 0 0  . Khi đó 0 0 bằng 2 4 A. . B. 0 . C. . D. 2 . 3 3
Câu 137. Cho ba điểm không thẳng hàng A3;0;0, B 0;3;0, C 0;0;3. Hai mặt cầu có phương trình S  2 2 2
: x  y  z  2x  4y  6z  9  0
S : x  y  z 8x  4z 8  0 2  2 2 2 1 và
cắt nhau theo đường tròn
C. Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa C và tiếp xúc với ba đường thẳng AB, BC,CA? A. vô số B. 1 C. 3 D. Không có x  2  t 
Câu 138. Cho mặt cầu S  x   y  2   z  2 2 : 1
1  1 và đường thẳng d : y  t . Hai mặt phẳng z  t  
P,Q chứa d , tiếp xúc với S tại T và T '. Điểm H  ;a ;bc là trung điểm của đoạn TT ', giá trị
của biểu thức T  a  b  c là 1 2 A. 0 . B. . C. . D. 1. 3 3 x  y  z 
Câu 139. Cho mặt cầu S  2 2 2
: x  y  z  2x  4y  6z 13  1 2 1 0 và đường thẳng d :   . 1 1 1 Điểm M  ; a ;
b c,a  0 nằm trên đường thẳng d sao cho từ M kẻ được ba tiếp tuyến M , A MB, MC
đến mặt cầu S  ( ,
A B, C là các tiếp điểm) và  0 AMB  60 ,  0 BMC  60 ,  0 CMA 120 . Tính 3 3 3 a  b  c 173 112 23 A. 3 3 3 a  b  c  . B. 3 3 3 a  b  c  . C. 3 3 3 a  b  c  8 . D. 3 3 3 a  b  c  . 9 9 9
Vấn đề 5. Tọa độ hóa bài toán hình trong Không gian
Câu 140. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  , a BC  a 3, SA  a và SA
vuông góc với đáy ABCD . Tính sin với  là góc tạo bởi đường thẳng BD và mặt phẳng (SBC) . 2 A. sin  7 . B. sin  3 . C. sin  3 . D. sin  . 4 8 5 2
Câu 141. . Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA  2a vuông góc với đáy.
Gọi M là trung điểm cạnh SD. Tính cos của góc tạo bởi hai mặt phẳng (AMC) và (SBC). 5 5 3 2 A. . B. . C. . D. . 5 3 2 3
Câu 142. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , biết SO  a và SO
vuông góc với mặt đáy  ABCD . Gọi M , N là trung điểm của S ,
A BC . Gọi  là góc giữa đường thẳng
MN và mặt phẳng SBD . Tính cos . 2 21 5 2 A. . B. . C. . D. . 7 7 10 5
Câu 143. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA  a và SA vuông góc với
đáy. Gọi M là trung điểm SB và N là điểm thuộc cạnh SD sao cho SN  2ND . Tính thể tích khối tứ diện ACMN . 1 1 1 1 A. 3 V  a . B. 3 V  a . C. 3 V  a . D. 3 V  a . 12 8 6 36
Document Outline

  • Đề cương Toán 12 - Đại số - Gửi HS
  • Đề cương Toán 12 - Hình - Gửi HS