Trần Kim Ngân K9A Chương 1:
KHÁI LƯỢC VỀ LOGIC HỌC
I. ĐỐI TƯỢNG CỦA LOGIC HỌC 1. Thu t
ậ ngữ logic
- Thay đổi giờ h c ọ , giờ Logos: làm 10 năm trước
 Từ ngữ, lời nói, câu, quy tắc viết => chưa đ nh giá á đc đầy
đủ nguyên nhân tắc
 Sự lập luận/ cái k thể khác (tất yếu)/ tính có QUY LUẬT LOGIC đường  Tính QL trong s v
ự ận động & phát triển c a
ủ SVHT (logic khách quan)
 Cơ sở hạ tầng, hệ
- Là các QL trong hiện thực khách quan.
thống đường xá (cấm
(diễn ra tất yếu, không phụ thuộc ý thức của con người)
xe máy vào nội đô, e ơi
QL chỉ những mlh có t/c bên trong, b n ả ch t ấ , t t
ấ yếu, bền vững, lặp đi lặp HN ph , ố ngõ ngách,
lại giữa các đối tượng ho c
ặ giữa các thành t c ố
ấu thành nên các đối tượng đó. tập quán, ĐK sinh Khách quan t n t ồ i
ạ bên ngoài con ngoài, t n t ồ i
ạ phát triển không ph t ụ huộc hoạt)
ý thức con người.
 Ý thức người dân - H c
ọ logic khách quan ở các b m
ộ ôn KH cụ thể
tham gia phương tiện - ng t Tư duy có vận độ heo QL công c ng, ộ …
=> QL của tư duy gọi là logic ch quan ủ
 Tính QL trong tư tưởng, lập luận (logic chủ quan)
- Biểu thị các QL bắt buộc mà QT tư duy phải tuân theo nh m
ằ phản - M i
ọ bột giặt đều chứa
ánh đúng hiện thực cũng như các quy tắc, lập luận khoa học chất làm ạ
h i da tay, trừ
=> QL của tư duy bột gi t ặ này.
- Nếu tư duy k có tính QL thì? Phản ánh sai hiện thực, tư duy k thể - Cấm k
đổ rác ở đây,
hiện tính đúng đắn =>lập luận có vấn đề phạt 50k.
- Ở đâu rẻ nh t
ấ , ở đây rẻ  KH nghiên c u v ứ
ề tư duy (logic học ) hơn. 2. Thu t
ậ ngữ logic h c ọ
- Tư duy phản ánh k chân thực (sai) - xét về h u ậ qu ả => ng ộ  Thườ ầ
ng do nh m lẫn, hiểu sai về ả b n chất đối tượ ,… ng biện nguy hi ểm hơn  Nguyên nhân - x t
é về PL cụ thể => + khách quan – ng bi
ộ ện: phương tiên nhận thức, sự vận n
độ g, biến đổi nguỵ biện nguy hi ểm hơn của SVHT + ch quan ủ ngu –
ỵ biện: năng lực nhận thức hạn chế - n á Tư duy phả nh chân thực (đúng)
Thi TRẮC NGHIỆM Đúng ngẫu nhiên
Đúng tất yếu
 Học chắc kiến
- K dựa trên QL/qui tắc + bằng chứng - Dựa trên QL/qui tắc + bằng ch n ứ g
thức, k/n sai ít KH KH  Vào random =>
- Có thể xuất hiện k/n sai
- Không có (hoặc k nhiều) k/n sai đúng ngẫu nhiên
=> mục đích nghiên cứu logic học: nghiên cứu tư duy đúng tất yếu (tư duy tiếp Trời mưa => đường ướt cận chân lí)
Đường ướt => trời mưa? Logic h c
ọ nghiên cứu gì về tư duy đúng đắn?
- Logic học vs tư cách là 1 bộ môn KH nghiên cứu về tư duy dưới góc độ cấu trúc & mlh giữa các b ph ộ ận của nó - Tư duy
 Nội dung (tính chân thực): toàn bộ những mặt, những thuộc tính cấu thành nên đối tượng
=> Tri thức khác nhau đc khái quát lại thành mệnh đề tư tưởng có nghĩa (có tính chân thực ) Trần Kim Ngân K9A
 Hình thức (tính đúng đắn): toàn bộ phương thức t n ổ t i
ạ , phát triển, nh ng ữ
mlh mang tính ổn định
giữa các bộ phận c ng
ấu thành nên đối tượ
=> kết cấu đc cấu thành từ những yếu tố gì, phương th c ứ liên kết c a ủ các b
ộ phận của tư tương (kết hợp 2 khái niệm, sử d ng t ụng lượ ừ
Logic học quan tâm, nghiên cứu hình thức & các QL của tư duy đúng đắn
- các hình thức CB của tư duy: KN Phán đoán , , Suy luận, Chứng minh - Các QL CB c ủa tư duy
 QL CB: QL đồng nhất, QL cấm mâu thuẫn, QL bài trung, QL lý do đầy đủ
 QL k CB: t/đ đến từng loại hình tư duy
Logic học đại cương chỉ nghiên cứu Logic h c
ọ hình thức ?
=> LOGIC lưỡng trị: Logic h u v
ọc đại cương là KH nghiên cứ ề các hình th c
ứ & các QL của TD đúng cho phép 2 giá trị
đắn để phản ánh đối tượng ở mặt hình thức của nó hay ns cách khác là để phản (Đ hoặc S)
ánh đối tượng ở trạng thái đứng im tương đối
=> là LOGIC HÌNH THỨC (phân biệt vs logic biến chứng ph – ản ánh sự vật ở trạng thái vận độ ồ ng kh ừ n ng ng)
Nhiệm vụ CB của logic hình thức ? - Làm sáng t
ổ những ĐK cần để đạt tới tri th c
ứ chân thực, phân tích kết cấu của QT tư duy, vạch ra nh ng ữ
thao tác logic & pp lập luận chính xác
II. KHÁI LƯỢC CÁC GIAI ĐOẠN PHÁT TRIỂN CỦA LOGIC HỌC 1. LGH c ổ đại
- Vs tư cách là 1 KH, logic học đ nh c hì
thành từ TK IV – TCN & đc đánh dấu bằng bộ sách Organon (công
cụ nhận thức) của triết gia người Hy Lạp Aristote.
- Aristote (384 – 322 TCN) đc coi là người sáng lập ra logic học. Ông đã bao quát đc toàn bộ phạm vi & nắm
đc thực chết, đtg của logic học, đặt nền tảng cho KH logic, đó là sự tổng kết những hình thức CB của tư duy & n ng ữ QL CB của tư duy. c
Đặ Biệt Aristote đã xd hoàn chỉnh lý thuyết về tam đoạn luận, hình th c ứ CB
nhất của suy lý diễn dịc h
2. GĐ phát triển mới của logic học hình thức - Vào thời kỳ Ph t
ục Hưng, mặ tích cực, tinh thần khách quan KH của logic Aristote đc phục h i ồ & phát huy để c ố h ng lại thầ ọ
n h c. Tuy nhiên, bấy giờ nó đã bộc lộ sự c ậ h t hẹ ạ
p, h n chế trước tiến bộ của KH - F.Bacon (1561
– 1626): triết gia người Anh đã xd 1 cách KH logic ms vs t/p Novum Organum (công c ụ
ms). Ông đặc biệt chú ý phương pháp suy lu n ậ qui n p ạ
- R. Descarates (1596 1
– 650) nhà triết học người Pháp, trong khi Bacon đề cao qui nạp & KH th c ự nghiệm
thì R. Descarates lại đề cao pp diễn dịch & toán học . 3. Logic h c
ọ hiện đại - Logic hình th c ứ c
ổ điển dưới hình thức toán b c ộ l nh ộ ng h ữ ạn chế. T ừ đó xuất hi ng ện 2 khuynh hướ
 Thứ nhất, ra sức hoàn thiện những công trình logic, hình th c
ứ hóa & toán học hóa để nhằm khắc phục
các mâu thuẫn & nghịch lý logic.
 Thứ 2, xét lại 1 số QL CB của logic cổ điể
n, phát triển thành logic phi cổ điển - Đặc m điể chung c a
ủ logic hình twhcs phi cổ điển là logic đa trị khác hẳng vs logic hình th c ứ cổ điển như
loic tam trị của Lukasiewicz (1878
– 1956), logic tam trị xác suất c a ủ H. Reichenbach (1891 – 1953), logic
trực giác của L. E. Brower và A. Heiting, Logic kiến thiết c a
ủ A.A. Marcov, A. N. Kolmogorov, V.I.Glivenko, logic mờ c a
ủ L.A.Zadeh, logic tình thái, logic thời gian.
III. Ý NGHĨA CỦA LOGIC H C Ọ - Logic h c
ọ giúp chúng ta chuyển t
ừ tư duy logic tự phát sang t gi ự ác - Nắm vững tri th c ứ logic h c
ọ giúp ta lập luận, diễn gi v
ải cũng như CM, bác bỏ ấn đề có sức thuyết phục .
- Logic còn giúp chúng ta chính xác hoá ngôn ngữ thể hiện ở việc dùng từ chính xác, đặt câu rõ ràng, k mơ hồ Trần Kim Ngân K9A Chương 2: KHÁI NIỆM
I. KHÁI LƯỢC VỀ KHÁI NIỆM 1. Bản ch t ấ của KN
 cảm giác: sự tác ng độ - K
N là hình thức CB của tư duy trừu tượng, trong đó phản ánh các dấu hiệu CB
của SVHT lên các giác
khác biệt của 1 SVHT hay 1 l m
ớp SV => Đặc điể c a ủ KN quan
 tri giác: t p ậ h p ợ c a ủ  KN là hình th c ứ CB của tư duy
nhiều cảm giác => sự
tác động lên các giác quan tr ở nên rõ ràng NHẬN THỨC hơn TRỰC QUAN
 biểu tượng: dù ta k SINH ĐỘNG TƯ DUY TRỪU TƯỢNG nhìn th y
ấ 1 cách trực
tiếp, SVHT k còn tác (Nhận thức cảm tính) (Nhận thức lý tính)
động lên tri giác thì
vẫn có thể tưởng tượng
về SVHT đó Cảm Tri Biểu KN PĐ SL CM
=> tiếp tục đi lên 1 mức giác giác tượng
độ cao hơn: dù nhận
thức đã gần như hoàn
=> Khái niệm là hình thức cơ bản đầu tiên c ủa tư duy
chỉnh nhưng vẫn mang tính c m
ả tính, hiểu biết
 KN phản ánh đối tượng thông qua các dấu hiệu CB khác biệt
mang tính bề ngoài,
+ đối tượng của tư duy là SVHT
chưa phân biệt đc bản
+ Mỗi đối tượng luôn 3 g m ồ 3 yếu tố
chất, cái chung, cái
riêng => c n ầ 1 nh n ậ thức
cao hơn => tư duy trừu
YẾU TỐ THUỘC TÍNH (DẤU HIỆU)
tượng => khái quát hoá, = t t
ấ cả những gì t n ồ t i
ạ bên trong đối
đưa ra tri thức cụ thể.
tượng (thuộc tính), đc đối tượng ộ b c lộ
(thể hiện) ra bên ngoài, trở thành dấu
hiện để nhận biết đối tượng. => giúp chúng ta  Nhận th ức đc về ĐT  Phân bi ệt các ĐT vs nhau
 Gọi tên (định danh) ĐT
=> Đây là yếu tố mà KN quan tâm VD: hình vuông
- Dấu hiệu k bản chất: là những dấu hiệu bên ngoài, k quyết địn s
ự vận động và - K BC: có 1 c nh ạ = 8cm phát triển của SVHT - BC chung: là 1 d ng ạ
- Dấu hiệu b n c ả h t
ấ : là những dấu hiệu bên trong, quyết định sự vận động và phát hình h c ọ ph ng ẳ triển của SVHT
- BC khác biệt: là 1 hình
 Dấu hiệu bản ch t ấ CHUNG: là nh ng ữ dấu hiệu tất yếu t n
ồ tại ở đtg nhưng có 4 c nh ạ b ng ằ nhau và cũng tồn tại ở ững đtg/ lớp đtg khác nh 4 góc vuông
 Dấu hiệu bản chất KHÁC BIỆT: là dấu hiểu BC tồn tại trong 1 đtg/ lớp
đtg khiến chúng khác biệt vs đtg/ lớp đtg khác Trần Kim Ngân K9A
2. KN & từ KN TỪ - là 1 hình th c ứ logic c ủa tư duy
- là sự quy ước mang tính riêng biệt c a ủ m i ỗ c ng ộ
đồng, phương tiện để gắ ết, lưu giữ n k tư tưở ng - là 1 phạm trù logic h c ọ
- là 1 phạm trù của ngôn ngữ học
- KN đc hình thành trên cơ sở những từ xđ có nghĩa - T ừ V là cơ sở C của KN  K thể có KN ngoài t ừ
 Mọi KN đều đc thể hiện bằng TỪ hay CỤM TỪ  K có t t
ừ hì k thể hình thành & sd đc KN
 Nhưng k phải từ nào cũng thể hiện KN - va KN đóng i trò N D - T ừ đóng vai trò hình th c ứ => 1 KN có thể di t ễn đạ bằng nhiều t ừ => 1 t c
ừ ó thể biểu đạt nhiều KN khác nhau (ĐỒNG NGHĨA KHÁC ÂM) (ĐỒNG ÂM KHÁC NGHĨA)
Từ k thể hiện KN: từ cảm thán,… Vd: đàn, đống, lũ
3. Cấu trúc của KN: n i
ộ hàm – ngoại diên a. Nội hàm:
- là tập hợp tất cả những dấu hiệu bản chất đặc trưng, n
vố có của các SVHT đc Nội hàm của KN “số
phản ánh trong khái niệm
chẵn” là dấu hiệu “chia - là n i ộ dung c m
ủa KN, đặc trưng cho KN về ặt chất hết cho 2” - Có thể đc biểu di
ễn dưới dang: A(a,b,c,d,…) KN “ số c ẵn” h có ngoại b. Ngo i ạ diên: diên là t p
ậ hợp các s ố
- là tập hợp tất cả các SVHT có chung nh n
ữ g dấu hiệu BC đặc trưn n á g đc phả nh 2,4,6 trong n i ộ hàm KN - m Đặc trưng cho KN về ng ặt lượ
=> Ngoại diên của KN là phạm vi đối tượng mà khái niệm phản ánh c. mqh - N i
ộ hàm & ngoại diên là 2 b ph ộ
ận hợp thành KN, có mqh chặt chẽ vs nhau, làm
tiền đề tồn tại cho nhau.
- Mqh ngược - nghịch biến: nội hàm càng r n
ộ g thì ngoại diên càng hẹp & ngược lại 4. Các lo i ạ hình KN
- Dựa vào nội hàm: 6 loại (3 cặp) Trần Kim Ngân K9A - D a ự vào ngoại diên
5. QH giữa các KN
a. QH tương thích (điều hoà, trung lặp): Ngoại diên c a
ủ chúng có ít nhất 1 đối tượng chung nhau (ít nhất 1
phần ngoại diên trùng nhau) b. QH k tương thích u hoà, k trùng l (k điề ặp): Ngoại diên c a ủ chúng k có bất k
ỳ đối tượng nào chung nhau Trần Kim Ngân K9A
II. THAO TÁC LOGIC ĐỐI VỚI KHÁI NIỆM
1. Thu hẹp và mở r n ộ g KN
- Thu hẹp KN: là 1 thao tác logic giúp ta chuyển từ KN có ngoại diên rộng đến KN có ngoại diên hẹp hơn
bằng cách thêm vào KN ban đầu những dấu hiệu mới mà chỉ thuộc về 1 bộ ận đối ph tượng nằm trong ngoại
diên của đối tượng ban đầu - Mở r ng ộ
KN: là 1 thao tác logic giúp ta chuyển từ KN có ngoại diên hẹp sang KN có ngoại diên rộng hơn
bằng cách tước bỉ những dấu diệu chỉ thuộc về nh m
ững đtg nằ trong ngoại diên của KN ban đâu 2. Định nghĩa KN
- là 1 thao tác logic giúp chúng ta chỉ ra n i
ộ hàm của KN & làm rõ GT, ý nghĩa của ngoại diên biểu thị K N - Kết cấu logic c ủa định nghĩa KN  KN đc định nghĩa
 KN dùng để định nghĩa
- Các quy tắc định nghĩa KN
 Định nghĩa phải cân đối, có nghĩa là ngoại diên của KN cần định nghĩa phải ừa v đúng bằng ngoại diên c
ủa KN dùng để định nghĩa
 Định nghĩa phải rõ ràng, ngắn gọn, chính xác, k đc dùng hình tượng ví von, ss,…
 Định nghĩa k đc vòng quanh, luẩn ẩn, qu
có nghĩa là nội hàm của KN cần phải định nghĩa đc xđ qua
nội hàm của KN khác, mà nội hàm của KN khác ấy lại đc xđ là nội hàm của KN cần phải định nghĩa
 Trong đa số TH, ĐN k đc là ĐN theo lối phủ định, vì việc phủ đị h
n 1 cái gì đó k giúp cho chúng ta
vạch ra đc những dấu hiệu bản chất khác biệt của đối tượng cầ ải ĐN n ph - Các kiểu ĐN
 Căn cứ vào đối tượng đc ĐN + ĐN thực + ĐN duy danh
 Căn cứ vào t/c của KN dùng để ĐN
+ ĐN qua giống gần nhất & khác biệt loài + ĐN theo quan hệ + ĐN theo nguồn gốc + Mô tả + SS 3. Phân chia KN
a. Bản chất của phân chia KN
Phân chia KN là 1 thao tác logic giúp chúng ta tìm hiểu ngoại diên của 1 KN nào đó có bn bộ phận hợp thành b. Kết cấu c a ủ phân chia KN - KN bị phân chia - KN phân chia - Cơ sở phân chia
c. Các qui tắc phân chia KN - Phân chia ph i ải cân đố
- Các KN thành phần sau phân chia phải nằm trong hệ thống ngang hàng
- Phân chia k đc vượt cấp
- Trong 1 phép phân chia chỉ đc dựa vào 1 cơ sở duy nhất Trần Kim Ngân K9A Chương 3: PHÁN ĐOÁN
I. KHÁI LƯỢC VỀ PHÁN ĐOÁN 1. Phán đoán đơn
- là phán đoán được hình thành dựa trên sự liên kết 2 KN
Chủ từ - vị từ là xương sống
- Dạng tổng quát của phán đoán đơn
Tính chu diên của các thu t
ậ ngữ trong phán đoán đơn
- Tính chu diên l à sự thể hiện mqh giữa S và P c ủa phán đoán đơn.
=> việc xác định tính chu diên chỉ đc đặt ra và xem xét khi các thuật ngữ đó tồn tại trong mqh xác định tạo
nên 1 phán đoán đơn bất kì Trần Kim Ngân K9A Toàn b
ộ SV ĐHKS đều phải học logic h c ọ S P Cách xđ chu diên Chu diên (+) Không chu diên (-)
Thuật ngữ là chu diên (+) nếu như ngoại diên Thuật ngữ k chu diên (-) khi ngoại diên của nó
của nó hoàn toàn nằm trong hoặc hoàn toàn chỉ có 1 ph n ầ n m ằ trong ho c ặ có 1 ph n ầ nằm
nằm ngoài ngoại diên của thuật ng c ữ òn lại
ngoài ngoại diên của thuật ngữ còn lại
Thuật ngữ nào đc xét đến toàn bộ lớp đối
Thuật ngữ nào chỉ xét đến 1 phần lớp đối
tượng thì thuật ngữ đó là chu diên
tượng thì thuật ngữ k c đó hu diên
- Chủ từ của PĐ toàn thể (A,E) luôn chu diên (S+)
- Chủ từ c ph ủa PĐ bộ n (
ậ I,O) luôn không chu diên (S-)
- Vị từ của PĐ phủ định (E,O) luôn chu diên (P+)
- Vị từ của PĐ khẳng định (I,A) luôn chu diên khi ngo i
ạ diên c a nó < ho ủ
ặc = ngoại diên S Trần Kim Ngân K9A
- SV ĐHKS vừa h c ọ gi i ỏ ,
2. Phán đoán phức
vừa có lỷ luật tốt (1)
- Là PĐ đc tạo thành từ các PĐ đơn thành phần nhờ các liên t
ừ logic (thể hiện (a) SV ĐHKS học giỏi
quan hệ giữa các PĐ đơn thành phần)
(b) SV ĐHKS có kỷ luật - Kí hiệu: a, b,c, d, …. tốt - D a
ự vào quan hệ của các PĐ thành phần mà chia làm 5 loại:
=> (1) = a ˄ b
 PĐ liên kết (PHÉP HỘI)
 PĐ phân liệt (PHÉP TUYỂN)
 PĐ có điều kiện (PHÉP KÉO THEO)
 PĐ tương đương (PHÉP TƯƠNG ĐƯƠNG)
 PĐ phủ định (PHÉP PHỦ ĐỊNH) TUYỂN Mạnh Yếu
ự tồn tại < sự t n ồ tại của PĐ này của 1 PĐ k TƯƠNG HỘI KÉO THEO
loại trừ hoàn loại trừ hoàn ĐƯƠNG PHỦ ĐỊ NH
toàn sự tồn
toàn sự tồn tại của PĐ
tại của các còn lại> PĐ còn lại QH Thể hiện mqh
Thể hiện quan hệ lựa chọn tồn Mqh nhân –
Mqh nhân quả Thể hiện sự k
biểu đồng thời tồn tại gi t ữa các PĐ hành phần, quả 1 chiều 2 chiều tồn tại của thị tại gi a ữ các
trong đó, phải có ít nhất 1 PĐ (a-NN; b- (a,b v a ừ là NN, PĐTP PĐTP là t n t ồ ại KQ) vừa là KQ)
Liên Và, vừa, tuy
Hay, hoặc, hay… hay…, hoặc
Nếu… thì…
Khi và chỉ khi K, k có từ …nhưng, … hoặc… Vì… nên…
Nếu và chỉ nếu chuyện, làm
logic chẳng những
Muốn (hễ/
gì có chuyện … mà còn, mà, để)… thì… song… Do… nên… Cấu trúc a˄b a v 𝒃 a v b a →𝒃 𝒂↔𝒃 𝒂 , 7a Cách  Đ khi các
 Đ khi 1 PĐTP  S khi các  S khi a=1,  Đ khi PĐTP Luôn có GT xđ PĐTP cùng Đ Đ PĐTP cùng S b=0 cùng giá trị logic đối lập
GT  S khi có ít nhất  S khi các  Đ khi có ít  Còn lại Đ  S khi PĐTP k vs GT logic logic 1 PĐTP S PĐTP cùng Đ nhất 1 PĐTP cùng giá trị của PĐ cho hoặc S Đ trước Trần Kim Ngân K9A
Tuyển mạnh:
- Đi thi hoặc đỗ, hoặc trượt
- Trong tam giác vuông ABC, ho c
ặ A vuông, hoặc B vuông, ho c ặ C vuông
Tuyển yếu:
- Cuốn sách này ho c ặ b í ổ ch, ho c ặ thú vị
BẢNG GIÁ TRỊ N
LOGIC PĐ PHỨC CƠ BẢ a b 7b a˄b a v b a v b a →𝒃
𝒂 ↔ 𝒃 7(a˄b) 1 1 0 1 0 1 1 1 0 1 0 1 0 1 1 0 0 1 0 1 0 0 1 1 1 0 1 0 0 1 0 0 0 1 1 1
3. Phán đoán đa phức hợp Lan học gi i ỏ = a
- là những PĐ đc tạo thành từ các phán đoán phức CB (hoặc những PĐ có từ 2 = k có chuyện Lan học
loại liên từ logic trở lên) không gi i ỏ = 7(7a)
=> việc tín giá trị logic của PĐ đa ph c ứ hợp ph ụ thu c
ộ vào giá trị của các PĐ phức thành phần.
Tính đẳng trị của PĐ phức (= suy luận diễn dịch trực tiếp xuất phát từ tiền đề là PĐ phức) = tìm cách di t
ễn đạ khác vs cách diễn đạt ban đầu cho nội dung và giá trị logic k thay đổi nhưng cấu trúc thì thay đổi a→b = 7a→ 7b = 7a v b = 7(a˄7b)
a˄b = 7(a→7b)=7((b→7a)=7(7a v 7b) a=7(7a)
a v b = 7a→b = 7b→a = 7(7a˄7b) Cách l p ậ b n
ả g giá trị logic
{[(a→b)˄(a→c)] ˄ (7b v 7c)} → 7a Số biến = n = 3 Số cột = n + s
ố phán đoán thành phần = 3+9 = 12
Số dòng chứa giá trị = 2𝑛 = 8
Số lượng giá trị 1 hoặc 0 liền nhau ở cột đầu tiên = 2𝑛 : 2 =4
Cột sau sẽ là phân đội của cột trước
Đặt: I = (a→b)˄(a→c) II = I ˄ (7b v 7c) III = II → 7a a b c 7a 7b 7c a→b a→c 7b v 7c I II III 1 1 1 0 0 0 1 1 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 0 0 0 1 1 0 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 Trần Kim Ngân K9A Chương 4:
CÁC QUY LUẬT LOGIC HÌNH THỨC CỦA TƯ DUY
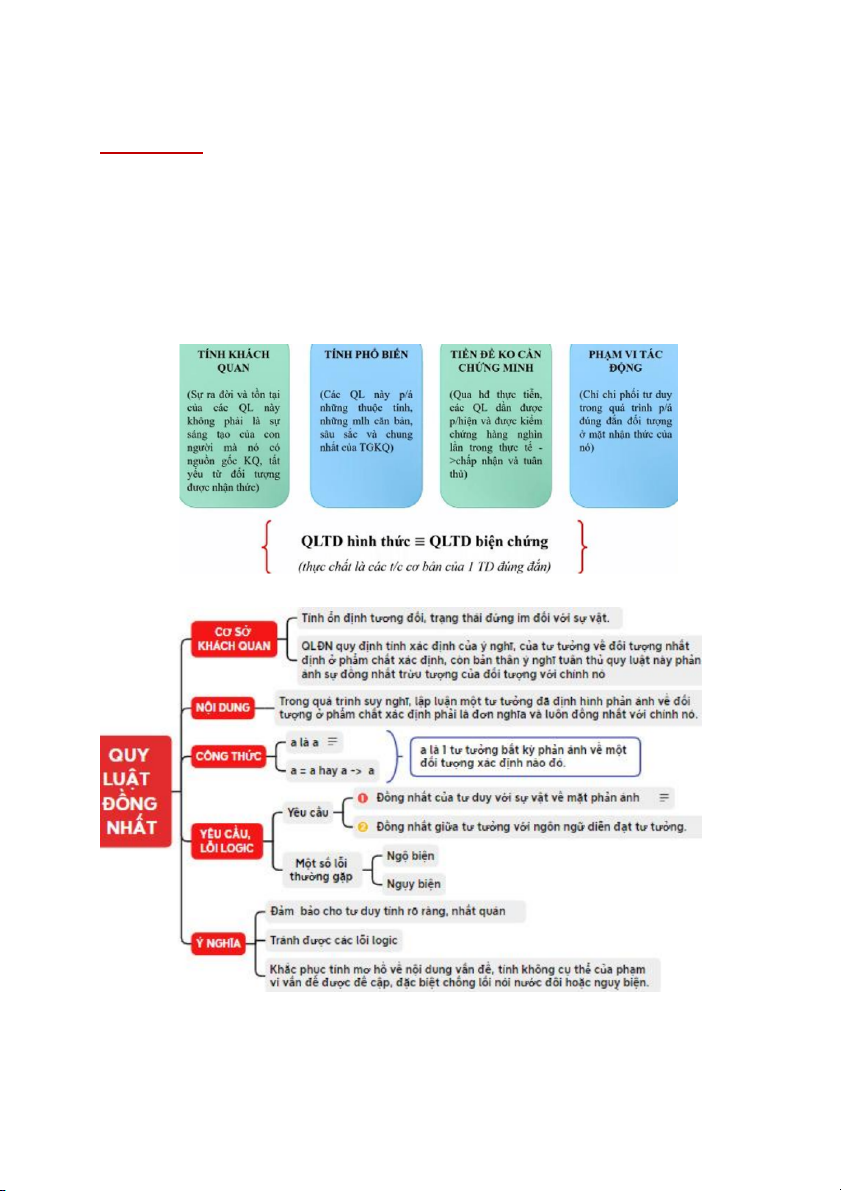
Quy luật là nh ng ữ
mlh khách quan, bên trong, bản chất, tất yếu, bền vững, lặp đi p
lặ lại giữa các đối tượng
hoặc giữa các thành tố cấu tạo nên chúng. Đặc trưng của tư duy
- các hình thức của tư duy
- mlh giữa các tư tưởng (mlh n i
ộ dung –mlh hình thức) Quy lu t
ậ CB của tư duy?
- tác động mọi hình thức tư duy: KN, CM, Phán đoán, suy luận - nh s Quy đị
ự tác động của các quy luật khác, k CB
T/c chung của các QLCB tư duy Trần Kim Ngân K9A Trần Kim Ngân K9A Trần Kim Ngân K9A Chương 5:
SUY LUẬN DIỄN DỊCH VÀ QUI NẠP
I. KHÁI LƯỢC VỀ SUY LUẬN Có nh ng ữ TH k thể trực 1. KN tiếp sử ụ d ng các giác
- Tri thức trực tiếp = tri thức có được nhờ các giác quan, mang tính đơn lẻ, rời rạc = quan: tìm nguyên nhân
1 phần đáng kể trong tri thức con người của QT bắt nguồn cách
- Tri thức gián tiếp = tri thức được rút ra từ tri thức đã biết khác = cách thức rút ra đây hàng triệu năm tri th c
ứ 1 cách gián tiếp = SUY LUẬN
SUY LUẬN là 1 hình thức của tư duy, trong đó từ 1 hay 1 s t
ố ri thức đã có, ta rút KN, PĐ – hình thức biểu
ra đc tri thức ms => Tri th c
ứ hoạt động sản sinh ra tri thức mới thị tư duy - Vai trò của SL
SL – cũng biểu thị tư duy
 Gắn kết – làm phong phú tri thức
về đtg nhưng cũng là
thao tác của tư duy (gắn  Tác d n
ụ g ở nơi giác quan con người bất lực (tìm hiểu về QK thông qua hóa thạch)
kết các tư tưởng theo các cách th nh) ức xác đị
 Nhận thức QK – TL (dự đoán mức độ tăng trưởng ,….) - Vai trò c a
ủ SL vs KH pháp lý: nhận định về thời gian, cách thức phạm t i ộ , khoanh vùng đtg
2. Cấu tạo của SL
Tiền đề thường rơi vào
 Tiền đề (tri thức đã biết): quan sát trực tiếp, tiếp thu thông qua học tập, lđ, các TH: giao tiếp, nghiên c u, ho ứ
ặc là kết quả của các SL trước đó
 Sự thật hiển nhiên
 Kết luận (tri thức ms): là những tri thức mới nhận được từ các tiền đề và các khách quan (nước chảy hệ quả của chúng
chỗ trũng, hêt ngày đến
 Cơ sở Logic: các QL, quy tắc mà việc tuân thủ chúng cho phép chúng ta rút đêm) ra KL chân thực t c
ừ ác tiền đề chân thực đã có
 Những QL, định luật
(tồn tại trong suy nghĩ của chính ta – khi c n
ầ kiểm tra SL chính xác, hợp logic mang tính KH đã đc CM
k thì đem ra để áp dụng, kiểm tra)
(lương đổi chất đổi, vạn
- Xác định tiền đề & KL dựa vào:
vật hấp dẫn ,…)
 Từ chỉ thị tiền đề: vì, bởi, do, vì rằng, …
 Vấn đề chân lí mang
 Từ chỉ thị KL: do đó, vậy, bởi vậy, vì vậy, từ đó, suy ra ,… tính xh - k ph i ả CM
nhưng ta mặc định nó là chân lí (có t t ậ gi t ậ mình, tình m u ẫ
tử “mẹ xót con”, …)
3. SL đúng & SL hợp logic
- ĐK để có SL đúng (kết luận tất yếu chân thực )  Xuất phát từ các ti c ền đề hân thực A B  Tuân th c
ủ ác quy tắc logic (=SL hợp logic)
=> SL đúng (A) là SL hợp logic (B), nhưng SL hợp logic chưa chắc là SL đúng
- SL & mlh vs ngôn ngữ:
 SL luôn là mlh của 1 số câu (2 hoặc nhiều hơn) đc diễn đạt bằng những từ như: suy ra, có nghĩa là,
như vậy là, vì rằng, …
 Trật tự sắp xếp [ti -
ền đề kết luận] trong SL là tương đối 4. Phân lo i ạ SL: d a
ự vào cách thức lập luận - t
Vđ từ ri thức chung => riêng: DIỄN DỊCH
 Diễn dịch trực tiếp - ti
ền đề là 1 PĐ (đơn = phức )
 Diễn dịch gián tiếp - ti c
ền đề ó từ 2 PĐ trở lên (đơn = phức ) - t
Vđ từ ri thức riêng => chung: QUY NẠP Trần Kim Ngân K9A  Quy nạp hoàn toàn  Quy nạp hoàn toàn - LOẠI SUY (p. tương t )
ự : là dạng SL đặc biệt trên cơ
sở rút ra những KL về sự gi ng ố nhau c a ủ các dấu hiệu thuộc về a
các đtg dự trên sự giống nhau của các dấu hiệu hoặc của các đtg đó => sử dụng như 1 pp bổ trợ II. SUY LUẬN DIỄN DỊCH
1. Diễn dịch trực tiếp
- là SL mà KL đc rút ra từ ti
ền đề là 1 PĐ (đơn hoặc phức)
 Từ tiền đề là PĐ đơn
 Từ tiền đề là PĐ phức (=tính đẳng trị của PĐ phức )
a. Phép chuyển hóa (phép đổi chất )
- Thay đổi sắc thái của câu nói, PĐ, tạ ững ý tưở o nh
ng mới, phong phú hơn ban đầu
=> Khẳng định mang hình thức ph
ủ định và ngược lại - Gi : ữ
 LƯỢNG của PĐ tiền đề  VỊ TRÍ của S P – - Đổi:  CHẤT của ti t
ền đề ừ KĐ sang phủ định ở KL (hoặc từ phủ đị sang KĐ) nh
 VỊ TỪ ở tiềng đề thành vị từ phủ định trong KL
b. Phép đảo ngược (phép đổi chỗ)
- Hoán vị giữa chủ từ (S) & vị từ (P) của PĐ tiền đề để thu đc KL ms có chất & GT k thay đổi
 Giữ: Chất của KL đc giữ ngu
yên như chất của tiền đề  Đổi:
+ Vị trí c a ủ chủ t ừ ở ti t ền đề hành vị t ừ ở KL và vị t ừ ở ti t ền đề hành c t ủ ừ ở KL (𝑆 ↔𝑃)
+ Lượng từ sẽ thay đổi từ ti
ền đề xuống KL theo quy tắc: thuật ngữ k chu diên ở tiền đề, thì cũng k đc
phép chu diên ở KL Trần Kim Ngân K9A
c. Phép đối lập vị từ (đổi chất kết hợp vs đổi chỗ)
- Yêu cầu: tuân theo các qui tắc của đổi chất và đổi ch ỗ - Th c ự hiên:
 B1: Đổi chất của PĐ tiền đề
 B2: Đổi chỗ các thuật ngữ của PĐ trung gian vừa thu đc sau B1
d. Phép đối lập chủ từ (đổi chỗ kết hợp vs đổi chất)
- Yêu cầu: tuân theo các qui tắc của đổi chất và đổi ch ỗ - Th c ự hiên:
 B1: Đổi chỗ của PĐ tiền đề
 B2: Đổi chất của PĐ trung gian vừa thu đc sau B1
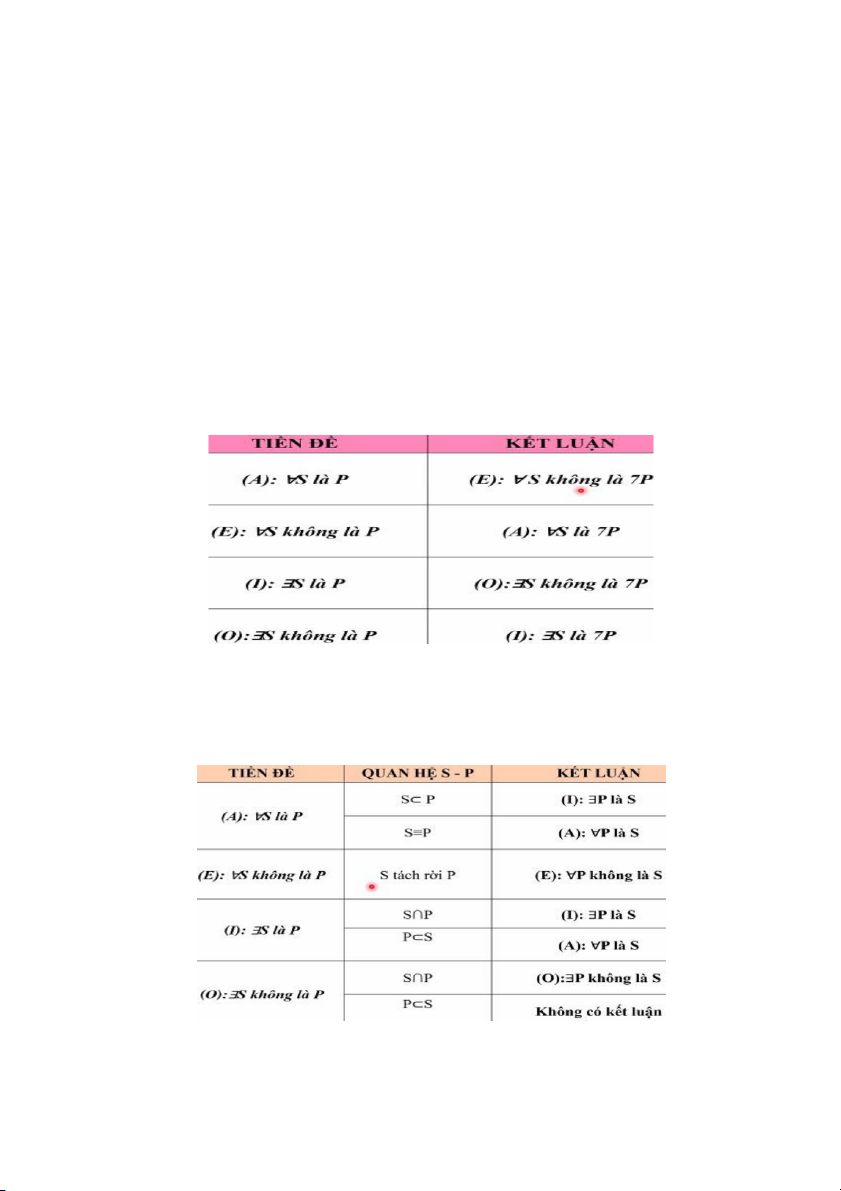
d. SL trực tiếp theo quan hệ giữa các PĐ trên hình vuông logic
2. Diễn dịch gián tiếp
a. Tam đoạn luận (suy luận gián tiếp t ừ ti ền đề là PĐ đơn)
-Tam đoạn luận nhất quyết đơn là suy luận diễn dịch trong đó kết luận là PĐ nhất quyết đơn đc rút ra từ mlh
logic tất yếu giữa 2 ti
ền đề là các PĐ đơn thành phần
- Cấu trúc của tam đoạn luận: (2 TĐ – 1 KL – 3 TN) Trần Kim Ngân K9A
CÁC LOẠI HÌNH TAM ĐOẠN LUẬN
 Để xđ tam đoạn luận thuộc loại nào thì phải dựa vào vị trí (M)
 Thuật ngữ (M) chỉ xuất hiện ở ti , K ền đề XUẤT HIỆN Ở KL
 Cấu trúc của mỗi tam đoạn lu C
ận là QUY ƯỚ BẮT BUỘC => k đc phép thay đổi
 Trật tự của tam đoạn luận luôn phải đc đưa về DẠNG THUẬN Các qui t c
ắ của tam đoạn luận (8) - 3 Quy t c
ắ cho THUẬT NGỮ
 Q/t 1: Trong tam đoạn luận chỉ đc phép có 3 thuậ t ngữ (S, P, M) i
VD: Ngườ là chúa tể muôn loài. Tôi là người
=> Tôi là chúa tể muôn loài
 Q/t 2: Thuật ngữ trung gian (M) phải chu diên ít nhất 1 lần ở 1 trong 2 tiền đề VD: Tr m
ộ cắp là hành vi VPPL. Tr n t
ố huế là hành vi VPPL.
=> Trốn thuế là tr m ộ c p ắ
 Q/t 3: Nếu thuật ngữ S & P k chu diên ở tiền đề thì cũng k chu diên ở tiền đề thì cũng k đc phép chu diên ở KL
VD: Mọi kẻ ph m ạ t u c ội đề
ó hành vi nguy hiểm cho xh. Nam không là kẻ ph m ạ tội
=> Nam không có hành vi nguy hiểm cho xh - 5 Quy t c ắ cho TI ỀN ĐỀ
 Q/t 4: Nếu 2 tiền đề đều là PĐ phủ định thì k rút ra đc KL
VD: Mọi SV đang học t p k ậ
phải thực hiện nghĩa vụ quân sự. A k phải là SV đang học t p = ậ > ???
 Q/t 5: Nếu 1 tiền đề là PĐ phủ định thì KL ph
ải là PĐ phủ định Trần Kim Ngân K9A
VD: Mọi SV đang học tập k ph i
ả thực hiện nghĩa vụ quân sự. A là SV đang học t p ậ => A k ph i
ả thực hiện nghĩa vụ quân sự
 Q/t 6: Nếu 2 tiền đề cùng là PĐ bộ phận thì k rút ra đc KL
VD: Có những loài th o m ả c
ộ có t/d chữa bệnh. 1 s ố ch t
ấ có t/d chữa bệnh là độc t = ố > ??
 Q/t 7: Nếu 1 tiền đề là PĐ bộ phận thì KL là PĐ bộ phậ n
VD: Đi làm thêm là cách tự t o t ạ hu nh p. N ậ
hiều SV đi làm thêm
=>Nhiều SV có k/n tự t o t ạ hu nh p ậ
 Q/t 8: Nếu 2 tiền đề nh t là PĐ khẳng đị hì KL ph nh
ải là PĐ khẳng đị
VD: Mọi SV ĐHKS đều ph i
ả học LGH. Có SV ĐHKS là người Huế i
=> Có ngườ Huế k ph i ả h c ọ LGH
QUY TẮC RIÊNG: là s c ự ụ thể hóa c a
ủ quy tắc chung vào t ng l ừ
oại hình tam đoạn luận
Đ vs tất cả quy tắc chung => Đ vs quy tắc riêng S vs quy t c
ắ chung => S vs quy t c ắ riêng  QTR lo i
ạ (I): tiền đề nhỏ phải là PĐ khẳng định, tiền đề lớn là PĐ toàn thể
=> Các kiểu t/m QTR: AAA, EAE, AII, EIO  QTR lo i
ạ (II): 1 trong 2 tiền đề ph ải là PĐ phủ định, ti l
ền đề ớn phải là PĐ toàn thể
=> Các kiểu t/m QTR: EAE, AEE, EIO, AOO  QTR lo i
ạ (III): tiền đề nhỏ phải là PĐ khẳng định, KL phải là PĐ bộ phận
=> Các kiểu t/m QTR: AAI, IAI, AII, EAO, OAO, EIO  QTR lo i ạ (IV): 1 tiền đề
là PĐ phủ định thì tiền đề lớn phải là PĐ toàn thể
TĐ lớn là PĐ khẳng định thì TĐ nhỏ ải là PĐ toàn thể ph
TĐ nhỏ là PĐ khẳng đị
nh thì KL phải là PĐ bộ phận
=> Các kiểu t/m QTR: AAI, AEE, IAI, EAO, EIO
b. Tam đoạn luận rút gọn - n l Tam đoạ uận thiếu ti l ền đề ớn
 Phải giữ nguyên 2 PĐ đã có
 PĐ đưa thêm vào lấp chỗ thiế ải là PĐ châ u ph n thực - n l Tam đoạ uận thiếu ti nh ền đề ỏ - n l Tam đoạ uận thiếu KL
* CÁCH THỨC KHÔI PHỤC TĐL rút gọn
 B1: Xđ bộ phận đã có? Bộ phận còn thiếu? của TĐL
 B2: KHÔI PHỤC
Vs TĐL thiếu tiền đề lớn (hoặc tiền đề nhỏ), đã có KL => Xđ (S), (P)
=> Xđ tiền đề đã có và tiế
n hành khôi phục tiền đề còn thiếu
Vs TĐL thiếu KL, đã có tiền đề lớn và tiền đề nhỏ
=> Xđ thuật ngữ trung gian (M)
=> Xd KL phù hợp Trần Kim Ngân K9A
c. Tam đoạn luận phức - Là s l
ự iên kết tam đoạn luận đơn s/c KL của tam đoạn luận trước đc dùng làm tiền đề cho tam đoạn luận sau d. SL ĐK
- SL ĐK là SL trong đó, có ít nhất 1 tiền đề là PĐ kéo theo. - D a
ự vào việc có 1 hay tất cả tiền đề ng
là PĐ kéo theo mà SL ĐK chia làm 2 dạ
 SL ĐK xác định (1 tiền đề là PĐ kéo theo)
 SL ĐK thuần túy (tất cả tiền đề là PĐ kéo theo) Trần Kim Ngân K9A
e. SL phân liệt: Là SL diễn dịch trong đó 1 hay 1 số ti ền đề t
là PĐ phân liệ (phép tuyển)
- SL phân liệt thuần túy (l a
ự chọn thuần túy): là SL phân liệt trogn đó, tất cả các tiền đề và KL là PĐ phân
liệt tương đối (tuyển yếu)  Cấu tạo:
 VD: Hôm nay, An phải h c ọ Toán ho c
ặc Văn hoặ Sử.
- SL phân liệt nhất quyết (l a
ự chọn xđ): 1 tiền đề là PĐ phân liệt tuyệt đối (tuyển mạnh); 1 tiền đề còn lại + KL là các PĐ đơn.
- SL phân liệt có điều kiện (lựa chọn có điều kiện): là sự kết hợp giữa phép tuyển và phép kéo theo (song đề)