Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.

ĐỀ THI SỐ 4
Cho hệ tuyến tính bất biến có phương trình mô tả quan hệ vào ra: y[n ] = x[n] − x[n− 2]
1. Tìm biểu thức và vẽ đồ thị của đáp ứng xung đơn vị của hệ (1 điểm)
2. Tìm biểu thức của đáp ứng tần số (*) của hệ (1 điểm)
3. Tìm biểu thức và vẽ đồ thị của đáp ứng biên độ của hệ. Hệ khuếch đại, làm suy
giảm, và làm triệt tiêu hoàn toàn (nếu có) biên độ của các tín hiệu sin phức có tần
số cụ thể bằng những giá trị nào (3 điểm)  n 
4. Xét tín hiệu x[n] = 2 − 3cos
. Dùng công thức Euler (**) để biểu diễn x[n]   2  
dưới dạng tổ hợp tuyến tính các tín hiệu sin phức. Từ đó kết luận x[n] gồm những
thành phần tần số nào, biên độ và pha của mỗi tần số có giá trị bằng bao nhiêu? (3 điểm)
5. Dùng kết quả của câu 2 và câu 4, xác định biểu thức của tín hiệu ra y[n] cho tín
hiệu đầu vào x[n] ở câu 4 đi qua hệ (2 điểm) Gợi ý: +
- (*): H (e j ) =  h[n].e− jn n=−
- (**): e jx = cos x + j sin x, e− jx = cos x − j sin x Giải đề 4:
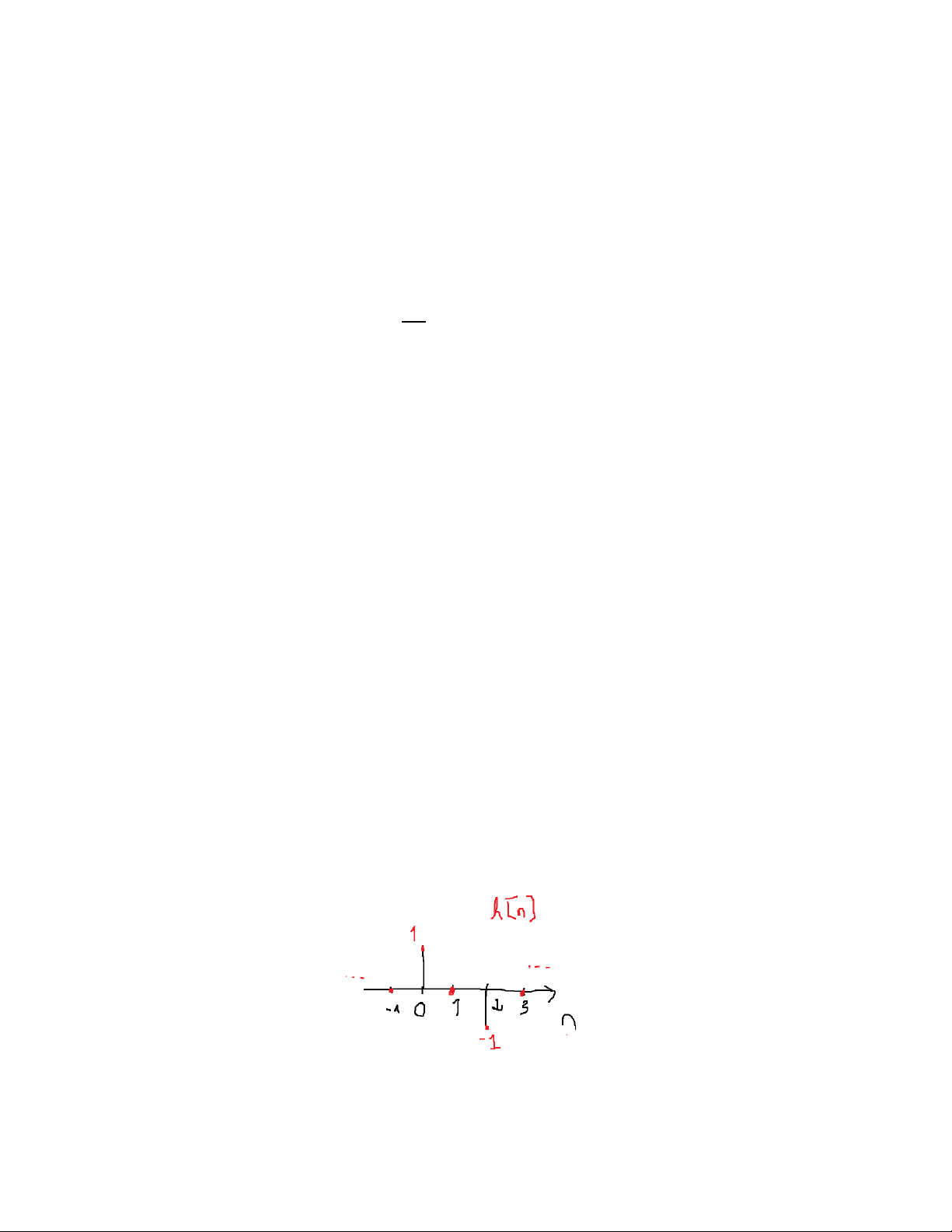
1. Với x[n] =  [n] thì ta có đáp ứng xung: h[n] =  [n] −  [n − 2] Suy ra:
h[n] = 1; 0; −1  n = 0 Đồ thị của h[n]:
2. Biểu thức của đáp ứng tần số của hệ là: + 2
H (e j ) =  h[n].e− jn = h[n].e− jn n=− n=0
= h[0].e− j0 + h[1].e− j1 + h[2].e− j2
= 1 + 0.e− j1 −1.e− j2
= 1 − e− j 2
= 1 − cos(2) + jsin(2)
3. Biểu thức đáp ứng biên độ của hệ là:
H (e j ) = 1 − cos(2) + j sin(2)
= (1 − cos(2))2 + sin2 (2) = 2 − 2 cos(2)
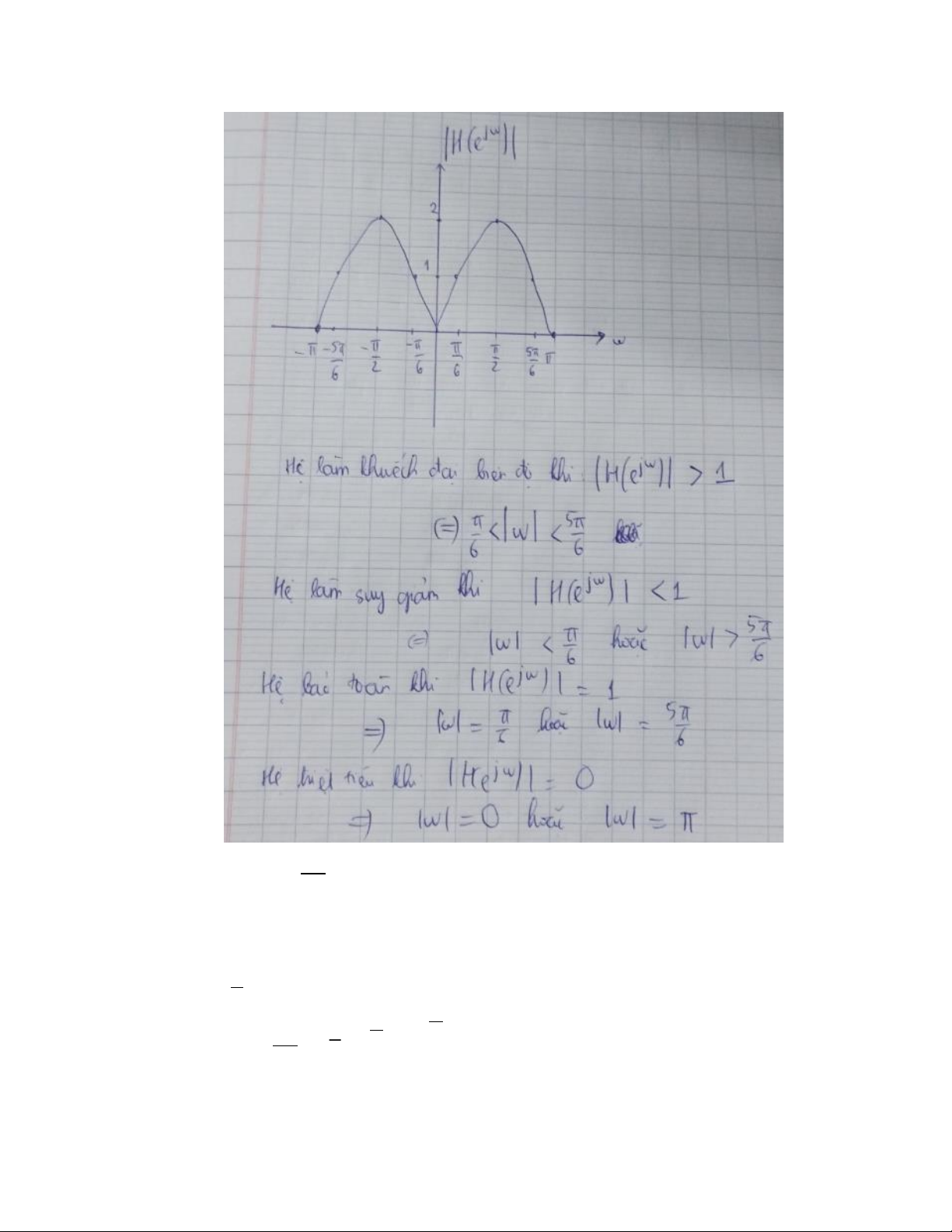
Đồ thị đáp ứng biên độ của tín hiệu 4.  n 
x[n] = 2 − 3cos   2  
Ta có: e jx = cos x + j sin x và e− jx = cos x − j sin x nên: 1
cos x = (e jx + e− jx ) 2  n    − n  1  n j j Suy ra: cos
 =  e 2 + e 2   2  2      n   n  3  n − j n − j j 3  j
Nên ta có: x[n] = 2 −  e 2 + e 2  = 2.e j.0 −  e 2 + e 2  2   2   −  Vậy 
x[n] được tạo nên từ các thành phần tần số  = ;0;   2 2  
Trong đó biên độ, pha của tần số  = 0 lần lượt là 2 và 0  3 n
Trong đó biên độ, pha của tần số  = lần lượt là và +  2  2 2 3 
Trong đó biên độ, pha của tần số  = lần lượt là và − n  +   2 2 2   5.
Đáp ứng ra của một hệ thống có tín hiệu đầu vào x[n] = e jn có dạng:
y[n ] = e jn.H (e j )  n    − n  3  n j j
Do đó, với tín hiệu đầu vào x[n] = 2 − 3cos
 = 2.e j.0 −  e 2 + e 2  thì tín  2  2     − j.  −  j n = j n  j. 3 3
hiệu ra sẽ là: y[n ] 2e j.0.H (e j.0 ) − .e 2 .H  e 2  − .e 2 .H  e 2  2   2  
Ở câu 2, ta có: H (e j ) = 1− cos(2) + jsin(2) , ta tính được:
H (e j.0 ) = 1− cos 0 + j sin 0 = 0   j. 
H  e 2  = 1− cos  + j sin  = 2    − j. 
H  e 2  = 1 − cos(− ) + j sin(− ) = 2   − − 3 jn 3 jn jn jn
Vậy y[n ] = − .e 2 .2 − .e 2 .2 = −3e 2 − 3e 2 2 2
Ta có: e jx = cos x + j sin x, e− jx = cos x − j sin x nên e jx + e− jx = 2 cos x n −n  j j n 
Do đó: e 2 + e 2 = 2cos    2  jn − jn  n   n 
Vậy: y[n ] = −3.e 2 − 3.e 2 = −3.2cos  = 6cos +    2   2  Cách 2:
Ở câu 2, ta có: H (e j ) = 1− cos(2) + jsin(2)  sin(2) Suy ra đáp ứng pha là:
H ( e j ) =  () = arctan 1− cos(2)
Và đáp ứng biên độ: H (e j ) =
Vậy khi cho tín hiệu đầu vào x[n] đi qua hệ thì ta sẽ thu được y[n] là:   j.   n     n   n 
y[n] = 2. H (e j.0 ) − 3 H  e 2  .cos
+    = −6 cos  = 6 cos +      2  2   2   2 