Đề cương môn Truyền động điện - Trường Đại học bách khoa - Đại học đà nẵng.

ĐẠI HỌC ĐÀ NẴNG
TRƯỜNG ĐẠI HỌC BÁCH KHOA KHOA ĐIỆN
BÁO CÁO CUỐI KỲ
HỌC PHẦN: ĐIỀU KHIỂN TRUYỀN ĐỘNG ĐIỆN TRONG CÔNG NGHIỆP
ĐỀ TÀI: RESET AND CLOCK CONTROL (RCC)
GV hướng dẫn: TS. Trần Thái Thanh Âu
Sinh viên thực hiện: Nguyễn Hoàng Min Bùi Văn Bình Nhóm: 8
Lớp học phần: 20.32 Đà Nẵng, tháng 10/2024
CHƯƠNG 1: MÔ HÌNH HÓA, ĐIỀU KHIỂN VÀ THIẾT KẾ QUỸ ĐẠO
1.1 Giới thiệu
Việc tích hợp một bộ điều khiển chuyển động và servo đa trục vào một chip duy
nhất, sau đó áp dụng vào bàn XYZ, máy CNC (Điều khiển số hóa) hoặc hệ thống robot,
v.v., nhằm giảm kích thước hệ thống và tăng cường hiệu suất cũng như độ ổn định của
chuyển động, đã trở thành một chủ đề nghiên cứu phổ biến trong các tài liệu [1–5]. Thêm
vào đó, trong các ứng dụng điển hình, việc áp dụng động cơ đồng bộ nam châm vĩnh cửu
(PMSM) làm bộ truyền động trong thiết bị đa trục tự động là một xu hướng kỹ thuật chủ
đạo nhờ vào mật độ công suất cao và khả năng điều khiển chuyển động vượt trội, phản
hồi nhanh và định vị chính xác [6–8]. Trong các máy móc truyền thống, thường sử dụng
một bộ điều khiển trung tâm để lập kế hoạch quỹ đạo chuyển động và nhiều bộ vi xử lý để
điều khiển hệ thống động cơ servo đa trục nhằm thiết lập một bộ điều khiển chuyển động
đa trục. Trong kiến trúc này, việc phối hợp và giao tiếp giữa bộ điều khiển trung tâm và
các bộ vi xử lý là một nhiệm vụ đầy thách thức trong thiết bị đa trục tự động.Tuy nhiên
một số nhược điểm xuất hiện, chẳng hạn như kích thước lớn, dễ bị ảnh hưởng bởi nhiễu,
chi phí đắt đỏ, và thiếu linh hoạt. Ngoài ra, việc giao tiếp dữ liệu và giao thức bắt tay giữa
bộ điều khiển trung tâm và nhiều bộ vi xử lý chắc chắn làm chậm tốc độ thực thi của hệ
thống. Để giải quyết vấn đề này, FPGA cung cấp giải pháp tối ưu so với các bộ vi xử lý
thương mại cao cấp khác nhờ vào khả năng tính toán nhanh, xử lý song song, đặc tính có
thể lập trình trường (field-programmable), và môi trường SoPC có thể thực hiện các
nhiệm vụ kết hợp phần cứng-phần mềm [9–12]. Ví dụ, trong thiết kế bộ điều khiển servo
PMSM sử dụng FPGA, chỉ mất chưa đến 2 µs để thực hiện thuật toán SVPWM, chưa đến
3 µs để thực hiện bộ điều khiển vector dòng, và chưa đến 3 µs để thực thi thuật toán điều
khiển mờ trong vòng điều chỉnh tốc độ. Các đặc tính tính toán nhanh và xử lý song song
cho phép tích hợp các bộ điều khiển servo đa trục và chức năng lập kế hoạch quỹ đạo
chuyển động vào một FPGA duy nhất. Gần đây, một công việc đồng mô phỏng bởi
Electronic Design Automation (EDA) Simulator Link đã dần dần được áp dụng để kiểm
tra hiệu quả của mã HDL (Hardware Description Language) trong hệ thống điều khiển
động cơ [13–15]. EDA Simulator Link [16] cung cấp giao diện đồng mô phỏng giữa
Simulink và ModelSim [17], cho phép sử dụng các mô hình Simulink làm băng thử
nghiệm để tạo tín hiệu kích thích cho ModelSim và phân tích phản hồi của mô phỏng
[16]. Vì vậy, trước khi hiện thực FPGA, công việc đồng mô phỏng qua EDA Simulator
Link sẽ được áp dụng vào hệ thống điều khiển chuyển động đa trục trong bài báo này. Các
động cơ PMSM đa trục, các biến tần đa trục, chức năng lập kế hoạch quỹ đạo chuyển
động và phản hồi vị trí chuyển động được thực hiện trong Simulink, còn bộ điều khiển vị
trí/tốc độ/dòng điện IP (Intellectual Property) được mô tả bằng mã VHDL sẽ được thực
hiện trong ModelSim. Sau khi kiểm tra thành công trong mô phỏng, IP điều khiển vị
trí/tốc độ/dòng điện có thể được sử dụng trực tiếp trong FPGA.
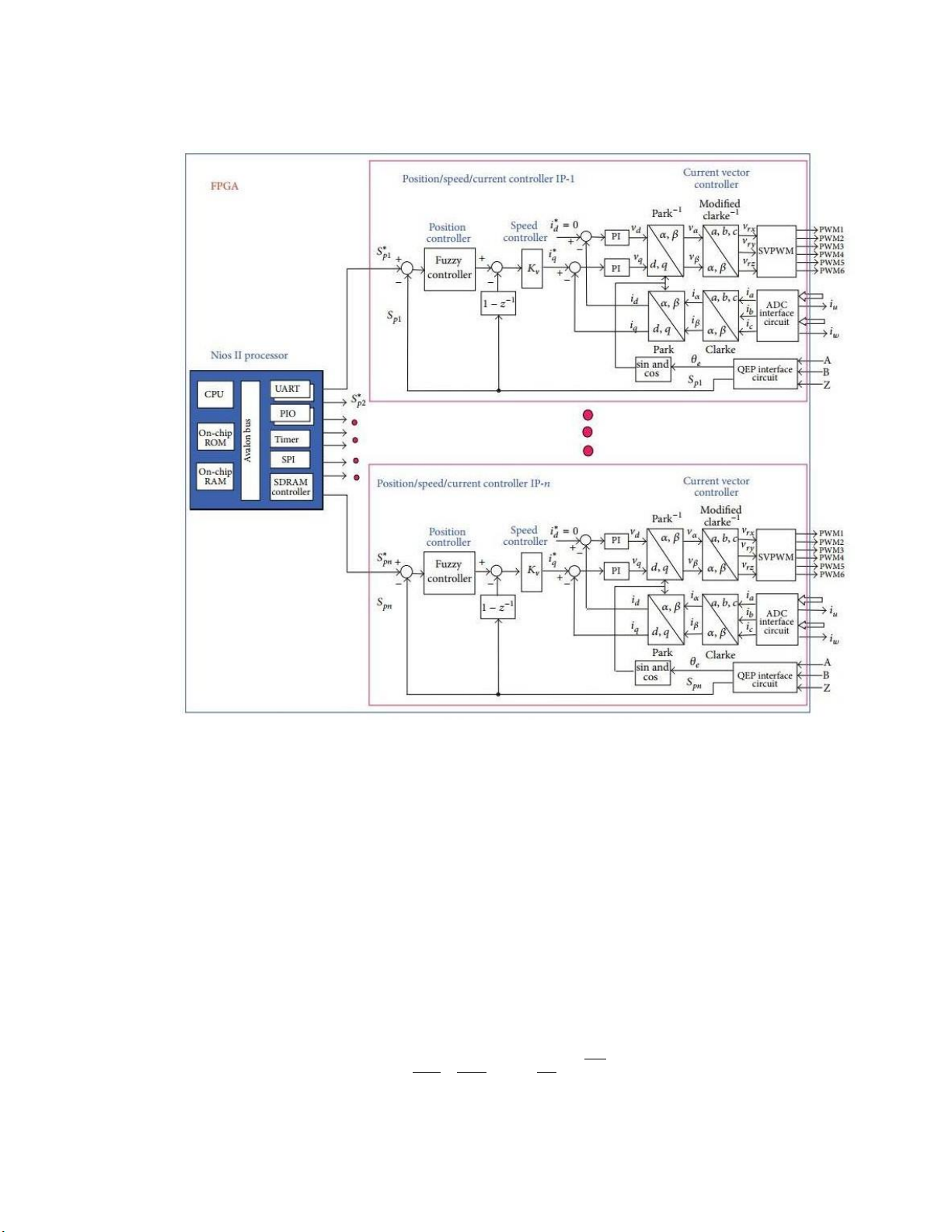
Việc hiện thực trong bài báo này sử dụng công nghệ SoPC, trong đó FPGA tích hợp
bộ xử lý Nios II được thiết lập để phát triển một vi mạch điều khiển chuyển động đa trục,
được minh họa trong Hình 1. Nó bao gồm nhiều IP điều khiển servo và một bộ xử lý Nios
II trong FPGA. Mỗi IP điều khiển servo thực hiện chức năng điều khiển vị trí/tốc độ/dòng
điện cho từng bộ truyền động PMSM, và bộ xử lý Nios II thực hiện chức năng lập kế
hoạch quỹ đạo chuyển động. Ngoài ra, cấu trúc chi tiết bên trong của IC điều khiển
chuyển động đa trục được đề xuất trong FPGA được trình bày trong Hình 2. Trong IP điều
khiển servo, điều khiển vector được áp dụng trong vòng điều khiển dòng điện, bộ điều
khiển P được sử dụng trong vòng điều khiển tốc độ, và bộ điều khiển mờ được áp dụng
trong vòng điều khiển vị trí cho từng bộ truyền động PMSM. Tuy nhiên, IC điều khiển
chuyển động đa trục trong Hình 1 có thể được áp dụng cho các thiết bị tự động đa trục,
chẳng hạn như bàn XYZ, cánh tay robot SCARA, cánh tay robot dạng đứng và máy CNC.
1.2 Mô hình hóa, Điều khiển, và Thiết kế Quỹ đạo Chuyển động
Hình: Hệ thống tích hợp nhiều bộ điều khiển servo
Hình 1.1 minh họa việc tích hợp nhiều bộ điều khiển servo IP và một bộ xử lý Nios
II trong FPGA. Mỗi bộ điều khiển servo IP thực hiện chức năng điều khiển vị trí/tốc
độ/dòng điện cho một hệ truyền động PMSM, trong khi bộ xử lý Nios II thực hiện chức
năng lập kế hoạch quỹ đạo chuyển động. Phương pháp thiết kế chi tiết được mô tả như sau:
1.2.1 Mô hình Toán học của Bàn Trượt Đơn Trục
Mô hình toán học điển hình của động cơ PMSM được mô tả trong hệ quy chiếu
xoay đồng bộ hai trục d-q như sau: ⅆi −r L d s q 1 ⅆ = i +ω i + V t L d e d L q L d d d ⅆi L r λ q d s f 1 ⅆ =−ω i − i −ω + V t e L d q e L L q q L d q d Trong đó:
- Vd , Vq: Điện áp trên trục d và q
- id, iq : Dòng điện trên trục d và - r s
: Điện trở cuộn dây pha
- Ld, Lq: Độ tự cảm trên trục d và q - ωe
: Tốc độ quay của từ thông nam châm - λf
: Liên kết từ thông của nam châm vĩnh cửu
Bộ điều khiển vòng dòng điện của hệ truyền động PMSM trong Hình 1.1 dựa trên
phương pháp điều khiển vector. Điều này có nghĩa là nếu dòng id được điều khiển về 0,
PMSM sẽ hoạt động tương tự như động cơ DC. Do đó, sau khi tách biệt, mô-men xoắn
của PMSM có thể được biểu diễn bằng phương trình sau: 3 P T =
λ i ≡K i e 4 f q t q 3 P k = λ t 4 f
Trong đó, Te là mô-men xoắn của động cơ và P là số cặp cực. Khi xét đến tải cơ học,
phương trình động học tổng quát của hệ thống bàn trượt tuyến tính được xác định như sau: ⅆ2 s ⅆ S T −T 2 π ⋅ pi + B pi e L=Jm r ⅆ ⅆt b t 2 m
Kt là hằng số lực; Jm là giá trị quán tính; Bm là tỷ lệ suy giảm; TL là mô-men xoắn
bên ngoài; spi đại diện cho độ dịch chuyển trên trục i, rb là độ dẫn của vít bi.
1.2.2 Thiết kế Bộ điều khiển mờ (FC)
FC trong nghiên cứu này sử dụng bộ làm mờ đơn, hàm thành viên tam giác, quy tắc
suy diễn sản phẩm, và phương pháp giải mờ trung bình trung tâm. Trong Hình 1.1, sai số
theo dõi e và sự thay đổi sai số de được định nghĩa như sau:
ⅇ(k )=s¿ (k )−S (k ) pi pi
de (k )=ⅇ(k )−ⅇ(k−1) ¿
Trong đó μf là đầu ra của FC; s ( k ) S (k ) lần pi và pi
lượt là lệnh vị trí trục I và phản hồi
vị trí trục I. Quy trình thiết kế của FC được mô tả như sau
a) Lấy e, de làm biến đầu vào của FC và định nghĩa các biến ngôn ngữ của
chúng là E và dE. Các giá trị ngôn ngữ của E và dE là {A0, A1, A2, A3, A4,
A5, A6} và {B0, B1, B2, B3, B4, B5, B6}, tương ứng. Mỗi giá trị ngôn ngữ
của E và dE dựa trên hàm thành viên tam giác đối xứng.
b) Tính độ thành viên của e và de. Chỉ có hai giá trị ngôn ngữ được kích hoạt
(kết quả là một giá trị thành viên không bằng 0) ở bất kỳ giá trị đầu vào nào.
Do đó, độ thành viên μAi có thể được xác định bằng: μ (e)=e −ⅇ Ai i+1/ 2 μ (ⅇ)=1−μ (ⅇ) Ai+1 Ai Và e ≡−6+2.( i+1
i +1). Kết quả tương tự có thể đạt được khi tính độ thành viên μ (de ) Bj .
c) Chọn các quy tắc FC ban đầu dựa trên đặc tính đáp ứng động, chẳng hạn: “Nếu e là A ”
i và Δe là Bj thì uf là C j ,i
Với i , j=0 6. Trong đó, Ai và Bj là các số mờ và cj, i là các số thực.
d) Thiết lập hệ thống mờ uf(e,Δe) bằng cách sử dụng bộ làm mờ dạng
singleton, quy tắc suy luận tích và phương pháp giải mờ trung bình trọng tâm.
Mặc dù có tổng cộng 49 quy tắc mờ sẽ được suy luận, nhưng thực tế chỉ có 4
quy tắc mờ có thể được kích hoạt hiệu quả để tạo ra đầu ra khác 0. Do đó, đầu
ra của suy luận mờ có thể được tính bằng công thức sau:
Σi+1 Σj+1 c [ μA ( ⅇ)⋅ μ β ( Δⅇ)]
u ( ⅇ , Δe )= m=i m= j m, n n m
≡Σi +1 Σ j+1 c ⋅d f
Σi+1 Σ j+1 μA (ⅇ)⋅ μ β ( Δⅇ) n=i m= j m,n n ,m
n=i m= j n m
Với d ≡μA (ⅇ) ⋅ μ β ( Δⅇ) và Σi+1 Σ j+1 d =1 n , m n m n=i m = j n ,m
1.2.3 Lập quỹ đạo chuyển động
1.2.3.1 Quỹ đạo đường cong
Sử dụng lý thuyết đường cong Bézier để thực hiện thuật toán vẽ đường cong:
- Đường cong Bézier là một đường cong tham số thường được sử dụng trong
đồ họa máy tính và một số lĩnh vực khác. Dạng tổng quát hóa của đường
cong Bézier trong không gian nhiều chiều được gọi là mặt phẳng Bézier,
trong đó tam giác Bézier là một trường hợp đặc biệt.
- Đường cong Bézier được công bố lần đầu vào năm 1962 bởi một kỹ sư người
Pháp Pierre Bézier, người sử dụng nó để thiết kế thân ôtô. Nhưng việc nghiên
cứu những đường cong này thực tế đã bắt đầu từ năm 1959 bởi nhà toán học
Paul de Casteljau, ông sử dụng giải thuật De Casteljau để đánh giá các đường cong đó.
- Về mặt ứng dụng, đường cong Bézier thường được sử dụng trong đồ họa
vector để mô hình hóa các đường cong mượt (smooth curves) và những
đường cong đó có thể được phóng to hoặc thu nhỏ theo một tỉ lệ không giới
hạn. "Đường dẫn" (path), một khái niệm được sử dụng trong các chương trình
xử lý ảnh, được tạo ra bằng cách liên kết các đường cong Bézier với nhau.
Đường cong Bézier còn thường được sử dụng như là một công cụ để điều
khiển sự chuyển động (animation).
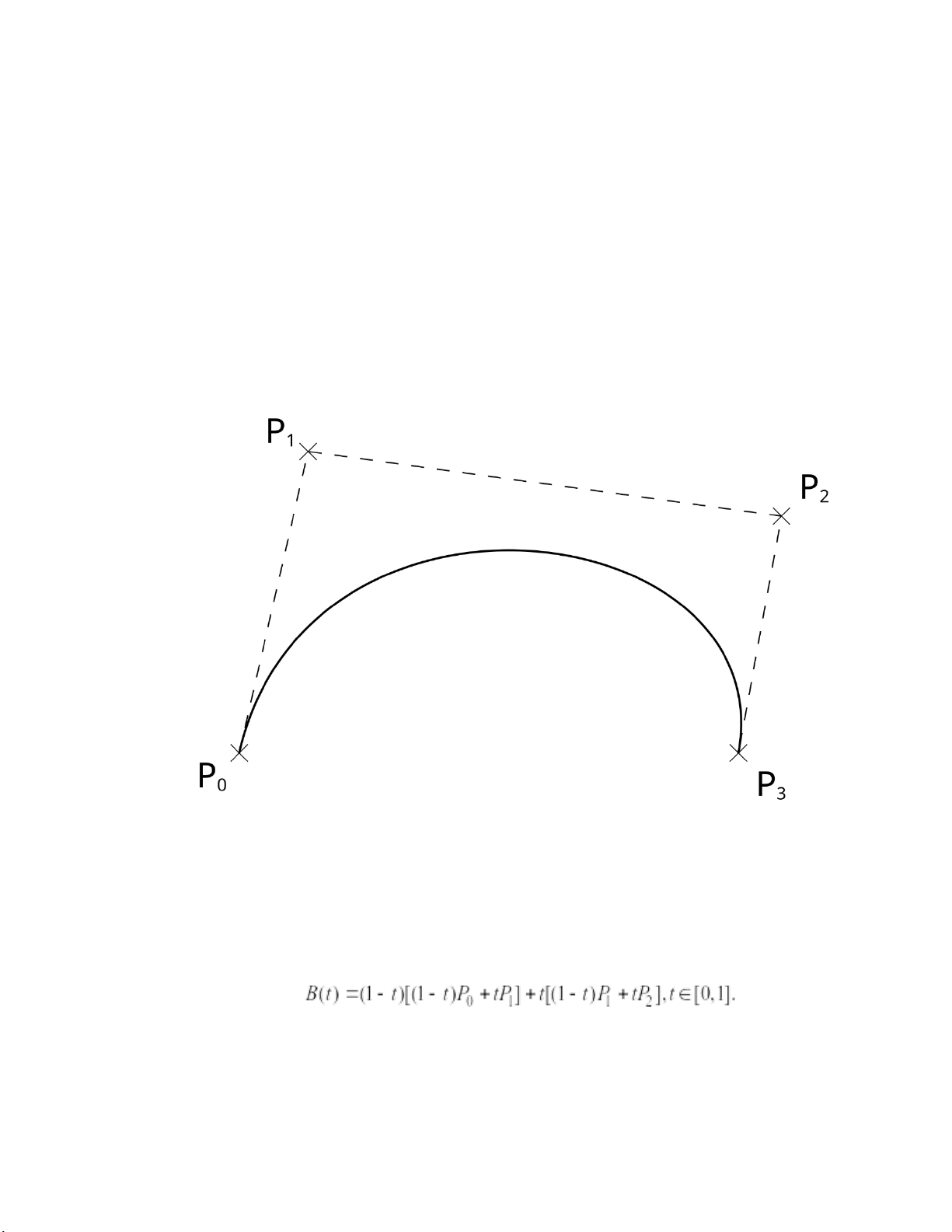
Hình: Đường cong Bézier bậc 3
Đường cong Bézier toàn phương hay bậc hai (quadratic):
- Đường cong Bézier bậc 2 được tạo bởi một hàm B(t), với các điểm P 0, P1 và P2 cho trước, khi đó:
Và có thể biểu diễn thành tập hợp các điểm tương ứng trong đường Bézier
tuyến tính được tạo bởi hai đường Bézier tuyến tính từ P0 tới P1, và từ P1 tới
P2. Nói một cách tường minh, thì nó có thể viết lại thành:
- Đường cong này xuất phát từ P0, tiến đến P1 rồi chuyển hướng dần đến P2
1.2.3.2 Quỹ đạo đường thẳng
Mặt phẳng Oxy: Một cách tổng quát: Với: S: Bước nhảy
Mặt phẳng Oz:
Nếu hệ thống tiến đến điểm có tọa độ z lớn hơn tọa độ z ban đầu thì: Ngược lại: Với S: bước nhảy
CHƯƠNG 2: MÔ PHỎNG HỆ THỐNG
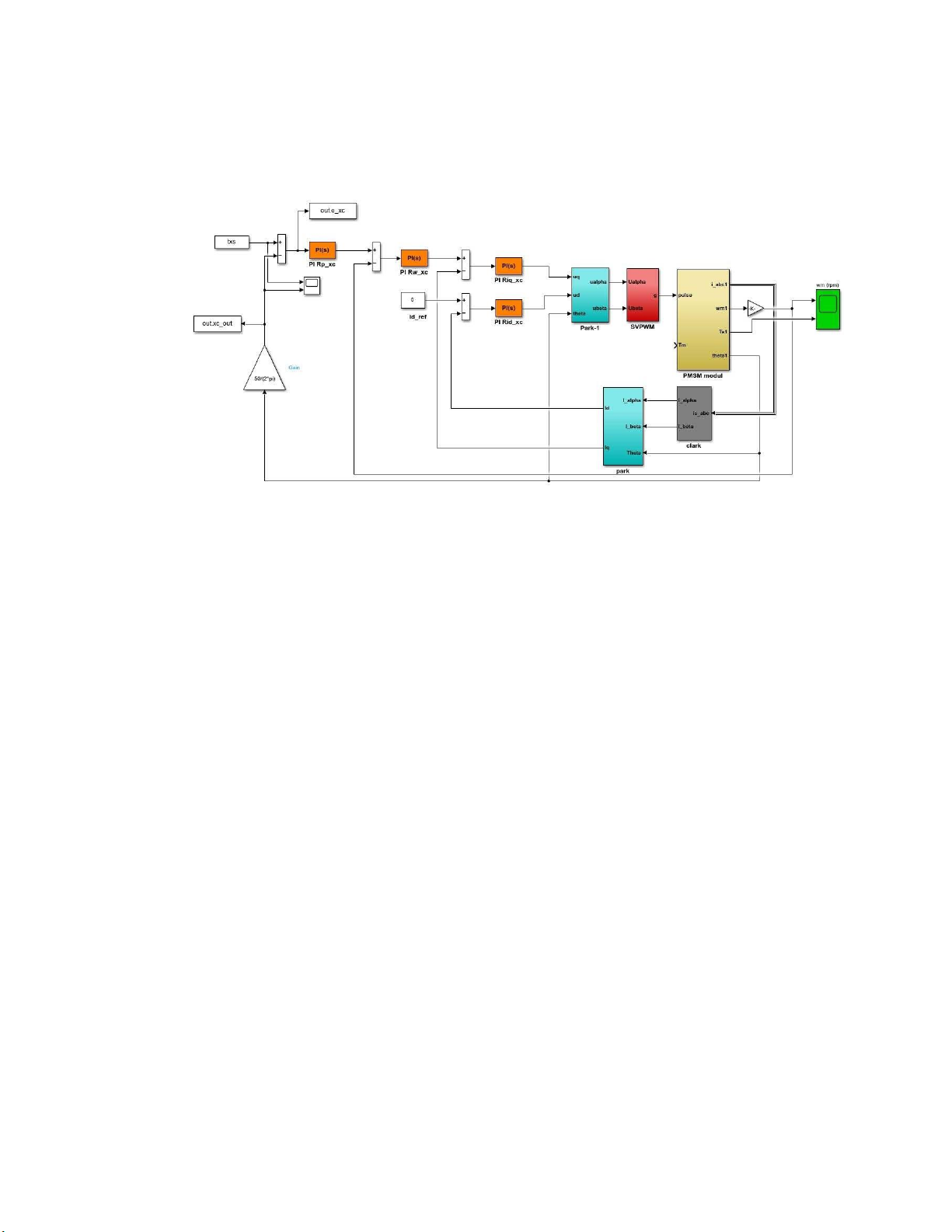
2.1 Sơ đồ mô phỏng Simulink
Hình 2.1: Sơ đồ điều khiển động cơ PMSM
Hệ thống điều khiển động cơ PMSM gồm 3 vòng điều khiển: điều khiển dòng điện,
điều khiển tốc độ và điều khiển vị trí.
Đầu vào hệ thống là giá trị theo thời gian vị trí tọa độ theo yêu cầu.
Mỗi hệ trục tương đương 1 hệ thống điều khiển động cơ PMSM gồm 3 vòng điều khiển như trên.
2.2 Hàm đường cong
Hàm này sử dụng định lý đường cong Bézier để xác định các đường cong mong muốn
function [xs, ys, zs, i] = drawCurve(xs, ys, zs, x1, y1, xc, yc, x2, y2, numPoints, i)
% Hàm này vẽ đường cong Bezier bậc hai trên mặt phẳng XY từ điểm (x1, y1) đến (x2, y2),
% với điểm điều khiển (xc, yc) và số lượng điểm nội suy numPoints.
% Tính toán các điểm trên đường cong
for t = linspace(0, 1, numPoints) i = i + 1;
% Công thức Bezier bậc hai
xs(i) = (1 - t)^2 * x1 + 2 * (1 - t) * t * xc + t^2 * x2;
ys(i) = (1 - t)^2 * y1 + 2 * (1 - t) * t * yc + t^2 * y2;
zs(i) = zs(i - 1); % Giữ z không thay đổi end end Với
xs, ys, zs: các mảng lưu giá trị của tọa độ XYZ
x1, y1: tọa độ vị trí đầu
xc, yc: tọa điểm điểm nội suy, quyết định hướng cong vào độ cong
x2, y2: tọa độ ví trị sau
numPoint: số điểm mong muốn, xác định khoảng cách t
i: giá trị tham số của mảng lưu giá trị
2.3 Hàm đường thẳng trên tọa độ Oxy
Hàm này dùng để vẽ đường thẳng giữa 2 điểm trên hệ Oxy
function [xs, ys, zs, i] = moveXY(xs, ys, zs, x1, y1, x2, y2, S, i)
% Calculate the length between the points (x1, y1) and (x2, y2)
length = sqrt((x2 - x1)^2 + (y2 - y1)^2);
% Calculate the angle between the two points (x1, y1) and (x2, y2)
angle = atan2(y2 - y1, x2 - x1); % Angle in radians
% Calculate the increments in x and y based on the angle and step size
dx = cos(angle) * S; % Increment in x-direction
dy = sin(angle) * S; % Increment in y-direction a = 0; while a < length i = i + 1;
xs(i) = xs(i - 1) + dx; % Increment in x-direction
ys(i) = ys(i - 1) + dy; % Increment in y-direction zs(i) = zs(i - 1); % No change in z-direction a = a + S; % Update the progress end end Với:
xs, ys, zs: các mảng lưu giá trị tọa độ XYZ
x1, y1: tọa độ điểm đầu
x2, y2: tọa độ điểm sau S: bước nhảy
i: tham số mảng lưu giá trị
2.4 Quỹ đạo đường tròn
2.5 Quỹ đạo hình sao
2.6 Quỹ đạo bất kỳ
CHƯƠNG 3: KẾT QUẢ