Đề cương ôn tập HK2 Toán 11 năm 2018 – 2019 trường Hai Bà Trưng – TT Huế

Đề cương ôn tập HK2 Toán 11 năm học 2018 – 2019 trường THPT Hai Bà Trưng – Thừa Thiên Huế gồm 81 trang trình bày các nội dung kiến thức Toán 11 học sinh cần ôn tập để chuẩn bị cho kỳ thi học kỳ 2 môn Toán 11,

34 17 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TrườngTHPTHaiBàTrưng–Huế  Trang1/81

TRƯỜNG THPT HAI BÀ TRƯNG ĐỀ CƯƠNG ÔN TẬP HKII NĂM HỌC 2018 - 2019

TỔ TOÁN

MÔN TOÁN – KHỐI 11



Họ và tên: PHAN PHƯỚC BẢO; Trường: HAI BÀ TRƯNG; Lớp: 11 

A. Nội dung

I. Giải tích: Từ§1chươngIV.Giớihạnđến§5chươngV.Đạohàm.

II. Hình học:Từ§1đến§5chươngIII.Vectơtrongkhônggian.Quanhệvuônggóc.

B. Một số bài tập tham khảo

Xem lại các bài tập trong SGK và SBT Đại số & Giải tích, Hình học 11 cơ bản.

 CHỦ ĐỀ I. GIỚI HẠN

Câu 1. Dãysốnàosauđâycógiớihạnbằng

?



 



 

 

. B.

 



 

 

. C.







n n

. D.

 

u n n

.



Lời giải:Vì

lim

lim 0 lim 0

n n

u u





   











Câu 2. Phátbiểunàotrongcácphátbiểusaulàsai?

lim 0









| | 1



. B.

lim

c c



. C.

lim 0











. D.

lim 0



.

Lời giải:

Theođịnhlý

lim 0



khi





| | 1



.

Câu 3. Tínhgiớihạn

lim .

3 2

n n



 





 B.

 C.



 D.



Lời giải:

Tự luận :

lim lim .

1 2

3 2

lim .

lim

1 2

im lim .

1 2

3 2

n n





 

 





 



   

 



MTCT: NHẬP

 10

3 2

CALC x

x x





  

 



Câu 4. Cho

2 3 2

5 1

lim

a n n n

n bn a

  



 

.Cóbaonhiêugiátrị

nguyêndươngđể





0;4

b

?

. B.

. C.

. D.

.

Lời giải:

 

 

2 3 2 2

5 1

lim 0;4 0 4, 1;2;3;4

4 4

a n n n a

a a a

n bn a

  

       

 





TrườngTHPTHaiBàTrưng–Huế  Trang2/81

Câu 5. Cóbaonhiêugiátrịnguyêncủathamsố

thuộc





10;10



để





2 3

lim 5 3 2n a n

 

   

 

?

. B.

. C.

. D.

.

Lời giải:

   

   

2 3 2 3 2

lim 5 3 2 lim 3 2 2 0

 10;10 , 9; 8;...; 2;2;3;...;8;9

n a n a n a

do a a a





 

            



 

 





       





Câu 6. Tínhgiớihạn

2 3

3 2

7 2 1

lim .

3 2 1

n n

 



 



. B.



. C.

. D.

.

Lời giải:

2 3

3 2

7 1

7 2 1 2

lim lim

2 1

3 2 1 3

n n

 

 

 

 

 

   

 

 

 

 

 



MTCT: NHẬP

2 3

10

3 2

7 2 1 2

0,666

3 2 1 3

Calc

x x

  

 

 



Câu 7. Biết

3 2

2 4 1

lim

2 2

n n

 





với

làthamsố.Tính

a a



.



. B.



. C.

. D.



.

Lời giải:

Tacó

3 2

1 4

2 4 2 1

lim lim 4

2 2

n n

an a

n a

 

 

 

 

 

    



 



 

 



Vậy

2 2

4 4 12

a a

    

Câu 8. Chohaisốthực

;

a b

thỏamãn

3 2 3

5 3

lim 1

5 4 2

an n

n n bn

 

 

  

.Tính

S a b

 

.



. B.

 

. C.



. D.

 

.

Lời giải:

Dotửcóbậc2nêngiớihạnđãchovề1sốkháckhôngkhitửvàmẫucùngbậc

Suyra

 



Từđó

5 3

lim 1 2

4 2 2

an n a

 

     

 



Vậy

2 ( 5) 3

S a b

      



TrườngTHPTHaiBàTrưng–Huế  Trang3/81

Câu 9. Chodãysố





với

  

1 1 1

...

1.3 3.5 2 1 2 1

n n

   

 

.Tính

lim

.

A.

. B.

. C.

. D.

.

Lời giải:

Tự luận:

  

1 1 1 1 1 1 1 1 1 1 1

... 1 ... 1

1.3 3.5 2 1 2 1 2 3 3 5 2 1 2 1 2 2 1

1 1 1

 1

2 2 1 2

n n n n n

lim u lim

   

            

   

    

   

 

  

 



 



MTCT CASIO – 580 : Bấm như sau

q[a1R(2[p1)(2[+1)$$1E100=



HIỂN THỊ

KẾT QUẢ



Câu 10. Cóbaonhiêugiátrịnguyênlớnhơn



củathamsố

để





lim 4 3 5n mn

    

?

A.

. B.

. C.

. D.

.

Lời giải:





2 2

3 5

lim 4 3 5 lim  4 2 0

n mn n m m

n n

 

           

 

 







, 10 2 9; 8;...;1

m m m       



có11giátrịm.

Câu 11. Cóbaonhiêugiátrịnguyêncủathamsố

thuộckhoảng





0;2018

đểcó

9 3 1

lim

5 9 2187

n n

n n a







?

2011

. B.

2016

. C.

2019

. D.

2009

.

Lời giải:

Bước 1:DùngMTCTCASI0-580sửdụngcôngcụFACT

2187=qx



Xuất hiện ởmànhìnhMTCT 



Bước 2:

9 1

9 3 1 1

lim lim lim 7

5 9 3 3

9 1

n n

n n a a

n a



 



 



 

    



 



 

 



thuộckhoảng





0;2018

nên





7;8;...;2017

a 

có2011giátrịanguyênthỏamãn.



TrườngTHPTHaiBàTrưng–Huế  Trang4/81

Câu 12. Tínhgiớihạn

2 2 2

1 1 1

lim 1 1 ... 1

2 3 n

 

    

  

    

 

    

 

.

A.1. B.

. C.

. D.

. 

Lời giải:

Tự luận: nhớ lại hằng đẳng thức và áp dụng









2 2

2 2 2

1 1 1 1 1 1 1 1 1

lim 1 1 ... 1 lim 1 1 1 1 ... 1 1

2 3 2 2 3 3

1 3 2 1 1 1 1 1

lim . . ... . . 1 lim . 1

2 2 3 1 2 2

a b a b a b

n n n

n n

n n n n

   

 

            

         

            

 

            

 



       

    

       



       



MTCT CASIO - 580

Q[1pa1R[d$$2$100=



Xuấthiệnởmànhìnhkếtquả

 

KẾT QUẢ





Câu 13. Tínhtổngtấtcảcácgiátrịthựccủathamsố

để

 





2 2 2

lim 2 1 2

n a n n a n

     

.



. B.



 C.

. D.

.

Lời giải:

 









 

2 2 2

2 1

lim 2 1 lim

2 1

lim 2 6 0

2 1

1 1

1 V

n a n n a n

n a a

a a

n n n

S theo iet

    

      

    

 

  

 

 

 

     

 



   

 

 

 



TrườngTHPTHaiBàTrưng–Huế  Trang5/81

Câu 14. Tínhtổng

1 1 1 1

1 ... ...

3 9 27 3



 

       

 

 

với

n



.



. B.



. C.

 

. D.



.

Lời giải:

Tự luận

Nhắclạitổngcủa1cấpsốnhânlùivôhạn







1 1 1 1 1 3

1 ... ...

3 9 27 3 4



 

         

 

 

 

 

 

 



MTCT CASIO -580VN

q[(ap1R3$)^[$$0E100=



Xuất hiện ở màn hình kết quả



Câu 15. Giảsửtacó





lim

f x a





và





lim

g x b





.Trongcácmệnhđềsau,mệnhđềnàosai?

A.









lim

f x g x ab





 

 

. B.









lim

f x g x a b



  

 

 

.

C.





 

lim

f x

g x b





.  D.









lim

f x g x a b



  

 

 

.



Lời giải:





 

lim

f x

g x b





vìcóthể





lim 0

g x b



 



Câu 16. Chocácgiớihạn





lim 2

x x

f x





;





lim 3

x x

g x





.Tínhgiớihạn









lim 3 4

x x

f x g x





 

 

. B.

. C.



. D.

.

Lời giải:









lim 3 4 3.2 4.3 6

x x

f x g x



    

 

 



Câu 17. Tínhgiớihạn

2 3

lim

1 3





.

. B.



. C.



. D.



.

Lời giải:

Tự luận

2 3 2

lim lim

1 3 3

x x

 

 



 



 

  



 



 

 



MTCT CASIO -580VN

 

 10

2 3 2

1 3 3

Calc x



 

 





a2[p3R1p3[r10^10==

kếtquảxuấthiệnởmànhìnhMTCT



TrườngTHPTHaiBàTrưng–Huế  Trang6/81

Câu 18. Cho





lim 5 5

x ax x



   

thì

là

nghiệmcủaphươngtrìnhnàotrongcácphươngtrìnhsau?

11 10 0

x x

  

. B.

5 6 0

x x

  

. C.

8 15 0

x x

  

. D.

9 10 0

x x

  

.

Lời giải:

 

2 2

lim 5 lim lim

5 5

lim lim 5 10

1 1

x x x

x x

x a

x ax x

x x

x a x a

x x

  

 

 



 

  

 

     

  

   

 

   

   

     



 

   

   

 

 



Mà D.

9 10 0

x x





   



 



.(thỏa)



Câu 19. Tínhgiớihạn





lim 4 1

I x x x



   

.

 

. B.

 

. C.



. D.

 

.

Lời giải:

Tự luận:





2 2

4 1

lim 4 1 lim lim 2

4 1

1 1

x x x

I x x x

x x x

x x

  



  

       

  

   



MTCT CASIO -580VN





 10

4 1 2

Calc x

x x x



   



s[d+4[+1$+[rp10^10==



kếtquảmànhìnhxuấthiện

  



Câu 20. Cho





lim 5

f x









.Tínhgiớihạn





 

lim

1 4 9 3

f x

x f x





  

.

. B.

. C.

. D.

.

Lời giải:

Bình luận:khigiảidạngnàytaluônđốichiếuvớiđịnhnghĩađạohàm













 

lim 5 lim ' .

1 10

' 1 5

x x x

f x f x f x

f x

x x x

 

 

  

 















 





 

1 1

10 10

1 1

lim lim . 5. 1

4.10 9 3

1 4 9 3 4 9 3

x x

f x f x

x f x f x

 



 



  



 

    



TrườngTHPTHaiBàTrưng–Huế  Trang7/81



Câu 21. Tínhgiớihạn





3 2

lim 3 5 9 2 2017

x x x



  

.

A.



. B.

. C.



. D.



.

Lời giải:

Bìnhluận:cácgiớihạnkhixtiếnvề+ vô cùng(hoặc–vôcùng)tachỉquantâmđếnbậclớnnhất

củax

 

3 2 3

2 3

5 9 2 2017

lim 3 5 9 2 2017 lim 3

x x

x x x x

x x x

 

 

        

 

 

.

Câu 22. Chohaisốthực

và

thoảmãn

4 3 1

lim 0

2 1

x x

ax b



 

 

  

 



 

.Tính

a b





. B.



. C.

. D.



.

Lời giải:

Tự luận:



 

4 3 1 5

2 1 2 2 1

4 3 1 5

lim lim 2 0

2 1 2 2 1

x x

ax b x ax b

x x

 

 

  

 

 

 

 

 

 

 

       

 

 

 

 

 

 

 

 

 



vì

lim 0

2 1







nên

x ax b







   



 







Vậy

2 2 2. 3

a b

 

     

 

 



* MTCT CASIO -580VN ( sau khi thi xong và hè sẽ luyện tập MTCT thêm)

dùng thủ thuật Calc 100 (lấy 2 chữ số)

ta có 97,5 > 50 ta lấy 97,5 - 100 = 2,5 sau đó làm tròn hàng tiếp theo lên 1 đơn vị :

tức 1 + 1 = 2 < 50. ta có



 100

4 3 1 5

197,5... 2

2 1 2

Calc x

x x



 

  



Câu 23. Tínhgiớihạn

3 2

lim









.



. B.

. C.



. D.

.

Lời giải:









2 2

lim 3 2 7, lim 2 0, 2 2 2 0

3 2

lim

x x

x x x x x

 



 



         



  





MTCT CASIO -580VN 



x 1,9999

3 2

Calc











TrườngTHPTHaiBàTrưng–Huế  Trang8/81

Câu 24. Biết

2 2

1 1

lim

3 4 4 12 20

x x x x



 



 

   

 

làmộtphânsốtốigiản

 

0 .



Tính

S a b

 

.

 

. B.



. C.



. D.



.

Lời giải:

Tự luận

     

    

 

   

    

2 2

1 1 1 1

lim lim

3 4 4 12 20 2 3 2 2 10

4 2

1 3x 2 10

lim . lim

2 3 2 10 2 3 2 10

4 4 1

lim

3 2 10 8. 8 16

0 16; 1

x x

x x x x x x x x

x x x x x x

x x b

b b a

 



 

 

  

 

 

       

 

 



  

 

     



   

  

    



 

6 6. 1 16 10

S a b

      



MTCT CASIO -580VN

a1R3[dp4[p4$+a1R[dp12[+20

mànhìnhxuấthiện



tiếptục

r1.9999==



mànhìnhxuấthiện  



p0.0625=



kết quả

0,0625



  



TrườngTHPTHaiBàTrưng–Huế  Trang9/81

Câu 25. Biết

 





lim 4 3 1 0

x x ax b



    

.Tính

a b



.

. B.

. C.



. D.

.

Lời giải:

Tự luận

cách 1:

 





lim 4 3 1 0 0

x x ax b a



      



 

2 2 2 2

4 3 1

4 3 1 2

lim 4 3 1 lim lim 0

3 1

4 3 1

x x x

x x ax b

x x a x abx b

x x ax b

x a

x x x

  

   

    

      

 

   

 

 

khi bậc tử < bậc mẫu

tức là

4 0

4 2 4. 5

3 2a 0

a b





 





     

 

 

  







cách 2 : bí kíp

 





 

lim

lim . ... lim

...

n n n

x x

f x

f x a x bx b f x ax





 







 



 

     

 





 

2 2

4 3 1

lim 2

4 3 1 4 3 3

lim 4 3 1 2 lim

2 2 4

4 3 1 2

x x

x x x

b x x x

x x x



 

 

 

    

      



  



MTCT CASIO -580VN

as4[dp3[+1R[r10^10==



x 10

4 3 1

Calc

x x



 

 

 

s4[dp3[+1$p2[r10^10==



x 102

4 3 1 2

Calc

x x x





   

 

TrườngTHPTHaiBàTrưng–Huế  Trang10/81

Câu 26. Tínhgiớihạn

2 2

4 1

lim

2 3

x x x



  



.



. B.



. C.



. D.

.

Lời giải:

Tự luận

 

2 2

1 1 1 1

1 4 1 4

1 2

4 1 1

lim lim lim

3 3

2 3 2 2

2 2

x x x

x x

x x x x

x x x

x x

  

   

      

   

 

  

   

   



   

 

   

   



MTCT CASIO -580VN

2 2

x 10

4 1 1

2 3 2

Calc

x x x



  







as[dp[$ps4[d+1R2[+3rp10^10

==

xuất hiện 



Câu 27. Cho

1 2017 1

lim

2018 2

a x



 





;





lim 1 2

x bx x



   

.Tính

P a b

 

.



. B.

 

. C.



. D.



.

Lời giải:

 

2 2

1 1

1 2017 1 2017

1 2017

lim lim lim

2018 2018 2018

1 2017

1 1

lim

2018

1 2 2

x x x

a x a x

a x

x x

x x x

x a

x x

  



    

 

 

  

 

  

 



 

     

 



 

 



 

2 2

lim 1 lim lim 2 4

1 1

x x x

x b

x bx x b

x bx x

x x

  

 



 

  

 

        



 

  

 

 



4 4 4 2

P a b

 

     

 

 



TrườngTHPTHaiBàTrưng–Huế  Trang11/81

Câu 28. Giátrịcủasốthực

saocho









2 1 3

lim 6

4 7

x mx

x x



 



 

là

A.

 

. B.



. C.



. D.

 

.

Lời giải:

Tự luận

 

2 3

1 3

2 1 3

lim lim 6 3

4 7

4 7 1

x x

x x m

x mx

x x

 

   

 

   

 

   

    

 

 

 

 

 



* MTCT CASIO -580VN

gánm=Y

thửđápánAtacó

a(2[dp1)(Q)[+3)R[^3$+4[+7r

10^10=p3==



     

  

thửđápánBtacó 

a(2[dp1)(Q)[+3)R[^3$+4[+7r

10^10=3==



Câu 29. Chohàmsố





y f x



xácđịnhtrên





\ 1





cóđồthịnhưhìnhvẽ.Khẳngđịnhnàođúng?



A.





 





lim ; lim

f x f x

 



 

   

. B.





 





lim ; lim

f x f x

 



 

   

.

C.





 





lim ; lim

f x f x

 



 

   

. D.





 





lim ; lim

f x f x

 



 

   

.



Lời giải:

Bình luận

Khigặpdangđồthịcầnnhớ:

khixtừphíalớnhơnvềvịtríkhôngxácđịnh(kíhiệulà+)nhánhđồthìhướnglênlà+vôcùng

khixtừphíanhỏhơnvềvịtríkhôngxácđịnh(kíhiệulà-)nhánhđồthìhướngxuốnglà-vôcùng



TrườngTHPTHaiBàTrưng–Huế  Trang12/81

Câu 30. Tínhgiớihạn

3 1 4

lim

3 4



 

 

.

A.



. B.



. C.



. D.



.

Lời giải:tự luận dạngvôđịnh

nhân liên hợp khử vô định





 





 





 

5 5

3 4 3 1 4 3 1 4

3 1 4

lim lim .

3 4

3 4 3 4 3 1 4

3 4 3 4

3 5

3 1 16 3 3 3 9

lim . lim .

9 4 5 1 4 4 4

3 1 4 3 1 4

x x

x x x

x x

 

     

 



 

     

   



  

    

     

   



MTCT CASIO -580VN

cách 1: dùng Calc

x 4,99999

3 1 4 9

3 4

Calc



 

 

 

as3[+1$p4R3ps[+4r4.99999==



   

xuấthiện



sauđó

Wp2.25=







cách 2: dùng công cụ đạo hàm

aqys3[+1$p4$5 

Rqy3ps[+4$$5  



TrườngTHPTHaiBàTrưng–Huế  Trang13/81

Câu 31. Tínhgiớihạn

2 3

lim

x x



 





.



 B.



 C.



 D.





Lời giải:dạngvôđịnh



tự luận nhân liên hợp khử vô định





  





 

  

 

  

 

1 1 1

1 1

2 3 2 3

2 3 4 3

lim lim . lim

1 1 1

2 3 1 1 2 3

1 4 3 4 3

lim lim

1 1 2 3 1 2 3

x x x

x x

x x x x

x x x

x x x x x x

x x x

x x x x x x x

  

 

   

   

  

  

     

  

  

      



MTCT CASIO -580VN tương tự câu 30 ( bấm tại lớp để rèn luyện và học hỏi)



Câu 32. Tínhgiớihạn

7 2

lim

x x x



   



.





.

Lời giải:dạngvôđịnh



tự luận nhân liên hợp khử vô định

   

 





   

  

 

2 2

3 3

1 1

2 2

1 7 2, 2 2

7 2 7 2 2 2

lim lim

1 1 1

7 8 2 4

lim

1 2 2

1 7 2 7 4

1 2

lim

1 2 2

1 7 2 7 4

x x

x x x x

x x x x x x

x x x

x x

x x x

 



      

 

        

 

 

  

 

 

 

    

 

 

 

   

 

    

 

 

 

 

 

 



 

 

 

   

 

    

 

 

 



 





2 2

lim

2 2

7 2 7 4

1 3 2

12 4 3

x x



 

 





 

 

  

 

   

 

 

 

   



MTCT CASIO -580VN tương tự câu 30 ( bấm tại lớp để rèn luyện và học hỏi)

TrườngTHPTHaiBàTrưng–Huế  Trang14/81

Câu 33. Tínhgiớihạn





3 3

lim

x a

x a x a

x a



  



.

A.



. B.



. C.



. D.



.

Lời giải:dạngvôđịnh



tự luận













 





 

3 3 2

2 2 2 2

1 1 1

lim lim lim

x a x a x a

x a x a x a x x

x a a

x a x xa a x xa a

  

     



  



    



MTCT CASIO -580VN tương tự câu 30 ( bấm tại lớp để rèn luyện và học hỏi)

gána=3(vìmẫucókếtquảbội3)



Câu 34. Chohàmsố





y f x



liêntụctrên





;

a b

.Điềukiệncầnvàđủđểhàmsốliêntụctrên





;

a b

là









lim

x a

f x f a







và









lim

x b

f x f b







. B.









lim

x a

f x f a







và









lim

x b

f x f b







.









lim

x a

f x f a







và









lim

x b

f x f b







. D.









lim

x a

f x f a







và









lim

x b

f x f b







.

Lời giải:

địnhlýsgk

Câu 35. Tìmthamsốthực

đểhàmsố





y f x



khi 4

1khi 4

x x

mx x



 

 











  



liêntụctạiđiểm

 

.

A.



. B.



. C.



. D.



.

Lời giải:

Đểhàmsố





y f x



liêntụctạiđiểm

 

thì

   









4 4 4

4 3

4 4 1 4 1

4 4

7 4 1 2

x x x

x x

lim f x f lim m lim m

x x

m m

  

 

        

 

      



Câu 36. Cótấtcảbaonhiêugiátrịcủa

đểhàmsố

( 2) 2

khi 1

( )

3 2

8 khi 1

ax a x

f x

a x



  







 





 



liêntụctại



?

. B.

. C.

. D.

.

Lời giải:

đểhàmsố

( )

f x

liêntụctại



thì

   

  





 

2 2

1 1 1

2 2

1 2 3 2

( 2) 2

1 8 8

3 4

3 2

2 .4 8 4 0

x x x

x ax x

ax a x

lim f x f lim a lim a

a a a a

  

   

  

      

 





       









Vậy có 2 giá trị a.

Câu 37. Hàmsốnàotrongcáchàmsốdướiđâykhôngliêntụctrên





A.

y x



. B.





. C.

sin

y x



. D.

2 1







.

Lời giải:

bí kíp:Cáchàmsốkhôngliêntụctrên



làcáchàmphânthứcvớimẫubằng0cónghiệm

TrườngTHPTHaiBàTrưng–Huế  Trang15/81

Câu 38. Chohàmsố

 

khi 1

 



3 khi 1

mx n x

f x

mnx x



 







 





liêntụctrên



.Tính

2 2



m n

.

. B.

. C.

. D.

.

Lời giải:

Đểhàmsố





f x

liêntụctrên



thì

         

2 2

1 1 1 1

2 2 2 2

lim lim lim lim 2 3 2 3

2 2 3 3.

x x x x

f x f x mx n mnx m n mn

m mn n mn m n

   

   

        

       



Câu 39. Gọi

làhaisốthựcđểhàmsố

 

khi 1

2 1 khi 1

x ax b

f x

ax x



 













 



liêntụctrên



.Tính

a b



.

A.

. B.



. C.



. D.

.

Lời giải:

Đểhàmsố





f x

liêntụctrên



thì



   

1 1

lim 1 lim 2 1

x x

x ax b

f x f ax

 

 

   





suyrax=1lànghiệmcủatử

0 1 0

x ax b a b



      

nghiệmcònlạilàx=b(đlViet)



vậy

   









1 1 1

lim 1 lim 2 1 lim 2 1

1 1

1 0 3

1 2 1 4

x x x

x x b

x ax b

f x f a a

x x

a b a

a b

b a b

  

 

 

      

 

   

 

    

 

    

 



bí kíp: MTCT 580 VN

đốivớiphânthứctalấyđạohàmtửtạix=1vàchiachođạohàmmẫutạix=1,

cònđathứcthayx=1.

lưu ýhàmphânthứccótửvàmẫuchung1nghiệm(dạng

)

 

2 2 1 3

1 0 4

x ax b

a a a

a b b

a b

 





      





     

 



Câu 40. Chohàmsố





f x

xácđịnhtrên





;

a b

.Tìmmệnhđềđúng.

A.Nếuhàmsố





f x

liêntụctrên





;

a b

và









f a f b



thìphươngtrình





f x



khôngcó

nghiệmtrongkhoảng





;

a b

.

B.Nếu









f a f b



thìphươngtrình





f x



cóítnhấtmộtnghiệmtrongkhoảng





;

a b

.

C.Nếuhàmsố





f x

liêntục,tăngtrên





;

a b

và









f a f b



thìphươngtrình





f x



không

cónghiệmtrongkhoảng





;

a b

.

D.Nếuphươngtrình





f x



cónghiệmtrongkhoảng





;

a b

thìhàmsố





f x

liêntụctrên





;

a b

.

Lời giải:

địnhlýsgk

TrườngTHPTHaiBàTrưng–Huế  Trang16/81

Câu 41. Phươngtrìnhnàodướiđâycónghiệmtrongkhoảng





0;1

2 3 4 0

x x

  

. B.



 

1 2 0

x x

   

.C.

4 2

3 4 5 0

x x

  

. D.

2017

3 8 4 0

x x

  

.

Lời giải:

thay

0, 1

x x

 

vàocácđápánA,B,C,D.

biểuthứcnàochokếtquảtráidấu(1kếtquảâmvà1kếtquảdương)đólàđápán.

Câu 42. Chophươngtrình





4 2

2 5 1 0 1

x x x   

.Khẳngđịnhnàosauđâylàđúng?

A.





cónghiệmtrongkhoảng





1;1



. B.





chỉcómộtnghiệmtrongkhoảng





2;1



.

C.





cóítnhấthainghiệmtrong





1;2

. D.





khôngcónghiệmtrongkhoảng





2;0



.

Lời giải:dùng công cụ Table

MTCT CASIO -580VN là Mode 8

kiểm tra các vùng đổi dấu

Tự luận

Đặt





4 2

2 5 1

f x x x x

   











       

0 0

1 1, 0 1

1 0 0 1;0 , 0

f f

f f x f x

   

      



TrườngTHPTHaiBàTrưng–Huế  Trang17/81

Câu 43. Chophươngtrình

















2 2 3

3 1 4 3 0 1

m x x x     

, với

 làthamsố.Khẳngđịnhnàosau

đâyvềphươngtrình





làkhẳngđịnhđúng?





cóđúng

nghiệmphânbiệt. B.





vônghiệm.





cóítnhất

nghiệmphânbiệt. D.





cóđúngmộtnghiệm.

Lời giải:

Bí kíp:

chọncácgiátrịxsaochobiểuthứckhôngcònphụthuộcm(hoặcbiểuthứccómxácđịnh1loaik

dấu)

chẳng hạn













12 2

3 1 4 0

1 2

3 2 5 

2 11

m x x

x P

P x x P

x P





   

  

      

   



! số nghiệm của 1 phương trình nhỏ hơn hoặc bằng bậc của phương trình

Tự luận

Đặt

















2 2 3

3 1 4 3

f x m x x x

     



ta có

 

   

 

2 2 3 3 2

2 3

3 2

1 4 3

lim lim 3 1 4 3 lim 3 1 1 1

lim 3 1 0

x x x

f x m x x x x m

x x x

x m

  



 

  

 

           

  

 

 

  

 

     





 

2 11 0

2 5 0

  

  



 

   

 

2 2 3 3 2

2 3

3 2

1 4 3

lim lim 3 1 4 3 lim 3 1 1 1

lim 3 1 0

x x x

f x m x x x x m

x x x

x m

  



 

  

 

           

  

 

 

  

 

     

Vậy phương trình đã cho có 3 nghiệm.

MTCT CASIO -580VN

giá trị cực đại . giá trí cực tiểu > 0 thì pt có 1 nghiệm

giá trị cực đại . giá trí cực tiểu = 0 thì pt có 2 nghiệm

giá trị cực đại . giá trí cực tiểu < 0 thì pt có 3 nghiệm

chom=y=1,x=100

kếtquả 



dùng Calc 100suyra





3 2

3 4 16 19

f x x x x

   



Mode 9 chọn 2 chọn 3 nhập 



sauđóbấm=liêntiếp

  

kết luận:3nghiệm.hihi. lợi hại quá



TrườngTHPTHaiBàTrưng–Huế  Trang18/81

Câu 44. Tìmtấtcảcácgiátrịthựccủa

đểphươngtrình





 

2020

2019

1 2 2 3 0

m x x x

    

vônghiệm.



 B.

 



 C.



 D. Khôngcógiátrị



Lời giải:

Bí kíp : pt bậc lẻ luôn có nghiệm





 

2020

2019

1 2 2 3 0

m x x x

    

bậc4039nênluôncónghiệm.

Tự luận

Đặt

 





 

2020

2019

1 2 2 3

f x m x x x

    



ta có

























0 0

1 1 0, 2 1 0, 1 . 2 0 1;2 , 0.

f f f f x f x

         

Vậy pt luôn có nghiệm.

------------------------

. CHỦ ĐỀ 2. ĐẠO HÀM

Câu 45. Cho

y x

 

.Gọi



làsốgiacủađốisốtại

và



làsốgiatươngứngcủahàmsố,tính



.

2 3

3 3 .

x x x x

   

. B.

2 2

3 3 .

x x x x

   

. C.

2 2

3 3 .

x x x x

   

. D.

2 3

3 3 .

x x x x

   

.

Lời giải:

   

 









3 2 2

2 2

1 1 3 3

3 3

x x x x x x x x

f x x f x

x x x x

         

  



       

   



Câu 46. Sốgia



củahàmsố

2 5

y x x

  

tạiđiểm



là

A.

 

2 5

x x

   

. B.

 

x x

  

. C.

 

x x

  

. D.

 

x x

  

.

Lời giải:

       





 

2 2

1 1 1 2 1 5 1 2.1 5 4

y x x x x x

f f

                  



Câu 47. Chohàmsố





y f x



cóđạohàmthỏamãn





6 2.





Giátrịcủabiểuthức









lim

f x f





bằng

12.

 B.

. C.

 D.



Lời giải:theođịnhnghĩađạohàm









 

lim 6 2.

f x f







 





Câu 48. Chohàmsố

 

1, 1

2 , 1.

x x

y f x

x x



 

 







Mệnhđềsailà

A.





1 2





. B.









. C.





0 2.





D.





2 4.







Lời giải:

   

 

2 1

1, 1

2, 1.

2 , 1.

' 1 ' 1 2

x x

y f x f x

x x

f f







  

   

 





  



nêntồntạiđạohàmtạix=1.

TrườngTHPTHaiBàTrưng–Huế  Trang19/81

Câu 49. Chohàmsố

 

1 khi 0

ax bx x

f x

ax b x



  





  



.Biết





f x

cóđạohàmtại



.Tính

T a b

 

.

A.

 

. B.



. C.

 

. D.



.

Lời giải:

 

     

   

0 0

1 khi 0

lim lim 0 1 1 2

1 khi 0 2 khi 0

1 khi 0 khi 0

' 0 ' 0

x x

ax bx x

f x

ax b x

f x f x f b b

ax bx x ax b x

f x f x

ax b x a x

f f a b

a b

 

 

 



  





  



        

 

    

  

 

   

 

  

  



2 6

T a b

   



Câu 50. Đạohàmcủahàmsố

5 3 2

2 4

y x x x

  

là

4 2

10 3 2

y x x x



  

. B.

4 2

5 12 2

y x x x



  

.C.

4 2

10 12 2

y x x x



  

.D.

4 2

10 12 2

y x x x



  

.

Lời giải:

5 3 2

2 4y x x x

   

4 2

10 12 2

y x x x



  



Câu 51. Chohàmsố

 

2 1

f x







xácđịnhtrên





\ 1



.Đạohàmcủahàmsố





f x

là

A.

 

f x







. B.

 

f x







. C.

 

f x









. D.

 

f x







.

Lời giải:nhắclạicôngthứcđạohàmnhanh

 

ax b a bc

cx d

 

 



 



 





 

2 1

f x



 



 

f x









MTCT CASIO -580VN

và nhân với bình phương mẫu 



dùngCalc100kếtquả vậy tử=3.



Câu 52. Tínhđạohàmcủahàmsố

2 2 3

x x

 



 

.

x x



 

. B.

 

6 3

x x



 

. C.

 

x x 

. D.

x x



 

.

Lời giải:

 

2 2 3 6 3

x x x

y y

x x

  

  

 



MTCT CASIO -580VN

tươngtự 

kếtquảCalc100là:603suyratử=6x+3

TrườngTHPTHaiBàTrưng–Huế  Trang20/81



Câu 53. Chohàmsố





















1 2 3 4

f x x x x x x

    

.Tính







. B.

. C.



. D.

.

Lời giải:

 

























   

0 0

0 1 2 3 4

0 lim lim 1 . 2 ...( 4) 4! 24

x x

f x f x x x x x

x x

 

    



       





dạng này tổng quát





























   

0 1 2 3 4 ...

' 0 1 . !

' 1 1 . !

f x x x x x x x n

f n



      

 



ứng dụng đạo hàm giải 2 câu trong đề Trấn Biên - ĐN

Câu 38(TB-ĐN) Cho

 

    

1 2 ... 2018

f x

x x x



  

.Tính





' 0

Lời giải:

 

        

          

0 0

0 1 2 ... 2018

0 lim lim

0 0

1 1 1

lim

1 2 ... 2018 1 . 2 ... 2018 2018!

x x

f x f x x x

x x

x x x

 





   



 

 

  

     



Câu 40(TB-ĐN) Cho

2018

2017

lim

x x a

x x b



 



 

.Tính

2 2

a b





Dạng

dùng MTCT 580 VN như sau

qy[^2018$+[p2$1=



2019





qy[^2017$+[p2$1=



 

2018





Suy ra:

2 2

4037

a b 

TrườngTHPTHaiBàTrưng–Huế  Trang21/81

Câu 54. Cho

 

2 2

2 3 5

x x ax bx c



 

   



 



 

.Tính

S a b c

  

.

A.



. B.



. C.

 

. D.



.

Lời giải:

tự luận

   

2 2 2

2 2

2 3 5 2 12 4

2, 12, 4.

3 3

x x x x ax bx c

a b c

x x



 

     

     

 



 

 



MTCT CASIO -580VN



Calc100phântích1/88/04thìtử=

2 12 4 2, 12, 4

x x a b c

     



2 12 4 18

S a b c

      



Câu 55. Biết

 

3 2

4 1 4 1 4 1

x ax b

x x x



 

 



 

  

 

.Tính



 

. B.

 

. C.

 

. D.



.

Lời giải:





 

   

4 3 2

2 4 1

4 4 1 4 3 2

3 2 8 8

2 4 1

4 1

4 1 2 4 1 4 1 2 4 1 4 1

4 4

4, 4

4 1 4 1 4 1 4 1

x x

x x x x x

x ax b

a b

x x x x



  



   

  

 



  

 



    

 

  

     

   



  



Câu 56. Tínhđạohàmcủahàmsố

 

2 1

y x x

  

2 2 1

x x

 







. B.

2 2 1

x x

 







. C.

2 2 1

x x

 







. D.

2 2 1

x x

 







.

Lời giải:

 

2 1

y x x

   

2 2 1

x x

 









Câu 57. Hàmsốnàosauđâykhôngcóđạohàmtrên



?

A.

y x

 

. B.

4 5

y x x

  

. C.

sin

y x



. D.

2 cos

y x

 

.

Lời giải:

cáchàmgiátrịtuyệtđốikhôngcóđạohàmtạinghiệmcủanó.

   

1 1

1  1

' 1 1 ' 1 1

x khix

y x

x khix

f f

 

 



  



 



   



Câu 58. Tínhđạohàmcủahàmsố





y x x

  

tạiđiểm

 

.

A.

. B.



. C.

. D.



.

Lời giải:





 

' 3 1 2 1

' 1 81

y x x x

   

  



TrườngTHPTHaiBàTrưng–Huế  Trang22/81

Câu 59. Cho hàmsố

   

3 2

2 2

f x x m x x

    

. Đểđạohàm





f x



bằng bìnhphươngcủa mộtnhị

thứcbậcnhấtthìgiátrị

là



hoặc

. B.

hoặc

. C.



hoặc

. D. Khôngcógiátrịnào.

Lời giải:

   

3 2

2 2

2 2 1

f x x m x x

f x mx m x

    



   



Đểđạohàm





f x



bằngbìnhphươngcủamộtnhịthứcbậcnhấtthì

 



 

4 2 4 0

m m





     











Câu 60. Tìmtấtcảcácgiátrịcủathamsố

đểhàmsố





3 2 3

1 2

y x m x x m

    

có

' 0,y x

  



.

A.

1 2 6; 1 2 6

 

   

 

.B.

1 2 6;1 2 6

 

 

 

.C.

1 6; 1 6

 

   

 

.D.

1 6;1 6

 

 

 

.

Lời giải:





 

3 2 3

1 2

' 3 2 1 2 0,

3 0

2 5 0 1 6 1 6

4 1 4.3.2 0

y x m x x m

y x m x x

m m m

    

      











          

 

 

  











Câu 61. Chohàmsố

 

3 2

4 7 11

f x x x x

    

.Tậpnghiệmcủabấtphươngtrình





f x





là

A.





1;7

. B.









;1 7;

  

. C.





7; 1

 

. D.





1;7



.

Lời giải:

 

3 2

4 7 11

8 7 0 1 7

f x x x x

    



       



Câu 62. Chohàmsố

 

5 14 9

f x x x

   

.Tậphợpcácgiátrịcủa

để





f x





là

;

 



 

 

. B.

7 9

;

5 5

 

 

 

. C.

 

 

 

. D.

;

 



 

 

.

Lời giải:

 

5 14 9, 1;

10 14 9 7

5 5

2 5 14 9

f x x x D

f x x

x x

 

    

 

 

 



    

  



TrườngTHPTHaiBàTrưng–Huế  Trang23/81

Câu 63. Biếthàmsố









f x f x



cóđạohàmbằng

tại



vàđạohàmbằng

1000

tại



.Tínhđạo

hàmcủahàmsố









f x f x



tại



.

2018

. B.

1982

. C.

2018



. D.

1018

.

Lời giải:

















   

2 ' ' 2 ' 2

1 ' 1 2 ' 2 18

2 ' 2 2 ' 4 1000

' 1 4 ' 4 2018

f x f x f x f x

x f f

f f

   

 

   

  



Vậy

















   

4 ' ' 4 ' 4

1 ' 1 4 ' 4 2018

f x f x f x f x

x f f

   

 

   



Câu 64. Chohàmsố





f x x

 

và





2 3

g x x x

  

.Đạohàmcủahàmsố









y g f x



tại



bằng

A.

. B.

. C.

. D.

.

Lời giải:

cách 1:





















' ' ' . '

y g f x f x g f x

 

 

 



 





   

1 3

' 1 ' 1 1

f x x

f x f



  



  















 

2 3 ' 2 2

' 3 4

g x x x g x x

     





Đạohàmcủahàmsố









y g f x



tại



tacó





















' 1 . ' 1 ' 1 . ' 3 1.4 4

f g f f g

  



cách 2:

















   

 

2 3

2 2 2 3 2 3

' 2 2

' 1 4

y g f x f x f x

x x x x

y x

   

       

 





Câu 65. Chohàmsố





y f x



cóđạohàmvớimọi





vàthỏa









2 4cos . 2

f x x f x x

 

.Tính







.

. B.



. C.

. D.

.

Lời giải:









     

2 ' 4cos . 2 '

2 ' 2 4sin 4cos . ' 2

0 2 ' 0 0 4 ' 0 2 ' 0 1

f x x f x x

f x xf x x f x

x f f f

    

   

    

      



TrườngTHPTHaiBàTrưng–Huế  Trang24/81

Câu 66. Hệsốgóctiếptuyếncủađồthịhàmsố

3 4







tạiđiểmcótungđộ

 

là



. B.

. C.



. D.

.

Lời giải:

3 4 1

2 3

y x



    





 

3 4 5

' '



 

 

 



 





Hệsốgóctiếptuyếnlà

1 5 9

3 5

 

 

 

 

 



 

 



Câu 67. Chođườngcong





cóphươngtrình







.Gọi

làgiaođiểmcủa





vớitrụctung.Tiếp

tuyếncủa





tại

cóphươngtrìnhlà

2 1

y x

  

. B.

2 1

y x

 

. C.

2 1

y x

 

. D.

y x

 

.

Lời giải:



làgiaođiểmcủa











vớitrụctungnên

0, 1

M M

x y

  



 

' ' 0 2

y y

  



.Tiếptuyếncủa





tại

cóphươngtrìnhlà

2 1

y x

 



Câu 68. Phươngtrìnhcáctiếptuyếncủađồthịhàmsố

4 2

3 1

y x x

  

tạicácđiểmcótungđộbằng

là

20 35

y x

 

. B.

20 35

y x

  

và

20 35

y x

 

.

20 35

y x

 

và

20 35

y x

  

. D.

20 35

y x

  

.

Lời giải:

4 2 4 2

3 1 5 3 4 0 2

' 4 6

y x x x x x

y x x

          

 



Phươngtrìnhcáctiếptuyếnlà

20 35

y x

 

và

20 35

y x

  

.



Câu 69. Chohàmsố

4 2

6 3

y x x

  

.Tiếptuyếncủađồthịhàmsốtạiđiểm

cóhoànhđộ



cắtđồthị

hàmsốtạiđiểm

(

khác

).Tọađộđiểm

là

A.





3; 24

B 

. B.





1; 8

 

. C.





3;24

. D.





0; 3



.

Lời giải:

4 2

6 3

' 4 12

y x x

  

 



Tiếptuyếncủađồthịhàmsốtạiđiểm

cóhoànhđộ



là





















' 1 1 1 8 1 8 8

y y x y x x

         



phươngtrìnhhoànhđộgiaođiểm

4 2 4 2

8 6 3 6 8 3 0

x x x x x x

        



MTCT CASIO -580VN chọn4 

nhập hệ số ta có 



 Tọađộđiểm

là





3; 24

B 

TrườngTHPTHaiBàTrưng–Huế  Trang25/81



Câu 70. Chohàmsố





cos sin 2

y x m x C

 

(

làthamsố).Tìmtấtcảcácgiátrị

đểtiếptuyếncủa







tạiđiểmcóhoànhđộ





,





songsonghoặctrùngnhau.

A.

m  

. B.

2 3

m  

. C.

m  . D.

2 3

m   .



Lời giải:







' cos sin 2 ' sin 2 . s2

y x m x x m co x

    



 Đểtiếptuyếncủa





tạiđiểmcóhoànhđộ





,





songsonghoặctrùngnhauthì

 

3 1 3

' ' 2 2 .

3 2 2 6

y y m m m





   

       

   

   



Câu 71. Hìnhbênlàđồthịcủahàmsố





y f x



.Biếtrằngtạicácđiểm

,

đồthịhàmsốcótiếp

tuyếnđượcthểhiệntrênhìnhvẽbêndưới.



Mệnhđềnàodướiđâyđúng?













C A B

f x f x f x

  

 

. B.













B A C

f x f x f x

  

 

.













A C B

f x f x f x

  

 

. D.













A B C

f x f x f x

  

 

.

Lời giải:

Hệsốgóccủatiếptuyếndươngkhiđườngthẳngđiquagócphântưthứnhâtvàthứba.

Hệsốgóccủatiếptuyếnâmkhiđườngthẳngđiquagócphântưthứhaivàthứtư.

Từđồthịđềchotacó













B A C

f x f x f x

  

  



Câu 72. Trên đồthị

 

C y







 có bao nhiêu điểm

 mà tiếp tuyến với





 tại

 song song với

đườngthẳng

: 1

d x y

 

.

. B.

. C.

. D.

.

Lời giải:



: 1 1

d x y y x

     



 

1 1

: ' 0, 2

C y y x

 

     





 tiếptuyếnvới





tại

songsongvớiđườngthẳng

: 1

d x y

 

thì

 

' 1 2 1

y x







      











khi

1 0

x y

  

tiếptuyếnlà

y x d

   

(loại)

khi

3 2

x y

  

tiếptuyếnlà





3 2 5 / /

y x x d

      

(thỏa)



Lưu ý:cẩmthậnkhigặploạinàyvìchủquannghĩrằngcó2nghiệmsẽcó2tiếptuyến//d.

TrườngTHPTHaiBàTrưng–Huế  Trang26/81



Câu 73. Tìmphươngtrìnhtiếptuyếncủađồthịhàmsố







,biếttiếptuyếnvuônggócvớiđườngthẳng

y x

 

vàtiếpđiểmcóhoànhđộdương.

A.

3 10

y x

  

. B.

3 2

y x

  

. C.

3 6

y x

  

. D.

3 2

y x

  

.

Lời giải:

 









 tiếptuyếnvuônggócvớiđườngthẳng

y x

 



 

3 1

. 1 1 1







     











 dotiếpđiểmcóhoànhđộdươngnên





 Vậyphươngtrìnhtiếptuyếnlà

3 10

y x

  



Câu 74. Phươngtrìnhtiếptuyếnvớiđồthị





3 2

: 2 6 3

C y x x

  

cóhệsốgócnhỏnhấtlà

A.

6 5 0

x y

  

. B.

6 5 0

x y

  

. C.

6 3 0

x y

  

. D.

6 7 0

x y

  

.

Lời giải:

 

' 6 12 6 1 6 6

y x x x

      



Vậyhệsốgócnhỏnhấtbằng-6khix=1.Suyraphươngtrìnhtiếptuyếnlà

6 5 0

x y

  

.



Câu 75. Cótấtcảbaonhiêutiếptuyếncủađồthịhàmsố

3 2

y x x x

  

điquađiểm





1;0

A 

?

. B.

. C.

. D.

.

Lời giải:

Gọi





: 1

d y k x

 

điqua





1;0

A 

.

dtiếpxúc





3 2

: 3 2

C y x x x

  

khi

 





   

2 3 2

3 2

3 6 2 1 3 2  1

1 3 2

3 6 2

x x x x x x

k x x x x

k x x



     

   

 



 

  



  







sốnghiệm(1)làsốtiếptuyếnnênMTCT CASIO -580VN nhập

tathấycó3nghiệm,suyaracó3tiếptuyếnđiquaA.

Câu 76. Gọi

làtiếptuyếncủahàmsố







tạiđiểmcóhoànhđộbằng



.Khiđó

tạovớihaitrục

tọađộmộttamgiáccódiệntíchlà

169

S 

. B.

121

S 

. C.

S 

. D.

S 

.

Lời giải:

làtiếptuyếncủahàmsố







tạiđiểmcóhoànhđộbằng



cóphươngtrìnhlà:





3 3 4 3 13

y x x

    





cắthaitrụctọađộtại

 

0;13 , ;0

A B



 

 

 

.

 TamgiácOABcódiệntíchlà

1 169

. .

2 6

S OAOB 



TrườngTHPTHaiBàTrưng–Huế  Trang27/81

Câu 77. Chohàmsố

x b











 

.Biếtrằng

và

làcácgiátrịthỏamãntiếptuyếncủađồthị

hàmsốtạiđiểm





1; 2



songsongvớiđườngthẳng

: 3 4 0

d x y

  

.Tính

a b



.

A.



. B.

. C.



. D.

.

Lời giải:

: 3 4 0 3 4

d x y y x

      



 

 







Tiếptuyếncủađồthịhàmsốtạiđiểm





1; 2



songsongvớiđườngthẳng

: 3 4 0

d x y

  

nên

 

   

 

2 3

5 15 10 0

2 3

2 2 3 3 2

1, 1

A C

b a

a a

b a

a a a

a l

a b





   



  







  

 

 

  

 

  

      







 













 





Vậy

3 2.

a b

  



Câu 78. Phươngtrìnhtiếptuyến củađồthị hàmsố

2 3







biếttiếptuyếnđócắttrụctungvàcắttrục

hoànhtạihaiđiểmphânbiệt

,

saochotamgiác

OAB

cânlà

y x

  

. B.

y x

 

. C.

y x

 

. D.

y x

  

.

Lời giải:

Bình luận:

 Tiếptuyếnđócắttrụctungvàcắttrụchoànhtạihaiđiểmphânbiệt

,

saochotamgiác

OAB



cânlàkhicóhệsốgócbằng1hoặc-1.

 

' 1 2 3 1

2 3

y x

 





      



 







 Khi

1, 1

x y

  

phươngtrìnhtiếptuyếnlà





1 1 1

y x x

     

(loạivìđiquaO).

 Khi

2, 0

x y

  

phươngtrìnhtiếptuyếnlà





1 2 2

y x x

     

(thỏa)



Câu 79. Chohàmsố





y f x



cóđạohàmliêntụctrên



,thỏamãn









2 2 1 2 12

f x f x x

  

.Phương

trìnhtiếptuyếncủađồthịhàmsố





y f x



tạiđiểmcóhoànhđộbằng

là

2 2

y x

 

. B.

4 6

y x

 

. C.

2 6

y x

 

. D.

4 2

y x

 

.

Lời giải:











2 2 1 2 12

f x f x x

  











   

 

0 2 0 1 0

0 1

1 2

2 1 0 3

x f f

   

 



 



 



   









Đạohàm2vếtacó









4 ' 2 2 ' 1 2 24

f x f x x

  











   

 

0 4 ' 0 2 ' 1 0

' 0 2

' 1 4

4 ' 1 2 ' 0 12

x f f

   





 



 



   







 Phươngtrìnhtiếptuyếncủađồthịhàmsố





y f x



tạiđiểmcóhoànhđộbằng

là



















' 1 1 1 4 1 2 4 2

y f x f x x

       



TrườngTHPTHaiBàTrưng–Huế  Trang28/81



Câu 80. Mộtvậtrơitựdovớiphươngtrìnhchuyểnđộnglà



S gt

trongđó

tínhbằnggiây(s),

tính

bằngmét

và

9,8



m / s

.Vậntốccủavậttạithờiđiểm



là?

9,8



m / s

 B.

78,4



m / s

 C.

39,2





m / s

 D.

=

19,6



m / s



Lời giải:

nhắc lại

' ''

v S

a v S



 





 

 

4 9,8.4 39,2 /

S gt v gt

t v m s

  

   



Câu 81. Mộtchấtđiểmchuyểnđộngtheoquyluật

3 2

4 9

S t t t

   

với

(giây)làkhoảngthờigiantínhtừ

lúcbắtđầuchuyểnđộngvà

(mét)làquãngđườngvậtchuyểnđộngtrongthờigianđó.Hỏitrong

khoảngthờigian

giâykểtừlúcbắtđầuchuyểnđộng,vậntốclớnnhấtcủachấtđiểmlà





88 m/s .

 B.





25 m/s .

 C.





100 m/s .

 D.





11 m/s .



Lời giải:

 

3 2

4 9

' 8 9

0 10

8 9

S t t t

v S t t

v t t

   

    

 





 



    











* MTCT CASIO -580VN sử dụng chức năng Mode 9



bấm=liêntiếptacó

 



Câu 82. Tínhđạohàmcủahàmsố





sin 2 cos3

f x x x

 

.

A.

2sin 4 3sin 3

x x



. B.

2sin 4 3sin 3

x x



. C.

sin 4 3sin 3

x x



. D.

2sin 2 3sin 3

x x





Lời giải:









' sin 2 cos3 ' 4 2 cos2 3sin 3 2sin 4 3sin3

f x x x sin x x x x x

     



Câu 83. Tínhđạohàmcủahàmsố

cos4

3sin 4

y x

 

.

A.

12cos 4 2sin 4

x x



. B.

12cos 4 2sin 4

x x



.C.

12cos 4 2sin 4

x x

 

.D.

3cos 4 sin 4

x x



.

Lời giải:

cos 4

' 3sin 4 ' 12cos4 2sin 4

y x x x

 

   

 

 



TrườngTHPTHaiBàTrưng–Huế  Trang29/81

Câu 84. Tínhđạohàmcủahàmsố

tan

y x



 

 

 

 

.

cos





 

 



 

 

. B.

cos







 



 

 

. C.

sin







 



 

 

. D.

sin





 

 



 

 

.

Lời giải:

tan

y x



 

  

 

 

cos





 

 



 

 



Câu 85. Tínhđạohàmcủahàmsố

cos 2

y x



.

sin 2

2 cos2





. B.

sin 2

cos 2







. C.

sin 2

cos 2





. D.

sin 2

2 cos2







.

Lời giải:

cos2

y x

 

sin 2

cos 2









Câu 86. Tínhđạohàmcủahàmsốsau

sin

sin cos

x x





.

A.

 

sin cos

x x









. B.

 

sin cos

x x







.C.

 

sin cos

x x









.D.

 

sin cos

x x







.

Lời giải:

sin

sin cos

x x

 



 

sin cos

x x











Câu 87. Tínhđạohàmcủahàmsố

6 6 2 2

sin cos 3sin cos

y x x x x

   .

. B.

. C.

. D.

.

Lời giải:









6 6 2 2 2 2 2 2

sin cos 3sin cos sin cos sin cos 1

' 0

y x x x x x x x x

      





Câu 88. Đạohàmcủahàmsố

2 cos 2

y x

 

bằng

A.

sin 2

2 cos 2









. B.

sin 4

2 2 cos 2









.C.

cos 2

2 cos 2







. D.

sin 4

2 cos 2









.

Lời giải:

2 cos 2

y x

  

sin 4

2 cos 2











Câu 89. Đạohàmcủahàmsố

sin

y x x



là

A.

sin cos

y x x x



 

. B.

sin cos

y x x x



 

.C.

cos

y x x





. D.

cos

y x x



 

.

Lời giải:

sin

y x x

 

sin cos

y x x x



 



Câu 90. Chohàmsố

sin

y x

 .Tìmhệthứcliênhệgiữa

và



khôngphụthuộcvào

.

A.

 

4 4

y y



 

. B.

 

2 4 1

y y



 

. C.

   

2 2

1 2 1

y y



  

.D.

 

4 4

y y



 

.

Lời giải:





' sin ' 2. . s 2

y x sinx co x sin x

  



   

     

 

   

2 2

2 2 2 2 2

 2 2 1

1 2 2 1 2s 2 2 1

y sin x

do sin x cos x

y y sin x in x sin x cos x





 



        



TrườngTHPTHaiBàTrưng–Huế  Trang30/81

Câu 91. Viphâncủahàmsố





f x x x

 

tạiđiểm



ứngvới

0,1

 

là

0,07



. B.

. C.

1,1

. D.

0,4



.

Lời giải:





 

6 1

2, 0,1 6.2 1 .0,1 1,1

y x x

x x y

   

       





Câu 92. Chohàmsố

3 2

9 12 5

y x x x

   

.Viphâncủahàmsốlà





d 3 18 12 d

y x x x

  

. B.





d 3 18 12 d

y x x x

   





d 3 18 12 d

y x x x

   

. D.





d 3 18 12 d

y x x x

  

.

Lời giải:

3 2

9 12 5

y x x x

   



có vi phân





d 3 18 12 d

y x x x

  



Câu 93. Hàmsố





cóviphânlà

A.

 

d d

y x







. B.

 

d d

y x





. C.

d d

y x







. D.

d d

y x





.

Lời giải:







cóviphânlà

 

d d

y x









Câu 94. Hàmsố

tan cot

y x x

 

cóviphânlà

d d

cos 2

y x



. B.

d d

sin 2

y x



. C.

d d

cos 2

y x



. D.

d d

sin 2

y x



.

Lời giải:



tan cot

y x x

 

cóviphânlà

d d

sin 2

y x





Câu 95. Viphâncủahàmsố

sin 2

y x

 

là

2 2

cos 2 .

d d

y x





. B.

cos 2 .

d d

y x

x 



.

cos 2

d d

y 





. D.

( 1)

cos 2 .

d d

y x





.

Lời giải:

 Viphâncủahàmsố

sin 2

y x

 

là

cos 2

d d

y 







Câu 96. Hàmsố

tan

y 

cóviphânlà

sin

d d

cos

y x



. B.

2sin

d d

cos

y x



. C.

sin

d d

2cos

y x



. D.

d tan d

y x

 



 

 

.

Lời giải: Hàmsố

tan

y 

cóviphânlà

sin

d d

cos

y x





TrườngTHPTHaiBàTrưng–Huế  Trang31/81



Câu 97. Hàmsố

cot 2

y x



cóviphânlà

1 cot 2

d d

cot 2

y x





. B.





1 cot 2

d d

cot 2

y x

 



.C.

1 tan 2

d d

cot 2

y x





.D.





1 tan 2

d d

cot 2

y x

 



.

Lời giải:

 Hàmsố

cot 2

y x



cóviphânlà





1 cot 2

d d

cot 2

y x

 





Câu 98. Hàmsố

sin cos

y x x x

 

cóviphânlà





d cos – sin d

y x x x x



. B.





d cos d

y x x x



.





d cos – sin d

y x x x



. D.





d sin d

y x x x



.

Lời giải:

 Hàmsố

sin cos

y x x x

 

cóviphânlà





d cos d

y x x x





Câu 99. Chohàmsố

y x x

  

.Mệnhđềnàosauđâyđúng?

1 d d 0

x y y x

  

.  B.

1 d d 0

x x y

  

.

d 1 d 0

x x x y

  

.  D.

1 d d 0

x y y x

  

.

Lời giải:





2 2 2

2 2

1 .

1 1 1

1. . 1. . 0.

x x

x y

dy dx dx dx

x x x

x dy y dx x dy y dx

 

 

   

 

  

 

      



Câu 100. Tínhđạohàmcấphaicủahàmsố





3 2

f x x x

  

tạiđiểm



.





2 14





. B.





2 10





. C.





2 28





. D.





2 1





.

Lời giải:





 

' 3 2

'' 6 2

'' 2 6.2 2 10.

f x x x

f x x

 

  



Câu 101. Đạohàmcấphaicủahàmsố







y f x

sin 3

 

x x

làbiểuthứcnàotrongcácbiểuthứcsau?

2cos sin

x x x



. B.

sin

x x



. C.

sin cos

x x x



. D.

1 cos



.

Lời giải:





' sin 3 ' . s

y x x sinx x co x

   



'' 2cos sin

y x x x

 



Câu 102. Mộtchấtđiểmchuyểnđộngcóphươngtrình

4 2

2 6 3 1

S t t t

   

với

tínhbằnggiây(s)và

tính

bằngmét(m).Hỏigiatốccủachuyểnđộngtạithờiđiểm

3( )

t s



bằngbaonhiêu?





m/s

. B.

228





m/s

. C.





m/s

. D.





m/s

.

Lời giải:

 

4 2

2 6 3 1

' 8 12 3

' '' 24 12

3 228 /

S t t t

v S t t

a v S t

t a m s

   

   

   

  



TrườngTHPTHaiBàTrưng–Huế  Trang32/81

Câu 103. Một chất điểm chuyển động trong

giây đầu tiên có phương trình

 

4 3 2

6 10

s t t t t t

   

,

trongđó



với

tínhbằnggiây





và





s t

tínhbằngmét





.Hỏitạithờiđiểmgiatốccủavật

đạtgiátrịnhỏnhấtthìvậntốccủavậtbằngbaonhiêu?

A.





17 m/s

. B.





18 m/s

. C.





28 m/s

. D.





13 m/s

.

Lời giải:

 

4 3 2

3 2

min

6 10

' 3 12 10

' 6 12 3 3 3

3 3 28 /

s t t t t t

v s t t t

a v t t t

a t v m s

   

    

       

    



Câu 104. Chochuyểnđộngthẳngxácđịnhbởiphươngtrình

3 2

3 9

S t t t

   

,trongđó

tínhbằnggiâyvà



tínhbằngmét.Tínhvậntốccủachuyểnđộngtạithờiđiểmgiatốctriệttiêu.

12m/s

. B.

0m/s

. C.

11m/s

. D.

6m/s

.

Lời giải:



3 2

3 9

' 3 6 9

' 6 6

S t t t

v S t t

a v t

   

    

   



 Khigiatốctriệttiêu





0 1 12 /

a t v m s

    





Câu 105. Chohàmsố

y x x

 

.Mệnhđềnàosauđâylàđúng?

. 1 0

y y 







. B.

. 1 0

y y 







. C.

3 . 1 0.

y y

 



. D.

2 . 3 0.

y y

 





Lời giải:

 

   

2 2 2 2

2 1

2 2 2 2

'' . '' 1 0

x x

x x x

x x

x x x x x x x x

y y y







   



  



   



   





Câu 106. Chohàmsố

sin 2

y x



.Khẳngđịnhnàosauđâylàđúng?

A.

 

y y



 

. B.

4 0

y y



 

. C.

4 0

y y



 

. D.

.tan 2

y y x





.

Lời giải:

' 2 s2

'' 4.sin2 4

'' 4 0

y co x

y x y

y y



   

 





TrườngTHPTHaiBàTrưng–Huế  Trang33/81

Câu 107. Chohàmsố

.cos

y x x



.Chọnkhẳngđịnhđúng?









2 cos 1

x y x y y

 

   

. B.









2 cos 0

x y x y y

 

   

.









2 cos 1

x y x y y

 

   

. D.









2 cos 0

x y x y y

 

   

.

Lời giải:

' s .

'' 2 . s 2

'' 2

y co x x sinx

y sinx x co x sinx y

y y sinx

 

     

  











2 cos 0

x y x y y

 

    



Câu 108. Chohàmsố

 

2 1

y f x



 



.Phươngtrình









f x f x

 

 

cónghiệmlà



. B.

 

. C.

 

. D.





Lời giải:

 

   

2 3

3 6

' '' 0

1 1

1 2 3

f x

f x f x

x x









   

 

    



Câu 109. Tính



,biết

y x x

 

.





 

2 2

3 2

1 1

x x







 

.B.





 

2 3 2

x x









. C.





 

3 2

x x









. D.





 

2 1

x x









.

Lời giải:

y x x

 







 

2 2

3 2

1 1

x x







 



Câu 110. Đạohàmcấp

củahàmsố

ax b







là

( )

2 . . !

( )

n n

a n

ax b







. B.

 

( )

1 . . !

( 1)

a n









. C.

 

( )

1 . !

( )

ax b









. D.

 

( )

1 . . !

( )

a n

ax b









.

Lời giải:

ax b







 

1. .1!

1 . .2!

ax b















....



 

( )

1 . . !

( )

a n

ax b











TrườngTHPTHaiBàTrưng–Huế  Trang34/81

. CHỦ ĐỀ 3. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC

Câu 111. Chotứdiện

ABCD

.Hỏicóbaonhiêuvectơkhácvectơ



màmỗivectơcóđiểmđầu,điểmcuốilà

haiđỉnhcủatứdiện

ABCD

?

. B.

. C.

. D.

.

Lời giải:

Sốvectơkhácvectơ



màmỗivectơcóđiểmđầu,điểmcuốilàhaiđỉnhcủatứdiện

ABCD

làsố

cácchỉnhhợpchập2củaphầntử



sốvectơlà



.



Câu 112. Chotứdiện

ABCD

.Gọi

,

M N

lầnlượtlàtrungđiểmcủacáccạnh

,

AD BC

và

làtrungđiểm

của

.Mệnhđềnàosauđâyđúng?





NM AB DC

 

  

. B.

AB AC AD AG

  

   

.

AB AC AD

  

   

.  D.

AB AC A

  

   

.

Lời giải:



Gọi

,

M N

lầnlượtlàtrungđiểmcủacáccạnh

,

AD BC

và

làtrungđiểmcủa

nên

là

trọngtâmcủatứdiện

ABCD

dođó:

 

AB AM NB

N AB DC

DC DM MN NC



  



  



  





   

  

   

A sai

GA GB GC GD

   

    



4 0

GA AB AC AD

    

    





AG AB AC AD

   

   

B,C sai

Câu 113. Cho hình lăng trụ

ABC A B C

  

 với

 là trọng tâm của tam giác

A B C

  

 Đặt

AA a





 

,

AB b



 

,

AC c



 

.Khiđó





bằng

A.





a b c

 

  

 B.







a b c

 

  

 C.





a b c

 

  

 D.





a b c

 

  



Lời giải:



làtrọngtâmcủatamgiác





A B C A G A B A C

      

  

  











1 1

' ' ' .

3 3

AG AA A G AA A B A C a b c

   

       

        



TrườngTHPTHaiBàTrưng–Huế  Trang35/81

Câu 114. Chotứdiệnđều

ABCD

.Tíchvôhướng

AB CD

 

bằng

. B.

. C.

. D.



.

Lời giải:



Chotứdiệnđều

ABCD

có4mặtlà4tamgiácđều.







0 0

. . . . .

. D. s60 . D. s60 0

AB CD AC CB CD AC CD CB CD CACD CB CD

CAC co CB C co AB CD

      

     

        

  

 



Câu 115. Chotứdiện

ABCD

vàcácđiểm

,

xácđịnhbởi

2 3

AM AB AC

 

  

;

DN DB xDC

 

  

.Tìm



đểcácvéctơ



,



,



đồngphẳng.

 

. B.

 

. C.

 

. D.



.

Lời giải:

Phântíchhướnggiải:Khigặploạinàychúngtavẽhình

2 3

AM AB AC

 

  



Đặt

2 , 3

AB AE AC AF

  

   

AM AE AF

  

  



Mlàđỉnhthứ4củahìnhbìnhhànhAEMF.

/ /

DN DB xDC xDC DN DB BN BN DC

      

      



Giải như sau:

Tacó





3 2

MN MA AD DN AC AB AD DB xDC

       

        

.





3 3 2 2

AD DC AD DB AD DB xDC

      

      











2 3 2 3

AD DB x DC AD BC CD x DC

        

      







2 2

AD BC x DC

   

  

.

Bavéctơ



,



,



đồngphẳngkhivàchỉkhi

2 0 2

x x

    

.



Câu 116. Trongkhônggian,chocácmệnhđềsau,mệnhđềnàolàmệnhđềđúng?

A.Mộtđườngthẳngvuônggócvớimộttronghaiđườngthẳngvuônggócthìvuônggócvớiđường

thẳngcònlại.

B.Haiđườngthẳngcùngsongsongvớiđườngthẳngthứbathìsongsongvớinhau

C.Mộtđườngthẳngvuônggócvớimộttronghaiđườngthẳngsongsongthìvuônggócvớiđường

thẳngcònlại.

D.Haiđườngthẳngcùngvuônggócvớiđườngthẳngthứbathìvuônggócvớinhau.

Lời giải:

DựavàođịnhnghĩahaiđườngthẳngvuônggóctrongkhônggiantasuyrađápánCđúng.



TrườngTHPTHaiBàTrưng–Huế  Trang36/81

Câu 117. Chohìnhlậpphương

ABCD EFGH

.Gócgiữacặpvectơ



và



bằng

. B.

. C.

. D.

Lời giải:



Nhậnxét

EG AC



 

nên











; ;

AF EG AF AC FAC

 

   

.

Tamgiác

FAC

làtamgiácđềunên



FAC 

.

Câu 118. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhbìnhhành,

SA SB a

 

,

AB a



.Gọi



làgóc

giữahaivéctơ



và



.Tính

cos



cos



 

. B.

cos



 

. C.

cos





. D.

cos





.

Lời giải:



Tacó





SB AS AB

 

 

2 2 2

2 .

SB AS AS AB AB

   

 



AS CD

 

 

AS BA



 

AS AB

 

 

2 2 2

SB SA AB

 

 

.

Vậy

cos









cos ,

CD AS

 

CD AS



 

a a









.



TrườngTHPTHaiBàTrưng–Huế  Trang37/81

Câu 119. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhchữnhậtvới

AB a



,

BC a



.Cáccạnhbêncủa

hìnhchópcùngbằng

.Tínhgócgiữahaiđườngthẳng

và

.



. B.



. C.



. D.

arctan 2

.

Lời giải:



Tacó

AB CD

nên















; ;

AB SC CD SC SCD

 

.

Gọi

làtrungđiểmcủa

.Tamgiác

SCM

vuôngtại

vàcó

SC a



,

CM a



nênlàtam

giácvuôngcântại

nên



SCD

 

.Vậy







; 45

AB SC

 

.



Câu 120. Chotứdiệnđều

ABCD

,

làtrungđiểmcủacạnh

.Khiđó





cos ,

AB DM

bằng

A.

. B.

. C.

.  D.

.

Lời giải:



Giảsửtứdiệnđều

ABCD

cócạnhbằng

tacó:

DM 

.

Talạicó:

 

cos ,

AB DM



 



. .

AB DB AB BM





   



. .cos60 . .cos120

a a a a

 







.

Vậy

 

cos ,

AB DM 

.

Cách 2: dùng bí kíp góc



 

2 2 2 2

D D

4 4

cos ,

2. . 6

2. .

A BM AM B

AB DM

a a



  

  



 hehe - quá lợi hại phải không



TrườngTHPTHaiBàTrưng–Huế  Trang38/81



Tương tự câu 120.

Chotứdiện

ABCD

biết

AB BC CA

  

,



,



,



.Gócgiữa haiđườngthẳng

và

bằng?

A.

120



. B.



. C.

150



. D.



.

Hướngdẫngiải

ChọnB



Khiđó







. . . .cos . .cos

AB CD CB CA CD CB CD BCD CACD ACD

   

    



2 2 2 2 2 2

. . . .

2. . 2. .

CB CD BD CA CD AD

CB CD CACD

   

 

2 2 2 2

CB AD BD CA  

  



Suyra

 

cos ,

AB CD



 

12 1

4.6 2

 







, 60

AB CD

  

.

hoặc dùng bí kíp ra liền

TrườngTHPTHaiBàTrưng–Huế  Trang39/81

Câu 121. Chohìnhlăngtrụtamgiácđều

ABC A B C

  

cócạnhbên

AA a





,gócgiữađườngthẳng

A B



với

mặtphẳng





ABC

là

.Gọi

làtrungđiểm

.Tínhcosincủagócgiữa

A C



và

.

. B.

. C.

. D.

.

Lời giải:



. 0

AM BC AM BC

  

 



Gócgiữađườngthẳng

A B



vớimặtphẳng





ABC

là



' 60

A BA 



' '

2 3

AA a AB a

A C A B a

AM a a



  

 













 

 

' . ' . . s ' , ' . ' . . .

. . . s

. . s . s

s ' ,

' . '

A C AM A C AM co A C AM A A AB BC AM A A AM AB AM BC AM

AB AM AB AM co BAM

AB AM co BAM AB co BAM

co A C AM

A C AM A C

      

 

        

     

 

 

2 3

 





TrườngTHPTHaiBàTrưng–Huế  Trang40/81

Câu 122. Cho

hình

chóp

S ABC

cóđáy

ABC

vuôngtại

,

vuônggócvớiđáy.Khẳngđịnhnàosai?

SB AC



 B.

SA AB



 C.

SB BC



 D.

SA BC





Lời giải:



Nếu

SB AC





Từ





SA ABC SA AC

  

dođó

 

AC SB

AC SAB AC AB

AC SA





   









Điềunàylàvôlývì

ABC



vuôngtại

nênđápánAsai.

Tacó





, 

SA ABC SA AB SA BC

   

nênđápánBvàDđúng.

Lạicó

 

BC AB

BC SAB BC SB

BC SA





   







nênđápánCđúng.



Câu 123. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuông.

vuônggócvới





ABCD

và

làhình

chiếuvuônggóccủa

lên

.Khẳngđịnhnàosauđâylàsai?

AH BC



. B.

AH SC



. C.

BD SC



. D.

AC SB



.

Lời giải:



Tacó



BC SA

và



BC AB

nên







BC SAB











 

SBC SAB

.

Mặtkhác









 

SBC SAB SB

.Dođótừ

kẻ



AH SB







 

AH SBC





AC SA



,ACkhôngvuônggócABnên

AC SB



là sai



TrườngTHPTHaiBàTrưng–Huế  Trang41/81

Câu 124. Cho hình chóp

S ABC

 có

SA SB SC

 

 và tam giác

ABC

vuông tại

. Vẽ





SH ABC







H ABC



.Khẳngđịnhnàosauđâyđúng?

A.

trùngvớitrựctâmtamgiác

ABC

. B.

trùngvớitrọngtâmtamgiác

ABC

.

C.

trùngvớitrungđiểm

. D.

trùngvớitrungđiểm

.

Lời giải:

Gọi

làtrungđiểmcủa

BM AM CM AC

   

.

SAC



cântại







SM AC 

.

SMA



vuôngtại

2 2 2

SA AM SM

  



2 2 2

SB BM SM

  

.



SMB



vuôngtại

hay





SM BM

.

Từ





và





suyra:





SM ABC



.

Theogiảthiết:





SH ABC







H ABC



H M

 

.

Vậy

trùngvớitrungđiểm

.



Câu 125. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

,

vuônggócvớimặtđáy,gócgiữa

cạnh

vàmặtđáybằng



.Độdàicạnh

bằng

. B.

2 3

. C.

. D.

.

Lời giải:



 



vuônggócvớimặtđáy,gócgiữacạnh

vàmặtđáybằng





D 30

S A 



D 2

s30

A a SD a

   



2 3





TrườngTHPTHaiBàTrưng–Huế  Trang42/81



Câu 126. Chotứdiện

OABC

có

,

đôimộtvuônggócvớinhau.Kẻ

vuônggócvớimặt

phẳng





ABC

tại

.Khẳngđịnhnàosauđâylàsai?

2 2 2 2

1 1 1 1

OH OA OB OC

  

. B.

làtrựctâmtamgiác

ABC

.

OA BC



. D.





AH OBC



.

Lời giải:



Tacó





OH ABC OH BC

  

và





OA OBC OA BC

  

.

Suyra









BC AOH BC AH  



Talạicó





OH ABC OH AC

  

và





OB OAC OB AC

  



Suyra









AC BOH AC BH  



Từ





và





suyra

làtrựctâmtamgiác

ABC

.

Gọi

làchânđườngvuônggóccủa

lênđườngthẳng



Tacó

2 2 2 2 2 2

1 1 1 1 1 1

OH OI OA OB OC OA

    

.

VậyDlàđápánsai.



Câu 127. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngvà

vuônggócđáy.Mệnhđềnàosai?





BC SAB



. B.





AC SBD



. C.





BD SAC



. D.





CD SAD



.

Lời giải:



Tacó:

+

 

BC AB

BC SAB

BC SA





 







.

+

 

CD AD

CD SAD

CD SA





 







.

+

 

BD AC

BD SAC

BD SA





 







.

Suyra:đápánBsai.



TrườngTHPTHaiBàTrưng–Huế  Trang43/81

Câu 128. Chohìnhchóp

S ABCD

đáylàhìnhvuôngcạnh

,tâm

.Cạnhbên

SA a



vàvuônggócvới

mặtphẳngđáy.Gọi



làgóctạobởiđườngthẳng

vàmặtphẳngđáy.Mệnhđềnàođúng?

A.



 

. B.



 

. C.

tan 1





. D.

tan 2





.

Lời giải:



Tacó

làhìnhchiếuvuônggóccủa

lênmặtphẳng





ABCD

.

 









,SC ABCD SCA



  

.

Tamgiác

SAC

vuôngtại

có

tan





,với

AC a



thì

tan 2





.



Câu 129. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

a SD a



và

vuônggócvớimặt

phẳngđáy.Tínhgócgiữađườngthẳng

vàmặtphẳng





SBD

.



. B.





arcsin 1/ 4

. C.



. D.



.

Lời giải:







   

D D D

D D

 D

S ABC S AC

AC SB AO SB

AC B

  





   













 Gócgiữađườngthẳng

vàmặtphẳng





SBD

là



ASO





 

sin 30

SA a

AO a

ASO ASO



  







TrườngTHPTHaiBàTrưng–Huế  Trang44/81



Câu 130. Chohìnhchóp

S ABC



cóđáy

ABC

làtamgiácđềucạnh

,cạnhbên

vuônggócvớimặtđáyvà



SA a

.Gọi

làtrungđiểmcủa

.Tínhcôsincủagóc



làgócgiữa

và





ABC

.

cos





. B.

2 7

cos





. C.

cos





. D.

cos





.

Lời giải:



GọiHlàtrungđiểmACtacóMHlàđườngtrungbìnhcủatam

giácSACnênMHsongsongSA.

SAvuônggóc(ABC)thìMHvuônggóc(ABC)

suyragócgiữa

và





ABC

là



MBH



2 2 2

2 2

3 3

2 2

HM a

BH AB a

BM MH BH

a a



 

 

  





Câu 131. Chohìnhlậpphương

ABCD A B C D

   

(hìnhbên).Tínhgócgiữa



vàmặtphẳng





BDD B

 

.



. B.



. C.



. D.



.

Lời giải:



GọiOlàgiaođiểmACvàBD.TacóAOvuônggóc(BDD’B’)

Gócgiữa



vàmặtphẳng





BDD B

 

là



AB O



 

' ' 30

' 2

sinAB O AB O

    



 



TrườngTHPTHaiBàTrưng–Huế  Trang45/81



Câu 132. Chohìnhchóp

S ABCD

cóđáylàhìnhthangvuôngtại

,đáylớn

AD cm



,

BC cm



,



vuônggócvớimặtđáyvà

SA cm



.Gọi

làtrungđiểmcủa

.Mặtphẳng





điqua

và

vuônggócvới

.Tínhdiệntíchthiếtdiệncủahìnhchópcắtbởimặtphẳng





.

. B.

. C.

. D.

.

Lời giải:



Gọi

,

và

lầnlượtlàtrungđiểmcủa

,

và

.

Tacó:









P SAB MQ

 

,









P ABCD MN

 

,









P SCD NP

 

.

Dođó,thiếtdiệncủahìnhchóp

S ABCD

cắtbởimặtphẳng





làtứgiác

MNPQ

.

Dễthấy

MNPQ

làhìnhthangvuôngtại

,

và

MQ PQ

 

,



.

Vậydiệntíchhìnhthang

MNPQ

là:









. 4. 9 4

2 2

MNPQ

MQ MN PQ

 

  

.



Câu 133. Trongcáckhẳngđịnhsaukhẳngđịnhnàolàđúng?

A. Hìnhlăngtrụđứnglàhìnhlăngtrụđều. 

B. Hìnhlăngtrụcóđáylàmộtđagiácđềulàmộthìnhlăngtrụđều. 

C. Hìnhlăngtrụđứngcóđáylàmộtđagiácđềulàhìnhlăngtrụđều. 

D. Hìnhlăngtrụtứgiácđềulàhìnhlậpphương.

Lời giải:

Theođịnhnghĩa:Hìnhlăngtrụđềulàhìnhlăngtrụđứngcóđáylàmộtđagiácđều.



Câu 134. Mệnhđềnàodướiđâysai?

A.Hìnhchópđềucócáccạnhbêntạovớimặtphẳngđáycácgócbằngnhau. 

B.Hìnhchópđềucótấtcảcáccạnhbằngnhau. 

C.Hìnhchópđềucócácmặtbênlàcáctamgiáccânbằngnhau.

D.Mộthìnhchópcóđáylàmộtđagiácđềuvàcóchânđườngcaotrùngvớitâmcủađagiácđáyđó

làhìnhchópđều.

Lời giải:

Theođịnhnghĩa:

Mộthìnhchópcóđáylàmộtđagiácđềuvàcóchânđườngcaotrùngvớitâmcủađagiácđáyđólà

hìnhchópđều.

Hìnhchópđềucócáccạnhbêntạovớimặtphẳngđáycácgócbằngnhau. 

Hìnhchópđềucócácmặtbênlàcáctamgiáccânbằngnhau. 

Hìnhchópđềucócáccạnhbênbằngnhau,đáylàđagiácđều(tamgiácđềuhoặchìnhvuông)



TrườngTHPTHaiBàTrưng–Huế  Trang46/81



Câu 135. Chohaimặtphẳngcắtnhau







và







.

làmộtđiểmnằmngoàihaimặtphẳngtrên.Qua



dựngđượcbaonhiêumặtphẳngđồngthờivuônggócvới







vàvuônggócvới







A.Vôsố. B.Một. C.Hai. D.Không.

Lời giải:

Chohaimặtphẳngcắtnhau







và







tạoragiaotuyếnlà1đườngthẳngd

QuaMdựngđượcduynhất1mặtphẳngvuônggócvớid,khiđócũngvuônggócvới







vàvuông

gócvới









Câu 136. Chohìnhchóp

S ABC

có





SA ABC



tamgiác

ABC

vuôngtại

.Kếtluậnnàosauđâysai?









SAC SBC



. B.









SAB ABC



. C.









SAC ABC



. D.









SAB SBC



.

Lời giải:

ChọnA

Tacó:





   

SA ABC

SA SAB SAC































SAB SAC ABC







B,Cđúng.





SA ABC SA BC

  

mà

BC AB

















;

BC SAB BC SBC

 















SAB SBC







Dđúng.

VậyđápánsailàA.



Câu 137. Chohìnhchóp

S ABC

cóđáy

ABC

làtamgiácvuôngcântại

và

AB a



.Biết





SA ABC





và

SA a



.Tínhgócgiữahaimặtphẳng





SBC

và





ABC



. B.



. C.



. D.



.

Lời giải:



 KẽADvuônggócBCsuyragócgiữahaimặtphẳng





SBC

và





ABC

là



S A





ABC

làtamgiácvuôngcântại

và

2 D

AB a A a

  





D 1 D 45

tanS A S A  



TrườngTHPTHaiBàTrưng–Huế  Trang47/81



Câu 138. Chohìnhchóp

S ABCD

đáy

ABCD

làhìnhchữnhật,

AB a



,

AD a



.Cạnhbên

vuônggóc

vớiđáy





ABCD

,

SA a



.Tính

tang

củagócgiữahaimặtphẳng





SBD

và





ABCD

.

. B.

. C.

. D.

.

Lời giải:



Kẻ

AH BD



,





H BD



(1).









BD SA SA ABCD

BD AH



 

















BD SAH

 



BD SH

 

(2).

Và:









SBD ABCD BD

 

(3).

Từ(1)(2)và(3)suyra:gócgiữahaimặtphẳng





SBD

và





ABCD

là



SHA

.

Xét

ABD



vuôngtại

:

2 2 2

1 1 1

AH AB AD

 

2 2

1 1

a a

 





AH 

.

Xét

SAH



vuôngtại

:



tan 5

SHA

 

.



TrườngTHPTHaiBàTrưng–Huế  Trang48/81



Câu 139. Chohìnhlăngtrụđều

ABC A B C

  

cócạnhđáybằng

,cạnhbênbằng

.Tínhgócgiữahaimặt

phẳng





AB C

 

và





A B C

  

.



. B.



. C.

arccos

. D.

arcsin

.

Lời giải:

Gọi

làtrungđiểmcủa

B C

 

.Tacó:

 

B C A I

B C AIA

B C A A

  





  

 



  







Khiđó:









AB C A B C B C

AI B C

A I B C

      

 



 







  









gócgiữahaimặtphẳng





AB C

 

và





A B C

  

làgóc



AIA



.

Xéttamgiác

AIA



vuôngtại



tacó:



tan

AIA

A I







3 3

 



AIA





 

.



Câu 140. Chohìnhchóp

S ABCD

cóđáylàhìnhvuôngcạnh

,





SA ABCD



.Gọi

và

làhaiđiểm

thayđổitrêncạnh

và

saocho

CM x



,

CN x





 

 

 

 

.Tìmhệthứcliênhệgiữa



và

để









SAM SMN



.

a x



. B.





2 3 0

a a x

 

4 0

x ax

 

. D.

3 0

x ax

 

.

Lời giải:







 

   

SAM MN

SA MN

SAM SMN

AM MN

MN SMN

 







  

 













VậytamgiácAMNvuôngtạiM.

     

2 2 2

2 2 2 2 2 2 2

2 2 2

2 2

4 0

AM AB BM

MN MC NC

AN AM MN AB BM MC NC

AN A DN AB BM MC NC

a a x a a x x x

x ax

 

     

       

  





TrườngTHPTHaiBàTrưng–Huế  Trang49/81



Câu 141. Khẳngđịnhnàosauđâylàkhẳngđịnhsai?

A. Khoảngcáchtừmộtđiểmđếnmộtmặtphẳnglàkhoảngcáchtừđiểmđóđếnhìnhchiếucủanó

lênmặtphẳng.

B. Khoảngcáchgiữahaimặtphẳngsongsonglàkhoảngcáchtừmộtđiểmtuỳýtrênmặtphẳngnày

đếnmặtphẳngkia.

C. Khoảngcáchgiữahaiđườngthẳngchéonhaubằngkhoảngcáchgiữahaimặtphẳngsongsong

vớinhaulầnlượtchứahaiđườngthẳngđó.

D. Khoảngcáchgiữahaiđườngthẳngchéonhaulàkhoảngcáchtừmộtđiểmtuỳýtrênđườngthẳng

nàyđếnđườngthẳngkia.

Lời giải:



D saivìkhoảngcáchgiữahaiđườngthẳngchéonhaubằngkhoảngcáchgiữahaimặtphẳngsong

songvớinhaulầnlượtchứahaiđườngthẳngđó.



Cách tính khoảng cách giữa hai đường thẳng chéo nhau d và d’

Cách 1: 

+Xácđịnhđườngthẳngvuônggócchungcủadvàd’

+Tínhđộdàiđoạnvuônggócchung.

Cách 2:

Kẽd’vàsongsongvớid,suyramp(P)chứad’vàsongsongd.

+Khiđó

( , ') ( ,( )) ( ,( ))

d d d d d P d A P

 

vớiAlàmộtđiểmbấtkỳthuộcd

Chú ý:mp(P) có thể có sẵn hoặc chúng ta phải dựng

(Cách dựng: qua một điểm

B d



dựng đường thẳng ∆ song song với d, lúc đó mp(P)≡(d’,∆)).

Các ví dụ mẫu cho cách 1

Ví dụ 1:ChotứdiệnABCDcóAB=a,tấtcảcáccạnhcònlạibằng3a.Tính

( , )

d AB CD



Giải:

+GọiI,JlầnlượtlàtrungđiểmcủaCDvàAB.

+VìACDvàACDlàcáctamgiácđềunên:

, ( ) (1)

CD AI CD BI CD AIB CD IJ

     



Mặtkhác,

ACD ACD

  

nêntamgiácAIBcântạiI.Dođó,

(2)

IJ AB





+Từ(1),(2)suyra:IJlàđườngvuônggócchungcủaABvàCD.

+Tacó:

2 2

3 3 26

2 2 2

a a a

IJ AI AJ

 

    

 

 

.

Vậy

( , )

d AB CD 



TrườngTHPTHaiBàTrưng–Huế  Trang50/81



Ví dụ 2:ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuôngcạnha.GọiM,Nlầnlượtlàtrung

điểmcủaABvàAD,HlàgiaođiểmcủaCNvàDM,

( ), 3

SH ABCD SH a

 

.Tính

( , )

d DM SC



Giải:

+Trongmp(SCH)kẻ

(1), (K SC)

HK SC

 

.

+Mặtkhác,

( )

(*)

( )

SH ABCD

SH DM

DM ABCD





 









XéthaitamgiácvuôngAMDvàDNCcóAM=DN,

AD=DC

AMD DNC

   

.

Từđótacó:



0 0

90 90

AMD DNC

ADM DCN DNC ADM NHD

AMD ADM







     





 





hay

(**)

DM CN



.

Từ(*),(**)suyra:

( ) (2)

DM SCH DM HK

  

.

Từ(1),(2)suyra:HKlàđoạnvuônggócchungcủaDMvàSC.

+Tacó:

HCD DCN

 



2 2

2 3

CD a a

CD DN

   



.

XéttamgiácvuôngSHCtacó:

2 2 2 2

1 1 1 5 15

HK HC HS a

    



Vậy

( , )

d DM SC HK 



các ví dụ cho cách 2

Ví dụ 1:ChohìnhlăngtrụđứngABC.A’B’C’,đáyABClà

tamgiácđềucạnha,

AA 

.

Tính

( , ')

d AB CB



Giải:+GọiI,JlầnlượtlàtrungđiểmcủaABvàA’B’.

+Tacó:

/ /( ' ') ( , ') ( ,( ' ')) ( ,( ' '))

AB CA B d AB CB d AB CA B d I CA B

  



+Trongmp(CIJ)kẻ

(1),(H CJ)

IH CJ

 



Tacó:

' ' ( )

A B IJ



(vìABC.A’B’C’làhìnhlăngtrụđứng)và

' '

IC A B



(vì∆ABClàtamgiácđều)

nên

' ' ( ) ' '(2)

A B CIJ IH A B

  

.

Từ(1),(2)suyra:

( ' ')

IH CA B



hay

( , ')

d AB CB IH





+XéttamgiácvuôngCIJcó:

2 2 2 2 2 2

1 1 1 4 2 10 30

3 3

IH IC IJ a a a

      



Vậy

( , ')

d AB CB IH 



TrườngTHPTHaiBàTrưng–Huế  Trang51/81

Ví dụ 2:ChohìnhchóptứgiácđềuS.ABCDcóđáyABCDlàhìnhvuôngcạnha,cạnhbênbằng

.Tính

( , )

d AD SB



Giải:+Vì





AD / / SBC ( , ) ( ,( ))

d AD SB d AB SBC

 



+GọiOlàgiaođiểmcủaACvàBD.I,Jlầnlượtlàtrungđiểm

củaADvàBC.

+Trongmp(SIJ)kẻ

,( )(1)

IH SJ H SJ

 

.

Theogiảthiếttacó:

( )

/ /

(2)

SO ABCD SO BC

BC SIJ

IJ AB IJ BC

IH BC

  



 



 



 



Từ(1),(2)suyra:

( )

IH SBC



hay

( , )

d AD SB IH





+XéttamgiácSIJcó:

1 1 .

. .

2 2

SIJ

SO IJ

S IH SJ SO IJ IH

   

.Với:IJ=a,

2 2 2 2

3 . 7

. ,

2 4

SO SA AO a SJ SB BJ     

.Suyra:

. 2 21

SO IJ a

 



Vậy

2 21

( , )

d AD SB IH 



Ví dụ 3:ChohìnhchópS.ABCD,cóđáyABCDlàhìnhvuôngcạnha,tamgiácSADlàtamgiácđều,

(SAD)vuônggócvớimặtphẳngđáy.Tính

( , )

d SA BD



Giải:+QuaAkẻđườngthẳngdsongsongvớiBD.GọiOlàgiaođiểmcủaACvàBD;I,Mlầnlượt

làtrungđiểmcủaADvàOD;NlàgiaođiểmcủadvàIM.

+Tacó:

( , ) (( , ), )

( ,( , ))

d SA BD d SA d BD

d M SA d

 





+Trongmp(SMN)kẻ

(1),(H SN)

MH SN

 



Theogiảthiết:

( ) (*)

( ) ( )

SI AD

SI ABCD SI d

SAD ABCD





   







Mặt

kháctacó:

/ /

(**)

/ /

d BD

BD AO d MN

AO MN





  







.Từ(*),(**)

suyra:

( ) (2)

d SMN d MH

  

.Từ(1),(2)suyra:

( , )

MH SA d



.

+XéttamgiácSMNcó:

1 1 .

. .

2 2

SMN

SI MN

S MH SN SI MN MH

   



với

2 2

3 2 10

, ,

2 2 4

a a a

SI MN AO SN SI IN     

.Dođó,

. 15

SI MN a

 

.Vậy

( , )

d SA BD 



TrườngTHPTHaiBàTrưng–Huế  Trang52/81

Ví dụ 4:ChohìnhchópS.ABCcóđáyABClàtamgiácvuôngtaiB,AB=BC=2a,haimặtphẳng

(SAB)và(SAC)cùngvuônggócvớimặtphẳng(ABC).GọiMlàtrungđiểmcủaAB,mặtphẳngqua

SMvàsongsongvớiBCcắtACtạiN,gócgiữahaimặtphẳng(SBC)và(ABC)bằng60

.Tính

( , )

d AB SN



Giải:

+GọiIlàtrungđiểmcủaBC.

DoMN//BCnênNlàtrungđiểmcủaAC.Dođó,IN//AB

hay

( , ) ( ,( ))

d AB SN d AB SNI



.

+Trongmp(ABC)kẻ

,( )(*)

AJ IN J IN

 



Trongmp(SAJ)kẻ

,( )(1)

AH SJ H SJ

 



+Theogiảithiếttacó:

( ) ( )

( ) (**)

( ) ( )

SAB ABC

SA ABC SA IN

SAC ABC





   









Từ(*),(**)tacó:

( ) (2)

IN SAJ IN AH

  

.

Từ(1),(2)tacó:

( ) ( , )

AH SIN d AB SN AH

  

.

+Tacó:



0 0

(( ),( )) 60 .tan 60 2 3

SBC ABC SBA SA AB a

    

;

AJ BI a

 

.

+XéttamgiácvuôngSAJcó:

2 2 2 2

1 1 1 13 12

AH a

AH SA AJ a

    

.

Vậy

. 156

( , )

d AB SN AH 



TrườngTHPTHaiBàTrưng–Huế  Trang53/81



Câu 142. Chohìnhchóptứgiácđều

S ABCD

cócácmặtbênlàcáctamgiácđềucạnh

.Tínhkhoảngcách

từ

đếnmặtphẳng

( )

ABCD

. 

2 2

. B.

. C.

. D.

.

Lời giải:



Chohìnhchóptứgiácđều

S ABCD

cócácmặtbênlàcáctam

giácđềucạnh

.

GọiOlàgiaođiểmACvàBDnênSOvuônggóc(ABCD)

(tính chất hình chóp đều)

ABCDlàhìnhvuôngcạnh

2 2 2

a AC a

 



 





2 2 2 2

2 2 2

SO SA AO a a a

    



SO a

 



Câu 143. Cho hình chóp

S ABCD

có đáy

ABCD

 là hình vuông cạnh

,



SA a

,







SA ABCD

. Tính

khoảngcáchtừ

đếnmặtphẳng





SBC

.

. B.

. C.

. D.

.

Lời giải:



Tacó



BC SA

và



BC AB

nên







BC SAB











 

SBC SAB

.

Mặtkhác









 

SBC SAB SB

.Dođótừ

kẻ



AH SB







 

AH SBC



hay









,

AH d A SBC

.Trongtamgiácvuông

SAB

tacó

2 2 2

1 1 1

 

AH SA AB

2 2 2

1 1 4

3 3

  

a a a

.

Vậy



.



TrườngTHPTHaiBàTrưng–Huế  Trang54/81



Câu 144. Cho hình lăng trụ đứng

ABC A B C

  

. Cạnh bên

AA a





,

ABC

 là tam giác vuông tại

 có

BC a



,

AB a

 .Tínhkhoảngcáchtừđỉnh

đếnmặtphẳng





A BC



.

. B.

.  C.

. D.

.

Lời giải:



Lăngtrụđứng

ABC A B C

  

cóđáy

ABC

làtamgiácvuôngtại



BC a



, 3

AB a AC a

  

.

 khoảngcáchtừđỉnh

đếnmặtphẳng





A BC



là



2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 7

' 3 3

AH AA AB AC a a a a

      





 

, '

A A BC

d AH 



Câu 145. Chohình chóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

,mặtbên

SAB

làtamgiácđều và

nằmtrongmặtphẳngvuônggócvớimặtphẳngđáy.Tínhkhoảngcách

từđiểm

đếnmặtphẳng





SCD

.

h 

. B.

h a



. C.

h 

. D.

h 

.

Lời giải:



GọiMvàFlàtrungđiểmAB,CD











 

SAB ABC

SM ABC

SM AB

SM a

MF a

 



 













 

, D , D

/ / D

A SC M SC

AB C

AB SC d d h

AB SC





   











2 2 2

1 1 1

h SM MF

 



h 



TrườngTHPTHaiBàTrưng–Huế  Trang55/81



Câu 146. Chohình lậpphương

ABCD A B C D

   

cócạnh bằng

.Khoảngcáchtừđiểm

đếnmặtphẳng





AD B

 

bằng

. B.

. C.

. D.

.

Lời giải:



Gọi

,



lầnlượtlàtâmcủahìnhvuông

ABCD

và

A B C D

   

.

Tacó





BO B O AB D

   







BO AB D

 



.

Dựng

OK AO





,tacó

B D A C

B D AA

   







  









B D AA C C OK

   

  

B D OK

 

 

.





OK AB D

 

 

.









d B AB D

 











d O AB D

 



.

Xét

AOO





vuôngtại

có

làđườngcao.

2 2 2

1 1 1

OK OA OO

  





2 2

1 1 3

a a

  

 

 

 

OK 

.



Câu 147. Cho hình chóp

S ABCD

 có đáy là hình vuông tâm

 cạnh

,

 vuông góc với mặt phẳng





ABCD

và

SO a



.Tínhkhoảngcáchgiữa

và

.

2 5

. B.

. C.

2 3

. D.

.

Lời giải:



Gọi

làtrungđiểm

;

làhìnhchiếuvuônggóccủa

lên

.

Tacó





























, , , 2 , 2

d AB SC d AB SCD d A SCD d O SCD OH

   

.

Xéttamgiác

SMO

vuôngtại

có:

2 2 2 2 2 2

1 1 1 4 1 5

OH OM OS a a a

    

OH 

.

Vậy

 

2 5

d AB SC 

.



TrườngTHPTHaiBàTrưng–Huế  Trang56/81

Câu 148. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

,cạnh

SA a



vàvuônggócvớimặt

đáy





ABCD

.Tínhkhoảngcáchgiữahaiđườngthẳng

và

. B.

. C.

. D.

.

Lời giải:



Tacó





 

 D

SA ABC SA BD

B SAC

AC B

AC B O

OH SC

OH SAC OH B

   



 









 



  





VậyOHlàđoạnvuônggócchungcủaBDvàSC.

 



. . .

2. 3

SC DB

a a

AC SA

d OH OC sinHCO OC sinDCA

    







Câu 149. Cho hình lăng trụ đứng

ABC A B C

  

 có đáy

ABC

 là tam giác vuông,

BA BC a

 

, cạnh bên

AA a





,

làtrungđiểmcủa

.Tínhkhoảngcáchgiữahaiđườngthẳng

và

B C



.

. B.

. C.

. D.

.

Lời giải:



Phương pháp 2 xác định khoảng cách giữa 2 đường chéo nhau

Bước 1: dưng mặt phẳng song song

GọiDlàtrungđiểmBB’

tacó





D / / ' D / / '

M B C AM B C





Bước 2: tỉ lệ khoảng cách

 

, '

' , D ', D , D

AM B C

B C AM B AM B AM

d d d d h

   





ABC

làtamgiácvuông,



BA BC a B   



Bí kíp: công thức tam diện vuông

( 3 đường đôi 1 vuông góc nhau)

2 2 2 2

1 1 1 1

h BA BM

    



TrườngTHPTHaiBàTrưng–Huế  Trang57/81



Luyện tập tương tự



Cho hình lăng trụ đứng

ABC A B C

  

 có đáy

ABC

 là tam giác vuông,

BA BC a

 

, cạnh bên

AA a





,

làtrungđiểmcủa

.Khoảngcáchgiữahaiđườngthẳng

và

B C



bằng

A.

. B.

. C.

. D.

.

Lờigiải

ChọnD



Gọi

làtrungđiểm



nên

MN B C

















; ;

d AM B C d B C AMN

 

 









;

d C AMN













;

d B AMN



.

Gọi

làhìnhchiếucủa

lên





AMN

,do tứ diện

B AMN

là tứ diện vuông đỉnh

nên

2 2 2 2

1 1 1 1

BH BA BM BN

  



2 2 2 2

1 4 1 6

a a a a

   

.

Vậy

BH 

.



TrườngTHPTHaiBàTrưng–Huế  Trang58/81



Câu 150. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhchữnhật,

AB a



,

BC a



,

vuônggócvớimặt

phẳngđáyvà

SA a



.Tínhkhoảngcáchgiữahaiđườngthẳng

và

.

A.

. B.

. C.

. D.

.

Lời giải:

Phương pháp 2 xác định khoảng cách giữa 2 đường chéo nhau



Bước 1:kẻđườngthẳngdđiquaBvàsongsongAC

Bước 2:kẻAEvuônggócxuốngđườngd.

Bước 3:KẻAHvuônggócSE.



Tacó





 

, ,

/ /

AC SB

AC SBE A SBE

AC SBE d d d AH h

    





2 2 2

1 1 1

h A SA

 





SA a





 

2 2 2 2 2

1 1 1 1 1

D D

D AC

A d k

k A DC A AB

 

   



suyra

2 2 2 2 2

1 1 1 1 9 2

4 4 3

h a

h a a a a

     





Bí kíp: công thức tam diện vuông ( 3 đường đôi 1 vuông góc nhau)

 

2 2 2 2

1 1 1 1

AC SB

d SA AB A

  



--- HẾT ---



TrườngTHPTHaiBàTrưng–Huế  Trang59/81



BÀI TẬP TRẮC NGHIỆM 1.5.2019

1. Cho hình chóp 

S ABC

 có cạnh

 vuông góc với mặt phẳng





ABC

, biết

AB AC a

 

,

BC a

 .Tínhgócgiữahaimặtphẳng





SAB

và





SAC

.

A.



. B.

150



. C.



. D.

120



.

Lờigiải

ChọnD



Vì





SA ABC



nên

SA AB



và

SA AC



.

tacó:









SAB SAC SA

SA AB

SA AC

 















   















, ,

SAB SAC AB AC BAC

  

.

Xét

ABC



có



2 2 2

cos

2. .

AB AC BC

BAC

AB AC

 









2 2

2. . 2

a a a

a a

 

  





120

BAC

  

.

Vậy

   







, 120

SAB SAC

 

.

2. Chohìnhchóp

ABC

có

vuônggócvớimặtphẳng





ABC

vàđáylàtamgiácvuôngtại

,

AB SA a

 

.Gọi

làhìnhchiếucủa

trên

.Khoảngcáchgiữa

và

bằng:

A.

. B.

. C.

. D.

.

Lờigiải

ChọnA



Tacó

AH SB



(nên

AH HB



).

 

BC AB

BC SAB BC AH

BC SA





   







(nên

BC BH



).

Dođó,





d BC AH HB



.

Tamgiác

SAB

vuôngcântại

,

làđườngcao

2 2

SB a a a



   

.

Vậy

 

d BC AH 

.

TrườngTHPTHaiBàTrưng–Huế  Trang60/81



3. Cho hình chóp

S ABC

 có

,

 tạo với mặt đáy các góc bằng nhau và bằng



. Biết

BC a



,



BAC

 

.Tínhkhoảngcách

từđỉnh

đếnmặtphẳng





ABC

.

A.

h a

 . B.

h 

. C.

h 

. D.

h 

.

Lờigiải

ChọnB



Gọi

làhìnhchiếuvuônggóccủa

lên





ABC

,suyra









d S ABC SH



và



SAH SBH SCH

   



HA HB HC

  

.

Dođó

làtâmđườngtrònngoạitiếptamgiác

ABC

.

Xét

ABC



,có:

sin

BC a

HA HA

  

.

Xét

SAH



vuôngtại

,

có



.tan . 3

a a

SH AH SAH   .

4. Cho hình chóp

S ABCD

 có đáy

ABCD

 là hình chữ nhật,

AB a



,

AD a



,

vuônggócvớiđáyvà

SA a



.Tínhgócgiữa

và





SAB

.

A.



. B.



. C.



. D.



.

Lờigiải

ChọnD



Tacó:

 

BC AB

SA SAB

BC SA





  







làhìnhchiếuvuônggóccủa

lên





SAB

 



SC SAB CSB

  .

Tamgiác

SAB

vuôngtại

có:

2 2

SB SA AB a

  

.

Tamgiác

SBC

vuôngtại

có:

 

tan 30

CSB CSB

    

.



60°

45°

TrườngTHPTHaiBàTrưng–Huế  Trang61/81

5. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

,cạnh

SA a



vàvuônggócvớimặt

đáy





ABCD

.Khoảngcáchgiữahaiđườngthẳng

và

bằng

A.

. B.

. C.

. D.

.

Lờigiải

ChọnD



Do

BD AC



và

BD SA



nên





BD SAC



.

Trongmặtphẳng





SAC

dựng

OH SC



tại

.



làđườngvuônggócchungcủa

và

.

Gọi

làtrungđiểm

.Tamgiác

OIC

vuôngtại

cóđườngcao

.

Tacó

2 2 2

2 2

1 1 1 . 6

OI OC a

OH OI OC

OI OC

    



.



6. Chotứdiệnđều

ABCD

cạnh

.Tínhkhoảngcáchgiữahaiđườngthẳng

và



A.

. B.

. C.

. D.

.

Hướngdẫngiải

ChọnD



Gọi

làtrungđiểmcủa

.

Qua

kẻđườngthẳngvuônggócvới

cắt

tạitrungđiểm

(

AMN



cântại

)

Suyra





d AB CD MN



2 2

3 2

2 2 2

a a a

BM BN

 

    

 

 

.



TrườngTHPTHaiBàTrưng–Huế  Trang62/81



7. Chohìnhlăngtrụđứng

ABC A B C

  

cóđáy

ABC

làtamgiácvuôngtại

,

AB a



,

AA a





.Tính

khoảngcáchtừđiểm

đếnmặtphẳng





A BC



.

A.

2 5

. B.

2 5

. C.

. D.

3 5

.

Lờigiải

ChọnB



Dựng

AH A B





.

Tacó

 

BC AB

BC A AB

BC AA







 









BC AH

 



Vậy





AH A BC













d A A BC AH



 

.

Xéttamgiácvuông

A AB



có

2 2 2

1 1 1

AH AA AB

 





2 2 2 2

. 2 . 2 5

AA AB a a a

AA AB a a



   



 

.



8. Chochóp

S ABC

có

vuônggócvới đáy,tamgiác

ABC

vuôngtại

. Biết

SA AB



.

Tínhgócgiữađườngthẳng

vàmặtphẳng





SAC

A.



. B.



. C.



. D.

cos

arc

.

Lờigiải

ChọnA

Gọi

làtrungđiểmcủa

BI AC

 

(vì

ABC





vuôngcântại

).







Mặtkhác:

SA BI



(vì





SA ABC



)







Từ





và





,suyra:





BI SAC



.



làhìnhchiếucủa

lên





SAC

.

 



 



, ,

SB SAC SB SI

 



BSI



.

Xét

BSI



vuôngtại

,tacó:



sin

BSI





BSI

  

.



TrườngTHPTHaiBàTrưng–Huế  Trang63/81

9. Cho hìnhchóp

S ABCD

có đáy là hìnhthang vuôngtại

 và

;

vuông gócvớimặtđáy

( )

ABCD

;



AD a

;

SD a

Tínhkhoảngcáchgiữađườngthẳng

vàmặtphẳng





SAB

.

A.

. B.

. C.

. D.

.

Lờigiải

ChọnA



Gọi

làhìnhchiếuvuônggóccủa

trên

.Khiđótacó:











AB AD

AB SD





 

AB SDA

 

AB DH

;













DH AB

DH SA





 

DH SAB

.

Tacó





CD SAB

















, , 

d CD SAB d D SAB





2 2





SD AD

2 2



.



10. Cho hình chóp

ABC

 trong đó

,

 vuông góc với nhau từng đôi một. Biết

3 ,

SA a

AB a

 .Tínhkhoảngcáchtừđiểm

đếnmặtphẳng





SBC



A.



 B.

2 5



 C.



 D.





Hướngdẫngiải

ChọnD



Hạ

AH SB



.

Ta có

BC SA



 và

BC AB



 nên





BC SAB



BC AH

 

 do đó





AH SBC



 hay









;

AH d A SBC



.

Khiđó

2 2 2

1 1 1

AH SA AB

 

2 2

1 1

3 3

a a

 

AH 

.



TrườngTHPTHaiBàTrưng–Huế  Trang64/81

11. Chohìnhchóp

S ABCD

có

SA a



,

SB a



,

SC a



,



ASB BSC

  

,



CSA

 

.Gọi



là

gócgiữahaiđườngthẳng

và

.Tính

cos



.

A.

cos





. B.

cos



 

. C.

cos 0





. D.

cos





.

Lờigiải

ChọnA

cos cos( , )

SA BC





 

SA BC



 

.( )

SA SC SB

SA BC





  

. .

SA SC SA SB

SA BC





   

2 2

.S .cos90 . .cos60

. 4 9 2.2 .3 .cos 60

SA C SA SB

a a a a a

  



  



.

12. Chohìnhchóp

S ABCD

cóđáylàhìnhvuôngcạnh

.Biết

vuônggócvớiđáyvà

SA a



.Tính

khoảngcáchtừđiểm

đếnmp





SBD

.

A.

. B.

. C.

2 3

. D.

.

Lờigiải

ChọnB

Gọi

làgiaođiểmcủa

và

.

Tacó

 

BD AC

BD SAC

BD SA





 







,





BD SBD













SBD SAC

 

và









SAC SBD SO

 



Trongmặtphẳng





SAC

,kẻ

AH SO



thì





AH SBD













AH d A SBD

 

.

Mặtkhác

Tamgiác

SAO

vuôngtại

có

OA AC 

,

SA a



và

2 2 2

1 1 1

AH SA OA

 



2 2 2 2

1 2 1 3

AH a a a

   



AH 



Vậy

 

d A SBD 

.

TrườngTHPTHaiBàTrưng–Huế  Trang65/81

13. Chotứdiện

ABCD

cótamgiác

BCD

đềucạnh

,

vuônggócvới





mp BCD

,

AB a



.

là

trungđiểmđoạn

,gọi



làgócgiữa

với





mp BCD

.khiđó:

A.

tan





. B.

2 3

tan





. C.

3 2

tan





. D.

tan





Lờigiải.

ChọnB

Gọi

làtrungđiểm

.

Tacógócgiữa

với





mp BCD

bằnggóc



MCN

.

+

MN a

 

.

CN 

.

Vậy

2 2 3

tan .



   .



14. Hìnhchóp

S ABCD

cóđáylàhìnhthoicạnh

,góc



BAC 

,

vuônggócvới





mp ABCD



gócgiữahaimặtphẳng





SBC

và





ABCD

bằng



.Khoảngcáchtừ

đến





mp SBC

bằng:

A.

. B.

. C.

. D.

.

Lờigiải.

ChọnC



+

ABCD

làhìnhthoi,góc



BAC 

nêntacótamgiác

ABC

đều.

+Gọi

làtrungđiểm

tacógócgiữa





SBC

vàđáy





ABCD

bằnggóc



SMA 

.

+Gọi

làhìnhchiếuvuônggóccủa

lên

tacó:

+

BC SA

BC AM



















BC SAM





BC AH



.

Lạicó:

AH SM











AH SBC













d A SBC AH



.

+

AM 

sin 60

  





3 3 3

2 2 4

a a

AH  

.



TrườngTHPTHaiBàTrưng–Huế  Trang66/81

15. Chohìnhchóp

S ABC

có

,

đôimộtvuônggócvớinhauvà

SA SB SC a

  

.Gọi



làtrungđiểmcủa

.Tínhgócgiữahaiđườngthẳng

và

.

A.



. B.



. C.



. D.

120



.

Lờigiải

ChọnA



Gọi

làtrungđiểmcủa

.Khiđógócgiữa

và



bằnggócgiữa

và

.

Tacó:



AB BC CA

 





SM AB



(trungtuyếntrongtamgiácvuôngứngvớicạnh

huyền).



SN AC



(trungtuyếntrongtamgiácvuôngứngvớicạnh

huyền).



MN BC



.

Suyra

SM MN SN

 

haytamgiác

SMN

đều.Dođó









; 60

SM BC SMN

  

16. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

.





SA ABCD





và

SA a

 .Khiđókhoảngcáchtừđiểm

đếnmặtphẳng





SAC

bằng



A.









d B SAC a



. B.









, 2

d B SAC a



.

C.









, 2

d B SAC a



. D.

 

d B SAC 

.

Lờigiải

ChọnD



Gọi

làtâmhìnhvuông

ABCD

.

Tacó:

BO AC

BO SA















BO SAC

 











d B SAC





.



TrườngTHPTHaiBàTrưng–Huế  Trang67/81

17. Chohìnhchóptứ giácđều

S ABCD

cótấtcảcáccạnh bằng



Gọi

làđiểmtrênđoạn

saocho

SM MD



.Tangócgiữa

đườngthẳng

vàmặtphẳng





ABCD

là

A.

. B.

. 

C.

. D.

.

Lờigiải

ChọnD



Tacó

BD a



OD 

.

Xéttamgiác

SOD

vuôngtại

có:

2 2 2

2 2

a a

SO SD OD a

 

    

 

 

.

Kẻ

MH BD



tại

nên

 







;

BM ABCD MBH





Do

MH BD



MH SO



.Tacó

MH MD HD

SO SD OD

  

.

3 6

SO a

MH  

và

1 2

3 6

HD OD 

2 5 2

6 6

a a

BH BD HD a     

.

Xéttamgiác

BHM

vuôngtại

có:

 



tan ;

BM ABCD MBH

 

 

tan ;

BM ABCD

 

.



TrườngTHPTHaiBàTrưng–Huế  Trang68/81

18. Chohìnhchóp

S ABCD

cóđáylàhìnhvuôngcạnh

,





SA ABCD



và

SA a

 Gọi



làgóc

tạobởigiữađườngthẳng

vàmặtphẳng





SAC

,khiđó



thỏamãnhệthứcnàosauđây:

A.

cos





. B.

sin





. C.

sin





. D.

cos





.

Lờigiải

ChọnC



Gọi

làtâmcủađáy

ABCD

.

Tacó

BO AC



và

BO SA



nên

làhìnhchiếucủa

trên





SAC

.

Suyra



BSO





.

Lạicó

BO 

,

2 2

SB SA AB a

  

.Suyra

sin



 

.

19. Chohìnhchóp

S ABCD

cóđáylàhìnhvuôngcạnh

.

vuônggócvớimặtphẳng





ABCD

và

SA a

 (hìnhvẽ).Gọi



làgócgiữađườngthẳng

vàmặtphẳng





SAC

.Tính

sin



tađược

kếtquảlà

 

A.

. B.

. C.

. D.

.

Lờigiải

ChọnA



Gọi

làtâmhìnhvuông

ABCD

thì





BO SAC





 



SB SAC



 



BSO



.

Tacó

SB a

 ,

sin





.



TrườngTHPTHaiBàTrưng–Huế  Trang69/81

20. Chohìnhchóp

S ABCD

cócáccạnhbênbằngnhauvàbằng

,đáylàhìnhchữnhật

ABCD

có

AB a



,

AD a



.Gọi

làđiểmthuộc

saocho

3 2 0

BK CK

 

  

.Tínhkhoảngcáchgiữahai

đườngthẳng

và

.

A.

165

. B.

2 165

. C.

2 135

. D.

135

.

Lờigiải

ChọnB

Gọi

làtâmcủahìnhchữnhật

ABCD

thì

làchiềucaocủahìnhchóp

S ABCD

.

2 2 2

5 11

4 2

a a

SO SA OA a     .

Do





SK SBC



mà

BC AD

nênkhoảngcáchgiữahaiđườngthẳng

và

làkhoảngcách

giữađườngthẳng

vàmặtphẳng





SBC

khôngphụthuộc

.

Gọi

,

lầnlượtlàtrungđiểmcủa

,

suyra

2 2

SI SO OI  

.

Trongtamgiác

SMI

dựngđườngcao

thì

làkhoảngcáchcầntìm.

Tacó:

. .

MH SI SO MI



. 2 165

SO MI a

  

.



21. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

,

vuônggócvớiđáy,

SA a

 .

Khoảngcáchgiữahaiđườngthẳng

và

là

A.

. B.

. C.

. D.

.

Lờigiải

ChọnD

a 3



Tacó:





BC SAB



BC SB

 

và

BC DC



.

Dođó,

chínhlàđoạnvuônggócchungcủahaiđườngthẳng

và

.

Nênkhoảngcáchgiữahaiđườngthẳng

và

là

BC a



.



TrườngTHPTHaiBàTrưng–Huế  Trang70/81

22. Chohình chóp

S ABCD

đềucó

AB a



,

SO a



với

làgiaođiểmcủa

và

.Khoảng

cáchtừ

đếnmặtphẳng





SCD

bằng

A.

. B.

. C.

. D.

.

Lờigiải

ChọnD



Gọi

làtrungđiểmcủacạnh

,tacó

CD OM

CD SO















CD SOM

 





SCD SOM

 

.

Trongmặtphẳng





SOM

kẻ

OH SM



,





H SM



thì

làkhoảngcáchtừđiểm

đếnmặt

phẳng





SCD

.

Tacó

2 2 2

1 1 1

OH OM SO

 

2 2

1 1

a a

 



OH 

.

23. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhchữnhật,

AB a



,

AD a



.

vuônggócvớimặt

phẳngđáy.

SA a

 .Cosincủagócgiữa

vàmặtđáybằng

A.

. B.

. C.

. D.

.

Lờigiải

ChọnD



Hìnhchiếucủa

lên





ABCD

là



Dođó

 



SC ABCD SCA

 

 



Tacó

2 2 2 2

4 5

AB ADA a aC

   



2 2

SC a

 



Trongtamgiácvuông

SAC

:



5 10

cos

2 2

AC a

SCA

   .



TrườngTHPTHaiBàTrưng–Huế  Trang71/81

24. Chohìnhchóp

S ABC

cótamgiác

ABC

vuôngcântại

,

AB BC a

 

,

SA a

 ,





SA ABC



.

Gócgiữahaimặtphẳng





SBC

và





ABC

là

A.



. B.



. C.



. D.



.

Lờigiải

ChọnB



Tacó





BC SAB



BC SA

 

.Gócgiữahaimặtphẳng





SBC

và





ABC

làgóc



SBA

.



tan

SBA





SBA

  

.

25. Chohìnhchóp

SABCD

cóđáy

ABCD

làhìnhthoicạnh

,



ADC

 

.Gọi

làgiaođiểmcủa

và

,





SO ABCD



và

SO a



.Gócgiữađườngthẳng

vàmặtphẳng





ABCD

bằng

A.



. B.



. C.



. D.



.

Lờigiải

ChọnC



Tacó

ABCD

làhìnhthoicạnh

,và



ADC

 

nên

ACD



đềuvà

2 . 3

OD a

 

.

Gócgiữađườngthẳng

vàmặtphẳng





ABCD

là



SDO

và



tan

SDO

 

suyra



SDO

 

.



TrườngTHPTHaiBàTrưng–Huế  Trang72/81

26. Chohìnhlăngtrụtamgiácđều

ABC A B C

  

cótấtcảcáccạnhbằng

.Khoảngcáchtừ

đếnmặt

phẳng





A BC



bằng

A.

. B.

. C.

. D.

.

Lờigiải

ChọnC



Gọi

làtrungđiểmcủa

,

làhìnhchiếucủa

trên

A M



tacó:

 

BC AM

BC AA M

BC AA







 









mà





AH AA M





BC AH

 

.

AH BC

AH A M

















AH A BC



 

nên









d A A BC AH





.

Trongtamgiác

AA M



vuôngtại

có

2 2

.AM AA

AM AA











 



 

 



.

27. Chohìnhchóp

S ABCD

cóđáylàhìnhchữnhật,

AB a



,

AD a



và





SA ABCD



.Gọi

là

trungđiểmcủađoạnthẳng

(thamkhảohìnhvẽ).Gócgiữahaimặtphẳng





SAC

và





SDM



bằng

A.



. B.



. C.



. D.



.

Lờigiải

ChọnD

Gọi

N AC DM

 

.Tacó

AM AD

BC AB

 

,dođóhaitamgiác

ABC

và

DAM

đồngdạng,suyra



AMN MAN

  

.

Vậy

AC DM







DM SAC

 

mà





DM SDM





nêngócgiữahaimặtphẳng





SAC

và





SDM

là



.

TrườngTHPTHaiBàTrưng–Huế  Trang73/81

28. Chohìnhchóptứgiácđều

S ABCD

cócạnhđáybằng

.Gócgiữacạnhbênvàmặtphẳngđáybằng



.Tínhkhoảngcáchtừđỉnh

đếnmặtphẳng





ABCD

.

A.

. B.

. C.

.

Lờigiải

ChọnB



Trong





ABCD

gọi

làgiaođiểmcủa

và

.

Tacó:





SO ABCD



.









d S ABCD SO

 

.

Talạicó:

làhìnhchiếucủa

lênmặtphẳng





ABCD



 



 



, , 60

SB ABCD SB OB SBO

    

.

Xét

SOB



vuôngtại

,tacó:



2 6

.tan .tan 60

2 2

a a

SO OB SBO   

.

Vậy

 

d S ABCD 

.

29. Chohìnhchóp

S ABC

cóđáylàtamgiácvuôngcântại

,

AB a



.Biết

vuônggócvớiđáy





ABC

(Hìnhthamkhảo).Khoảngcáchtừđiểm

đếnmặtphẳng





SAC

bằng



A.

. B.

. C.

. D.

.

Lờigiải

ChọnC



Tacó:

2 2

AC a



.Gọi

làtrungđiểm

.

Tacó:

BM AC

BM SA















BM SAC

 

 

, 2

d B SAC BM a

   

.

TrườngTHPTHaiBàTrưng–Huế  Trang74/81



30. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhchữnhật

AB a



,

AD a

 .Cạnhbên

vuông

gócvớiđáyvà

SA a



.Tínhkhoảngcách

từđiểm

đếnmặtphẳng





SBD

.

A.

2 57

d 

. B.

d 

. C.

d 

. D.



Lờigiải

ChọnA



Gọi

làhìnhchiếucúa

lên

.

Gọi

làhìnhchiếucủa

lên

.Suyra





AK SBD



tại

nên









d A SBD AK



.

Tamgiác

ABD

vuôngtại

có

AH BD





 

2 2 2 2

1 1 1 1 1

AH AB AD a

    

AH 



AH 



Tamgiác

SAH

vuôngtại

có

AK SH





 

2 2

2 2 2 2

1 1 1 1 1 19

AK SA AH a

     

 

 

 

AK 

2 57

AK 

.

Gọi

I AC BD

 











I AC SBD

 











 

d A SBD

d C SBD

 

. Mà

ABCD

làhìnhchữnhật nên

làtrungđiểm

nên



nên

 

2 57

, ,

d C SBD d A SBD 

.



TrườngTHPTHaiBàTrưng–Huế  Trang75/81



31. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuông,

vuônggócvớimặtđáy(thamkhảohình

vẽbên).Gócgiữahaimặtphẳng





SCD

và





ABCD

bằng



A.Góc



SDA

. B.Góc



SCA

. C.Góc



SCB

. D.Góc



ASD

.

Lờigiải

ChọnA

Tacó





   

 



CD SAD

ABCD SCD SDA

ABCD SCD CD





 



 





32. Cho hình chóp

S ABCD

 có đáy là hình vuông cạnh bằng

,

 vuông góc với mặt phẳng





ABCD

.Biếtgócgiữa

vàmặtphẳng





ABCD

bằng



.Tínhkhoảngcách

từ

đếnmặt

phẳng





SCD

.

A.

. B.

. C.

. D.

.

Lờigiải

ChọnD

Tacó





AB SCD

nên

















, ,

h d B SCD d A SCD AH

  



Vì













CD SAD SCD SAD

  

theogiaotuyến

,dựng





AH SD AH SCD

  

.

Theođềgócgiữa

vàmặtphẳng





ABCD

bằng



nên



SCA

 

.

Tacó:

tan 60 6

SA a

   



Và

2 2 2

1 1 1 42

AH SA AD

   

.



TrườngTHPTHaiBàTrưng–Huế  Trang76/81

33. Chohìnhlậpphương

ABCD A B C D

   

cócạnhbằng

tínhkhoảngcáchcủahaiđườngthẳng



và



A.

. B.

. C.

. D.

.

Lờigiải

ChọnC



Tacóvì

OC BD

ABCD A B C D

OC CC





   

















làkhoảngcáchcủahaiđườngthẳng



và



Mà

ABCD

làhìnhvuôngcócạnhbằng

2 2

a AC a OC a

   

.

34. Cho hình chóp

S ABCD

, đáy

ABCD

 là hình vuông cạnh

và





SA ABCD



. Biết

SA 

.

Gócgiữa

và





ABCD

là:

A.



. B.



. C.



. D.



.

Lờigiải

ChọnB

a 6



Tacó:





SA ABCD



.

Dođó

làhìnhchiếucủa

lên





ABCD

.









SC ABCD







SC AC





SCA



.

Xéttamgiác

SAC

vuôngtại

có



tan

SCA

  

.



SCA

  

.

Vậygócgiữa

và





ABCD

là



.

TrườngTHPTHaiBàTrưng–Huế  Trang77/81

35. Chohìnhchóp

S ABCD

cóđáy

ABCD

làhìnhvuôngcạnh

có





ABCD



và

SA a



.Gọi

làtrungđiểm

.Tính

tan

gócgiữađườngthẳng

và





ABCD

.

A.

. B.

. C.

. D.

.

Lờigiải

ChọnD

Gọi

làtrungđiểm

.

Tacó:

làđườngtrungbìnhcủa

SAB



nên

MN SA

và

1 2

2 2

MN SA 

.

Lạicó:





ABCD



.

Dođó





ABCD









.

Suyra



.

Tacó:

làhìnhchiếuvuônggóccủa

lên





ABCD

(do





)và

làhìnhchiếuvuônggóccủa

lên





ABCD

.

Suyra













; ;

DM ABCD DM ND





MDN



(



MDN

nhọnvì

MND



vuôngtại

).

Tacó:

2 2

DN AD AN

 



.

Xét

MND



vuôngtại

,có:

tan

MDN



.

Vậy

 

tan ;

DM ABCD 

.



TrườngTHPTHaiBàTrưng–Huế  Trang78/81

36. Chohìnhlậpphương

ABCD A B C D

   

cócạnhlà



.Khiđó,khoảngcáchgiữahaiđườngthẳng

chéonhau



và



là

A.

. B.

. C.

. D.

.

Lờigiải

ChọnB



Gọi

làtâmhìnhvuông

ABCD

.Trongmặtphẳng





ACC A

 

,kẻ

CH C O





tại

,

mà

CH BD



(do





BD ACC A

 



)nên





CH C BD









;

d C C BD CH



 



Tacó:





AB C BD

 





























, , , ,

d AB BC d AB C BD d A C BD d C C BD CH

     

    



Xét



C CO



vuôngtại

,đườngcao

:

2 2 2 2

1 1 1 3 3

CH CO CC a

    



.

37. Chotứdiện

ABCD

cótấtcảcáccạnhđềubằng



.Khiđókhoảngcáchtừđỉnh

đến





mp BCD

bằng

A.

. B.

. C.

. D.

.

Lờigiải

ChọnA



Gọi

làtrọngtâmtamgiác

BCD



















;

AO BCD d A BCD AO

  

.

Gọi

làtrungđiểm

.

Tacó:

2 3

3 3

BO BI 

,

2 2

AO AB BO  

.

Vậy

 

;

d A BCD 

.



TrườngTHPTHaiBàTrưng–Huế  Trang79/81

38. Chohìnhlậpphương

ABCD A B C D

   

.Gọi



làtrungđiểmcủacủa

A C

 

.Tính

tan



với



là

góctạobởi



vàmặtphẳng





ABCD

.

A.

. B.

. C.

. D.

.

Lờigiải

ChọnB



Đặtcạnhhìnhlậpphươngbằng

.

Tacó

 







 







, ,

BO ABCD BO A B C D

     



.

Tacó

O B

 

làhìnhchiếucủa



trên





A B C D

  



 







BO ABCD











BO B O

  





BO B



 

 

,

tan

O B







 

  .



TrườngTHPTHaiBàTrưng–Huế  Trang80/81

39. Chohìnhchóptứgiácđều

S ABCD

,cóđáy

ABCD

làhìnhvuông,cạnhbênbằngcạnhđáyvàbằng

.Gọi

làtrungđiểmcủa

.Gócgiữahaimặtphẳng





MBD

và





ABCD

bằng

A.



. B.



. C.



. D.



Lờigiải

ChọnC



Gọi

làtâmhìnhvuông

ABCD

,Tacó:



BD SO

BD AC















BD SOC

 

BD OM

 

.











MBD ABCD BD

BD OM

BD OC

 













   







MBD ABCD









OM OC





MOC



.





MOC

 

cântại

;

OC 

.





cos cos

MOC MCO





MOC

  

.

Vậy

   







, 45

MBD ABCD

 

.



TrườngTHPTHaiBàTrưng–Huế  Trang81/81

40. Hìnhchóp

S ABCD

đáyhìnhvuôngcạnh

,





SA ABCD



;

SA a

 . Khoảngcáchtừ

đến

mặtphẳng





SCD

bằng:

A.

. B.

. C.

2 3

. D.

.

Lờigiải

ChọnB

a 3



Tacó:





AB SCD

















, ,

d B SCD d A SCD

 

.

Kẻ

AH SD









.

CD SA



,

CD AD







CD SAD AH

  

CD AH

 







.

Từ





,





tacó:





AH SCD











d A SCD AH

 

.

Trongtamgiácvuông

SAD

:

2 2 2

1 1 1

AH SA AD

 

AH 

.

Bấm Tải xuống để xem toàn bộ.

| 1/81

| | Tải xuống

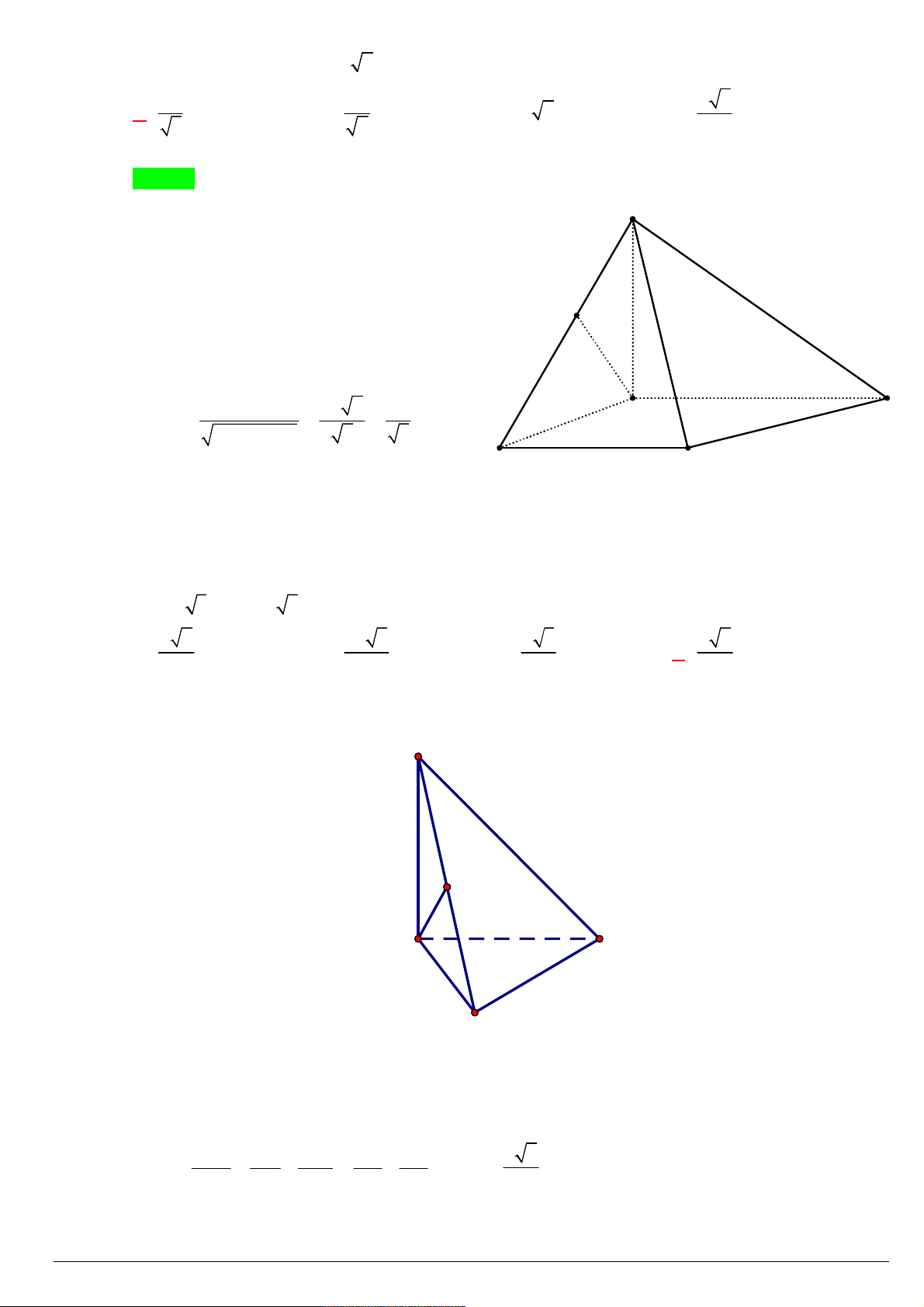
Preview text:

TRƯỜNG THPT HAI BÀ TRƯNG
ĐỀ CƯƠNG ÔN TẬP HKII NĂM HỌC 2018 - 2019 TỔ TOÁN MÔN TOÁN – KHỐI 11 
Họ và tên: PHAN PHƯỚC BẢO; Trường: HAI BÀ TRƯNG; Lớp: 11 A. Nội dung
I. Giải tích: Từ §1 chương IV. Giới hạn đến §5 chương V. Đạo hàm.
II. Hình học: Từ §1 đến §5 chương III. Vectơ trong không gian. Quan hệ vuông góc.
B. Một số bài tập tham khảo
Xem lại các bài tập trong SGK và SBT Đại số & Giải tích, Hình học 11 cơ bản.
 CHỦ ĐỀ I. GIỚI HẠN
Câu 1. Dãy số nào sau đây có giới hạn bằng 0 ? n n  2    6  3 n  3n A. u  . B. u  . C. u  . D. 2
u  n  4n . n   n   n n  3   5  n 1 lim u  n Lời giải: Vì 
 lim u  0  lim u  0 n n u  1   n
Câu 2. Phát biểu nào trong các phát biểu sau là sai? 1 1 A. lim n
q  0 | q |  
1 . B. lim c  c . C. lim  0 k   1 . D. lim  0 . k n n Lời giải: Theo định lý lim n
q  0 khi | q |   1 . 3 n  2n Câu 3. Tính giới hạn lim . 2 3n  n  2 1 A.  .  B. . C. .  D. 0. 3 Lời giải: 2 3 1 2 n  2n lim  lim . n n 2 3n  n  2 1 2 3   2 n n lim . n   2 Tự luận : 1 2 1 lim n  1 2 3 3   2 n n 2 3 1 2 n  2n  im  lim . n n   2 3n  n  2 1 2 3   2 n n 3 10 x  2x CALC x 1  0 MTCT: NHẬP     2 3x  x  2 2 3 2
a n  5n  n 1 Câu 4. Cho lim
 b . Có bao nhiêu giá trị a nguyên dương để b 0; 4 ? 3
4n  bn  a A. 0 . B. 4 . C. 16 . D. 2 . 2 3 2 2
a n  5n  n 1 a Lời giải: lim 
 0; 4  0  a  4, a    a  1; 2;3; 4 3    
4n  bn  a 4
Trường THPT Hai Bà Trưng – Huế Trang 1/81
Câu 5. Có bao nhiêu giá trị nguyên của tham số a thuộc  10  ;10 để  n   2 a   3 lim 5 3 2 n    ?   A. 16 . B. 3 . C. 5 . D. 10 . Lời giải: a  2 lim 5n  3 2 a  2 3
n     lim 3 2 a  2 3 2
n    a  2  0     a   2  do a   10 
;10 , a    a  9  ; 8  ;...; 2; 2;3;...;8;  9 2 3 7n  2n 1
Câu 6. Tính giới hạn I  lim . 3 2 3n  2n 1 7 2 A. . B.  . C. 0 . D. 1. 3 3 Lời giải:  7 1 3  n  2  2 3  3  7n  2n 1  n n  2 I  lim  lim   3 2 3n  2n 1  2 1 3  3 n 3    3   n n  2 3 10 7x  2x 1  Calc 2 MTCT: NHẬP 10   0  , 666  3 2 3x  2x 1 3 3 2 2n  n  4 1 Câu 7. Biết lim 
với a là tham số. Tính 2 a  a . 3 an  2 2 A. 12 . B. 2 . C. 0 . D. 6 . Lời giải:  1 4 3  n 2   3 2  3  2n  n  4  n n  2 1 Ta có lim  lim    a  4 3 an  2  2 3  a 2 n a     n  Vậy 2 2
a  a  4  4  12  2 an  5  3n
Câu 8. Cho hai số thực a;b thỏa mãn lim
 1. Tính S  a  b . 3 2 3
5n  4  2n  bn A. S  5 . B. S  3  . C. S  3 . D. S  5  . Lời giải:
Do tử có bậc 2 nên giới hạn đã cho về 1 số khác không khi tử và mẫu cùng bậc Suy ra b  5 2 an  5  3n a Từ đó lim   1   a  2  2 4   2n 2
Vậy S  a  b  2   ( 5  )  3
Trường THPT Hai Bà Trưng – Huế Trang 2/81 1 1 1
Câu 9. Cho dãy số u với u    ...  . Tính lim u . n  n 1.3 3.5 2n   1 2n   1 n 1 1 A. 0 . B. . C. . D. 1. 2 4 Lời giải: Tự luận: 1 1 1 1  1 1 1 1 1  1  1  u    ...   1    ...    1 n     1.3 3.5 2n   1 2n   1 2  3 3 5 2n 1 2n 1  2  2n 1  1  1  1
lim u  lim 1  n   2  2n  1  2
MTCT CASIO – 580 : Bấm như sau q[a1R(2[p1)(2[+1)$$1E100= HIỂN THỊ 1 KẾT QUẢ  2
Câu 10. Có bao nhiêu giá trị nguyên lớn hơn 1
 0 của tham số m để  2 lim
4n  3  mn  5   ? A. 9 . B. 10 . C. 11. D. 12 . Lời giải:   lim  3 5 2
4n  3  mn  5  lim n 4   m 
    2  m  0 2 2  n n    Do m  , 10 
 m  2  m  9  ; 8;  ...;1 có 11 giá trị m. n n 1 9  3  1
Câu 11. Có bao nhiêu giá trị nguyên của tham số a thuộc khoảng 0; 2018 để có lim  ?
5n  9na 2187 A. 2011 . B. 2016 . C. 2019 . D. 2009 . Lời giải:
Bước 1: Dùng MTCT CASI0 -580 sử dụng công cụ FACT 2187=qx Xuất hiện ở màn hình MTCT n 1    n 3 9 1 n n 1   9  3  9n   1 1 Bước 2: lim  lim  lim   a  7 n na n a 7 5  9   na 5 3 3 9 1   5n  
Do a thuộc khoảng 0; 2018 nên a 7;8;...; 
2017 có 2011 giá trị a nguyên thỏa mãn.
Trường THPT Hai Bà Trưng – Huế Trang 3/81  1   1   1 
Câu 12. Tính giới hạn lim 1 1 ... 1  . 2   2   2   2   3   n  1 1 3 A. 1. B. . C. . D. . 2 4 2 Lời giải:
Tự luận: nhớ lại hằng đẳng thức và áp dụng 2 2
a  b  a  ba  b  1   1   1   1   1  1  1   1   1  lim 1 1 ... 1  lim 1 1 1 1 ... 1 1  2   2   2               2   3   n   2   2  3  3   n   n  1  3 2   n n 1   1  1  1  1  lim . . ... . . 1  lim . 1         
2  2 3   n 1 n   n  2  n  2 MTCT CASIO - 580 Q[1pa1R[d$$2$100=
Xuất hiện ở màn hình kết quả 1 KẾT QUẢ  2
Câu 13. Tính tổng tất cả các giá trị thực của tham số a để  2 2 2 lim
n  a n  n  a  2 n 1  2. A. 1  . B. 5 C. 1. D. 5 . Lời giải: 2 2 2
n  a n  n  a  n  lim  2 1 2 2 2
n  a n  n  a  2 n 1    lim  2 2 2
n  a n  n  a  2 n 1  2 1 
n a  a  2    2  n  a  a  2 2 lim 
 2  a  a  6  0 2   2 a a  2 1 n  1  1   2  n n n   
 S  1theo Viet a 
Trường THPT Hai Bà Trưng – Huế Trang 4/81 n 1  1 1 1  1 
Câu 14. Tính tổng S  1    ...    ...   với * n   . 3 9 27  3  3 3 A. S  1 . B. S  . C. S   . D. S  . 4 2 Lời giải: Tự luận u
Nhắc lại tổng của 1 cấp số nhân lùi vô hạn 1 S  n 1 q n 1  1 1 1  1  1 3 S  1    ...    ...     3 9 27  3   1  4 1     3  MTCT CASIO -580VN q[(ap1R3$)^[$$0E100=
Xuất hiện ở màn hình kết quả
Câu 15. Giả sử ta có lim f  x  a và lim g  x  b . Trong các mệnh đề sau, mệnh đề nào sai? x x
A. lim  f  x g  x  ab   .
B. lim  f  x  g  x  a  b   . x x f  x a C. lim  .
D. lim  f  x  g  x  a  b   .
x g  x b x f  x a Lời giải: lim 
vì có thể lim g  x  b  0
x g  x b x
Câu 16. Cho các giới hạn lim f  x  2 ; lim g  x  3 . Tính giới hạn lim 3 f  x  4g  x   . xx xx x x 0 0 0 A. 5 . B. 2 . C. 6  . D. 3 . Lời giải: lim 3
 f  x  4g  x  3.2  4.3  6   xx0 2x  3
Câu 17. Tính giới hạn lim .
x 1  3x 2 2 3 A. . B.  . C.  . D. 3  . 3 3 2 Lời giải:  3  x 2    2x  3  x  2 Tự luận lim  lim   x 1 3 x x   1  3 x  3    x  MTCT CASIO -580VN 10 2x  3  Calc x 2 10   1 3x 3 a2[p3R1p3[r10^10==
kết quả xuất hiện ở màn hình MTCT
Trường THPT Hai Bà Trưng – Huế Trang 5/81 Câu 18. Cho  2 lim
x  ax  5  x  thì a là 1 nghiệm của phương trình nào trong các phương trình sau?   5 x A. 2
x 11x 10  0 . B. 2
x  5x  6  0 . C. 2
x  8x 15  0 . D. 2
x  9x 10  0 . Lời giải:  5  x a  2 2  
x  ax   x  x lim x ax x        x  5 2 5  lim lim x 2 x  ax  5 x  x  a 5 x 1   x 2 x x  5   5  x a  x a       x   x  a lim  lim   5  a  10  x a 5 x  a 5  2   x 1   x x  1  1 2  2 x x x x    x  1 Mà D. 2
x  9x 10  0   . (thỏa) x  10  
Câu 19. Tính giới hạn I     .   2 lim x 4x 1 x x  A. I  2  . B. I  4  . C. I  1. D. I  1. Lời giải: 1 2 2 4 
x  4x 1 x Tự luận:  lim x I
x  x   x     x  2 4 1  lim lim 2 x 2 x  4x 1 x  x  4 1  1  1 2 x x MTCT CASIO -580VN 10 2 Calc x 10 x 4x 1 x       2  s[d+4[+1$+[rp10^10==
kết quả màn hình xuất hiện f  x 10 f  x 10 Câu 20. Cho lim  5 . Tính giới hạn lim . x 1  x 1 x 1   x  
1  4 f x  9  3 5 A. 1. B. 2 . C. 10 . D. . 3 Lời giải:
Bình luận: khi giải dạng này ta luôn đối chiếu với định nghĩa đạo hàm f  x 10
f  x  f  x0  lim  5  lim  f ' x . 0  x 1  x 1 xx0 x  x0  f   1  10
  f ' 1  5       x f x f x    1 10 10 11 lim  lim .  5.  1 x 1   x  
1  4 f  x  9  3 x 1  x 1
 4 f x9 3 4.10  9  3
Trường THPT Hai Bà Trưng – Huế Trang 6/81 Câu 21. Tính giới hạn  3 2
lim 3x  5x  9 2x  2017 . x A.  . B. 3 . C. 3  . D.  . Lời giải:
Bình luận: các giới hạn khi x tiến về + vô cùng (hoặc – vô cùng) ta chỉ quan tâm đến bậc lớn nhất của x   lim  5 9 2 2017 3 2
3x  5x  9 2x  2017 3  lim x  3       . 2 3 x x  x x x    2
 4x  3x 1 
Câu 22. Cho hai số thực a và b thoả mãn lim
 ax  b  0  
. Tính a  2b . x 2x 1   A. 4  . B. 5  . C. 4 . D. 3  . Lời giải: Tự luận: 7 2 4x  3x  1 5 2  2x   2x 1 2 2x 1  7   2
 4x  3x 1   5 2   lim
 ax  b  lim    2x    
  ax  b  0 x 2x 1 x 2 2x  1         7 a  2 5  vì 2 lim  0 nên 2x 
 ax  b   5
x 2x 1 2 b     2  5 
Vậy a  2b  2  2.   3    2 
* MTCT CASIO -580VN ( sau khi thi xong và hè sẽ luyện tập MTCT thêm)
dùng thủ thuật Calc 100 (lấy 2 chữ số)
ta có 97,5 > 50 ta lấy 97,5 - 100 = 2,5 sau đó làm tròn hàng tiếp theo lên 1 đơn vị : 5
tức 1 + 1 = 2 < 50. ta có 2x  2 2 4x  3x 1 Calc x 5 100
197,5...  2x  2x 1 2 3  2x
Câu 23. Tính giới hạn lim . x 2  x  2 3 A.  . B. 2 . C.  . D. . 2 Lời giải:
lim 3  2x  7, lim  x  2  0, x  2  x  2  x  2  0 x2 x2 3  2x  lim   x2 x  2 MTCT CASIO -580VN 3  2x x Calc 1  ,9999    x  2
Trường THPT Hai Bà Trưng – Huế Trang 7/81  1 1  a Câu 24. Biết lim  
là một phân số tối giản b  0. Tính 2
S  6a  b . 2 2 
x2  3x  4x  4
x 12x  20  b A. S  10  . B. S  10 . C. S  32 . D. S  21. Lời giải: Tự luận 1 1  1 1    lim   lim   2 2    x2 x2
 3x  4x  4
x 12x  20 
 x  23x  2  x  2 x 10   1 3x  2  x 10 4 x  2  lim .  lim
x2  x  2 3x  2 x 10
x2  x  23x  2 x 10 4 4 1 a  lim   
x2 3x  2 x 10 8.8 16 b
b  0  b  16; a  1
S  a  b   2 2 6 6. 1 16  10 MTCT CASIO -580VN a1R3[dp4[p4$+a1R[dp12[+20 màn hình xuất hiện tiếp tục r1.9999== màn hình xuất hiện p0.0625= 1  kết quả  0  , 0625  16
Trường THPT Hai Bà Trưng – Huế Trang 8/81 Câu 25. Biết    
 . Tính a  4b .   2 lim 4x
3x 1 ax b 0 x A. 3 . B. 5 . C. 1  . D. 2 . Lời giải: Tự luận cách 1:          2 lim 4x
3x 1 ax b 0 a 0 x 2 2 2 2 2 2
x  x   ax  b
x  x   a x  abx  b lim
x  x   ax  b    x  4 3 1 4 3 1 2 2 4 3 1     lim lim 0 x 2
4x  3x 1  ax  b x  3 1 b  x  4    a  2  x x x  
khi bậc tử < bậc mẫu a  2 2 4  a  0  3 tức là   
3  a  4b  2  4.  5 3   2ab  0 b   4    4  f  x a  lim  n x x 
cách 2 : bí kíp lim  f  x   n n 1 .
a x  bx   ...  b  lim  f  x n  ax      x x  .  ..   2 4x  3x 1 a  lim  2 x x 2 2
x  x   x   b  lim
x  x   x    x  4 3 1 4 3 3 2 4 3 1 2  lim x  2
x  x   x 2  2 4 4 3 1 2 MTCT CASIO -580VN as4[dp3[+1R[r10^10== 2 10 4x  3x 1 Calc x 10     2 x s4[dp3[+1$p2[r10^10== 10  Calc 3 2 x 10
4x  3x 1  2x    4
Trường THPT Hai Bà Trưng – Huế Trang 9/81 2 2
x  x  4x 1
Câu 26. Tính giới hạn lim . x 2x  3 1 1 A.  . B.  . C.  . D. . 2 2 Lời giải: Tự luận  1 1   1 1  x  1  4    x  1  4   2 2 2 2
x  x  4x 1 x x x x      1 2 1 lim  lim  lim   x 2x  3 x  3 x   3  2 2 x 2  x 2       x   x  MTCT CASIO -580VN 2 2 10
x  x  4x 1 Calc  1 x 10   2x  3 2 as[dp[$ps4[d+1R2[+3rp10^10 == xuất hiện 2 a x 1  2017 1 Câu 27. Cho lim  ;
x  bx   x  . Tính P  4a  b . x  2 lim 1  2 x x  2018 2 A. P  3 . B. P  1. C. P  2 . D. P  1 . Lời giải: 1 1 a x 1  2017 a x 1  2017 2   2 2 a x 1  2017 x x lim  lim  lim x x  2018 x x  2018 x x  2018  1 2017  x  a 1   2 x x   a 1 1  lim    a   x  2018  1 2 2 x 1    x   1  x b  2 2  
x  bx   x  x  b lim
x  bx   x      b  x  1 2 1  lim lim 2 4 x 2 x  bx 1 x  x   b 1  11 x  1  1 2  x x    1 
P  4a  b  4   4  2    2 
Trường THPT Hai Bà Trưng – Huế Trang 10/81  2 2x   1 mx  3
Câu 28. Giá trị của số thực m sao cho lim  6 là 3 x x  4x  7 A. m  3  . B. m  3 . C. m  2 . D. m  2  . Lời giải: Tự luận  1   3 2   2 x  x m  2x  1 mx 3 2  2       x   x  2m lim  lim   6  m  3 3 x x  4x  7 x  4 7 3  1 x 1   2 3   x x  * MTCT CASIO -580VN gán m = Y thử đáp án A ta có a(2[dp1)(Q)[+3)R[^3$+4[+7r 10^10=p3== thử đáp án B ta có a(2[dp1)(Q)[+3)R[^3$+4[+7r 10^10=3==
Câu 29. Cho hàm số y  f  x xác định trên  \  1 
có đồ thị như hình vẽ. Khẳng định nào đúng?
A. lim f  x   ;
 lim f  x   .
B. lim f  x   ;
 lim f  x   . x 1     x  1 x 1  x  1
C. lim f  x  ;
 lim f  x   .
D. lim f  x  ;
 lim f  x   . x 1     x  1 x 1  x  1 Lời giải: Bình luận
Khi gặp dang đồ thị cần nhớ :
khi x từ phía lớn hơn về vị trí không xác định (kí hiệu là +) nhánh đồ thì hướng lên là + vô cùng
khi x từ phía nhỏ hơn về vị trí không xác định (kí hiệu là -) nhánh đồ thì hướng xuống là - vô cùng
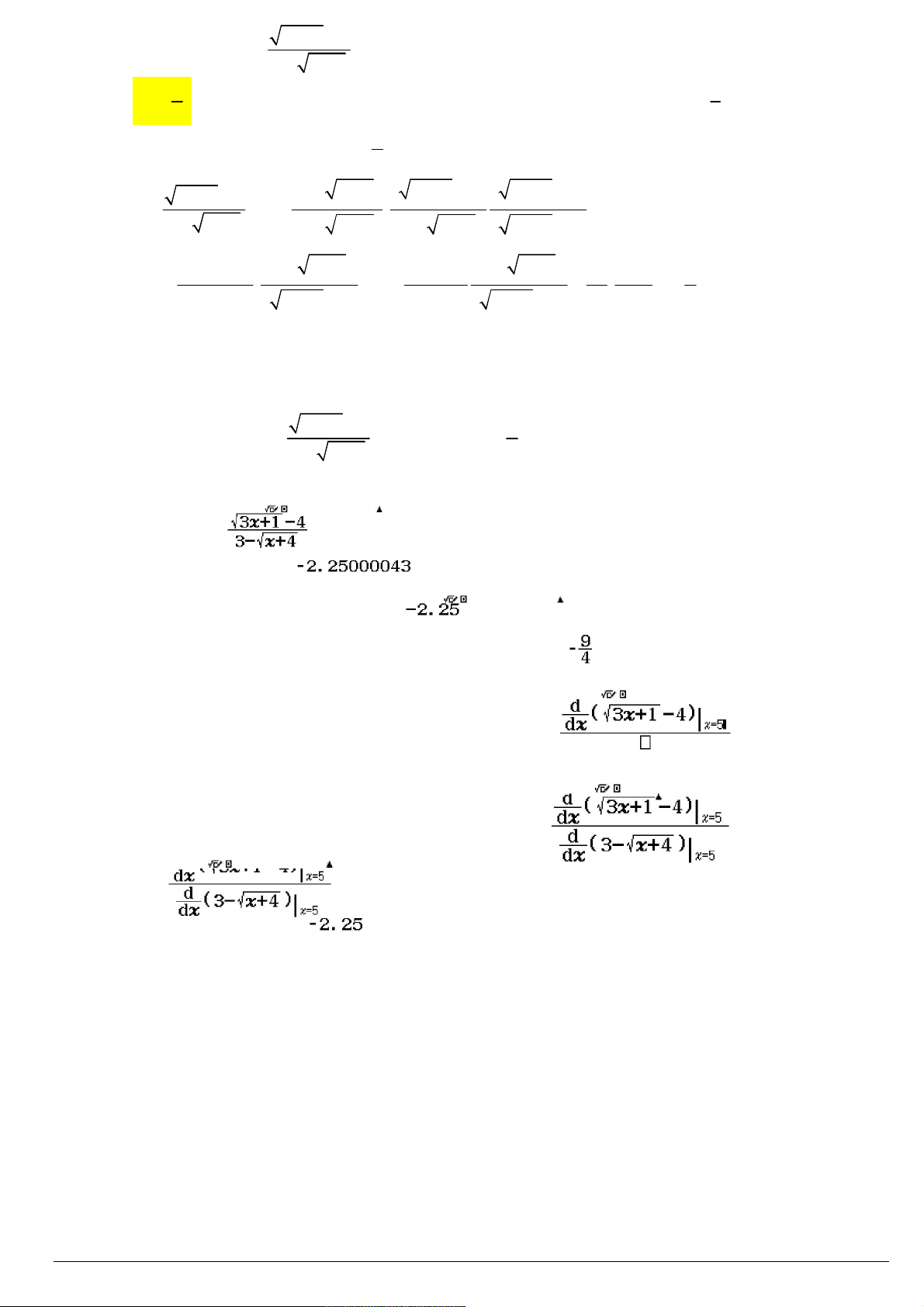
Trường THPT Hai Bà Trưng – Huế Trang 11/81 3x 1  4
Câu 30. Tính giới hạn lim .
x5 3  x  4 9 3 A.  . B. 3  . C. 18  . D.  . 4 8 0
Lời giải: tự luận dạng vô định
nhân liên hợp khử vô định 0 x  
3 x  4  3x 1 4  3x 1 4 3 1 4  lim  lim . x5 x5 3  x  4
3 x  4 3 x  4  3x 1 4
3x  116 3  x  4 
 x   3  x  4 3 5  3 33 9  lim .  lim  .   x5
9  x  4  3x 1  4 x5 x 5  3x 1  4 1  4  4 4 MTCT CASIO -580VN 3x 1  4 Calc  9 cách 1: dùng Calc x 4,99999    3  x  4 4 as3[+1$p4R3ps[+4r4.99999== xuất hiện sau đó Wp2.25=
cách 2: dùng công cụ đạo hàm aqys3[+1$p4$5 Rqy3ps[+4$$5 =
Trường THPT Hai Bà Trưng – Huế Trang 12/81 2x  x  3
Câu 31. Tính giới hạn I  lim . 2 x 1  x 1 7 3 3 3 A. I  . B. I  . C. I  . D. I  . 8 2 8 4 0
Lời giải: dạng vô định 0
tự luận nhân liên hợp khử vô định x  x 
2x  x 3 2x  x 3 2 3  2 4x  x  3 I  lim  lim .  lim 2 x 1  x 1 x 1   x   1  x   1
2x  x 3 x 1   x   1  x  
1 2x  x  3  x   1 4x  3 4x  3 7  lim  lim  x 1   x   1  x  
1 2x  x  3 x 1   x  
1 2x  x  3 8
MTCT CASIO -580VN tương tự câu 30 ( bấm tại lớp để rèn luyện và học hỏi) 3 2
x  7  x  x  2
Câu 32. Tính giới hạn lim . x 1  x 1 1 3 2 A. B.  C.  D.  . 12 2 3 0
Lời giải: dạng vô định 0
tự luận nhân liên hợp khử vô định 3 2 x  1 
x  7  2, x  x  2  2 3 2 3 2 x 7 x x 2  x 7 2 x x 2 2           lim  lim    x 1  x 1 x 1   x 1 x 1      2  x  7  8
x  x  2  4   lim    x 1
  x  3 1
 x  72  2 x  7  4  x   1  2 3
x  x  2  2           x 1  x   1  x  2   lim    x 1
  x  3 1
 x  72  2 x  7  4  x   1  2 3
x  x  2  2           1  x  2   lim    x 1   3 
 x  72  2 x  7  4  2 3
x  x  2  2        1 3 2     12 4 3
MTCT CASIO -580VN tương tự câu 30 ( bấm tại lớp để rèn luyện và học hỏi)
Trường THPT Hai Bà Trưng – Huế Trang 13/81 2
x  a   1 x  a
Câu 33. Tính giới hạn lim . 3 3 x a x  a a 1 a  1 a 1 A. . B.  . C. . D. . 2 3a 2 3a 3a 0
Lời giải: dạng vô định 0 2
x  a   1 x  a
 x  a x   1  x   1 a 1 tự luận lim  lim  lim  3 3 x a x a x  a
 x  a 2 2
x  xa  a  xa  2 2
x  xa  a  2 3a
MTCT CASIO -580VN tương tự câu 30 ( bấm tại lớp để rèn luyện và học hỏi)
gán a = 3 ( vì mẫu có kết quả bội 3 )
Câu 34. Cho hàm số y  f  x liên tục trên a;b . Điều kiện cần và đủ để hàm số liên tục trên a;b là
A. lim f  x  f a và lim f  x  f b .
B. lim f  x  f a và lim f  x  f b . x a  x b  x a  x b 
C. lim f  x  f a và lim f  x  f b .
D. lim f  x  f a và lim f  x  f b . x a  x b  x a  x b  Lời giải: định lý sgk 2
 x  x 12  khi x  4 
Câu 35. Tìm tham số thực m để hàm số y  f  x   x  4
liên tục tại điểm x  4  . 0
mx 1 khi x  4   A. m  4 . B. m  3 . C. m  2 . D. m  5 . Lời giải:
Để hàm số y  f  x liên tục tại điểm x  4  thì 0 2 x  x 12
 x  4 x  3
lim f  x  f 4  lim
 4m 1  lim  4  m 1 x4 x 4  x4 x  4 x  4  7  4
 m  1  m  2 2
 ax  (a  2)x  2 khi x 1 
Câu 36. Có tất cả bao nhiêu giá trị của a để hàm số f (x)   x  3  2
liên tục tại x  1 ?  2
8  a khi x  1  A. 1. B. 0 . C. 3 . D. 2 . Lời giải:
để hàm số f (x) liên tục tại x  1 thì 2 ax  a  x   x   1 ax  2 x  3  2 ( 2) 2 2  
lim f  x  f   2 1  lim
 8  a  lim  8  a x 1  x 1  x 1 x  3  2  x  3  4 a  0  a  2 2 2
.4  8  a  a  4a  0  a  4  Vậy có 2 giá trị a.
Câu 37. Hàm số nào trong các hàm số dưới đây không liên tục trên  ? x 2x 1 A. y  x . B. y  .
C. y  sin x . D. y  . x  1 2 x 1 Lời giải:
bí kíp: Các hàm số không liên tục trên  là các hàm phân thức với mẫu bằng 0 có nghiệm
Trường THPT Hai Bà Trưng – Huế Trang 14/81  
 mx  n2 khi x  1
Câu 38. Cho hàm số f  x  
liên tục trên  . Tính 2 2 m  n .
2mnx  3 khi x  1  A. 1. B. 2 . C. 3. D. 4 . Lời giải:
Để hàm số f  x liên tục trên  thì
lim f  x  lim f  x  lim mx  n2  lim 2mnx  3  m  n2  2mn  3 x 1 x 1 x 1 x 1     2 2 2 2
 m  2mn  n  2mn  3  m  n  3. 2
 x  ax  b  khi x  1
Câu 39. Gọi a , b là hai số thực để hàm số f  x   x 1
liên tục trên  . Tính a  b . 2ax 1 khi x  1  A. 0 . B. 1  . C. 5  . D. 7 . Lời giải:
Để hàm số f  x liên tục trên  thì 2
x  ax  b
lim f  x  f   1  lim  2ax 1 x 1  x 1  x 1
suy ra x = 1 là nghiệm của tử 2 x 1 x ax b    
 0  1 a  b  0 nghiệm còn lại là x = b (đl Viet) 2
x  ax  b  x   1  x  b
lim f  x  f   1  lim  2a 1  lim  2a 1 x 1  x 1  x 1 x 1  x 1 vậy 1
  a  b  0 a  3    
 a  b  7
1 b  2a 1 b  4    bí kíp: MTCT 580 VN
đối với phân thức ta lấy đạo hàm tử tại x =1 và chia cho đạo hàm mẫu tại x=1, còn đa thức thay x =1. 0
lưu ý hàm phân thức có tử và mẫu chung 1 nghiệm (dạng ) 0  2
x  ax  b x 1 2a 
 2  a  2a 1  a  3 1  x   1 x  1
1 a  b  0  b  4  a  b  7
Câu 40. Cho hàm số f  x xác định trên a;b . Tìm mệnh đề đúng.
A. Nếu hàm số f  x liên tục trên a;b và f a f b  0 thì phương trình f  x  0 không có
nghiệm trong khoảng a;b .
B. Nếu f a f b  0 thì phương trình f  x  0 có ít nhất một nghiệm trong khoảng a;b .
C. Nếu hàm số f  x liên tục, tăng trên a;b và f a f b  0 thì phương trình f  x  0 không
có nghiệm trong khoảng a;b .
D. Nếu phương trình f  x  0 có nghiệm trong khoảng a;b thì hàm số f  x liên tục trên a;b . Lời giải: định lý sgk
Trường THPT Hai Bà Trưng – Huế Trang 15/81
Câu 41. Phương trình nào dưới đây có nghiệm trong khoảng 0;  1 A. 2
2x  3x  4  0 . B. x  5 7
1  x  2  0 . C. 4 2
3x  4x  5  0 . D. 2017 3x  8x  4  0 . Lời giải:
thay x  0, x  1 vào các đáp án A,B,C,D.
biểu thức nào cho kết quả trái dấu ( 1 kết quả âm và 1 kết quả dương) đó là đáp án. Câu 42. Cho phương trình 4 2
2x  5x  x 1  0 
1 . Khẳng định nào sau đây là đúng? A.  
1 có nghiệm trong khoảng  1   ;1 . B.  
1 chỉ có một nghiệm trong khoảng  2   ;1 . C.  
1 có ít nhất hai nghiệm trong 1; 2 . D.  
1 không có nghiệm trong khoảng  2  ;0 .
Lời giải: dùng công cụ Table MTCT CASIO -580VN là Mode 8
kiểm tra các vùng đổi dấu Tự luận
Đặt f  x 4 2
 2x  5x  x 1 f   1  1  , f 0  1 f  
1 f 0  0  x   1  ;0 , f x  0 0    0 
Trường THPT Hai Bà Trưng – Huế Trang 16/81
Câu 43. Cho phương trình  2
m   x   2 x   3 3 1
4  x  3  0  
1 , với m là tham số. Khẳng định nào sau
đây về phương trình   1 là khẳng định đúng? A.  
1 có đúng 4 nghiệm phân biệt. B.   1 vô nghiệm. C.  
1 có ít nhất 2 nghiệm phân biệt. D.   1 có đúng một nghiệm. Lời giải: Bí kíp:
chọn các giá trị x sao cho biểu thức không còn phụ thuộc m ( hoặc biểu thức có m xác định 1 loaik dấu)  2
m  3 x   1  2 x  4 x 1    0 x2
x  1  P  2 chẳng hạn 3
P  x  3 x  2  P  5  x  2   P  11
! số nghiệm của 1 phương trình nhỏ hơn hoặc bằng bậc của phương trình Tự luận
Đặt f  x   2
m   x   2 x   3 3 1 4  x  3 ta có   1  4  3 
lim f  x  lim  2
m  3 x   1  2 x  4 3 3
 x  3  lim x  2 m  3     1 1 1    2  3  x x x   x  x  x  3  lim x  2 m  3   1    0 x
f 2  11  0 f 2  5   0   1  4  3 
lim f  x  lim  2
m  3 x   1  2 x  4 3 3
 x  3  lim x  2 m  3     1 1 1    2  3  x x x   x  x  x  3  lim x  2 m  3   1    0 x
Vậy phương trình đã cho có 3 nghiệm. MTCT CASIO -580VN
giá trị cực đại . giá trí cực tiểu > 0 thì pt có 1 nghiệm
giá trị cực đại . giá trí cực tiểu = 0 thì pt có 2 nghiệm
giá trị cực đại . giá trí cực tiểu < 0 thì pt có 3 nghiệm cho m =y =1, x =100 kết quả
dùng Calc 100 suy ra f  x 3 2
 3x  4x 16x 19
Mode 9 chọn 2 chọn 3 nhập sau đó bấm = liên tiếp
kết luận: 3 nghiệm. hihi. lợi hại quá
Trường THPT Hai Bà Trưng – Huế Trang 17/81
Câu 44. Tìm tất cả các giá trị thực của m để phương trình m  x
  x  2020 2019 1 2
 2x  3  0 vô nghiệm. A. m  1 B. m    C. m  0
D. Không có giá trị m Lời giải:
Bí kíp : pt bậc lẻ luôn có nghiệm m  x
  x  2020 2019 1 2
 2x  3  0 bậc 4039 nên luôn có nghiệm. Tự luận
Đặt f  x  m  x
  x  2020 2019 1 2  2x  3 ta có f   1  1
  0, f 2  1  0, f  
1 . f 2  0  x  1; 2 , f x  0. 0    0  Vậy pt luôn có nghiệm. ------------------------
. CHỦ ĐỀ 2. ĐẠO HÀM y  Câu 45. Cho 3
y  x  1. Gọi x là số gia của đối số tại x và y là số gia tương ứng của hàm số, tính . x  A. 2 3 3x  3 . x x   x . B. 2 2 3x  3 . x x   x . C. 2 2 3x  3 . x x   x . D. 2 3 3x  3 . x x   x . Lời giải: 3 y
f  x  x
   f  x
 x  x 1  3 x   1 x   2 2 3x  3x x   x  2 2   
 3x  3xx  x  x  x  x  x 
Câu 46. Số gia  của hàm số 2
y  x  2x  5 tại điểm x  1 là y 0
A.  2  2  5 . B.    . C.    . D.    . x 2 4 x 2 4 x 2 2 x x x x x Lời giải:
  f     f      2             2 2 1 1 1 2 1 5 1 2.1 5  4 y x x x x x
f  x  f 6
Câu 47. Cho hàm số y  f  x có đạo hàm thỏa mãn f 6  2. Giá trị của biểu thức lim bằng x6 x  6 1 1 A. 12. B. 2 . C. . D. . 3 2
f  x  f 6
Lời giải: theo định nghĩa đạo hàm lim
 f 6  2. x6 x  6 2
x 1, x  1
Câu 48. Cho hàm số y  f  x   Mệnh đề sai là 2x, x  1.  A. f   1  2 . B. f   1  . C. f 0  2. D. f 2  4. Lời giải: 2
x 1, x  1 2 x  1
y  f  x  
 f ' x   2x, x  1. 2, x  1.  
f '1   f '1  2
nên tồn tại đạo hàm tại x =1.
Trường THPT Hai Bà Trưng – Huế Trang 18/81 2
ax  bx 1 khi x  0
Câu 49. Cho hàm số f  x  
. Biết f  x có đạo hàm tại x  0 . Tính T  a  2b . ax  b 1 khi x  0  A. T  4  . B. T  0 . C. T  6  . D. T  4 . Lời giải: 2
ax  bx 1 khi x  0
f  x  ax b1 khi x  0 
lim f  x  lim f  x  f 0  1  b  1  b  2  x 0 x 0   2
ax  bx 1 khi x  0 2ax  b khi x  0
f  x  
 f  x   ax  b 1 khi x  0 a khi x  0  
f '0   f '0   a  b a  b  2
T  a  2b  6 
Câu 50. Đạo hàm của hàm số 5 3 2
y  2x  4x  x là A. 4 2
y  10x  3x  2x . B. 4 2
y  5x 12x  2x .C. 4 2
y  10x 12x  2x .D. 4 2
y  10x 12x  2x . Lời giải: 5 3 2
y  2x  4x  x  4 2
y  10x 12x  2x 2x 1
Câu 51. Cho hàm số f  x 
xác định trên  \  
1 . Đạo hàm của hàm số f  x là x 1 1 2 1  3
A. f  x  .
B. f  x  .
C. f  x  .
D. f  x  .  x  2 1  x  2 1  x  2 1  x  2 1 '  ax  b  d a  bc
Lời giải: nhắc lại công thức đạo hàm nhanh     cx  d  cx  d 2 2x 1 3 f  x 
 f  x  x 1  x  2 1 MTCT CASIO -580VN
và nhân với bình phương mẫu dùng Calc 100 kết quả vậy tử = 3. 2 2x  2x  3
Câu 52. Tính đạo hàm của hàm số y  . 2 x  x  3 3 6x  3 3 x  3 A. 2  . B. . C. . D. . 2 x  x  3  2
x  x  32 2
x  x  32 2 x  x  3 Lời giải: 2 2x  2x  3 6x  3 y   y '  2 x  x  3  2
x  x  32 MTCT CASIO -580VN tương tự
kết quả Calc 100 là : 603 suy ra tử = 6x+3
Trường THPT Hai Bà Trưng – Huế Trang 19/81
Câu 53. Cho hàm số f  x  x  x  
1  x  2 x  3  x  4 . Tính f 0 . A. 42 . B. 24 . C. 2  4 . D. 0 . Lời giải:
f  x  f 0 x  x  
1  x  2 x  3 x  4 f 0  lim  lim    1 .2...( 4  )  4!  24 x0 x0 x  0 x dạng này tổng quát
f  x   x  0 x  
1  x  2 x  3 x  4... x  n n
f '0    1 .n! n f '  1    1 1 .n!
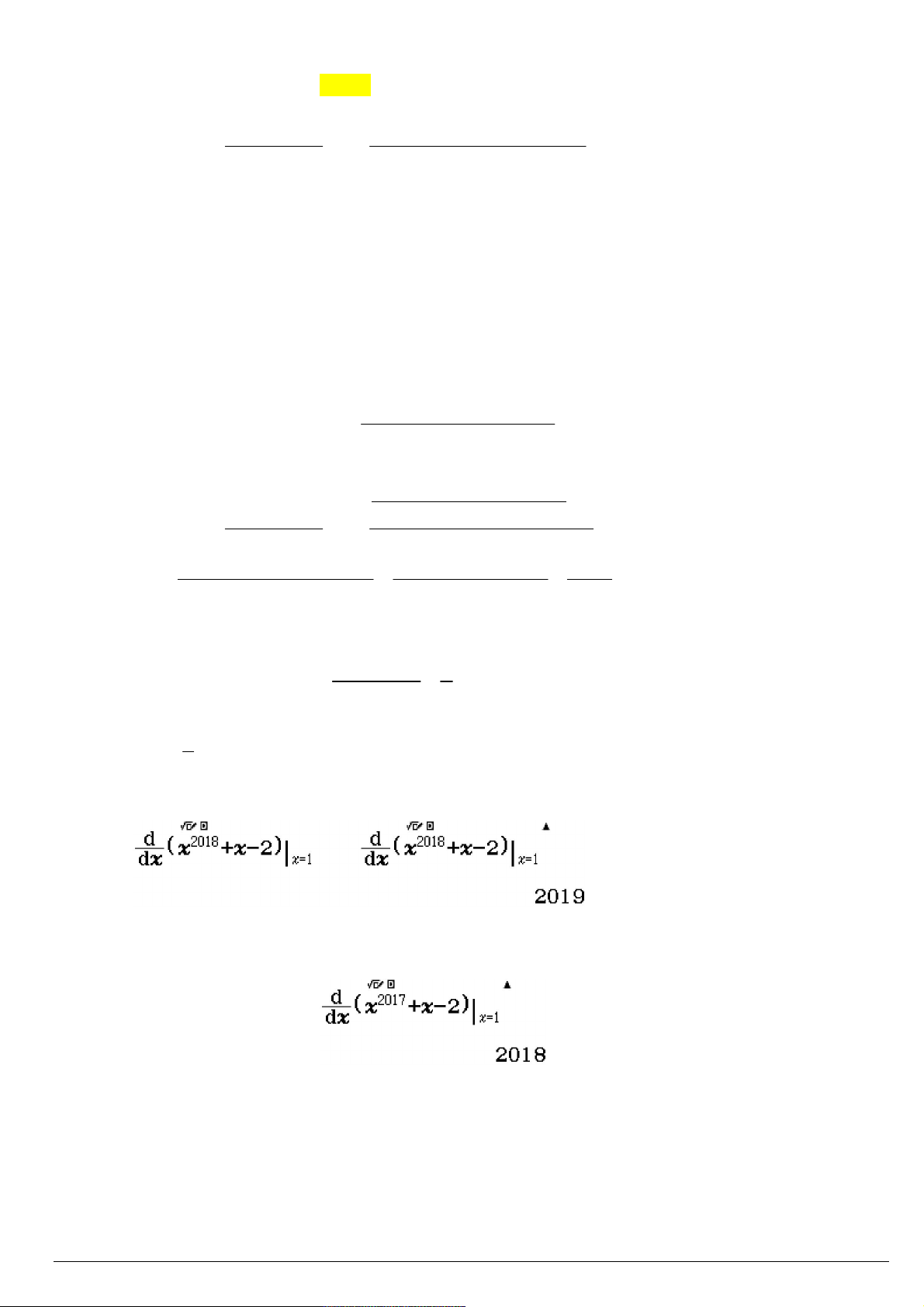
ứng dụng đạo hàm giải 2 câu trong đề Trấn Biên - ĐN x
Câu 38(TB-ĐN) Cho f  x  . Tính f '0 .  x  
1  x  2... x  2018 Lời giải: x  0
f  x  f 0  x  
1  x  2... x  2018 f 0  lim  lim x0 x0 x  0 x  0 1 1 1  lim  
x0  x  
1  x  2... x  2018   1 . 2  ...2018 2018! 2018 x  x  2 a Câu 40(TB-ĐN) Cho lim  . Tính 2 2 a  b 2017 x 1  x  x  2 b 0 Dạng dùng MTCT 580 VN như sau 0 qy[^2018$+[p2$1= a  2019 qy[^2017$+[p2$1= b  2018 Suy ra: 2 2
a  b  4037
Trường THPT Hai Bà Trưng – Huế Trang 20/81 2  2
 2x  3x  5 
ax  bx  c Câu 54. Cho   
. Tính S  a  b  c . x  3    x  32 A. S  0 . B. S  12 . C. S  6  . D. S  18 . Lời giải: tự luận 2  2 2
 2x  3x  5  2x 12x  4
ax  bx  c  
 a  2,b  12, c  4.   x  3    x  32  x  32 MTCT CASIO -580VN
Calc 100 phân tích 1/88/04 thì tử = 2
2x 12x  4  a  2,b  12, c  4
S  a  b  c  2 12  4  18  3 2x    ax  b a Câu 55. Biết    . Tính E  .  4x 1  4x   1 4x 1 b A. E  1  . B. E  4 . C. E  2 . D. E  4 . Lời giải: 4 3  2x 2 4x 1   3  2x   4 2 4x 1 4x   1  4 3  2x 8  x  8       4x 1  4x   1 24x   1 4x 1 2 4x   1 4x 1 4  x  4 ax  b    a  4  , b  4 4x   1 4x 1 4x   1 4x 1 a E   1  b
Câu 56. Tính đạo hàm của hàm số y   x   2 2 x 1 . 2 2x  2x 1 2 2x  2x  1 2 2x  2x  1 2 2x  2x  1 A. y  . B. y  . C. y  . D. y  . 2 x 1 2 x  1 2 x 1 2 x 1 Lời giải: 2 2x  2x  1
y   x   2 2
x 1  y  2 x 1
Câu 57. Hàm số nào sau đây không có đạo hàm trên  ?
A. y  x 1 . B. 2 y 
x  4x  5 .
C. y  sin x . D. y  2  cos x . Lời giải:
các hàm giá trị tuyệt đối không có đạo hàm tại nghiệm của nó.
x 1 khix  1
y  x 1  1 x khix 1 
f '1   1  f '1   1 
Câu 58. Tính đạo hàm của hàm số y   x  x  3 2 1 tại điểm x  1  . A. 27 . B. 27  . C. 81. D. 81  . Lời giải:
y   x  x  2 2 ' 3 1 2x   1 y '  1  81 
Trường THPT Hai Bà Trưng – Huế Trang 21/81 m
Câu 59. Cho hàm số f  x 3 
x  m   2
2 x  x  2 . Để đạo hàm f  x bằng bình phương của một nhị 3
thức bậc nhất thì giá trị m là A. 1  hoặc 1. B. 1 hoặc 4 . C. 4  hoặc 4 .
D. Không có giá trị nào. Lời giải: m f  x 3 
x  m  2 2 x  x  2 3 f  x 2
 mx  2 m  2 x 1
Để đạo hàm f  x bằng bình phương của một nhị thức bậc nhất thì   0 m    m  2 1 4 2  4m  0   m  4 
Câu 60. Tìm tất cả các giá trị của tham số m để hàm số 3
y  x  m   2 3
1 x  2x  m có y '  0, x   . A.  1   2 6; 1   2 6  .B. 1
  2 6;1 2 6  . C.  1
  6; 1 6  . D. 1   6;1 6  .         Lời giải: 3
y  x  m   2 3
1 x  2x  m 2
y '  3x  2 m  
1 x  2  0,x   3     0 a 0  2    
 m  2m  5  0  1 6  m  1 6   0  4  m  2 1  4.3.2  0  1
Câu 61. Cho hàm số f  x 3 2  
x  4x  7x 11. Tập nghiệm của bất phương trình f  x  0 là 3 A. 1;7. B.  
;1 7;  . C.  7  ;   1 . D.  1  ; 7 . Lời giải: 1 f  x 3 2  
x  4x  7x 11 3 f  x 2
 x  8x  7  0  1  x  7
Câu 62. Cho hàm số f  x 2  5
 x 14x  9 . Tập hợp các giá trị của x để f  x  0 là  7   7 9   7   7  A. ;    . B. ;   . C. 1;   . D. ;    .  5   5 5   5   5  Lời giải:  9  f  x 2  5
 x 14x  9, D  1;  5   10x 14 9 7
f  x   0   x  2 5 5 2 5
 x 14x  9
Trường THPT Hai Bà Trưng – Huế Trang 22/81
Câu 63. Biết hàm số f  x  f 2x có đạo hàm bằng 18 tại x  1 và đạo hàm bằng 1000 tại x  2 . Tính đạo
hàm của hàm số f  x  f 4x tại x  1. A. 2018 . B. 1982 . C. 2018  . D. 1018 . Lời giải:
 f  x  f 2x '  f ' x  2 f '2x  
x  1  f ' 
1  2 f '2  18
x  2  f '2  2 f '4  1000  f ' 
1  4 f '4  2018
 f  x  f 4x '  f ' x  4 f '4x   Vậy
x  1  f ' 
1  4 f '4  2018
Câu 64. Cho hàm số f  x  x  2 và g  x 2
 x  2x  3 . Đạo hàm của hàm số y  g  f  x tại x 1 bằng A. 4 . B. 1. C. 3 . D. 2 . Lời giải:
cách 1: y '  g  f  x '  f ' x.g ' f  x    f   1  3
f  x  x  2  
 f ' x  1  f '  1  1  g  x 2
 x  2x  3  g ' x  2x  2 g '3  4
Đạo hàm của hàm số y  g  f  x tại x 1 ta có f ' 
1 .g ' f   1   f ' 
1 .g '3  1.4  4 cách 2:
y  g  f  x 2
 f  x  2 f  x  3
  x  22  2 x  2 2
 3  x  2x  3 y '  2x  2 y '  1  4
Câu 65. Cho hàm số y  f  x có đạo hàm với mọi x   và thỏa f 2x  4 cos .
x f  x  2x . Tính f 0 .  A. 1. B. . C. 2 . D. 0 . 2 Lời giải:
 f 2x '  4 cos .
x f  x  2x '    
 2 f '2x  4
 sin xf  x  4 cos .
x f ' x  2
x  0  2 f '0  0  4 f '0  2  f '0  1
Trường THPT Hai Bà Trưng – Huế Trang 23/81 3  4x
Câu 66. Hệ số góc tiếp tuyến của đồ thị hàm số y 
tại điểm có tung độ y  1  là x  2 9 5 5 A. 10  . B. . C.  . D. . 5 9 9 Lời giải: 3  4x 1 y   1   x  x  2 3  3  4x  5 y '  '     x  2   x  22  1  5 9
Hệ số góc tiếp tuyến là y '     2  3   1 5   2    3  x 1
Câu 67. Cho đường cong C  có phương trình y 
. Gọi M là giao điểm của C  với trục tung. Tiếp x  1
tuyến của C  tại M có phương trình là
A. y  2x 1 .
B. y  2x 1.
C. y  2x 1.
D. y  x  2 . Lời giải: x 1
M là giao điểm của C  y 
với trục tung nên x  0, y  1  x  1 M M 2 y ' 
 y ' 0  2 . Tiếp tuyến của C  tại M có phương trình là y  2x 1 2    x   1
Câu 68. Phương trình các tiếp tuyến của đồ thị hàm số 4 2
y  x  3x 1 tại các điểm có tung độ bằng 5 là
A. y  20x  35 . B. y  20 
x  35 và y  20x  35 .
C. y  20x  35 và y  20  x  35 . D. y  20  x  35 . Lời giải: 4 2 4 2
y  x  3x 1  5  x  3x  4  0  x  2 3
y '  4x  6x
Phương trình các tiếp tuyến là y  20x  35 và y  20  x  35 . Câu 69. Cho hàm số 4 2
y  x  6x  3. Tiếp tuyến của đồ thị hàm số tại điểm A có hoành độ x  1 cắt đồ thị
hàm số tại điểm B ( B khác A ). Tọa độ điểm B là A. B  3  ; 24 . B. B  1  ; 8 . C. B 3;24 . D. B 0; 3   . Lời giải: 4 2
y  x  6x  3 3
y '  4x 12x
Tiếp tuyến của đồ thị hàm số tại điểm A có hoành độ x  1 là y  y '  1  x   1  y   1  8   x   1   8    8  x
phương trình hoành độ giao điểm 4 2 4 2 8
 x  x  6x  3  x  6x  8x  3  0 MTCT CASIO -580VN chọn 4 nhập hệ số ta có
Tọa độ điểm B là B  3  ; 24
Trường THPT Hai Bà Trưng – Huế Trang 24/81
Câu 70. Cho hàm số y  cos x  m sin 2x C  ( m là tham số). Tìm tất cả các giá trị m để tiếp tuyến của C  
tại điểm có hoành độ x   , x 
song song hoặc trùng nhau. 3 3 2 3 A. m   . B. m   . C. m  3 . D. m  2 3 . 6 3 Lời giải:
y '  cos x  msin 2x  '  s  inx  2 . m s co 2x 
Để tiếp tuyến của C  tại điểm có hoành độ x   , x 
song song hoặc trùng nhau thì 3    3  1  3
y '   y '  2m    2 . m  m        3  2  2  6
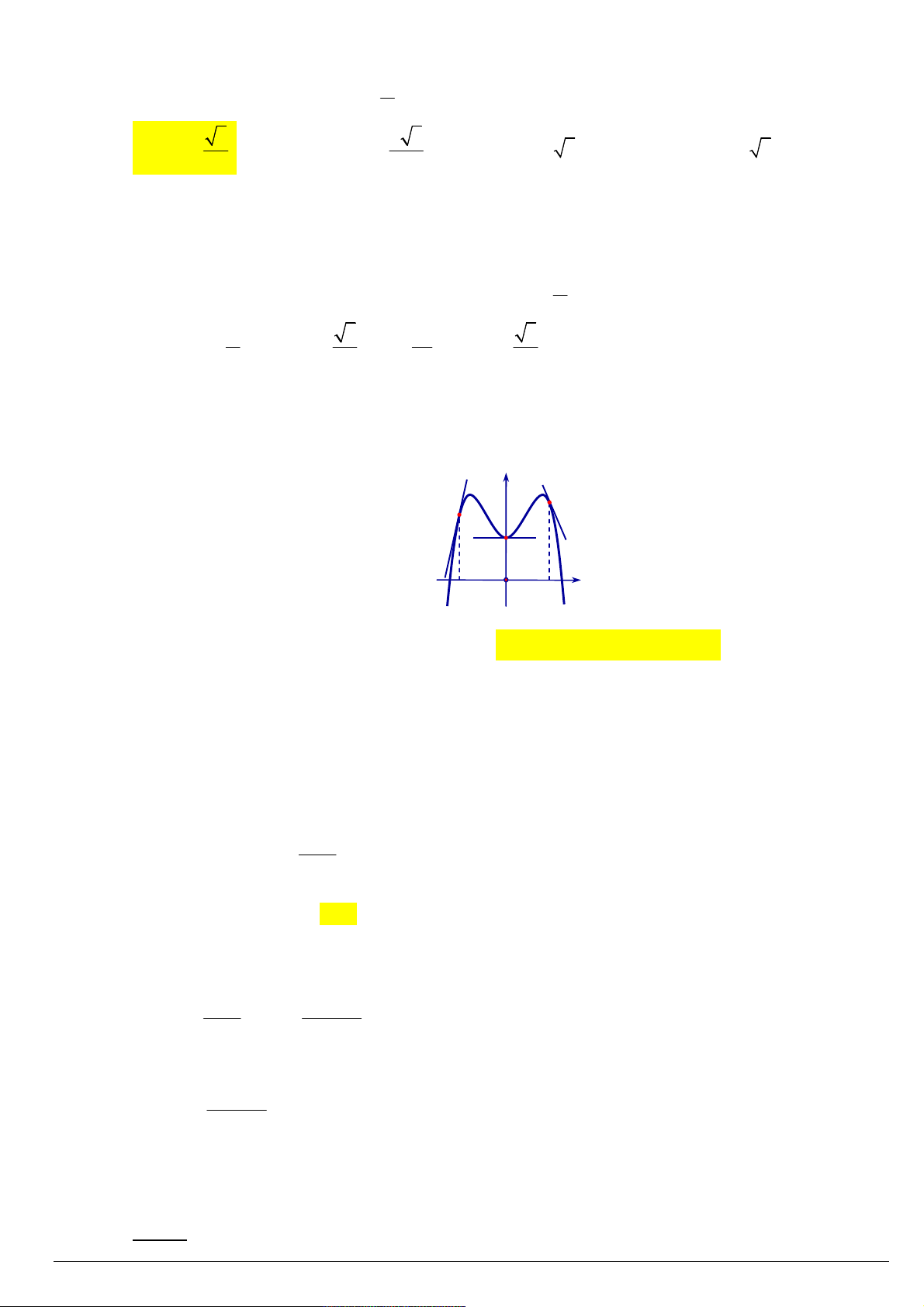
Câu 71. Hình bên là đồ thị của hàm số y  f  x . Biết rằng tại các điểm A , B , C đồ thị hàm số có tiếp
tuyến được thể hiện trên hình vẽ bên dưới. y B C A x x x C O x A B
Mệnh đề nào dưới đây đúng? A. f  x  f  x  f  x . B. f  x  f  x  f  x . B   A   C  C   A   B  C. f  x  f  x  f  x . D. f  x  f  x  f  x . A   B   C  A   C   B  Lời giải:
Hệ số góc của tiếp tuyến dương khi đường thẳng đi qua góc phân tư thứ nhât và thứ ba.
Hệ số góc của tiếp tuyến âm khi đường thẳng đi qua góc phân tư thứ hai và thứ tư.
Từ đồ thị đề cho ta có f  x   0  f  x  f  x B  A   C  x 1
Câu 72. Trên đồ thị C  : y 
có bao nhiêu điểm M mà tiếp tuyến với C  tại M song song với x  2
đường thẳng d : x  y  1 . A. 0 . B. 1. C. 2 . D. 4 . Lời giải:
d : x  y  1  y  x 1 x 1 1 C : y   y '   0,x  2 x  2  x  22
tiếp tuyến với C  tại M song song với đường thẳng d : x  y  1 thì 1   x  1 y '  1    x  2  1  2  2   x  2 x  3 
khi x  1  y  0 tiếp tuyến là y  x 1  d (loại)
khi x  3  y  2 tiếp tuyến là y    x  3  2  x  5 / /d (thỏa)
Lưu ý: cẩm thận khi gặp loại này vì chủ quan nghĩ rằng có 2 nghiệm sẽ có 2 tiếp tuyến //d.
Trường THPT Hai Bà Trưng – Huế Trang 25/81 x  2
Câu 73. Tìm phương trình tiếp tuyến của đồ thị hàm số y 
, biết tiếp tuyến vuông góc với đường thẳng x 1 1 y 
x  5 và tiếp điểm có hoành độ dương. 3 A. y  3  x 10 . B. y  3  x  2 . C. y  3  x  6 . D. y  3  x  2 . Lời giải: 3 y '   x  2 1 1 3 1  x  0
tiếp tuyến vuông góc với đường thẳng y  x  5 .  1  x 1  1  2  2  3  x   1 3 x  2 
do tiếp điểm có hoành độ dương nên x  2
Vậy phương trình tiếp tuyến là y  3  x 10
Câu 74. Phương trình tiếp tuyến với đồ thị C  3 2
: y  2x  6x  3 có hệ số góc nhỏ nhất là
A. 6x  y  5  0 .
B. 6x  y  5  0 .
C. 6x  y  3  0 .
D. 6x  y  7  0 . Lời giải: y  x 
x   x  2 2 ' 6 12 6 1  6  6
Vậy hệ số góc nhỏ nhất bằng -6 khi x = 1. Suy ra phương trình tiếp tuyến là 6x  y  5  0 .
Câu 75. Có tất cả bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y  x  3x  2x đi qua điểm A 1;0 ? A. 1. B. 2 . C. 3 . D. 4 . Lời giải:
Gọi d : y  k  x  
1 đi qua A 1;0 . d tiếp xúc C  3 2
: y  x  3x  2x khi k   x   3 2
1  x  3x  2x   2
3x  6x  2 x   3 2
1  x  3x  2x   1    2 2
k  3x  6x  2 
k  3x  6x  2 
số nghiệm (1) là số tiếp tuyến nên MTCT CASIO -580VN nhập
ta thấy có 3 nghiệm, suya ra có 3 tiếp tuyến đi qua A. x 1
Câu 76. Gọi d là tiếp tuyến của hàm số y 
tại điểm có hoành độ bằng 3
 . Khi đó d tạo với hai trục x  2
tọa độ một tam giác có diện tích là 169 121 25 49 A. S  . B. S  . C. S  . D. S  . 6 6 6 6 Lời giải: x 1
d là tiếp tuyến của hàm số y 
tại điểm có hoành độ bằng 3  có phương trình là: x  2
y  3 x  3  4  3x 13  13  
d cắt hai trục tọa độ tại A0;13 , B ; 0   .  3  1 169
Tam giác OAB có diện tích là S  . . OA OB  2 6
Trường THPT Hai Bà Trưng – Huế Trang 26/81 x  b
Câu 77. Cho hàm số y  ab  2
  . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị ax  2
hàm số tại điểm A 1;  2 song song với đường thẳng d : 3x  y  4  0 . Tính a  3b . A. 2  . B. 4 . C. 1  . D. 5 . Lời giải:
d : 3x  y  4  0  y  3  x  4 2   ab y '  ax  22
Tiếp tuyến của đồ thị hàm số tại điểm A 1;  2 song song với đường thẳng d : 3x  y  4  0 nên  1 b AC    2   2  a  2 b   2  a  3  5
 a 15a 10  0     2 ab    2   a      2
 a  3  3a  2 3 2 b  2  a  3   a  22 
a  2 l 
 a 1,b 1 
Vậy a  3b  2.  x  2
Câu 78. Phương trình tiếp tuyến của đồ thị hàm số y 
biết tiếp tuyến đó cắt trục tung và cắt trục 2x  3
hoành tại hai điểm phân biệt A , B sao cho tam giác OAB cân là
A. y  x  2 .
B. y  x  2 .
C. y  x  2 .
D. y  x  2 . Lời giải: Bình luận:
Tiếp tuyến đó cắt trục tung và cắt trục hoành tại hai điểm phân biệt A , B sao cho tam giác OAB
cân là khi có hệ số góc bằng 1 hoặc -1. 1   x  1  y '   1   2x  3  1  2  2  2x  3 x  2  
Khi x  1, y  1 phương trình tiếp tuyến là y  1   x  
1 1  x (loại vì đi qua O).
Khi x  2, y  0 phương trình tiếp tuyến là y  1 x  2  x  2 (thỏa)
Câu 79. Cho hàm số y  f  x có đạo hàm liên tục trên  , thỏa mãn f  x  f   x 2 2 2 1 2  12x . Phương
trình tiếp tuyến của đồ thị hàm số y  f  x tại điểm có hoành độ bằng 1 là
A. y  2x  2 .
B. y  4x  6 .
C. y  2x  6 .
D. y  4x  2 . Lời giải:
f  x  f   x 2 2 2 1 2  12x
x  0  2 f 0  f   1  0  f   0  1   1   x   2 f    1  f 0  3 f    1  2   2
Đạo hàm 2 vế ta có 4 f '2x  2 f '1 2x  24x
x  0  4 f '0  2 f '  1  0  f '   0  2  1   x   4 f '   
1  2 f '0  12 f '    1  4   2
Phương trình tiếp tuyến của đồ thị hàm số y  f  x tại điểm có hoành độ bằng 1 là y  f '  1  x   1  f   1  4  x   1  2  4x  2
Trường THPT Hai Bà Trưng – Huế Trang 27/81 1
Câu 80. Một vật rơi tự do với phương trình chuyển động là 2 S 
gt , trong đó t tính bằng giây (s), S tính 2
bằng mét m và g  9,8 2
m / s . Vận tốc của vật tại thời điểm t  4s là? A. v  9,8 m / s B. v  78, 4 m / s C. v  39, 2 m / s D. v = 19, 6 m / s Lời giải: v  S ' nhắc lại
a  v '  S ' 1 2 S 
gt  v  gt 2
t  4  v  9,8.4  39, 2 m / s 1
Câu 81. Một chất điểm chuyển động theo quy luật 3 2
S   t  4t  9t với t (giây) là khoảng thời gian tính từ 3
lúc bắt đầu chuyển động và S (mét) là quãng đường vật chuyển động trong thời gian đó. Hỏi trong
khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của chất điểm là A. 88m/s. B. 25m/s. C. 100 m/s. D. 11m/s. Lời giải: 1 3 2
S   t  4t  9t 3 2
v  S '  t   8t  9 0  t  10  b t    v  t   t    a ma  4 2 8 9 2 x max v  25  x ma
* MTCT CASIO -580VN sử dụng chức năng Mode 9 bấm = liên tiếp ta có
Câu 82. Tính đạo hàm của hàm số f  x 2
 sin 2x  cos 3x .
A. 2sin 4x  3sin 3x .
B. 2sin 4x  3sin 3x . C. sin 4x  3sin 3x .
D. 2sin 2x  3sin 3x Lời giải:
f  x   2 '
sin 2x  cos 3x'  4sin2x cos 2x  3sin 3x  2sin 4x  3sin 3x cos 4x
Câu 83. Tính đạo hàm của hàm số y   3sin 4x . 2 1
A. 12 cos 4x  2 sin 4x . B. 12 cos 4x  2 sin 4x .C. 12 
cos 4x  2 sin 4x . D. 3cos 4x  sin 4x . 2 Lời giải:  cos 4x  y ' 
 3sin 4x '  12 cos 4x  2 sin 4x    2 
Trường THPT Hai Bà Trưng – Huế Trang 28/81   
Câu 84. Tính đạo hàm của hàm số y  tan  x   .  4  1 1 1 1 A. y   . B. y  . C. y  . D. y   .         2     cos  x 2 2 2   cos  x   sin  x   sin  x    4   4   4   4  Lời giải:    1 y  tan  x    y    4    2  cos  x    4 
Câu 85. Tính đạo hàm của hàm số y  cos 2x . sin 2x sin 2x sin 2x  sin 2x A. y  . B. y  . C. y  . D. y  . 2 cos 2x cos 2x cos 2x 2 cos 2x sin 2x Lời giải: y 
cos 2x  y  cos 2x sin x
Câu 86. Tính đạo hàm của hàm số sau y  . sin x  cos x 1  1 1  1 A. y  . B. y  .C. y  .D. y  .
sin x  cos x2
sin x  cos x2
sin x  cos x2
sin x  cos x2 Lời giải: sin x 1  y   y  sin x  cos x
sin x  cos x2
Câu 87. Tính đạo hàm của hàm số 6 6 2 2
y  sin x  cos x  3sin x cos x . A. 1 . B. 0 . C. 2 . D. 3 . Lời giải: y  x  x  x x  x  x   x  x3 6 6 2 2 2 2 2 2 sin cos 3sin cos sin cos sin cos  1 y '  0
Câu 88. Đạo hàm của hàm số 2
y  2  cos 2x bằng  sin 2x  sin 4x cos 2x  sin 4x A. y  . B. y  . C. y  . D. y  . 2 2  cos 2x 2 2 2  cos 2x 2 2  cos 2x 2 2  cos 2x Lời giải:  sin 4x 2
y  2  cos 2x  y  2 2  cos 2x
Câu 89. Đạo hàm của hàm số y  x sin x là
A. y  sin x  x cos x . B. y  sin x  x cos x . C. y  x cos x .
D. y  x cos x . Lời giải:
y  x sin x  y  sin x  x cos x Câu 90. Cho hàm số 2
y  sin x . Tìm hệ thức liên hệ giữa y và y không phụ thuộc vào x . 2 2 A.  y2 2 4  y  4 . B.  y2 2 2  4 y  1 .
C.  y  1 2y  1 .D.  y2 2  4 y  4 . Lời giải: y   2 '
sin x'  2.si . nx s
co x  sin2x
 y2  sin2x2
do sin2x2  cos2x2  1 2
  y2  1 2 y2  sin2x2  1 2sin x  sin2x2  cos2x2 2  1
Trường THPT Hai Bà Trưng – Huế Trang 29/81
Câu 91. Vi phân của hàm số f  x 2
 3x  x tại điểm x  2 ứng với x   0,1 là A. 0  , 07 . B. 10 . C. 1,1 . D. 0  , 4 . Lời giải: y   6x   1 x 
x  2, x  0,1  y  6.2   1 .0,1  1,1 Câu 92. Cho hàm số 3 2
y  x  9x 12x  5 . Vi phân của hàm số là A. y   2 d
3x 18x 12dx . B. y   2 d 3
 x 18x 12dx . C. y    2 d
3x 18x 12dx . D. y   2 d
3x 18x 12dx . Lời giải: 3 2
y  x  9x 12x  5
có vi phân y   2 d
3x 18x 12dx x
Câu 93. Hàm số y  có vi phân là 2 x 1 2 1 x 1 2 1 x 2x A. dy  dx . B. dy  dx . C. dy  dx . D. dy  dx .  2 2 x  2 2 1 x  2 2 1 x 1 x 1 Lời giải: x 2 1 x y 
có vi phân là dy  dx 2 x 1 x  2 2 1
Câu 94. Hàm số y  tan x  cot x có vi phân là 1 4 4 1 A. dy  dx . B. dy  dx . C. dy  dx . D. dy  dx . 2 cos 2x 2 sin 2x 2 cos 2x 2 sin 2x Lời giải: 4
y  tan x  cot x có vi phân là dy  dx 2 sin 2x
Câu 95. Vi phân của hàm số 2
y  sin 2  x là 2x  2 x A. 2 dy 
cos 2  x .dx . B. 2 dy  
cos 2  x .dx . 2 2  x 2 2  x x (x 1) C. 2 dy  cos 2  x d . x . D. 2 dy 
cos 2  x .dx . 2 2  x 2 2  x Lời giải: x Vi phân của hàm số 2
y  sin 2  x là 2 dy  cos 2  x d . x 2 2  x x Câu 96. Hàm số 2 y  tan có vi phân là 2 x x x sin 2sin sin  x  A. 2 dy  dx . B. 2 dy  dx . C. 2 dy  dx . D. 3 dy  tan dx   . 3 x x x  2 cos 3 cos 3 2 cos  2 2 2 x sin x Lời giải: Hàm số 2 y  tan có vi phân là 2 dy  dx 2 3 x cos 2
Trường THPT Hai Bà Trưng – Huế Trang 30/81
Câu 97. Hàm số y  cot 2x có vi phân là 2 2 2 1 cot 2x  1 cot 2x 2 1 tan 2x  1 tan 2x A. dy  dx . B. dy  dx .C. dy  dx .D. dy  dx . cot 2x cot 2x cot 2x cot 2x Lời giải:   2 1 cot 2x
Hàm số y  cot 2x có vi phân là dy  dx cot 2x
Câu 98. Hàm số y  x sin x  cos x có vi phân là
A. dy   x cos x – sin x dx .
B. dy   x cos x dx .
C. dy  cos x – sin x dx .
D. dy   x sin x dx . Lời giải:
Hàm số y  x sin x  cos x có vi phân là dy   x cos x dx Câu 99. Cho hàm số 2
y  x  x 1 . Mệnh đề nào sau đây đúng? A. 2 1 x dy  d y x  0 . B. 2
1 x dx  dy  0 . C. 2 d
x x  1 x dy  0 . D. 2 1 x dy  d y x  0 . Lời giải:  x   2 x  x 1 y dy  1 dx  .dx  dx   2 2 2  x 1  x  1 x 1 2 2  x 1.dy  . y dx  x 1.dy  . y dx  0.
Câu 100. Tính đạo hàm cấp hai của hàm số f  x 3 2
 x  x 1 tại điểm x  2 .
A. f  2  14 .
B. f  2  10 .
C. f  2  28 .
D. f  2  1. Lời giải: f  x 2 '  3x  2x
f '  x  6x  2
f ' 2  6.2  2  10.
Câu 101. Đạo hàm cấp hai của hàm số y  f  x  x sin x  3 là biểu thức nào trong các biểu thức sau?
A. 2 cos x  x sin x . B. x sin x .
C. sin x  x cos x . D. 1 cos x . Lời giải:
y '   x sin x  3 '  sinx  . x cosx
y '  2 cos x  x sin x
Câu 102. Một chất điểm chuyển động có phương trình 4 2
S  2t  6t  3t 1 với t tính bằng giây (s) và S tính
bằng mét (m). Hỏi gia tốc của chuyển động tại thời điểm t  3(s) bằng bao nhiêu? A. 64  2 m/s  . B. 228  2 m/s  . C. 88  2 m/s  . D. 76  2 m/s  . Lời giải: 4 2
S  2t  6t  3t 1 3
v  S '  8t 12t  3 2
a  v '  S '  24t 12
t  3  a  228 2 m / s 
Trường THPT Hai Bà Trưng – Huế Trang 31/81 1
Câu 103. Một chất điểm chuyển động trong 20 giây đầu tiên có phương trình s t  4 3 2 
t  t  6t 10t , 12
trong đó t  0 với t tính bằng giây  s và s t  tính bằng mét m . Hỏi tại thời điểm gia tốc của vật
đạt giá trị nhỏ nhất thì vận tốc của vật bằng bao nhiêu? A. 17 m/s . B. 18m/s . C. 28m/s . D. 13m/s . Lời giải: 1 s t  4 3 2 
t  t  6t 10t 12 1 3 2 v  s ' 
t  3t 12t 10 3
a  v '  t  6t 12  t  32 2  3  3 a
 3  t  3  v  28 m / s min  
Câu 104. Cho chuyển động thẳng xác định bởi phương trình 3 2 S  t
  3t  9t , trong đó t tính bằng giây và S
tính bằng mét. Tính vận tốc của chuyển động tại thời điểm gia tốc triệt tiêu. A. 12 m/ s . B. 0 m/ s . C. 11m/ s . D. 6 m/ s . Lời giải: 3 2 S  t
  3t  9t 2 v  S '  3
 t  6t  9 a  v '  6  t  6
Khi gia tốc triệt tiêu a  0  t  1  v  12m / s Câu 105. Cho hàm số 2
y  2x  x . Mệnh đề nào sau đây là đúng ? A. 3
y .y  1  0 . B. 2
y .y  1  0 . C. 2
3y .y  1  0. . D. 3
2 y .y  3  0. Lời giải: 1 x y '  2 2x  x 1 x 2  2x  x  1 x 2x  x
 2x  x   1 x2 2 2 1  y '    2 2x  x  2 2x  x  2 2x  x  2 2x  x  2 2x  x 1  3 y ' 
 y .y ' 1  0 3 y
Câu 106. Cho hàm số y  sin 2x . Khẳng định nào sau đây là đúng?
A. y   y2 2  4 .
B. 4 y  y  0 .
C. 4 y  y  0 .
D. y  y . tan 2x . Lời giải: y '  2 s2 co x y '  4.  sin2x  4  y
y '  4 y  0
Trường THPT Hai Bà Trưng – Huế Trang 32/81
Câu 107. Cho hàm số y  .
x cos x . Chọn khẳng định đúng?
A. 2cos x  y  x  y  y  1.
B. 2cos x  y  x  y  y  0 .
C. 2cos x  y  x  y  y  1.
D. 2cos x  y  x  y  y  0 . Lời giải: y '  s co x  . x sinx y '  2  sinx  . x s co x  2  sinx  y
y '  y  2sinx
 2 cos x  y  x  y  y  0 2x  1
Câu 108. Cho hàm số y  f  x 
. Phương trình f  x  f   x  0 có nghiệm là 1 x 3 1 1 A. x  3 . B. x   . C. x   . D. x  . 2 2 2 Lời giải: 3
f ' x  1 x2 6
f '  x  1 x3 3 6 
f ' x  f '  x  0   1 x2 1 x3 1 x  2   x  3
Câu 109. Tính y , biết 2
y  x 1  x . x  2 3  2x  2x  2 3  2x  x  2 3  2x  x  2 1 x  A. y  . B. y  . C. y  . D. y  .  2 1 x  2 1 x  2 3 1 x 3 2  2 1 x  2  2 1 x  Lời giải: 2
y  x 1  x x  2 3  2x  y   2 1 x  2 1 x 1
Câu 110. Đạo hàm cấp n của hàm số y  , a  0 là ax  b n n n 2 . n n a .n! 1  . n a .n! 1  .n! 1  . n a .n! (n)   (n)   (n)   A. (n) y  . B. y  . C. y  . D. y  . n 1 (ax  b)  n 1 (x 1)  n 1 (ax  b)  n 1 (ax  b)  Lời giải: 1
y  ax  b 1.  .1 a !
y '  axb2  2 2 1 .a .2! y '  ax  b3 .... n 1  . n a .n! (n)   y  n 1 (ax  b) 
Trường THPT Hai Bà Trưng – Huế Trang 33/81
. CHỦ ĐỀ 3. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC 
Câu 111. Cho tứ diện ABCD . Hỏi có bao nhiêu vectơ khác vectơ 0 mà mỗi vectơ có điểm đầu, điểm cuối là
hai đỉnh của tứ diện ABCD ? A. 12 . B. 4 . C. 10 . D. 8 . Lời giải: 
Số vectơ khác vectơ 0 mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD là số
các chỉnh hợp chập 2 của phần tử  số vectơ là 2 A  12 . 4
Câu 112. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của các cạnh AD, BC và G là trung điểm
của MN . Mệnh đề nào sau đây đúng?  1  
    A. NM 
 AB  DC.
B. AB  AC  AD  3AG . 2
   
   
C. AB  AC  AD  0 .
D. AB  AC  AD  4. G A . Lời giải:
Gọi M , N lần lượt là trung điểm của các cạnh AD, BC và G là trung điểm của MN nên G là
trọng tâm của tứ diện ABCD do đó:
   
AB  AM  MN  NB    1   + 
    MN   AB  DC A sai 2
DC  DM  MN  NC 
    
      1   
+ GA  GB  GC  GD  0  4GA  AB  AC  AD  0  AG 
AB  AC  AD B,C sai 4
   
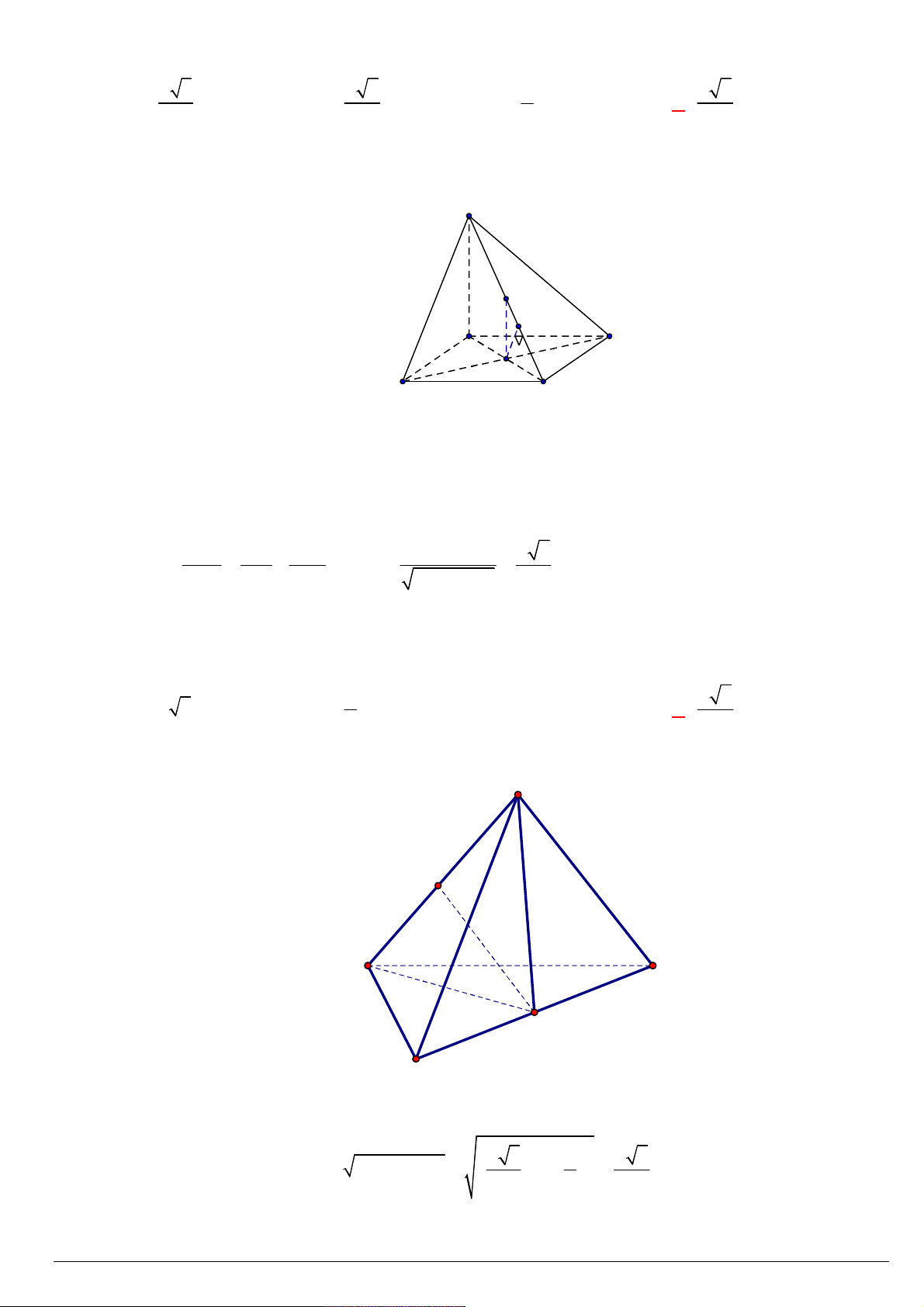
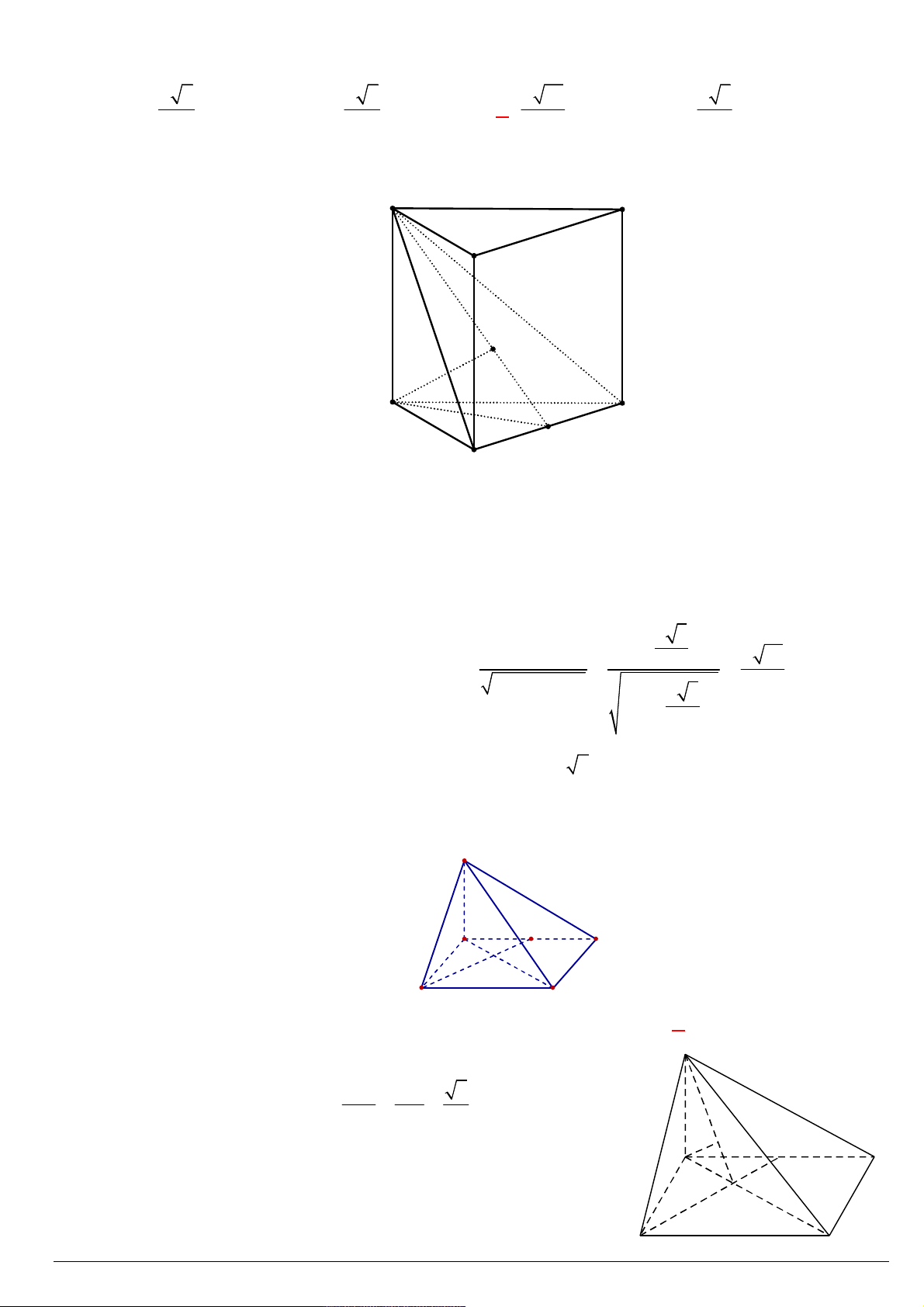
Câu 113. Cho hình lăng trụ ABC.AB C
  với G là trọng tâm của tam giác AB C
 . Đặt AA  a , AB  b ,   
AC  c . Khi đó AG bằng  1    1    1    1  
A. a  b  c. B. a  b  c. C. a  b  c. D. a  b  c. 3 4 6 2 Lời giải: A C B A' C' G I B'
 1  
G là trọng tâm của tam giác AB C
   A'G   A B
   AC 3
    1     
AG  AA  A G  AA   A B
   AC 1 ' ' '
 a  b  c. 3 3
Trường THPT Hai Bà Trưng – Huế Trang 34/81  
Câu 114. Cho tứ diện đều ABCD . Tích vô hướng A . B CD bằng 2 a 2 a A. 2 a . B. . C. 0 . D.  . 2 2 Lời giải: D A C B
Cho tứ diện đều ABCD có 4 mặt là 4 tam giác đều.
       
   .
AB CD   AC  CBCD  AC.CD  . CB CD  C  . A CD  C . B CD   0 0  C  . A CD. s co 60  . CB CD. s
co 60  0  AB  CD  
   
Câu 115. Cho tứ diện ABCD và các điểm M , N xác định bởi AM  2 AB  3AC ; DN  DB  xDC . Tìm x
  
để các véctơ AD , BC , MN đồng phẳng. A. x  1  . B. x  3  . C. x  2  . D. x  2 . Lời giải:   
Phân tích hướng giải: Khi gặp loại này chúng ta vẽ hình AM  2 AB  3AC    
  
Đặt 2AB  AE, 3
 AC  AF  AM  AE  AF
M là đỉnh thứ 4 của hình bình hành AEMF.   
   
DN  DB  xDC  xDC  DN  DB  BN  BN / / DC Giải như sau:
        
Ta có MN  MA  AD  DN  3AC  2AB  AD  DB  xDC .       
 3AD  3DC  2AD  2DB  AD  DB  xDC   
   
 2AD  DB   x  3 DC  2AD  BC  CD   x  3 DC   
 2AD  BC   x  2 DC .
  
Ba véc tơ AD , BC , MN đồng phẳng khi và chỉ khi x  2  0  x  2  .
Câu 116. Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì vuông góc với đường thẳng còn lại.
B. Hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau
C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
D. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau. Lời giải:
Dựa vào định nghĩa hai đường thẳng vuông góc trong không gian ta suy ra đáp án C đúng.
Trường THPT Hai Bà Trưng – Huế Trang 35/81  
Câu 117. Cho hình lập phương A .
BCD EFGH . Góc giữa cặp vectơ AF và EG bằng A. o 0 . B. o 60 . C. o 90 . D. o 30 . Lời giải: B C A D F G E H      
Nhận xét EG  AC nên  AF EG   AF AC   ; ;  FAC .
Tam giác FAC là tam giác đều nên  o FAC  60 .
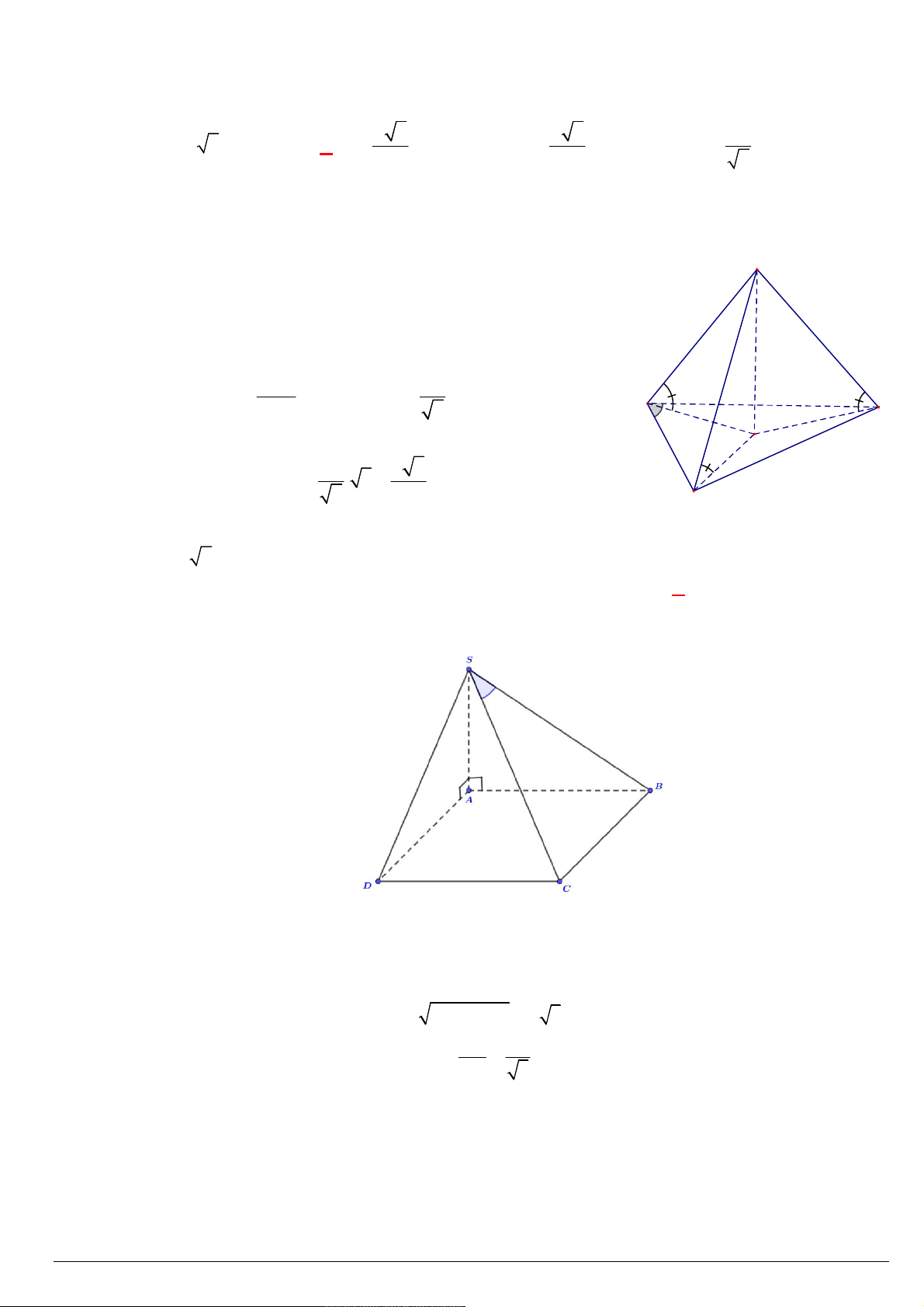
Câu 118. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, SA  SB  2a , AB  a . Gọi  là góc  
giữa hai véc tơ CD và AS . Tính cos ? 7 1 7 1 A. cos   . B. cos   . C. cos  . D. cos  . 8 4 8 4 Lời giải:     Ta có    2 2 SB AS AB 2 2 2
 SB  AS  2 AS.AB  AB       2 2 2
SB  SA  AB 2 a
 AS.CD  AS.BA  AS.AB    . 2 2   2 a    C . D AS 1
Vậy cos  cos CD, AS   2   . C . D AS . a 2a 4
Trường THPT Hai Bà Trưng – Huế Trang 36/81
Câu 119. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  2a , BC  a . Các cạnh bên của
hình chóp cùng bằng a 2 . Tính góc giữa hai đường thẳng AB và SC . A. 45 . B. 30 . C. 60 . D. arctan 2 . Lời giải: S A D M B C
Ta có AB//CD nên  AB SC   CD SC  ; ;  SCD .
Gọi M là trung điểm của CD . Tam giác SCM vuông tại M và có SC  a 2 , CM  a nên là tam
giác vuông cân tại M nên 
SCD  45 . Vậy   ; AB SC   45 .
Câu 120. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos  AB, DM  bằng 3 2 3 1 A. . B. . C. . D. . 6 2 2 2 Lời giải: A B D M C a 3
Giả sử tứ diện đều ABCD có cạnh bằng a ta có: DM  . 2  
      AB DM A . B DB  . AB BM . a . a cos 60  . a . a cos120 3 Ta lại có: AB DM  . cos ,
      . AB . DM a 3 a 3 6 . a . a 2 2 3
Vậy cos  AB, DM   . 6 Cách 2: dùng bí kíp góc 2 a 3 2 2 2 2 2  a
AD  BM  AM  BD 4 4 3
cos  AB, DM     2.A . B DM 3 6 2. . a a 2
hehe - quá lợi hại phải không
Trường THPT Hai Bà Trưng – Huế Trang 37/81 Tương tự câu 120.
Cho tứ diện ABCD biết AB  BC  CA  4 , AD  5 , CD  6 , BD  7 . Góc giữa hai đường thẳng AB và CD bằng? A. 120 . B. 60 . C. 150 . D. 30 . Hướng dẫn giải Chọn B A B D C  
  
Khi đó AB CD  CB  CA   . .CD  C . B .
CD cos BCD  C . A C . D cos ACD 2 2 2 2 2 2
CB  CD  BD
CA  CD  AD 2 2 2 2
CB  AD  BD  CA  C . B . CD  C . A . CD   12  2. . CB CD 2. . CA CD 2   A . B CD 12 1 Suy ra 
cos  AB,CD   
  AB,CD  60 . A . B CD 4.6 2
hoặc dùng bí kíp ra liền
Trường THPT Hai Bà Trưng – Huế Trang 38/81
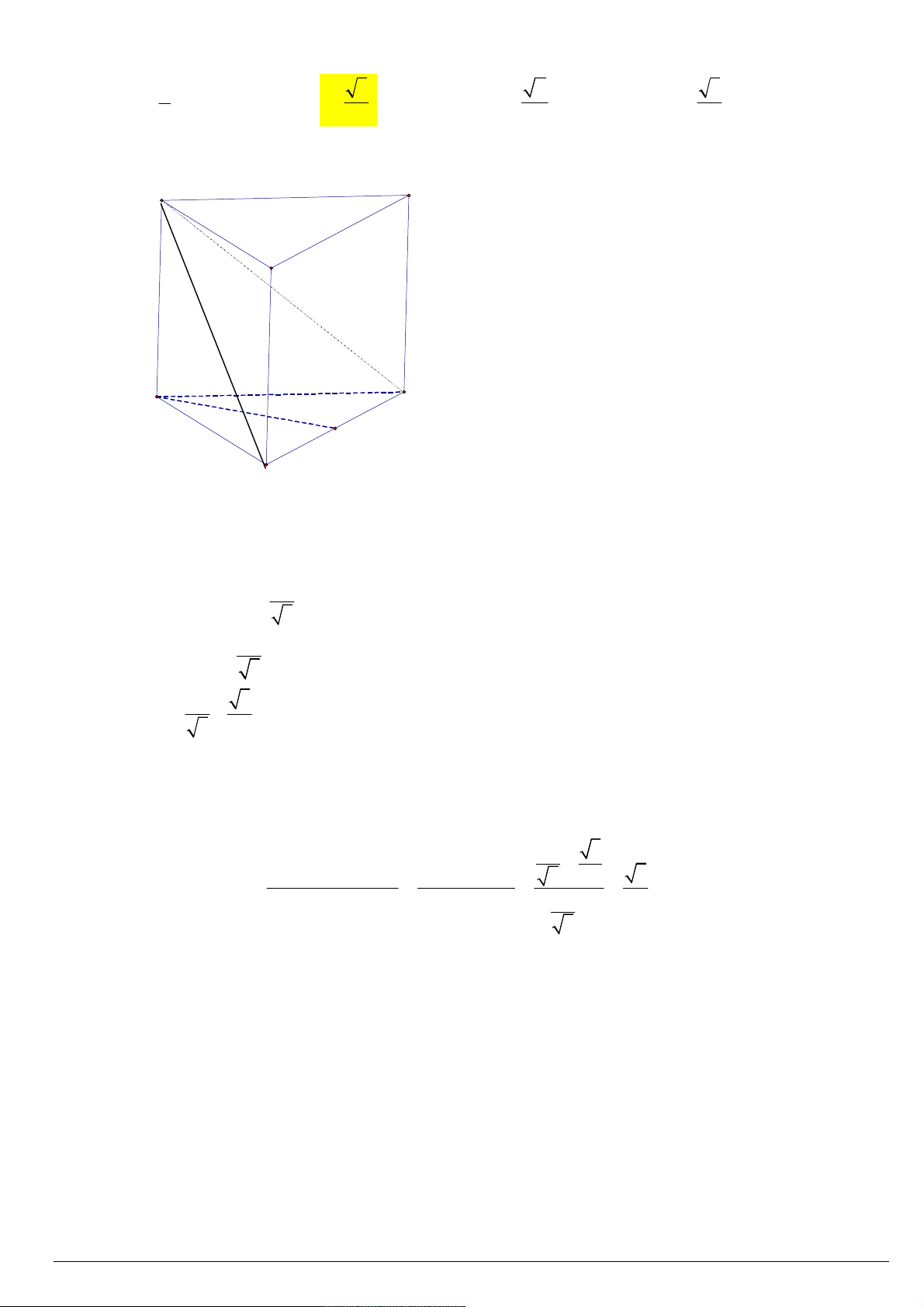
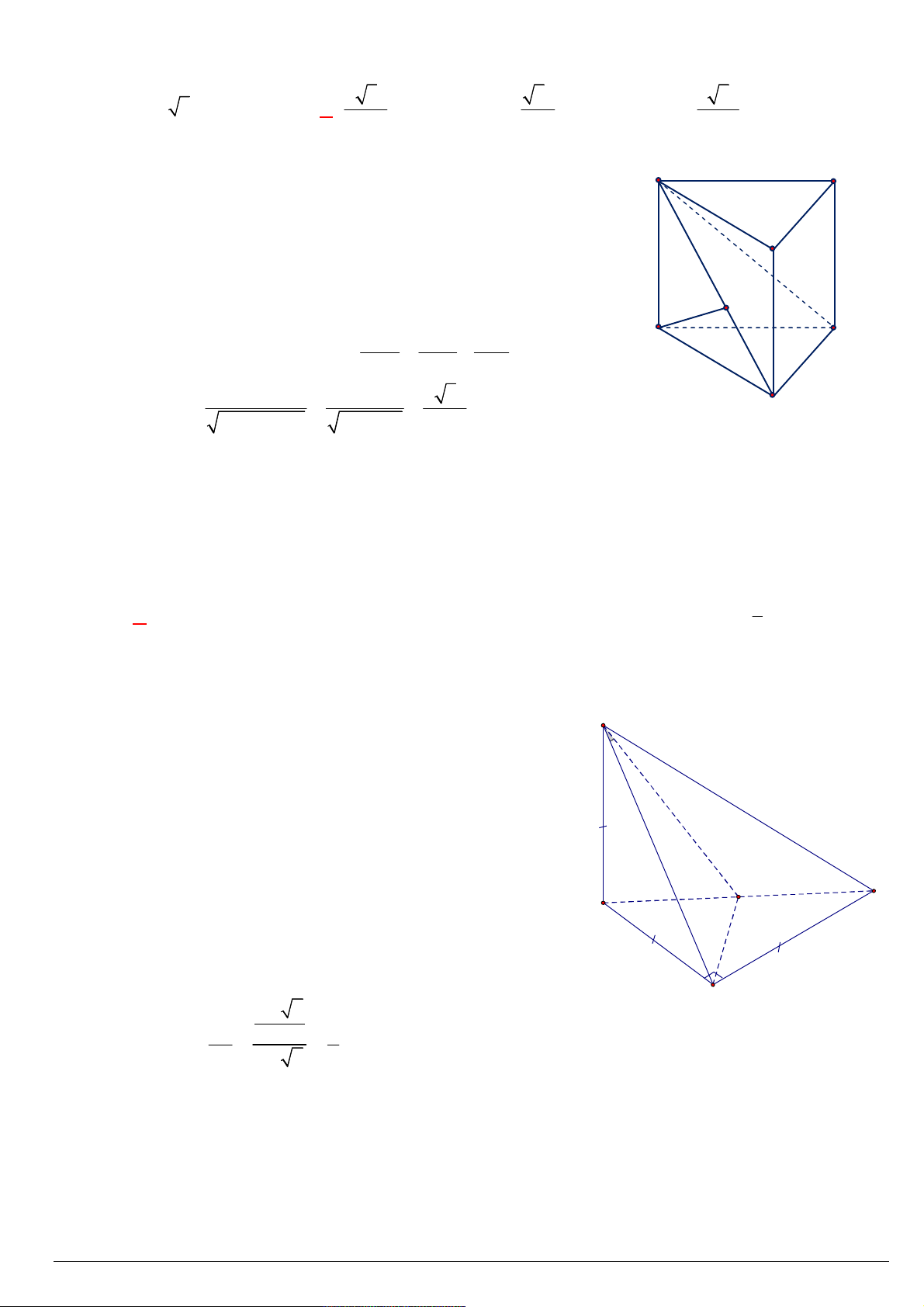
Câu 121. Cho hình lăng trụ tam giác đều ABC.AB C
  có cạnh bên AA  2a , góc giữa đường thẳng AB với
mặt phẳng  ABC  là 0
60 . Gọi M là trung điểm BC . Tính cosin của góc giữa AC và AM . 1 3 2 3 A. . B. . C. . D. . 2 4 4 2 Lời giải: C' A' B' A C M B  
AM  BC  AM .BC  0
Góc giữa đường thẳng AB với mặt phẳng   ABC  là 0 60 0
 A' BA  60 2
AA  2a  AB  a 3 4
A'C  A' B  a 3 2 3 AM  . a  a 3 2
 
 
         
A 'C.AM  A'C.AM . s
co  A'C, AM    A' A  AB  BC .AM  A' . A AM  .
AB AM  BC.AM     A . B AM  A . B AM . s co BAM 2 3
    . a 3 2 3
co  A C AM  A . B AM . s co BAM . AB s co BAM s ' ,     A'C.AM A'C 4 4 a 3
Trường THPT Hai Bà Trưng – Huế Trang 39/81
Câu 122. Cho hình chóp S.ABC có đáy ABC vuông tại B , SA vuông góc với đáy. Khẳng định nào sai? A. SB  AC. B. SA  A . B C. SB  BC. D. SA  BC. Lời giải: S A C B
Nếu SB  AC.  AC  SB
Từ SA   ABC   SA  AC, do đó 
 AC   SAB  AC  . AB AC  SA 
Điều này là vô lý vì A
 BC vuông tại B nên đáp án A sai.
Ta có SA   ABC   SA  AB, SA  BC nên đáp án B và D đúng. BC  AB Lại có 
 BC   SAB  BC  SB nên đáp án C đúng. BC  SA 
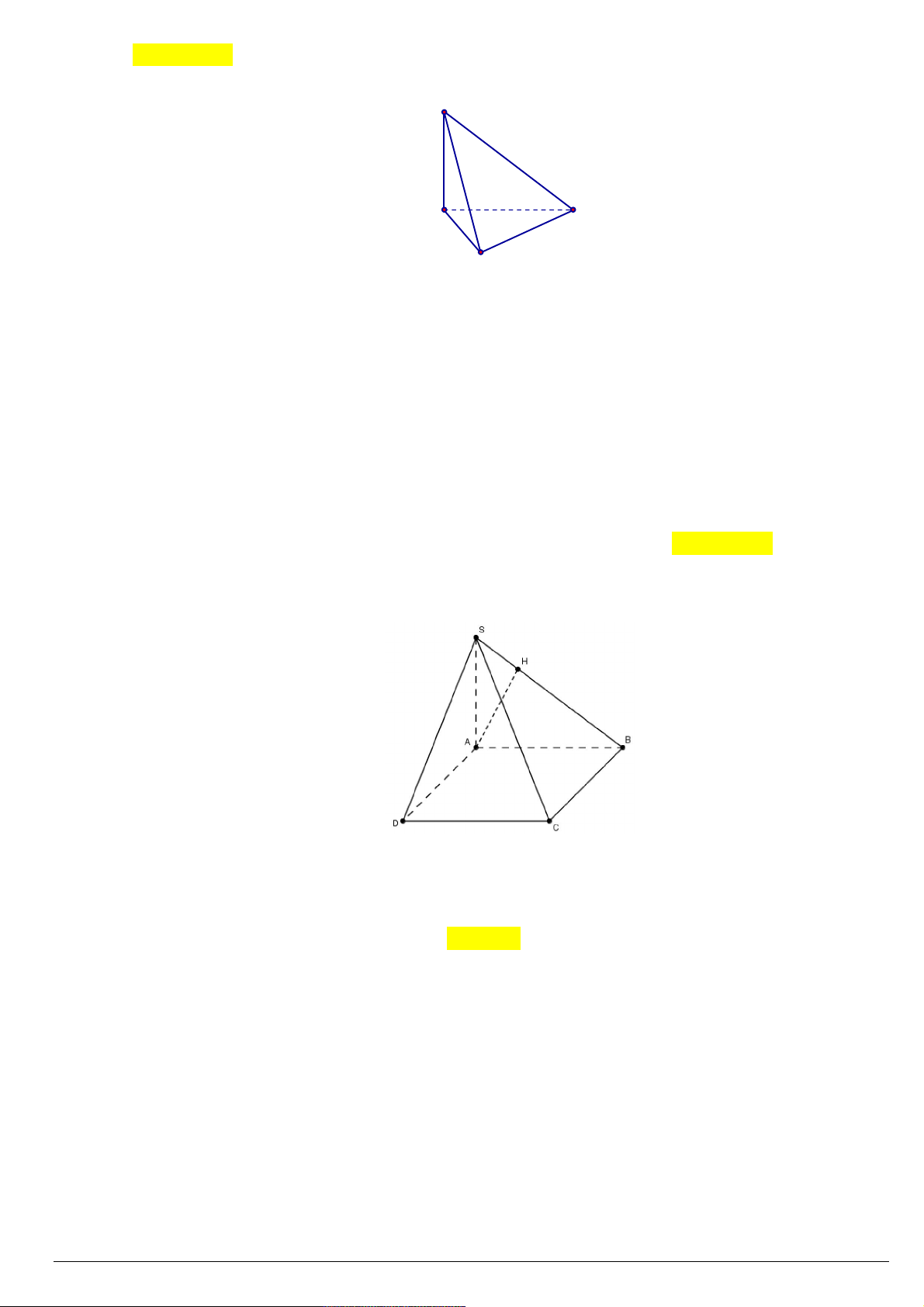
Câu 123. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA vuông góc với  ABCD và H là hình
chiếu vuông góc của A lên SB . Khẳng định nào sau đây là sai? A. AH  BC . B. AH  SC . C. BD  SC . D. AC  SB . Lời giải:
Ta có BC  SA và BC  AB nên BC   SAB   SBC    SAB .
Mặt khác SBC    SAB  SB . Do đó từ A kẻ AH  SB  AH  SBC 
AC  SA , AC không vuông góc AB nên AC  SB là sai
Trường THPT Hai Bà Trưng – Huế Trang 40/81
Câu 124. Cho hình chóp S.ABC có SA  SB  SC và tam giác ABC vuông tại B . Vẽ SH   ABC  ,
H   ABC  . Khẳng định nào sau đây đúng?
A. H trùng với trực tâm tam giác ABC .
B. H trùng với trọng tâm tam giác ABC .
C. H trùng với trung điểm AC .
D. H trùng với trung điểm BC . Lời giải: S A C M B 1
Gọi M là trung điểm của AC  BM  AM  CM  AC . 2 S
 AC cân tại S  SM  AC   1 . S
 MA vuông tại M 2 2 2
 SA  AM  SM 2 2 2
 SB  BM  SM .  . S
 MB vuông tại M hay SM  BM 2 . Từ  
1 và 2 suy ra: SM   ABC  .
Theo giả thiết: SH   ABC  , H  ABC   H  M .
Vậy H trùng với trung điểm AC .
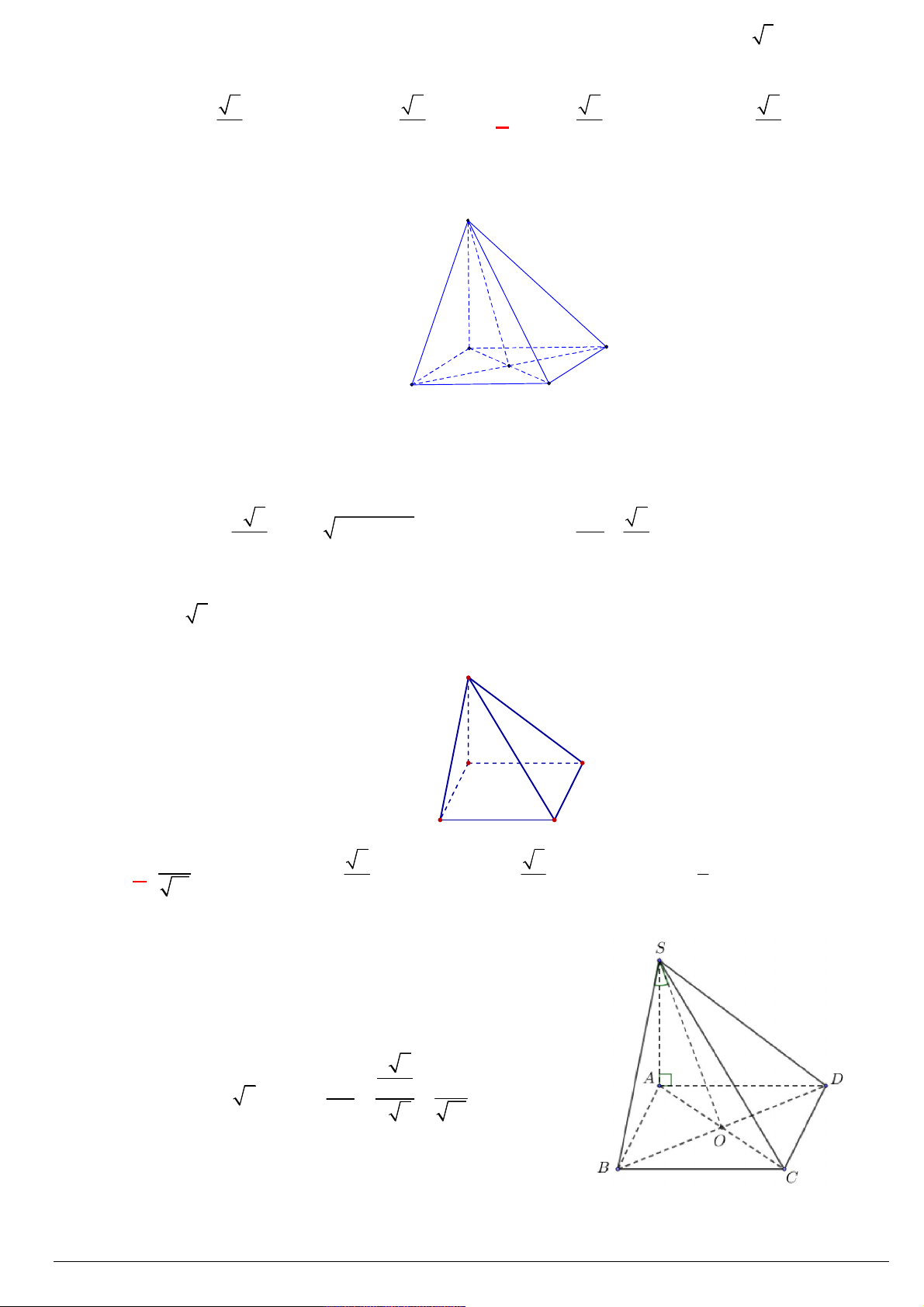
Câu 125. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt đáy, góc giữa
cạnh SD và mặt đáy bằng 30 . Độ dài cạnh SD bằng 2a 3 a A. 2a . B. . C. . D. a 3 . 3 2 Lời giải: S A D O B C 
SA vuông góc với mặt đáy, góc giữa cạnh SD và mặt đáy bằng 30 0  D S A  30 D A 2 2a 3
AD  a  SD   a  0 s30 co 3 3
Trường THPT Hai Bà Trưng – Huế Trang 41/81
Câu 126. Cho tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt
phẳng  ABC  tại H . Khẳng định nào sau đây là sai? 1 1 1 1 A.    .
B. H là trực tâm tam giác ABC . 2 2 2 2 OH OA OB OC B. OA  BC .
D. AH  OBC  . Lời giải: A H B O I C
Ta có OH   ABC   OH  BC và OA  OBC   OA  BC .
Suy ra BC   AOH   BC  AH   1
Ta lại có OH   ABC   OH  AC và OB  OAC   OB  AC
Suy ra AC   BOH   AC  BH 2 Từ  
1 và 2 suy ra H là trực tâm tam giác ABC .
Gọi I là chân đường vuông góc của O lên đường thẳng BC 1 1 1 1 1 1 Ta có      . 2 2 2 2 2 2 OH OI OA OB OC OA Vậy D là đáp án sai.
Câu 127. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sai?
A. BC  SAB .
B. AC  SBD .
C. BD  SAC  .
D. CD  SAD . Lời giải: S Ta có: BC  AB + 
 BC   SAB . BC  SA  C  D  AD + 
 CD  SAD . CD  SA  A BD  AC D + 
 BD  SAC  . BD  SA  Suy ra: đáp án B sai. B C
Trường THPT Hai Bà Trưng – Huế Trang 42/81
Câu 128. Cho hình chóp S.ABCD đáy là hình vuông cạnh a , tâm O . Cạnh bên SA  2a và vuông góc với
mặt phẳng đáy. Gọi  là góc tạo bởi đường thẳng SC và mặt phẳng đáy. Mệnh đề nào đúng? A.   60 . B.   75 . C. tan   1. D. tan   2 . Lời giải: S A D  B C
Ta có AC là hình chiếu vuông góc của SC lên mặt phẳng  ABCD .
 SC  ABCD     ,  SCA   . SA
Tam giác SAC vuông tại A có tan  
, với AC  a 2 thì tan   2 . AC
Câu 129. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SD  a và SD vuông góc với mặt
phẳng đáy. Tính góc giữa đường thẳng SA và mặt phẳng  SBD . A. 45 . B. arcsin 1/ 4 . C. 30 . D. 60 . Lời giải: S D C O A B D S   A D BC   D S  AC  
  AC   SBD  AO   SBD
AC  BD 
Góc giữa đường thẳng SA và mặt phẳng  SBD là  ASO SA  a 2 2 AO  a 2  1  0 sin ASO   ASO  30 2
Trường THPT Hai Bà Trưng – Huế Trang 43/81
Câu 130. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với mặt đáy và
SA  2a . Gọi M là trung điểm của SC . Tính côsin của góc  là góc giữa BM và  ABC  . 7 2 7 5 21 A. cos  . B. cos  . C. cos  . D. cos  . 14 7 7 7 Lời giải:
Gọi H là trung điểm AC ta có MH là đường trung bình của tam
giác SAC nên MH song song SA.
SA vuông góc (ABC) thì MH vuông góc (ABC) 
suy ra góc giữa BM và  ABC  là MBH SA HM   a. 2 3 3 BH  . AB  a 2 2 2 2 2
BM  MH  BH 3 a BH 21 2 s co     BM 3 7 2 2 a  a 4
Câu 131. Cho hình lập phương . ABCD AB C  D
  (hình bên). Tính góc giữa AB và mặt phẳng  BDD B   . A. 60 . B. 90 . C. 45 . D. 30 . Lời giải:
Gọi O là giao điểm AC và BD. Ta có AO vuông góc (BDD’B’)
Góc giữa AB và mặt phẳng  BDD B   là  AB 'O 2 a  AO 1 2  0 sin AB 'O   
 AB 'O  30 AB ' a 2 2
Trường THPT Hai Bà Trưng – Huế Trang 44/81
Câu 132. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A , đáy lớn AD  10 cm , BC  8cm , SA
vuông góc với mặt đáy và SA  8cm . Gọi M là trung điểm của AB . Mặt phẳng  P đi qua M và
vuông góc với AB . Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng  P . A. 2 26 cm . B. 2 20 cm . C. 2 52 cm . D. 2 18 cm . Lời giải: S 8 P Q 10 A D M N B 8 C
Gọi N , P và Q lần lượt là trung điểm của CD , SC và SB .
Ta có:  P   SAB  MQ ,  P   ABCD  MN ,  P   SCD  NP .
Do đó, thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng  P là tứ giác MNPQ .
Dễ thấy MNPQ là hình thang vuông tại M , Q và MQ  PQ  4 , MN  9 . .
MQ MN  PQ 4.9  4
Vậy diện tích hình thang MNPQ là: S    26 . MNPQ 2 2
Câu 133. Trong các khẳng định sau khẳng định nào là đúng?
A. Hình lăng trụ đứng là hình lăng trụ đều.
B. Hình lăng trụ có đáy là một đa giác đều là một hình lăng trụ đều.
C. Hình lăng trụ đứng có đáy là một đa giác đều là hình lăng trụ đều.
D. Hình lăng trụ tứ giác đều là hình lập phương. Lời giải:
Theo định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là một đa giác đều.
Câu 134. Mệnh đề nào dưới đây sai?
A. Hình chóp đều có các cạnh bên tạo với mặt phẳng đáy các góc bằng nhau.
B. Hình chóp đều có tất cả các cạnh bằng nhau.
C. Hình chóp đều có các mặt bên là các tam giác cân bằng nhau.
D. Một hình chóp có đáy là một đa giác đều và có chân đường cao trùng với tâm của đa giác đáy đó là hình chóp đều. Lời giải: Theo định nghĩa :
Một hình chóp có đáy là một đa giác đều và có chân đường cao trùng với tâm của đa giác đáy đó là hình chóp đều.
Hình chóp đều có các cạnh bên tạo với mặt phẳng đáy các góc bằng nhau.
Hình chóp đều có các mặt bên là các tam giác cân bằng nhau.
Hình chóp đều có các cạnh bên bằng nhau, đáy là đa giác đều (tam giác đều hoặc hình vuông)
Trường THPT Hai Bà Trưng – Huế Trang 45/81
Câu 135. Cho hai mặt phẳng cắt nhau   và    . M là một điểm nằm ngoài hai mặt phẳng trên. Qua M
dựng được bao nhiêu mặt phẳng đồng thời vuông góc với   và vuông góc với    ? A. Vô số. B. Một. C. Hai. D. Không. Lời giải:
Cho hai mặt phẳng cắt nhau   và    tạo ra giao tuyến là 1 đường thẳng d
Qua M dựng được duy nhất 1 mặt phẳng vuông góc với d, khi đó cũng vuông góc với   và vuông góc với   
Câu 136. Cho hình chóp S.ABC có SA   ABC  , tam giác ABC vuông tại B . Kết luận nào sau đây sai?
A.  SAC    SBC  .
B.  SAB   ABC  . C. SAC    ABC  . D. SAB   SBC  . Lời giải: S Chọn A SA    ABC  Ta có: 
  SAB , SAC    ABC   B, C đúng. SA  
SAB,SAC   A C
SA   ABC   SA  BC mà BC  AB  BC  SAB; BC   SBC 
 SAB   SBC   D đúng. Vậy đáp án sai là A. B
Câu 137. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB  a 2 . Biết SA   ABC 
và SA  a . Tính góc giữa hai mặt phẳng  SBC  và  ABC  . A. 30 . B. 45 . C. 60 . D. 90 . Lời giải: S H B A D C
Kẽ AD vuông góc BC suy ra góc giữa hai mặt phẳng  SBC  và  ABC  là  D S A
ABC là tam giác vuông cân tại A và AB  a 2  D A  a   0 tan D S A  1  D S A  45
Trường THPT Hai Bà Trưng – Huế Trang 46/81
Câu 138. Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, AB  a , AD  2a . Cạnh bên SA vuông góc
với đáy  ABCD , SA  2a . Tính tang của góc giữa hai mặt phẳng  SBD và  ABCD . 1 2 5 A. . B. . C. 5 . D. . 5 5 2 Lời giải: S 2a 2a A D a H B C
Kẻ AH  BD ,  H  BD (1). 
BD  SA SA   ABCD 
 BD  SAH   BD  SH (2). BD  AH 
Và:  SBD   ABCD  BD (3).
Từ (1) (2) và (3) suy ra: góc giữa hai mặt phẳng  SBD và  ABCD là  SHA . 1 1 1 1 1 5 2a Xét A
 BD vuông tại A :       AH  . 2 2 2 AH AB AD 2 2 a 4a 2 4a 5 SA Xét SA 
H vuông tại A :  tan SHA   5 . AH
Trường THPT Hai Bà Trưng – Huế Trang 47/81
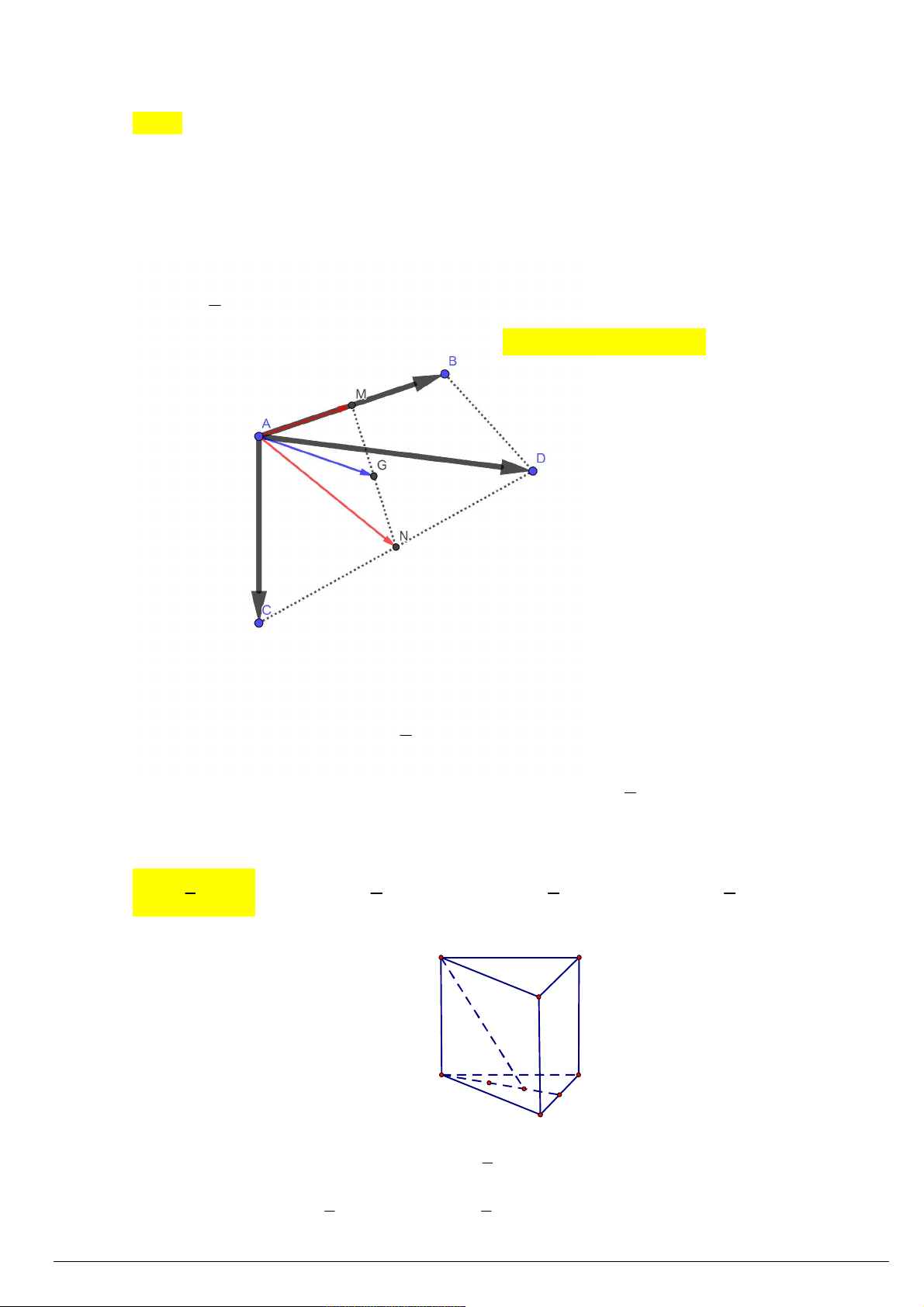
Câu 139. Cho hình lăng trụ đều ABC.AB C
  có cạnh đáy bằng 2a , cạnh bên bằng a . Tính góc giữa hai mặt phẳng  AB C   và  A B  C   .   3 3 A. . B. . C. arccos . D. arcsin . 6 3 4 4 Lời giải: A C B A C  I B B C
   AI
Gọi I là trung điểm của B C   . Ta có:   B C
    AIA B C
   AA    AB C
    AB C    B C   
Khi đó: AI  B C  
 AI  B C    
 góc giữa hai mặt phẳng  AB C   và  A B  C
  là góc AIA . AA a 1 
Xét tam giác AIA vuông tại A ta có:  tan AIA      AIA  . AI a 3 3 6
Câu 140. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA   ABCD . Gọi M và N là hai điểm  a 
thay đổi trên cạnh CB và CD sao cho CM  2x , CN  x 0  x  
 . Tìm hệ thức liên hệ giữa a  2 
và x để SAM   SMN  . A. 2a  x .
B. 2a a  3x  0 . C. 2
4x  ax  0 . D. 2
x  3ax  0 . Lời giải: S SA  MN 
SAM   MN   
   SAM    SMN  AM  MN 
MN   SMN 
Vậy tam giác AMN vuông tại M. 2 2 2
AM  AB  BM 2 2 2
MN  MC  NC 2 2 2 2 2 2 2
AN  AM  MN  AB  BM  MC  NC A D 2 2 2 2 2 2 2
AN  AD  DN  AB  BM  MC  NC N
 a  a  x2  a  a  2x2  2x2 2 2 2  x B M C 2
 4x  ax  0
Trường THPT Hai Bà Trưng – Huế Trang 48/81
Câu 141. Khẳng định nào sau đây là khẳng định sai?
A. Khoảng cách từ một điểm đến một mặt phẳng là khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
B. Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm tuỳ ý trên mặt phẳng này đến mặt phẳng kia.
C. Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song
với nhau lần lượt chứa hai đường thẳng đó.
D. Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ một điểm tuỳ ý trên đường thẳng
này đến đường thẳng kia. Lời giải:
D sai vì khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song
song với nhau lần lượt chứa hai đường thẳng đó.
Cách tính khoảng cách giữa hai đường thẳng chéo nhau d và d’ Cách 1:
+ Xác định đường thẳng vuông góc chung của d và d’
+ Tính độ dài đoạn vuông góc chung. Cách 2:
Kẽ d’ và song song với d, suy ra mp(P) chứa d’ và song song d.
+ Khi đó d(d, d ')  d (d,(P))  d ( ,
A (P)) với A là một điểm bất kỳ thuộc d
Chú ý: mp(P) có thể có sẵn hoặc chúng ta phải dựng
(Cách dựng: qua một điểm B  d ' dựng đường thẳng ∆ song song với d, lúc đó mp(P)≡(d’,∆)).
Các ví dụ mẫu cho cách 1
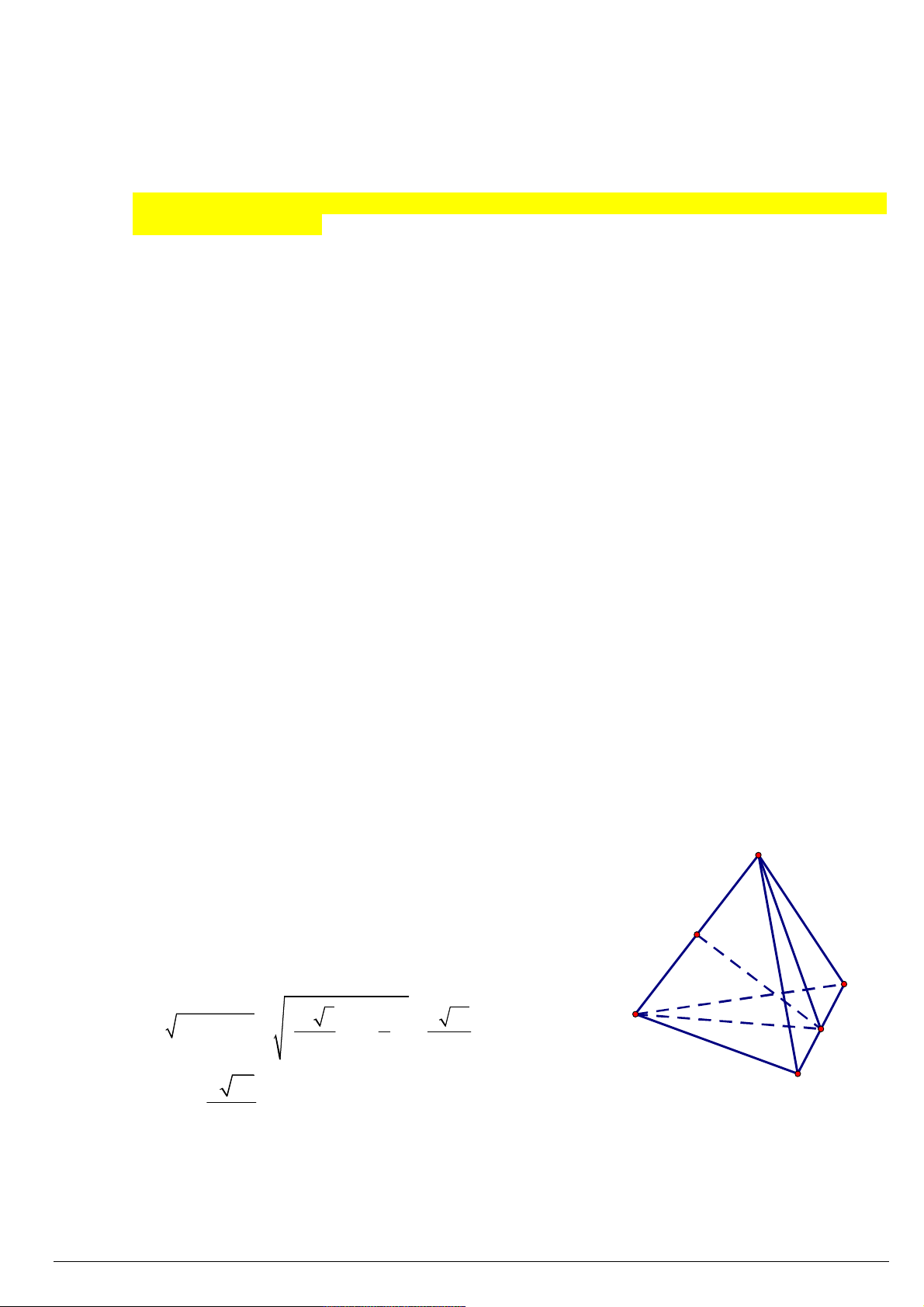
Ví dụ 1: Cho tứ diện ABCD có AB=a, tất cả các cạnh còn lại bằng 3a. Tính d ( AB,CD) Giải:
+ Gọi I, J lần lượt là trung điểm của CD và AB. A
+ Vì ACD và ACD là các tam giác đều nên:
CD  AI , CD  BI  CD  ( AIB)  CD  IJ (1) Mặt khác, AC 
D  ACD nên tam giác AIB cân tại I. Do đó, J IJ  AB (2)
+ Từ (1), (2) suy ra: IJ là đường vuông góc chung của AB và CD. D 2 2   B + Ta có: 2 2 3a 3  a  a 26 IJ 
AI  AJ        . I 2  2  2   a 26 C
Vậy d ( AB,CD)  2
Trường THPT Hai Bà Trưng – Huế Trang 49/81
Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung
điểm của AB và AD, H là giao điểm của CN và DM, SH  ( ABCD), SH  a 3 . Tính d (DM , SC) Giải: S
+ Trong mp(SCH) kẻ HK  SC(1), (K  SC) .
SH  ( ABCD)  + Mặt khác,
  SH  DM (*) K
DM  ( ABCD)
Xét hai tam giác vuông AMD và DNC có AM = DN, AD = DC  A  MD  D  NC . D C Từ đó ta có: N   AMD DNC   H       0  0 ADM  DCN
  DNC  ADM  90  NHD  90 hay   A 0 M B
AMD ADM  90 
DM  CN (**) .
Từ (*), (**) suy ra: DM  (SCH )  DM  HK (2) .
Từ (1), (2) suy ra: HK là đoạn vuông góc chung của DM và SC. 2 2 CD a 2a 3 + Ta có: H  CD  D
 CN  HC    . 2 2 CN 3 CD  DN 1 1 1 5 a 15
Xét tam giác vuông SHC ta có:     HK  2 2 2 2 HK HC HS 3a 5 a 15
Vậy d (DM , SC)  HK  C 5 A các ví dụ cho cách 2 I
Ví dụ 1: Cho hình lăng trụ đứng ABC.A’B’C’, đáy ABC là B a 2
tam giác đều cạnh a, AA'  . 2 H Tính d (A , B CB')
Giải: + Gọi I, J lần lượt là trung điểm của AB và A’B’. C' A' + Ta có: J
AB / /(CA' B ')  d ( AB,CB ')  d ( AB, (CA' B '))  d (I , (CA' B ')) B'
+ Trong mp(CIJ) kẻ IH  CJ (1), (H  CJ)
Ta có: A' B '  (IJ ) (vì ABC. A’B’C’ là hình lăng trụ đứng) và IC  A' B ' (vì ∆ABC là tam giác đều)
nên A' B '  (CIJ )  IH  A' B ' (2) .
Từ (1), (2) suy ra: IH  (CA ' B ') hay d ( A , B CB ')  IH 1 1 1 4 2 10 a 30
+ Xét tam giác vuông CIJ có:       IH  2 2 2 2 2 2 IH IC IJ 3a a 3a 10 a 30 Vậy d(A ,
B CB')  IH  10
Trường THPT Hai Bà Trưng – Huế Trang 50/81
Ví dụ 2: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên bằng
a 2 . Tính d ( A , D ) SB S
Giải: + Vì AD / / SBC  d(A ,
D SB)  d(A , B (SBC))
+ Gọi O là giao điểm của AC và BD. I, J lần lượt là trung điểm của AD và BC.
+ Trong mp(SIJ) kẻ IH  SJ , (H  SJ ) (1) . H A
SO  ( ABCD)  SO  BC  B
  BC  (SIJ )
Theo giả thiết ta có: IJ / / AB  IJ  BC  I O J
 IH  BC (2) D C
Từ (1), (2) suy ra: IH  (SBC) hay d ( A , D SB)  IH 1 1 S . O IJ
+ Xét tam giác SIJ có: S  IH.SJ  S . SIJ O IJ  IH  . Với: IJ=a, 2 2 SJ 2 2 3 2 2 . a 7 S . O IJ 2a 21 SO 
SA  AO  a. , SJ  SB  BJ  . Suy ra: IH   . 2 4 SJ 7 2a 21
Vậy d (AD, SB)  IH  7
Ví dụ 3: Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a, tam giác SAD là tam giác đều,
(SAD) vuông góc với mặt phẳng đáy. Tính d (S , A BD)
Giải: + Qua A kẻ đường thẳng d song song với BD. Gọi O là giao điểm của AC và BD; I, M lần lượt
là trung điểm của AD và OD; N là giao điểm của d và IM. d ( , SA BD)  d (( , SA d ), BD)  S
+ Ta có:  d(M,( , SA d ))
+ Trong mp(SMN) kẻ MH  SN (1), (H  SN) Theo giả thiết: H D SI  AD  C
  SI  ( ABCD)  SI  d (*) Mặt
(SAD)  ( ABCD) M I O d / / BD  N  A B
khác ta có: BD  AO   d  MN (**) . Từ (*), (**) AO / /MN  
suy ra: d  (SMN )  d  MH (2) . Từ (1), (2) suy ra: MH  (S , A d ) . 1 1 SI.MN
+ Xét tam giác SMN có: S  MH.SN  SI. SMN MN  MH  2 2 SN a 3 a 2 a 10 SI.MN a 15 với 2 2 SI  , MN  AO 
, SN  SI  IN  . Do đó, MH   . Vậy 2 2 4 SN 5 a 15 d (S , A BD)  5
Trường THPT Hai Bà Trưng – Huế Trang 51/81
Ví dụ 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tai B, AB = BC = 2a, hai mặt phẳng
(SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC). Gọi M là trung điểm của AB, mặt phẳng qua
SM và song song với BC cắt AC tại N, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 600. Tính d ( A , B SN) S Giải:
+ Gọi I là trung điểm của BC.
Do MN//BC nên N là trung điểm của AC. Do đó, IN//AB H
hay d ( AB, SN )  d ( AB, (SNI )) . J
+ Trong mp(ABC) kẻ AJ  IN , (J  IN ) (*) A
Trong mp(SAJ) kẻ AH  SJ , (H  SJ ) (1) N + Theo giải thiết ta có: C
(SAB)  ( ABC )  M
  SA  ( ABC)  SA  IN (**) I
(SAC)  ( ABC ) B
Từ (*), (**) ta có: IN  (SAJ )  IN  AH (2) .
Từ (1), (2) ta có: AH  (SIN )  d ( AB, SN )  AH .  + Ta có: 0 0
((SBC),( ABC))  SBA  60  SA  .
AB tan 60  2a 3 ; AJ  BI  a . 1 1 1 13 12
+ Xét tam giác vuông SAJ có:     AH  . a . 2 2 2 2 AH SA AJ 12a 13 . a 156
Vậy d ( AB, SN )  AH  13
Trường THPT Hai Bà Trưng – Huế Trang 52/81
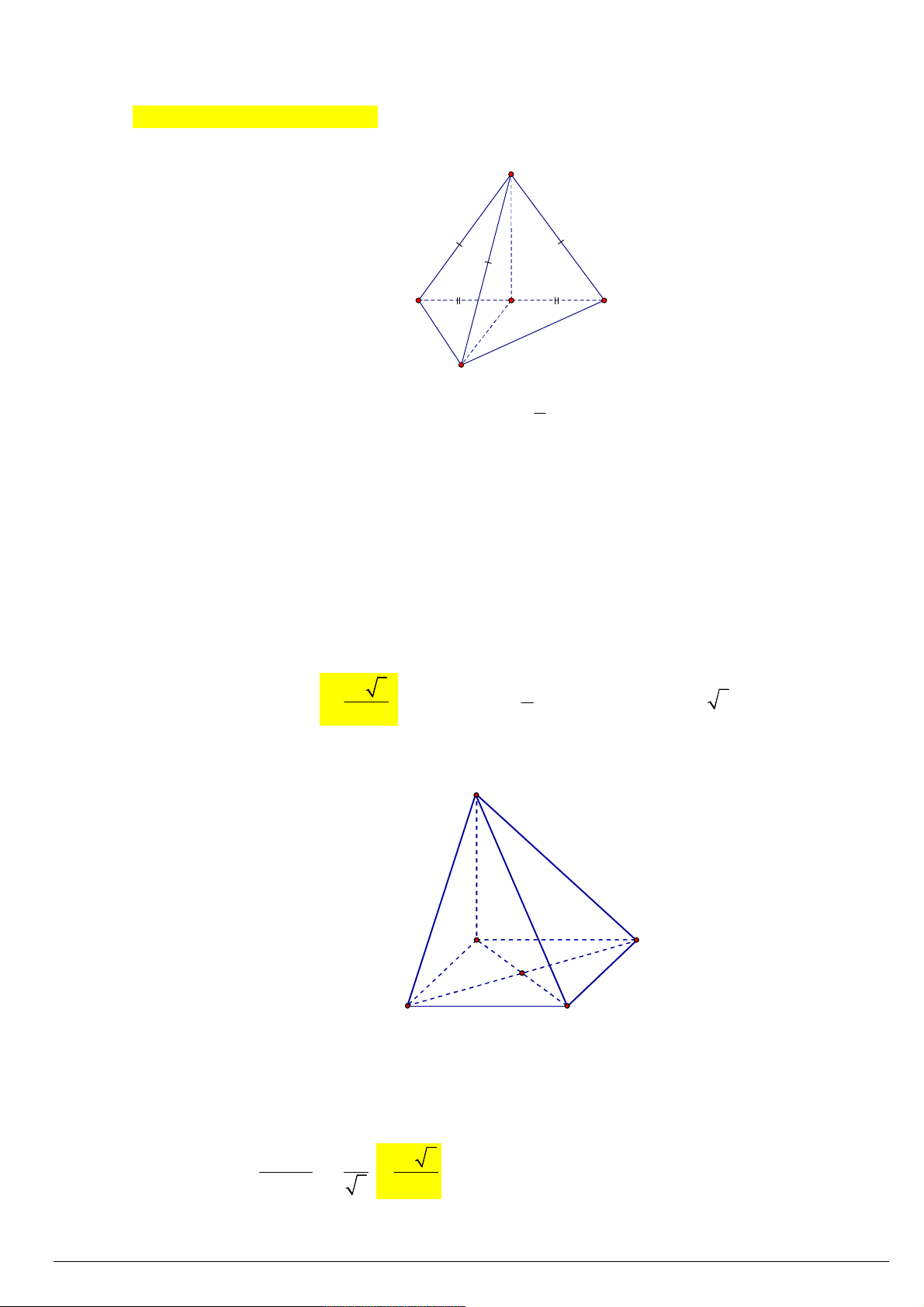
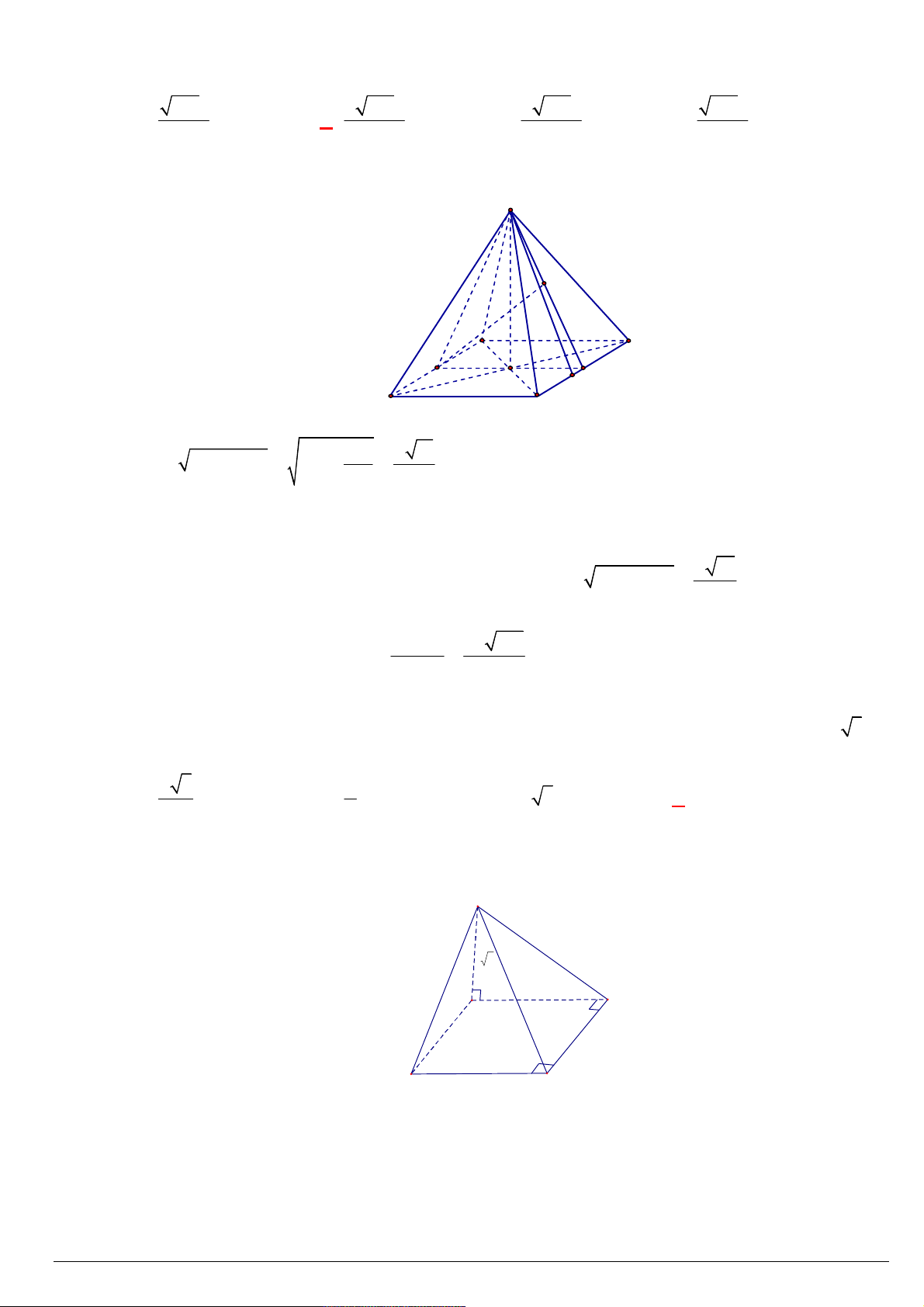
Câu 142. Cho hình chóp tứ giác đều S.ABCD có các mặt bên là các tam giác đều cạnh 2a . Tính khoảng cách
từ S đến mặt phẳng ( ABCD) . A. 2a 2 . B. 2a . C. a 2 . D. a . Lời giải: S
Cho hình chóp tứ giác đều S.ABCD có các mặt bên là các tam
giác đều cạnh 2a .
Gọi O là giao điểm AC và BD nên SO vuông góc (ABCD)
(tính chất hình chóp đều)
ABCD là hình vuông cạnh 2a  AC  2a 2 A D
SO  SA  AO   a  a 2 2 2 2 2 2 2 2  2a O B C  SO  a 2
Câu 143. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA  a 3 , SA   ABCD . Tính
khoảng cách từ A đến mặt phẳng  SBC  . a 3 2 a 3 A. . B. . C. . D. a . 2 a 3 4 Lời giải:
Ta có BC  SA và BC  AB nên BC   SAB   SBC    SAB .
Mặt khác SBC    SAB  SB . Do đó từ A kẻ AH  SB  AH  SBC 
hay AH  d  ,
A  SBC  . Trong tam giác vuông SAB ta có 1 1 1 1 1 4      . 2 2 2 AH SA AB 2 2 2 3a a 3a a 3 Vậy AH  . 2
Trường THPT Hai Bà Trưng – Huế Trang 53/81
Câu 144. Cho hình lăng trụ đứng ABC.AB C
  . Cạnh bên AA  a , ABC là tam giác vuông tại A có
BC  2a , AB  a 3 . Tính khoảng cách từ đỉnh A đến mặt phẳng  A B  C  . a 7 a 21 a 21 a 3 A. . B. . C. . D. . 21 21 7 7 Lời giải: A C
Lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại A
BC  2a , AB  a 3  AC  a . B
khoảng cách từ đỉnh A đến mặt phẳng  A B  C  là 1 1 1 1 1 1 1 7        H 2 2 2 2 2 2 2 2 AH AA' AB AC a 3a a 3a A C a 21 d  AH 
 A, A'BC 7 B
Câu 145. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm A đến mặt phẳng SCD . a 21 a 3 a 3 A. h  . B. h  a . C. h  . D. h  . 7 4 7 Lời giải:
Gọi M và F là trung điểm AB, CD
SAB   ABCD SM  ABCD SM  AB   3 SM  a 2 MF  a AB / /CD  
  AB / /  SCD  d  d  h AB   D SC   A,S D C  M ,S D C    1 1 1 a 21    h  2 2 2 h SM MF 7
Trường THPT Hai Bà Trưng – Huế Trang 54/81
Câu 146. Cho hình lập phương AB . CD A B  C  D
  có cạnh bằng a . Khoảng cách từ điểm B đến mặt phẳng  AD B   bằng a 3 a 2 a 6 A. . B. . C. . D. a . 3 2 3 Lời giải: A a B O
Gọi O , O lần lượt là tâm của hình vuông C D a ABCD và A B  C  D   . K      a Ta có BO // B O
 AB D   BO //  AB D   .
Dựng OK  AO , ta có B D    A C     B D
    AAC C    OK B D    AA   B D    OK . A' B' O'
 OK   AB D   . D' C'
 d  B, AB D
   d O, AB D    OK . Xét AOO 
 vuông tại O có OK là đường cao. 1 1 1 1 1 3 a 3        OK  . 2 2 2 OK OA OO 2 2 2  2 a a a  3   2  
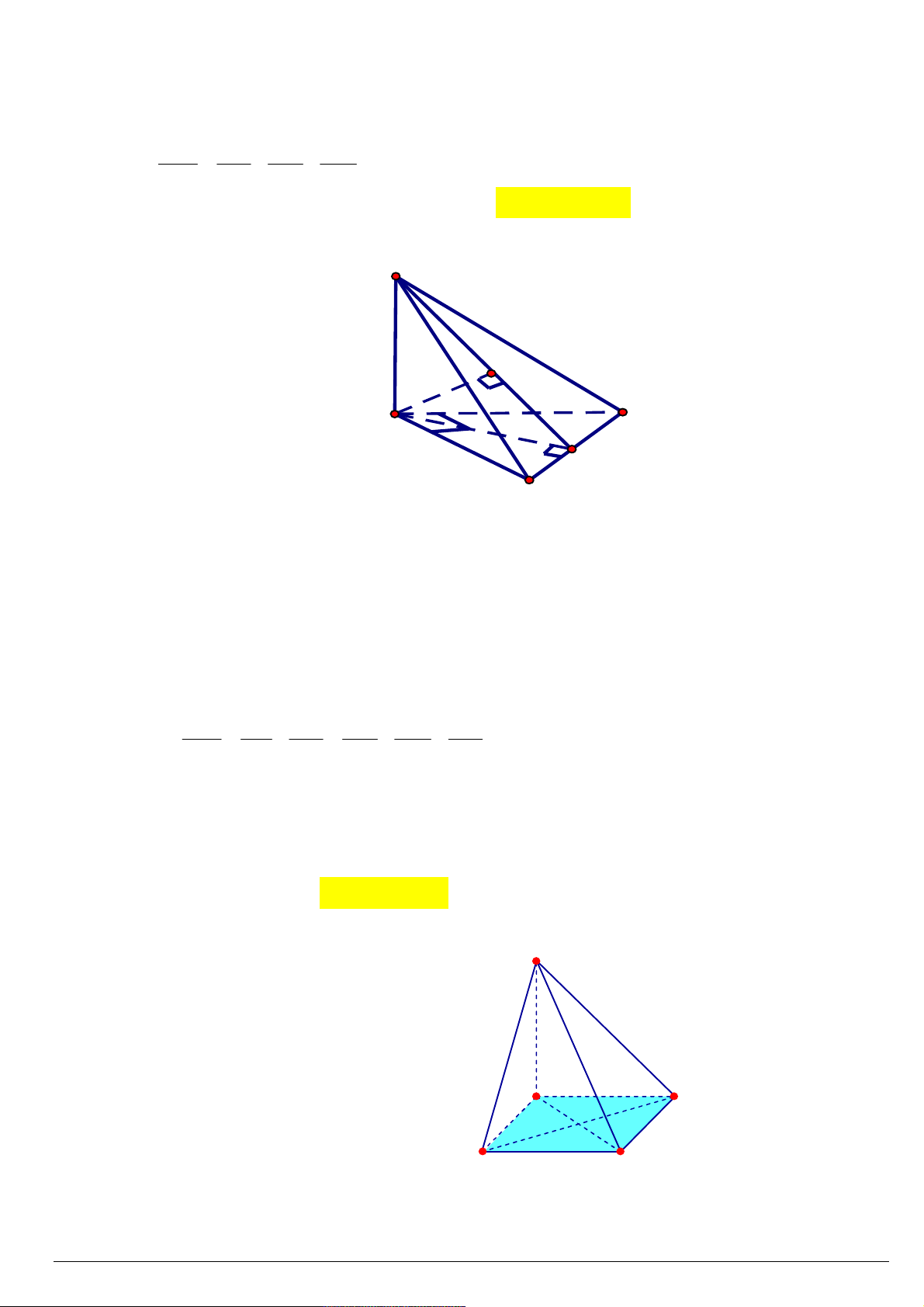
Câu 147. Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a , SO vuông góc với mặt phẳng
 ABCD và SO  a . Tính khoảng cách giữa SC và AB . 2a 5 a 5 2a 3 a 3 A. . B. . C. . D. . 5 5 15 15 Lời giải: S a H A D M O B a C
Gọi M là trung điểm CD ; H là hình chiếu vuông góc của O lên SM .
Ta có d  AB, SC   d  AB, SCD  d  ,
A SCD  2d O, SCD  2OH . 1 1 1 4 1 5 a 5
Xét tam giác SMO vuông tại O có:       OH  . 2 2 2 2 2 2 OH OM OS a a a 5 2a 5
Vậy d  AB, SC   . 5
Trường THPT Hai Bà Trưng – Huế Trang 55/81
Câu 148. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh SA  a và vuông góc với mặt
đáy  ABCD . Tính khoảng cách giữa hai đường thẳng SC và BD . a 3 a 6 a a 6 A. . B. . C. . D. . 4 3 2 6 Lời giải:
SA   ABCD  SA  BD  D B  SAC  AC  D B 
Ta có AC  BD  O OH  SC
OH   SAC   OH  D B
Vậy OH là đoạn vuông góc chung của BD và SC.   2 AC SA a .a a 6 2 d
 OH  OC.sinHCO  OC.sinDCA  .   SC,DB 2 SC 2.a 3 6
Câu 149. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông, BA  BC  a , cạnh bên
AA  a 2 , M là trung điểm của BC . Tính khoảng cách giữa hai đường thẳng AM và B C  . a 2 a 3 a 5 a 7 A. . B. . C. . D. . 2 3 5 7 Lời giải:
Phương pháp 2 xác định khoảng cách giữa 2 đường chéo nhau
Bước 1: dưng mặt phẳng song song
Gọi D là trung điểm BB’
ta có MD / / B 'C   A D
M  / /B 'C
Bước 2: tỉ lệ khoảng cách d  d  d  d  h
 AM ,B'C 
B'C , AMD B', A D M  B, A D M 
ABC là tam giác vuông,  0
BA  BC  a  B  90
Bí kíp: công thức tam diện vuông
( 3 đường đôi 1 vuông góc nhau) 1 1 1 1 a 7     h  2 2 2 2 h BA BM BD 7
Trường THPT Hai Bà Trưng – Huế Trang 56/81 Luyện tập tương tự
Cho hình lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông, BA  BC  a , cạnh bên
AA  2a , M là trung điểm của BC . Khoảng cách giữa hai đường thẳng AM và B C  bằng a 2 a 3 a 5 a 6 A. . B. . C. . D. . 2 3 5 6 Lời giải Chọn D
Gọi N là trung điểm BB nên MN //B C
  d  AM ; B C
   d B C
 ; AMN   d C; AMN 
 d B; AMN  .
Gọi H là hình chiếu của B lên  AMN  , do tứ diện .
B AMN là tứ diện vuông đỉnh B nên 1 1 1 1 1 4 1 6        . 2 2 2 2 BH BA BM BN 2 2 2 2 a a a a a 6 Vậy BH  . 6
Trường THPT Hai Bà Trưng – Huế Trang 57/81
Câu 150. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a , BC  2a , SA vuông góc với mặt
phẳng đáy và SA  a . Tính khoảng cách giữa hai đường thẳng AC và SB . 6a 2a a a A. . B. . C. . D. . 2 3 2 3 Lời giải:
Phương pháp 2 xác định khoảng cách giữa 2 đường chéo nhau
Bước 1: kẻ đường thẳng d đi qua B và song song AC
Bước 2: kẻ AE vuông góc xuống đường d.
Bước 3: Kẻ AH vuông góc SE.
Ta có AC / /  SBE   d  d  d  AH  h  AC ,SB
 AC,SBE
 A,SBE 1 1 1   2 2 2 h AE SA SA  a AE  d  k  D,AC  1 1 1 1 1     2 2 2 2 2 k D A DC D A AB 1 1 1 1 9 2 suy ra      h  a 2 2 2 2 2 h a a 4a 4a 3
Bí kíp: công thức tam diện vuông ( 3 đường đôi 1 vuông góc nhau) 1 1 1 1    2 2 2 2 d SA AB AD  AC ,SB --- HẾT ---
Trường THPT Hai Bà Trưng – Huế Trang 58/81
BÀI TẬP TRẮC NGHIỆM 1.5.2019 1.
Cho hình chóp S.ABC có cạnh SA vuông góc với mặt phẳng  ABC  , biết AB  AC  a ,
BC  a 3 . Tính góc giữa hai mặt phẳng  SAB và  SAC  . A. 30 . B. 150 . C. 60 . D. 120 . Lời giải Chọn D S B C A
Vì SA   ABC  nên SA  AB và SA  AC . 
 SAB   SAC   SA 
ta có: SA  AB 
  SAB SAC        AB AC  , ,  BAC . SA  AC 
AB  AC  BC
a  a  a 2 2 2 3 1 Xét A  BC có  2 2 2 cos BAC       BAC  120 . 2. . AB AC 2. . a a 2
Vậy  SAB, SAC     120. 2.
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  và đáy là tam giác vuông tại B ,
AB  SA  a . Gọi H là hình chiếu của A trên SB . Khoảng cách giữa AH và BC bằng: a 2 a a 3 A. . B. a . C. . D. . 2 2 2 Lời giải Chọn A
Ta có AH  SB (nên AH  HB ).
BC  AB  BC  SAB  BC  AH (nên BC  BH ). BC  SA 
Do đó, d  BC, AH   HB .
Tam giác SAB vuông cân tại A , AH là đường cao 2 2 SB a  a a  BH    . 2 2 2 a
Vậy d  BC, AH   . 2
Trường THPT Hai Bà Trưng – Huế Trang 59/81 3.
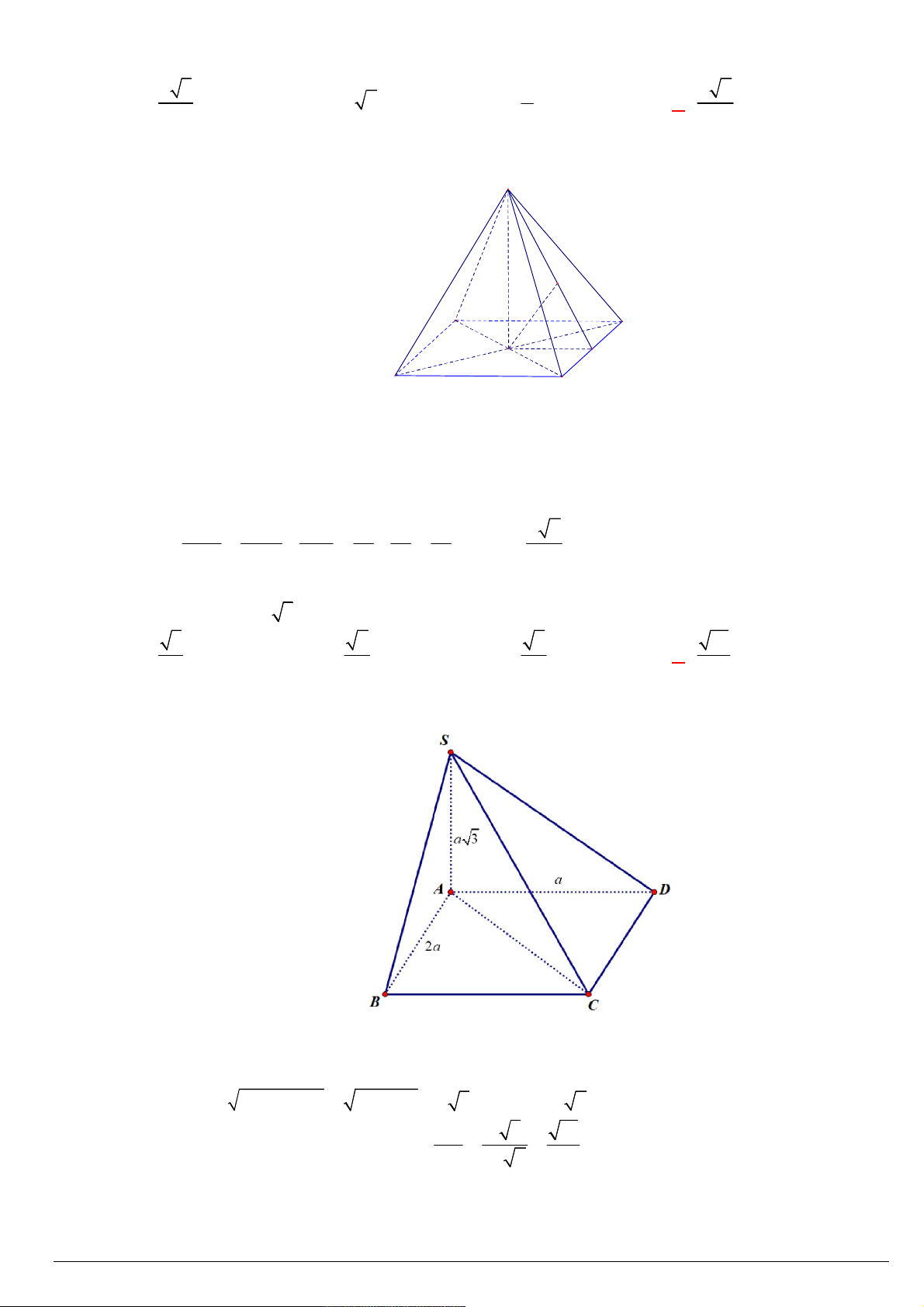
Cho hình chóp S.ABC có SA , SB , SC tạo với mặt đáy các góc bằng nhau và bằng 60 . Biết BC  a , 
BAC  45 . Tính khoảng cách h từ đỉnh S đến mặt phẳng  ABC  . a 6 a 6 a A. h  a 6 . B. h  . C. h  . D. h  . 2 3 6 Lời giải Chọn B
Gọi H là hình chiếu vuông góc của S
S lên  ABC  , suy ra
d S, ABC   SH và   
SAH  SBH  SCH  60
 HA  HB  HC .
Do đó H là tâm đường tròn ngoại tiếp tam giác ABC . BC a Xét A  BC , có:
 2HA  HA  . 60° sin A A 2 C 45° Xét SA 
H vuông tại H , H a a a có  6
SH  AH. tan SAH  . 3  . 2 2 B 4.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB  a 2 , AD  a , SA vuông góc với đáy và SA  a . Tính góc giữa SC và  SAB . A. 90 . B. 60 . C. 45 . D. 30 . Lời giải Chọn D BC  AB Ta có: 
 SA  SAB  SB là hình chiếu vuông góc của SC lên BC  SA 
SAB  SC SAB   ,  CSB .
Tam giác SAB vuông tại A có: 2 2 SB 
SA  AB  a 3 .  BC 1 
Tam giác SBC vuông tại B có: tan CSB    CSB  30 . SB 3
Trường THPT Hai Bà Trưng – Huế Trang 60/81 5.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh SA  a và vuông góc với mặt
đáy  ABCD . Khoảng cách giữa hai đường thẳng SC và BD bằng a 3 a 6 a a 6 A. . B. . C. . D. . 4 3 2 6 Lời giải Chọn D S I H A D O B C
Do BD  AC và BD  SA nên BD   SAC  .
Trong mặt phẳng  SAC  dựng OH  SC tại H .
 OH là đường vuông góc chung của BD và SC .
Gọi I là trung điểm SC . Tam giác OIC vuông tại O có đường cao OH . 1 1 1 OI.OC a 6 Ta có    OH   . 2 2 2 2 2 OH OI OC 6 OI  OC 6.
Cho tứ diện đều ABCD cạnh a . Tính khoảng cách giữa hai đường thẳng AB và CD a a 2 A. a 2 . B. . C. a . D. . 2 2 Hướng dẫn giải Chọn D A N B D M C
Gọi M là trung điểm của CD .
Qua M kẻ đường thẳng vuông góc với AB cắt AB tại trung điểm N ( AMN  cân tại M ) 2 2  a 3   a  a 2
Suy ra d  AB,CD  MN 2 2 
BM  BN        .  2   2  2  
Trường THPT Hai Bà Trưng – Huế Trang 61/81 7.
Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại B , AB  a , AA  2a . Tính
khoảng cách từ điểm A đến mặt phẳng  A B  C  . 2 5a 5a 3 5a A. 2 5a . B. . C. . D. . 5 5 5 Lời giải Chọn B A C
Dựng AH  AB . BC  AB  B Ta có
  BC   AAB  BC  AH BC  AA     H Vậy AH  A BC  d  ,
A  A BC   AH . A C 1 1 1
Xét tam giác vuông AAB có   2 2 2 AH AA AB AA .AB 2 . a a 2 5a  AH    . B 2 2 2 2  5 AA  AB 4a  a 8.
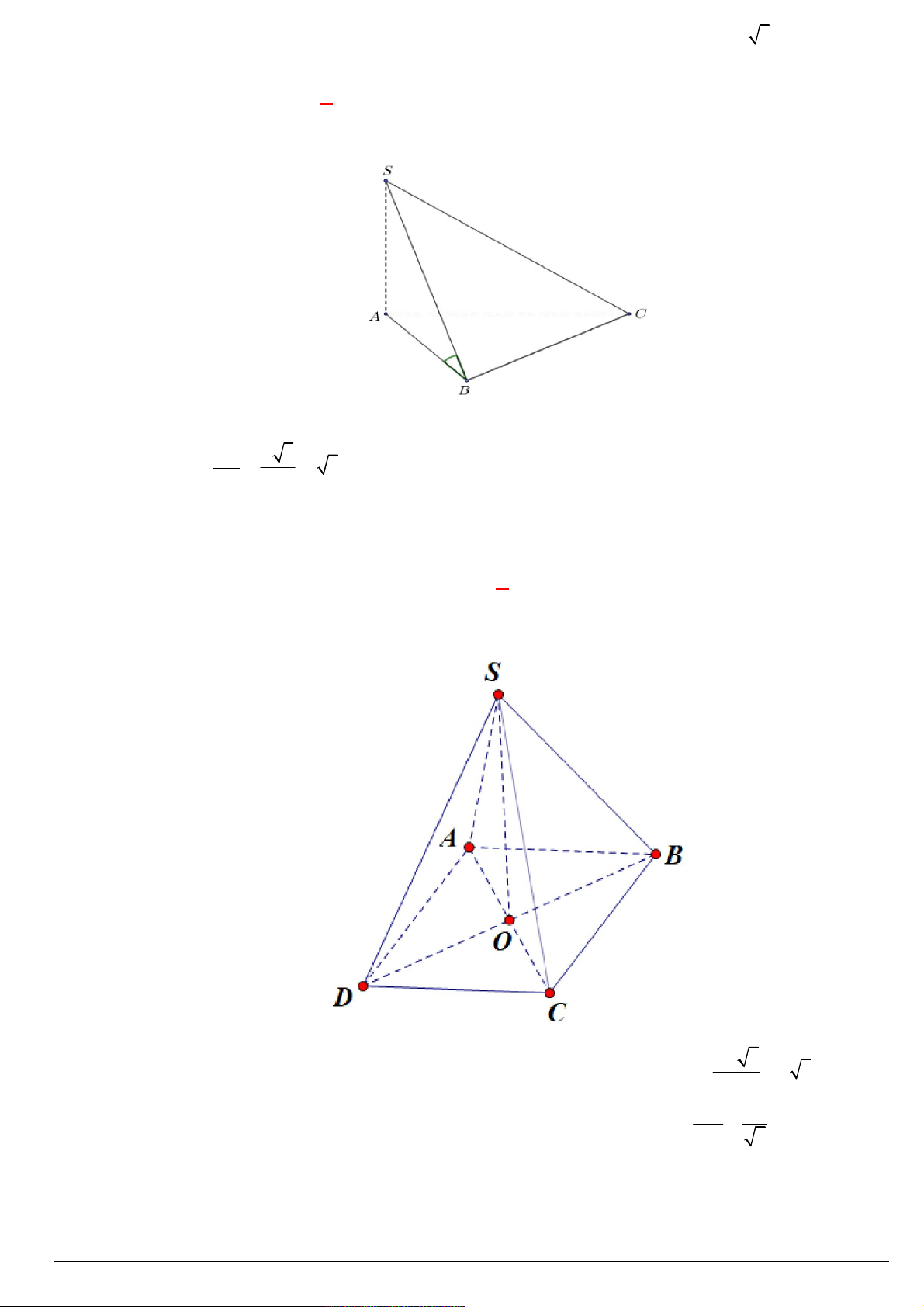
Cho chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông tại B . Biết SA  AB  BC .
Tính góc giữa đường thẳng SB và mặt phẳng  SAC  . 1 A. 30 . B. 45 . C. 60 . D. arc cos . 3 Lời giải Chọn A S
Gọi I là trung điểm của AC  BI  AC (vì A  BC
vuông cân tại A ).   1
Mặt khác: SA  BI (vì SA   ABC  ) 2 Từ  
1 và 2 , suy ra: BI   SAC  .
 SI là hình chiếu của SB lên  SAC  . I C A
  SB  SAC    SB SI   , ,   BSI . Xét BSI 
vuông tại I , ta có: B AB 2  BI 1 sin BSI  2     BSI  30 . SB AB 2 2
Trường THPT Hai Bà Trưng – Huế Trang 62/81 9.
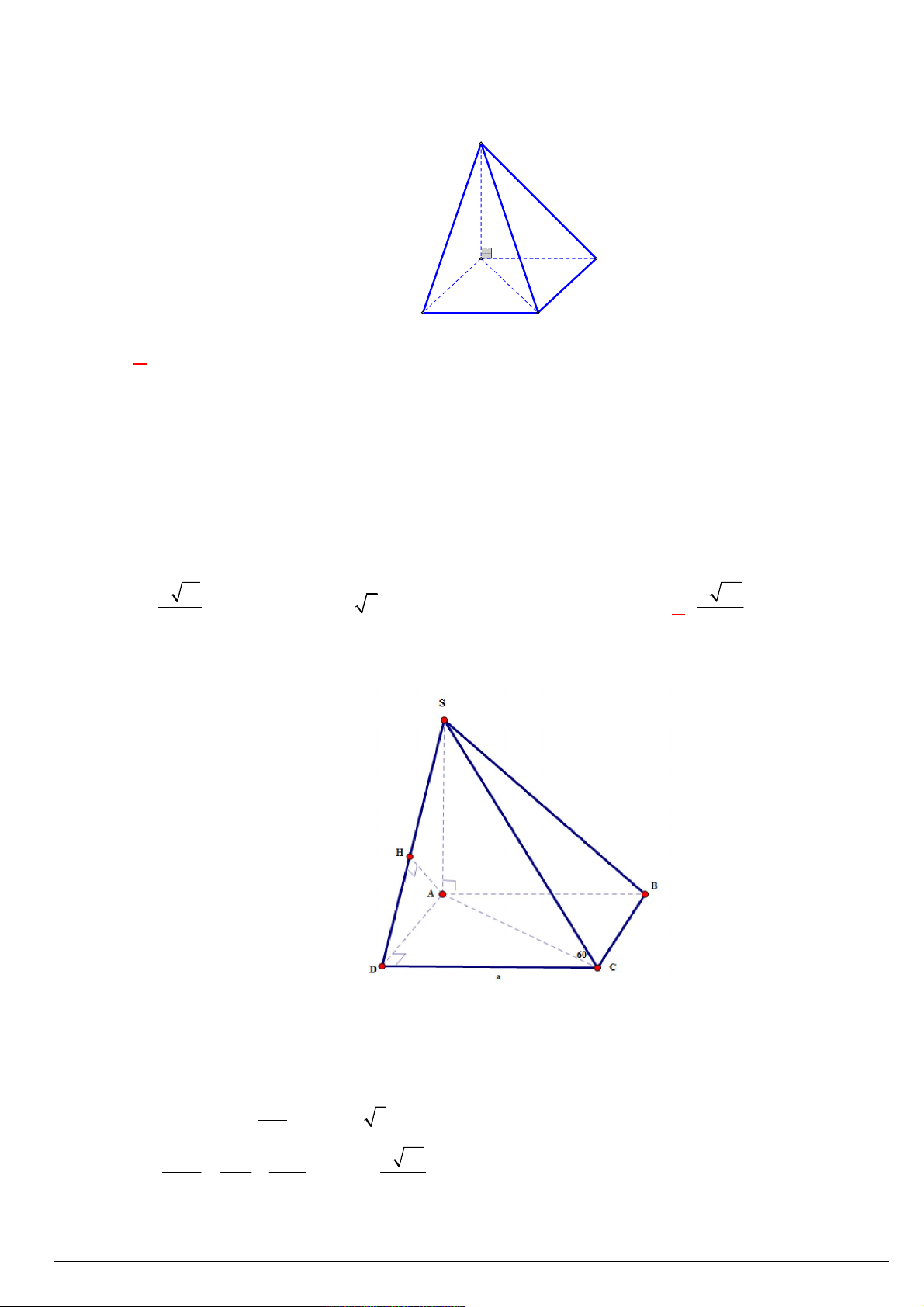
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D ; SD vuông góc với mặt đáy
( ABCD) ; AD  2a ; SD  a 2. Tính khoảng cách giữa đường thẳng CD và mặt phẳng  SAB . 2a a a 3 A. . B. . C. a 2 . D. . 3 2 3 Lời giải Chọn A S
Gọi H là hình chiếu vuông góc của D trên SA . Khi đó ta có: AB  AD 
 AB   SDA  AB  DH ; AB   SD H DH  AB 
 DH  SAB . DH   SA
Ta có CD //  SAB  d CD, SAB  d D, SAB C . SD AD 2a 2 2a D  DH    . 2 2 SD  AD 6 3 A B 10.
Cho hình chóp S.ABC trong đó SA , AB , BC vuông góc với nhau từng đôi một. Biết
SA  a 3 , AB  a 3 . Tính khoảng cách từ điểm A đến mặt phẳng  SBC  . a 2 2a 5 a 3 a 6 A.  B.  C.  D.  3 5 2 2 Hướng dẫn giải Chọn D S H A C B
Hạ AH  SB .
Ta có BC  SA và BC  AB nên BC   SAB  BC  AH do đó AH  SBC  hay AH  d  ;
A SBC  . 1 1 1 1 1 a 6 Khi đó      AH  . 2 2 2 AH SA AB 2 2 3a 3a 2
Trường THPT Hai Bà Trưng – Huế Trang 63/81 11.
Cho hình chóp S.ABCD có SA  a , SB  2a , SC  3a ,  
ASB  BSC  60 , 
CSA  90 . Gọi  là
góc giữa hai đường thẳng SA và BC . Tính cos . 7 7 2 A. cos  . B. cos   . C. cos  0 . D. cos  . 7 7 3 Lời giải Chọn A  
     . SA BC .( SA SC  SB) cos  cos( , SA BC)   . SA BC . SA BC
    . SA SC  . SA SB .
SA SC.cos 90  . SA . SB cos 60 7    . . SA BC 2 2 .
a 4a  9a  2.2 .3 a . a cos 60 7 12.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Biết SA vuông góc với đáy và SA  a . Tính
khoảng cách từ điểm A đến mp  SBD . 2a a a a 2 A. . B. . C. . D. . 3 3 2 3 6 Lời giải Chọn B S H A D O B C
Gọi O là giao điểm của AC và BD . BD  AC Ta có 
 BD  SAC  , BD   SBD   SBD   SAC  và  SAC    SBD  SO BD  SA 
Trong mặt phẳng  SAC  , kẻ AH  SO thì AH  SBD  AH  d  ,
A  SBD . Mặt khác 1 a 1 1 1
Tam giác SAO vuông tại A có OA  AC  , SA  a và   2 2 2 2 2 AH SA OA 1 2 1 3 a      AH  2 2 2 2 AH a a a 3 a Vậy d  ,
A  SBD  . 3
Trường THPT Hai Bà Trưng – Huế Trang 64/81 13.
Cho tứ diện ABCD có tam giác BCD đều cạnh a , AB vuông góc với mp  BCD , AB  2a . M là
trung điểm đoạn AD , gọi  là góc giữa CM với mp  BCD . khi đó: 3 2 3 3 2 6 A. tan   . B. tan   . C. tan   . D. tan   . 2 3 2 3 Lời giải. Chọn B A
Gọi N là trung điểm BC .
Ta có góc giữa CM với mp  BCD bằng góc  MCN . 2a M AB + MN   a . 2 a 3 + CN  . B D N 2 a φ MN 2 2 3 Vậy tan    . a  . CN a 3 3 C 14.
Hình chóp S.ABCD có đáy là hình thoi cạnh a , góc  0
BAC  60 , SA vuông góc với mp  ABCD
góc giữa hai mặt phẳng  SBC  và  ABCD bằng 60 . Khoảng cách từ A đến mp SBC  bằng: a 2 3a A. . B. 2a . C. . D. a . 3 4 Lời giải. S Chọn C
+ ABCD là hình thoi, góc  0
BAC  60 nên ta có tam giác ABC đều. H A D
+ Gọi M là trung điểm BC ta có góc giữa  SBC  và đáy
 ABCD bằng góc  0 SMA  60 . B M C
+ Gọi H là hình chiếu vuông góc của A lên SM ta có: BC  SA + 
 BC  SAM   BC  AH . BC  AM 
Lại có: AH  SM  AH  SBC   d  ,
A  SBC   AH . a 3 AH 3 a 3 3 3a + AM  .  sin 60   AH  .  . 2 AM 2 2 2 4
Trường THPT Hai Bà Trưng – Huế Trang 65/81 15.
Cho hình chóp S.ABC có SA , SB , SC đôi một vuông góc với nhau và SA  SB  SC  a . Gọi M
là trung điểm của AB . Tính góc giữa hai đường thẳng SM và BC . A. 60 . B. 30 . C. 90 . D. 120 . Lời giải Chọn A C
Gọi N là trung điểm của AC . Khi đó góc giữa SM và BC
bằng góc giữa SM và MN . Ta có:
AB  BC  CA 1 N SM 
AB (trung tuyến trong tam giác vuông ứng với cạnh 2 huyền). 1 B S SN 
AC (trung tuyến trong tam giác vuông ứng với cạnh 2 M huyền). 1 MN  BC . A 2
Suy ra SM  MN  SN hay tam giác SMN đều. Do đó  SM BC  ;  SMN  60 . S 16.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . SA   ABCD
và SA  a 3 . Khi đó khoảng cách từ điểm B đến mặt phẳng  SAC  bằng D C
A. d  B, SAC   a .
B. d  B, SAC   a 2 . a A B
C. d  B, SAC   2a .
D. d  B, SAC   . 2 Lời giải Chọn D
Gọi O là tâm hình vuông ABCD . BO  AC Ta có: 
 BO   SAC  BO  SA  a 2
 d  B, SAC   BO  . 2
Trường THPT Hai Bà Trưng – Huế Trang 66/81 17.
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng . a S
Gọi M là điểm trên đoạn SD sao cho SM  2MD .Tan góc giữa
đường thẳng BM và mặt phẳng  ABCD là 1 5 M A. . B. . 3 5 A D 3 1 C. . D. . 3 5 B C Lời giải Chọn D S M A D H O B C a 2
Ta có BD  a 2  OD  . 2 2  a 2  a 2
Xét tam giác SOD vuông tại O có: 2 2 2
SO  SD  OD  a     .  2  2  
Kẻ MH  BD tại H nên  BM  ABCD  ;  MBH MH MD HD 1
Do MH  BD  MH // SO . Ta có    . SO SD OD 3 SO a 2 1 a 2 a 2 5a 2  MH   và HD  OD 
 BH  BD  HD  a 2   . 3 6 3 6 6 6
Xét tam giác BHM vuông tại H có:  MH
BM  ABCD  tan ;  MBH  
BM  ABCD 1 tan ;  . BH 5
Trường THPT Hai Bà Trưng – Huế Trang 67/81 18.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA   ABCD và SA  a 3 Gọi  là góc
tạo bởi giữa đường thẳng SB và mặt phẳng  SAC  , khi đó  thỏa mãn hệ thức nào sau đây: 2 2 2 2 A. cos  . B. sin  . C. sin  . D. cos  . 8 8 4 4 Lời giải Chọn C S D A O B C
Gọi O là tâm của đáy ABCD .
Ta có BO  AC và BO  SA nên SO là hình chiếu của SB trên  SAC  . Suy ra    BSO . a 2 BO 2 Lại có BO  , 2 2 SB 
SA  AB  2a . Suy ra sin   . 2 SB 4 19.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . SA vuông góc với mặt phẳng  ABCD và
SA  a 6 (hình vẽ). Gọi  là góc giữa đường thẳng SB và mặt phẳng  SAC  . Tính sin ta được kết quả là S A D B C 1 2 3 1 A. . B. . C. . D. . 14 2 2 5 Lời giải Chọn A
Gọi O là tâm hình vuông ABCD thì BO  SAC 
   SB SAC   ,   BSO . a 2 BO 1
Ta có SB  a 7 , sin  2   . SB a 7 14
Trường THPT Hai Bà Trưng – Huế Trang 68/81 20.
Cho hình chóp S.ABCD có các cạnh bên bằng nhau và bằng 2a , đáy là hình chữ nhật ABCD có   
AB  2a , AD  a . Gọi K là điểm thuộc BC sao cho 3BK  2CK  0 . Tính khoảng cách giữa hai
đường thẳng AD và SK . 165a 2 165a 2 135a 135a A. . B. . C. . D. . 15 15 15 15 Lời giải Chọn B S H D C M I O K A B
Gọi O là tâm của hình chữ nhật ABCD thì SO là chiều cao của hình chóp S.ABCD . 2 5a a 11 2 2 2 SO  SA  OA  4a   . 4 2
Do SK  SBC  mà BC//AD nên khoảng cách giữa hai đường thẳng AD và SK là khoảng cách
giữa đường thẳng AD và mặt phẳng  SBC  không phụ thuộc SK . a 15
Gọi I , M lần lượt là trung điểm của BC , AD suy ra 2 2 SI  SO  OI  . 2
Trong tam giác SMI dựng đường cao MH thì MH là khoảng cách cần tìm. . SO MI 2a 165
Ta có: MH.SI  . SO MI  MH   . SI 15 21.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy, SA  a 3 .
Khoảng cách giữa hai đường thẳng SB và CD là a 3 a A. . B. . C. a 3 . D. a . 2 2 Lời giải Chọn D S a 3 A B a D C
Ta có: BC   SAB  BC  SB và BC  DC .
Do đó, BC chính là đoạn vuông góc chung của hai đường thẳng SB và DC .
Nên khoảng cách giữa hai đường thẳng SB và DC là BC  a .
Trường THPT Hai Bà Trưng – Huế Trang 69/81 22.
Cho hình chóp S.ABCD đều có AB  2a , SO  a với O là giao điểm của AC và BD . Khoảng
cách từ O đến mặt phẳng  SCD bằng a 3 a a 2 A. . B. a 2 . C. . D. . 2 2 2 Lời giải Chọn D S H A D M O B C C  D  OM
Gọi M là trung điểm của cạnh CD , ta có 
 CD   SOM    SCD  SOM . CD  SO 
Trong mặt phẳng  SOM  kẻ OH  SM ,  H  SM  thì OH là khoảng cách từ điểm O đến mặt phẳng  SCD . 1 1 1 1 1 2 a 2 Ta có       OH  . 2 2 2 OH OM SO 2 2 a a 2 a 2 23.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  2a , AD  a . SA vuông góc với mặt
phẳng đáy. SA  a 3 . Cosin của góc giữa SC và mặt đáy bằng 5 7 6 10 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn D
Hình chiếu của SC lên  ABCD là AC 
Do đó SC  ABCD  ,   SCA   Ta có 2 2 2 2 AC  AB  AD 
4a  a  a 5  SC  2a 2 AC a
Trong tam giác vuông SAC :  5 10 cos SCA    . SC 2a 2 4
Trường THPT Hai Bà Trưng – Huế Trang 70/81 24.
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B , AB  BC  a , SA  a 3 , SA   ABC  .
Góc giữa hai mặt phẳng  SBC  và  ABC  là A. 45 . B. 60 . C. 90 . D. 30 . Lời giải Chọn B
Ta có BC   SAB  BC  SA . Góc giữa hai mặt phẳng  SBC  và  ABC  là góc  SBA .  SA a 3 tan SBA    3   SBA  60 . AB a 25.
Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh 2a , 
ADC  60 . Gọi O là giao điểm của
AC và BD , SO   ABCD và SO  a . Góc giữa đường thẳng SD và mặt phẳng  ABCD bằng A. 60 . B. 75 . C. 30 . D. 45 . Lời giải Chọn C 2 . a 3
Ta có ABCD là hình thoi cạnh 2a , và 
ADC  60 nên A
 CD đều và OD   a 3 . 2  SO 1
Góc giữa đường thẳng SD và mặt phẳng  ABCD là 
SDO và tan SDO   suy ra DO 3  SDO  30 .
Trường THPT Hai Bà Trưng – Huế Trang 71/81 26.
Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng a . Khoảng cách từ A đến mặt phẳng  A B  C  bằng a 2 a 6 a 21 a 3 A. . B. . C. . D. . 2 4 7 4 Lời giải Chọn C A' C' B' H A C M B
Gọi M là trung điểm của BC , H là hình chiếu của A trên A M  ta có: BC  AM 
 BC   AA M 
 mà AH   AAM   BC  AH . BC  AA   AH  BC 
 AH   ABC  nên d  , A  A B
 C   AH .
AH  AM  a 3 . a AM .AA a 21
Trong tam giác AAM vuông tại A có AH  2   . 2 2 AM  AA 2   7 2 a 3 a    2   27.
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB  a 2 , AD  a và SA   ABCD . Gọi M là
trung điểm của đoạn thẳng AB (tham khảo hình vẽ). Góc giữa hai mặt phẳng  SAC  và  SDM  bằng S A M B D C A. 45 . B. 60 . C. 30 . D. 90 . Lời giải S Chọn D AM AD 2
Gọi N  AC  DM . Ta có   , do đó hai tam giác BC AB 2 H
ABC và DAM đồng dạng, suy ra  
AMN  MAN  90 . A M B
Vậy AC  DM  DM   SAC  mà DM  SDM 
nên góc giữa hai mặt phẳng  SAC  và  SDM  là 90 . N D C
Trường THPT Hai Bà Trưng – Huế Trang 72/81 28.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Góc giữa cạnh bên và mặt phẳng đáy bằng
60 . Tính khoảng cách từ đỉnh S đến mặt phẳng  ABCD . a 6 a 3 A. a 2 . B. . C. . C. a . 2 2 Lời giải S Chọn B
Trong  ABCD gọi O là giao điểm của AC và BD .
Ta có: SO   ABCD .
 d  S, ABCD  SO . A B
Ta lại có: OB là hình chiếu của SB lên mặt phẳng  ABCD a O D
  SB  ABCD   SB OB  , ,  SBO  60 . C a a Xét SOB 
vuông tại O , ta có:  2 6 SO  . OB tan SBO  . tan 60  . 2 2 a
Vậy d S  ABCD 6 ,  . 2 29.
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  2a . Biết SA vuông góc với đáy
 ABC  (Hình tham khảo). Khoảng cách từ điểm B đến mặt phẳng SAC  bằng S A C B 3a a 2 A. 2a . B. . C. 2a . D. . 2 2 Lời giải Chọn C S A M C B
Ta có: AC  2 2a . Gọi M là trung điểm AC . BM  AC AC Ta có: 
 BM   SAC   d  B,SAC   BM   a 2 . BM  SA  2
Trường THPT Hai Bà Trưng – Huế Trang 73/81 30.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB  a , AD  a 3 . Cạnh bên SA vuông
góc với đáy và SA  2a . Tính khoảng cách d từ điểm C đến mặt phẳng  SBD . 2a 57 2a a 5 a 57 A. d  . B. d  . C. d  . D. 19 5 2 19 Lời giải Chọn A S K A D I H B C
Gọi H là hình chiếu cúa A lên BD .
Gọi K là hình chiếu của A lên SH . Suy ra AK  SBD tại K nên d  ,
A  SBD  AK .
Tam giác ABD vuông tại A có AH  BD 1 1 1 1 1 3a a 3      2  AH   AH  2 2 2 2 AH AB AD a a 32 4 2
Tam giác SAH vuông tại A có AK  SH 1 1 1 1 1 19 2 12a 2a 57       2  AK   AK  . 2 2 2 AK SA AH 2a2 2 2 12  a 3 a  19 19   2   d  , A  SBD IA
Gọi I  AC  BD  I  AC  SBD  
. Mà ABCD là hình chữ nhật nên
d C, SBD IC IA a
I là trung điểm AC nên
 1 nên d C SBD  d  A  SBD 2 57 , ,  . IC 19
Trường THPT Hai Bà Trưng – Huế Trang 74/81 31.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy (tham khảo hình
vẽ bên). Góc giữa hai mặt phẳng  SCD và  ABCD bằng S A D B C A. Góc  SDA . B. Góc  SCA . C. Góc  SCB . D. Góc  ASD . Lời giải Chọn A C  D   SAD Ta có 
  ABCD SCD  ,  SDA .  ABCD 
 SCD  CD  32.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a , SA vuông góc với mặt phẳng
 ABCD. Biết góc giữa SC và mặt phẳng  ABCD bằng 60 . Tính khoảng cách h từ B đến mặt phẳng SCD . a 10 a 42 A. . B. a 2 . C. a . D. . 5 7 Lời giải Chọn D
Ta có AB// SCD nên h  d  B,SCD  d  ,
A SCD  AH
Vì CD   SAD   SCD   SAD theo giao tuyến SD , dựng AH  SD  AH   SCD .
Theo đề góc giữa SC và mặt phẳng  ABCD bằng 60 nên  SCA  60 . SA Ta có: tan 60   SA  a 6 AC 1 1 1 a 42 Và    AH  . 2 2 2 AH SA AD 7
Trường THPT Hai Bà Trưng – Huế Trang 75/81 33.
Cho hình lập phương A . BCD AB C  D
  có cạnh bằng a 2 tính khoảng cách của hai đường thẳng CC và B . D a 2 a 2 A. . B. . C. a . D. a 2 . 2 3 Lời giải Chọn C A' D' B' C' A D O B C O  C  BD Ta có vì ABC . D A B  C  D     OC  CC 
 OC là khoảng cách của hai đường thẳng CC và BD
Mà ABCD là hình vuông có cạnh bằng a 2  AC  2a  OC  a . a 6 34.
Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh a và SA   ABCD . Biết SA  . 3
Góc giữa SC và  ABCD là: A. 45 . B. 30 . C. 75 . D. 60 . Lời giải Chọn B S a 6 3 A D a B a C
Ta có: SA   ABCD .
Do đó AC là hình chiếu của SC lên  ABCD .
  SC, ABCD   SC, AC    SCA . a 6 SA 3
Xét tam giác SAC vuông tại A có  3 tan SCA    . AC a 2 3   SCA  30 .
Vậy góc giữa SC và  ABCD là 30 .
Trường THPT Hai Bà Trưng – Huế Trang 76/81 35.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a có SA   ABCD và SA  a 2 . Gọi
M là trung điểm SB . Tính tan góc giữa đường thẳng DM và  ABCD . 5 2 2 10 A. . B. . C. . D. . 5 5 5 5 Lời giải Chọn D S M A D N B C
Gọi N là trung điểm AB . 1 a 2
Ta có: MN là đường trung bình của SAB 
nên MN //SA và MN  SA  . 2 2
Lại có: SA   ABCD .
Do đó MN   ABCD   1 .
Suy ra MN  DN .
Ta có: N là hình chiếu vuông góc của M lên  ABCD (do  
1 ) và D là hình chiếu vuông góc của
D lên  ABCD .
Suy ra  DM ; ABCD   DM ; ND   MDN ( 
MDN nhọn vì MND  vuông tại N ). a 5 Ta có: 2 2 DN  AD  AN  . 2 Xét MND  vuông tại N , có: MN 10 tan MDN   . DN 5 Vậy
DM  ABCD 10 tan ;  . 5
Trường THPT Hai Bà Trưng – Huế Trang 77/81 36.
Cho hình lập phương ABC . D A B  C  D
  có cạnh là a  0 . Khi đó, khoảng cách giữa hai đường thẳng
chéo nhau AB và BC là a 3 a 3 a 2 a 6 A. . B. . C. . D. . 2 3 3 3 Lời giải Chọn B
Gọi O là tâm hình vuông ABCD . Trong mặt phẳng  ACC A
  , kẻ CH  C O  tại H ,
mà CH  BD (do BD   ACC A
  ) nên CH  C BD 
  d C;C BD    CH
Ta có: AB // C BD 
  d  AB , BC  d  AB ,C BD    d  , A C BD 
  d C,C BD    CH Xét  C CO 
vuông tại C , đường cao CH : 1 1 1 3 a 3     CH  . 2 2 2 2 CH CO CC a 3 37.
Cho tứ diện ABCD có tất cả các cạnh đều bằng a  0 . Khi đó khoảng cách từ đỉnh A đến
mp  BCD bằng a 6 a 3 a 8 a 2 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn A
Gọi O là trọng tâm tam giác BCD  AO   BCD  d  ;
A  BCD  AO .
Gọi I là trung điểm CD . 2 a 3 a Ta có: BO  BI  , 2 2 6 AO  AB  BO  . 3 3 3 a
Vậy d  A  BCD 6 ;  . 3
Trường THPT Hai Bà Trưng – Huế Trang 78/81 38. Cho hình lập phương . ABCD AB C  D
  . Gọi O là trung điểm của của AC . Tính tan  với  là
góc tạo bởi BO và mặt phẳng  ABCD . 2 A. 3 . B. 2 . C. 1. D. . 2 Lời giải Chọn B
Đặt cạnh hình lập phương bằng a . Ta có BO ,   ABCD  
  BO ,A B C D   . Ta có O B
  là hình chiếu của BO trên  A B  C  D   BB a  BO ,   ABCD    
 BO , B O     BO B     , tan     2 . O B   a 2
Trường THPT Hai Bà Trưng – Huế Trang 79/81 39.
Cho hình chóp tứ giác đều S.ABCD , có đáy ABCD là hình vuông, cạnh bên bằng cạnh đáy và bằng
a . Gọi M là trung điểm của SC . Góc giữa hai mặt phẳng  MBD và  ABCD bằng A. 90 . B. 30 . C. 45 . D. 60 . Lời giải Chọn C
Gọi O là tâm hình vuông ABCD , Ta có: BD  SO 
 BD  SOC   BD  OM . BD  AC  
 MBD   ABCD  BD    BD  OM
  MBD, ABCD  
  OM,OC  MOC . BD  OC  SC a a 2 OM  MC  
 MOC cân tại M ; OC  . 2 2 2 a 2 OC 2  
cos MOC  cos MCO  2     MOC  45 . SC a 2
Vậy  MBD, ABCD     45.
Trường THPT Hai Bà Trưng – Huế Trang 80/81 40.
Hình chóp S.ABCD đáy hình vuông cạnh a , SA   ABCD ; SA  a 3 . Khoảng cách từ B đến
mặt phẳng  SCD bằng: a 3 a 3 A. a 3 . B. . C. 2a 3 . D. . 2 4 Lời giải Chọn B S H a 3 A D B a C
Ta có: AB // SCD  d  B, SCD  d  ,
A SCD .
Kẻ AH  SD   1 .
CD  SA , CD  AD  CD   SAD  AH  CD  AH 2 . Từ  
1 , 2 ta có: AH   SCD  d  ,
A  SCD  AH . 1 1 1 2 3a a 3
Trong tam giác vuông SAD :   2  AH   AH  . 2 2 2 AH SA AD 4 2
Trường THPT Hai Bà Trưng – Huế Trang 81/81

Đề cương ôn tập HK2 Toán 11 năm 2018 – 2019 trường Hai Bà Trưng – TT Huế

Thông tin :

Tài liệu liên quan:

Đề cuối kỳ 2 Toán 11 năm 2023 – 2024 trường THPT Trần Cao Vân – Gia Lai

Đề cuối học kì 2 Toán 11 năm 2023 – 2024 trường THPT Phạm Thành Trung – Tiền Giang

Đề cuối kì 2 Toán 11 năm 2023 – 2024 trường THPT Phan Ngọc Hiển – Cà Mau

Đề cuối học kỳ 2 Toán 11 năm 2023 – 2024 trường THPT Tam Đảo 2 – Vĩnh Phúc

Đề cuối học kỳ 2 Toán 11 năm 2023 – 2024 trường THPT Dĩ An – Bình Dương