Đề cương ôn tập thi học kỳ 2 Toán 11 – Đặng Ngọc Hiền

Tài liệu ôn tập thi học kỳ 2 Toán 11 do thầy Đặng Ngọc Hiền sưu tầm và biên soạn. Nội dung đề cương gồm:

+ Các chủ đề cần ôn tập
+ Tóm tắt lý thuyết và các công thức tính toán
+ Bài tập trắc nghiệm có đáp án

 

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 11

Môn: Toán 11

Thông tin:

29 trang 6 tháng trước

Tác giả:

Profile Kim Oanh
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page1
SỞ GIÁO DỤC & ĐÀO TẠO MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2016 – 2017
TỈNH BÀ RỊA – VŨNG TÀU MÔN: TOÁN KHỐI 11
I. CHỦ ĐỀ CHÍNH
A. Đại số và Giải tích
Chương IV: Giới hạn
1. Giới hạn của dãy số.
2. Giới hạn của hàm số.
3. Hàm số liên tục (hàm số liên tục tại điểm, trên tập I, tính chất hàm số liên tục).
4. Chứng minh về số nghiệm của phương trình.
Chương V: Đạo hàm
1. Đạo hàm (định nghĩa đạo hàm, quy tắc tính đạo hàm, đạo hàm của hàm số lượng giác).
2. Tiếp tuyến của đồ thị hàm số.
B. Hình học
1. Vectơ trong không gian.
2. Chứng minh quan hệ vuông góc.
3. Bài toán liên quan đến góc.
4. Bài toán liên quan đến khoảng cách.
5. Thiết diện vuông góc.
II. MA TRẬN
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I I
Môn: TOÁN – Lớp: 11
Thời gian làm bài: 90 phút
Tên chủ đề Nhận biết - Thông hiểu
Vận dụng
Tổng
Cấp độ thấp Cấp độ cao
Chương IV.
Giới hạn –
Hàm số liên
tục
- Giới hạn dãy số.
- Giới hạn hàm số tại một điểm.
- Giới hạn một bên.
- Giới hạn vô cực, tại vô cực.
- Xét tính liên tục của hàm số tại một
điểm, trên khoản
g
.
Chứng minh về số
nghiệm của
phương trình.
Số câu TN
Số điểm
Tỷ lệ %
5
1,0
10%
5
1,0
10%
Số câu TL
Số điểm
Tỷ lệ %
3
2,0
20%
1
0,75
7,5%
4
2,75
27,5%
Chương V.
Đạo hàm
*Biết dùng quy tắc để tính đạo hàm
*Tính được đạo hàm các hs l.giác
*Giải phương trình, bất pt, chứng minh
hệ thức có chứa đạo hàm.
Lập phương trình
tiếp tuyến với đồ
thị tại một
điểm,biết hệ số
góc(song song
hoặc vuông góc
với đường thẳng
cho trước
)
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page2
Số câu TN
Số điểm
Tỷ lệ %
4
0,8
8%
2
0,4
4%
6
1,2
12%
Số câu TL
Số điểm
Tỷ lệ %
1
0,75
7,5%
1
0,75
7,5%
Chương III.
Vec tơ trong
k.gian-Quan
hệ vuông góc
- Nhận biết quan hệ vuông góc giữa hai
đường thẳng ở dạng đơn giản
-Chứng minh hai đường thẳng vuông
góc
-Chứng minh đường thẳng vuông góc
với mặt phẳng
-Chứng minh hai
mặt phẳng vuông
góc
*Xác định và tính
góc giữa các đối
tượng véc
tơ,đường thẳng,
mặt phẳng
*Xác định và tính
khoảng cách giữa
các đối tượng:
điểm, đường
thẳng, mặt phẳng
* Xác định thiết
diện vuông góc đt,
m
p
Số câu TN
Số điểm
Tỷ lệ %
5
1,0
10%
2
0,4
4 %
7
1,4
14%
Số câu TL
Số điểm
Tỷ lệ %
1
1,0
10%
1
1,0
10%
2
2,0
20%
Bài tập tổng
hợp
Sử dụng tổng
hợp các kiến
thức
Số câu TN
Số điểm
T
ỷ
lệ %
2
0,4
4%
2
0,4
4%
Số câu TL
Số điểm
T
ỷ
lệ %
1
0,5
5%
1
0,5
5%
Tổng số câu
Tổng số điểm
Tỉ lệ%
14TN+4TL
2,8+3,0=5,8
58%
4TN+3TL
0,8+2,5=3,3
33%
2TN+1TL
0,4+0,5=0,9
9%
20 TN+8TL
4,0+6,0=10,0
100%
III. CẤU TRÚC ĐỀ
Trắc nghiệm : 20 câu : Thời gian 35 phút
Tự luận : Thời gian 55 phút
Bài 1.(1,5 điểm) : Chủ đề 1 (Giới hạn)
Bài 2.(1,0 điểm) : Chủ đề 1 (Tính liên tục của hàm số)
Bài 3.(1,0 điểm) : Chủ đề 2 (Đạo hàm hàm số)
Bài 4.(2,0 điểm) : Chủ đề 3 (Hình học)
Bài 5.(0.5 điểm) : Tổng hợp
IV. HÌNH THỨC KIỂM TRA VÀ THỜI GIAN
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page3
- Hình thức tự luận và trắc nghiệm.
- Thời gian làm bài : 35 phút trắc nghiệm và 55 phút tự luận.
Lưu ý : + Các trường tự soạn đề ôn tập theo ma trận đề trên.
+ Trong mỗi câu tự luận có thể gồm nhiều ý.
+ Học sinh làm phần trắc nghiệm lên phiếu trả lời trắc nghiệm, phần tự luận làm trên tờ giấy thi.
Bà Rịa-Vũng Tàu, ngày 26 tháng 2 năm 2017
GIỚI HẠN DÃY SỐ
KIẾN THỨC CẦN NHỚ
I. Giới hạn hữu hạn
1. Giới hạn đặc biệt



*
11
lim 0 ; lim 0
lim 0 1
lim


k
n
kN
nn
qq
c c c la hang so
2. Định lý
A.
Nếu
lim ,lim
nn
ua vb
thì:



*lim
*lim
*lim . .
*lim 0



nn
nn
nn
n
n
uv ab
uv ab
uv ab
ua
b
vb
B.Nếu 0, lim
nn
unvaua thì
0lim
n
ava u a
C. Nếu lim lim
nn
uathi u a
3. Tổng của cấp số nhân lùi vô hạn

2
1
11 1
... 1
1

u
S u uq uq q
q
II. Giới hạn vô cực
1. Giới hạn đặc biệt
lim 
k
n
với k nguyên dương
lim 1
n
qq
2. Định lý
A.
Nếu lim , lim
nn
ua v thì lim 0
n
n
u
v
B. Nếu
lim , lim , 0
nnn
ua v v n
thì
lim 
n
n
u
v
C. Nếu lim , lim 0
nn
uva thì lim . 
nn
uv
CÂU HỎI TRẮC NGHIỆM
Câu 1.
Với k là số nguyên dương thì
1
lim
k
n
bằng
A.

. B.  . C.
0
. D. 1.
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
A.

11
lim lim ; 
k
k
nn
.
B. lim 0
n
q nếu 1q .
C.
lim cc
(
c
là hằng số).
D.
33
lim lim
nn
uu.
Câu 3. Dãy số nào sau đây có giới hạn khác 0?
A.
1
1n
. B.
1
n
. C. 0 D.
cosn
n
.
Câu 4. Dãy số nào sau đây có giới hạn bằng 0?
A.
3
2



n
. B.
5
4



n
. C.
2
3



n
. D.
4
3



n
.
Câu 5. Dãy nào sau đây không có giới hạn?
A.
2
3



n
. B.
2
3



n
. C.

0,99
n
. D.

1
n
.
Câu 6.
1
lim
2
n
n
có giá trị bằng
A.
1
2
.
B. 0 . C. 1 . D.
1
2
.
Câu 7. Dãy số nào sau đây có giới hạn khác 0?
A.
1
.
3
n
B.
1
.
n
n
C.
5
.
4



n
D.
2
2
.
n
Câu 8.
12
lim
4
n
n
có giá trị bằng
A.
1
4
.
B.
1
4
. C.
1
2
.
D.
1
2
.
Câu 9.
35
lim
5
nn
n
có giá trị bằng
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page4
A.
1
. B. 0 . C.
3
5
.
D.
8
5
.
Câu 10.
1
751
lim
3.4 7

nn
nn
có giá trị bằng
A. 7 . B. 0 . C. 1 . D.
1
3
.
Câu 11.
2
22
32
lim
332


nn n
nn n
có giá trị bằng
A.
1
3
.
B.
1
4
.
C.

. D. 1 .
Câu 12.
3
4
25
lim
22


nn
nn
có giá trị bằng
A.  . B. 2 . C.
0
. D.
6
.
Câu 13. Gọi
sin3
lim 4

n
L
n
thì L bằng số nào
sau đây?
A.
0.
B.
2.
C.
2
. D.
4.
Câu 14.
4
4
21
lim
32

nn
nn
có giá trị bằng
A. 0 . B.
2
3
.
C.  . D.
2
5
.
Câu 15.
32
2
24
lim
23


nn
nn
có giá trị bằng
A.
2
. B. 0 . C.  . D.
2
.
Câu 16.


2
2
23
lim
12 5


nn
nn
có giá trị bằng
A. 0 . B.
1
2
.
C. 1. D.  .
Câu 17. Tổng của cấp số nhân lùi vô hạn
2
11 1
... ...
55 5

n
S
có giá trị bằng
A.
1
5
.
B.
1
4
.
C.
2
5
.
D.
5
4
.
Câu 18. Cho các dãy số

,, ,
nn n n
uvw với
22
31 2
,
112


n
nn
n
n
uv
n
,
2017
4
n
n
w ,
41
2017 2
n
n
n
. Có bao nhiêu dãy số có giới
hạn bằng
0
trong các dãy số trên?
A. 1. B. 2 . C.
3
. D. 4 .
Câu 19. Biết
41
lim
2
n
a
n
. Hỏi
a
là nghiệm của
phương trình nào sau đây?
A.
2
40x
. B.
2
540xx
.
C.
2
540xx
. D.
2
4
0
54

x
xx
.
Câu 20.
32
lim 3 1nn có giá trị bằng
A. 2 . B. 1 . C.  . D.  .
Câu 21.
22
lim 2 nn n có giá trị bằng
A. 0 . B. 1. C.  . D.
1
2
.
Câu 22.
22
lim 2 nn n có giá trị bằng
A. 12 . B.  . C. 1 . D.  .
Câu 23.
2
2
2
lim
42


nnn
nn n
có giá trị bằng
A. 4. B. 2. C.
1
2
.
D.
1
2
.
Câu 24.
33
lim 1nn có giá trị bằng
A. 0 . B. 1. C.  . D.  .
Câu 25.
2
1 3 5 ... (2 1)
lim
32

n
n
có giá trị bằng
A. 0 . B. 1. C.
1
3
.
D.  .
Câu 26. ? có giá trị bằng
A. 0 . B.
2
. C.
1
. D. 1.
Câu 27. Cho dãy

1
1
1
:
1
n
n
n
n
u
u
u
u
u
. Lúc đó,
lim
n
u
bằng
A. 0 . B. 2. C. 1 . D. 1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
C B C C D B C D A A B C C B C B B C B C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D D A A C D A
GIỚI HẠN HÀM SỐ
KIẾN THỨC CẦN NHỚ
1.Định nghĩa :Giới hạn hữu hạn ,giới hạn vô cực
2.Các giới hạn đặc biệt
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page5
0
0
lim
xx
x
0
0
lim
xx
x
x (c: hằng số)
lim 0

x
c
x
(c: hằng số)
1
lim 0

k
x
x
lim


k
x
x
( *k )
lim

k
x
x
neáu k chaün
neáu k leû
3.Các định lí về giới hạn hữu hạn
Nếu
0
lim ( )
xx
f
xL
và
0
lim ( )
xx
g
xM
, thì:
0
lim . ( ) .
xx
cf x cL (với C là hằng số)
0
lim[ () ()]

xx
f
xgx L M
0
lim [ ( ) ( )]

xx
f
xgx L M
0
lim [ ( ). ( )] .
xx
f
xgx L M
0
()
lim
()
xx
f
xL
g
xM
(M
0)
0
lim ( )
xx
f
xL
0
3
3
lim ( )
xx
f
xL
Nếu
0
lim ( )

xx
fx thì
0
1
lim 0
()
xx
fx
- Nếu
0fx
và
0
lim ( )
xx
f
x L thì
0L
và
0
lim ( )
xx
f
xL
Chú ý: Định lí 1 vẫn đúng khi

x
Định lí 2.
0
00
lim() lim()lim()



xx
xx xx
f
xL fx fxL
4.Qui tắc về giới hạn vô cực:
Qui tắc tìm giới hạn của tích f(x).g(x)
Qui tắc tìm giới hạn của thương
f
(x)
g
(x)
CÂU HỎI TRẮC NGHIỆM
Câu 1.
Với
k
là số nguyên dương. Giá trị của

lim 2 1

k
x
x bằng:
A.
 . B. 0. C. 1. D. .
Câu 2.
Giá trị của
3
lim 4 6


x
xx bằng:
A.

. B. 0. C. 1. D. .
Câu 3. Giá trị của
1
23
lim
2
x
x
x
bằng:
A.
5. B.
3
.
2
C. 1. D. 2.
Câu 4.
Giá trị của
5
221
lim
5

x
x
x
bằng:
A.
.
B.
1.
C.
2.
D. .
Câu 5.
Giá trị của
2
210
lim
2
x
x
x
bằng:
A.
. B. 5. C. 2. D. .
Câu 6.
Giá trị của
3
3
36
lim
25


x
xx
x
bằng:
A.
. B.
1
.
2
C. 1. D. .
Câu 7.
Giá trị của
2
2
2
32
lim
310



x
xx
xx
bằng:
A.
1.
B.
0.
C.
1
.
7
D.
1.
Câu 8. Giá trị của
2
sin 2 3cos
lim
1


x
x
x
xx
bằng:
A.
2.
B.
0.
C.
4.
D.
5.
Câu 9.
Cho hàm số

32
52 fx x x
. Trong các
khẳng định sau, khẳng định nào
sai?
A.
Hàm số có giới hạn bên trái và giới hạn bên phải
tại
1
x
bằng nhau.
B. Hàm số có giới hạn bên trái và giới hạn bên phải
tại
0x không bằng nhau.
C. Hàm số có giới hạn tại mọi điểm.
D. Hàm số có tập xác định .DR
Câu 10. Giá trị của
22
lim 2 3 2 5


x
xx bằng:
A.
0. B. 22. C. 35. D. .
Câu 11.
Giá trị của
22
lim 2 3 2 5


x
xx
bằng:
A.
0. B. 22. C. 35. D. .
Câu 12.
Giá trị của
2
3
3
lim
815

x
xx
xx
bằng:
A.
3
.
2
B.
1.
C.
3
.
2
D.
1.
Câu 13.
Giá trị của
2
2
253
lim
4

x
x
x
bằng:
A. . B.
3
.
4
C.
1
.
12
D. 0.
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page6
Câu 14. Trong các giới hạn sau, giới hạn nào bằng 0?
A.
2
3
lim .
5

x
x
x
x
B.
3
24
lim .
1
x
x
x
C.
2
lim 4 5 2 .


x
x
x
D.
1
3
lim .
1
x
x
x
Câu 15. Cho hàm số

2
3
32khi 2
2 8 khi 2


xx x
fx
xx
.
Khi đó
2
lim
x
f
x
bằng:
A.
1
. B.
8.
C.
10
. D. Không tồn tại.
Câu 16. Giá trị của

42
21
lim
21 3



x
xx
xx
bằng:
A.
1
.
2
B.
1
.
2
C. . D. .
Câu 17. Giá trị của
3
3
lim
235

x
x
x
bằng:
A.
4
.
3
B. 0. C.
4
.
3
D. .
Câu 18. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
2
2
33
lim .
55


x
xx
xx
B.
0
1
lim .

x
x
C.
3
21 3
2
lim .
32 3


x
xx
x
D.
2
25
lim .
2

x
x
x
Câu 19. Giá trị của
2
31
lim
32


x
x
x
x
bằng:
A. 0. B. 1. C. 2. D. 3.
Câu 20. Tìm m để hàm số

2
2
23 1 2
32
2
2


xmxkhix
fx
xx
khi x
x
có giới hạn
khi
2.x
A.
2.
m
B.
1.
m
C.
1.
m
D.
2.
m
Câu 21. Giá trị của
2
4
213
lim
54


x
x
xx
bằng:
A.0. B.
1
.
9
C.
2
.
9
D. .
Câu 22. Giá trị của
3
12
lim
52


x
x
x
bằng:
A. . B. . C. 1. D. 0.
Câu 23. Giá trị của
2
2
40 5
lim
412 2




x
xx x
bằng:
A.
.
B. . C.
5
.
8
D.
5
.
8
Câu 24. Giá trị của
2
2
11
lim
56 2




x
xx x
bằng:
A. . B. . C. 0. D. 1.
Giá trị của
22
lim 5 8


x
xxx bằng:
A.
0.
B.
5
.
2
C.
5
.
2
D.
.
Câu 25. Giá trị của
22
lim 5 8


x
xxx bằng:
A.
0.
B.
5
.
2
C.
5
.
2
D.
.
Câu 26. Giá trị của

34
7
252
lim
1


x
x
x
x
bằng:
A.
8.
B.
2.
C.
2.
D.
8.
Câu 27. Giá trị của
3
3
23 76
lim
3

x
xx
x
bằng:
A. 0. B.
2
.
27
C.
16
.
27
D. .
Câu 28. Giới hạn nào sau đây có giá trị bằng
3?
A.
54
lim .
22



x
x
x
B.
1
25
lim .
1
x
x
x
C.

2
22
lim .
2

x
x
x
D.
2
3
23 5
lim .
2



x
xx
x
Câu 29. Giá trị của
322
lim
2





x
x
bằng:
A.
.
B.
0.
C.
1.
D. .
Câu 30. Giá trị của
1
54
lim
295



x
x
x
bằng:
A.
4
.
5
B.
4
.
5
C.
0.
D. .
Câu 31. Giá trị của

42
4
352
lim
3


x
x
x
x
bằng:
A. . B. 81. C. 81. D. .
Câu 32. Giá trị của
2
0
cos6 cos 2
lim
x
x
x
x
bằng:
A. 16. B. 2. C. 0. D. .
Câu 33. Giá trị của
22
1
lim tan
2
x
x
x
bằng:
A.
.
B. . C.
1
.
4
D.
1
.
4
Câu 34. Tìm giới hạn của hàm số

2
3 5 khi 2
2khi2

xx x
fx
x
.
A.
2. B. 2. C. 5. D. Không tồn tại.
Câu 35.
Giá trị của

2
0
12cos
lim
sin 2
x
x
x
x
bằng:
A.
1.
B.
1
.
2
C.
0.
D. .
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page7
Câu 36. Cho hàm số
4
() ( 0) fx ax bx ca . Khẳng
định nào sau đây là đúng?
A. Hàm số
()
f
x
có giới hạn là

khi

x
và
0a
.
B.
Hàm số
()
f
x
có giới hạn là

khi 
x
và
0a .
C. Hàm số
()
f
x
có giới hạn là

khi

x
và
0
a
.
D.
Hàm số ()
f
x có giới hạn là

khi

x
và
0a
.
Câu 37. Cho hàm số
() ( 0, 0)

ax b
fx c ad cb
cx d
.
Khẳng định nào sau đây là sai?
A.
lim ( )

x
a
fx
c
.
B.
lim ( )

x
a
fx
c
.
C.
lim ( )





d
x
c
fx
khi 0ad cb .
D.
lim ( )





d
x
c
fx
khi
0.ad cb
Câu 38. Cho hàm số
2
23
()
1

xx
fx
x
. Đặt

()
lim , lim ( )
 

xx
fx
abfxax
x
. Khi đó:
A.
1, 1ab
. B.
1, 2ab
.
C.
1, 1 ab
. D. 1ab .
Câu 39.
Cho hàm số
2
1
,khi 1
()
1
2 1, khi 1

x
x
fx
x
mx x
có giới
hạn hữu hạn khi
1x . Khi đó giá trị m
bằng:
A.
1
2
.
B.
1
2
.
C.
3
2
.
D.
3
2
.
Câu 40.
Cho 3ab và
32
1
21
lim 2
1

x
ax x bx
x
.
Khẳng định nào sau đây là đúng?
A. 34ab . B. 36ab .
C.
36ab . D. 34ab .
Câu 41.
Cho
22ab
và
2
2
4
lim 5
2

x
ax bx
x
. Khẳng
định nào sau đây là đúng?
A.
3
,1
2
ab.
B. 1, 0ab.
C.
1, 4 ab. D. 2,6 ab.
Câu 42.
Cho
2
2006
lim
2007


x
mx
L
xx
. Tìm
m để
0L
.
A.
0m
. B.
0m
.
C.
0m
. D.
11 m
Câu 43.
Cho hàm số ()yfx có đồ thị như hình vẽ:
Khẳng định nào sao đây là
sai?
A. lim ( )


x
fx . B. lim ( ) 0

x
fx .
C.
1
lim ( ) 2
x
fx . D.
2017
lim ( )

x
fx .
Câu 44. Cho hàm số ()yfx có đồ thị như hình vẽ:
Khẳng định nào sau đây là
sai?
A. lim ( ) 1

x
fx . B. lim ( ) 1

x
fx .
C.
(1)
lim ( )


x
fx
.
D.
(1)
lim ( )


x
fx
.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
D A A D A B C B B D A C C C B A A D B C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B C D B D D B D B A D A D D B D D A B B
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
A B D D
HÀM SỐ LIÊN TỤC
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page8
1 Hàm số liên tục tại một điểm
Định nghĩa:
Giả sử hàm số
f
xác định trên khoảng
; ab và
0
;
x
ab . Hàm số
f
được gọi là liên tục tại điểm
0
x
nếu:
() ( )
0
0
xx
lim f x f x
Theo định nghĩa trên, hàm số

f
x xác định trên khoảng
; ab là liên tục tại điểm
0
;
x
ab nếu và chỉ
nếu
()
0
xx
lim f x
và
()
0
xx
lim f x
tồn tại và
() () ( )
00
0
xx xx
limfx limfx fx



2 Hàm số liên tục trên một khoảng
Hàm số

f
x xác định trên khoảng

; ab được gọi là liên tục trên khoảng đó, nếu nó liên tục tại mọi
điểm của khoảng đó.
Chú ý: Đồ thị của một hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
Tính liên tục của một số hàm số:
Tổng, hiệu, tích, thương của hai hàm số liên tục tại một điểm là những hàn số liên tục tại điểm đó (giá trị
của mẫu tại điểm đó phải khác 0).
Hàm đa thức và hàm phân thức hữu tỉ liên tục trên tập xác định của chúng.
Các hàm sin, cos, tan, cotyxyxy xyx liên tục trên tập xác định của chúng.
3 Tính chất của hàm số liên tục
Nếu hàm
f
liên tục trên
; ab
và
.0fa fb
thì phương trình
0fx
có nghiệm trên khoảng

;ab
.
CÂU HỎI TRẮC NGHIỆM
Câu 1. Xét hai mệnh đề
I. Hàm số
02 1, khi
()
1 , khi 0
xx
fx
xx
liên
tục trên
II. Hàm số
21
, khi
()
2, khi
0
0
x
x
fx
x
x
liên tục tại
0x
Mệnh đề nào đúng?
A. Chỉ I. B. Chỉ II .
C. Cả I và II. D. Không có .
Câu 2. Cho

22
x
x
fx
x
với 0x . Phải
bổ sung thêm giá trị
0
f
bằng bao nhiêu thì hàm số
liên tục trên
.
A.
0.
B.
1.
C.
1
.
2
D.
1
.
22
Câu 3. Cho hàm số

2
khi 1, 0
0 khi 0
khi 1


x
xx
x
fx x
xx
.
Hàm số
f
x liên tục tại:
A. mọi điểm thuộc
.
B.
mọi điểm trừ 0x .
C. mọi điểm trừ
1
x
.
D.
mọi điểm trừ 0x và 1
x
.
Câu 4. Hàm số
f
x có đồ thị
như hình bên
không liên tục tại
điểm có hoành độ là bao nhiêu?
A.
0x
.
B.
1
x
.
C.
2x .
D.
3x .
Câu 5. Cho hàm số
2
2
1
() , ()
5x 6

x
f
xfx
x
liên tục
trên các khoản nào sau đây?
A. (3;2) . B. (3; ) C. (;3) . D. (2;3).
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page9
Câu 6. Cho
2
710
khi 2
() .
2
khi 2

xx
x
fx
x
ax
Hàm số
liên tục tại
2x
thì giá trị của
a
là:
A.
3.
B.
2.
C.
5.
D. Một số khác.
Câu 7. Cho
2
2
2
khi 2
6
() .
2
khi 2
5

xx
x
xx
fx
x
Hàm số
bị gián đoạn tại điểm nào sau đây?
A. 2.x B. 3.x
C. 0.x D. Một điểm khác.
Câu 8. Cho
2
1 khi 1
() .
2khi1

ax x
fx
x
Hàm số liên
tục trên
khi a có giá trị là:
A. 2. B. 0.
C. 1. D. Một số khác.
Câu 9. Cho
2
4
() .
2
x
x
fx
x
Để hàm số liên tục trên
thì phải định nghĩa (0)
f
bằng giá trị nào sau đây?
A.
0.
B.
4.
C.
2.
D.
2.
Câu 10. Cho
3
() .
11

x
fx
x
Để hàm số liên tục tại
0x thì phải định nghĩa (0)
f
bằng giá trị nào sau
đây?
A. 3. B. 6. C. 4. D. 0.
Câu 11. Cho
44
() .
2

x
x
fx
x
Để hàm số liên
tục tại
0x
thì phải định nghĩa
(0)
f
bằng giá trị nào
sau đây?
A.
1
.
4
B.
1
.
2
C. 0. D. 4.
Câu 12. Cho
1
() .
1
fx
x
Để hàm số liên tục tại 1
x
thì phải định nghĩa (1)
f
bằng giá trị nào sau đây?
A. 0. B. 2.
C.
1.
D. Không xác định được (1).
f
Câu 13. Cho
2
2sin5
() .
x
x
fx
x
Để hàm số liên tục
tại
0x thì phải định nghĩa (0)
f
bằng giá trị nào sau
đây?
A. 2. B. 0.
C. 5. D. Không xác định được (1).
f
Câu 14. Cho hàm số

3
8
khi { 2; 0}
2
( ) 6 khi 1 .
5 khi 0


x
x
xx
fx x
x
Khẳng định nào sau
đây đúng?
A. Hàm số không xác định tại 2.x
B. Hàm số không xác định tại 0.x
C. Hàm số liên tục tại 0.x
D. Hàm số liên tục tại 2.x
Câu 15. Cho hàm số

3
11
2 1

xkhix
fx
khi x
. Khi đó
1
lim
x
f
x
bằng
A.
1
. B.
2
.
C. 0 . D. không tồn tại.
Câu 16. Cho hàm số

33
x
x
fx
x
với
0x . Để hàm số

f
x
liên tục trên
thì
0
f
bằng
A.
23
3
.
B.
3
3
.
C. 1. D. 0 .
Câu 17. Cho hàm số

2
32
1

xx
fx
x
với
1
x
. Để
hàm số
f
x liên tục trên
thì

1
f
bằng
A. 2. B. 1. C. 0 . D. 1 .
Câu 18. Cho hàm số

42

x
fx
x
với
0x . Để
hàm số
f
x liên tục trên thì
0
f
bằng
A. 0 . B. 2. C. 4. D. 1.
Câu 19. Cho hàm số

3
8
2
48
3 2


x
khi x
fx
x
khi x
.
Hàm số
f
x liên tục tại
A. 2x . B. 3x . C. 2x . D. 3x .
Câu 20. Cho hàm số

2
43
khi 3
3
khi 3

xx
x
fx
x
ax
. Để hàm số
f
x liên tục tại 3x thì a bằng
A. 2. B. 4. C. 0 . D. 2 .
Câu 21. Cho hàm số

2
-5 6
khi 3
4-3-
1 khi 3

xx
x
fx
xx
ax x
. Để hàm số
f
x liên tục tại 3x thì a bằng
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page10
A.
4
3
.
B. 3 . C. 0 . D.
2
3
.
Câu 22. Cho hàm số

54
khi 1
1
( 4) khi 1


xx
x
fx
x
ax x
.
Để hàm số
f
x liên tục trên thì a bằng
A. 3. B. 1 . C. 1. D. 0 .
Câu 23. Cho hàm số

3
31 26
khi 1
1
khi 1


xx
x
fx
x
ax x
. Để hàm số

f
x
liên tục trên
thì
a
bằng
A. 2. B. 1. C.
1
4
.
D.
5
4
.
Câu 24. Cho hàm số

3
322
khi 2
2
khi 2

x
x
fx
x
ax
. Để hàm số
f
x
liên tục trên thì a bằng
A. 0 . B.
2
. C.
1
4
.
D.
1
.
Câu 25. Cho hàm số

2
1
khi 3, 1
1
4 khi 1
1 khi 3



x
x
x
x
fx x
xx
.
Hàm số
f
x liên tục tại:
A. mọi điểm thuộc .
B. mọi điểm trừ 1
x
.
C. mọi điểm trừ 3x .
D. mọi điểm trừ 1
x
và 3x .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A C A B D A B C D B A D C D B B D C A A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A B D C C
ĐẠO HÀM
KIẾN THỨC CẦN NHỚ
1. Định nghĩa đạo hàm tại một điểm
1.1. Định nghĩa : Cho hàm số

y
fx xác định trên khoảng
;abvà

0
;
x
ab, đạo hàm của hàm số tại
điểm
0
x
là :

0
0
0
0
'lim
xx
f
xfx
fx
xx
.
1.2. Chú ý :
Nếu kí hiệu
00 0
;
x
xx y fx x fxthì :

0
00
0
0
0
'lim lim




xx x
fx x fx
y
fx
x
xx
.
Nếu hàm số
yfxcó đạo hàm tại
0
x
thì nó liên tục tại điểm đó.
2. Ý nghĩa của đạo hàm
2.1. Ý nghĩa hình học: Cho hàm số
y
fx có đồ thị
C

0
'
f
x là hệ số góc của tiếp tuyến đồ thị

C của hàm số

yfx tại
000
,
M
xy C.
Phương trình tiếp tuyến của đồ thị hàm số
yfxtại điểm
000
,
M
xy Clà :
000
'
y
fx xx y.
2.2. Ý nghĩa vật lí :
Vận tốc tức thời của chuyển động thẳng xác định bởi phương trình :
s
st tại thời điểm
0
t là
00
'vt s t .
Cường độ tức thời của điện lượng

QQttại thời điểm
0
t là :
00
'It Q t .
3. Qui tắc tính đạo hàm và công thức tính đạo hàm
3.1. Các quy tắc : Cho
;;:uux vvx C là hằng số.
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page11
'''uv u v

. ' '. '. . .
 uv u v v u Cu Cu

22
'. '. .
,0




uuvvu C Cu
v
vv uu
Nếu
,.


x
ux
yfuuux y yu
.
3.2. Các công thức :

0; 1

Cx
 

11
...,,2



nn nn
xnx unuun n




1
,0 ,0
22


u
xxu u
xu
 
sin cos sin . cos


x
xuuu
 
cos sin cos .sin

 
x
xuuu
 
22
1
tan tan
cos cos


u
xu
x
u
 
22
1
cot cot
sin sin

 
u
xu
x
u
.
1. ĐỊNH NGHĨA ĐẠO HÀM
Câu 1:
Số gia của hàm số
2
41
f
xx x ứng
với
x
và
x
là
A.

24.xx x B. 2.
x
x
C.
.2 4 .
x
xx D.
24.
x
x
Câu 2: Cho hàm số ()yfx có đạo hàm tại
0
x
là
0
'( )
f
x
. Khẳng định nào sau đây sai?
A.
0
0
0
0
() ( )
() lim .
xx
f
xfx
fx
xx
B.
00
0
0
()()
() lim .
x
f
xxfx
fx
x


C.
00
0
0
()()
()lim .
h
f
xh fx
fx
h

D.
0
00
0
0
()()
() lim .
xx
f
xx fx
fx
xx

Câu 3: Xét ba mệnh đề sau:
(1) Nếu hàm số
f
x có đạo hàm tại điểm
0
x
x
thì
f
x liên tục tại điểm đó.
(2) Nếu hàm số
f
x liên tục tại điểm
0
x
x
thì
f
x
có đạo hàm tại điểm đó.
(3) Nếu
f
x gián đoạn tại
0
x
x
thì chắc chắn
f
x không có đạo hàm tại điểm đó.
Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Câu 4: Cho hàm số
2
khi 1
()
2
khi 1
x
x
fx
ax b x

.
Với giá trị nào sau đây của a, b thì hàm số có đạo hàm
tại 1
x
?
A.
1
1; .
2
ab
B.
11
;.
22
ab
C.
11
;.
22
ab
D.
1
1; .
2
ab
Câu 5: Số gia của hàm số

2
2
x
fx ứng với số gia
x
của đối số
x
tại
0
1x 
là
A.

2
1
.
2
x
x B.

2
1
.
2
x
x



C.

2
1
.
2
x
x



D.

2
1
.
2
x
x
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page12
Câu 6: Tỉ số
y
x
của hàm số
21fx xxtheo
x
và
x
là
A. 42 2.xx B.

2
42 2.xx
C. 42 2.xx D.

2
42 2.
x
xx x
Câu 7: Số gia của hàm số
3
f
xx ứng với
0
2x
và
1
x

bằng bao nhiêu?
A. 19 . B. 7 . C. 19. D. 7 .
2. ĐẠO HÀM CỦA HÀM ĐA THỨC – HỮU TỈ-
CĂN THỨC
Câu 8:
Cho hàm số
2
23
2
xx
y
x

. Đạo hàm
y
của hàm số là biểu thức nào sau đây?
A.
2
3
1
(2)x

.
B.
2
3
1
(2)x
.
C.
2
3
1
(2)x

.
D.
2
3
1
(2)x
.
Câu 9: Đạo hàm của hàm số
42
31yx x x
là
A.
32
'4 6 1.yxx
B.
32
'4 6 .yxxx
C.
32
'4 3 .yxxx
D.
32
'4 3 1.yxx
Câu 10: Đạo hàm của hàm số
32
11
y
x
x

bằng biểu
thức nào sau đây?
A.
43
31
.
x
x
B.
43
32
.
x
x
C.
43
32
.
x
x
D.
43
31
.
x
x
Câu 11: Đạo hàm của hàm số
7
2
y
xx bằng
biểu thức nào sau đây?
A.
6
14 2 .
x
x
B.
6
2
14 .x
x

C.
6
1
14 .
2
x
x
 D.
6
1
14 .x
x

Câu 12:
Đạo hàm của
2
52
2yx x là
A.
963
10 28 16 .yx xx

B.
963
10 14 16 .yxxx

C.
93
10 16 .yxx

D.
63
7616.yxx x

Câu 13: Đạo hàm của hàm số
322016
(2)yx x
là:
A.
322015
2016( 2 ) .yxx

B.
3 2 2015 2
2016( 2 ) (3 4 ).yxxxx

C.
322
2016( 2 )(3 4 ).yxxxx

D.
322
2016( 2 )(3 2 ).yxxxx

Câu 14:
Cho hàm số
() .
f
xaxb
Trong các mệnh
đề sau, mệnh đề nào
đúng?
A.
() .
f
xa

B.
() .
f
xb

C.
() .
f
xa
D.
() .
f
xb
Câu 15: Cho hàm số

1
fx
x
. Đạo hàm của
f
tại
2x
là
A.
1
.
2
B.
1
.
2
C.
1
.
2
D.
1
.
2
Câu 16: Cho hàm số


2
2
31fx x. Giá trị
1f
là
A. 4. B. 8. C. -4. D. 24.
Câu 17: Cho hàm số
1
f
xx
. Đạo hàm của
hàm số tại
1
x
là
A.
1
2
. B. 1. C.
0
D. Không tồn tại.
Câu 18: Cho hàm số
2
1yx thì
2f
là kết quả
nào sau đây?
A.
2
(2) .
3
f
B.
2
(2) .
3
f
C.
2
(2) .
3
f
D. Không tồn tại.
Câu 19: Cho hàm số 4yxx . Nghiệm của
phương trình
0y
là
A.
1
.
8
x
B.
1
.
8
x
C.
1
.
64
x
D.
1
.
64
x 
Câu 20: Cho hàm số
3
325.yx
Các nghiệm của
phương trình
0y
là.
A.
5
3
x 
. B.
3
5
x 
. C.
0x
. D.
5x 
.
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page13
Câu 21: Cho hàm số

32
1
22 8 1
3
f
xx xx
.
Tập hợp những giá trị của
x
để
0fx
là:
A.
22
.
B.
2; 2
.
C.
42
.
D.
22
.
Câu 22: Cho hàm số
32
31yxx
. Để 0y
thì
x
nhận các giá trị thuộc tập nào sau đây
A.
2
;0 .
9



B.
9
;0 .
2



C.
9
;0;.
2

 

D.
2
;0;.
9

 

Câu 23: Cho hàm số
3
1
y
x
. Để 0
y thì
x
nhận
các giá trị thuộc tập nào sau đây?
A. 1. B. 3. C.
. D. .
Câu 24:
Cho hàm số
32
31.fx x x Đạo hàm
của hàm số
f
x âm khi và chỉ khi.
A. 02x. B. 1
x
.
C. 0x
hoặc 1.x D. 0x
hoặc 2.x
Câu 25: Cho hàm số
3
() 2
f
xmxmx
. Số
1
x
là
nghiệm của bất phương trình
() 1fx
khi và chỉ khi:
A. 1.m B. 1.m 
C. 11.m D. 1.m 
Câu 26: Cho hàm số 23yxx . Để
0y
thì x
nhận các giá trị thuộc tập nào sau đây?
A.

;.  B.
1
;.
9




C.
1
;.
9




D.
.
3. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
Câu 27:
Hàm số cot 2yx có đạo hàm là:
A.
2
1tan2
.
cot 2
x
y
x
B.
2
(1 tan 2 )
.
cot 2
x
y
x

C.
2
1cot2
.
cot 2
x
y
x
D.
2
(1 cot 2 )
.
cot 2
x
y
x

Câu 28: Đạo hàm của hàm số 3sin 2 cos3yxxlà:
A. 3cos2 sin3 .yxx
 B. 3cos2 sin3 .yxx

C. 6cos2 3sin3 .yxx
 D. 6cos2 3sin3 .yxx

Câu 29: Đạo hàm của hàm số
sin cos
sin cos
x
x
y
x
x
là:
A.

2
sin 2
.
sin cos
x
y
x
x
B.

22
2
sin cos
.
sin cos
x
x
y
x
x
C.

2
2 2sin 2
.
sin cos
x
y
x
x

D.

2
2
.
sin cos
y
x
x
Câu 30: Hàm số
sin
x
y
x
có đạo hàm là:
A.
2
sin cos
.
x
xx
y
x
B.
2
cos sin
.
x
xx
y
x
C.
2
cos sin
.
x
xx
y
x
D.
2
sin cos
.
x
xx
y
x
Câu 31: Cho hàm số
1
()
sin
yfx
x

. Giá trị
2
f



là:
A.1. B.
1
.
2
C. 0. D. Không tồn tại.
Câu 32: Cho hàm số
3
cos 4
() cot
3sin 3
x
yfx x
x
 .
Giá trị đúng của
3
f



bằng:
A.
8
.
9
B.
9
.
8
C.
9
.
8
D.
8
.
9
Câu 33: Cho hàm số
2
2
cos
()
1sin
x
yfx
x

. Biểu thức
3
44
ff



bằng
A. 3 . B.
8
3
C. 3. D.
8
3

Câu 34: Cho hàm số

2
tan
3
fx x




. Giá trị
0f
bằng
A.
3
. B. 4 . C. 3 . D.
3
.
Câu 35: Cho hàm số

cos
12sin
x
yfx
x

. Chọn kết
quả
SAI
A.
5
64
f




B.

02f
 .
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page14
C.
1
23
f




D.
2f

.
Câu 36: Cho hàm số
2
cos 2
3
y
x




. Khi đó
phương trình
0y
có nghiệm là:
A. 2
3
x
k
 . B.
32
k
x
 .
C.
3
x
k
 . D.
32
k
x
 .
Câu 37: Cho hàm số
sin
32




x
y
. Khi đó phương
trình
'0y
có nghiệm là:
A.
2
3

x
k
. B.
3

x
k
.
C.
2
3

x
k
. D.
3

x
k
.
4. ĐẠO HÀM CẤP CAO
Câu 38:
Hàm số nào dưới đây có đạo hàm cấp hai là
6
x
?
A.
2
3.yx
B.
3
2.yx
C.
3
.yx
D.
2
.yx
Câu 39: Cho hàm số
32
33 5yxxx
. Khi
đó
(3)
(3)y
bằng:
A. 54 . B. 18 . C. 0 . D. 162 .
Câu 40: Cho hàm số cos 2yx . Khi đó ''(0)y bằng
A. 2 . B.
23
C. 4 . D.
23
.
Câu 41: Cho hàm số
2
cosyx
. Khi đó
(3)
3
y



bằng:
A. 2 . B.
23
. C.
23
. D. 2 .
Câu 42: Cho 3sin 2cosyxx. Tính giá trị biểu
thức
''
A
yy
là:
A.
0A
.
B.
2
A
.
C.
4cos .
A
x
D.
6sin 4cos .
A
xx
Câu 43: Cho hàm số
1
y
x
. Khi đó
()
()
n
yx
bằng:
A.
1
!
(1)
n
n
n
x
. B.
1
!
n
n
x
.
C.
!
(1).
n
n
n
x
.
D.
!
n
n
x
.
Câu 44: Cho hàm số
cos
y
x
. Khi đó
(2016)
()yx
bằng
A.
cos
x
.
B.
sin
x
. C.
sin
x
. D.
cos
x
.
Câu 45: Cho hàm số
432
34521yxxxx
.
Hỏi đạo hàm đến cấp nào thì ta được kết quả triệt tiêu
(bằng 0 )?
A. 2 . B. 4 . C. 5. D. 3.
5. VI PHÂN
Câu 46:
Cho hàm số

2
1yfx x. Biểu thức
nào sau đây là vi phân của hàm số đã cho?
A.

d2 1dyxx
. B.

d2 1yx
.
C.
d1dyx x
. D.

2
d1dyx x .
Câu 47: Vi phân của hàm số
2
3
f
xxx
tại điểm
2x , ứng với
0,1x
là:
A.
0,07
. B.
10
. C.
1,1
. D.
0,4
.
Câu 48: Vi phân của
cot 2017yx
là:
A.
d 2017sin 2017 d .yxx
B.

2
2017
dd.
sin 2017
yx
x
C.

2
2017
dd.
cos 2017
yx
x

D.

2
2017
dd.
sin 2017
yx
x

Câu 49: Cho hàm số y =
2
1
1
x
x
x

. Vi phân của hàm
số là:
A.
2
2
22
dd
(1)
xx
yx
x


B.
2
21
dd
(1)
x
yx
x
C.
2
21
dd
(1)
x
yx
x

D.
2
2
22
dd
(1)
xx
yx
x

Câu 50: Cho hàm số
3
12
x
y
x
. Vi phân của hàm số
tại
3x 
là:
A.
1
dd.
7
yx
B.
d7d.yx
C.
1
dd.
7
yx
D.
d7d.yx
Câu 51: Vi phân của
tan 5yx
là :
A.
2
5
dd.
cos 5
x
yx
x
B.
2
5
dd.
sin 5
yx
x

TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page15
C.
2
5
dd.
cos 5
yx
x
D.
2
5
dd.
cos 5
yx
x

Câu 52: Cho
dcos2 dyxx
. Khi đó
8
3
y
y






có giá
trị nào sau đây?
A. 1 B.
2
C.
2
D.
0
6. TIẾP TUYẾN – Ý NGHĨA CỦA ĐẠO HÀM
Câu 53:
Cho hàm số
24
3
x
y
x
có đồ thị là
(H)
.
Phương trình tiếp tuyến tại giao điểm của
(H)
với trục hoành là:
A.
24yx
. B.
31yx
.
C.
24yx
. D.
2yx
.
Câu 54: Hệ số góc của tiếp tuyến của đồ thị hàm số
23
1
x
y
x
tại giao điểm của đồ thị hàm số
với trục hoành bằng :
A.
9
. B.
1
.
9
C.
9.
D.
1
.
9
Câu 55: Phương trình tiếp tuyến của đồ thị hàm số
32
23
f
xx x x
tại điểm có hoành độ
0
1x 
là:
A.
10 4.yx
B.
10 5.yx
C.
24.yx
D.
25.yx
Câu 56: Tiếp tuyến của đồ thị hàm số
3
2
32
3
x
yx có hệ số góc
9,k 
có phương trình
là :
A.
16 9( 3).yx
B.
9( 3).yx
C.
16 9( 3).yx
D.
16 9( 3).yx
Câu 57: Hệ số góc của tiếp tuyến của đồ thị hàm số
1
1
x
y
x
tại giao điểm với trục tung bằng :
A.
2.
B.
2.
C.
1.
D.
1.
Câu 58: Cho hàm số
32
3yx x
có đồ thị
.C
Có
bao nhiêu tiếp tuyến của

C
song song đường thẳng
910?yx
A.
1. B. 3. C. 2. D. 4.
Câu 59: Cho hàm số
2
65yx x
có tiếp tuyến
song song với trục hoành. Phương trình tiếp tuyến đó
là:
A. 3.x  B.
4.y 
C.
4.y
D. 3.x
Câu 60: Trong các tiếp tuyến tại các điểm trên đồ thị
hàm số
32
32yx x
, tiếp tuyến có hệ số góc nhỏ
nhất bằng
A.
3
. B.
3
. C. 4 . D.
0
.
Câu 61: Hệ số góc của tiếp tuyến của đồ thị hàm số
ytan
x
tại điểm có hoành độ
0
4
x
là
A.
1
.
2
B.
2
.
2
C.
1.
D.
2.
Câu 62: Cho hàm số
4
2y
x
 có đồ thị

.
H
Đường thẳng
vuông góc với đường thẳng
: 2dy x
và tiếp xúc với
H
thì phương trình
của
là
A.
4.yx
B.
2
4
yx
yx


.
C.
2
6
yx
yx


. D. Không tồn tại.
Câu 63: Lập phương trình tiếp tuyến của đường cong
32
(): 3 8 1Cyx x x 
, biết tiếp tuyến đó song song
với đường thẳng
:2017yx
?
A.
2018yx
. B.
4yx
.
C.
4yx
;
28yx
. D.
2018yx
.
Câu 64: Cho hàm số
32
y2x 3x 1
có đồ thị

C
,
tiếp tuyến với

C
nhận điểm
00
3
;
2
M
y



làm tiếp
điểm có phương trình là:
A.
9
2
yx .
B.
927
24
yx.
C.
923
24
yx.
D.
931
24
x
y .
Câu 65: Hoành độ tiếp điểm của tiếp tuyến song song
với trục hoành của đồ thị hàm số
3
32yx x
là
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page16
A.
1
x
và
1x 
. B.
3x 
và
3x
.
C.
1
x
và
0x
. D.
2x
và
1x 
.
Câu 66: Phương trình tiếp tuyến của đồ thị hàm số
42
21yx x
tại điểm có tung độ tiếp
điểm bằng 2 là:
A.
86, 86.yx y x
B.
86, 86.yx y x
C.
88, 88.yx y x
D.
40 57.yx
Câu 67: Cho đồ thị
2
():
1
x
Hy
x
và điểm
()AH
có tung độ
4y
. Hãy lập phương trình tiếp tuyến của
()H
tại điểm
A
.
A.
2yx
. B.
311yx
.
C.
311yx
. D.
310yx
.
Câu 68: Cho hàm số
1
(C)
1
x
y
x
. Có bao nhiêu
cặp điểm
A
, B
thuộc

C
mà tiếp tuyến tại đó song
song với nhau:
A.
0
. B. 2 . C. 1. D. Vô số.
Câu 69: Cho hàm số
32
22yx x x
có đồ thị (C).
Gọi
12
,
x
x
là hoành độ các điểm
M
, N
trên

C
, mà
tại đó tiếp tuyến của

C
vuông góc với đường thẳng
2017yx
. Khi đó
12
x
x
bằng:
A.
4
3
.
B.
4
3
.
C.
1
3
.
D. 1 .
Câu 70: Trên đồ thị của hàm số
1
1
y
x
có điểm
M
sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo
thành một tam giác có diện tích bằng 2. Tọa độ
M
là:
A.

2;1 .
B.
1
4; .
3



C.
34
;.
47




D.
3
;4.
4



Câu 71: Cho ha
m sô
32
1
2
3
yxx co
đô
thi
ha
m
sô

C
. Phương trı
nh tiê
p tuyê
n cu
a

C
ta
i điê
m co
hoa
nh đô
la
nghiê
m cu
a phương trı
nh
"0y
la
A.
7
3
yx
B.
7
3
yx
C.
7
3
yx
D.
7
3
yx
Câu 72: Tiếp tuyê
n cu
a đô
thi
ha
m sô
1
5
x
y
x
ta
i
điê
m
1; 0A
co
hê
sô
go
c bă
ng
A.
1
6
B.
6
25
C.
1
6
D.
6
25
Câu 73: Cho hàm sô
2
43yx x
co
đô
thi
P
.
Nê
u tiê
p tuyê
n ta
i điê
m
M
cu
a
P
co
hê
sô
go
c bă
ng
8
thı
hoa
nh đô
điê
m
M
la
:
A. 12 B.
6
C. 1 D.
5
Câu 74: Cho hàm sô
32
32yx x
co
đô
thi

C
.
Đươ
ng thă
ng na
o sau đây la
tiê
p tuyê
n cu
a

C
va
co
hê
sô
go
c nho
nhâ
t:
A.
33yx
B.
0y
C.
510yx
D.
33yx
Câu 75: Cho hàm số
32
3(1)yx mx m xm
.
Gọi
A
là giao điểm của đồ thị hàm số với
Oy
. Tìm m
để tiếp tuyến của đồ thị hàm số tại
A
vuông góc với
đường thẳng
23yx
.
A.
3
2
B.
1
2
C.
3
2
D.
1
2
Câu 76: Cho hàm số
32
33yx x
có đồ thị

C
.
Số tiếp tuyến của

C
vuông góc với đường thẳng
1
2017
9
yx là:
A.1 B. 2 C.
3
D.
0
Câu 77: Cho chuyển động thẳng xác định bởi phương
trình
32
392
s
ttt (t tính bằng giây;
s
tính bằng
mét). Khẳng định nào sau đây đúng ?
A. Vận tốc của chuyển động bằng 0 khi 0t hoặc
2t .
B. Vận tốc của chuyển động tại thời điểm 2t là
18 /vms .
C. Gia tốc của chuyển động tại thời điểm 3t là
2
12 /ams
.
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page17
D. Gia tốc của chuyển động bằng 0 khi 0t .
Câu 78: Cho chuyển động thẳng xác định bởi phương
trình
32
3
s
tt (t tính bằng giây;
s
tính bằng mét).
Khẳng định nào sau đây đúng?
A. Gia tốc của chuyển động khi 4ts là
2
18am/s .
B. Gia tốc của chuyển động khi 4ts là
2
9am/s .
C. Vận tốc của chuyển động khi 3ts là 12vm/s .
D. Vận tốc của chuyển động khi 3ts là 24vm/s .
Câu 79: Giá trị m để hàm số

32
1
1311
3
yxmx mx có
0,
yx
là:
A. 0m B. 1m C. 01m D.
0
1
m
m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A D A A A C C C A B C A B C B D D D C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D A C A D C D C D B C B C B A D C C B C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
B A A D C A C D D A C B C A A A B C B A
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
D C C C A A D D A D A C B A A B B A C
HAI ĐƯỜNG THẲNG VUÔNG GÓC
Câu 1.
Trong không gian cho ba đường thẳng phân
biệt a, b, c. Khẳng định nào sau đây đúng?
A. Nếu a và b cùng vuông góc với c thì a//b
B. Nếu a//b và c a thì c b.
C. Nếu góc giữa a và c bằng góc giữa b và c thì a//b
D. Nếu a và b cùng nằm trong mp ( ) // c thì góc
giữa a và c bằng góc giữa b và c
Câu 2. Cho tứ diện ABCD có AC = a, BD = 3a. Gọi
M và N lần lượt là trung điểm của AD và BC. Biết AC
vuông góc với BD. Tính MN
A. MN =
10
2
a
B. MN =
6
3
a
C. MN =
32
2
a
D. MN =
23
3
a
Câu 3. Cho hình hộp ABCD.A’B’C’D’ có tất cả các
cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề
nào có thể
sai?
A. A’C’BD B. BB’BD
C. A’BDC’ D. BC’A’D
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B A B
ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
KIẾN THỨC CẦN NHỚ
Dạng 1 Chứng minh đường th
ẳ
ng vuông góc với mặt ph
ẳ
ng.
Phương pháp : * Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau trong mặt
phẳng
* Sử dụng sự liên hệ giữa quan hệ song song và quan hệ vuông góc
Dạng 2 Chứng minh hai đường thẳng vuông góc.
Phương pháp : * Chứng minh đường thẳng này vuông góc với mặt phẳng chứa đường thẳng kia
* Sử dụng định lý ba đường vuông góc
* Sử dụng sự liên hệ giữa quan hệ song song và quan hệ vuông góc
Dạng 3 Tìm thiết diện của đa diện và mặt phẳng vuông góc với đường thẳng cho trước.
Phương pháp : Tìm hai đường thẳng cắt nhau vuông góc với đường thẳng cho trước
Khi đó thiết diện song song với hai đường thẳng vừa tìm được
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page18
Dạng 4 Tính góc giữa đường th
ẳ
ng a và
m
ặt ph
ẳ
ng
.
Phương pháp : Tìm đường thẳng a’ là hình chiếu của a lên mặt phẳng
Khi đó
góc giữa đường thẳng a và mặt phẳng
là góc giữa đường thẳng a và a’.
CÂU HỎI TRẮC NGHIỆM
Câu 1.
Khẳng định nào sau đây sai ?
A. Nếu đường thẳng d () thì d vuông góc với hai
đường thẳng trong ()
B. Nếu đường thẳng d vuông góc với hai đường
thẳng nằm trong () thì d ()
C. Nếu đường thẳng d vuông góc với hai đường
thẳng cắt nhau nằm trong () thì d vuông góc với
bất kì đường thẳng nào nằm trong ().
D. Nếu d () và đường thẳng a // () thì d a
Câu 2. Trong không gian cho đường thẳng và
điểm O. Qua O có mấy đường thẳng vuông góc với
cho trước?
A. 1 B. 2 C. 3 D. Vô số
Câu 3. Qua điểm O cho trước, có bao nhiêu mặt
phẳng vuông góc với đường thẳng cho trước?
A. 1 B. 2 C. 3 D. Vô số
Câu 4. Mệnh đề nào sau đây có thể sai ?
A. Hai đường thẳng phân biệt cùng vuông góc với
một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một
đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với
một đường thẳng thứ ba thì song song.
D. Một đường thẳng và một mặt phẳng (không chứa
đường thẳng đã cho) cùng vuông góc với một đường
thẳng thì song song nhau.
Câu 5. Cho hình chóp S.ABC có SA (ABC) và
ABC vuông ở B. AH là đường cao của SAB. Khẳng
định nào sau đây
sai?
A. SA BC B. AH BC
C. AH AC D. AH SC
Câu 6. Trong không gian tập hợp các điểm M cách
đều hai điểm cố định A và B là:
A. Mặt phẳng trung trực của đoạn thẳng AB.
B. Đường trung trực của đoạn thẳng AB.
C. Mặt phẳng vuông góc với AB tại A
D. Đường thẳng qua A và vuông góc với AB
Câu 7. Câu 11: Cho tứ diện ABCD có AB = AC và
DB = DC. Khẳng định nào sau đây đúng?
A. AB (ABC) B. AC BD
C. CD (ABD) D. BC AD
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là
hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng
định nào sau đây
đúng?
A. SO (ABCD) B. CD (SBD)
C. AB (SAC) D. CD AC
Câu 9. Cho hình chóp S.ABC có SA= SB = SC và
tam giác ABC vuông tại B. Vẽ SH (ABC),
H(ABC). Khẳng định nào sau đây đúng?
A. H trùng với trọng tâm tam giác ABC
B. H trùng với trực tâm tam giác ABC.
C. H trùng với trung điểm của AC
D. H trùng với trung điểm của BC
Câu 10. Cho hình chóp S.ABC có cạnh SA (ABC)
và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt
là trung điểm của AB và SB. Khẳng định nào sau đây
có thể
sai ?
A. CH SA B. CH SB
C. CH AK D. AK SB
Câu 11. Cho hình chóp S.ABC có SA= SB = SC. Gọi
O là hình chiếu của S lên mặt đáy ABC. Khẳng định
nào sau đây đúng?
A. O là trọng tâm tam giác ABC
B. O là tâm đường tròn ngoại tiếp tam giác ABC
C. O là trực tâm tam giác ABC
D. O là tâm đường tròn nội tiếp tam giác ABC
Câu 12. Cho hình chóp S.ABCD có SA (ABCD) và
đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD
và I là trung điểm của S
C. Khẳng định nào sau đây sai
?
A. BC SB
B. (SAC) là mặt phẳng trung trực của đoạn BD
C. IO (ABCD)
D. Tam giác SCD vuông ở D.
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là
hình vuông và SA (ABCD). Gọi I, J, K lần lượt là
trung điểm của AB, BC và SB. Khẳng định nào sau đây
sai ?
A. (IJK) // (SAC) B. BD (IJK)
C. Góc giữa SC và BD có số đo 60
0
D. BD (SAC)
Câu 14. Cho hình tứ diện ABCD có AB, BC, CD đôi
một vuông góc nhau. Hãy chỉ ra điểm O cách đều bốn
điểm A, B, C, D.
A. O là tâm đường tròn ngoại tiếp tam giác ABC
B. O là trọng tâm tam giác ACD
C. O là trung điểm cạnh BD
D. O là trung điểm cạnh AD
Câu 15. Cho hình chóp S.ABC có SA (ABC) và AB
BC. Gọi O là tâm đường tròn ngoại tiếp tam giác
SBC.H là hình chiếu vuông góc của O lên (ABC).
Khẳng định nào sau đây đúng ?
A. H là trung điểm cạnh AB
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page19
B. H là trung điểm cạnh AC
C. H là trọng tâm tam giác ABC
D. H là tâm đường tròn nội tiếp tam giác ABC
Câu 16. Cho tứ diện ABCD. Vẽ AH (BCD).Biết H
là trực tâm tam giác BCD. Khẳng định nào sau đây
không
sai ?
A. AB = CD B. AC = BD
C. AB CD D. CD BD
Câu 17. Cho hình chóp S.ABCD, đáy ABCD là hình
vuông có tâm O, SA (ABCD). Gọi I là trung điểm
của SC. Khẳng định nào sau đây
sai ?
A. IO (ABCD).
B. (SAC) là mặt phẳng trung trực của đoạn BD
C. BD SC D. SA= SB= SC.
Câu 18. Cho hình vuông ABCD có tâm O và cạnh
bằng 2a. Trên đường thẳng qua O vuông góc với
(ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) có
số đo bằng 45
0
. Tính độ dài SO.
A. SO = a 3 B. SO= a 2
C. SO =
3
2
a
D. SO=
2
2
a
Câu 19. Cho hình chóp S.ABCD có các cạnh bên
bằng nhau SA = SB = SC = SD. Gọi H là hình chiếu
của S lên mặt đáy ABCD. Khẳng định nào sau đây
sai
?
A. HA = HB = HC = HD
B. Tứ giác ABCD là hình bình hành
C. Tứ giác ABCD nội tiếp được trong đường tròn.
D. Các cạnh SA, SB, SC, SD hợp với đáy ABCD
những góc bằng nhau.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B D A C C A D A C D B B C D B C D B B
HAI MẶT PHẲNG VUÔNG GÓC
KIẾN THỨC CẦN NHỚ
Dạng 1 Xác định và tính góc giữa hai mặt ph
ẳ
ng () và ().
Phương pháp : Tìm giao tuyến của () và ().
Từ một điểm trên giao tuyến ta dựng hai đường thẳng nằm trong () và ()
Sao cho hai đường thẳng đó cùng vuông góc với giao tuyến
Lúc đó góc giữa hai mặt phẳng () và () là hai đường thẳng vừa dựng
Dạng 2 Chứng minh hai mặt phẳng vuông góc.
Phương pháp : * Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với
mặt phẳng kia
* Chứng minh góc giữa hai mặt phẳng là 90
o
* Sử dụng sự liên hệ giữa quan hệ song song và quan hệ vuông góc
Dạng 3 Chứng minh đường thẳng vuông góc với mặt phẳng.
Phương pháp : * Sử dụng định lý : Khi hai mặt phẳng vuông góc với nhau một đường
thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia
* Sử dụng định lý : Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ
ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ ba.
CÂU HỎI TRẮC NGHIỆM
Câu 1.
Cho hình chóp S.ABC có SA (ABC) và
đáy ABC vuông ở A. Khẳng định nào sau đây
sai ?
A. (SAB) (ABC)
B. (SAB) (SAC)
C. Vẽ AH BC , H BC góc AHS là góc giữa
hai mặt phẳng (SBC) và (ABC)
D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc
SCB .
Câu 2. Cho tứ diện ABCD có AC = AD và BC =
BD. Gọi I là trung điểm của CD. Khẳng định nào sau
đây
sai ?
A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc
.
A
IB
B. (BCD) (AIB)
C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc
CBD
D. (ACD) (AIB)
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page20
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là
hình chữ nhật tâm O và khoảng cách từ A đến BD bằng
2
5
a
. Biết SA (ABCD) và SA = 2a. Gọi là góc giữa
hai mặt phẳng (ABCD) và (SBD). Khẳng định nào sau
đây
sai ?
A. (SAB) (SAD) B. (SAC) (ABCD)
C. tan =
5
D. =
SOA
.
Câu 4. Cho hình lăng trụ ABCD.A’B’C’D’ có đáy
ABCD là hình thoi, AC = 2a. Các cạnh bên AA’,
BB’… vuông góc với đáy và AA’ = a. Khẳng định nào
sau đây
sai ?
A. Các mặt bên của hình lăng trụ là các hình chữ
nhật.
B. Góc giữa hai mặt phẳng (AA’C’C) và (BB’D’D)
có số đo bằng 60
0
.
C. Hai mặt bên (AA’C) và (BB’D) vuông góc với
hai đáy.
D. Hai hai mặt bên AA’B’B và AA’D’D bằng nhau.
Câu 5. Cho hình lăng trụ ABCD.A’B’C’D’. Hình
chiếu vuông góc của A’ lên (ABC) trùng với trực tâm
H của tam giác ABC. Khẳng định nào sau đây
đúng?
A. (AA’B’B)(BB’C’C)
B. (AA’H)(A’B’C’)
C. BB’C’C là hình chữ nhật.
D. (BB’C’C)(AA’H)
Câu 6. Cho hình chóp S.ABC có SA (ABC) và
đáy ABC là tam giác cân ở A. Gọi H là hình chiếu
vuông góc của A lên (SBC). Khẳng định nào sau đây
đúng?
A. H SB B. H trùng với trọng tâm tam giác SBC
C. H SC D. H SI (I là trung điểm của BC)
Câu 7. Cho hình chóp S.ABC có hai mặt bên (SBC)
và (SAC) vuông góc với đáy (ABC). Khẳng định nào
sau đây
sai?
A. SC (ABC)
B. Nếu A’ là hình chiếu vuông góc của A lên (SBC)
thì A’ SB
C. (SAC) (ABC)
D. BK là đường cao của tam giác ABC thì BK
(SAC).
Câu 8. Cho hình chóp S.ABC có hai mặt bên (SAB)
và (SAC) vuông góc với đáy (ABC), tam giác ABC
vuông cân ở A và có đường cao AH (H BC). Gọi O là
hình chiếu vuông góc của A lên (SBC). Khẳng định
nào sau đây
sai?
A. SC (ABC)
B. (SAH) (SBC)
C. O SC
D. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc
SBA.
Câu 9. Cho tứ diện ABCD có hai mặt bên ACD và
BCD là hai tam giác cân có đáy CD. Gọi H là hình
chiếu vuông góc của B lên (ACD). Khẳng định nào sau
đây
sai?
A. AB nằm trên mặt phẳng trung trực của CD
B. HAM (M là trung điểm CD)
C. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc
ADB.
D. (ABH) (ACD).
Câu 10. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy
ABC là tam giác vuông cân ở A. H là trung điểm BC.
Khẳng định nào sau đây sai?
A. Các mặt bên của ABC.A’B’C’ là các hình chữ
nhật bằng nhau.
B. (AA’H) là mặt phẳng trung trực của BC
C. Nếu O là hình chiếu vuông góc của A lên (A’BC)
thì O A’H
D. Hai mặt phẳng (AA’B’B) và (AA’C’C) vuông
góc nhau.
Câu 11. Hình hộp ABCD.A’B’C’D’ trở thành hình
lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau
đây?
A. Tất cả các cạnh đáy bằng nhau và cạnh bên
vuông góc với mặt đáy.
B. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc
với mặt đáy
C. Có một mặt bên vuông góc với mặt đáy và đáy là
hình vuông.
D. Các mặt bên là hình chữ nhật và mặt đáy là hình
vuông
Câu 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’.
Khẳng định nào sau đây không đúng?
A. Hình hộp có 6 mặt là 6 hình chữ nhật.
B. Hai mặt ACC’A’ và BDD’B’ vuông góc nhau
C. Tồn tại điểm O cách đều tám đỉnh của hình hộp
D. Hình hộp có 4 đường chéo bằng nhau và đồng
qui tại trung điểm của mỗi đường.
Câu 13. Cho hình lập phương ABCD.A’B’C’D’ cạnh
bằng A. Khẳng định nào sau đây
sai ?
A. Hai mặt ACC’A’ và BDD’B’ vuông góc nhau
B. Bốn đường chéo AC’, A’C, BD’, B’D bằng nhau
và bằng a
3
C. Hai mặt ACC’A’ và BDD’B’là hai hình vuông
bằng nhau
D. AC BD’
Câu 14. Cho hình lăng trụ tứ giác đều
ABCD.A’B’C’D’ có cạnh đáy bằng a, góc giữa hai mặt
phẳng (ABCD) và (ABC’) có số đo bằng 60
0
. Cạnh bên
của hình lăng trụ bằng:
A. 3a B. a 3 C. 2a D. a 2
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page21
Câu 15. Cho hình lăng trụ đứng ABC.A’B’C’ có AB
= AA’ = a, BC = 2a, CA = a
5
. Khẳng định nào sau
đây sai ?
A. Đáy ABC là tam giác vuông.
B. Hai mặt AA’B’B và BB’C’ vuông góc nhau
C. Góc giữa hai mặt phẳng (ABC) và (A”BC) có số
đo bằng 45
0
D. AC’ = 2a
2
Câu 16. Cho hình lăng trụ lục giác đều
ABCDEF.A’B’C’D’E’F’ có cạnh bên bằng a và
ADD’A’ là hình vuông. Cạnh đáy của lăng trụ bằng:
A. a B.
2
a
C.
3
3
a
D.
2
2
a
Câu 17. Cho hình lăng trụ tứ giác đều
ABCD.A’B’C’D’ có ACC’A’ là hình vuông, cạnh
bằng A. Cạnh đáy của hình lăng trụ bằng:
A.
2
2
a
B. a
2
C.
3
3
a
D. a
3
Câu 18. Cho hình lăng trụ tam giác đều ABC.A’B’C’
có cạnh đáy bằng 2a
3 và cạnh bên bằng 2a. Gọi G và
G’ lần lượt là trọng tâm của hai đáy ABC và
A’B’C’.Khẳng định nào sau đây đúng khi nói về
AA’G’G?
A. AA’G’G là hình chữ nhật có hai kích thước là 2a
và 3a.
B. AA’G’G là hình vuông có cạnh bằng 2a.
C. AA’G’G là hình chữ nhật có diện tích bằng 6a
2
D. AA’G’G là hình vuông có diện tích bằng 8a
2
Câu 19. Cho hình lập phương ABCD.A’B’C’D’ có
cạnh bằng A. Khẳng định nào sau đây
sai?
A. Tam giác AB’C là tam giác đều.
B. Nếu là góc giữa AC’ và (ABCD)thì cos =
2
3
C. ACC’A’ là hình chữ nhật có diện tích bằng 2a
2
D. Hai mặt AA’C’C và BB’D’D ở trong hai mặt
phẳng vuông góc với nhau.
Câu 20. Cho hình chóp S.ABC có đường cao SH. Xét
các mệnh đề sau:
I) SA = SB = SC
II) H trùng với tâm đường tròn ngoại tiếp tam giác
ABC.
III) Tam giác ABC là tam giác đều.
IV) H là trực tâm tam giác ABC.
Các yếu tố nào chưa đủ để kết luận S.ABC là hình
chóp đều?
A. (I ) và (II ) B. (II) và (III )
C. (III ) và (IV ) D. (IV ) và (I )
Câu 21. Cho hình chóp đều S.ABC có cạnh đáy bằng
a, góc giữa một mặt bên và mặt đáy bằng 60
0
. Tính độ
dài đường cao SH.
A. SH =
2
a
B. SH =
3
2
a
C. SH =
2
3
a
D. SH =
3
3
a
Câu 22. Cho ba tia Ox, Oy, Oz vuông góc nhau từng
đôi một. Trên Ox, Oy, Oz lần lượt lấy các điểm A, B, C
sao cho OA = OB = OC = a. Khẳng định nào sau đây
sai?
A. O.ABC là hình chóp đều.
B. Tam giác ABC có diện tích S =
2
3
2
a
C. Tam giác ABC có chu vi 2p =
32
2
a
D. Ba mặt phẳng (OAB), (OBC), (OCA)vuông góc
với nhau từng đôi một.
Câu 23. Cho hình thoi ABCD có cạnh bằng a và Â =
60
0
. Trên đường thẳng vuông góc với mặt phẳng
(ABCD) tại O (O là tâm của ABCD), lấy điểm S sao
cho tam giác SAC là tam giác đều. Khẳng định nào sau
đây đúng?
A. S.ABCD là hình chóp đều
B. Hình chóp S.ABCD có các mặt bên là các tam
giác cân.
C. SO =
3
2
a
D. SA và SB hợp với mặt phẳng (ABCD) những góc
bằng nhau.
Câu 24. Cho hình chóp cụt đều ABC.A’B’C’ với đáy
lớn ABC có cạnh bằng A
. Đáy nhỏ A’B’C’ có cạnh
bằng
2
a
, chiều cao OO’ =
2
a
. Khẳng định nào sau đây
sai ?
A. Ba đường AA’, BB’, CC’ đồng qui tại S.
B. AA’= BB’= CC’ =
2
a
C. Góc giữa cạnh bên mặt đáy là góc SIO (I là trung
điểm BC)
D. Đáy lớn ABC có diện tích gấp 4 lần diện tích đáy
nhỏ A’B’C’.
Câu 25. Cho hình chóp cụt tứ giác đều
ABCD.A’B’C’D’cạnh của đáy nhỏ ABCD bằng
3
a
và
cạnh của đáy lớn A’B’C’D’bằng A. Góc giữa cạnh bên
và mặt đáy bằng 60
0
. Tính chiều cao OO’ của hình
chóp cụt đã cho.
A. OO’=
3
3
a
B. OO’ =
3
2
a
C. OO’ =
26
3
a
D. OO’ =
32
4
a
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page22
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
D C D B B D B A C A D B C B D B A B C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A C C B A
KHOẢNG CÁCH
KIẾN THỨC CẦN NHỚ
D
ạ
ng 1 Khoảng cách từ đi
ể
m A đ
ế
n đ
ư
ờng th
ẳ
ng Δ
Phương pháp : Tìm hình chiếu H của A lên Δ. Lúc đó d(A , Δ) = AH
Dạng 2 Khoảng cách từ điểm A đến mặt phẳng ()
Phương pháp : Tìm hình chiếu H của A lên (). Lúc đó d(A , ) = AH
Dạng 3 Khoảng cách giữa đường thẳng Δ và mặt phẳng () với Δ //
Phương pháp : Chọn điểm A bất kỳ trên Δ. Lúc đó d(Δ, ) = d(A , )
Dạng 4 Khoảng cách giữa hai mặt phẳng song song ,
Phương pháp : Chọn điểm A bất kỳ trên . Lúc đó d( , ) = d(A , )
Dạng 5 Khoảng cách giữa hai đường thẳng chéo nhau a , b
Phương pháp : * Dựng đoạn vuông góc chung : MN
a , MN
b , M a , N b
Lúc đó d(a , b) = MN
* d(a , b) = d(a , ) = d( , ) , với a , // b và b , // a
CÂU HỎI TRẮC NGHIỆM
Câu 1.
Cho tứ diện SABC trong đó SA, SB, SC
vuông góc với nhau từng đôi một và SA = 3a, SB = a,
SC=2a. Khoảng cách từ A đến đường thẳng BC bằng:
A.
32
2
a
B.
75
5
a
C.
83
3
a
D.
56
6
a
Câu 2. Cho hình chóp A.BCD có cạnh AC (BCD)
và BCD là tam giác đều cạnh bằng a. Biết AC = a
2
và M là trung điểm của BD. Khoảng cách từ C đến
đường thẳng AM bằng:
A. a
2
3
B. a
6
11
C. a
7
5
D. a
4
7
Câu 3. Cho hình chóp A.BCD có cạnh AC (BCD)
và BCD là tam giác đều cạnh bằng a. Biết AC = a
2
và M là trung điểm của BD. Khoảng cách từ A đến
đường thẳng BD bằng:
A.
32
2
a
B.
23
3
a
C.
45
3
a
D.
11
2
a
Câu 4. Cho hình chóp S.ABCD có SA (ABCD) đáy
ABCD là hình thoi cạnh bằng a và
ˆ
B
= 60
0
. Biết SA=
2a. Tính khỏang cách từ A đến SC
A.
32
2
a
B.
43
3
a
C.
25
5
a
D.
56
2
a
Câu 5. Cho hình chóp S.ABCD có SA (ABCD),
SA= 2a, ABCD là hình vuông cạnh bằng A. Gọi O là
tâm của ABCD, tính khoảng cách từ O đến SC.
A.
3
3
a
B.
3
4
a
C.
2
3
a
D.
2
4
a
Câu 6. Cho hình chóp S.ABC trong đó SA, AB, BC
vuông góc với nhau từng đôi một. Biết SA = 3a,
AB=a
3 , BC = a 6 . Khỏang cách từ B đến SC bằng:
A. a 2 B. 2a C. 2a 3 D. a 3
Câu 7. Cho hình chóp S.ABC trong đó SA, AB, BC
vuông góc với nhau từng đôi một. Biết SA = a
3,
AB=a
3 . Khỏang cách từ A đến (SBC) bằng:
A.
3
2
a
B.
2
3
a
C.
25
5
a
D.
6
2
a
Câu 8. Cho hình chóp S.ABCD có SA (ABCD),
đáy ABCD là hình chữ nhật. Biết AD = 2a, SA = a.
Khỏang cách từ A đến (SCD) bằng:
A.
32
2
a
B.
23
3
a
C.
2
5
a
D.
3
7
a
Câu 9. Cho hình chóp tam giác đều S.ABC cạnh đáy
bằng 2a và chiều cao bằng a
3 . Tính khaỏng cách từ
tâm O của đáy ABC đến một mặt bên:
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page23
A.
5
2
a
B.
23
3
a
C. a
3
10
D. a
2
5
Câu 10. Cho hình chóp tứ giác đều S.ABCD có cạnh
đáy bằng a và chiều cao bằng a
2 . Tính khỏang cách
từ tâm O của đáy ABCD đến một mặt bên:
A.
3
2
a
B.
2
3
a
C.
25
3
a
D.
2
a
Câu 11. Cho hình chóp S.ABCD có SA (ABCD),
đáy ABCD là hình thang vuông có chiều cao AB = a.
Gọi I và J lần lượt là trung điểm của AB và CD. Tính
khỏang cách giữa đường thẳng IJ và (SAD).
A.
2
2
a
B.
3
3
a
C.
2
a
D.
3
a
Câu 12. Cho hình thang vuông ABCD vuông ở A và
D, AD = 2a. Trên đường thẳng vuông góc tại D với
(ABCD) lấy điểm S với SD = a
2
. Tính khỏang cách
giữa đường thẳng DC và (SAB).
A.
2
3
a
B.
2
a
C. a 2 D.
3
3
a
Câu 13. Cho hình chóp O.ABC có đường cao OH =
2
3
a
. Gọi M và N lần lượt là trung điểm của OA và OB.
Khỏang cách giữa đường thẳng MN và (ABC) bằng:.
A.
2
a
B.
2
2
a
C.
3
a
D.
3
3
a
Câu 14. Cho tứ diện đều ABCD có cạnh bằng a. Tính
khoảng cách giữa AB và CD.
A.
3
2
a
b )
2
3
a
C.
2
2
a
D.
3
3
a
Câu 15. Cho hình chóp S.ABCD có SA (ABCD),
đáy ABCD là hình chữ nhật với AC = a
5
và
BC=a
2
. Tính khoảng cách giữa SD và BC
A.
3
4
a
B.
2
3
a
C.
3
2
a
D. a 3
Câu 16. Cho hình lập phương ABCD.A’B’C’D’ có
cạnh bằng a. Khoảng cách giữa BB’ và AC bằng:
A.
2
a
B.
3
a
C.
2
2
a
D.
3
3
a
Câu 17. Cho hình lập phương ABCD.A’B’C’D’ có
cạnh bằng 1 (đvd). Khoảng cách giữa AA’ và BD’
bằng:
A.
3
3
B.
2
2
C.
22
5
D.
35
7
Câu 18. Cho hình lăng trụ tứ giác đều
ABCD.A’B’C’D’ có cạnh đáy bằng a
. Gọi M, N, P lần
lượt là trung điểm của AD, DC, A’D’. Tính khoảng
cách giữa hai mặt phẳng (MNP) và (ACC’).
A.
3
3
a
B.
4
a
C.
3
a
D.
2
4
a
Câu 19. Cho hình lăng trụ tam giác ABC.A’B’C’ có
các cạnh bên hợp với đáy những góc bằng 60
0
, đáy
ABC là tam giác đều cạnh a và A’ cách đều A, B, C.
Tính khoảng cách giữa hai đáy của hình lăng trụ.
A. a B. a 2 C.
3
2
a
D.
2
3
a
Câu 20. Cho tứ diện đều ABCD có cạnh bằng
.a
Khoảng cách từ A đến (BCD) bằng:
A.
6
2
a
B.
6
3
a
C.
3
6
a
D.
3
3
a
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B B D C A B D C C B C A D C D C B D A B
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page24
PHẦN 3 – MỘT SỐ ĐỀ MINH HỌA
ĐỀ SỐ 1
(Theo ma trận Bà Rịa – Vũng Tàu)
I. PHÂ
N TRĂ
C NGHIÊ
M ( 4 điểm)
Câu 1.
12
651
lim
3.6 6


nn
nn
có giá trị bằng
A. 6 . B. 0 . C. 1 . D.
1
3
.
Câu 2. Giá trị của
2
210
lim
2
x
x
x
bằng:
A.
. B. 5. C. 2. D. .
Câu 3.
Giá trị của
22
lim 2 3 2 5


x
xx bằng:
A.
0.
B.
22.
C.
35.
D.
.
Câu 4.
Giá trị của
2
4
213
lim
54


x
x
xx
bằng:
A.
0.
B.
1
.
9
C.
2
.
9
D.
.
Câu 5. Cho
44
() .
2

x
x
fx
x
Để hàm số liên tục tại
0x
thì phải định nghĩa (0)
f
bằng giá trị nào sau
đây?
A.
1
.
4
B.
1
.
2
C. 0. D. 4.
Câu 6. Cho hàm số
2
23
2
xx
y
x

. Đạo hàm
y
của hàm số là biểu thức nào sau đây?
A.
2
3
1
(2)x

.
B.
2
3
1
(2)x
.
C.
2
3
1
(2)x

.
D.
2
3
1
(2)x
.
Câu 7. Cho hàm số


2
2
31fx x. Giá trị
1f
là
A. 4. B. 8. C. -4. D. 24.
Câu 8. Cho hàm số
32
31yxx
. Để
0y
thì
x
nhận các giá trị thuộc tập nào sau đây
A.
2
;0 .
9



B.
9
;0 .
2



C.
9
;0;.
2

 

D.
2
;0;.
9

 

Câu 9. Đạo hàm của hàm số
3sin2 cos3yxx
là:
A.
3cos2 sin3 .yxx

B.
3cos2 sin3 .yxx

C.
6cos2 3sin3 .yxx

D.
6cos2 3sin3 .yxx

Câu 10. Phương trình tiếp tuyến của đồ thị hàm số
32
23
f
xx x x
tại điểm có hoành độ
0
1x 
là:
A.
10 4.yx
B.
10 5.yx
C.
24.yx
D.
25.yx
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page25
Câu 11. Lập phương trình tiếp tuyến của đường cong
32
(): 3 8 1Cyx x x 
, biết tiếp tuyến đó song song với
đường thẳng
:2017yx
?
A.
2018yx
. B.
4yx
.
C.
4yx
;
28yx
. D.
2018yx
.
Câu 12. Trong không gian cho ba đường thẳng phân biệt ,,abc. Khẳng định nào sau đây đúng?
A. Nếu
a
và
b
cùng vuông góc với
c
thì
//ab
.
B. Nếu //ab và ca thì cb .
C. Nếu góc giữa a và c bằng góc giữa b và c thì //ab.
D. Nếu a và b cùng nằm trong )/(/mp c
thì góc giữa a và c bằng góc giữa b và c.
Câu 13. Trong không gian cho đường thẳng và điểm O. Qua O có mấy đường thẳng vuông góc với cho
trước?
A. 1 B. 2 C. 3 D. Vô số
Câu 14. Cho hình chóp .SABC có
SA ABC và
A
BC
vuông ở B. AH là đường cao của
SAB
. Khẳng
định nào sau đây
sai?
A.
SA BC
B.
AH BC
C.
AH AC
D.
AH SC
Câu 15. Cho hình chóp .SABCD có

SA ABCD và đáy ABCD là hình chữ nhật. Gọi O là tâm của ABC D
và
I là trung điểm của SC . Khẳng định nào sau đây sai ?
A. BC SB B.

SAC
là mặt phẳng trung trực của đoạn BD
C.
IO ABCD D. Tam giác
SCD
vuông ở
D
.
Câu 16. Cho hình chóp
.SABCD
có
SA A BCD
, đáy
ABCD
là hình chữ nhật. Biết
2AD a
,
SA a
.
Khoảng cách từ
A đến

SCD
bằng:
A.
32
2
a
B.
23
3
a
C.
2
5
a
D.
3
7
a
.
Câu 17. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy, 3SC a . Khi đó góc
giữa SB với mặt phẳng
A
BCD bằng
A.
0
45 . B.
0
60 . C.
0
90 . D.
0
30 .
Câu 18. Gọi
là góc giữa hai đường thẳng
12
,dd lần lượt có vectơ chỉ phương
12
,
 
uu. Ta luôn có :
A.
12
cos cos ,
 
uu . B.
12
cos cos ,


uu .
C.

12
cos cos ,

uu . D.
12
cos cos ,
 
uu .
Câu 19. Tất cả các giá trị m để hàm số

32
1
11
3
 yxmxmxm
có
0,

yxR
là:
A.
0m
B.
3m
C.
30m
D.
3
0
m
m

Câu 20.
Cho chuyển động thẳng xác định bởi phương trình
32
392st t t
(t tính bằng giây;
s
tính bằng
mét). Khẳng định nào sau đây đúng ?
A. Vận tốc của chuyển động bằng
0
khi
0t
hoặc
2t
.
B. Vận tốc nhỏ nhất của chuyển động tại thời điểm 1 ts
C. Vận tốc của chuyển động tại thời điểm
3t
là
2
3m/s .
D. Vận tốc của chuyển động bằng 5 khi 2t .
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page26
II. PHÂ
N TƯ
LUÂ
N(6điểm)
Bài 1:
(2,0điểm)a)Tính các giới hạn sau:
3
3
231
lim
325


nn
A
nn
;
1
813
lim
1

x
x
B
x
b)Tìm
a
để hàm số

2
2
56
khi 3
3
4 khi 3


xx
x
fx
x
xa x
liên tục tại trên
3x
.
Bài 2: (1,5điểm)a)Chứng minh các phương trình sau luôn có nghiệm thực với mọi
m
:
420175
1320 mm x x
b)Viết phương trình tiếp tuyến với đồ thị hàm số

21
2

x
yfx
x
, biết tiếp tuyến vuông góc với
đường thẳng
1
2
5
 yx
Bài 3: (2,0điểm)Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
,2.SA ABCD SA a
a)Chứng minh:
,.
B
CSBSAC SBD
b)Tính các góc



,,,SC ABCD SAC ABCD .
c)Tính


,dADSBC
d)Tìm thiết diện hình chóp với mặt phẳng
chứa
A
D và vuông góc với
mp SBC
.
Bài 4: (0,5điểm)Cho hàm số
1
x
y
x
có đồ thị
H
. Tìm tọa độ điểm
M
thuộc đồ thị
H
để tiếp tuyến
của
H tại
M
cắt đường tròn
22
: 2 –2 –2 0 Cx y x y tại 2 điểm ,
A
B sao cho tam giác IAB
vuông, với
I
là tâm của
C .
-----------------HẾT-----------------
ĐỀ SỐ 2
(Theo ma trận Bà Rịa – Vũng Tàu)
I. PHÂ
N TRĂ
C NGHIÊ
M ( 4 điểm)
Câu 1.
3
4
25
lim
22
nn
nn


có giá trị bằng
A.

. B.
2
. C. 0 . D. 6 .
Câu 2.
2
7
23
lim
49
x
x
x

có giá trị bằng
A. 1. B. 1 . C. 2 . D.
1
56
.
Câu 3.
2
2
2
2
lim
x
x
x
x
có giá trị bằng
A.
3
. B. 3. C. 0 . D. 1.
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page27
Câu 4.
1
3
lim
1
x
x
x
có giá trị bằng
A.  . B.

. C. 1. D.
3
.
Câu 5. Cho
44
() .
2

x
x
fx
x
Để hàm số liên tục tại
0x thì phải định nghĩa
(0)
f
bằng giá trị nào sau
đây?
A.
1
.
4
B.
1
.
2
C.
0.
D.
4.
Câu 6. Cho hàm số

2
43
khi 3
3
khi 3
xx
x
fx
x
ax

. Để hàm số

f
x liên tục tại 3x thì
a
bằng
A. 2 . B. 4 . C.
0
. D. 2 .
Câu 7. Cho hai hàm số
2
3
() 25
2
fx x ;
2
1
()
2

g
xx x. Giá trị của
x
là bao nhiêu để
(x) ( )
f
gx

?
A. 2 . B. 0. C.
1
4
.
D.
1
2
.
Câu 8. Cho hàm số
3
2
() 2
3

f
xmxx
. Với giá trị nào của m thì
1x 
là nghiệm của bất phương trình
() 2fx
?
A. 0m . B. 0m . C. 0m . D. 1m .
Câu 9. Đạo hàm của hàm số tan 2yx bằng biểu thức nào sau đây?
A.
2
2
cos 2
x
. B.
2
2
cos 2
x
. C.
2
1
cos 2
x
. D.
2
2
sin 2
x
.
Câu 10. Cho hàm số
32
33yx x
có đồ thị

C
. Số tiếp tuyến của

C
vuông góc với đường thẳng
1
2017
9
yx
là:
A.1 B. 2 C.
3
D.
0
Câu 11. Cho hàm sô
2
43yx x
co
đô
thi

P
. Nê
u tiê
p tuyê
n ta
i điê
m
M
cu
a
P
co
hê
sô
go
c bă
ng
8
thı
hoa
nh đô
điê
m
M
la
:
A. 12 B.
6
C. 1 D.
5
Câu 12.
Trong các mệnh đề sau, mệnh đề nào sai?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho
trước.
B. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với hai đường thẳng chéo
nhau cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho
trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Câu 13. Cho hai đường thẳng phân biệt a, b và mặt phẳng (P). Mệnh đề nào sau đây là đúng?
A. Nếu a b, (P) a thì (P) // b. C. Nếu a // b, (P) a thì (P) b.
B. Nếu a // (P), b a thì b (P). D. Nếu a // (P), b a thì b // (P).
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page28
Câu 14. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy. Trong các tam giác cho dưới
đây, tam giác nào
không phải tam giác vuông?
A.
SAB
. B.
SAD
. C.
SAC
. D.
SCD
.
Câu 15.
Cho hình chóp S.ABCD có SA vuông góc với đáy. Khi đó, góc giữa đường thẳng SB với mặt phẳng đáy
bằng góc nào dưới đây?
A.
SCA
. B.
SBA
. C.
SBD
. D.
B
AB .
Câu 16. :Cho hình chóp
.SABCD
có đáy
ABCD
là hình thoi tâm
I
, cạnh bên
SA
vuông góc với đáy. Khẳng
định nào sau đây đúng ?
A.
()()SBC SIA
B.
()()SBD SAC
C.
()()SDC SAI
D.
()()SCD SAD
Câu 17. Cho hình chóp .SABCDcó đáy là hình vuông cạnh
a
. Đường thẳng SA vuông góc với mặt phẳng đáy,
SA a
. Khoảng cách giữa hai đường thẳng
SB
và
CD
nhận giá trị nào trong các giá trị sau?
A.
2a
B.
a
C.
3a
D.
2a
Câu 18.
Cho hình chóp
.SABC
có đáy là tam giác đều
ABC
cạnh
a
, cạnh bên
SA
vuông góc với mặt đáy và
a
SA
2
. Tính góc giữa hai mặt phẳng
ABC
và
SBC
là:
A. 30
0
B. 45
0
C. 60
0
D. 90
0
Câu 19. Một vật rơi tự do theo phương trình
2
1
s gt (m),
2
với
2
9,8 m/sg . Vận tốc tức thời của vật tại thời
điểm
10 st là:
A. 122, 5 (m/s) B. 49 (m/s) C. 10 (m/s) D. 98 (m/s)
Câu 20.
Chóp tam giác .SABCcó SA SB SC, ABC là tam giác đều. I là trung điểm của BC .Chọn mệnh
đề đúng?
A.
BC AC
B.
BC SAC
C.
BC SAB
D.
BC SAI
II. PHÂ
N TƯ
LUÂ
N(6điểm)
Bài 1:
(2,0điểm)a)( 2 điểm ) Tính các giới hạn sau:
32
32
33
lim
221


nn
A
nn
1
31 22
lim
1

x
xx
B
x
.
b)Xét tính liên tục của hàm số sau tại điểm
0
2x  :
2
4
khi 2
() .
2
4 khi 2


x
x
fx
x
x
Bài 2: (1,5điểm)a)Chứng minh rằng với mọi giá trị của tham số m phương trình sau luôn có nghiệm:
42
–
2–3–20.xmx m x
b)Viết phương trình tiếp tuyến của đồ thị hàm số
32
–
3–3 1yx x x, biết rằng tiếp tuyến đó song
song với đường thẳng
6–1yx .
Bài 3: (2,0điểm)Cho hình chóp .SABCD có đáy ABC D là hình vuông, hình chiếu vuông góc của S trên mặt
phẳng
ABCD là trung điểm H của AB . Biết AB SH a.
a)Chứng minh:
BC SAB . b)Gọi M là trung điểm đoạn BC . Chứng minh BD SM .
c)Tính khoảng cách từ điểm
A đến
mp SCD d)Tính góc giữa SC và mặt đáy.
e)Tính góc giữa
mp SCD và mặt đáy.
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424Page29
f)Gọi
là mặt phẳng qua
M
và vuông góc với
BC
. Tìm thiết diện của
cắt hình chóp
.SABCD
.
Bài 4: (0,5điểm)Cho hàm số
2
21 yx x C
và đường thẳng
: dyxm
. Tìm
m
để
d
cắt

C
tại 2
điểm phân biệt
,AB
sao cho các tiếp tuyến của
C tại
A
và
B
vuông góc nhau.
-----------------HẾT-----------------
| 1/29
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
SỞ GIÁO DỤC & ĐÀO TẠO MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2016 – 2017
TỈNH BÀ RỊA – VŨNG TÀU MÔN: TOÁN KHỐI 11 I. CHỦ ĐỀ CHÍNH
A. Đại số và Giải tích
Chương IV: Giới hạn
1. Giới hạn của dãy số.
2. Giới hạn của hàm số.
3. Hàm số liên tục (hàm số liên tục tại điểm, trên tập I, tính chất hàm số liên tục).
4. Chứng minh về số nghiệm của phương trình.
Chương V: Đạo hàm
1. Đạo hàm (định nghĩa đạo hàm, quy tắc tính đạo hàm, đạo hàm của hàm số lượng giác).
2. Tiếp tuyến của đồ thị hàm số. B. Hình học
1. Vectơ trong không gian.
2. Chứng minh quan hệ vuông góc.
3. Bài toán liên quan đến góc.
4. Bài toán liên quan đến khoảng cách.
5. Thiết diện vuông góc. II. MA TRẬN
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I I
Môn: TOÁN – Lớp: 11
Thời gian làm bài: 90 phút Vận dụng Tên chủ đề
Nhận biết - Thông hiểu Cấp độ thấp Cấp độ cao Tổng Chương IV. - Giới hạn dãy số. Chứng minh về số Giới hạn –
- Giới hạn hàm số tại một điểm. nghiệm của Hàm số liên - Giới hạn một bên. phương trình. tục
- Giới hạn vô cực, tại vô cực.
- Xét tính liên tục của hàm số tại một
điểm, trên khoảng. Số câu TN 5 5 Số điểm 1,0 1,0 Tỷ lệ % 10% 10% Số câu TL 3 1 4 Số điểm 2,0 0,75 2,75 Tỷ lệ % 20% 7,5% 27,5% Chương V.
*Biết dùng quy tắc để tính đạo hàm Lập phương trình Đạo hàm
*Tính được đạo hàm các hs l.giác tiếp tuyến với đồ
*Giải phương trình, bất pt, chứng minh thị tại một
hệ thức có chứa đạo hàm. điểm,biết hệ số góc(song song hoặc vuông góc với đường thẳng cho trước)
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 1
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 Số câu TN 4 2 6 Số điểm 0,8 0,4 1,2 Tỷ lệ % 8% 4% 12% Số câu TL 1 1 Số điểm 0,75 0,75 Tỷ lệ % 7,5% 7,5%
- Nhận biết quan hệ vuông góc giữa hai -Chứng minh hai
đường thẳng ở dạng đơn giản mặt phẳng vuông
-Chứng minh hai đường thẳng vuông góc góc *Xác định và tính
-Chứng minh đường thẳng vuông góc góc giữa các đối với mặt phẳng tượng véc Chương III. tơ,đường thẳng, Vec tơ trong mặt phẳng k.gian-Quan *Xác định và tính hệ vuông góc khoảng cách giữa các đối tượng: điểm, đường thẳng, mặt phẳng * Xác định thiết diện vuông góc đt, mp Số câu TN 5 2 7 Số điểm 1,0 0,4 1,4 Tỷ lệ % 10% 4 % 14% Số câu TL 1 1 2 Số điểm 1,0 1,0 2,0 Tỷ lệ % 10% 10% 20% Bài tập tổng Sử dụng tổng hợp hợp các kiến thức Số câu TN 2 2 Số điểm 0,4 0,4 Tỷ lệ % 4% 4% Số câu TL 1 1 Số điểm 0,5 0,5 Tỷ lệ % 5% 5% Tổng số câu 14TN+4TL 4TN+3TL 2TN+1TL 20 TN+8TL Tổng số điểm 2,8+3,0=5,8 0,8+2,5=3,3
0,4+0,5=0,9 4,0+6,0=10,0 Tỉ lệ% 58% 33% 9% 100% III. CẤU TRÚC ĐỀ
Trắc nghiệm : 20 câu : Thời gian 35 phút
Tự luận : Thời gian 55 phút
Bài 1.(1,5 điểm) : Chủ đề 1 (Giới hạn)
Bài 2.(1,0 điểm) : Chủ đề 1 (Tính liên tục của hàm số)
Bài 3.(1,0 điểm) : Chủ đề 2 (Đạo hàm hàm số)
Bài 4.(2,0 điểm) : Chủ đề 3 (Hình học)
Bài 5.(0.5 điểm) : Tổng hợp
IV. HÌNH THỨC KIỂM TRA VÀ THỜI GIAN
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 2
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
- Hình thức tự luận và trắc nghiệm.
- Thời gian làm bài : 35 phút trắc nghiệm và 55 phút tự luận.
Lưu ý : + Các trường tự soạn đề ôn tập theo ma trận đề trên.
+ Trong mỗi câu tự luận có thể gồm nhiều ý.
+ Học sinh làm phần trắc nghiệm lên phiếu trả lời trắc nghiệm, phần tự luận làm trên tờ giấy thi.
Bà Rịa-Vũng Tàu, ngày 26 tháng 2 năm 2017 GIỚI HẠN DÃY SỐ KIẾN THỨC CẦN NHỚ
I. Giới hạn hữu hạn
II. Giới hạn vô cực
1. Giới hạn đặc biệt
1. Giới hạn đặc biệt 1 1 lim k
n   với k nguyên dương lim  0 ; lim  0 k N k  *   n n lim n
q   q   1 lim n
q  0  q   1 2. Định lý u
lim c c c la hang so
A.Nếu limu a, limv   thì lim n  0 n n v 2. Định lý n u
A.Nếu limu a,limv b thì:
B. Nếu limu a, lim v  , v  0 n thì lim n   n n n n n vn *limu v a b n n   
C. Nếu limu  , limv a  0 thì limu .v   n n n n *limu v a b n n    *limu .v a b n n   . u a *lim n  b  0 v b n
B.Nếu u  0,n va limu a thì n n
a  0 va lim u a n
C. Nếu limu a thi lim u a n n
3. Tổng của cấp số nhân lùi vô hạn u 2 1
S u u q u q  ...  q  1 1 1 1   1 q
CÂU HỎI TRẮC NGHIỆM  2 n  2 n n 1
A.   . B.    . C.  0,  99 . D.   1  n .
Câu 1. Với k là số nguyên dương thì lim bằng  3   3  k n n A.  . B.  . C. 0 . D. 1.   1 Câu 6. lim có giá trị bằng
Câu 2. Trong các khẳng định sau, khẳng định nào sai? n  2 1 1 1 1 A. lim  lim ; k   . A. . B. 0 . C. 1  . D.  . kn n 2 2 B. lim n
q  0 nếu q  1.
Câu 7. Dãy số nào sau đây có giới hạn khác 0? n
C. limc c ( c là hằng số). 1  1  5 n 2 A. . B. . C. .   D. . D. 3 3
lim u  limu . 3n n  4  2 n n n
Câu 3. Dãy số nào sau đây có giới hạn khác 0? 1 2n Câu 8. lim có giá trị bằng 1 1 cos n 4n A. . B. . C. 0 D. . n 1 n n 1 1 1 1 A. . B.  . C. . D.  .
Câu 4. Dãy số nào sau đây có giới hạn bằng 0? 4 4 2 2 n n  3 n  5 n  2 n  4 n 3  5
A.   . B.    . C.   . D.    . Câu 9. lim có giá trị bằng n  2   4   3   3  5
Câu 5. Dãy nào sau đây không có giới hạn?
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 3
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 3 8 n A. 1. B. 0 . C. . D. . 4 1   
. Có bao nhiêu dãy số có giới 5 5 n 2017  2n n 1 7   5n 1
hạn bằng 0 trong các dãy số trên? Câu 10. lim có giá trị bằng 3.4n  7n A. 1. B. 2 . C. 3 . D. 4 . 1 4n 1 A. 7  . B. 0 . C. 1  . D. . Câu 19. Biết lim
a . Hỏi a là nghiệm của 3 2  n n n 2   3  2 n
phương trình nào sau đây? Câu 11. lim có giá trị bằng n n 2n2 x   x x   3  3  2 A. 2 4 0 . B. 2 5 4 0 . 1 1 x  4 A. . B. . C.  . D. 1  . C. 2
x  5x  4  0 . D.  0 . 2 3 4 x  5x  4 3 2
n n  5 Câu 20.  3 2
lim 3n n   1 có giá trị bằng Câu 12. lim có giá trị bằng 4 n  2n  2 A. 2  . B. 1  . C.  . D.  . A.  . B. 2  . C. 0 . D. 6  . Câu 21.  2 2 lim
n n n  2  có giá trị bằng sin 3
Câu 13. Gọi  lim 4  n L
thì L bằng số nào n 1 A. 0 . B. 1. C.  . D. . sau đây? 2 A. 0. B. 2. C. 2 . D. 4. Câu 22.  2 2 lim
n n n  2  có giá trị bằng 4 2n n 1 Câu 14. lim có giá trị bằng
A. 1 2 . B.  . C. 1  . D.  . 4 3n  2n 2 2 2
n  2n n A. 0 . B. . C.  . D. . Câu 23. lim có giá trị bằng 2 3 5
4n n  2n 3 2 2n n  4 1 1 Câu 15. lim có giá trị bằng A. 4 . B. 2 . C.  . D. . 2 n  2n  3 2 2 A. 2 . B. 0 . C.  . D. 2  . Câu 24. 3 3
lim n 1  n  có giá trị bằng
n  2 2n 3 A. 0 . B. 1. C.  . D.  . Câu 16. lim  có giá trị bằng 2 n   1 2n  5
1 3  5  ... (2n 1) Câu 25. lim có giá trị bằng 2 1 3n  2 A. 0 . B. . C. 1. D.  . 1 2 A. 0 . B. 1. C. . D.  .
Câu 17. Tổng của cấp số nhân lùi vô hạn 3 1 1 1
Câu 26. ? có giá trị bằng S   ... ... có giá trị bằng A. 0 . B. 2 . C. 1  . D. 1. 2 5 5 5nu  1 1 2 5 1 1 A. . B. . C. . D. .  5 4 5 4
Câu 27. Cho dãy u u . Lúc đó, limu n  : un n n 1  
Câu 18. Cho các dãy số u , v , w ,  với u 1  n n n n n 3n 1 2n 2017 bằng u  , v  , w  , A. 0 . B. 2 . C. 1  . D. 1. n 2 n 2 1 n 1 2 n n 4n 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
C B C C D B C D A A B C C B C B B C B C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 D D A A C D A GIỚI HẠN HÀM SỐ
KIẾN THỨC CẦN NHỚ
1.Định nghĩa :Giới hạn hữu hạn ,giới hạn vô cực
2.Các giới hạn đặc biệt
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 4
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 c
lim x x
lim x x (c: hằng số) lim
 0 (c: hằng số) 0 0 xxx x 0 x 0 x 1    neáu k chaün lim  0 lim k
x   ( k   * ) lim k x    k x x x x  neáu k leû
3.Các định lí về giới hạn hữu hạn
Nếu lim f (x)  L và lim g(x)  M , thì: xx 0 x 0 x lim . c f (x)  .
c L (với C là hằng số) lim [ f (x)  g(x)]  L M xx 0 x 0 x
lim [ f (x)  g(x)]  L M
lim [ f (x).g(x)]  L . M xx 0 x 0 x f (x) L lim  (M 0)
lim f (x)  L
xx g ( x) M x 0 0 x 1  3 3 lim
f (x)  L
Nếu lim f (x)    thì lim  0 xxxx f (x) 0 x 0 x 0
- Nếu f x  0 và lim f (x)  L thì L  0 và lim f (x)  L xx 0 x 0 x
Chú ý: Định lí 1 vẫn đúng khi x  
Định lí 2. lim f (x)  L  lim f (x)  lim f (x)  L   x 0 x xx xx 0 0
4.Qui tắc về giới hạn vô cực:
Qui tắc tìm giới hạn của tích f(x).g(x)
Qui tắc tìm giới hạn của thương f(x) g(x) CÂU HỎI TRẮC NGHIỆM
Câu 1. Với k là số nguyên dương. Giá trị của
sin 2x  3cos x
Câu 8. Giá trị của lim bằng: lim 2x   1 k bằng: 2 x x x 1 x A. 2. B. 0. C. 4. D. 5. A.  . B. 0. C. 1. D. . 
Câu 9. Cho hàm số f x 3 2
x  5x  2 . Trong các
Câu 2. Giá trị của  3
lim x  4x  6 bằng: x
khẳng định sau, khẳng định nào sai? A.  . B. 0. C. 1. D. . 
A. Hàm số có giới hạn bên trái và giới hạn bên phải 2x  3
Câu 3. Giá trị của lim bằng:
tại x  1 bằng nhau. x 1  x  2
B. Hàm số có giới hạn bên trái và giới hạn bên phải 3
tại x  0 không bằng nhau. A. 5.  B.  . C. 1. D. 2. 2
C. Hàm số có giới hạn tại mọi điểm. 2x  21
D. Hàm số có tập xác định D  . R
Câu 4. Giá trị của lim bằng: 2 2 x 5  x  5
Câu 10. Giá trị của lim x x bằng: x  2 3 2 5   A. .  B. 1. C. 2. D. .  2x 10 A. 0. B. 2 2. C. 3  5. D. . 
Câu 5. Giá trị của lim bằng: 2 2 x 2  2  x
Câu 11. Giá trị của lim x x bằng: x  2 3 2 5   A. .  B. 5  . C. 2  . D. .  3  x  3x  6 A. 0. B. 2 2. C. 3 5. D. . 
Câu 6. Giá trị của lim bằng: xx  3 3 x 2x  5
Câu 12. Giá trị của lim bằng:  2 1 x 3  x  8x 15 A. .  B. . C. 1. D. .  2 3 3 A. . B. 1. C.  . D. 1.  2 x  3x  2 2 2
Câu 7. Giá trị của lim bằng: 2 2x  5  3
x2 x  3x 10
Câu 13. Giá trị của lim bằng: 2 1 x2 x  4 A. 1. B. 0. C. . D. 1. 7 3 1 A. .  B. . C. . D. 0. 4 12
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 5
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Câu 14. Trong các giới hạn sau, giới hạn nào bằng 0? Giá trị của x x x bằng: x  2 2 lim  5   8   2 x  3x 2x  4 A. lim . B. lim . 5 5 x x  5 x 3  x 1 A. 0. B. . C. . D. .  3x 2 2 C. x x D. lim . x  2 lim 4  5  2 .  x 1  x 1
Câu 25. Giá trị của x x x bằng: x  2 2 lim  5   8   2
x  3x  2 khi x  2
Câu 15. Cho hàm số f x   . 5 5 3 2x 8 khi x  2 A. 0. B. . C. . D. .  2 2
Khi đó lim f x bằng:
2x 532  x4 x2
Câu 26. Giá trị của lim bằng: A. 1. B. 8. C. 10 . D. Không tồn tại. 7 x x 1 4 2 x  2x 1 A. 8. B. 2. C. 2. D. 8.
Câu 16. Giá trị của lim bằng: 3 x   x
x 2x   1  x  3 2 3 7 6
Câu 27. Giá trị của lim bằng: x 3  x  3 1 1 A. . B.  . C. .  D. .  2 16 2 2 A. 0. B. . C. . D. .  x  3 27 27
Câu 17. Giá trị của lim bằng:
Câu 28. Giới hạn nào sau đây có giá trị bằng 3? x 3  2  3x  5 x  5  4 2x  5 4 4 A. lim . B. lim . A.  . B. 0. C. . D. .  x  x x 1  x 1 3 3 2 2
Câu 18. Trong các mệnh đề sau, mệnh đề nào đúng? x  2  2
23xx 52 C. lim . D. lim . 2 x  3x 3  1 x2 x  2 3 x x  2 A. lim  . B. lim   .  2
x x  5x 5 x 0  xx 3  2 2 
2x  1x 3
Câu 29. Giá trị của lim bằng: 2 2x  5   x   C. lim  . D. lim   .  2   3 x 3x  2 3 x 2  2  x A. .  B. 0. C. 1. D. .  3x 1
Câu 19. Giá trị của lim bằng: x  5  4 x 2 x  3  2x
Câu 30. Giá trị của lim bằng: x 1  2  9  5x A. 0. B. 1. C. 2. D. 3. Câu 20. Tìm 4 4 m để hàm số A.  . B. . C. 0. D. .  5 5 2
2x  3mx 1 khi x  2
3x 54 2  x2 f x  2
  x 3x  2
có giới hạn Câu 31. Giá trị của lim bằng:  khi x  2 4 x x  3  x  2 A. .  B. 81. C. 81. D. .  khi x  2. cos6x  cos 2x A. m  2.  B. m  1.
C. m 1. D. m  2.
Câu 32. Giá trị của lim bằng: 2 x0 x 2x 1  3
Câu 21. Giá trị của lim bằng: A. 16. B. 2. C. 0. D. .  2
x4 x  5x  4 1
Câu 33. Giá trị của 2 2 lim x tan bằng: 1 2 x 2x A. 0. B. . C. . D. .  9 9 1 1 A. .  B. .  C.  . D. . x 1  2 4 4
Câu 22. Giá trị của lim bằng: x 3  5  x  2 Câu 34. Tìm giới hạn của hàm số 2 A. .  B. .  C. 1. D. 0.
f x x  3x  5 khi x  2   .  40  5  2 khi x  2
Câu 23. Giá trị của lim  bằng:  x  2 
2  x  4x 12 x  2  A. 2. B. 2. C. 5.
D. Không tồn tại. 5 5 x 2 1 2cos xA. .  B. .  C.  . D. .
Câu 35. Giá trị của lim bằng: 8 8 x0 sin 2x  1 1 
Câu 24. Giá trị của lim  bằng:  1   A. 1. B. . C. 0. D. .  x  2 
2  x  5x  6 x  2  2 A. .  B. .  C. 0. D. 1.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 6
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 Câu 36. Cho hàm số 4
f (x)  ax bx c (a  0) . Khẳng 2 ax bx  4
Câu 41. Cho 2a b  2 và lim  5. Khẳng
định nào sau đây là đúng? x2 x  2
A. Hàm số f (x) có giới hạn là  khi x   và
định nào sau đây là đúng? a  0 . 3
A. a  ,b  1  .
B. a  1,b  0 .
B. Hàm số f (x) có giới hạn là  khi x   và 2 a  0 . C. a  1,  b  4 . D. a  2  ,b  6 .
C. Hàm số f (x) có giới hạn là  khi x   và mx  2006 Câu 42. Cho lim
L . Tìm m để a  0 . x 2 x x  2007
D. Hàm số f (x) có giới hạn là  khi x   và L  0 . a  0 .
A. m  0 . B. m  0 .
C. m  0 . D. 1   m 1 ax b
Câu 37. Cho hàm số f (x) 
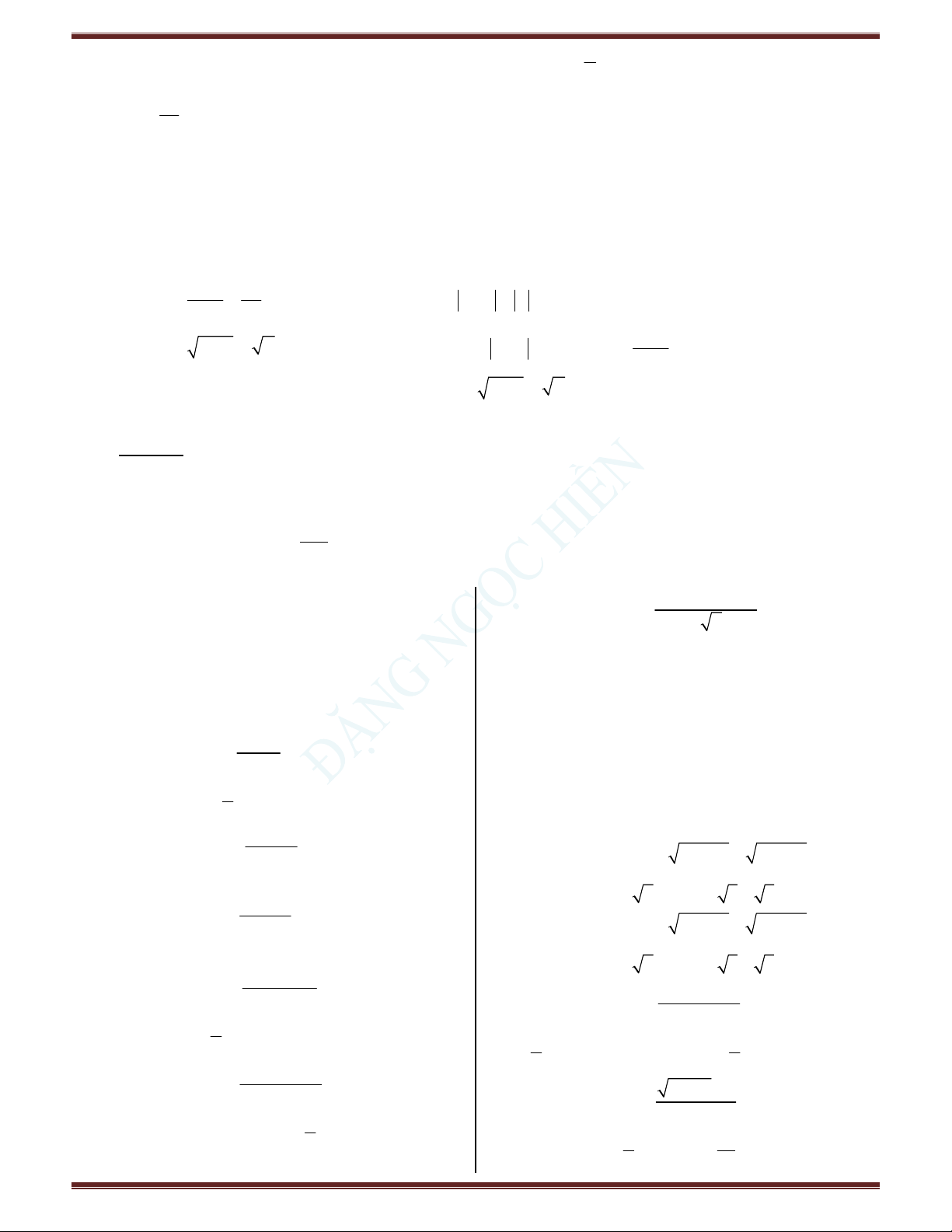
(c  0, ad cb  0) . Câu 43. Cho hàm số y f (x) có đồ thị như hình vẽ: cx d
Khẳng định nào sau đây là sai? a
A. lim f (x)  . x c a
B. lim f (x)  . x c
C. lim f (x)   khi ad cb  0 .   d x     c
D. lim f (x)   khi ad cb  0.   d x     c
Khẳng định nào sao đây là sai? 2 x  2x  3
A. lim f (x)   .
B. lim f (x)  0 . Câu 38. Cho hàm số f (x)  . Đặt x x x 1
C. lim f (x)  2 .
D. lim f (x)   . f (x) x 1  x2017 a  lim
, b  lim  f (x)  ax. Khi đó:
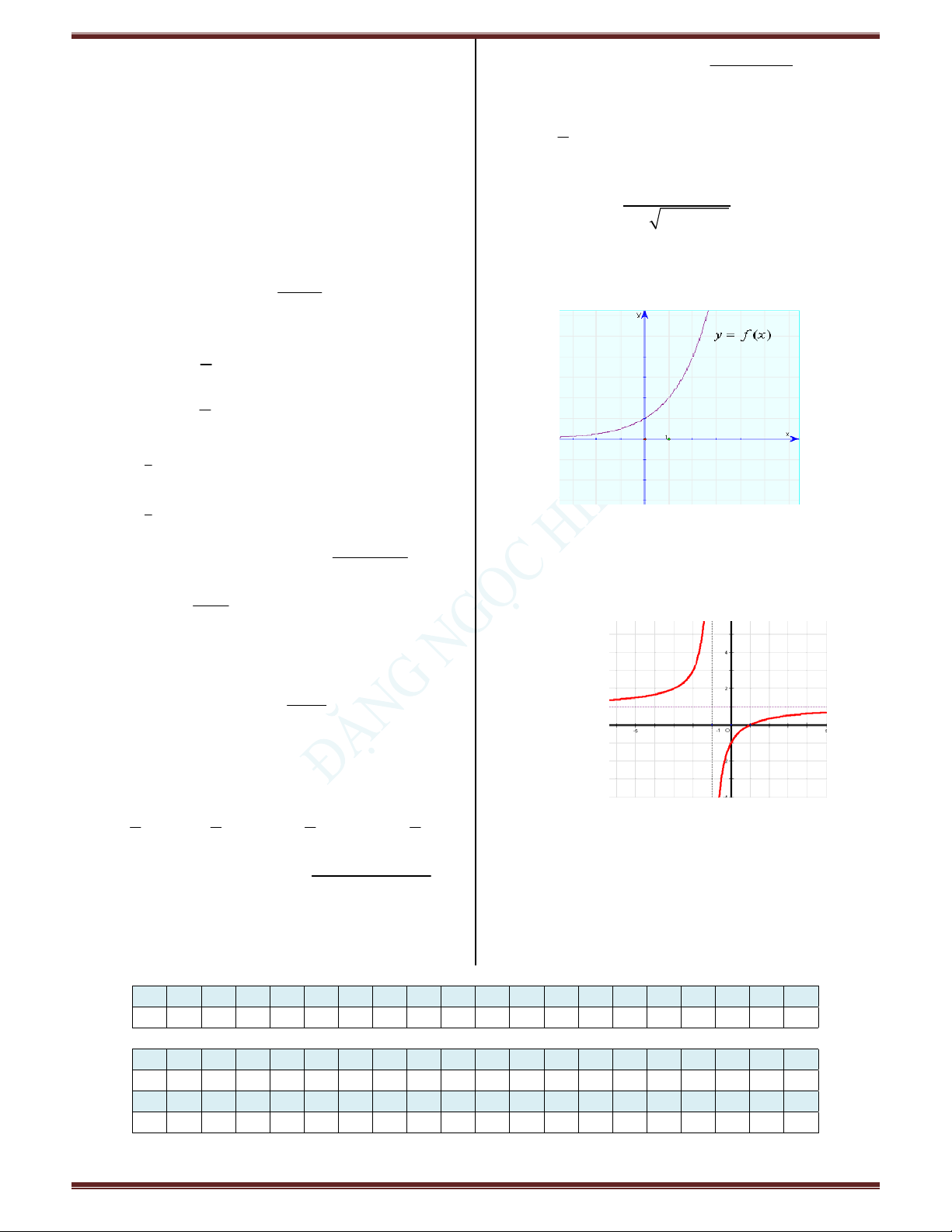
Câu 44. Cho hàm số y f (x) có đồ thị như hình vẽ: x x x
A. a  1, b  1  .
B. a  1, b  2 . C. a  1,  b 1.
D. a b  1. 2  x 1  , khi x  1
Câu 39. Cho hàm số f (x)   x 1 có giới
2mx 1, khix 1
hạn hữu hạn khi x 1 . Khi đó giá trị m bằng: 1 1 3 3
Khẳng định nào sau đây là sai? A.  . B. . C. . D.  . 2 2 2 2
A. lim f (x)  1.
B. lim f (x)  1. x x 3 2
ax  2x bx 1
Câu 40. Cho a b  3 và lim  2 .
C. lim f (x)   .
D. lim f (x)   . x ( 1)   x ( 1)   x 1  x 1
Khẳng định nào sau đây là đúng?
A. 3a b  4 .
B. 3a b  6 .
C. a  3b  6 .
D. a  3b  4 . 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
D A A D A B C B B D A C C C B A A D B C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B C D B D D B D B A D A D D B D D A B B
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 A B D D HÀM SỐ LIÊN TỤC
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 7
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
1 Hàm số liên tục tại một điểm Định nghĩa:
Giả sử hàm số f xác định trên khoảng a; b và x a; b . Hàm số f được gọi là liên tục tại điểm x 0   0
nếu: lim f (x)  f (x ) 0 x0 x
Theo định nghĩa trên, hàm số f x xác định trên khoảng a; b là liên tục tại điểm x a; b nếu và chỉ 0  
nếu lim f (x) và lim f (x) tồn tại và lim f (x)  lim f (x)  f (x ) 0 x         0 x x 0 x x 0 x x 0 x
2 Hàm số liên tục trên một khoảng
Hàm số f x xác định trên khoảng a; b được gọi là liên tục trên khoảng đó, nếu nó liên tục tại mọi
điểm của khoảng đó.
Chú ý: Đồ thị của một hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
Tính liên tục của một số hàm số:
Tổng, hiệu, tích, thương của hai hàm số liên tục tại một điểm là những hàn số liên tục tại điểm đó (giá trị
của mẫu tại điểm đó phải khác 0).
Hàm đa thức và hàm phân thức hữu tỉ liên tục trên tập xác định của chúng.
Các hàm y sin x, y cos x, y tan x, y cot x liên tục trên tập xác định của chúng.
3 Tính chất của hàm số liên tục
Nếu hàm f liên tục trên a; b và f a. f b  0 thì phương trình f x  0 có nghiệm trên khoảng a;b.
CÂU HỎI TRẮC NGHIỆM 2  x
khi x  1, x  0  x
Câu 1. Xét hai mệnh đề 
Câu 3. Cho hàm số f x  0 khi x  0 .
2x 1, khi x  0
I. Hàm số f (x)   liên  x khi x  1 1
  x, khi x  0   tục trên  2x 1
Hàm số f x liên tục tại:  , khi x  0
II. Hàm số f (x)   x
A. mọi điểm thuộc  . 2, khi x  0
B. mọi điểm trừ x  0 .
C. mọi điểm trừ x  1.
liên tục tại x  0
D. mọi điểm trừ x  0 và x  1. Mệnh đề nào đúng? A. Chỉ I. B. Chỉ II .
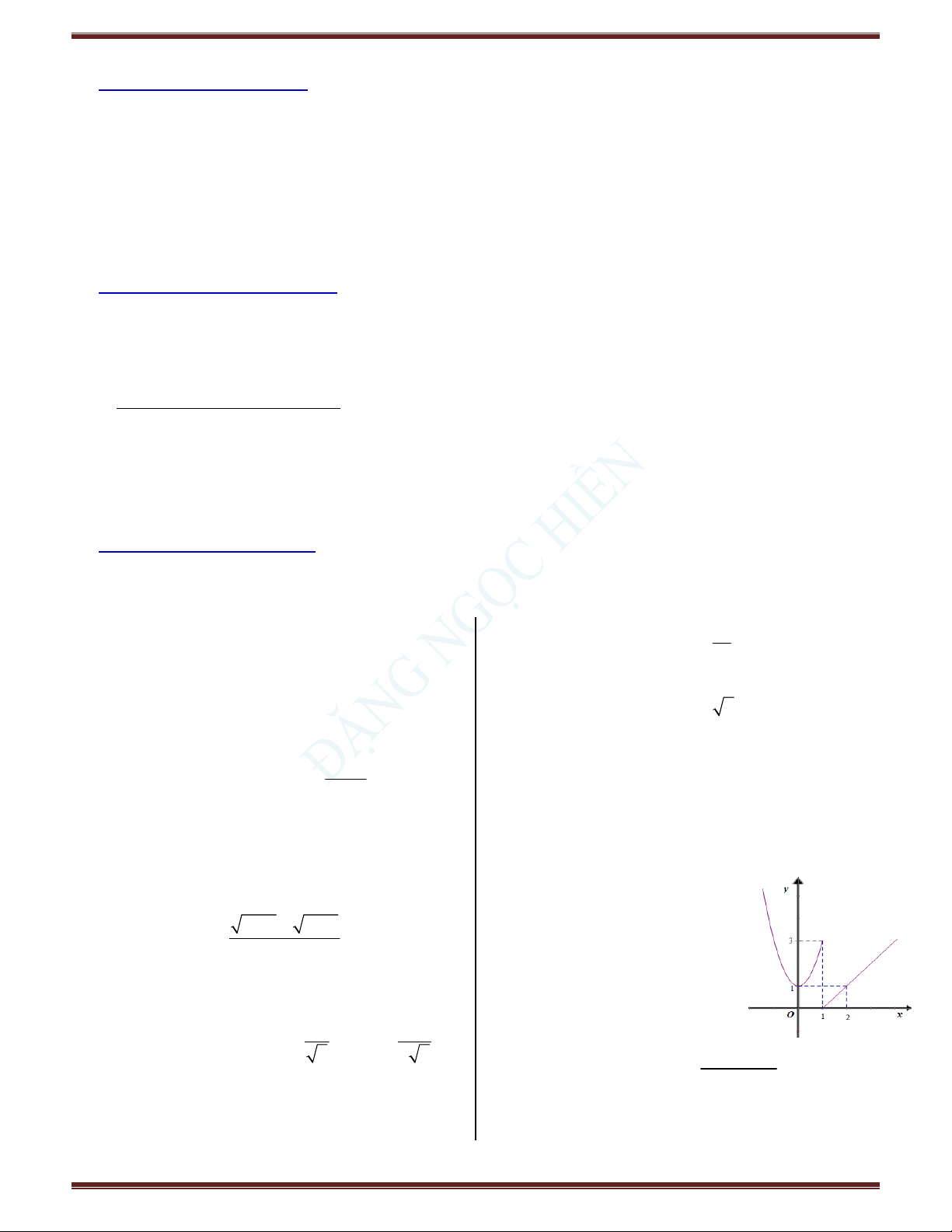
Câu 4. Hàm số f x có đồ thị C. Cả I và II. D. Không có .
như hình bên không liên tục tại   
điểm có hoành độ là bao nhiêu? Câu 2. Cho   2 2  x x f x
với x  0 . Phải x
A. x  0 .
bổ sung thêm giá trị f 0 bằng bao nhiêu thì hàm số B. x  1.
C. x  2 . liên tục trên  .
D. x  3 . 1 1 A. 0. B. 1. C. . D. . 2 2 2 2 x 1
Câu 5. Cho hàm số f (x) 
, f (x) liên tục 2 x  5x  6
trên các khoản nào sau đây?
A. (3;2) . B. ( 3  ;) C. ( ;  3) . D. (2;3) .
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 8
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 2
x  7x 10 Câu 14. Cho hàm số  khi x  2
Câu 6. Cho f (x)   x  2 . Hàm số 3  x  8  khi x { 2; 0}  a khi x  2 xx  2 
liên tục tại x  2 thì giá trị của a là: f (x)   6  khi x  1  .Khẳng định nào sau A. 3.  B. 2. 5  khi x  0 C. 5.
D. Một số khác.   2  x  2x  khi x  2  2  đây đúng? Câu 7. Cho x x  6 f (x)   . Hàm số 2
A. Hàm số không xác định tại x  2.  khi x  2 
B. Hàm số không xác định tại x  0. 5
C. Hàm số liên tục tại x  0.
bị gián đoạn tại điểm nào sau đây?
D. Hàm số liên tục tại x  2. A. x  2.  B. x  3. 3
x 1 khi x 1 C. x  0.
D. Một điểm khác.
Câu 15. Cho hàm số f x   . Khi đó 2 khi x  1 2
ax 1 khi x  1
Câu 8. Cho f (x)  
. Hàm số liên lim f x bằng 2 khi x  1 x 1 
tục trên  khi a có giá trị là: A. 1. B. 2 . A. 2. B. 0. C. 0 . D. không tồn tại. C. 1.
D. Một số khác.    Câu 16. Cho hàm số   3 3  x x f x với 2  4 x
Câu 9. Cho ( )  x x f x
. Để hàm số liên tục trên 2x
x  0 . Để hàm số f x liên tục trên  thì f 0 bằng
 thì phải định nghĩa f (0) bằng giá trị nào sau đây? 2 3 3 A. 0. B. 4. C. 2. D. 2. A. . B. . C. 1. D. 0 . 3 3 3x
Câu 10. Cho f (x) 
. Để hàm số liên tục tại 2 x  3x  2 x 1 1
Câu 17. Cho hàm số f x  với x  1. Để x 1
x  0 thì phải định nghĩa f (0) bằng giá trị nào sau hàm số f x liên tục trên  thì f  1 bằng đây? A. 3. B. 6. C. 4. D. 0. A. 2 . B. 1. C. 0 . D. 1  . x  4  4 
Câu 18. Cho hàm số f x  với x  0 . Để
Câu 11. Cho ( )  x x f x . Để hàm số liên x  4  2 2x
tục tại x  0 thì phải định nghĩa f (0) bằng giá trị nào hàm số f x liên tục trên  thì f 0 bằng sau đây? A. 0 . B. 2 . C. 4 . D. 1. 1 1 3  x  8 A. . B. . C. 0. D. 4.  khi x  2  4 2
Câu 19. Cho hàm số f x  4x  8 . 1 3  khi x  2 
Câu 12. Cho f (x) 
. Để hàm số liên tục tại x  1 x 1
Hàm số f x liên tục tại
thì phải định nghĩa f (1) bằng giá trị nào sau đây? A. x  2
 . B. x  3. C. x  2 . D. x  3 . A. 0. B. 2. 2
x  4x  3 C. 1.
D. Không xác định được f (1).  khi x  3
Câu 20. Cho hàm số f x   x  3 2 2  sin 5
Câu 13. Cho ( )  x x f x . Để hàm số liên tục a khi x  3 x x
tại x  0 thì phải định nghĩa f (0) bằng giá trị nào sau . Để hàm số f x liên tục tại 3 thì a bằng đây? A. 2 . B. 4 . C. 0 . D. 2  . 2 A. 2. B. 0.  x -5x  6  khi x  3 C. 5.
D. Không xác định được f (1).
Câu 21. Cho hàm số f x   4x -3 - x 1   ax khi x  3
. Để hàm số f x liên tục tại x  3 thì a bằng
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 9
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 4 2 Câu 24. Cho hàm số A.  . B. 3 . C. 0 . D. . 3 3 3  3x  2  2   khi x  2 5  4x f x 
. Để hàm số f x  x  khi x  1 x  2
Câu 22. Cho hàm số f x   1 x . a khi x  2 (a  4)x khi x  1
liên tục trên  thì a bằng
Để hàm số f x liên tục trên  thì a bằng 1 A. 0 . B. 2 . C. . D. 1. A. 3 . B. 1  . C. 1. D. 0 . 4 Câu 23. Cho hàm số 2
x 1 khi x  3, x 1  3  3x 1  2   6x x 1  f x  khi x  1   f x   x x 1
. Để hàm số Câu 25. Cho hàm số   4 khi 1 .   a x khi x  1
x 1 khi x  3  
f x liên tục trên  thì a bằng
Hàm số f x liên tục tại: 1 5 A. 2 . B. 1. C. . D. . 4 4
A. mọi điểm thuộc  .
B. mọi điểm trừ x  1.
C. mọi điểm trừ x  3 .
D. mọi điểm trừ x  1 và x  3 . 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
A C A B D A B C D B A D C D B B D C A A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 A B D C C ĐẠO HÀM
KIẾN THỨC CẦN NHỚ
1. Định nghĩa đạo hàm tại một điểm
1.1. Định nghĩa : Cho hàm số y f x xác định trên khoảng a ; b và x a ; b , đạo hàm của hàm số tại 0   f x f x
điểm x là : f ' x  lim . 0     0 0 x 0 x x x0 1.2. Chú ý :
 Nếu kí hiệu x x x ; y f x  x f x thì : 0  0   0
f x  x f xy f ' x  lim  lim . 0   0   0 xxx 0 0 x xx 0
 Nếu hàm số y f x có đạo hàm tại x thì nó liên tục tại điểm đó. 0
2. Ý nghĩa của đạo hàm
2.1. Ý nghĩa hình học: Cho hàm số y f x có đồ thị C
f 'x là hệ số góc của tiếp tuyến đồ thị Ccủa hàm số y f x tại M x , y C . 0  0 0    0 
 Phương trình tiếp tuyến của đồ thị hàm số y f x tại điểm M x , y C là : 0  0 0   
y f ' x x x y . 0   0  0
2.2. Ý nghĩa vật lí :
 Vận tốc tức thời của chuyển động thẳng xác định bởi phương trình : s st tại thời điểm t là 0
vt s ' t . 0   0
 Cường độ tức thời của điện lượng Q Qt tại thời điểm t là : I t Q' t . 0   0 0
3. Qui tắc tính đạo hàm và công thức tính đạo hàm
3.1. Các quy tắc : Cho u u x ; v vx ; C : là hằng số.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 10
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
 u v'  u ' v'   .
u v'  u '.v v'.u
 C.u  C.u 
u u v v uC C u  '. '. .  , v  0      2     2  v vu u
 Nếu y f u, u ux  y  y.u . x u x
3.2. Các công thức :
 C 0 ; x  1   n x  n 1   n x   n u  n 1 .  . 
n u .u , n  , n  2   u  1  x  
,  x  0   u   , u  0 2 x 2 u
 sin x  cos x  sinu  . u cosu
 cos x  sin x
 cosu  u .sinu   1 tan  tan     u x u 2   2 cos x cos u  1 cot  cot       u x u . 2   2 sin x sin u
1. ĐỊNH NGHĨA ĐẠO HÀM
(3) Nếu f x gián đoạn tại x x thì chắc chắn 0
f x không có đạo hàm tại điểm đó.
Câu 1: Số gia của hàm số f x 2
x  4x 1 ứng Trong ba câu trên:
với x và x là
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai. A. x   x   2x  4. B. 2x   . x
C. Cả ba đều đúng. D. Cả ba đều sai. C.  .
x 2x  4 x  . D. 2x  4 . x 2  x
Câu 2: Cho hàm số y f (x) có đạo hàm tại x là  khi x  1 0
Câu 4: Cho hàm số f (x)   2 .
f '(x ) . Khẳng định nào sau đây sai?
ax b khi x 1 0
f (x)  f (x )
Với giá trị nào sau đây của a, b thì hàm số có đạo hàm A. 0 f (  x )  lim . 0 x 0 x x x0 tại x  1?
f (x x  )  f (x ) B. 0 0 f (  x )  lim . 1 1 1 0 x  0 x
A. a  1;b   .
B. a  ;b  . 2 2 2
f (x h)  f (x ) C. 0 0 f (  x )  lim . 1 1 1 0 h0 h
C. a  ;b   .
D. a  1;b  . 2 2 2
f (x x )  f (x ) D. 0 0 f (  x )  lim . 0 2 xx 0 x x x0
Câu 5: Số gia của hàm số f x  ứng với số gia 2
Câu 3: Xét ba mệnh đề sau:
x của đối số x tại x  1
(1) Nếu hàm số f x có đạo hàm tại điểm 0 là
x x thì f x liên tục tại điểm đó. 1    1     0 A. x2 . x B. x2 x . 2 2  
(2) Nếu hàm số f x liên tục tại điểm x x thì 0 1 1 C.  x  2  x  . x    . x
f x có đạo hàm tại điểm đó. 2   D.  2 2
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 11
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 y
Câu 13: Đạo hàm của hàm số 3 2 2016   là: Câu 6: Tỉ số
của hàm số f x  2xx   1 theo y (x 2x ) xA. 3 2 2015
y  2016(x  2x ) . x và x là B. 3 2 2015 2
y  2016(x  2x ) (3x  4x).
A. 4x  2 x   2.
B. x   x  2 4 2  2. C. 3 2 2
y  2016(x  2x )(3x  4x). D. 3 2 2
y  2016(x  2x )(3x  2x).
C. 4x  2 x   2. D. x x    x  2 4 2  2 . x
Câu 14: Cho hàm số f (x)  ax  . b Trong các mệnh
Câu 7: Số gia của hàm số   3
f x x ứng với x  2 0
đề sau, mệnh đề nào đúng? và x  1 bằng bao nhiêu? A. f (  x)   . a B. f (  x)   . b A. 19 . B. 7 . C. 19 . D. 7 . C. f (  x)  . a D. f (  x)  . b
2. ĐẠO HÀM CỦA HÀM ĐA THỨC – HỮU TỈ-
Câu 15: Cho hàm số   1
f x  . Đạo hàm của f tại CĂN THỨC x 2
x  2x  3 x  2 là
Câu 8: Cho hàm số y  . Đạo hàm yx  2 1 1 1 1 A. . B.  . C. . D.  .
của hàm số là biểu thức nào sau đây? 2 2 2 2 3 3   A. 1   . B. 1 .
Câu 16: Cho hàm số f x  x 2 2 3
1 . Giá trị f   1 2 (x  2) 2 (x  2) 3 3 là C. 1   . D. 1 . 2 (x  2) 2 (x  2) A. 4. B. 8. C. -4. D. 24.
Câu 9: Đạo hàm của hàm số 4 2
y x  3x x 1 là
Câu 17: Cho hàm số f x  x 1 . Đạo hàm của A. 3 2
y '  4x  6x 1. B. 3 2
y '  4x  6x  . x
hàm số tại x  1 là C. 3 2
y '  4x  3x  . x D. 3 2
y '  4x  3x 1. 1 A. . B. 1. C. 0 D. Không tồn tại. 1 1 2
Câu 10: Đạo hàm của hàm số y   bằng biểu 3 2 x x Câu 18: Cho hàm số 2
y  1 x thì f 2là kết quả thức nào sau đây? nào sau đây? 3 1 3 2 A.  . B.  . 2 2  4 3 x x 4 3 x x A. f (2  )  . B. f (2  )  . 3 2 3 1 3 3 C.  . D.  . 4 3 x x 4 3 x x 2 C. f (2  )  . D. Không tồn tại. 3 
Câu 11: Đạo hàm của hàm số 7
y  2x x bằng
Câu 19: Cho hàm số y  4x x . Nghiệm của biểu thức nào sau đây?
phương trình y  0 là 2 A. 6 14x  2 x. B. 6 14  x  . x 1 1 1 1 1 1 A. x  . B. x  . C. x  . D. x   . C. 6 14  x  . D. 6 14  x  . 8 8 64 64 2 x x Câu 20: Cho hàm số 3
y  3x  25. Các nghiệm của
Câu 12: Đạo hàm của y  x x 2 5 2 2 là
phương trình y  0 là. A. 9 6 3
y  10x  28x 16x . 5 3
A. x   . B. x   . C. x  0 . D. x  5  . B. 9 6 3
y  10x 14x 16x . 3 5 C. 9 3
y  10x 16x . D. 6 3
y  7x  6x 16 . x
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 12
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 1 sin x  cos x
Câu 21: Cho hàm số f x 3 2
x  2 2x  8x 1. Câu 29: Đạo hàm của hàm số y  là: 3 sin x  cos x
Tập hợp những giá trị của x để f  x  0 là: sin 2x 2 2 sin x  cos x A. y  . B. y  .
sin x cos x2
sin x cos x2
A. 2 2. B. 2; 2 . C. 4 2. D. 2 2. 2   2sin 2x 2 C. y  . D. y  . Câu 22: Cho hàm số 3 2
y  3x x 1. Để y  0 thì x
sin x cos x2
sin x cos x2
nhận các giá trị thuộc tập nào sau đây sin x
Câu 30: Hàm số y  có đạo hàm là:  2   9  x A.  ;0 .  B.  ;0 . 9     2   
x sin x  cos x
x cos x  sin x A. y  . B. y  .  9   2  2 x 2 x C. ;   0;  . D. ;   0;  . 2    9   
x cos x  sin x
x sin x  cos x C. y  . D. y  . 2 x 2 x 3
Câu 23: Cho hàm số y
. Để y  0 thì x nhận 1 x 1
Câu 31: Cho hàm số y f (x)  . Giá trị sin x
các giá trị thuộc tập nào sau đây? A. 1. B. 3. C. . D. .    f   là:  2 
Câu 24: Cho hàm số f x 3 2
x  3x 1. Đạo hàm 1
của hàm số f x âm khi và chỉ khi. A.1. B. . C. 0. D. Không tồn tại. 2
A. 0  x  2 . B. x  1. cos x 4
Câu 32: Cho hàm số y f (x)    cot x .
C. x  0 hoặc x 1.
D. x  0 hoặc x  2. 3 3sin x 3 Câu 25: Cho hàm số 3
f (x)  2mx mx . Số x 1 là   
Giá trị đúng của f   bằng:
nghiệm của bất phương trình f (
x)  1 khi và chỉ khi:  3  A. m 1. B. m  1.  8 9 9 8 A. . B.  . C. . D.  . C. 1   m 1. D. m  1.  9 8 8 9 2
Câu 26: Cho hàm số y  2 
x  3x . Để y  0 thì x cos x
Câu 33: Cho hàm số y f (x)  . Biểu thức 2 1 sin x
nhận các giá trị thuộc tập nào sau đây?        1  f  3 f      bằng A.  ;  . B. ;  .    4   4   9   1  8 8 C. ;  .   D. .  A. 3  . B. C. 3 . D.    9  3 3
3. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC   
Câu 34: Cho hàm số f x 2  tan x    . Giá trị
Câu 27: Hàm số y  cot 2x có đạo hàm là:  3  2 1 tan 2x 2 (1 tan 2x) f 0 bằng A. y  . B. y  . cot 2x cot 2x A.  3 . B. 4 . C. 3  . D. 3 . 2 1 cot 2x 2 (1 cot 2x) C. y  . D. y  . x cot 2x cot 2x
Câu 35: Cho hàm số y f x cos  . Chọn kết 1 2sin x
Câu 28: Đạo hàm của hàm số y  3sin 2x  cos3x là: quả SAI
A. y  3cos 2x  sin 3 .
x B. y  3cos 2x  sin 3 . x    5
C. y  6 cos 2x  3sin 3 .
x D. y  6c  os2x 3sin3 . x A. f      
B. f 0  2  .  6  4
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 13
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11    1
Câu 44: Cho hàm số y  cos x . Khi đó (2016) y (x) C. f      
D. f    2  .  2  3 bằng  2 
Câu 36: Cho hàm số y  cos  2x   . Khi đó
A.  cos x . B. sin x .
C. sin x . D. cos x .  3  Câu 45: Cho hàm số 4 3 2
y  3x  4x  5x  2x 1.
phương trình y  0 có nghiệm là:
Hỏi đạo hàm đến cấp nào thì ta được kết quả triệt tiêu   k
A. x    k2 . B. x   . (bằng 0 )? 3 3 2   kA. 2 . B. 4 . C. 5 . D. 3 .
C. x    k . D. x    . 3 3 2 5. VI PHÂN   x
Câu 37: Cho hàm số y  sin 
Câu 46: Cho hàm số y f x   x  2 1 . Biểu thức   . Khi đó phương  3 2 
nào sau đây là vi phân của hàm số đã cho?
trình y '  0 có nghiệm là:
A. dy  2 x   1 dx .
B. dy  2 x   1 .   A. x   k2 . B. x   k.
C. dy   x   1 dx .
D. y   x  2 d 1 dx . 3 3  
C. x    k 2 .
D. x    k .
Câu 47: Vi phân của hàm số f x 2
 3x x tại điểm 3 3
x  2 , ứng với x   0,1 là:
4. ĐẠO HÀM CẤP CAO
A. 0, 07 . B. 10 . C. 1,1 . D. 0, 4 .
Câu 38: Hàm số nào dưới đây có đạo hàm cấp hai là Câu 48: Vi phân của y  cot2017x là: 6x ? A. dy  201  7sin 2017xd . x A. 2
y  3x . B. 3
y  2x . C. 3
y x . D. 2 y x . 2017 B. dy  d . x Câu 39: Cho hàm số 3 2
y  3x  3x x  5 . Khi 2 sin 2017x đó (3) y (3) bằng: 2017 2017 C. dy   d .
x D. dy   d . x 2 cos 2017x 2 sin 2017xA. 54 . B. 18 . C. 0 . D. 162 . 2
Câu 40: Cho hàm số y  cos 2x . Khi đó y ''(0) bằng x x 1
Câu 49: Cho hàm số y = . Vi phân của hàm A. 2 . B.  2 3 C. 4 . D. 2 3 . x 1 số là:    2 Câu 41: Cho hàm số 2   
y  cos x . Khi đó (3) y x 2x 2 2x 1   A. dy  
dx B. dy  dx  3  2 (x 1) 2 (x 1) bằng: 2x 1 2 x  2x  2 C. dy   dx D. dy  dx 2 (x 1) 2 (x 1) A. 2 . B. 2 3 .
C. 2 3 . D. 2 . x  3
Câu 42: Cho y  3sin x  2cosx . Tính giá trị biểu Câu 50: Cho hàm số y  . Vi phân của hàm số 1 2x
thức A y '' y là: tại x  3  là: 1 A. A  0 . B. A  2 . A. dy  d . x B. dy  7d . x C. A  4cos . x
D. A  6sin x  4cos . x 7 1 1
C. dy   d . x D. dy  7  d . x
Câu 43: Cho hàm số y  . Khi đó (n) y (x) bằng: 7 x
Câu 51: Vi phân của y  tan 5x là : n! n! A. ( 1  )n . B. . 5x 5 n 1    x n 1 x A. dy d . x B. dy d . x 2 cos 5x 2 sin 5x n n! n ! C. ( 1  ) . . D. . n x n x
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 14
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 5 5    C. dy  d . x D. dy   d . x Câu 59: Cho hàm số 2 y x
6x 5 có tiếp tuyến 2 cos 5x 2 cos 5x
song song với trục hoành. Phương trình tiếp tuyến đó    y  là:  8 Câu 52: Cho 
dy  cos 2x dx . Khi đó có giá    A. x  3.
B. y  4. C. y  4. D. x  3. y   3 
Câu 60: Trong các tiếp tuyến tại các điểm trên đồ thị trị nào sau đây? hàm số 3 2
y x  3x  2 , tiếp tuyến có hệ số góc nhỏ A. 1 B. 2 C.  2 D. 0 nhất bằng
6. TIẾP TUYẾN – Ý NGHĨA CỦA ĐẠO HÀM A. 3  . B. 3 . C. 4 . D. 0 . 2x  4
Câu 61: Hệ số góc của tiếp tuyến của đồ thị hàm số
Câu 53: Cho hàm số y  có đồ thị là (H) . x  3 
Phương trình tiếp tuyến tại giao điểm của
y  tan x tại điểm có hoành độ x  là 0 4 (H) với trục hoành là:
A. y  2x  4 .
B. y  3x 1 . 1 2 A. . B. . C. 1. D. 2.
C. y  2x  4 .
D. y  2x . 2 2
Câu 54: Hệ số góc của tiếp tuyến của đồ thị hàm số 4
Câu 62: Cho hàm số y  2  có đồ thị H . 2  3x y
tại giao điểm của đồ thị hàm số x x 1
Đường thẳng  vuông góc với đường thẳng với trục hoành bằng : 1 1 A. 9 . B. . C. 9.  D.  .
d : y  x  2 và tiếp xúc với H  thì phương trình 9 9 của  là
Câu 55: Phương trình tiếp tuyến của đồ thị hàm số
y x  2 f x 3 2
x  2x  3x tại điểm có hoành độ x  1 là:
A. y x  4. B.  . 0
y x  4
A. y  10x  4.
B. y  10x  5.
y x  2
C. y  2x  4.
D. y  2x  5. C.  . D. Không tồn tại.
y x  6
Câu 56: Tiếp tuyến của đồ thị hàm số Câu 63: Lập phương trình tiếp tuyến của đường cong 3 x 3 2 2 y
 3x  2 có hệ số góc k  9, có phương trình (C) : y x  3x  8x 1, biết tiếp tuyến đó song song 3
với đường thẳng  : y x  2017 ? là :
A. y x  2018 .
B. y x  4 .
A. y 16  9(x  3).
B. y  9(x  3).
C. y x  4 ; y x  28 . D. y x  2018 .
C. y 16  9(x  3).
D. y 16  9(x  3).    C
Câu 57: Hệ số góc của tiếp tuyến của đồ thị hàm số Câu 64: Cho hàm số 3 2 y 2x 3x 1 có đồ thị   , x 1  3  y
tại giao điểm với trục tung bằng :
tiếp tuyến với C nhận điểm M ; y   làm tiếp x 1 0 0  2  A. 2.  B. 2. C. 1. D. 1. 
điểm có phương trình là: Câu 58: Cho hàm số 3 2
y x  3x có đồ thị C. Có 9 9 27
A. y x .
B. y x  . 2 2 4
bao nhiêu tiếp tuyến của C song song đường thẳng 9 23 9x 31
C. y x  . D. y   .
y  9x 10 ? 2 4 2 4
Câu 65: Hoành độ tiếp điểm của tiếp tuyến song song A. 1. B. 3. C. 2. D. 4.
với trục hoành của đồ thị hàm số 3
y x  3x  2 là
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 15
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
A. x 1và x  1  . B. x  3  và x  3. 7 7
A. y  x
B. y  x
C. x 1và x  0 .
D. x  2 và x  1  . 3 3
Câu 66: Phương trình tiếp tuyến của đồ thị hàm số 7 7
C. y x
D. y x 4 2
y x  2x 1 tại điểm có tung độ tiếp 3 3 điểm bằng 2 là: x 1
A. y  8x  6, y  8x  6.
Câu 72: Tiếp tuyến của đồ thi ̣ hàm số y  ta ̣i x  5
B. y  8x  6, y  8x  6.
C. y  8x  8, y  8x  8. điểm A 1
 ;0 có hê ̣ số góc bằng
D. y  40x  57. 1 6 1 6 A. B. C.D.x  2 6 25 6 25
Câu 67: Cho đồ thị (H ) : y
và điểm A (H ) x 1
Câu 73: Cho hàm số 2
y  x  4x  3 có đồ thi ̣P .
có tung độ y  4 . Hãy lập phương trình tiếp tuyến của Nếu tiếp tuyến tại điểm M của P có hệ số góc bằng
(H ) tại điểm A .
8 thı̀ hoành đô ̣ điểm M là:
A. y x  2 .
B. y  3x 11.
C. y  3x 11 .
D. y  3x 10 . A. 12 B. 6  C. 1 D. 5 x 1
Câu 74: Cho hàm số 3 2
y x  3x  2 có đồ thi ̣ C .
Câu 68: Cho hàm số y  (C) . Có bao nhiêu x 1
Đường thẳng nào sau đây là tiếp tuyến của C và có
cặp điểm A, B thuộc C mà tiếp tuyến tại đó song hê ̣ số góc nhỏ nhất: song với nhau:
A. y  3x  3 B. y  0 A. 0 . B. 2 . C. 1. D. Vô số.
C. y  5x 10
D. y  3x  3 Câu 69: Cho hàm số 3 2
y x  2x  2x có đồ thị (C). Câu 75: Cho hàm số 3 2
y x  3mx  (m 1)x m .
Gọi x , x là hoành độ các điểm M , N trên C , mà Gọi A là giao điểm của đồ thị hàm số với Oy . Tìm m 1 2
tại đó tiếp tuyến của C vuông góc với đường thẳng để tiếp tuyến của đồ thị hàm số tại A vuông góc với
đường thẳng y  2x  3 .
y  x  2017 . Khi đó x x bằng: 1 2 3  1 3 1 4 4 1 A. B. C. D. A. . B. . C. . D. 1  . 2 2 2 2 3 3 3 Câu 76: Cho hàm số 3 2
y  x  3x  3 có đồ thị C . 1
Câu 70: Trên đồ thị của hàm số y  có điểm M x 1
Số tiếp tuyến của C vuông góc với đường thẳng
sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo 1
y x  2017 là:
thành một tam giác có diện tích bằng 2. Tọa độ M là: 9  1  A. 2;  1 . B. 4; . A.1 B. 2 C. 3 D. 0    3 
Câu 77: Cho chuyển động thẳng xác định bởi phương  3 4   3  C.  ;  .   D. ; 4 .   trình 3 2
s t  3t  9t  2 ( t tính bằng giây; s tính bằng  4 7   4 
mét). Khẳng định nào sau đây đúng ? 1
Câu 71: Cho hàm số 3 2
y x x  2 có đồ thi ̣ hàm 3
A. Vận tốc của chuyển động bằng 0 khi t  0 hoặc t  2 .
số C . Phương trı̀nh tiếp tuyến của C ta ̣i điểm có
B. Vận tốc của chuyển động tại thời điểm t  2 là
v  18 m / s .
hoành đô ̣ là nghiê ̣m của phương trı̀nh y"  0 là
C. Gia tốc của chuyển động tại thời điểm t  3 là 2
a  12 m / s .
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 16
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
D. Gia tốc của chuyển động bằng 0 khi t  0 . Câu 79: Giá trị m để hàm số
Câu 78: Cho chuyển động thẳng xác định bởi phương 1 3
y x  m   2
1 x  3m  
1 x 1 có y  0,x   trình 3 2
s t  3t (t tính bằng giây; s tính bằng mét). 3
Khẳng định nào sau đây đúng? là:
A. Gia tốc của chuyển động khi t  4s là 2 a 18  m/ s . m 0
A. m  0 B. m  1
C. 0  m  1 D.
B. Gia tốc của chuyển động khi t  4s là 2 a 9m/ s . m 1
C. Vận tốc của chuyển động khi t  3s là v 12  m/ s.
D. Vận tốc của chuyển động khi t  3s là v24m/ s. 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
A D A A A C C C A B C A B C B D D D C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D A C A D C D C D B C B C B A D C C B C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
B A A D C A C D D A C B C A A A B C B A
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
D C C C A A D D A D A C B A A B B A C
HAI ĐƯỜNG THẲNG VUÔNG GÓC a 10 a 6
Câu 1. Trong không gian cho ba đường thẳng phân A. MN = B. MN = 2 3
biệt a, b, c. Khẳng định nào sau đây đúng? 3a 2 2a 3
A. Nếu a và b cùng vuông góc với c thì a//b C. MN = D. MN =
B. Nếu a//b và c  a thì c  b. 2 3
C. Nếu góc giữa a và c bằng góc giữa b và c thì a//b
Câu 3. Cho hình hộp ABCD.A’B’C’D’ có tất cả các
D. Nếu a và b cùng nằm trong mp ( ) // c thì góc
cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề
giữa a và c bằng góc giữa b và c
nào có thể sai?
Câu 2. Cho tứ diện ABCD có AC = a, BD = 3a. Gọi A. A’C’BD B. BB’BD
M và N lần lượt là trung điểm của AD và BC. Biết AC C. A’BDC’ D. BC’A’D
vuông góc với BD. Tính MN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 B A B
ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
KIẾN THỨC CẦN NHỚ
Dạng 1 Chứng minh đường thẳng vuông góc với mặt phẳng.
Phương pháp : * Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng
* Sử dụng sự liên hệ giữa quan hệ song song và quan hệ vuông góc
Dạng 2 Chứng minh hai đường thẳng vuông góc.
Phương pháp : * Chứng minh đường thẳng này vuông góc với mặt phẳng chứa đường thẳng kia
* Sử dụng định lý ba đường vuông góc
* Sử dụng sự liên hệ giữa quan hệ song song và quan hệ vuông góc
Dạng 3 Tìm thiết diện của đa diện và mặt phẳng vuông góc với đường thẳng cho trước.
Phương pháp : Tìm hai đường thẳng cắt nhau vuông góc với đường thẳng cho trước
Khi đó thiết diện song song với hai đường thẳng vừa tìm được
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 17
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Dạng 4 Tính góc giữa đường thẳng a và mặt phẳng  .
Phương pháp : Tìm đường thẳng a’ là hình chiếu của a lên mặt phẳng  Khi đó
góc giữa đường thẳng a và mặt phẳng  là góc giữa đường thẳng a và a’.
CÂU HỎI TRẮC NGHIỆM
Câu 9. Cho hình chóp S.ABC có SA= SB = SC và
Câu 1. Khẳng định nào sau đây sai ?
tam giác ABC vuông tại B. Vẽ SH  (ABC),
A. Nếu đường thẳng d () thì d vuông góc với hai
H(ABC). Khẳng định nào sau đây đúng? đường thẳng trong ()
A. H trùng với trọng tâm tam giác ABC
B. Nếu đường thẳng d vuông góc với hai đường
B. H trùng với trực tâm tam giác ABC.
thẳng nằm trong () thì d ()
C. H trùng với trung điểm của AC
C. Nếu đường thẳng d vuông góc với hai đường
D. H trùng với trung điểm của BC
thẳng cắt nhau nằm trong () thì d vuông góc với
Câu 10. Cho hình chóp S.ABC có cạnh SA (ABC)
bất kì đường thẳng nào nằm trong ().
và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt
D. Nếu d () và đường thẳng a // () thì d  a
là trung điểm của AB và SB. Khẳng định nào sau đây
Câu 2. Trong không gian cho đường thẳng  và có thể sai ?
điểm O. Qua O có mấy đường thẳng vuông góc với  A. CH  SA B. CH  SB cho trước? C. CH  AK D. AK  SB A. 1 B. 2 C. 3 D. Vô số
Câu 11. Cho hình chóp S.ABC có SA= SB = SC. Gọi
Câu 3. Qua điểm O cho trước, có bao nhiêu mặt
O là hình chiếu của S lên mặt đáy ABC. Khẳng định
phẳng vuông góc với đường thẳng  cho trước? nào sau đây đúng? A. 1 B. 2 C. 3 D. Vô số
A. O là trọng tâm tam giác ABC
Câu 4. Mệnh đề nào sau đây có thể sai ?
B. O là tâm đường tròn ngoại tiếp tam giác ABC
A. Hai đường thẳng phân biệt cùng vuông góc với
C. O là trực tâm tam giác ABC
một mặt phẳng thì song song.
D. O là tâm đường tròn nội tiếp tam giác ABC
B. Hai mặt phẳng phân biệt cùng vuông góc với một Câu 12. Cho hình chóp S.ABCD có SA (ABCD) và
đường thẳng thì song song.
đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD
C. Hai đường thẳng phân biệt cùng vuông góc với
một đường thẳng thứ ba thì song song.
và I là trung điểm của SC. Khẳng định nào sau đây sai
D. Một đường thẳng và một mặt phẳng (không chứa ?
đường thẳng đã cho) cùng vuông góc với một đường A. BC  SB thẳng thì song song nhau.
B. (SAC) là mặt phẳng trung trực của đoạn BD
Câu 5. Cho hình chóp S.ABC có SA  (ABC) và C. IO  (ABCD)
ABC vuông ở B. AH là đường cao của SAB. Khẳng
D. Tam giác SCD vuông ở D.
định nào sau đây sai?
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là A. SA  BC B. AH  BC
hình vuông và SA (ABCD). Gọi I, J, K lần lượt là C. AH  AC D. AH  SC
trung điểm của AB, BC và SB. Khẳng định nào sau đây
Câu 6. Trong không gian tập hợp các điểm M cách sai ?
đều hai điểm cố định A và B là: A. (IJK) // (SAC) B. BD  (IJK)
A. Mặt phẳng trung trực của đoạn thẳng AB.
C. Góc giữa SC và BD có số đo 600 D. BD  (SAC)
B. Đường trung trực của đoạn thẳng AB.
Câu 14. Cho hình tứ diện ABCD có AB, BC, CD đôi
C. Mặt phẳng vuông góc với AB tại A
một vuông góc nhau. Hãy chỉ ra điểm O cách đều bốn
D. Đường thẳng qua A và vuông góc với AB điểm A, B, C, D.
Câu 7. Câu 11: Cho tứ diện ABCD có AB = AC và
A. O là tâm đường tròn ngoại tiếp tam giác ABC
DB = DC. Khẳng định nào sau đây đúng?
B. O là trọng tâm tam giác ACD A. AB  (ABC) B. AC  BD
C. O là trung điểm cạnh BD C. CD  (ABD) D. BC  AD
D. O là trung điểm cạnh AD
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là
Câu 15. Cho hình chóp S.ABC có SA (ABC) và AB
hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng
BC. Gọi O là tâm đường tròn ngoại tiếp tam giác
định nào sau đây đúng?
SBC.H là hình chiếu vuông góc của O lên (ABC). A. SO  (ABCD) B. CD  (SBD)
Khẳng định nào sau đây đúng ? C. AB  (SAC) D. CD AC
A. H là trung điểm cạnh AB
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 18
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
B. H là trung điểm cạnh AC
(ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) có
C. H là trọng tâm tam giác ABC
số đo bằng 450. Tính độ dài SO.
D. H là tâm đường tròn nội tiếp tam giác ABC A. SO = a 3 B. SO= a 2
Câu 16. Cho tứ diện ABCD. Vẽ AH  (BCD).Biết H
là trực tâm tam giác BCD. Khẳng định nào sau đây a 3 a 2 C. SO = D. SO= không sai ? 2 2 A. AB = CD B. AC = BD
Câu 19. Cho hình chóp S.ABCD có các cạnh bên C. AB CD D. CD BD
bằng nhau SA = SB = SC = SD. Gọi H là hình chiếu
Câu 17. Cho hình chóp S.ABCD, đáy ABCD là hình
của S lên mặt đáy ABCD. Khẳng định nào sau đây sai
vuông có tâm O, SA (ABCD). Gọi I là trung điểm ?
của SC. Khẳng định nào sau đây sai ? A. HA = HB = HC = HD
B. Tứ giác ABCD là hình bình hành A. IO (ABCD).
C. Tứ giác ABCD nội tiếp được trong đường tròn.
B. (SAC) là mặt phẳng trung trực của đoạn BD
D. Các cạnh SA, SB, SC, SD hợp với đáy ABCD C. BD SC D. SA= SB= SC. những góc bằng nhau.
Câu 18. Cho hình vuông ABCD có tâm O và cạnh
bằng 2a. Trên đường thẳng qua O vuông góc với 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
B D A C C A D A C D B B C D B C D B B
HAI MẶT PHẲNG VUÔNG GÓC
KIẾN THỨC CẦN NHỚ
Dạng 1 Xác định và tính góc giữa hai mặt phẳng () và ().
Phương pháp : Tìm giao tuyến của () và ().
Từ một điểm trên giao tuyến ta dựng hai đường thẳng nằm trong () và ()
Sao cho hai đường thẳng đó cùng vuông góc với giao tuyến
Lúc đó góc giữa hai mặt phẳng () và () là hai đường thẳng vừa dựng
Dạng 2 Chứng minh hai mặt phẳng vuông góc.
Phương pháp : * Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia
* Chứng minh góc giữa hai mặt phẳng là 90o
* Sử dụng sự liên hệ giữa quan hệ song song và quan hệ vuông góc
Dạng 3 Chứng minh đường thẳng vuông góc với mặt phẳng.
Phương pháp : * Sử dụng định lý : Khi hai mặt phẳng vuông góc với nhau một đường thẳng nằm trong
mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia
* Sử dụng định lý : Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ
ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ ba.
CÂU HỎI TRẮC NGHIỆM
Câu 2. Cho tứ diện ABCD có AC = AD và BC =
Câu 1. Cho hình chóp S.ABC có SA  (ABC) và
BD. Gọi I là trung điểm của CD. Khẳng định nào sau
đáy ABC vuông ở A. Khẳng định nào sau đây sai ? đây sai ? A. (SAB)  (ABC)
A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc B. (SAB)  (SAC)  A . IB
C. Vẽ AH BC , H BC  góc AHS là góc giữa B. (BCD)  (AIB)
hai mặt phẳng (SBC) và (ABC)
C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc
D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc   CBD SCB . D. (ACD)  (AIB)
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 19
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là
Câu 9. Cho tứ diện ABCD có hai mặt bên ACD và
hình chữ nhật tâm O và khoảng cách từ A đến BD bằng BCD là hai tam giác cân có đáy CD. Gọi H là hình 2a
chiếu vuông góc của B lên (ACD). Khẳng định nào sau
. Biết SA  (ABCD) và SA = 2a. Gọi  là góc giữa 5 đây sai?
hai mặt phẳng (ABCD) và (SBD). Khẳng định nào sau
A. AB nằm trên mặt phẳng trung trực của CD đây sai ?
B. HAM (M là trung điểm CD)
C. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc A. (SAB) (SAD) B. (SAC) (ABCD) ADB. C. tan = 5 D.  =  SOA . D. (ABH)  (ACD).
Câu 4. Cho hình lăng trụ ABCD.A’B’C’D’ có đáy
Câu 10. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy
ABCD là hình thoi, AC = 2a. Các cạnh bên AA’,
ABC là tam giác vuông cân ở A. H là trung điểm BC.
BB’… vuông góc với đáy và AA’ = a. Khẳng định nào
Khẳng định nào sau đây sai? sau đây sai ?
A. Các mặt bên của ABC.A’B’C’ là các hình chữ
A. Các mặt bên của hình lăng trụ là các hình chữ nhật bằng nhau. nhật.
B. (AA’H) là mặt phẳng trung trực của BC
B. Góc giữa hai mặt phẳng (AA’C’C) và (BB’D’D)
C. Nếu O là hình chiếu vuông góc của A lên (A’BC) có số đo bằng 600. thì O A’H
C. Hai mặt bên (AA’C) và (BB’D) vuông góc với
D. Hai mặt phẳng (AA’B’B) và (AA’C’C) vuông hai đáy. góc nhau.
D. Hai hai mặt bên AA’B’B và AA’D’D bằng nhau. Câu 11. Hình hộp ABCD.A’B’C’D’ trở thành hình
Câu 5. Cho hình lăng trụ ABCD.A’B’C’D’. Hình
lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau
chiếu vuông góc của A’ lên (ABC) trùng với trực tâm đây?
H của tam giác ABC. Khẳng định nào sau đây đúng?
A. Tất cả các cạnh đáy bằng nhau và cạnh bên
A. (AA’B’B)(BB’C’C)
vuông góc với mặt đáy.
B. (AA’H)(A’B’C’)
B. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc
C. BB’C’C là hình chữ nhật. với mặt đáy
D. (BB’C’C)(AA’H)
C. Có một mặt bên vuông góc với mặt đáy và đáy là
Câu 6. Cho hình chóp S.ABC có SA  (ABC) và hình vuông.
đáy ABC là tam giác cân ở A. Gọi H là hình chiếu
D. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông
vuông góc của A lên (SBC). Khẳng định nào sau đây
Câu 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’. đúng?
Khẳng định nào sau đây không đúng?
A. H  SB B. H trùng với trọng tâm tam giác SBC
A. Hình hộp có 6 mặt là 6 hình chữ nhật.
C. H  SC D. H  SI (I là trung điểm của BC)
B. Hai mặt ACC’A’ và BDD’B’ vuông góc nhau
Câu 7. Cho hình chóp S.ABC có hai mặt bên (SBC)
C. Tồn tại điểm O cách đều tám đỉnh của hình hộp
và (SAC) vuông góc với đáy (ABC). Khẳng định nào
D. Hình hộp có 4 đường chéo bằng nhau và đồng sau đây sai?
qui tại trung điểm của mỗi đường. A. SC  (ABC)
Câu 13. Cho hình lập phương ABCD.A’B’C’D’ cạnh
B. Nếu A’ là hình chiếu vuông góc của A lên (SBC)
bằng A. Khẳng định nào sau đây sai ? thì A’  SB
A. Hai mặt ACC’A’ và BDD’B’ vuông góc nhau C. (SAC)  (ABC)
B. Bốn đường chéo AC’, A’C, BD’, B’D bằng nhau
D. BK là đường cao của tam giác ABC thì BK  và bằng a 3 (SAC).
C. Hai mặt ACC’A’ và BDD’B’là hai hình vuông
Câu 8. Cho hình chóp S.ABC có hai mặt bên (SAB) bằng nhau
và (SAC) vuông góc với đáy (ABC), tam giác ABC D. AC  BD’
vuông cân ở A và có đường cao AH (H BC). Gọi O là Câu 14. Cho hình lăng trụ tứ giác đều
hình chiếu vuông góc của A lên (SBC). Khẳng định
ABCD.A’B’C’D’ có cạnh đáy bằng a, góc giữa hai mặt
nào sau đây sai?
phẳng (ABCD) và (ABC’) có số đo bằng 600. Cạnh bên A. SC  (ABC)
của hình lăng trụ bằng: B. (SAH)  (SBC) A. 3a B. a 3 C. 2a D. a 2 C. O SC
D. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc SBA.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 20
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Câu 15. Cho hình lăng trụ đứng ABC.A’B’C’ có AB a a 3 A. SH = B. SH =
= AA’ = a, BC = 2a, CA = a 5 . Khẳng định nào sau 2 2 đây sai ? a 2 a 3 C. SH = D. SH =
A. Đáy ABC là tam giác vuông. 3 3
B. Hai mặt AA’B’B và BB’C’ vuông góc nhau
Câu 22. Cho ba tia Ox, Oy, Oz vuông góc nhau từng
C. Góc giữa hai mặt phẳng (ABC) và (A”BC) có số
đôi một. Trên Ox, Oy, Oz lần lượt lấy các điểm A, B, C đo bằng 450
sao cho OA = OB = OC = a. Khẳng định nào sau đây D. AC’ = 2a 2 sai?
Câu 16. Cho hình lăng trụ lục giác đều
A. O.ABC là hình chóp đều.
ABCDEF.A’B’C’D’E’F’ có cạnh bên bằng a và 2 a 3
ADD’A’ là hình vuông. Cạnh đáy của lăng trụ bằng:
B. Tam giác ABC có diện tích S = 2 a a 3 a 2 A. a B. C. D. 3a 2 2 3 2
C. Tam giác ABC có chu vi 2p =
Câu 17. Cho hình lăng trụ tứ giác đều 2
D. Ba mặt phẳng (OAB), (OBC), (OCA)vuông góc
ABCD.A’B’C’D’ có ACC’A’ là hình vuông, cạnh
với nhau từng đôi một.
bằng A. Cạnh đáy của hình lăng trụ bằng:
Câu 23. Cho hình thoi ABCD có cạnh bằng a và Â = a 2 a 3
600. Trên đường thẳng vuông góc với mặt phẳng A. B. a 2 C. D. a 3 2 3
(ABCD) tại O (O là tâm của ABCD), lấy điểm S sao
Câu 18. Cho hình lăng trụ tam giác đều ABC.A’B’C’
cho tam giác SAC là tam giác đều. Khẳng định nào sau
có cạnh đáy bằng 2a 3 và cạnh bên bằng 2a. Gọi G và đây đúng?
G’ lần lượt là trọng tâm của hai đáy ABC và
A. S.ABCD là hình chóp đều
A’B’C’.Khẳng định nào sau đây đúng khi nói về
B. Hình chóp S.ABCD có các mặt bên là các tam giác cân. AA’G’G? 3a
A. AA’G’G là hình chữ nhật có hai kích thước là 2a C. SO = và 3a. 2
B. AA’G’G là hình vuông có cạnh bằng 2a.
D. SA và SB hợp với mặt phẳng (ABCD) những góc
C. AA’G’G là hình chữ nhật có diện tích bằng 6a2 bằng nhau.
D. AA’G’G là hình vuông có diện tích bằng 8a2
Câu 24. Cho hình chóp cụt đều ABC.A’B’C’ với đáy
Câu 19. Cho hình lập phương ABCD.A’B’C’D’ có
lớn ABC có cạnh bằng A. Đáy nhỏ A’B’C’ có cạnh
cạnh bằng A. Khẳng định nào sau đây sai? a a
bằng , chiều cao OO’ = . Khẳng định nào sau đây
A. Tam giác AB’C là tam giác đều. 2 2
B. Nếu  là góc giữa AC’ và (ABCD)thì cos = sai ? 2
A. Ba đường AA’, BB’, CC’ đồng qui tại S. 3 a
B. AA’= BB’= CC’ =
C. ACC’A’ là hình chữ nhật có diện tích bằng 2a2 2
D. Hai mặt AA’C’C và BB’D’D ở trong hai mặt
C. Góc giữa cạnh bên mặt đáy là góc SIO (I là trung
phẳng vuông góc với nhau. điểm BC)
Câu 20. Cho hình chóp S.ABC có đường cao SH. Xét
D. Đáy lớn ABC có diện tích gấp 4 lần diện tích đáy các mệnh đề sau: nhỏ A’B’C’.
Câu 25. Cho hình chóp cụt tứ giác đều I) SA = SB = SC
II) H trùng với tâm đường tròn ngoại tiếp tam giác a
ABCD.A’B’C’D’cạnh của đáy nhỏ ABCD bằng và ABC. 3
III) Tam giác ABC là tam giác đều.
cạnh của đáy lớn A’B’C’D’bằng A. Góc giữa cạnh bên
IV) H là trực tâm tam giác ABC.
và mặt đáy bằng 600. Tính chiều cao OO’ của hình
Các yếu tố nào chưa đủ để kết luận S.ABC là hình chóp cụt đã cho. chóp đều? A. (I ) và (II ) B. (II) và (III ) a 3 a 3 A. OO’= B. OO’ = C. (III ) và (IV ) D. (IV ) và (I ) 3 2
Câu 21. Cho hình chóp đều S.ABC có cạnh đáy bằng 2a 6 3a 2
a, góc giữa một mặt bên và mặt đáy bằng 600. Tính độ C. OO’ = D. OO’ = 3 4 dài đường cao SH.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 21
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
D C D B B D B A C A D B C B D B A B C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 A C C B A KHOẢNG CÁCH
KIẾN THỨC CẦN NHỚ
Dạng 1 Khoảng cách từ điểm A đến đường thẳng Δ
Phương pháp : Tìm hình chiếu H của A lên Δ. Lúc đó d(A , Δ) = AH
Dạng 2 Khoảng cách từ điểm A đến mặt phẳng ()
Phương pháp : Tìm hình chiếu H của A lên (). Lúc đó d(A , ) = AH
Dạng 3 Khoảng cách giữa đường thẳng Δ và mặt phẳng () với Δ // 
Phương pháp : Chọn điểm A bất kỳ trên Δ. Lúc đó d(Δ, ) = d(A , )
Dạng 4 Khoảng cách giữa hai mặt phẳng song song  , 
Phương pháp : Chọn điểm A bất kỳ trên . Lúc đó d( , ) = d(A , )
Dạng 5 Khoảng cách giữa hai đường thẳng chéo nhau a , b
Phương pháp : * Dựng đoạn vuông góc chung : MN  a , MN  b , M  a , N  b Lúc đó d(a , b) = MN
* d(a , b) = d(a , ) = d( , ) , với   a ,  // b và   b ,  // a
CÂU HỎI TRẮC NGHIỆM
Câu 5. Cho hình chóp S.ABCD có SA (ABCD),
Câu 1. Cho tứ diện SABC trong đó SA, SB, SC
SA= 2a, ABCD là hình vuông cạnh bằng A. Gọi O là
vuông góc với nhau từng đôi một và SA = 3a, SB = a,
tâm của ABCD, tính khoảng cách từ O đến SC.
SC=2a. Khoảng cách từ A đến đường thẳng BC bằng: a 3 a 3 a 2 a 2 3a 2 7a 5 8a 3 5a 6 A. B. C. D. A. B. C. D. 3 4 3 4 2 5 3 6
Câu 6. Cho hình chóp S.ABC trong đó SA, AB, BC
Câu 2. Cho hình chóp A.BCD có cạnh AC  (BCD)
vuông góc với nhau từng đôi một. Biết SA = 3a,
và BCD là tam giác đều cạnh bằng a. Biết AC = a 2
AB=a 3 , BC = a 6 . Khỏang cách từ B đến SC bằng:
và M là trung điểm của BD. Khoảng cách từ C đến A. a 2 B. 2a C. 2a 3 D. a 3 đường thẳng AM bằng:
Câu 7. Cho hình chóp S.ABC trong đó SA, AB, BC 2 6 7 4 A. a B. a C. a D. a
vuông góc với nhau từng đôi một. Biết SA = a 3 , 3 11 5 7
AB=a 3 . Khỏang cách từ A đến (SBC) bằng:
Câu 3. Cho hình chóp A.BCD có cạnh AC  (BCD)
và BCD là tam giác đều cạnh bằng a. Biết AC = a 2 a 3 a 2 2a 5 a 6 A. B. C. D.
và M là trung điểm của BD. Khoảng cách từ A đến 2 3 5 2
Câu 8. Cho hình chóp S.ABCD có SA  (ABCD), đường thẳng BD bằng:
đáy ABCD là hình chữ nhật. Biết AD = 2a, SA = a. 3a 2 2a 3 4a 5 a 11 A. B. C. D.
Khỏang cách từ A đến (SCD) bằng: 2 3 3 2
Câu 4. Cho hình chóp S.ABCD có SA (ABCD) đáy 3a 2 2a 3 2a 3a A. B. C. D. 2 3 5 7
ABCD là hình thoi cạnh bằng a và ˆB = 600. Biết SA=
Câu 9. Cho hình chóp tam giác đều S.ABC cạnh đáy
2a. Tính khỏang cách từ A đến SC
bằng 2a và chiều cao bằng a 3 . Tính khaỏng cách từ 3a 2 4a 3 2a 5 5a 6 A. B. C. D.
tâm O của đáy ABC đến một mặt bên: 2 3 5 2
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 22
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 a 5 2a 3 3 2
Câu 15. Cho hình chóp S.ABCD có SA  (ABCD), A. B. C. a D. a 2 3 10 5
đáy ABCD là hình chữ nhật với AC = a 5 và
Câu 10. Cho hình chóp tứ giác đều S.ABCD có cạnh
BC=a 2 . Tính khoảng cách giữa SD và BC
đáy bằng a và chiều cao bằng a 2 . Tính khỏang cách 3a 2a a 3
từ tâm O của đáy ABCD đến một mặt bên: A. B. C. D. a 3 4 3 2 a 3 a 2 2a 5 a A. B. C. D.
Câu 16. Cho hình lập phương ABCD.A’B’C’D’ có 2 3 3 2
cạnh bằng a. Khoảng cách giữa BB’ và AC bằng:
Câu 11. Cho hình chóp S.ABCD có SA  (ABCD), a a a 2 a 3
đáy ABCD là hình thang vuông có chiều cao AB = a. A. B. C. D. 2 3 2 3
Gọi I và J lần lượt là trung điểm của AB và CD. Tính
Câu 17. Cho hình lập phương ABCD.A’B’C’D’ có
khỏang cách giữa đường thẳng IJ và (SAD).
cạnh bằng 1 (đvd). Khoảng cách giữa AA’ và BD’ a 2 a 3 a a bằng: A. B. C. D. 2 3 2 3 3 2 2 2 3 5
Câu 12. Cho hình thang vuông ABCD vuông ở A và A. B. C. D. 3 2 5 7
D, AD = 2a. Trên đường thẳng vuông góc tại D với
Câu 18. Cho hình lăng trụ tứ giác đều
(ABCD) lấy điểm S với SD = a 2 . Tính khỏang cách
ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P lần
giữa đường thẳng DC và (SAB).
lượt là trung điểm của AD, DC, A’D’. Tính khoảng 2a a a 3
cách giữa hai mặt phẳng (MNP) và (ACC’). A. B. C. a 2 D. 3 2 3 a 3 a a a 2 A. B. C. D.
Câu 13. Cho hình chóp O.ABC có đường cao OH = 3 4 3 4 2a
Câu 19. Cho hình lăng trụ tam giác ABC.A’B’C’ có
. Gọi M và N lần lượt là trung điểm của OA và OB. 3
các cạnh bên hợp với đáy những góc bằng 600, đáy
Khỏang cách giữa đường thẳng MN và (ABC) bằng:.
ABC là tam giác đều cạnh a và A’ cách đều A, B, C.
Tính khoảng cách giữa hai đáy của hình lăng trụ. a a 2 a a 3 A. B. C. D. 2 2 3 3 a 3 2a A. a B. a 2 C. D.
Câu 14. Cho tứ diện đều ABCD có cạnh bằng a. Tính 2 3
khoảng cách giữa AB và CD.
Câu 20. Cho tứ diện đều ABCD có cạnh bằng .
a Khoảng cách từ A đến (BCD) bằng: a 3 a 2 a 2 a 3 A. b ) C. D. 2 3 2 3 a 6 a 6 a 3 a 3 A. B. C. D. 2 3 6 3 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
B B D C A B D C C B C A D C D C B D A B
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 23
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
PHẦN 3 – MỘT SỐ ĐỀ MINH HỌA ĐỀ SỐ 1
(Theo ma trận Bà Rịa – Vũng Tàu)
I. PHẦN TRẮC NGHIỆM ( 4 điểm) n 1  n2 6  5 1 Câu 1. lim có giá trị bằng 3.6n  6n 1 A. 6 . B. 0 . C. 1  . D. . 3 2x 10
Câu 2. Giá trị của lim bằng: x 2  2  x A. .  B. 5. C. 2. D. . 
Câu 3. Giá trị của x x bằng: x  2 2 lim 2  3  2  5   A. 0. B. 2 2. C. 3  5. D. .  2x 1  3
Câu 4. Giá trị của lim bằng: 2
x4 x  5x  4 1 2 A. 0. B. . C. . D. .  9 9  4  4 
Câu 5. Cho ( )  x x f x
. Để hàm số liên tục tại x  0 thì phải định nghĩa f (0) bằng giá trị nào sau 2x đây? 1 1 A. . B. . C. 0. D. 4. 4 2 2
x  2x  3
Câu 6. Cho hàm số y
. Đạo hàm y của hàm số là biểu thức nào sau đây? x  2 3 3 3 3 A. 1   . B. 1 . C. 1   . D. 1 . 2 (x  2) 2 (x  2) 2 (x  2) 2 (x  2)
Câu 7. Cho hàm số f x   x  2 2 3
1 . Giá trị f   1 là A. 4. B. 8. C. -4. D. 24. Câu 8. Cho hàm số 3 2
y  3x x 1. Để y  0 thì x nhận các giá trị thuộc tập nào sau đây  2   9  A.  ;0 .  B.  ;0 . 9     2     9   2  C. ;   0;  . D. ;   0;  . 2    9   
Câu 9. Đạo hàm của hàm số y  3sin 2x  cos 3x là:
A. y  3cos 2x  sin 3 . x
B. y  3cos 2x  sin 3 . x
C. y  6 cos 2x  3sin 3 . x
D. y  6 cos 2x  3sin 3 . x
Câu 10. Phương trình tiếp tuyến của đồ thị hàm số f x 3 2
x  2x  3x tại điểm có hoành độ x  1 là: 0
A. y  10x  4.
B. y  10x  5.
C. y  2x  4.
D. y  2x  5.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 24
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Câu 11. Lập phương trình tiếp tuyến của đường cong 3 2
(C) : y x  3x  8x 1, biết tiếp tuyến đó song song với
đường thẳng  : y x  2017 ?
A. y x  2018 .
B. y x  4 .
C. y x  4 ; y x  28 .
D. y x  2018 .
Câu 12. Trong không gian cho ba đường thẳng phân biệt , a ,
b c. Khẳng định nào sau đây đúng?
A. Nếu a và b cùng vuông góc với c thì a / /b .
B. Nếu a / /b và c a thì c b .
C. Nếu góc giữa a và c bằng góc giữa b và c thì a / /b .
D. Nếu a và b cùng nằm trong m (
p  ) / /c thì góc giữa a và c bằng góc giữa b và c .
Câu 13. Trong không gian cho đường thẳng  và điểm O . Qua O có mấy đường thẳng vuông góc với  cho trước? A. 1 B. 2 C. 3 D. Vô số
Câu 14. Cho hình chóp .
S ABC có SA   ABC và ABC vuông ở B . AH là đường cao của SAB . Khẳng
định nào sau đây sai?
A. SA BC
B. AH BC
C. AH AC
D. AH SC
Câu 15. Cho hình chóp .
S ABCD có SA   ABCD và đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD
và I là trung điểm của SC . Khẳng định nào sau đây sai ?
A. BC SB
B. SAC là mặt phẳng trung trực của đoạn BD
C. IO  ABCD
D. Tam giác SCD vuông ở D .
Câu 16. Cho hình chóp .
S ABCD có SA   ABCD, đáy ABCD là hình chữ nhật. Biết AD  2a, S A a .
Khoảng cách từ A đến SCD bằng: 3a 2 2a 3 2a 3a A. B. C. D. . 2 3 5 7
Câu 17. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy, SC a 3 . Khi đó góc
giữa SB với mặt phẳng  ABCD bằng A. 0 45 . B. 0 60 . C. 0 90 . D. 0 30 .  
Câu 18. Gọi  là góc giữa hai đường thẳng d , d lần lượt có vectơ chỉ phương u , u . Ta luôn có : 1 2 1 2    
A. cos  cosu ,u .
B. cos  cosu ,u . 1 2  1 2     
C. cos  cosu ,u .
D. cos  cosu ,u . 1 2  1 2  1
Câu 19. Tất cả các giá trị m để hàm số 3
y   x  m   2
1 x  m  
1 x m có y  0,x R là: 3 m 3
A. m  0
B. m  3
C. 3  m  0 D. m 0
Câu 20. Cho chuyển động thẳng xác định bởi phương trình 3 2
s t  3t  9t  2 ( t tính bằng giây; s tính bằng
mét). Khẳng định nào sau đây đúng ?
A. Vận tốc của chuyển động bằng 0 khi t  0 hoặc t  2.
B. Vận tốc nhỏ nhất của chuyển động tại thời điểm t  1 s
C. Vận tốc của chuyển động tại thời điểm t  3 là  2 3 m/s  .
D. Vận tốc của chuyển động bằng 5 khi t  2.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 25
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
II. PHẦN TỰ LUẬN(6điểm) Bài 1:
(2,0điểm)a)Tính các giới hạn sau: 3 2n  3n 1 8x 1  3 A  lim ; B  lim 3 3n  2n  5 x 1  x 1 2
x  5x  6  khi x  3
b)Tìm a để hàm số f x   x  3
liên tục tại trên x  3 .  2
x  4a khi x  3 Bài 2:
(1,5điểm)a)Chứng minh các phương trình sau luôn có nghiệm thực với mọi m :  4
m m   2017 5 1 xx  32  0 x
b)Viết phương trình tiếp tuyến với đồ thị hàm số y f x 2 1 
, biết tiếp tuyến vuông góc với x  2 1
đường thẳng y   x  2 5 Bài 3:
(2,0điểm)Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA   ABCD,SA  2 . a
a)Chứng minh: BC SB,SAC  SBD.
b)Tính các góc SC ABCD  
 SAC ABCD  , , , .
c)Tính d AD,SBC
d)Tìm thiết diện hình chóp với mặt phẳng   chứa AD và vuông góc với mpSBC . x Bài 4:
(0,5điểm)Cho hàm số y
có đồ thị H  . Tìm tọa độ điểm M thuộc đồ thị H  để tiếp tuyến x 1
của H  tại M cắt đường tròn C 2 2
: x y  2x – 2 y – 2  0 tại 2 điểm ,
A B sao cho tam giác IAB
vuông, với I là tâm của C .
-----------------HẾT----------------- ĐỀ SỐ 2
(Theo ma trận Bà Rịa – Vũng Tàu)
I. PHẦN TRẮC NGHIỆM ( 4 điểm) 3 2
n n  5 Câu 1. lim có giá trị bằng 4 n  2n  2 A.  . B. 2  . C. 0 . D. 6 . 2  x  3 Câu 2. lim có giá trị bằng 2 x7 x  49 1 A. 1. B. 1  . C. 2 . D.  . 56 2 x  2 Câu 3. lim có giá trị bằng  2 x2 x x A. 3 . B. 3 . C. 0 . D. 1.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 26
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11 x  3 Câu 4. lim có giá trị bằng x 1  1 x A.  . B.  . C. 1. D. 3 .  4  4 
Câu 5. Cho ( )  x x f x
. Để hàm số liên tục tại x  0 thì phải định nghĩa f (0) bằng giá trị nào sau 2x đây? 1 1 A. . B. . C. 0. D. 4. 4 2 2
x  4x  3  khi x  3 Câu 6.
Cho hàm số f x   x  3
. Để hàm số f x liên tục tại x  3 thì a bằng a khi x  3 A. 2 . B. 4 . C. 0 . D. 2  . 3 1
Câu 7. Cho hai hàm số 2
f (x)  x  25 ; 2
g(x)  x x . Giá trị của x là bao nhiêu để f (x)   g (x) ? 2 2 1 1 A. 2  . B. 0. C. . D. . 4 2 2 Câu 8. Cho hàm số 3 f (x)  2
mx x . Với giá trị nào của m thì x  1
 là nghiệm của bất phương trình 3 f (  x)  2 ? A. m  0 . B. m  0 . C. m  0 . D. m  1.
Câu 9. Đạo hàm của hàm số y  tan 2x bằng biểu thức nào sau đây? 2 2 1 2 A. . B.  . C. . D.  . 2 cos 2x 2 cos 2x 2 cos 2x 2 sin 2x Câu 10. Cho hàm số 3 2
y  x  3x  3 có đồ thị C . Số tiếp tuyến của C vuông góc với đường thẳng 1
y x  2017 là: 9 A.1 B. 2 C. 3 D. 0
Câu 11. Cho hàm số 2
y  x  4x  3 có đồ thi ̣P . Nếu tiếp tuyến ta ̣i điểm M của P có hê ̣ số góc bằng 8
thı̀ hoành đô ̣ điểm M là: A. 12 B. 6  C. 1 D. 5
Câu 12. Trong các mệnh đề sau, mệnh đề nào sai?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
B. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với hai đường thẳng chéo nhau cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Câu 13. Cho hai đường thẳng phân biệt a, b và mặt phẳng (P). Mệnh đề nào sau đây là đúng?
A. Nếu a b, (P) a thì (P) // b.
C. Nếu a // b, (P) a thì (P) b.
B. Nếu a // (P), b a thì b (P).
D. Nếu a // (P), b a thì b // (P).
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 27
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
Câu 14. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy. Trong các tam giác cho dưới
đây, tam giác nào không phải tam giác vuông?
A. SAB .
B. SAD .
C. SAC .
D. SCD .
Câu 15. Cho hình chóp S.ABCD có SA vuông góc với đáy. Khi đó, góc giữa đường thẳng SB với mặt phẳng đáy
bằng góc nào dưới đây? A. SCA . B. SBA. C. SBD . D. BAB .
Câu 16. :Cho hình chóp .
S ABCD có đáy ABCD là hình thoi tâm I , cạnh bên SA vuông góc với đáy. Khẳng
định nào sau đây đúng ?
A. (SBC)  (SI ) A
B. (SBD)  (SAC)
C. (SDC)  (SAI )
D. (SCD)  (SAD)
Câu 17. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt phẳng đáy,
SA a . Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau? A. 2a B. a C. a 3 D. a 2
Câu 18. Cho hình chóp .
S ABC có đáy là tam giác đều ABC cạnh a , cạnh bên SA vuông góc với mặt đáy và a
SA  . Tính góc giữa hai mặt phẳng ABC và SBC là: 2 A. 300 B. 450 C. 600 D. 900 1
Câu 19. Một vật rơi tự do theo phương trình 2
s  gt (m), với g   2
9,8 m/s  . Vận tốc tức thời của vật tại thời 2 điểm t  10  s là: A. 122, 5 (m/s) B. 49 (m/s) C. 10 (m/s) D. 98 (m/s)
Câu 20. Chóp tam giác .
S ABC có SA SB SC , ABC là tam giác đều. I là trung điểm của BC .Chọn mệnh đề đúng? A. BC  AC
B. BC  SAC
C. BC  SAB
D. BC  SAI
II. PHẦN TỰ LUẬN(6điểm) Bài 1:
(2,0điểm)a)( 2 điểm ) Tính các giới hạn sau: 3 2 3n n  3
3x 1  2x  2 A  lim B  lim . 3 2 2n  2n 1 x 1  x 1 2  x  4  khi x  2 
b)Xét tính liên tục của hàm số sau tại điểm x  2
 : f (x)   x  2 . 0  4  khi x  2  Bài 2:
(1,5điểm)a)Chứng minh rằng với mọi giá trị của tham số m phương trình sau luôn có nghiệm: 4 2
x mx – 2m–  3 x – 2  0.
b)Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y x – 3x – 3x 1, biết rằng tiếp tuyến đó song
song với đường thẳng y  6x –1. Bài 3: (2,0điểm)Cho hình chóp .
S ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của S trên mặt
phẳng ABCD là trung điểm H của AB. Biết AB SH a.
a)Chứng minh: BC  SAB .
b)Gọi M là trung điểm đoạn BC . Chứng minh BD SM .
c)Tính khoảng cách từ điểm A đến mpSCD d)Tính góc giữa SC và mặt đáy.
e)Tính góc giữa mpSCD và mặt đáy.
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 28
TRƯỜNG THPT ĐINH TIÊN HOÀNG -ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 2- KHỐI 11
f)Gọi   là mặt phẳng qua M và vuông góc với BC . Tìm thiết diện của   cắt hình chóp . S ABCD . Bài 4: (0,5điểm)Cho hàm số 2
y x  2x 1 C và đường thẳng d : y x m. Tìm m để d cắt C tại 2 điểm phân biệt ,
A B sao cho các tiếp tuyến của C tại A và B vuông góc nhau.
-----------------HẾT-----------------
Sưu tầm và biên soạn: Đặng Ngọc Hiền ĐT: 0977802424 Page 29