













Preview text:
ĐỀ CƯƠNG ÔN TẬP TOÁN 10 GIỮA HỌC KỲ I NĂM HỌC 2022-2023 I. PHẦN TRẮC NGHIỆM Chủ đề 1: Mệnh đề
Câu 1.1: Phát biểu nào sau đây không phải là mệnh đề ?
A. Bức tranh đẹp quá. B. 13 là hợp số. C. 92 là số lẻ. D. 7 là số nguyên tố.
Câu 1.2: Trong các câu sau, câu nào là mệnh đề?
A. Hôm nay là thứ mấy? B. Các bạn hãy học bài đi!
C. Bạn An học Toán giỏi quá! D.Việt Nam là một nước thuộc Châu Á.
Câu 1.3: Khẳng định nào sau đây là mệnh đề 2x 2
A. 3x 2 y 10. B. .
C. x 0 . D. 5 . y
Câu 1.4: . Khẳng định nào sau đây là mệnh đề :
A. 3x + 5 = 8 B. 3x + 2y – z = 12 C. 1500 D. 3 + > 6
Câu 2.1: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều di chuyển”.
A. Mọi động vật đều không di chuyển.
B. Mọi động vật đều đứng yên.
C. Có ít nhất một động vật không di chuyển.
D. Có ít nhất một động vật di chuyển.
Câu 2.2: Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề nào sau đây:
A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.
B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.
C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.
D. Mọi số vô tỷ đều là số thập phân tuần hoàn.
Câu 2.3: Cho mệnh đề P: “ 2 x
R :9x 1 0 ”. Mệnh đề phủ định của P là: A. 2 P :" x
R :9x 1 0". B. 2 P :" x
R :9x 1 0". C. 2 P :" x
R :9x 1 0". D. 2 P :" x
R :9x 1 0".
Câu 2.4: Cho mệnh đề A : “ 2 x
: x x ”. Phủ định của mệnh đề A là: 2 2 2 2 A. x
: x x B. x : x x C. x : x x D. x : x x
Câu 3.1: Cách phát biểu nào sau đây không thể dùng để phát biểu mệnh đề: A B .
A. Nếu A thì B .
B. A kéo theo B .
C. A là điều kiện đủ để có B .
D. A là điều kiện cần để có B .
Câu 3.2 :Trong các mệnh đề nào sau đây mệnh đề nào sai?
A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.
B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông.
C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.
D. Một tam giác là đều khi và chỉ khi chúng có 2 đường trung tuyến bằng nhau và có 1 góc bằng 60 .
Câu 3.3: Mệnh đề nào sau đây sai?
A. Tứ giác ABCD là hình chữ nhật tứ giác ABCD có ba góc vuông.
B. Tam giác ABC là tam giác đều A 60 .
C. Tam giác ABC cân tại A AB AC .
D. Tứ giác ABCD nội tiếp đường tròn tâm O OA OB OC OD .
Câu 3.4 : Trong các câu sau, câu nào là mệnh đề đúng?
A. Nếu a b thì 2 2 a
b . B. Nếu a chia hết cho 9 thì a chia hết cho 3.
C. Nếu em chăm chỉ thì em thành công. D. Nếu tam giác có một góc bằng 60 thì tam giác đó đều.
Câu 4.1: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Không có số chẵn nào là số nguyên tố. B. 2 x , x 0. C. n , n n 11
6 chia hết cho 11. D. Phương trình 2 3x 6 0 có nghiệm hữu tỷ.
Câu 4.2: Trong các mệnh đề sau đây, mệnh đề nào sai? A. 2 x , 2x 8 0. B. 2 n , n
11n 2 chia hết cho 11.
C. Tồn tại số nguyên tố chia hết cho 5. D. 2 n , n 1 chia hết cho 4.
Câu 4.3: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Với mọi số thực x , nếu x 2 thì 2 x
4. B. Với mọi số thực x , nếu 2 x 4 thì x 2.
C. Với mọi số thực x , nếu x 2 thì 2 x
4. D. Với mọi số thực x , nếu 2 x 4 thì x 2.
Câu 4.4: Trong các mệnh đề sau đây, mệnh đề nào đúng? A. 2 x , x x. B. 2 x , x x. C. x , x 1 x 1. D. 2 x , x x.
Câu 5.1:Mệnh đề “ 2 x
: x 4” khẳng định rằng:
A. Bình phương của mỗi số thực bằng 4 B. Có ít nhất một số thực mà bình phương của nó bằng 4
C. Chỉ có một số thực bình phương bằng 4 D. Nếu x là một số thực thì 2 x 4
Câu 5.2: Mệnh đề “ 2 x
: x 0 ” khẳng định rằng:
A.Mọi số thực có bình phương không âm. B. Mọi số thực có bình phương lớn hơn 0.
C. Có số thực có bình phương không âm. D. Có ít nhất một số thực có bình phương không âm.
Câu 5.3: Cho mệnh đề P: “Có số thực mà bình phương nhỏ hơn nó”.Cách viết nào dưới đây đúng.? 2 2 A. x
: x x B. x : x x 2 2 C. x
: x x D. x : x x
Câu 5.4: Cho mệnh đề P: “Mọi số nguyên đều có bình phương không âm”.Cách viết nào dưới đây đúng.? A. 2 n
: n 0 B. 2 2 2 n : n 0 C. n : n 0 D. n : n 0 . Chủ đề 2: Tập hợp
Câu 6.1: Kí hiệu nào sau đây dùng để viết đúng mệnh đề '' 7 là số tự nhiên '' ? A. 7 . B. 7 . C. 7 . D. 7 .
Câu 6.2: Kí hiệu nào sau đây dùng để viết đúng mệnh đề '' 2 không phải là số hữu tỉ '' ? A. 2 . B. 2 . C. 2 . D. 2 .
Câu 6.3: Cho A là một tập hợp. Trong các mệnh đề sau, mệnh đề nào đúng A. A . A B. . A C. A . A D. A A .
Câu 6.4: Cho x là một phần tử của tập hợp .
A Xét các mệnh đề sau: (I) x . A (II) x . A (III) x . A (IV) x . A
Trong các mệnh đề trên, mệnh đề nào đúng? A. I và II. B. I và III. C. I và IV. D. II và IV.
Câu 7.1: Cho tập hợp A {x
/ x 5} . Tập A được viết dưới dạng liệt kê là:
A. A {0,1, 2, 4,5} .
B. A {0,1, 2,3, 4,5}. C. A {0;5}.
D. A {1, 2,3, 4,5}.
Câu 7.2: Cho tập hợp A {x / 1 x
2}. Khi đó tập hợp A bằng với tập hợp: A. [ 1;2] B. {0;1;2} C. { 1; 0;1;2} D. ( 1;2)
Câu 7.3: Cho tập hợp X = { n N | n chia hết cho 5, 0< n<40} các phần tử của tập hợp X là:
A. X={10, 20, 30, 40} .
B. X = {5, 10, 15, 20, 25, 30, 35} .
C. X={5, 10, 15, 20, 25, 30, 35, 40} . D. .
Câu 7.4: Hãy liệt kê các phần tử của tập hợp X 2 x
| 2x 3x 1 0 . 1 3 A. X 0 B. X 1 C. X 1 ; D. X 1 ; 2 2
Câu 8.1: Số tập con của tập hợp 𝑋 = {𝑎; 𝑏; 𝑐} là A. 1 B. 3 C. 5 D. 8
Câu 8.2: Số tập con 1 phần tử của tập hợp A 0,1, 2,3, 4, 5 là: A. 5 B. 6 C. 7 D. 4
Câu 8.3: Tập hợp nào sau đây có đúng một tập con A. . B. 1 . C. . D. , 1 .
Câu 8.4: Cho tập hợp A gồm 4 phân tử. Khi đó số tập con của A có 3 phần tử bằng:
A. 6 B. 14 C.4 D. 10
Câu 9.1: Cho tập hợp X 1; 5 ,Y 1;3;
5 . Tập X Y là tập hợp nào sau đây? A. 1 B.1;
3 C.{1;3;5} D.1; 5
Câu 9.2: Cho tập hợp X 1; 5 ,Y 1;3;
5 . Tập X Y là tập hợp nào sau đây? A. 1 B.1;
3 C.{1;3;5} D.1; 5
Câu 9.3: Cho tập hợp X ; a ; b
c ,Y a; ;
x y; z . Tập X Y là tập hợp nào sau đây? A. ; a ; b c B. ; x y; z C. ; a ; b ; c ; x y; z D. a
Câu 9.4: Cho tập hợp X ; a ; b
c ,Y a; ;
x y; z . Tập X Y là tập hợp nào sau đây? A. ; a ; b c B. ; x y; z C. ; a ; b ; c ; x y; z D. a
Câu 10.1: Cho các tập hợp: A {cam, táo, mít, dừa}, B {táo, cam}, C {dừa, ổi, cam, táo, xoài}. Chọn mệnh đề đúng.
A. A \ B C có ba phần tử
B. A \ B C có hai phần tử
C. A \ B C là một tập con của tập B
D. A \ B C là một tập con của tập A
Câu 10.2: Cho tập hợp A. Chọn khẳng định đúng:
A. A A. B. A A. C. A . D. A .
Câu 10.3: Tập hai tập hợp: A 2 ;
3 ; B 1;6. Tìm mệnh đề đúng?
A. “ A B là một khoảng có chứa dương vô tận” B. “ A B là một khoảng có chứa âm vô tận”
C. “ A B là một nửa khoảng” D. “ A B là một khoảng”
Câu 10.4: Tập hai tập hợp: A 2 ;
3 ; B 1;6. Tìm mệnh đề đúng?
A. “ A B có 5 phần tử là số nguyên” B. “ A B có 6 phần tử là số nguyên”
C. “ A B có 8 phần tử là số nguyên” D. “ A B l có 7 phần tử là số nguyên” Câu 11.1:
Cho tập hợp A x | 3 x
1 . Tập A là tập nào sau đây? A. 3 ; 1 B.3; 1 C.3; 1 D. 3 ;1 Câu 11.2:
Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp 1;4 ? A. B. C. D. Câu 11.3:
Cho tập hợp X x |1 x
3 thì X được biểu diễn là hình nào sau đây? A. B. C. D. Câu 11.4:
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A x 4 x 9 :
A. A 4;9.
B. A 4;9.
C. A 4;9.
D. A 4;9. Câu 12.1:
Cho tập hợp A ;
1 và tập B 2;
. Khi đó A B là: A. 2; B. 2 ; 1 C. D. Câu 12.2:
Cho hai tập hợp A 5
;3, B 1;. Khi đó A B là tập nào sau đây? A. 1;3 B. 1; 3 C.5; D.5; 1 Câu 12.3: Cho A 2 ;1 , B 3
;5 . Khi đó A B là tập hợp nào sau đây? A.2; 1 B. 2 ; 1 C. 2 ;5 D. 2 ;5
Câu 12.4: Cho A 2 ;1 , B 3
;5 . Khi đó A B là tập hợp nào sau đây? A.2; 1 B. 2 ; 1 C. 2 ;5 D. 3 ;5 Câu 13.1:
Cho hai tập hợp A 1;5; B 2;7. Tập hợp A \ B là: A. 1;2 B. 2;5 C. 1 ;7 D. 1; 2 Câu 13.2:
Cho tập hợp A 2; . Khi đó C A là: R A.2; B. 2; C. ; 2 D. ; 2 Câu 13.3:
Cho tập hợp A 2 ;
3 . Khi đó C A bằng:
A. 2;3 B. ; 2
3; C. ; 2 3; D. ; 2 Câu 13.4:
Cho tập hợp A 2
;1 . Khi đó C A bằng: A.2; 1 B. ; 2 1; C. ; 2 1; D. ; 2
Câu 14.1: Cho hai tập hợp A x 2
7x 3x 41 x
0 , B x 3x 2 1 5 khi đó 4 4 A \ B 1 ; 0 .
A. A \ B 1
;0; ;1. B. A \ B 1 ; . C.
D. A \ B 7 7
Câu 14.2: Cho hai tập hợp A x 2
(2x 7x 5)(x 2) 0 ,B x 3 2x 1 8 khi đó 5 5
A. A \ B ; 2
B. A \ B 2 ; 1 ;0;1;2; . 2 2
C. A \ B 1 ;0;1; 2 .
D. A \ B 1 .
Câu 14.3: Cho 2 tập hợp A 2 x
(2x 1)(x 5x 6)
0 , B 0;1; 2; 3 . Khi đó tập hợp
X A B 1;3; 5 là 1 3 ;2;3; 5 . 1; 2 ;3; 5 . A. ;2;3;5. B. 1; 2;3; 5 . C. D. 2 Câu14.4: Cho 3 tập hợp A 2 x
(2x 1)(x 5x 6) 0 , B 4 ;2; 3 , C 2 x
(5x 3)(x 7x 12)
0 Khi đó tập hợp X A B A C là 3 2; 3 . 3 A. ;2;3;5. B. 2;3; 4 . C. D. ;2;3;4. 5 5
Chủ đề 3: Bất phương trình bậc nhất hai ẩn
Câu 15.1: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 2
2x 3y 0. B. 2 2 x y 2. C. 2 x y 0.
D. x y 0.
Câu 15.2: Cho bất phương trình 2x 3y 6 0 (1) . Chọn khẳng định đúng trong các khẳng định sau: A. Bất PT
1 chỉ có một nghiệm duy nhất. B. Bất PT 1 vô nghiệm. C. Bất PT
1 luôn có vô số nghiệm. D. Bất PT 1 có tập nghiệm là .
Câu 15.3: Cho bất PT: 2
x 3y 2 0 có tập nghiệm là S . Khẳng định nào sau đây là đúng? 2 A. 1 ;1 S . B. ;0 S . C. 1; 2 S .
D. 1;0 S . 2
Câu 15.4: Cặp số ( ; x y) 2;
3 là nghiệm của bất phương trình nào sau đây?
A. 4x 3y . B. x – 3y 7 0 .
C. 2x – 3y –1 0 .
D. x – y 0 .
Câu 16.1: Điểm A1;3 là điểm thuộc miền nghiệm của bất phương trình: A. 3
x 2y 4 0. B. x 3y 0. C. 3x y 0. D. 2x y 4 0.
Câu 16.2: Cặp số 2;3 là nghiệm của bất phương trình nào sau đây ?
A. 2x – 3y –1 0. B. x – y 0 . C. 4x 3y . D. x – 3y 7 0 .
Câu 16.3: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x y 1? A. 2 ; 1 . B. 3; 7 . C. 0; 1 . D. 0;0 .
Câu 16.4: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình x 4y 5 0 ? A. 5;0. B. 2 ; 1 . C. 1; 3 . D. 0;0 .
Câu 17.1: Câu nào sau đây sai?.
Miền nghiệm của bất phương trình x 2 2 y 2 21 x là nửa mặt phẳng không chứa điểm
nào trong các điểm sau ? A. M 0;0 . B. N 1; 1 .
C. P 4; 2 . D. Q 1; 1 .
Câu 17.2: Câu nào sau đây đúng?.
Miền nghiệm của bất phương trình 3 x
1 4 y 2 5x 3 là nửa mặt phẳng chứa điểm A. 0;0 . B. 4 ;2 . C. 2 ;2 .
D. 5;3 .
Câu 17.3: Câu nào sau đây sai?.
Miền nghiệm của bất phương trình x 3 22y 5 21 x là nửa mặt phẳng chứa điểm A. 3 ; 4 . B. 2 ; 5 . C. 1 ;6. D. 0;0 .
Câu 17.4: Câu nào sau đây đúng?.
Miền nghiệm của bất phương trình 4 x
1 5 y 3 2x 9 là nửa mặt phẳng chứa điểm A. 0;0 . B. 1; 1 . C. 1 ;1 . D. 2;5 .
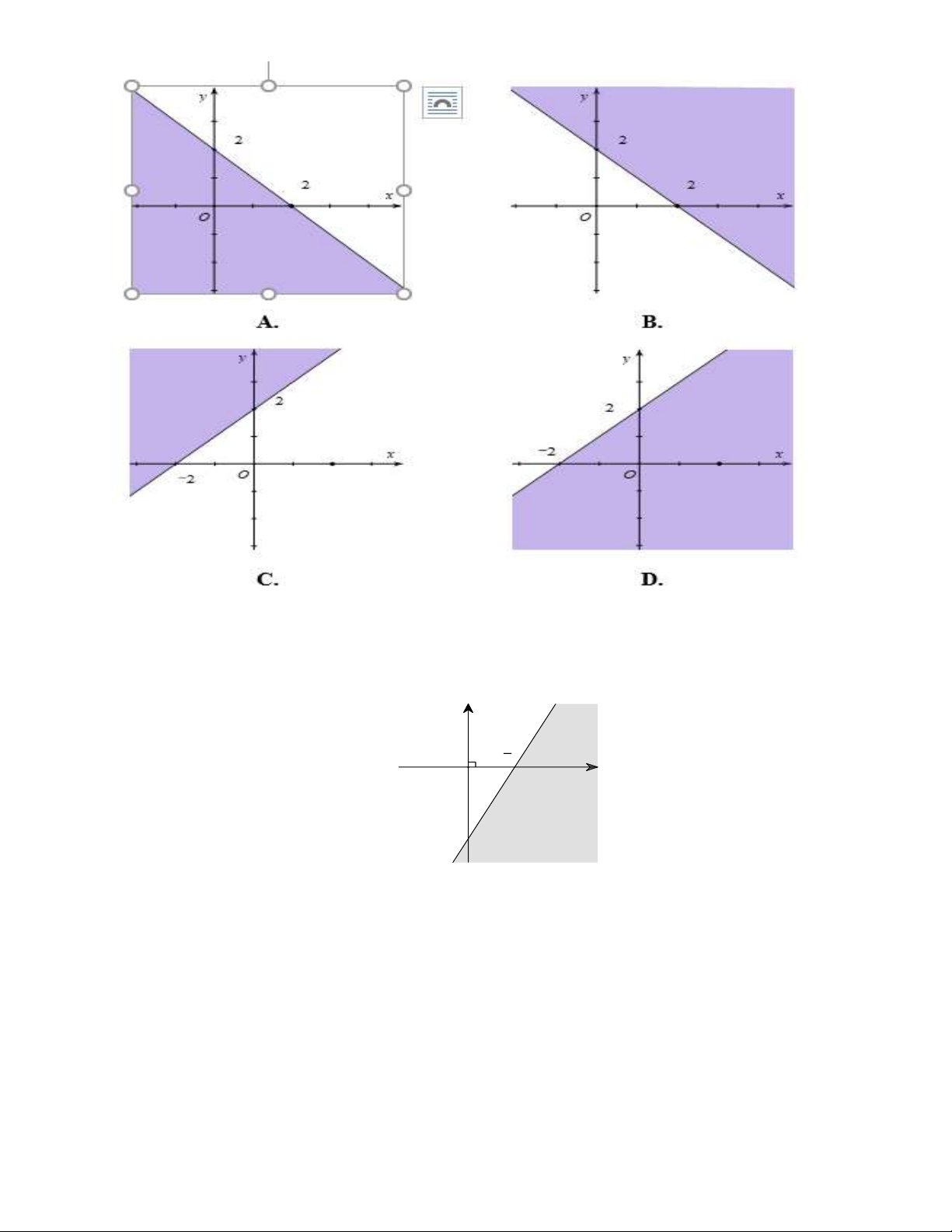
Câu 18.1: Miền nghiệm của bất phương trình x y 2 là phần tô đậm trong hình vẽ nào sau đây?
Câu 18.2: Phần tô đậm trong hình vẽ sau, biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau? y 3 2 x O - 3
A. 2x y 3. B. 2x y 3.
C. x 2 y 3.
D. x 2y 3.
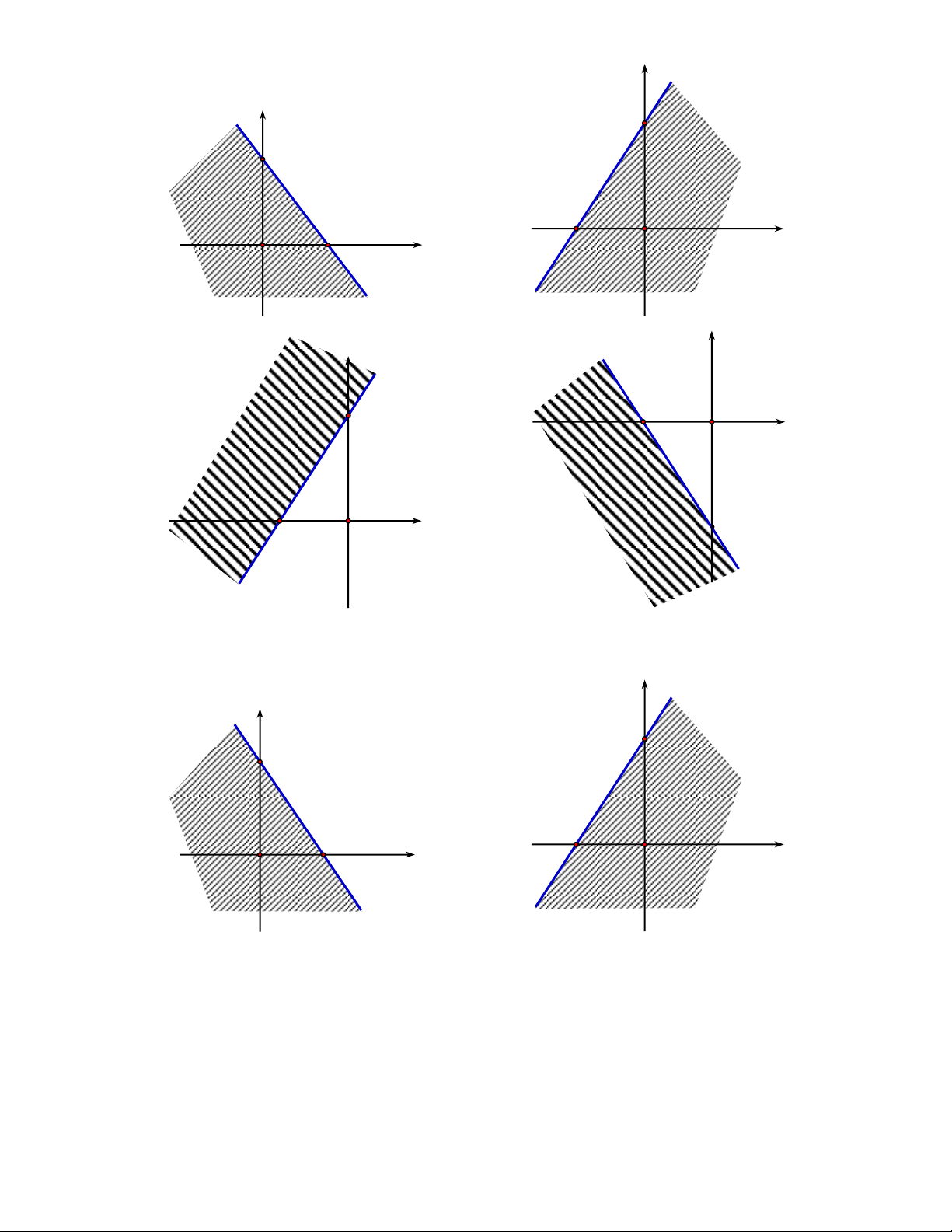
Câu 18.3: Miền nghiệm của bất phương trình 3x 2y 6 là y y 3 3 A. B. 2 2 x O x O y y 2 3 O x C. D. 3 2 O x
Câu 18.4: Miền nghiệm của bất phương trình 3x 2 y 6 là y y 3 3 A. B. 2 2 x O x O y y 2 3 O x C. D. 3 2 O x
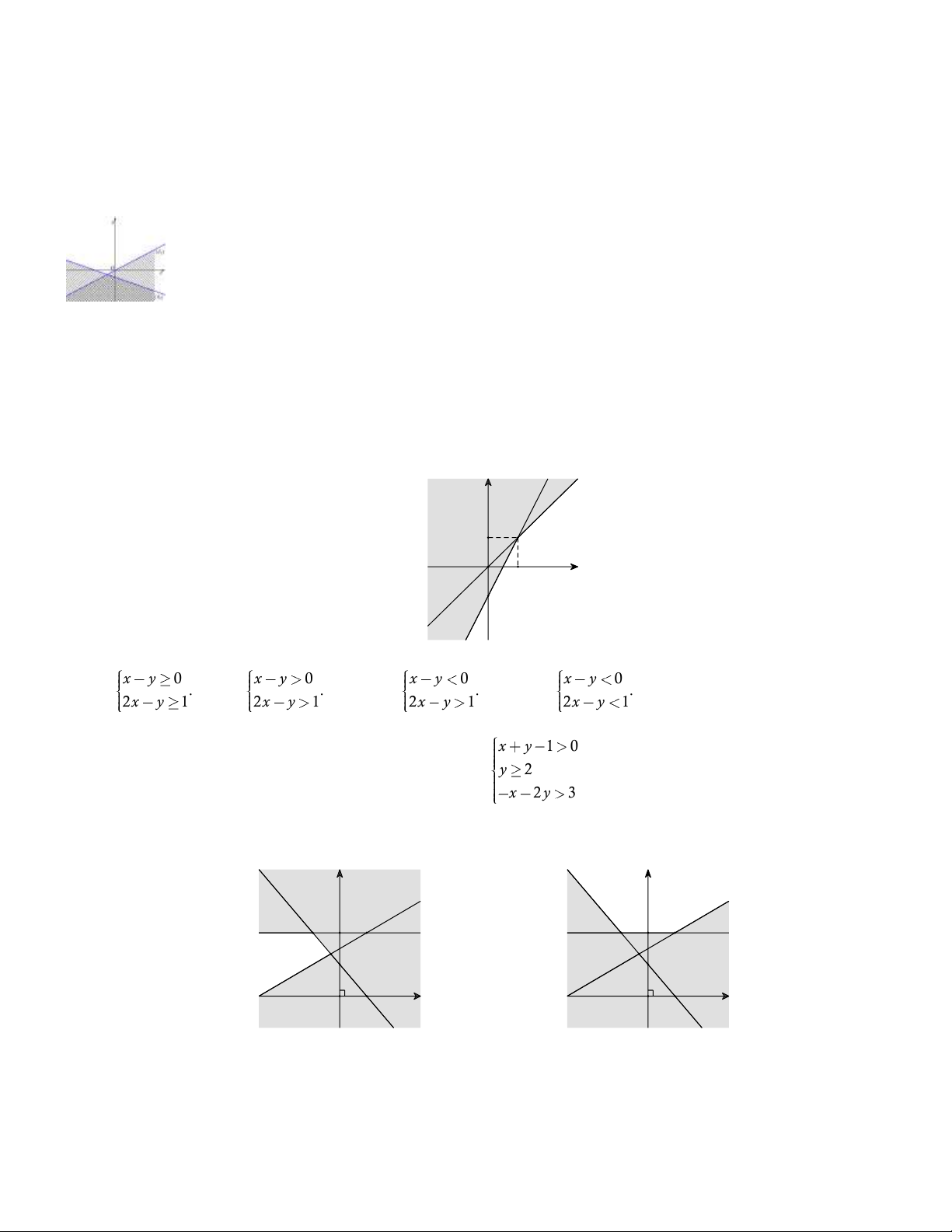
x y 2 0
Câu 19.1: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình là
2x 3y 2 0 A. 0;0 . B. 1; 1 . C. 1 ;1 . D. 1 ; 1 . x y 0
Câu 19.2: Cho hệ bất phương trình
có tập nghiệm là S . Khẳng định nào sau đây là khẳng
2x 5y 0 định đúng? 1 1 2 A. 1 ;1 S . B. 1 ; 1 S . C. 1; S . D. ; S . 2 2 5
2x 3y 1 0
Câu 19.3: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình ?
5x y 4 0 A. 1; 4 . B. 2
;4 . C. 0;0 . D. 3; 4 . x 0
Câu 19.4: Cho hệ bất phương trình
có tập nghiệm là S . Khẳng định nào sau đây là đúng?
x 3y 1 0 A. 1; 1 S .
B. 1; 3S . C. 1 ; 5S . D. 4 ; 3S .
2x 5y 1 0
Câu 20.1: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2x y 5 0 ?
x y 1 0 A. 0;0 . B. 1;0 . C. 0; 2 . D. 0; 2 .
2x 5y 1 0
Câu 20.2: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2x y 5 0 ?
x y 1 0 A. 0;0 . B. 1;0 . C. 0; 2 . D. 0; 2 . 3
x y 9 x y 3
Câu 20.3: Miền nghiệm của hệ bất phương trình
là phần mặt phẳng chứa điểm 2 y 8 x y 6 A. 0;0 . B. 1; 2 . C. 2; 1 . D. 8; 4 .
3x y 6
x y 3
Câu 20.4: Miền nghiệm của hệ bất phương trình
là phần mặt phẳng chứa điểm: 2 y 8 x y 4 A. 2; 1 . B. 6;4 . C. 0;0 . D. 1;2 .
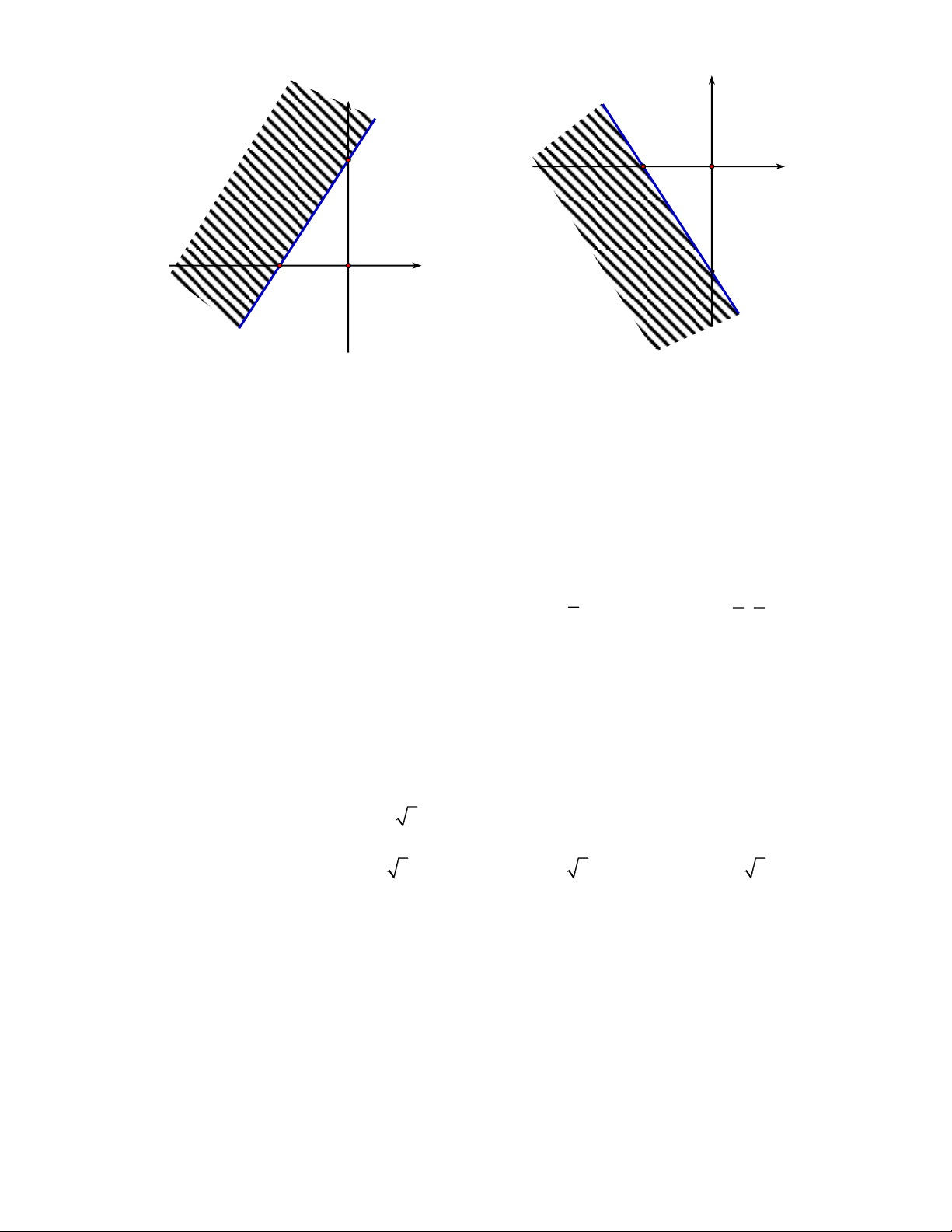
Câu 21.1: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? y 3 2 x O y 0 y 0 x 0 x 0 A. . B. . C. . D. . 3
x 2y 6 3
x 2y 6 3
x 2y 6 3
x 2y 6
Câu 21.2: : Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D?
x 2y 0 y 0 x 0 x 0 A. .B. . C. . D. .
x 3y 2 3
x 2y 6 3
x 2y 6 3
x 2y 6
Câu 21.3: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ
bất phương trình nào trong các hệ bất phương trình sau? y 1 x O 1 - 1 x y 0 x y 0 x y 0 x y 0 A. . B. . C. . D. . 2x y 1 2x y 1 2x y 1 2x y 1 x y 1 0
Câu 21.4: Miền nghiệm của hệ bất phương trình y 2
là phần không tô đậm của hình vẽ nào x 2y 3 trong các hình vẽ sau? y y 2 2 1 1 x 1 x 1 -3 O -3 O A. B. y y 2 2 1 1 x 1 x 1 -3 O -3 O C. D.
Chủ đề 4: GTLG của góc từ 0 đến 180 độ
Câu 22.1: Giá trị của tan180 là A. 1. B. 0 . C. –1.
D. Không xác định.
Câu 22.2: . Giá trị 0 0 cos 45 sin 45 bằng bao nhiêu? A. 1. B. 2. C. 3. D. 0.
Câu 22.3: Giá trị của 0 0 tan30 cot 30 bằng bao nhiêu? 4 1 3 2 A. . B. . C. . D. 2. 3 3 3
Câu 22.4: Trong các đẳng thức sau đây đẳng thức nào là đúng? 3 3 1 A. O sin150 . B. O cos150 . C. O tan150 . D. O cot150 3. 2 2 3
Câu 23.1: Tính giá trị biểu thức P cos30 cos60 sin30 sin 60 . 3 A. P 3. B. P . C. P 1. D. P 0. 2
Câu 23.2: Tính giá trị biểu thức P sin30 cos60 sin 60 cos30 . A. P 1. B. P 0. C. P 3. D. P 3.
Câu 23.3: Trong các đẳng thức sau, đẳng thức nào sai? A. O O sin 45 cos 45 2. B. O O sin30 cos60 1. C. O O sin 60 cos150 0. D. O O sin120 cos30 0.
Câu 23.4: Trong các đẳng thức sau, đẳng thức nào sai? A. O O sin0 cos0 0. B. O O sin 90 cos90 1. 3 1 C. O O sin180 cos180 1. D. O O sin 60 cos 60 . 2
Câu 24.1: Khẳng định nào sau đây sai? A. cos75 cos50 . B. sin 80 sin 50 . C. tan 45 tan 60 . D. cos30 sin 60 .
Câu 24.2: . Khẳng định nào sau đây đúng? A. sin 90 sin100 . B. cos 95 cos100 . C. tan 85 tan125 . D. cos145 cos125 .
Câu 24.3: Trong các khẳng định sau đây, khẳng định nào sai? A. O O cos 45 sin 45 . B. O O cos 45 sin135 . C. O O cos30 sin120 . D. O O sin 60 cos120 .
Câu 24.4: Tính giá trị biểu thức 2 2 2 2 S sin 15 cos 20 sin 75 cos 110 . A. S 0. B. S 1. C. S 2. D. S 4.
Câu 25.1: Cho hai góc nhọn và phụ nhau. Hệ thức nào sau đây là sai?
A. cot tan .
B. cos sin .
C. cos sin .
D. sin cos .
Câu 25.2: Trong các đẳng thức sau, đẳng thức nào đúng? A. 0
sin 180 – a – cos a . B. 0
sin 180 – a sin a . C. sin 0
180 – a sin a. D. sin 0 180 – a c s o a .
Câu 25.3: Cho và là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai? A. sin sin . B. cos cos . C. tan tan . D. cot cot .
Câu 25.4: Trong các công thức sau, công thức nào sai? 1 A. 2 2 sin cos 1 . B. 2 1 tan
k ,k . 2 cos 2 1 k C. 2 1 cot
k,k .
D. tan cot 1 , k . 2 sin 2
Câu 26.1: Cho là góc tù. Khẳng định nào sau đây là đúng? A. sin 0. B. cos 0. C. tan 0. D. cot 0.
Câu 26.2: . Cho hai góc nhọn và trong đó
. Khẳng định nào sau đây là sai? A. cos cos . B. sin sin . C. cot cot . D. tan tan 0.
Câu 26.3: Cho hai góc và với
90 . Tính giá trị của biểu thức P sin cos sin cos . A. P 0. B. P 1. C. P 1. D. P 2.
Câu 26.4: Cho hai góc và với
90 . Tính giá trị của biểu thức P cos cos sin sin . A. P 0. B. P 1. C. P 1. D. P 2.
Chủ đề 5: Hệ thức lượng trong tam giác
Câu 27.1: Tam giác ABC có cosB bằng biểu thức nào sau đây? 2 2 2 2 2 2 A. b c a B. 2 a c b 1 sin B
C. cos( A + C) D. 2bc 2ac
Câu 27.2: Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 2 2 2
a b c 2bc cos A. B. 2 2 2
a b c 2bc cos A. C. 2 2 2
a b c 2bc cosC . D. 2 2 2
a b c 2bc cos B .
Câu 27.3: Cho tam giác ABC . Tìm công thức sai: a a c sin A A. 2R. B. sin A .
C. b sin B 2R. D. sin C . sin A 2R a
Câu 27.4: Cho ABC
với các cạnh AB , c AC ,
b BC a . Gọi ,
R r, S lần lượt là bán kính đường tròn
ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai? abc a A. S . B. R . 4R sin A 1 C. S absin C . D. 2 2 2
a b c 2ab cosC . 2
Câu 28.1: Chọn công thức đúng trong các đáp án sau: 1 1 1 1
A. S bc sin A. B. S ac sin A.
C. S bc sin B.
D. S bc sin B. 2 2 2 2
Câu 28.2: Cho tam giác ABC. Đẳng thức nào sai: B C A
A. sin ( A+ B – 2C ) = sin 3C B. cos sin 2 2
A B 2C C C.sin( A+ B) = sinC D. cos sin 2 2
Câu 28.3: Cho tam giác ABC có a2 + b2 – c2 > 0 . Khi đó :
A. Góc C > 900 B.Góc C < 900 C.Góc C = 900
D. Không thể kết luận được gì về góc C
Câu 28.4: Cho tam giác ABC thoả mãn : b2 + c2 – a2 = 3bc . Khi đó : A. A = 300 B. A= 450 C. A = 600 D.A = 750
Câu 29.1: Cho tam giác ABC có a 8,b 10 , góc C bằng 0
60 . Độ dài cạnh c là? A. c 3 21 . B. c 7 2 . C. c 2 11 . D. c 2 21 . Câu 29.2: Cho ABC có 0
b 6, c 8, A 60 . Độ dài cạnh a là: A. 2 13. B. 3 12. C. 2 37. D. 20. Câu 29.3: Cho ABC có 0
B 60 , a 8, c 5. Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Câu 29.4: Cho ABC
có AB 9 ; BC 8; 0
B 60 . Tính độ dài AC . A. 73 . B. 217 . C. 8 . D. 113 .
Câu 30.1:Tam giác ABC có AB 5, BC 7, CA
8 . Số đo góc A bằng:
A. 30 . B. 45 . C. 60 . D. 90 .
Câu 30.2: Tam giác ABC có AB 2, AC
1 và A 60 . Tính độ dài cạnh BC . A. BC 1. B. BC 2. C. BC 2. D. BC 3.
Câu 30.3: Tam giác ABC có AB 2, AC 3 và C
45 . Tính độ dài cạnh BC . 6 2 6 2 A. BC 5. B. BC . C. BC . D. BC 6. 2 2
Câu 30.4: Tam giác ABC có B 60 , C
45 và AB 5. Tính độ dài cạnh AC . 5 6 A. AC . B. AC 5 3. C. AC 5 2. D. AC 10. 2
Câu 31.1:Cho hình thoi ABCD có cạnh bằng a . Góc BAD 30 . Diện tích hình thoi ABCD là 2 a 2 a 2 a 3 A. . B. . C. . D. 2 a . 4 2 2 Câu 31.2:
Tính diện tích tam giác ABC biết AB 3, BC 5, CA 6 . A. 56 B. 48 . C. 6 . D. 8 . Câu 31.3: Cho ABC
có a 6,b 8, c 10. Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30. Câu 31.4: Cho ABC có 0
a 4, c 5, B 150 .Diện tích của tam giác là: A. 5 3. B. 5. C. 10. D. 10 3.
Câu 32.1: Tam giác ABC có BC 10 và O A
30 . Tính bán kính R của đường tròn ngoại tiếp ABC 10 A. R 5 . B. R 10 . C. R . D. R 10 3 . 3
Câu 32.2: . Tam giác ABC có AB 3, AC
6 và A 60 . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. R 3 . B. R 3 3 . C. R 3 . D. R 6 .
Câu 32.3: Tam giác ABC có BC
21cm, CA 17cm, AB 10cm . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . 85 7 85 7 A. R cm . B. R cm . C. R cm . D. R cm . 2 4 8 2
Câu 32.4: Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R . Khi đó bán kính R bằng: a 3 a 2 a 3 a 3 A. R . B. R . C. R . D. R . 2 3 3 4
Câu 33.1: Tam giác ABC có AB 3, AC 6, BAC
60 . Tính diện tích tam giác ABC . 9 3 9 A. S 9 3 . B. S . C. S 9 . D. S . ABC ABC 2 ABC ABC 2
Câu 33.2: Tam giác ABC có AC 4, BAC
30 , ACB 75 . Tính diện tích tam giác ABC . A. S 8 . B. S 4 3 . C. S 4 . D. S 8 3 . ABC ABC ABC ABC
Câu 33.3: Tam giác ABC có a 21, b 17, c
10 . Diện tích của tam giác ABC bằng: A. S 16 . B. S 48 . C. S 24 . D. S 84 . ABC ABC ABC ABC
Câu 33.4: Tam giác ABC có AB 8 cm, AC
18 cm và có diện tích bằng 64 2
cm . Giá trị sin A ằng: 3 3 4 8 A. sin A . B. sin A . C. sin A . D. sin A . 2 8 5 9
Câu 34.1: Tam giác ABC có AB 5, AC 8 và 0 BAC
60 . Tính bán kính r của đường tròn nội tiếp tam giác đã cho. A. r 1 . B. r 2 . C. r 3 . D. r 2 3 .
Câu 34.2: Tam giác ABC có a 21, b 17, c
10 . Tính bán kính r của đường tròn nội tiếp tam giác đã cho. 7 A. r 16 . B. r 7 . C. r . D. r 8 . 2
Câu 34.3: Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a . a 3 a 2 a 3 a 5 A. r . B. r . C. r . D. r . 4 5 6 7
Câu 34.4: Tam giác ABC vuông tại A có AB 6 cm, BC
10 cm. Tính bán kính r của đường tròn nội tiếp tam giác đã cho. A. r 1 cm. B. r 2 cm. C. r 2 cm. D. r 3 cm.
Câu 35.1: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78o24 ' . Biết CA 250 ,
m CB 120 m . Khoảng cách AB bằng bao nhiêu? A. 266 . m B. 255 . m C. 166 . m D. 298 . m
Câu 35.2 : Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A , đi thẳng theo hai hướng tạo với nhau một góc 0
60 . Tàu thứ nhất chạy với tốc độ 30 km / h , tàu thứ hai chạy với tốc độ 40 km / h . Hỏi sau 2 giờ
hai tàu cách nhau bao nhiêu km ? A. 13. B. 20 13. C. 10 13. D. 15. Câu 35.3:
Từ một đỉnh tháp chiều cao CD 80 m , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 72 12 ' và 0 34 26 ' . Ba điểm , A ,
B D thẳng hàng. Tính khoảng cách AB ? A. 71 . m B. 91 . m C. 79 . m D. 40 . m Câu 35.4:
Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 0 56 16' . Biết
CA 200 m , CB 180 m . Khoảng cách AB bằng bao nhiêu? A. 180 . m B. 224 . m C. 112 . m D. 168 . m II. TỰ LUẬN:
Câu 1(VDT) (1.0 điểm). Cho hai tập hợp A, B là các khoảng, nửa khoảng, đoạn Tìm A B, A
B, A \ B, C A
Câu 2(VDT)(1.0 điểm). Áp dụng định lý sin hoặc cosin để tính một cạnh(góc) và diện tích (hoặc R,r) của tam giác.
Câu 3(VDC)(1.0 điểm). Cho đẳng thức lượng giác, tính giá trị biểu thức lượng giác(hoặc chứng minh
đẳng thức lượng giác)
Chú ý học sinh được phép sử dụng các hằng đẳng thức(bài 3.3 trang 37 sách giáo khoa KNTT) mà không cần chứng minh.




