-
Thông tin
-
Hỏi đáp
Đề cương ôn tập toán cao cấp | trường Đại học Huế
1. Hàm số và biến số thực1.1. Hàm số, giới hạn và tính liên tục + Hàm số: các khái niệm cơ bản + Giới hạn cÿa hàm số: Định nghĩa, tính chất, vô cùng bé, vô cùng lớn + Tính liên tục của hàm một biến, phân loại iểm gián đoạn. 1.2. Phép tính vi phân cÿa hàm một biến + Đạo hàm và vi phân cấp một, ứng dụng vi phân tính gần úng.+ Đạo hàm và vi phân cấp cao, quy tắc L’hospital, khai triển Taylor, khai triển Maclaurin. 1.3. Phép tính tích phân của hàm một biến + Tích phân bất ịnh. + Tích phân xác định, ứung dụng tính thểtích, diện tích.+ Tích phân suy rộng: Định nghĩa, các quy tắc xét sự hội tụ. 2. Hàm số nhiều biến số thực .2.1. Hàm số nhiều biến, giới hạn và tính liên tục của hàm nhiều biến. + Khái niệm hàm nhiều biến, định nghĩa giới hạn, tính liên tục và các tính chất. 2.2. Đạo hàm riêng và vi phân toàn phần của hàm nhiều biến. Āng dụng vi phân toàn phần vào tính gần úng.2.3. Đạo hàm của hàm hợp và hàm ẩn. 2.4. Đạo hàm và vi phân cấp cao. 2.5. Cực trị(không điều kiện) của hàm nhiều biến. 2.6. Tích phân hàm nhiều biến. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Toán rời rạc (ĐHH) 7 tài liệu
Đại học Huế 272 tài liệu
Đề cương ôn tập toán cao cấp | trường Đại học Huế
1. Hàm số và biến số thực1.1. Hàm số, giới hạn và tính liên tục + Hàm số: các khái niệm cơ bản + Giới hạn cÿa hàm số: Định nghĩa, tính chất, vô cùng bé, vô cùng lớn + Tính liên tục của hàm một biến, phân loại iểm gián đoạn. 1.2. Phép tính vi phân cÿa hàm một biến + Đạo hàm và vi phân cấp một, ứng dụng vi phân tính gần úng.+ Đạo hàm và vi phân cấp cao, quy tắc L’hospital, khai triển Taylor, khai triển Maclaurin. 1.3. Phép tính tích phân của hàm một biến + Tích phân bất ịnh. + Tích phân xác định, ứung dụng tính thểtích, diện tích.+ Tích phân suy rộng: Định nghĩa, các quy tắc xét sự hội tụ. 2. Hàm số nhiều biến số thực .2.1. Hàm số nhiều biến, giới hạn và tính liên tục của hàm nhiều biến. + Khái niệm hàm nhiều biến, định nghĩa giới hạn, tính liên tục và các tính chất. 2.2. Đạo hàm riêng và vi phân toàn phần của hàm nhiều biến. Āng dụng vi phân toàn phần vào tính gần úng.2.3. Đạo hàm của hàm hợp và hàm ẩn. 2.4. Đạo hàm và vi phân cấp cao. 2.5. Cực trị(không điều kiện) của hàm nhiều biến. 2.6. Tích phân hàm nhiều biến. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Toán rời rạc (ĐHH) 7 tài liệu
Trường: Đại học Huế 272 tài liệu
Thông tin:
Tác giả:
Preview text:
lO M oARcPSD| 45467232
ĐỀ CƯƠNG ÔN TÀP BÀI THI TOÁN CAO CÂP
1. Hàm số một biến số thực
1.1. Hàm số, giới hạn và tính liên tục
+ Hàm số: các khái niệm cơ bản
+ Giới hạn cÿa hàm số: Định nghĩa, tính chất, vô cùng bé, vô cùng lớn +
Tính liên tục cÿa hàm một biến, phân loại iểm gián oạn.
1.2. Phép tính vi phân cÿa hàm một biến
+ Đạo hàm và vi phân cấp một, āng dụng vi phân tính gần úng.
+ Đạo hàm và vi phân cấp cao, quy tắc L’hospital, khai triển Taylor, khai triển Maclaurin.
1.3. Phép tính tích phân cÿa hàm một biến + Tích phân bất ịnh.
+ Tích phân xác ịnh, āng dụng tính thể tích, diện tích.
+ Tích phân suy rộng: Định nghĩa, các quy tắc xét sự hội tụ.
2. Hàm số nhiều biến số thự
2.1. Hàm số nhiều biến, giới hạn và tính liên tục cÿa hàm nhiều biến.
+ Khái niệm hàm nhiều biến, ịnh nghĩa giới hạn, tính liên tục và các tính chất.
2.2. Đạo hàm riêng và vi phân toàn phần cÿa hàm nhiều biến. Āng dụng vi
phân toàn phần vào tính gần úng.
2.3. Đạo hàm cÿa hàm hợp và hàm ẩn.
2.4. Đạo hàm và vi phân cấp cao.
2.5. Cực trị (không iều kiện) cÿa hàm nhiều biến.
2.6. Tích phân hàm nhiều biến
+ Tích phân hai lớp, các công thāc ổi biến. 1 lO M oARcPSD| 45467232
+ Tích phân ba lớp, các công thāc ổi biến.
+ Tích phân ường loại một, tích phân ường loại hai, công thāc Green, ịnh lý
bốn mệnh ề tương ương.
+ Tích phân mặt loại một, tích phân mặt loại hai, công thāc Ostrogradski.
3. Lý thuyết chuỗi 3.1. Chuỗi số
+ Định nghĩa, tính chất.
+ Chuỗi số dương và các tiêu chuẩn hội tụ cÿa chuỗi số dương.
+ Chuỗi có dấu tùy ý, chuỗi an dấu, tiêu chuẩn Leibniz. 3.2. Chuỗi hàm
+ Khái niệm, miền hội tụ. + Chuỗi lũy thừa.
4. Phương trình vi phân
4.1. Phương trình vi phân cấp một
+ Phương trình khuyết, phương trình phân li biến số, phương trình thuần
nhất, phương trình vi phân toàn phần.
+ Phương trình tuyến tính cấp một, phương trình Bernoul i, phương trình
Lagrange, phương trình Clairaut.
4.2. Phương trình vi phân cấp hai
+ Phương trình tuyến tính thuần nhất cấp hai với hệ số hằng.
+ Phương trình tuyến tính không thuần nhất cấp hai với hệ số hằng.
4.3. Đại số tuyến tính
4.4. Ma trận và các phép toán trên ma trận
4.5. Định thāc và cách tính ịnh thāc
4.6. Hệ phương trình tuyến tính + Hệ phương trình Cramer.
+ Hệ phương trình tuyến tính thuần nhất.
+ Hệ phương trình tuyến tính tổng quát.
5. Tài liệu tham khÁo:
- Toán cao cấp (tập 1, tập 2, tập 3), Nguyễn Đình Trí chÿ biên, NXB Giáo dục, năm 2006. 2 lO M oARcPSD| 45467232
- Bài tập Toán cao cấp (tập 1, tập 2, tập 3), Nguyễn Đình Trí chÿ biên, NXB Giáo dục, năm 2006.
MỘT SỐ BÀI TẬP THAM KHẢO BÀI THI TOÁN CAO CẤP
1. HÀM SỐ MỘT BIẾN SỐ THỰC
1.1. Đạo hàm, vi phân
Bài 1. Xét tính khả vi cÿa hàm số: ÿÿāāÿĀ ý khi |ý| f 1 Ą(ý) = {ÿ ý 2 1 ĀąĀ ý + khi |ý| > 1 4 2 Hướng dẫn giải Ta có: |ý| < 1 Ą′(ý) = {1 + ý |ý| > 1
+ Kiểm tra tính khả vi tại ý = 1. Ta có: 㔋 ý21 㔋 2 2 1
Ą+′ (1) = þ㕖ÿ+ 4 ý 2 12 4 =; ý→1 㔋 ÿÿāāÿĀ ý 2 Ą ′ 2 (1) = ý→1þ㕖ÿ2 ý 2 1
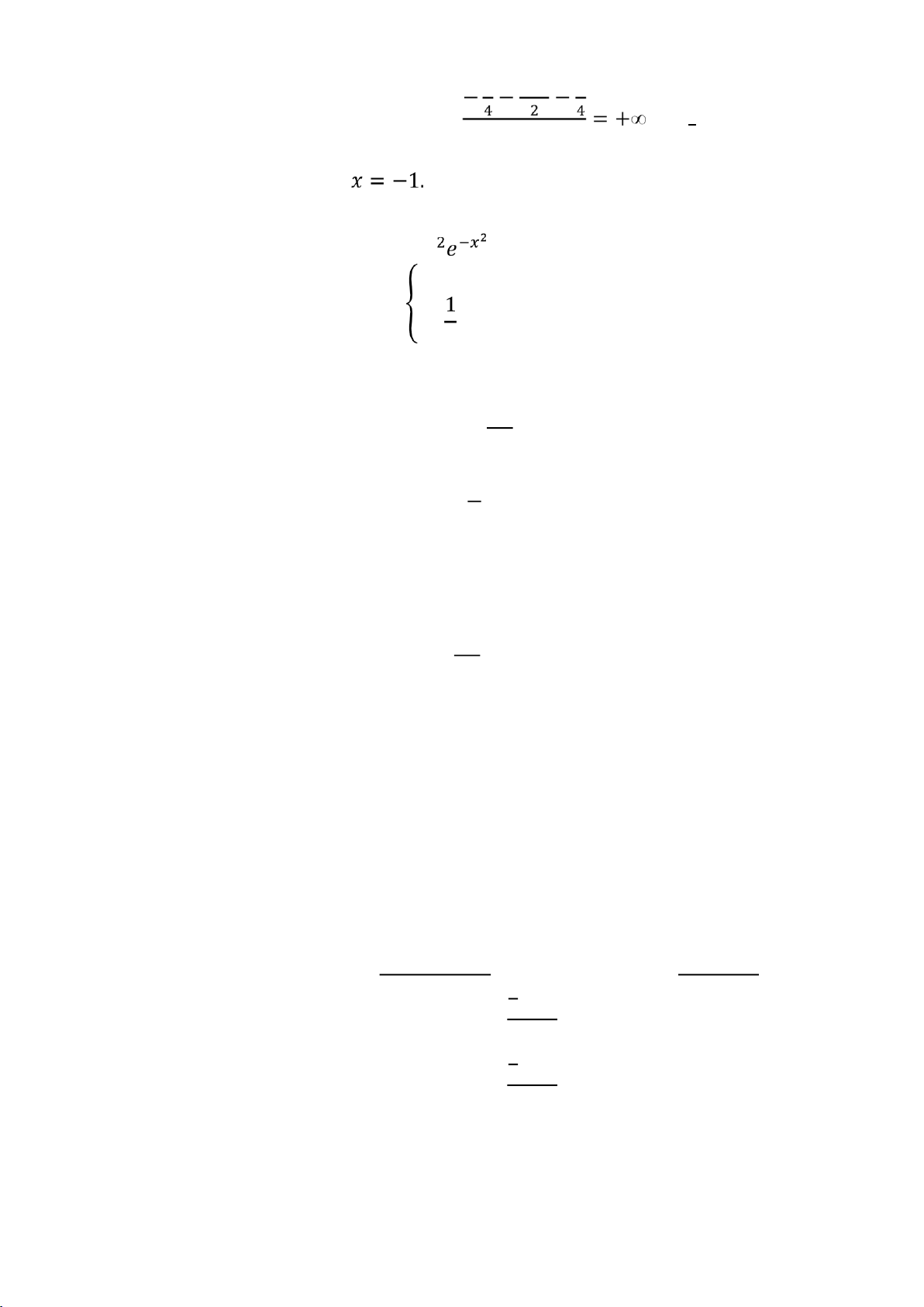
4 = ÿÿāāÿĀý′ (1) = Do ó Ą′(1) =
+ Kiểm tra tính khả vi tại ý = 21: 㔋 ÿÿāāÿĀ ý + Ą ′ + (21) = þ㕖ÿ+ ý + 1
4 = ÿÿāāÿĀý′ (21) =; ý→21 㔋 ý21 㔋 3 lO M oARcPSD| 45467232 Ą ′ 2 (21) = þ㕖ÿ ý→21 ý + 1
Suy ra Ą không khả vi tại
Bài 2. Xét tính khả vi cÿa hàm số: ý khi |ý| f 1 Ą(ý) = khi |ý| > 1 ă
Bài 3. Xét tính khả vi cÿa hàm số: 1 ÿÿāāÿĀ khi ý b 0 Ą(ý) = { |ý| ÿ khi ý = 0 2
Bài 4. Xác ịnh các giá trị ÿ, Ā, ā ể hàm số khả vi trên R: ÿ + Āý2 khi |ý| < 1 Ą(ý) = { 1 khi |ý| g 1 |ý| Hướng dẫn giải
+ Với ∀ý b ±1, hàm số Ą(ý) luôn khả vi, ta chỉ cần tìm iều kiện cÿa a và b ể hàm số khả vi tại ý = ±1
+ Hàm số khả vi tại ý = ±1 ⇒ Ą(ý) liên tục tại ý = ±1
⇔ þ㕖ÿ Ą(ý) = Ą(±1) ⇔ ÿ + Ā = 1 ⇒ ÿ = 1 2 Ā ý→+1 + Tại ý = 1, ta có 1
′ (1) = þ㕖ÿ Ą(ý) 2 Ą(1) = þ㕖ÿ ý 2 1 = þ㕖ÿ 1 2 ý = 21 Ą+ + ý 2 1 ý→1+ ý 2 1 ý→1+ ý(ý 2 1) ý→1 1 Ą(ý) 2 Ą(1) 2 1 1 2 ý ′ 4 lO M oARcPSD| 45467232 Ą+(1) = þ 㕖ÿ+ ý 2 1 = ý→1þ㕖 ÿ+ ý 2 1ý
= ý→1þ㕖ÿ+ ý(ý 2 1) = 21 ý→1
Vậy với Ā = 2 ; ÿ = thì hàm số Ą(ý) khả vi tại ý = 1 + Tại ý = 21, ta có 1
′ (21) =þ㕖ÿ Ą(ý) 2 Ą(21) = þ㕖ÿ 2 ý 2 1 = þ㕖 ÿ 2(1 + ý) = 1 Ą2 2
ý + 1 ý→212 ý + 1 ý→212 ý(ý + 1) ý→21 Ą(ý) 2 Ą(21) ÿ + Āý2 2 1 Āý2 2 Ā Ą+′ (21) = þ㕖ÿ+ ý + 1 = ý→21þ㕖ÿ+ ý + 1 = ý→21þ㕖ÿ+ ý + 1 = 22Ā ý→21 Vậy với Ā = 2
; ÿ = thì hàm số Ą(ý) khả vi tại ý = 21.
Bài 5. Xác ịnh các giá trị ÿ, Ā, ā ể hàm số khả vi trên R: 4ý khiý f 0 Ą(ý) = {ÿý2 + Āý + ā khi0 < ý < 1 3 2 2ý khiý g 1
Bài 6. Tìm khai triển Maclaurin cÿa hàm số Ą(ý) = þĀ(ý2 + 3ý + 2) Hướng dẫn giải
+ Do khai triển Maclaurin là khai triển Taylor trong lân cận iểm x=0 nên ta chỉ
xét ý trong lân cận cÿa 0 sao cho ý + 1 > 0, ý + 2 > 0. + Biến ổi
Ą(ý) = þĀ( ý2 + 3ý + 2) = þĀ(ý + 1)(ý + 2) = þĀ( ý + 1) + þĀ( ý + 2)
+ Áp dụng khai triển cơ bản
þĀ( 1 + ý) = ý 2 ý2 + ý3 2 ý4 + ⋯ + (21)㕛21 ý 㕛 + ā(ý㕛) 2 3 4 Ā + Ta ược : ý þĀ( 2 + ý) = þĀ 2 ý 2 ý 3 ý 㕛 5 lO M oARcPSD| 45467232 = þĀ 2 + ý ( ) ( ) 㕛21 + ā(ý㕛 2 2 3 Ā 㕛 ýý = þĀ 2 + ∑ý21 2 ýý + ā(ý㕛) + Từ ó 㕛 1 ýý
þĀ( ý2 + 3ý + 2) = þĀ 2 + ∑(21)ý21 (1 + ) + ā(ý㕛) 2 ý
Bài 7. Tìm khai triển Maclaurin cÿa hàm số 3 + ý Ą(ý) = þĀ 2 2 ý
Bài 8. Tìm khai triển Maclaurin cÿa hàm số 1 þ = √1 + ý
1.2. Tích phân và ÿng dụng
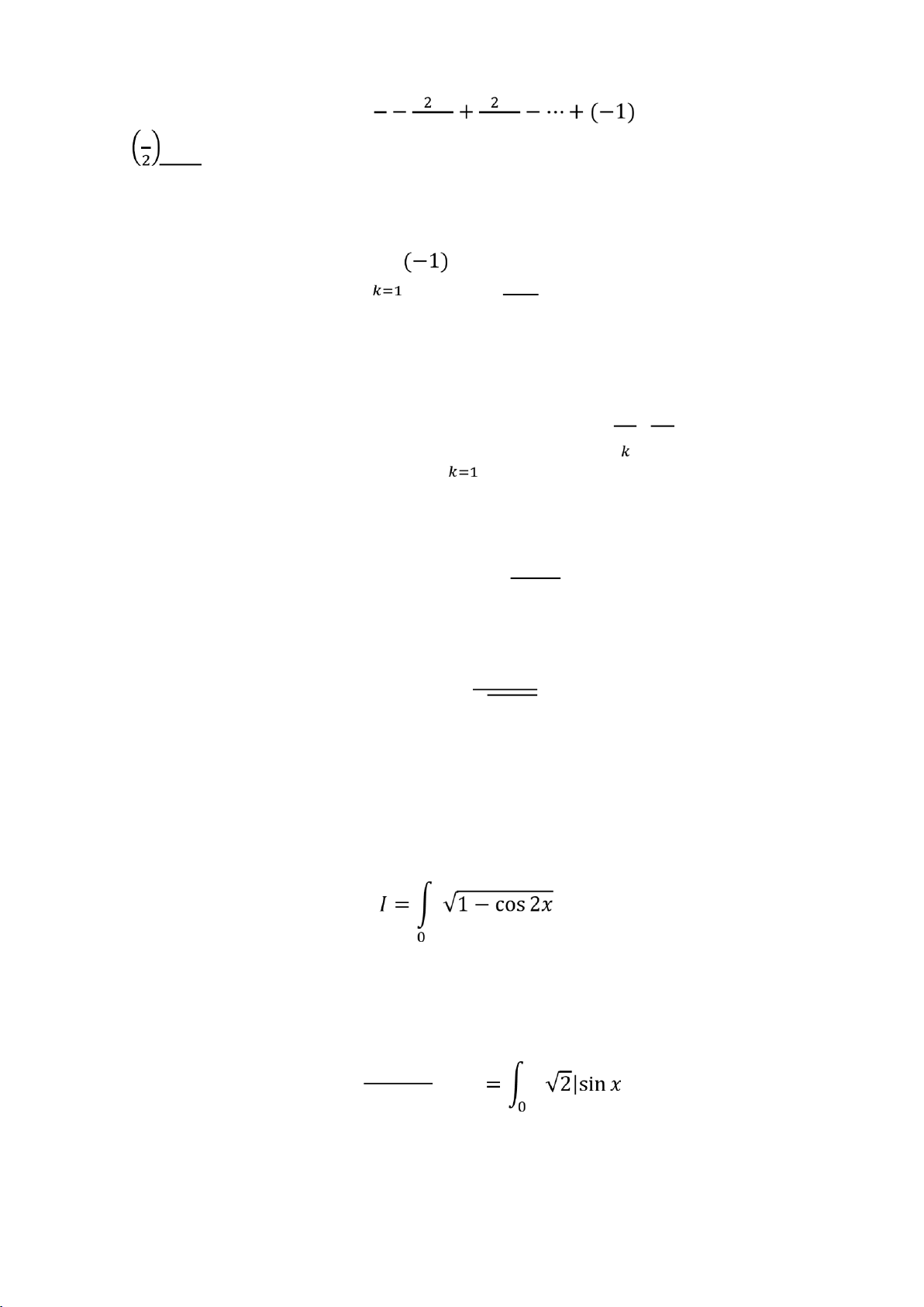
1.2.1. Tích phân xác ịnh Bài 1. Tính 2㔋 Ăý H°ớng d¿n giÁi + Viết Ā dưới dạng: 2㔋 2㔋 Ā=∫ √ 2 sin 2 0 ý Ăý |Ăý
+ Dựa vào sự biến thiên cÿa hàm sin (ý) trên oạn [0; 2ÿ] ta có: 6 lO M oARcPSD| 45467232 㔋 2㔋 Ā =
Bài 2. Tính tích phân xác ịnh 㔋
Bài 3. Tính tích phân xác ịnh 1 ýĂý Ā = ∫ ý2 + ý + 1 21
Bài 4. Tính tích phân xác ịnh 㔋 ý Ăý
1.2.2. þng dụng tích phân
Bài 1. Tính diện tích hình phẳng giới hạn bởi các ồ thị hàm số þ = 2ý2 +
3ý 2 2 , þ = ý 2 1 và þ = 2 2 ý. H°ớng d¿n giÁi
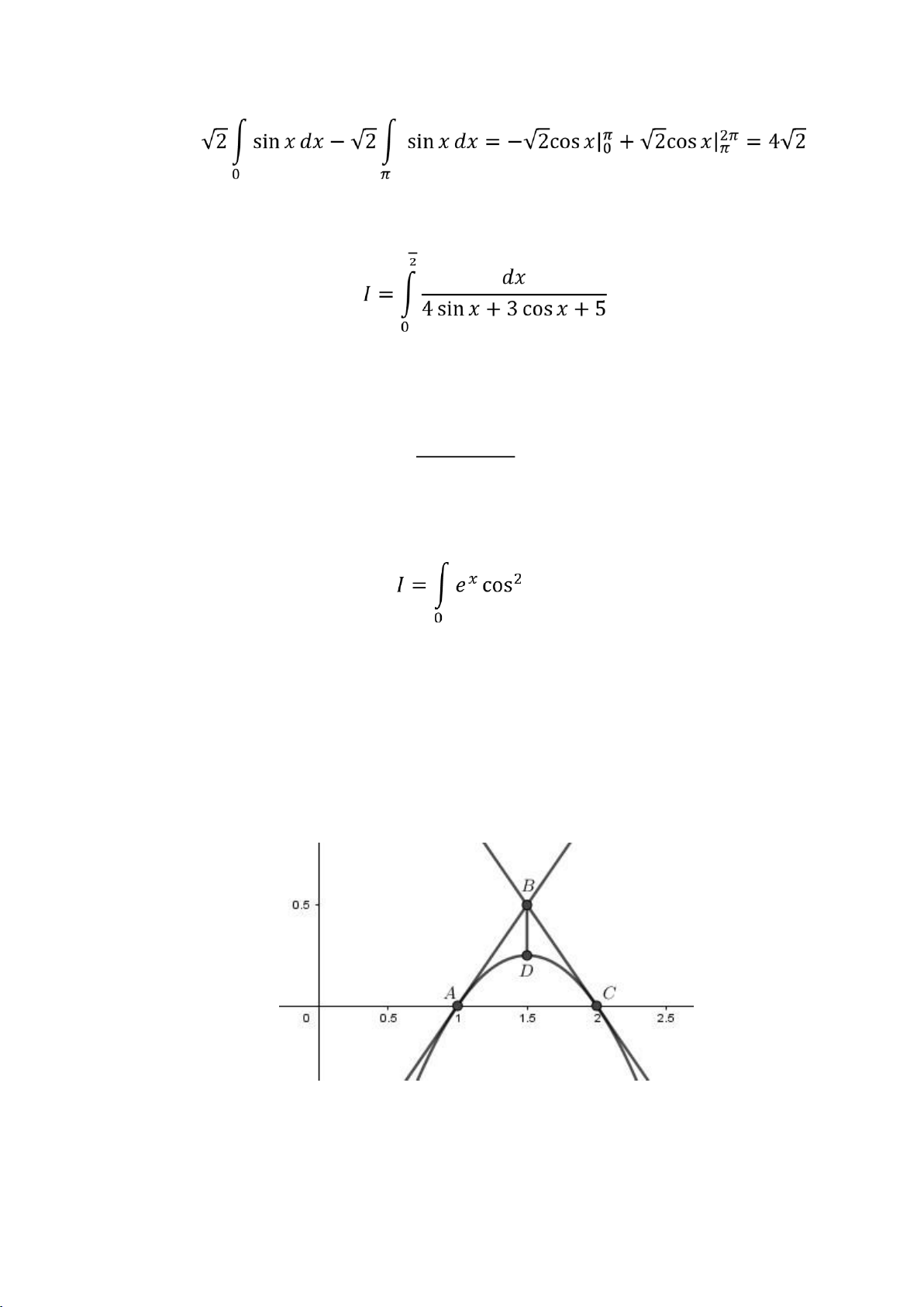
+ Vẽ hình xác ịnh hình phẳng cần tính diện tích 7 lO M oARcPSD| 45467232
+ Gọi A là giao iểm cÿa þ = 2ý2 + 3ý 2 2 và þ = ý 2 1; B là giao iểm cÿa þ = ý 2
1 và þ = 2 2 ý; C là giao iểm cÿa þ = 2ý2 + 3ý 2 2 và þ = 2 2 ý. + Tìm ược tọa
ộ:ý(1,0); þ (3 , 1) ; ÿ(2,0). Đường thẳng ý = 3/2 cắt cung ýÿ 2 2 tại iểm Ā ( ; 0).
+ Diện tích hình phẳng cần tìm là diện tích tam giác cong ABC, ta có
Ăýþÿ = ĂýþĀ + ĂþÿĀ
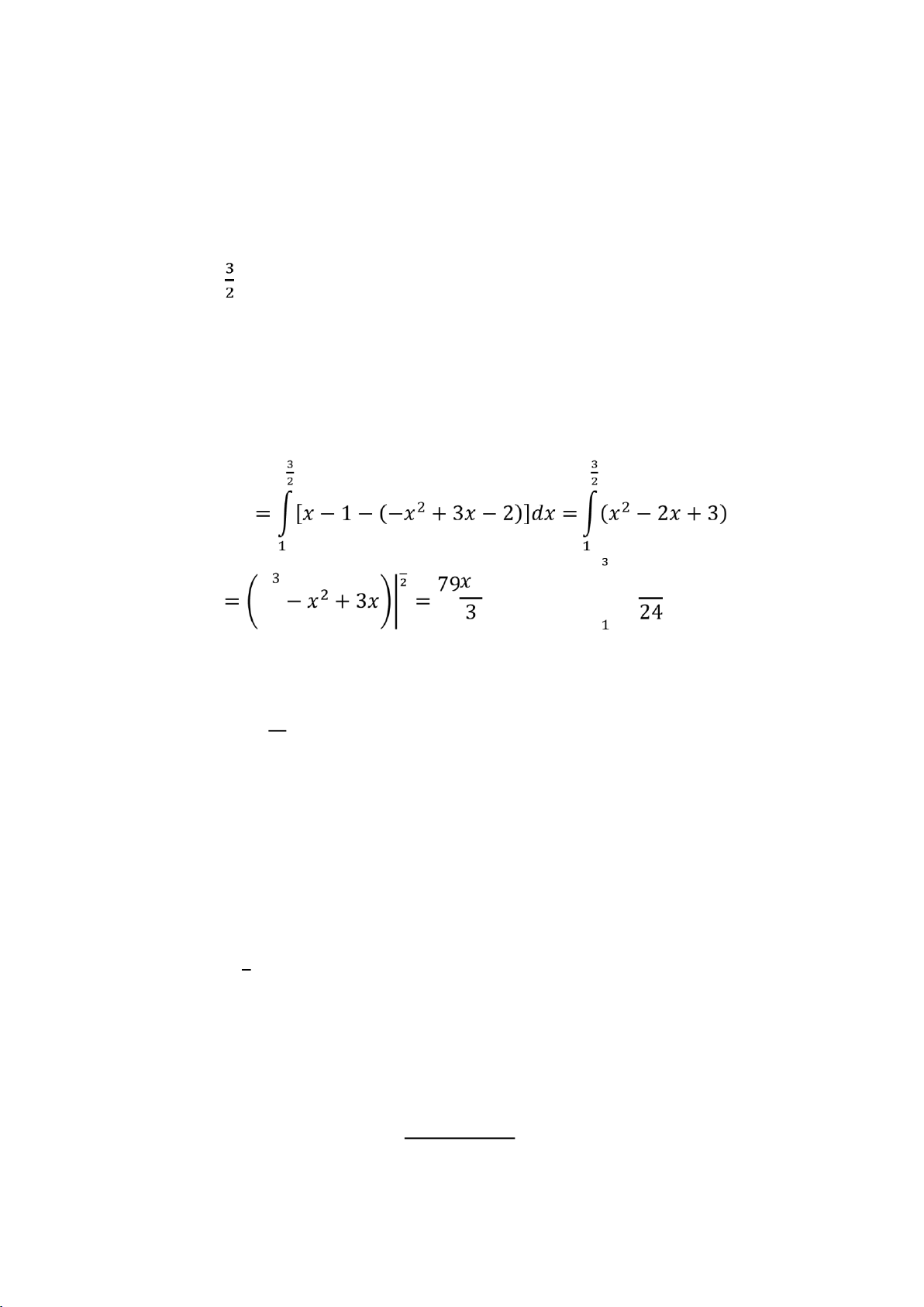
+ Tính diện tích tam giác cong ABD. ĂýþĀ Ăý
+ Tương tự có: ĂþÿĀ = 79/24. + Vậy Ăýþÿ = 12 79
Bài 2. Tính diện tích hình phẳng giới hạn bởi ồ thị hàm số þ = ý2 2 4ý + 5 và hai
tiếp tuyến với ồ thị hàm số tại hai tiếp iểm có hoành ộ lần lượt là 1 và 4.
Bài 3. Tính diện tích hình phẳng giới hạn bởi các ồ thị hàm số þ = |ý2 2 1|, þ = |ý| + 5.
Bài 4. Tính diện tích hình phẳng giới hạn bởi các ồ thị hàm số þ = 4 2 |ý| và 1 2. parabal þ =ý 2
1.2.3. Tích phân suy ráng
Bài 1. Xét sự hội tụ và tính tích phân suy rộng sau +∞ Ăý Ā = ∫ ý2 + 4ý + 9 2∞ 8 lO M oARcPSD| 45467232 H°ớng d¿n giÁi - Xét sự hội tụ
+ Viết tích phân dưới dạng: +∞ Ăý
Ā = ∫2∞ ý2 + 4ý + 9 21 Ăý 1 Ăý +∞ Ăý = ∫2
ý2 + 4ý + 9 + ∫21 ý2 + 4ý + 9 + ∫1 ý2 + 4ý + 9 ∞ = Ā1 + Ā2 + Ā3
+ Tích phân I2 là tích phân xác ịnh nên hội tụ + Xét Ā1 ý
2+4㕑ýý+9 + Đặt Ą . Chọn ą . Hai hàm số Ą(ý),ą(ý) không âm trong ý (2∞,1]. Có lim ÿ(ý) = 1 ý→+∞ Ā(ý) + Mặt khác tích phân
Ăýhội tụ (ÿ = 2 > 1) nên tích phân
Ą(ý)Ăý hội tụ hay Ā1 hội tụ.
+ Xét Ā3 tương tự như Ā1, cũng nhận ược kết quả Ā3 hội tụ.
+ Vậy Ā = Ā1 + Ā2 + Ā3 hội tụ. - Tính
+∞ Ăý +∞ Ăý 1 ý + 2 +∞ ÿÿāāÿĀ | 2∞ 1 ÿ ÿ ÿ = ( + ) =
Bài 2. Xét sự hội tụ và tính tích phân suy rộng: +∞ Ăý 9 lO M oARcPSD| 45467232 Ā = ∫ ý√ý2 + ý + 1 1
Bài 3. Xét sự hội tụ và tính tích phân suy rộng: +∞ Ăý Ā = ∫
Bài 4. Xét sự hội tụ và tính tích phân suy rộng: 2ýĂý
Bài 5. Xét sự hội tụ và tính tích phân suy rộng: 1 Ăý Ā = ∫ H°ớng d¿n giÁi - Xét sự hội tụ + Viết Ā dưới dạng: Ăý + Xét Ā1: Đặt Ą . Chọn ą
. Hai hàm số Ą(ý),ą(ý) không âm trong . Có lim ÿ(ý) = 1 ý→0+ Ā(ý) + Mặt khác +0 ą(ý)Ăý hội tụ (ÿ =
< 1). Do ó, +0 Ą(ý)Ăý hội tụ hay Ā1 hội tụ. 10 lO M oARcPSD| 45467232 ( 1 ) + Xét Ā2: Đặt Ą
. Chọn ą ý = √12ý. Hai hàm số Ą(ý), ą(ý) không âm trong . Có lim ÿ(ý) = 1 ý→12 Ā(ý) 1 + Mặt khác 1 ą = ( ý + ) 1 Ăý 㕑ý hội tụ (ÿ =< 1). Do ó, 1 Ą(ý)Ăý hội √ 2 tụ 12ý hay Ā2 hội tụ.
+ Vậy Ā = Ā1 + Ā2 hội tụ. - Tính Ăý 1 2Ăý ÿÿā sin(2ý 2 1)| 0 ÿ = ÿ Bài 6.
Xét sự hội tụ và tính tích phân 1 Ăý Ā = ∫
Bài 7. Xét sự hội tụ và tính tích phân 1 ý4Ăý Ā = ∫ 11 lO M oARcPSD| 45467232
2. HÀM SÞ NHIÀU BI¾N SÞ THþC
2.1. Đ¿o hàm, vi phân hàm nhiÁu bi¿n Bài 1. Tính 㔕ÿ⃗ và ąÿÿĂ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗Ă
tại ý0 = (1,2,1) biết hàm Ă = ý2 + þ2 2 23 ÿ3 và þ⃗ = 㔕þ
⃗ý⃗⃗⃗⃗0⃗⃗ý⃗⃗⃗⃗1⃗, ý1 = (2,0,3) H°ớng d¿n giÁi + Ta có: 㔕Ă 㔕Ă 㔕Ă 2 = 2ý; = 2þ; = 22ÿ 㔕 ý 㔕þ 㔕ÿ + Từ giả thiết:
þ⃗ = ⃗ý⃗⃗⃗⃗0⃗⃗ý⃗⃗⃗⃗1⃗ = (1; 22; 2) ⇒ āāĀ ÿ = ; āāĀ Ā = 2 ; āāĀ ā = + Tính ược 㔕Ă 㔕Ă 㔕Ă
㔕ý (ý0) = 2; 㔕þ (ý0) = 4; 㔕ÿ (ý0) = 22 ⇒ ąÿÿĂ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗Ă(ý0) = (2; 4; 22) + Vậy 㔕Ă 㔕þ⃗ (ý0) = 2 2 = 2
Bài 2.Cho hàm số ẩn ÿ = ÿ(ý, þ) xác ịnh bởi ý3 + 2þ3 + ÿ3 2 3ýþÿ 2 2þ + 3 = 0. Tìm ÿ ′ ′ ý , ÿþ . H°ớng d¿n giÁi
+ Đặt 㔹(ý, þ, ÿ) = ý3 + 2þ3 + ÿ3 2 3ýþÿ 2 2þ + 3 = 0 + Từ ó suy ra : 12 lO M oARcPSD| 45467232 㔹 ′ ′ ′
ý = 3ý1 2 3þÿ; 㔹þ = 6þ2 2 3ýÿ 2 2; 㔹ÿ = 3ÿ2 2 3ýþ + Vậy :
′ = 2 㔹㔹 ′ ý ′ = 33þÿÿ2 2
32 3ýþý2 = þÿÿ2 22ýþý2 ÿý ÿ
′ = 2 㔹㔹þÿ′′ = ÿþ
Bài 3. Cho hàm số ÿ = ăý+þ Ā㕖Ā( ý 2 þ) tính Ăÿ(0, 0) và
ý = ÿ. ÿýý′′ 2 (ÿý′ )2 2 ÿ. ÿþþ′′ + (ÿþ′ )2
Bài 4.Cho hàm số Ă(ý, þ) = ý. þ. þĀ( ý + þ). Tính 㔕2Ă 㔕2Ă 㔕2Ă ý2(ý2 2 þ2)
4 + þ4ýℎ㕖 (ý; þ) b (0; 0) Ą(ý, þ) = { ý ÿ
ýℎ㕖(ý; þ) = (0; 0) H°ớng d¿n giÁi + Ta có Ą(0; 0) = ÿ 1 , 㔕þ2 , 㔕ý㔕þ 㔕ý
Bài 5. Cho hàm số ÿ =
2ýþ2 + ý2 + ý1 2 þ1. Chāng minh rằng ý2ÿ ′ ý + þ2ÿ ′ þ = ýþ3
Bài 6.Xét tính liên tục tại iểm (0;0) cÿa hàm số theo a: 13 lO M oARcPSD| 45467232
+ Xét dãy iểm ý㕛(㕛1 ; 㕛1) → (0; 0)(Ā → +∞ , khi ó Ą(ý㕛) → 0(Ā → +∞
+ Xét dãy iểm þ㕛 (㕛2 ; 㕛 1) → (0; 0)(Ā → +∞ , ýhi ó Ą(þ㕛) → (Ā → +∞
+ Vậy không tồn tại giới hạn cÿa Ą(ý, þ) khi (ý; þ) → (0; 0) nên không tồn tại giá
trị cÿa a ể hàm số liên tục.
Bài 7.Xét tính liên tục cÿa hàm số sau theo a ýþ 2 þ2
āāĀ () ýℎ㕖(ý, þ) b (0,0) Ą(ý, þ) = { ý
ÿ ýℎ㕖(ý, þ) = (0,0)
Bài 8.Chāng minh rằng hàm số ÿ = þĄ(ý2 2 þ2) với Ą(ā) là hàm số có ạo hàm
liên tục thỏa mãn ẳng thāc ý1 ÿ ′ ′ ý + þ1 ÿþ 2 þ ÿ2 = 0.
Bài 9. Dùng vi phân toàn phần tính gần úng Ā =
Bài 10.Tìm hàm số ÿ = ÿ(ý, þ) biết rằng 㔕ÿ = ý2+þ2 và ÿ(ý, þ) = Ā㕖Ā þ khi ý = 㔕ý ý 1.
2.2. Bài toán cÿc trị
Bài 1. Tìm cực trị cÿa hàm ÿ(ý, þ) = ý4 + þ4 2 2ý2 + 4ýþ 2 2þ2 H°ớng d¿n giÁi ÿ ′ ý = 4ý3 2 4ý + 4þ = 0(1)
+ Tìm iểm tới hạn {ÿþ′ = 4þ3 + 4ý 2 4þ = 0(2)
+ Lấy (1) + (2) ược: ý3 + þ3 = 0 ⇔ ý = 2þ
+ Thay vào (1) ược: 4ý3 2 8ý = 0 ⇔ ý = 0, ±
+ Vậy có 3 iểm tới hạn ý1(0,0),ý và ý
+ Đạo hàm cấp 2: ý = ÿ ′′ ′′ ′′ ý 2 = 12ý2 2 4, þ = ÿýþ = 4, ÿ = ÿþ 2 = 12þ2 2 4 14 lO M oARcPSD| 45467232
+ Tại ý2,ý3: ý2 2 þÿ = 2384 < 0, ý = 20 > 0. Vậy M2 và M3 là các iểm cực tiểu.
+ Tại M1: với M(k,k) thì ÿ(ý) 2 ÿ(ý1) = 2ý4 g 0, ∀ý trong khi với M(k,0) thì ÿ(ý) 2 ÿ(ý
. Vậy M1 không là iểm cực trị.
+ Kết luận: hàm số có hai iểm cực tiểu ý .
Bài 2. Tìm cực trị cÿa hàm ÿ(ý, þ) = ăý
Bài 3.Tìm cực trị cÿa hàm ÿ(ý, þ) = ý2þ2 2 4ýþ + ý2 2 4ý
Bài 4. Tìm cực trị cÿa hàm ÿ(ý, þ) = 4ýþ ý þ
Bài 5. Tìm cực trị cÿa hàm số Ą(ý, þ) = 8ý 2 ý þ 2 12ý2 2.3. Tích phân bái
Bài 1. Tính tích phân Ā = ,Ā ý2(ý2 + þ2)ĂýĂþ với D là miền giới hạn bởi ường
tròn ý2 + þ2 = 2 nằm trong góc phần tư thā nhất. H°ớng d¿n giÁi
+ Vẽ hình xác ịnh miền lấy tích phân Ā = {(ý, þ): ý2 + þ2 f 2, ý g 0, þ g 0} ý = ÿ. āāĀ 㔑
+ Đổi biến tọa ộ cực: { ⇒ ā(ÿ, 㔑) = ÿ þ = ÿ. Ā㕖Ā 㔑
+ Miền D thành Ā′: 0 f ÿ f ,0 f 㔑 f 㔋 2 + Ā = +0 +0㔋/2 ÿ5 āāĀ2 㔑 Ă㔑 0㔋/2 āāĀ2 㔑 Ă㔑 㔋 6 √ 2 ÿ 㔑 Ā㕖Ā2㔑 2 ÿ = | . ( + )| =
Bài 2. Tính tích phân -㕉 ýþ2Ă㕉 với V là miền giới hạn bởi mặt paraboloid
elliptic ÿ = ý2 + þ2 và mặt phẳng ÿ = 4. H°ớng d¿n giÁi
+ Vẽ miền lấy tích phân V
+ Hình chiếu D cÿa V trên mặt phẳng Oxy là hình tròn tâm O, bán kính bằng 2
+ Miền 㕉 = {(ý, þ, ÿ): (ý, þ) ∈ Ā, ý2 + þ2 f ÿ f 4} 15 lO M oARcPSD| 45467232
+ Đổi biến sang tọa ộ trụ ý = ÿ āāĀ 㔑
{þ = ÿ Ā㕖Ā 㔑 ; ā(ÿ, 㔑, ÿ) = ÿ ÿ = ÿ
+ Miền 㕉′ = {(ÿ, 㔑, ÿ): 0 f 㔑 f 2ÿ; 0 f ÿ f 2; ÿ2 f ÿ f 4} + Ta có
Ā = ∭ ÿ4. āāĀ 㔑 . Ā㕖Ā2 㔑 ĂÿĂ㔑Ăÿ 㕉′ 2 2 Ā㕖Ā3 㔑 2㔋 = ∫ ÿ4Ăÿ ∫ Ăÿ × )| 0 ÿ2
Bài 3. Tính tích phân -㕉 ÿ(þ + 2) ĂýĂþĂÿ với V là miền giới hạn bởi mặt trụ ý2
+ þ2 = 4 và các mặt phẳng ÿ = 0, ÿ = 2. =
Bài 4. Tính tích phân I
x x2( 2 + y dxdy2) với D là miền giới hạn bởi ường D
tròn x2 + =y2 2 nằm trong góc phần tư thā nhất. =
Bài 5. Tính tích phân I
(x−2 )y dxdy với D là miền giới hạn bởi các ường D
y x= 3, x y+ =2 và trục tung.
Bài 6.Tính tích phân cÿa hàm số Ą(ý, þ, ÿ) = 1 2 ý 2 þ 2 ÿtrên miền giới hạn bởi
mặt phẳng ý + þ + ÿ = 1 và các mặt phẳng tọa ộ, nằm trong góc phần tám thā nhất.
Bài 7.Tính thể tích cÿa miền V giới hạn bởi 1 2 2ÿ f ý2 + þ2 + ÿ2 f 1. H°ớng d¿n giÁi
+ V là miền giới hạn bởi hai hình cầu: ý2 + þ2 + (ÿ 2 1)2 g 2 và ý2 + þ2 + ÿ2 f 1
+ Miền V ược xác ịnh bởi: f ÿ f 16 lO M oARcPSD| 45467232
+ Hình chiếu V xuống mặt phẳng Oxy là miền D: ý2 + þ2 f 1 + Ta có I =
dxdy 1 21− −x y2x y2 2 2 dz − − − D = ( )
1− − + − − −x2
y2 2 x2 y2 1 dxdy D ý = ÿ āāĀ 㔑
+ Chuyển sang tọa ộ cực { ⇒ ā = ÿ þ = ÿ Ā㕖Ā 㔑
+ Miền D: ý2 + þ2 f 1 ⇒ Ā′: 0 f ÿ f 1,0 f 㔑 f 2ÿ 1 2 㔋 Ā=∫ Ăÿ ∫
ÿ ( √ 12 ÿ 2 + √ 22 ÿ 2 21 ) 0 0 1 2 √ 2 =2 ÿ ( 2 + ) 2 3 Ă㔑
Bài 8. Tính diện tích phần mặt cầu ý2 + þ2 + ÿ2 = 4nằm ở phía trên mặt phẳng
Oxy bị cắt bởi mặt trụ
Bài 9.Tìm thể tích vật thể nằm trong góc phần tám thā nhất giới hạn bởi các mặt
paraboloid ÿ = ý2 + 3þ2, mặt phẳng ÿ = 0, mặt trụ þ = ý2 và þ = ý
Bài 10. Tính thể tích cÿa vật thể giới hạn bởi các mặt cong ÿ = ý2 + þ2; ÿ = .
2.4. Tích phân °ờng
Bài 1. Tính tích phân Ā = .ÿ 2(ý2 + þ2)Ăý + (ý + þ)2Ăþ trong ó C là biên cÿa
tam giác ABC lấy theo chiều dương với A(1,1), B(2,2), C(1,3). H°ớng d¿n giÁi + Ta có:
Ā = ∫ 2(ý2 + þ2)Ăý + (ý + þ)2Ăþ + ∫ 2(ý2 + þ2)Ăý + (ý + þ)2Ăþ 17 lO M oARcPSD| 45467232 ýþ þÿ
+ ∫ 2(ý2 + þ2)Ăý + (ý + þ)2Ăþ ÿý = Ā1 + Ā2 + Ā3
+ Đường thẳng AB: þ = ý cóĀ1 = +12 8ý2Ăý =
+ Đường thẳng BC: þ = 2ý + 4 ta có Ā2 = 4 +21(ý2 2 4ý + 7)Ăý =
+ Đường thẳng CA: ý = 1 ta cóĀ3 = +31(1 + þ)2Ăþ = + Kết quả: Ā = .
Bài 2.Tính tích phân Ā = .㔿(ý2 + ýþ2)Ăý + (3þ + 2ý2þ)Ăþtrong ó L là biên
cÿa miền giới hạn bởi các ường ý = 0, þ = 0, þ = 2 2 ý. H°ớng d¿n giÁi + Vẽ
các ường lấy tích phân
+ L là một ường cong kín, xác ịnh một miền D hình tam giác
+ Miền Ā = {(ý, þ): 0 f ý f 2,0 f þ f 2 2 ý} ÿ(ý, þ) = ý2 + ýþ2 ÿ ′ þ = 2ýþ
+ Đặt {Ā(ý, þ) = 3þ + 2ý2þ ⇒ {Āý′ = 4ýþ
+ Áp dụng công thāc Green, ta ược: Ā = , ′ ′
Ā(Āý 2 ÿþ )ĂýĂþ = ,Ā 2ýþĂýĂþ + Ta có
Bài 2.Tính Ā = +㕂ýþ(āāĀ þ 2 1)ăýĂý + (2þ 2 Ā㕖Ā þ)ăýĂþ trong ó OAB là
ường gấp khúc O(0,0), A(1,1), B(2,0).
Bài 3. Tính tích phân Ā = .㔿(2ýþ + ý2)Ăý + (3þ2 + 2ýþ)Ăþ , trong đó L là
biên của miền giới hạn bởi þ = 0, þ = 2ý, ý = 2.
Bài 4.Tính tích phân Ā = + 㕑 ÿ ý2þ
Ā trong ó C là oạn thẳng þ = ý2 2 2 nằm
giữa các iểm A(0,-2) và B(4,0). 18 lO M oARcPSD| 45467232 H°ớng d¿n giÁi + Vẽ hình + Ta có ĂĀ Ăý Ăý Ā= √ 5 þ Ā 2 ý = ā + āāĀ ā
Bài 5.Tính ộ dài cung { với 0 f ā f ÿ þ = Ā㕖Ā ā
Bài 6. Tính tích phânĀ = +ÿ √ý2 + þ2ĂĀ trong ó C là ường xoắn hình nón ý = ā
āāĀ ā , þ = ā Ā㕖Ā ā , ÿ = ā với 0 f ā f ā0.
2.5. Tích phân mặt
Bài 1. Tính tích phân ,㕆 2ýĂýĂþ + þĂÿĂý 2 ÿĂþĂÿvới (S) là phía ngoài mặt cầu ý2 + þ2 + ÿ2 = 4. H°ớng d¿n giÁi + Vẽ mặt cong (S)
+ (S) và một mặt cong kín, xác ịnh một miền V là hình cầu tâm O, bán kính bằng 2,
hướng cÿa mặt là phía ngoài.
+ Với ÿ(ý, þ, ÿ) = 2ÿ, Ā(ý, þ, ÿ) = þ, ā(ý, þ, ÿ) = 2ý, ta có ÿ ′ ′ ′ ý = 0, Āþ = 1, āÿ = 0
+ Áp dụng công thāc Ostrogradsky, ta ược Ā ′ ′ ′
3 = -㕉(ÿý + Āþ + āÿ )ĂýĂþĂÿ + Ā = - 㔋
㕉 ĂýĂþĂÿ =thể tích khối cầu tâm O, bán kính 2. VậyĀ = 323
Bài 2. Tính tích phân ,㕆 ý2ĂþĂÿ 2 þ2ĂÿĂý + 2þÿĂýĂþ với (S) là nửa mặt cầu ÿ =
, hướng cÿa (S) là hướng lên trên.
Bài 3. Tính tích phân ,㕆 2ýĂýĂþ 2 þĂÿĂý + ÿĂþĂÿ với (S) là phía ngoài mặt cầu ý2 + þ2 + ÿ2 = 4. 19 lO M oARcPSD| 45467232
Bài 4.Tính tích phân Ā = ,㕆 þĀ ÿ dS trong ó S là mặt cầu xác ịnh bởi ý2 + þ2 + ÿ2 = 1, f ÿ f 1 H°ớng d¿n giÁi
+ Mặt S có phương trình ÿ =
với hình chiếu cÿa S xuống mặt
phẳng Oxy là miền D giới hạn bởi ường tròn ý2 + þ2 = 3 . 4 ′ 2 ′ 2
ĂĂ = √ 1+ ÿ ý + ÿ þ ĂýĂþ = ĂýĂþ þ √ 12 ý 2 2 þ 2 + Ā = , 㕛 Ā √12ý22þ2 ĂýĂþ ý = ÿ. āāĀ 㔑
+ Chuyển sang tọa ộ cực { ⇒ ā(ÿ, 㔑) = ÿ þ = ÿ. Ā㕖Ā 㔑
+ Miền D:ý2 + þ2 f 3 ⇒ Ā′: 0 f ÿ f , 0 f 㔑 f 2ÿ 4 + Thay vào tính ược Ā = ÿĂÿ × + 2㔋 0 Ă㔑 = ÿ(þĀ 2 2 1)
Bài 5.Tính tích phân Ā = ,㕆 ý2þ2ÿĂĂ trong ó S là mặt nón ý2 + þ2 = ÿ2, 0 f ÿ f 1.
Bài 6.Tính diện tích cÿa phần mặt paraboloid ÿ = ýþ với hình chiếu xuống mặt
phẳng Oxy là hình tròn xác ịnh bởi ý2 + þ2 f 1. 20