
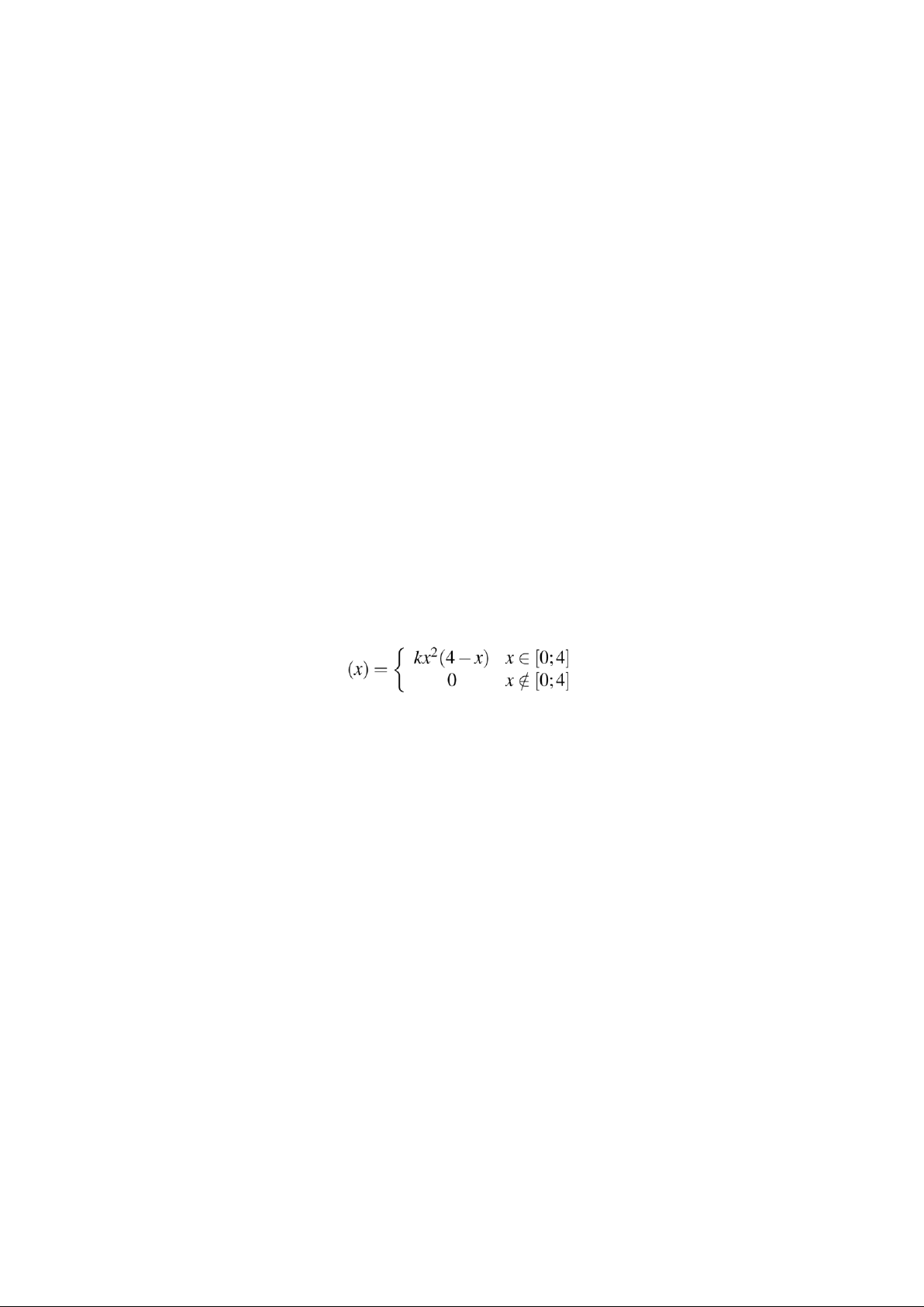


Preview text:
lO M oARcPSD| 47110589 ĐẠI HỌC HUẾ
ĐỀ CƯƠNG ÔN TẬP HỌC PHẦN
KHOA KỸ THUẬT VÀ CÔNG NGHÊ
Tên HP: TOÁN VÀ THỐNG KÊ 2
Câu 1 Với a,b,x ∈Rn, A ∈Rm×n Tính dạo hàm các hàm sau:
a. f(x) = aTx
b. f(x) = Ax
c. f(x) = xTAx d. aTxTxb
Câu 2. Cho X và Y là các biến ngẫu nhiên rời rạc. Chứng minh rằng X và Y là độc lập khi và chỉ khi
fX,Y(x,y) = fX(x)fY(y) với mọi x và y.
Câu 3. Trong một lớp học có 30 sinh viên, 18 sinh viên học giỏi Toán, 15 sinh viên học giỏi Vật lý
và 10 sinh viên học giỏi cả Toán và Vật lý. Nếu chọn ngẫu nhiên một sinh viên, tính xác suất để sinh
viên đó học giỏi Vật lý, biết rằng sinh viên đó học giỏi Toán.
Câu 4. Một công ty thăm dò dầu mỏ hiện có hai dự án đang hoạt động,một ở châu Á và một ở
châu Âu. Gọi A là biến cố rằng dự án châu Á thành công và B là sự kiện dự án châu Âu thành công.
Giả sử A và B là các sự biến cố độc lập với P(A) = 0.4 và P(B) = 0.7.
a. Nếu dự án châu Á không thành công thì khả năng dự án châu Âu cũng không thành công là baonhiêu?
b. Xác suất để ít nhất một trong hai dự án sẽ thành công là bao nhiêu?
c. Biết rằng ít nhất một trong hai dự án thành công,xác suất để chỉ có dự án châu Á thành công làbao nhiêu?
Câu 5. Một nhà thầu có xác suất hoàn thành công việc đúng hạn là 0.9 và xác suất hoàn thành
công việc đạt chất lượng là 0.85. Tính xác suất để nhà thầu hoàn thành công việc vừa đúng hạn vừa
đạt chất lượng, biết rằng hai sự kiện này là độc lập
Câu 6. Một cỗ máy sản xuất lần lượt từng sản phẩm. Xác suất để sản phẩm sản xuất ra là phế
phẩm của cỗ máy là 0,01.
a. Cho máy sản xuất 20 sản phẩm. Tính xác suất để có 2 phế phẩm.
b. Máy cần sản xuất ít nhất bao nhiêu sản phẩm để xác suất có ít nhất một chính phẩm trên 0,99. lO M oARcPSD| 47110589
Câu 7. Cho ba biến ngẫu nhiên độc lập X,Y,Z trong đó X có phân phối N(50;0,36), Y có phân phối
B(15;0,5) và Z có phân phối Poisson với λ = 3. Tính E(U),V(U) biết U = X +2Y −3Z.
Câu 8.). Một phân xưởng có ba máy M1,M2,M3 .Trong một giờ, mỗi máy sản xuất được 10 sản
phẩm. Số sản phẩm không đạt tiêu chuẩn trong 10 sản phẩm của M1,M2,M3 lần lượt là 1, 2, 1. Lấy
ngẫu nhiên 1 sản phẩm từ 10 sản phẩm do mỗi máy sản xuất. Gọi X là số sản phẩm không đạt tiêu
chuẩn trong 3 sản phẩm được lấy ra.
1. Lập bảng phân phối xác suất của X.
2. Tìm E(X),Var(X),Mod(X).
3. Tính P(X ≤ 1).
Câu 9.). Một nhóm kỹ sư đang kiểm tra độ bền nén của một loại bê tông mới. Họ lấy mẫu ngẫu
nhiên 30 khối bê tông và đo được độ bền trung bình là 40 MPa với độ lệch chuẩn là 5 MPa. Ước
lượng khoảng tin cậy 95% cho độ bền trung bình của bê tông này.
Câu 10.). Trong một dự án xây dựng, người ta kiểm tra 200 mối hàn và phát hiện 15 mối hàn có
lỗi. Ước lượng khoảng tin cậy 95% cho tỷ lệ mối hàn có lỗi trong toàn bộ dự án.
Câu 11.). Tuổi thọ của một loại bóng đèn nào đó là một biến số ngẫu nhiên liên tục X (đơn vị
năm) với hàm mật độ như sau: f a. Tìm k.
b. Tìm xác suất để bóng đèn hỏng trước khi nó được 1 năm tuổi.
Câu 12.). Một công ty xây dựng kiểm tra trọng lượng của các viên gạch và phát hiện trọng lượng
trung bình là 2.5 kg với độ lệch chuẩn là 0.1 kg từ 25 mẫu gạch. Ước lượng khoảng tin cậy 95% cho
phương sai trọng lượng của gạch.
Câu 13.). Một loại xi măng được cho là có độ bền nén trung bình là 50 MPa. Một kỹ sư nghi ngờ rằng
độ bền thực tế thấp hơn. Anh ta lấy mẫu 25 khối xi măng và đo được độ bền trung bình là 48 MPa
với độ lệch chuẩn là 4 MPa. Sử dụng mức ý nghĩa 0.05, kiểm định giả thuyết rằng độ bền thực tế của
xi măng này không thấp hơn 50 MPa.
Câu 14.). Trong một dự án xây dựng, tỷ lệ lỗi kỹ thuật được cho là không vượt quá 5%. Một kỹ sư
lấy mẫu ngẫu nhiên 100 công việc và phát hiện 8 lỗi kỹ thuật. Sử dụng mức ý nghĩa 0.05, kiểm định
giả thuyết rằng tỷ lệ lỗi kỹ thuật vượt quá 5%.
Câu 15.). Một công ty xây dựng muốn so sánh độ bền của hai loại bê tông A và B. Họ lấy mẫu ngẫu
nhiên 15 khối bê tông A với độ bền trung bình là 42 MPa và độ lệch chuẩn là 4 MPa, và 20 khối bê
tông B với độ bền trung bình là 40 MPa và độ lệch chuẩn là 5 MPa. Sử dụng mức ý nghĩa 0.05, kiểm
định giả thuyết rằng độ bền trung bình của hai loại bê tông này là như nhau. lO M oARcPSD| 47110589
Câu 16.). Trong một công trình xây dựng, tỷ lệ các lỗi của hai loại vật liệu xây dựng được so sánh.
Trong 200 mẫu của vật liệu A, có 30 mẫu có lỗi. Trong 150 mẫu của vật liệu B, có 20 mẫu có khuyết
tật. Sử dụng mức ý nghĩa 0.05, kiểm định giả thuyết rằng tỷ lệ khuyết tật của hai loại vật liệu là như nhau.
Câu 17.). Đo đường kính của 100 trục máy do một nhà máy sản xuất thì được bảng số liệu:
Đường kính (cm) 9,75 9,8 9,85 9,9 Số trục máy 5 37 42 16
a. Hãy ước lượng đường kính trung bình của trục máy với độ tin cậy 97%.
b. Để ước lượng đường kính trung bình của trục máy có độ chính xác 0,006cm thì đảm bảo độ tincậy là bao nhiêu?
c. Muốn ước lượng đường kính trung bình của trục máy có độ chính xác lớn hơn 0,003cm với
độtin cậy 99% thì phải đo tối đa bao nhiêu trục máy nữa?
Câu 18.). Để kiểm tra một loại súng thể thao, người ta cho bắn 1.000 viên đạn vào một tấm bia
thì có 670 viên trúng mục tiêu. Sau đó, người ta cải tiến kỹ thuật và kiểm tra lại thì thấy tỉ lệ trúng
của súng lúc này là 70%. Trong kiểm định giả thuyết : “tỉ lệ bắn trúng của loại súng thể thao này
trước cải tiến là 70%”, với mức ý nghĩa 3% có giá trị thống kê và kết luận như thế nào?
Câu 19.). Giả sử biến ngẫu nhiên X có hàm mật độ như sau: f a.
Tìm mean(X) và Var(X). b.
Tìm mean(Y) và Var(Y) với Y = −3X +2. Câu 20.). Thang máy trong siêu thị Go Huế
có biển “tối đa 10 người, hoặc nhiều nhất là 800kg.” Giả sử cân nặng của một người là biến
ngẫu nhiên tuân theo quy luật phân phối chuẩn N(70,10)kg. Tính xác suất để 10 khách hàng sẽ làm thang máy quá tải?
Câu 21.). Tuổi thọ (tháng) của thiết bị là biến ngẫu nhiên có phân phối chuẩn. Người ta kiểm tra ngẫu nhiên tuổi thọ của 15 thiết bị loại , có kết quả:
114;78;96;137;78;103;126;86;99;114;72;104;73;86;117.
Kiểm tra tuổi thọ 17 thiết bị loại thấy có trung bình là 84 tháng và độ lệch chuẩn đã hiệu chỉnh là 19
tháng. Kiểm định giả thuyết : “tuổi thọ trung bình của thiết bị loại A và B là như nhau với mức ý
nghĩa 3%” có giá trị thống kê và kết luận là:
A. t = 2,1616; tuổi thọ trung bình của 2 loại thiết bị như nhau; B.
t = 2,1616; tuổi thọ trung bình của loại thiết bị lớn hơn;
C. t = 2,4616; tuổi thọ trung bình của 2 loại thiết bị như nhau;
D. t = 2,4616; tuổi thọ trung bình của loại thiết bị lớn hơn.
Câu 22.). Giả sử X là biến ngẫu nhiên với hàm mật độ như sau: lO M oARcPSD| 47110589 f a. Tìm k.
b. Tìm hàm phân phối của X.
c. Tìm P(X < 3/2). d. Tìm E[X].
Câu 23.). Cho X là biến số ngẫu nhiên liên tục có hàm phân phối xác suất sau: 1 1 x F(x) = + arctan 2 π 2
1. Tính P(0 < X < 1.
2. Tìm hàm mật độ xác suất của X HẾT



