





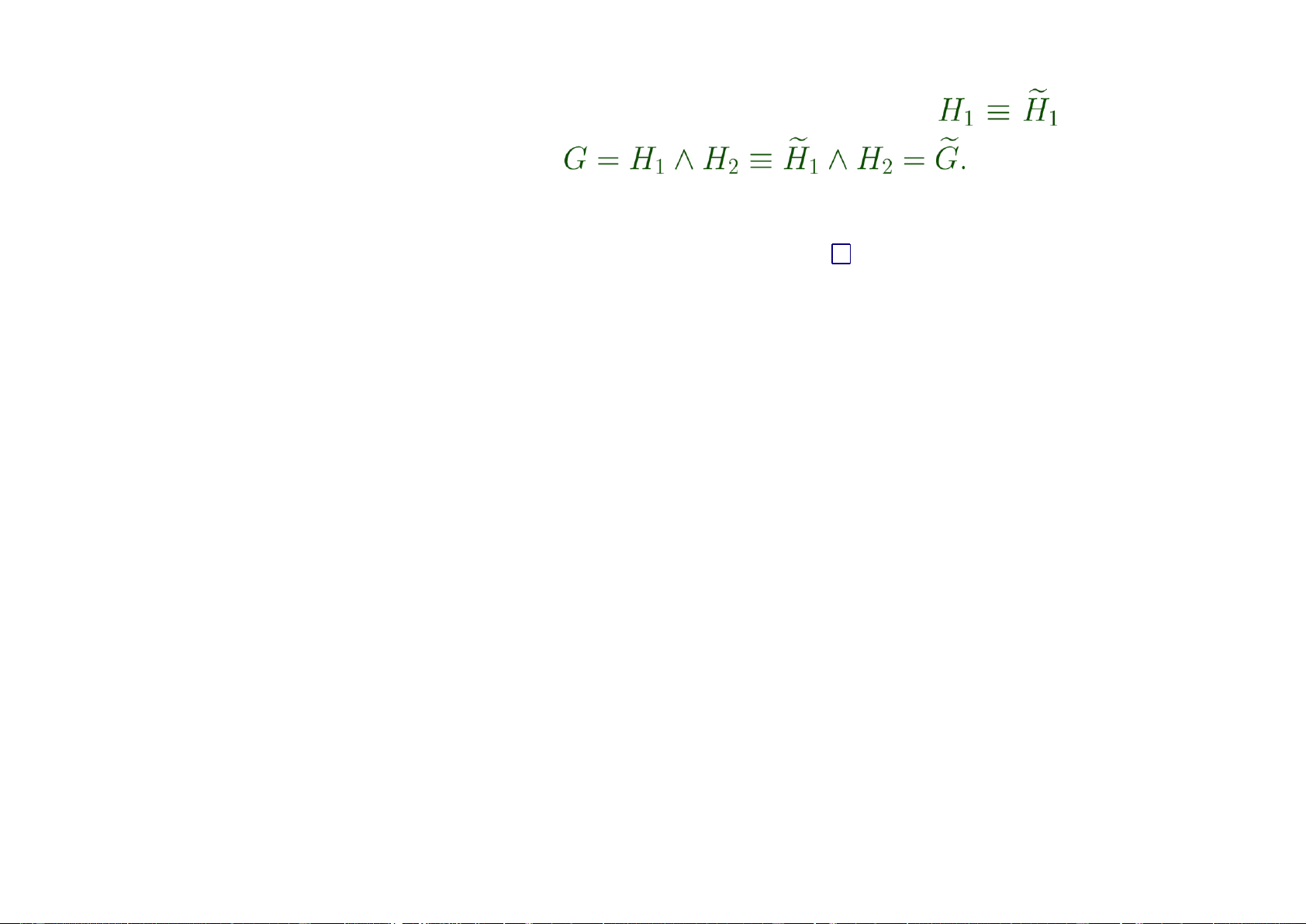










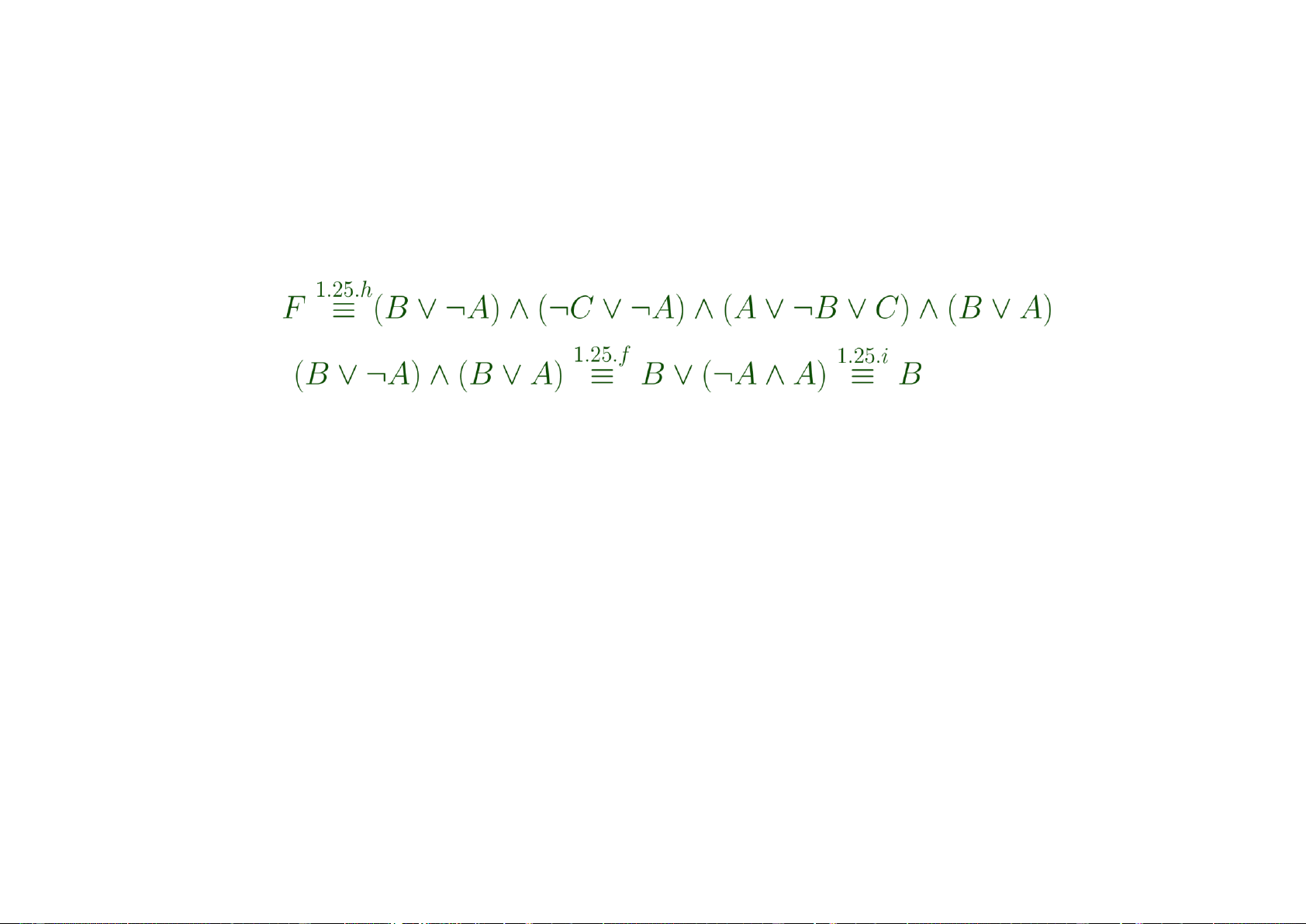


Preview text:
lO M oARcPSD| 47110589 lO M oARcPSD| 47110589 Hue University of Education Department of Mathematics ⋆ ⋆ ⋆
THE PRINCIPLE OF MATHEMATICS 1 LE NGOC LONG - TRAN N.K. LINH lO M oARcPSD| 47110589 HUE, March 8, 2022 1.3
Tautologies, Absurdities, and Contingencies
Definition 1.13. Let F be a logical formula.
(a) If F is always true, it is called a tautology.
(b) If F is always false, it is called an absurdity.
(c) If F is sometimes true and sometimes false, it is called a contingency.
One of the main purposes of logic is to ferret out tautologies, for these are the
theorems, or laws, of logic. We shall be concerned only with testing for
tautologies, checking the truth tables of formulas for the last column having only 1’s.
Example 1.14. (a) The logical formula F ⇒ (F ∧ G) is a contingency. Indeed, we have
F G F ∧ G F ⇒ (F ∧ G) 1 1 1 1 12
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589 1 0 0 0 0 1 0 1 0 0 0 1
Thus the formula F ⇒ (F ∧G) is true if, for instance, F and G both are true;
while it is false if F is true and G is false.
(b) The formula F ∨¬F is a tautology which follows from the following truth table.
F ¬F F ∨ ¬F 1 0 1 0 1 1
(c) The formula F ∧ ¬F is an absurdity as the following truth table shows.
F ¬F F ∧ ¬F 1 0 0 0 1 0 13
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(d) Similarly, we can check that (F ∧ G) ⇒ F and (F ∧ G) ⇔ (G ∧ F) are tautologies.
Remark 1.15. A logical formula F is a tautology if and only if ¬F is an absurdity.
✍ 1.16. Let F,G,H be logical formulas. Determine whether each logical formula
is a tautology, an absurdity, or a contingency.
(a) (G ∧ (F ⇒ G)) ⇒ F.
(b) (¬G ∧ (F ⇒ G)) ⇒ ¬F. (c)
(¬F ∧ (F ⇒ G)) ⇒ ¬G.
(d) (F ∧ G) ⇒ (G ⇒ H).
(e) ¬F ⇒ (F ⇒ G).
(f) (F ∨ ¬F) ⇒ (G ∧ ¬G).
Definition 1.17. Two logical formulas F and G are called equivalent if the
formula F ⇔ G is a tautology (i.e., F and G have the same truth tables). In this
case we write F ≡ G. 14
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
Example 1.18. (a) We have F ∧ (F ∨ G) ≡ F, because
F G F ∨ G F ∧ (F ∨ G)
F ∧ (F ∨ G) ⇔ F 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 0 0 0 0 1
Here notice that the truth values of the first column are equal to the truth values of the fourth column.
(b) We have (F ⇒ G) ≡ (¬F ∨ G), since
F G ¬F F ⇒ G ¬F ∨ G 1 1 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 1 1 1
where the last two columns have the same values. Similarly, we have 15
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(F ⇔ G) ≡ ((F ⇒ G) ∧ (G ⇒ F))
≡ ((¬F ∨ G) ∧ (¬G ∨ F)) ≡ ((F ∧ G) ∨ (¬F ∧ ¬G)).
Theorem 1.19. Let F1,F2 be two logical formulas with F1 ≡ F2, let G be a logical
formula such that F1 is a subformula appearing in G. If Ge is the formula obtained
from G by replacing F1 by F2, then we have .
Proof. We proceed by induction on the construction of the formula G by
Definition 1.9. If G is an atomic formula, then G = F1, and so Ge = F2 ≡ G. Next
we consider the following three cases.
If G is of the form G = ¬H, then F1 is a subformula of H and Ge = ¬He, where He
is obtained from H by replacing F1 by F2. By induction hypothesis, , and hence .
Let G be of the form G = H1∧H2 with logical formulas . Without loss of
generality, we may assume that F1 is a subformula of H1. Let H1 be obtained 16
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
from H1 by replacing F1 by F2. By induction hypothesis, . By the
definition of conjunction, we get
Finally, if G is of the form G = H1 ∨ H2 with logical formulas H1,H2, we can
similarly argue as the second case and get the claim.
Definition 1.20. Calling the implication F ⇒ G the given formula, we then call
G ⇒ F the converse, ¬F ⇒ ¬G the inverse, and ¬G ⇒ ¬F the contrapositive.
✍ 1.21. Rewrite each statement as an implication.
(a) If F, then G. (b) G, if F.
(c) G only if F.
(d) G is necessary for F.
(e) G is sufficient for F.
(f) A necessary condition for F is G. 17
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(g) A sufficient condition for F is G.
✍ 1.22. Write the converse, inverse, and contrapositive of each statement.
(a) If today is Monday, then tomorrow is Tuesday.
(b) The base angles of an isosceles triangle are equal.
(c) x + y = z implies x < z.
Lemma 1.23. The given formula and its contrapositive are logically equivalent;
the inverse and the converse are equivalent. This given formula is not equivalent
to its converse. Symbolically,
(F ⇒ G) ≡ (¬G ⇒ ¬F),
(¬F ⇒ ¬G) ≡ (G ⇒ F), but
(F ⇒ G) 6≡ (G ⇒ F).
Proof. One can use the truth table to prove this result. Alternatively, we can
directly prove (F ⇒ G) ≡ (¬G ⇒ ¬F) as follows. By Example 1.18.b, we have 18
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(F ⇒ G) ≡ (¬F ∨ G) ≡ (G ∨ ¬F) ≡ (¬G ⇒ ¬F).
The next two theorem lists some important tautologies, whose proofs are left for the reader.
Theorem 1.24. For logical formulas F,G,H, the following are tautologies.
(a) ¬(F ∧ ¬F) (Law of Contradiction).
(b) F ∨ ¬F (Law of Excluded Middle).
(c) (F ∧ (F ⇒ G)) ⇒ G (Law of Detachment).
(d) (F ∧ G) ⇒ F (Law of Simplification).
(e) F ⇒ (F ∨ G) (Law of Addition).
(f) (¬F ∧ (F ∨ G)) ⇒ G (Law of Disjunction).
(g) ((F ⇒ G) ∧ (G ⇒ H)) ⇒ (F ⇒ H) (Law of Syllogism).
Theorem 1.25. For logical formulas F,G,H, we have: 19
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(a) (F ∧ F) ≡ F and (F ∨ F) ≡ F (Idempotent Laws).
(b) ¬(¬F)) ≡ F (Law of Double Negation).
(c) ¬(F ∧ G) ≡ (¬F ∨ ¬G), ¬(F ∨ G) ≡ (¬F ∧ ¬G) (De Morgan’s Laws).
(d) (F ∨ G) ≡ (G ∨ F), (F ∧ G) ≡ (G ∧ F) (Commutative Laws).
(e) ((F ∨G)∨H) ≡ (F ∨(G∨H)), ((F ∧G)∧H) ≡ (F ∧(G∧H)) (Associative Laws).
(f) (F ∧(G∨H)) ≡ ((F ∧G)∨(F ∧H)), (F ∨(G∧H)) ≡ ((F ∨G)∧(F ∨H)) (Distributive Laws).
(g) (F ∧ (F ∨ G)) ≡ F, F ∨ (F ∧ G) ≡ F (Laws of Absorption).
(h) If F is a tautology, then F∨G ≡ F and F∧G ≡ G.
(Law of Tautologies). (i) If
F is an absurdity, then (F ∨ G) ≡ G and (F ∧ G) ≡ F. (Law of Absurdities).
✍ 1.26. Define F/G to mean ¬F ∨ ¬G.
(a) Show that ¬F ≡ (F/F). 20
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(b) Show that (F ∨ G) ≡ ((F/F)/(G/G)).
✍ 1.27. Shortly after the birth of the twins Herakles and Eurystheus, there was
a dispute between Herakles and Eurystheus: who of them was the legitimate
ruler. For this, the three most famous Oracles were consulted.
Ammonion announced that the Oracle from the Klaros was always wrong.
Likewise, the Oracle from Klaros also announced that the Oracle from Delphi
was wrong since the beginning. However, the Oracle from Delphi claimed that
both the statements of Ammonions and the Oracles from Klaros were never
true. In addition, suppose that every oracle is either always right or always
wrong. Who should you believe?
✍ 1.28. A report of police contains the following information about a
housebreaking: The offenders are sure to be some of three people, namely Anna,
Bill, Christian. If Christian is an offender, then both Anna and Bill are involved in
the housebreaking. Bill is guilty or Christian is unguilty only if Anna is not an offender. 21
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
a) Write a logical formula F for the above situation. b) Who broke in the house?
✍ 1.29. Aladdin finds three trunks A, B and C in a cave. He knows that only one
trunk contains a treasure and the other two contain fatal traps. Moreover, he
heard the following three secret massages:
Message 1: The gold is not in trunk A.
Message 2: The gold is not in trunk B.
Message 3: The gold is in trunk B.
He knows that only one message is true and the other two are false.
a) Write a logical formula F for the above situation.
b) Can Aladdin choose a trunk and be sure that he will find the treasure? If
thisis the case, which trunk should he open? 22
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
✍ 1.30. The police in Ingolstadt is looking for the resident of a house who
caused the fire of the house in the last weekend. Both Anton and Brian are
under suspicion, but they both said that they do not know anything about the
incident. The following statements are given by other residents of the house.
Statement 1: “Anton is not lying and Brian is not innocent”.
Statement 2: “Anton and Brian are both not innocent”.
Statement 3: “If Anton is lying then Brian is innocent”.
Statement 4: “From these three claims it follows that Anton is lying or guilty”.
a) Write the above statements as propositional logic formulas.
b) Suppose that the statements 1,2,3 are true. Using a truth table, determine
whether the statement 4 is true. 1.4
Conjunctive and Disjunctive Normal Form
In the view of Theorems 1.19 and 1.25, one can bring a logic formula into standard forms. 23
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
Definition 1.31. (a) A literal L is an atomic formula or the negation of an
atomic formula. In the first case L is called a positive literal, in the second
case L is called a negative literal.
(b) A logical formula F is called in conjunctive normal form (CNF) if it is a
conjunction of disjunctions of literals, i.e., if F is of the form with literals Lij:
F = (L11 ∨ ··· ∨ L1k1) ∧ ··· ∧ (Ln1 ∨ ··· ∨ Lnkn).
(c) A logical formula F is called in disjunctive normal form (DNF) if it is a
disjunction of conjunctions of literals, i.e., if F is of the form with literals Lij:
F = (L11 ∧ ··· ∧ L1k1) ∨ ··· ∨ (Ln1 ∧ ··· ∧ Lnkn).
Example 1.32. Let A, B, C be propositions. 24
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(a) The formula F = (A∨¬B∨C)∧(¬A∨C)∧(¬A∨B) is a conjunctive normal form (CNF).
(b) The formula G = (¬A∧B∧C)∨(A∧¬B∧C)∨(A∧B∧¬C) is a disjunctive normal form (DNF).
Theorem 1.33. Any logical formula F has an equivalent formula in CNF and an
equivalent formula in DNF.
Instead of giving the proof of the theorem, we present the algorithm which
can bring a logical formula in CNF.
Algorithm 1.34. Let F be a logical formula. Perform the following instructions:
(0) Eliminate ⇒ and ⇔ using Example 1.18.b.
(1) Replace in F every subformula of the form ¬¬G by G.
(2) Replace in F every subformula of the form ¬(G ∧ H) by (¬G ∨ ¬H). If a
subformula of the form ¬¬K appears, then apply Step (1). 25
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(3) Replace in F every subformula of the form ¬(G ∨ H) by (¬G ∧ ¬H). If a
subformula of the form ¬¬K appears, then apply Step (1).
(4) Repeat Steps (2) and (3) if possible.
(5) Replace in F every subformula of the form (G ∨ (H ∧ I)) by ((G ∨ H) ∧ (G ∨ I)).
(6) Replace in F every subformula of the form ((G∧H)∨I) by ((G∨I)∧(H∨I)).
(7) Repeat Steps (5) and (6) if possible.
The resulting formula is then in CNF.
Example 1.35. Let F = ((A ⇔ (B ∧ ¬C)) ∧ (¬B ⇒ A)) be a logical formula, where
A,B,C are atomic formulas. We apply the algorithm to bring F into CNF. (0) Eliminate ⇒ and ⇔:
F ≡ (((A ∧ (B ∧ ¬C)) ∨ (¬A ∧ ¬(B ∧ ¬C))) ∧ (¬¬B ∨ A)).
(1) Replace in F every subformula of the form ¬¬G by G:
F ≡ ((A ∧ B ∧ ¬C) ∨ (¬A ∧ ¬(B ∧ ¬C))) ∧ (B ∨ A). 26
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
(2-3) Replace in F every subformula of the form ¬(G ∧ H) by (¬G ∨ ¬H), resp. of
the form ¬(G ∨ H) by (¬G ∧ ¬H):
F ≡ ((A ∧ B ∧ ¬C) ∨ (¬A ∧ (¬B ∨ ¬¬C))) ∧ (B ∨ A).
(1) Replace in F every subformula of the form ¬¬G by G:
F ≡ ((A ∧ B ∧ ¬C) ∨ (¬A ∧ (¬B ∨ C))) ∧ (B ∨ A).
(5) Replace in F every subformula of the form (G∨(H∧I)) by ((G∨H)∧(G∨I)):
F ≡ (((A ∧ B ∧ ¬C) ∨ ¬A) ∧ ((A ∧ B ∧ ¬C) ∨ (¬B ∨ C))) ∧ (B ∨ A).
(6) Replace in F every subformula of the form ((G∧H)∨I) by ((G∨I)∧(H∨I)):
F ≡(((A ∨ ¬A) ∧ (B ∨ ¬A) ∧ (¬C ∨ ¬A)) ∧ ((A ∨ (¬B ∨ C)) 27
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
∧(B ∨ (¬B ∨ C)) ∧ (¬C ∨ (¬B ∨ C)))) ∧ (B ∨ A) ≡(A ∨
¬A) ∧ (B ∨ ¬A) ∧ (¬C ∨ ¬A) ∧ (A ∨ ¬B ∨ C) ∧ (B ∨ ¬B ∨ C)
∧ (¬C ∨ ¬B ∨ C) ∧ (B ∨ A).
This formula is in CNF. We can use Theorem 1.25 to simplify the formula. Observe , and so 1.25.d,f,i F ≡
(¬C ∨ ¬A) ∧ (A ∨ ¬B ∨ C) ∧ B 1.25.f,i
≡ (¬C ∨ ¬A) ∧ (A ∨ C) ∧ B.
✍ 1.36. Let A,B,C be propositions and let
F = (¬(A ∧ B)) ∧ (C ⇒ B) ∧ ((¬A ∧ B) ⇒ ¬C) ∧ C. (a) Bring F into CNF.
(b) Simplify F and show that ¬F is a tautology. 28
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589 (c) Bring F into DNF.
✍ 1.37. After Ensel and Krete have pushed the witch into the oven, they want
to devour the gingerbread house. But it is well known that one must be very
careful when eating this kind of house, since these houses tend to be unstable.
They first turn to a wall consisting of three pieces of gingerbread. Since Ensel
successfully studied civil engineering, he knows that they have to carefully respect the following rules:
1) Of the first two pieces of gingerbread they may remove at most one.
2) If the third piece is removed, the second one also needs to be removed.
3) If the second one is removed and the first one not, then they cannot remove the third.
Because Krete knows logic, she deduces that it is better not to start by removing the third piece.
a) Show that you can prove this by showing that the following formula is notsatisfiable: 29
L.N. Long & T.N.K. Linh lO M oARcPSD| 47110589
F = (¬(A ∧ B)) ∧ (C ⇒ B) ∧ ((¬A ∧ B) ⇒ ¬C) ∧ C.
b) Write F in conjunctive normal form (CNF).
c) Simplify F such that you can show that F is not satisfiable.
✍ 1.38. Emil would like to celebrate his birthday. Unfortunately, his friends,
Anne, Bernd, Christine and Dirk, are difficult people. Anne only participates if
Bernd attends. Bernd only attends if Christine takes part. If Christine takes part
then Dirk takes part. If Bernd and Dirk take part, then Christine won’t attend.
Dirk takes part only if Anne or Bernd takes part.
a) Write a logical formula for the above situation.
b) Using a truth table, show that none of Emil’s friends comes to his birthday party. 30
L.N. Long & T.N.K. Linh



