Đề cương ôn thi HK2 môn Toán lớp 11 GDTX Quảng Điền

Đề cương ôn thi HK2 môn Toán lớp 11 GDTX Quảng Điền – Hoàng Hữu Tài. Đề cương ôn thi HK2 môn Toán lớp 11 GDTX Quảng Điền – Hoàng Hữu Tài.

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

5 trang 6 tháng trước

Tác giả:

Profile Kim Oanh
GV: Hoàng Hữu Tài
TRUNG TÂM GDTX QUẢNG ĐIỀN
ĐỀ CƯƠNG ÔN THI HỌC KÌ II
MÔN TOÁN - LỚP 11
Câu 1. Cho cấp số cộng
()
n
u
, biết
1
5u 
, d = 3.
a) Viết số hạng tổng quát của CSC.
b) Tìm
15
u
và tính tổng 15 số hạng đầu tiên của CSC.
c) Số 100 là số hạng thứ bao nhiêu.
Câu 2. Cho cấp số nhân
()
n
u
với
3
4u
và
4
8u
.
a) Tính
1
u
và q.
b) Viết số hạng tổng quát của CSN.
c) Tính
7
u
và tổng 7 số hạng đầu của CSN.
Câu 3. Tính giới hạn các hàm số sau:
a)
b)
4
lim( 2)nn
c)
34
lim
5
nn
n
Câu 4. Tính giới hạn các hàm số sau:
a)
4
2
lim
2
x
x
x
b)
2
2
2
lim
21
x
xx
x

c)
3
lim( 3 2)
x
xx

d)
2
2
56
lim
2
x
xx
x

Câu 5. Tìm đạo hàm của các hàm số sau:
a)
2
5y x x
b)
2
2 3 1y x x
c)
83y x x
d)
( 2)(2 1)y x x
e)
52
23
x
y
x
f)
4
( 4)yx
g)
2sin tany x x
h)
2cos 2
2
yx




Câu 6. Chứng minh rằng phương trình
3
2sin 1 0x 
có ít nhất một nghiệm thuộc khoảng
0;
2



Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, O là giao điểm của AC và
BD, cạnh bên
2SA SB SC SC a
.
a) Chứng minh
()SO ABCD
.
b) Chứng minh
( ) ( )SAC SBD
.
c) Tính khoảng cách từ S đến (ABCD)
d) Tính khoảng cách từ O đến (SAB).
GV: Hoàng Hữu Tài
HƯỚNG DẪN GIẢI VÀ ĐÁP SỐ
Câu 1.
a) Số hạng tổng quát
1
( 1) 5 ( 1).3 3 8
n
u u n d n n
với
1n
b)
15
3.15 8 37u
Tổng 15 số hạng đầu của CSC là
1 15
15
15
15 5 37
240
22
uu
S

c) Giả sử 100 là số hạng thứ k. Khi đó:
1
( 1). 100
5 ( 1) 3 100
36
k
u u k d
k
k

Vậy 100 là số hạng thứ 36.
Câu 2.
a)
4
3
8
2
4
u
q
u
Ta có
22
3 1 1 1
. 4 .2 1u u q u u
b) Số hạng tổng quát
1 1 1
1
. 1.2 2 ( 1)
n n n
n
u u q n
c)
66
71
. 1.2 64u u q
Tổng 7 số hạng đầu của CSN là
77
1
7
(1 ) 1.(1 2 )
127
1 1 2
uq
S
q


.
Câu 3.
a)
2
2
2
2
21
1
2 1 1
lim lim
1
2 1 2
2
nn
nn
n
n




b)
44
34
12
lim( 2) lim 1n n n
nn



Ta có
4
limn
và
34
12
lim 1 1
nn



nên
44
34
12
lim( 2) lim 1n n n
nn




c)
3 4 3 4 3 4
lim lim lim lim 0
5 4 5 4 5
n n n n
nn
n




Câu 4.
GV: Hoàng Hữu Tài
a)
4
2 4 2
lim 3
2 4 2
x
x
x



b)
2
2
2
2
1
21
lim lim
1
2 1 2
2
xx
xx
x
x
x
 

c)
33
23
32
lim ( 3 2) lim 1
xx
x x x
xx
 



Ta có
3
lim
x
x


và
23
32
lim 1 1
x
xx




nên
3
23
32
lim 1
x
x
xx




d)
2
2 2 2
23
56
lim lim lim( 3) 2 3 1
22
x x x
xx
xx
x
xx



.
Câu 5.
a)
''
''
22
' 5 5 0 1 2 1 2y x x x x x x
b)
''
''
22
' 2 3 1 2 3 1 4 3y x x x x x
c)
' ' '
''
14
' 8 3 8 3 8 3 8. 3.1 3
2
y x x x x x x
xx
d)
'
'
( 2)(2 1) 2 (2 1) ( 2)(2 1) 1.(2 1) ( 2).2y x x x x x x x x
2 1 2 4 4 3x x x
Chú ý: Có thể khai triển rồi tính đạo hàm như sau:
'
'
2
( 2)(2 1) 2 3 2 4 3x x x x x
e)
''
'
'
22
5 2 2 3 5 2 2 3 5. 2 3 5 2 .2
52
23
2 3 2 3
x x x x x x
x
y
x
xx




22
10 15 10 4
19
2 3 2 3
xx
xx


f)
'
' 3 3
4
' ( 4) 4. 4 4 4 4y x x x x
g)
' ' '
2
1
' 2sin tan 2sin tan 2cos
cos
y x x x x x
x
h)
''
'
' 2cos 2 2. cos 2 2. 2 sin 2
2 2 2 2
y x x x x
2.2sin 2 4sin 2
22
xx

GV: Hoàng Hữu Tài
Câu 6.
Xét hàm số
3
( ) 2sin 1f x x
.
Ta có
3
(0) 2.0 1 1f
và
3
2.1 1 1
2
f



. Do đó
(0). 0
2
ff



Hàm số
3
( ) 2sin 1y f x x
liên tục trên đoạn
0;
2



Do đó phương trình
3
2sin 1 0x 
có ít nhất một nghiệm trong khoảng
0;1
.
Câu 7. S
A D
M O
B C
a) Vì tứ giác ABCD là hình vuông nên O là trung điểm của AC
SO là trung tuyến của tam
giác SAC. Hơn nữa SA = SC nên tam giác SAC là tam giác cân tại S. Do đó SO cũng là đường
cao của tam giác SAC. Suy ra
SO AC
.
Lập luận tương tự, ta có
SO BD
. Do đó
SO ABCD
.
b) Ta có
AC SO
và
AC BD
(tính chất 2 đường chéo vuông góc của hình vuông)
Nên
AC SBD
. Suy ra
SAC SBD
c) Vì
SO ABCD
nên
,d S ABCD SO
Áp dụng định lí Pytago vào các tam giác vuông ABC và SOA, ta có:
2 2 2 2
1 1 1 2
2 2 2 2
a
AO AC AB BC a a
Suy ra
2
2
22
2 14
2
22
aa
SO SA AO a



GV: Hoàng Hữu Tài
d) Gọi M là trung điểm của AB. Kẻ OH vuông góc với SM (H thuộc SM).
Vì
AB SO
và
AB OM
nên
AB SOM
, suy ra
AB OH
Mà
OH SM
nên OH vuông góc với (SAB).
Do đó
( ,( ))d O SAB OH
Ta có
11
22
OM BC a
Xét tam giác vuông SOM, ta có
2 2 2
1 1 1
OH OS OM

Vậy
2
7
30
a
OH
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GV: Hoàng Hữu Tài
TRUNG TÂM GDTX QUẢNG ĐIỀN
ĐỀ CƯƠNG ÔN THI HỌC KÌ II MÔN TOÁN - LỚP 11
Câu 1. Cho cấp số cộng (u ) , biết u  5  , d = 3. n 1
a) Viết số hạng tổng quát của CSC.
b) Tìm u và tính tổng 15 số hạng đầu tiên của CSC. 15
c) Số 100 là số hạng thứ bao nhiêu.
Câu 2. Cho cấp số nhân (u ) với u  4 và u  8 . n 3 4 a) Tính u và q. 1
b) Viết số hạng tổng quát của CSN.
c) Tính u và tổng 7 số hạng đầu của CSN. 7
Câu 3. Tính giới hạn các hàm số sau: 2 n  2n 1 3n  4n a) lim b) 4
lim(n n  2) c) lim 2 2  n 1 5n
Câu 4. Tính giới hạn các hàm số sau: x  2 2 x  2x 2 x  5x  6 a) lim lim c) 3
lim (x  3x  2) d) lim x4 x  b) 2 2
x 2x 1 x x2 x  2
Câu 5. Tìm đạo hàm của các hàm số sau: a) 2
y  5  x x b) 2
y  2x  3x 1
c) y  8 x  3x
d) y  (x  2)(2x 1) 5x  2    e) y y x
g) y  2sin x  tan x
h) y  2cos 2x    2x  f) 4 ( 4) 3  2 
Câu 6. Chứng minh rằng phương trình 3
2sin x 1  0 có ít nhất một nghiệm thuộc khoảng    0;    2 
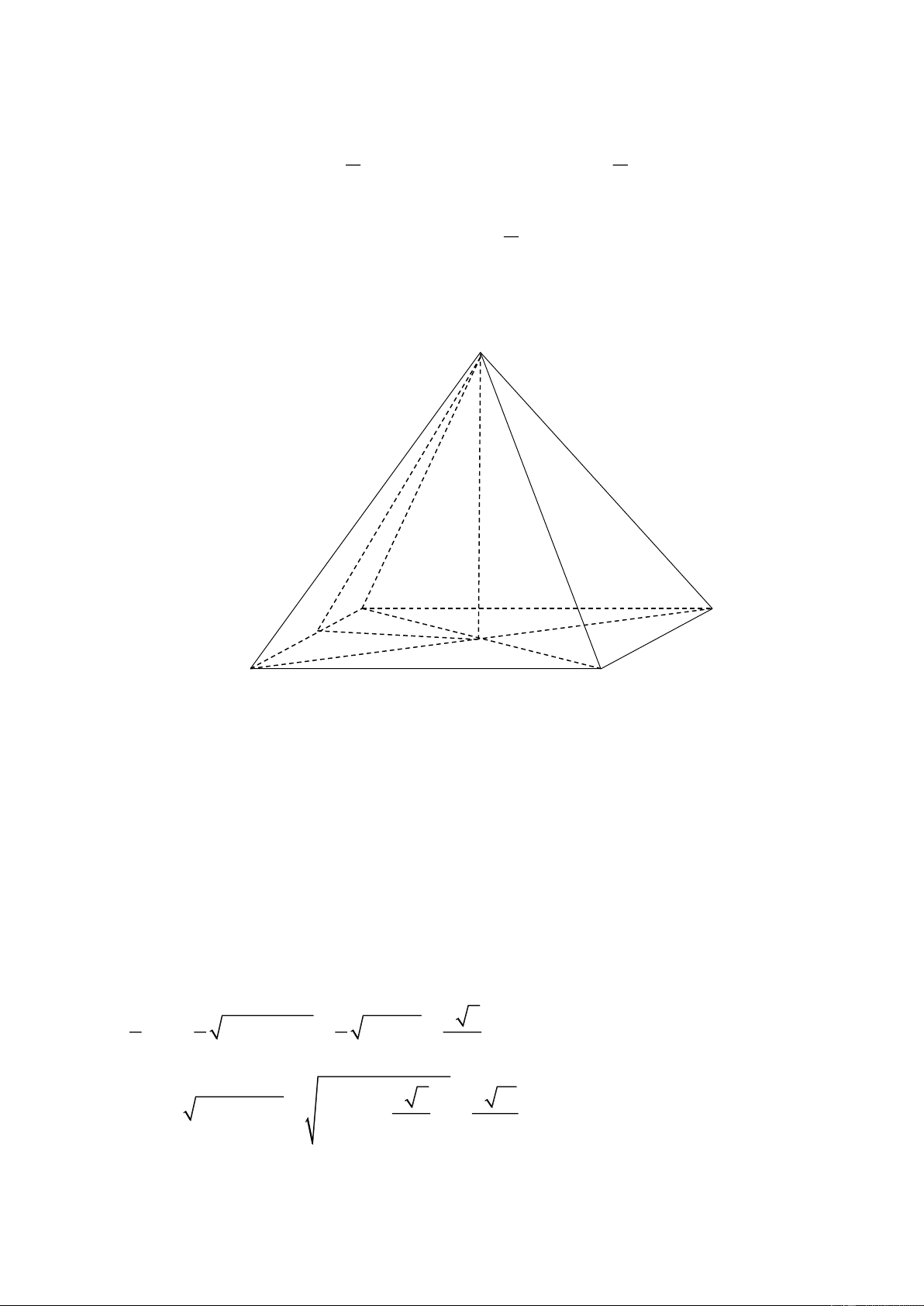
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, O là giao điểm của AC và
BD, cạnh bên SA SB SC SC  2a .
a) Chứng minh SO  (ABC ) D .
b) Chứng minh (SAC)  (SB ) D .
c) Tính khoảng cách từ S đến (ABCD)
d) Tính khoảng cách từ O đến (SAB). GV: Hoàng Hữu Tài
HƯỚNG DẪN GIẢI VÀ ĐÁP SỐ Câu 1.
a) Số hạng tổng quát u u  (n 1)d  5
  (n 1).3  3n  8 với n 1 n 1
b) u  3.15  8  37 15 15u u 15 5   37 1 15   
Tổng 15 số hạng đầu của CSC là S    240 15 2 2
c) Giả sử 100 là số hạng thứ k. Khi đó:
u u  (k 1).d  100 k 1  5
  (k 1)  3 100  k  36
Vậy 100 là số hạng thứ 36. Câu 2. u 8 a) 4 q    2 u 4 3 Ta có 2 2
u u .q  4  u .2  u  1 3 1 1 1    b) Số hạng tổng quát n 1 n 1 n 1
u u .q  1.2  2 (n  1) n 1 c) 6 6
u u .q  1.2  64 7 1 7 7 u (1 q ) 1.(1 2 )
Tổng 7 số hạng đầu của CSN là 1 S   127 . 7 1 q 1 2 Câu 3. 2 1   2 1 2 n  2n 1 1 a) lim  lim n n  2 2  n 1 1 2  2   2 n  1 2  b) 4 4
lim(n n  2)  lim n 1    3 4  n n   1 2   1 2  Ta có 4
limn   và lim 1  1   nên 4 4
lim(n n  2)  lim n 1      3 4  n n  3 4  n n n n n n 3n  4n  3   4    3   4  c) lim  lim        lim  lim  0     5n  4 5       4   5    Câu 4. GV: Hoàng Hữu Tài x  2 4  2 a) lim   3 x4 x  2 4  2 2  2 1 x  2x 1 b) lim  lim x  2
x 2x 1 x 1 2 2  2 x  3 2  c) 3 3
lim (x  3x  2)  lim x 1      2 3 x x  x x   3 2   3 2  Ta có 3
lim x   và lim 1     1    nên 3 lim x 1        x 2 3 x  x x  2 3 x  x x  2 x  5x  6
x  2x 3 d) lim  lim
 lim(x  3)  2  3  1  x2 x2 x2 x  2 x  . 2 Câu 5. ' ' ' ' a) y   2
x x      x   2 ' 5 5
x   0 1 2x  1 2x ' ' ' ' b) y   2
x x     2 ' 2 3 1
2x   3x    1  4x  3 ' ' ' ' ' 1 4
c) y '  8 x  3x  8 x   3x  8 x   3x  8.  3.1   3 2 x x d) y x x   x  ' ' ( 2)(2 1)
2 (2x 1)  (x  2)(2x 1)  1.(2x 1)  (x  2).2
 2x 1 2x  4  4x  3
Chú ý: Có thể khai triển rồi tính đạo hàm như sau:  x
x     x x  ' ' 2 ( 2)(2 1) 2 3 2  4x  3 '  5x  2  5x  2
2x  3  5x  2 2x  3
5. 2x  3  5x  2 .2 '  '     '     e) y       2x  3  2x 32 2x 32
10x 15  10x  4 19    2x  32 2x 32 ' ' 3 3 f) y   4 '
(x  4)   4. x  4  x  4  4 x  4 ' ' ' 1
g) y '  2sin x  tan x  2sin x  tan x  2cos x  2 cos x ' ' '              
h) y '  2cos 2x   2. cos 2x   2  . 2x  sin 2x              2     2    2   2         2  .2sin 2x   4  sin 2x       2   2  GV: Hoàng Hữu Tài Câu 6. Xét hàm số 3
f (x)  2sin x 1.       Ta có 3
f (0)  2.0 1  1  và 3 f  2.1 1 1  
. Do đó f (0). f  0    2   2     Hàm số 3 y f ( )
x  2sin x 1 liên tục trên đoạn 0;    2  Do đó phương trình 3
2sin x 1  0 có ít nhất một nghiệm trong khoảng 0;  1 . Câu 7. S A D M O B C
a) Vì tứ giác ABCD là hình vuông nên O là trung điểm của AC  SO là trung tuyến của tam
giác SAC. Hơn nữa SA = SC nên tam giác SAC là tam giác cân tại S. Do đó SO cũng là đường
cao của tam giác SAC. Suy ra SO AC .
Lập luận tương tự, ta có SO BD . Do đó SO   ABCD .
b) Ta có AC SO và AC BD (tính chất 2 đường chéo vuông góc của hình vuông)
Nên AC  SBD . Suy ra SAC   SBD
c) Vì SO   ABCD nên d S, ABCD  SO
Áp dụng định lí Pytago vào các tam giác vuông ABC và SOA, ta có: 1 1 1 a 2 2 2 2 2 AO AC AB BC a a  2 2 2 2 2   2 a 2 a 14 Suy ra 2 2 SO
SA AO  2a     2 2   GV: Hoàng Hữu Tài
d) Gọi M là trung điểm của AB. Kẻ OH vuông góc với SM (H thuộc SM).
Vì AB SO và AB OM nên AB  SOM  , suy ra AB OH
Mà OH SM nên OH vuông góc với (SAB). Do đó d( , O (SA ) B )  OH Ta có 1 1 OM BC a 2 2 1 1 1
Xét tam giác vuông SOM, ta có   2 2 2 OH OS OM 2 7a Vậy OH  30