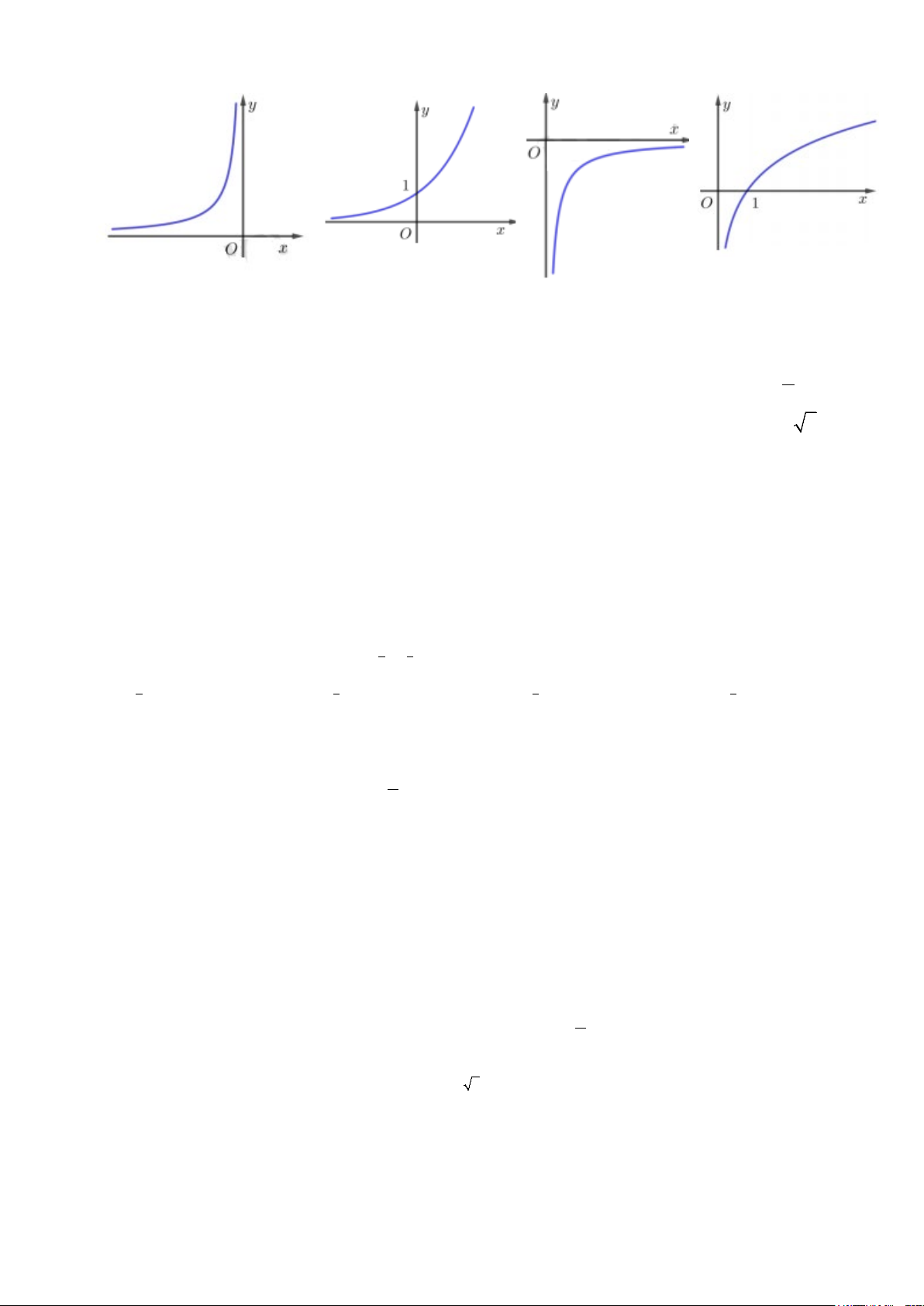

Preview text:
TRƯỜNG THPT PHAN ĐÌNH PHÙNG
ĐỀ KIỂM TRA GIỮA HỌC KỲ II TỔ: TOÁN – TIN NĂM HỌC 2024 - 2025 ĐỀ CHÍNH THỨC MÔN: TOÁN, KHỐI 11
(Đề kiểm tra có 03 trang)
Thời gian làm bài: 60 phút, không kể thời gian phát đề MÃ ĐỀ 844
Họ và tên học sinh: ………………………………… Số báo danh: …………
PHẦN 1: TRẮC NGHIỆM (5,0 điểm–Thời gian: 30 phút, mỗi câu hỏi học sinh chỉ chọn một phương án)
Câu 1. Theo số liệu thống kê đầu năm 2022, diện tích Thành phố Hà Nội là 2
3360 km và mật độ dân số là 2
2511 ngöôøi / km , tỉ lệ tăng dân số là r =1,4% . Biết rằng sau t năm tính từ đầu năm 2022, dân số Hà
Nội được tính theo công thức rt
S = A⋅e , trong đó A là số dân của năm lấy làm mốc. Giả sử tỉ lệ tăng dân
số r không đổi theo các năm, hỏi đến đầu năm bao nhiêu thì dân số của Hà Nội đạt ngưỡng 13 triệu người? A. 2053. B. 2051. C. 2050. D. 2052.
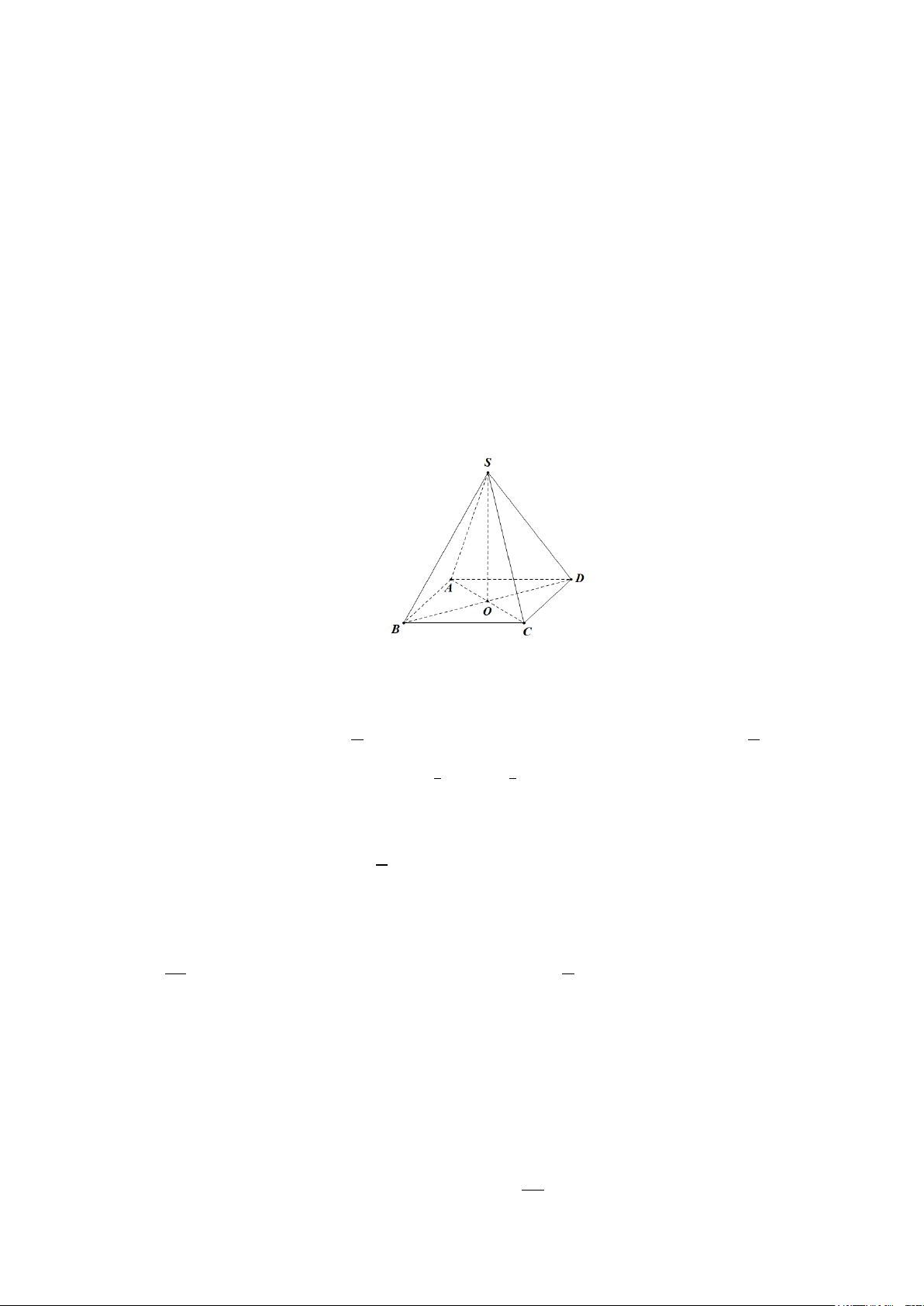
Câu 2. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng nhau (tham khảo hình vẽ bên dưới).
Số đo góc giữa hai đường thẳng SD và BC bằng A. 90 .° B. 60 .° C. 45 .° D. 30 .°
Câu 3. Nghiệm của phương trình log 2x +1 = 2 là 2 ( ) A. x = 4. B. 5 x = . C. x = 2. D. 3 x = . 2 2 4 1
Câu 4. Với những giá trị nào của a thì (a − )5 > (a − )2 1 1 ? A. a ∈(1;2). B. a > 2. C. a >1. D. a ∈(0; ) 1 . x
Câu 5. Tập xác định của hàm số 1 y = là 2
A. D = [1;+∞).
B. D = (1;+∞). C. D = .
D. D = (0;+∞).
Câu 6. Tập nghiệm T của phương trình 5x = 5 − là A. 1 T − = . B. T = {− } 1 . C. 1 T = . D. T = . ∅ 2 2
Câu 7. Cho số a >1. Mệnh đề nào sau đây là đúng?
A. Tập xác định của hàm số y = log x là a .
B. Tập giá trị của hàm số x
y = a là .
C. Tập giá trị của hàm số y = log x là a .
D. Tập xác định của hàm số x
y = a là (0;+∞).
Câu 8. Cho hai số dương x, y và hai số thực ,
m n . Đẳng thức nào sau đây là sai? m
A. ( m )n n m x = x . B. ( ⋅ )n n n
x y = x ⋅ y . C. x m−n = x . D. m n m n x x x + ⋅ = . n x Mã đề 844 Trang 1/3
Câu 9. Cho các số dương a,b,c và a ≠1. Đẳng thức nào sau đây là đúng? A. log bc = b⋅ c B. log bc = b − c a ( ) loga loga . a ( ) loga loga . C. log bc = b + c D. log bc = b + a a ( ) loga logc . a ( ) loga loga .
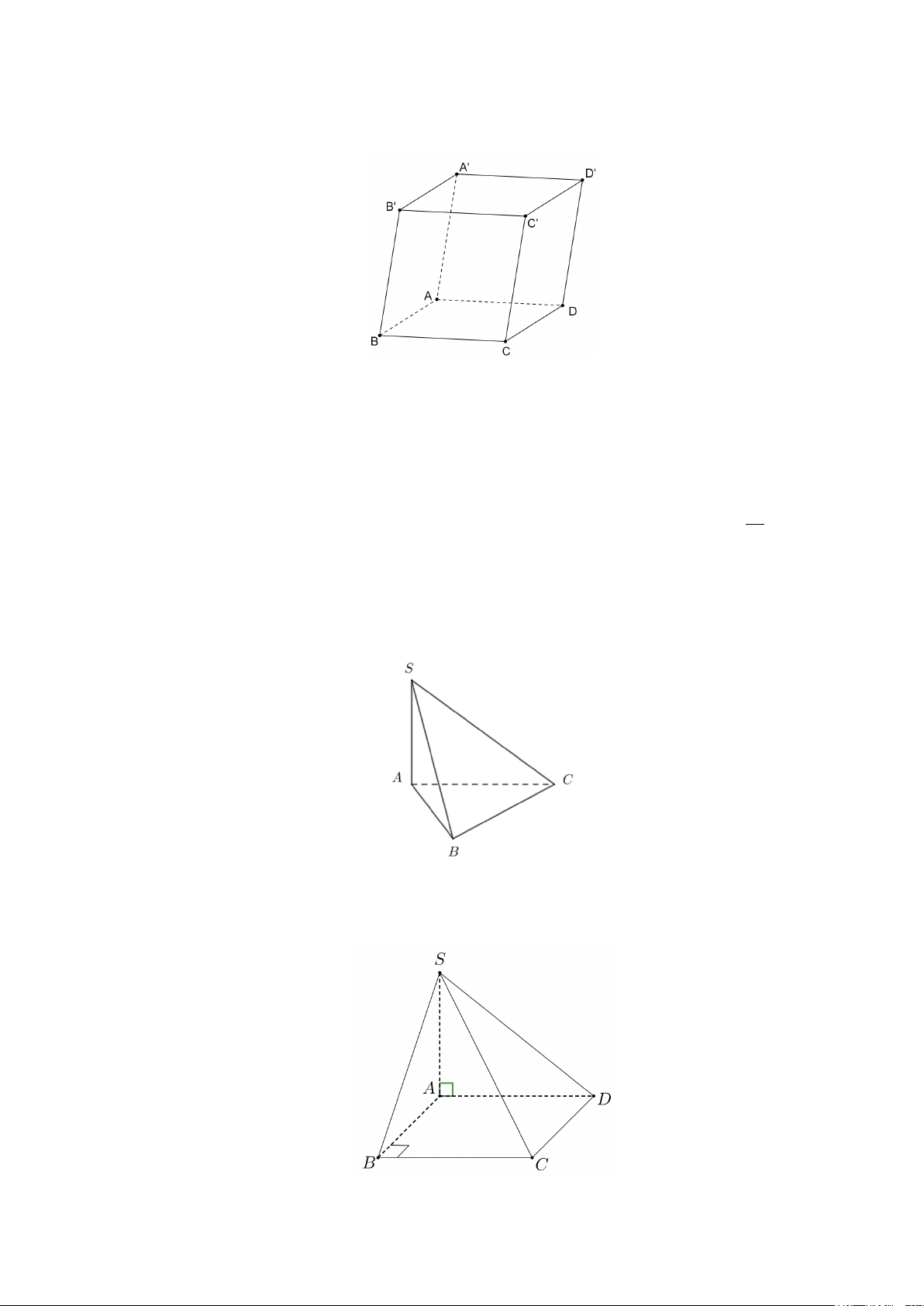
Câu 10. Cho hình hộp ABC . D A′B C ′ D
′ ′ có tất cả các cạnh bằng nhau (tham khảo hình vẽ bên dưới).
Mệnh đề nào sau đây là sai?
A. BB′ ⊥ B . D
B. A′C′ ⊥ B . D
C. A′B ⊥ C′ . D
D. BC′ ⊥ A′ . D
Câu 11. Tìm tất cả các giá trị của tham số m để hàm số y = ( 2 ln x − 2mx + )
1 xác định với mọi x∈ .
A. m∈(−∞ ) ;1 . B. m∈( 1; − ) 1 . C. m∈( ; −∞ − ) 1 ∪(1;+∞). D. m∈[ 1; − ] 1 . 3
Câu 12. Cho các số thực a,b lớn hơn 1 và thỏa mãn 2 8log + log b a b − b + = . Tính giá a 1 loga 2log 0 2 ( ) 2 a
trị biểu thức P = 4log a + log ab . 2 a ( ) A. P = 5. B. P = 2.
C. P =1+ 2log 3. 2 D. P = 3.
Câu 13. Cho hình chóp S.ABC có đáy là tam giác vuông tại A và SA ⊥ ( ABC) (tham khảo hình vẽ bên dưới).
Mệnh đề nào sau đây là đúng?
A. AB ⊥ (SBC).
B. AB ⊥ (SAC).
C. BC ⊥ (SAB).
D. BC ⊥ (SAC).
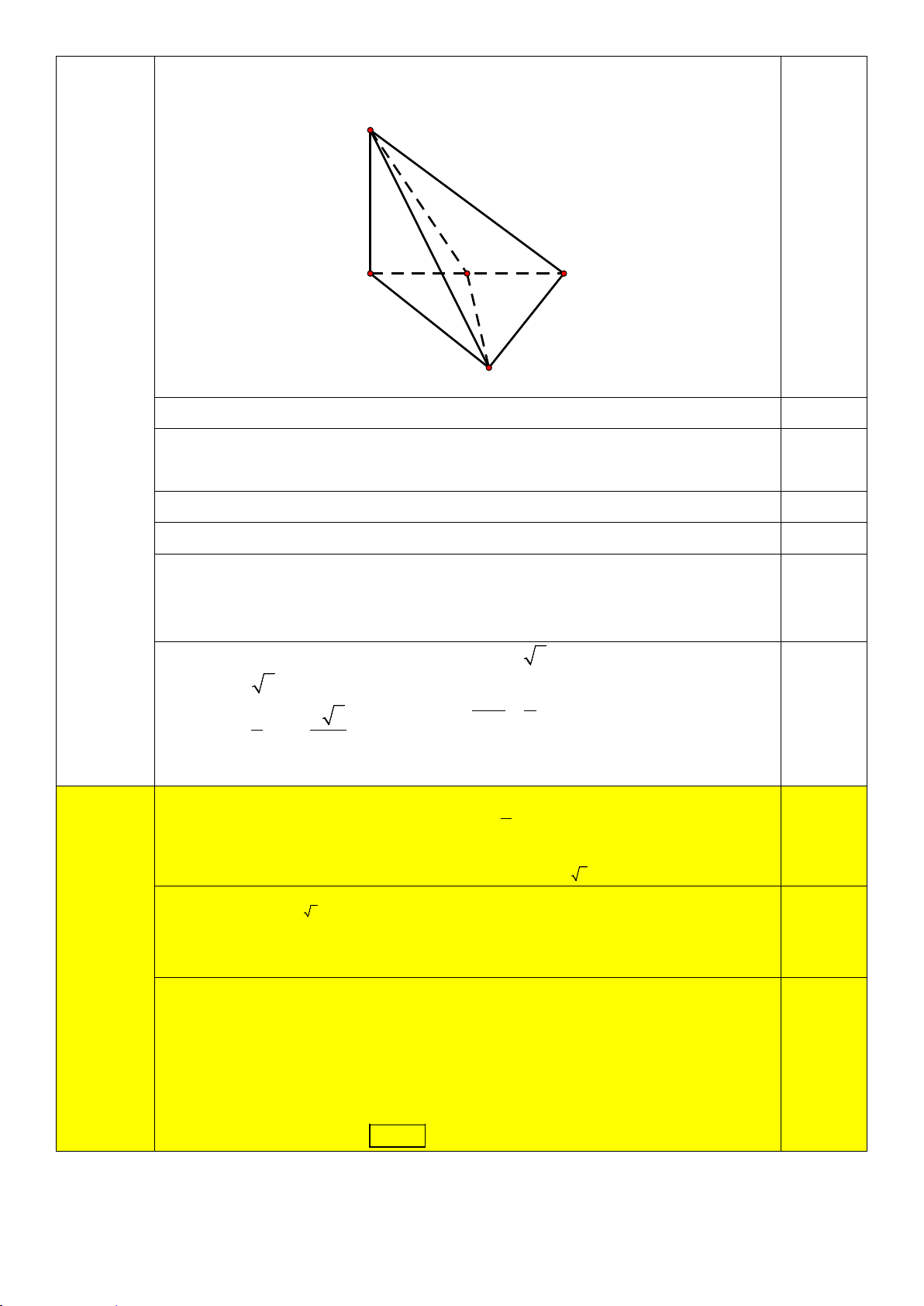
Câu 14. Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ ( ABCD) (tham khảo hình vẽ bên dưới).
Đường thẳng nào sau đây vuông góc với mặt phẳng (SAD)? A. . CD B. BC. C. AC. D. SC. Mã đề 844 Trang 2/3
Câu 15. Cho số a >1. Đồ thị hàm số x
y = a có dạng nào sau đây? A. B. C. D.
Câu 16. Số nghiệm của phương trình log ( 2
−x + 3x + 2 = log x −1 là 7 ) 7 ( ) A. 0. B. 2. C. 1. D. 3.
Câu 17. Cho số dương a khác 1. Đẳng thức nào sau đây là đúng? A. log a =
B. log a = a C. log a = = a 1. a . a 0. D. 1 log a a . a
Câu 18. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Tam giác SAB đều và SC = a 2 . Gọi
H, K lần lượt là trung điểm của AB,CD . Mệnh đề nào sau đây là sai?
A. BC ⊥ (SAB).
B. AB ⊥ (SAD).
C. SH ⊥ ( ABCD).
D. CD ⊥ (SHK ).
Câu 19. Trong không gian, mệnh đề nào sau đây là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại. 2 1
Câu 20. Cho số dương a . Biểu thức 3 2 a ⋅a bằng 7 1 4 1 A. 6 a . B. 3 a . C. 3 a . D. 6 a .
PHẦN 2: TỰ LUẬN (5,0 điểm – Thời gian làm: 30 phút) x
Câu 21 (1,0 điểm). Giải phương trình 1 1+2 = 3 x . 3
Câu 22 (1,0 điểm). Cho các số dương a,b khác 1 và thỏa mãn log b = . a 3
Tính giá trị biểu thức 4 2 2
P = 494log b + log ab 3 a a ( ).
Câu 23 (1,0 điểm). Đặt x = log 2 , hãy biểu diễn T = log 49 theo x . 7 28
Câu 24 (1,5 điểm). Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B và SA ⊥ ( ABC) .
a) Chứng minh tam giác SBC là tam giác vuông.
b) Biết rằng AB = AS = a , tính góc giữa đường thẳng SB với mặt phẳng (SAC). 2
x −(m+2)x
Câu 25 (0,5 điểm). Tìm giá trị của tham số m để phương trình 1 27 =
5 có hai nghiệm phân biệt 5
a và b thỏa mãn điều kiện ( log log a b b − b + = a ) 2log 4 0 a . ------- HẾT ------- Mã đề 844 Trang 3/3
TRƯỜNG THPT PHAN ĐÌNH PHÙNG
HƯỚNG DẪN CHẤM KIỂM TRA TỔ TOÁN – TIN
BÀI THI GIỮA KÌ II KHỐI 11
MÔN TOÁN NĂM HỌC 2024 - 2025
Thời gian làm bài : 60 Phút
Đáp án phần trắc nghiệm: Câu
Mã 841 Mã 842 Mã 843 Mã 844 1 D D A A 2 D A D B 3 B D A D 4 D B D B 5 C B C C 6 B C B D 7 B B B C 8 B C C A 9 A A C C 10 A C D A 11 C D B B 12 C C C B 13 C A B B 14 A A B A 15 C C C B 16 A D D C 17 D B B C 18 C A D B 19 B D C A 20 B B A A
Đáp án phần tự luận: Câu Nội dung Điểm x
Giải phương trình 1 1+2 = 3 x . 3 21 − x 1+2 ⇔ 3 = 3 x. 0,25
(1,0 điểm) ⇔ −x =1+ 2 .x 0,25 ⇔ 3 − x =1. 0,25 1 x − ⇔ = . Vậy 1 x − = là nghiệm duy nhất. 0,25 3 3
Cho các số dương a,b khác 1 và thỏa mãn log b = . a 3
Tính giá trị biểu thức 4 2 2
P = 494log b + log ab 3 . a a ( ) 22 4
(1,0 điểm) P = 494⋅ log b + (log a + 2log b)2 0,5 3 a a a 4
P = 494⋅ ⋅3+ (1+ 2⋅3)2 = 2025. 0,5 3
Đặt x = log 2 , hãy biểu diễn T = log 49 theo x . 7 28 log 49 7 T = log 28 0,25 7 2 Câu 23 T = 0,25 (1,0 điểm) log 4 + log 7 7 7 2 T = 2log 2 +1 0,25 7 2 T = 0,25 2x +1
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B và SA ⊥ ( ABC) .
a) Chứng minh tam giác SBC là tam giác vuông. S M A C B Câu 24
Do SA ⊥ ( ABC) nên SA ⊥ BC . 0,25
(1,5 điểm) Có BC vuông góc với S ,A AB, và SA cắt AB trong mặt phẳng (SAB) 0,5
nên suy ra BC ⊥ (SAB) .
Do BC ⊥ (SAB) nên suy ra BC ⊥ SB , vậy tam giác SBC vuông tại B . 0,25
b) Biết rằng AB = AS = a , tính góc giữa đường thẳng SB với mặt phẳng (SAC).
Gọi M là trung điểm AC , do tam giác ABC cân tại B nên BM ⊥ AC .
Từ đó chứng minh được M là hình chiếu của B trên (SAC). 0,25
Vậy góc giữa SB với (SAC) bằng góc BSM .
Có tam giác ABC vuông cân tại B nên AC = a 2 . SB = a 2 Có BM 1 a 2 nên 1 sin BSM = = , 0,25 BM = AC = SB 2 2 2
suy ra góc giữa SB với (SAC) bằng 30° . 2
x −(m+2)x
Tìm giá trị của tham số m để phương trình 1 27 = 5 có hai nghiệm phân 5
biệt a và b thỏa mãn điều kiện ( log log a b b − b + = a ) 2log 4 0 a . ( logab b − b + = ⇔ b − b + = ⇔
b = ⇔ b = a a ) 2 2 log 2log 4 0 log a a 4loga 4 0 loga 2
Vậy ta cần tìm m để phương trình 2
x − (m + 2) x + 27 = 0 có hai nghiệm a,b 0,25 Câu 25
dương, phân biệt, khác 1, và thỏa mãn 2 b = a .
(0,5 điểm) Giả sử phương trình có hai nghiệm a,b, theo định lý Viete, ta có:
a + b = m + 2
a + b = m + 2 a = 3 3 ab 27 a 27 b = ⇔ = ⇔ = 9 2 2 0,25 a = b a = b
m + 2 = 12 ⇔ m = 10
Thử lại m =10 , ta thấy phương trình 2
x −12x + 27 = 0 có hai nghiệm 3;9 thỏa
mãn yêu cầu bài toán. Vậy m =10 .
Xem thêm: ĐỀ THI GIỮA HK2 TOÁN 11
https://toanmath.com/de-thi-giua-hk2-toan-11
Document Outline
- Ma_de_844
- Hướng dẫn chấm Kiểm tra giữa HK2 khối 11 năm 2024-2025
- GK2 - 11





