














Preview text:
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
Chủ đề 9: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
A. TỌA ĐỘ ĐIỂM - VECTƠ y
I. Hệ trục toạ độ ĐỀ-CÁC trong mặt phẳng : j x'Ox : trục hoành i x x' y'Oy : trục tung O O : gốc toạ độ y'
i, j : véc tơ đơn vị ( i j 1 vaø i j )
Quy ước : Mặt phẳng mà trên đó có chọn hệ trục toạ độ Đề-Các vuông góc Oxy được gọi là mặt phẳng
Oxy và ký hiệu là : mp(Oxy)
II. Toạ độ của một điểm và của một véc tơ:
1. Định nghĩa 1: Cho M m (
p Oxy) . Khi đó véc tơ OM được biểu diển một cách duy nhất theo
y i, j bởi hệ thức có dạng : OM xi y j vôùi x,y . Q M j
Cặp số (x;y) trong hệ thức trên được gọi là toạ độ của điểm M. i ' x x O P
Ký hiệu: M(x;y) ( x: hoành độ của điểm M; y: tung độ của điểm M ) y' ñ / n
M(x; y) OM xi y j
Ý nghĩa hình học: y Q M y x ' x O x P
x OP vaø y=OQ ' y
2. Định nghĩa 2: Cho a mp(Oxy) . Khi đó véc tơ a được biểu diển một cách duy nhất theo
i, j bởi hệ thức có dạng : a a i a j vôùi a ,a . 1 2 1 2 Cặp số (a y
1;a2) trong hệ thức trên được gọi là toạ độ của véc tơ a . a e2
Ký hiệu: a (a ; a ) 1 2 e1 x ' x O ñ/ n P a=(a ;a ) a a i a j 1 2 1 2 y'
Ý nghĩa hình học: y B K B 2 A A 2 H x a ' x
A B vaø a =A B 1 1 1 2 2 2 O A B 1 1 y' 199
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
III. Các công thức và định lý về toạ độ điểm và toạ độ véc tơ :
Định lý 1: Nếu ( A x ; y ) vaø B(x ; y ) thì A A B B B(x ; y ) B B
AB (x x ; y y ) B A B A ( A x ; y ) A A
Định lý 2: Nếu a (a ;a ) vaø b (b ;b ) thì a 1 2 1 2 a b * 1 1 a b b a b 2 2
* a b (a b ;a b ) 1 1 2 2
* a b (a b ; a b ) 1 1 2 2
* k.a (ka ;ka ) (k ) 1 2
IV. Sự cùng phương của hai véc tơ: Nhắc lại
Hai véc tơ cùng phương là hai véc tơ nằm trên cùng một đường thẳng hoặc nằm trên hai đường thẳng song song .
Định lý về sự cùng phương của hai véc tơ:
Định lý 3 : Cho hai véc tơ a vaø b vôùi b 0 a a cuø
ng phöông b !k sao cho a k.b b
Nếu a 0 thì số k trong trường hợp này được xác định như sau: b
k > 0 khi a cùng hướng b a a b
k < 0 khi a ngược hướng b a 2 5 C k a b , b - a b 5 2 B A
Định lý 4 : , A B,C thaú ng haø
ng AB cuøng phöông AC
(Điều kiện 3 điểm thẳng hàng )
Định lý 5: Cho hai véc tơ a (a ;a ) vaø b (b ;b ) ta có : 1 2 1 2 a cuø
ng phöông b a .b a .b 0 (Điều kiện cùng phương của 2 véc tơ) 1 2 2 1 200
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
V. Tích vô hướng của hai véc tơ: Nhắc lại: y B . a b
a . b .cos( , a b) b b b 2 2 O a a x ' x A O a a a a b . a b 0
Định lý 6: Cho hai véc tơ a (a ;a ) vaø b (b ;b ) ta có : ' y 1 2 1 2 .
a b a b a b (Công thức tính tích vô hướng theo tọa độ) 1 1 2 2
Định lý 7: Cho hai véc tơ a (a ;a ) ta có : 1 2 2 2
a a a
(Công thức tính độ dài véc tơ ) 1 2
Định lý 8: Nếu ( A x ; y ) vaø B(x ; y ) thì A A B B 2 2
AB (x x ) (y y ) (Công thức tính khoảng cách 2 điểm) B A B A
Định lý 9: Cho hai véc tơ a (a ;a ) vaø b (b ;b ) ta có 1 2 1 2
a b a b a b 0 (Điều kiện vuông góc của 2 véc tơ) 1 1 2 2
Định lý 10: Cho hai véc tơ a (a ;a ) vaø b (b ;b ) ta có 1 2 1 2 . a b a b a b 1 1 2 2 cos( , a b)
(Công thức tính góc của 2 véc tơ) 2 2 2 2 a . b
a a . b b 1 2 1 2
VI. Điểm chia đoạn thẳng theo tỷ số k:
Định nghĩa: Điểm M được gọi là chia đoạn AB theo tỷ số k ( k 1 ) nếu như : MA k.MB A M B
Định lý 11 : Nếu (
A x ; y ) , B(x ; y ) và MA k.MB ( k 1 ) thì A A B B x k.x A B x M 1 k y k.y A B y M 1 k 201
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN x x A B x M Đặc biệt : 2
M là trung điểm của AB y y A B y M 2
VII. Một số điều kiện xác định điểm trong tam giác : A x x x A B C xG G . 1 l G a t øroïng t aâm t am g iaù c A B C G
A GB GC 3 0 y y y C B A B C yG 3 A AH BC AH.BC 0 H 2. H laø tröïc taâm tam giaù c ABC
A C BH AC BH.AC 0 B ' AA BC 3. ' A laø chaân ñöôø ng cao keû töø A C B A' '
BA cuøng phöông BC A IA=IB 4. I laø taâm ñöôø ng troø n ngoaïi tieáp tam giaù c ABC IA=IC I B C AB 5. D laø chaân ñöôø ng phaân giaù c trong cuû a goù c A cuû a ABC DB .DC AC A AB 6. ' ' D B ' D laø chaân ñöôø ng phaân giaù c ngoaø i cuû a goù c A cuû a ABC .D C AC A AB C 7. J laø taâm ñöôø ng troø n noäi tieáp A BC JA .JD B D BD J C B. ĐƯỜNG THẲNG D B
I. Các định nghĩa về VTCP và VTPT (PVT) của đường thẳng: ñn a
a là VTCP của đường thẳng ( ) 0
a coù giaù song song hoaëc truøng vôùi ( ) ñn n
n là VTPT của đường thẳng ( ) 0
n coù giaù vuoâng goùc vôùi ( ) a n a () * Chú ý: ()
Nếu đường thẳng ( ) có VTCP a (a ;a ) thì có VTPT là n (a ;a ) 1 2 2 1
Nếu đường thẳng ( ) có VTPT n ( ;
A B) thì có VTCP là a ( ; B A) 202
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
II. Phương trình đường thẳng :
1. Phương trình tham số và phương trình chính tắc của đường thẳng :
a. Định lý : Trong mặt phẳng (Oxy). Đường thẳng ( ) qua M0(x0;y0) và nhận a (a ;a ) làm 1 2 VTCP sẽ có : y
x x t.a 0
Phương trình tham số là : () : 1 (t ) a
y y t.a 0 2 M (x; y) x O x x y y
M ( x ; y ) 0 0 0
Phương trình chính tắc là : 0 0 () : a ,a 0 1 2 a a 1 2
2. Phương trình tổng quát của đường thẳng :
a. Phương trình đường thẳng đi qua một điểm M0(x0;y0) và có VTPT n ( ; A B) là: y n M ( ; x y) x O
M ( x ; y ) 0 0 0 () : (
A x x ) B(y y ) 0 ( 2 2 A B 0 ) 0 0
b. Phương trình tổng quát của đường thẳng :
Định lý :Trong mặt phẳng (Oxy). Phương trình đường thẳng ( ) có dạng : n y ( ; A B)
M (x ; y ) 0 0 0 Ax + By + C = 0 với 2 2 A B 0 x O
a (B; A)
a (B;A) Chú ý:
Từ phương trình ( ):Ax + By + C = 0 ta luôn suy ra được :
1. VTPT của ( ) là n ( ; A B)
2. VTCP của ( ) là a ( ; B A) hay a ( ; B A)
3. M (x ; y ) ( ) Ax By C 0 0 0 0 0 0
Mệnh đề (3) được hiểu là :
Điều kiện cần và đủ để một điểm nằm trên đường thẳng là tọa độ điểm đó
nghiệm đúng phương trình của đường thẳng . 203
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
3. Các dạng khác của phương trình đường thẳng :
a. Phương trình đường thẳng đi qua hai điểm A(xA;yA) và B(xB;yB) : x x y y (AB) : A A AB
x x (AB) : y y x x y ( ) : y A A B A B A y y A(x ; y ) y B(x ; y ) A A B B M (x; y) B(x ; y ) y A(x ; y ) B B A A A x x y y A B x A B x O x A(x ; y ) A A y B(x ; y ) B B B
b. Phương trình đường thẳng theo đoạn chắn:
Định lý: Trong mp(Oxy) phương trình đường thẳng ( ) cắt trục hoành tại điểm A(a;0) và trục tung tại điểm B(0;b) với a, b x y 0 có dạng: 1 a b
c. Phương trình đường thẳng đi qua một điểm M0(x0;y0) và có hệ số góc k:
Định nghĩa: Trong mp(Oxy) cho đường thẳng . Gọi (Ox,) thì k tg được gọi là hệ số góc của đường thẳng y
Định lý 1: Phương trình đường thẳng qua M (x ; y ) có hệ số góc k là : 0 0 0 y x O M ( ; x y) y0
x y - y = k(x - x ) (1) 0 0 O x0
Chú ý 1: Phương trình (1) không có chứa phương trình của đường thẳng đi qua M0 và vuông góc
Ox nên khi sử dụng ta cần để ý xét thêm đường thẳng đi qua M0 và vuông góc Ox là x = x0
Chú ý 2: Nếu đường thẳng có phương trình y ax b thì hệ số góc của đường thẳng là k a
Định lý 2: Gọi k1, k2 lần lượt là hệ số góc của hai đường thẳng , ta có : 1 2
// k k 1 2 1 2
k .k 1 1 2 1 2
c. Phương trình đt đi qua một điểm và song song hoặc vuông góc với một đt cho trước:
i. Phöông trinh ñöôøng thaúng ( ) //( ): Ax+By+C=0 coù daïng: Ax+By+m =0 1 1 ii. Phöông trinh ñöôø ng thaú ng ( ) ( ): Ax+By+C=0 coù daïng: Bx-Ay+m =0 1 2 204
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
Chú ý: m ; m được xác định bởi một điểm có tọa độ đã biết nằm trên ; 1 2 1 2 y
: Ax By m 0 1 1 y B x A y m : 0 1 2
: Ax By C 0 1 x O x0 x M 1 O x0 M 1 :A x B y C 0 1
III. Vị trí tương đối của hai đường thẳng : y y y 1 2 1 x x x O O O 1 2 2 // ca ét 1 2 1 2 1 2
Trong mp(Oxy) cho hai đường thẳng : ( ) : A x B y C 0 1 1 1 1
( ) : A x B y C 0 2 2 2 2
Vị trí tương đối của ( ) vaø ( ) phụ thuộc vào số nghiệm của hệ phương trình : 1 2
A x B y C 0
A x B y C 1 1 1 hay 1 1 1 (1) A x
B y C 0 A x B y C 2 2 2 2 2 2
Chú ý: Nghiệm duy nhất (x;y) của hệ (1) chính là tọa độ giao điểm M của ( ) vaø ( ) 1 2 Định lý 1: .
i Heä (1) voâ nghieäm ( ) //( ) 1 2 i . i Heä (1) coù
nghieäm duy nhaát ( ) caét ( ) 1 2 ii . i Heä (1) coù
voâ soá nghieäm ( ) ( ) 1 2
Định lý 2: Nếu A ;B ;C khác 0 thì 2 2 2 B .
i ( ) caét ( ) A1 1 1 2 A B 2 2 A B C i . i ( ) // ( ) 1 1 1 1 2 A B C 2 2 2 B C ii .
i ( ) ( ) A1 1 1 1 2 A B C 2 2 2 205
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
IV. Góc giữa hai đường thẳng
1.Định nghĩa: Hai đường thẳng a, b cắt nhau tạo thành 4 góc. Số đo nhỏ nhất trong các số đo
của bốn góc đó được gọi là góc giữa hai đường thẳng a và b (hay góc hợp bởi hai
đường thẳng a và b). Góc giữa hai đường thẳng a và b đước kí hiệu là a,b
Khi a và b song song hoặc trùng nhau, ta nói rằng góc của chúng bằng 0 0
2. Công thức tính góc giữa hai đường thẳng theo VTCP và VTPT
a) Nếu hai đường thẳng có VTCP lần lượt là u v v thì u.v cos a, b cos u, v u . v
b) Nếu hai đường thẳng có VTPT lần lượt là n v n ' thì n.n' cos a, b cos n, n ' n . n '
( ) : A x B y C 0
Định lý : Trong mp(Oxy) cho hai đường thẳng : 1 1 1 1
( ) : A x B y C 0 2 2 2 2 Gọi ( 0 0
0 90 ) là góc giữa ( ) vaø ( ) ta có : 1 2 y A A B B 1 1 2 1 2 cos 2 2 2 2
A B . A B 1 1 2 2 x O 2 Hệ quả:
( ) ( ) A A B B 0 1 2 1 2 1 2
V. Khoảng cách từ một điểm đến một đường thẳng :
Định lý 1: Trong mp(Oxy) cho hai đường thẳng (): Ax By C 0 và điểm M (x ;y ) 0 0 0
Khoảng cách từ M đến đường thẳng
được tính bởi công thức: 0 () M 0 y H
Ax By C 0 0 d(M ; ) 0 x 2 2 A B O () 206
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN C. ĐƯỜNG TRÒN
I. Phương trình đường tròn:
1. Phương trình chính tắc:
Định lý : Trong mp(Oxy). Phương trình của đường tròn (C) tâm I(a;b), bán kính R là : y I (a; b) b 2 2 2
(C) : (x a) (y b) R (1) R M (x; y) x O a
Phương trình (1) được gọi là phương trình chính tắc của đường tròn
Đặc biệt: Khi I O thì 2 2 2
(C) : x y R
2. Phương trình tổng quát:
Định lý : Trong mp(Oxy). Phương trình : 2 2
x y 2ax 2by c 0 với 2 2
a b c 0
là phương trình của đường tròn (C) có tâm I(a;b), bán kính 2 2
R a b c
II. Phương trình tiếp tuyến của đường tròn:
Định lý : Trong mp(Oxy). Phương trình tiếp tuyến với đường tròn 2 2
M (x ; y )
(C) : x y 2ax 2by c 0 tại điểm M(x ; y )(C) là : 0 0 0 0 0 (C)
() : x x y y (
a x x ) b(y y ) c 0 0 0 0 0 I(a;b) ()
VI. Các vấn đề có liên quan:
1. Vị trí tương đối của đường thẳng và đường tròn: (C) (C) (C) I I I R R R H H M Định lý: M H M
() (C) d(I;) > R
() tieáp xuùc (C) d(I;) = R
() caét (C) d(I;) < R
Lưu ý: Cho đường tròn 2 2
(C) : x y 2ax 2by c 0 và đường thẳng : Ax By C 0. Tọa độ giao điềm
(nếu có) của (C) và ( ) là nghiệm của hệ phương trình: 2 2
x y 2ax 2by c 0 (1) (*) Ax
By C 0 (2)
Cách giải (*): Sử dụng phép thế
+ Rút x hoặc y từ (2) thay vào (1) để được phương trình 1 ẩn. 207
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
2. Vị trí tương đối của hai đường tròn : C C 1 C 1 C C 1 1 2 C C 2 2 I R R 1 2 R R R 1 I I 1 2 I R I 2 1 1 1 2 I I 1 I 2 2 2 C2 (C ) vaø
(C ) khoâng caét nhau I I > R R 1 2 1 2 1 2 (C ) vaø
(C ) caét nhau R R < I I < R R 1 2 1 2 1 2 1 2 (C ) vaø (C ) tieáp xuù c ngoaø
i nhau I I = R R 1 2 1 2 1 2 (C ) vaø (C ) tieáp xuù
c trong nhau I I = R R 1 2 1 2 1 2
Lưu ý: Cho đường tròn 2 2
(C) : x y 2ax 2by c 0
và đường tròn C 2 2
' : x y 2a ' x 2b ' y c ' 0 .
Tọa độ giao điểm (nếu có) của (C) và (C’) là nghiệm của hệ phương trình: 2 2 x
y 2ax 2by c 0 (1) (*) 2 2 x
y 2a'x 2b' y c' 0 (2)
Cách giải (*): Sử dụng phép cộng và phép thế.
+ Trừ vế với vế hai phương trình (1) và (2) để được phương trình 1 ẩn. Từ phương trình 1 ẩn tìm được rút x hoặc
y và thay vào (1) hoặc (2) để tiếp tục được phương trình 1 ẩn. Giải phương trình nầy ta sẽ được kết quả cần tìm.
D. RÈN LUYỆN KỸ NĂNG GIẢI TOÁN
I. CÁC BÀI TOÁN CƠ BẢN VỀ PHƯƠNG PHÁP TỌA ĐỘ
Bài 1. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng : x 2y 3 0 và hai điểm A1; 1 , B1; 2
1) Viết phương trình đường thẳng d đi qua A và song song với đường thẳng 1
2) Viết phương trình đường thẳng d đi qua B và vuông góc với đường thẳng 2
3) Viết phương trình đường thẳng AB 3
Bài 2. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có M ; 0 là trung điểm đoạn AC . Phương 2
trình các đường cao AH , BK lần lượt là 2x y 2 0 và 3x 4 y 13 0 . Xác định tọa độ các đỉnh của tam giác ABC .
Bài 3. Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD , đường thẳng BC có phương trình
x y 4 0 , điểm M 1;
1 là trung điểm của đoạn AD . Xác định tọa độ các đỉnh của hình chữ nhật ABCD ,
biết đường thẳng AB đi qua điểm E 1 ;1 . 208
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
Bài 4. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC . Điểm M 2;
0 là trung điểm của AB . Đường
trung tuyến và đường cao kẻ từ A lần lượt có phương trình 7x 2 y 3 0 và 6x y 4 0 . Viết phương trình đường thẳng AC .
Bài 5. Trong mặt phẳng với hệ tọa độ Oxy , cho hình thang vuông ABCD có 0
B C 90 . Phương trình các
đường thẳng AC và DC lần lượt là x 2y 0 và x y3 0. Xác định tọa độ các đỉnh của hình thang 3 3
ABCD , biết trung điểm cạnh AD là M ; . 2 2
Bài 6. Trong mặt phẳng Oxy, cho tam giác ABC biết A B 4 0; 1 ; 3; 0 ;C ;3 3
1) Tìm tọa độ điểm E sao cho AB BE
2) Tìm tọa độ điểm F sao cho AC CF
Bài 7. Trong mặt phẳng Oxy, cho điểm A 1
;1 và đường thẳng : x 2y 6 0 . Tìm tọa độ điểm M trên
đường thẳng sao cho AM 5.
Bài 8. Trong mặt phẳng Oxy, cho điểm A1;
2 và đường thẳng : x 2 y 1 0 . Tìm tọa độ điểm M trên
đường thẳng sao cho AM 2 2 .
Bài 9. Trong mặt phẳng Oxy, cho tam giác ABC biết A1; 2; B2;
1 . Tìm tọa độ điểm I thỏa mãn IA 4 và IB 2 .
Bài 10. Trong mặt phẳng Oxy, cho tam giác ABC biết A 4 ; 8 ; B5;
4 và đường thẳng : 3x y 4 0
Tìm tọa độ điểm M trên đường thẳng sao cho MA MB .
Bài 11. Trong mặt phẳng Oxy, cho tam giác ABC biết A 17 1 0;1 ; B ;
và đường thẳng : x 2 y 3 0 5 5
Tìm tọa độ điểm M trên đường thẳng sao cho MA AB .
Bài 12. Trong mặt phẳng Oxy, cho điểm A5; 4
và đường thẳng :3x y 4 0
Tìm tọa độ điểm A' đối xứng với điểm A qua đường thẳng .
Bài 13. Trong mặt phẳng Oxy, cho điểm A 2 ;0, B1
;1 và đường thẳng : x 3y 3 0 .
1) Viết phương trình đường thẳng d đi qua A và tạo với một góc 0 45 . 1
2) Viết phương trình đường thẳng d đi qua A và cách B một khoảng bằng 2 2 . 2 209
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
II. CÁC BÀI TOÁN CƠ BẢN VỀ HÌNH HỌC PHẲNG 1
Bài 1. Cho hình vuông ABCD . Gọi M là trung điểm của BC , N là điểm trên cạnh AC sao cho AN AC . 4
Chứng minh rằng tam giác DMN vuông tại N . Gợi ý chứng minh
Lấy điểm phụ F là trung điểm của DI sẽ giúp tìm ra lời giải bài toán.
Bài 2. Cho hình vuông ABCD . Gọi M là trung điểm của BC , N là điểm trên CD sao cho CN 2ND . Chứng minh 0 MAN 45 . Gợi ý chứng minh
Cách 1: Chứng minh A DN ∽
AHM , từ đó sẽ suy ra được đpcm.
Cách 2: Tính độ dài ba cạnh của tam giác AMN theo a (cạnh hình vuông).
Áp dụng định lý Côsin vào tam giác AMN sẽ được đpcm.
Bài 3. Cho hình chữ nhật ABCD . Gọi H là hình chiếu vuông góc của B trên đường chéo AC . Các điểm M, K
lần lượt là trung điểm của AH và DC . Chứng minh rằng BM KM . Gợi ý chứng minh
Lấy điểm phụ E là trung điểm của BH sẽ giúp tìm ra lời giải bài toán. 210
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
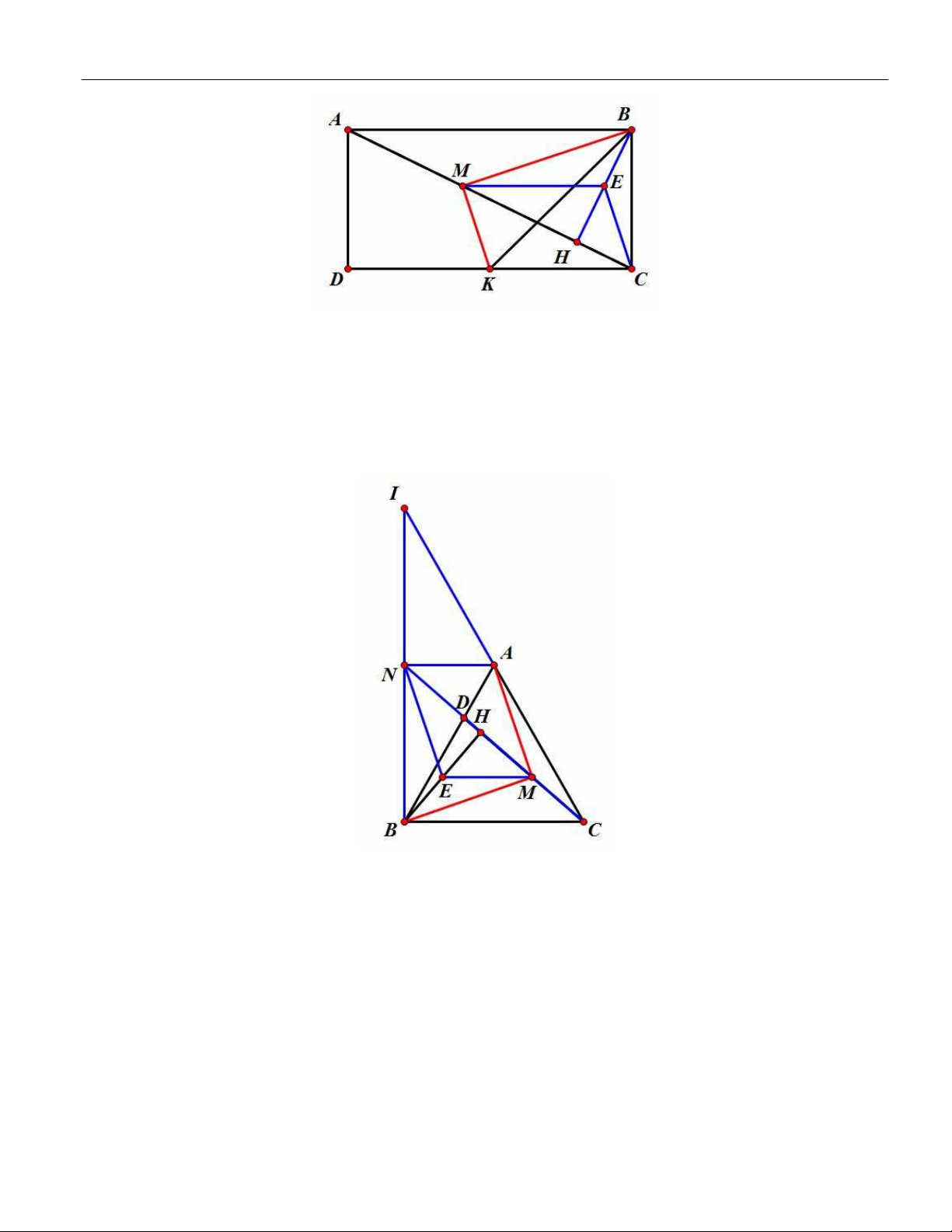
Bài 4. Cho tam giác ABC cân tại A . Gọi D là điểm trên cạnh AB sao cho AB 3AD và H là hình chiếu
vuông góc của B trên CD , M là trung điểm của HC . Chứng minh rằng AM BM . Gợi ý chứng minh
Gọi N, I là giao điểm của đường thẳng qua B vuông góc với BC với các đường thẳng CD,CA
Chứng minh tứ giác NAME là hình bình hành và E là trực tâm tam giác NBM sẽ suy ra được đpcm.
Bài 5. Cho hình chữ nhật ABCD . Gọi M là điểm đối xứng của B qua C , N là hình chiếu vuông góc của B
trên đường thẳng MD . Chứng minh rằng AN CN . Gợi ý chứng minh
Tứ giác BCND và tứ giác ABCN nội tiếp sẽ giúp ta tìm ra lời giải bài toán. 211
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
Bài 6. Cho tam giác ABC cân tại A , D là trung điểm đoạn AB . I , E lần lượt là tâm đường tròn ngoại tiếp tam
giác ABC , trọng tâm tam giác ADC và G là giao điểm của AI và CD . Chứng minh rằng DG IE . Gợi ý chứng minh
Chứng minh G là trực tâm tam giác DEI
Bài 7. Cho hình vuông ABCD . Gọi M, N lần lượt là trung điểm của các cạnh AB, BC . Gọi I là giao điểm của
CM và DN . Chứng minh rằng AI AD . Gợi ý chứng minh
Lấy điểm phụ P là trung điểm của DC sẽ giúp tìm ra lời giải bài toán.
Bài 8. Cho hình thang vuông ABCD 0
A D 90 và DC 2AB, H là hình chiếu của D trên đường chéo
AC , M là trung điểm của đoạn thẳng HC . Chứng minh rằng BM MD . Gợi ý chứng minh 212
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
Lấy điểm phụ E là trung điểm của DH sẽ giúp tìm ra lời giải bài toán.
Bài 9. Cho hình thang vuông ABCD 0
A B 90 và BC 2AD , H là hình chiếu vuông góc của điểm B trên
cạnh CD , M là trung điểm của đoạn thẳng BC . Chứng minh rằng AH MH . Gợi ý chứng minh
Tứ giác BDHM và tứ giác AHMD nội tiếp sẽ giúp ta tìm ra lời giải bài toán.
Bài 10: Cho tam giác ABC nội tiếp đường tròn O, R, phân giác trong của góc A cắt BC tại D , tiếp tuyến tạI
A với đường tròn cắt BC tại E . Chứng minh tam giác ADE cân tại E .
Bài 11: Cho hình vuông ABCD có điểm M là trung điểm của đoạn AB và N là điểm thuộc đoạn AC sao cho
AN 3NC . Tính độ dài đoạn IN biết rằng MN 10 .
Bài 12: Cho tam giác nhọn ABC nội tiếp đường tròn ,
O R, H là trực tâm tam giác, AH cắt BC tại K và cắt
đường tròn tại D . Chứng minh K là trung điểm của HD .
Bài 13: Cho tam giác nhọn ABC nội tiếp đường tròn O, R, M, N là chân các đường cao kẻ từ đỉnh B và C .
Gọi I, J lần lượt là giao điểm của BM,CN với đường tròn. Chứng minh AO IJ .
Bài 14: Cho hình vuông ABCD . M là một điểm tùy ý trên đường thẳng BD M B, M D, H, K lần lượt là
hình chiếu vuông góc của M trên các đường thẳng AB, AD . Chứng minh rằng CM HK .
Bài 15: Cho tam giác ABC nội tiếp đường tròn ,
O R, K là tâm đường tròn nội tiếp tam giác, AK cắt đường
tròn O, R tại D . Chứng minh rằng DB DC DK 213
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN
III. CÁC BÀI TOÁN THI CĐ - TSĐH NĂM 2014. Bài 1. (CĐ)
Trong mặt phẳng với hệ tọa độ Oxy , cho điểm (
A 2;5) và đường thẳng (d ) : 3x 4 y 1 0 . Viết phương trình
đường thẳng đi qua A và vuông góc với (d) . Tìm tọa độ điểm M thuộc (d) sao cho AM 5. Đáp án Bài 2. (ĐH-K.D)
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có chân đường phân giác trong của góc A là điểm D(1; 1
) . Đường thẳng AB có phương trình 3x 2y 9 0 , tiếp tuyến tại A của đường tròn ngoại tiếp tam giác
ABC có phương trình x 2 y 7 0 . Viết phương trình đường thẳng BC . Đáp án Bài 3. (ĐH-K.B)
Trong mặt phẳng với hệ tọa độ Oxy , cho hình bình hành ABCD . Điểm M ( 3
;0) là trung điểm của cạnh AB , điểm
H (0; 1) l hình chiếu vuông góc của B trên AD và điểm 4 G ;3
là trọng tâm tam giác BCD. Tìm tọa độ 3
các điểm B và D . Đáp án 214
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN Bài 4. (ĐH-K.A)
Trong mặt phẳng với hệ tọa độ Oxy , cho hình vuông ABCD có điểm M là trung điểm của đoạn AB và N là
điểm thuộc đoạn AC sao cho AN 3NC . Viết phương trình đường thẳng CD , biết rằng M (1;2) và N(2;1) . Đáp án 215
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN VI. CÁC DẠNG TOÁN THI
Dạng 1: Tìm tọa độ điểm thỏa mãn điều kiện cho trước.
Bài toán tổng quát: Tìm điểm M : ax by c 0 thỏa điều kiện cho trước. Phương pháp 1
B1. Đặt tọa độ cho điểm M . a mc b mc M ; m ,b 0 hoặc M ; m ,a 0 b a
B2. Khai thác tính chất hình học của điểm M . + Tính đối xứng + Khoảng cách + Góc
+ Quan hệ song song, vuông góc
+ Tính chất của điểm và đường đặc biệt trong tam giác. + Tam giác đồng dạng
+ Ba điểm thẳng hàng, hai vectơ cùng phương
Chuyển tính chất hình học sang phương trình với ẩn m . Giải phương trình tìm m M . Phương pháp 2
B1. Xem điểm M là giao điểm của hai đường (đường thẳng, đường tròn).
B2. Lập phương trình các đường. Giải hệ tìm M .
Ví dụ 1. Cho điểm A 1;3 và đường thẳng có phương trình x 2y 2 0 . Dựng hình vuông ABCD sao cho
hai đỉnh B, C nằm trên và các tọa độ đỉnh C đều dương. Tìm tọa độ các đỉnh B, C, D. Bài giải
Đường thẳng (d) đi qua A và vuông góc với có phương trình: 2x y m 0
A 1;3 2 3 m 0 m 1
Suy ra: d : 2x y 1 0 x 2y 2 x 0
Tọa độ B là nghiệm của hệ phương trình: B0; 1 2x y 1 y 1
Suy ra: BC AB 1 4 5 C x 2y 2 0 x 2y 2
Đặt C x ; y với x , y 0 , ta có: 0 0 0 0 0 0 0 0 BC 5 x y 2 1 5 x y 2 2 2 1 5 0 0 0 0 216
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN x 2 x 2
Giải hệ này ta được: 0 C 2; 2 y hoặc 0 2 y (loại). Suy ra: 0 0 0 x 2 1 0 x 1
Do ABCD là hình vuông nên: CD BA D D 1;4 y 2 3 1 y 4 D D D Vậy B0
;1 , C 2; 2, D1;4
Ví dụ 2. Trong mặt phẳng Oxy, cho tam giác ABC vuông tại A. Biết A 1;4, B1; 4
và đường thẳng BC đi qua điểm 1 I 2;
. Tìm tọa độ đỉnh C. 2 Bài giải
Phương trình đường thẳng BC: 9x 2y 17 0 AB 2;8
Do C BC nên ta có thể đặt 9c 17 C c;
, ta có 9c 25 2 AC c 1; 2 9c 25
Theo giả thiết tam giác ABC vuông tại A nên: AB.AC 0 c 1 4. 0 c 3 2 Vậy C3;5.
Ví dụ 3. Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có diện tích bằng 12, 9 3 I ;
và tâm của hình chữ 2 2
nhật là M 3;0 là trung điểm của cạnh AD. Tìm tọa độ các đỉnh của hình chữ nhật. Bài giải 9 9
Do MI là đường trung bình của tam giác ABD nên AB 2MI 2 3 2 4 4 12 Vì S AB.AD 12 nên AD 2 2 MA MD 2 ABCD AB
Đường thẳng AD qua M 3;0 và nhận 3 3 IM ;
làm VTPT có phương trình là: 2 2 3 3
x 3 y0 0 x y3 0 2 2
Phương trình đường tròn tâm M bán kính R 2 là: 2 2 x 3 y 2
Tọa độ A và D là nghiệm của hệ phương trình: x y 3 0 y 3 x x 3 x 2 x 4 2 y 2 x 3 2 3 x2 2 2 y 1 y 1 Suy ra: ta chọn A 2 ;1 , D 4; 1
x 2x x 9 2 7
Vì I là trung điểm của AC nên: C I A C7;2 y 2y y 3 1 2 C I A 217
Tài liệu ôn thi môn Toán THPTQG HĐBM-TỔ TOÁN x 2x x 5
Vì I là trung điểm của BD nên: B I D B5;4 y 2y y 4 B I D
Vậy tọa độ các đỉnh của hình chữ nhật là A2
;1 , B5; 4,C7;2, D4; 1 .
Ví dụ 4. Trong mặt phẳng Oxy, cho tam giác ABC với A 2;4, B0;2 và trọng tâm G thuộc đường thẳng
3x y 1 0 . Hãy tìm tọa độ của C biết rằng tam giác ABC có diện tích bằng 3. Bài giải
Do G là trọng tâm của tam giác ABC nên: 1 1 S S .3 1 GAB ABC 3 3 x 2 y 4
Phương trình đường thẳng AB là: x y 2 0 2 2
Đặt G a;b , do G d:3x y1 0 nên 3a b 1 0, ta có: 1 1 S 1 .AB.d G, AB 1 .2 2.d G, AB 1 GAB 2 2 1 d G, AB 2 a b 2 1 2 2 a b 2 1 1 a
Tọa độ G là nghiệm của hệ: 3a b 1 3a b 1 a 1 2 a b 1 a b 3 1 b 2 b 2 1 1
Suy ra: G ; hoặc G 1;2 2 2 7 x 3x x x C G A B 7 9 Với 1 1 G ; thì 2 C ; 2 2 9 2 2 y 3y y y C G A B 2 x 3x x x 5 C G A B
Với G 1;2 thì C 5 ;0 y 3y y y 0 C G A B 7 9
Vậy có hai điểm C thỏa đề bài là : C 5
;0 và C ; . 2 2
Ví dụ 5. Trong mặt phẳng Oxy, cho đường thẳng d : x y 1 0 và đường tròn 2 2
C : x y 2x 4y 0 .
Tìm tọa độ điểm M thuộc đường thẳng (d) mà qua đó có thể kẻ được hai tiếp tuyến MA và MB với (C) (A,B là hai tiếp điểm) sao cho 0 AMB 60 . 218




