Đề giữa học kì 1 Toán 11 năm 2023 – 2024 trường THPT Marie Curie – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kì 1 môn Toán 11 năm học 2023 – 2024 trường THPT Marie Curie, quận 3, thành phố Hồ Chí Minh; đề thi gồm 01 trang, hình thức tự luận với 09 bài toán, thời gian làm bài 60 phút, có đáp án và thang điểm.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Thông tin:

2 trang 6 tháng trước

Tác giả:

Profile H. Phượng
ĐÁP ÁN KIỂM TRA GIỮA KÌ I - KHỐI 11 – NH 2023- 2024
N
Ộ
I DUNG
ĐI
M
N
Ộ
I DUNG
ĐI
M
Câu 1. (1.0 điểm)
a) Trên đường tròn lượng giác gốc
A
, biết góc lượng giác
,
OA OM
có số đo
410
. Hỏi điểm
M
nằm ở góc phần
tư thứ mấy?
410 360 50
Điểm
M
nằm ở góc phần tư thứ nhất.
b) Không dùng máy tính hãy tính giá trị
13
sin
6
.
13 1
sin sin
6 6 2
.
Câu 2. (1.0 điểm) Cho góc
thỏa mãn
3
cos
5
,
0
2
.
a) Tính giá trị
sin
.
Vì
0
2
nên
sin 0
.
(N)
(L)
2 2
4
sin
16
5
sin 1 cos
425
sin
5
b) Tính giá trị
cos 2
2
.
24
cos 2 sin2 2sin cos
2 25
Câu 3. (0.5 điểm) Chứng minh đẳng thức lượng giác sau
trong điều kiện biểu thức có nghĩa
2
1 cos 1
0
1 cos
sin
.
2 2
2 2
2 2
1 cos sin
1 cos sin
0
sin 1 cos sin 1 cos
VT
Câu 4. (0.5 điểm) Tìm tập xác định của hàm số
2003
cos 2004
sin
y x
x
.
Điều kiện:
sin 0 ,
x x k k
.
\ |D k k .
Câu 5. (1.0 điểm) Giải các phương trình lượng giác
a)
3
cos
2
x
cos cos 2 ,
6 6
x x k k
b)
sin cos 0
7
x os os
7 2
c c x
5
2
14
( )
9
2
14
x k
k
x k
Câu 6. (1.0 điểm) Cho dãy số
n
u
, biết
2 1
2
n
n
u
n
.
Số
167
84
là số hạng thứ bao nhiêu của dãy?
167 2 1 167
84 2 84
250
n
n
u
n
n
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0.5
Câu 7. (1.0 điểm) Cho cấp số cộng
n
u
có số hạng
tổng quát
3 1
n
u n .
a) Xác định ba số hạng đầu tiên của cấp số cộng
đó . Suy ra công sai
d
của cấp số cộng
n
u
.
1 2 3
4; 7; 10
u u u
2 1
3
d u u
b) Tính tổng 50 số hạng đầu tiên của cấp số cộng
đó.
50
50
2.4 49.3 3875
2
S
Câu 8. (1.0 điểm) Vào năm 2023, nhiệt độ trung
bình của thành phố A là
29,5
C
. Giả sử do biến
đổi khí hậu nên nhiệt độ trung bình của thành phố
A mỗi năm đều tăng lên khoảng
0,1
C
. Hãy ước
tính kể từ năm nào thì nhiệt độ trung bình của
thành phố A đạt từ
35
C
trở lên.
1
29,5 , 0,1
u C d C
35 29,5 1 .0,1 35
56
n n
u u n
n
1
u
là nhiệt độ năm 2023.
56
u
là nhiệt độ năm 2078.
Câu 9. (3.0 điểm) Cho hình chóp
.
S ABCD
,
,
M N
lần lượt là trung điểm các cạnh
,
SA AB
.
P
là điểm
nằm trên cạnh
SD
, sao cho
1
4
SP SD
.
a) Đường thẳng
MP
có nằm trên mặt phẳng
SAD
không? Giải thích vì sao?
M SA SAD
MP SAD
P SD SAD
b) Tìm giao tuyến của hai mặt phẳng
MNP
và
ABCD
.
M MNP ABCD
Trong
SAD
, gọi
E MP AD
E MP MNP
E MNP ABCD
E AD ABCD
ME MNP ABCD
c) Tìm giao điểm của đường thẳng
NP
và mặt
phẳng
SAC
.
Trong
ABCD
, gọi
O AC ND
.
SAC SND SO
Trong
SND
,
K NP SO
K NP
K NP SAC
K SAC
.
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
| 1/2
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐÁP ÁN KIỂM TRA GIỮA KÌ I - KHỐI 11 – NH 2023- 2024 NỘI DUNG ĐIỂM NỘI DUNG ĐIỂM Câu 1. (1.0 điểm)
Câu 7. (1.0 điểm) Cho cấp số cộng u có số hạng n
a) Trên đường tròn lượng giác gốc A , biết góc lượng giác
tổng quát u  3n  1 .  n
OA,OM  có số đo 410 . Hỏi điểm M nằm ở góc phần
a) Xác định ba số hạng đầu tiên của cấp số cộng tư thứ mấy?
0,25 đó . Suy ra công sai d của cấp số cộng u . n  410  360  50 Điểm 0,25 0,25
M nằm ở góc phần tư thứ nhất.
u  4; u  7; u  10  d u u  3 1 2 3 2 1 0,25 1 3
b) Tính tổng 50 số hạng đầu tiên của cấp số cộng
b) Không dùng máy tính hãy tính giá trị sin . 6 đó. 0,25 0,25 1 3   1 50 sin  sin  S  2.4 49.3 3875 50       . 0,25 0,25 6  6  2 2
Câu 8. (1.0 điểm) Vào năm 2023, nhiệt độ trung 3
Câu 2. (1.0 điểm) Cho góc thỏa mãn cos ,
bình của thành phố A là 29, 
5 C . Giả sử do biến 5
đổi khí hậu nên nhiệt độ trung bình của thành phố 0   .
A mỗi năm đều tăng lên khoảng 0,1C . Hãy ước 2
a) Tính giá trị sin.
tính kể từ năm nào thì nhiệt độ trung bình của
thành phố A đạt từ 3  5 C trở lên. Vì 0   nên sin 0 . 2
u  29, 5 C ,d  0,1C 1  0,25  4 sin (N) 0,25
u  35  u  29, 5  n 0,25 n n   1.0,1  35  16 2   2    5 sin 1 cos 0,25  n  56 0,25 25  4 sin  (L)
u là nhiệt độ năm 2023. u là nhiệt độ năm 2078.  5 1 56 0,25
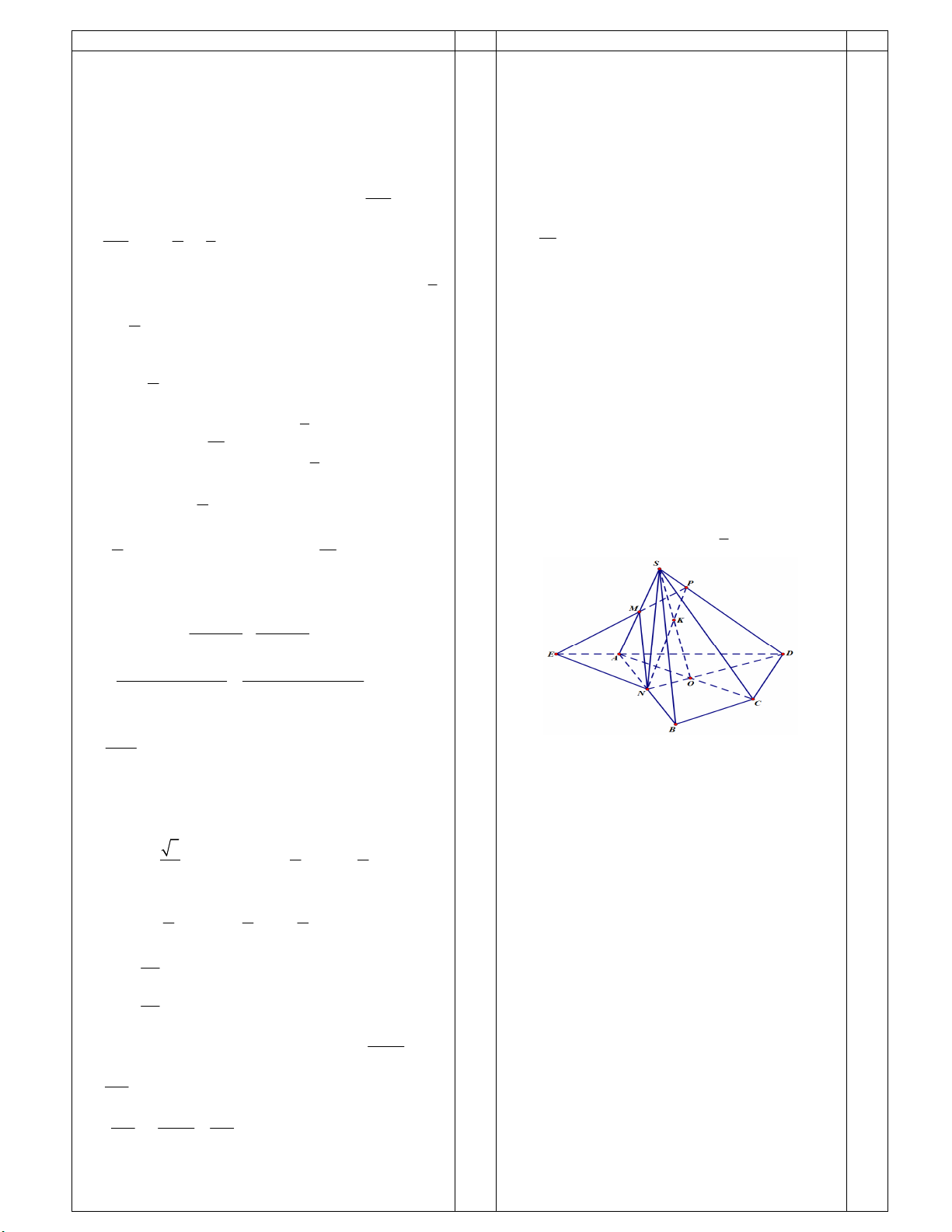
Câu 9. (3.0 điểm) Cho hình chóp .
S ABCD , M , N  b) Tính giá trị cos   2  .
lần lượt là trung điểm các cạnh SA, AB . P là điểm  2  1   24 0,25
nằm trên cạnh SD , sao cho SP SD . cos  2  sin
2  2 sincos   0,25 4  2  25
Câu 3. (0.5 điểm) Chứng minh đẳng thức lượng giác sau
trong điều kiện biểu thức có nghĩa 1  cos 1   0 . 2 sin 1  cos 0,25 2 2 1  2 2 1  cos  sin
cos  sin  0,25 VT    0 2
sin 1  cos 2
sin 1  cos
Câu 4. (0.5 điểm) Tìm tập xác định của hàm số 2003 y
 cos x  2004 .
a) Đường thẳng MP có nằm trên mặt phẳng sin x
SAD không? Giải thích vì sao? Điều kiện: sin x 0,25
 0  x k , k   . 0,25  0,25  D    \ k |k    . M SA   SAD
MP  SAD 0,25
Câu 5. (1.0 điểm) Giải các phương trình lượng giác P SD   SAD  0,5 3 0,25
b) Tìm giao tuyến của hai mặt phẳng MNP và a) cos x   cos x  cos  x    k  2 , k   2 6 6 0,25 ABCD .
M   MNP   ABCD  0,25 b) sin x  cos  0  cos  cos   x  7 7  2 
0,25 Trong SAD , gọi E MP AD 0,25  5  x    k  E MP   MNP  2 0,25  
E   MNP   ABCD 0,25   14 (k  ) E AD   ABCD   9 x    k  2   14
ME  MNP   ABCD 0,25 2n  1
Câu 6. (1.0 điểm) Cho dãy số u , biết u  .
c) Tìm giao điểm của đường thẳng NP và mặt n n n  2 phẳng SAC . 167 Số
là số hạng thứ bao nhiêu của dãy?
Trong  ABCD , gọi O AC ND . 84 167 2n  1 167
 SAC  SND  SO u    0,5 0,25 n 84 n  2 84
Trong SND , K NP SO 0,25  n  250 K   NP 0,25 0.5  
K NP  SAC . K  0,25  SAC 
Document Outline

  • Doc1
  • dap-an-kttt-k11-2023-2024-de-1_2510202382640