Đề giữa học kì 1 Toán 9 năm 2022 – 2023 phòng GD&ĐT Hà Đông – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề khảo sát chất lượng giữa học kì 1 môn Toán 9 năm học 2022 – 2023 phòng Giáo dục và Đào tạo quận Hà Đông, thành phố Hà Nội; đề thi gồm 01 trang với 05 bài toán dạng tự luận, thời gian học sinh làm bài thi là 60 phút (không kể thời gian phát đề); đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm. Mời bạn đọc đón xem.

44 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

5 trang 9 tháng trước

Tác giả:

Profile Hà Việt Anh
https://thcs.toanmath.com/de-thi-giua-hk1-toan-9
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
QUẬN HÀ ĐÔNG
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG GIỮA HỌC KÌ I
Năm học 2022 – 2023
Môn TOÁN 9
Bài
Ý
NỘI DUNG
Điểm
Bài 1
(2
điểm)
a
(1
điểm)
3
50
9 3 3 8 27
9
A
3
23
2
25.2
3 3 3 4.2 3
3
2
0,5
0,25
0,25
b
(1
điểm)
2
2 16
2 3 6
3
31
B
2
2 3 1
4
2 3 6
3
3 1 3 1

2 3 1
4
2 3 6.
2
3
(do
23
nên
2 3 2 3
)
2 3 3 1 8 3
1 8 3

0,5
0,25
0,25
Bài 2
(2
điểm)
a
(1
điểm)
5 9 9 2 4 4 1 36x x x
(Điều kiện:
1x 
)
5 9( 1) 2 4( 1) 1 36x x x
15 1 4 1 1 36x x x
12 1 36
13
19
8( )
x
x
x
x TM

Vậy phương trình có nghiệm duy nhất
8x
0,25
0,25
0,25
0,25
b
(1
điểm)
Với điều kiện
-1x
. Ta có
0,25
2
2
2
4 4 1 1
2 1 1
2 1 1
2 1 1
2 1 1
2
0
x x x
xx
xx
xx
xx
x TM
x TM
Vậy tập nghiệm của phương trình là
2;0S
0,25
0,25
0,25
Bài 3
(2,5
điểm)
a
(0,75
điểm)
Thay
9x
(TMĐK) vào biểu thức
B
ta có:
4 9 2
4 3 2
4.5
20
3 2 1
92
B
Vậy giá trị của
20B
tại
9x
.
0,25
0,5
b
(1,25
điểm)
2 2 4
4
22
2 2 4
22
22
x x x
A (x 0; x 4)
x
xx
x x x
xx
xx





2 2 2 2
4
4
2 2 2 2
x x x x
x
x
x x x x
4 4 4 4 4
4
x x x x x
x
48
4
xx
x
42
22
4
2
xx
xx
x
x

Vậy
4
2
x
A
x
với
(x 0; x 4)
0,25
0,25
0,25
0,25
0,25
3
c
(0,5
điểm)
Ta có
A
M
B
42
4
:
22
x
x
xx

42
22
42
x x x
xx
x

Với
0x
;
4x
thì
0M
Xét
2
1M M M M
Vì
0x
;
4x
thì
x -2
M = 0, M -1 = <0
x +2 x +2
,
2
0MM
2
M M M M
Vậy với
0x
;
4x
thì
MM
0,25
0,25
Bài 4
(3
điểm)
a
(1,5
điểm)
0,25
Xét
ABC
vuông tại
A
, đường cao
AH
. Ta có
2
. AH HB HC
(Hệ thức về cạnh và đường cao)
2
4.9 36
6 cm
AH
AH

.
Xét
ABH
vuông tại
H
có
6
tan
4
AH
ABH
BH

(Tỉ số lượng giác của góc nhọn)
56ABC
0,75
0,5
b
(1
điểm)
Xét
AHB
vuông tại
H
, đường cao
HD
. Ta có
2
. HB BD AB
(Hệ thức về cạnh và đường cao) (1)
Xét
AHC
vuông tại
H
, đường cao
HE
. Ta có
2
. HC CE AC
(Hệ thức về cạnh và đường cao) (2)
Xét
ABC
vuông tại
A
, đường cao
AH
. Ta có
2
. AH HB HC
(Hệ thức về cạnh và đường cao) (3)
Từ (1), (2) và (3) suy ra
4
. . .CE BD AC AB AH
0,25
0,25
0,25
0,25
I
4
c
(0,5
điểm)
Chứng minh I là trung điểm BC.
+) Chứng minh
AED
đồng dạng
ABC
(c.g.c)
AED B
(hai góc tương ứng)
Mà
90
o
BC
(gt)
90
o
AED EAI
(gt)
EAI C IAC
cân
IC IA
(đ/n) (*)
+) Chứng minh tương tự: IA = IB (**)
Từ (*), (**)
IC IB
Vậy I là trung điểm BC
0,25
0,25
Bài 5
(0,5
điểm)
Với x, y, z dương, chứng minh được:
1 1 4
x y x y

(1)
Dấu “=” xảy ra khi x = y
Ta có:
1 1 1
P =
2023
11
+
2023xz 2023yz z x y




Áp dụng bất đẳng thức (1)
2
1 1 1 4 1 4 1
P =
2023 2023 2023
2
16
2023
z x y z x y
x y z
P








Dấu “=” xảy ra khi
1
4
1
1
2
xy
xy
x y z
z
z x y





Vậy GTNN của
16
2023
P
khi
11
,
42
x y z
0,25
0,25
Ghi chú: Học sinh giải cách khác đúng cho đủ điểm theo từng phần
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

https://thcs.toanmath.com/de-thi-giua-hk1-toan-9
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN HÀ ĐÔNG
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG GIỮA HỌC KÌ I
Năm học 2022 – 2023 Môn TOÁN 9 Bài Ý NỘI DUNG Điểm Bài 1 a 50 3 A  9  3  3 8  27 (2 (1 9 điểm) điểm) 25.2 2 3 3  3  3  3 4.2  3 2 3 0,5  35 2  6 2 3 0,25 0,25 2 b B    2 2 16 2 3   6 (1 3 1 3 điểm)    2 2 3 1 4  0,5 2  3    3   1  3   6 1 3 2 3   1 4  2  3   6.
(do 2  3 nên 2  3  2  3 ) 2 3 0,25  2  3  3 18 3  0,25 1 8 3 a 5
9x  9  2 4x  4 
x 1  36 (Điều kiện: x  1  ) 0,25 Bài 2 (1
 5 9(x 1)  2 4(x 1)  x 1  36 điểm) (2 điểm)
 15 x 1  4 x 1  x 1  36 0,25  12 x 1  36 x 1  3 0,25 x 1  9  x  8(TM ) 0,25
Vậy phương trình có nghiệm duy nhất x  8 b Với điều kiện x -1. Ta có 0,25 (1 điểm) 2 2 4x 4x 1 x 1 0,25 2 2x 1 x 1 2x 1 x 1 2x 1 x 1 0,25 2x 1 x 1 x 2 TM 0,25 x 0 TM
Vậy tập nghiệm của phương trình là S 2;0 a Thay x
9 (TMĐK) vào biểu thức B ta có: 0,25 (0,75 4 9  2 43 2 điểm) 4.5 B     20 Bài 3 9  2 3  2 1 0,5 (2,5
Vậy giá trị của B  20 tại x  9 . điểm) b   (1,25 x 2 x 2 4x A   
(x 0; x 4) điểm) x  2 x  2 4  x x  2 x  2 4x    x  2 x  2
x 2 x 2 0,25
x 2 x 2  x 2 x 2 4x    
x  2 x  2  x  2 x  2 x  4 0,25
x  4 x  4  x  4 x  4  4x x  4 0,25 4x  8 x x  4
4 x x  2 0,25
  x 2 x 2 4 x0,25 x  2 4 x Vậy  A   x  với (x 0; x 4) 2 3 c 4  xx 2 4  A 4 x x  2 x Ta có M   :    (0,5 B x  2 x  2
x  2 4 x  2 x  2 điểm)
Với x  0 ; x  4 thì M  0 Xét 2
M M M M   1 0,25 x -2
Vì x  0 ; x  4  thì M = 0, M - 1 = < 0 , x + 2 x + 2 2
M M  0 0,25 2
M M M M
Vậy với x  0 ; x  4 thì M M Bài 4 (3 điểm) I 0,25 a (1,5 điểm) Xét ABC
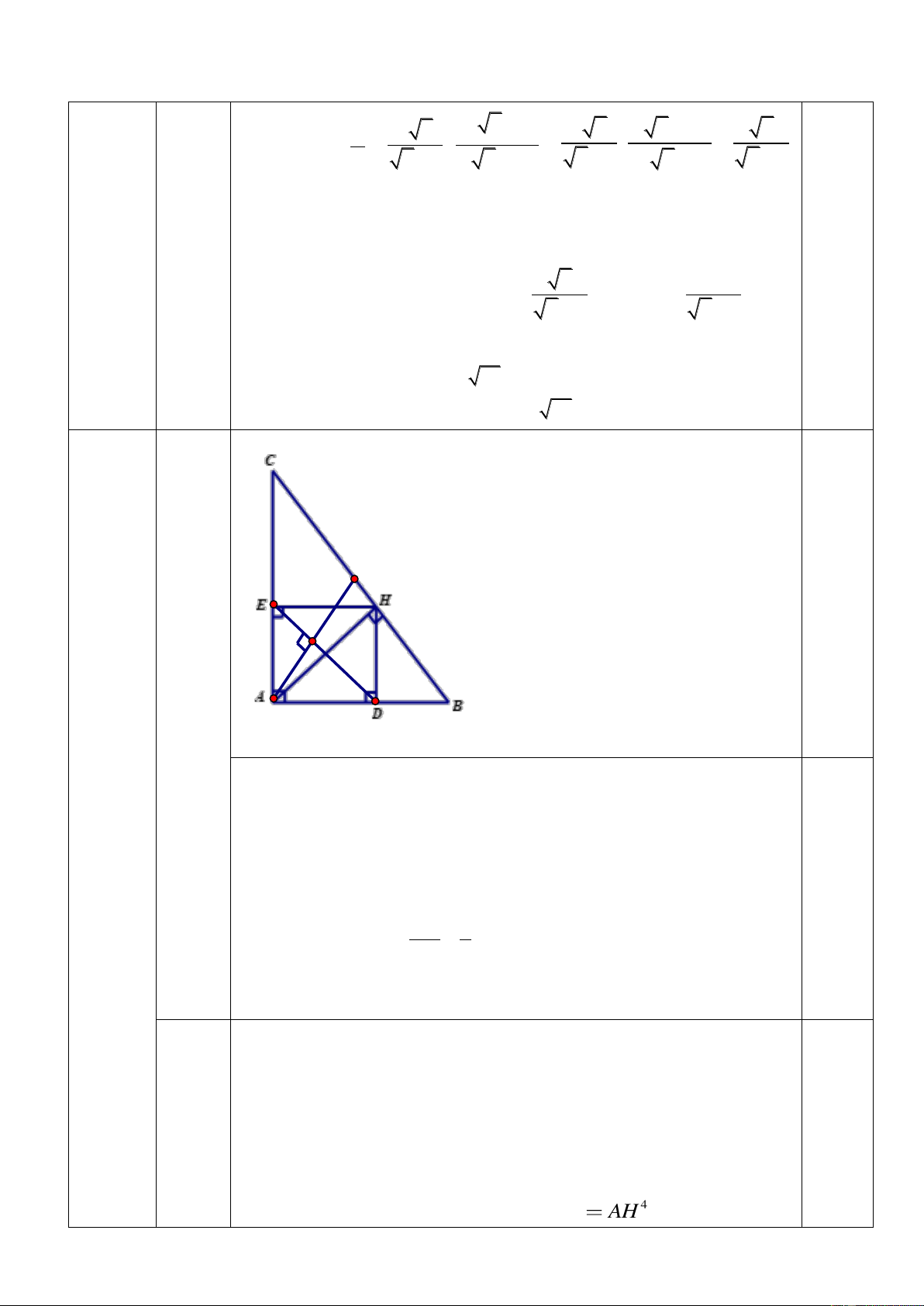
vuông tại A , đường cao AH . Ta có 2 AH H .
B HC (Hệ thức về cạnh và đường cao) 2  AH  4.9  36  0,75 AH  . 6cm Xét ABH  vuông tại H có AH 6 tan ABH
 (Tỉ số lượng giác của góc nhọn) BH 4  ABC  56 0,5 b Xét A
HB vuông tại H , đường cao HD . Ta có (1 2 HB B .
D AB (Hệ thức về cạnh và đường cao) (1) 0,25 điểm) Xét A
HC vuông tại H , đường cao HE . Ta có 2 0,25 HC C .
E AC (Hệ thức về cạnh và đường cao) (2) Xét ABC
vuông tại A , đường cao AH . Ta có 0,25 2 AH H .
B HC (Hệ thức về cạnh và đường cao) (3) 0,25 Từ (1), (2) và (3) suy ra 4 C . E B . D A . C AB AH 4 c
Chứng minh I là trung điểm BC. (0,5 +) Chứng minh AED  đồng dạng ABC  (c.g.c)
điểm) AED B (hai góc tương ứng) Mà   90o B C (gt) 0,25   90o AED EAI (gt)
EAI C I
AC cân  IC IA (đ/n) (*)
+) Chứng minh tương tự: IA = IB (**)
Từ (*), (**)  IC IB 0,25 Vậy I là trung điểm BC Bài 5
Với x, y, z dương, chứng minh được: (0,5 1 1 4 điể   m) x y x  (1) y
Dấu “=” xảy ra khi x = y 1 1 1  1 1  Ta có: P = +     2023xz 2023yz 2023z x y
Áp dụng bất đẳng thức (1) 1  1 1  4 1 4 1 P =        2 2023z x
y  2023z x y
2023  x y z     2  0,25 16  P  2023 1 x y x y     4     
Dấu “=” xảy ra khi x y z 1  1   0,25
z x y z    2 16 1 1 Vậy GTNN của P
khi  x y  , z  2023 4 2
Ghi chú: Học sinh giải cách khác đúng cho đủ điểm theo từng phần
Document Outline

  • https
  • HDC_ KSCL giữa kì 1_Toán 9