Đề giữa học kì 1 Toán 9 năm 2023 – 2024 trường Lương Thế Vinh – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra giữa học kì 1 môn Toán 9 năm học 2023 – 2024 trường THCS & THPT Lương Thế Vinh, thành phố Hà Nội. Mời bạn đọc đón xem.
Preview text:
ĐỀ KIỂM TRA GIỮA HỌC KÌ I Môn Toán Lớp 9 Năm học 2023 – 2024
TRƯỜNG THCS & THPT LƯƠNG THẾ VINH
Thời gian làm bài: 90 phút
Bài 1. (2,0 điểm) Thực hiện phép tính: a) 7 1 81 − 16 . b) ( − )2 7 4 + 7 . 9 2 c) 8 50 − 24 + . 12 . d) 1 1 + . 3 3 5 + 2 3 5 − 2 3
Bài 2. (1,5 điểm) Giải các phương trình sau: a) + 4(x x
− 3) + 9x − 27 =10 . b)
8 = x +2. c) 2x −4x+4 = 3x+1. x − 2 Bài 3. +
(2,5 điểm) Cho hai biểu thức x + 2 A = và x 20 1 6 B = + +
, với x ≥ 0; x ≠ 4 . x + 5 x − 4 x + 2 2 − x
a) Tính giá trị của biểu thức A khi x =16 . b) Chứng minh x − 3 B = . x + 2 c) Tìm x để 1 AB < . 2
Bài 4. (3,5 điểm) A
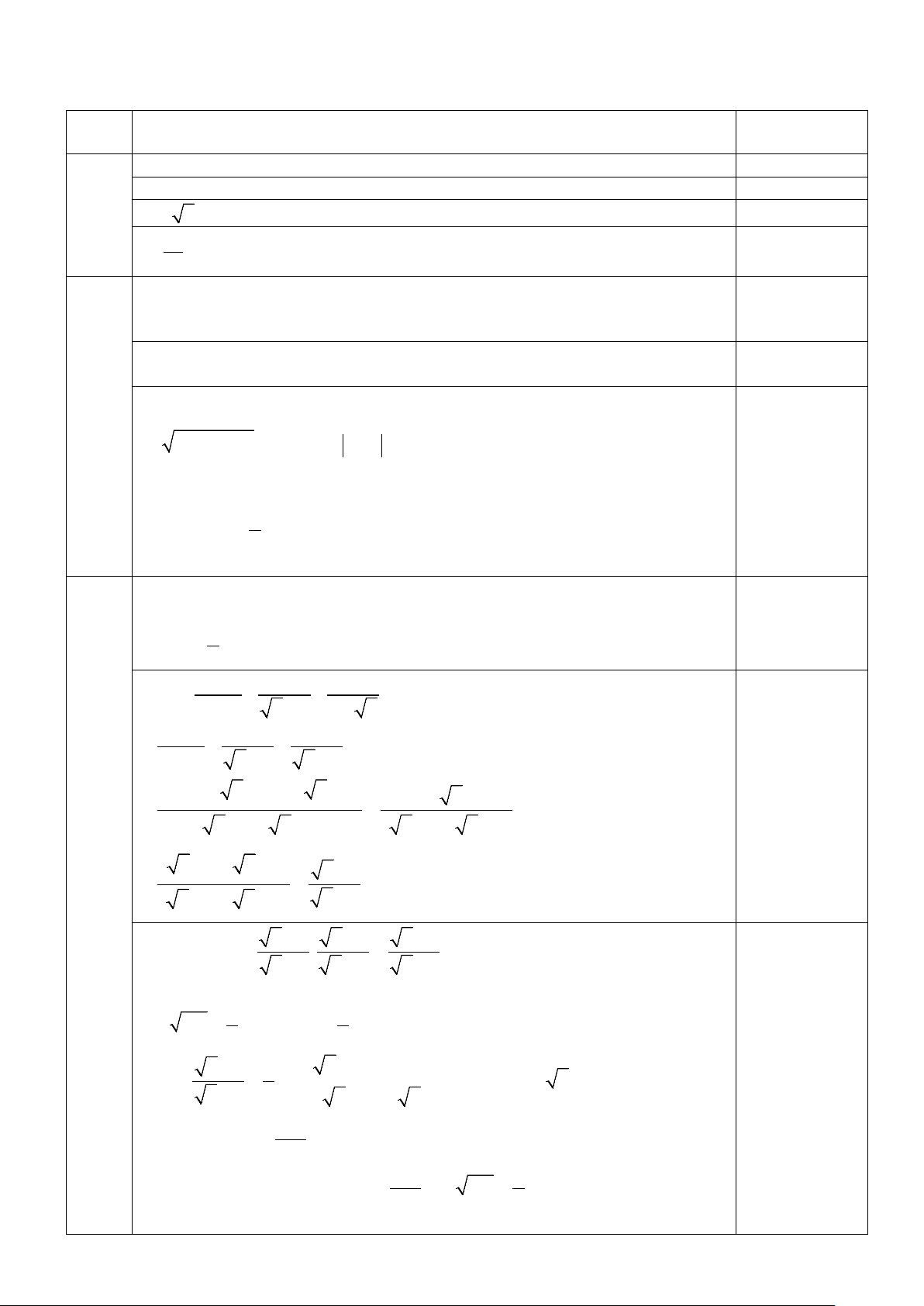
1) Từ đỉnh A của một ngọn đèn biển cao 45m so với mặt nước biển 36°
, người ta nhìn thấy một con tàu ở vị trí B dưới góc 36ο so với
phương nằm ngang (hình vẽ). Hỏi khoảng cách từ tàu đến chân đèn bằng bao nhiêu mét ?
( Làm tròn kết quả đến chữ số thập phân thứ nhất) B C 2) Cho đường tròn ( ;
O R) . Lấy hai điểm ,
A B thuộc đường tròn (O) sao cho AB < 2R . Vẽ các đường
thẳng đi qua A vuông góc với OA và đi qua B vuông góc với OB , hai đường thẳng đó cắt nhau tại M . a) Chứng minh 4 điểm ,
A B, M ,O cùng thuộc một đường tròn và chỉ rõ tâm, bán kính của đường tròn này.
b) Qua M vẽ đường thẳng d nằm trong góc OMB cắt đường tròn tại hai điểm C và D ( MC < MD ).
H là trung điểm của CD , đường thẳng OH cắt đường thẳng MA tại K . Chứng minh . KA KM = .
KO KH và AH < OM .
c) Đường thẳng qua O vuông góc với OM cắt hai đường thẳng ,
MA MB lần lượt tại E và F . Tìm vị
trí điểm M để diện tích tam giác MEF là nhỏ nhất.
Bài 5. (0,5 điểm) Giải phương trình: 2 2 2 x − x + x − x + = x ( 2 3 2 6 10 29 9 8 − 9x ) −11. --- Hết ---
(Học sinh được sử dụng máy tính bỏ túi. Cán bộ trông kiểm tra không giải thích gì thêm).
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ THI GIỮA HỌC KÌ I TOÁN 9 NĂM HỌC 2023 -2024 TT ĐÁP ÁN THANG ĐIỂM a) 5. 0,5 đ b) 4 . 0,5 đ Bài 1 c) 2 2 . 0,5 đ d) 10 . 0,5 đ 13 a) ĐKXĐ: x ≥ 3 0,25 đ
Tìm được x = 7 (TMĐK). 0,25 đ
b) ĐKXĐ: 0 ≤ x ≠ 4 0,25 đ
Tìm được x =16 (TMĐK). 0,25 đ x < 2 Bài 2
2 − x = 3x +1 c) 2
x − 4x + 4 = 3x +1 ⇔ x − 2 = 3x +1 ⇔ 0,25 đ . x ≥ 2
x − 2 = 3x +1 Tìm được 1 x = . 0,25 đ 4
a) Thay x =16 (tmđk) vào biểu thức A ta được: 0,25 đ A( ) 2 16 = . 3 0,25 đ b) x + 20 1 6 B = + + x − 4 x + 2 2 − x x + 20 1 6 = + − x − 4 x + 2 x − 2 0,25 đ
x + 20 + x − 2 − 6( x + 2) x − 5 x + 6 = ( = x + 2)( x − 2) ( x +2)( x −2) 0,75 đ (
x − 2)( x −3) x − 3 = = . Bài 3
( x +2)( x −2) x +2 0,5 đ c) Ta có x + 2 x − 3 x − 3 A.B = . = . x + 5 x + 2 x + 5 Để 1 1
AB < ⇔ 0 ≤ AB < 2 4 0,25 đ x − 3 1 x −3 ≥ 0 ⇒ 0 ≤ < ⇔
(vì x ≥ 0 ⇒ x + 5 > 0 ). x + 5 4
4 x −12 < x + 5 Tìm được 289 9 ≤ x < . 9 Đối chiếu với ĐKXĐ 289 ⇒ 9 ≤ x < thì 1 AB < . 9 2 0,25 đ
1. Viết đúng được công thức tính BC AC.tan 54ο = . 0,25 đ
Tính được BC 45.tan 54ο = ≈ 61,9 m. 0,25 đ 2a)
- Vẽ đúng hình đến câu a)
Gọi I là trung điểm của OM . 0,25 đ
- Chứng minh được các điểm O, M , A thuộc đường tròn ; OM I (1). 2 0,25 đ
- Chứng minh được các điểm O, M , B thuộc đường tròn ; OM I (2). 0,25 đ 2
- Từ (1) và (2) suy ra 4 điểm ,
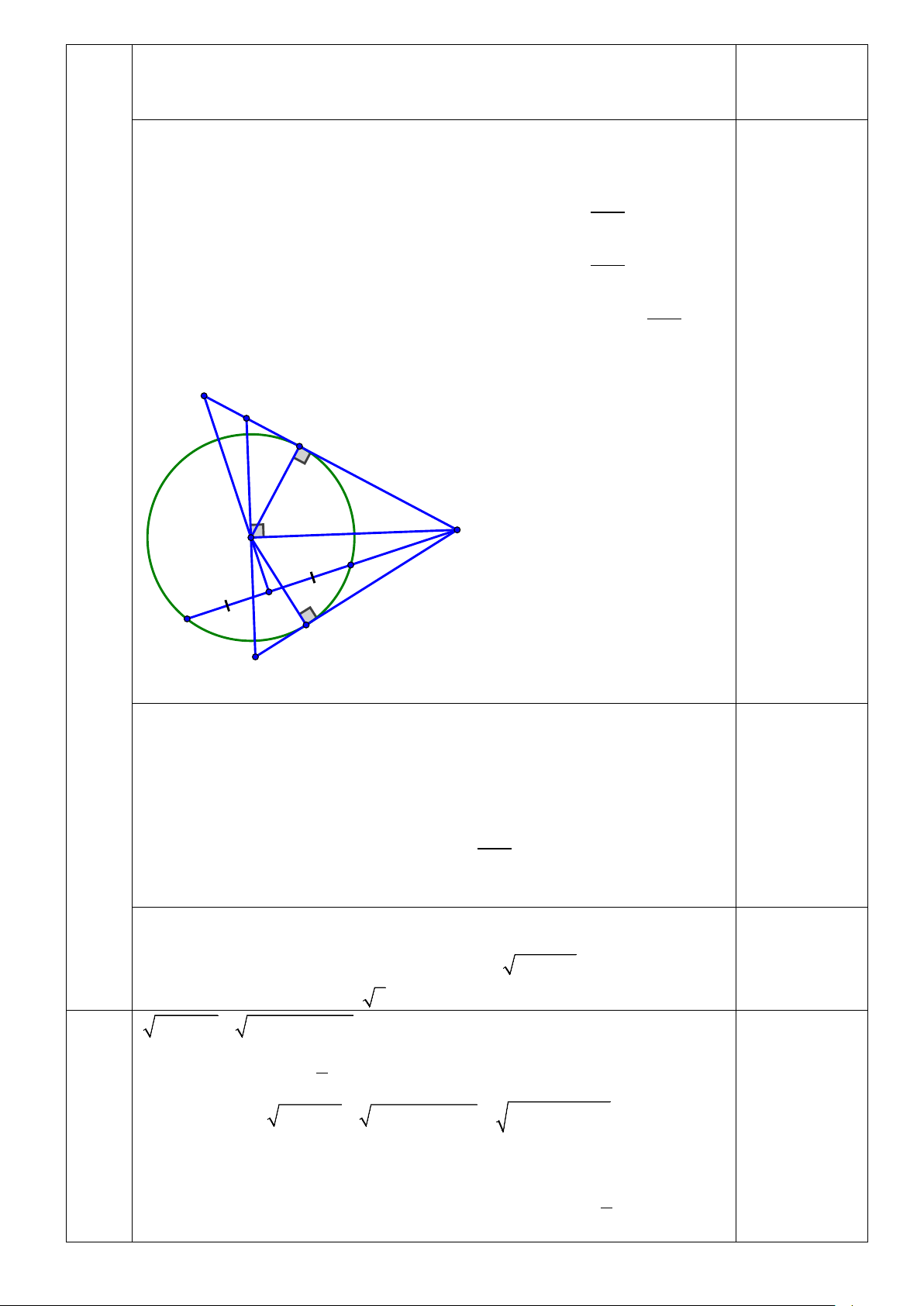
A B,O, M cùng thuộc đường tròn ; OM I . 2 0,5 đ K E A Bài 4 M O C H D B F b)
- Chỉ ra được: OH ⊥ CD . 0,25 đ - Chỉ ra được: KA ∆ O KH ∆ M (g.g). 0,25 đ - Suy ra được: . KA KM = . KO KH . 0,25 đ - Chứng minh H OM
thuộc thuộc đường tròn I; . 0,25 đ 2
- Chỉ ra AH là dây OM là đường kính nên AH < OM . 0,25 đ c) - Chứng minh được S = S = = + ≥ = . 0,25 đ ∆ OA ME OA AE AM R AE AM R MEF MOE ( ) 2 2 . . .2 . 2
- Dấu bằng xảy ra khi: MO = 2.R . 0,25 đ 2 2 2 x − x + x − x + = x ( 2 3 2 6 10 29 9 8 − 9x ) −11. - ĐKXĐ: x ≤ 0 và 2 x ≥ . 3 2 2
Bài 5 - Đánh giá VT = 3x − 2x + 6x −10x + 29 ≥ (3x − 2)2 + 25 ≥ 5.
VP = x ( − x ) − = −( x − )2 2 2 2 9 8 9 11 9 4 + 5 ≤ 5 . 0,25 đ ( 2
3x − 2x)( 2
6x −10x + 29) = 0 - Dấu bằng xảy ra khi 2 ⇔ x = (TMĐK). 2 9 0,25 đ x − 4 = 0 3