8 trang 11 lượt tải

Đề giữa học kì 2 Toán 8 năm 2024 – 2025 trường THCS Phước Bửu – BR VT có đáp án

22

Đề giữa học kì 2 Toán 8 năm 2024 – 2025 trường THCS Phước Bửu – BR VT có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 8 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem. 

Chủ đề: Đề giữa HK2 Toán 8 153 tài liệu

Môn: Toán 8 1.9 K tài liệu

Tác giả:

Profile

Kim Ngân Lê

3 tháng trước
Danh sách Quiz
/8
TRƯỜNG THCS PHƯỚC BỬU ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TỔ TOÁN - TIN MÔN: TOÁN 8
NĂM HỌC: 2024 – 2025
Thời gian làm bài 90 phút (không kể giao đề)
Đề gồm có 02 trang Kiểm tra, ngày 18 tháng 03 năm 2025.
Phần I. Câu trắc nghiệm nhiều lựa chọn (3,0 điểm).
Mỗi câu hỏi học sinh chỉ ghi một phương án vào bài làm:
Câu 1. Cho mt phng ta đ
Oxy
v đim
A
(như hnh v).
Khi đ ta đ ca đim
A
l:
A.
(1;2)
. B.
(2;1)
. C.
(1; 2)−
. D.
(2; 1)−
.
Câu 2. Trong các hàm số sau, hàm số bậc nhất là
A.
. B.
21yx=+
. C.
21=+yx
. D.
2
1=+y
x
.
Câu 3. Hàm số
( )
1– –2025xym=
là hàm số bậc nhất khi:
A
1=m
. B.
1=−m
. C.
1m
. D.
1−m
.
Câu 4. Đường thng
23= − −yx
có hệ số góc là
A
2− x
. B.
3−
. C.
2
. D.
2−
.
Câu 5. Đường thng tạo với trục Ox mt góc nhn là:
A.
32=−yx
. B.
23=−yx
. C.
21= − +yx
. D.
3= − +yx
.
Câu 6. Đường thng song song với đường thng
23=−yx
là:
A.
23=−yx
. B.
32= − +yx
. C.
31= − +yx
. D.
23= − −yx
.
Câu 7. Đ th ca hm số
36yx=+
v hm số
5y ax=+
l hai đường thng ct nhau, khi đ hệ số a
nhận nhng gi tr:
A.
3=a
. B.
6=a
. C.
3a
. D.
0a
.
Câu 8. Cho hai đoạn thng: MN = 15cm, PQ = 25cm. Khi đ tỉ số
MN
PQ
=
A.
25
15
. B.
5
3
. C.
10
20
. D.
3
5
.
Câu 9. Hệ thức theo Đnh lí Thalès ca hnh bên l
A.
CE CD
CB CA
=
. B.
BE CA
CB AD
=
.
C.
CE AD
BE CD
=
. D.
DE AC
AB AD
=
.
Câu 10. Nếu
' ' 'ABC A B C
theo tỉ số k = 2 thì
' ' 'A B C ABC
theo tỉ số là
A. 2. B.
1
4
. C.
1
2
. D. 4.
Đề chẵn
Câu 11. Hai tam gic no đng dạng với nhau khi biết đ dài các cạnh ca chúng lần lượt là
A. 3 cm; 4 cm; 5 cm và 4 cm; 8 cm; 10 cm. B. 3 cm; 4 cm; 6 cm và 9 cm; 12 cm; 16 cm.
C. 4 cm; 7 cm; 10 cm và 8 cm; 13 cm; 20 cm. D. 2 cm; 3 cm; 4 cm và 10 cm; 15 cm; 20 cm.
Câu 12 Cho hình v, biết MN // BC. Khi đ đ di đoạn thng MN là
A. 3. B. 4.
C. 12. D. 1,5.
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh ghi Đ (đúng) hoặc S (sai) vào bài làm:
Câu 1. Cho hàm số
2
( ) 2 5= = −y f x x
. Khi đ:
a)
(0) 3=−f
. b)
(1) 3=−f
. c)
( 1) 7− = −f
d)
( 2) 3−=f
Câu 2. Trong mt phng ta đ Oxy:
a) Đim thuc trục honh c tung đ bằng 0.
b) Đim thuc trục honh c honh đ bằng 0.
c) Đim thuc trục tung c honh đ bằng 0.
d) Đim thuc trục tung c honh đ bằng tung đ.
Câu 3. Xc đnh các hệ số a, b ca hàm số bậc nhất:
a) Hàm số bậc nhất
23=−yx
có các hệ số a, b lần lượt là 2; 3.
b) Hàm số bậc nhất
3( 1)=+yx
có các hệ số a, b lần lượt là 3; 1.
c) Hàm số bậc nhất
2( 3)yx=−
có các hệ số a, b lần lượt là 2; – 6.
d) Hàm số bậc nhất
52=−yx
có các hệ số a, b lần lượt là –2; 5.
Câu 4. Trong hình v bên:
a) C 3 đường trung bình ca tam giác MNP.
b) AC không phải l đường trung bình ca tam giác MNP.
c) AB và BC l hai đường trung bình ca tam giác MNP.
d) Chỉ c AB l đường đường trung bình ca tam giác MNP.
Phần III. Tự luận (3,0 điểm).
Bài 1 (1,25 điểm).
a) Cho hàm số
1=−y ax
. Tìm hệ số a, biết đ th hàm số đi qua đin A(1; 1)..
b) V đ th ca hàm số
21=−yx
.
Bài 2 (0,5 điểm). V trí nhà ca 3 bạn An, Bnh, Chi được đnh dấu trên mt phng ta đ Oxy là 3 đim
A(2; 3); B(0; – 1) và C(1; 1). Chứng tỏ nhà ca các bạn ấy cùng nằm trên mt con đường thng.
Bài 3 (1,25 điểm).
a) Cho tam giác DEF, DK là tia phân giác góc EDF (K
EF).
Tính đ dài KF biết DE = 24cm, DF = 32cm và EK = 15cm.
b) Người ta tiến hnh đo đạc các yếu tố cần thiết đ tính chiều
rng ca mt khúc sông mà không cần phải sang bờ bên kia sông
(như hnh v). Biết BC = 30m, DE = 45m, và BD = 20m.
Tính chiều rng AB ca khúc sông?
--- Hết ---
H và tên hc sinh ......................................................................
Ch ký giám th ..........................................................................
B
C
A
M
N
P
TRƯỜNG THCS PHƯỚC BỬU HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HKII
TỔ TOÁN - TIN MÔN TOÁN 8
NĂM HỌC 2024 – 2025
Hướng dẫn gồm 02 trang
Phần I. Trắc nghiệm (3,0 điểm). Mỗi câu đúng cho 0,25.
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi Câu: Đúng 1 ý cho 0,1; đúng 2 ý cho 0,25; đúng 3 ý cho 0,5; đúng 4 ý cho 1,0.
Phần III. Tự luận (3,0 điểm).
Bài 1 (1,25đ)
a) Cho hàm số
1=−y ax
. Tìm hệ số a, biết đ th hàm số đi qua đin A(1; 1)..
b) V đ th ca hàm số
21=−yx
.
Bài 2 (0,5 điểm). V trí nhà ca 3 bạn An, Bnh, Chi được đnh dấu trên mt phng ta đ Oxy là 3 đim
A(2; 3); B(0; – 1) và C(1; 1). Chứng tỏ nhà ca các bạn ấy cùng nằm trên mt con đường thng.
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đp n
A
B
C
D
A
C
C
D
A
C
D
B
Câu
1a
1b
1c
1d
2a
2b
2c
2d
3a
3b
3c
3d
4a
4b
4c
4d
Đp
án
S
Đ
S
Đ
Đ
S
Đ
S
S
S
Đ
Đ
S
Đ
S
Đ
Bài
Hướng dẫn
Đim
Bài 1 a)
Đ th hàm số
1=−y ax
đi qua đin A(1; 1).
Suy ra 1 = a.1 – 1
1 = a – 1
a = 2
Vậy a = 2.
0,25
0,25
Bài 1 b)
Cho x = 0, suy ra y = – 1. Ta c đim (0; – 1)
Cho y = 0, suy ra x =
1
2
. Ta c đim (
1
2
; 0)
Đ th hàm số y = 2x – 1 l đường thng đi qua hai đim (0; – 1) và (
1
2
; 0)
Ghi chú: Học sinh có thể xác định hai điểm khác thuộc đồ thị để vẽ đồ thị.
0,25
0,5
Đề chẵn
Bài 3 (1,25 điểm).
a) Cho tam giác DEF, DK là tia phân giác góc EDF (K
EF).
Tính đ dài KF biết DE = 24cm, DF = 32cm và EK = 15cm.
b) Người ta tiến hnh đo đạc các yếu tố cần thiết đ tính chiều
rng ca mt khúc sông mà không cần phải sang bờ bên kia sông
(như hnh v). Biết BC = 30m, DE = 45m, và BD = 20m.
Tính chiều rng AB ca khúc sông?
---HẾT---
Bài
Hướng dẫn
Đim
Bài 2
Gi (d): y = ax + b (a ≠ 0) l đường thng đi qua A v B
V (d) đi qua B(0 ; – 1) suy ra b = – 1
(d) đi qua A(2; 3) suy ra: 3 = a.2 – 1
a = 2
Nên ta có (d): y = 2x – 1
0,25
Thay x
C
= 1 vo (d) ta được: y = 2.1 – 1 = 1 = y
C
Nên C(1; 1)
(d). Do đ A, B, C thng hàng.
Vậy nhà ca các bạn An, Bình, Chi cùng nằm trên mt con đường thng
0,25
Bài
Hướng dẫn
Đim
Bài 3 a)
Xét tam giác DEF, có DK là tia phân giác ca góc EDF
Theo tính chất đường phân giác trong tam giác ta có:
15 15.32
20
24 32 24
EK KF KF
KF
DE DF
= = = =
0,75
Bài 3 a)
Xét tam giác ADE có BC // DE (cùng vuông góc với AD)
Theo hệ quả đnh lí Thalès ta có:
AB BC
AD DE
=
30 2
40
20 45 20 3
xx
x
xx
= = =
++
Vậy chiều rng khúc sông là 40m.
0,25
0,25
D
E
F
K
24
32
15
TRƯỜNG THCS PHƯỚC BỬU ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TỔ TOÁN - TIN MÔN: TOÁN 8
NĂM HỌC: 2024 – 2025
Thời gian làm bài 90 phút (không kể giao đề)
Đề gồm có 02 trang Kiểm tra, ngày 18 tháng 03 năm 2025.
Phần I. Câu trắc nghiệm nhiều lựa chọn (3,0 điểm).
Mỗi câu hỏi học sinh chỉ ghi một phương án vào bài làm:
Câu 1. Cho mt phng ta đ
Oxy
v đim
A
(như hnh v).
Khi đ ta đ ca đim
A
l:
A.
(1;2)
. B.
(2;1)
. C.
(1; 2)−
. D.
(2; 1)−
.
Câu 2. Trong các hàm số sau, hàm số bậc nhất là
A.
2
2=+yx
. B.
2
2=yx
. C.
32=−yx
. D.
3
2=+y
x
.
Câu 3. Hàm số
( )
2– 2025xym=+
là hàm số bậc nhất khi:
A
2=m
. B.
2=−m
. C.
2−m
. D.
2m
.
Câu 4. Đường thng
32= − −yx
có hệ số góc là
A
3− x
. B.
3−
. C.
3
. D.
2−
.
Câu 5. Đường thng tạo với trục Ox mt góc tù là:
A.
3= − +yx
. B.
23=+yx
. C.
21=+yx
. D.
32=−yx
.
Câu 6. Đường thng song song với đường thng
32=−yx
là:
A.
23= − +yx
. B.
32= − +yx
. C.
21= − +yx
. D.
23=+yx
.
Câu 7. Đ th ca hm số
25=+yx
v hm số
2=+y ax
l hai đường thng ct nhau, khi đ hệ số a
nhận nhng gi tr:
A.
2=a
. B.
5=a
. C.
0a
. D.
2a
.
Câu 8. Cho hai đoạn thng: CD = 12cm, EF = 20cm. Khi đ tỉ số
EF
CD
=
A.
12
20
. B.
5
3
. C.
3
5
. D.
2
1
.
Câu 9. Hệ thức theo Đnh lí Thalès ca hnh bên l
A.
=
DM EN
DE NF
. B.
=
ME NE
MD NF
.
C.
=
DE EN
EF EM
. D.
=
DE NF
ME EF
.
Câu 10. Nếu
' ' 'ABC A B C
theo tỉ số k = 4 thì
' ' 'A B C ABC
theo tỉ số là
A. 2. B.
1
2
. C.
1
4
. D. 4.
Đề lẻ
Câu 11. Hai tam gic no đng dạng với nhau khi biết đ dài các cạnh ca chúng lần lượt là
A. 8 cm; 10 cm; 6 cm và 4 cm; 9 cm; 12 cm. B. 3 cm; 4 cm; 6 cm và 6 cm; 8 cm; 12 cm.
C. 4 cm; 7 cm; 10 cm và 8 cm; 13 cm; 20 cm. D. 2 cm; 3 cm; 4 cm và 10 cm; 15 cm; 18cm.
Câu 12 Cho hình v, biết MN // BC. Khi đ đ di đoạn thng BC là
A. 9. B. 3.
C. 12. D. 18.
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh ghi Đ (đúng) hoặc S (sai) vào bài
làm:
Câu 1. Cho hàm số
2
( ) 3 2= = −y f x x
. Khi đ:
a)
(1) 2=−f
. b)
( 1) 1−=f
. c)
(2) 10=f
d)
( 2) 14− = −f
Câu 2. Trong mt phng ta đ Oxy:
a) Đim thuc trục tung c tung đ bằng 0.
b) Đim thuc trục tung c honh đ bằng 0.
c) Đim thuc trục hoành có tung đ bằng 0.
d) Đim thuc trục hoành c honh đ luôn dương.
Câu 3. Xc đnh các hệ số a, b ca hàm số bậc nhất:
a) Hàm số bậc nhất
23= − +yx
có các hệ số a, b lần lượt là –2; 3.
b) Hàm số bậc nhất
2( 1)=+yx
có các hệ số a, b lần lượt là 2; 2.
c) Hàm số bậc nhất
3( 2)=−yx
có các hệ số a, b lần lượt là 2; – 2.
d) Hàm số bậc nhất
25=−yx
có các hệ số a, b lần lượt là 2; –5.
Câu 4. Trong hình v bên:
a) Có 2 đường trung bình ca tam giác DEF.
b) MN l đường trung bình ca tam giác DEF.
c) MP và NP không phải đường trung bình ca tam giác DEF.
d) PM và MN là hai đường trung bình ca tam giác DEF.
Phần III. Tự luận (3,0 điểm).
Bài 1 (1,25 điểm).
a) Cho hàm số
1=+y ax
Tìm hệ số a, biết đ th hàm số đi qua đin B(1; 3)..
b) V đ th ca hàm số
21=+yx
.
Bài 2 (0,5 điểm). V trí nhà ca 3 bạn Minh, Nam, Phi được đnh dấu trên mt phng ta đ Oxy là 3
đim M(–1; –1); N(0; 1) và P(2; 5). Chứng tỏ nhà ca các bạn ấy cùng nằm trên mt con đường thng.
Bài 3 (1,25 điểm).
a) Cho tam giác MNP, MI là tia phân giác góc NMP (I
NP). Tính
đ dài NI biết MN = 28cm, MP = 35cm và IP = 15cm.
b) Người ta tiến hnh đo đạc các yếu tố cần thiết đ tính chiều rng
ca mt khúc sông mà không cần phải sang bờ bên kia sông (như hnh
v). Biết BE= 40m, BC = 20m, và CD = 60m.
Tính chiều rng AB ca khúc sông?
--- Hết ---
H và tên hc sinh ......................................................................
Ch ký giám th ..........................................................................
D
E
F
M
N
P
TRƯỜNG THCS PHƯỚC BỬU HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HKII
TỔ TOÁN - TIN MÔN TOÁN 8
NĂM HỌC 2024 – 2025
Hướng dẫn gồm 02 trang
Phần I. Trắc nghiệm (3,0 điểm). Mỗi câu đúng cho 0,25.
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi Câu: Đúng 1 ý cho 0,1; đúng 2 ý cho 0,25; đúng 3 ý cho 0,5; đúng 4 ý cho 1,0.
Phần III. Tự luận (3,0 điểm).
Bài 1 (1,25đ)
a) Cho hàm số
1=+y ax
Tìm hệ số a, biết đ th hàm số đi qua đin B(1; 3)..
b) V đ th ca hàm số
21=+yx
.
Bài 2 (0,5 điểm). V trí nhà ca 3 bạn Minh, Nam, Phi được đnh dấu trên mt phng ta đ Oxy là 3
đim M(–1; –1); N(0; 1) và P(2; 5). Chứng tỏ nhà ca các bạn ấy cùng nằm trên mt con đường thng.
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đp n
B
C
D
B
A
C
D
B
B
C
B
A
Câu
1a
1b
1c
1d
2a
2b
2c
2d
3a
3b
3c
3d
4a
4b
4c
4d
Đp
án
S
Đ
Đ
S
S
Đ
Đ
S
Đ
Đ
S
S
S
Đ
Đ
S
Bài
Hướng dẫn
Đim
Bài 1 a)
Đ th hàm số
1=+y ax
đi qua đin B(1; 3).
Suy ra 3 = a.1 + 1
3 = a + 1
a = 2
Vậy a = 2.
0,25
0,25
Bài 1 b)
Cho x = 0, suy ra y = 1. Ta c đim (0; 1)
Cho y = 0, suy ra x =
1
2
−
. Ta c đim (
1
2
−
; 0)
Đ th hàm số y = 2x – 1 l đường thng đi qua hai đim (0; 1) và (
1
2
−
; 0)
Ghi chú: Học sinh có thể xác định hai điểm khác thuộc đồ thị để vẽ đồ thị.
0,25
0,5
Đề lẻ
Bài 3 (1,25 điểm).
a) Cho tam giác MNP, MI là tia phân giác góc NMP (I
NP). Tính
đ dài NI biết MN = 28cm, MP = 35cm và IP = 15cm.
b) Người ta tiến hnh đo đạc các yếu tố cần thiết đ tính chiều rng
ca mt khúc sông mà không cần phải sang bờ bên kia sông (như hnh
v). Biết BE= 40m, BC = 20m, và CD = 60m.
Tính chiều rng AB ca khúc sông?
---HẾT---
Bài
Hướng dẫn
Đim
Bài 2
Gi (d): y = ax + b (a ≠ 0) l đường thng đi qua M và N
V (d) đi qua N(0 ; 1) suy ra b = 1
(d) đi qua M(–1; –1) suy ra: –1 = a.(–1) + 1
a = 2
Nên ta có (d): y = 2x + 1
0,25
Thay x
P
= 2 vo (d) ta được: y = 2.2 + 1 = 5 = y
P
Nên P(2; 5)
(d). Do đ M, N, P thng hàng.
Vậy nhà ca các bạn Minh, Nam, Phi cùng nằm trên mt con đường thng
0,25
Bài
Hướng dẫn
Đim
Bài 3 a)
Xét tam giác MNP, có MI là tia phân giác ca góc NMP
Theo tính chất đường phân giác trong tam giác ta có:
15 15.28
12
28 35 35
NI IP NI
NI
MN MP
= = = =
0,75
Bài 3 b)
Xét tam giác ACD có BE // CD (cùng vuông góc với AC)
Theo hệ quả đnh lí Thalès ta có:
AB BE
AC CD
=
40 2
40
20 60 20 3
xx
x
xx
= = =
++
Vậy chiều rng khúc sông là 40m.
0,25
0,25

Tài liệu khác của Toán 8

Preview text:

TRƯỜNG THCS PHƯỚC BỬU
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TỔ TOÁN - TIN MÔN: TOÁN 8
NĂM HỌC: 2024 – 2025 Đề chẵn
Thời gian làm bài 90 phút (không kể giao đề)
Đề gồm có 02 tran g
Kiểm tra, ngày 18 tháng 03 năm 2025.
Phần I. Câu trắc nghiệm nhiều lựa chọn (3,0 điểm).
Mỗi câu hỏi học sinh chỉ ghi một phương án vào bài làm:
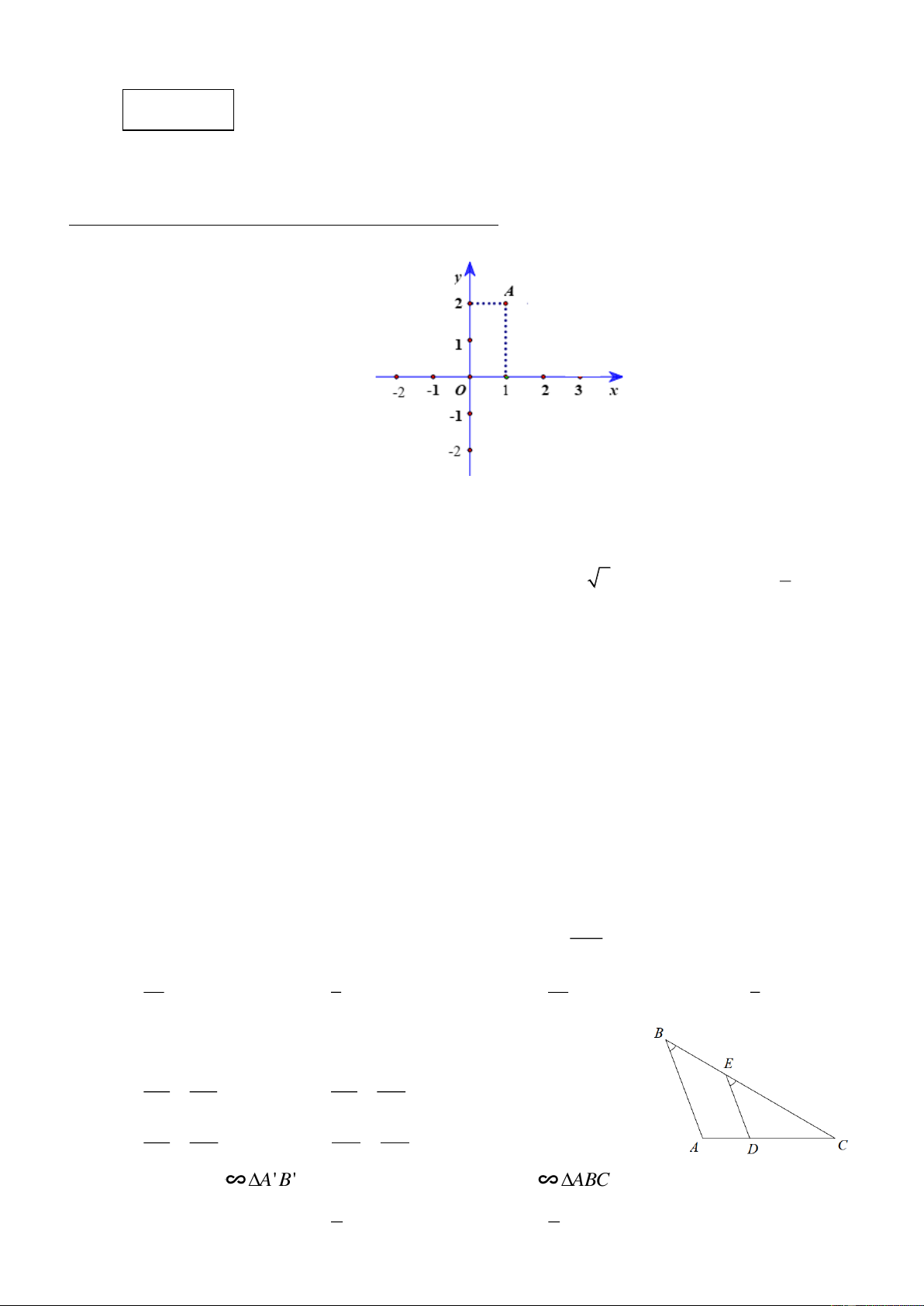
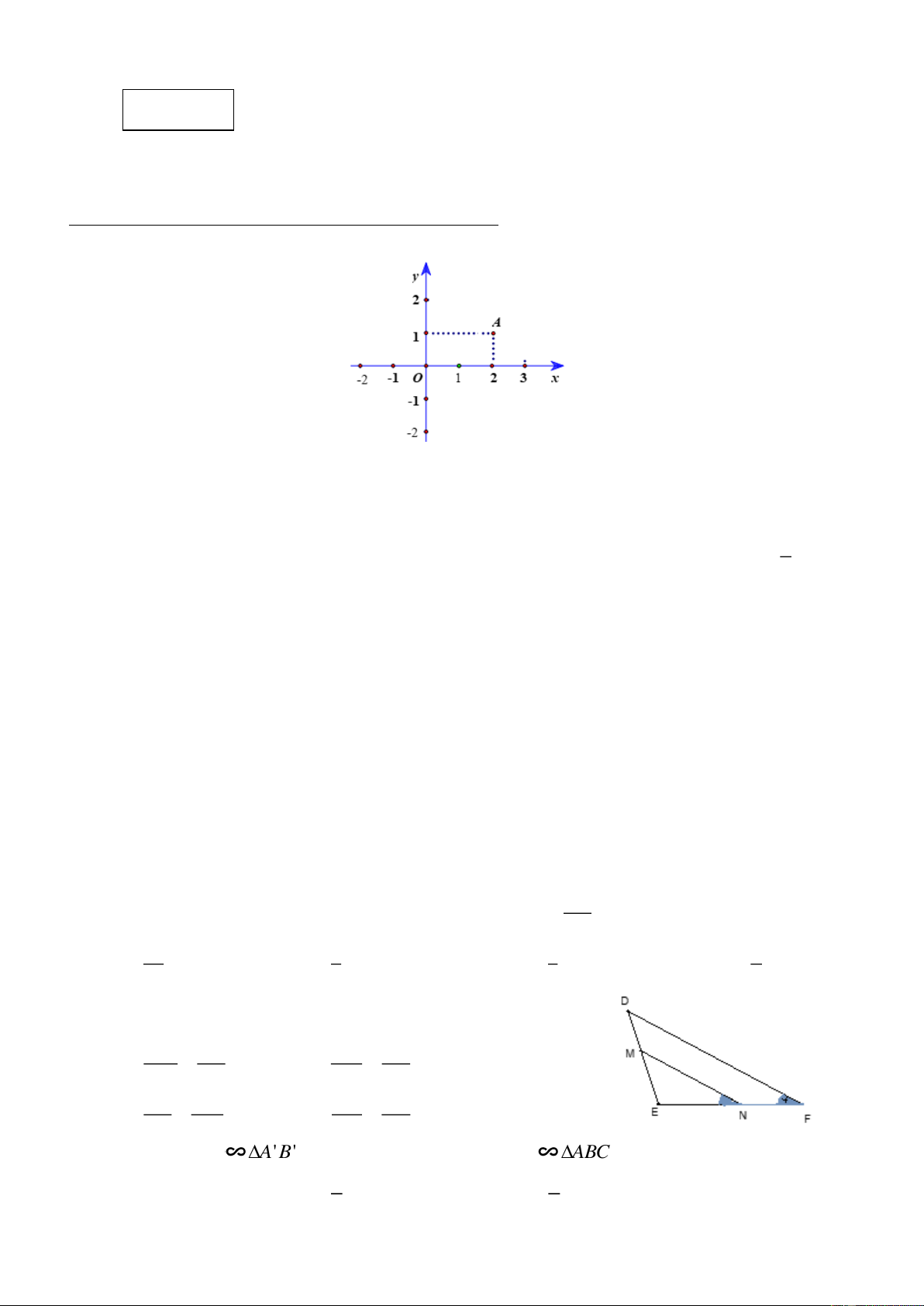
Câu 1. Cho mặt phẳng tọa độ Oxy và điểm A (như hình vẽ).
Khi đó tọa độ của điểm A là: A. (1;2) . B. (2;1) . C. (1; 2 − ) . D. (2; 1 − ) .
Câu 2. Trong các hàm số sau, hàm số bậc nhất là 2 A. 2
y = 2x +1.
B. y = 2x +1.
C. y = 2 x +1. D. y = +1. x
Câu 3. Hàm số y = (1– m) x – 2025 là hàm số bậc nhất khi: A m =1. B. m = 1 − . C. m 1. D. m  1 − .
Câu 4. Đường thẳng y = 2
− x−3 có hệ số góc là A 2 − x . B. 3 − . C. 2 . D. −2 .
Câu 5. Đường thẳng tạo với trục Ox một góc nhọn là:
A. y = 3x − 2 .
B. y = 2 −3x . C. y = 2 − x +1.
D. y = −x + 3.
Câu 6. Đường thẳng song song với đường thẳng y = 2 −3x là:
A. y = 2x −3 . B. y = 3 − x+2 . C. y = 3 − x +1. D. y = 2 − x−3.
Câu 7. Đồ thị của hàm số y = 3x + 6 = + và hàm số y
ax 5 là hai đường thẳng cắt nhau, khi đó hệ số a
nhận những giá trị: A. a = 3. B. a = 6 . C. a  3 . D. a  0 . MN
Câu 8. Cho hai đoạn thẳng: MN = 15cm, PQ = 25cm. Khi đó tỉ số = PQ 25 5 10 3 A. . B. . C. . D. . 15 3 20 5
Câu 9. Hệ thức theo Định lí Thalès của hình bên là A. CE CD = BE CA . B. = . CB CA CB AD CE AD DE AC C. = . D. = . BE CD AB AD Câu 10. Nếu ABC A
 'B'C' theo tỉ số k = 2 thì A  'B'C' A
BC theo tỉ số là 1 1 A. 2. B. 4 . C. 2 . D. 4.
Câu 11. Hai tam giác nào đồng dạng với nhau khi biết độ dài các cạnh của chúng lần lượt là
A. 3 cm; 4 cm; 5 cm và 4 cm; 8 cm; 10 cm.
B. 3 cm; 4 cm; 6 cm và 9 cm; 12 cm; 16 cm.
C. 4 cm; 7 cm; 10 cm và 8 cm; 13 cm; 20 cm.
D. 2 cm; 3 cm; 4 cm và 10 cm; 15 cm; 20 cm.
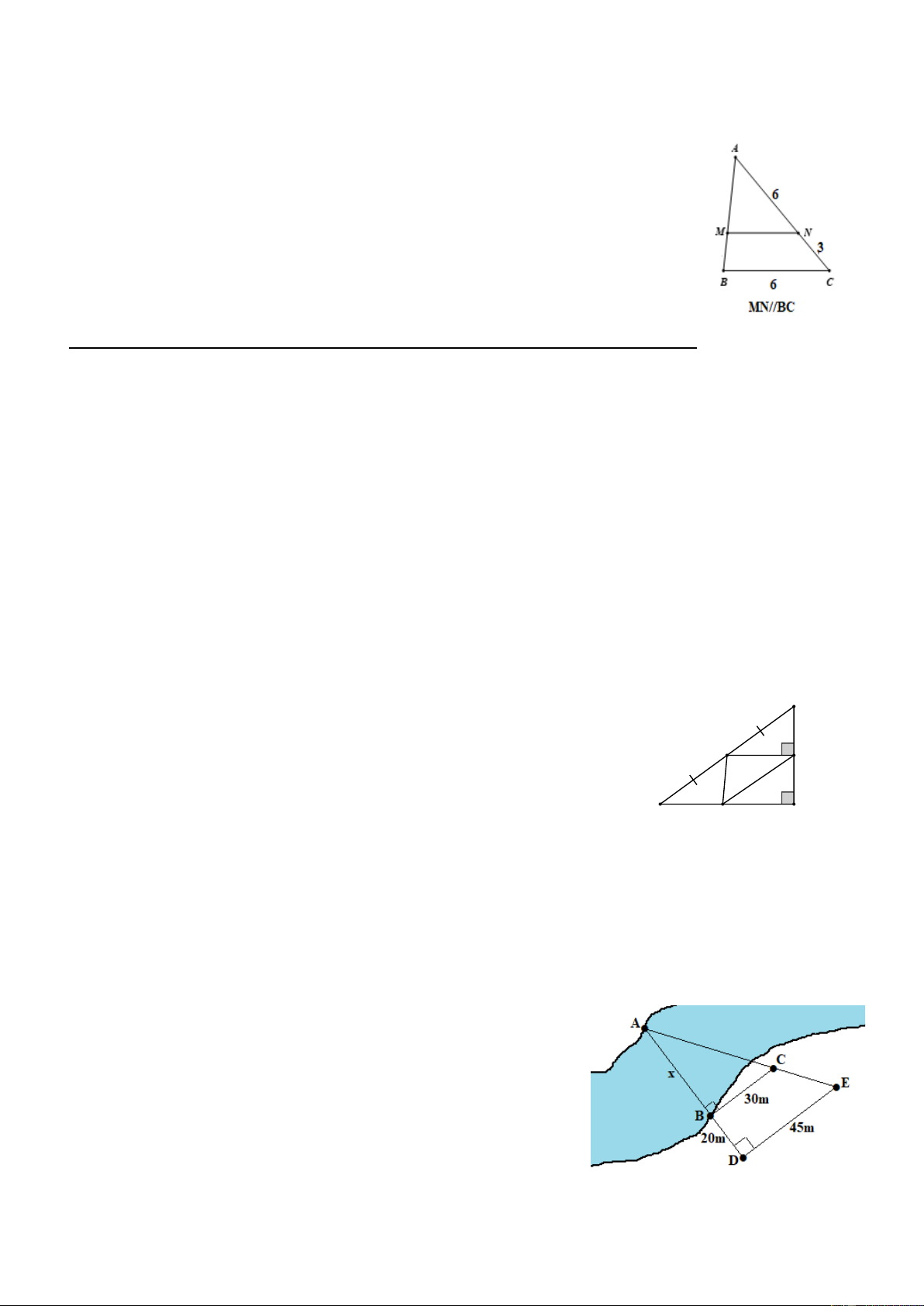
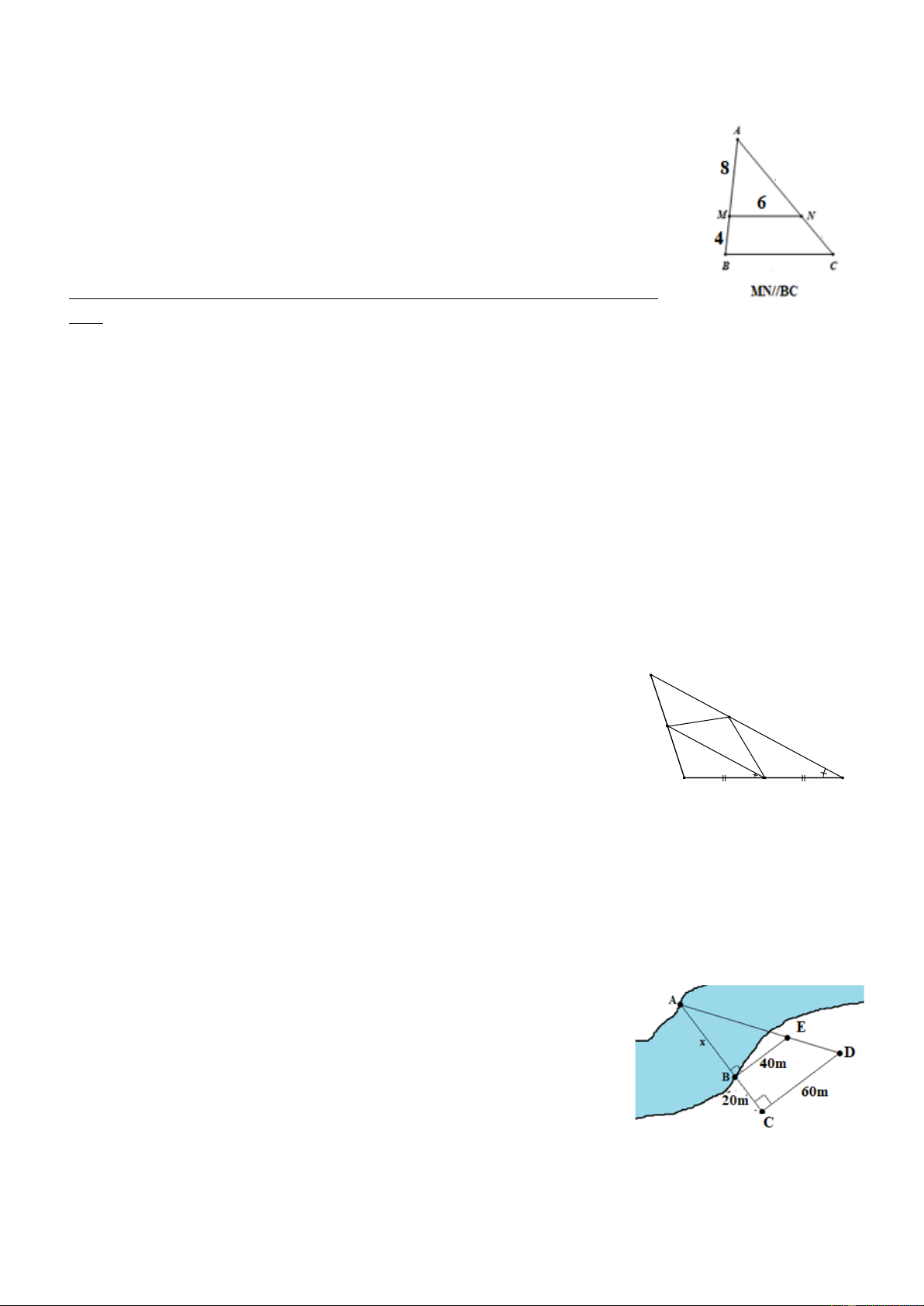
Câu 12 Cho hình vẽ, biết MN // BC. Khi đó độ dài đoạn thẳng MN là A. 3. B. 4. C. 12. D. 1,5.
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh ghi Đ (đúng) hoặc S (sai) vào bài làm: Câu 1. Cho hàm số 2
y = f (x) = 2x − 5 . Khi đó: a) f (0) = 3 − . b) f (1) = 3 − . c) f ( 1 − ) = 7 − d) f ( 2 − ) = 3
Câu 2. Trong mặt phẳng tọa độ Oxy:
a) Điểm thuộc trục hoành có tung độ bằng 0.
b) Điểm thuộc trục hoành có hoành độ bằng 0.
c) Điểm thuộc trục tung có hoành độ bằng 0.
d) Điểm thuộc trục tung có hoành độ bằng tung độ.
Câu 3. Xác định các hệ số a, b của hàm số bậc nhất:
a) Hàm số bậc nhất y = 2x −3 có các hệ số a, b lần lượt là 2; 3.
b) Hàm số bậc nhất y = 3(x +1) có các hệ số a, b lần lượt là 3; 1.
c) Hàm số bậc nhất y = 2(x −3) có các hệ số a, b lần lượt là 2; – 6.
d) Hàm số bậc nhất y = 5− 2x có các hệ số a, b lần lượt là –2; 5.
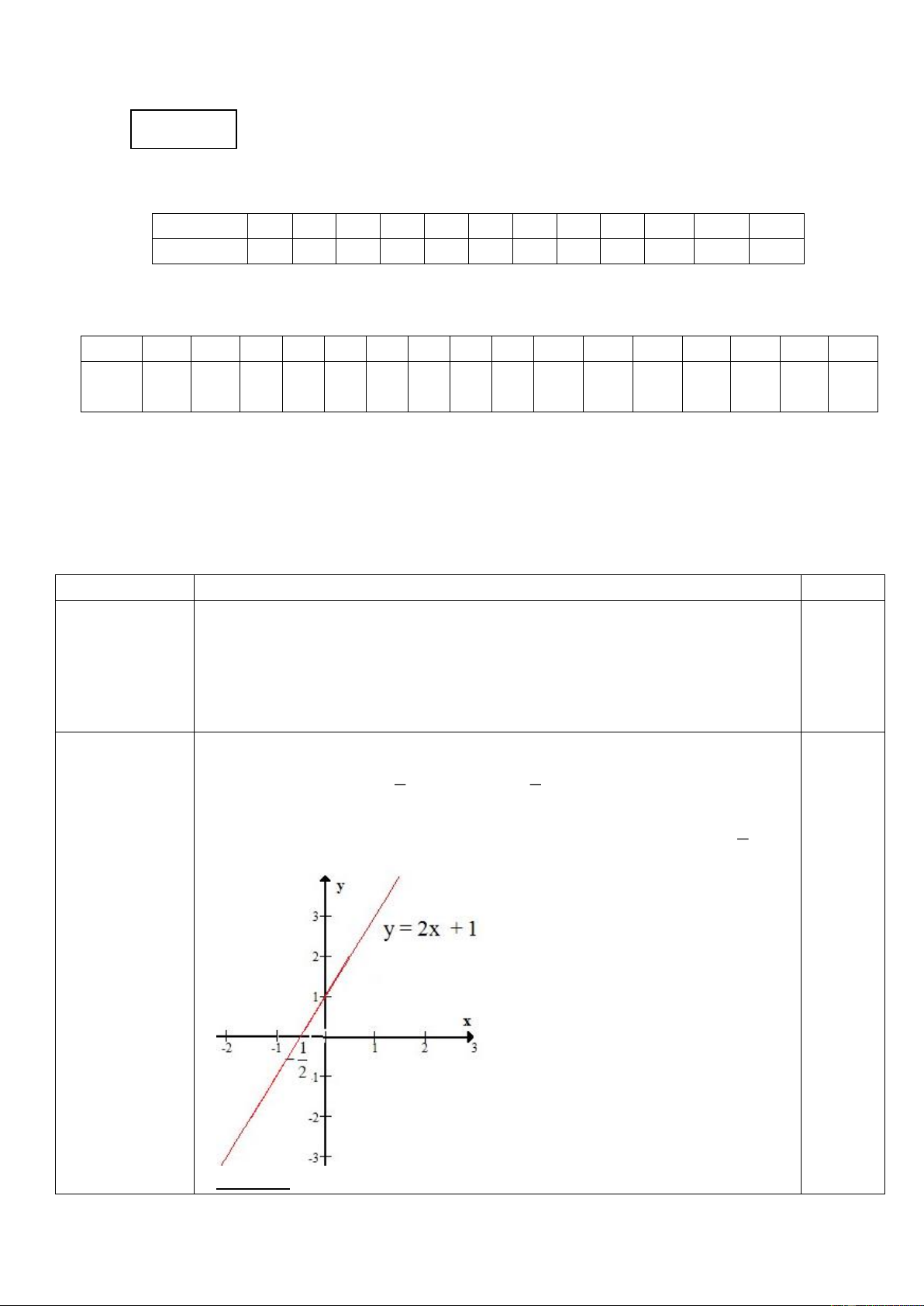
Câu 4. Trong hình vẽ bên: M
a) Có 3 đường trung bình của tam giác MNP.
b) AC không phải là đường trung bình của tam giác MNP.
c) AB và BC là hai đường trung bình của tam giác MNP. A B
d) Chỉ có AB là đường đường trung bình của tam giác MNP.
Phần III. Tự luận (3,0 điểm). N C P Bài 1 (1,25 điểm).
a) Cho hàm số y = ax −1. Tìm hệ số a, biết đồ thị hàm số đi qua điển A(1; 1)..
b) Vẽ đồ thị của hàm số y = 2x −1.
Bài 2 (0,5 điểm). Vị trí nhà của 3 bạn An, Bình, Chi được đánh dấu trên mặt phẳng tọa độ Oxy là 3 điểm
A(2; 3); B(0; – 1) và C(1; 1). Chứng tỏ nhà của các bạn ấy cùng nằm trên một con đường thẳng. Bài 3 (1,25 điểm).
a) Cho tam giác DEF, DK là tia phân giác góc EDF (K  EF).
Tính độ dài KF biết DE = 24cm, DF = 32cm và EK = 15cm.
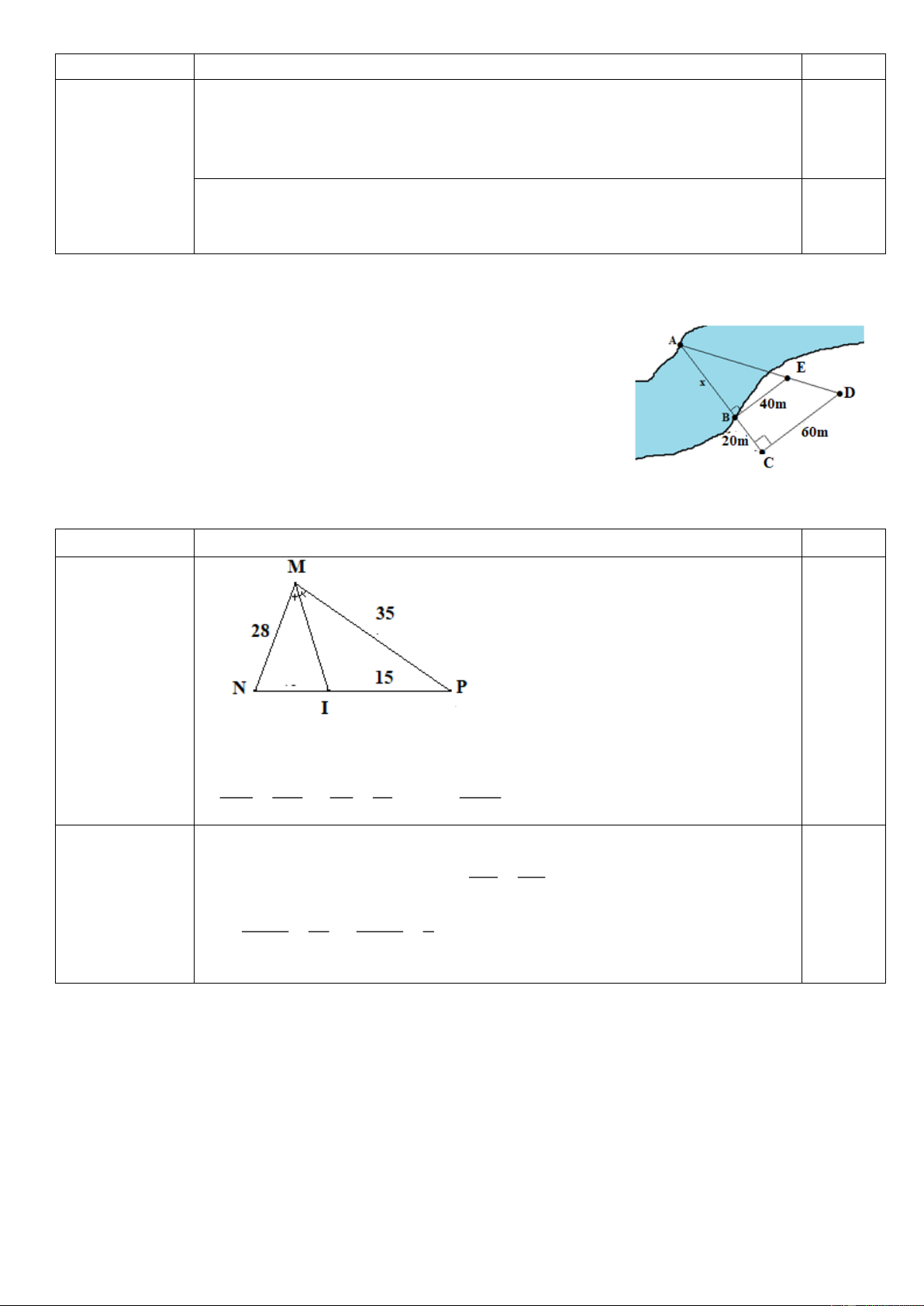
b) Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều
rộng của một khúc sông mà không cần phải sang bờ bên kia sông
(như hình vẽ). Biết BC = 30m, DE = 45m, và BD = 20m.
Tính chiều rộng AB của khúc sông? --- Hết ---
Họ và tên học sinh ......................................................................
Chữ ký giám thị ..........................................................................
TRƯỜNG THCS PHƯỚC BỬU HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HKII
TỔ TOÁN - TIN MÔN TOÁN 8
NĂM HỌC 2024 – 2025 Đề chẵn
Hướng dẫn gồm 02 trang
Phần I. Trắc nghiệm (3,0 điểm). Mỗi câu đúng cho 0,25. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A B C D A C C D A C D B
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi Câu: Đúng 1 ý cho 0,1; đúng 2 ý cho 0,25; đúng 3 ý cho 0,5; đúng 4 ý cho 1,0. Câu 1a 1b 1c 1d 2a 2b 2c 2d 3a 3b 3c 3d 4a 4b 4c 4d Đáp S Đ S Đ Đ S Đ S S S Đ Đ S Đ S Đ án
Phần III. Tự luận (3,0 điểm). Bài 1 (1,25đ)
a) Cho hàm số y = ax −1. Tìm hệ số a, biết đồ thị hàm số đi qua điển A(1; 1)..
b) Vẽ đồ thị của hàm số y = 2x −1. Bài Hướng dẫn Điểm Bài 1 a)
Đồ thị hàm số y = ax −1 đi qua điển A(1; 1). Suy ra 1 = a.1 – 1 0,25 1 = a – 1 a = 2 0,25 Vậy a = 2. Bài 1 b)
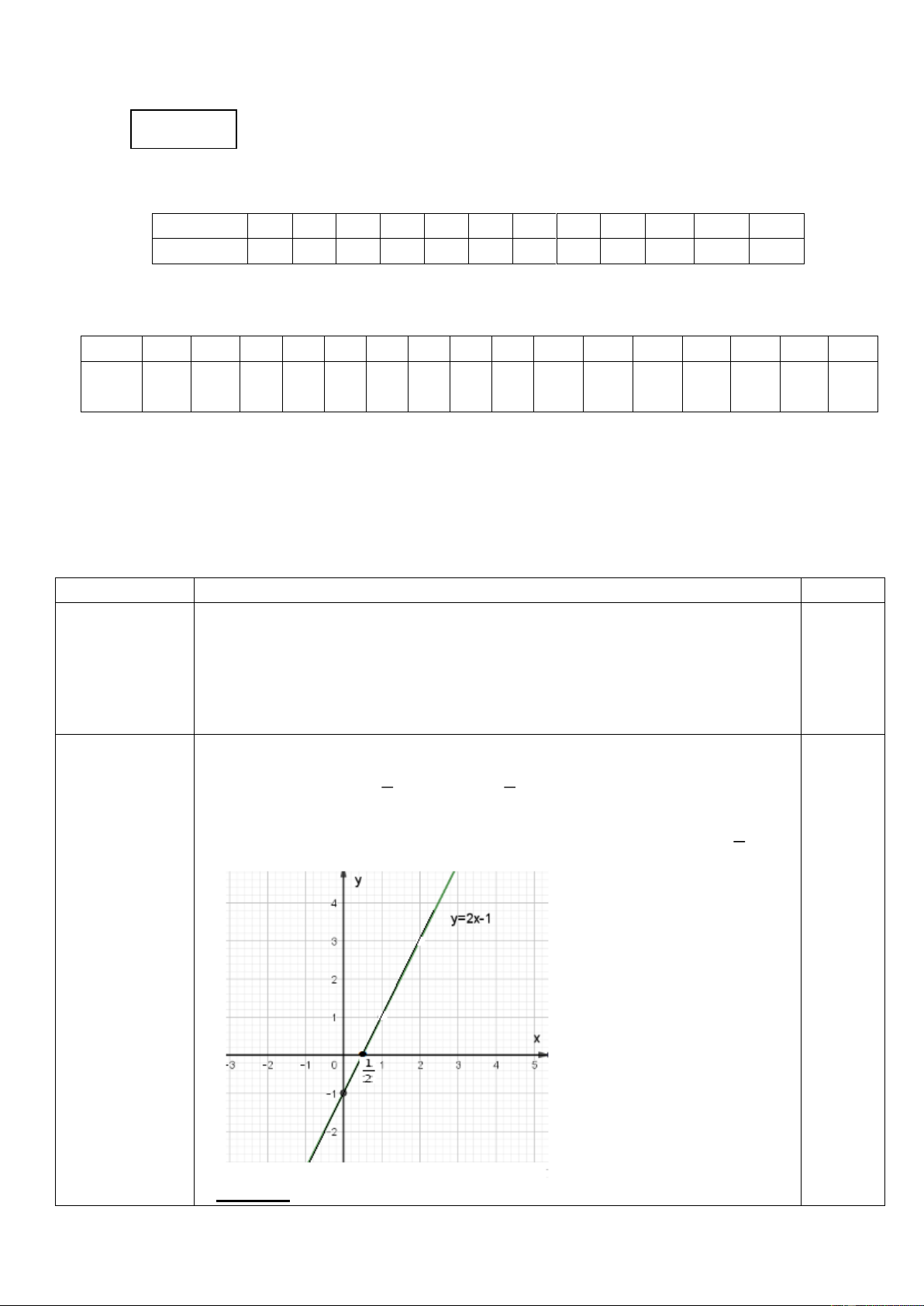
Cho x = 0, suy ra y = – 1. Ta có điểm (0; – 1) 1 1 0,25 Cho y = 0, suy ra x = . Ta có điể 2 m ( 2 ; 0) 1
Đồ thị hàm số y = 2x – 1 là đường thẳng đi qua hai điểm (0; – 1) và ( 2 ; 0) 0,5
Ghi chú: Học sinh có thể xác định hai điểm khác thuộc đồ thị để vẽ đồ thị.
Bài 2 (0,5 điểm). Vị trí nhà của 3 bạn An, Bình, Chi được đánh dấu trên mặt phẳng tọa độ Oxy là 3 điểm
A(2; 3); B(0; – 1) và C(1; 1). Chứng tỏ nhà của các bạn ấy cùng nằm trên một con đường thẳng. Bài Hướng dẫn Điểm
Gọi (d): y = ax + b (a ≠ 0) là đường thẳng đi qua A và B
Vì (d) đi qua B(0 ; – 1) suy ra b = – 1 0,25
(d) đi qua A(2; 3) suy ra: 3 = a.2 – 1 a = 2 Bài 2 Nên ta có (d): y = 2x – 1
Thay xC= 1 vào (d) ta được: y = 2.1 – 1 = 1 = yC
Nên C(1; 1)  (d). Do đó A, B, C thẳng hàng. 0,25
Vậy nhà của các bạn An, Bình, Chi cùng nằm trên một con đường thẳng Bài 3 (1,25 điểm).
a) Cho tam giác DEF, DK là tia phân giác góc EDF (K  EF).
Tính độ dài KF biết DE = 24cm, DF = 32cm và EK = 15cm.
b) Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều
rộng của một khúc sông mà không cần phải sang bờ bên kia sông
(như hình vẽ). Biết BC = 30m, DE = 45m, và BD = 20m.
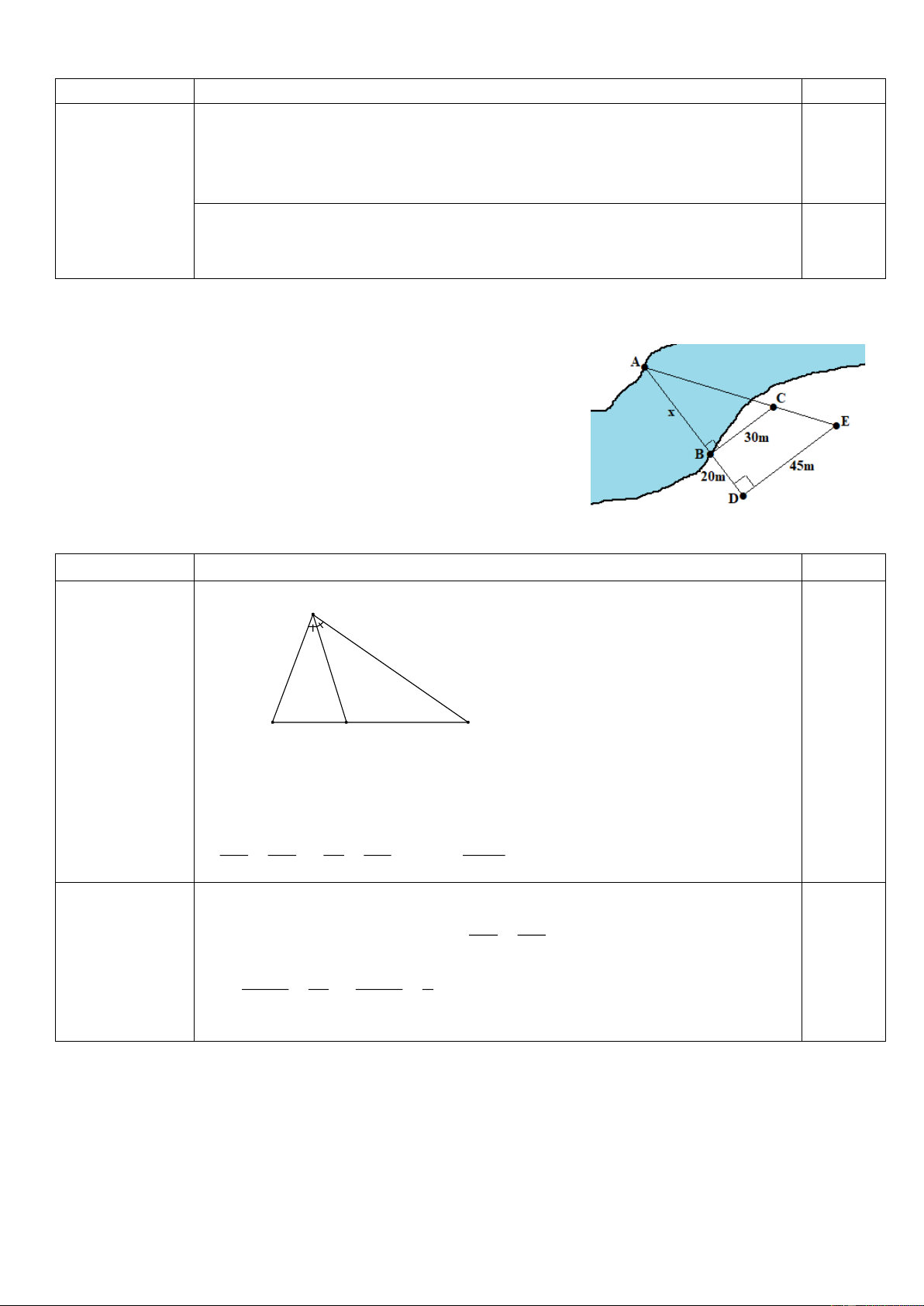
Tính chiều rộng AB của khúc sông? Bài Hướng dẫn Điểm Bài 3 a) D 24 32 15 0,75 E F K
Xét tam giác DEF, có DK là tia phân giác của góc EDF
Theo tính chất đường phân giác trong tam giác ta có: EK KF 15 KF 15.32 =  =  KF = = 20 DE DF 24 32 24 Bài 3 a)
Xét tam giác ADE có BC // DE (cùng vuông góc với AD) AB BC
Theo hệ quả định lí Thalès ta có: = AD DE 0,25 x 30 x 2  =  =  x = 40 x + 20 45 x + 20 3
Vậy chiều rộng khúc sông là 40m. 0,25 ---HẾT---
TRƯỜNG THCS PHƯỚC BỬU
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TỔ TOÁN - TIN MÔN: TOÁN 8
NĂM HỌC: 2024 – 2025 Đề lẻ
Thời gian làm bài 90 phút (không kể giao đề)
Đề gồm có 02 tran g
Kiểm tra, ngày 18 tháng 03 năm 2025.
Phần I. Câu trắc nghiệm nhiều lựa chọn (3,0 điểm).
Mỗi câu hỏi học sinh chỉ ghi một phương án vào bài làm:
Câu 1. Cho mặt phẳng tọa độ Oxy và điểm A (như hình vẽ).
Khi đó tọa độ của điểm A là: A. (1;2) . B. (2;1) . C. (1; 2 − ) . D. (2; 1 − ) .
Câu 2. Trong các hàm số sau, hàm số bậc nhất là 3 A. 2
y = x + 2 . B. 2 y = 2x .
C. y = 3x − 2 . D. y = + 2. x
Câu 3. Hàm số y = (2 – m) x + 2025 là hàm số bậc nhất khi:
A m = 2 . B. m = 2 − . C. m  2 − .
D. m  2 .
Câu 4. Đường thẳng y = 3
− x−2 có hệ số góc là A 3 − x. B. 3 − . C. 3 . D. −2 .
Câu 5. Đường thẳng tạo với trục Ox một góc tù là:
A. y = −x + 3.
B. y = 2 +3x .
C. y = 2x +1.
D. y = 3x − 2 .
Câu 6. Đường thẳng song song với đường thẳng y = 3− 2x là: A. y = 2 − x+3 . B. y = 3 − x+2 . C. y = 2 − x +1.
D. y = 2x +3.
Câu 7. Đồ thị của hàm số y = 2x +5 y = ax + và hàm số
2 là hai đường thẳng cắt nhau, khi đó hệ số a
nhận những giá trị: A. a = 2 . B. a = 5 . C. a  0 . D. a  2 . EF
Câu 8. Cho hai đoạn thẳng: CD = 12cm, EF = 20cm. Khi đó tỉ số = CD 12 5 3 2 A. . B. . C. . D. . 20 3 5 1
Câu 9. Hệ thức theo Định lí Thalès của hình bên là
A. DM = EN ME NE . B. = . DE NF MD NF DE EN DE NF C. = . D. = . EF EM ME EF Câu 10. Nếu ABC A
 'B'C' theo tỉ số k = 4 thì A  'B'C' A
BC theo tỉ số là 1 1 A. 2. B. 2 . C. 4 . D. 4.
Câu 11. Hai tam giác nào đồng dạng với nhau khi biết độ dài các cạnh của chúng lần lượt là
A. 8 cm; 10 cm; 6 cm và 4 cm; 9 cm; 12 cm.
B. 3 cm; 4 cm; 6 cm và 6 cm; 8 cm; 12 cm.
C. 4 cm; 7 cm; 10 cm và 8 cm; 13 cm; 20 cm.
D. 2 cm; 3 cm; 4 cm và 10 cm; 15 cm; 18cm.
Câu 12 Cho hình vẽ, biết MN // BC. Khi đó độ dài đoạn thẳng BC là A. 9. B. 3. C. 12. D. 18.
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh ghi Đ (đúng) hoặc S (sai) vào bài làm: Câu 1. Cho hàm số 2
y = f (x) = 3x − 2 . Khi đó: a) f (1) = 2 − . b) f ( 1 − ) =1. c) f (2) =10 d) f ( 2 − ) = 1 − 4
Câu 2. Trong mặt phẳng tọa độ Oxy:
a) Điểm thuộc trục tung có tung độ bằng 0.
b) Điểm thuộc trục tung có hoành độ bằng 0.
c) Điểm thuộc trục hoành có tung độ bằng 0.
d) Điểm thuộc trục hoành có hoành độ luôn dương.
Câu 3. Xác định các hệ số a, b của hàm số bậc nhất:
a) Hàm số bậc nhất y = 2
− x+3 có các hệ số a, b lần lượt là –2; 3.
b) Hàm số bậc nhất y = 2(x +1) có các hệ số a, b lần lượt là 2; 2.
c) Hàm số bậc nhất y = 3(x − 2) có các hệ số a, b lần lượt là 2; – 2.
d) Hàm số bậc nhất y = 2−5x có các hệ số a, b lần lượt là 2; –5.
Câu 4. Trong hình vẽ bên: D
a) Có 2 đường trung bình của tam giác DEF.
b) MN là đường trung bình của tam giác DEF. P M
c) MP và NP không phải đường trung bình của tam giác DEF.
d) PM và MN là hai đường trung bình của tam giác DEF.
Phần III. Tự luận (3,0 điểm). E N F Bài 1 (1,25 điểm).
a) Cho hàm số y = ax +1 Tìm hệ số a, biết đồ thị hàm số đi qua điển B(1; 3)..
b) Vẽ đồ thị của hàm số y = 2x +1.
Bài 2 (0,5 điểm). Vị trí nhà của 3 bạn Minh, Nam, Phi được đánh dấu trên mặt phẳng tọa độ Oxy là 3
điểm M(–1; –1); N(0; 1) và P(2; 5). Chứng tỏ nhà của các bạn ấy cùng nằm trên một con đường thẳng. Bài 3 (1,25 điểm).
a) Cho tam giác MNP, MI là tia phân giác góc NMP (I  NP). Tính
độ dài NI biết MN = 28cm, MP = 35cm và IP = 15cm.
b) Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng
của một khúc sông mà không cần phải sang bờ bên kia sông (như hình
vẽ). Biết BE= 40m, BC = 20m, và CD = 60m.
Tính chiều rộng AB của khúc sông? --- Hết ---
Họ và tên học sinh ......................................................................
Chữ ký giám thị ..........................................................................
TRƯỜNG THCS PHƯỚC BỬU HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HKII
TỔ TOÁN - TIN MÔN TOÁN 8
NĂM HỌC 2024 – 2025 Đề lẻ
Hướng dẫn gồm 02 trang
Phần I. Trắc nghiệm (3,0 điểm). Mỗi câu đúng cho 0,25. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B C D B A C D B B C B A
Phần II. Câu trắc nghiệm “đúng – sai” (4,0 điểm).
Trong mỗi Câu: Đúng 1 ý cho 0,1; đúng 2 ý cho 0,25; đúng 3 ý cho 0,5; đúng 4 ý cho 1,0. Câu 1a 1b 1c 1d 2a 2b 2c 2d 3a 3b 3c 3d 4a 4b 4c 4d Đáp S Đ Đ S S Đ Đ S Đ Đ S S S Đ Đ S án
Phần III. Tự luận (3,0 điểm). Bài 1 (1,25đ)
a) Cho hàm số y = ax +1 Tìm hệ số a, biết đồ thị hàm số đi qua điển B(1; 3)..
b) Vẽ đồ thị của hàm số y = 2x +1. Bài Hướng dẫn Điểm Bài 1 a)
Đồ thị hàm số y = ax +1 đi qua điển B(1; 3). Suy ra 3 = a.1 + 1 0,25 3 = a + 1 a = 2 0,25 Vậy a = 2. Bài 1 b)
Cho x = 0, suy ra y = 1. Ta có điểm (0; 1) 1 1 0,25 Cho y = 0, suy ra x = − . Ta có điể − 2 m ( 2 ; 0) 1
Đồ thị hàm số y = 2x – 1 là đường thẳng đi qua hai điểm (0; 1) và ( − 2 ; 0) 0,5
Ghi chú: Học sinh có thể xác định hai điểm khác thuộc đồ thị để vẽ đồ thị.
Bài 2 (0,5 điểm). Vị trí nhà của 3 bạn Minh, Nam, Phi được đánh dấu trên mặt phẳng tọa độ Oxy là 3
điểm M(–1; –1); N(0; 1) và P(2; 5). Chứng tỏ nhà của các bạn ấy cùng nằm trên một con đường thẳng. Bài Hướng dẫn Điểm
Gọi (d): y = ax + b (a ≠ 0) là đường thẳng đi qua M và N
Vì (d) đi qua N(0 ; 1) suy ra b = 1 0,25
(d) đi qua M(–1; –1) suy ra: –1 = a.(–1) + 1 a = 2 Bài 2 Nên ta có (d): y = 2x + 1
Thay xP = 2 vào (d) ta được: y = 2.2 + 1 = 5 = yP
Nên P(2; 5)  (d). Do đó M, N, P thẳng hàng. 0,25
Vậy nhà của các bạn Minh, Nam, Phi cùng nằm trên một con đường thẳng Bài 3 (1,25 điểm).
a) Cho tam giác MNP, MI là tia phân giác góc NMP (I  NP). Tính
độ dài NI biết MN = 28cm, MP = 35cm và IP = 15cm.
b) Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng
của một khúc sông mà không cần phải sang bờ bên kia sông (như hình
vẽ). Biết BE= 40m, BC = 20m, và CD = 60m.
Tính chiều rộng AB của khúc sông? Bài Hướng dẫn Điểm Bài 3 a) 0,75
Xét tam giác MNP, có MI là tia phân giác của góc NMP
Theo tính chất đường phân giác trong tam giác ta có: NI IP NI 15 15.28 =  =  NI = =12 MN MP 28 35 35 Bài 3 b)
Xét tam giác ACD có BE // CD (cùng vuông góc với AC) AB BE
Theo hệ quả định lí Thalès ta có: = AC CD 0,25 x 40 x 2  =  =  x = 40 x + 20 60 x + 20 3
Vậy chiều rộng khúc sông là 40m. 0,25 ---HẾT---

Tài liệu liên quan: