Đề giữa học kỳ 1 Toán 11 năm 2023 – 2024 trường THPT Thiệu Hóa – Thanh Hóa

TRƯỜNG THPT THIỆU HÓA
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TỔ TOÁN-TIN
NĂM HỌC 2023 – 2024
MÔN: TOÁN – KHỐI 11
Thời gian làm bài: 90 phút
(Đề gồm có 4 trang) ĐỀ CHÍNH THỨC Mã đề thi
Họ và tên:………………………………….Mã học sinh:…….............……..…… 111
I. PHẦN TRẮC NGHIỆM  2023 
Câu 1. Phương trình cos 3x + − sin  
(3x − 2023 ) = 3 tương đương với phương trình nào sau đây?  2  3 3 3 3 A. sin 3x = . B. cos 3x = . C. cos 3x = − . D. sin 3x = − . 2 2 2 2
Câu 2. Thêm hai số thực dương x và y vào giữa hai số 5 và 320 để được bốn số 5; ;
x y; 320 theo thứ tự
đó lập thành cấp số nhận. Khẳng định nào sau đây là đúng? x = 20 x =15 x = 30 x = 25 A.  . B.  . C.  . D.  . y = 80 y = 45 y = 90 y =125
Câu 3. Tính tổng tất cả các số hạng của một cấp số nhân, biết số hạng đầu bằng 18, số hạng thứ hai bằng 54
và số hạng cuối bằng 39366. A. 24576 . B. 59040 . C. 49152 . D. 54090 .
Câu 4. Phương trình 2cos x −1 = 0 có nghiệm là   A. x = 
+ k , k  . B. x = 
+ k , k  . 3 6   C. x = 
+ k2 , k  . D. x = 
+ k2 , k  . 3 6
Câu 5. Nghiệm của phương trình cos x = 1 là
A. x =  + k 2 , k  .
B. x = k , k  . 
C. x = k 2 , k  . D. x =
+ k , k  . 2
Câu 6. Chọn khẳng định đúng trong các khẳng định sau: A. 2
cos 2 = 1 − 2sin  . B. 2
cos 2 = 2sin  −1. C. 2
cos 2 = 2 cos  + 1. D. 2
cos 2 = 1 − 2 cos  .
Câu 7. Khẳng định nào sau đây đúng?
A. Hàm số y = tan x có tập xác định là .
B. Hàm số y = cot x có tập xác định là
\ k , k   .  
C. Hàm số y = cot x có tập xác định là
\  + k , k   .  2 
D. Các hàm số lượng giác có tập xác định là .
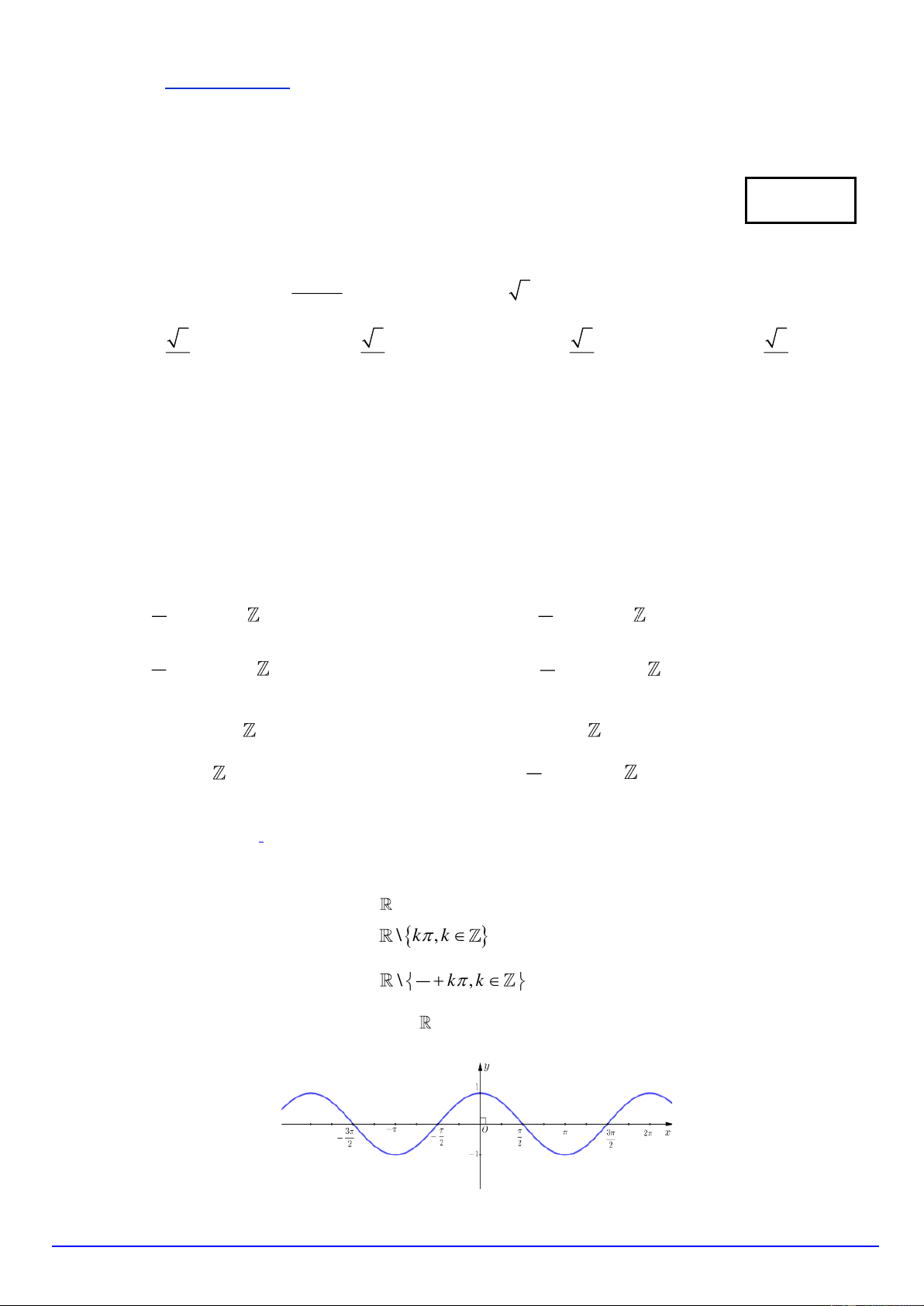
Câu 8. Cho hàm số y = cos x có đồ thị như hình bên dưới:
Mệnh đề nào sau đây đúng? Trang 1/4 - Mã đề 111       
A. Hàm số đồng biến trên − ; .  
B. Hàm số đồng biến trên − ; 0 .    2 2   2         
C. Hàm số đồng biến trên 3 − ; − .  
D. Hàm số đồng biến trên 3 ; .    2 2   2 2  1 1
Câu 9. Cho  ,  là hai góc nhọn thỏa mãn tan = , tan  =
. Góc  +  có giá trị bằng: 2 3     A. . B. . C. . D. . 6 3 2 4 u  = 1 −
Câu 10. Cho dãy số (u xác định bởi hệ thức truy hồi 1 
(n  2). Giá trị của u bằng n ) u = 3u + n  3 n n 1 − A. 0 . B. 3. C. 2 . D. 1 .
Câu 11. Cho cấp số cộng (u có u = 0
− ,1; d = 0,1. Số hạng thứ 7 của cấp số cộng là n ) 1 A. 1, 6 . B. 6 . C. 0, 5 . D. 0, 6 .
Câu 12. Cho cấp số nhân (u có u = 3 và u = 9 . Công bội của cấp số nhân đã cho bằng n ) 1 2 1 1 A. − . B. −2 . C. . D. 3 . 2 3
Câu 13. Với a,b là các góc bất kì. Trong các công thức sau, công thức nào đúng?
A. cos (a + b) = cos . a cos b + sin . a sin b
B. cos (a − b) = cos . a sin b + sin .
a sin b .
C. sin (a − b) = sin .
a cos b − cos .
a sin b .
D. sin (a + b) = sin .
a cos b − cos .
a sin b . 3 cot a + tan a
Câu 14. Cho sin a =
, 0  a  90 . Tính E = . 5 cot a − tan a 25 1 13 19 A. E = . B. E = − . C. E = − . D. E = − . 7 3 7 3
Câu 15. Khán đài A của một sân bóng có 16 hàng ghế. Biết hàng ghế đầu tiên có 8 ghế, mỗi hàng sau nhiều
hơn hàng trước 2 ghế. Hỏi khán đài A của sân bóng chứa được bao nhiêu người biết rằng mỗi người chỉ ngồi 1 ghế.
A. 365 người.
B. 366 người.
C. 367 người.
D. 368 người. 1
Câu 16. Cho sin = − .Tính cos 2 3 8 − 8 7 − 7 A. . B. . C. . D. . 9 9 9 9
Câu 17. Trong các đẳng thức sau đây, đẳng thức nào đúng?       A. tan − = tan   ( ) B. cot − = cot   ( ).  2   2        C. sin − = cos   ( ) . D. sin − = sin   ( ).  2   2  1 1
Câu 18. Cho sin.cos  = ; cos.sin  =
. Tính sin ( +  ) . 2 3 A. ( +  ) 1 sin = − . B. ( +  ) 5 sin = . 6 6 C. ( +  ) 2 sin = . D. ( +  ) 1 sin = . 3 6
Câu 19. Hàm số y = 2023sin 2x tuần hoàn với chu kì
A. T = 2 .
B. T = 2023 .
C. T = 3 .
D. T =  . Trang 2/4 - Mã đề 111 n
Câu 20. Cho dãy số u , n biết u =
. Chọn đáp án đúng. n 2n 1 1 1 1 A. u = . B. u = . C. u = . D. u = . 5 32 3 8 4 4 5 16
Câu 21. Tìm chu kì T của hàm số y = tan x + cot 3x  A. T = .
B. T = 4.
C. T = 3.
D. T = . 3
Câu 22. Cho cấp số cộng (u với u = 2 và u = 10 . Công sai của cấp số cộng đã cho bằng n ) 1 3 A. 3 . B. −4 . C. 8 . D. 4 .   
Câu 23. Tìm tất cả các nghiệm của phương trình sin x + =1   .  6    A. x = −
+ k2 (k  ) . B. x =
+ k2 (k  ) . 6 3 5  C. x =
+ k2 (k  ) . D. x =
+ k (k  ) . 6 3
Câu 24. Phương trình tan x =
3 có tập nghiệm là      A. −
+ k2 , k  .
B.  + k , k   .  3   6     
C.  + k 2 , k   .
D.  + k , k   .  6   3 
Câu 25. Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2 − sin x + 2 . C. y = 2 − sin x . D. y = 2 − cos x + 2 .   
Câu 26. Phương trình 2cos x + = 1  
có số nghiệm thuộc đoạn 0;2 là  3  A. 1 B. 2 C. 0 D. 3 n  
Câu 27. Cho dãy (u với 1 u = +1, * n   . Tính S
= u + u + u + ...+ u
, ta được kết quả n ) n    2  2023 1 2 3 2023 4047 1 1 6069 A. . B. 2024 − .. C. 2024 + . D. . 2 2023 2 2023 2 2
Câu 28. Trong các dãy số (u
cho bởi số hạng tổng quát u sau, dãy số nào là dãy số tăng? n ) n 1 n + 5 2n −1 1 A. u = . B. u = . u = . u = . n n n 3n + C. 1 n n + D. 1 n 2n
Câu 29. Cho cấp số nhân (u với u = −5 và công bội q = 3.Giá trị của u bằng n ) 1 5 A. 405 . B. 1875 . C. 405 − . D. 15 − .
Câu 30. Cho cấp số cộng (u có u = 2 và công sai d = 4 . . Tính u ? n ) 1 3
A. u = 8 .
B. u = 10 .
C. u = 12 .
D. u = 6 . 3 3 3 3  3   3 
Câu 31. Biểu thức A = cos(5 − x) − sin + x + tan
− x + cot(3 − x)     bằng  2   2  A. 0 . B. 1.
C. tan x .
D. 2 cos x . 1 2 3 4
Câu 32. Cho dãy số có các số hạng đầu là: , ,
, .... Số hạng tổng quát của dãy số này là: 2 3 4 5 n +1 n n −1 2 n − n A. u = . B. u = u = . D. u = n n n n + . C. 1 n n n n + . 1 Trang 3/4 - Mã đề 111
Câu 33. Cho một cấp số cộng (u
với u = 5 và u = 11
− . Khi đó số hạng u của cấp số cộng đã cho là n ) 1 9 4 A. −1. B. 2 . C. −2 D. 11.
Câu 34. Tìm tập xác định D của hàm số 2023 y = cos x   A. D =
\  + k , k  . B. D = \   0 .  2  C. D =
\ k , k  . D. D = .
Câu 35. Phương trình 2 cos 2x = có nghiệm là 2   A. x = 
+ k (k  ) . B. x = −
+ k2 (k  ) . 8 4 3  C. x = 
+ k2 (k  ) . D. x =
+ k (k  ) . 4 4 II. PHẦN TỰ LUẬN Câu 1: (1 điểm) 3
a) Giải phương trình sin 2x = . 2
b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số 4 4
y = 7 + 3cos x − 3sin x Câu 2: ( 1 điểm) u
 − u + u = 15
a) Cho cấp số cộng (u thỏa mãn 1 3 5 
. Tính tổng 10 số hạng đầu của cấp số cộng trên. n ) u + u = 27  1 6
b) Tìm giá trị x dương để 5x − 4;3 ;
x 5x + 4 lập thành cấp số nhân.
Câu 3 : ( 0.5 điểm)
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được cho bởi   
một hàm số y = 4sin (t −60) +10   với t 
và 0  t  365 . Vào ngày nào trong năm thì 178 
thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Câu 4: ( 0.5 điểm) Đầu mùa thu hoạch dưa hấu, ông A đã bán cho người thứ nhất nửa số dưa hấu thu hoạch
được và tặng thêm 1 quả, bán cho người thứ hai nửa số dưa hấu còn lại và tặng thêm 1 quả. Ông cứ
tiếp tục cách bán như trên thì đến người thứ chín số dưa hấu của ông được bán hết. Tính số dưa hấu
mà ông A thu hoạch được
------------- HẾT ------------- Trang 4/4 - Mã đề 111
ĐÁP ÁN CÁC MÃ ĐỀ
------------------------ Mã đề [111] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 A A B C C A B B D A C D C A D D C B
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D C D D B D C B B C C B A B A A A Mã đề [112] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 B B D A A C B A A D A C D B C C C B
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B A C C D C D B D B B D D C A A A Mã đề [113] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 B A A C C A D C A B B A D D B C B B
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A D C B A A D A D C D B D C C C B Mã đề [114] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 A C C D C D A B B D C C B B A C B A
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B A A C D B A D A B D A C D C D B Mã đề [115] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 B C C A B A D D B A D B C C B D A B
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C D C A D C D A D A A B C A C B B Mã đề [116] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 D A B B C A A B D C D C C A D B B B
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B B C C D C B A A D A D C A C D A
HƯỚNG DẪN GIẢI PHẦN TỰ LUẬN ĐỀ LẺ
Lưu ý: Học sinh làm cách khác nếu đúng thì cho điểm tối đa II. TỰLUẬN Bài Đáp án Điểm 3
a) Giải phương trình sin 2x = . 2 Ta có: 0,25 3 sin 2x =
⇔ sin 2x = sinπ  1 2  3    (1,0đ)  π  π 2x = + k2π x = + kπ 3 ⇔  (k∈) 6 ⇔  (k∈) 0,25 2π π 2x = + k2π x = + kπ  3  3
b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số 4 4
y = 7 + 3cos x − 3sin x 4 4
y = 7 + 3cos x − 3sin x = 7 + 3cos 2x 0,25 Vì 1
− ≤ cos 2x ≤1 nên 4 ≤ y = 7 +3cos2x ≤10 0,25
Giá trị lớn nhất bằng 10 khi x = kπ , nhỏ nhất bằng 4 khi π x = + kπ 2 u
 − u + u = 15
a) Cho cấp số cộng (u thỏa mãn 1 3 5
Tính tổng 10 số hạng đầu của cấp số n )  . u + u =  27 1 6 cộng trên. 2 u
 − u + u = 15 u  + 2d = 15 u  = 21 0,25 (1,0đ) Ta có: 1 3 5 1 1  ⇔  ⇔ u  u 27 2u 5d 27  + = + = d = 3 − 1 6 1
Tính tổng 10 số hạng đầu của cấp số cộng đã cho là: 0,25 10(2u + 9d 1 ) S = = 5 2.21 9. 3 75. 10 ( + (− )) = 2
b) Tìm giá trị x dương để 5x − 4;3 ;
x 5x + 4 lập thành cấp số nhân. Để 5x − 4;3 ;
x 5x + 4 lập thành cấp số nhân thì 0,25 3
 x = (5x − 4).q 
⇔ (3x)2 = (5x − 4)(5x + 4). 5  x + 4 = 3 . x q ⇔ (x)2 16 = 16 ⇔ x = 1 ± ⇒ x =1 0,25 Cho phương trình 2
(sin x +1).(sin 2x − msin x) = mcos x . Tìm tham số m để phương trình  π 
có nghiệm trên khoảng 0; . 6    Ta có 2
(sin x +1).(sin 2x − msin x) = mcos x . 3
⇔ (sin x +1).(sin 2x − msin x) = m(1− sin x).(1+ sin x) . (1) (0,5đ) 0,25  π Với x 0;  ∈ ⇒ 1+ sin x ≠  
0 , thì phương trình (1) tương đương:  6 
sin 2x − msin x = m(1− sin x) .
⇔ sin 2x = m .      Khi π  3 3 x ∈0; ⇒  sin 2x ∈0;  ⇒ m ∈0;  6  2 2      0,25
Đầu mùa thu hoạch dưa hấu, ông A đã bán cho người thứ nhất nửa số dưa hấu thu hoạch được
và tặng thêm 1 quả, bán cho người thứ hai nửa số dưa hấu còn lại và tặng thêm 1 quả. Ông cứ
tiếp tục cách bán như trên thì đến người thứ chín số dưa hấu của ông được bán hết. Tính số dưa
hấu mà ông A thu hoạch được
Gọi x là số quả dưa hấu mà ông A thu hoạch được 1 x + 2
Khi đó số quả dưa hấu mà người thứ nhất mua và được tặng là: x +1 = 2 2 4 1  x 2  x + 2 0,25
(0,5đ) Số quả dưa hấu mà người thứ hai mua và được tặng là: x + − +1 =   2 2  2  2 ... x + 2
Số quả dưa hấu mà người thứ chín mua và được tặng là: 9 2 x + 2 x + 2 x + 2  1 1 1 Khi đó: ... x x 2 ...  + + + = ⇔ + + + + =   x 2 9 ( ) 2 9 2 2 2  2 2 2  9 0,25  1 1  −   ⇔ (x + 2) 1  2  511 . = x ⇔
(x + 2) = x ⇔ x =1022 2 1 512 1− 2
HƯỚNG DẪN GIẢI PHẦN TỰ LUẬN ĐỀ CHẴN
Lưu ý: Học sinh làm cách khác nếu đúng thì cho điểm tối đa II. TỰLUẬN Bài Đáp án Điểm a) Giải phương trình 1 sin 2x = . 2 Ta có: 0,25 1
sin 2x = ⇔ sin 2x = sinπ    1 2  6  (1,0đ)  π  π 2x = + k2π x = + kπ 6 ⇔  (k∈) 12 ⇔  (k∈) 0,25 5π 5π 2x = + k2π x = + kπ  6  12
b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số 4 4
y = 6 + 4cos x − 4sin x 4 4
y = 6 + 4cos x − 4sin x = 6 + 4cos 2x 0,25 Vì 1
− ≤ cos 2x ≤1 nên 2 ≤ y = 6+ 4cos2x ≤10 0,25
Giá trị lớn nhất bằng 10 khi x = kπ , nhỏ nhất bằng 2 khi π x = + kπ 2 u
 − u + u = 9
a) Cho cấp số cộng (u thỏa mãn 1 3 5
Tính tổng 10 số hạng đầu của cấp n )  . u + u =  21 1 6 số cộng trên. 2  0,25
Ta có: u − u + u = 9 u 2d 9 u 3 1 3 5  + =  =  . ⇔  1 ⇔ 1 (1,0đ)  u + u =  21 2u 5d 21 d 3 1 6  + = =  1 
Tính tổng 10 số hạng đầu của cấp số cộng đã cho là: 0,25 10(2u + 9d 1 ) S = = 5 2.3 9. 3 165. 10 ( + ( )) = 2
b) Tìm giá trị x dương để 5x − 4;3 ;
x 5x + 4 lập thành cấp số nhân. Để 5x − 3;4 ;
x 5x + 3lập thành cấp số nhân thì 0,25
4x = (5x − 3).q 
⇔ (4x)2 = (5x − 3)(5x + 3) . 5  x + 3 = 4 . x q ⇔ (x)2 9 = 9 ⇔ x = 1 ± ⇒ x =1 0,25 Cho phương trình 2
(sin x +1).(cos 2x − msin x) = mcos x . Tìm tham số m để phương trình  π 
có nghiệm trên khoảng 0; . 6    Ta có 2
(sin x +1).(cos 2x − msin x) = mcos x .
⇔ (sin x +1).(cos 2x − msin x) = m(1− sin x).(1+ sin x) . (1) 0,25 3  π Với x 0;  ∈ ⇒ 1+ sin x ≠  
0 , thì phương trình (1) tương đương: (0,5đ)  6 
cos 2x − msin x = m(1− sin x) .
⇔ cos 2x = m .  π Khi   1   1 x
0;  cos2x  ;1 m  ;1 ∈ ⇒ ∈ ⇒ ∈  6 2 2        0,25
Đầu mùa thu hoạch dưa hấu, ông A đã bán cho người thứ nhất nửa số dưa hấu thu hoạch được
và tặng thêm 1 quả, bán cho người thứ hai nửa số dưa hấu còn lại và tặng thêm 1 quả. Ông cứ
tiếp tục cách bán như trên thì đến người thứ tám số dưa hấu của ông được bán hết. Tính số dưa
hấu mà ông A thu hoạch được
Gọi x là số quả dưa hấu mà ông A thu hoạch được 1 x + 2
Khi đó số quả dưa hấu mà người thứ nhất mua và được tặng là: x +1 = 4 2 2 (0,5đ) 1  x 2  x + 2 0,25
Số quả dưa hấu mà người thứ hai mua và được tặng là: x + − +1 =   2 2  2  2 ... x + 2
Số quả dưa hấu mà người thứ tám mua và được tặng là: 8 2 x + 2 x + 2 x + 2  1 1 1 Khi đó: ... x x 2 ...  + + + = ⇔ + + + + =   x 2 8 ( ) 2 8 2 2 2  2 2 2  8 0,25  1 1  −   ⇔ (x + 2) 1  2  255 . = x ⇔
(x + 2) = x ⇔ x = 510 2 1 255 1− 2
Document Outline

• Made 111
• Dap an