Đề giữa học kỳ 1 Toán 9 năm 2022 – 2023 trường THCS Giảng Võ – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra đánh giá chất lượng giữa học kỳ 1 môn Toán 9 năm học 2022 – 2023 trường THCS Giảng Võ, quận Ba Đình, thành phố Hà Nội; kỳ thi được diễn ra vào thứ Ba ngày 01 tháng 11 năm 2022. Mời bạn đọc đón xem.
Preview text:
UBNN QUẬN BA ĐÌNH
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 TRƯỜNG THCS GIẢNG VÕ NĂM HỌC 2022-2023 Môn: TOÁN 9 ĐỀ CHÍNH THỨC Ngày kiểm tra: 01/11/2022 (Đề thi gồm 01 trang)
Thời gian làm bài: 90 phút
Bài I. (2,0 điểm) Rút gọn các biểu thức sau: a) A 2 3 3 5 80 6; b) 18 4 3 3 ; 4 B 6 5 1 1 3 0 tan29 1 c) C 2 0 sin 33 2 0 .cos 60 2 0 sin 57 . 0 cot61 2
Bài II. (2,0 điểm) Giải các phương trình sau: 1 a) 9 x 2 9x 18 24 ; b) 2
x 6x 9 2 x 3 0. 3 x x 1 1
Bài III. (2,0 điểm) Cho hai biểu thức: A 2 và B với x 0, x 4 . x x 4 x 2 x 2
a) Tính giá trị của biểu thức A khi x 25;
b) Rút gọn biểu thức B ; c) Cho M . A B . Tìm x để M M. Bài IV. (3,5 điểm)
1) Một người đứng ở trên đỉnh một ngọn hải đăng cao 150m so
với mực nước biển và quan sát thấy một chiếc thuyền ở xa với một góc nghiêng 0
40 so với phương nằm ngang. Hỏi chiếc thuyền đang
ở cách chân ngọn hải đăng bao nhiêu m ? (Kết quả làm tròn đến chữ số hàng đơn vị).
2) Cho hình chữ nhật ABCD . Gọi H là hình chiếu của điểm D trên đường thẳng AC . a) Giả sử AD 9c ,
m AB 12cm . Tính độ dài đoạn thẳng DH ; số đo
DAC (số đo góc làm tròn đến phút). 2 DC CH b) Chứng minh rằng: ; 2 BC AH
c) Gọi M và N lần lượt là hình chiếu của điểm H trên đường thẳng AD và DC . Chứng minh rằng: SBAC 1 1 . S 2 2 DMN sin DAC cos HDC
Bài V. (0,5 điểm) Cho các số thực x, y 0 thỏa mãn x y 2 . Tìm giá trị nhỏ nhất của biểu
thức: P x y 2022 xy .
----------------------Hết---------------------
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA KÌ I MÔN TOÁN 9 Năm học 2022-2023 A. HƯỚNG DẪN CHUNG:
+) Điểm toàn bài để lẻ đến 0,25, trong cùng một bài có 2 lỗi trừ 1/8 thì trừ 1/4.
+) Bài III giải phương trình, HS có thể không tìm ĐK mà thử lại thấy x thỏa mãn phương trình thì vẫn cho điểm tối đa.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Bài hình vẽ hình sai thì không cho điểm.
B. HƯỚNG DẪN CHẤM CỤ THỂ: Bài Ý Đáp án Điểm a) A 2 3 3 5 80 6 0,75 4 3 3 5 .4 5 6 0,25 4 3 5 3 5 6 0,25 2 5 3 0,25 b) 18 4 3 3 B 0,75 6 5 1 1 3 4 5 1 3 3 1 Bài I 3 0,25 2,0 điểm 5 1 3 1 3 5 1 3 0,25 5 1 0,25 c) 0 2 0 tan29 1 2 0 2 0 C sin 33 .cos 60 sin 57 0 cot61 2 0,5 2 0 2 0 2 0 tan 29 1 1 sin 33 cos 33 . 0,25 0 tan 29 2 2 1 1 1 1 0,25 8 8 1 9 x 2 9x 18 24 1,0 Bài II a) 3 2,0 điểm ĐK: x 2 . 0,25
9 x 2 x 2 24 0,25 8 x 2 24 x 2 3 0,25 x 2 9
x 7 (TMĐK). Vậy phương trình có nghiệm x 7 . 0,25 b) 2
x 6x 9 2 x 3 0 1,0 ĐK: x 3 . 0,25 2
x 6x 9 2 x 3 (x 2 3) 4(x 3) 0,25 (x 3)(x 7) 0 x 3 0 x 3 (TMDK ) 0,25 x 7 0 x 7 (TMDK )
Phương trình có tập nghiệm là S 3;7. 0,25
a) Tính giá trị của biểu thức A khi x 25. 0,5 25 2
Thay x 25 (TMĐK) vào biểu thức A ta có: A 0,25 25 Tính được 7 A 5 0,25 x 1 1 b) Rút gọn biểu thức B x 4 x 1,0 2 x 2 x x 2 x 2 B 0,25
x 2 x 2 x 2 x 2 x 2 x 2 x x 2 x 2 B 0,25 x 2 x 2 x 2 x Bài III B 2,0 điểm x 2 x 2 x x 2 B 0,25 x 2 x 2 x 0,25 B x 2 c) Cho M . A B . Tìm x để M M. 0,5 x 2 x x M A B 2 . x x 2 x 2 x 2 0,25 Có M M M 0 0 (do x 2 0) x 2
x 2 0 x 2 x 4 0,25
KHĐKXĐ: M M 0 x 4 1)
Một người đứng ở trên đỉnh một ngọn hải đăng cao 150m so với mực 0,5
nước biển và quan sát thấy một chiếc thuyền ở xa với một góc nghiêng 0
40 so với phương nằm ngang. Hỏi chiếc thuyền đang ở cách chân ngọn
hải đăng bao nhiêu m? (Kết quả làm tròn đến chữ số hàng đơn vị).
Xét MNP vuông tại M ta có: tan MN MN NPM MP 0,25 MP tan NPM MN 150 MP 179 (m). tan NPM tan 40o 0,25
Vậy chiếc thuyền đang ở cách chân ngọn hải đăng khoảng 179m .
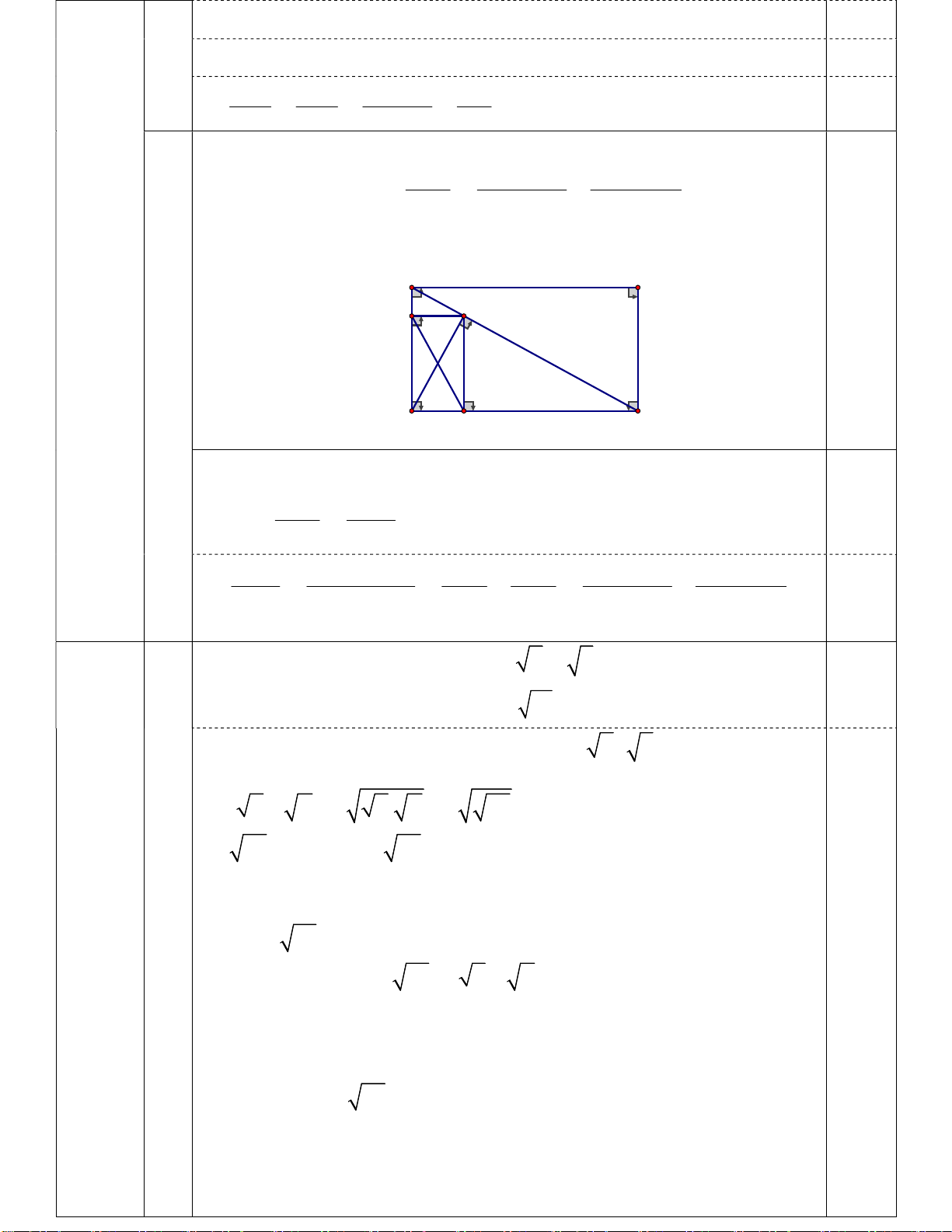
2) Cho hình chữ nhật ABCD . Gọi H là hình chiếu của điểm D trên đường thẳng AC .
a) Giả sử AD 9cm, AB 12cm . Tính độ dài đoạn thẳng DH , số đo
DAC (số đo góc làm tròn đến phút) 2 DC CH b) Chứng minh rằng . 2 BC AH
c) Gọi M, N lần lượt là hình chiếu của điểm H trên đường thẳngAD và SBAC 1 1 DC . Chứng minh rằng: Bài IV 2 S 2 DMN sin DAC cos HDC 3,0 điểm
Hình vẽ đúng đến hết câu a) A B H 0,5 D C
a) Giả sử AD 9cm, AB 12cm . Tính độ dài đoạn thẳng DH ; số đo 1,0
DAC (số đo góc làm tròn đến phút)
Theo định lí Py-ta-go, tính được AC = 15 cm 0,25
Áp dụng HTL trong ADC vuông tại D đường cao DH ta có: AD.DC DH AC AD DC DH 9.12 . . 7,2 (cm) 0,25 AC 15 0,25 Ta có 12 4 tanDAC . 9 3 Suy ra 53 8 o DAC '. 0,25 2 b) Chứng minh rằng DC CH . 2 BC AH 1,0
Áp dụng HTL trong ADC vuông tại D đường cao DH ta có: 2 )DC CH.AC 0,25 +) 2 AD AH.AC 0,25
Mà ABCD là hình chữ nhật AD BC 0,25 2 2 DC DC AC.CH CH (đpcm) 2 2 BC AD AC.AH AH 0,25
c) Gọi M và N lần lượt là hình chiếu của điểm H trên đường thẳngAD và SBAC 1 1 DC . Chứng minh rằng: 2 S 2 DMN sin DAC cos HDC . A B 0,5 H M D C N +) Chứng minh được: D MN ∽ DCA ∽ BAC 2 S AC 0,25 BAC 2 S MN DMN 2 2 2 2 2 1 1 ) AC AD DC AD DC 2 2 2 2 2 MN DH DH DH 2 sin DAC cos HDC 0,25 (Đpcm)
Cho các số thực x, y 0 thỏa mãn x y 2 . Tìm giá trị nhỏ 0,5
nhất của biểu thức: P x y 2022 xy .
Áp dụng bất đẳng thức Cô-si cho hai số dương x , y ta có 2 x y 2 x. y 2 xy xy 1 2 022 xy 2 022 (1)
Áp dụng bất đẳng thức Cô-si cho hai số dương x,y Bài V 0,5 điểm x y 2 xy 2 2
2x 2y x y 2 xy ( x y ) 2 4 x y 2 (2) 0,25
Cộng vế với vế của (1) và (2) ta có
P x y 2022 xy 2 2022 2020.
Dấu bằng xảy ra khi x y 1. Vậy P 2 020 khi x y 1. min 0,25