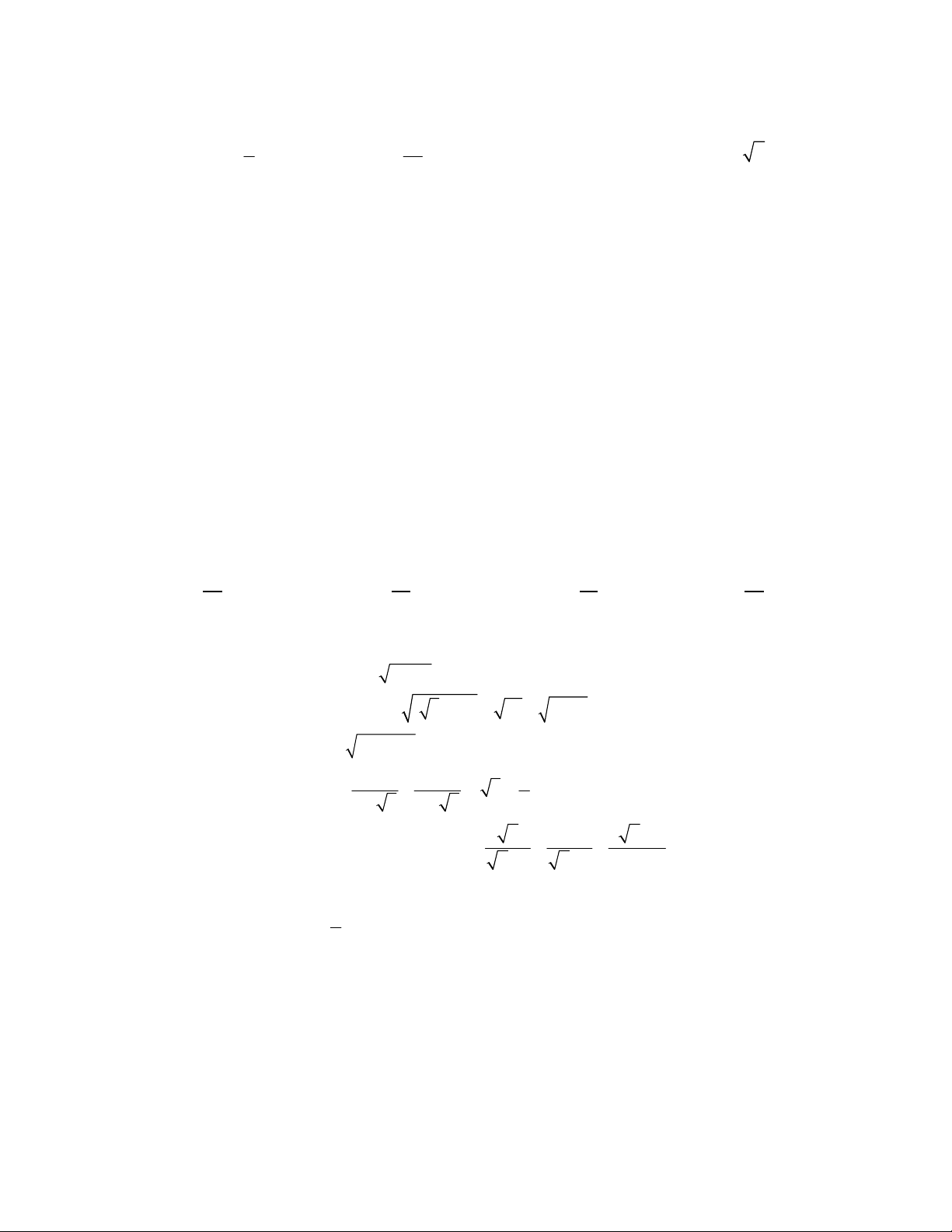

Preview text:
PHÒNG GD&ĐT LẠNG GIANG
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THCS HƯƠNG SƠN
NĂM HỌC 2022 – 2023 MÔN: TOÁN 9 Mã đề 901
Thời gian làm bài 90 phút, không kể thời gian giao
I. TRẮC NGHIỆM (3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng
trước phương án đó vào bài làm.
Câu 1: Kết quả của phép tính 3 3 + 2 3 bằng: 3 1 A. 3
3. B. 3. C. 3 3. D. 3.
Câu 2: Căn bậc hai số học của 4 là:
A. 2 B. 2 và -2 C. 16 D. 16 và -16
Câu 3: Các căn bậc hai của 16 là: A. ±4 B. 4 C. - 4 D. ± 2
Câu 4: Căn bậc ba của (-27) là: A. 3
B. -3 C . 3 và - 3 D. 9 và -9
Câu 5: Với 16x - 25x = -3 khi đó x bằng: A. 3 B. 0 C. -9 D. 9
Câu 6: Điều kiện xác định của căn thức : 6 2x là: A. x 3 B. x 0 C. x 3 D. x 6
Câu 7: Với x > 0 biểu thức 2 (3 2x) bằng A. 3 - 2x.
B. 2x - 3. C. 3 – 2x hoặc 2x - 3. D. 3 – 2x và 2x - 3 .
Câu 8: Phép tính nào có kết quả đúng: A. 100 1
0 B. 1 2 3 C. 9 4 5 D. 10 : 2 5 2
Câu 9: Biểu thức 3 5 sau khi bỏ dấu căn là: A. 3 5 B. 5 3 C. 2 5 D. 5 3
Câu 10: Kết quả so sánh 3 và 10 là: A. 3 10 B. 3 10 C. 3 10 D. 3 10 1
Câu 11: Rút gọn biểu thức là: 2 1 A. 2 1 B. 2 1 C. 2 D. 2
Câu 12. Trong các hàm số sau, hàm số nào là số bậc nhất ?
A. y = 1- 1 . B. y = 2 5. C. y = x + 1. D. y = 2 x 1. x 3x
Câu 13. Cho hàm số y f (x) 3x 1. Khẳng định nào sau đây là đúng ? 1
A. f (5) f (7).
B. f (3) f (4).
C. f (1) f (3). D. f (2) f (1).
Câu 14. Hệ số góc của đường thẳng y = 2 - 3x là? A. -3 B. 2. C. 3 . D. -1
Câu 15. Cho hàm số y m - 3 x 5, hàm số đồng biến khi A. m 3. B. m 3. C. m 3. D. m 3 .
Câu 16. Tam giác MNP vuông tại M , khẳng định nào sau đây là đúng ? A. MP N .
P SinN. B. MP N . P Sin . P C. MP N . P CosN. D.
MP MN.Co t N.
Câu 17: Một cột điện cao 5m có bóng trên mặt đất dài 4 .
m Khi đó phương tia nắng tạo với
mặt đất một góc xấp xỉ bằng (làm tròn đến phút) A. 0 38 40'. B. 0 53 8'. C. 0 36 52'. D. 0 51 20'.
Câu 18: : Cho tam giác ABC vuông tại A có đường cao AH ,Sin B bằng
A .ு B. ு C. D. ு
Câu 19. Cho tam giác ABC vuông tại A có AB = 6 cm; AC = 8cm. Khi đó bán kính
đường tròn ngoại tiếp tam giác đó bằng:
A. 7 cm B. 3cm C. 4 cm D. 5 cm
Câu 20: Cho tam giác ABC vuông tại .
A Biết AB : AC 5: 6 và đường cao AH 30c . m
Độ dài đoạn BH bằng A. 30 cm. B. 12 cm. C. 36 cm. D. 25 cm.
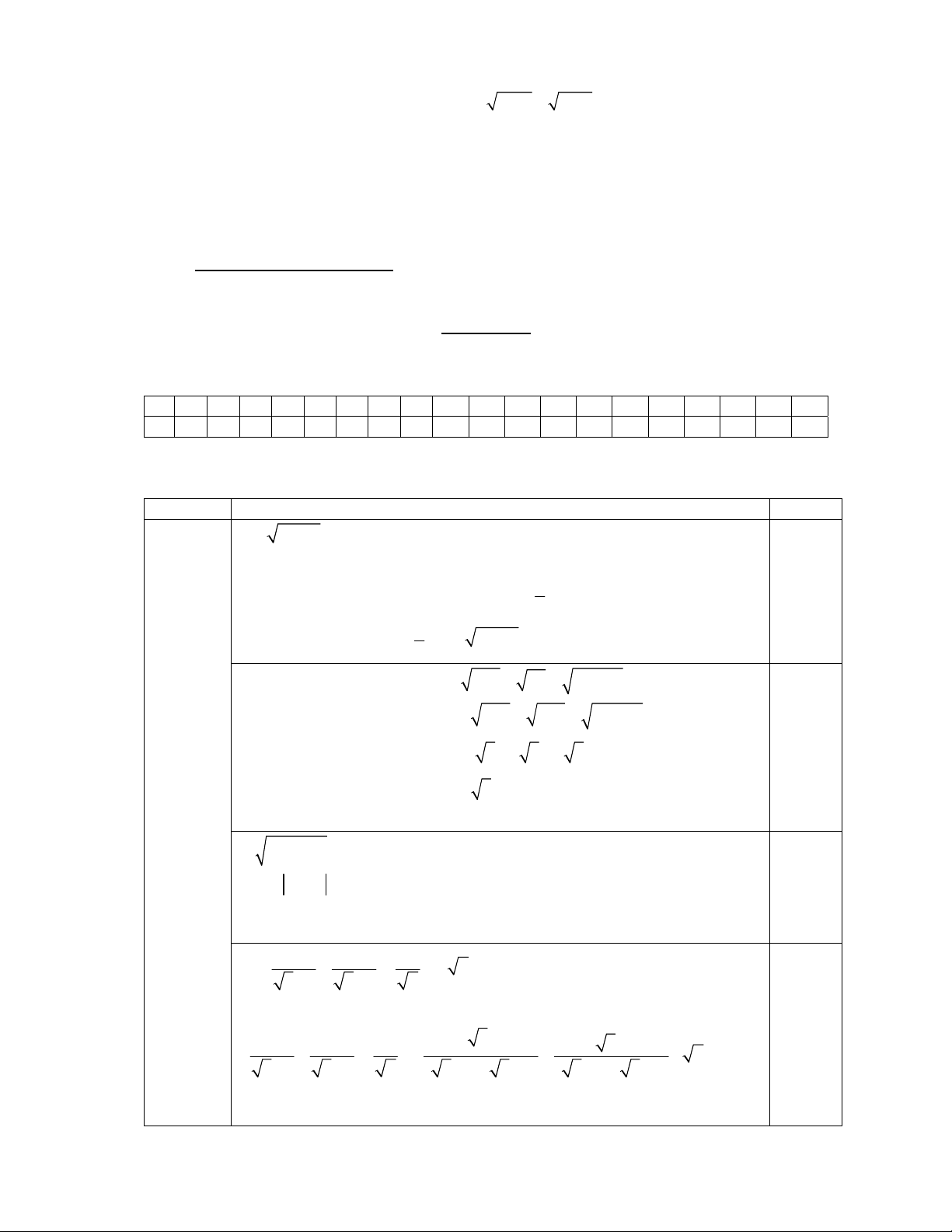
PHẦN II. TỰ LUẬN (7 điểm) Câu 21: ( 3 điểm)
a) Tìm điều kiện của x để 3 6x xác định.
b) Tính giá trị của biểu thức: 2 2 2 .3 27 ( 5) .3 c) Giải phương trình: 2 (2 x1) 3 d) Chứng minh rằng: 2 2 1 : 2 2 3 1 3 1 2 x x
Câu 22: ( 1,5 điểm) Cho biểu thức 3 6 4 M
với x 0; x 1 x 1 x 1 x 1 a) Rút gọn biểu thức M b) Tìm x để M< 3 4
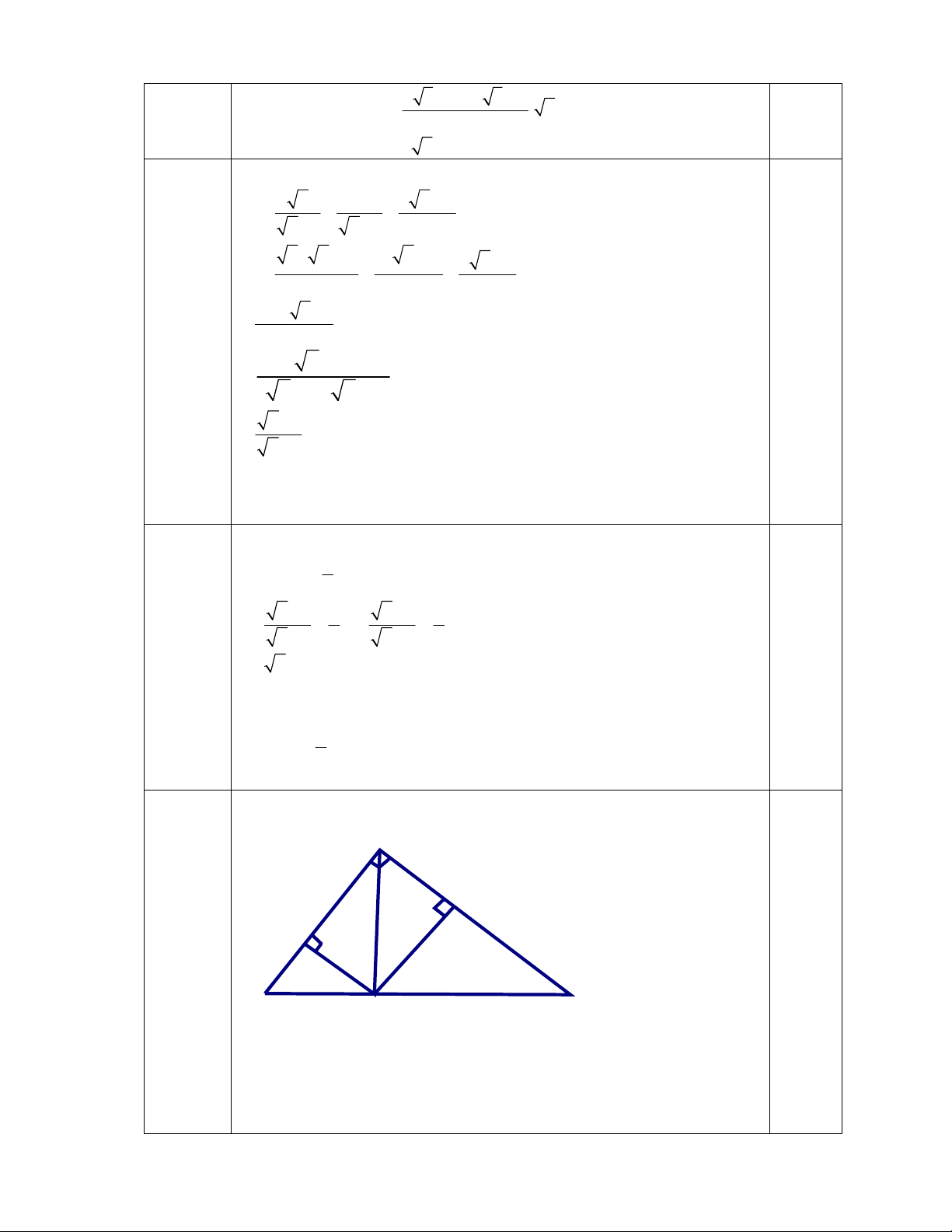
Câu 23: (2 điểm) Cho ∆ABC vuông tại A, đường cao AH (HBC). Vẽ HE vuông góc
với AB tại E, HD vuông góc với AC tại D
a) Cho biết AB = 9cm, AC = 12cm Tính các độ dài BC, AH.
b) Chứng minh bốn điểm A, E, H, D cùng thuộc một đường tròn.
c) Chứng minh: AE.EB + AD.DC = AH2
Câu 24: (0,5 điểm). Cho các số thực dương a, b thỏa mãn ab 2020a 2021b
Chứng minh bất đẳng thức: a b 2 2020 2021 2
..........................HẾT ..................................
PHÒNG GD&ĐT LẠNG GIANG
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THCS HƯƠNG SƠN
NĂM HỌC 2022 – 2023 MÔN: TOÁN 9 Mã đề 902
Thời gian làm bài 90 phút, không kể thời gian giao
I. TRẮC NGHIỆM (3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1: Căn bậc hai số học của 4 là:
A. 2 B. 2 và -2 C. 16 D. 16 và -16
Câu 2: Với 16x - 25x = -3 khi đó x bằng: A. 3 B. 0 C. -9 D. 9
Câu 3: Kết quả của phép tính 3 3 + 2 3 bằng: 3 1 A. 3 3. B. 3. C. 3 3. D. 3.
Câu 4: Điều kiện xác định của căn thức : 6 2x là: A. x 3 B. x 0 C. x 3 D. x 6
Câu 5: Phép tính nào có kết quả đúng: A. 100 1
0 B. 1 2 3 C. 9 4 5 D. 10 : 2 5
Câu 6: Các căn bậc hai của 16 là: A. ±4 B. 4 C. - 4 D. ± 2 2
Câu 7: Biểu thức 3 5 sau khi bỏ dấu căn là: A. 3 5 B. 5 3 C. 2 5 D. 5 3
Câu 8: Căn bậc ba của (-27) là: A. 3
B. -3 C . 3 và - 3 D. 9 và -9
Câu 9: Kết quả so sánh 3 và 10 là: A. 3 10 B. 3 10 C. 3 10 D. 3 10
Câu 10: Với x > 0 biểu thức 2 (3 2x) bằng A. 3 - 2x.
B. 2x - 3. C. 3 – 2x hoặc 2x - 3. D. 3 – 2x và 2x - 3 . 1
Câu 11: Rút gọn biểu thức là: 2 1 A. 2 1 B. 2 1 C. 2 D. 2
Câu 12. Hệ số góc của đường thẳng y = 2 - 3x là? A. -3 B. 2. C. 3 . D. -1
Câu 13. Cho hàm số y m - 3 x 5, hàm số đồng biến khi 3 A. m 3. B. m 3. C. m 3. D. m 3 .
Câu 14. Trong các hàm số sau, hàm số nào là số bậc nhất ?
A. y = 1- 1 . B. y = 2 5. C. y = x + 1. D. y = 2 x 1. x 3x
Câu 15. Cho hàm số y f (x) 3x 1. Khẳng định nào sau đây là đúng ?
A. f (5) f (7).
B. f (3) f (4).
C. f (1) f (3). D. f (2) f (1).
Câu 16. Tam giác MNP vuông tại M , khẳng định nào sau đây là đúng ? A. MP N .
P SinN. B. MP N . P Sin . P C. MP N . P CosN. D.
MP MN.Co t N.
Câu 17. Cho tam giác ABC vuông tại A có AB = 6 cm; AC = 8cm. Khi đó bán kính
đường tròn ngoại tiếp tam giác đó bằng:
A. 7 cm B. 3cm C. 4 cm D. 5 cm
Câu 18: Cho tam giác ABC vuông tại .
A Biết AB : AC 5: 6 và đường cao AH 30c . m
Độ dài đoạn BH bằng A. 30 cm. B. 12 cm. C. 36 cm. D. 25cm.
Câu 19: Một cột điện cao 5m có bóng trên mặt đất dài 4 .
m Khi đó phương tia nắng tạo với
mặt đất một góc xấp xỉ bằng (làm tròn đến phút) A. 0 38 40'. B. 0 53 8'. C. 0 36 52'. D. 0 51 20'.
Câu 20: : Cho tam giác ABC vuông tại A có đường cao AH ,Sin B bằng
A .ு B. ு C. D. ு
PHẦN II. TỰ LUẬN (7 điểm) Câu 21: ( 3 điểm)
e) Tìm điều kiện của x để 3x 6 xác định.
f) Tính giá trị của biểu thức: 2 2 ( 3 2) 12 ( 2) g) Giải phương trình: 2 (3x 1) 5 h) Chứng minh rằng: 1 1 1 : 5 3 5 3 5 2 x x
Câu 22: ( 1,5 điểm) Cho biểu thức 3 6 4 M
với x 0;x 1 x 1 x 1 x 1 a) Rút gọn biểu thức M b) Tìm x để M< 1 2
Câu 23: (2 điểm) Cho ∆ABC vuông tại A, đường cao AH (HBC). Vẽ HE vuông góc
với AB tại E, HD vuông góc với AC tại D
a) Cho biết AB = 9cm, AC = 12cm Tính các độ dài BC, AH.
b) Chứng minh bốn điểm A, E, H, D cùng thuộc một đường tròn.
c) Chứng minh: AE.EB + AD.DC = AH2
Câu 24: (0,5 điểm). Cho các số thực dương a, b thỏa mãn ab 2020a 2021b 4
Chứng minh bất đẳng thức: a b 2 2020 2021
..........................HẾT ..................................
IV. ĐÁP ÁN VÀ THANG ĐIỂM
PHÒNG GD&ĐT LẠNG GIANG HƯỚNG DẪN CHẤM
TRƯỜNG THCS HƯƠNG SƠN
ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC: 2022-2023
Môn: TOÁN – Lớp 9 ĐỀ SỐ 901
A- Trắc nghiệm : (Mỗi câu đúng 0,15đ)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B A D B D C B D A B A C C A B A D B D D B- Tự luận : (7đ)
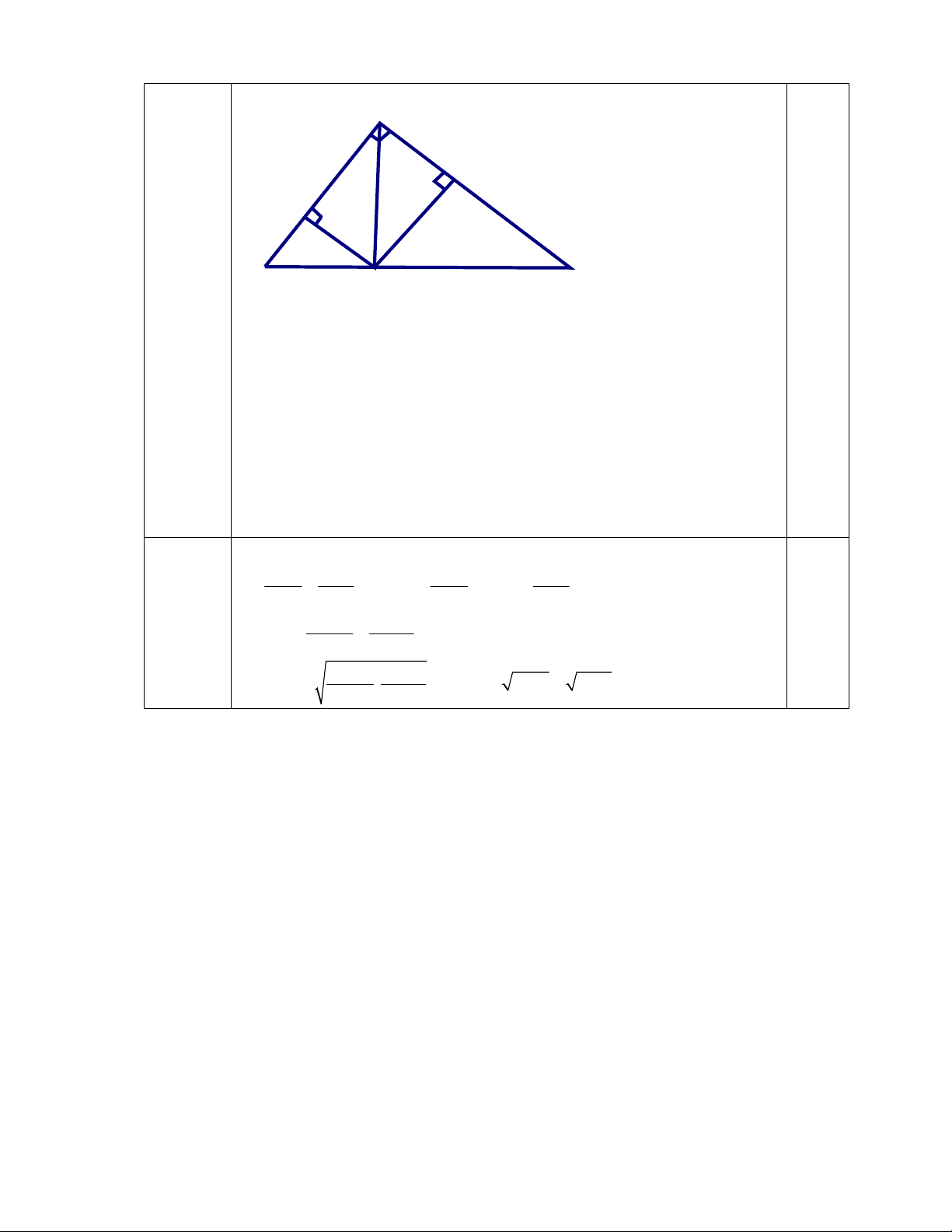
Bài Lời giải sơ lược Điểm Câu 21
1) 3 6x xác định khi và chỉ khi 3 - 6 x 0 (3,0 0, 25 điểm) -6 x -3 x 1 0,25 3 Vậy với x 1
thì 3 6x xác định. 0,25 3
2)Tính giá trị của biểu thức: a) 2 2 2 .3 27 ( 5) .3 2 2 2 2 .3 3 .3 ( 5) .3 0,25 = 2 3 3 3 5 3 = 0,25 4 3 = 0,25 x 2 3) 2 1 3
2x 1 3 0,25
Giải ra được x = 2 hoặc x = - 1 0,25 KL... 0,25 2 2 1 4) : 2 2 3 1 3 1 2
Biến đổi vế trái ta có: 2. 3 1 2 2 1 2( 3 1) : . 2 0,25 3 1 3 1 2
( 3 1).( 3 1) ( 3 1).( 3 1) 0,25 0,25 5 2 3 2 2 3 2 . 2 2 2 2
Vậy đẳng thức được cm Câu 22
a) Với x 0; x 1, ta có: ( 1,5đ) x 3 6 x 4 M x 1 x 1 x 1 x x 1 3 x 1 6 x 4 M 0,25đ x 1 x 1 x 1 x 2 x 1 x 1 2 ( x 1) 0,25đ
( x 1)( x 1) x 1 0,25đ x 1 KL 0,25đ
b) ) với x 0; x 1 Ta có M< 3 4 x 1 < 3 x 1 - 3 < 0 x 1 4 x 1 4 0,25
x 7 < 0 x < 49
Kết hợp điều kiện bài cho ta được 0 x 49 và x 1
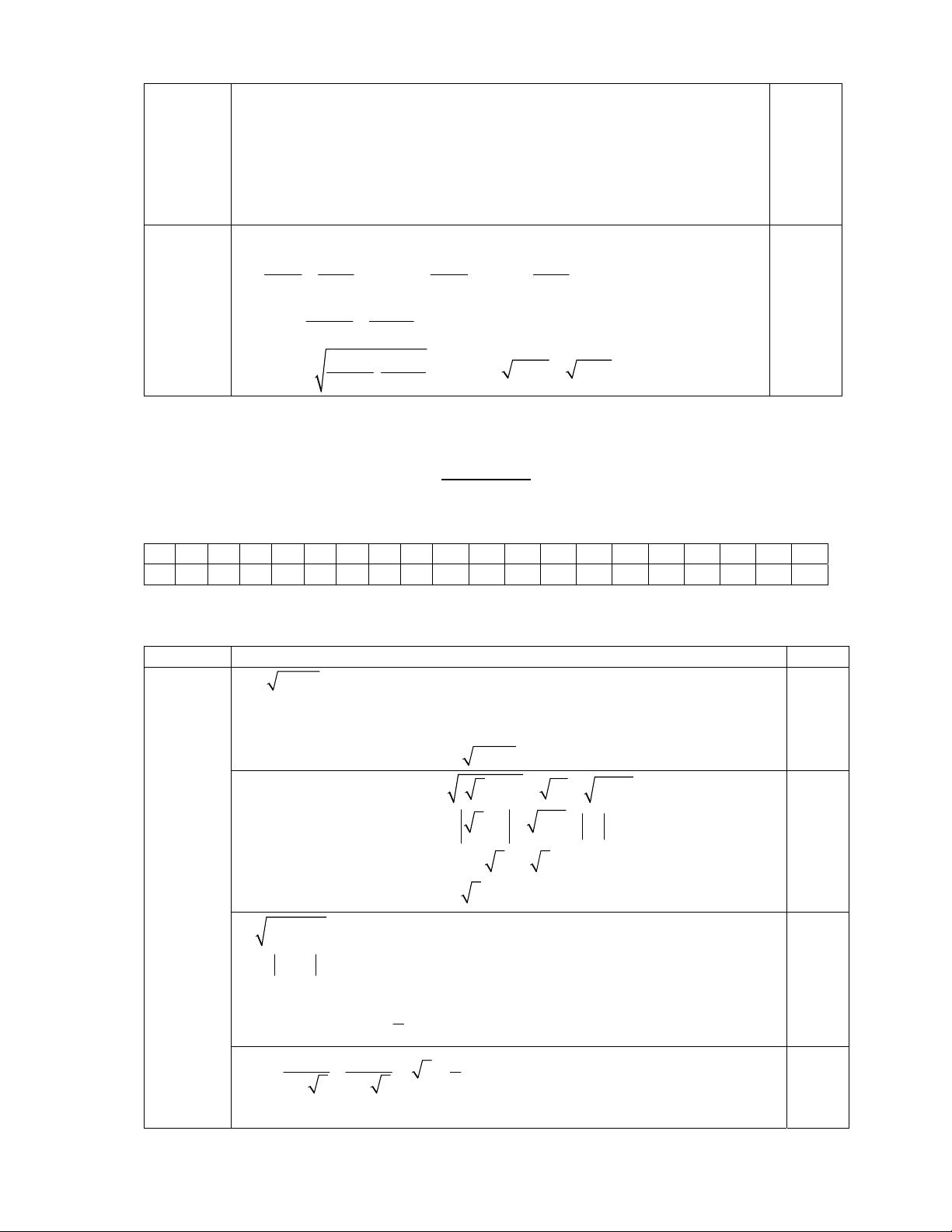
Vậy M< 3 thì 0 x 49 và x 1. 4 0,25đ Câu 23 Vẽ hình: (2điểm) A D E B C H a) Tính được BC 0,25 Tính được AH 0,25 KL 0,25
b) Chứng minh được tứ giác AEHD là hình chữ nhật 0,5 0,25 6
=> A, E, H, D cùng thuộc đường tròn .
c) Chứng minh được EH2 = AE.EB. HD2 = AD.DC 0,25
EH2 + HD2 = AE. EB + AD.DC ED2= AE. EB + AD.DC Mà ED = AH ( AEHD là HCN) 0, 25 đpcm Câu 24
Từ giả thiết ab 2020a 2021b suy ra: (0,5điểm) 2020 2021 2020 2021 1 a b a b a b b a b a 2020a 2021b 2020 2021 0,25 b a 2020a 2021b 0,25 2020 2 .
2021 2020 20212 b a
Học sinh làm cách khác chặt chẽ, chính xác vẫn chấm điểm tối đa. ĐỀ SỐ 902
A- Trắc nghiệm : (Mỗi câu đúng 0,15đ)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A D B C D D A B B B A A B C C A D D D B B- Tự luận : (7đ)
Bài Lời giải sơ lược Điểm Câu 21
1) 3x 6 xác định khi và chỉ khi 3x - 6 0 0,25 (3,0 điểm) 3 x 6 0,25 x 2 0,25
Vậy với x 2 thì 3x 6 xác định. ( 3 2 2) 12 ( 2 2) 3 2 2 2 .3 2
2)Tính giá trị của biểu thức: 0,25 2 3 2 3 2 0,25 3 0,25 x 2 3) 3 1 5 3x 1 5
3x -1 = 5 hoặc 3x-1 = -5 0,25 0,25 x = 2 hoặc x = 4 KL... 0,25 3 1 1 1 4. : 5 3 5 3 5 2
Biến đổi vế trái ta có: 7 1 1 : 5 3 5 3 5 3 5 3 5 1 . (3 5)(3 5) (3 5)(3 5) 5 2 5 1 . 9 5 5 0,25 1 2 0,25
Vậy đẳng thức được cm 0,25 Câu 22
a) Với x 0; x 1, ta có: ( 1,5đ) x 3 6 x 4 M x 1 x 1 x 1 x x 1 3 x 1 6 x 4 M 0,25đ x 1 x 1 x 1 x 2 x 1 x 1 2 ( x 1) 0,25đ
( x 1)( x 1) x 1 0,25đ x 1 0,25đ KL
b) ) với x 0; x 1 Ta có M< 1 2 x 1 < 1 x 1 - 1 < 0 0,25 x 1 2 x 1 2
x 3< 0 x < 9
Kết hợp điều kiện bài cho ta được 0 x 9 và x 1 0,25
Vậy M < 1 thì 0 x 9 và x 1. 2 Câu 23 Vẽ hình: (2điểm) 8 A D E B C H a) Tính được BC 0,25 Tính được AH 0,25 KL 0,25
b) Chứng minh được tứ giác AEHD là hình chữ nhật 0,25
=> A, E, H, D cùng thuộc đường tròn . 0,25
c) Chứng minh được EH2 = AE.EB. HD2 = AD.DC
EH2 + HD2 = AE. EB + AD.DC 0,25 ED2= AE. EB + AD.DC Mà ED = AH ( AEHD là HCN) đpcm 0, 25 Câu 24
Từ giả thiết ab 2020a 2021b suy ra: (0,5điểm) 2020 2021 2020 2021 1 a b a b a b b a b a 2020a 2021b 2020 2021 0,25 b a 2020a 2021b 0,25 2020 2 .
2021 2020 20212 b a
Học sinh làm cách khác chặt chẽ, chính xác vẫn chấm điểm tối đa. 9