

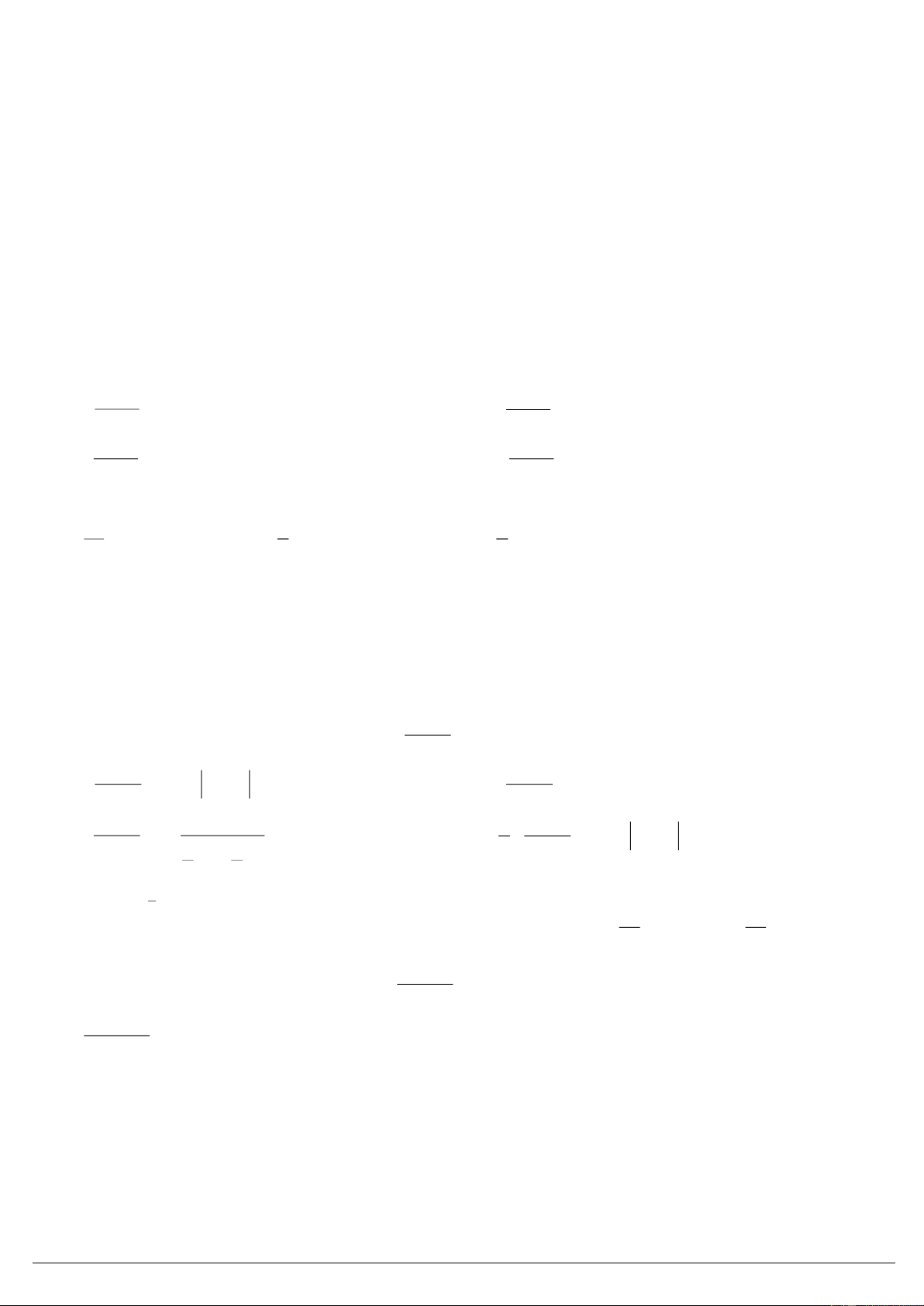
Preview text:
TRƯỜNG THPT THỐNG NHẤT A
ĐỀ KIỂM TRA GIỮA HỌC KỲ II Điểm:
Năm học: 2021 – 2022
Môn: TOÁN HỌC – 12. Thời gian làm bài: 90 phút Mã đề: 104
I. PHẦN TRẮC NGHIỆM (35 câu – 7 điểm)
Câu 1. Cho hàm số f liên tục và không âm trên đoạn a; b
. Công thức tính diện tích S của hình thang
cong giới hạn bởi đồ thị hàm số y = f (x) , trục Ox và hai đường thẳng có phương trình x = ; a x = b là b b b b 2 A. S = f (x) dx .
B. S = f (x)dx .
C. S = f (x) dx . D. S = f ( x) dx . a a a a
Câu 2. Hàm số F(x) = sin x + 1 là một nguyên hàm của hàm số nào?
A. f (x) = c s
o x + x .
B. f (x) = − cos x .
C. f (x) = cos x .
D. f (x) = − c s o x + x .
Câu 3. Cho hàm số f (x) là hàm số liên tục trên đoạn a; b
. Giả sử F (x) là một nguyên hàm của f (x)
trên đoạn a; b
. Mệnh đề nào dưới đây là ĐÚNG? b b
A. f (x)dx = F(b) − F(a) .
B. f (x)dx = f (b) − f (a) . a a b b
C. f (x)dx = F(a) − F(b) .
D. f (x)dx = F(a) + F(b) . a a
Câu 4. Cho hàm số y = f ( x) liên tục trên đoạn a;b . Mệnh đề nào dưới đây SAI? b a a b b b
A. f (x)dx = − f (x)dx
. B. f (x)dx = 1 .
C. dx = b − a
. D. f (x)dx = f (t)dt . a b a a a a
Câu 5. Cho hai hàm số f (x) , g (x) liên tục trên . Trong các mệnh đề sau, mệnh đề nào SAI? A. f
(x).g(x)dx = f (x)d .x g
(x)dx. B. f
(x)− g(x)dx = f
(x)dx− g (x)dx.
Trang 1/4 - Mã đề thi 104 C. f
(x)+ g(x)dx = f
(x)dx+ g
(x)dx. D. kf
(x)dx = k f
(x)dx ( k ,k 0).
Câu 6. Trong không gian Oxyz , cho mặt cầu có phương trình 2 2 2
x + y + z − 2x + 4y − 6z + 9 = 0 . Tọa độ tâm
I và bán kính R của mặt cầu là
A. I (1; − 2; 3) và R = 5 .
B. I (1; − 2; 3) và R = 5 . C. I ( 1
− ; 2; − 3) và R = 5 . D. I ( 1
− ; 2; − 3) và R = 5 .
Câu 7. Cho f (x) là hàm số liên tục trên đoạn ; b c và a ; b c
. Tìm một mệnh đề đúng. b c c c b a A. f
(x)dx− f
(x)dx = f
(x)dx . B. f
(x)dx+ f
(x)dx = f (x)dx . a a c a c b b c b b a b C. f
(x)dx+ f
(x)dx = f
(x)dx . D. f
(x)dx+ f
(x)dx = f (x)dx . a a c a c c
Câu 8. Khẳng định nào sau đây ĐÚNG?
A. 2xdx = 2 + xdx
B. 2xdx = 2dx + xdx
C. 2xdx = 2d .x xdx
D. 2xdx = 2 xdx
Câu 9. Tìm nguyên hàm của hàm số ( ) x f x = e . x+1 A. x x−1 e dx = xe + C . B. x x
e dx = e + C . C. x e e dx = + C . D. x x
e dx = xe + C . x + 1
Câu 10. Trong không gian với hệ trục tọa độ Oxyz, cho a = −i + 2j − 3k . Tọa độ của vectơ a là A. ( 3 − ; 2; − ) 1 . B. (2; 1 − ; 3 − ). C. (2; 3 − ; − ) 1 . D. ( 1 − ; 2; 3 − ).
Câu 11. Trong không gian Oxyz , điểm nào dưới đây nằm trên mặt phẳng (P) : 2x − y + z − 2 = 0 . A. P (2; 1 − ; − ) 1 . B. N (1; 1 − ; 1 − ) . C. M (1;1; 1 − ) . D. Q(1; 2 − ; 2) .
Câu 12. Trong không gian với hệ toạ độ Oxyz , cho ba vectơ a = ( 1
− ;1;0) , b = (1;1;0) , c = (1;1;−1). Trong
các mệnh đề sau, mệnh đề nào sai?
A. b,c = a ⊥ . C. c = 2 a = . . B. a c . D. 2
Câu 13. Giả sử f là hàm số liên tục trên khoảng K và a, b là số bất kỳ trên khoảng K . Khẳng định nào sau đây sai? b a b b A. f
(x)dx = − f
(x)dx . B. f
(u)du = f (x)dx . a b a a a b b C. f
(x)dx = 1. D. kf
(x)dx = k f
(x)dx ( k là hằng số) a a a
Câu 14. Trong không gian Oxyz , mặt phẳng (P) : x + 2y − 3z + 3 = 0 có một vectơ pháp tuyến là A. (1; 2; 3 − ) . B. (1; 2; 3) . C. (1; 2 − ; 3) . D. ( 1 − ; 2; 3 − ) . 3 3 Câu 15. Cho f
(x)dx = 1. Khi đó J = f
(x)−2dx bằng A. 2 . B. 5
− . C. −7 . D. 4 . 0 0 6
Câu 16. Cho hàm số f (x) liên tục trên và F (x) là nguyên hàm của f (x) , biết f
(x)dx = 9 và 0
F (0) = 1 . Tính F (6) .
A. F (6) = 10 .
B. F (6) = 8 .
C. F (6) = 6 . D. F (6) = 6 − .
Câu 17. Trong không gian Oxyz, cho điểm A(1; 2
− ; 3) . Hình chiếu vuông góc của điểm A trên mặt
phẳng (Oyz) là điểm M. Tọa độ của điểm M là
Trang 2/4 - Mã đề thi 104
A. M (1; 0; 0) . B. M (1; 2 − ;0) .
C. M (1; 0; 3) . D. M (0; 2 − ; 3) . Câu 18. Để tìm 4 sin . x cos xdx
cách làm nào sau đây phù hợp nhất?
A. Dùng phương pháp đổi biến số đặt t = sin x . 4 u = sin x
B. Dùng phương pháp nguyên hàm từng phần đặt .
dv = cos xdx
C. Dùng phương pháp đổi biến số đặt t = cos x . u = cos x
D. Dùng phương pháp nguyên hàm từng phần đặt . 4
dv = sin xdx
Câu 19. Hàm số F(x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu A. f (
x) = −F(x), x K . B. f (
x) = F(x), x K . C. F (
x) = − f (x), x K . D. F (
x) = f (x), x K .
Câu 20. Chọn một khẳng định đúng. 1 1 A.
dx = − cot x + C B.
dx = − t anx + C 2 os c x 2 os c x 1 1 C.
dx = t anx + C D.
dx = cot x + C 2 os c x 2 os c x
Câu 21. Họ nguyên hàm của hàm số 5
y = (2x + 1) là 1 1 1 A. 6
(2x + 1) + C . B. 6
(2x + 1) + C . C. 6
(2x + 1) + C . D. 4
10(2x + 1) + C . 12 6 2
Câu 22. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A(6; 2; − 5) , B( 4 − ; 0; 7) . Viết phương
trình mặt cầu đường kính AB . 2 2 2 2 2 2
A. (x + 5) + (y + )
1 + (z − 6) = 62 . B. (x + )
1 + (y + 1) + (z + 1) = 62 . 2 2 2 2 2 2
C. (x − 5) + (y − 1) + (z + 6) = 62 . D. (x − )
1 + (y −1) + (z − 1) = 62 . 2x + 1
Câu 23. Tìm nguyên hàm của hàm số f (x) = . 2 x + x 2x + 1 2x + 1 A. 2
dx = ln x + x + C B. dx = ln
( 2x +x +C 2 ) 2 x + x x + x 2 2x + 1 x + x 1 2x + 1 C. dx = + C D. 2
dx = ln x + x + C 2 x + x 1 2 + 3 1 2 2 x + x x x 3 2 2 1 1
Câu 24. Tính (2 − x)sin d x x . A. 1 − . B. 1 . C. . D. − . 50 50 0 +
Câu 25. Họ nguyên hàm của hàm số ( ) 3 3x x f x = là x 3 3x + 2x A. + C . B. 4 2
12x + 2x + C . C. 3
x + x + C . D. 2 3x + 1 + C . 4 1 2 2 Câu 26. Cho f
(x)dx = 2, f
(x)dx = 4, khi đó f (x)dx = ?
A. 2 . B. 3 . C. 1 . D. 6 . 0 1 0
Câu 27. Trong không gian Oxyz , cho hai điểm A( 1 − ; 2; )
1 và B(2;1; 0) . Mặt phẳng qua A và vuông góc
với AB có phương trình là
A. 3x − y − z − 6 = 0 .
B. 3x − y − z + 6 = 0 .
C. x + 3y + z − 5 = 0 .
D. x + 3y + z − 6 = 0 .
Trang 3/4 - Mã đề thi 104
Câu 28. Trong không gian Oxyz cho mặt phẳng (P) : 2x − 2y + z + 5 = 0 . Khoảng cách từ M ( 1 − ; 2; − 3) 4 4 2 4
đến mặt phẳng (P) bằng A. − . B. . C. . D. . 3 3 3 9
Câu 29. Tìm nguyên hàm F (x) của hàm số f (x) = sin x + x thoả mãn F (0) = 2 . x x A. F (x) 2 = −cos x + + 3 B. F (x) 2 = cos x + + 1 2 2 x C. F (x) 2 = cos x − + 1
D. F (x) = −cos x + 3 2 2 sin 2xdx
Câu 30. Xét tích phân I =
. Nếu đặt t = 1+ cos x , ta được: + 0 1 cos x 2 1 3 4t − 4t 2 1 3 4 − t + 4t A. I = 4
− ( 2t −1)dt B. I = dt
C. I = 4 ( 2t +1)dt D. I = dx t t 1 2 1 2 1
Câu 31. Cho tích phân = ( + 3) x I x
e dx = ae + b , với a,b . Mệnh đề nào dưới đây là ĐÚNG? 0
A. a − b = 5 − . B. ab = 6 − . C. 3 3
a + b = 28 .
D. a + 2b = 7 .
Câu 32. Với C là hằng số, mệnh đề nào trong các mệnh đề sau ĐÚNG? 1
A. dx = C . B.
dx = ln x + C . x 1 1 C. +1 x dx = x + C( R) = + . D. . + t anxdx C 1 2 sin x 5 dx Câu 33. Giả sử = ln c
. Giá trị của c là A. 81 B. 8 C. 9 D. 3 2x − 1 1 b
Câu 34. Cho hàm số f (x) có f (x) liên tục trên đoạn a; b
, f (a) = 3 và f
(x)dx =10 giá trị của f (b) a bằng A. 13 . B. −7 . C. 7 . D. 13 − .
Câu 35. Trong không gian Oxyz , cho hai mặt phẳng (P) : x + 2y − 2z − 6 = 0 và (Q) : x + 2y − 2z + 3 = 0 .
Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng A. 6 . B. 9 . C. 3 . D. 1 .
II. PHẦN TỰ LUẬN (4 câu – 3 điểm) 2
Câu 36. (1 điểm) Tính tích phân A =
1 + 3 cos x sin xdx . 0
Câu 37. (1 điểm) Cho mặt cầu (S) có tâm I, bán
kính R = 5. Một mặt phẳng (P) cắt (S) theo giao
tuyến là đường tròn (C) có tâm H, bán kính r = 4.
Mặt nón (N) có đỉnh A và đường tròn đáy là (C).
Tính diện tích xung quanh của hình nón (N).
(Tham khảo hình vẽ bên).
Câu 38. ( 0,5 điểm) Tìm một nguyên hàm F(x) của hàm số f(x) = xsin2x biết F(0) = 3. 1 −
Câu 39. ( 0,5 điểm) Tính tích phân B = l n(x + 3)dx . 2 − --- HẾT ---
Trang 4/4 - Mã đề thi 104
ĐÁP ÁN TỰ LUẬN TOÁN 12 – KT GIỮA KỲ 2 (Năm học 2021-2022).
Người ra đề: Nguyễn Lê Quỳnh 2
Câu 36. (1 điểm) Tính tích phân A 1 3cos x sin xdx . 0
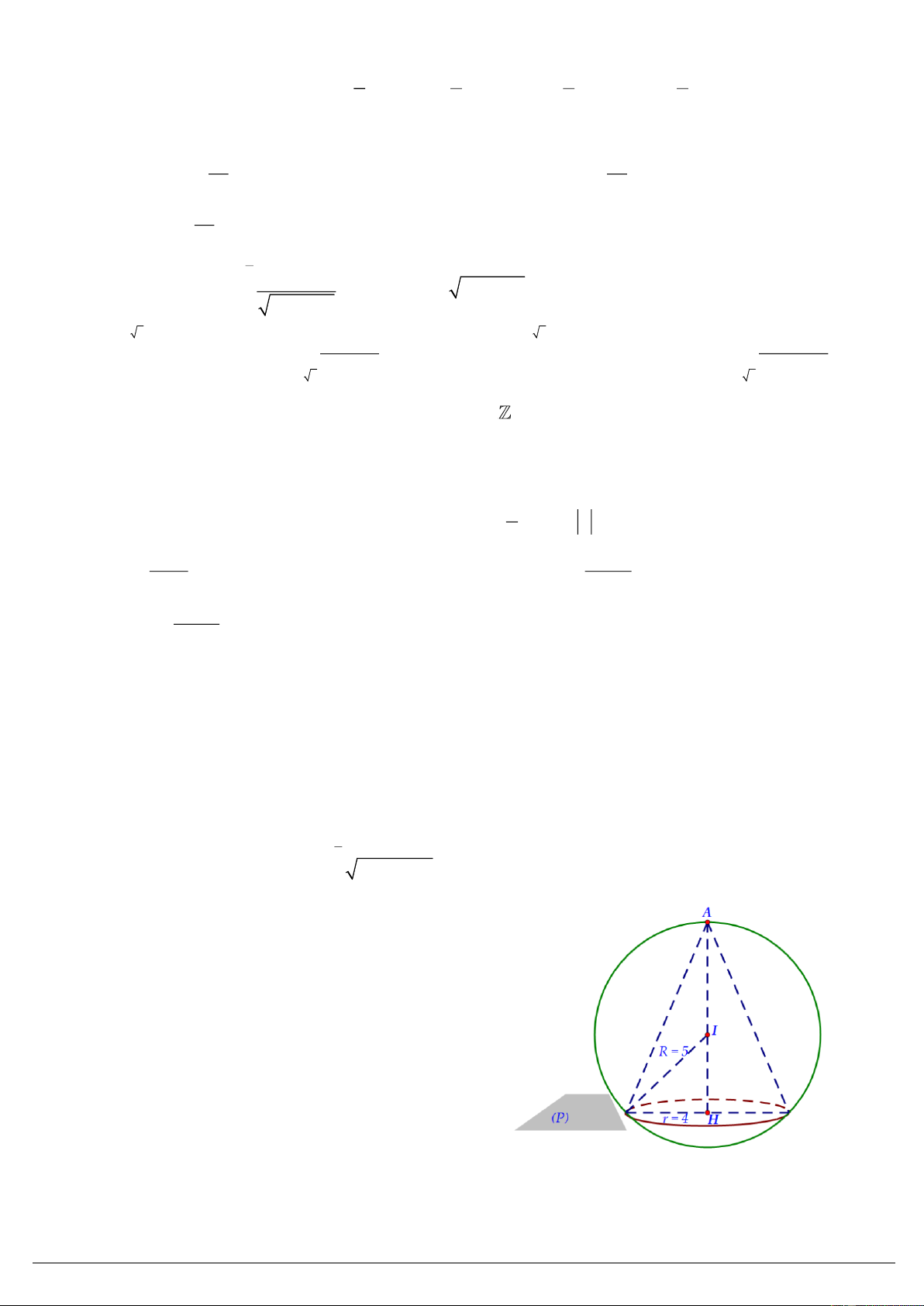
Câu 37. (1 điểm) Cho mặt cầu (S) có tâm I, bán
kính R = 5. Một mặt phẳng (P) cắt (S) theo giao
tuyến là đường tròn (C) có tâm H, bán kính r = 4.
Mặt nón (N) có đỉnh A và đường tròn đáy là (C).
Tính diện tích xung quanh của hình nón (N).
(Tham khảo hình vẽ bên).
Câu 38. ( 0,5 điểm) Tìm một nguyên hàm F(x) của hàm số f(x) = xsin2x biết F(0) = 3. 1
Câu 39. ( 0,5 điểm) Tính tích phân B ln(x 3)dx . 2 Câu Nội dung Điểm Đặt 2 2
t 1 3cos x t 1 3cos x sin xdx tdt 0,25 3 36 2 x 0 t 2; x t 1, do đó 2 2 A t dt (1 điểm) 2 3 0,25 1 2 2 3 14 t . 0,25 + 0,25 1 9 9
Đọc được IH = 3 và AH = 8. 0,25 37
Độ dài đường sinh của hình nón là 2 2 l r AH 4 5 . 0,25
(1 điểm) Diện tích xung quanh của (N) là S rl . xq 16 5 0,25 + 0,25 u x du dx F(x) xsin2xdx . Đặt 1
dv sin 2xdx v cos 2x 2 0,25 38 x 1 F(x) cos 2x cos 2xdx (0,5 điểm) 2 2 x 1
cos 2x sin 2x C 2 4 0,25
Mà F(0) = 3 nên tìm được C = 3. Vậy x 1
F(x) cos 2x sin 2x 3 . 2 4 1 Đặt u ln(x 3) du dx x 3 0,25 dv dx v x 3 39 1 (0,5 điểm) Nên 1
B (x 3)ln(x 3) dx 0,25 2 2ln 2 1 2
Nếu học sinh không khéo chọn v = x + 3 thì giáo viên tự chia điểm theo
tiến trình làm bài của học sinh.
Document Outline
- TOAN 12 - GIUA KI 2 - MD 104
- ĐÁP ÁN TOÁN 12




