Đề giữa học kỳ 2 Toán 12 năm 2023 – 2024 trường chuyên Biên Hòa – Hà Nam

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kỳ 2 môn Toán 12 năm học 2023 – 2024 trường THPT chuyên Biên Hòa, tỉnh Hà Nam; đề thi có đáp án trắc nghiệm mã đề Đề 101 Đề 102 Đề10 3 Đề 104 Đề 105 Đề 106 Đề 107 Đề 108. Mời bạn đọc đón xem!

60 30 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

13 trang 6 tháng trước

Tác giả:

Profile M. Hậu
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NAM
TRƯỜNG THPT CHUYÊN BIÊN HÒA
(Đề thi có 06 trang)
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
NĂM HỌC 2023-2024
Môn: Toán. Lớp: 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Họ tên: ........................................................................Số báo danh: ............................. ......
Câu 1. Cho hàm số
3 2
2 4 khi 4
1
khi 4
4
x x
f x
x x x x
. Tích phân
2
2
0
2sin 3 sin 2 df x x x
bằng
A.
341
96
. B.
28
3
. C. 8. D.
341
48
Câu 2. Cho
F x
là một nguyên hàm của hàm số
2
1
1
f x
x
. Giá trị của
' 2 2 ' 0
F F
là:
A.
2
3
B.
. C.
1
3
. D.
Câu 3. Chướng ngại vật “tường cong” trong một sân thi đấu X-Game là một khối bê tông có chiều cao từ mặt đất
lên là 3 m. Giao của mặt tường cong và mặt đất là đoạn thẳng
2AB
m. Thiết diện của khối tường cong cắt bởi
mặt phẳng vuông góc với
AB
tại
A
là một hình tam giác vuông cong
ACE
với
4
AC
m,
3
CE
m và cạnh
cong
AE
nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí
M
là trung điểm của
AC
thì tường cong có độ cao 1 m
Thể tích khối tường cong đó là
A.
3
14
m .
3
B.
3
35
m .
3
C.
3
24 m .
D.
3
28
m .
3
Câu 4. Cho khối nón có đỉnh
S
, chiều cao bằng 8 và thể tích bằng
800
3
. Gọi
A
và
B
là hai điểm thuộc đường
tròn đáy sao cho
12AB
, khoảng cách từ tâm của đường tròn đáy đến mặt phẳng
SAB
bằng
A.
4 2
. B.
24
5
. C.
5
24
. D.
8 2
.
Mã đề 101
2
Câu 5. Cho hàm số
f x
liên tục trên
.
Biết
,
F x G x
lần lượt là các nguyên hàm của các hàm số
f x
và
1
f x
thỏa mãn
2 2 4.
G F
Tính tích phân
2
0
.I G x F x xdx
A.
3
20
. B. 20. C.
20
3
. D. 8.
Câu 6. Biết
cos 2 d sin 2 cos 2
x x x ax x b x C
với
a
,
b
là các số hữu tỉ. Tính tích
ab
.
A.
1
8
ab
. B.
1
8
ab
. C.
1
4
ab
. D.
1
4
ab
.
Câu 7. Cho hàm số
3
2
4 0
4 0
x khi x
f x
x khi x
. Tích phân
4
3
f x dx
bằng
A. 46. B. 45. C. 47. D.
13
12
.
Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số
2
2
,
1
x
y x y
x
là
ln 2
a b
với
là các số hữu
tỷ. Giá trị
a b
là
A. 1. B.
11
.
3
C.
7
.
3
D.
5.
Câu 9. Nguyên hàm của hàm số
2
ln 2
f x x x
là:
A.
2 2
2
2
ln 2
2 2
x x
x C
. B.
2 2
2
2
ln 2
2 2
x x
x C
C.
2 2 2
2 ln 2
x x x C
. D.
2
2 2
2 ln 2
2
x
x x C
Câu 10. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 6 1 0
S x y z x y z
. Tâm của (S) có tọa độ là
A.
2;4;6
. B.
2; 4; 6
. C.
1; 2; 3
. D.
1; 2;3
.
Câu 11. Tính
sin 2 dx x x
.
A.
2
cos 2
2
x
x C
. B.
2
cos2
2
x
x C
. C.
2
cos2
2 2
x x
C
. D.
2
sin
2
x
x C
.
Câu 12. Cho
2
0
d 5
f x x
. Tính
2
0
2cos dI f x x x
.
A.
3
I
. B.
5I
.
C.
7
I
. D.
5
2
I
.
Câu 13. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
2; 2;1
M
trên mặt phẳng
Oxy
có tọa độ là
A.
0; 2;1
. B.
0;0;1
. C.
2; 2;0
. D.
2;0;1
.
Câu 14. Diện tích hình phẳng giới hạn bởi hai đường thẳng
0
x
,
x
, đồ thị hàm số
cosy x
và trục
Ox
là
A.
0
cos dS x x
. B.
2
0
cos dS x x
. C.
0
cos dS x x
. D.
0
cos dS x x
.
3
Câu 15. Biết
3
1
2
ln ,
x
dx a b c
x
với
, , , 9.
a b c c
Tính tổng
.S a b c
A.
6
S
. B.
5
S
. C.
7
S
. D.
8
S
.
Câu 16. Cho hàm số
f x
có đạo hàm trên đoạn
1;2
,
1 1
f
và
2 2
f
. Tích phân
2
1
I f x dx
bằng
A. 2. B. 3. C. 0. D. 1.
Câu 17. Giả sử tích phân
5
1
1
ln 3 ln5 , ,
1 3 1
I dx a b c a b c
x
. Giá trị của giá trị biểu thức
P a b c
là
A.
7
.
3
P
B.
5
.
3
P
C.
8
.
3
P
D.
4
.
3
P
Câu 18. Cho biết
2 13
ln 1 ln 2
1 2
x
dx a x b x C
x x
với a, b là các số nguyên và C là hằng số thực.
Mệnh đề nào sau đây đúng?
A.
8
a b
. B.
8
a b
. C.
2 8
a b
. D.
2 8
a b
.
Câu 19. Cho
3
2
, 0;
1
x
I dx x
x

. Bằng phép đổi biến
2
1
u x
, khẳng định nào sau đây sai?
A.
2
1 .I u udu
. B.
3
3
u
I u C
. C.
xdx udu
. D.
2 2
1
x u
.
Câu 20. Giá trị
2
1
2 3
dx
x
bằng
A.
7
2ln
5
. B.
1
ln 35
2
. C.
1 7
ln
2 5
. D.
7
ln
5
.
Câu 21. Cho
F x
là một nguyên hàm của
1
1
f x
x
trên khoảng
1;

thỏa mãn
1 4
F e
. Tìm
F x
.
A.
4ln 1
x
. B.
ln 1 3
x
. C.
ln 1 3
x
. D.
2ln 1 2
x
.
Câu 22. Trong không gian
Oxyz
, cho hai điểm
5;2;1
A
và
1;0;1
B
. Phương trình của mặt cầu đường kính
là
A.
2 2 2
3 1 1 20
x y z
. B.
2 2 2
3 1 1 5
x y z
.
C.
2 2 2
3 1 1 20
x y z
. D.
2 2 2
3 1 1 5
x y z
.
Câu 23. Tính tích phân
1
0
e d
x
I x
.
A. -1. B.
1
1
e
. C.
1
e
. D.
1
1
e
.
Câu 24. Cho hàm số
y f x
có đồ thị trên
2;6
như hình vẽ bên. Biết các miền A, B, C có diện tích lần lượt là
32; 2; 3. Tích phân
2
2
2 2 1
f x dx
bằng
4
A. 41. B. 37. C.
45
2
. D.
41
2
.
Câu 25. Họ nguyên hàm của hàm số
2
2
cos
x
x
e
y e
x
là
A.
2 tan
x
e x C
. B.
2 tan
x
e x C
. C.
1
2
cos
x
e C
x
. D.
1
2
cos
x
e C
x
.
Câu 26. Cho
2
1
2,
f x dx
2
1
1
g x dx
. Khi đó
2
1
2 3
I x f x g x dx
bằng
A.
1
.
2
I
B.
17.
I
C.
17
.
2
I
D.
15
.
2
I
Câu 27. Cho
F x
là một nguyên hàm của hàm số
1
ln
f x
x x
thỏa mãn
1
2
e
F
và
e ln 2.
F
Giá trị của
biểu thức
2
2
1
e
e
F F
bằng
A.
3ln2 2
. B.
ln2 1
. C.
ln2 2
. D.
2ln2 1
.
Câu 28. Cho
2
2
d 1f x x
,
4
2
d 4
f t t
. Tính
4
2
df y y
.
A.
5
I
. B.
3
I
. C.
3
I
. D.
5
I
.
Câu 29. Trong không gian
Oxyz
, cho hai vectơ
1;2; 2
u
và
2; 2;3
v
. Tọa độ của vectơ
u v
là
A.
3;0;1
. B.
1; 4;5
. C.
1; 4; 5
. D.
3;0; 1
.
Câu 30. Cho
1
2
0
1
2ln ln3
3 2
I dx a b
x x
, với
*
, .
a b
Giá trị
ab
bằng
A. 12. B. 6. C. 2. D.
3
.
Câu 31. Cho
F x
là một nguyên hàm của hàm số
2
4 2
x
f x e x
thỏa mãn
0 1
F
. Hàm số
F x
là:
A.
2 2
4 3
x
F x e x
. B.
2 2
2 1
x
F x e x
. C.
2 2
2 1
x
F x e x
. D.
2 2
2 1
x
F x e x
.
Câu 32. Cho hàm số
f x
có đạo hàm liên tục trên
. Biết
3 1
f
và
1
0
3 d 1
xf x x
, khi đó
3
2
0
d
x f x x
bằng
A.
9
. B. 7. C.
25
3
. D. 3.
5
Câu 33. Cho hàm số
( )f x
thỏa mãn
(2)
f e
và
2
( ) ( )
x
f x e f x
với mọi
.
x
Giá trị của
(1)f
bằng
A.
2.
. B.
2
.e
C.
. D.
e
.
Câu 34. Cho hàm số
4
2
2 3
x
f x
x
. Khẳng định nào sau đây đúng?
A.
3
3
2
f x dx x C
x
. B.
3
2 3
3
x
f x dx C
x
.
C.
3
2 3
3
x
f x dx C
x
. D.
3
2 3
3 2
x
f x dx C
x
.
Câu 35. Biết rằng hàm số
f x
liên tục trên
;a b
và có một nguyên hàm là
F x
. Khẳng định nào trong các
khẳng định sau là đúng?
A.
.
b
a
f x dx F a F b
B.
.
b
a
f x dx F a F b
C.
.
b
a
f x dx F b F a
D.
.
b
a
f x dx f a f b
Câu 36. Biết
4
*
0
1 sin 2 , , , 5 .
2
b
a
x xdx a b a
Giá trị của tích ab bằng
A. 4. B. 12. C. 2. D. 6.
Câu 37. Tìm nguyên hàm của hàm số
1
5 2
f x
x
.
A.
d
ln 5 2
5 2
x
x C
x
. B.
d 1
ln 5 2
5 2 2
x
x C
x
.
C.
d
5ln 5 2
5 2
x
x C
x
. D.
d 1
ln 5 2
5 2 5
x
x C
x
.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
1;0;3
A
,
2;3; 4
B
,
3;1;2
C
. Tìm tọa độ điểm
D
sao cho
ABCD
là hình bình hành.
A.
4;2;9
D
. B.
4; 2;9
D
. C.
4; 2;9
D
. D.
4;2; 9
D
.
Câu 39. Hàm số
3
x
F x e
là một nguyên hàm của hàm số
A.
3
2
3
x
e
f x
x
. B.
3
2
3 .
x
f x x e
. C.
3
x
f x e
. D.
3
3 1
.
x
f x x e
.
Câu 40. Tìm
222x
e dx
.
A.
222
.
222
x
e
B.
222 x
e
. C.
222
.
222
x
e
x
D.
222
222 .
x
e
Câu 41. Trong không gian
Oxyz
, cho hai điểm
1;3;0
A
và
5;1; 2
B
. Mặt phẳng trung trực của đoạn thẳng
AB
có phương trình là:
A.
3 2 14 0
x y z
. B.
2 3 0
x y z
. C.
2 5 0
x y z
. D.
2 5 0
x y z
.
6
Câu 42. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ) : ( 1) ( 2) ( 3) 1
S x y z
và điểm
(2;3;4)
A
. Xét các điểm
M
thuộc
( )S
sao cho đường thẳng
AM
tiếp xúc với
( )S
,
M
luôn thuộc mặt phẳng có phương trình là
A.
7 0
x y z
. B.
7 0
x y z
.
C.
2 2 2 15 0
x y z
. D.
2 2 2 15 0
x y z
.
Câu 43. Trong không gian với hệ trục tọa độ
Oxyz
, tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
2 2 2 2
2 2 3 2 3 3 0
x y z mx m y z m
là phương trình mặt cầu:
A.
7 1
m
. B.
7
1
m
m
. C.
1 7
m
. D.
1
7
m
m
.
Câu 44. Trong không gian
,Oxyz
cho mặt cầu
2 2 2
( ) : ( 1) ( 1) ( 2) 9.
S x y z
Viết phương trình mặt phẳng
( )
tiếp xúc với
( )S
tại điểm
(0;3;0).
M
A.
2 2 12 0
x y z
. B.
2 2 6 0
x y z
. C.
2 2 6 0
x y z
. D.
4 2 12 0
x y z
.
Câu 45. Trong không gian
Oxyz
, mặt phẳng
Oxz
có phương trình là.
A.
0
y
. B.
0
x y z
. C.
0
x
. D.
0
z
.
Câu 46. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
: 2 5 0
Q x y z
và mặt cầu
2 2
2
: 1 2 15
S x y z
. Mặt phẳng
P
song song với mặt phẳng
Q
và cắt mặt cầu
S
theo giao tuyến
là một đường tròn có chu vi bằng
6
đi qua điểm nào sau đây?
A.
0; 1; 5
. B.
2; 2;1
. C.
1; 2;0
. D.
2;2; 1
.
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
3; 2;6 , 0;1;0
A B
và mặt cầu
2 2 2
: 1 2 3 25
S x y z
. Mặt phẳng
: 2 0
P ax by cz
đi qua
,A B
và cắt
S
theo giao tuyến
là đường tròn có bán kính nhỏ nhất. Tính
T a b c
A.
5
T
. B.
4T
. C.
3
T
. D.
2T
.
Câu 48. Trong không gian
Oxyz
, cho 3 điểm
1;0;0
A
,
0;2;0
B
và
0;0;3
C
. Mặt phẳng
ABC
có phương
trình là
A.
1
1 2 3
x y z
. B.
1
1 2 3
x y z
. C.
1
1 2 3
x y z
. D.
1
1 2 3
x y z
.
Câu 49. Trong không gian
Oxyz
, mặt phẳng
: 1 0
P x y z
có một vectơ pháp tuyến là
A.
2
1; 1;1
n
. B.
4
1;1; 1
n
. C.
3
1;1;1
n
. D.
1
1;1;1
n
.
Câu 50. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2;4;1 ; 1;1;3
A B
và mặt phẳng
: 3 2 5 0
P x y z
. Một mặt phẳng
Q
đi qua hai điểm
,A B
và vuông góc với mặt phẳng
P
có dạng
11 0
ax by cz
. Khẳng định nào sau đây là đúng?
A.
15
a b c
. B.
5
a b c
. C.
15
a b c
. D.
5
a b c
.
-----------------------------------Hết -----------------------------
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NAM
TRƯỜNG THPT CHUYÊN BIÊN HÒA
(Đề thi có 06 trang)
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
NĂM HỌC 2023-2024
Môn: Toán. Lớp: 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Họ tên: ........................................................................Số báo danh: ..............................
Câu 1. Họ nguyên hàm của hàm số
2
2
cos
x
x
e
ye
x




là
A.
2 tan
x
e x C
. B.
2 tan
x
e x C
. C.
1
2
cos
x
eC
x

. D.
1
2
cos
x
eC
x

.
Câu 2. Cho
Fx
là một nguyên hàm của hàm số
2
42
x
f x e x
thỏa mãn
01F
. Hàm số
Fx
là:
A.
22
21
x
F x e x
. B.
22
43
x
F x e x
. C.
22
21
x
F x e x
. D.
22
21
x
F x e x
Câu 3. Biết
4
*
0
1 sin 2 , , , 5 .
2
b
a
x xdx a b a
Giá trị của tích ab bằng
A. 2. B. 12. C. 6. D. 4.
Câu 4. Biết
cos2 d sin2 cos2x x x ax x b x C
với
a
,
b
là các số hữu tỉ. Tính tích
ab
.
A.
1
8
ab 
. B.
1
4
ab 
. C.
1
4
ab
. D.
1
8
ab
.
Câu 5. Cho
1
2
0
1
2ln ln3
32
I dx a b
xx

, với
*
,.ab
Giá trị
ab
bằng
A.
3
. B. 2. C. 12. D. 6.
Câu 6. Hàm số
3
x
F x e
là một nguyên hàm của hàm số
A.
3
31
.
x
f x x e
. B.
3
2
3
x
e
fx
x
. C.
3
2
3.
x
f x x e
. D.
3
x
f x e
.
Câu 7. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
2; 2;1M
trên mặt phẳng
Oxy
có tọa độ là
A.
0;0;1
. B.
2;0;1
. C.
2; 2;0
. D.
0; 2;1
.
Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số
2
2
,
1
x
y x y
x

là
ln2ab
với
,ab
là các số hữu
tỷ. Giá trị
ab
là
A.
7
.
3
B. 1. C.
5.
D.
11
.
3
Câu 9. Biết
3
1
2
ln ,
x
dx a b c
x

với
, , , 9.a b c c
Tính tổng
.S a b c
A.
5S
. B.
7S
. C.
8S
. D.
6S
.
Mã đề 102
2
Câu 10. Trong không gian
Oxyz
, cho hai điểm
5;2;1A
và
1;0;1B
. Phương trình mặt cầu đường kính
AB
là
A.
2 2 2
3 1 1 20 x y z
. B.
2 2 2
3 1 1 5 x y z
.
C.
2 2 2
3 1 1 5 x y z
. D.
2 2 2
3 1 1 20 x y z
.
Câu 11. Cho
2
2
d1f x x
,
4
2
d4f t t

. Tính
4
2
df y y
.
A.
3I
. B.
5I 
. C.
3I 
. D.
5I
.
Câu 12. Cho
Fx
là một nguyên hàm của hàm số
2
1
1
fx
x
. Giá trị của
' 2 2 ' 0FF
là:
A.
2
3
. B.
2
3
C.
8
9
D.
1
3
.
Câu 13. Cho hàm số
y f x
có đồ thị trên
2;6
như hình vẽ bên. Biết các miền A, B, C có diện tích lần lượt là
32; 2; 3. Tích phân
2
2
2 2 1f x dx



bằng
A.
45
2
. B. 41. C. 37. D.
41
2
.
Câu 14. Cho
Fx
là một nguyên hàm của
1
1
fx
x
trên khoảng
1; 
thỏa mãn
14Fe
. Tìm
Fx
.
A.
2ln 1 2x
. B.
4ln 1x
. C.
ln 1 3x
. D.
ln 1 3x
.
Câu 15. Tìm nguyên hàm của hàm số
1
52
fx
x
.
A.
d1
ln 5 2
5 2 5
x
xC
x
. B.
d1
ln 5 2
5 2 2
x
xC
x
.
C.
d
5ln 5 2
52
x
xC
x
. D.
d
ln 5 2
52
x
xC
x
.
Câu 16. Giá trị
2
1
23
dx
x
bằng
A.
1
ln35
2
. B.
7
2ln
5
. C.
17
ln
25
. D.
7
ln
5
.
Câu 17. Trong không gian
Oxyz
, cho hai vectơ
1;2; 2u
và
2; 2;3v
. Tọa độ của vectơ
uv
là
A.
3;0;1
. B.
1;4; 5
. C.
3;0; 1
. D.
1; 4;5
.
3
Câu 18. Cho
3
2
, 0;
1
x
I dx x
x

. Bằng phép đổi biến
2
1ux
, khẳng định nào sau đây sai?
A.
3
3
u
I u C
. B.
2
1.I u udu
. C.
xdx udu
. D.
22
1xu
.
Câu 19. Tính tích phân
1
0
ed
x
Ix
.
A.
1
1
e

. B.
1
e
. C.
1
1
e

. D. -1.
Câu 20. Biết rằng hàm số
fx
liên tục trên
;ab
và có một nguyên hàm là
Fx
. Khẳng định nào trong các
khẳng định sau là đúng?
A.
.
b
a
f x dx f a f b
B.
.
b
a
f x dx F a F b
C.
.
b
a
f x dx F b F a
D.
.
b
a
f x dx F a F b
Câu 21. Cho hàm số
fx
liên tục trên
.
Biết
,F x G x
lần lượt là các nguyên hàm của các hàm số
fx
và
1fx
thỏa mãn
2 2 4.GF
Tính tích phân
2
0
.I G x F x xdx


A. 8. B.
20
3
. C. 20. D.
3
20
.
Câu 22. Cho hàm số
32
2 4 khi 4
1
khi 4
4
xx
fx
x x x x

. Tích phân
2
2
0
2sin 3 sin2 df x x x
bằng
A.
341
48
B.
28
3
. C.
341
96
. D. 8.
Câu 23. Tìm
222x
e dx
.
A.
222
.
222
x
e
x
B.
222
.
222
x
e
C.
222x
e
. D.
222
222 .
x
e
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
1;0;3A
,
2;3; 4B
,
3;1;2C
. Tìm tọa độ điểm
D
sao cho
ABCD
là hình bình hành.
A.
4;2;9D
. B.
4; 2;9D
. C.
4; 2;9D 
. D.
4;2; 9D
.
Câu 25. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 6 1 0S x y z x y z
. Tâm của (S) có tọa độ là
A.
2; 4; 6
. B.
2;4;6
. C.
1; 2; 3
. D.
1;2;3
.
Câu 26. Cho khối nón có đỉnh
S
, chiều cao bằng 8 và thể tích bằng
800
3
. Gọi
A
và
B
là hai điểm thuộc đường
tròn đáy sao cho
12AB
, khoảng cách từ tâm của đường tròn đáy đến mặt phẳng
SAB
bằng
A.
42
. B.
24
5
. C.
5
24
. D.
82
.
4
Câu 27. Cho hàm số
()fx
thỏa mãn
(2)fe
và
2
( ) ( )
x
f x e f x
với mọi
.x
Giá trị của
(1)f
bằng
A.
2.
. B.
2
e
. C.
e
. D.
2
.e
Câu 28. Nguyên hàm của hàm số
2
ln 2f x x x
là:
A.
2
22
2 ln 2
2
x
x x C
. B.
22
2
2
ln 2
22
xx
xC
.
C.
22
2
2
ln 2
22
xx
xC
. D.
2 2 2
2 ln 2x x x C
.
Câu 29. Cho
2
0
d5f x x
. Tính
2
0
2cos dI f x x x



.
A.
5
2
I

. B.
7I
. C.
3I
. D.
5I

.
Câu 30. Cho hàm số
fx
có đạo hàm liên tục trên . Biết
31f
và
1
0
3 d 1
xf x x
, khi đó
3
2
0
d
x f x x
bằng
A. 7. B.
25
3
. C.
9
. D. 3.
Câu 31. Tính
sin2 dx x x
.
A.
2
cos2
2
x
xC
. B.
2
cos2
2
x
xC
. C.
2
sin
2
x
xC
. D.
2
cos2
22
xx
C
.
Câu 32. Cho hàm số
4
2
23x
fx
x
. Khẳng định nào sau đây đúng?
A.
3
23
3
x
f x dx C
x
. B.
3
3
2f x dx x C
x
.
C.
3
23
32
x
f x dx C
x
. D.
3
23
3
x
f x dx C
x
.
Câu 33. Chướng ngại vật “tường cong” trong một sân thi đấu X-Game là một khối bê tông có chiều cao từ mặt đất
lên là 3 m. Giao của mặt tường cong và mặt đất là đoạn thẳng
2AB
m. Thiết diện của khối tường cong cắt bởi
mặt phẳng vuông góc với
AB
tại
A
là một hình tam giác vuông cong
ACE
với
4AC
m,
3CE
m và cạnh
cong
AE
nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí
M
là trung điểm của
AC
thì tường cong có độ cao 1 m
5
Thể tích khối tường cong đó là
A.
3
28
m.
3
B.
3
24m .
C.
3
14
m.
3
D.
3
35
m.
3
Câu 34. Diện tích hình phẳng giới hạn bởi hai đường thẳng
0x
,
x
, đồ thị hàm số
cosyx
và trục
Ox
là
A.
0
cos dS x x
. B.
2
0
cos dS x x
. C.
0
cos dS x x
. D.
0
cos dS x x
.
Câu 35. Cho
Fx
là một nguyên hàm của hàm số
1
ln
fx
xx
thỏa mãn
1
2
e
F



và
e ln2.F
Giá trị của
biểu thức
2
2
1
e
e
FF



bằng
A.
ln2 2
. B.
2ln2 1
. C.
3ln2 2
. D.
ln2 1
.
Câu 36. Cho hàm số
3
2
40
40
x khi x
fx
x khi x


. Tích phân
4
3
f x dx
bằng
A. 45. B. 46. C. 47. D.
13
12
.
Câu 37. Cho
2
1
2,f x dx
2
1
1g x dx

. Khi đó
2
1
23I x f x g x dx


bằng
A.
15
.
2
I
B.
17.I
C.
1
.
2
I
D.
17
.
2
I
Câu 38. Cho hàm số
fx
có đạo hàm trên đoạn
1;2
,
11f
và
22f
. Tích phân
2
1
I f x dx
bằng
A. 3. B. 1. C. 0. D. 2.
Câu 39. Cho biết
2 13
ln 1 ln 2
12
x
dx a x b x C
xx

với a, b là các số nguyên và C là hằng số thực.
Mệnh đề nào sau đây đúng?
A.
8ab
. B.
8ab
. C.
28ab
. D.
28ab
.
Câu 40. Giả sử tích phân
5
1
1
ln3 ln5 , ,
1 3 1
I dx a b c a b c
x

. Giá trị của giá trị biểu thức
P a b c
là
A.
8
.
3
P
B.
4
.
3
P
C.
5
.
3
P
D.
7
.
3
P
Câu 41. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
: 2 5 0Q x y z
và mặt cầu
22
2
: 1 2 15S x y z
. Mặt phẳng
P
song song với mặt phẳng
Q
và cắt mặt cầu
S
theo giao tuyến
là một đường tròn có chu vi bằng
6
đi qua điểm nào sau đây?
A.
1; 2;0
. B.
2;2; 1
. C.
2; 2;1
. D.
0; 1; 5
.
6
Câu 42. Trong không gian với hệ trục tọa độ
Oxyz
, tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
2 2 2 2
2 2 3 2 3 3 0x y z mx m y z m
là phương trình mặt cầu:
A.
71m
. B.
17m
. C.
7
1
m
m

. D.
1
7
m
m

.
Câu 43. Trong không gian
Oxyz
, mặt phẳng
Oxz
có phương trình là.
A.
0y
. B.
0z
. C.
0x
. D.
0 x y z
.
Câu 44. Trong không gian
,Oxyz
cho mặt cầu
2 2 2
( ):( 1) ( 1) ( 2) 9.S x y z
Viết phương trình mặt phẳng
()
tiếp xúc với
()S
tại điểm
(0;3;0).M
A.
2 2 12 0x y z
. B.
2 2 6 0x y z
. C.
2 2 6 0x y z
. D.
4 2 12 0x y z
.
Câu 45. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ):( 1) ( 2) ( 3) 1S x y z
và điểm
(2;3;4)A
. Xét các điểm
M
thuộc
()S
sao cho đường thẳng
AM
tiếp xúc với
()S
,
M
luôn thuộc mặt phẳng có phương trình là
A.
2 2 2 15 0x y z
. B.
2 2 2 15 0x y z
.
C.
70x y z
. D.
70x y z
.
Câu 46. Trong không gian
Oxyz
, mặt phẳng
: 1 0 P x y z
có một vectơ pháp tuyến là
A.
1
1;1;1n
. B.
4
1;1; 1n
. C.
3
1;1;1n
. D.
2
1; 1;1n
.
Câu 47. Trong không gian
Oxyz
, cho hai điểm
1;3;0A
và
5;1; 2B
. Mặt phẳng trung trực của đoạn thẳng
AB
có phương trình là:
A.
2 5 0x y z
. B.
3 2 14 0x y z
. C.
2 5 0x y z
. D.
2 3 0x y z
.
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2;4;1 ; 1;1;3AB
và mặt phẳng
: 3 2 5 0P x y z
. Một mặt phẳng
Q
đi qua hai điểm
,AB
và vuông góc với mặt phẳng
P
có dạng
11 0ax by cz
. Khẳng định nào sau đây là đúng?
A.
5abc
. B.
15abc
. C.
15abc
. D.
5abc
.
Câu 49. Trong không gian
Oxyz
, cho 3 điểm
1;0;0A
,
0;2;0B
và
0;0;3C
. Mặt phẳng
ABC
có phương
trình là
A.
1
1 2 3
x y z
. B.
1
1 2 3
x y z
. C.
1
1 2 3
x y z
. D.
1
1 2 3
x y z
.
Câu 50. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
3; 2;6 , 0;1;0AB
và mặt cầu
2 2 2
: 1 2 3 25S x y z
. Mặt phẳng
: 2 0P ax by cz
đi qua
,AB
và cắt
S
theo giao tuyến
là đường tròn có bán kính nhỏ nhất. Tính
T a b c
A.
4T
. B.
5T
. C.
3T
. D.
2T
.
-----------------------------------Hết-----------------------------------
Đề 101
Đề 102
Đề10 3
Đề 104
Đề 105
Đề 106
Đề 107
Đề 108
1. A
1. A
1. A
1. C
1. D
1. B
1. B
1. B
2. B
2. A
2. D
2. A
2. C
2. B
2. B
2. A
3. D
3. C
3. A
3. C
3. D
3. D
3. B
3. A
4. A
4. D
4. C
4. B
4. B
4. D
4. D
4. B
5. C
5. B
5. D
5. A
5. B
5. A
5. A
5. B
6. B
6. C
6. B
6. B
6. C
6. B
6. D
6. C
7. B
7. C
7. B
7. B
7. A
7. A
7. D
7. D
8. B
8. D
8. B
8. B
8. D
8. D
8. D
8. D
9. B
9. B
9. B
9. B
9. D
9. A
9. D
9. D
10. D
10. B
10. A
10. B
10. B
10. C
10. D
10. C
11. C
11. B
11. A
11. D
11. C
11. A
11. D
11. B
12. C
12. A
12. A
12. A
12. D
12. D
12. A
12. C
13. C
13. D
13. B
13. B
13. A
13. B
13. B
13. A
14. D
14. C
14. D
14. C
14. B
14. A
14. A
14. D
15. C
15. A
15. C
15. C
15. C
15. C
15. B
15. C
16. D
16. C
16. C
16. C
16. C
16. C
16. B
16. C
17. D
17. A
17. B
17. A
17. A
17. B
17. A
17. C
18. B
18. B
18. C
18. C
18. D
18. D
18. D
18. D
19. A
19. C
19. A
19. A
19. B
19. B
19. D
19. A
20. C
20. C
20. D
20. A
20. A
20. D
20. A
20. C
21. C
21. B
21. A
21. C
21. A
21. B
21. C
21. C
22. B
22. C
22. C
22. C
22. C
22. C
22. B
22. C
23. B
23. B
23. C
23. A
23. C
23. A
23. A
23. C
24. D
24. C
24. D
24. C
24. A
24. B
24. B
24. D
25. A
25. D
25. D
25. A
25. D
25. A
25. D
25. A
26. C
26. A
26. D
26. B
26. B
26. A
26. D
26. B
27. A
27. B
27. C
27. C
27. A
27. A
27. C
27. A
28. A
28. C
28. D
28. A
28. B
28. B
28. C
28. D
29. A
29. B
29. B
29. A
29. D
29. D
29. B
29. D
30. C
30. C
30. A
30. D
30. C
30. B
30. C
30. B
31. B
31. D
31. A
31. A
31. C
31. A
31. A
31. A
32. A
32. D
32. D
32. D
32. D
32. D
32. A
32. A
33. C
33. A
33. B
33. C
33. B
33. D
33. D
33. B
34. B
34. D
34. D
34. B
34. A
34. A
34. B
34. B
35. C
35. C
35. C
35. D
35. C
35. C
35. C
35. D
36. D
36. A
36. B
36. D
36. D
36. D
36. C
36. D
37. D
37. D
37. C
37. C
37. B
37. D
37. D
37. B
38. B
38. B
38. A
38. D
38. B
38. B
38. D
38. B
39. B
39. B
39. B
39. D
39. C
39. C
39. B
39. C
40. A
40. B
40. A
40. D
40. D
40. C
40. C
40. C
41. D
41. B
41. D
41. A
41. D
41. D
41. A
41. A
42. B
42. A
42. A
42. B
42. A
42. A
42. C
42. D
43. A
43. A
43. B
43. C
43. B
43. C
43. A
43. A
44. B
44. C
44. A
44. B
44. A
44. D
44. A
44. A
45. A
45. D
45. D
45. C
45. A
45. A
45. C
45. A
46. D
46. C
46. B
46. A
46. B
46. A
46. A
46. A
47. C
47. A
47. C
47. D
47. B
47. A
47. D
47. D
48. A
48. D
48. D
48. B
48. A
48. C
48. C
48. A
49. C
49. D
49. B
49. D
49. C
49. C
49. B
49. A
50. D
50. C
50. B
50. D
50. B
50. B
50. B
50. B
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NAM
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT CHUYÊN BIÊN HÒA NĂM HỌC 2023-2024 Môn: Toán. Lớp: 12
(Đề thi có 06 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Họ tên: ........................................................................Số báo danh: ............................. .... M .. ã đề 101  2x  4 khi x  4  2
Câu 1. Cho hàm số f x  2  1 . Tích phân f
 2sin x  3sin 2 d x x bằng 3 2
x x x khi x  4   4 0 341 28 341 A. . B. . C. 8. D. 96 3 48 1
Câu 2. Cho F x là một nguyên hàm của hàm số f x 
. Giá trị của F '2 2   F '0 là: 2 x 1 2 2 1 8 A. B.  . C. . D.  3 3 3 9
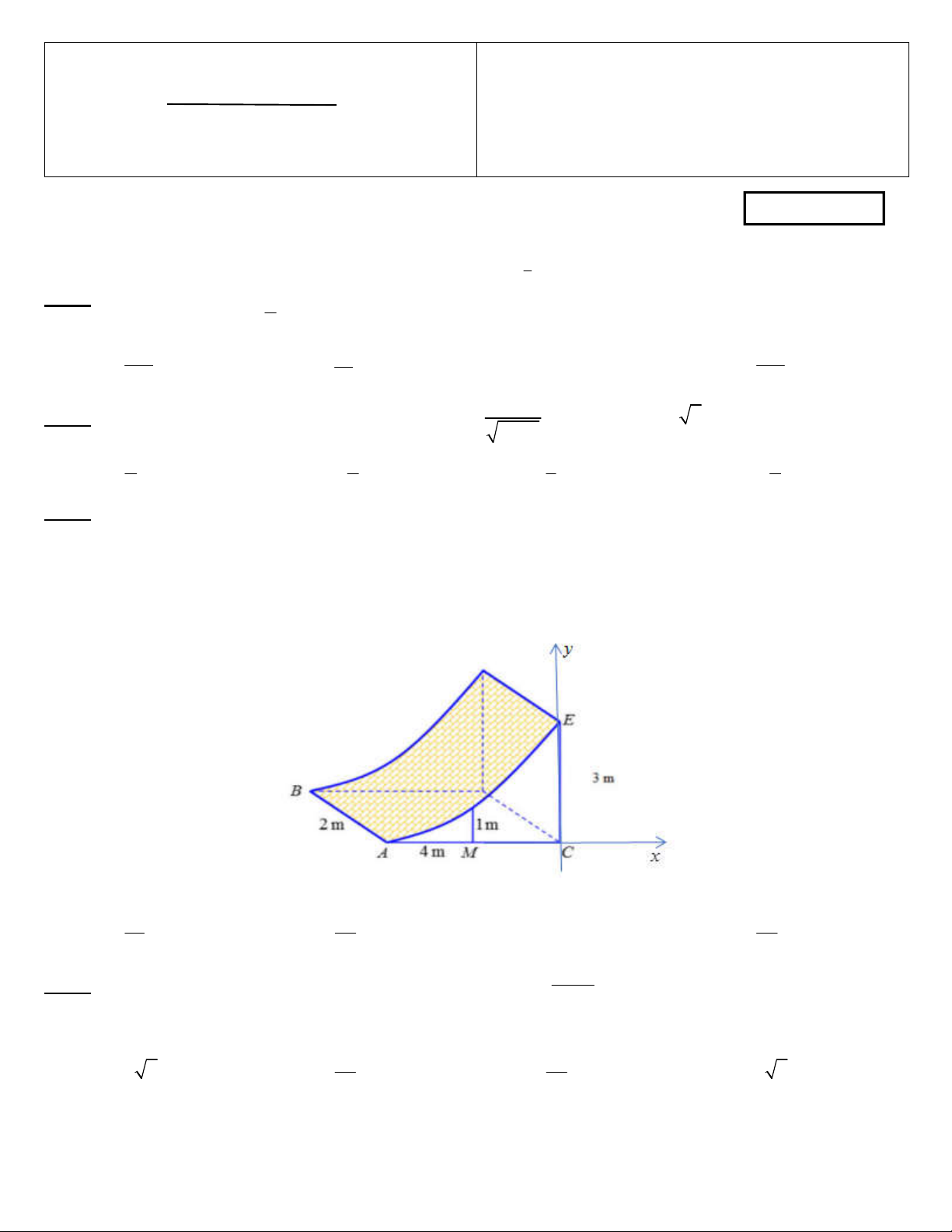
Câu 3. Chướng ngại vật “tường cong” trong một sân thi đấu X-Game là một khối bê tông có chiều cao từ mặt đất
lên là 3 m. Giao của mặt tường cong và mặt đất là đoạn thẳng AB  2 m. Thiết diện của khối tường cong cắt bởi
mặt phẳng vuông góc với AB tại A là một hình tam giác vuông cong ACE với AC  4 m, CE  3 m và cạnh
cong AE nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí M là trung điểm của AC
thì tường cong có độ cao 1 m
Thể tích khối tường cong đó là 14 35 28 A. 3 m . B. 3 m . C. 3 24 m . D. 3 m . 3 3 3 800
Câu 4. Cho khối nón có đỉnh S , chiều cao bằng 8 và thể tích bằng
. Gọi A và B là hai điểm thuộc đường 3
tròn đáy sao cho AB  12 , khoảng cách từ tâm của đường tròn đáy đến mặt phẳng SAB bằng 24 5 A. 4 2 . B. . C. . D. 8 2 . 5 24 1
Câu 5. Cho hàm số f x liên tục trên .
 Biết F x,G x lần lượt là các nguyên hàm của các hàm số f x và 2
f x 1 thỏa mãn G 2  F 2  4. Tính tích phân I
G x  F x xd . x    0 3 20 A. . B. 20. C. . D. 8. 20 3
Câu 6. Biết x cos 2 d
x x ax sin 2x b cos 2x C
với a , b là các số hữu tỉ. Tính tích ab . 1 1 1 1 A. ab   . B. ab  . C. ab   . D. ab  . 8 8 4 4 3
x  4 khi x  0 4
Câu 7. Cho hàm số f x   . Tích phân
f xdx 2  bằng
x  4 khi x  0  3  13 A. 46. B. 45. C. 47. D. . 12 2x
Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số 2
y x , y
là a b ln 2 với a, b là các số hữu x 1
tỷ. Giá trị a b là 11 7 A. 1. B. . C. . D. 5. 3 3
Câu 9. Nguyên hàm của hàm số f x  x  2 ln 2  x  là: 2 2 x  2 x 2 2 x  2 x A. ln  2 x  2   C . B. ln  2 x  2   C 2 2 2 2 2 x C.  2 x    2 x   2 2 ln 2  x C . D.  2 x    2 2 ln x  2   C 2
Câu 10. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  2x  4 y  6z 1  0 . Tâm của (S) có tọa độ là A. 2; 4;6 . B.  2  ; 4  ; 6   . C.  1  ; 2  ; 3   . D. 1; 2;3 .
Câu 11. Tính  x  sin 2xdx  . 2 2 2 cos 2x x x cos 2x x A. 2 x   C . B.
 cos 2x C . C.   C . D.
 sin x C . 2 2 2 2 2   2 2 Câu 12. Cho
f xdx  5 
. Tính I   f x  2cos x dx    . 0 0  A. I  3 .
B. I  5   . C. I  7 . D. I  5  . 2
Câu 13. Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2; 2; 
1 trên mặt phẳng Oxy có tọa độ là A. 0; 2;  1 . B. 0;0;  1 . C. 2; 2;  0 . D. 2;0;  1 .
Câu 14. Diện tích hình phẳng giới hạn bởi hai đường thẳng x  0 , x   , đồ thị hàm số y  cos x và trục Ox là    
A. S  cos x dx  . B. 2
S  cos x dx  . C. S   cos x dx  . D. S  cos x dx  . 0 0 0 0 2 3 x  2 Câu 15. Biết
dx a b ln c, 
với a, b, c  , c  9. Tính tổng S a b  . c x 1 A. S  6 . B. S  5. C. S  7 . D. S  8 . 2
Câu 16. Cho hàm số f x có đạo hàm trên đoạn 1; 2 , f  
1  1 và f 2  2 . Tích phân I f  xdx  bằng 1 A. 2. B. 3. C. 0. D. 1. 5 1
Câu 17. Giả sử tích phân I
dx a b ln 3  c ln 5a, , b c   
 . Giá trị của giá trị biểu thức 1 3x 1 1
P a b c là 7 5 8 4 A. P  . B. P  . C. P  . D. P  . 3 3 3 3 2x 13 Câu 18. Cho biết
dx a ln x 1  b ln x  2  C
với a, b là các số nguyên và C là hằng số thực.  x   1  x  2
Mệnh đề nào sau đây đúng?
A. a b  8 .
B. a b  8 .
C. 2a b  8 .
D. a  2b  8 . 3 x
Câu 19. Cho I d , x x 0;   . Bằng phép đổi biến 2 u
x  1 , khẳng định nào sau đây sai? 2 x 1 3 u A. I   2 u    1 .udu . B. I   u C .
C. xdx udu . D. 2 2 x u 1 . 3 2 dx Câu 20. Giá trị  bằng 2x  3 1 7 1 1 7 7 A. 2 ln . B. ln 35 . C. ln . D. ln . 5 2 2 5 5 1
Câu 21. Cho F x là một nguyên hàm của f x 
trên khoảng 1;  thỏa mãn F e  
1  4 . Tìm F x . x 1
A. 4 ln  x   1 .
B. ln  x   1  3 .
C. ln  x   1  3 .
D. 2 ln  x   1  2 .
Câu 22. Trong không gian Oxyz , cho hai điểm A 5; 2;  1 và B 1;0; 
1 . Phương trình của mặt cầu đường kính AB là 2 2 2 2 2 2
A. x  3   y   1   z   1  20 .
B. x  3   y   1   z   1  5 . 2 2 2 2 2 2
C. x  3   y   1   z   1  20 .
D. x  3   y   1   z   1  5 . 1
Câu 23. Tính tích phân  ex I dx  . 0 1 1 1 A. -1. B.  1 . C. . D. 1   . e e e
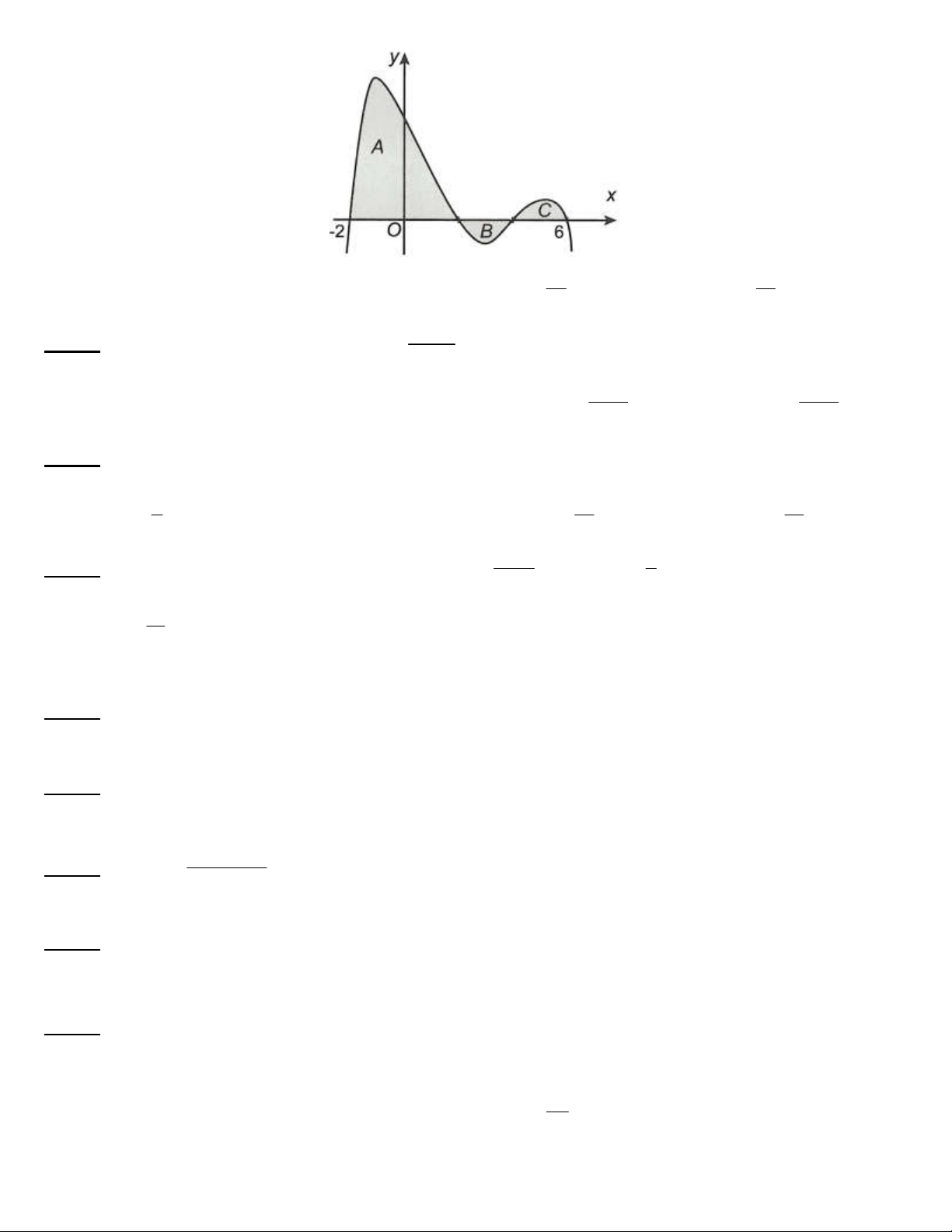
Câu 24. Cho hàm số y f x có đồ thị trên  2
 ; 6 như hình vẽ bên. Biết các miền A, B, C có diện tích lần lượt là 2 32; 2; 3. Tích phân
f 2x  2 1 dx    bằng 2  3 45 41 A. 41. B. 37. C. . D. . 2 2  xe
Câu 25. Họ nguyên hàm của hàm số x y e 2   là 2  cos x   x 1 x 1 A. 2 x
e  tan x C . B. 2 x
e  tan x C . C. 2e   C . D. 2e   C . cos x cos x 2 2 2 Câu 26. Cho
f xdx  2, 
g xdx  1   . Khi đó I
x  2 f x  3g xdx    bằng 1  1  1  1 17 15 A. I  . B. I  17. C. I  . D. I  . 2 2 2 1  1 
Câu 27. Cho F x là một nguyên hàm của hàm số f x  thỏa mãn F  2  
và F e  ln 2. Giá trị của x ln x  e   1  biểu thức FF    2 e bằng 2   e  A. 3ln 2  2 . B. ln 2 1. C. ln 2  2. D. 2ln 2 1. 2 4 4 Câu 28. Cho
f x dx  1  ,
f t dt  4   . Tính
f y dy  . 2  2  2 A. I  5  . B. I  3  . C. I  3 . D. I  5 .    
Câu 29. Trong không gian Oxyz , cho hai vectơ u  1;2; 2
  và v  2; 2  ; 
3 . Tọa độ của vectơ u v là A. 3; 0;  1 . B. 1; 4;5 .
C. 1; 4; 5 . D. 3;0;  1  . 1 1
Câu 30. Cho I
dx  2 ln a b ln 3  , với *
a, b   . Giá trị ab bằng 2 x  3x  2 0 A. 12. B. 6. C. 2. D. 3.
Câu 31. Cho F x là một nguyên hàm của hàm số   2  4 x f x e
 2x thỏa mãn F 0  1. Hàm số F x là:
A. F x 2 x 2  4ex  3 .
B. F x 2 x 2  2ex 1.
C. F x 2 x 2  2e
x 1. D. F x 2 x 2  2ex  1 . 1 3 2
Câu 32. Cho hàm số f x có đạo hàm liên tục trên  . Biết f 3  1 và  xf 3xdx  1, khi đó 
x f xdx 0 0 bằng 25 A. 9  . B. 7. C. . D. 3. 3 4
Câu 33. Cho hàm số f (x) thỏa mãn f (2)  e và  x
f x e f x 2 ( ) ( ) với mọi x  .
 Giá trị của f (1) bằng A. 2. . B. 2 e  . C. 2 e . D. e . 4 2x  3
Câu 34. Cho hàm số f x 
. Khẳng định nào sau đây đúng? 2 x 3 3 2x 3 A. f x 3 dx  2x   C  . B.
f xdx    C  . x 3 x 3 2x 3 3 2x 3 C.
f xdx    C  . D.
f xdx    C  . 3 x 3 2x
Câu 35. Biết rằng hàm số f x liên tục trên  ;
a b và có một nguyên hàm là F x . Khẳng định nào trong các
khẳng định sau là đúng? b b A.
f xdx F a  F b.  B.
f xdx F a  F b.  a a b b C.
f xdx F b  F a.  D.
f xdx f a  f b.  a a  4 a
Câu 36. Biết 1 xsin 2xdx  ,   *
a, b   , a  5. Giá trị của tích ab bằng 2b 0 A. 4. B. 12. C. 2. D. 6. 1
Câu 37. Tìm nguyên hàm của hàm số f x  . 5x  2 dx dx 1 A.
 ln 5x  2  C  . B.  
ln 5x  2  C  . 5x  2 5x  2 2 dx dx 1 C.
 5 ln 5x  2  C  . D.
ln 5x  2  C  . 5x  2 5x  2 5
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho các điểm A 1; 0;3 , B 2;3;  4 , C 3;1; 2 . Tìm tọa độ điểm
D sao cho ABCD là hình bình hành.
A. D 4; 2;9 .
B. D 4;  2;9 .
C. D 4;  2;9 .
D. D 4; 2;  9 . Câu 39. Hàm số   3 x
F x e là một nguyên hàm của hàm số 3 x e
A. f x  . B.   3 2  3 . x f x x e . C.   3 x f x e . D.   3 3 1 . x f x x e   . 2 3x Câu 40. Tìm 222 x e dx  . 222 x e 222 x e A. . B. 222x e . C. . D. 222 222 x e . 222 222x
Câu 41. Trong không gian Oxyz , cho hai điểm A1;3;0 và B 5;1; 2 . Mặt phẳng trung trực của đoạn thẳng AB
có phương trình là:
A. 3x  2y z 14  0 .
B. x y  2z  3  0 .
C. 2x y z  5  0 .
D. 2x y z  5  0 . 5
Câu 42. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S ) : (x 1)  ( y  2)  (z  3)  1 và điểm (
A 2;3; 4) . Xét các điểm
M thuộc (S) sao cho đường thẳng AM tiếp xúc với (S) , M luôn thuộc mặt phẳng có phương trình là
A. x y z  7  0 .
B. x y z  7  0 .
C. 2x  2 y  2z 15  0 .
D. 2x  2y  2z 15  0 .
Câu 43. Trong không gian với hệ trục tọa độ Oxyz , tìm tập hợp tất cả các giá trị của tham số m để phương trình 2 2 2
x y z mx  m  2 2 2
3 y  2z 3m  3  0 là phương trình mặt cầu: m  7  m  1  A. 7
  m  1. B. . C. 1
  m  7 . D. . m  1  m  7 
Câu 44. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S ) : (x 1)  ( y 1)  (z  2)  9. Viết phương trình mặt phẳng
() tiếp xúc với (S) tại điểm M (0;3;0).
A. x  2y  2z 12  0 .
B. x  2y  2z  6  0 .
C. x  2y  2z  6  0 .
D. x  4y  2z 12  0 .
Câu 45. Trong không gian Oxyz , mặt phẳng Oxz  có phương trình là. A. y  0 .
B. x y z  0 . C. x  0 . D. z  0 .
Câu 46. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng Q : x  2 y z  5  0 và mặt cầu
S   x  2  y   z  2 2 : 1 2
 15 . Mặt phẳng  P song song với mặt phẳng Q và cắt mặt cầu S  theo giao tuyến
là một đường tròn có chu vi bằng 6 đi qua điểm nào sau đây?
A. 0; 1; 5 . B. 2;  2;  1 . C. 1;  2;0 . D.  2  ; 2;   1 .
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3; 2
 ;6, B 0;1;0 và mặt cầu
S   x  2   y  2   z  2 : 1 2 3
 25 . Mặt phẳng  P : ax by cz  2  0 đi qua ,
A B và cắt S  theo giao tuyến
là đường tròn có bán kính nhỏ nhất. Tính T a b c A. T  5 . B. T  4 . C. T  3. D. T  2 .
Câu 48. Trong không gian Oxyz , cho 3 điểm A 1; 0; 0 , B 0; 2; 0 và C 0; 0;3 . Mặt phẳng  ABC  có phương trình là x y z x y z x y z x y z A.    1. B.    1. C.    1. D.    1. 1  2 3 1 2 3  1 2  3 1 2 3
Câu 49. Trong không gian Oxyz , mặt phẳng  P : x y z 1  0 có một vectơ pháp tuyến là     A. n  1; 1  ;1 . B. n  1;1; 1  .
C. n  1;1;1 . D. n  1  ;1;1 . 1   3   4   2  
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho điểm A2; 4  ;1 ; B  1  ;1;3 và mặt phẳng
P : x  3y  2z  5  0 . Một mặt phẳng Q đi qua hai điểm ,
A B và vuông góc với mặt phẳng  P có dạng
ax by cz 11  0 . Khẳng định nào sau đây là đúng?
A. a b c  1  5 .
B. a b c  5  .
C. a b c  15 .
D. a b c  5 .
-----------------------------------Hết ----------------------------- 6
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NAM
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT CHUYÊN BIÊN HÒA NĂM HỌC 2023-2024 Môn: Toán. Lớp: 12
(Đề thi có 06 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Họ tên: ........................................................................Số báo danh: .............................. M ã đề 102 xe
Câu 1. Họ nguyên hàm của hàm số x
y e  2   là 2  cos x x 1 x 1 A. 2 x
e  tan x C . B. 2 x
e  tan x C . C. 2e   C . D. 2e   C . cos x cos x
Câu 2. Cho F x là một nguyên hàm của hàm số   2  4 x f x e
 2x thỏa mãn F 0 1. Hàm số F x là:
A. F x 2 x 2
 2e x 1.
B. F x 2 x 2
 4e x  3 .
C. F x 2 x 2
 2e x 1.
D. F x 2 x 2
 2e x 1  4 a
Câu 3. Biết  1 xsin 2xdx  ,  * a, b
, a  5. Giá trị của tích ab bằng 2b 0 A. 2. B. 12. C. 6. D. 4.
Câu 4. Biết x cos 2 d
x x ax sin 2x b cos 2x C
với a , b là các số hữu tỉ. Tính tích ab . 1 1 1 1 A. ab   . B. ab   . C. ab  . D. ab  . 8 4 4 8 1 1
Câu 5. Cho I
dx  2 ln a b ln 3  , với * a,b
. Giá trị ab bằng 2 x  3x  2 0 A. 3 . B. 2. C. 12. D. 6. Câu 6. Hàm số   3 x
F x e là một nguyên hàm của hàm số 3 x e A.   3 3 1 . x f x x e   .
B. f x  . C.   3 2  3 . x f x x e . D.   3 x f x e . 2 3x
Câu 7. Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2; 2; 
1 trên mặt phẳng Oxy có tọa độ là A. 0;0;  1 . B. 2;0;  1 . C. 2; 2;0 . D. 0; 2;  1 . 2x
Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số 2
y x , y a b
với a,b là các số hữu x  là ln 2 1
tỷ. Giá trị a b là 7 11 A. . B. 1. C. 5. D. . 3 3 3 x  2 Câu 9. Biết
dx a b ln c,  với a, ,
b c  , c  9. Tính tổng S a b  . c x 1 A. S  5 . B. S  7 . C. S  8 . D. S  6 . 1
Câu 10. Trong không gian Oxyz , cho hai điểm A5; 2  ;1 và B 1;0; 
1 . Phương trình mặt cầu đường kính AB là 2 2 2 2 2 2
A. x  3   y   1   z   1  20 .
B. x  3   y   1   z   1  5. 2 2 2 2 2 2
C. x  3   y   1   z   1  5 .
D. x  3   y   1   z   1  20 . 2 4 4 Câu 11. Cho f
 xdx 1, f tdt  4   . Tính
f y dy  . 2  2  2 A. I  3 . B. I  5 . C. I  3 . D. I  5 . 1
Câu 12. Cho F x là một nguyên hàm của hàm số f x 
. Giá trị của F '2 2   F '0 là: 2 x 1 2 2 8 1 A.  . B. C. D. . 3 3 9 3
Câu 13. Cho hàm số y f x có đồ thị trên 2;6 như hình vẽ bên. Biết các miền A, B, C có diện tích lần lượt là 2 32; 2; 3. Tích phân  f
  2x21dx  bằng 2  45 41 A. . B. 41. C. 37. D. . 2 2
Câu 14. Cho F x là một nguyên hàm của f x 1 
trên khoảng 1;  thỏa mãn F e  
1  4 . Tìm F x . x 1
A. 2 ln  x   1  2 .
B. 4 ln  x   1 .
C. ln  x   1  3.
D. ln  x   1  3 .
Câu 15. Tìm nguyên hàm của hàm số f x 1  . 5x  2 dx 1 dx 1 A.
 ln 5x  2  C  . B.
  ln 5x  2  C  . 5x  2 5 5x  2 2 dx dx C.
 5ln 5x  2  C  . D.
 ln 5x  2  C  . 5x  2 5x  2 2 dx Câu 16. Giá trị  bằng 2x  3 1 1 7 1 7 7 A. ln 35 . B. 2 ln . C. ln . D. ln . 2 5 2 5 5
Câu 17. Trong không gian Oxyz , cho hai vectơ u  1; 2; 2 và v  2; 2;3 . Tọa độ của vectơ u v là A. 3;0  ;1 . B.  1  ;4; 5   . C. 3;0;  1  . D. 1; 4  ;5 . 2 3 x
Câu 18. Cho I dx, x  
0;. Bằng phép đổi biến 2 u
x 1 , khẳng định nào sau đây sai? 2 x 1 3 u A. I   u C . B. I   2 u   1.udu .
C. xdx udu . D. 2 2 x u 1 . 3 1
Câu 19. Tính tích phân  ex I dx  . 0 1 1 1 A. 1   . B. . C.  1 . D. -1. e e e
Câu 20. Biết rằng hàm số f x liên tục trên a;b và có một nguyên hàm là F x . Khẳng định nào trong các
khẳng định sau là đúng? b b A.
f xdx f a   f b. B.
f xdx F a   F b. a a b b C.
f xdx F b   F a. D.
f xdx F a   F b. a a
Câu 21. Cho hàm số f x liên tục trên . Biết F x,G x lần lượt là các nguyên hàm của các hàm số f x và 2
f x 1 thỏa mãn G 2  F 2  4. Tính tích phân I  G
  x F x xd .x  0 20 3 A. 8. B. . C. 20. D. . 3 20   2x  4 khi x  4  2
Câu 22. Cho hàm số f x   2 1 . Tích phân f
 2sin x3sin2 d x x bằng 3 2
x x x khi x  4 4 0 341 28 341 A. B. . C. . D. 8. 48 3 96 Câu 23. Tìm 222 x e dx  . 222 x e 222 x e A. . B. . C. 222x e . D. 222 222 x e . 222x 222
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho các điểm A1;0;3 , B 2;3;  4 , C  3
 ;1;2 . Tìm tọa độ điểm
D sao cho ABCD là hình bình hành. A. D  4  ;2;9 .
B. D 4;  2;9 . C. D  4  ; 2;9 .
D. D 4; 2;  9 .
Câu 25. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  2x  4 y  6z 1  0 . Tâm của (S) có tọa độ là A.  2  ; 4  ; 6   . B. 2; 4;6 . C.  1  ; 2  ; 3   . D. 1; 2;3 . 800
Câu 26. Cho khối nón có đỉnh S , chiều cao bằng 8 và thể tích bằng
. Gọi A và B là hai điểm thuộc đường 3
tròn đáy sao cho AB  12 , khoảng cách từ tâm của đường tròn đáy đến mặt phẳng SAB bằng 24 5 A. 4 2 . B. . C. . D. 8 2 . 5 24 3 
Câu 27. Cho hàm số f (x) thỏa mãn f (2)  e và x
f x e f x 2 ( )
( ) với mọi x  . Giá trị của f (1) bằng A. 2. . B. 2 e . C. e . D. 2 e  .
Câu 28. Nguyên hàm của hàm số f x  x  2 ln 2  x  là: x 2 2 x  2 x
A. x    x   2 2 2 2 ln 2   C . B. ln  2 x  2   C . 2 2 2 2 2 x  2 x C. ln  2 x  2   C . D.  2 x    2 x   2 2 ln 2  x C . 2 2   2 2 Câu 29. Cho f
 xdx  5. Tính I   f
  x2cosxdx  . 0 0  A. I  5  . B. I  7 . C. I  3 .
D. I  5   . 2 1 3
Câu 30. Cho hàm số f x có đạo hàm liên tục trên
. Biết f 3  1 và  xf 3xdx  1, khi đó 2 
x f xdx 0 0 bằng 25 A. 7. B. . C. 9 . D. 3. 3
Câu 31. Tính x sin 2xdx . 2 x 2 2 cos 2x x x cos 2x A.
 cos 2x C . B. 2 x   C . C.
 sin x C . D.   C . 2 2 2 2 2 2x  3
Câu 32. Cho hàm số f x 4 
. Khẳng định nào sau đây đúng? 2 x x 3 A. f  x 3 2 3 dx    C . B. f  x 3 dx  2x   C . 3 x x x x C. f  x 3 2 3 dx    C . D. f  x 3 2 3 dx    C . 3 2x 3 x
Câu 33. Chướng ngại vật “tường cong” trong một sân thi đấu X-Game là một khối bê tông có chiều cao từ mặt đất
lên là 3 m. Giao của mặt tường cong và mặt đất là đoạn thẳng AB  2 m. Thiết diện của khối tường cong cắt bởi
mặt phẳng vuông góc với AB tại A là một hình tam giác vuông cong ACE với AC  4 m, CE  3 m và cạnh
cong AE nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí M là trung điểm của AC
thì tường cong có độ cao 1 m 4
Thể tích khối tường cong đó là 28 14 35 A. 3 m . B. 3 24 m . C. 3 m . D. 3 m . 3 3 3
Câu 34. Diện tích hình phẳng giới hạn bởi hai đường thẳng x  0 , x   , đồ thị hàm số y  cos x và trục Ox là    
A. S  cos x dx  . B. 2
S  cos x dx  .
C. S   cos x dx  . D. S  cos x dx  . 0 0 0 0  1 
Câu 35. Cho F x là một nguyên hàm của hàm số f x 1  thỏa mãn F  2  
và F e  ln 2. Giá trị của x ln x  e   1  biểu thức FF    2e bằng 2   e  A. ln 2  2 . B. 2 ln 2 1 . C. 3ln 2  2 . D. ln 2 1. 3
x  4 khi x  0 4
Câu 36. Cho hàm số f x   . Tích phân f
 xdx bằng 2
x  4 khi x  0 3 13 A. 45. B. 46. C. 47. D. . 12 2 2 2 Câu 37. Cho f
 xdx  2, gxdx  1  
. Khi đó I  x  2 f
x3g xdx    bằng 1  1  1  15 1 17 A. I  . B. I  17. C. I  . D. I  . 2 2 2 2
Câu 38. Cho hàm số f x có đạo hàm trên đoạn 1;2 , f  
1  1 và f 2  2 . Tích phân I f
 xdx bằng 1 A. 3. B. 1. C. 0. D. 2. 2x 13
Câu 39. Cho biết      
  với a, b là các số nguyên và C là hằng số thực. 
x   dx a ln x 1 b ln x 2 C x 1 2
Mệnh đề nào sau đây đúng?
A. a b  8 .
B. a b  8 .
C. 2a b  8 .
D. a  2b  8 . 5 1
Câu 40. Giả sử tích phân I
dx a b ln 3  c ln 5 
a, ,bc  . Giá trị của giá trị biểu thức 1 3x 1 1
P a b c là 8 4 5 7 A. P  . B. P  . C. P  . D. P  . 3 3 3 3
Câu 41. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng Q : x  2 y z  5  0 và mặt cầu
S x  2  y z  2 2 : 1 2
15. Mặt phẳng P song song với mặt phẳng Q và cắt mặt cầu S  theo giao tuyến
là một đường tròn có chu vi bằng 6 đi qua điểm nào sau đây? A. 1;  2;0 . B.  2  ;2;  1 . C. 2;  2  ;1 .
D. 0; 1;  5 . 5
Câu 42. Trong không gian với hệ trục tọa độ Oxyz , tìm tập hợp tất cả các giá trị của tham số m để phương trình 2 2 2
x y z mx  m   2 2 2
3 y  2z  3m  3  0 là phương trình mặt cầu: m  7  m  1 A. 7   m 1. B. 1
  m  7 . C. . D. .m 1 m  7
Câu 43. Trong không gian Oxyz , mặt phẳng Oxz có phương trình là. A. y  0 . B. z  0 . C. x  0 .
D. x y z  0 .
Câu 44. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x 1)  ( y 1)  (z  2)  9. Viết phương trình mặt phẳng
( ) tiếp xúc với (S) tại điểm M (0;3;0).
A. x  2 y  2z 12  0 .
B. x  2 y  2z  6  0 .
C. x  2 y  2z  6  0 .
D. x  4 y  2z 12  0 .
Câu 45. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : (x 1)  ( y  2)  (z  3)  1 và điểm (
A 2;3; 4) . Xét các điểm
M thuộc (S ) sao cho đường thẳng AM tiếp xúc với (S ) , M luôn thuộc mặt phẳng có phương trình là
A. 2x  2 y  2z 15  0 .
B. 2x  2 y  2z 15  0 .
C. x y z  7  0 .
D. x y z  7  0 .
Câu 46. Trong không gian Oxyz , mặt phẳng  P : x y z 1  0 có một vectơ pháp tuyến là A. n  1  ;1;1 .
B. n  1;1; 1 .
C. n  1;1;1 .
D. n  1; 1;1 . 2   3   4   1  
Câu 47. Trong không gian Oxyz , cho hai điểm A1;3;0 và B 5;1; 2
  . Mặt phẳng trung trực của đoạn thẳng AB
có phương trình là:
A. 2x y z  5  0 .
B. 3x  2 y z 14  0 .
C. 2x y z  5  0 .
D. x y  2z  3  0 .
Câu 48. Trong không gian với hệ tọa độ Oxyz , cho điểm A2; 4  ;1 ; B  1  ;1;3 và mặt phẳng
P: x 3y  2z 5  0. Một mặt phẳng Q đi qua hai điểm ,
A B và vuông góc với mặt phẳng  P có dạng
ax by cz 11  0 . Khẳng định nào sau đây là đúng?
A. a b c  5 .
B. a b c  15 .
C. a b c  15  .
D. a b c  5 .
Câu 49. Trong không gian Oxyz , cho 3 điểm A 1
 ;0;0, B0;2;0 và C 0;0;3. Mặt phẳng  ABC có phương trình là x y z x y z x y z x y z A.   1    . C.   1    1 2 3  . B. 1 1 2 3 1 2  . D. 1 3 1  . 2 3
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3; 2
 ;6, B0;1;0 và mặt cầu
S x  2  y  2 z  2 : 1 2 3
 25. Mặt phẳng P : ax by cz  2  0 đi qua ,
A B và cắt S  theo giao tuyến
là đường tròn có bán kính nhỏ nhất. Tính T a b c A. T  4 . B. T  5 . C. T  3. D. T  2 .
-----------------------------------Hết----------------------------------- 6 Đề 101 Đề 102 Đề10 3 Đề 104 Đề 105 Đề 106 Đề 107 Đề 108 1. A 1. A 1. A 1. C 1. D 1. B 1. B 1. B 2. B 2. A 2. D 2. A 2. C 2. B 2. B 2. A 3. D 3. C 3. A 3. C 3. D 3. D 3. B 3. A 4. A 4. D 4. C 4. B 4. B 4. D 4. D 4. B 5. C 5. B 5. D 5. A 5. B 5. A 5. A 5. B 6. B 6. C 6. B 6. B 6. C 6. B 6. D 6. C 7. B 7. C 7. B 7. B 7. A 7. A 7. D 7. D 8. B 8. D 8. B 8. B 8. D 8. D 8. D 8. D 9. B 9. B 9. B 9. B 9. D 9. A 9. D 9. D 10. D 10. B 10. A 10. B 10. B 10. C 10. D 10. C 11. C 11. B 11. A 11. D 11. C 11. A 11. D 11. B 12. C 12. A 12. A 12. A 12. D 12. D 12. A 12. C 13. C 13. D 13. B 13. B 13. A 13. B 13. B 13. A 14. D 14. C 14. D 14. C 14. B 14. A 14. A 14. D 15. C 15. A 15. C 15. C 15. C 15. C 15. B 15. C 16. D 16. C 16. C 16. C 16. C 16. C 16. B 16. C 17. D 17. A 17. B 17. A 17. A 17. B 17. A 17. C 18. B 18. B 18. C 18. C 18. D 18. D 18. D 18. D 19. A 19. C 19. A 19. A 19. B 19. B 19. D 19. A 20. C 20. C 20. D 20. A 20. A 20. D 20. A 20. C 21. C 21. B 21. A 21. C 21. A 21. B 21. C 21. C 22. B 22. C 22. C 22. C 22. C 22. C 22. B 22. C 23. B 23. B 23. C 23. A 23. C 23. A 23. A 23. C 24. D 24. C 24. D 24. C 24. A 24. B 24. B 24. D 25. A 25. D 25. D 25. A 25. D 25. A 25. D 25. A 26. C 26. A 26. D 26. B 26. B 26. A 26. D 26. B 27. A 27. B 27. C 27. C 27. A 27. A 27. C 27. A 28. A 28. C 28. D 28. A 28. B 28. B 28. C 28. D 29. A 29. B 29. B 29. A 29. D 29. D 29. B 29. D 30. C 30. C 30. A 30. D 30. C 30. B 30. C 30. B 31. B 31. D 31. A 31. A 31. C 31. A 31. A 31. A 32. A 32. D 32. D 32. D 32. D 32. D 32. A 32. A 33. C 33. A 33. B 33. C 33. B 33. D 33. D 33. B 34. B 34. D 34. D 34. B 34. A 34. A 34. B 34. B 35. C 35. C 35. C 35. D 35. C 35. C 35. C 35. D 36. D 36. A 36. B 36. D 36. D 36. D 36. C 36. D 37. D 37. D 37. C 37. C 37. B 37. D 37. D 37. B 38. B 38. B 38. A 38. D 38. B 38. B 38. D 38. B 39. B 39. B 39. B 39. D 39. C 39. C 39. B 39. C 40. A 40. B 40. A 40. D 40. D 40. C 40. C 40. C 41. D 41. B 41. D 41. A 41. D 41. D 41. A 41. A 42. B 42. A 42. A 42. B 42. A 42. A 42. C 42. D 43. A 43. A 43. B 43. C 43. B 43. C 43. A 43. A 44. B 44. C 44. A 44. B 44. A 44. D 44. A 44. A 45. A 45. D 45. D 45. C 45. A 45. A 45. C 45. A 46. D 46. C 46. B 46. A 46. B 46. A 46. A 46. A 47. C 47. A 47. C 47. D 47. B 47. A 47. D 47. D 48. A 48. D 48. D 48. B 48. A 48. C 48. C 48. A 49. C 49. D 49. B 49. D 49. C 49. C 49. B 49. A 50. D 50. C 50. B 50. D 50. B 50. B 50. B 50. B
Document Outline

  • Toán_12-Mã_101
  • Toán_12-Mã_102.1
  • Đáp-án_Giữa-kỳ-2-toán-12-2023-2024