SỞ GD&ĐT ĐIỆN BIÊN
ĐỀ KIỂM TRA, ĐÁNH GIÁ GIỮA HỌC KÌ I
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN NĂM HỌC 2023 - 2024
MÔN TOÁN - KHỐI LỚP 11
(Đề có 4 trang)
Thời gian làm bài : 90 Phút; (Đề có 39 câu)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 157
PHẦN I: TRẮC NGHIỆM (7,0 ĐIỂM): Thí sinh tô đáp án của mình vào phiếu trả lời trắc nghiệm.
Câu 1: Nghiệm của phương trình tan x = 3 là A. π π π π
x = + kπ (k ∈) . B. x = + k2π (k ∈) . C. x = + kπ (k ∈) . D. x = + k2π (k ∈) . 3 6 6 3
Câu 2: Đổi góc lượng giác có số đo 12° sang đơn vị rađian ta được π π π A. . B. 2 . C. . D. π . 15 15 5 3 Câu 3: Nếu cos 1
a = thì cos2a bằng: 6 A. 17 − . B. 2 − . C. 17 . D. 2 . 18 3 18 3
Câu 4: Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành một cấp số nhân.
A. x  64. B. x 14. C. x  32. D. x  68.
Câu 5: Công thức nào sau đây đúng? A. 2 1 cos 2 cos a a − = . B. 2 1 cos 2 cos a a + = . C. 2 1 cos cos a a + = . D. 2 1 cos cos a a − = . 2 2 2 2
Câu 6: Với giá trị nào của m thì phương trình cos x −1= 2m có nghiệm? A. 1 3 m  ;  ∈  . B. m∈( 1; − 0) . C. D. m∈[ 1; − 0]. 2 2  
Câu 7: Phương trình ( 0
2cos 2x −10 ) = 3 có nghiệm: 0 0 0 0 0 0 0 0
A. x = 20 + k360 x = 20 + k360 x = 20 + 180 k x = 20 + 180 k  . B.  . C.  D.  . 0 0
x = 80 + k360 0 0 x = 10 − + k360 0 0 x = 10 − + 180 k 0 0 x = 80 + 180 k Câu 8: Rút gọn  π   π M cos x  cos x  = + + − 
ta được kết quả: 4 4      A. 2 cos x . B. 2cos x . C. 2 − cos x .
D. − 2 cos x .
Câu 9: Cho cấp số nhân (u với u = 3; u = 6
− . Số 192 là số hạng thứ mấy của (u ? n ) n ) 1 2
A. Số hạng thứ 7 .
B. Không là số hạng của cấp số đã cho.
C. Số hạng thứ 6 .
D. Số hạng thứ 5.
Câu 10: Trong các công thức sau, công thức nào đúng? A.  π  1 3  π cos 
 x +  = cos x − sin .x B. 3 1 cos x +  = cos x + sin .x  3  2 2  3  2 2 C.  π  1 3  π cos 
 x +  = cos x + sin .x D. 3 1 cos x +  =
cos x − sin .x  3  2 2  3  2 2 Trang 1/4 - Mã đề 157
Câu 11: Tập giá trị của hàm số y = 2cos3x −1 là: A. [−2;2]. B. [ 1; − ] 1 . C. [ 2; − 0]. D. [ 3 − ; ] 1 .  
Câu 12: Trên đường tròn lượng giác, điểm 1 15 M  ;−
biểu diễn cho góc lượng giác α . Khi đó 4 4     
giá trị sinα bằng: A. 15 − . B. 1 . C. 15 . D. 1 − . 4 4 4 4 π
Câu 13: Cho góc lượng giác α thỏa mãn 3
cosα = − với < α < π và. Khi đó tanα bằng 5 2 A. 3 − . B. 4 − . C. 3 . D. 4 . 2 3 2 3
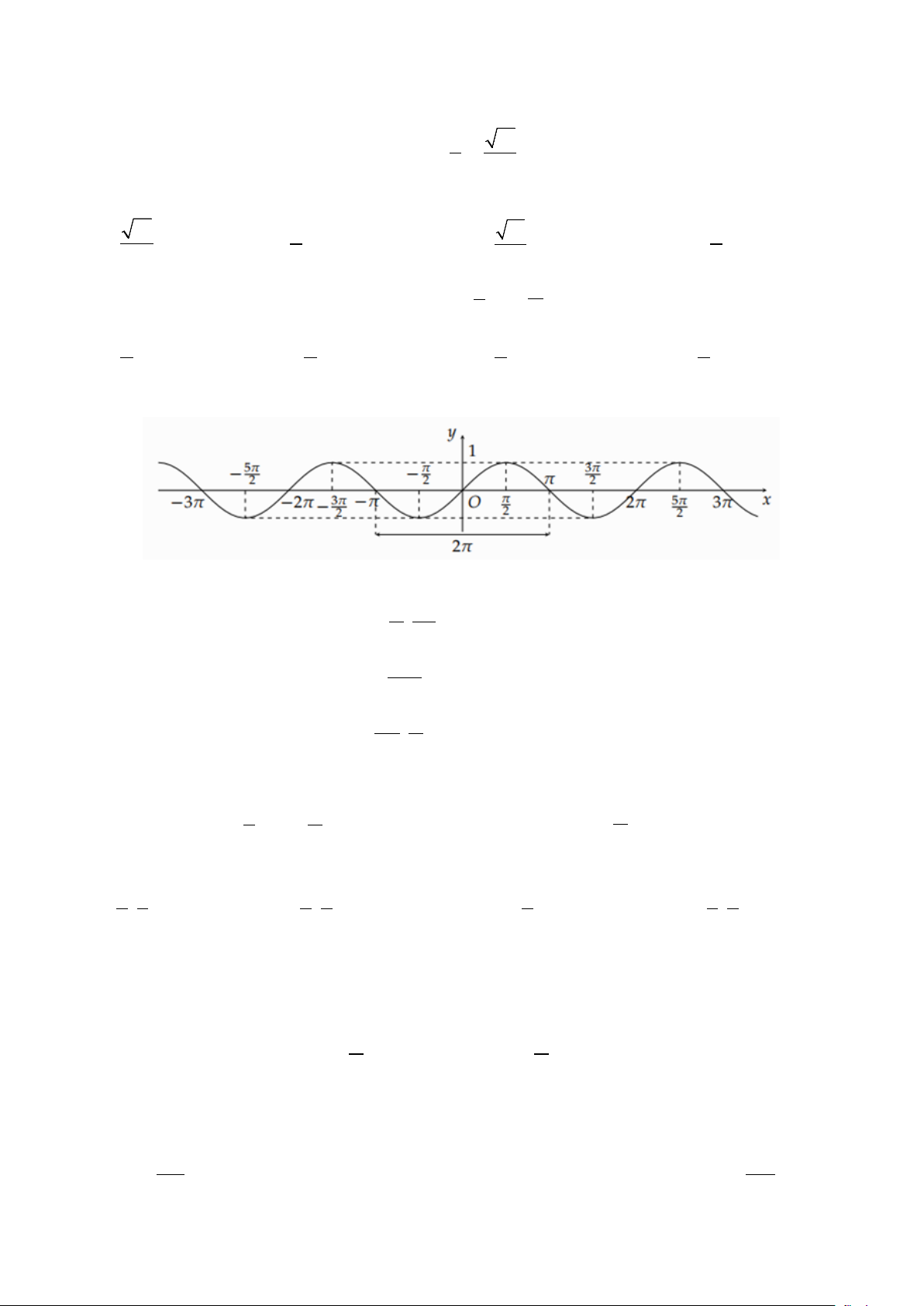
Câu 14: Cho đồ thị hàm số y = sin x như hình vẽ sau Mệnh đề nào sai? A. Hàm số  π π
y = sinx nghịch biến trên 3 ;   . 2 2    B. Hàm số  − π
y = sinx nghịch biến trên 3 ; π  −  . 2    C. Hàm số  π − π
y = sinx đồng biến trên ;   . 2 2   
D. Hàm số y = sinx đồng biến trên (0;π ) . Câu 15: Cho 4 π  π sinα 
= − và − < α < 0. Giá trị của biểu thức cos
−α thuộc khoảng nào dưới 5 2  6    đây? A.  1 1 ;         . B. 4 8  ; . C. 1 0; . D. 5 3  ; .  4 3   5 9   5   8 4 
Câu 16: Cho cấp số cộng (u có u = 28 và công sai d = 6 − . Hỏi 32
− là số hạng thứ mấy của cấp n ) 1 số cộng? A. 9. B. 10. C. 12. D. 11.
Câu 17: Rút gọn biểu thức  π   π S  = cos − 
x sin(π + x) − sin − 
x cos(π − x) ta được  2   2 
A. S = sin 2x.
B. S = cos2x . C. S = 1. D. S = 1 − .
Câu 18: Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2 − .Tính S . n ) 1 6 A. 155 S = − . B. S = 315 − . C. S = 315. D. 315 S = − . 6 3 6 6 6 3 Trang 2/4 - Mã đề 157
Câu 19: Cho một cấp số cộng (u có u = 5;
− u = 30 . Công sai của cấp số cộng bằng n ) 1 8 A. 5. B. 4. C. 6. D. 3.
Câu 20: Chọn khẳng định đúng trong các khẳng định sau đây. A. cos( α  π
− ) = −cosα . B. cos(π −α ) = cosα . C. sin (π +α ) = sinα D. sin α  − =   cosα .  2 
Câu 21: Tập xác định của hàm số 1+ cos2x y = là sin x −1 A. π
 \{kπ | k ∈ }  . B.  \  kπ | k  + ∈ . 2    C. π
 \{k2π | k ∈ }  . D.  \  k2π | k  + ∈ . 2    2
Câu 22: Cho dãy số  2n 1
u , biết u 
. Tìm số hạng u . n n 2 n 3 5 A. 7 1 17 71 u  . B. u  . C. u  . D. u  . 5 4 5 4 5 12 5 39
Câu 23: Phương trình cos x = cosα có tập nghiệm là:
A. S = {α + kπ, α
− + kπ | k ∈ }  .
B. S = {α + kπ;π −α + kπ | k ∈ }  .
C. S = {α + k2π; α
− + k2π | k ∈ }  .
D. S = {α + k2π;π −α + k2π | k ∈ }  .
Câu 24: Cho dãy số ( u  = 5 u với 1
. Năm số hạng đầu của dãy là: n ) u  = +  + u n n 1 n A. 5;5;6;7;8. B. 5;5;6;8;11. C. 5;6;8;11;15. D. 5;6;7;8;9.
Câu 25: Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2
− . Số hạng thứ sáu của (u n ) n ) 1 là: A. u = 320 − . B. u = 320 . C. u =160 . D. u = 160 − . 6 6 6 6 Câu 26: Cho 3π π < a <
. Trong các khẳng định sau, khẳng định nào đúng ? 2
A. sin a < 0, cosa > 0. B. sin a > 0 , cosa > 0. C. sin a < 0, cosa < 0. D. sin a > 0 , cosa < 0.
Câu 27: Nghiệm của phương trình  π   3π sin 2x  sin  x  − = +  là 4 4      A. π 2π π π π π x = − + k
; x = π + kπ (k ∈ 2 2 ) .
B. x = + k ; x = − + k (k ∈) . 6 3 6 3 2 3 C. π π π
x = + k2π; x = π + k2π (k ∈ 2 ) .
D. x = + k
; x = π + k2π (k ∈). 6 6 3 Câu 28: Tập π D  \  kπ ,k  = +
∈ là tập xác định của hàm số nào sau đây? 2   
A. y = tan 2x .
B. y = cot x .
C. y = cot 2x .
D. y = tan x .
Câu 29: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin 2 .x
B. y = cot .x
C. y = tan3 .x
D. y = cos .x Trang 3/4 - Mã đề 157
Câu 30: Bạn An cần xếp 15 cột đồng xu theo thứ tự cột thứ nhất có 2 đồng xu, các cột tiếp theo cứ
tăng ba đồng một cột so với cột đứng trước. Hỏi bạn An cần bao nhiêu đồng xu để xếp?
A. 360 (đồng xu).
B. 345 (đồng xu).
C. 500 (đồng xu).
D. 400 (đồng xu).
Câu 31: Cho cấp số cộng (u có u = 2
− và công sai d = 3. Số hạng tổng quát u là n ) 1 n
A. u = n − .
B. u = − n + .
C. u = − n + .
D. u = n − . n 3 5 n 3 2 n 2 3 n 3 2
Câu 32: Tập xác định của hàm số  π y cot 2x  = −  là 4   
A. D =  \{kπ, k ∈ }  B. D =  C. π π π  \ k D   , k  = + ∈ .
D. D =  \  + kπ, k ∈ 8 2      4 
Câu 33: Dãy số nào sau đây là cấp số cộng? A. 2, − 2,4,6,8 . B. 7,3, 1 − , 5 − , 9 − . C. 1,4,7,10,14. D. 1,3,5,7,11.
Câu 34: Dãy số có các số hạng cho bởi: 1 2 3 4
0; ; ; ; ;. có số hạng tổng quát là công thức nào dưới 2 3 4 5 đây? 2 A. n −1 u + = B. n u = C. n − n D. n 1 u = n . n . n . u = n . n n +1 n +1 n
Câu 35: Trong các dãy số u
u sau, dãy số nào bị chặn trên?
n  cho bởi số hạng tổng quát n
A. u  2n. B. 2 u  n . C. 1 u  .
D. u  n1. n n n n n
PHẦN II: TỰ LUẬN (3,0 ĐIỂM) Câu 36(1,0 điểm): 1. Cho 3 π  π
cosα = − và < α < π. Tính sin 2α  + 5 2 4   
2. Tìm tập xác định của hàm số 2sin x − 5 y = 3 tan x −1  + = Câu 37(0,75 điểm): u 4u 17
Cho cấp số cộng (u thỏa mãn: 5 2 . n ) 2u −u =  9 7 10
1. Tìm số hạng đầu và công sai của (u . n )
2. Tính S = u + u +....+ u . 31 32 50
Câu 38(0,75 điểm): Giải phương trình: sin 2x + cos x −1− 2sin x = 0 . 2cos x + 3
Câu 39(0,5 điểm): Anh Tâm vay ngân hàng 50 triệu đồng, mỗi tháng trả góp cho ngân hàng 3 triệu
đồng và phải chịu lãi suất của số tiền chưa trả là 0,7% / tháng. Hỏi sau 15 tháng anh Tâm còn nợ
ngân hàng bao nhiêu tiền ?
------ HẾT ------ Trang 4/4 - Mã đề 157
SỞ GD&ĐT ĐIỆN BIÊN
ĐỀ KIỂM TRA, ĐÁNH GIÁ GIỮA HỌC KÌ I
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN NĂM HỌC 2023 - 2024
MÔN TOÁN - KHỐI LỚP 11(CƠ BẢN)
(Đề có 4 trang)
Thời gian làm bài : 90 Phút; (Đề có 39 câu)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 258
PHẦN I: TRẮC NGHIỆM (7,0 ĐIỂM): Thí sinh tô đáp án của mình vào phiếu trả lời trắc nghiệm.
Câu 1: Cho cấp số cộng (u có u = 28 và công sai d = 6 − . Hỏi 32
− là số hạng thứ mấy của cấp số n ) 1 cộng? A. 10. B. 11. C. 12. D. 9. Câu 2: Cho dãy số ( u  = 5 u với 1
. Năm số hạng đầu của dãy là: n ) u  = +  + u n n 1 n A. 5;5;6;8;11. B. 5;6;7;8;9. C. 5;6;8;11;15. D. 5;5;6;7;8.
Câu 3: Phương trình cos x = cosα có tập nghiệm là:
A. S = {α + k2π;π −α + k2π | k ∈ }  .
B. S = {α + kπ, α
− + kπ | k ∈ }  .
C. S = {α + kπ;π −α + kπ | k ∈ }  .
D. S = {α + k2π; α
− + k2π | k ∈ }  .
Câu 4: Nghiệm của phương trình  π   3π sin 2x  sin  x  − = +  là 4 4      A. π 2π π x = − + k
; x = π + kπ (k ∈) .
B. x = + k2π; x = π + k2π (k ∈) . 6 3 6 C. π 2π π 2π π π x = + k ; x = − + k (k ∈ 2 ) .
D. x = + k
; x = π + k2π (k ∈). 6 3 2 3 6 3
Câu 5: Trong các dãy số u
u sau, dãy số nào bị chặn trên?
n  cho bởi số hạng tổng quát n
A. u  n1. B. 2 u  n .
C. u  2n. D. 1 u  . n n n n n
Câu 6: Chọn khẳng định đúng trong các khẳng định sau đây.
A. cos(π −α ) = cosα . B.  π sin α  − =   cosα . C. cos( α − ) = −cosα .
D. sin(π +α ) = sinα  2 
Câu 7: Cho cấp số nhân (u với u = 3; u = 6
− . Số 192 là số hạng thứ mấy của (u ? n ) n ) 1 2
A. Số hạng thứ 6 .
B. Số hạng thứ 7 .
C. Số hạng thứ 5.
D. Không là số hạng của cấp số đã cho. Câu 8: Tập π D  \  kπ ,k  = +
∈ là tập xác định của hàm số nào sau đây? 2   
A. y = tan 2x .
B. y = cot 2x .
C. y = cot x .
D. y = tan x .
Câu 9: Tập giá trị của hàm số y = 2cos3x −1 là: A. [ 2; − 0]. B. [ 1; − ] 1 . C. [ 3 − ; ] 1 . D. [−2;2]. π
Câu 10: Cho góc lượng giác α thỏa mãn 3
cosα = − với < α < π và. Khi đó tanα bằng 5 2 A. 4 − . B. 3 − . C. 4 . D. 3 . 3 2 3 2 Trang 1/4 - Mã đề 258
Câu 11: Dãy số có các số hạng cho bởi: 1 2 3 4
0; ; ; ; ;. có số hạng tổng quát là công thức nào dưới 2 3 4 5 đây? 2 A. n − n n − n n + u = B. 1 u = C. u = D. 1 u = n . n . n . n . n +1 n n +1 n Câu 12: Rút gọn  π   π M cos x  cos x  = + + − 
ta được kết quả: 4 4      A. 2cos x .
B. − 2 cos x . C. 2 cos x . D. 2 − cos x .
Câu 13: Cho một cấp số cộng (u có u = 5;
− u = 30 . Công sai của cấp số cộng bằng n ) 1 8 A. 4. B. 3. C. 5. D. 6.
Câu 14: Dãy số nào sau đây là cấp số cộng? A. 1,3,5,7,11. B. 2, − 2,4,6,8 . C. 1,4,7,10,14. D. 7,3, 1 − , 5 − , 9 − .  
Câu 15: Trên đường tròn lượng giác, điểm 1 15 M  ;−
biểu diễn cho góc lượng giác α . Khi đó 4 4     
giá trị sinα bằng: A. 1 − . B. 15 − . C. 15 . D. 1 . 4 4 4 4
Câu 16: Công thức nào sau đây đúng? A. 2 1 cos cos a a − = . B. 2 1 cos cos a a + = . C. 2 1 cos 2 cos a a − = . D. 2 1 cos 2 cos a a + = . 2 2 2 2
Câu 17: Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2
− . Số hạng thứ sáu của (u n ) n ) 1 là: A. u = 160 − . B. u =160 . C. u = 320 − . D. u = 320 . 6 6 6 6
Câu 18: Trong các công thức sau, công thức nào đúng? A.  π  1 3  π cos 
 x +  = cos x + sin .x B. 3 1 cos x +  =
cos x − sin .x  3  2 2  3  2 2 C.  π  1 3  π cos 
 x +  = cos x − sin .x D. 3 1 cos x +  = cos x + sin .x  3  2 2  3  2 2
Câu 19: Phương trình ( 0
2cos 2x −10 ) = 3 có nghiệm: 0 0 0 0 0 0 0 0
A. x = 20 + k360 x = 20 + 180 k x = 20 + k360 x = 20 + 180 k  . B.  . C.  . D.  0 0
x = 80 + k360 0 0 x = 80 + 180 k 0 0 x = 10 − + k360 0 0 x = 10 − + 180 k
Câu 20: Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2 − .Tính S . n ) 1 6 A. S = 315 − . B. S = 315. C. 155 315 6 6 S = − . D. S = − . 6 3 6 3
Câu 21: Tập xác định của hàm số 1+ cos2x y = là sin x −1 A. π
 \{k2π | k ∈ }  . B.  \  k2π | k  + ∈ . 2    C. π
 \{kπ | k ∈ }  . D.  \  kπ | k  + ∈ . 2    Trang 2/4 - Mã đề 258
Câu 22: Cho cấp số cộng (u có u = 2
− và công sai d = 3. Số hạng tổng quát u là n ) 1 n
A. u = n − .
B. u = − n + .
C. u = n − .
D. u = − n + . n 3 2 n 3 2 n 2 3 n 3 5
Câu 23: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = tan3 .x
B. y = cot .x
C. y = cos .x
D. y = sin 2 .x
Câu 24: Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành một cấp số nhân.
A. x  68. B. x  32. C. x  64. D. x 14. Câu 25: Nếu cos 1
a = thì cos2a bằng: 6 A. 17 . B. 17 − . C. 2 . D. 2 − . 18 18 3 3
Câu 26: Với giá trị nào của m thì phương trình cos x −1= 2m có nghiệm? A. m∈( 1; − 0) . B. m∈[ 1; − 0]. C. 1 3 m  ;  ∈  . D. 2 2   Câu 27: Cho 3π π < a <
. Trong các khẳng định sau, khẳng định nào đúng ? 2
A. sin a < 0, cosa > 0. B. sin a > 0 , cosa < 0. C. sin a < 0, cosa < 0. D. sin a > 0 , cosa > 0.
Câu 28: Rút gọn biểu thức  π   π S  = cos − 
x sin(π + x) − sin − 
x cos(π − x) ta được  2   2  A. S = 1 − .
B. S = sin 2x.
C. S = cos2x . D. S = 1.
Câu 29: Tập xác định của hàm số  π y cot 2x  = −  là 4   
A. D =  \{kπ, k ∈ }  B. D =  C. π π π D k  \   kπ , k  = + ∈
D. D =  \  + , k ∈ . 4      8 2  2
Câu 30: Cho dãy số  2n 1
u , biết u 
. Tìm số hạng u . n n 2 n 3 5 A. 17 1 7 71 u  . B. u  . C. u  . D. u  . 5 12 5 4 5 4 5 39
Câu 31: Bạn An cần xếp 15 cột đồng xu theo thứ tự cột thứ nhất có 2 đồng xu, các cột tiếp theo cứ
tăng ba đồng một cột so với cột đứng trước. Hỏi bạn An cần bao nhiêu đồng xu để xếp?
A. 500 (đồng xu).
B. 360 (đồng xu).
C. 345 (đồng xu).
D. 400 (đồng xu).
Câu 32: Nghiệm của phương trình tan x = 3 là A. π π
x = + kπ (k ∈ π π
) . B. x = + kπ (k ∈) . C. x = + k2π (k ∈) . D. x = + k2π (k ∈) . 6 3 6 3 Trang 3/4 - Mã đề 258
Câu 33: Đổi góc lượng giác có số đo 12° sang đơn vị rađian ta được π π π A. 2 . B. . C. . D. π . 15 5 15 3 Câu 34: Cho 4 π  π sinα 
= − và − < α < 0. Giá trị của biểu thức cos
−α thuộc khoảng nào dưới 5 2  6    đây? A.  1 0;         . B. 1 1  ; . C. 5 3  ; . D. 4 8  ; .  5   4 3   8 4   5 9 
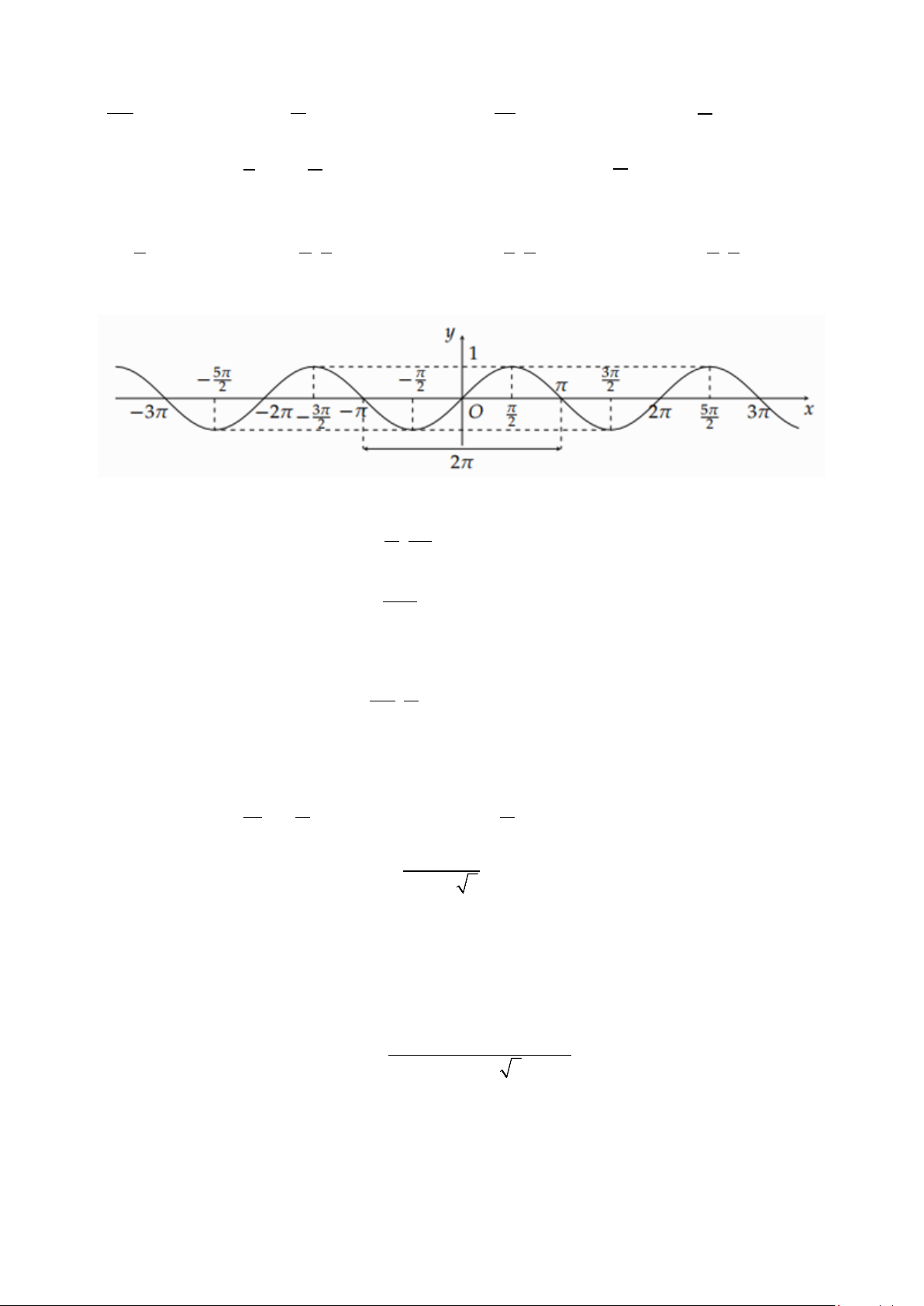
Câu 35: Cho đồ thị hàm số y = sin x như hình vẽ sau Mệnh đề nào sai?  π 3π ;   
A. Hàm số y = sinx nghịch biến trên 2 2  .  3 − π ; π  −  
B. Hàm số y = sinx nghịch biến trên 2  .
C. Hàm số y = sinx đồng biến trên(0;π ) .  π − π ;   
D. Hàm số y = sinx đồng biến trên 2 2 .
PHẦN II: TỰ LUẬN (3,0 ĐIỂM) Câu 36(1,0 điểm):  π 1. Cho 5 π sinα =
và < α < π. Tính cos2α  − 13 2 3   
2. Tìm tập xác định của hàm số 2cos x + 5 y = cot x + 3 2u − u = 5
Câu 37(0,75 điểm): Cho cấp số cộng (u thỏa mãn: 10 15 . n ) 4u +u =  15 3 8
1. Tìm số hạng đầu và công sai của (u . n )
2. Tính S = u + u +....+ u . 51 52 80
Câu 38(0,75 điểm): Giải phương trình: sin 2x −sin x −1+ 2cos x = 0 . 2sin x − 3
Câu 39(0,5 điểm): Anh Tâm vay ngân hàng 50 triệu đồng, mỗi tháng trả góp cho ngân hàng 3 triệu
đồng và phải chịu lãi suất của số tiền chưa trả là 0,7% / tháng. Hỏi sau 15 tháng anh Tâm còn nợ
ngân hàng bao nhiêu tiền ?
------ HẾT ------ Trang 4/4 - Mã đề 258
SỞ GD&ĐT ĐIỆN BIÊN
DE KIEM TA – NĂM HỌC 2023 - 2024
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN
MÔN TOÁN - KHỐI LỚP 11
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm: 157 258 356 455 1 A B C A 2 A C D A 3 A D C C 4 C D C A 5 B D D B 6 D B B C 7 C B A B 8 A D D A 9 A C A A 10 A A A C 11 D B C B 12 A C D C 13 B C B D 14 D D B C 15 C B C A 16 D D C A 17 B A A A 18 D C A D 19 A D B C 20 D D D A 21 D B B A 22 A A B C 23 C C D D 24 C B C D 25 D B C B 26 C B A B 27 D C A C 28 D C A C 29 D D D B 30 B C B B 31 D C D D 32 C B D C 33 B C D D 34 A A D C 35 C C D D ĐÁP ÁN TỰ LUẬN ĐỀ 157+356 CÂU ĐÁP ÁN BIỂU ĐIỂM Câu 36  π Cho 3 π
cosα = − và < α < π. Tính sin 2α  + 5 2 4    1 3 π cosα 0.25
= − và < α < π nên 4 sinα = 5 2 5 Tính được 24 sin2α = − , 7 cos2α = − 5 25  π  31 2 0.25 ⇒ sin 2α + = −  4    50
Tìm tập xác định của hàm số 2sin x − 5 y = 3 tan x −1 0.25 cos x ≠ 0  π x ≠ + kπ  ĐKXĐ:   2  1 ⇔  (k ∈Z ) tan x ≠ π  3 x ≠ +  kπ  6 π π 0.25 TXĐ: D  \  kπ , kπ ,k Z  = + + ∈ 2 6    Câu 37 u  + 4u =17
Cho cấp số cộng (u thỏa mãn: 5 2 . n ) 2u −u =  9 7 10
1. Tìm số hạng đầu và công sai của (u . n )
2. Tính S = u + u +....+ u . 31 32 50
Gọi số hạng đầu là u , công sai là d . Ta có 0.25 1 u  + 
4d + 4 u + d =17 1 ( 1 ) 5  u + 8d =17 1  ⇔  2
 (u + 6d − u + 9d = 9 u +  3d = 9 1 ) ( 1 ) 1 u  = 3 − 0.25 1  d = 4
Ta có S = S − S = ..... 0.25 50 30 Câu 38
Giải phương trình: sin 2x + cos x −1− 2sin x = 0 2cos x + 3 π 0.25 ĐK: 3 5 cos x ≠ − ⇔ x ≠ ±
+ k2π ,k ∈ Z 2 6
Với mọi x thoả mãn ĐK, PT ⇔ sin 2x + cos x −1− 2sin x = 0
⇔ 2sin x cos x + cos x −1− 2sin x = 0 ⇔ (2sin x + ) 1 (cos x − ) 1 = 0 2  π 0.25 x − = + k2π  6 2sin x 1 0  + =  7π ⇔ ⇔ x = + k2π (k ∈  Z ) cos x −1 = 0  6 x = k2π    π 0.25 x − = + k2π
Kết hợp điều kiện ta được:  6
(k ∈ Z ) là nghiệm của PT  x = k2π Câu 39
Anh Tâm vay ngân hàng 50 triệu đồng, mỗi tháng trả góp cho ngân hàng 3
triệu đồng và phải chịu lãi suất của số tiền chưa trả là 0,7% / tháng. Hỏi sau
15 tháng anh Tâm còn nợ ngân hàng bao nhiêu tiền ?
Đặt A = 50 triệu đồng; r = 0,7% ; m = 3 triệu đồng. 0.25
Số tiền anh Tâm còn nợ sau tháng thứ nhất là: T = A 1+ r − m. 1 ( ) Số tiền anh Tâm còn nợ sau tháng thứ hai là:
T = T (1+ r) − m = A(1+ r)2 − m 1+ r − m . 2 1 ( ) …………
Số tiền anh Tâm còn nợ sau tháng thứ n là: n − + r −
T = A + r − m + r
− − m + r − m = A + r − m . n ( )n ( )n 1 ( ) ( )n (1 ) 1 1 1 ... 1 1 . r
Do đó số tiền anh Tâm còn nợ ngân hàng sau tháng thứ 15 là: 0.25 + −
T = A( + r) (1 r)15 15 1 1 − . m = ....... 15 r ĐỀ 258+455 CÂU ĐÁP ÁN BIỂU ĐIỂM Câu 36  π Cho 5 π sinα =
và < α < π. Tính cos2α  − 13 2 3    5 π sinα 0.25 = và < α < π nên 12 cosα = − 13 2 13 Tính được 120 sin2α = − , 119 cos2α = 169 169  π  119 3 120 0.25 ⇒ cos 2α − − =  3    338
Tìm tập xác định của hàm số 2cos x + 5 y = cot x + 3 3 si 0.25  n ≠ 0 x ≠ k x π ĐKXĐ:   ⇔  π (k ∈Z ) cot x ≠ − 3
x ≠ − + kπ  3  π 0.25
TXĐ: D  \ kπ, kπ ,k Z  = − + ∈ 3    Câu 37 2u − u = 5
Cho cấp số cộng (u thỏa mãn: 10 15 . n ) 4u +u =  15 3 8
1. Tìm số hạng đầu và công sai của (u . n )
2. Tính S = u + u +....+ u . 51 52 80
Gọi số hạng đầu là u , công sai là d . Ta có 0.25 1
2(u + 9d − u +14d = 5 1 ) ( 1 ) u  + 4d = 5 1  ⇔  4
 (u + 2d + u + 7d = 15 5  u +15d = 15 1 ) ( 1 ) 1 u  = 3 − 0.25 1  d = 2
Ta có S = S − S = ..... 0.25 80 50 Câu 38
Giải phương trình: sin 2x − sin x −1+ 2cos x = 0 2sin x − 3  π 0.25 x ≠ + k2π  ĐK: 3  3 sin x ≠ ⇔  (k ∈Z ) 2 2π x ≠ + k2π  3
Với mọi x thoả mãn ĐK, PT ⇔ sin 2x − sin x −1+ 2cos x = 0
⇔ 2sin x cos x − sin x −1+ 2cos x = 0 ⇔ (sin x + ) 1 (2cos x − ) 1 = 0  π 0.25 x − = + k2π  2 sin x 1 0  + = π  ⇔ ⇔ x = + k2π (k ∈  Z ) 2cos x −1 = 0  3  π
x = − + k2π  3  π 0.25 x − = + k2π 
Kết hợp điều kiện ta được: 2 
(k ∈ Z ) là nghiệm của PT π
x = − + k2π  3 Câu 39
Anh Tâm vay ngân hàng 50 triệu đồng, mỗi tháng trả góp cho ngân hàng 3
triệu đồng và phải chịu lãi suất của số tiền chưa trả là 0,7% / tháng. Hỏi sau
15 tháng anh Tâm còn nợ ngân hàng bao nhiêu tiền ? 4
Đặt A = 50 triệu đồng; r = 0,7% ; m = 3 triệu đồng. 0.25
Số tiền anh Tâm còn nợ sau tháng thứ nhất là: T = A 1+ r − m. 1 ( ) Số tiền anh Tâm còn nợ sau tháng thứ hai là:
T = T (1+ r) − m = A(1+ r)2 − m 1+ r − m . 2 1 ( ) …………
Số tiền anh Tâm còn nợ sau tháng thứ n là: n − + r −
T = A + r − m + r
− − m + r − m = A + r − m . n ( )n ( )n 1 ( ) ( )n (1 ) 1 1 1 ... 1 1 . r
Do đó số tiền anh Tâm còn nợ ngân hàng sau tháng thứ 15 là: 0.25 + −
T = A( + r) (1 r)15 15 1 1 − . m = ....... 15 r 5
Document Outline