Đề giữa kì 1 Toán 11 năm 2023 – 2024 trường THPT Nguyễn Huệ – TT Huế

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kì 1 môn Toán 11 năm học 2023 – 2024 trường THPT Nguyễn Huệ, tỉnh Thừa Thiên Huế

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang
1
/
4
-
Mã
đ
ề 198
TRƯỜNG THPT NGUYỄN HUỆ
TỔ TOÁN
KIỂM TRA GIỮA KÌ I
NĂM HỌC 2023 - 2024
Môn: TOÁN - Lớp 11
ĐỀ CHÍNH THỨC
(Đề kiểm tra có 4 trang)
ời gian: 90
phút (Không k
ể thời gian phát đề)
Họ và tên:............................................................................
Mã đề thi
198
SBD:.......................................Lớp:.....................................
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN (7 điểm)
Câu 1. Phương trình
tan 3
x
có tất cả các nghiệm là:
A.
x ( ).
3
k k
B.
x 2 ( ).
3
k k
C.
x ( ).
6
k k
D.
x ( ).
3
k k
Câu 2. Cho các dãy số
,
n
u
,
n
v
,
n
w
với
2 1
,
n
n
u
n
2
2 ,
n
v n
2 1.
n
n
w
Có bao nhiêu dãy số bị
chặn?
A.
3.
B.
0.
C.
1.
D.
2.
Câu 3. Đơn giản biểu thức
cos sin tan
2
A
, ta được:
A.
o
sin
c s
–A
. B.
tan
A
. C.
in
cos sA
. D.
2sin
A
.
Câu 4. Cho dãy số
n
u
xác định bởi
1
1
1
.
2 3; 2
n n
u
u u n
Khẳng định nào sau đây SAI?
A.
4
29.
u
B.
2
5.
u
C.
5
58.
u
D.
3
13.
u
Câu 5. Cho cấp số nhân có các số hạng lần lượt là
3 3 3
3; ; ; ; ...
2 4 8
. Tìm số hạng tổng quát
n
u
của cấp số
nhân đã cho.
A.
1
1
3. .
2
n
n
u
B.
1
1
.3 .
2
n
n
u
C.
1
1
.3 .
2
n
n
u
D.
1
1
3. .
2
n
n
u
Câu 6. Cho góc
thỏa mãn
3
sin
5
và
2
. Tính
2
tan
.
1 tan
P
A.
12
.
25
P
B.
3
.
7
P
C.
12
.
25
P
D.
3.
P
Câu 7. Tính tổng
2 12
S 1 10 10 10 .
A.
13
1
.(1 10 ).
9
S
B.
12
1
.(1 10 ).
9
S
C.
13
1
.(10 1).
9
S
D.
12
1
.(10 1).
9
S
Câu 8. Trên đường tròn lượng giác có điểm gốc là
A
lấy điểm
M
thuộc đường tròn sao cho
sđ
0
( , ) 45
OA OM
. Gọi
N
là điểm đối xứng với
M
qua trục
Ox
, số đo của các góc lượng giác
( , )
OA ON
bằng:
A.
0
225
. B.
0 0
45 360 ,k k
.
C.
0 0
135 360 , .
k k
D.
0
135
.
Câu 9. Trong các hàm số sau hàm số nào tuần hoàn với chu kỳ
?
A.
cot .
2
x
y
B.
sin 2 .
y x
C.
tan 2 .
y x
D.
cos .
y x
Câu 10. Mức thưởng tết (triệu đồng) của các công nhân trong một nhà máy được cho trong bảng sau:
Mức thưởng
5;10
10;15
15;20
20;25
25;30
Số công nhân 19 30 42 6 3
Trang
2
/
4
-
Mã
đ
ề 198
Tính mốt của mẫu số liệu ghép nhóm.
A.
16,25.
B.
20, 25.
C.
21,25.
D.
15,25.
Câu 11. Tìm điều kiện xác định của hàm số
tan cot .
y x x
A.
2
k
x
,
k
. B.
2
x k
,
k
.
C.
x
. D.
x k
,
k
.
Câu 12. Cho
1
cos
3
. Khi đó
3
sin
2
bằng:
A.
2
.
3
B.
2
.
3
C.
1
.
3
D.
1
.
3
Câu 13. Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
2 .
n
u n
B.
2 .
n
n
u
C.
2
.
n
u n
D.
2
.
n
u
Câu 14. Tìm m để phương trình
sin 0
x m
vô nghiệm .
A.
1 1.
m
B.
1.
m
C.
1
.
1
m
m
D.
1.
m
Câu 15. Tuổi thọ (năm) của một loại bóng đèn được cho trong bảng sau:
Tu
ổ
i t
h
ọ
(năm)
2;3,5
3,5;5
5;6,5
6,5;8
8;9,5
Số bóng đèn
8 32 34 11 15
Nhóm chứa trung vị là nhóm thứ mấy?
A. Thứ 4. B. Thứ 3. C. Thứ 5. D. Thứ 2.
Câu 16. Cho cấp số cộng
n
u
có
1
4
u
và
3.
d
Khẳng định nào sau đây ĐÚNG?
A.
4 3 1 .
n
u n
B.
4 3 .
n
u n
C.
4 3 1 .
n
u n
D.
4 3 1.
n
u n
Câu 17. Cho cấp số cộng
n
u
có
1
27
u
và
4
3
u
. Tổng
20 1 2 3 20
.....
S u u u u
bằng:
A.
20
980.
S
B.
20
1250
S
. C.
20
1960.
S
D.
20
1060.
S
Câu 18. Trong các đẳng thức sau, đẳng thức nào ĐÚNG?
A.
2 2
sin sin sin sin
a b a b b a
. B.
2 2
sin sin sin sin
a b a b a b
C.
2 2
sin sin cos cos
a b a b a b
. D.
2 2
sin sin sin sin
a b a b a b
.
Câu 19. Tập giá trị của hàm số
4 sin 3 1
y x
là:
A.
2;2 .
B.
2;4 .
C.
4 2;8 .
D.
4 2 1;7 .
Câu 20. Cho cấp số cộng
n
u
có
2 3
n
u n
. Công sai của cấp số cộng là:
A.
1.
d
B.
2.
d
C.
5.
d
D.
8.
d
Câu 21. Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A.
1;1;1;1;...
B.
1 1 1
1, , , ;...
5 25 125
C.
1 1 1
; ; ; 1;...
8 4 2
D.
1;3;9;18;...
Câu 22. Khảo sát nhiệt độ (
0
C
) tại một địa điểm trong 40 ngày thu được mẫu số liệu ghép nhóm sau:
Nhiệt độ (
0
C
)
20;23
23;26
26;29
29;32
32;35
S
ố
n
g
ày
7
6
10
8
9
Số ngày có nhiệt độ từ
0
29
C đến dưới
0
32
C là:
A. 8. B. 40. C. 10. D. 9.
Câu 23. Cân nặng (kg) của 45 học sinh lớp 11 được cho trong bảng sau:
Cân n
ặ
n
g
(k
g
)
41,5;46,5
46,5;51,5
51,5;56,5
56,5;61,5
61,5;66,5
66,5;71,5
Số học sinh 10 8 17 4 3 3
Cân nặng (kg) trung bình là:
Trang
3
/
4
-
Mã
đ
ề 198
A.
55.
x
B.
53.
x
C.
54.
x
D.
52.
x
Câu 24. Biểu thức
sin7 .sin os7 . os
x x c x c x
bằng:
A.
sin8 .
x
B.
6 .
cos x
C.
8 .
cos x
D.
sin6 .
x
Câu 25. Trong các dãy số sau, dãy số nào là cấp số cộng?
A.
1; 4;7;10;14.
B.
3;1;5;9;14.
C.
5;2; 1; 4; 7.
D.
1 2 4
; ;1; ;2.
3 3 3
Câu 26. Giải phương trình lượng giác
2cos 3 0
2
x
có nghiệm là:
A.
5
2 ( ).
6
x k k
B.
5
4 ( ).
6
x k k
C.
5
4 ( ).
3
x k k
D.
5
2 ( ).
3
x k k
Câu 27. Cho các dãy số sau. Dãy số nào là dãy số giảm?
A.
3;7;13;21;31;...
B.
1; 1; 1; 1; 1;...
C.
2;4;8;16;32;...
D.
3; 1; 1; 3; 5;...
Câu 28. Trong các đẳng thức sau, đẳng thức nào SAI?
A.
2
cos 2 1 2sin
a a
. B.
2
2 tan
tan 2
1 tan
a
a
a
.
C.
sin 2 2sin cos
a a a
. D.
2 2
cos 2 cos sin
a a a
.
Câu 29. Một cấp số nhân có
1
3
u
và
2
q
. Số 384 là số hạng thứ mấy của cấp số nhân này?
A. 7. B. 6. C. 9. D. 8.
Câu 30. Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
3
1
.
2 1
n
u
n
B.
4 1
.
1
n
n
u
n
C.
1
.
4
n
n
u
D.
2
4 .
n
u n
Câu 31. Cho
5
cos 2
4
và
2
4
. Khẳng định nào sau đây ĐÚNG?
A.
3 3
sin
3
10
. B.
3 3
sin
3 2
.
C.
3 3
sin
3
2 10
. D.
3 3
sin
3
2 10
.
Câu 32. Cho lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo thứ tự
đó và các điểm
,
B C
có tung độ dương. Khi đó số đo của các góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng :
A.
0
120
. B.
0
240 .
C.
0 0
120 360 ,k k
. D.
0 0
240 360 ,k k
.
Câu 33. Cho dãy số
n
u
, biết
2
2
sin cos .
4 3
n
n n
u
Bốn số hạng đầu tiên của dãy số đó lần lượt là
những số nào dưới đây?
A.
1 3 1
0; ; ; .
2 2 2
B.
1 1 1
0; ; ; .
2 2 2
C.
1 1 3 1
; ; ; .
2 2 2 2
D.
1 1 3 1
; ; ; .
2 2 2 2
Câu 34. Trong các hàm số sau đây, hàm số nào có đồ thị nhận trục tung làm trục đối xứng?
A.
cos
y x
. B.
tan
y x
. C.
3
sin
y x
. D.
sin
y x
.
Câu 35. Hàm số
sin
y x
đồng biến trên khoảng nào sau đây?
A.
5 7
;
4 4
. B.
9 11
;
4 4
. C.
7
;3
4
. D.
7 9
;
4 4
.
PHẦN II: TỰ LUẬN (3 điểm)
Câu 36. (1,0 điểm) Cho
2
cos , .
3 2
Tính các giá trị lượng giác còn lại của góc
.
Trang
4
/
4
-
Mã
đ
ề 198
Câu 37. (1,0 điểm) Khảo sát thời gian (phút) tập thể dục trong ngày của 1 số học sinh lớp 11 thu được
mẫu số liệu ghép nhóm sau:
Thời gian (phút)
0;10
10;20
20;30
30;40
40;50
Số học sinh 5 10 13 9 7
a. Tính thời gian (phút) trung bình của một học sinh tập thể dục trong ngày.
b. Tìm số a sao cho có 25% số học sinh tập thể dục với thời gian ít nhất là a (phút).
Câu 38. (0,5 điểm) Số giờ có ánh sáng mặt trời của thành phố B trong ngày thứ t (ở đây t là số ngày tính
từ ngày mùng 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số :
2
( ) 12 2,83sin 80
365
S t t
với
t
và
0 365
t
. Hỏi vào ngày nào trong năm thì thành phố B có
khoảng
10
giờ ánh sáng mặt trời?
Câu 39. (0,5 điểm) Dân số của một thành phố A hiện nay là 4 triệu người. Biết rằng tỉ lệ tăng dân số hàng
năm của thành phố A là 3%. Hãy ước tính dân số của thành phố A sau 10 năm nữa?
------------- HẾT -------------
BẢNG ĐÁP ÁN
1.A
2.C
3.B
4.C
5.D
6.A
7.C
8.B
9.B
10.A
11.A
12.D
13.A
14.C
15.B
16.C
17.A
18.D
19.D
20.B
21.D
22.A
23.B
24.B
25.C
26.C
27.D
28.B
29.D
30.B
31.C
32.C
33.A
34.A
35.D
PHẦN 1: TRẮC NGHIỆM
Câu 1: Phương trình
tan 3= −
x
có tất cả các nghiệm là:
A.
x ( ).
3
kk
π
π
=−+ ∈
B.
x 2 ( ).
3
kk
π
π
=−+ ∈
C.
x ( ).
6
kk
π
π
=+∈
D.
x ( ).
3
kk
π
π
=+∈
Lời giải
Chọn A
( )
tan 3
3
x x kk
π
π
−
=− ⇔= + ∈
.
Câu 2: Cho các dãy số
( )
,
n
u
( )
,
n
v
( )
,
n
w
với
21
,
n
n
u
n
+
=
2
2,
n
vn=
2 1.
n
n
w = +
Có bao nhiêu dãy số bị
chặn?
A.
3.
B.
0.
C.
1.
D.
2.
Lời giải
Chọn C
Ta có
21 1
2
n
n
u
nn
+
= = +
.
Với mọi
*n
∈
ta có:
1
22 3 2 3
n
u
n
<+ ≤⇔< ≤
nên dãy số
( )
n
u
bị chặn.
Do đó có 1 dãy số bị chặn.
Câu 3: Đơn giản biểu thức
( )
( )
cos sin tan
2
A
π
α απ πα

= − + −+ +


, ta được:
A.
osin cs–A
α
α
=
. B.
tan=A
α
. C.
incos sA
αα
= +
. D.
2sinA
α
=
.
Lời giải
Chọn B
( )
( )
( )
cos sin tan cos sin tan
22
A
ππ
α απ πα α πα α
 
= − + −+ += − − −+
 
 
sin sin tan tanA
ααα α
=−+ =
.
Câu 4: Cho dãy số
( )
n
u
xác định bởi
1
1
1
.
2 3; 2
nn
u
uu n
−
=
= +≥
Khẳng định nào sau đây SAI?
A.
4
29.u =
B.
2
5.u =
C.
5
58.u =
D.
3
13.u =
Lời giải
Chọn C
1 21 32 43 54
1; 2 3 5; 2 3 13; 2 3 29; 2 3 61uuu uu uu uu
= = += = += = += = +=
.
Câu 5: Cho cấp số nhân có các số hạng lần lượt là
333
3; ; ; ; ...
248
. Tìm số hạng tổng quát
n
u
của cấp
số nhân đã cho.
A.
1
1
3. .
2
n
n
u
−

=


B.
1
1
.3 .
2
n
n
u
−
=
C.
1
1
.3 .
2
n
n
u
−
=
D.
1
1
3. .
2
n
n
u
−

=


Lời giải
Chọn D
Cấp số nhân có các số hạng lần lượt là
333
3; ; ; ; ...
248
.nên nó có công bội
1
1
; 3.
2
qu= =
Do đó số hạng tổng quát là
1
1
1
1
. 3. .
2
n
n
n
u uq
−
−

= =


Câu 6: Cho góc
α
thỏa mãn
3
sin
5
α
=
và
2
π
απ
<<
. Tính
2
tan
.
1 tan
P
α
α
=
+
A.
12
.
25
P
= −
B.
3
.
7
P
=
C.
12
.
25
P =
D.
3.P = −
Lời giải
Chọn A
Do
2
π
απ
<<
nên
cos 0
α
<
do đó
2
94
cos 1 sin 1
25 5
αα
=−− =−− =−
, vậy
3
tan
4
α
= −
,
suy ra
2
tan 12
1 tan 25
P
α
α
= = −
+
.
Câu 7: Tính tổng
2 12
S 1 10 10 10 .
=++ ++
A.
13
1
.(1 10 ).
9
S = −
B.
12
1
.(1 10 ).
9
S = −
C.
13
1
.(10 1).
9
S = −
D.
12
1
.(10 1).
9
S = −
Lời giải
Chọn C
S là tổng của 13 số hạng đầu của cấp số nhân có
1
1, 10uq= =
.
Vậy
(
)
(
)
13
2 12 13
1 1 10
1
S 1 10 10 10 . 10 1 .
1 10 9
−
=++ ++ = = −
−
Câu 8: Trên đường tròn lượng giác có điểm gốc là
A
lấy điểm
M
thuộc đường tròn sao cho
sđ
0
( , ) 45OA OM =
. Gọi
N
là điểm đối xứng với
M
qua trục
Ox
, số đo của các góc lượng giác
(, )OA ON
bằng:
A.
0
225
. B.
00
45 360 ,kk−+ ∈
.
C.
00
135 360 , .kk+∈
D.
0
135
.
Lời giải
Chọn B
Có số đo của các góc lượng giác
(, )OA ON
bằng
00
45 360 ,kk−+ ∈
.
Câu 9: Trong các hàm số sau hàm số nào tuần hoàn với chu kỳ
π
?
A.
cot .
2
x
y =
B.
sin 2 .yx=
C.
tan 2 .yx=
D.
cos .yx=
Lời giải
Chọn B
Hàm số
sin 2
yx=
tuần hoàn với chu kỳ
π
.
Câu 10: Mức thưởng tết (triệu đồng) của các công nhân trong một nhà máy được cho trong bảng sau:
Tính mốt của mẫu số liệu ghép nhóm.
A.
16,25.
B.
20,25.
C.
21, 25.
D.
15,25.
Lời giải
Chọn A
Nhóm có tần số lớn nhất là nhóm
[
)
15;20
. Vậy mốt của mẫu số liệu trên là
( ) (
)
42 30 5
15 .5 15 16,25.
42 30 42 6 4
o
M
−
= + = +=
−+−
Câu 11: Tìm điều kiện xác định của hàm số
tan cot .y xx= +
A.
2
π
≠
k
x
,
∈
k
. B.
2
π
π
≠+xk
,
∈k
.
C.
x ∈
D.
π
≠xk
,
∈k
.
Lời giải
Chọn A
tan cot .y xx= +
Điều kiện
sin 0
sin 2 0 2
cos 0
2
x
k
x xk x
x
π
π
≠
⇔ ≠⇔ ≠ ⇔≠
≠
,
∈k
.
Câu 12: Cho
1
cos
3
=
α
. Khi đó
3
sin
2

−


π
α
bằng:
A.
2
.
3
B.
2
.
3
−
C.
1
.
3
−
D.
1
.
3
Lời giải
Chọn D
31
sin sin 2 sin cos
2 2 23
ππ π
α απ α α
 
− = +− = + = =
 
 
.
Câu 13: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
2.
n
un
=
B.
2.
n
n
u =
C.
2
.
n
un=
D.
2
.
n
u
n
=
Lời giải
Chọn A
2
n
un=
là cấp số cộng vì
( )
1
2 12 2
nn
uu n n
+
− = +− =
.
Câu 14: Tìm m để phương trình
sin 0
−=
xm
vô nghiệm.
A.
1 1.m−≤ ≤
B.
1.m ≤−
C.
1
.
1
m
m
<−
>
D.
1.m ≥
Lời giải
Chọn C
sin 0 sin
xm x m
−=⇔ =
vô nghiệm
1
.
1
m
m
<−
⇔
>
Câu 15: Tuổi thọ (năm) của một loại bóng đèn được cho trong bảng sau:
Tuổi thọ (năm)
c
[
)
3, 5;5
[
)
5; 6, 5
[
)
6, 5;8
[
)
8;9,5
Số bóng đèn
8
32
34
11
15
Nhóm chứa trung vị là nhóm thứ mấy?
A. Thứ 4. B. Thứ 3. C. Thứ 5. D. Thứ 2.
Lời giải
Chọn B
8 32 34 11 15 100n =++++=
.
Suy ra
(
)
50 51
1
2
e
M xx= +
mà
[
)
50 51
, 5;6,5xx∈
[
)
5; 6, 5
e
M⇒∈
⇒
Nhóm chứa trung vị là nhóm thứ 3.
Câu 16: Cho cấp số cộng
( )
n
u
có
1
4u =
và
3.d =
Khẳng định nào sau đây ĐÚNG?
A.
( )
43 1
n
un=++
.B.
43
n
un= +
. C.
( )
43 1
n
un=+−
. D.
43 1
n
un=+−
.
Lời giải
Chọn C
Áp dụng công thức
( )
1
1
n
uu n d=+−
Suy ra
( ) ( )
4 13 4 3 1
n
un n=+− =+ −
Vậy số hạng tổng quát
( )
43 1
n
un=+−
.
Câu 17: Cho cấp số cộng
( )
n
u
có
1
27u = −
và
4
3u = −
. Tổng
20 1 2 3 20
.....S uu u u=++ +
bằng:
A.
20
980S
=
. B.
20
1250S =
. C.
20
1960S
=
. D.
20
1060S
=
.
Lời giải
Chọn A
Áp dụng công thức
( )
( )
1
21
2
n
n
S un d= +−
( )
20 1
20
2 19
2
S ud⇒= +
.
Theo giả thiết ta có
1
4
27
3
u
u
= −
= −
1
1
27
33
u
ud
= −
⇔
+=−
1
27
8
u
d
= −
⇔
=
Suy ra
( ) ( )
( )
20 1
20
2 19 10. 2. 27 19.8 980
2
S ud= + = −+ =
.
Vậy
20
980S =
Câu 18: Trong các đẳng thức sau, đẳng thức nào ĐÚNG?
A.
( ) (
)
22
sin sin sin sin
+ −= −ab ab b a
. B.
( ) ( )
22
sin sin sin sin+ −= +
ab ab a b
.
C.
( ) ( )
22
sin sin cos cos+ −= −ab ab a b
. D.
( ) ( )
22
sin sin sin sin+ −= −ab ab a b
.
Lời giải
Chọn D
Áp dụng công thức
( ) ( )
( )
1
sin .sin cos cos
2
α β αβ αβ
= −− +
⇒
( ) ( )
( ) ( )
(
)
1
sin sin cos cos
2
ab ab abab abab+ − = +−+ − ++−
( ) ( )
( )
1
cos 2 cos 2
2
ba= −
( )
22
1
1 2sin 1 2sin
2
ba= − −+
22
sin sinab= −
Vậy
( ) ( )
22
sin sin sin sin+ −= −ab ab a b
Câu 19: Tập giá trị của hàm số
4 sin 3 1= +−yx
là:
A.
2;2


. B.
[ ]
2; 4
. C.
4 2;8


. D.
4 2 1; 7

−

.
Lời giải
Chọn D
Ta có
1 sin 1 ,xx
−≤ ≤ ∀∈
2sin 34x⇔≤ +≤
2 sin 3 2x⇔ ≤ +≤
4 2 4 sin 3 8x⇔ ≤ +≤
4 2 1 4 sin 3 1 7x⇔ −≤ + −≤
Vậy tập giá trị của hàm số
4 sin 3 1= +−yx
là
4 2 1; 7

−

Câu 20: Cho cấp số cộng
( )
n
u
có
23
n
un= −
. Công sai của cấp số cộng là
A.
1d =
. B.
2d =
. C.
5d = −
. D.
8d =
.
Lời giải
Chọn B
Ta có
23
n
un= −
1
12.1 3
u =
−=
⇒−
và
2
12.2 3u = −=
(
)
21
1 12du u⇒ = − =−− =
.
Vậy công sai của cấp số cộng là
2d
=
.
Câu 21: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A.
1;1;1;1;......
. B.
11 1
1; ; ; ;.......
5 25 125
−− − −
.
C.
111
; ; ; 1;.....
842
−−−−
. D.
1;3;9;18;......
.
Lời giải
Chọn D
Dãy số
1;1;1;1;......
là một cấp số nhân với
1
1; 1uq= =
.
Dãy số
11 1
1; ; ; ;.......
5 25 125
−− − −
là một cấp số nhân với
1
1
1;
5
uq=−=
.
Dãy số
111
; ; ; 1;.....
842
−−−−
là một cấp số nhân với
1
1
;2
8
uq=−=
.
Dãy số
1;3;9;18;......
không phải là một cấp số nhân vì
3 9 18
13 9
= ≠
.
Câu 22: Khảo sát nhiệt độ
( )
C°
tại một địa điểm trong
40
ngày thu được mẫu số liệu ghép nhóm sau:
Số ngày có nhiệt độ từ
29 C°
đến dưới
32 C°
là
A.
8
. B.
40
. C.
10
. D.
9
.
Lời giải
Chọn A
Số ngày có nhiệt độ từ
29
C°
đến dưới
32 C°
là
8
.
Câu 23: Cân nặng (kg) của
45
học sinh lớp 11 được cho trong bảng sau:
Cân nặng (kg) trung bình là:
A.
55x
=
. B.
53x =
. C.
54x =
. D.
52x =
.
Lời giải
Chọn B
Cân nặng (kg) trung bình là:
44.10 49.8 54.17 59.4 64.3 69.3
53
45
x
++ +++
= =
.
Câu 24: Biểu thức
sin 7 .sin cos7 .cosxx x x+
bằng
A.
sin8x
. B.
cos6x
. C.
cos8
x
. D.
sin 6x
.
Lời giải
Chọn B
Ta có
(
)
sin 7 .sin cos7 .cos cos 7 cos6
x x x x xx x
+ = −=
.
Câu 25: Trong các dãy số sau, dãy số nào là cấp số cộng?
A.
1; 4;7;10;14
. B.
3;1;5;9;14−
. C.
5;2; 1; 4; 7−− −
. D.
12 4
;;1;;2
33 3
.
Lời giải
Chọn C
Ta có
(
) ( )
25 12 4 1 7 4 3− =−− =−−− =−−− =−
.
Suy ra dãy số
5;2; 1; 4; 7
−− −
là một cấp số cộng có
1
5; 3ud
= = −
.
Câu 26: Giải phương trình lượng giác
2cos 3 0
2
+=
x
có nghiệm là
A.
( )
5
2
6
x kk
π
π
=±+ ∈
. B.
( )
5
4
6
x kk
π
π
=±+ ∈
.
C.
( )
5
4
3
x kk
π
π
=±+ ∈
. D.
( )
5
2
3
x kk
π
π
=±+ ∈
.
Lời giải
Chọn C
Phương trình lượng giác
( )
3 55
2cos 3 0 cos cos cos 4
2 22 2 6 3
x xx
x kk
ππ
π
+=⇔=−⇔= ⇔=±+ ∈
.
Vậy phương trình có nghiệm là
( )
5
4
3
x kk
π
π
=±+ ∈
.
Câu 27: Cho các dãy số sau. Dãy số nào là dãy số giảm?
A.
3;7;13;21;31;
. B.
1; 1; 1; 1; 1;−−−−−
.
C.
2; 4;8;16;32;
. D.
3; 1;1;3;5;
−−−
.
Lời giải
Chọn D
Dãy số
3; 1;1;3;5;−−−
là dãy số giảm.
Câu 28: Trong các đẳng thức sau, đẳng thức nào SAI?
A.
2
cos 2 1 2sinaa= −
. B.
2
2 tan
tan 2
1 tan
a
a
a
=
+
.
C.
sin 2 2sin cos
a aa=
. D.
22
cos 2 cos sina aa= −
.
Lời giải
Chọn B
Đẳng thức sai là
2
2 tan
tan 2
1 tan
a
a
a
=
+
.
Câu 29: Một cấp số nhân có
1
3u =
và
2
q =
. Số 384 là số hạng thứ mấy của cấp số nhân này?
A.
7
. B.
6
. C.
9
. D.
8
.
Lời giải
Chọn D
Ta có
1
1
n
n
u uq
−
=
nên
1
384 3.2 8
n
n
−
= ⇔=
.
Câu 30: Trong các dãy số
( )
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
3
1
21
n
u
n
=
+
. B.
41
1
n
n
u
n
−
=
+
. C.
1
4
n
n
u =
. D.
2
4
n
un
= −
.
Lời giải
Chọn B
Xét dãy số
41
1
n
n
u
n
−
=
+
ta có
(
)
(
)
( )
(
)
1
4 11
41 5
0
11 1 1 2
nn
n
n
uu
n n nn
+
+−
−
−= − = >
++ + + +
.
Suy ra dãy số
41
1
n
n
u
n
−
=
+
là dãy số tăng.
Câu 31: Cho
5
cos 2
4
= −
α
và
24
<<
ππ
α
. Khẳng định nào sau đây ĐÚNG?
A.
33
sin
3
10
+

+=


π
α
. B.
33
sin
32
+

+=


π
α
.
C.
33
sin
3
2 10
+

+=


π
α
. D.
33
sin
3
2 10
−

+=


π
α
.
Lời giải
Chọn C
Vì
sin 0, 0
2
cos
4
ππ
α αα
< <⇒ > >
.
2
19 3
sin
2 10
10
cos 2
sin
α
αα
−
= =⇒=
và
2
1
1 sin
10
cos
αα
=−=
Khi đó
31 1 33 3
sin sin . .sin . .
3 3 32 2
10 10 2 10
cos cos
π ππ
αα α
+

+= + = + =


.
Câu 32: Cho Cho lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo
thứ tự đó và các điểm
,BC
có tung độ dương. Khi đó số đo của các góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng :
A.
0
120−
. B.
0
240
.
C.
00
120 360 ,kk
+∈
. D.
00
240 360 ,kk
+∈
.
Lời giải
Chọn C
Ta có
( )
00
0
, 12 360 ,sđ kOA OC k
=+∈
.
Câu 33: Cho dãy số
( )
n
u
, biết
2
2
sin cos .
43
n
nn
u
ππ
= +
Bốn số hạng đầu tiên của dãy số đó lần lượt là
những số nào dưới đây?
A.
13 1
0;;;
22 2
−
. B.
1 11
0; ; ;
2 22
−
. C.
113 1
;;;
222 2
−
. D.
1131
;;;
2222
.
Lời giải
Chọn A
Ta có
22 2
12 3
2 41 3 3
sin cos 0; sin cos ; sin cos 2
43 232 2 2
uu u
ππ ππ π
π
=+==+== +=
;
2
4
81
sin cos
32
u
π
π
=+=−
.
Câu 34: Trong các hàm số sau đây, hàm số nào có đồ thị nhận trục tung làm trục đối xứng?
A.
cos=yx
. B.
tan
yx=
. C.
3
sin=yx
. D.
sinyx=
.
Lời giải
Chọn A
Hàm số
cos=yx
là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng
Câu 35: Hàm số
sin=yx
đồng biến trên khoảng nào sau đây?
A.
57
;
44



ππ
. B.
9 11
;
44



ππ
. C.
7
;3
4



π
π
. D.
79
;
44



ππ
.
Lời giải
Chọn D
Hàm số
sin
=yx
đồng biến trên các khoảng
2; 2 ,
22
k kk
ππ
ππ

−+ + ∈


nên đồng biên trên
khoảng
79
;
44



ππ
.
PHẦN 2: TỰ LUẬN
Câu 36: Cho
2
cos , .
32
=− <<
π
α απ
Tính các giá trị lượng giác của góc
.
α
Lời giải
Do
sin 0
2
<<⇒ >
π
απ α
2
45
sin 1 cos 1
93
= − = −=
αα
sin 5 2 5
tan :
cos 3 3 2
−−
= = =
α
α
α
1 25
cot
tan 5
−
= =
α
α
.
Câu 37: Khảo sát thời gian (phút) tập thể dục trong ngày của 1 số học sinh lớp 11 thu được mẫu số liệu
ghép nhóm sau:
a. Tính thời gian (phút) trung bình của một học sinh tập thể dục trong ngày.
b. Tìm số a sao cho có 25% số học sinh tập thể dục với thời gian ít nhất là a (phút).
Lời giải
a) Trong mỗi khoảng thời gian, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có
bảng sau:
Tổng số học sinh là:
44.n =
Thời gian trung bình của một học sinh tập thể dục trong ngày là:
5.5 10.15 13.25 9.35 7.45
25, 7
44
x
++++
= ≈
(phút)
b) Số a chính là tứ phân vị thứ 3.
Gọi
1 44
,...,xx
là thời gian tập thể dục (phút) trong ngày của 44 học sinh lớp 11 và giả sử dãy này
được xếp theo thứ tự tăng dần.
Khi đó, tứ phân vị thứ 3 là
33 34
2
xx+
. Do
33 34
;xx
đều thuộc nhóm
[
)
30;40
nên nhóm này chứa
3
.Q
Do đó
4 4 1 2 3 54
4; 30; 9; 5 10 13 28; 10.p a m mmm aa= = = + + =++= −=
3
3.44
28
320
4
30 .10 35,6
99
Q
−
=+=≈
Vậy có 25% số học sinh tập thể dục với thời gian ít nhất là 35,6 (phút).
Câu 38: Số giờ có ánh sáng mặt trời của thành phố B trong ngày thứ
t
(ở đây
t
là số ngày tính từ ngày
mùng
1
tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số :
(
)
2
( ) 12 2,83sin 80
365

=+−


St t
π
với
∈t
và
0 365<≤t
. Hỏi vào ngày nào trong năm thì thành
phố B có khoảng
10
giờ ánh sáng mặt trời?
Lời giải
Thành phố B có khoảng
10
giờ ánh sáng mặt trời
( )
10St⇔=
( )
( )
2 22
12 2,83sin 80 10 sin 80
365 365 2,83
tt
ππ
−

⇔+ −=⇔ −=


( )
( )
22
80 arcsin 2
365 2,83
22
80 arcsin 2
365 2,83
tk
tk
π
π
π
ππ
−

−= +


⇔
−

−=− +


( )
365 2
80 arcsin 365
2 2,83
525 365 2
arcsin 365
2 2 2,83
tk
k
tk
π
π
−

=++


⇔∈
−

=−+


.
Ta có các nghiệm
0 365<≤t
khi
0k =
suy ra
365 2
80 arcsin 34,7
2 2,83
t
π
−

=+≈


,
525 365 2
arcsin 308,3
2 2 2,83
t
π
−

=−≈


nên vào các ngày thứ
34
,
35
,
308
và
309
là các ngày
thành phố B có khoảng
10
giờ ánh sáng mặt trời.
Câu 39: Dân số của một thành phố A hiện nay là 4 triệu người. Biết rằng tỉ lệ tăng dân số hàng năm của
thành phố A là 3%. Hãy ước tính dân số của thành phố A sau 10 năm nữa?
Lời giải
Theo đề bài, số dân số của thành phố A trong từng năm lập thành 1 cấp số nhân có số hạng đầu
1
4u =
và công bội
1,03.q =
Dân số của thành phố A sau 10 năm nữa là:
10 10
11 1
. 4.1,03 5,4u uq= = ≈
(triệu người)
Vậy dân số của thành phố A sau 10 năm nữa là khoảng 5,4 triệu người.
------------- HẾT -------------
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT NGUYỄN HUỆ
KIỂM TRA GIỮA KÌ I TỔ TOÁN NĂM HỌC 2023 - 2024 Môn: TOÁN - Lớp 11 ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
(Đề kiểm tra có 4 trang) Mã đề thi
Họ và tên:............................................................................ 198
SBD:.......................................Lớp:.....................................
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN (7 điểm)
Câu 1. Phương trình tan x   3 có tất cả các nghiệm là:   A. x  
k (k  ). B. x  
k 2 (k  ). 3 3   C. x 
k (k  ). D. x 
k (k  ). 6 3 2n 1
Câu 2. Cho các dãy số u , vw với u  , 2
v  2n , w  2n 1. Có bao nhiêu dãy số bị n  , n  , n n n n n chặn? A. 3. B. 0. C. 1. D. 2.   
Câu 3. Đơn giản biểu thức A  cos    sin  
    tan    , ta được:  2 
A. A  sin – o c s .
B. A  tan .
C. A  cos  sin .
D. A  2sin . u   1
Câu 4. Cho dãy số u xác định bởi 1 
. Khẳng định nào sau đây SAI? n u  2u  3; n  2  n n 1 
A. u  29.
B. u  5.
C. u  58.
D. u  13. 4 2 5 3 3 3 3
Câu 5. Cho cấp số nhân có các số hạng lần lượt là 3; ;
; ; ... . Tìm số hạng tổng quát u của cấp số 2 4 8 n nhân đã cho. 1n n 1   1  1 1  1  A. u  3. . B. 1 u  .3 n. C. n 1 u .3   . D. u  3. . n   n n n    2  2 2  2  3  tan
Câu 6. Cho góc  thỏa mãn sin   và
    . Tính P  . 5 2 2 1 tan  12 3 12 A. P   . B. P  . C. P  . D. P  3  . 25 7 25 Câu 7. Tính tổng 2 12
S  110 10 10 . 1 1 1 1 A. 13 S  .(110 ). B. 12 S  .(110 ). C. 13 S  .(10 1). D. 12 S  .(10 1). 9 9 9 9
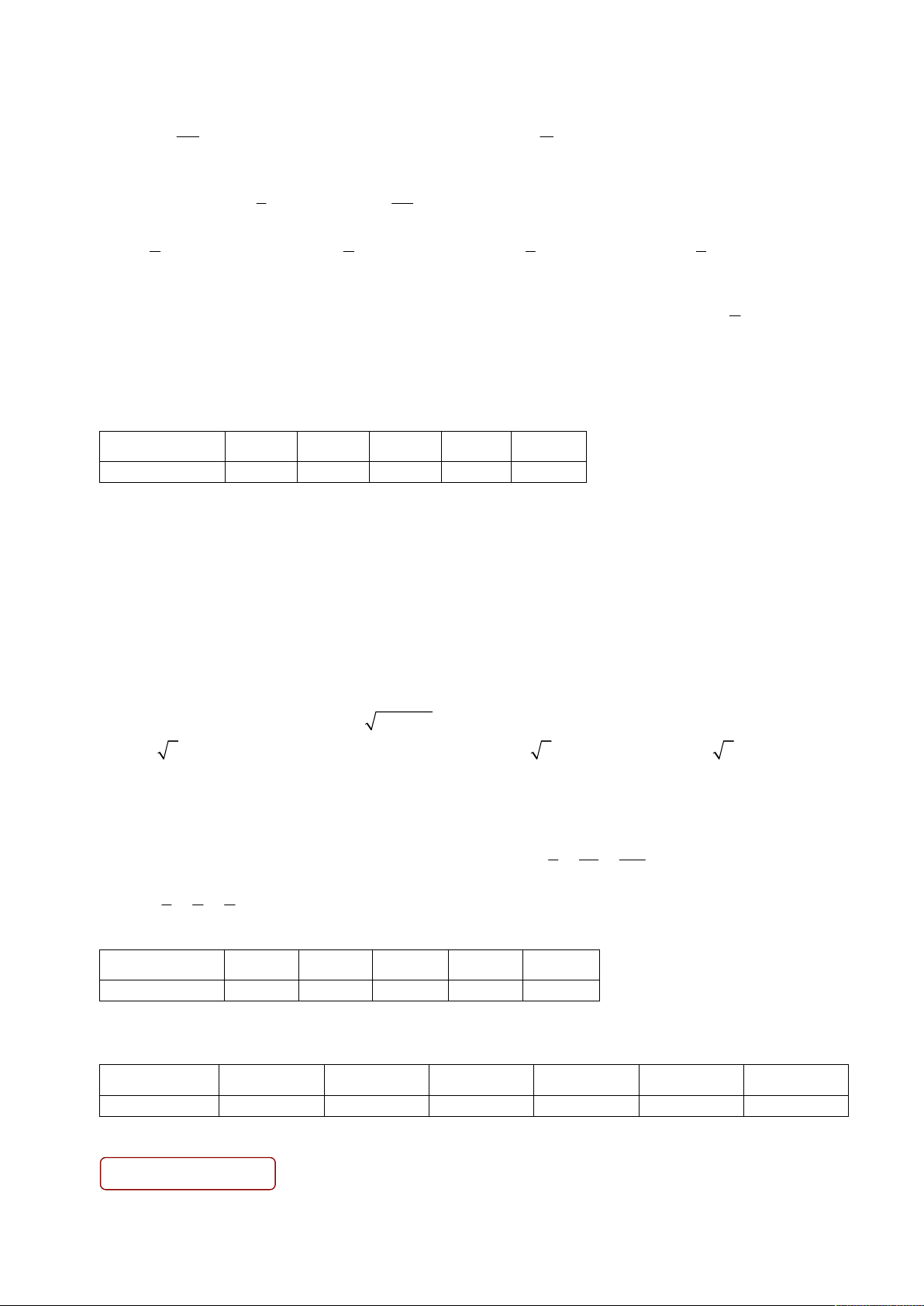
Câu 8. Trên đường tròn lượng giác có điểm gốc là A lấy điểm M thuộc đường tròn sao cho sđ 0 (O ,
A OM )  45 . Gọi N là điểm đối xứng với M qua trục Ox , số đo của các góc lượng giác ( , OA ON ) bằng: A. 0 225 . B. 0 0
 45  k360 , k . C. 0 0
135  k360 , k  .  D. 0 135 .
Câu 9. Trong các hàm số sau hàm số nào tuần hoàn với chu kỳ  ? x A. y  cot . B. y  sin 2 . x
C. y  tan 2 . x D. y  cos . x 2
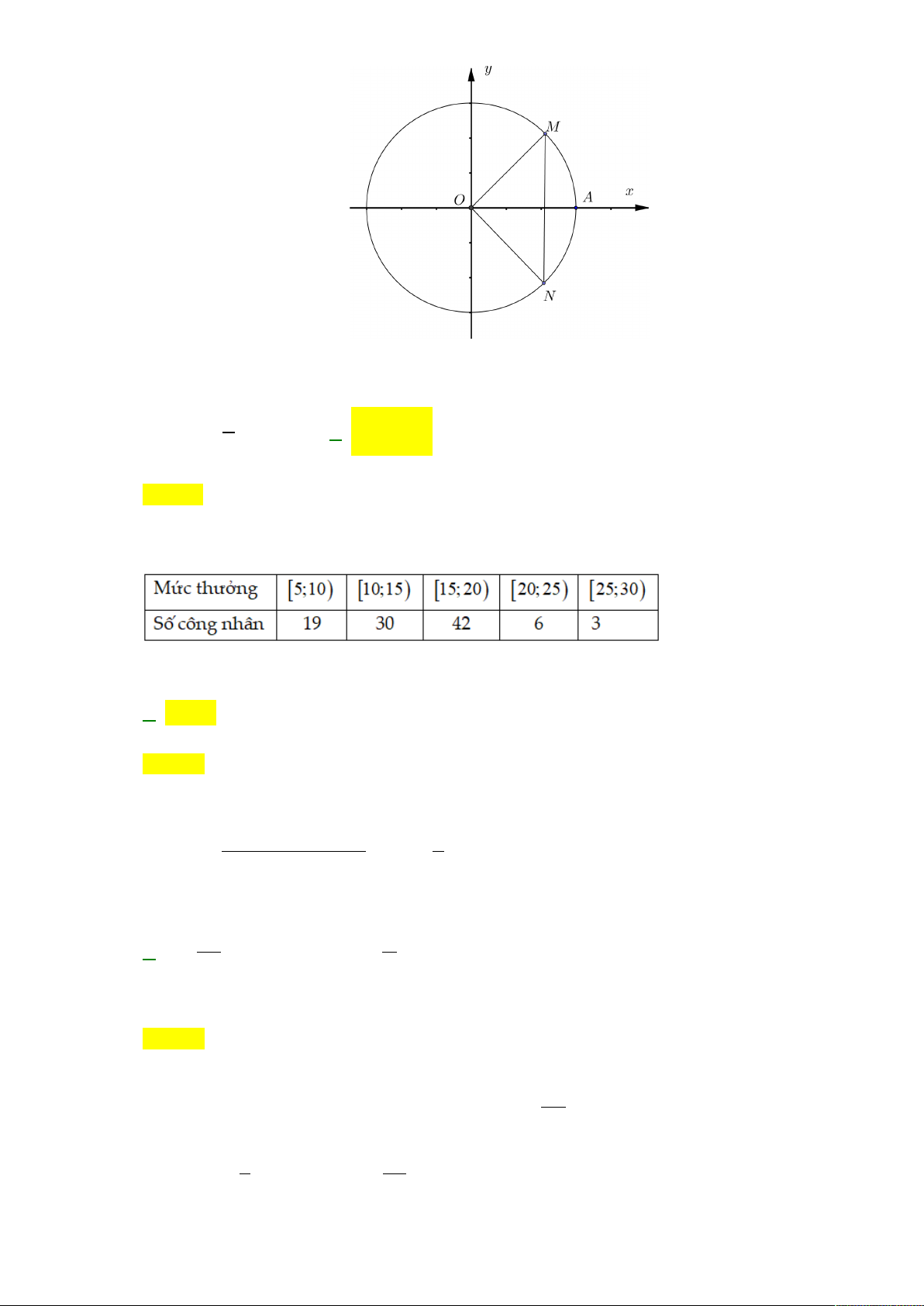
Câu 10. Mức thưởng tết (triệu đồng) của các công nhân trong một nhà máy được cho trong bảng sau: Mức thưởng
5;10 10;15 15;20 20;25 25;30 Số công nhân 19 30 42 6 3 Trang 1/4 - Mã đề 198
Tính mốt của mẫu số liệu ghép nhóm. A. 16, 25. B. 20, 25. C. 21, 25. D. 15, 25.
Câu 11. Tìm điều kiện xác định của hàm số y  tan x  cot . x k  A. x
, k . B. x
k , k . 2 2
C. x .
D. x k , k . 1  3  Câu 12. Cho cos  . Khi đó sin     bằng: 3  2  2 2 1 1 A. . B.  . C.  . D. . 3 3 3 3
Câu 13. Trong các dãy số sau đây, dãy số nào là cấp số cộng? 2 A. u  2 . n
B. u  2n. C. 2
u n . D. u  . n n n n n
Câu 14. Tìm m để phương trình sin x m  0 vô nghiệm . m  1 A. 1
  m  1. B. m  1  . C. . 
D. m  1. m  1 
Câu 15. Tuổi thọ (năm) của một loại bóng đèn được cho trong bảng sau: Tuổi thọ (năm)
2;3,5 3,5;5 5;6,5 6,5;8 8;9,5 Số bóng đèn 8 32 34 11 15
Nhóm chứa trung vị là nhóm thứ mấy? A. Thứ 4. B. Thứ 3. C. Thứ 5. D. Thứ 2.
Câu 16. Cho cấp số cộng u có u  4 và d  3. Khẳng định nào sau đây ĐÚNG? n  1
A. u  4  3n   1 .
B. u  4  3 . n
C. u  4  3 n
D. u  4  3n 1. n   1 . n n n
Câu 17. Cho cấp số cộng u có u  27  và u  3  . Tổng S
u u u .....  u bằng: n  1 4 20 1 2 3 20 A. S  980. B. S  1250 . C. S  1960. D. S  1060. 20 20 20 20
Câu 18. Trong các đẳng thức sau, đẳng thức nào ĐÚNG? A. a b a b 2 2 sin sin
 sin b  sin a . B. a b a b 2 2 sin sin
 sin a  sin b C. a b a b 2 2 sin sin
 cos a  cos b . D. a b a b 2 2 sin sin
 sin a  sin b .
Câu 19. Tập giá trị của hàm số y  4 sin x  3 1 là: A.  2; 2  .
B. 2; 4. C. 4 2;8   .
D. 4 2 1;7.
Câu 20. Cho cấp số cộng u có u  2n  3 . Công sai của cấp số cộng là: n n
A. d  1.
B. d  2.
C. d  5.
D. d  8.
Câu 21. Trong các dãy số sau, dãy số nào không phải là một cấp số nhân? 1 1 1 A. 1;1;1;1;... B. 1,  ,  ,  ;... 5 25 125 1 1 1
C.  ;  ;  ; 1;...
D. 1;3;9;18;... 8 4 2
Câu 22. Khảo sát nhiệt độ ( 0 C ) tại một địa điểm trong 40 ngày thu được mẫu số liệu ghép nhóm sau: Nhiệt độ ( 0 C )
20;23 23;26 26;29 29;32 32;35 Số ngày 7 6 10 8 9
Số ngày có nhiệt độ từ 0 29 C đến dưới 0 32 C là: A. 8. B. 40. C. 10. D. 9.
Câu 23. Cân nặng (kg) của 45 học sinh lớp 11 được cho trong bảng sau: Cân nặng (kg)
41,5;46,5 46,5;51,5 51,5;56,5 56,5;61,5 61,5;66,5 66,5;71,5 Số học sinh 10 8 17 4 3 3
Cân nặng (kg) trung bình là: Trang 2/4 - Mã đề 198
A. x  55.
B. x  53.
C. x  54.
D. x  52.
Câu 24. Biểu thức sin 7 . x sin x  o c s7 . x o
c sx bằng: A. sin 8 . x B. cos6 . x C. co 8 s . x D. sin 6 . x
Câu 25. Trong các dãy số sau, dãy số nào là cấp số cộng? 1 2 4
A. 1; 4; 7;10;14.
B. 3;1;5;9;14.
C. 5; 2; 1; 4; 7. D. ; ;1; ; 2. 3 3 3 x
Câu 26. Giải phương trình lượng giác 2 cos
 3  0 có nghiệm là: 2 5 5 A. x  
k 2 (k  ). B. x  
k 4 (k  ). 6 6 5 5 C. x  
k 4 (k  ). D. x  
k 2 (k  ). 3 3
Câu 27. Cho các dãy số sau. Dãy số nào là dãy số giảm?
A. 3; 7;13; 21;31;...
B. 1; 1; 1; 1; 1;...
C. 2; 4;8;16;32;...
D. 3; 1; 1; 3; 5;...
Câu 28. Trong các đẳng thức sau, đẳng thức nào SAI? 2 tan a A. 2
cos 2a  1 2 sin a . B. tan 2a  . 2 1 tan a
C. sin 2a  2sin a cos a . D. 2 2
cos 2a  cos a  sin a .
Câu 29. Một cấp số nhân có u  3 và q  2 . Số 384 là số hạng thứ mấy của cấp số nhân này? 1 A. 7. B. 6. C. 9. D. 8.
Câu 30. Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào là dãy số tăng? n n 1 4n 1 1 A. u  . B. u  . C. u  . D. 2
u  4n . n 3 2n 1 n n 1 n 4n n 4  
Câu 31. Cho cos 2   và   
. Khẳng định nào sau đây ĐÚNG? 5 4 2    3  3    3  3 A. sin     . B. sin     .  3  10  3  2    3  3    3  3 C. sin     . D. sin     .  3  2 10  3  2 10
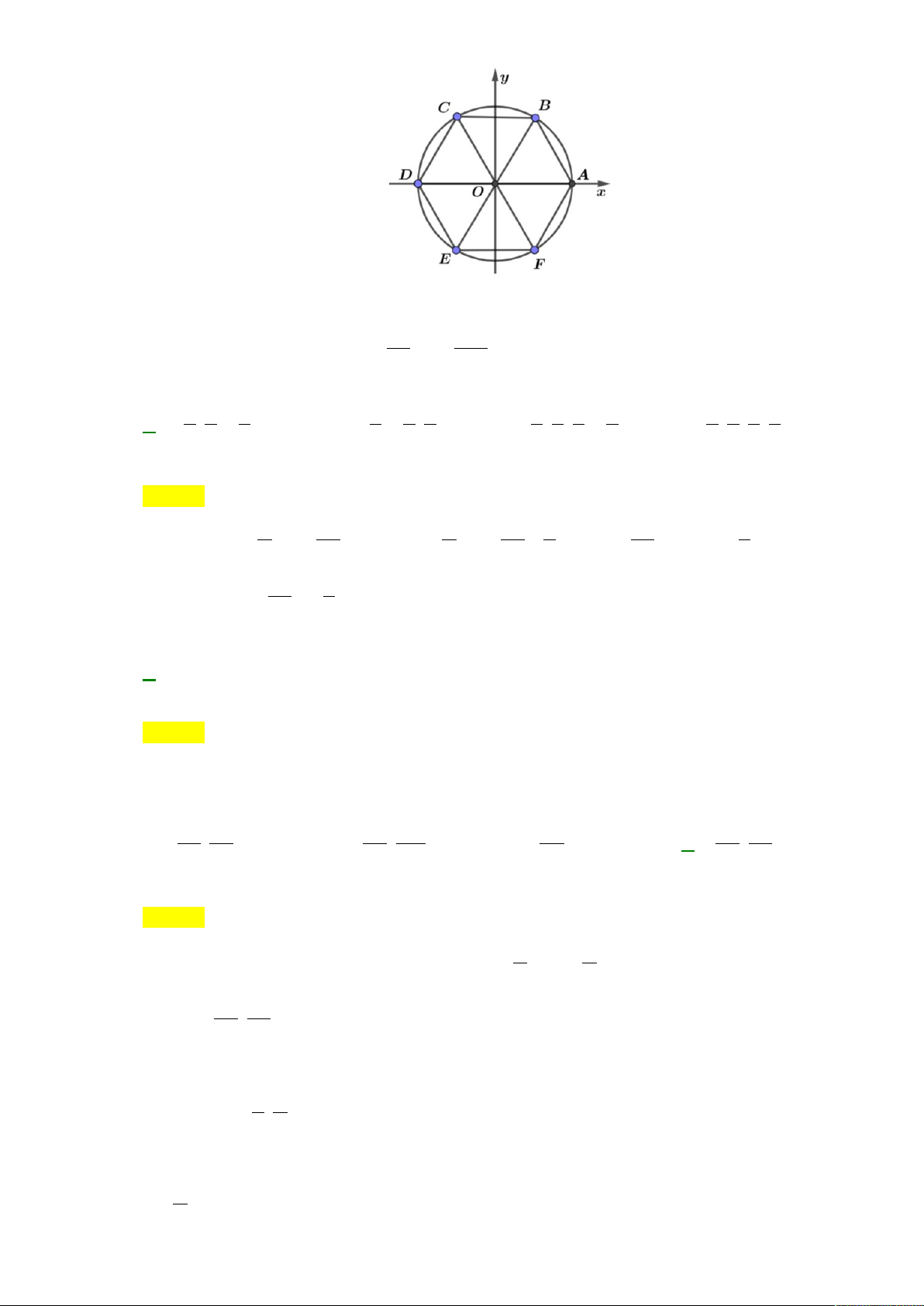
Câu 32. Cho lục giác đều ABCDEF nội tiếp đường tròn lượng giác có gốc là A , các đỉnh lấy theo thứ tự
đó và các điểm B, C có tung độ dương. Khi đó số đo của các góc lượng giác có tia đầu OA , tia cuối OC bằng : A. 0 12  0 . B. 0 240 . C. 0 0
120  k360 , k   . D. 0 0
240  k360 , k   . n 2n
Câu 33. Cho dãy số u , biết 2 u  sin  cos
. Bốn số hạng đầu tiên của dãy số đó lần lượt là n n 4 3
những số nào dưới đây? 1 3 1 1 1 1 1 1 3 1 1 1 3 1
A. 0; ; ;  .
B. 0; ;  ; . C. ; ; ;  . D. ; ; ; . 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Câu 34. Trong các hàm số sau đây, hàm số nào có đồ thị nhận trục tung làm trục đối xứng?
A. y  cos x .
B. y  tan x . C. 3
y  sin x .
D. y  sin x .
Câu 35. Hàm số y  sin x đồng biến trên khoảng nào sau đây?  5 7   9 11   7   7 9  A. ;   . B. ;   . C. ;3    . D. ;   .  4 4   4 4   4   4 4 
PHẦN II: TỰ LUẬN (3 điểm) 2 
Câu 36. (1,0 điểm) Cho cos   ,
    . Tính các giá trị lượng giác còn lại của góc . 3 2 Trang 3/4 - Mã đề 198
Câu 37. (1,0 điểm) Khảo sát thời gian (phút) tập thể dục trong ngày của 1 số học sinh lớp 11 thu được
mẫu số liệu ghép nhóm sau:
Thời gian (phút) 0;10 10;20 20;30 30;40 40;50 Số học sinh 5 10 13 9 7
a. Tính thời gian (phút) trung bình của một học sinh tập thể dục trong ngày.
b. Tìm số a sao cho có 25% số học sinh tập thể dục với thời gian ít nhất là a (phút).
Câu 38. (0,5 điểm) Số giờ có ánh sáng mặt trời của thành phố B trong ngày thứ t (ở đây t là số ngày tính
từ ngày mùng 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số :  2 
S(t)  12  2,83sin  
t  80  với t  và 0  t  365. Hỏi vào ngày nào trong năm thì thành phố B có  365 
khoảng 10 giờ ánh sáng mặt trời?
Câu 39. (0,5 điểm) Dân số của một thành phố A hiện nay là 4 triệu người. Biết rằng tỉ lệ tăng dân số hàng
năm của thành phố A là 3%. Hãy ước tính dân số của thành phố A sau 10 năm nữa?
------------- HẾT ------------- Trang 4/4 - Mã đề 198 BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.C 5.D 6.A 7.C 8.B 9.B 10.A 11.A 12.D 13.A 14.C 15.B 16.C 17.A 18.D 19.D 20.B 21.D 22.A 23.B 24.B 25.C 26.C 27.D 28.B 29.D 30.B 31.C 32.C 33.A 34.A 35.D
PHẦN 1: TRẮC NGHIỆM
Câu 1: Phương trình tan x = − 3 có tất cả các nghiệm là: A. π π
x = − + kπ (k ∈). B. x = − + k2π (k ∈). 3 3 C. π π
x = + kπ (k ∈). D. x = + kπ (k ∈). 6 3 Lời giải Chọn A π tan x 3 x − = − ⇔ =
+ kπ (k ∈) . 3
Câu 2: Cho các dãy số (u (v (w với 2n +1 u = 2
v = n w = 2n + Có bao nhiêu dãy số bị n 1. n 2 , n , n ) , n ) , n ) , n chặn? A. 3. B. 0. C. 1. D. 2. Lời giải Chọn C + Ta có 2n 1 1 u = = + . n 2 n n
Với mọi n∈* ta có: 1
2 < 2 + ≤ 3 ⇔ 2 < u ≤ nên dãy số (u bị chặn. n ) n 3 n
Do đó có 1 dãy số bị chặn.
Câu 3: Đơn giản biểu thức  π A cos α  = − + 
 sin (α −π ) + tan (π +α ) , ta được:  2 
A. A = sinα – o
c sα . B. A = tanα .
C. A = cosα + sinα . D. A = 2sinα . Lời giải Chọn B  π   π A cos α sin (α π ) tan (π α ) cos α  = − + − + + = − − sin (π −α ) +     tanα  2   2 
A = sinα − sinα + tanα = tanα . u  = 1
Câu 4: Cho dãy số (u xác định bởi 1 
. Khẳng định nào sau đây SAI? n ) u = u + ≥  − n n 2 n 3; 2 1 A. u = 29. u = 5. u = 58. u =13. 4 B. 2 C. 5 D. 3 Lời giải Chọn C
u =1;u = 2u + 3 = 5;u = 2u + 3 =13;u = 2u + 3 = 29;u = 2u + 3 = 61 1 2 1 3 2 4 3 5 4 .
Câu 5: Cho cấp số nhân có các số hạng lần lượt là 3 3 3
3; ; ; ; . .. Tìm số hạng tổng quát u của cấp 2 4 8 n số nhân đã cho. 1−n n 1 − A.  1 1 1 u  = B. 1 u − = C. n 1 u − = D.  1 u  = n 3.  . n .3 . n .3 .n n 3.  .  2  2 2  2  Lời giải Chọn D
Cấp số nhân có các số hạng lần lượt là 3 3 3 1
3; ; ; ; . ..nên nó có công bội q = ;u = 3. 2 4 8 1 2 n 1 −
Do đó số hạng tổng quát là n 1 −  1 u u q  = = n . 3.  . 1  2  3 π α sinα = < α < π tan P = .
Câu 6: Cho góc α thỏa mãn 5 và 2 . Tính 2 1+ tan α A. 12 P = − . B. 3 P = . C. 12 P = . D. P = 3. − 25 7 25 Lời giải Chọn A π
Do < α < π nên cosα < 0 do đó 2 9 4
cosα = − 1− sin α = − 1− = − , vậy 3 tanα = − , 2 25 5 4 α suy ra tan 12 P = = − . 2 1+ tan α 25 Câu 7: Tính tổng 2 12 S =1+10 +10 ++10 . A. 1 13
S = .(1−10 ). B. 1 12 S = .(1−10 ). C. 1 13
S = .(10 −1). D. 1 12 S = .(10 −1). 9 9 9 9 Lời giải Chọn C
S là tổng của 13 số hạng đầu của cấp số nhân có u =1,q =10 . 1 1( 13 1−10 2 12 ) Vậy 1 S =1+10 +10 ++10 = = .( 13 10 − ) 1 . 1−10 9
Câu 8: Trên đường tròn lượng giác có điểm gốc là A lấy điểm M thuộc đường tròn sao cho sđ 0 ( ,
OA OM ) = 45 . Gọi N là điểm đối xứng với M qua trục Ox , số đo của các góc lượng giác ( , OA ON) bằng: A. 0 225 . B. 0 0
− 45 + k360 ,k ∈. C. 0 0
135 + k360 ,k ∈ .  D. 0 135 . Lời giải Chọn B
Có số đo của các góc lượng giác( , OA ON) bằng 0 0
− 45 + k360 ,k ∈.
Câu 9: Trong các hàm số sau hàm số nào tuần hoàn với chu kỳ π ? A. cot x y = .
B. y = sin 2 .x
C. y = tan 2 .x
D. y = cos .x 2 Lời giải Chọn B
Hàm số y = sin 2x tuần hoàn với chu kỳ π .
Câu 10: Mức thưởng tết (triệu đồng) của các công nhân trong một nhà máy được cho trong bảng sau:
Tính mốt của mẫu số liệu ghép nhóm. A. 16,25. B. 20,25. C. 21,25. D. 15,25. Lời giải Chọn A
Nhóm có tần số lớn nhất là nhóm [15;20) . Vậy mốt của mẫu số liệu trên là 42 30 5 M − = + = + = o 15 ( − )+( − ).5 15 16,25. 42 30 42 6 4
Câu 11: Tìm điều kiện xác định của hàm số y = tan x + cot .x A. π π ≠ k x
, k ∈.
B. x ≠ + kπ , k ∈. 2 2
C. x∈
D. x ≠ kπ , k ∈. Lời giải Chọn A
y = tan x + cot . x si  n x ≠ 0 Điều kiện π  ⇔ sin 2 ≠ 0 ⇔ 2 k x
x ≠ kπ ⇔ x ≠ , k ∈. cos x ≠ 0 2 Câu 12: Cho 1 π cosα = . Khi đó  3 sin  α − bằng: 3  2    A. 2 . B. 2 − . C. 1 − . D. 1. 3 3 3 3 Lời giải Chọn D  3π   π   π  1 sin α − =  sin α + −  2π =  sin α + =   cosα =  .  2   2   2  3
Câu 13: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A. u = n B. u = C. 2 u = n D. 2 u = n . n . n 2 .n n 2 . n Lời giải Chọn A
u = n là cấp số cộng vì u − = + − = . + u n n n n 2 1 2 2 1 ( ) n 2
Câu 14: Tìm m để phương trình sin x − m = 0 vô nghiệm. m < 1 − A. 1 − ≤ m ≤1. B. m ≤ 1. − C.  .
D. m ≥1. m > 1 Lời giải Chọn C m < 1 −
sin x − m = 0 ⇔ sin x = m vô nghiệm ⇔  . m > 1
Câu 15: Tuổi thọ (năm) của một loại bóng đèn được cho trong bảng sau: Tuổi thọ (năm) c
[3,5;5) [5;6,5) [6,5;8) [8;9,5) Số bóng đèn 8 32 34 11 15
Nhóm chứa trung vị là nhóm thứ mấy? A. Thứ 4. B. Thứ 3. C. Thứ 5. D. Thứ 2. Lời giải Chọn B
n = 8 + 32 + 34 +11+15 =100 . Suy ra 1 M =
x + x mà x , x ∈ 5;6,5 ⇒ M ∈ e [5;6,5) 50 51 [ ) e ( 50 51) 2
⇒ Nhóm chứa trung vị là nhóm thứ 3.
Câu 16: Cho cấp số cộng (u có u = 4 và
Khẳng định nào sau đây ĐÚNG? n ) d = 3. 1
A. u = + n + .B. u = + n .
C. u = + n − . D. u = + n − . n 4 3 1 n 4 3( )1 n 4 3 n 4 3( )1 Lời giải Chọn C
Áp dụng công thức u = u + n − d n 1 1 ( )
Suy ra u = + n − = + n − n 4 ( ) 1 3 4 3( ) 1
Vậy số hạng tổng quát u = + n − . n 4 3( )1
Câu 17: Cho cấp số cộng (u có u = 27 − u = 3 −
S = u + u + u .....+ u 1 và 4 . Tổng 20 1 2 3 20 bằng: n )
A. S = 980 .
B. S =1250.
C. S =1960.
D. S =1060. 20 20 20 20 Lời giải Chọn A Áp dụng công thức n S =
u + n − d 20 ⇒ S = 2u +19d 20 ( 1 ) . n (2 1 1 ( ) ) 2 2 u  = 27 − u  = 27 − u  = 27 − Theo giả thiết ta có 1 1 ⇔ 1 ⇔ u  = 3 −    u +  3d = 3 − d = 8 4 1 Suy ra 20 S =
2u +19d =10. 2. 27 − +19.8 = 980 . 20 ( 1 ) ( ( ) ) 2 Vậy S = 980 20
Câu 18: Trong các đẳng thức sau, đẳng thức nào ĐÚNG? A.
(a + b) (a −b) 2 2 sin sin
= sin b − sin a . B.
(a + b) (a −b) 2 2 sin sin
= sin a + sin b . C.
(a + b) (a −b) 2 2 sin sin
= cos a − cos b . D.
(a + b) (a −b) 2 2 sin sin
= sin a − sin b . Lời giải Chọn D Áp dụng công thức 1
sinα.sin β = (cos(α − β ) − cos(α + β )) 2 1
⇒ sin (a + b)sin (a − b) = (cos(a + b − a + b) − cos(a + b + a − b)) 2 1
= (cos(2b) − cos(2a)) 2 1 = ( 2 2
1− 2sin b −1+ 2sin a ) 2 2 2
= sin a − sin b Vậy
(a + b) (a −b) 2 2 sin sin
= sin a − sin b
Câu 19: Tập giá trị của hàm số y = 4 sin x + 3 −1 là: A.  2;2   . B. [2;4] . C. 4 2;8   .
D. 4 2 −1;7 . Lời giải Chọn D Ta có 1
− ≤ sin x ≤1 , x ∀ ∈ 
⇔ 2 ≤ sin x + 3 ≤ 4
⇔ 2 ≤ sin x + 3 ≤ 2
⇔ 4 2 ≤ 4 sin x + 3 ≤ 8
⇔ 4 2 −1≤ 4 sin x + 3 −1≤ 7
Vậy tập giá trị của hàm số y = 4 sin x + 3 −1 là 4 2 −1;7
Câu 20: Cho cấp số cộng (u có u = n − . Công sai của cấp số cộng là n 2 3 n ) A. d =1. B. d = 2 . C. d = 5 − .
D. d = 8. Lời giải Chọn B
Ta có u = n − ⇒ u = 2.1− 3 = 1
− và u = 2.2 − 3 =1 n 2 3 1 2
⇒ d = u − u =1− 1 − = 2 . 2 1 ( )
Vậy công sai của cấp số cộng là d = 2 .
Câu 21: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân? 1 1 1 A. 1;1;1;1;....... B. 1 − ;− ;− ;− ;........ 5 25 125 1 1 1
C. − ;− ;− ;−1;...... D. 1;3;9;18;....... 8 4 2 Lời giải Chọn D
Dãy số 1;1;1;1;...... là một cấp số nhân với u =1;q =1. 1 1 1 1 Dãy số 1 − ;− ;− ;−
;....... là một cấp số nhân với 1 u = 1; − q = . 5 25 125 1 5 1 1 1
Dãy số − ;− ;− ;−1;..... là một cấp số nhân với 1 u = − ;q = 2. 8 4 2 1 8
Dãy số 1;3;9;18;...... không phải là một cấp số nhân vì 3 9 18 = ≠ . 1 3 9
Câu 22: Khảo sát nhiệt độ ( C
° ) tại một địa điểm trong 40 ngày thu được mẫu số liệu ghép nhóm sau:
Số ngày có nhiệt độ từ 29°C đến dưới 32°C là A. 8. B. 40 . C. 10. D. 9 . Lời giải Chọn A
Số ngày có nhiệt độ từ 29°C đến dưới 32°C là 8 .
Câu 23: Cân nặng (kg) của 45 học sinh lớp 11 được cho trong bảng sau:
Cân nặng (kg) trung bình là: A. x = 55 . B. x = 53 . C. x = 54 . D. x = 52 . Lời giải Chọn B
44.10 49.8 54.17 59.4 64.3 69.3
Cân nặng (kg) trung bình là: x + + + + + = = 53. 45
Câu 24: Biểu thức sin 7 .xsin x + cos7 .xcos x bằng A. sin8x . B. cos6x . C. cos8x . D. sin 6x . Lời giải Chọn B Ta có sin 7 .
x sin x + cos7 .xcos x = cos(7x − x) = cos6x .
Câu 25: Trong các dãy số sau, dãy số nào là cấp số cộng? A. 1;4;7;10;14 . B. 3 − ;1;5;9;14.
C. 5;2;−1;− 4;− 7 . D. 1 2 4 ; ;1; ;2 . 3 3 3 Lời giải Chọn C Ta có 2 − 5 = 1 − − 2 = 4 − − (− ) 1 = 7 − − ( 4 − ) = 3 − .
Suy ra dãy số 5;2;−1;− 4;− 7 là một cấp số cộng có u = 5;d = 3 − . 1
Câu 26: Giải phương trình lượng giác 2cos x + 3 = 0 có nghiệm là 2 π A. 5π 5 x = ±
+ k2π (k ∈) . B. x = ±
+ k4π (k ∈). 6 6 π π C. 5 x = ± + k4π (k ∈ 5 ) . D. x = ±
+ k2π (k ∈) . 3 3 Lời giải Chọn C
Phương trình lượng giác x x 3 x 5π 5π 2cos + 3 = 0 ⇔ cos = − ⇔ cos = cos ⇔ x = ±
+ k4π (k ∈) . 2 2 2 2 6 3 5π
Vậy phương trình có nghiệm là x = ±
+ k4π (k ∈) 3 .
Câu 27: Cho các dãy số sau. Dãy số nào là dãy số giảm? A. 3;7;13;21;31;. B. 1; − 1; − 1; − 1; − 1; −  . C. 2;4;8;16;32;. D. 3; 1; 1 − ; 3 − ; 5 − ; . Lời giải Chọn D Dãy số 3; 1; 1 − ; 3 − ; 5
− ; là dãy số giảm.
Câu 28: Trong các đẳng thức sau, đẳng thức nào SAI? A. 2 tan 2 a
cos 2a =1− 2sin a . B. tan 2a = . 2 1+ tan a
C. sin 2a = 2sin a cos a . D. 2 2
cos 2a = cos a −sin a . Lời giải Chọn B Đẳng thức sai là 2 tan tan 2 a a = . 2 1+ tan a
Câu 29: Một cấp số nhân có u = 3và q = 2 . Số 384 là số hạng thứ mấy của cấp số nhân này? 1 A. 7 . B. 6 . C. 9. D. 8 . Lời giải Chọn D Ta có n 1 u u q − = nên n 1 384 3.2 − = ⇔ n = 8 . n 1
Câu 30: Trong các dãy số (u
u sau, dãy số nào là dãy số tăng?
n ) cho bởi số hạng tổng quát n 1 A. 1 n − u = . B. 4 1 u = . C. u = . D. 2
u = − n . n 4 n 3 2n +1 n n +1 n 4n Lời giải Chọn B 4n −1 4(n + ) 1 −1 − Xét dãy số u = 4n 1 5 n u − = − = > . + u n n 0 n ta có +1 1
(n + )1+1 n +1 (n + )1(n + 2) 4n −1 Suy ra dãy số u = n n là dãy số tăng. +1 Câu 31: Cho π π cos 2 4
α = − và < α < . Khẳng định nào sau đây ĐÚNG? 5 4 2 π A.  π  3+ 3 sin   + α +  = . B. 3 3 sin α +  = .  3  10  3  2 C.  π  3+ 3 π sin   − α +  = . D. 3 3 sin α +  = .  3  2 10  3  2 10 Lời giải Chọn C π π
Vì < α < ⇒ sinα > 0,cosα > 0 . 4 2 2 1− cos 2α 9 3 sin α = = ⇒ sinα = và 2 1 cosα = 1− sin α = 2 10 10 10  π  π π Khi đó 3 1 1 3 3+ 3
sin α +  = sinα.cos + cosα.sin = . + . = .  3  3 3 10 2 10 2 2 10
Câu 32: Cho Cho lục giác đều ABCDEF nội tiếp đường tròn lượng giác có gốc là A , các đỉnh lấy theo
thứ tự đó và các điểm B,C có tung độ dương. Khi đó số đo của các góc lượng giác có tia đầu
OA, tia cuối OC bằng : A. 0 120 − . B. 0 240 . C. 0 0
120 + k360 ,k ∈. D. 0 0
240 + k360 ,k ∈ . Lời giải Chọn C Ta có sđ ( , OA OC) 0 0
= 120 + k360 ,k ∈ .
Câu 33: Cho dãy số (u , biết 2 nπ 2nπ u = +
Bốn số hạng đầu tiên của dãy số đó lần lượt là n sin cos . n ) 4 3
những số nào dưới đây? A. 1 3 1 0; ; ;− . B. 1 1 1 0; ;− ; . C. 1 1 3 1 ; ; ;− . D. 1 1 3 1 ; ; ; . 2 2 2 2 2 2 2 2 2 2 2 2 2 2 Lời giải Chọn A π π π π π Ta có 2 2 2 4 1 2 3 3 u = sin + cos = 0;u = sin + cos = ;u = sin + cos 2π = ; 1 2 3 4 3 2 3 2 2 2 2 8π 1 u = sin π + cos = − . 4 3 2
Câu 34: Trong các hàm số sau đây, hàm số nào có đồ thị nhận trục tung làm trục đối xứng?
A. y = cos x .
B. y = tan x . C. 3
y = sin x .
D. y = sin x . Lời giải Chọn A
Hàm số y = cos x là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng
Câu 35: Hàm số y = sin x đồng biến trên khoảng nào sau đây? A.  5π 7π π π π π π ;         . B. 9 11  ; . C. 7  ;3π . D. 7 9  ; . 4 4        4 4   4   4 4  Lời giải Chọn D  π π
Hàm số y = sin x đồng biến trên các khoảng k2π; k2π  − + + , k ∈   nên đồng biên trên  2 2  khoảng  7π 9π ;   . 4 4    PHẦN 2: TỰ LUẬN Câu 36: Cho 2 π
cosα = − , < α < π.Tính các giá trị lượng giác của góc α. 3 2 Lời giải
Do π < α < π ⇒ sinα > 0 2 2 4 5 sinα = 1− cos α = 1− = 9 3 sinα 5 2 − − 5 tanα = = : = cosα 3 3 2 1 2 − 5 cotα = = . tanα 5
Câu 37: Khảo sát thời gian (phút) tập thể dục trong ngày của 1 số học sinh lớp 11 thu được mẫu số liệu ghép nhóm sau:
a. Tính thời gian (phút) trung bình của một học sinh tập thể dục trong ngày.
b. Tìm số a sao cho có 25% số học sinh tập thể dục với thời gian ít nhất là a (phút). Lời giải
a) Trong mỗi khoảng thời gian, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:
Tổng số học sinh là: n = 44.
Thời gian trung bình của một học sinh tập thể dục trong ngày là: 5.5 10.15 13.25 9.35 7.45 x + + + + = ≈ 25,7 (phút) 44
b) Số a chính là tứ phân vị thứ 3.
Gọi x ,..., x là thời gian tập thể dục (phút) trong ngày của 44 học sinh lớp 11 và giả sử dãy này 1 44
được xếp theo thứ tự tăng dần.
Khi đó, tứ phân vị thứ 3 là x + x 33
34 . Do x ; x đều thuộc nhóm [30;40) nên nhóm này chứa Q . 2 33 34 3
Do đó p = 4;a = 30;m = 9;m + m + m = 5 +10 +13 = 28;a − a =10. 4 4 1 2 3 5 4 3.44 −28 4 320 Q = 30 + .10 = ≈ 35,6 3 9 9
Vậy có 25% số học sinh tập thể dục với thời gian ít nhất là 35,6 (phút).
Câu 38: Số giờ có ánh sáng mặt trời của thành phố B trong ngày thứ t (ở đây t là số ngày tính từ ngày
mùng 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số :  2π S(t) 12 2,83sin (  t 80) = + −
với t ∈ và 0 < t ≤ 365. Hỏi vào ngày nào trong năm thì thành 365   
phố B có khoảng 10 giờ ánh sáng mặt trời? Lời giải
Thành phố B có khoảng 10 giờ ánh sáng mặt trời ⇔ S (t) =10  2π ⇔ + (   π  t − ) 2  = ⇔ (  t − ) 2 12 2,83sin 80 10 sin 80 −  =  365   365  2,83  2π (  t )  2 80 arcsin −   − − = + 365 2     k2π t = 80 + arcsin +    k365 365  2,83   2π  2,83 ⇔   ⇔ (k ∈).  2π  525 365  2 −   (t )  2 80 π arcsin −  − = − +   k2π t = − arcsin +   k365 365  2,83   2 2π  2,83  365  2 − 
Ta có các nghiệm 0 < t ≤ 365 khi k = 0 suy ra t = 80 + arcsin ≈   34,7 , 2π  2,83  525 365  2 t arcsin −  = − ≈ 
 308,3 nên vào các ngày thứ 34 , 35 , 308 và 309 là các ngày 2 2π  2,83 
thành phố B có khoảng 10 giờ ánh sáng mặt trời.
Câu 39: Dân số của một thành phố A hiện nay là 4 triệu người. Biết rằng tỉ lệ tăng dân số hàng năm của
thành phố A là 3%. Hãy ước tính dân số của thành phố A sau 10 năm nữa? Lời giải
Theo đề bài, số dân số của thành phố A trong từng năm lập thành 1 cấp số nhân có số hạng đầu u = 4 q = 1 và công bội 1,03.
Dân số của thành phố A sau 10 năm nữa là: 10 10
u = u .q = 4.1,03 ≈ 5,4 (triệu người) 11 1
Vậy dân số của thành phố A sau 10 năm nữa là khoảng 5,4 triệu người.
------------- HẾT -------------
Document Outline

  • de-giua-ki-1-toan-11-nam-2023-2024-truong-thpt-nguyen-hue-tt-hue
  • TOÁN-11-GK1-THPT-NGUYỄN-HUỆ-HUẾ_23-24