PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG GIỮA KÌ I HUYỆN VỤ BẢN Năm học 2024-2025 Môn: Toán 9 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 90 phút)
Đề thi gồm:02 trang
Phần I. Trắc nghiệm (2,0 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
A. xy y  2 .
B. 3x y 4 .
C. 2  y  3 . D. 4 3x y  0 . x 5
Câu 2: Nghiệm tống quát của phương trình 2x − y = 3 là A. ( ;2
x x − 3) với mọi x∈ R . B. ( ;2
x x + 3) với mọi x∈ R . C. ( ;2
x y − 3) với mọi x, y ∈ R .
D. ( ;x y) với mọi x∈ R .
Câu 3: Cặp số (2; ) 1
− là nghiệm của hệ phương trình
A. x − 2y = 4 .
B. 2x − y =1 .
C. x − 2y = 4 .
D. x − 2y = 4 . 3      x + y = 2 3  x + y = 5 x + y = 1 x + y = 2
Câu 4: Điều kiện xác định của phương trình x + 3 x − 2 2 + = là 2 x −1 x x +1
A. x ≠ 0; x ≠ 1
± B. x = 0; x = 1
± C. x ≠ 0; x ≠ 1
D. x ≠ 0; x ≠ 1 −
Câu 5: Nghiệm của bất phương trình 2 − x > 3 − x − 3là A. x ≥ 3. B. x > 3. − C. x ≤ 3. − D. x < 3. Câu 6: Cho A
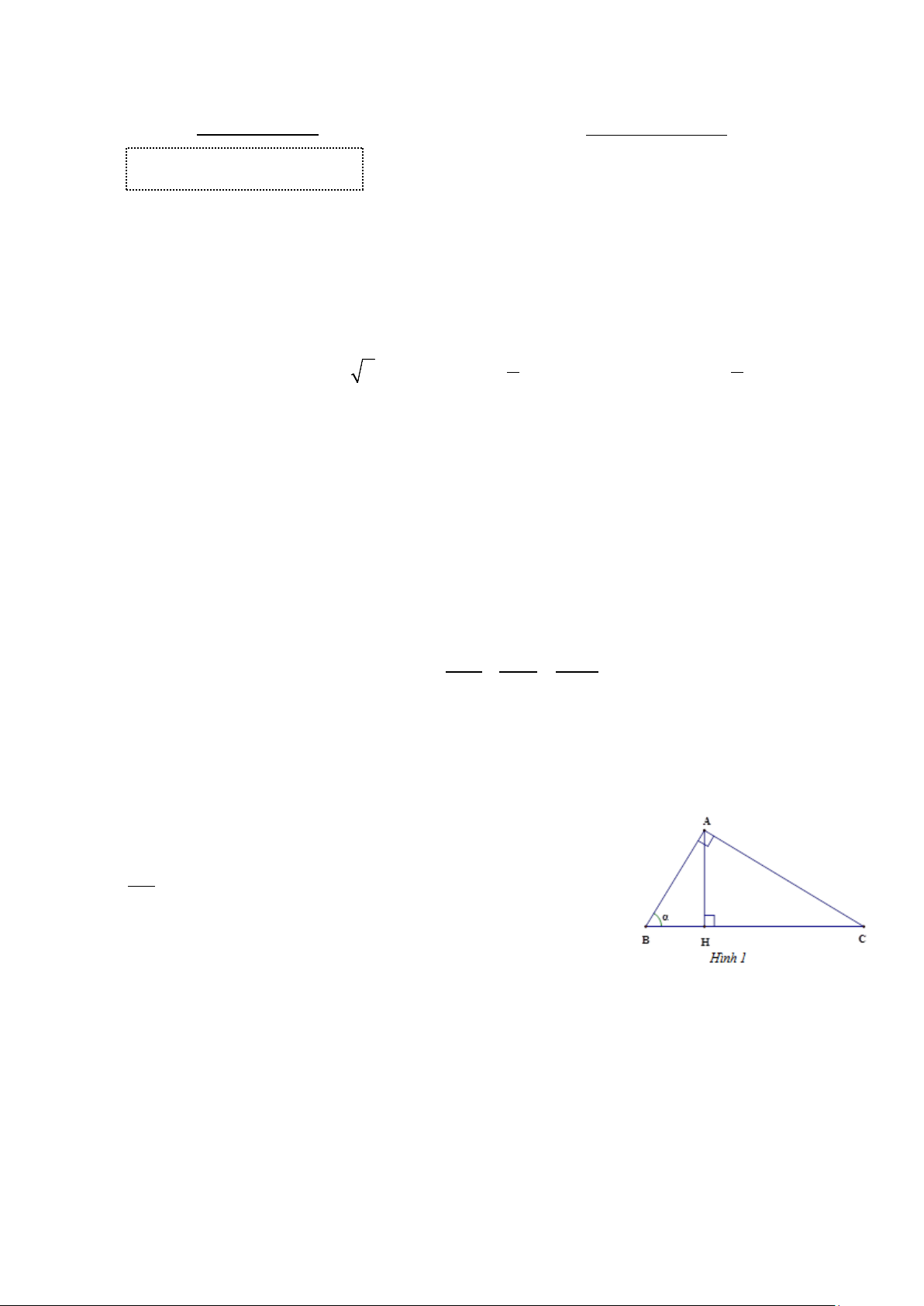
∆ BC vuông tại A , đường cao AH và B = α (Hình 1). Tỉ số HA bằng HB A. sinα . B. cosα . C. tanα . D. cotα .
Câu 7: Tam giác MNP vuông tại M thì
A. MP = MN.cot P .
B. MP = N . P sin P
C. NP = MN.tan P D. NP = . MP cos P .
Câu 8: Giá trị của biểu thức A = sin12°+ sin13°+ sin14°− cos78°− cos77°− cos76° là A. 1. − B. 0. C. 1. D. 2. 2
II. Phần tự luận (8,0 điểm).
Bài 1 (2,0 điểm). x − 2 x 2(1− 2x) 1) Giải phương trình − = . 2 x + 2 x − 2 x − 4
2) Giải bất phương trình (x + )2 1 − (x + ) 1 (x + 2) ≥ 2 − .
Bài 2 (2,0 điểm). Giải các hệ phương trình (Không sử dụng phương pháp dùng máy tính cầm tay). 2   x 4
2( x − y) − 3( x + y) = − a) 7  − = 5 
b) 3x + y −1 x − 2 5
 ( x − y) − 2( x + y) = 1 −   2x + y = 1 −
Bài 3 (3,0 điểm).
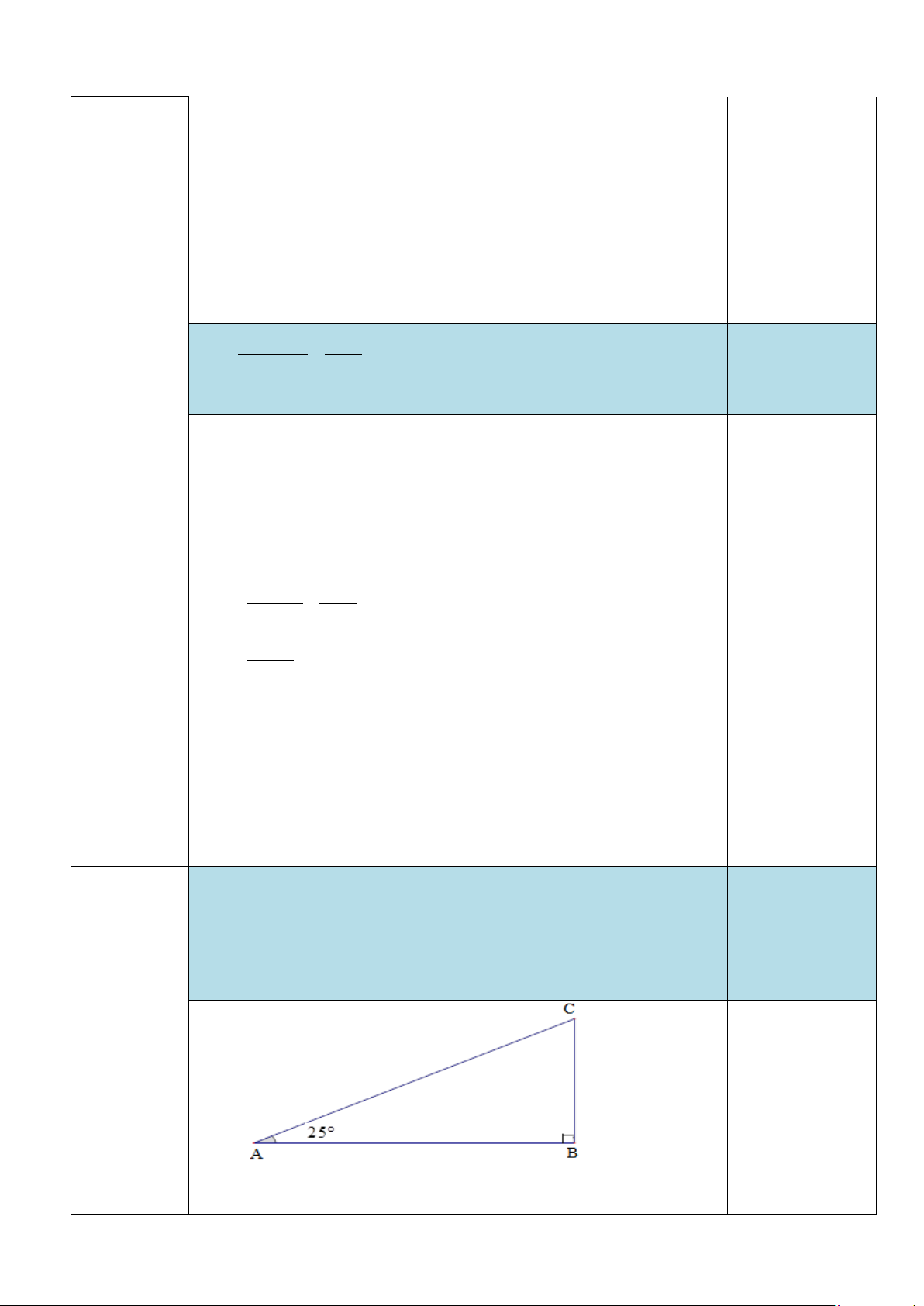
1) Một chiếc máy bay cất cánh với vận tốc
350km/h. Đường bay lên tạo với phương nằm
ngang một góc 25° (Hình 2). Hỏi sau 3 phút máy
bay bay lên cao được bao nhiêu km theo phương thẳng đứng?
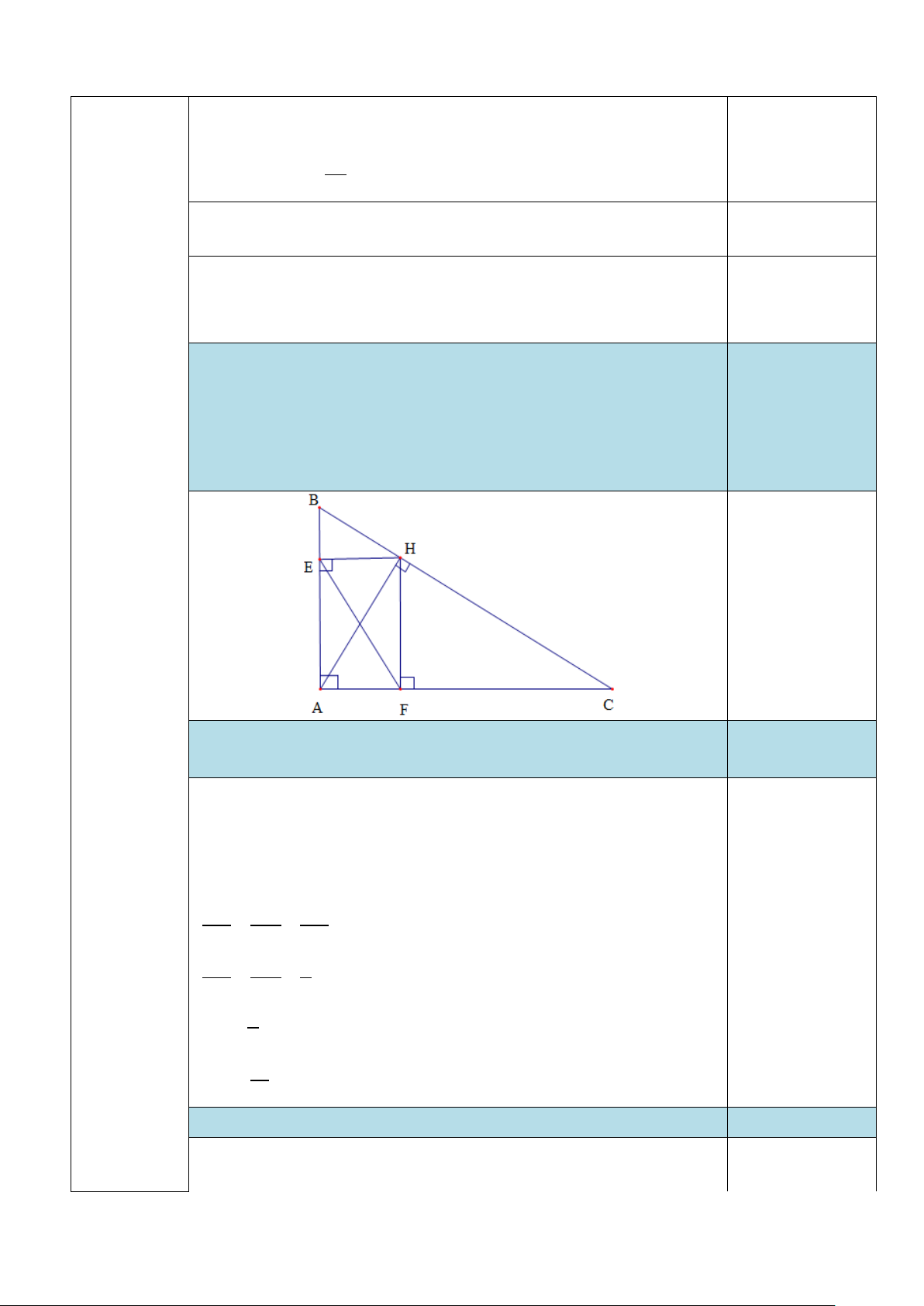
(làm tròn kết quả với độ chính xác 0,05). 2) Cho A
∆ BC vuông tại A , đường cao AH . Từ H kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB, F ∈ AC ) .
a) Biết AB = 3c , m AC = 4c .
m Tính độ dài các đoạn thẳng AH , HB . b) Chứng minh 2 E .
A EB + AF. FC = C . A
CF.tan C.
Bài 4 (1,0 điểm). 2 2 2
Cho a,b,c là các số thực dương tùy ý. Chứng minh rằng a b c + +
≥ a + b + c . b c a ---- Hết ---- 3
ĐÁP ÁN VÀ BIỂU ĐIỂM
Phần I. Trắc nghiệm (2,0 điểm). Mỗi đáp án đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 Đáp án D A C C B C A B
II. Phần tự luận (8,0 điểm). Bài Đáp án Điểm x − 2 x 2(1− 2x)
1) Giải phương trình − = . 2 x + 2 x − 2 x − 4 1,0
Điều kiện xác định của phương trình là: x ≠ 2 và x ≠ 2. − 0,25 x − 2 x 2(1− 2x) − = 2 x + 2 x − 2 x − 4 x − 2 x 2(1− 2x) − = . 0,25
x + 2 x − 2 (x − 2)(x + 2) 1 (x − )2 2 . x (x + 2) 2(1− 2x) (2,0 điểm) − = x + x − (x − )(x + ). 2 2 2 2 (x − )2 2 − .
x (x + 2) = 2(1− 2x). 2 2
x − 4x + 4 − x − 2x = 2 − 4 . x 0,25 2 − x = 2. −
x =1 ( Thỏa mãn điều kiện xác định). 0,25
Vậy phương trình có một nghiệm duy nhất x =1.
2) Giải bất phương trình (x + )2 1 − (x + ) 1 (x + 2) ≥ 2 − 1,0 2 x + x + − ( 2
2 1 x + 2x + x + 2) ≥ 2 − 0,25 2 2
x + 2x +1− x − 2x − x − 2 ≥ 2 − 0,25 −x ≥ 1 − x ≤1 0,25
Vậy nghiệm của bất phương trình là x ≤1 0,25
Giải các hệ phương trình sau:
2(x − y) −3(x + y) = 7 − a)  1,0 5
 ( x − y) − 2( x + y) = 1 −
2x − 2y − 3x − 3y = 7 −  0,25
5x − 5y − 2x − 2y = 1 −
−x − 5y = 7 −  0,25
3x − 7 y = 1 − 4
 x = 7 −5y ( ) 1 3 
 x − 7 y = 1 −  (2) 0,25
Thay x = 7 −5y vào (2) ta được 3(7 −5y) − 7y = 1 − Suy ra y =1 Thay y =1 vào ( ) 1 ta được x = 2 2
Vậy hệ phương trình đã cho có một nghiêm duy nhất 0,25 (2,0 điểm) ( ;x y) = (2; ) 1 2  x 4 b)  − = 5
3x + y −1 x − 2 1,0   2x + y = 1 −
Điều kiện: 3x + y −1≠ 0; x ≠ 2 0,25 2  x 4  − = 5 (3)
 x + 2x + y −1 x − 2 2x + y = 1 −  (4) 0,25 Thay 2x + y = 1 − vào (3) ta được 2 x 4 − = 5
x −1−1 x − 2 2 x − 4 = 5 x − 2 x + 2 = 5 0,25 x = 3
Thay x = 3 vào (4) ta được y = 7 −
Ta có x = 3và y = 7
− thỏa mãn điều kiện 0,25
Vậy hệ phương trình đã cho có một nghiệm duy nhất ( ;x y) = (3; 7 − )
1) Một chiếc máy bay cất cánh với vận tốc 350 km/h. Đường
bay lên tạo với phương nằm ngang một góc 25° (Hình 2).
Hỏi sau 3 phút máy bay bay lên cao được bao nhiêu km theo 1,0
phương thẳng đứng? (làm tròn kết quả với độ chính xác 0,05). 5
Quãng đường máy bay bay trong 3 phút là 0,25 3 AC = 350. = 17,5(km) 60 Xét A
∆ BC vuông tại B có
BC = AC.sin A 0,25 =17,5.sin 25° ≈ 7,4(km) 0,5
Vậy sau 3 phút máy bay bay lên cao được 7,4 km. 2) Cho A
∆ BC vuông tại A , đường cao AH . Từ H kẻ 3
HE ⊥ AB, HF ⊥ AC (E ∈ AB, F ∈ AC) .
(3,0 điểm) a) Biết AB =3c ,m AC = 4c .
m Tính độ dài các đoạn thẳng
AH , HB . b) Chứng minh 2 E .
A EB + AF. FC = C . A
CF.tan C.
a) Biết AB = 3c , m AC = 4c .
m Tính độ dài các đoạn thẳng AH , 1,0 HB . A
∆ BC vuông tại A có 2 2 2 2 2 2
BC = AB + AC = 3 + 4 = 5 0,25 BC = 5cm . HB ∆ Avà A ∆ BC có  = 
BHA BAC = 90°; B chung H ∆ BA ∽ A
∆ BC (g.g) 0,25 HB AH AB = = AB AC BC HB AH 3 = = 0,25 3 4 5 9 HB = cm 5 12 AH = cm 0,25 5 b) Chứng minh 2 E .
A EB + AF. FC = C . A
CF.tan C. 1,0
Chứng minh ΔHEB ∽ ΔAEH ( g.g) 6 EH BE = AE EH 2
AE. BE = EH 0,25
Chứng minh ΔHFA ∽ ΔCFH ( g.g) HF CF = 0,25 AF HF 2 AF.C F = HF
chứng minh tứ giác AEHF là hình chữ nhật từ đó suy ra EF = AH . E
∆ HF vuông tại H suy ra 2 2 2
EF = HE + HF 0,25
ΔAHC vuông tại H có đường cao HF nên cos FC CH C = = CH AC Suy ra 2 CH = . CACF Ta có 2 2 2 2
AE. BE + AF.CF = EH
+ HF = EF = AH 2 HC 0,25 2 2 = .AH = . CACF.tan C. 2 HC
Cho a,b,c là các số thực dương tùy ý. 2 2 2 a b c 1,0
Chứng minh rằng + + ≥ a + b + c. b c a 2 2 2 a b c
Ta chứng minh + + − a −b − c ≥ 0 b c a 2 2 2 a b c 4 VT = + +
− a − b − c b c a (1,0 điểm) 2 2 2       a b c
=  − 2a + b +  − 2b + c +  − 2c + a 0,5 b c a        2 2 2 2 2 2
 a − 2ab + b   b − 2bc + c   c − 2ca + a  =   +   + 0,25 b c  a       
(a −b)2 (b −c)2 (c − a)2 = + +
≥ 0 với mọi số thực dương a,b,c . b c a
Dấu “=” xảy ra khi a = b = c . 0,25
Vậy với mọi a,b,c là các số thực dương tùy ý thì 2 2 2 a b c + +
≥ a + b + c . b c a Lưu ý:
- Trên đây là sơ lược các bước giải, yêu cầu HS lập luận chặt chẽ khi trình bày bài.
- Các cách giải khác đúng và logic vẫn cho điểm tối đa.
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 9
https://thcs.toanmath.com/de-thi-giua-hk1-toan-9
Document Outline

• ĐỀ KHẢO SÁT CHẤT LƯỢNG GIỮA HỌC KỲ I TOÁN 9 VỤ BẢN
• XEM THEM - GIUA KY 1 - TOAN 9