Đề giữa kì 2 Toán 12 năm 2024 – 2025 trường chuyên Nguyễn Đình Chiểu – Đồng Tháp có đáp án
Đề giữa kì 2 Toán 12 năm 2024 – 2025 trường chuyên Nguyễn Đình Chiểu – Đồng Tháp có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 28 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem
Chủ đề: Đề giữa HK2 Toán 12 196 tài liệu
Môn: Toán 12 3.9 K tài liệu
Tác giả:
Preview text:
SỞ GD & ĐT TỈNH ĐỒNG THÁP
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG THPT CHUYÊN
Năm học : 2024 – 2025
NGUYỄN ĐÌNH CHIỂU
Môn: TOÁN – Khối 12 ĐỀ CHÍNH THỨC Thời gian: 90 phút
(không kể thời gian phát đề)
(Đề gồm có 06 trang ) Ngày kiểm tra: 12/3/2025 MÃ ĐỀ: 111
Họ và tên : .................................................................................... Số báo danh : ...................................
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm). Thí sinh trả lời từ câu 1
đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Họ tất cả các nguyên hàm của hàm số f (x) 4 3
= 5x − 8x − 6x là A. F (x) 5 4 2
= x − x − x + C. B. F (x) 5 4 2
= x + 2x − 3x + C.
C. F (x) 5 4 2
= x − 2x − 3x + C. D. F (x) 5 4 2
= x − 4x − 2x + C.
Câu 2: Khi cắt một vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x,
(− 3 ≤ x ≤ 3), mặt cắt là hình vuông có độ dài các cạnh là 2
3− x . Thể tích của vật thể đã cho bằng A. π 3 . B. 4 3 . C. 3 . D. 4π 3 .
Câu 3: Tìm nguyên hàm F (x) của hàm số f (x) = 6x + sin3x , biết F ( ) 2 0 = . 3 A. ( ) 2 cos3 = 3 x F x x − −1. B. ( ) 2 cos3 = 3 x F x x + +1. 3 3 C. F (x) 2 cos3x 2 = 3x − + . D. ( ) 2 cos3 = 3 x F x x − +1. 3 3 3 1 4 4 Câu 4: Cho f
∫ (x)dx = 2 và f
∫ (x)dx = 5, khi đó f (x)dx ∫ bằng 0 1 0 A. 3 − . B. 7 . C. 10. D. 6 .
Câu 5: Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Hãy chọn mệnh đề sai dưới đây: b a b
A. f (x)dx = f (x)dx ∫ ∫ .
B. kdx = k(b − a), k ∀ ∈ ∫ . a b a b c b b a
C. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ với c ∈[ ;
a b]. D. f (x)dx = − f (x)dx ∫ ∫ . a a c a b Trang 1/6 - Mã đề 111 3
Câu 6: Biết x + 2dx = a + blnc, ∫
với a,b,c ∈,c < 9. Tính tổng S = a + b + .c x 1 A. S = 8. B. S = 5 . C. S = 7. D. S = 6. Câu 7: Nếu f ∫ (x) 1
dx = + ln x + C thì f (x) là x A. f (x) 1
= − x + + ln x + C . B. f (x) 1 = − + ln x + C . x 2 x C. ( ) −1 f x x = .
D. f (x) = x + ln x + C . 2 x
Câu 8: Cho hàm số y = f (x) xác định và liên tục trên [ ;
a b]. Gọi (D) là hình phẳng giới
hạn bởi đồ thị hàm số y = f (x) trục hoành và hai đường thẳng x = a, x = b(a < b) .
Thể tích khối tròn xoay được tạo thành khi quay (D) quanh trục Ox được tính theo công thức nào sau đây b b b b A. 2
V = π f (x)dx ∫ . B. 2
V = 2π f (x)dx ∫ . C. 2 2 V = π f (x)dx ∫ . D. 2 V = π f (x)dx ∫ . a a a a
Câu 9: Nguyên hàm của hàm số y = sin x + 2cos x là
A. cos x + 2sin x + C ⋅
B. cos x − 2sin x + C ⋅
C. −cos x − 2sin x + C ⋅
D. −cos x + 2sin x + C ⋅ 1 1 Câu 10: Cho
f (x)dx = 3, g (x)dx = 2 − ∫ ∫ . Tính giá trị của biểu thức 0 0 1 I = 2 f
∫ (x)−3g(x)dx 0 A. 6 . B. y = 6 − . C. 12. D. 9 .
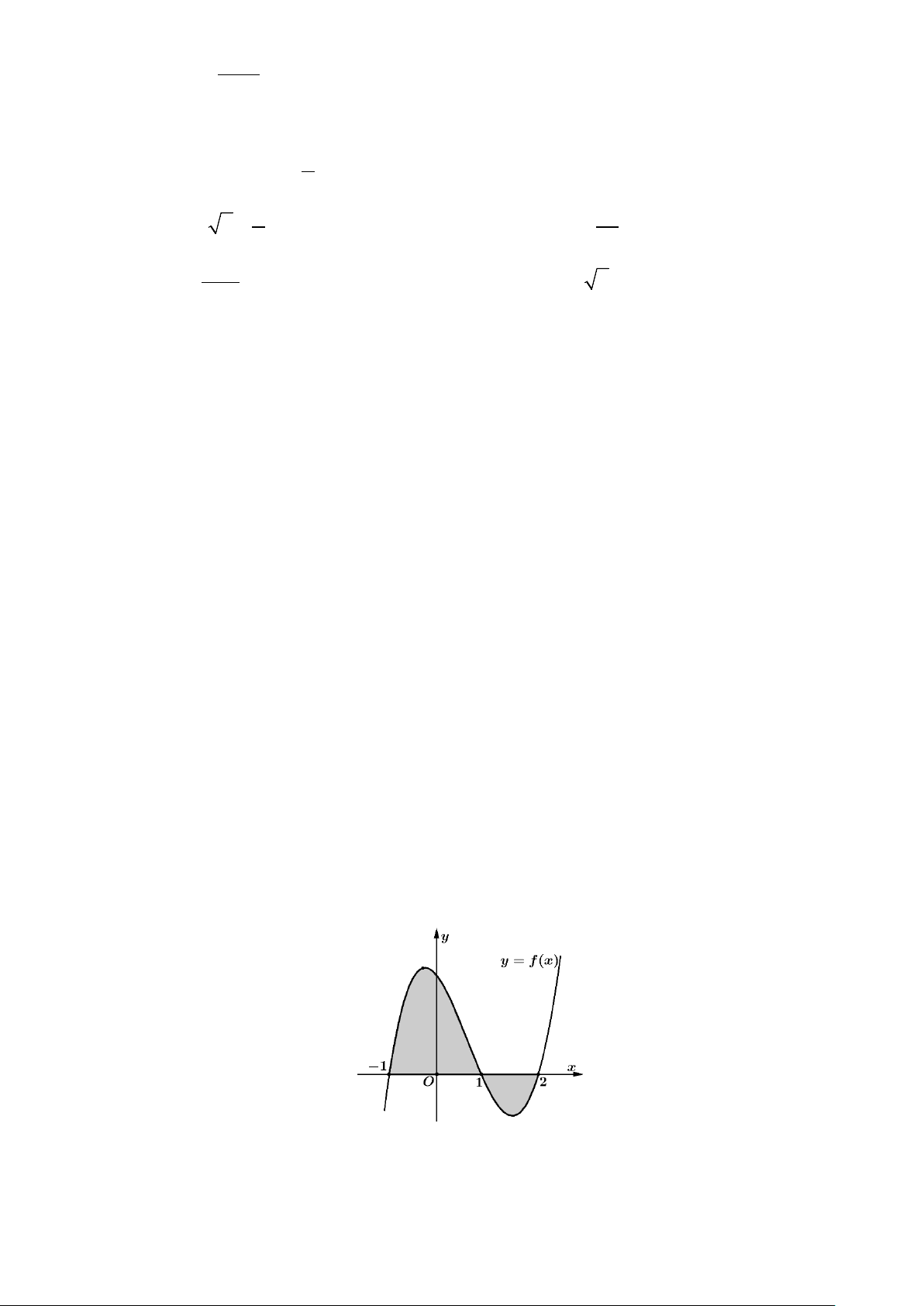
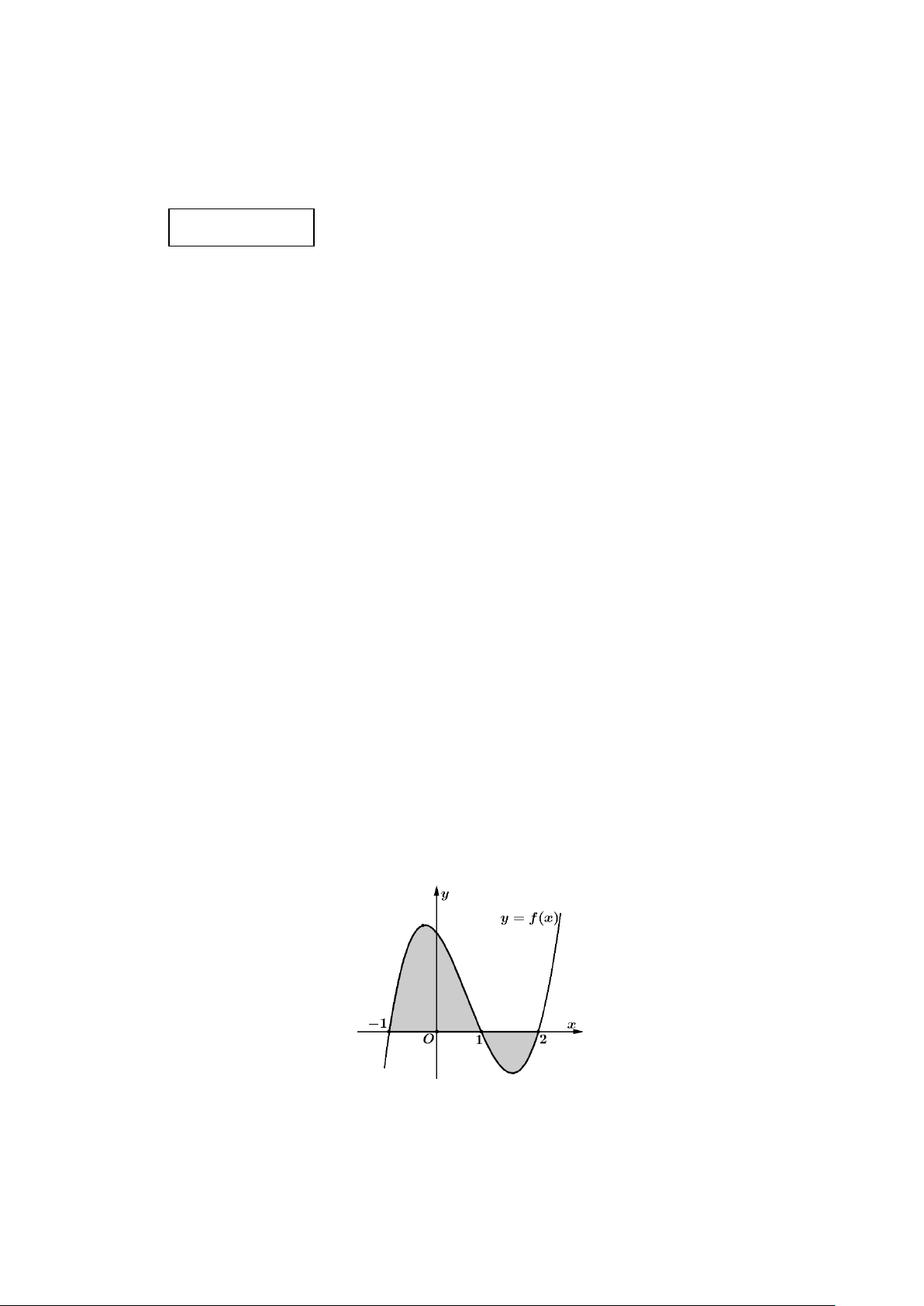
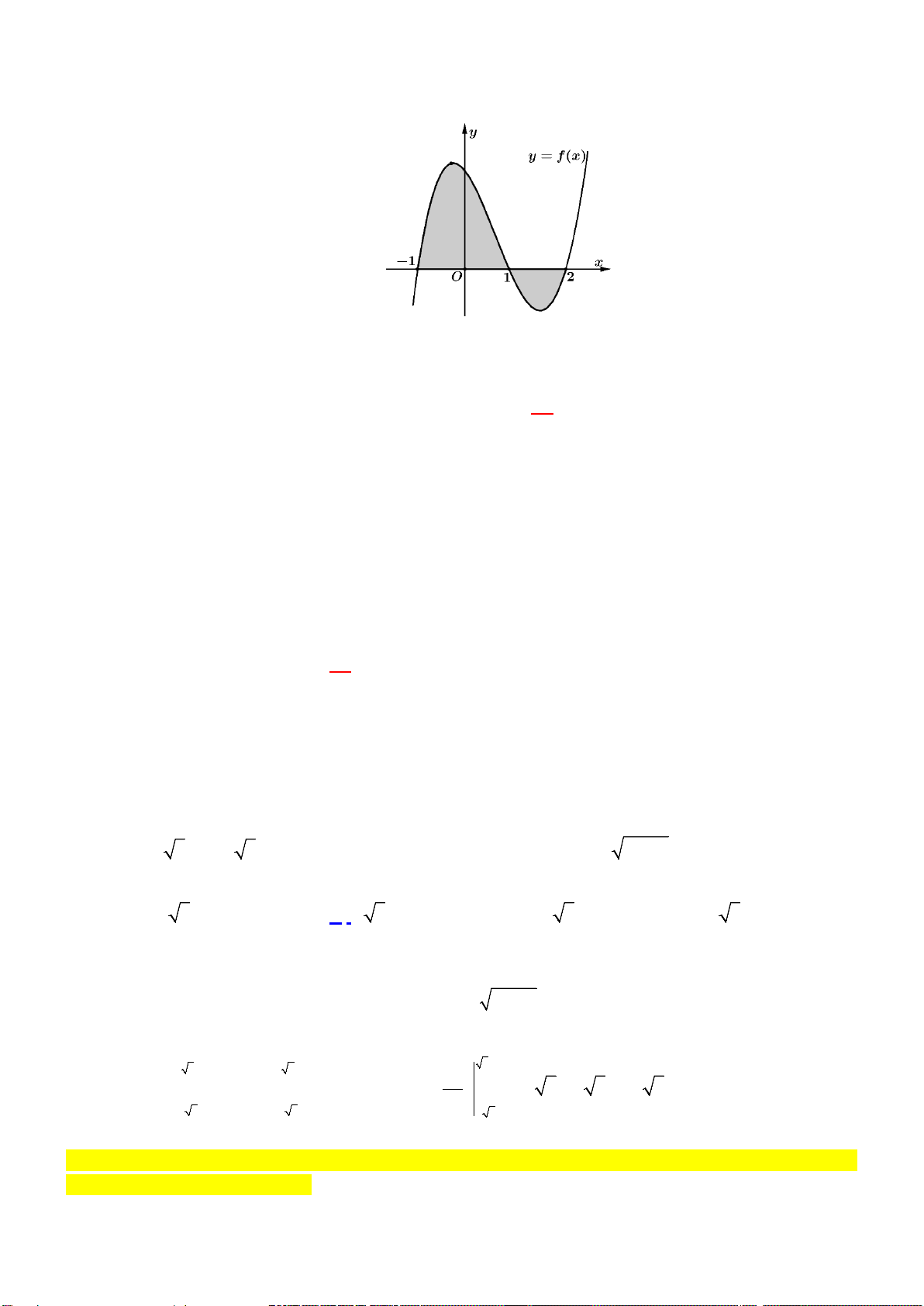
Câu 11: Cho hàm số f (x) liên tục trên . Gọi S là diện tích hình phẳng giới hạn bởi các
đường y = f (x), y = 0, x = 1,
− x = 2 . Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S = f
∫ (x) dx + f ∫ (x) dx. B. S = f
∫ (x) dx − f ∫ (x) dx. 1 − 1 1 − 1 1 2 1 2
C. S = − f
∫ (x) dx − f ∫ (x) dx.
D. S = − f
∫ (x) dx + f ∫ (x) dx . 1 − 1 1 − 1 Trang 2/6 - Mã đề 111 π π 2 2 Câu 12: Cho f
∫ (x)dx = 5. Tính I = f
∫ (x)+ 2sin xdx ? 0 0 A. I = 3. B. π I = 5 + . C. I = 5 +π D. I = 7 . 2
PHẦN II. Câu trắc nghiệm đúng sai (4,0 điểm). Thí sinh trả lời từ câu 1 đến câu 4. Trong
mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số y = f (x) liên tục trên đoạn [ ;
a b]. Gọi F (x) là một nguyên hàm của
hàm số y = f (x) trên đoạn [ ; a b]. b a b
A. Nếu a < c < b và f ∫ (x)dx = , m f
∫ (x)dx = n thì f
∫ (x)dx = m−n. a c c b B. f
∫ (x)dx = F (b)− F (a). a a b C. f
∫ (x)dx = − f ∫ (x)dx. b a b b D. 2024 f ∫
(x) + 2025dx = 2024 f
∫ (x)dx + 2025(a −b). a a
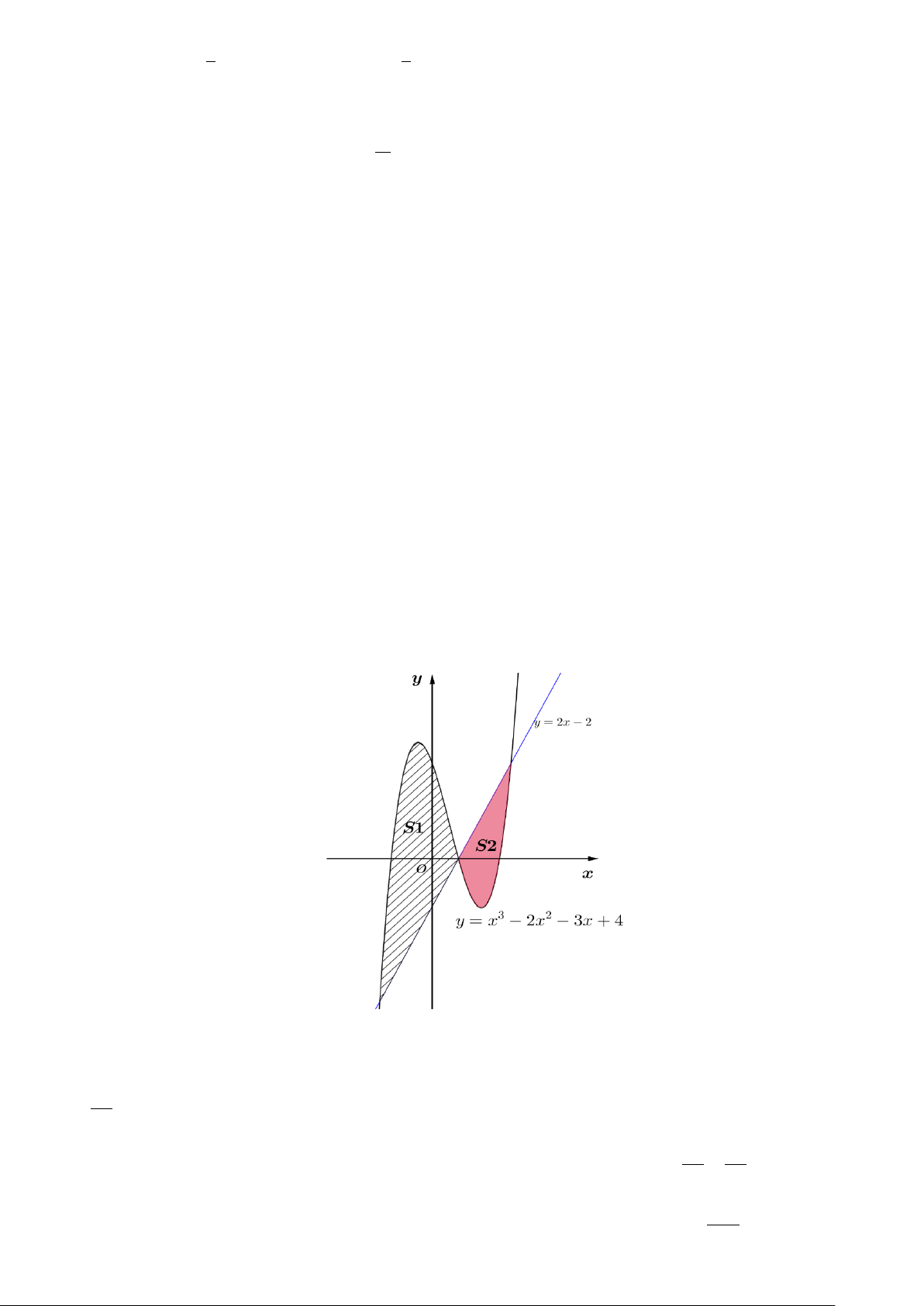
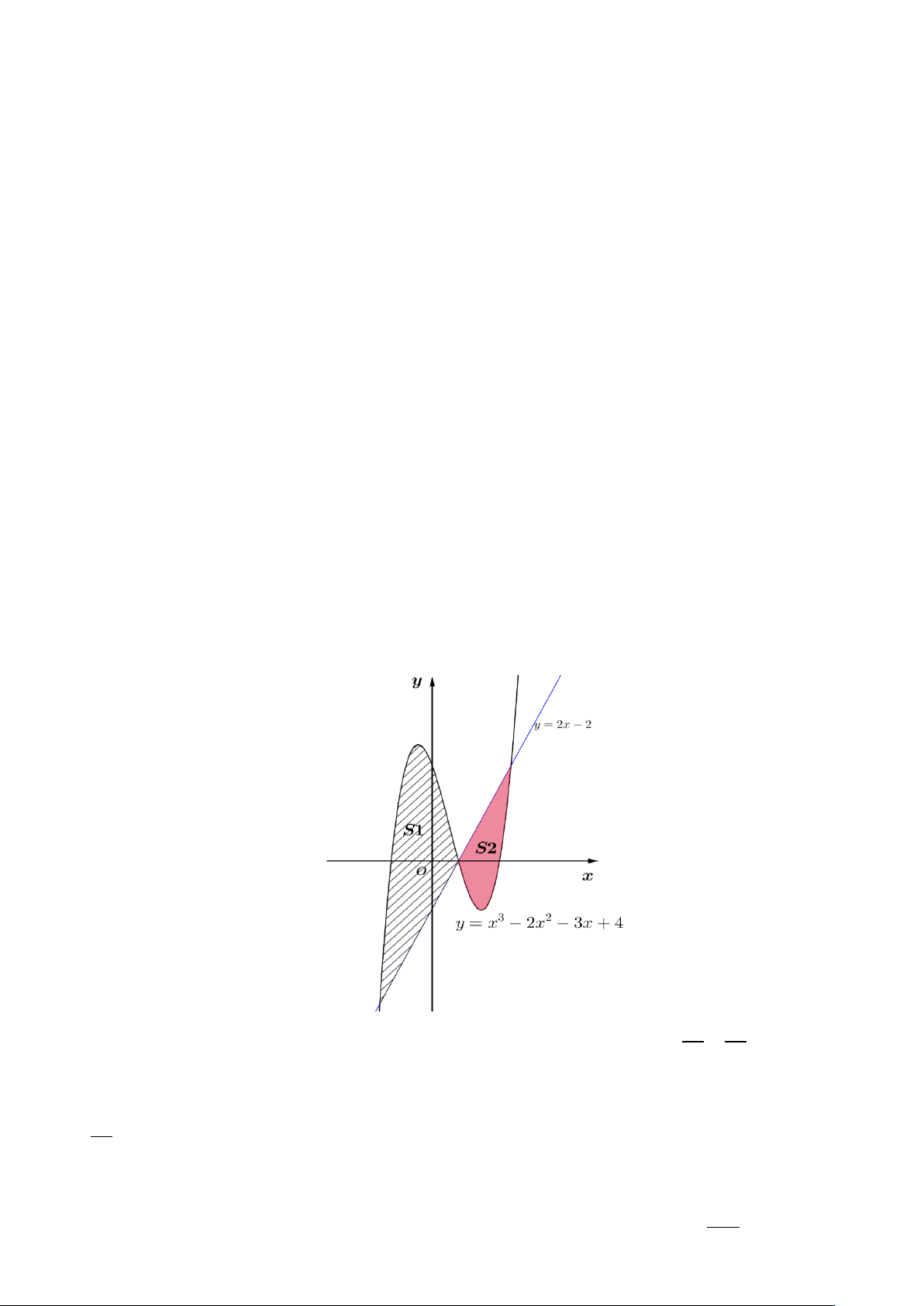
Câu 2: Cho đồ thị hàm số 3 2
y = x − 2x − 3x + 4(C) và đường thẳng d : y = 2x − 2 . Các
khẳng định sau là đúng hay sai?.
A. Đường thẳng d cắt đồ thị (C) tại ba điểm A( 2 − ; 6
− ), B(1;0),C (3;4) .
B. Diện tích hình phẳng giới hạn bởi đồ thị (C) , trục hoành, đường thẳng x = 1; − x = 2 bằng 21 . 4
C. Biết đường thẳng d cắt đồ thị (C) thành hai miền S và S . Tỉ số S1 63 = . 1 2 S 16 2
D. Diện tích hình phẳng giới hạn bởi đồ thị (C) và đường thẳng d bằng 253 . 12 Trang 3/6 - Mã đề 111
Câu 3: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang
phải) với gia tốc phụ thuộc vào thời gian t (s) là a(t) = t − ( 2
2 7 m/s ) . Biết vận tốc đầu bằng 6 (m/s)
A. Độ dịch chuyển của vật trong khoảng thời gian 1≤ t ≤ 7 là 18 m.
B. Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là t = 7 (s).
C. Tại thời điểm t = 7 (s), vận tốc của chất điểm là 6 (m/s).
D. Vận tốc tức thời của chất điểm tại thời điểm t (s) xác định bởi v(t) 2
= t − 7t +10 .
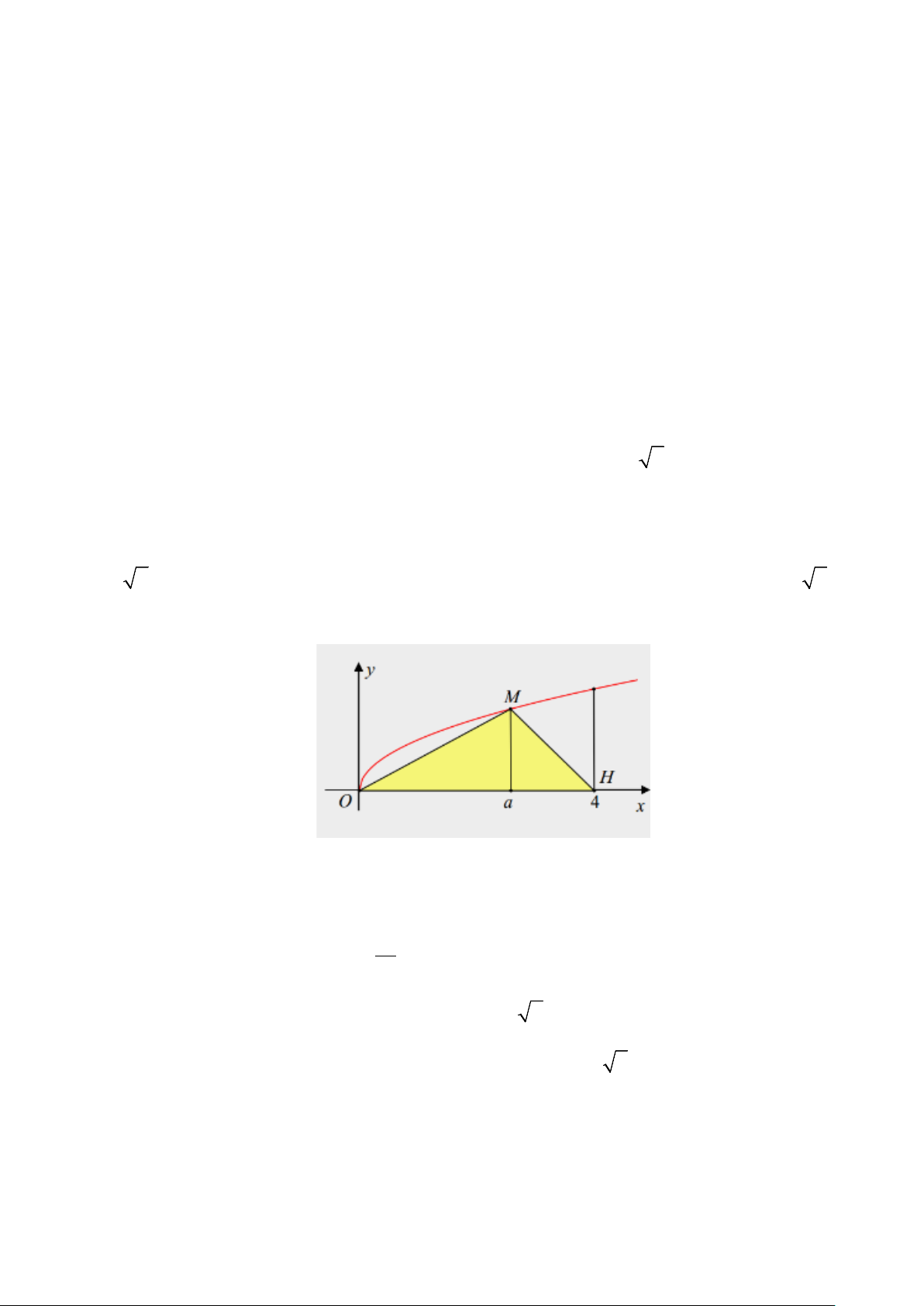
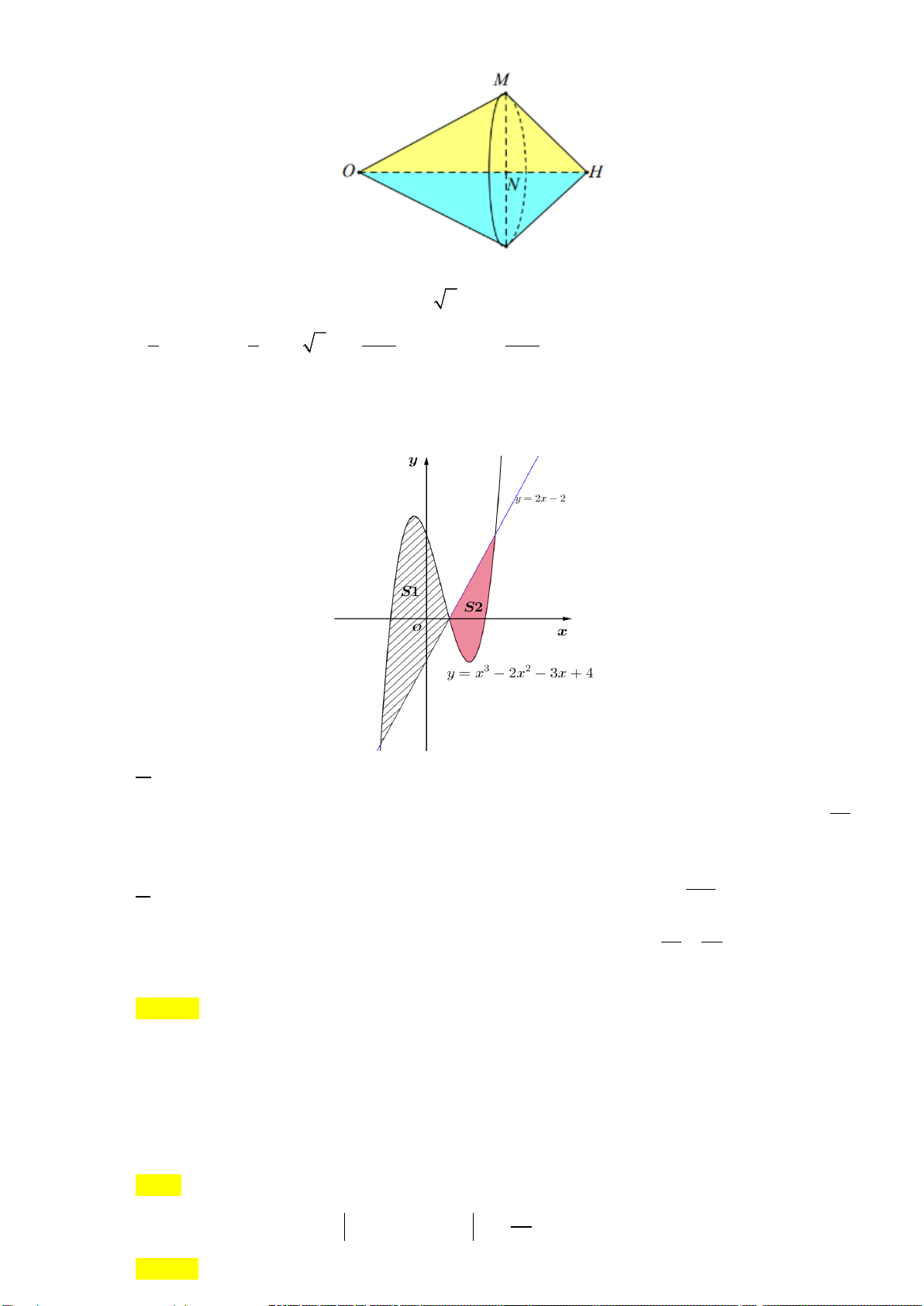
Câu 4: Cho hình phẳng (H ) giới hạn bởi đồ thị các hàm số y = x , trục hoành Ox và hai
đường thẳng x = 0, x = 4 . Các khẳng định sau là đúng hay sai?
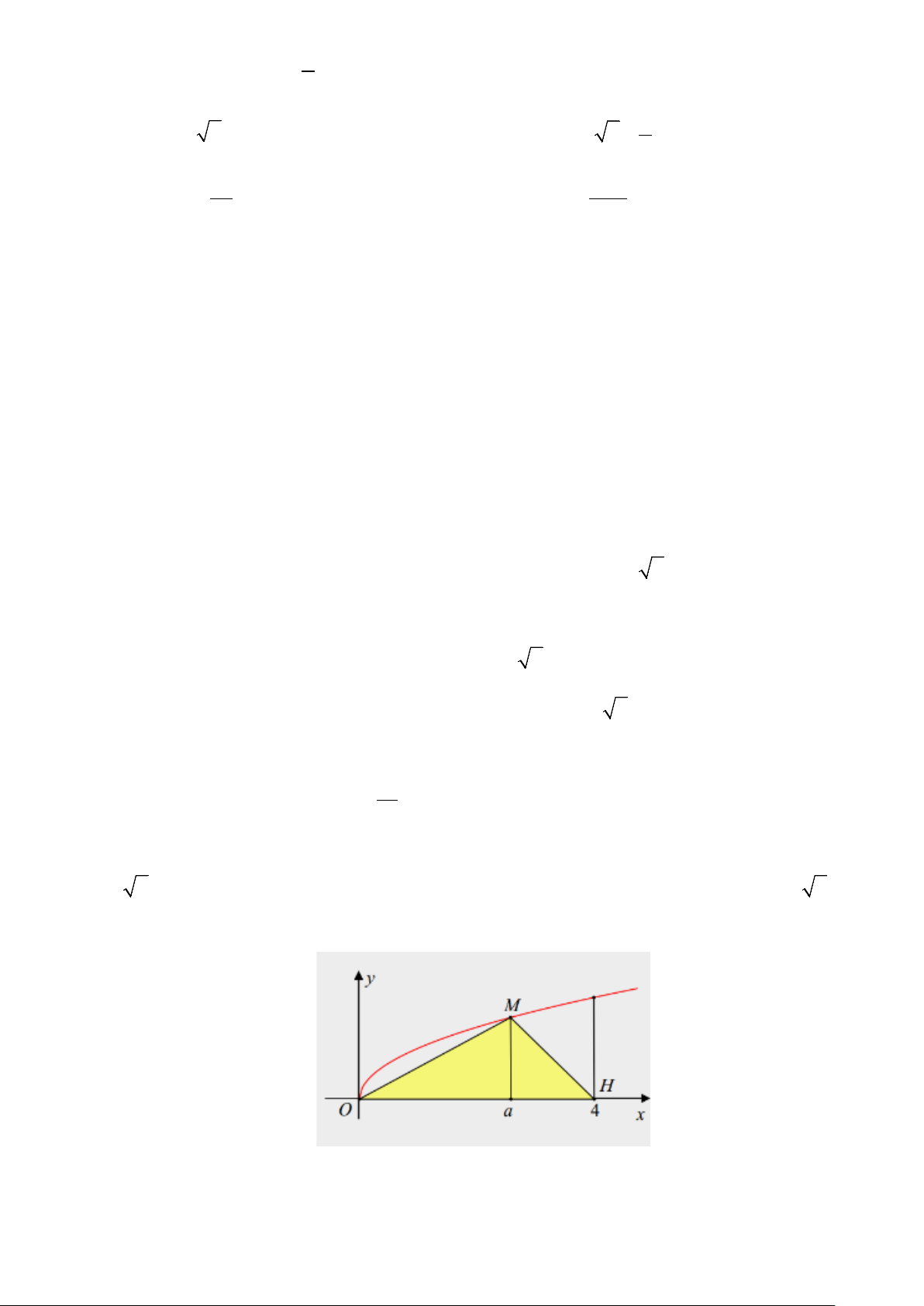
A. Gọi V là thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường
y = x , x = 0, x = 4 và trục Ox . Đường thẳng x = a(0 < a < 4) cắt đồ thị hàm số y = x tại M .
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác MOH quanh trục Ox . Biết 1
rằng V = 2V . Khi đó a = 3. 1
B. Diện tích hình phẳng (H ) là 19 . 6
C. Công thức tính diện tích hình phẳng (H ) là 4 xdx ∫ . 0
D. Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y = x , x = 0, x = 4 và trục hoành Ox là 8π . Trang 4/6 - Mã đề 111
PHẦN III. Câu trắc nghiệm trả lời ngắn (3,0 điểm). Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 2
− ≤ x ≤ 2), mặt cắt là tam giác vuông có một góc 0 45 và độ dài một cạnh góc vuông là 2
14 − 3x . Tính thể tích vật thể hình chiếc niêm trên.
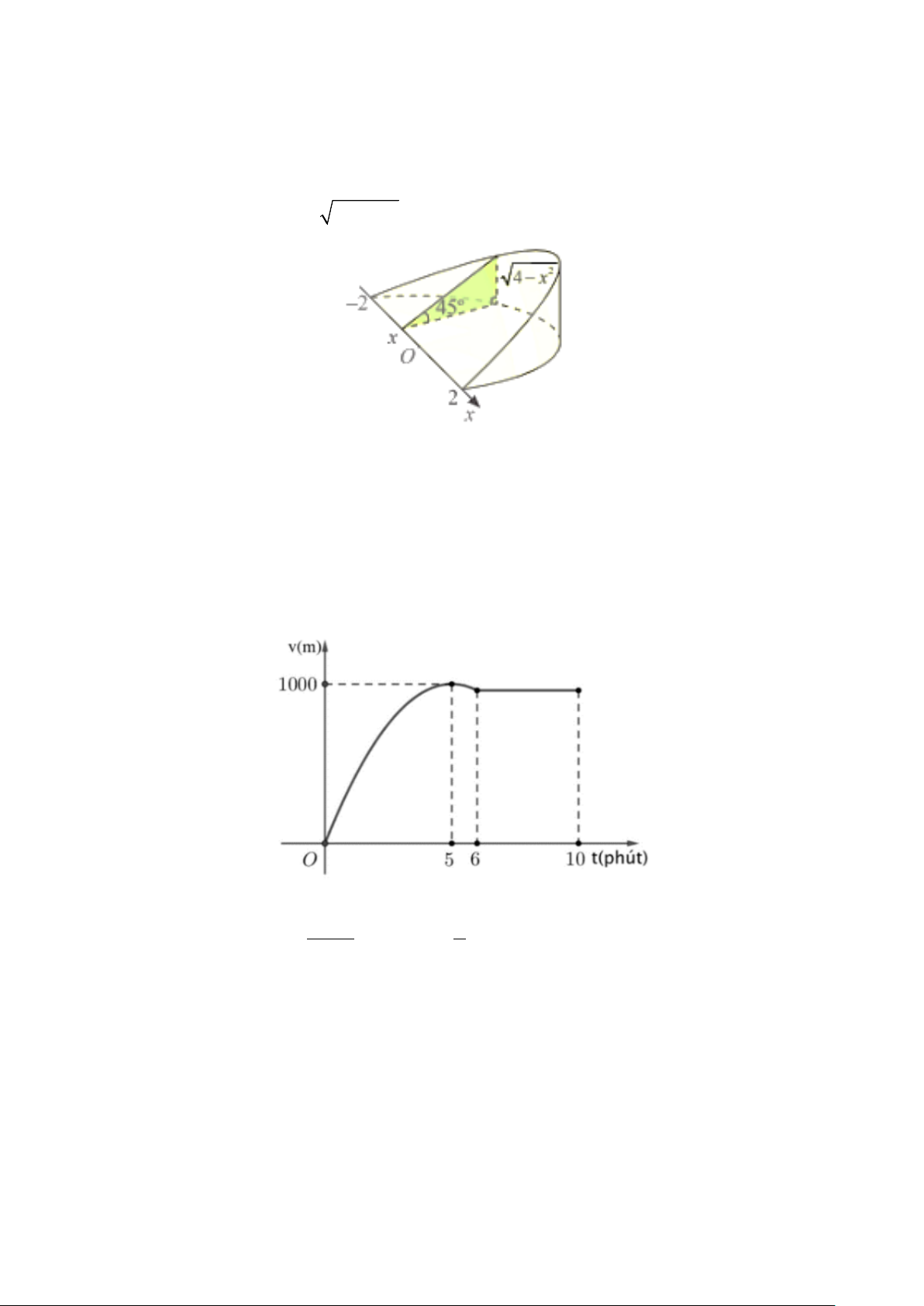
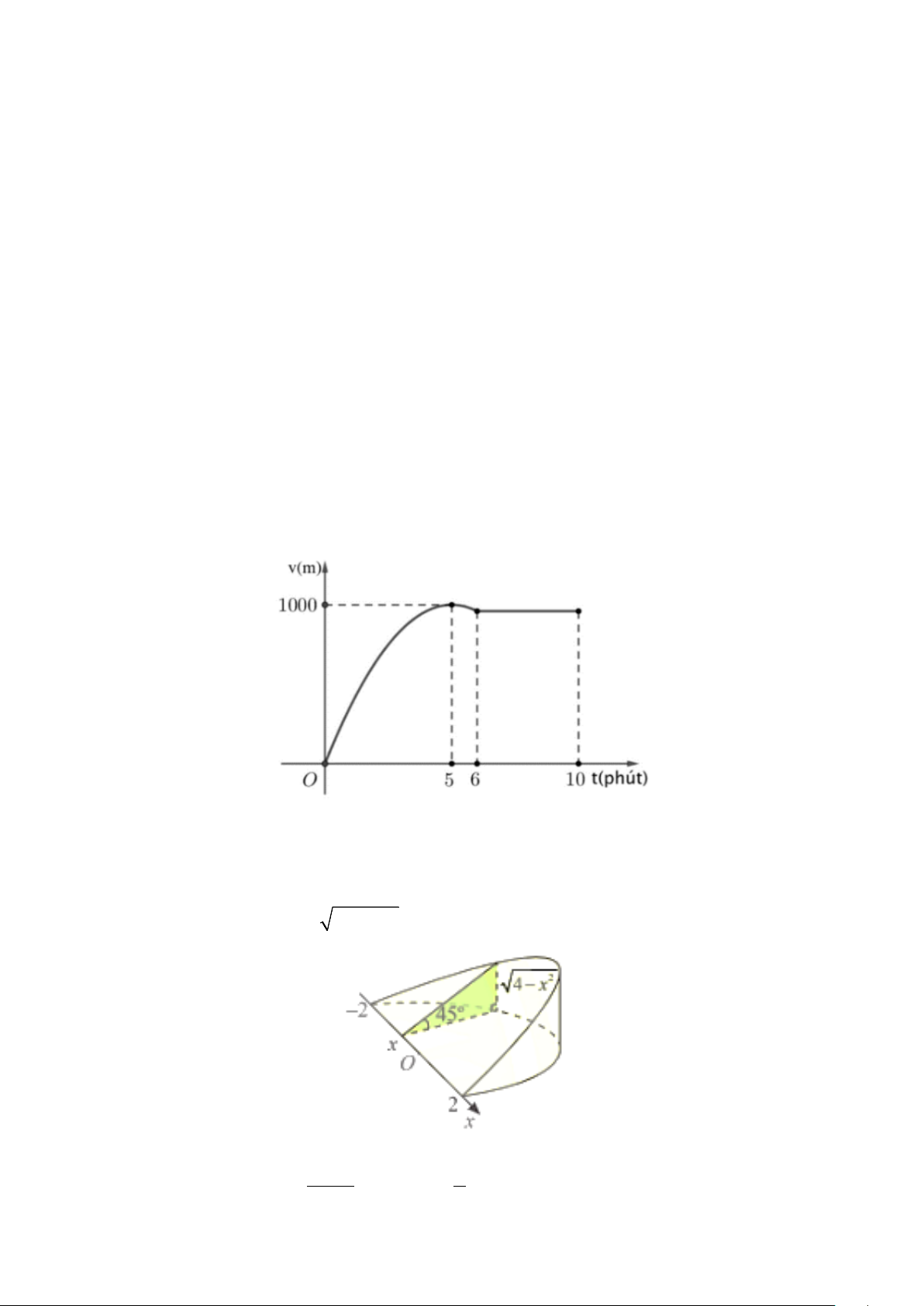
Câu 2: Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu chuyển động với vận tốc được biểu thị
bằng đồ thị là đường cong parabol. Biết rằng sau 5 phút thì xe đạt đến vận tốc cao
nhất 1 000 m/phút và bắt đầu giảm tốc, đi được 6 phút thì xe chuyển động đều (tham
khảo hình vẽ). Quãng đường xe đi được sau 10 phút đầu tiên kể từ khi hết đèn đỏ là bao nhiêu mét? 2 2 Câu 3: + Cho tích phân x 1 ∫ d = ln b x
a + , biết a,b,c là số nguyên. Tính tổng a + b + c . x c 1
Câu 4: Một hộ gia đình sản xuất cơ khí nhỏ mỗi ngày sản xuất được x sản phẩm
(0 ≤ x ≤ 20) . Chi phí biên để sản xuất x sản phẩm, tính bằng nghìn đồng, cho bởi
hàm số sau C (x) 2 '
= 3x − 4x +10. Biết rằng chi phí cố định ban đầu để sản xuất là
500 nghìn đồng. Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá 270 nghìn
đồng/sản phẩm. Tính lợi nhuận tối đa mà gia đình đó thu được khi sản xuất và bán sản phẩm? Trang 5/6 - Mã đề 111
Câu 5: Một viên đạn được bắn lên trời với vận tốc là 72(m / s) bắt đầu từ độ cao 2m . Hãy
xác định chiều cao của viên đạn sau thời gian 5s kể từ lúc bắn biết gia tốc trọng trường là ( 2
9,8 m / s ) (Làm tròn kết quả đến hàng phần mười).
Câu 6: Biết F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên và thoả mãn 4 f
∫ (x)dx = F (4)−G(0)+ 2m, với m > 0. Gọi S là diện tích hình phẳng giới hạn 0
bởi các đường y = F (x), y = G(x) ; x = 0 và x = 4. Khi S = 8 thì m bằng?
------ HẾT ------ Trang 6/6 - Mã đề 111
SỞ GD & ĐT TỈNH ĐỒNG THÁP
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG THPT CHUYÊN
Năm học : 2024 – 2025
NGUYỄN ĐÌNH CHIỂU
Môn: TOÁN – Khối 12 ĐỀ CHÍNH THỨC Thời gian: 90 phút
(không kể thời gian phát đề)
(Đề gồm có 06 trang ) Ngày kiểm tra: 12/3/2025 MÃ ĐỀ: 112
Họ và tên : .................................................................................... Số báo danh : ...................................
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm). Thí sinh trả lời từ câu 1
đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Hãy chọn mệnh đề sai dưới đây: b
A. kdx = k(b − a), k ∀ ∈ ∫ . a b c b
B. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ với c ∈[ ; a b]. a a c b a
C. f (x)dx = f (x)dx ∫ ∫ . a b b a
D. f (x)dx = − f (x)dx ∫ ∫ . a b
Câu 2: Cho hàm số f (x) liên tục trên . Gọi S là diện tích hình phẳng giới hạn bởi các
đường y = f (x), y = 0, x = 1,
− x = 2 . Mệnh đề nào dưới đây đúng? 1 2 1 2
A. S = − f
∫ (x) dx + f ∫ (x) dx . B. S = f
∫ (x) dx + f ∫ (x) dx. 1 − 1 1 − 1 1 2 1 2
C. S = − f
∫ (x) dx − f ∫ (x) dx. D. S = f
∫ (x) dx − f ∫ (x) dx. 1 − 1 1 − 1 Trang 1/6 - Mã đề 112
Câu 3: Họ tất cả các nguyên hàm của hàm số f (x) 4 3
= 5x − 8x − 6x là A. F (x) 5 4 2
= x + 2x − 3x + C. B. F (x) 5 4 2
= x − 2x − 3x + C. C. F (x) 5 4 2
= x − 4x − 2x + C. D. F (x) 5 4 2
= x − x − x + C. 1 1 Câu 4: Cho
f (x)dx = 3, g (x)dx = 2 − ∫ ∫ . Tính giá trị của biểu thức 0 0 1 I = 2 f
∫ (x)−3g(x)dx 0 A. 9 . B. y = 6 − . C. 12. D. 6 .
Câu 5: Nguyên hàm của hàm số y = sin x + 2cos x là
A. −cos x + 2sin x + C ⋅
B. cos x + 2sin x + C ⋅
C. cos x − 2sin x + C ⋅
D. −cos x − 2sin x + C ⋅
Câu 6: Khi cắt một vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x,
(− 3 ≤ x ≤ 3), mặt cắt là hình vuông có độ dài các cạnh là 2
3− x . Thể tích của vật thể đã cho bằng A. 4π 3 . B. π 3 . C. 4 3 . D. 3 . 3
Câu 7: Biết x + 2dx = a + blnc, ∫
với a,b,c ∈,c < 9. Tính tổng S = a + b + .c x 1 A. S = 7. B. S = 6. C. S = 8. D. S = 5 . π π 2 2 Câu 8: Cho f
∫ (x)dx = 5. Tính I = f
∫ (x)+ 2sin xdx ? 0 0 A. I = 3. B. I = 7 . C. I = 5 +π D. π I = 5 + . 2
Câu 9: Tìm nguyên hàm F (x) của hàm số f (x) = 6x + sin3x , biết F ( ) 2 0 = . 3 A. F (x) 2 cos3x 2 = 3x − + . B. ( ) 2 cos3 = 3 x F x x − −1. 3 3 3 C. ( ) 2 cos3 = 3 x F x x + +1. D. ( ) 2 cos3 = 3 x F x x − +1. 3 3 1 4 4 Câu 10: Cho f
∫ (x)dx = 2 và f
∫ (x)dx = 5, khi đó f (x)dx ∫ bằng 0 1 0 A. 10. B. 3 − . C. 6 . D. 7 . Trang 2/6 - Mã đề 112 Câu 11: Nếu f ∫ (x) 1
dx = + ln x + C thì f (x) là x
A. f (x) = x + ln x + C . B. f (x) 1
= − x + + ln x + C . x C. f (x) 1 − = − + ln x + C . D. ( ) 1 f x x = . 2 x 2 x
Câu 12: Cho hàm số y = f (x) xác định và liên tục trên [ ;
a b]. Gọi (D) là hình phẳng giới
hạn bởi đồ thị hàm số y = f (x) trục hoành và hai đường thẳng x = a, x = b(a < b) .
Thể tích khối tròn xoay được tạo thành khi quay (D) quanh trục Ox được tính theo công thức nào sau đây b b b b A. 2 2 V = π f (x)dx ∫ . B. 2
V = 2π f (x)dx ∫ . C. 2 V = π f (x)dx ∫ . D. 2
V = π f (x)dx ∫ . a a a a
PHẦN II. Câu trắc nghiệm đúng sai (4,0 điểm). Thí sinh trả lời từ câu 1 đến câu 4. Trong
mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hình phẳng (H ) giới hạn bởi đồ thị các hàm số y = x , trục hoành Ox và hai
đường thẳng x = 0, x = 4 . Các khẳng định sau là đúng hay sai?
A. Công thức tính diện tích hình phẳng (H ) là 4 xdx ∫ . 0
B. Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y = x , x = 0, x = 4 và trục hoành Ox là 8π .
C. Diện tích hình phẳng (H ) là 19 . 6
D. Gọi V là thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường
y = x , x = 0, x = 4 và trục Ox . Đường thẳng x = a(0 < a < 4) cắt đồ thị hàm số y = x tại M .
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác MOH quanh trục Ox . Biết 1
rằng V = 2V . Khi đó a = 3. 1 Trang 3/6 - Mã đề 112
Câu 2: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang
phải) với gia tốc phụ thuộc vào thời gian t (s) là a(t) = t − ( 2
2 7 m/s ) . Biết vận tốc đầu bằng 6 (m/s)
A. Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là t = 7 (s).
B. Tại thời điểm t = 7 (s), vận tốc của chất điểm là 6 (m/s).
C. Vận tốc tức thời của chất điểm tại thời điểm t (s) xác định bởi v(t) 2
= t − 7t +10 .
D. Độ dịch chuyển của vật trong khoảng thời gian 1≤ t ≤ 7 là 18 m.
Câu 3: Cho hàm số y = f (x) liên tục trên đoạn [ ;
a b]. Gọi F (x) là một nguyên hàm của
hàm số y = f (x) trên đoạn [ ; a b]. a b A. f
∫ (x)dx = − f ∫ (x)dx. b a b a b
B. Nếu a < c < b và f ∫ (x)dx = , m f
∫ (x)dx = n thì f
∫ (x)dx = m −n. a c c b C. f
∫ (x)dx = F (b)− F (a). a b b D. 2024 f ∫
(x) + 2025dx = 2024 f
∫ (x)dx + 2025(a −b). a a
Câu 4: Cho đồ thị hàm số 3 2
y = x − 2x − 3x + 4(C) và đường thẳng d : y = 2x − 2 . Các
khẳng định sau là đúng hay sai?.
A. Biết đường thẳng d cắt đồ thị (C) thành hai miền S và S . Tỉ số S1 63 = . 1 2 S 16 2
B. Diện tích hình phẳng giới hạn bởi đồ thị (C) , trục hoành, đường thẳng x = 1; − x = 2 bằng 21 . 4
C. Đường thẳng d cắt đồ thị (C) tại ba điểm A( 2 − ; 6
− ), B(1;0),C (3;4) .
D. Diện tích hình phẳng giới hạn bởi đồ thị (C) và đường thẳng d bằng 253 . 12 Trang 4/6 - Mã đề 112
PHẦN III. Câu trắc nghiệm trả lời ngắn (3,0 điểm). Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Biết F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên và thoả mãn 4 f
∫ (x)dx = F (4)−G(0)+ 2m, với m > 0. Gọi S là diện tích hình phẳng giới hạn 0
bởi các đường y = F (x), y = G(x) ; x = 0 và x = 4. Khi S = 8 thì m bằng?
Câu 2: Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu chuyển động với vận tốc được biểu thị
bằng đồ thị là đường cong parabol. Biết rằng sau 5 phút thì xe đạt đến vận tốc cao
nhất 1 000 m/phút và bắt đầu giảm tốc, đi được 6 phút thì xe chuyển động đều (tham
khảo hình vẽ). Quãng đường xe đi được sau 10 phút đầu tiên kể từ khi hết đèn đỏ là bao nhiêu mét?
Câu 3: Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 2
− ≤ x ≤ 2), mặt cắt là tam giác vuông có một góc 0 45 và độ dài một cạnh góc vuông là 2
14 − 3x . Tính thể tích vật thể hình chiếc niêm trên. 2 2 Câu 4: + Cho tích phân x 1 ∫ d = ln b x
a + , biết a,b,c là số nguyên. Tính tổng a + b + c . x c 1 Trang 5/6 - Mã đề 112
Câu 5: Một hộ gia đình sản xuất cơ khí nhỏ mỗi ngày sản xuất được x sản phẩm
(0 ≤ x ≤ 20) . Chi phí biên để sản xuất x sản phẩm, tính bằng nghìn đồng, cho bởi
hàm số sau C (x) 2 '
= 3x − 4x +10. Biết rằng chi phí cố định ban đầu để sản xuất là
500 nghìn đồng. Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá 270 nghìn
đồng/sản phẩm. Tính lợi nhuận tối đa mà gia đình đó thu được khi sản xuất và bán sản phẩm?
Câu 6: Một viên đạn được bắn lên trời với vận tốc là 72(m / s) bắt đầu từ độ cao 2m . Hãy
xác định chiều cao của viên đạn sau thời gian 5s kể từ lúc bắn biết gia tốc trọng trường là ( 2
9,8 m / s ) (Làm tròn kết quả đến hàng phần mười).
------ HẾT ------ Trang 6/6 - Mã đề 112
SỞ GD & ĐT ĐỒNG THÁP
ĐỀ KT GIỮA HKII, NĂM HỌC: 2024 - 2025 TRƯỜNG THPT CHUYÊN MÔN TOÁN - KHỐI 12 NGUYỄN ĐÌNH CHIỂU
Ngày kiểm tra: 12/3/2025
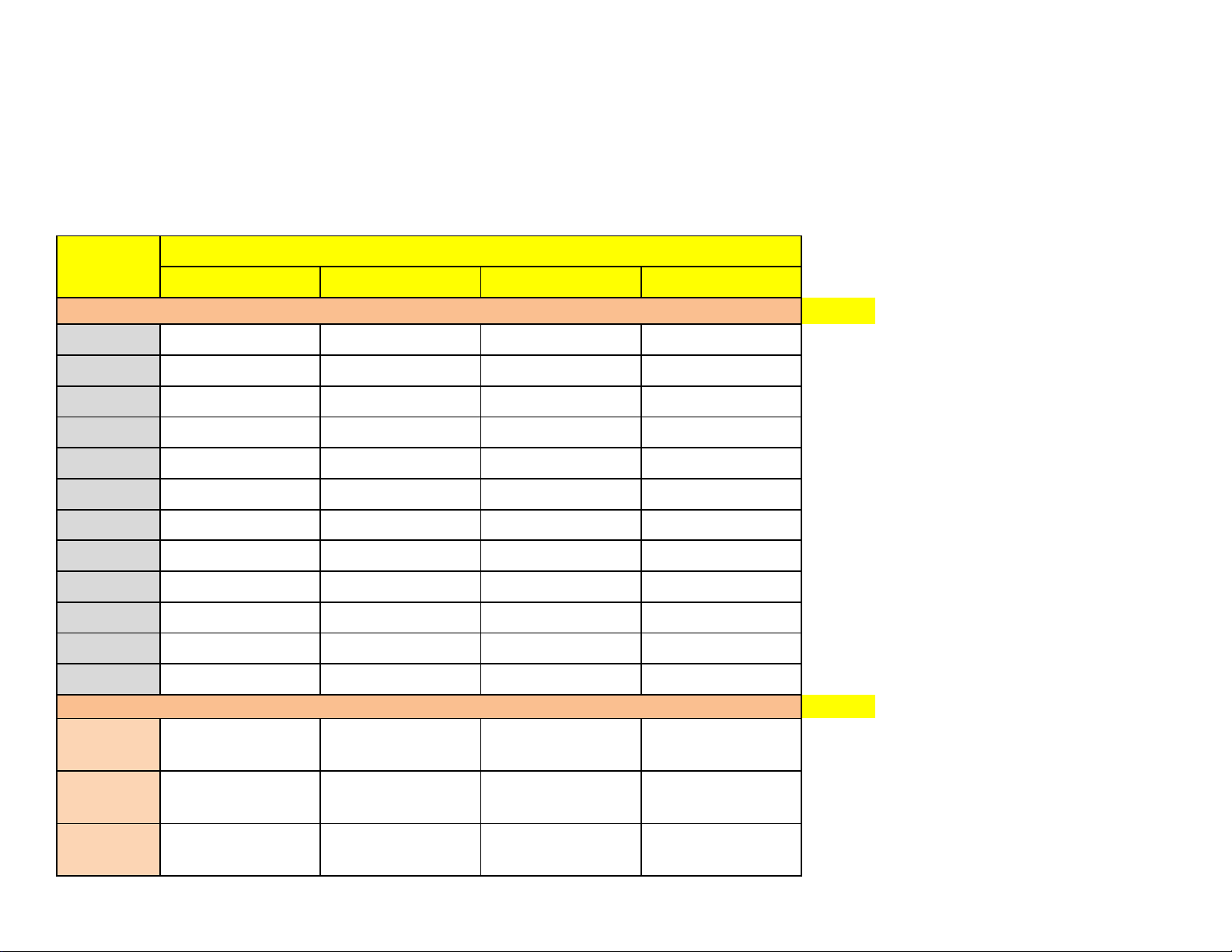
ĐÁP ÁN ĐỀ KT GIỮA HKII - LỚP 12 Mã đề kiểm tra Câu hỏi 111 112 113 114
CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
(MỖI CÂU ĐÚNG CHẤM 0,25 ĐIỂM) 1 C C A D 2 B D B A 3 D B D C 4 B C C B 5 A A A D 6 C C D B 7 C A D C 8 A B C A 9 D D D C 10 C D A D 11 B D C D 12 D D C C
CÂU TRẮC NGHIỆM ĐÚNG SAI
(MỖI CÂU ĐÚNG CHẤM 0,25 ĐIỂM)
A- S; B- Đ; C- Đ; A- Đ; B- Đ; C- S; A- S; B- S; C- Đ; A- Đ; B- Đ; C- S; 1 D- S; D- Đ; D- Đ; D- S;
A- Đ; B- S; C- S; A- S; B- Đ; C- S; A- S; B- Đ; C- S; A- Đ; B- S; C- S; 2 D- Đ; D- S; D- S; D- S;
A- S; B- S; C- Đ; A- Đ; B- S; C- Đ; A- S; B- S; C- Đ; A- S; B- S; C- Đ; 3 D- S; D- S; D- Đ; D- Đ;
A- Đ; B- S; C- Đ; A- S; B- S; C- Đ; A- Đ; B- Đ; C- S; A- Đ; B- Đ; C- S; 4 D- Đ; D- Đ; D- Đ; D- Đ;
CÂU TRẢ LỜI NGẮN ( MỖI CÂU ĐÚNG CHẤM 0,5 ĐIỂM )
(MỖI CÂU ĐÚNG CHẤM 0,5 ĐIỂM) 1 20 1 20 20 2 8160 8160 8160 8160 3 7 20 239,5 1 4 1300 7 7 239,5 5 239,5 1300 1 1300 6 1 239,5 1300 7 E E E E
CÂU CÓ ĐÁP ÁN 20 (HÌNH VÀ ĐỀ CHƯA KHỚP) VÀ 239,5 DO DƯ KÍ TỰ TRÊN PHIẾU TÔ (MÀU
VÀNG). THẦY /CÔ THÔNG BÁO HS LÀ CHẤM ĐỦ 0,5 ĐIỂM Ạ.
SỞ GD & ĐT TỈNH ĐỒNG THÁP
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG THPT CHUYÊN
Năm học : 2024 – 2025
NGUYỄN ĐÌNH CHIỂU
Môn: TOÁN – Khối 12 ĐỀ CHÍNH THỨC Thời gian: 90 phút
(không kể thời gian phát đề) (Đề gồm có … trang ) Ngày kiểm tra: 12/3/2025 ĐỀ GỐC
Họ và tên : .............................................................................. Số báo danh : ...................................
ĐÁP ÁN ĐỀ KT GK2 LỚP 12 NỘP TRƯỜNG
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nguyên hàm của hàm số y = sin x + 2cos x là
A. cos x − 2sin x + C ⋅
B. −cos x + 2sin x + C ⋅
C. cos x + 2sin x + C ⋅
D. −cos x − 2sin x + C ⋅ Lời giải Chọn B
Câu 2: Tìm nguyên hàm F (x) của hàm số f (x) = 6x + sin3x , biết F ( ) 2 0 = . 3 A. F (x) 2 cos3x 2 = 3x − + . B. ( ) 2 cos3 = 3 x F x x − −1. 3 3 3 C. ( ) 2 cos3 = 3 x F x x + +1. D. ( ) 2 cos3 = 3 x F x x − +1. 3 3 Lời giải ∫ ( ) = ∫( + ) 2 cos3 d 6 sin 3 d = 3 x f x x x x x x −
+ C = F (x). 3 F ( ) 2 0 = 1 2
⇔ 0 − .1+ C = ⇔ C = 1. Vậy ( ) 2 cos3 = 3 x F x x − +1. 3 3 3 3
Câu 3: Họ tất cả các nguyên hàm của hàm số f (x) 4 3
= 5x − 8x − 6x là A. F (x) 5 4 2
= x − 4x − 2x + C. B. F (x) 5 4 2
= x + 2x − 3x + C. C. F (x) 5 4 2
= x − 2x − 3x + C. D. F (x) 5 4 2
= x − x − x + C. Lời giải
Ta có F (x) = ∫( 4 3
x − x − x) 5 4 2 5 8
6 dx = x − 2x − 3x + C.
Vậy một nguyên hàm của hàm số f (x) là F (x) 5 4 2
= x − 2x − 3x + C. Câu 4: Nếu f ∫ (x) 1
dx = + ln x + C thì f (x) là x
A. f (x) = x + ln x + C . B. f (x) 1
= − x + + ln x + C . x C. f (x) 1 − = − + ln x + C . D. ( ) 1 f x x = . 2 x 2 x Lời giải ′ Ta có 1 1 1 −1 − + ln x x + C = − + = x 1 , suy ra f (x) = là hàm số cần tìm. 2 2 x x x x 2 x
Câu 5: Cho hàm số f (x) liên tục trên đoạn [a;b]. Hãy chọn mệnh đề sai dưới đây: b a b
A. f (x)dx = − f (x)dx ∫ ∫ .
B. kdx = k(b − a), k ∀ ∈ ∫ . a b a b c b
C. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫
với c ∈[a;b] . a a c b a
D. f (x)dx = f (x)dx ∫ ∫ . a b Lời giải Chọn D.
Theo tính chất tích phân A,B,C đúng b a
Đáp án D sai vì: f (x)dx = − f (x)dx ∫ ∫ . a b 1 4 4 Câu 6: Cho f
∫ (x)dx = 2 và f
∫ (x)dx = 5, khi đó f (x)dx ∫ bằng 0 1 0 A. 7 . B. 10. C. 3 − . D. 6 . Lời giải Chọn A 4 1 4 Ta có f
∫ (x)dx = f
∫ (x)dx + f
∫ (x)dx = 2 + 5 = 7. 0 0 1 1 1 1
Câu 7: Cho f (x)dx = 3, g (x)dx = 2 − ∫ ∫
. Tính giá trị của biểu thức I = 2 f
∫ (x) −3g(x)dx 0 0 0 A. y = 6 − . B. 12. C. 6 . D. 9. Lời giải Chọn B 1 1 1
Ta có I = 2 f
∫ (x) −3g(x)dx = 2 f
∫ (x)dx −3 g
∫ (x)dx = 2.3−3.( 2 − ) = 12 . 0 0 0 π π 2 2 Câu 8: Cho f
∫ (x)dx = 5. Tính I = f
∫ (x) + 2sin xdx ? 0 0 A. π I = 7 . B. I = 5 + . C. I = 3 . D. I = 5 + π 2 Lời giải Chọn A Ta có π π π π π 2 2 2 2 I = f
∫ (x)+ 2sin xdx = f
∫ (x)dx+2 sin xdx ∫ = f
∫ (x)dx − 2cos x 2 = 5− 2(0 − )1 = 7 . 0 0 0 0 0 3
Câu 9: Biết x + 2dx = a + bln c, ∫
với a,b,c ∈ ,c < 9. Tính tổng S = a + b + .c x 1 A. S = 7 . B. S = 5. C. S = 8 . D. S = 6 . Lời giải 3 3 3 3 Ta có x + 2 2 2 3 dx = 1+ dx = dx +
dx = 2 + 2ln x = 2 + ∫ ∫ 2ln 3. ∫ ∫ 1 x x x 1 1 1 1
Do đó a = 2,b = 2,c = 3 ⇒ S = 7.
Câu 10: Cho hàm số f (x) liên tục trên . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y = f (x), y = 0, x = 1,
− x = 2 . Mệnh đề nào dưới đây đúng? 1 2 1 2
A. S = − f x
∫ ( ) dx − f x ∫ ( ) dx.
B. S = f x
∫ ( ) dx + f x ∫ ( ) dx. 1 − 1 1 − 1 1 2 1 2
C. S = − f x
∫ ( ) dx + f x ∫ ( ) dx. D. S = f
∫ (x) dx − f
∫ (x) dx. 1 − 1 1 − 1 Lời giải 1 2
Dựa vào đồ thị, ta có S = f
∫ (x) dx − f ∫ (x) dx. 1 − 1
Câu 11: Cho hàm số y = f (x) xác định và liên tục trên [ ;
a b] . Gọi (D) là hình phẳng giới hạn bởi đồ
thị hàm số y = f (x) trục hoành và hai đường thẳng x = a, x = b(a < b) . Thể tích khối tròn
xoay được tạo thành khi quay (D) quanh trục Ox được tính theo công thức nào sau đây b b b b A. 2
V = 2π f (x)dx ∫ . B. 2
V = π f (x)dx ∫ . C. 2 V = π f (x)dx ∫ . D. 2 2 V = π f (x)dx ∫ . a a a a Lời giải Chọn B b
Áp dụng công thức tính thể tích vật thể tròn xoay quay quanh trục Ox ta có 2
V = π f (x)dx ∫ . a
Câu 12: Khi cắt một vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ,
(− 3 ≤ x ≤ 3), mặt cắt là hình vuông có độ dài các cạnh là 2
3 − x . Thể tích của vật thể đã cho bằng A. 3 . B. 4 3 . C. 4π 3 . D. π 3 . Lời giải Chọn B
Diện tích của mặt cắt hình vuông là S (x) = ( − x )2 2 2 3 = 3 − x .
Thể tích của vật thể đã cho là: 3 3 3 3 = ∫ ( ) = ∫ ( 2 3 − ) = 3 x V S x dx x dx x − = (2 3 + 2 3) = 4 3 . 3 − 3 − 3 − 3
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số y = f (x) liên tục trên đoạn [ ;
a b]. Gọi F (x) là một nguyên hàm của hàm số
y = f (x) trên đoạn [ ; a b]. b a) f
∫ (x)dx = F (b) − F (a) . a a b b) f
∫ (x)dx = − f ∫ (x)dx. b a b a b
c) Nếu a < c < b và f ∫ (x)dx = , m f
∫ (x)dx = n thì f
∫ (x)dx = m − n. a c c b b d) 2024 f ∫
(x) + 2025dx = 2024 f
∫ (x)dx + 2025(a −b). a a Lời giải a) Đúng. b Ta có: f
∫ (x)dx = F (x)b = F (b) − F (a). a a b) Đúng. a b Ta có: f
∫ (x)dx = F (x) a = F (a) − F (b) = −F
(b) − F (a) = − f ∫ (x)dx . b b a c) Sai. b c b b b c
Với a < c < b ta có f
∫ (x)dx = f
∫ (x)dx + f
∫ (x)dx ⇔ f
∫ (x)dx = f
∫ (x)dx − f ∫ (x)dx . a a c c a a c a Mặt khác f
∫ (x)dx = − f
∫ (x)dx =− n . a c b Từ đó ta được f
∫ (x)dx = m −(−n) = m + n. c d) Sai. b b b b Ta có: 2024 f ∫
(x) + 2025dx = 2024 f
∫ (x)dx + 2025 dx = 2024 f ∫
∫ (x)dx + 2025 b x a a a a a b = 2024 f
∫ (x)dx + 2025(b − a). a
Câu 2: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với
gia tốc phụ thuộc vào thời gian t (s) là a(t) = t − ( 2
2 7 m/s ) . Biết vận tốc đầu bằng 6 (m/s)
a) Vận tốc tức thời của chất điểm tại thời điểm t (s) xác định bởi v(t) 2
= t − 7t +10 .
b) Tại thời điểm t = 7 (s), vận tốc của chất điểm là 6 (m/s).
c) Độ dịch chuyển của vật trong khoảng thời gian 1 ≤ t ≤ 7 là 18 m.
d) Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là t = 7 (s). Lời giải
a) S, b) Đ, c) S, d) S.
a) Ta có v(t) = a
∫ (t) t = ∫( t − ) 2 d
2 7 dt = t − 7t + C . v(0) = 6 ⇒ C = 6 . Vậy v(t) 2
= t − 7t + 6 (m/s). nên mệnh đề sai
b) Tại thời điểm t = 7 (s) ta có v( ) 2
7 = 7 − 7 ⋅ 7 + 6 = 6 (m/s). nên mệnh đề đúng
c) Độ dịch chuyển của vật trong khoảng thời gian 1 ≤ t ≤ 7 là 7 7 7 3 2 = ∫ ( ) = ∫( 2 − + ) t 7 d 7 6 d t S v t t t t t = − + 6t = 18 − . nên mệnh đề SAI. 3 2 1 1 1
d) Tọa độ của chất điểm tại thời điểm t là ( ) = ∫ ( ) = ∫( − + ) 3 2 2 t 7 d 7 6 d t x t v t t t t t = − + 6t + C 3 2
Ta cần tìm giá trị lớn nhất của x(t) với t ∈[0;8] .
Ta có x′(t) = v(t) = 0 khi t = 1 hoặc t = 6 .
x(0) = C , x( ) 17 1 = + C , x(6) = 18 − + C , x( ) 16 8 = − + C . 6 3
Vậy giá trị lớn nhất của x(t) với t ∈[0;8] đạt được khi t = 1. nên mệnh đề sai
Câu 3: Cho hình phẳng (H ) giới hạn bởi đồ thị các hàm số y = x , trục hoành Ox và hai đường
thẳng x = 0, x = 4 . Các khẳng định sau là đúng hay sai?
a) Công thức tính diện tích hình phẳng (H ) là 4 xdx ∫ . 0
b) Diện tích hình phẳng (H ) là 19 . 6
c) Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y = x , x = 0, x = 4 và trục hoành Ox là 8π .
d) Gọi V là thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường
y = x , x = 0, x = 4 và trục Ox . Đường thẳng x = a(0 < a < 4) cắt đồ thị hàm số y = x tại M .
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác MOH quanh trục Ox . Biết rằng V = 2V . 1 1 Khi đó a = 3. Lời giải a) Đ b) S c) Đ d) Đ a) Ta có 4 S = xdx ∫ . Vậy a) Đúng. 0 3 b) 4 2 4 16 2 S = xdx = x = ∫ . Vậy b) Sai 0 0 3 3 c) Ta có 4 V = π ∫ ( x)2 4 dx π = xdx 8 = π ∫ . Vậy c) Đúng 0 0 d) 4 V = π ∫ ( x)2 4 dx π = xdx 8 = π ∫ V ⇒ V = = 4π 0 0 1 2
Tam giác MOH quanh trục Ox tạo nên hai khối nón chung đáy. Gọi N là hình chiếu vuông góc của
M trên trục Ox . Suy ra r = MN = y = y a = a . M ( ) 1 1 π ⇒ = π = π ( )2 2 4π . . . .4. . a V OH r a = . Suy ra 4 4 a π = ⇒ a = 3 1 3 3 3 3 Vậy d) Đúng.
Câu 4: Cho đồ thị hàm số 3 2
y = x − 2x − 3x + 4(C) và đường thẳng d : y = 2x − 2 . Các khẳng định sau là đúng hay sai?.
a) Đường thẳng d cắt đồ thị (C) tại ba điểm A( 2 − ; 6
− ), B(1;0),C (3;4).
b) Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành, đường thẳng x = 1; − x = 2 bằng 21 4 .
c) Diện tích hình phẳng giới hạn bởi đồ thị (C) và đường thẳng d bằng 253 . 12
d) Biết đường thẳng d cắt đồ thị (C) thành hai miền S và S . Tỉ số S1 63 = . 1 2 S 16 2 Lời giải a) Đúng
Ta có phương trình hoành độ giao điểm: 3 2 3 2
x − 2x − 3x + 4 = 2x − 2 ⇔ x − 2x − 5x + 6 = 0 x = 2 − x = 2 − ⇒ y = 6 − ⇔ x = 1
. Với: x = 1 ⇒ y = 0 .Vậy đường thẳng d cắt đồ thị (C) tại ba điểm x = 3 x = 3 ⇒ y = 4 A( 2 − ; 6
− ), B(1;0),C (3;4). b) Sai 2 Diện tích cần tính là: 3 2 97
S = x − 2x − 3x + 4dx = ∫ . − 12 1 c) Đúng