Đề giữa kỳ 1 Toán 10 năm 2023 – 2024 trường THPT Nguyễn Thị Minh Khai – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Năm học: 2023 – 2024
Môn TOÁN – Khối: 10 Thời gian: 60 phút
(Không kể thời gian phát đề) Bài 1:
a) Cho hai tập hợp A  1;2;3;  4 , B  3;4; 
5 . Xác định A B, A \ B . (1đ)
b) Cho hai tập hợp A  ; 
1 , B  0;5. Xác định A B, C A . (1đ) 
Bài 2: Tìm tập xác định của các hàm số:
a) y  f x  3 x 1. (1đ)
b) y  f x 1  . (1đ) xx   1
Bài 3: Xét tính đồng biến, nghịch biến của hàm số y  f x 2
 x  2 trên khoảng ;0 bằng định nghĩa. (1đ) Bài 4: Cho A
 BC với BC  a, CA  b, AB  c . Gọi S, h R r lần lượt là diện tích, chiều cao kẻ từ a , ,
đỉnh A , bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp của A  BC .
a) Chứng minh: h  R B C . (1đ) a 2 .sin .sin b) Biết    0
b 8, c 6, BAC  60 . Tính a, S, r . (3đ)
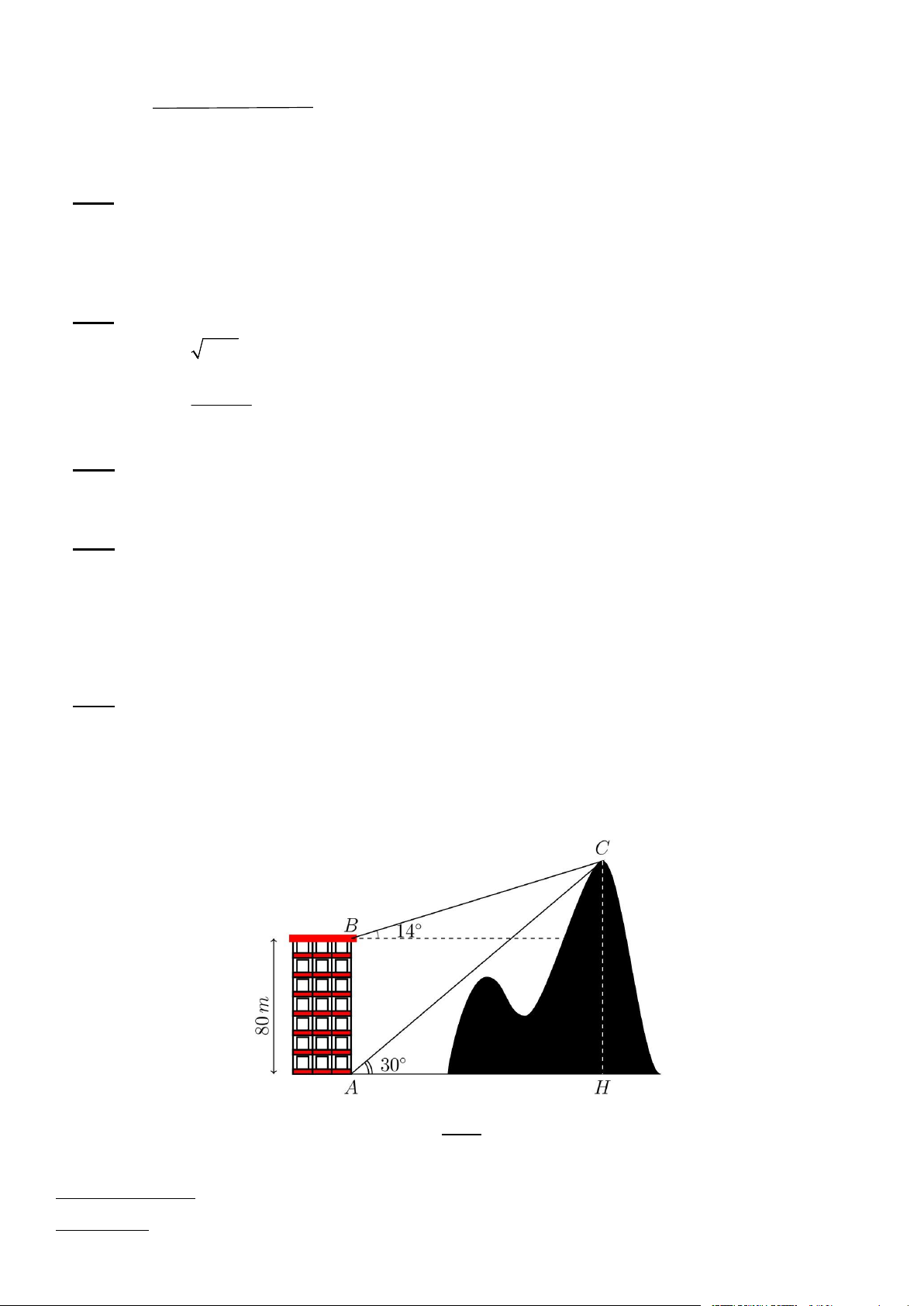
Bài 5: Từ hai vị trí ,
A B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi (hình vẽ). Biết rằng
độ cao AB bằng 80 m , phương nhìn AC tạo với phương nằm ngang góc 30 , phương nhìn BC tạo
với phương nằm ngang góc 14 . Tính chiều cao CH của ngọn núi so với mặt đất. (Làm tròn kết quả
đến 2 chữ số thập phân) (1đ) HẾT
Họ và tên học sinh: ………………………………………………………. ……………………………………………………………………………… Số báo danh:
………………………………………………………………………………………………………………………………………
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 2-TOÁN 10 Bài 1: 2đ
a) A  1;2;3;  4 , B  3;4; 
5 . Xác định A B, A \ B . 1đ
A B  3; 
4 , A \ B  1;  2 . 0.52
b) A  ; 
1 ,B  0;5. Xác định A B,C A.  1đ
A B  ;5, C A  1;  . 0.52
Bài 2: Tìm tập xác định của các hàm số sau: 2đ
a) y  f x  3 x 1 1đ
ĐKXĐ: 3 x  0  x  3 . Vậy D  ;  3 . 0.5+0.252
b) y  f x 1
 xx 1 1đ x 
ĐKXĐ: xx   0 1  0  
. Vậy D   \1;  0 . 0.5+0.252 x  1
Bài 3: Xét tính đồng biến, nghịch biến của hàm số y  f x 2
 x  2 trên khoảng ;0. 1đ x
 , x  ;0 : x  x 0.25 1 2   1 2  2 2
x  x (do x , x   ;  0 )
0.25 (không cần giải thích) 1 2   1 2  2 2
x  2  x  2  f x  f x . 0.25 2  1  2  1
Vậy hàm số f x nghịch biến trên khoảng ;0. 0.25 Cách 2: 0.254 x
 , x  ;0 : x  x 0.25 1 2   1 2
f x  f x  x  x x  x
0.25 (HS phải phân tích được thành tích) 1 
 2   1 2  1 2 
Chứng minh được f x  f x 0.25 1   2  Kết luận 0.25 Bài 4: Cho A  BC . 4đ
a) Chứng minh: h  R B C . a 2 .sin .sin 1đ 2S 2 abc bc VT  h    . Thế được: 2S h  (0.25), abc S  (0.25) a . 0.5 a a 4R 2R a a 4R
 2 sin .sin  2 . b c bc VP R B C R  . 2R 2R 2R 0.5 Thế được: sin b B  hoặc sin c C  (0.25), Kết luận (0.25) 2R 2R b) Biết    0
b 8, c 6, BAC  60 . Tính a, S, r . 3đ 2 2
a  b  c  2bc.cos A  2 13 . 1 S  b .
c sin A 12 3 . (0.5+0.5) 2 3 S 12 3 r   . p 13  7
HS ghi kết quả xấp xỉ thì GV ghi tha.
Bài 5: AB  80 m , phương nhìn AC tạo với phương nằm ngang góc 30 , phương nhìn BC
tạo với phương nằm ngang góc 14 . Tính chiều cao CH của ngọn núi so với mặt đất. (Làm 1đ
tròn kết quả đến 2 chữ số thập phân).     
        
ABC 90 14 104 , BAC 90 30
60 , ACB 180  104  60 16 . 0.25
Áp dụng định lý sin cho A  BC : AC AB AC 80 80.sin104     AC 
. (Công thức 0.25; Kết quả 0,25) 0.25x2 sin B sinC sin104 sin16 sin16 Xét 80.sin104 A
 HC :CH  AC.sin30  .sin30 140,81 m. sin16 0.25
Vậy ngọn núi cao khoảng 140,81 m .
Cách khác: Gọi K là chân đường vuông góc kẻ từ B đến CH. CK = AH.tan140 0.25
CH - CK = AH.tan300 - AH.tan140 = 80 0.25 Suy ra: AH 0.25 Suy ra: CH 0.25