Đề giữa kỳ 1 Toán 11 năm 2023 – 2024 trường chuyên Lê Khiết – Quảng Ngãi

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kỳ 1 môn Toán 11 năm học 2023 – 2024 trường THPT chuyên Lê Khiết, tỉnh Quảng Ngãi; đề thi mã đề 101, gồm 06 trang, cấu trúc 70% trắc nghiệm (35 câu) + 30% tự luận (04 câu), thời gian làm bài 90 phút.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Thông tin:

16 trang 7 tháng trước

Tác giả:

Profile Nguyễn Trang
Mã đề 101 Trang 1/6
TRƯỜ
NG THPT CHUYÊN
LÊ KHIẾT
KIỂM TRA GIỮA HỌC KỲ I - NĂM HỌC 2023-2024
Môn : Toán Lớp: 11
Thời gian làm bài: 90 phút.
Họ và tên:......................................................... Lớp: .........................................
I. PHẦN TRẮC NGHIỆM: (7 điểm - 35 câu)
Câu 1. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
cot
y x
. B.
sin
y x
. C.
tan
y x
. D.
cos
.
Câu 2. Cho dãy số
n
u
cho bởi công thức tổng quát
2 *
3 4 ,
n
u n n
. Khi đó
5
u
bằng
A.
97
. B.
503
. C.
23
. D.
103
.
Câu 3. Dãy số nào sau đây là cấp số nhân?
A.
1
1
1
.
3 , 1
n n
u
u u n
B.
1
1
1
.
1, 1
n n
u
u u n
C.
1
2
.
sin , 1
1
n
u
u n
n
D.
1
1
2
.
2 3, 1
n n
u
u u n
Câu 4. Trong các khẳng định sau, khẳng định nào đúng?
A.
sin sin cos cos sin
a b a a b b
. B.
sin sin cos cos sin
a b a b a b
.
C.
sin sin cos cos sin
a b a a b b
. D.
sin sin cos cos sin
a b a b a b
.
Câu 5. Phương trình
cos
x m
(m là tham số) vô nghiệm khi và chỉ khi
A.
1
m
. B.
1
m
. C.
1
1
m
m
. D.
1 1
m
.
Câu 6. Nghiệm của phương trình
sin 1
x
là
Mã đề 101
ĐỀ CHÍNH THỨC
(Đề gồm có 06 trang)
Mã đề 101 Trang 2/6
A.
,x k k
. B.
2 ,x k k
.
C.
2 ,
2
x k k
. D.
3
,
2
x k k
.
Câu 7. Hàm số
cot
y x
có tập xác định là
A.
\ |
2
k
D k
. B.
\ |
2
D k k
.
C.
\ 2 |D k k
. D.
\ |D k k
.
Câu 8. Cho
3
2
2
. Khẳng định nào sau đây là đúng?
A.
cot 0
. B.
tan 0
. C.
sin 0
. D.
cos 0
.
Câu 9. Thống kê về nhiệt độ tại một địa điểm trong
30
ngày, ta có bảng số liệu sau:
Nhiệt độ
0
C
18; 22
22; 25
25; 28
28; 31
31; 34
Số ngày 3 6 10 5 6
Số ngày có nhiệt độ thấp hơn
0
25
C
là
A.
10
. B.
19
. C.
9
. D.
3
.
Câu 10. Cho cấp số cộng
n
u
, biết
1
2
u
và công sai
3
d
. Khẳng định nào sau đây
đúng?
A.
2
1.
u
B.
2
5
u
. C.
2
1.
u
D.
2
5
u
.
Câu 11. Trên một đường tròn, cung có số đo 1 rad là
A. Cung có độ dài bằng đường kính của đường tròn đó.
B. Cung có độ dài bằng 1.
C. Cung tương ứng với góc ở tâm bằng
0
60
.
D. Cung có độ dài bằng bán kính của đường tròn đó.
Câu 12. Cho cấp số nhân
n
u
, biết
1 2
4, 2
u u
. Công bội của cấp số nhân là
A.
1
2
q
. B.
1
2
q
. C.
2
q
. D.
2
q
.
Câu 13. Chọn công thức đúng trong các công thức sau:
A.
1
sin .sin sin sin
2
a b a b a b
.
Mã đề 101 Trang 3/6
B.
1
sin .sin cos cos
2
a b a b a b
.
C.
1
sin .sin cos cos
2
a b a b a b
.
D.
1
sin .sin sin sin
2
a b a b a b
.
Câu 14. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Mốt. B. Tứ phân vị. C. Số trung vị. D. Số trung bình.
Câu 15. Dãy số nào sau đây là dãy tăng?
A.
1;3;5;6;9
. B.
10;8;6;4;2
. C.
1;1;1;1;1
. D.
1;5;3;7;9
.
Câu 16. Trong mẫu số liệu ghép nhóm, độ dài của nhóm
1;10
bằng bao nhiêu?
A.
8
. B.
9
. C.
10
. D.
5
.
Câu 17. Dãy số nào dưới đây không là cấp số cộng?
A.
1,1,1,1
. B.
1, 0, 1, 2
. C.
1, 2, 3, 4
. D.
1, 2, 4, 8
.
Câu 18. Phương trình lượng giác
3tan 3 0
x
có nghiệm là
A.
,
6
x k k
. B.
,
3
x k k
.
C. Vô nghiệm. D.
2 ,
6
x k k
.
Câu 19. Trong các dãy số
n
u
dưới đây, dãy số nào bị chặn dưới?
A.
2
n
u n
. B.
2
6
n
u n n
.
C.
1 2
n
u n
. D.
2
1 .
n
n
u n
.
Câu 20. Cho
0
2
. Chọn mệnh đề sai trong các mệnh đề sau:
A.
sin sin
2
. B.
tan cot
2
.
C.
sin cos
2
. D.
cos sin
2
.
Câu 21. Hỏi
1 1 3 1 5
; ; ; ;
2 2 8 4 32
là năm số hạng đầu của dãy số nào sau đây?
Mã đề 101 Trang 4/6
A.
n
w
với
*
2
n
n
n
w n
. B.
n
v
với
*
2
n
n
v n
n
.
C.
n
u
với
*
1
2
n
n
n
u n
. D.
n
t
với
*
1
1
n
t n N
n
.
Câu 22. Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối thu được
kết quả sau:
Thời gian
4; 5
5; 6
6; 7
7; 8
8; 9
Số học sinh
10
18
23
20
15
75%
số học sinh ngủ ít nhất bao nhiêu giờ trong một buổi tối?
A.
5,92
.
B.
7,68
.
C.
6,65
.
D.
5,64
.
Câu 23. Trên khoảng
( ; )
, đồ thị hàm số
sin
y x
được cho như hình vẽ.
Hàm số
sin
y x
nghịch biến trên khoảng nào sau đây?
A.
;0
. B.
0;
. C.
;
2
. D.
;
2 2
.
Câu 24. Cho góc
thỏa mãn
3
tan
5
. Tính
tan
4
P
.
A.
4.
P
B.
8
5
P
. C.
3
P
. D.
3
5
P
.
Câu 25. Cho
3
2
. Xác định dấu của biểu thức
sin .cot .
2
M
A.
0
M
. B.
0
M
. C.
0
M
. D.
0
M
.
Câu 26. Biết bốn số
2;8; ;128
x
theo thứ tự lập thành một cấp số nhân. Giá trị của
x
bằng
A.
64
x
. B.
24
x
. C.
32
x
. D.
16
x
.
Câu 27. Cho cấp số nhân có các số hạng lần lượt là
3;9;27;81; ...
. Tìm số hạng tổng quát
n
u
của cấp số nhân đã cho.
Mã đề 101 Trang 5/6
A.
3 3 .
n
n
u
B.
1
3 .
n
n
u
C.
1
3 .
n
n
u
D.
3 .
n
n
u
Câu 28. Tổng
n
số hạng đầu tiên của một cấp số cộng là
2
3 19
4
n
n n
S
với
*
n
. Tìm số
hạng đầu tiên
1
u
và công sai
d
của cấp số cộng đã cho.
A.
1
1
2;
2
u d
. B.
1
3
; 2
2
u d
.
C.
1
3
4;
2
u d
. D.
1
5 1
;
2 2
u d
.
Câu 29. Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x
trên đoạn
;
2 2
.
A.
2
S
. B.
6
S
. C.
3
S
. D.
5
6
S
.
Câu 30. Rút gọn
cos cos sin sin
M a b a b a b a b
.
A.
cos4
M b
. B.
sin2
M b
. C.
cos2
M b
. D.
sin4
M b
.
Câu 31. Biết
2
cos
3
và
3
2
. Giá trị
sin
bằng
A.
5
3
. B.
2
5
. C.
5
2
. D.
5
3
.
Câu 32. Tìm giá trị nhỏ nhất
m
của hàm số
2sin 2023 2024
y x
.
A.
1
m
. B.
2023 2
m
.
C.
2
m
. D.
2024 2
m
.
Câu 33. Người ta ghi lại tuổi thọ của một số con muỗi cái trong phòng thí nghiệm cho kết quả
như sau:
Tuổi thọ (ngày)
0; 20
20; 40
40; 60
60; 80
80;100
Số lượng
5
12
23
31
29
Muỗi cái có tuổi thọ khoảng bao nhiêu ngày là nhiều nhất?
A.
76
ngày. B.
90
ngày. C.
80
ngày. D.
66
ngày.
Câu 34. Cho dãy số
n
u
xác định bởi hệ thức truy hồi . Số hạng thứ bốn của
dãy số là
A.
14
. B.
28
. C.
10
. D.
8
.
1
1
4
n n
u
u u n
Mã đề 101 Trang 6/6
Câu 35. Cho cấp số cộng
n
u
có số hạng đầu
1
5
u
và công sai
3
d
. Số
94
là số hạng thứ
mấy của cấp số cộng?
A. 33. B. 20. C. 34. D. 35.
II
. PHẦN TỰ LUẬN (3 điểm- 4 câu)
Bài 1
.
(1 diểm)
Giải phương trình sau:
2sin 2 2cos 3 0
x x
.
Bài 2
.
( 1 điểm)
Cho một
cấp số cộng biết rằng tổng của số hạng thứ hai và số hạng thứ tư
bằng
6
, số hạng thứ sáu bằng
36
. Tính tổng 50 số hạng đầu của cấp số này.
Bài 3. (0,5 điểm) Với hình vuông như hình vẽ dưới đây, cách tô màu như phần gạch
sọc được gọi là cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như
hình bên, theo quy trình sau:
Bước 1: Tô màu “đẹp” cho hình vuông .
Bước 2: Tô màu “đẹp” cho hình vuông là hình vuông ở chính giữa khi chia hình
vuông thành phần bằng nhau như hình vẽ.
Bước 3: Tô màu “đẹp” cho hình vuông là hình vuông ở chính giữa khi chia hình
vuông thành phần bằng nhau…
Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu
chiếm ít nhất diện tích hình vuông .
Bài 4. (0,5 điểm) Số giờ có ánh sáng mặt trời của thành phố A trong ngày thứ
t
của năm
2023
được cho bởi hàm số
9 2cos 61
118
y t
,
*
t
. Vào ngày tháng nào trong năm
2023
thì thành phố A có số giờ có ánh sáng mặt trời nhiều nhất?
1 1 1 1
A B C D
1 1 1 1
A B C D
2 2 2 2
A B C D
1 1 1 1
A B C D
9
3 3 3 3
A B C D
2 2 2 2
A B C D
9
49,99%
1 1 1 1
A B C D
6
BẢNG ĐÁP ÁN
1.D 2.D 3.A 4.B 5.C 6.C 7.D 8.D 9.C 10.C
11.D 12.B 13.B 14.A 15.A 16.B 17.D 18.A 19.A 20.A
21.A 22.D 23.C 24.A 25.D 26.C 27.D 28.C 29.B 30.C
31.A 32.C 33.A 34.C 35.C
PHẦN 1: TRẮC NGHIỆM
Câu 1: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
cot .
y x
B.
sin .
y x
C.
tan .
y x
D.
cos .
y x
Lời giải
Chọn D
Hàm số chẵn là
cos .
y x
Câu 2: Cho dãy số
n
u
cho bởi công thức tổng quát
2 *
3 4 ,
n
u n n
. Khi đó
5
u
bằng
A.
97.
B.
503.
C.
23.
D.
103.
Lời giải
Chọn D
Ta có:
2
5
3 4 5 103.
u
Câu 3: Dãy số nào sau đây là cấp số nhân?
A.
1
1
1
.
3 , 1
n n
u
u u n
B.
1
1
1
.
1, 1
n n
u
u u n
C.
1
2
.
sin , 1
1
n
u
u n
n
D.
1
1
2
.
2 3, 1
n n
u
u u n
Lời giải
Chọn A
Đáp án A có:
1
1
3 3
n
n n
n
u
u u
u
không đổi, suy ra dãy số ở đáp án A là một cấp số nhân.
Câu 4: Trong các khẳng định sau, khẳng định nào đúng?
A.
sin sin cos cos sin .
a b a a b b
B.
sin sin cos cos sin .
a b a b a b
C.
sin sin cos cos sin .
a b a a b b
D.
sin sin cos cos sin .
a b a b a b
Lời giải
Chọn B
Theo công thức cộng, ta có:
sin sin cos cos sin .
a b a b a b
Câu 5: Phương trình
cos
x m
(
m
là tham số) vô nghiệm khi và chỉ khi
A.
1.
m
B.
1.
m
C.
1
.
1
m
m
D.
1 1.
m
Lời giải
7
Chọn C
Phương trình
sin
x m
có nghiệm
1 1
m
.
Do đó, phương trình
sin
x m
vô nghiệm
1
.
1
m
m
Câu 6: Nghiệm của phương trình
sin 1
x
là
A.
,x k k
B.
2 ,x k k
C.
2 ,
2
x k k
D.
3
,
2
x k k
Lời giải
Chọn C
Vì
sin 1 2 ,
2
x x k k
.
Câu 7: Hàm số
cot
y x
có tập xác định là
A.
\ |
2
k
D k
B.
\ | .
2
D k k
C.
\ 2 |D k k
D.
\ |D k k
Lời giải
Chọn D
Điều kiện xác định:
cos 0 , .
x x k k
Tập xác định của hàm số là
\ |D k k
Câu 8: Cho
3
2
2
. Khẳng định nào sau đây là đúng?
A.
cot 0.
B.
tan 0.
C.
sin 0.
D.
cos 0.
Lời giải
Chọn D
Câu 9: Thống kê về nhiệt độ tại một địa điểm trong 30 ngày, ta có bảng số liệu sau:
Số ngày có nhiệt độ thấp hơn
o
25
C
là
A.
10
B.
19
C.
9
D.
3
Lời giải
Chọn C
Câu 10: Cho cấp số cộng
n
u
, biết
1
2
u
và công sai
3
d
. Khẳng định nào sau đây đúng?
A.
2
1
u
B.
2
5
u
C.
2
1
u
D.
2
5
u
Lời giải
Chọn C
Ta có
2 1
2 3 1
u u d
.
Câu 11: Trên một đường tròn, cung có số đo 1 rad là
8
A. Cung có độ dài bằng đường kính của đường tròn đó.
B. Cung có độ dài bằng 1.
C. Cung tương ứng với góc ở tâm bằng
0
60
.
D. Cung có độ dài bằng bán kính của đường tròn đó.
Lời giải
Chọn D
Câu 12: Cho cấp số nhân
n
u
, biết
1 2
4, 2
u u
. Công bội của cấp số nhân là
A.
1
2
q
B.
1
2
q
C.
2
q
D.
2
q
Lời giải
Chọn B
2
1
2 1
.
4 2
u
q
u
Câu 13: Chọn công thức đúng trong các công thức sau:
A.
1
sin .sin sin sin
2
a b a b a b
B.
1
sin .sin cos cos
2
a b a b a b
C.
1
sin .sin cos cos
2
a b a b a b
D.
1
sin .sin sin sin
2
a b a b a b
Lời giải
Chọn B
Câu 14: Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Mốt B. Tứ phân vị C. Số trung vị D. Số trung bình
Lời giải
Chọn A
Câu 15: Dãy số nào sau đây là dãy tăng?
A.
1;3;5;6;9
B.
10;8;6;4;2
C.
1;1;1;1;1
D.
1;5;3;7;9
Lời giải
Chọn A
Câu 16: Trong mẫu số liệu ghép nhóm, độ dài của nhóm
1;10
bằng bao nhiêu?
A.
8
. B.
9
. C.
10
. D.
5
.
Lời giải
Chọn B
Độ dài của nhóm bằng
10 1 9
.
Câu 17: Dãy số nào dưới đây không là cấp số cộng?
A.
1,1,1,1
. B.
1, 0, 1, 2
. C.
1, 2, 3, 4
. D.
1, 2, 4, 8
.
9
Lời giải
Chọn D
1, 2, 4, 8
không là cấp số cộng vì
2 1 4 2
.
Câu 18: Phương trình lượng giác
3tan 3 0
x
có nghiệm là
A.
,
6
x k k
. B.
,
3
x k k
.
C. Vô nghiệm. D.
2 ,
6
x k k
.
Lời giải
Chọn A
3tan 3 0
3
tan
3
tan tan
6
6
,
x
x
x
x k k
Câu 19: Trong các dãy số
n
u
dưới đây, dãy số nào bị chặn dưới?
A.
2
n
u n
. B.
2
6
n
u n n
. C.
1 2
n
u n
. D.
2
1 .
n
n
u n
.
Lời giải
Chọn A
2 1
n
u n
,
n
nên
n
u
bị chặn dưới.
Câu 20: Cho
0
2
. Chọn mệnh đề sai trong các mệnh đề sau:
A.
sin sin
2
. B.
tan cot
2
.
C.
sin cos
2
. D.
cos sin
2
.
Lời giải
Chọn A
Câu A sai vì
sin cos
2
.
Câu 21: Hỏi
1 1 3 1 5
; ; ; ;
2 2 8 4 32
là năm số hạng đầu trong dãy số nào sau đây?
A.
n
w
với
*
2
n
n
n
w n
. B.
n
v
với
*
2
n
n
v n
n
.
C.
n
u
với
1
*
2
n
n
n
u n
. D.
n
t
với
1
*
1
n
t n
n
.
Lời giải
Chọn A
10
Với dãy số
n
w
ta có
1 2 3 4 5
2 3 4 5
1 2 1 3 3 4 1 5 5
; ; ; ; .
2 2 2 2 8 2 4 2 32
w w w w w
Câu 22: Phỏng vấn một số học sinh khối 11 về thời gian ngủ (giờ) của một buổi tối thu được kết quả sau
75%
số học sinh ngủ ít nhất bao nhiêu giờ trong một buổi tối?
A.
5,92
. B.
7,68
. C.
6,65
. D.
5,64
.
Lời giải
Chọn D
Tứ phân vị thứ nhất của mẫu số liệu trên là
1
5,64Q nên
75%
số học sinh ngủ ít nhất 5,64
giờ trong một buổi tối.
Câu 23: Trên khoảng
;
, đồ thị hàm số
siny x
được cho như hình vẽ.
Hàm số
siny x
nghịch biến trong khoảng nào sau đây?
A.
;0
. B.
0;
. C.
;
2
. D.
;
2 2
.
Lời giải
Chọn C
Dựa vào đồ thị suy ra hàm số
siny x
nghịch biến trên các khoảng
;
2
và
;
2
Câu 24: Cho góc
thỏa mãn
3
tan
5
. Tính
tan
4
P
.
A.
4P
. B.
8
5
P
. C.
3P
. D.
3
5
P
.
Lời giải
Chọn A
Có
3
1
tan tan
tan 1
5
4
tan 4
3
4 1 tan
1 tan .tan 1
4 5
.
Câu 25: Cho
3
2
. Xác định dấu của biểu thức
sin .cot .
2
M
A.
0M
. B.
0M
. C.
0M
. D.
0M
.
11
Lời giải
Chọn D
Có
2
cos
sin .cot cos .cot
2 sin
M
.
Với
3
2
thì
2
cos 0
sin 0
nên
0
M
.
Câu 26: Biết bốn số
2;8; ;128
x
theo thứ tự lập thành một cấp số nhân. Giá trị của
x
bằng
A.
64
x
. B.
24
x
. C.
32
x
. D.
16
x
.
Lời giải
Chọn C
Ta có
2;8; ;128
x
lập thành 1 cấp số nhân nên
2
8 2. 32
x x
Kiểm tra lại ta thấy
2
32 8.128
( thỏa mãn ).
Câu 27: Cho cấp số nhân có các số hạng lần lượt là
3;9;27;81;
. Tìm số hạng tổng quát
n
u
của cấp số
nhân đã cho.
A.
3 3
n
n
u
. B.
1
3
n
n
u
. C.
1
3
n
n
u
. D.
3
n
n
u
.
Lời giải
Chọn D
Ta có
1
3
u
2 1 1
9 3 .
u u u d
3
d
.
Do đó
1 1
1
. 3.3 3
n n n
n
u u d
.
Câu 28: Tổng
n
số hạng đầu tiên của một cấp số cộng là
2
3 19
4
n
n n
S
với
*
n
. Tìm số hạng đầu
tiên
1
u
và công sai
d
của cấp số cộng đã cho.
A.
1
1
2;
2
u d
. C.
1
3
4;
2
u d
. B.
1
3
; 2
2
u d
. D.
1
5 1
;
2 2
u d
.
Lời giải
Chọn C
Ta có công thức tổng
n
số hạng đầu tiên của một cấp số cộng
1 1
2 1
2 2
n n
n n
S u u u n d
Từ giả thiết
2
1
3 19
2 1
2 4
n n n
u n d
1
3 19
2
2 2
n
u d nd
với mọi
*
n
1
19
2
2
3
2
u d
d
1
3
2
4
d
u
.
Câu 29: Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x
trên đoạn
;
2 2
.
A.
2
S
. B.
6
S
. C.
3
S
. D.
5
6
S
.
12
Lời giải
Chọn B
Ta có
1
sin sin
2 6
x x sin
2
6
5
2
6
x k
x l
( với
;
k l Z
)
+Xét bất phương trình
2
2 6 2
k
1 1 1 1 1
2
2 6 2 3 6
k k
Do
0
6
k Z k x
+
5
2
2 6 2
l
1 5 1 2 1
2
2 6 2 3 6
l l
Do
l Z
nên không có giá trị
l
nguyên để
5
2
2 6 2
l
Vậy
6
x
là nghiệm duy nhất của phương trình thuộc
;
2 2
Vậy
6
S
.
Câu 30: Rút gọn
cos( ) cos( ) sin( )sin( )
M a b a b a b a b
.
A.
cos4
M b
. B.
sin2
M b
. C.
cos2
M b
. D.
sin4
M b
.
Lời giải
Chọn C
Ta có:
cos( )cos( ) sin( )sin( )
M a b a b a b a b
2
cos a b a b cos b
.
Câu 31: Biết
2
cos
3
và
3
2
. Giá trị
sin
bằng
A.
5
3
. B.
5
2
. C.
5
2
. D.
5
3
.
Lời giải
Chọn A
Vì
3
2
sin 0
Suy ra
2
2
2 5
sin 1 cos 1
3 3
Câu 32: Tìm giá trị nhỏ nhất
m
của hàm số
2 sin 2023 2024
y x .
A.
1
m
. B.
2023 2
m
. C.
2
m
. D.
2024 2
m
.
Lời giải
Chọn C
Ta có
, 1 sin 1
x x
Suy ra
1 sin 2023 2024 1
x
13
2 2 sin 2023 2024 2
x
Vậy giá trị nhỏ nhất
m
của hàm số
2sin 2023 2024
y x
là
2
m
.
Câu 33: Người ta ghi lại tuổi thọ của một số con muỗi cái trong phòng thí nghiệm cho kết quả như sau:
Muỗi cái có tuổi thọ khoảng bao nhiêu ngày là nhiều nhất?
A.
76
ngày. B.
90
ngày. C.
80
ngày. D.
66
ngày.
Lời giải
Chọn A
Số ngày muỗi cái có tuổi thọ nhiều nhất là mốt của mẫu số liệu.
Nhóm có tần số nhiều nhất là nhóm 4. Vì vậy nhóm chứa mốt là nhóm 4:
60;80
.
Ta có
4 4 3 5
4, 60, 31, 23, 29, 20
j a m m m h
.
Do đó
31 23
60 .20 76
31 23 31 29
o
M
.
Vậy Muỗi cái có tuổi thọ khoảng
76
ngày là nhiều nhất.
Câu 34: Cho dãy số
n
u
xác định bởi hệ thức truy hồi
1
1
4
n n
u
u u n
. Số hạng thứ bốn của dãy số là
A.
14
. B.
28
. C.
10
. D.
8
.
Lời giải
Chọn C
Ta có
1
1
4
n n
u
u u n
Suy ra
2 1
1 4 1 5
u u
.
3 2
2 5 2 7
u u
.
4 3
3 7 3 10
u u
.
Vậy Số hạng thứ bốn của dãy số là
4
10
u
.
Câu 35: Cho cấp số cộng
n
u
có số hạng đầu
1
5
u
và công sai
3
d
. Số
94
là số hạng thứ mấy của
cấp số cộng?
A.
33
. B.
20
. C.
34
. D.
35
.
Lời giải
Chọn C
Áp dụng công thức
1
1 .
n
u u n d
Suy ra
94 5 1 .3
n
3 102
n
34
n
.
Vậy số
94
là số hạng thứ
34
của cấp số cộng
n
u
.
PHẦN 2:TỰ LUẬN
Câu 36: Giải phương trình sau:
2sin 2 2cos 3 0
x x
.
Lời giải
14
Ta có
sin 1
2sin 2 2cos 3 0
3
cos .
2
x
x x
x
.
sin 1 2 ,
2
x x k k
.
3
cos cos cos 2 ,
2 6 6
x x x k k
.
Vậy phương trình có nghiệm
2 ; 2
6 2
S k k
.
Câu 37: Cho một cấp số cộng biết rằng tổng của số hạng thứ hai và số hạng thứ tư bằng
6
, số hạng thứ
sáu bằng
36
. Tính tổng
50
số hạng đầu của cấp số này.
Lời giải
Từ giả thiết ta có:
2 4 1 1 1
1
6 1 1
6 3 6 2 4 6
19
36
5 36 5 36
11.
u u u d u d u d
u
u
u d u d
d
Tổng
50
số hạng đầu của cấp số này là
1
50
2 1 50 2. 19 49.11
12525
2 2
n
n u n d
S S
Câu 38: Với hình vuông
1 1 1 1
A B C D
như hình vẽ dưới đây, cách tô màu như phần gạch sọc được gọi là
cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo
quy trình sau:
Bước 1: Tô màu “đẹp” cho hình vuông
1 1 1 1
A B C D
.
Bước 2: Tô màu “đẹp” cho hình vuông
2 2 2 2
A B C D
là hình vuông ở chính giữa khi chia hình
vuông
1 1 1 1
A B C D
thành phần bằng nhau như hình vẽ.
Bước 3: Tô màu “đẹp” cho hình vuông
3 3 3 3
A B C D
là hình vuông ở chính giữa khi chia hình
vuông
2 2 2 2
A B C D
thành phần bằng nhau…
Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu chiếm ít
nhất
49,99%
diện tích hình vuông
1 1 1 1
A B C D
.
Lời giải
9
9
15
Từ đề bài ta thấy được tỉ lệ diện tích giữa đa giác được tô màu so với hình vuông tương ứng là
4
9
và tỉ lệ diện tích giữa các hình vuông là
1
9
. Kí hiệu
n
u
là diện tích phần đa giác tô màu thứ
n
, khi đó
1 1 1 1
1
4 4 1
1
9 9 9
4 4
9
9 9
n n n n n n n n
n n n n n n n n
A B C D A B C D
n
n
A B C D A B C D
S S
u
u
S S
.
Khi đó dãy số
n
u
là một cấp số cộng có
1 1 1 1
1
4
9
A B C D
u S
và
1
9
q
.
Khi đó
1 1 1 1
1 1 1 1
1
1
4 1 9 8
9
49,99% 1 49,99% 4
1
9 9 4 9
1
9
n
n
n A B C D
S S A B C D n
.
Vậy ta cần làm ít nhất cần
4
bước để tổng diện tích phần được tô màu chiếm ít nhất
49,99%
diện tích hình vuông
1 1 1 1
A B C D
.
Câu 39: Số giờ có ánh sáng mặt trời của thành phố A trong ngày thứ
t
của năm
2023
được cho bởi hàm
số
9 2cos 61
118
y t
,
*
t
. Vào ngày tháng nào trong năm
2023
thì thành phố A có
số giờ có ánh sáng mặt trời nhiều nhất?
Lời giải
Ta có
1 cos 61 1 7 9 2cos 61 11 7 11
118 118
t t y
.
Vậy giá trị lớn nhất của
11
y
.
Khi
179
cos 61 11 61 2
118 118 236
t
t t k k
Mặt khác
1 365
t
nên
89 93
118 118
k
. Suy ra
0
k
hay
179
t
Vậy số giờ có ánh sáng mặt trường nhiều nhất của thành phố A trong một ngày là ngày thứ
179
trong năm
2023
.
Ta có số ngày từ tháng
1
đến tháng
5
là
31 28 31 30 31 151
ngày nên ngày có ánh
sáng nhiều nhất trong năm là ngày
28
tháng
6
năm
2023
.
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT CHUYÊN
KIỂM TRA GIỮA HỌC KỲ I - NĂM HỌC 2023-2024 LÊ KHIẾT Môn : Toán Lớp: 11
Thời gian làm bài: 90 phút. ĐỀ CHÍNH THỨC Mã đề 101
(Đề gồm có 06 trang)
Họ và tên:......................................................... Lớp: .........................................
I. PHẦN TRẮC NGHIỆM: (7 điểm - 35 câu)
Câu 1. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y  cot x .
B. y  sin x .
C. y  tan x .
D. y  cos x .
Câu 2. Cho dãy số u cho bởi công thức tổng quát 2 *
u  3  4n , n   . Khi đó u bằng n n 5 A. 97  . B. 503. C. 23. D. 103.
Câu 3. Dãy số nào sau đây là cấp số nhân? u   1   u  1 1  1 A.  . B.  . u   3  u , n 1  u
u 1, n 1 n 1  n  n 1  n  u    1   2  u   2   1 C.  .  .   D. u
 2u 3, n 1 u   sin   , n 1  n 1  n n  n1 
Câu 4. Trong các khẳng định sau, khẳng định nào đúng?
A. sin a b  sin a cos a  cosbsin b .
B. sin a b  sin a cosb  cos asin b .
C. sin a b  sin a cos a  cosbsin b .
D. sin a b  sin a cosb  cos asin b .
Câu 5. Phương trình cos x m (m là tham số) vô nghiệm khi và chỉ khi m  1 
A. m  1. B. m  1  . C.  . D. 1   m  1. m  1 
Câu 6. Nghiệm của phương trình sin x  1  là Mã đề 101 Trang 1/6
A. x    k , k   .
B. x    k 2 , k   .  3 C. x  
k 2 , k   . D. x
k , k   . 2 2
Câu 7. Hàm số y  cot x có tập xác định là  k   
A. D   \  | k  .
B. D   \   k | k  .  2   2 
C. D   \ k 2 | k    .
D. D   \ k | k    . 3 Câu 8. Cho
   2 . Khẳng định nào sau đây là đúng? 2
A. cot  0 .
B. tan  0 .
C. sin  0 . D. cos  0 .
Câu 9. Thống kê về nhiệt độ tại một địa điểm trong 30 ngày, ta có bảng số liệu sau:
Nhiệt độ  0C 18; 22 22; 25 25; 28 28; 3  1 31; 34 Số ngày 3 6 10 5 6
Số ngày có nhiệt độ thấp hơn 0 25 C là A. 10 . B. 19 . C. 9 . D. 3.
Câu 10. Cho cấp số cộng u , biết u  2 và công sai d  3 . Khẳng định nào sau đây n  1 đúng?
A. u  1. B. u  5  . C. u  1  . D. u  5. 2 2 2 2
Câu 11. Trên một đường tròn, cung có số đo 1 rad là
A. Cung có độ dài bằng đường kính của đường tròn đó.
B. Cung có độ dài bằng 1.
C. Cung tương ứng với góc ở tâm bằng 0 60 .
D. Cung có độ dài bằng bán kính của đường tròn đó.
Câu 12. Cho cấp số nhân u , biết u  4  ,u  2
 . Công bội của cấp số nhân là n  1 2 1 1 A. q   . B. q  .
C. q  2 . D. q  2 . 2 2
Câu 13. Chọn công thức đúng trong các công thức sau: 1 A. sin .
a sin b   sin a b  sin a b 2   . Mã đề 101 Trang 2/6 1 B. sin .
a sin b   cos a b  cosa b 2   . 1 C. sin . a sin b
cosa b  cosa b 2   . 1 D. sin . a sin b
sin a b  sin a b 2   .
Câu 14. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. Mốt.
B. Tứ phân vị.
C. Số trung vị. D. Số trung bình.
Câu 15. Dãy số nào sau đây là dãy tăng? A. 1;3;5;6;9 . B. 10;8;6;4;2. C. 1;1;1;1;1. D. 1;5;3;7;9.
Câu 16. Trong mẫu số liệu ghép nhóm, độ dài của nhóm 1;10 bằng bao nhiêu? A. 8. B. 9 . C. 10 . D. 5 .
Câu 17. Dãy số nào dưới đây không là cấp số cộng? A. 1, 1, 1, 1.
B. 1, 0, 1,  2 . C. 1, 2, 3, 4. D. 1, 2, 4, 8.
Câu 18. Phương trình lượng giác 3 tan x  3  0 có nghiệm là   A. x
k , k   . B. x
k , k   . 6 3 
C. Vô nghiệm. D. x
k 2 , k   . 6
Câu 19. Trong các dãy số u dưới đây, dãy số nào bị chặn dưới? n
A. u n  2 . B. 2
u  n  6n . n n n
C. u  1 2n . D. u   n . n   2 1 . n
Câu 20. Cho 0   
. Chọn mệnh đề sai trong các mệnh đề sau: 2       A. sin    sin   . B. tan    cot   .  2   2        C. sin   cos   . D. cos    sin   .  2   2  1 1 3 1 5 Câu 21. Hỏi ; ; ; ;
là năm số hạng đầu của dãy số nào sau đây? 2 2 8 4 32 Mã đề 101 Trang 3/6 n n
A. w với w  n   .
B. v với v  n   . n  *  n n n  *  n  2 n  2 n 1 1
C. u với u n    .
D. t với t n   N . n  *  n n n  *  n  2 n 1
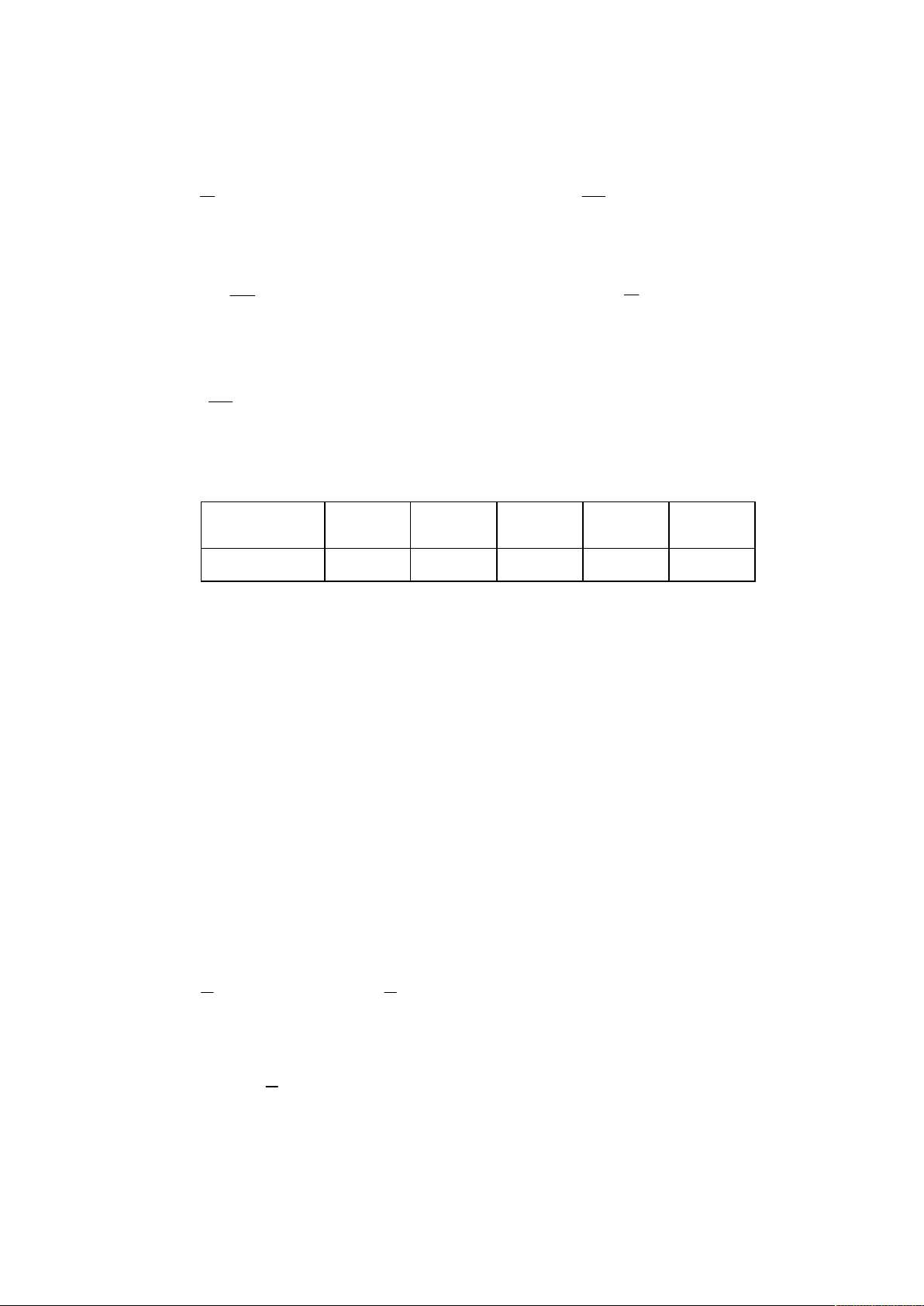
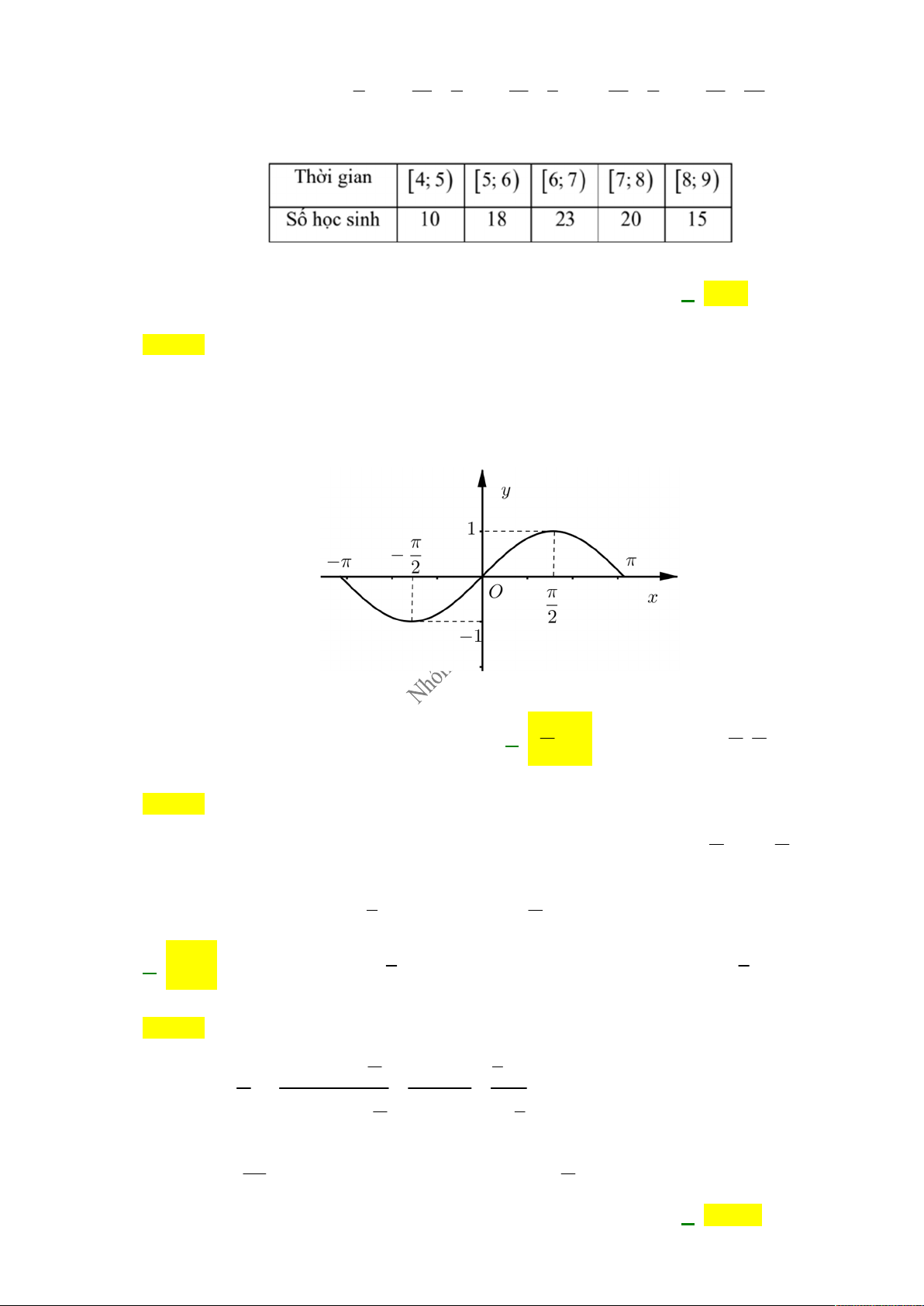
Câu 22. Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối thu được kết quả sau: Thời gian
4; 5 5; 6 6; 7 7; 8 8; 9 Số học sinh 10 18 23 20 15
75% số học sinh ngủ ít nhất bao nhiêu giờ trong một buổi tối? A. 5,92 . B. 7,68. C. 6,65 . D. 5,64 .
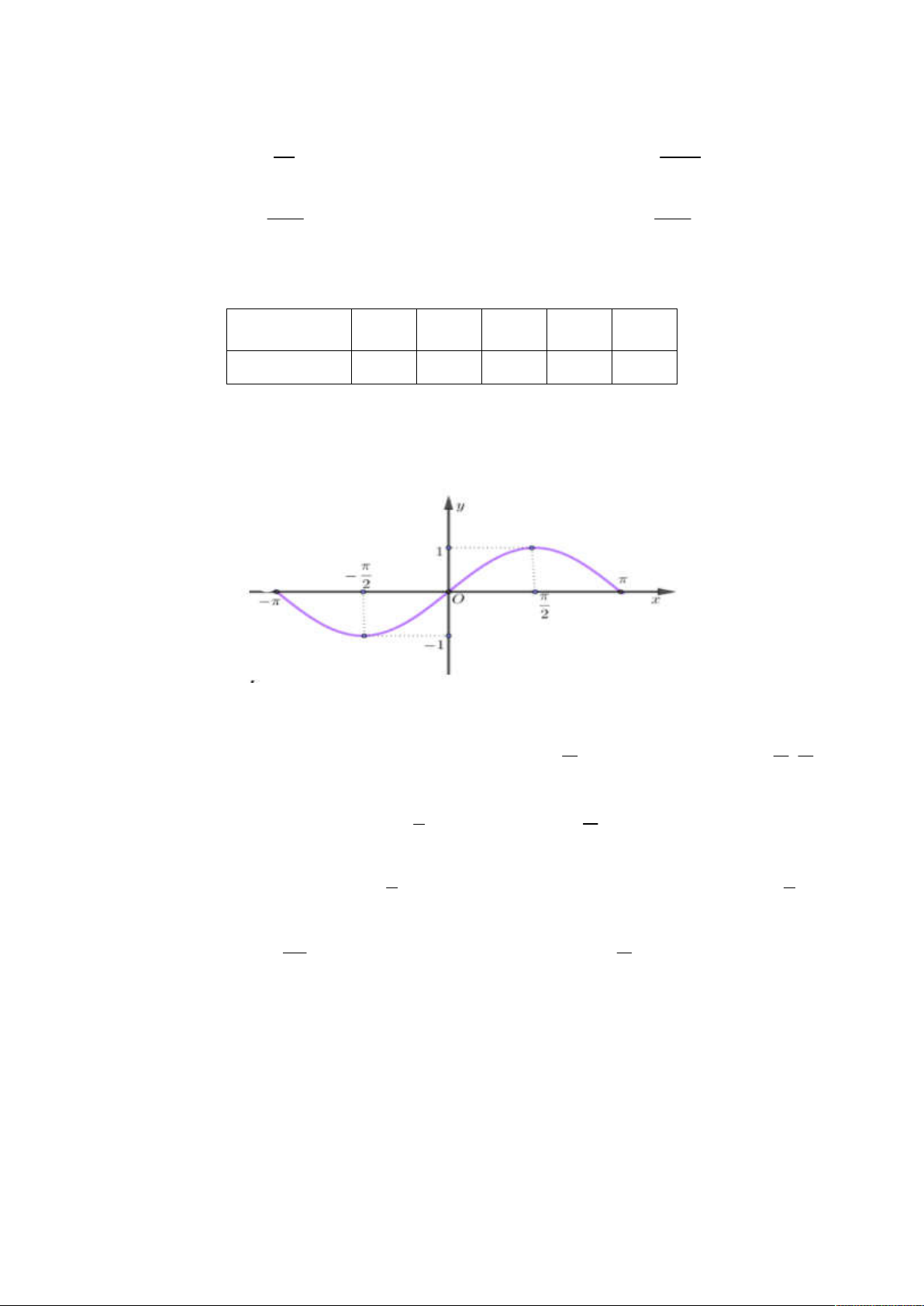
Câu 23. Trên khoảng ( 
 ; ) , đồ thị hàm số y  sin x được cho như hình vẽ.
Hàm số y  sin x nghịch biến trên khoảng nào sau đây?        A.    ;0 .
B. 0;  . C. ;   . D.  ;   .  2   2 2  3   
Câu 24. Cho góc  thỏa mãn tan 
. Tính P  tan     . 5  4  8 3
A. P  4. B. P  .
C. P  3. D. P  . 5 5 3   
Câu 25. Cho    
. Xác định dấu của biểu thức M  sin  .cot     . 2  2 
A. M  0 .
B. M  0 .
C. M  0 . D. M  0 .
Câu 26. Biết bốn số 2;8; ;
x 128 theo thứ tự lập thành một cấp số nhân. Giá trị của x bằng
A. x  64 .
B. x  24 .
C. x  32 . D. x  16 .
Câu 27. Cho cấp số nhân có các số hạng lần lượt là 3;9; 27;81; ... . Tìm số hạng tổng quát u n
của cấp số nhân đã cho. Mã đề 101 Trang 4/6  
A. u  3  3 . n B. n 1 u  3 . C. n 1 u  3 . D. u  3 . n n n n n 2 3n 19n
Câu 28. Tổng n số hạng đầu tiên của một cấp số cộng là S  với * n   . Tìm số n 4
hạng đầu tiên u và công sai d của cấp số cộng đã cho. 1 1 3
A. u  2; d   .
B. u   ; d  2 . 1 2 1 2 3 5 1
C. u  4; d  . D. u  ; d  . 1 2 1 2 2 1    
Câu 29. Tính tổng S của các nghiệm của phương trình sin x  trên đoạn  ; . 2  2 2       5 A. S  . B. S  . C. S  . D. S  . 2 6 3 6
Câu 30. Rút gọn M  cosa bcosa b  sin a bsin a b .
A. M  cos 4b .
B. M  sin 2b .
C. M  cos 2b .
D. M  sin 4b . 2 3
Câu 31. Biết cos   và     . Giá trị sin  bằng 3 2 5 5 5 5 A.  . B.  . C. . D. . 3 2 2 3
Câu 32. Tìm giá trị nhỏ nhất m của hàm số y   2 sin2023x  202  4 .
A. m  1. B. m  2  023 2 .
C. m   2 . D. m  2  024 2 .
Câu 33. Người ta ghi lại tuổi thọ của một số con muỗi cái trong phòng thí nghiệm cho kết quả như sau:
Tuổi thọ (ngày) 0; 20 20; 40 40; 60 60; 80 80; 100 Số lượng 5 12 23 31 29
Muỗi cái có tuổi thọ khoảng bao nhiêu ngày là nhiều nhất? A. 76 ngày. B. 90 ngày. C. 80 ngày. D. 66 ngày. u   4
Câu 34. Cho dãy số u xác định bởi hệ thức truy hồi 1 
. Số hạng thứ bốn của n uu nn 1  n dãy số là A. 14 . B. 28. C. 10 . D. 8. Mã đề 101 Trang 5/6
Câu 35. Cho cấp số cộng u có số hạng đầu u  5
 và công sai d  3. Số 94 là số hạng thứ n  1
mấy của cấp số cộng? A. 33. B. 20. C. 34. D. 35.
II. PHẦN TỰ LUẬN (3 điểm- 4 câu)
Bài 1. (1 diểm) Giải phương trình sau: 2sin x  22cos x  3  0 .
Bài 2. ( 1 điểm) Cho một cấp số cộng biết rằng tổng của số hạng thứ hai và số hạng thứ tư
bằng 6 , số hạng thứ sáu bằng 36 . Tính tổng 50 số hạng đầu của cấp số này.
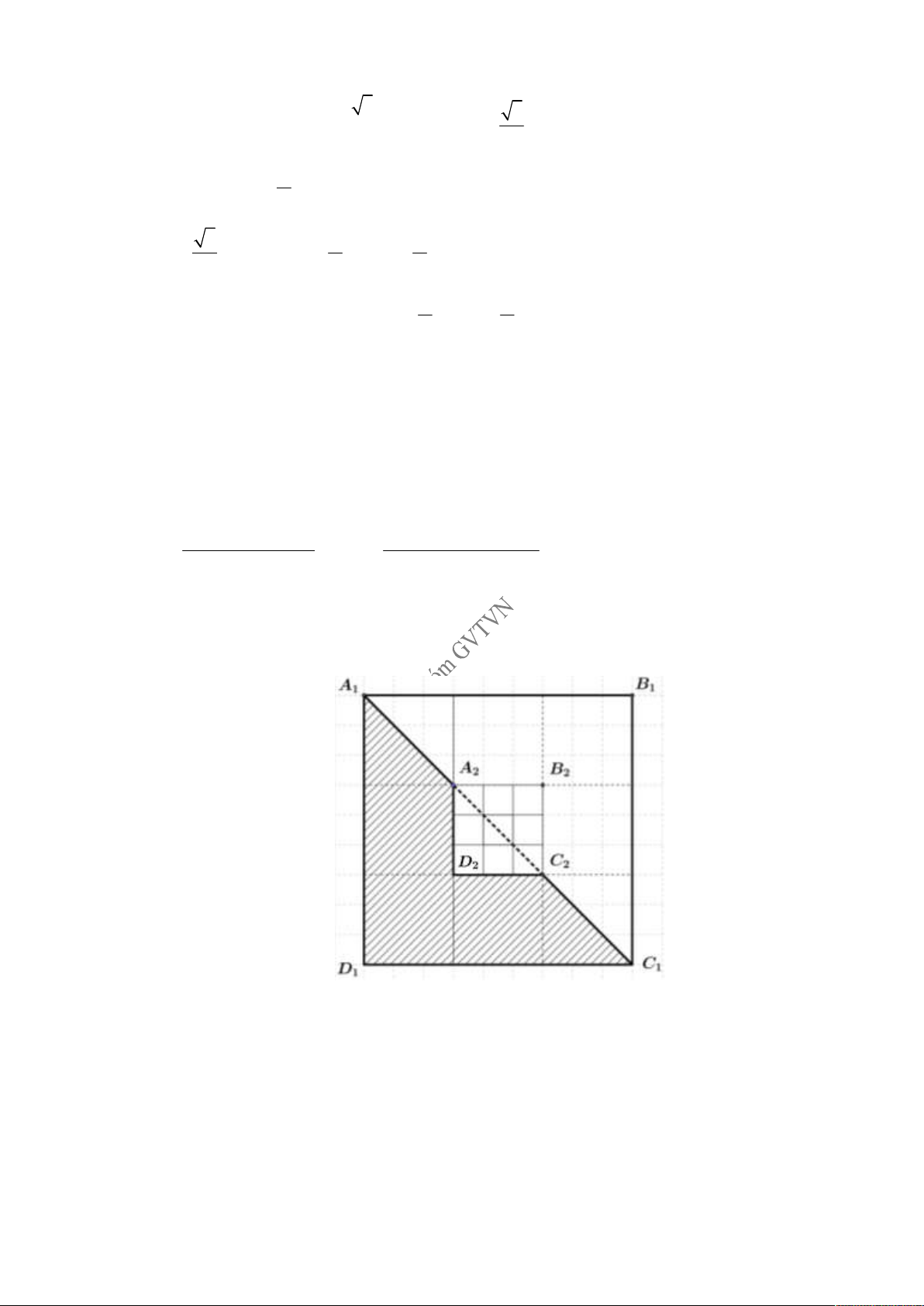
Bài 3. (0,5 điểm) Với hình vuông A B C D như hình vẽ dưới đây, cách tô màu như phần gạch 1 1 1 1
sọc được gọi là cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như
hình bên, theo quy trình sau:
Bước 1: Tô màu “đẹp” cho hình vuông A B C D . 1 1 1 1
Bước 2: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 2 2 2 2
vuông A B C D thành 9 phần bằng nhau như hình vẽ. 1 1 1 1
Bước 3: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 3 3 3 3
vuông A B C D thành 9 phần bằng nhau… 2 2 2 2
Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu
chiếm ít nhất 49, 99% diện tích hình vuông A B C D . 1 1 1 1
Bài 4. (0,5 điểm) Số giờ có ánh sáng mặt trời của thành phố A trong ngày thứ t của năm 2023 
được cho bởi hàm số y  9  2cos  t 6  1   , *
t   . Vào ngày tháng nào trong năm 2023 118   
thì thành phố A có số giờ có ánh sáng mặt trời nhiều nhất? Mã đề 101 Trang 6/6 BẢNG ĐÁP ÁN 1.D 2.D 3.A 4.B 5.C 6.C 7.D 8.D 9.C 10.C 11.D 12.B 13.B 14.A 15.A 16.B 17.D 18.A 19.A 20.A 21.A 22.D 23.C 24.A 25.D 26.C 27.D 28.C 29.B 30.C 31.A 32.C 33.A 34.C 35.C
PHẦN 1: TRẮC NGHIỆM Câu 1:
Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y  cot . x B. y  sin . x C. y  tan . x D. y  cos . x Lời giải Chọn D
Hàm số chẵn là y  cos . x Câu 2:
Cho dãy số u cho bởi công thức tổng quát 2 *
u  3  4n , n   . Khi đó u bằng n n 5 A. 97.  B. 503. C. 23. D. 103. Lời giải Chọn D Ta có: 2
u  3  4 5  103. 5 Câu 3:
Dãy số nào sau đây là cấp số nhân? u   1   u  1 1  1 A.  . B.  . u   3  u , n 1  u
u 1, n 1 n 1  n  n 1  n  u    1   2  u   2   1 C.  .  .   D. u
 2u 3, n 1 u   sin   , n 1  n 1  n n  n1  Lời giải Chọn A u Đáp án A có: n 1 u  3u  
 3 không đổi, suy ra dãy số ở đáp án A là một cấp số nhân. n 1  n un Câu 4:
Trong các khẳng định sau, khẳng định nào đúng?
A. sin a b  sin a cos a  cosbsin . b
B. sin a b  sin a cosb  cos a sin . b
C. sin a b  sin a cos a  cosbsin . b
D. sin a b  sin a cosb  cos a sin . b Lời giải Chọn B
Theo công thức cộng, ta có: sin a b  sin a cosb  cos a sin . b Câu 5:
Phương trình cos x m ( m là tham số) vô nghiệm khi và chỉ khi m  1 A. m  1. B. m  1  . C. .  D. 1   m  1. m  1  Lời giải 6 Chọn C
Phương trình sin x m có nghiệm  1   m  1. m  1
Do đó, phương trình sin x m vô nghiệm  .  m  1  Câu 6:
Nghiệm của phương trình sin x  1  là
A. x    k , k    B. x    k 2 , k     3 C. x  
k2 , k    D. x
k , k    2 2 Lời giải Chọn C  Vì sin x  1   x  
k2 , k   . 2 Câu 7:
Hàm số y  cot x có tập xác định là k   
A. D   \ 
| k   
B. D   \   k | k  .  2   2 
C. D   \ k2 | k    
D. D   \ k | k     Lời giải Chọn D
Điều kiện xác định: cos x  0  x k , k  . 
Tập xác định của hàm số là D   \ k | k     3 Câu 8: Cho
   2 . Khẳng định nào sau đây là đúng? 2
A. cot  0.
B. tan  0.
C. sin  0.
D. cos   0. Lời giải Chọn D Câu 9:
Thống kê về nhiệt độ tại một địa điểm trong 30 ngày, ta có bảng số liệu sau:
Số ngày có nhiệt độ thấp hơn o 25 C là A. 10  B. 19  C. 9  D. 3  Lời giải Chọn C
Câu 10: Cho cấp số cộng u , biết u  2 và công sai d  3
 . Khẳng định nào sau đây đúng? n  1
A. u  1
B. u  5 
C. u  1
D. u  5  2 2 2 2 Lời giải Chọn C
Ta có u u d  2  3  1  . 2 1
Câu 11: Trên một đường tròn, cung có số đo 1 rad là 7
A. Cung có độ dài bằng đường kính của đường tròn đó.
B. Cung có độ dài bằng 1.
C. Cung tương ứng với góc ở tâm bằng 0 60 .
D. Cung có độ dài bằng bán kính của đường tròn đó. Lời giải Chọn D
Câu 12: Cho cấp số nhân u , biết u  4  ,u  2
 . Công bội của cấp số nhân là n  1 2 1 1 A. q   B. q C. q  2 D. q  2 2 2 Lời giải Chọn B u 2  1 2 q    . u 4  2 1
Câu 13: Chọn công thức đúng trong các công thức sau: 1 A. sin . a sin b   s
 in a b  sin a b 2   1 B. sin .
a sin b   cosa b  cosa b 2   1 C. sin . a sin b
cosa b  cosa b 2   1 D. sin . a sin b
sin a b  sin a b 2   Lời giải Chọn B
Câu 14: Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. Mốt B. Tứ phân vị C. Số trung vị D. Số trung bình Lời giải Chọn A
Câu 15: Dãy số nào sau đây là dãy tăng? A. 1;3;5;6;9 B. 10;8;6;4;2 C. 1;1;1;1;1 D. 1;5;3;7;9 Lời giải Chọn A
Câu 16: Trong mẫu số liệu ghép nhóm, độ dài của nhóm 1;10 bằng bao nhiêu? A. 8 . B. 9 . C. 10 . D. 5 . Lời giải Chọn B
Độ dài của nhóm bằng 10 1  9 .
Câu 17: Dãy số nào dưới đây không là cấp số cộng? A. 1, 1, 1, 1.
B. 1, 0, 1,  2 . C. 1, 2, 3, 4 . D. 1, 2, 4, 8 . 8 Lời giải Chọn D
1, 2, 4, 8 không là cấp số cộng vì 2 1  4  2 .
Câu 18: Phương trình lượng giác 3 tan x  3  0 có nghiệm là   A. x
k , k   . B. x
k , k   . 6 3 
C. Vô nghiệm. D. x
k 2 , k   . 6 Lời giải Chọn A 3 tan x  3  0 3  tan x  3   tan x  tan 6   x
k , k   6
Câu 19: Trong các dãy số u dưới đây, dãy số nào bị chặn dưới? n n
A. u n  2 . B. 2
u  n  6n .
C. u  1 2n . D. u   n . n   2 1 . n n n Lời giải Chọn A
u n  2  1  , n
   nên u bị chặn dưới. n n
Câu 20: Cho 0   
. Chọn mệnh đề sai trong các mệnh đề sau: 2       A. sin   sin   . B. tan   cot    .  2   2        C. sin    cos   . D. cos    sin   .  2   2  Lời giải Chọn A    Câu A sai vì sin   cos   .  2  1 1 3 1 5 Câu 21: Hỏi ; ; ; ;
là năm số hạng đầu trong dãy số nào sau đây? 2 2 8 4 32 n n
A. w với w n    .
B. v với v n    . n  * n n n  * n  2 n  2 n 1 1
C. u với u n    .
D. t với t n    . n   * n n n  * n  2 n 1 Lời giải Chọn A 9 1 2 1 3 3 4 1 5 5
Với dãy số  w ta có w  ; w   ; w   ; w   ; w   . n  1 2 2 3 3 4 4 5 5 2 2 2 2 8 2 4 2 32
Câu 22: Phỏng vấn một số học sinh khối 11 về thời gian ngủ (giờ) của một buổi tối thu được kết quả sau
75% số học sinh ngủ ít nhất bao nhiêu giờ trong một buổi tối? A. 5, 92 . B. 7, 68 . C. 6, 65 . D. 5, 64 . Lời giải Chọn D
Tứ phân vị thứ nhất của mẫu số liệu trên là Q  5, 64 nên 75% số học sinh ngủ ít nhất 5,64 1
giờ trong một buổi tối.
Câu 23: Trên khoảng  
 ;  , đồ thị hàm số y  sin x được cho như hình vẽ.
Hàm số y  sin x nghịch biến trong khoảng nào sau đây?        A.    ; 0 . B. 0;  . C. ;   . D.  ;   .  2   2 2  Lời giải Chọn C      
Dựa vào đồ thị suy ra hàm số y  sin x nghịch biến trên các khoảng   ;    và ;    2   2  3   
Câu 24: Cho góc  thỏa mãn tan 
. Tính P  tan     . 5  4  8 3 A. P  4 . B. P  . C. P  3 . D. P  . 5 5 Lời giải Chọn A  3 tan   tan 1    tan 1 Có 4 5 tan       4   .  4   1 tan  3 1 tan . tan 1 4 5 3   
Câu 25: Cho    
. Xác định dấu của biểu thức M  sin  .cot     . 2  2  A. M  0 . B. M  0 . C. M  0 . D. M  0 . 10 Lời giải Chọn D 2    cos  Có M  sin
  .cot      cos.cot     .  2  sin  3 2 cos   0 Với     thì  nên M  0 . 2 sin   0 
Câu 26: Biết bốn số 2;8; x;128 theo thứ tự lập thành một cấp số nhân. Giá trị của x bằng
A. x  64 .
B. x  24 .
C. x  32 .
D. x  16 . Lời giải Chọn C
Ta có 2;8; x;128 lập thành 1 cấp số nhân nên 2
8  2.x x  32 Kiểm tra lại ta thấy 2 32  8.128 ( thỏa mãn ).
Câu 27: Cho cấp số nhân có các số hạng lần lượt là 3;9; 27;81; . Tìm số hạng tổng quát u của cấp số n nhân đã cho.
A. u  3  3n . B. 1 u 3n  . C. 1 u 3n  .
D. u  3n . n n n n Lời giải Chọn D
Ta có u  3 u  9  3u u .d d  3 . 1 2 1 1 Do đó n 1 n 1 u u .d  3.3     3n . n 1 2 3n  19n
Câu 28: Tổng n số hạng đầu tiên của một cấp số cộng là S  với *
n   . Tìm số hạng đầu n 4
tiên u và công sai d của cấp số cộng đã cho. 1 1 3 3 5 1
A. u  2;d   . C. u  4  ; d  .
B. u   ; d  2  . D. u  ;d  . 1 2 1 2 1 2 1 2 2 Lời giải Chọn C
Ta có công thức tổng n số hạng đầu tiên của một cấp số cộng n n S u u   u n d n  2 1 1 n  1   2 2   2 n 3n 19n Từ giả thiết 
2u n 1 d   1   2   4 3n 19
 2u d nd   với mọi * n   1 2 2  19  2u d    3 1  2    d      2 . 3   d     u 4    1 2 1    
Câu 29: Tính tổng S của các nghiệm của phương trình sin x  trên đoạn  ; . 2  2 2       5 A. S  . B. S  . C. S  . D. S  . 2 6 3 6 11 Lời giải Chọn B
x   k2 1   6 Ta có sin x
 sin x sin  
( với k; l Z ) 2 6  5x   l2  6   +Xét bất phương trình
  k2 1 1 1 1 1    2k    k  2 6 2 2 6 2 3 6
Do k Z k  0  x  6  5    +   l2 1 5 1 2 1    2l    l  2 6 2 2 6 2 3 6  5
Do l Z nên không có giá trị l nguyên để   l2 2 6 2     Vậy x
là nghiệm duy nhất của phương trình thuộc  ; 6  2 2    Vậy S  . 6
Câu 30: Rút gọn M  cos(a b) cos(a b)  sin(a b) sin(a b) .
A. M  cos 4b .
B. M  sin 2b .
C. M  cos 2b .
D. M  sin 4b . Lời giải Chọn C
Ta có: M  cos(a b) cos(a b)  sin(a b) sin(a b)
cos a ba b  cos2b   . 2 3
Câu 31: Biết cos   và     . Giá trị sin  bằng 3 2 5 5 5 5 A.  . B.  . C. . D. . 3 2 2 3 Lời giải Chọn A 3 Vì      sin   0 2 2  2  5 2
Suy ra sin    1  cos    1        3  3
Câu 32: Tìm giá trị nhỏ nhất m của hàm số y   2 sin 2023x  2024 . A. m  1  . B. m  2
 023 2 . C. m  2 . D. m  2  024 2 . Lời giải Chọn C Ta có x   ,  1  sinx 1 Suy ra 1
  sin2023x  202  4 1 12
  2   2 sin2023x  202  4  2
Vậy giá trị nhỏ nhất m của hàm số y   2 sin2023x  202 
4 là m   2 .
Câu 33: Người ta ghi lại tuổi thọ của một số con muỗi cái trong phòng thí nghiệm cho kết quả như sau:
Muỗi cái có tuổi thọ khoảng bao nhiêu ngày là nhiều nhất? A. 76 ngày. B. 90 ngày. C. 80 ngày. D. 66 ngày. Lời giải Chọn A
Số ngày muỗi cái có tuổi thọ nhiều nhất là mốt của mẫu số liệu.
Nhóm có tần số nhiều nhất là nhóm 4. Vì vậy nhóm chứa mốt là nhóm 4: 60;80 .
Ta có j  4, a  60, m  31, m  23, m  29, h  20 . 4 4 3 5 31 23 Do đó M  60  .20  76 . o
31 23  31 29
Vậy Muỗi cái có tuổi thọ khoảng 76 ngày là nhiều nhất. u  4
Câu 34: Cho dãy số u xác định bởi hệ thức truy hồi 1
. Số hạng thứ bốn của dãy số là n
u u nn 1  n A. 14 . B. 28 . C. 10 . D. 8 . Lời giải Chọn C u  4 Ta có 1  uu nn 1  n
Suy ra u u 1  4 1  5 . 2 1
u u  2  5  2  7 . 3 2
u u  3  7  3  10 . 4 3
Vậy Số hạng thứ bốn của dãy số là u  10 . 4
Câu 35: Cho cấp số cộng u có số hạng đầu u  5
 và công sai d  3. Số 94 là số hạng thứ mấy của n  1 cấp số cộng? A. 33 . B. 20 . C. 34 . D. 35 . Lời giải Chọn C
Áp dụng công thức u u n 1 .d n 1   Suy ra 94  5   n  
1 .3  3n  102  n  34 .
Vậy số 94 là số hạng thứ 34 của cấp số cộng u . n PHẦN 2:TỰ LUẬN
Câu 36: Giải phương trình sau: 2sin x  22cos x  3  0. Lời giải 13 sin x  1 
Ta có 2sin x 22cos x 3  0      3 . cos x  .  2 
sin x  1  x  
k 2 , k   . 2 3   cos x   cos x  cos  x  
k 2 , k   . 2 6 6    
Vậy phương trình có nghiệm S    k2 ;   k 2  .  6 2 
Câu 37: Cho một cấp số cộng biết rằng tổng của số hạng thứ hai và số hạng thứ tư bằng 6 , số hạng thứ
sáu bằng 36 . Tính tổng 50 số hạng đầu của cấp số này. Lời giải u   u  6 u
d u  3d  6
2u  4d  6 u   1  9 Từ giả thiết ta có: 2 4 1 1 1 1        u  36 u  5d  36 u  5d  36 d  11.  6  1  1 
Tổng 50 số hạng đầu của cấp số này là
n 2u n 1 d  50 2. 1  9  49.11  1     SS       12525 n 50 2 2
Câu 38: Với hình vuông A B C D như hình vẽ dưới đây, cách tô màu như phần gạch sọc được gọi là 1 1 1 1
cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình sau:
Bước 1: Tô màu “đẹp” cho hình vuông A B C D . 1 1 1 1
Bước 2: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 2 2 2 2
vuông A B C D thành 9 phần bằng nhau như hình vẽ. 1 1 1 1
Bước 3: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 3 3 3 3
vuông A B C D thành 9 phần bằng nhau… 2 2 2 2
Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu chiếm ít
nhất 49,99% diện tích hình vuông A B C D . 1 1 1 1 Lời giải 14
Từ đề bài ta thấy được tỉ lệ diện tích giữa đa giác được tô màu so với hình vuông tương ứng là 4 1
và tỉ lệ diện tích giữa các hình vuông là
. Kí hiệu u là diện tích phần đa giác tô màu thứ 9 9 n 4 4 1 S S n A 1 n B 1 n C 1  n D 1  n A n B Cn n D u 1 n , khi đó n 1  9 9 9    . u 4 4 9 n S S 9 A B C D A B C D n n n n 9 n n n n 4 1
Khi đó dãy số u là một cấp số cộng có u S và q  . n  1 1 1 1 1 9 A B C D 9 n  1  1 n   4  9   1  9  8  Khi đó S SA B C D 49, 99%   1  49, 99%  n  4 . n A B C D 1 1 1 1     1 1 1 1 9 1  9  4  9 1   9
Vậy ta cần làm ít nhất cần 4 bước để tổng diện tích phần được tô màu chiếm ít nhất 49,99%
diện tích hình vuông A B C D . 1 1 1 1
Câu 39: Số giờ có ánh sáng mặt trời của thành phố A trong ngày thứ t của năm 2023 được cho bởi hàm    số y  9  2 cos t   61  , *
t   . Vào ngày tháng nào trong năm 2023 thì thành phố A có 118   
số giờ có ánh sáng mặt trời nhiều nhất? Lời giải       Ta có 1  cos t   61  1  7  9  2 cos t   61
 11  7  y  11  . 118  118     
Vậy giá trị lớn nhất của y  11.     t  179 Khi cos t   61  11   t  
61    k 2  k   118    118 236 89 93
Mặt khác 1  t  365 nên  k
. Suy ra k  0 hay t  179 118 118
Vậy số giờ có ánh sáng mặt trường nhiều nhất của thành phố A trong một ngày là ngày thứ 179 trong năm 2023.
Ta có số ngày từ tháng 1 đến tháng 5 là 31  28  31  30  31  151 ngày nên ngày có ánh
sáng nhiều nhất trong năm là ngày 28 tháng 6 năm 2023. 15
Document Outline

  • de-giua-ky-1-toan-11-nam-2023-2024-truong-chuyen-le-khiet-quang-ngai
  • TOÁN-11-GK1-CHUYÊN LÊ KHIẾT-QUẢNG NGÃI_NH-23-24