SỞ GIÁO DỤC VÀ ĐÀO TẠO HẬU GIANG
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT CHUYÊN VỊ THANH NĂM HỌC 2023 - 2024
MÔN Toán – Khối lớp 11
Thời gian làm bài : 60 phút
(Đề thi có 03 trang)
(không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 111
I. PHẦN TRẮC NGHIỆM (20 câu – 5,0 điểm) – Học sinh chọn PA đúng và tô vào PTLTN
Câu 1. Cho dãy số (u xác định bởi 3, 9, 27, 81,... . Công thức số hạng tổng quát của dãy số này là n ) A. n 1 u + = − .
B. u = 3n − .
C. u = . D. 1 u − = . n 3n n 3n n 2 n 3 2
Câu 2. Với α là số thực bất kỳ, kết quả rút gọn biểu thức  π A cos α  = − +   sin (π +α ) bằng  2 
A. A = 2sinα .
B. A = 0 . C. A =1.
D. A = 2cosα .
Câu 3. Cho cấp số nhân (u với u = 3 và công bội
. Số hạng tổng quátu (n ≥ 2) bằng n ) q = 2 1 n A. 1 3.2n+ .
B. 3.2n . C. 2 3.2n+ . D. 1 3.2n− .
Câu 4. Phương trình sin x −1 = 0 có tập nghiệm là A. π π
x = + kπ , k ∈ .
B. x = − + k2π , k ∈ . 6 3 C. π π
x = + kπ , k ∈ .
D. x = + k2π , k ∈ . 2 2
Câu 5. Cho cấp số cộng (u với u = 2 và u = 7 . Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 5 − . C. 5. D. 7 . 7 2
Câu 6. Cho π < α < π . Kết quả đúng là 2
A. sinα > 0;cosα < 0 .
B. sinα < 0;cosα > 0 .
C. sinα > 0;cosα > 0 .
D. sinα < 0;cosα < 0 .
Câu 7. Phương trình tan x = 3 có tập nghiệm là A. π π  π   k2π ,k  +
∈ . B.  + kπ,k ∈ .
C.  + kπ,k ∈ . D. ∅. 3       3   6 
Câu 8. Trong các công thức sau, công thức nào luôn đúng ?
A. sin (a + b) = sin . a cosb − cos . a sin . b
B. sin (a – b) = sin . a cosb − cos . a sin . b
C. cos(a – b) = cos . a cosb − sin . a sin . b
D. cos(a + b) = cos . a cosb + sin . a sin . b Câu 9. Cho tanα  π = 2 . Tính tan α  −  ? 4    A. 1. B. 1 . C. 1 − . D. 2 . 3 3 3 Câu 10. Cho 1 sinα = ( o o
90 < α <180 ), khi đó giá trị góc α bằng 2 A. 0 120 . B. 0 150 . C. 0 30 . D. 0 135 . 1/3 - Mã đề 111 Câu 11. Giá trị 2 − x +1 lim bằng x 1+ → x −1 A. . −∞ B. 2 . C. 1. D. . +∞ 3 3
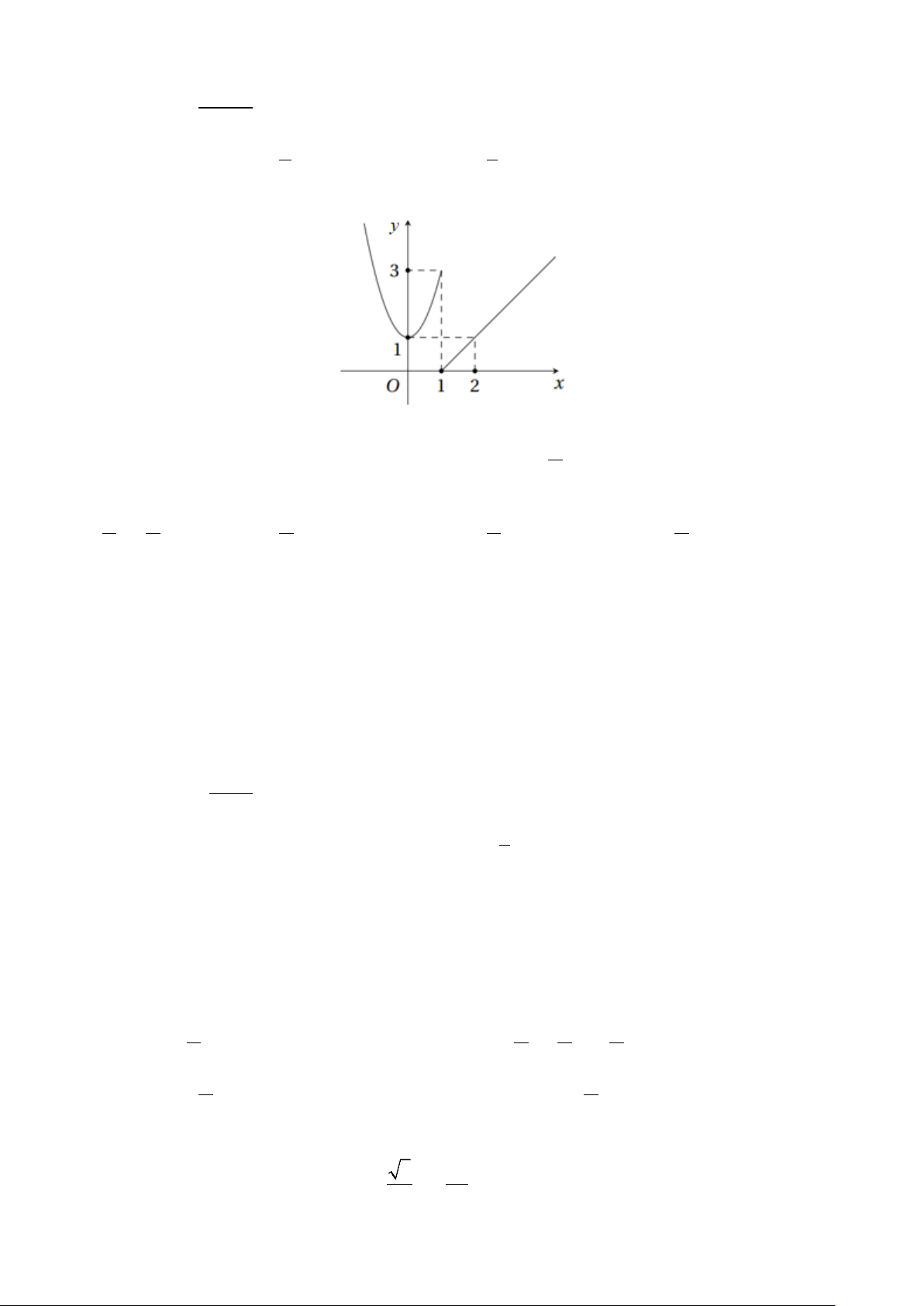
Câu 12. Hàm số y = f (x) có đồ thị như hình bên. Hàm số gián đoạn tại điểm có hoành độ bằng bao nhiêu? A. 2 . B. 3. C. 0 . D. 1.
Câu 13. Trên đường tròn lượng giác, cho góc lượng giác có số đo π (rad ) thì mọi góc lượng giác có cùng tia 2
đầu và tia cuối với góc lượng giác trên đều có số đo dạng A. π π π π π
+ k ,(k ∈) . B. + k2π ,(k ∈) . C. .
D. + kπ ,(k ∈). 2 2 2 2 2
Câu 14. Dãy số nào sau đây không phải là cấp số nhân?
A. 1; −1; 1; −1.
B. 32; 16; 8;4 .
C. 1; − 3; 9;10 . D. 1; 0; 0;0.
Câu 15. Cho cấp số cộng (u có các số hạng đầu lần lượt là 5; 9;13;17;.... thì số hạng tổng quát u của cấp n ) n số cộng là
A. u = n − .
B. u = n + .
C. u = n + .
D. u = n − . n 4 1 n 5 1 n 4 1 n 5 1
Câu 16. Cho dãy (u có limu = , dãy (v có limv = . Khi đó lim(u v bằng n. n ) n 5 n ) n 3 n ) A. 3. B. 8. C. 15. D. 5. Câu 17. Giá trị 3x −1 lim bằng x→+∞ x + 5 A. 3. B. 3 − . C. 1 − . D. 5. 5
Câu 18. Cho cấp số cộng (u có u =1 và u = 3 . Giá trị của u bằng n ) 1 2 3 A. 6. B. 4. C. 9. D. 5.
Câu 19. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin .xtan x
B. y = xcos .x
C. y = sin 2 .x
D. y = cos .xcot .x
Câu 20. Nghiệm của phương trình sin 3x = cos x là A. π π π π
x = kπ , x = + kπ , k ∈
B. x = + k , x = + kπ , k ∈ 4 8 2 4 C. π π
x = k2π , x = + k2π , k ∈
D. x = kπ , x = k , k ∈ 2 2
II. PHẦN TỰ LUẬN (05câu – 5,0 điểm) – Học sinh làm bài vào giấy kiểm tra quy định
Câu 21 (1,0 điểm). Tính sinα , biết 5 cosα π = và 3 < α < 2π . 3 2 2/3 - Mã đề 111
Câu 22 (1,0 điểm). Tính x −1 lim . x 1 → 1− x 2
Câu 23 (1,0 điểm). Cho sin x + cos x = 2 . Tính giá trị của biểu thức 2 2 + sin = cos 4 − sin x A x x − . 2 3tan x + 2
Câu 24 (1,0 điểm). Cho cấp số nhân (u có u + u = 4 và tổng của ba số hạng đầu tiên S =13. Hãy tính n ) 1 2 3
số hạng đầu tiên u và công bội q? 1
Câu 25 (1,0 điểm). Một công ty tuyển công nhân vào đầu tháng 01 của năm mới, trong thời hạn 5 năm và
đưa ra phương án trả lương như sau: Lương tháng khởi điểm là 4 triệu đồng và sau mỗi quý (04 tháng) lương
sẽ tăng thêm 500 nghìn đồng. Hỏi sau 5 năm làm việc thì tổng lương cần chi trả cho một công nhân là bao nhiêu?
------ HẾT ------ 3/3 - Mã đề 111 SỞ GD&ĐT HẬU GIANG
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT CHUYÊN VỊ THANH
MÔN Toán – Khối lớp 11
Thời gian làm bài : 60 phút
(Không kể thời gian phát đề)
I. Phần đáp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 20 111 112 113 114 1 C D A B 2 B A A D 3 D B D D 4 D D D B 5 C A C D 6 A A C A 7 B C A A 8 B C D A 9 B D C A 10 B D D B 11 A D D C 12 D D C C 13 B D B C 14 C A B C 15 B A B D 16 C A C A 17 A B D C 18 D D D B 19 A C A C 20 B C C A
II. Phần đáp án câu tự luận:
Câu 21. Tính sinα , biết 5 cosα π = và 3 < α < 2π . 3 2 Ta có: 2 2 sin α =1− cos α 0,25 đ Thay vào 2 2 5 4 sin α =1− cos α =1− = 9 9 0,25 đ Vậy 2 sinα = ± . 3 0,25 đ π
Do 3 < α < 2π nên sinα < 0 . Vậy 2 sinα = − . 2 3 0,25 đ 1 Câu 22. Tính x −1 lim . x 1 → 1− x 1 ( x x )2 2 − − 1 Ta có lim = lim 0,25 đ x 1 → x 1 1− x → 1− x x −1 ( x +1)( x −1) lim = lim x 1 → x 1 1− x → 1− x 0,25 đ x −1 lim = lim − + → → ( ( x 1)) x 1 x 1 1− x 0,25 đ Vậy x −1 lim = lim(− x −1) = 2 − x 1 → x 1 1− x → 0,25 đ 2
Câu 23. Cho sin x + cos x = 2 . Tính giá trị của biểu thức 2 2 + sin = cos 4 − sin x A x x − . 2 3tan x + 2
sin x + cos x = 2 2 2
⇒ sin x + 2sin x cos x + cos x = 2 ⇒1+ sin 2x = 2 ⇒ sin 2x =1. 0,25 đ 2 2 2 2 + sin + − = cos 4 − sin x A x x − 2 2 1 cos = cos 4 − sin x x x − 2 3tan x + 2 2 3tan x + 3−1 2 2 2 3− cos − = cos 4 − sin x x x − 2 3 cos = cos 4 − sin x x x − 0,25 đ 3( 2 tan x + ) 1 −1 3 −1 2 cos x ( 2 3− cos x) 2 cos x 2
= cos 4x − sin x − 2 2
= cos 4x − sin x − cos x 2 =1− 2sin 2x −1 0,25 đ 2 3− cos x 2 = 2 − sin 2x = 2 − . 0,25 đ
Câu 24. Cho cấp số nhân (u có u + u = 4 và S =13. Tính số hạng đầu tiên u và công bội q? n ) 1 2 3 1
Ta có u = S − S = 9 2 9
⇒ u q = 9 ⇒ u = 3 3 2 1 1 2 q 0,25 đ Vì S 9 9
= 4 nên u + u q = 4. Do đó + = 4 2
⇔ 4q − 9q − 9 = 0 ⇔ q = 3 hoặc 2 1 1 2 q q 3 0,25 đ q = − . 4
Với q = 3 thì u =1 1 0,25 đ Với 3
q = − thì u =16 4 1 0,25 đ
Câu 25. Một công ty tuyển công nhân vào đầu tháng 01 của năm mới, trong thời hạn 5 năm và đưa ra
phương án trả lương như sau: Lương tháng khởi điểm là 4 triệu đồng và sau mỗi quý (04 tháng) lương
sẽ tăng thêm 500 nghìn đồng. Hỏi sau 5 năm làm việc thì tổng lương cần chi trả cho một công nhân là bao nhiêu?
Mỗi quý 04 tháng thì một năm sẽ có 3 quý
5 năm có tất cả là 15 quý 0,25 đ Gọi u n∈
tiền lương mỗi tháng ở quý n n ( {1,2,..., } 15 ): 0,25 đ 2
Dãy (u là một cấp số cộng với công sai d = 0,5 (triệu đồng) n )
Tổng của 15 số hạng đầu tiên của cấp số cộng (u là n ) 15(u + u 0,25 đ 1 15 ) S =
= 15 u + 7d =112,5 (triệu đồng) 15 ( 1 ) 2
Tổng lương cần chi trả cho một công nhân trong 5 năm làm việc là
S =112,5× 4 = 450 (triệu đồng) 0,25 đ 3
SỞ GIÁO DỤC VÀ ĐÀO TẠO HẬU GIANG
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT CHUYÊN VỊ THANH NĂM HỌC 2023 - 2024
MÔN Toán – Khối lớp 11
Thời gian làm bài : 60 phút
(Đề thi có 03 trang)
(không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 115
I. PHẦN TRẮC NGHIỆM (20 câu – 5,0 điểm) – Học sinh chọn PA đúng và tô vào PTLTN
Câu 1. Phương trình sin 2x = cos x có nghiệm là  π  π π x = + k2π k  x = +  A. 6  (k ∈). B. 6 3  (k ∈). π  π x = + kπ   x = + k2π  2  2  π kπ  π π x = + k2  x = +  C. 6 3  (k ∈). D. 6 3  (k ∈). π  π x = + k2π   x = + k2π  3  2
Câu 2. Cho limu = − ; limv = . Khi đó lim(u − v bằng n n ) n 2 n 3 A. 5 − . B. 1 − . C. 1. D. 5. Câu 3. Cho 1 cosα = ( o o 90 −
< α < 0 ), khi đó giá trị góc α bằng 2 A. 0 30 . B. 0 120 . C. 0 60 . D. 0 60 − .
Câu 4. Cho α thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây A. cosα < 0 .
B. cotα < 0 . C. tanα < 0. D. sinα > 0. u  = 3
Câu 5. Cho dãy số (u biết 1 *  , n ∀ ∈ u . n )
 . Tìm số hạng tổng quát của dãy số ( n ) u =  + u n 3 1 n
A. u = 3n . B. 1 u + = . C. 1 u − = . D. n 1 u n + = . n 3n n 3n n n
Câu 6. Hàm số nào sau đây không liên tục tại x = 2 ? 2 A. 2
y = x − 3x + 2 .
B. y = x + 2 . C. x y = . D. 2 y = x . x − 2 Câu 7. Giá trị x + 2 lim bằng x 1− → x −1 A. 1 . B. 1 − . C. −∞ D. +∞ . 2 2
Câu 8. Mệnh đề nào sau đây đúng? A. ( − − ) tan x − tan tan y x y = . B. ( − ) tan x tan tan y x y = . 1− tan x tan y tan x tan y C. ( + − ) tan x − tan tan y x y = . D. ( − ) tan x tan tan y x y = . 1+ tan x tan y tan x tan y
Câu 9. Cho cấp số cộng có u = 3
− , d = 4 . Chọn khẳng định đúng trong các khẳng định sau? 1 1/3 - Mã đề 115
A. u =15.
B. u = 8.
C. u = 2 .
D. u = 5. 3 3 3 3
Câu 10. Cho cấp số cộng u có các số hạng đầu lần lượt là 5; 9;13;17;.... Tìm số hạng tổng quát u của cấp n n số cộng?
A. u = n − .
B. u = n + .
C. u = n + .
D. u = n − . n 4 1 n 4 1 n 5 1 n 5 1
Câu 11. Cho cấp số cộng (u có u =1 và u = 3 . Giá trị của u bằng n ) 1 2 3 A. 9. B. 5. C. 4. D. 6.
Câu 12. Rút gọn biểu thức: sin 54 .°cos 4° + sin 4 .°cos54° , ta được A. sin 50 .° B. sin 58 .° C. cos58 .° D. cos50 .°
Câu 13. Góc có số đo 120° đổi sang radian là A. π . B. 2π . C. 3π . D. π . 10 3 2 4
Câu 14. Phương trình tan x +1 = 0 có nghiệm là A. π π π
x = + kπ , x = − + kπ (k ∈) .
B. x = − + kπ (k ∈) . 4 4 2 C. π π
x = − + kπ (k ∈) .
D. x = + kπ (k ∈) . 4 4
Câu 15. Hàm số nào sau đây là hàm số lẻ?
A. y = 2x + cos x .
B. y = cos3x . C. 3
y = x cos x . D. 2
y = x sin (x + 3) .
Câu 16. Phương trình cos x =1 có nghiệm là A. π
x = + kπ , k ∈ .
B. x = k2π , k ∈ . 2 C. π π
x = + kπ , k ∈ .
D. x = ± + k2π , k ∈ . 3 3
Câu 17. Cho dãy số (u có các số hạng đầu là: 1, 3, 5, 7,.... thì công thức của số hạng tổng quát là n )
A. u = n − .
B. u = n − .
C. u = n − .
D. u = n − . n 2 1 n 4 3 n 3 2 n 8 7 Câu 18. Giá trị 3− 4 lim x bằng x→+∞ 5x + 2 A. 5 . B. 4 − . C. 5 − . D. 4 . 4 5 4 5 Câu 19. Cho 2
cos 2α = . Tính giá trị của biểu thức P = cosα.cos3α . 3 A. 7 P = . B. 7 P = . C. 5 P = . D. 5 . 9 18 9 18
Câu 20. Dãy số nào sau đây không phải là cấp số nhân?
A. 1;− 2;4;−8;16 .
B. 1;− 3;9;− 27;54 . C. 1;2;4;8;16 .
D. 1;−1;1;−1;1.
II. PHẦN TỰ LUẬN (05câu – 5,0 điểm) – Học sinh làm bài vào giấy kiểm tra quy định Câu 21  π
(1,0 điểm). Cho 2 cos x  x 0 = − < <
. Tính giá trị của sin x ? 5 2    3
Câu 22 (1,0 điểm). Tính x −1 lim x 1 → 1− x
Câu 23 (1,0 điểm). Chứng minh biểu thức 2/3 - Mã đề 115  π   π  2 P = 4cos −α sin −α − 3+     4sin α  6   3 
có giá trị không phụ thuộc vào α. u  + u + u = 91
Câu 24 (1,0 điểm). Cho cấp số nhân (u thỏa mãn 1 3 5 . n ) u  −u =  728 7 1
Tính số hạng đầu tiên u và công bội q? 1
Câu 25 (1,0 điểm). Một công ty nọ tuyển công nhân vào đầu tháng 01 của năm, trong thời hạn 5 năm và có
phương án trả lương như sau: Lương tháng khởi điểm là 4 triệu đồng và sau mỗi quý (04 tháng) lương sẽ
tăng thêm 500 nghìn đồng. Nhưng do năm thứ tư có dịch Covid 19, nên tiền lương vẫn giữ theo phương án
nhưng có trừ lương mỗi tháng là 5%. Hỏi sau 5 năm làm việc thì tổng lương nhận được của người công nhân là bao nhiêu?
------ HẾT ------ 3/3 - Mã đề 115 SỞ GD&ĐT HẬU GIANG
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT CHUYÊN VỊ THANH
MÔN Toán – Khối lớp 11
Thời gian làm bài : 60 phút
(Không kể thời gian phát đề)
I. Phần đáp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 20 115 116 117 118 1 D D D D 2 A A D A 3 D A C B 4 D B A A 5 A B B D 6 C C A C 7 C A D C 8 C D C C 9 D B B C 10 C D D C 11 B D B D 12 B A D D 13 B C C A 14 C A B A 15 C B A D 16 B A B A 17 D C C C 18 B D A D 19 D C B C 20 B A B A
II. Phần đáp án câu tự luận: Câu 21. Cho 2  π cos x  x 0 = − < <
. Hãy tính giá trị của sin x 5 2    Ta có 2 2
sin x + cos x =1 0,25 đ 2 2 2  2  1
⇒ sin x =1− cos x =1−  = 5  0,25 đ   5 Vậy 1 sin x = ± 5 0,25 đ Vì π
− < x < 0 ⇒ sin x < 0 nên 1 sin x = − . 2 5 0,25 đ 1 3 Câu 22. Tính x −1 lim x 1 → 1− x 3 2 x −1 (x −1)( + + Ta có l x x 1) im = lim 0,25 đ x 1 → x 1 1− x → 1− x 3 2 x −1 (x −1)( lim = lim x + x +1) 0,25 đ x 1 → x 1 1− x → −(x −1) 3 x −1 2 lim
= lim−(x + x +1) x 1   → x 1 x −1 → 0,25 đ 3 x −1 Vậy 2 lim
= lim−(x + x +1) = 3 − x 1   → x 1 x −1 → 0,25 đ
Câu 23. Chứng minh biểu thức  π   π  2 P = 4cos −α sin −α − 3+    
4sin α có giá trị không phụ thuộc  6   3  vào α. Ta có π π  π   π
−α và +α phụ nhau nên sin α   cos α  − = + . 3 6 3  6      0,25 đ Suy ra  π   π   π   π 4cos α sin α   4cos α  cos α  − − = − +  6 3 6  6          1   π π   π   π  = 4⋅ cos −α + +α +   cos −α − +α 2   6 6    6     6   0,25 đ  π  π = 2⋅ cos + cos( 2
− α ) = 2⋅cos + 2⋅cos2α  3    3 1 = 2⋅ + 2.( 2 1− 2sin α ) 2 2
= 1+ 2 − 4sin α = 3− 4sin α . 2 0,25 đ  π   π  2 P = 4cos −α sin −α − 3+ 4sin α =     0  6   3  0,25 đ u  + u + u = 91
Câu 24. Cho cấp số nhân (u thỏa mãn 1 3 5
. Tính số hạng đầu tiên u và công bội q? n ) u  −u =  728 1 7 1 u  + u + u = 91 u
 + u .q + u .q = 91 u  ( 2 4 2 4
1+ q + q = 91 (1) 1 ) Ta có: 1 3 5 1 1 1  ⇔  ⇔  6 u − 0,25 đ  u = 728 u
 .q − u = 728 u  ( 6 7 1 1 1 q −1 = 728 (2) 1 ) Chia từng vế của ( )
1 cho (2) ta được phương trình : 2 4 2 4 1+ q + q 1+ q + q 1 2 =
= ⇔ q = 9 ⇔ q = 3 * ± 0,25 đ 6 q −1 ( 2q − )1( 2 4 1+ q + q ) ( ) 8 2
Với q = 3 thay vào (2) ta được u =1. 1 0,25 đ Với q = 3
− thay vào (2) ta được u =1. 1 0,25 đ
Câu 25. Một công ty nọ tuyển công nhân vào đầu tháng 01 của năm, trong thời hạn 5 năm và có
phương án trả lương như sau: Lương tháng khởi điểm là 4 triệu đồng và sau mỗi quý (04 tháng) lương
sẽ tăng thêm 500 nghìn đồng. Nhưng do năm thứ tư có dịch Covid 19, nên tiền lương vẫn giữ theo
phương án nhưng có trừ lương mỗi tháng là 5%. Hỏi sau 5 năm làm việc thì tổng lương nhận được của
người công nhân là bao nhiêu?
Mỗi quý 04 tháng thì một năm sẽ có 3 quý
5 năm có tất cả là 15 quý Gọi u n∈
là tiền lương mỗi tháng ở quý thứ n 0,25 đ n ( {1,2,..., } 15 ):
Dãy (u là một cấp số cộng với công sai d = 0,5 (triệu đồng) n )
Tổng của 15 số hạng đầu tiên của cấp số cộng (u là n ) 15(u + u 0,25 đ 1 15 ) S =
= 15 u + 7d =112,5 (triệu đồng) 15 ( 1 ) 2
Trong năm thứ tư tiền lương của các quý: u , u , u và số tiền bị trừ là 10 11 12
4(u + u + u ×5% = 3u =12 u +10d ×5% =12 4 + 5 ×5% = 5,4 (triệu đồng) 0,25 đ 10 11 12 ) 11 ( 1 ) ( )
Tổng lương nhận được của một công nhân trong 5 năm làm việc là
S =112,5× 4 = 450 − 5,4 = 444,6 (triệu đồng) 0,25 đ 3
Document Outline

• de 111
• Dap an de 01
• de 115
• Dap an de 02