

Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 HIỆP HÒA NĂM HỌC 2022 - 2023 MÔN: Toán 9
(Đề gồm có 02 trang)
Thời gian làm bài: 90 phút
PHẦN TRẮC NGHIỆM (3,0 điểm).
Em hãy chọn chữ cái đứng trước ý trả lời đúng nhất trong các câu sau:
Câu 1. Căn bậc hai số học của 2 9 là A. 9 . B. 9 . C. 9 . D. 81.
Câu 2. Điều kiện để x 2022 có nghĩa là: A. x 202 2 B. x 202 2 C. x 20 22 D. x 202 2
Câu 3. Cho x 3 . Giá trị của biểu thức 2
P x 6x 9 là A. 2 . B. 0 . C. 2 . D. 6 .
Câu 4. Giá trị của biểu thức 2 2
T ( 5 1) ( 5) là: A. 2 5 1 B. 1 C. 1 2 5 D. 1 2 5
Câu 5. Với x 3,
giá trị của x thỏa mãn 4x 12 x 3 9x 27 4 bằng A. 4. B. 2. C. 5. D. 2. 4 x
Câu 6. Với y 0 , kết quả của phép tính 2 . y là 2 4y 2 x 2 x A. 2 x . B. 2 x . C. . D. . 2y 2y 1 1 Câu 7. Biểu thức có giá trị bằng 5 3 5 3 A. 5 3 . B. 5 3 . C. 5 . D. 3 .
Câu 8. Hàm số nào dưới đây là hàm số bậc nhất?
A. y x 2 5 .
B. y 2x 1. C. 2
y 2x x 1.
D. y 0x 1.
Câu 9. Giá trị của m để hai đường thẳng y m
1 x 2 và y 5x 2m song song là A. m 6. B. m 6 . C. m 1. D. m 5 .
Câu 10. Hàm số y 2 – 3m x 5m x là hàm số đồng biến khi A. 2 m . B. m 1. C. 2 m . D. m 1 3 3
Câu 11. Cho tam giác ABC vuông tại A , AB 4 và AC 3 . Khẳng định đúng là A. 3 sin B . B. 4 cosB . C. 4 tan B . D. 3 cot B . 5 5 3 4
Câu 12. Cho tam giác ABC vuông tại A có cạnh AB 6 cm, AC 8cm . Bán kính của đường
tròn ngoại tiếp tam giác ABC là A. 14cm . B. 10cm . C. 5cm. D. 7cm.
Câu 13. Cho tam giác ABC vuông tại A có BC AB 2 , biết đường cao AH 10 . Diện
tích tam giác vuông đó là: A. 100. B. 200 . C. 100 2 . D. 200 2 .
Câu 14. Một cột đèn có bóng trên mặt đất dài 7,5m . Các tia nắng mặt trời tạo với mặt đất một
góc xấp xỉ bằng 42 . Tính chiều cao của cột đèn (làm tròn đến chữ số thập phân thứ ba). A. 6, 753m . B. 6, 75m . C. 6, 751m . D. 6, 755m .
Câu 15. Cho đường tròn tâm O có bán kính bằng 10cm , dây AB =16cm . Gọi I là trung
điểm của dây AB . Tính độ dài OI . A. OI = 4cm . B. OI = 6cm . C. OI = 8cm . D. OI =10cm .
PHẦN TỰ LUẬN (7,0 điểm). Câu 16 ( 2 điểm)
1. Thực hiện phép tính 20 80 5 5: 5
2. Tính giá trị của biểu thức 3 3 2 A 1. 3 3 1 Câu 17 (2 điểm).
1. Tìm các giá trị của m để đường thẳng (d): y mx 2 (với m 0 ) đi qua điểm ( A 1; 2). x
2. Rút gọn biểu thức: 1 2 A :
.(với x 0; x 4 ) x 4 x 2 x 2 Câu 18 (2,5 điểm)
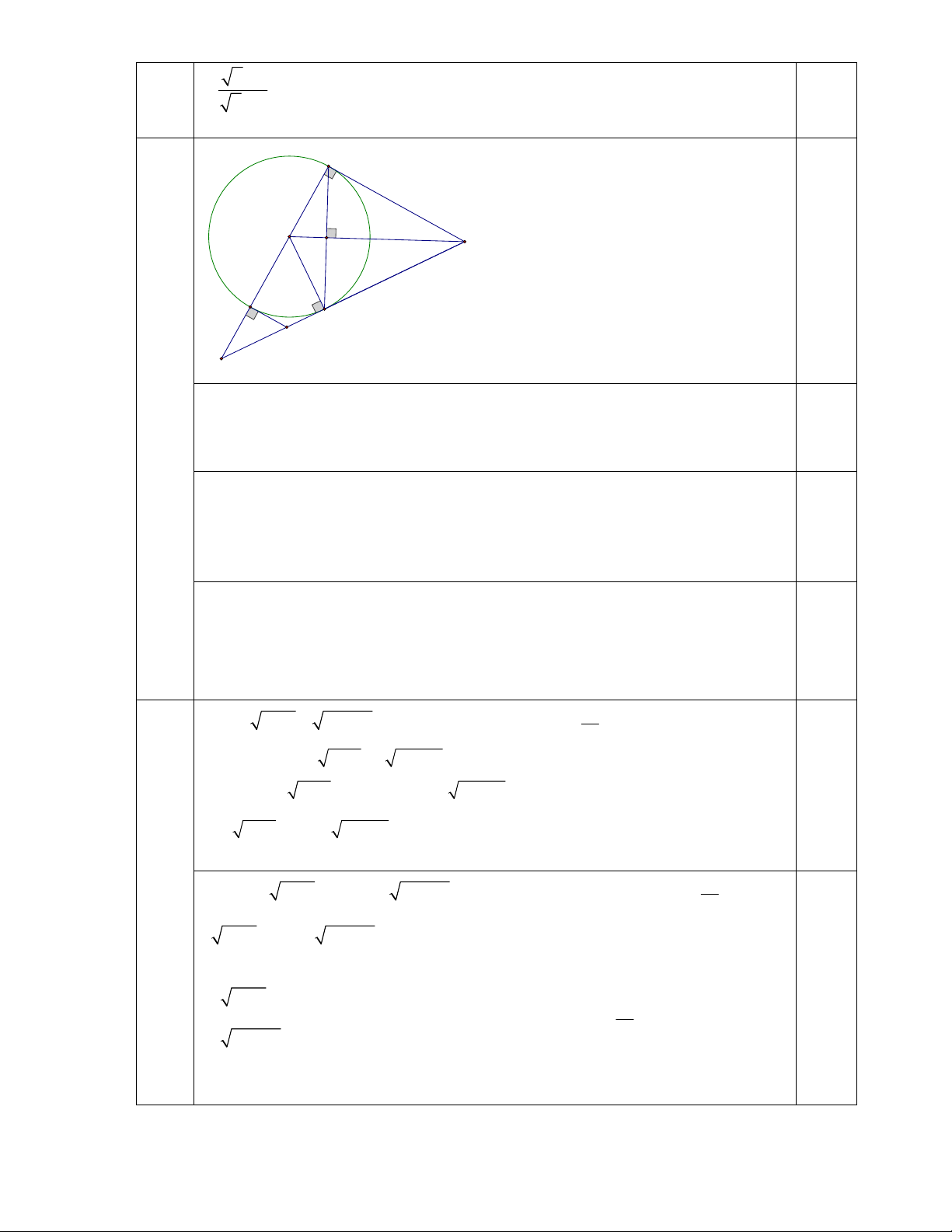
Cho tam giác ABC vuông tại A, đường cao AH có AB =15 cm, AC = 20 cm.
1. Tính độ dài các đoạn thẳng BC, BH, AH
2. Vẽ đường tròn (B), bán kính BA. Tia AH cắt đường tròn (B) tại D. Chứng minh
CD là tiếp tuyến của đường tròn (B).
3. Tia AB cắt đường tròn (B) tại E và cắt đường thẳng CD tại F. Từ E kẻ đường
thẳng song song với AC, đường thẳng này cắt CF tại G. Chứng minh G . D FC . FG CD
Câu 19 (0,5 điểm): Giải phương trình x2 10 3 x 5 . x
----------------Hết----------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên học sinh:........................................................ Số báo danh:.......................................
HƯỚNG DẪN CHẤM KIỂM TRA
GIỮA HỌC KÌ 1 NĂM HỌC 2022 – 2023 MÔN: Toán 9
I. TRẮC NGHIỆM (3 điểm)
Mỗi câu trả lời đúng được 0,15 điểm
Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A B B C D A C B A C Câu 11 12 13 14 15 Đáp án A,B C A A B
II. TỰ LUẬN (7 điểm) Câu
Nội dung cần đạt Điểm 16 2 2 20
80 5 5 : 5 ( 2 .5 4 .5 5 5) : 5 1) 0.5 (2 5 4 5 5 5) : 5 3 5 : 5 3 0.5 3 3 1 2 3 1 3 3 2 2) A 1 1 0.5 3 3 1 3 3 1
A 3 1 3 11 A 3 0.25 Kl… 0.25 Câu 17
Tìm các giá trị của m để đường thẳng (d): y mx 2 (với m 0 ) đi qua điểm ( A 1; 2). 1
Vì (d) đi qua A(1; 2). nên 2 m 2 0,5
Tìm được m 4 0,25 Kết luận 0,25
1. Với x 0; x 4 ta có: x 1 2 A : x 4 x 2 x 2 x 1 2 A 0,25
x 2 x 2 : x 2 x 2 2 x x 2 2
x 2 x 2 x 2 x 2 : x 2 2 x 2 x 2 0,25
x 2 x 2. 2 x 1 0,25 x 2 KL: 0,25 A B C E D G F 1, Tính được Câu BC=25 cm 0,5 18 AH = 12 cm 0,25 BH =9 cm; 0,25
2. Chứng minh được ABC DBC 0,25
Chứng minh được ABC DBC 0,25 Suy ra 0
BAC BDC 90
=> CD BD => CD là tiếp tuyến của (B) 0,25
3. Chứng minh được EG GD ; CD CA 0,25
Chứng minh được GEF CAF 0,25
GE.FC FG.CA . GD FC . FG CD 0,25 Vậy 10
Ta có x 2 10 3x 5 x 1 . ĐKXĐ: 2 x 3
1 10 2x 2 x 2 2 103x 0
x 2 2 x 2
1 10 3x 2 10 3x 1 0 0.25
x 2 2
1 10 3x 2 1 0 2 2 2 10 Câu Vì
x2 1 0; 103x 1 0với mọi 2 x nên 19 3
x 2 x 2 2 1 10 3 1 0
Dấu đẳng thức xảy ra khi và chỉ khi 0.25 x 2 2 1 0 x 3 10
(Thỏa mãn 2 x ) 3 x x 3 2 x 3 10 3 1 0
Vậy phương trình đã cho có nghiệm duy nhất x = 3




