Đề giữa kỳ 2 Toán 12 năm 2021 – 2022 trường THPT Bảo Thắng 3 – Lào Cai

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giữa học kì 2 môn Toán 12 năm học 2021 – 2022 .Mời bạn đọc đón xem.

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Lan Tường
1/4 - Mã đề 101
THPT SỐ 3 BẢO THẮNG
TỔ: TOÁN – TIN - CN
(Đề thi có 04 trang)
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM (8 điểm)
Câu 1. Họ tất cả các nguyên hàm của hàm số
( )
sin 3
fx x=
là:
A.
cos3xC+
. B.
cos3xC−+
. C.
1
cos3
3
xC
+
. D.
1
cos3
3
xC−+
.
Câu 2.
4
d
∫
x x
bằng
A.
3
4xC+
B.
C.
5
xC+
D.
5
5xC+
Câu 3. Trong không gian
Oxyz
, cho
3=+−
OM i j k


. Tọa độ điểm
M
là
A.
(
)
113M
;;
. B.
( )
113−−−M ;;
C.
( )
11 3−−M ;;
. D.
( )
11 3−M ;;
.
Câu 4. Mệnh đề nào dưới đây đúng?
A.
( )
32
3
d
′
= +
∫
x x xC
. B.
(
)
33
d
′
= +
∫
x xx C
. C.
( )
32
3d
′
=−+
∫
x x xC
. D.
( )
33
d
′
=−+
∫
x x xC
.
Câu 5. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 3 4 1 0xyz
α
− + −=
. Vectơ nào dưới đây là một vectơ
pháp tuyến của
( )
α
?
A.
(
)
2
2; 3; 4
n = −

. B.
( )
1
2; 3; 4n =

. C.
( )
4
2; 3; 4n = −

. D.
(
)
3
2; 3; 4n = −

.
Câu 6.
5
∫
x
dx
bằng
A.
5
+
x
C
. B.
5 .ln 5
+
x
C
. C.
1
5
1
+
+
+
x
C
x
D.
5
ln 5
+
x
C
.
Câu 7. Họ tất cả các nguyên hàm của hàm số
() 2
x
fx e
=
là
A.
1
2.
x
eC
+
+
B.
2.
x
eC−+
C.
2.
x
eC+
D.
1
2.
x
eC
+
−+
Câu 8. Giá trị
5
0
d
∫
x
bằng
A.
5
. B.
6
C.
5−
. D.
0.
Câu 9. Họ tất cả các nguyên hàm của hàm số
( )
sinfx x=
là
A.
cos xC+
. B.
2
1
sin
2
xC+
. C.
sin xC−+
. D.
cos
xC−+
.
Câu 10. Trong không gian
Oxyz
, cho mặt cầu
( ) ( )
2
22
: 29Sx y z+++ =
. Bán kính của
(
)
S
bằng
A.
3
. B.
18
. C.
9
. D.
6
.
Câu 11. Xét
( )
fx
là một hàm số tùy ý,
(
)
Fx
là một nguyên hàm của
( )
fx
trên đoạn
[ ]
7;8
. Mệnh đề nào
dưới đây đúng?
A.
( ) (
) ( )
8
7
d 78fx x F F
= −
∫
. B.
( ) (
) ( )
6
5
d 87fx x F F= +
∫
.
C.
( ) ( ) ( )
8
7
d 87fx x F F= −
∫
. D.
( ) ( ) ( )
6
5
d 78fx x F F=−−
∫
.
Câu 12. Trong không gian
Oxyz
cho điểm
( )
2;1; 3A
và điểm
( )
4; 3;1B −
. Toạ độ trung điểm
I
của đoạn
thẳng
AB
là
A.
. B.
( )
3; 1; 2−
. C.
( )
1;2;1−−
. D.
( )
2; 4; 2−−
.
Mã đề 101
2/4 - Mã đề 101
Câu 13. Cho hàm số
( )
fx
có đạo hàm
( )
′
fx
liên tục trên đoạn
[ ]
3; 5
và thỏa mãn
( )
3 2,
=
f
( )
5 10=f
. Giá
trị của
(
)
5
3
d
′
∫
fxx
bằng
A.
8
. B.
2
C.
12
. D.
8−
.
Câu 14. Cho hàm số
()fx
liên tục và không âm trên đoạn
[ ]
5; 6 .
Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số
()
y fx=
, trục
Ox
và
2
đường thẳng
5, 6xx
= =
được tính theo công thức nào
dưới đây?
A.
( )
6
5
d.S fx x
= −
∫
B.
(
)
6
5
d.S fx x
=
∫
C.
( )
6
2
5
d.S fx x
π
=


∫
D.
( )
6
5
d.S fx x
π
=
∫
Câu 15. Biết
(
)
2
1
d4=
∫
fx x
và
(
)
2021
2
d1fx x
= −
∫
. Khi đó
( )
2021
1
dfx x
∫
bằng
A.
3−
. B.
5
. C.
5−
. D.
3
.
Câu 16. Trong không gian
Oxyz
, cho ba điểm
(
)
3;0;0A
,
( )
0;1; 0B
và
( )
0;0; 2−C
. Mặt phẳng
(
)
ABC
có
phương trình là:
A.
1
312
++=
xyz
. B.
1
3 12
+ +=
−
xyz
. C.
1
31 2
++ =
−
xy z
. D.
1
312
++=
−
x yz
.
Câu 17. Mệnh đề nào dưới đây đúng?
A.
( )
33
3 d d 3d
xx
x x xx x+=−
∫ ∫∫
B.
( )
33
3 d d 3d
xx
x x xx x+=+
∫ ∫∫
.
C.
( )
33
3 d 3d d
xx
x x x xx+=−
∫ ∫∫
D.
(
)
33
3 d d. 3d
xx
x x xx x+=
∫ ∫∫
Câu 18. Biết
( )
2
1
2=
∫
f x dx
. Giá trị của
( )
2
1
3
∫
f x dx
bằng
A.
8
. B.
6
. C.
2
3
. D.
5
.
Câu 19. Xét hàm số
()fx
liên tục trên đoạn
[ ]
;ab
. Mệnh đề nào dưới
đây đúng?
A.
( ) ( )
3 d 3d
bb
aa
fxx f xx=
∫∫
. B.
(
)
( )
3 d 3d . d
b ba
a ab
fx x x fx x=
∫ ∫∫
.
C.
( )
( )
3 d3 d
bb
aa
fx x fx x=
∫∫
. D.
( )
( )
3 d3 d
bb
aa
fx x fxx= +
∫∫
.
Câu 20. Trong không gian
Oxyz
, cho hai điểm
( )
2; 2;1A −
và
( )
1; 1;3B −
. Véctơ
AB

có tọa độ là
A.
( )
1;1;2−
. B.
( )
3;3; 4−−
. C.
( )
3; 3;4−
. D.
( )
1; 1; 2−−
.
Câu 21. Biết
( )
3
2
d3=
∫
fx x
và
( )
3
2
d1=
∫
gx x
. Khi đó
( ) ( )
3
2
d+


∫
f x gx x
bằng
A.
2
. B.
2−
. C.
4
. D.
3
.
Câu 22. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
3, 0, 0, 1=+===yx y x x
. Gọi
V
là thể tích của
khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
( )
1
2
2
0
3
π
= +
∫
V x dx
B.
( )
1
2
0
3
π
= +
∫
V x dx
C.
( )
1
2
0
3= +
∫
V x dx
D.
( )
1
2
2
0
3= +
∫
V x dx
Câu 23. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
3; 2;1A
trên trục
Ox
có tọa độ là:
A.
( )
0;0;1
. B.
( )
0; 2;0
. C.
( )
0; 2;1
. D.
( )
3;0;0
.
3/4 - Mã đề 101
Câu 24. Mệnh đề nào dưới đây đúng?
A.
(
)
( )
53d 53 d+ =++
∫∫
x xx
x ex x e ex
. B.
( ) ( )
53d 53 5 d+ =++
∫∫
x xx
x ex x e ex
.
C.
( )
(
)
53d 53 5 d+ =+−
∫∫
x xx
x ex x e ex
. D.
( ) ( )
53d 53 d+ =+−
∫∫
x xx
x ex x e ex
.
Câu 25. Trong không gian
,Oxyz
khoảng cách từ điểm
( )
1; 3; 2A −
đến mặt phẳng
(
)
:2 2 3 0
P xy z
+− −=
bằng
A.
3
. B.
5
. C.
4
. D.
2
.
Câu 26. Cho hàm số bậc ba
( )
=
y fx
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( )
y fx=
,
0y =
,
1x = −
và
3
=x
. Mệnh đề nào dưới đây là đúng?
A.
( ) ( )
23
12−
= +
∫∫
S f x dx f x dx
. B.
( ) ( )
23
12−
= −
∫∫
S f x dx f x dx
.
C.
( ) ( )
23
12−
=−−
∫∫
S f x dx f x dx
. D.
( ) ( )
23
12−
=−+
∫∫
S f x dx f x dx
.
Câu 27. Cho hàm số
( )
y fx=
liên tục trên
và
( )
11
1
d 45=
∫
fx x
. Giá trị của
( )
2
0
5 1d+
∫
fx x
bằng
A.
9
. B.
10
. C.
90
. D.
91
.
Câu 28. Họ tất cả các nguyên hàm của hàm số
2
() 7=
x
fx
là
A.
l
4
27
9
n
+
x
C
. B.
1
4
1
9
+
+
+
x
C
x
. C.
2
l
49
n7
⋅+
x
C
D.
2.49 ln 7 +
x
C
.
Câu 29. Biết
( )
4
0
d5=
∫
fx x
và
( )
4
2
d1fx x
= −
∫
. Khi đó
( )
2
0
d
∫
fx x
bằng
A.
4−
. B.
6
. C.
4
. D.
6−
.
Câu 30. Họ tất cả các nguyên hàm của hàm số
( )
43
54=++
x
fx x x e
là
A.
1
54
1
+
++ +
+
x
e
xx C
x
.B.
32
20 12
+ ++
x
x xeC
. C.
54
+++
x
xxeC
. D.
54 1+
++ +
x
xxe C
.
Câu 31. Xét hàm số
()fx
liên tục trên
và
( )
( )
2
0
9521
d+ =
∫
fx x x
. Khi đó
( )
2
0
d
∫
fx x
bằng
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 32. Họ tất cả các nguyên hàm của hàm số
4
( ) 5 cos= +fx x x
là
A.
5
5 sin−+x xC
B.
5
sin−+x xC
C.
5
sin++x xC
D.
5
5 sin++x xC
Câu 33. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
2; 1; 2 ; 0;1; 0AB−
. Mặt cầu đường kính
AB
có phương
trình là
A.
( ) ( )
22
2
1 13x yz− + +− =
. B.
( ) ( ) ( )
222
2 2 22xyz+ +− ++ =
.
C.
( ) ( )
22
2
1 13x yz− + +− =
. D.
( ) ( )
22
2
1 1 12x yz− ++− =
.
Câu 34. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
24= +fx x
và thỏa mãn
( )
10=F
. Giá trị của
( )
3F
bằng
A.
15
. B.
16
. C.
17
. D.
14
.
4/4 - Mã đề 101
Câu 35. Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
(
)
fx
trên
. Giá trị của
(
)
3
1
1dfx x
+


∫
bằng.
A.
32
3
. B.
8
. C.
10
. D.
26
3
.
Câu 36. Trong không gian
Oxyz
, cho hai điểm
( )
1; 3; 0A
và
( )
5;1; 2B −
. Mặt phẳng trung trực của đoạn
thẳng
AB
có phương trình là
A.
2 70++−=xyz
. B.
2 50xyz−−+=
. C.
2 10− −−=xyz
. D.
2 50xyz
−−−=
.
Câu 37. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 3 5 20− + −=Pxyz
. Điểm nào dưới đây thuộc mặt
phẳng
( )
P
?
A.
( )
1;1; 7
N
. B.
(
)
4; 4; 2
Q
. C.
( )
4; 1; 3−P
. D.
( )
0;0; 2M
.
Câu 38. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
2
41=−+ +
yx x
và đường thẳng
21= +yx
bằng
A.
4
3
. B.
16
3
C.
4
. D.
20
3
.
Câu 39. Cho
(
)
2
6
45
1
1d
= +
∫
Ix xx
. Đặt
5
1= +tx
, mệnh đề nào dưới đây đúng?
A.
2
6
1
1
td.
5
=
∫
It
B.
33
6
2
5 d.=
∫
I tt
C.
33
6
2
d.=
∫
I tt
D.
33
6
2
1
d.
5
=
∫
I tt
Câu 40. Trong không gian
Oxyz
cho hai điểm
( )
4; 2; 1A
,
( )
2; 1; 4B −−
. Điểm
( )
;;
M abc
thỏa mãn
3 0+ =
 
AM BM
. Khi đó
2 ++
abc
bằng
A.
2
. B.
3
. C.
5
2
. D.
6
.
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hai hàm số
3
33=++yx x
và
2
53=++yx x
Câu 2. Trong không gian
Oxyz
, cho ba điểm
( )
0;1; 2A
,
( )
2;0;3B
và
( )
3; 4; 0C
. Viết phương trình mặt
phẳng
(
)
ABC
Câu 3. Cho hàm số bậc ba
32
2
7
y f x ax bx x d 
và
đường thẳng
( )
y gx=
có đồ thị như hình vẽ bên. Biết
2 65
7
=AB
,
diện tích hình phẳng giới hạn bởi hai đồ thị
y fx
và
( )
y gx=
bằng bao nhiêu?
Câu 4. Cho hàm số
()fx
liên tục trên
thỏa mãn
(
)
0
2
1
2
() 2 d13 3= −+ +
∫
f xx x xf x
. Giá trị của
( )
2
0
∫
f x dx
bằng
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ...................
1/4 - Mã đề 102
THPT SỐ 3 BẢO THẮNG
TỔ: TOÁN – TIN - CN
(Đề thi có 04 trang)
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM (8 điểm)
Câu 1. Biết
( )
2
1
d3=
∫
fx x
và
( )
2
1
d2
=
∫
gx x
. Khi đó
( ) ( )
2
1
d−


∫
f x gx x
bằng?
A.
1−
. B.
1
. C.
5
. D.
6
.
Câu 2. Giá trị
4
0
d
∫
x
bằng
A.
4
. B.
0.
C.
4
−
. D.
5
Câu 3. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
4; 5; 2A
trên trục
Ox
có tọa độ là
A.
(
)
0;0; 2
. B.
( )
0; 5; 2
. C.
( )
4;0;0
. D.
(
)
0; 5; 0
.
Câu 4. Xét hàm số
()fx
liên tục trên đoạn
[ ]
;ab
. Mệnh đề nào dưới
đây đúng?
A.
( ) ( )
4 d4 d
bb
aa
fx x fx x=
∫∫
. B.
( ) ( )
4 d 4d
bb
aa
fxx f xx=
∫∫
.
C.
( ) ( )
4 d 4d . d
b ba
a ab
fx x x fx x=
∫ ∫∫
. D.
(
) ( )
4 d4 d
bb
aa
fx x fxx= +
∫∫
.
Câu 5. Mệnh đề nào dưới đây đúng?
A.
(
)
44
5 d d. 5d
xx
x x xx x
+=
∫ ∫∫
B.
( )
44
5 d d 5d
xx
x x xx x+=+
∫ ∫∫
.
C.
( )
44
5 d 5d d
xx
x x x xx
+=−
∫ ∫∫
D.
( )
44
5 d d 5d
xx
x x xx x+=−
∫ ∫∫
Câu 6. Họ tất cả các nguyên hàm của hàm số
() 3
x
fx e=
là
A.
3.
x
eC+
B.
1
3.
x
eC
+
−+
C.
1
3.
x
eC
+
+
D.
3.
x
eC−+
Câu 7. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
4, 0, 1, 3=+===yx y x x
. Gọi
V
là thể tích của
khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
( )
3
2
1
4d= +
∫
Vx x
B.
( )
3
2
2
1
4d= +
∫
Vx x
C.
( )
3
2
1
4d
π
= +
∫
Vxx
D.
( )
3
2
2
1
4d
π
= +
∫
Vx x
Câu 8. Biết
( )
3
1
d5= −
∫
fxx
và
( )
5
3
d2=
∫
fxx
. Khi đó
(
)
5
1
d
∫
fxx
bằng
A.
1
. B.
3−
. C.
1−
. D.
3
.
Câu 9. Họ tất cả các nguyên hàm của hàm số
( )
sin 4fx x=
là:
A.
1
cos 4
4
xC−+
. B.
cos 4xC+
. C.
cos 4xC−+
. D.
1
cos 4
4
xC+
.
Câu 10. Trong không gian
Oxyz
, cho mặt cầu
( ) ( )
2
22
: 2 36++− =Sx y z
. Bán kính của
( )
S
bằng:
A.
36
. B.
72
. C.
6
. D.
12
.
Câu 11. Họ tất cả các nguyên hàm của hàm số
( )
cosfx x=
là
A.
cos xC
−+
. B.
2
1
cos
2
xC+
. C.
sin xC−+
. D.
sin
xC+
.
Câu 12. Xét
( )
fx
là một hàm số tùy ý,
( )
Fx
là một nguyên hàm của
( )
fx
trên đoạn
[ ]
5; 6
. Mệnh đề nào
dưới đây đúng?
Mã đề 102
2/4 - Mã đề 102
A.
( ) ( ) ( )
6
5
d 56fx x F F= −
∫
. B.
( ) ( ) ( )
6
5
d 65fx x F F= +
∫
.
C.
( ) (
)
( )
6
5
d 56fx x F F=−−
∫
. D.
( ) ( )
( )
6
5
d 65
fx x F F= −
∫
.
Câu 13. Trong không gian
Oxyz
, cho 3 điểm
( )
1;0;0
−A
,
(
)
0; 2;0
B
và
( )
0;0;3C
. Mặt phẳng
( )
ABC
có
phương trình là
A.
1
123
++=
xyz
. B.
1
12 3
++ =
−
xy z
. C.
1
123
++=
−
x yz
. D.
1
1 23
+ +=
−
xyz
.
Câu 14. Mệnh đề nào dưới đây đúng?
A.
( )
43
4
d
′
= +
∫
x x xC
. B.
(
)
44
d
′
=−+
∫
x x xC
.
C.
( )
44
d
′
= +
∫
x xx C
. D.
( )
43
4d
′
=−+
∫
x x xC
.
Câu 15. Trong không gian
Oxyz
, cho hai điểm
(
)
3; 2; 0A
và
( )
1; 4; 3B
. Véctơ
AB

có tọa độ là
A.
( )
2; 2; 3−−
. B.
(
)
2; 2;3−
. C.
( )
2; 2;3−
. D.
( )
2; 2;3
.
Câu 16.
3
∫
x dx
bằng.
A.
4
1
4
xC
B.
2
3xC
C.
4
xC
D.
4
4xC
Câu 17. Cho hàm số
( )
fx
có đạo hàm
( )
′
fx
liên tục trên đoạn
[ ]
5; 6
và thỏa mãn
( )
5 1,
=f
(
)
6 11
=
f
. Giá
trị của
( )
6
5
d
′
∫
fxx
bằng
A.
10
. B.
1
C.
10−
. D.
12
.
Câu 18. Biết
(
)
5
1
4=
∫
f x dx
. Giá trị của
( )
5
1
3
∫
f x dx
bằng
A.
7
. B.
12
. C.
4
3
. D.
64
.
Câu 19. Cho hàm số
()fx
liên tục và không âm trên đoạn
[ ]
3; 4 .
Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số
()y fx=
, trục
Ox
và
2
đường thẳng
3, 4xx
= =
được tính theo công thức nào
dưới đây?
A.
( )
4
3
d.S fx x
π
=
∫
B.
( )
4
3
d.S fx x= −
∫
C.
( )
4
2
3
d.S fx x
π
=


∫
D.
( )
4
3
d.S fx x=
∫
Câu 20.
2
∫
x
dx
bằng
A.
2
ln 2
+
x
C
. B.
2 +
x
C
. C.
1
2
1
+
+
+
x
C
x
D.
2 .ln 2 +
x
C
.
Câu 21. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 4 3 0x yz
α
+ −+=
. Véctơ nào dưới đây là véc tơ pháp
tuyến của
( )
α
?
A.
( )
2
2; 4;1n = −

. B.
( )
3
2; 4;1n = −

. C.
( )
1
2; 4; 1n = −

. D.
( )
1
2; 4;1n =

.
Câu 22. Trong không gian
Oxyz
, cho hai điểm
( )
1; 2; 3A −
,
( )
3; 4; 3B −
. Toạ độ trung điểm
I
của đoạn
thẳng
AB
là
A.
. B.
( )
1; 3; 0
. C.
( )
2;6;0
. D.
( )
2; 1; 3−−
.
Câu 23. Trong không gian
Oxyz
, cho
2= −−OM i j k


. Tọa độ điểm
M
là
A.
( )
211−−−M ;;
. B.
( )
211−M ;;
. C.
( )
2 11−−M ;;
D.
( )
211−−M ;;
.
3/4 - Mã đề 102
Câu 24. Cho hàm số bậc ba
(
)
=
y fx
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( )
, 0, 3= = = −y fx y x
và
1
=x
. Mệnh đề nào dưới đây là đúng?
A.
( ) ( )
11
31
−
−−
= +
∫∫
S f x dx f x dx
. B.
( ) ( )
11
31
−
−−
= −
∫∫
S f x dx f x dx
.
C.
( ) ( )
11
31
−
−−
=−+
∫∫
S f x dx f x dx
D.
( ) ( )
11
31
−−
−−
=−−
∫∫
S f x dx f x dx
.
Câu 25. Trong không gian
Oxyz
, cho hai điểm là
( )
1; 3; 1A
−
,
(
)
3; 1; 5B
−
. Điểm
(
)
;;
M abc
thỏa mãn
40+=
 
AM BM
. Khi đó
2++a bc
bằng
A.
6
. B.
31
5
. C.
9
. D.
8
.
Câu 26. Trong không gian
Oxyz
, khoảng cách từ điểm
( )
1; 0; 2−A
đến mặt phẳng
(
)
: 2 2 14 0+ −+=
Px y z
bằng
A.
2
. B.
4
. C.
5
. D.
3
.
Câu 27. Biết
( )
2
1
d2= −
∫
fx x
và
( )
3
1
d7=
∫
fx x
. Khi đó
( )
3
2
d
∫
fx x
bằng
A.
5−
. B.
5
. C.
9
. D.
9−
.
Câu 28. Họ tất cả các nguyên hàm của hàm số
2
() 5
x
fx
=
là
A.
1
25
1
x
C
x
+
+
+
. B.
2
l
25
n5
⋅+
x
C
C.
2.25 ln5 +
x
C
. D.
25
2ln 5
x
C
+
.
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
2
21=−+ −yx x
và đường thẳng
31=−−yx
bằng
A.
135
6
. B.
25
6
C.
7
. D.
125
6
.
Câu 30. Xét hàm số
()fx
liên tục trên
và
( )
( )
2
2
0
.2
03d1
+ =
∫
fx x x
Khi đó
(
)
2
0
d
∫
fx x
bằng
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 31. Mệnh đề nào dưới đây đúng?
A.
( ) ( )
32d 32 d+ =++
∫∫
x xx
xexxeex
. B.
( )
( )
32d 32 3 d+ =++
∫∫
x xx
xexxe ex
.
C.
( )
( )
32d 32 3 d+ =+−
∫∫
x xx
xexxe ex
. D.
( ) ( )
32d 32 d+ =+−
∫∫
x xx
xexxeex
.
Câu 32. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
26= +fx x
và thỏa mãn
( )
16= −
F
. Giá trị của
( )
3F
bằng
A.
15
. B.
17
. C.
16
. D.
14
.
Câu 33. Biết
( )
3
Fx x
=
là một nguyên hàm của hàm số
( )
fx
trên
. Giá trị của
( )
2
1
2 f x dx+


∫
bằng
A.
15
4
. B.
23
4
. C.
7
. D.
9
.
4/4 - Mã đề 102
Câu 34. Cho
( )
2
3
2
1
1d= +
∫
Ixxx
. Đặt
2
1tx= +
, mệnh đề nào dưới đây đúng?
A.
5
3
2
1
d.
2
=
∫
I tt
B.
2
3
1
1
td.
2
=
∫
It
C.
5
3
2
d.
=
∫
I tt
D.
5
3
2
2 d.=
∫
I tt
Câu 35. Trong không gian
Oxyz
, cho hai điểm
( )
2;1; 2A
và
(
)
6; 5; 4B
−
. Mặt phẳng trung trực của đoạn
thẳng
AB
có phương trình là
A.
2 2 3 17 0xyz+ −−=
.B.
2230
+−=
xyz
. C.
2 2 3 17 0xyz+ −+=
. D.
2 2 3 11 0xyz
+ +−=
.
Câu 36. Cho hàm số
( )
y fx=
liên tục trên
và
( )
5
1
d6=
∫
fx x
. Giá trị của
( )
2
0
2 1d+
∫
fx x
bằng
A.
12
. B.
3
. C.
4
. D.
13
.
Câu 37. Họ tất cả các nguyên hàm của hàm số
3
( ) 4 cos
= +fx x x
là
A.
4
4 sin−+x xC
B.
4
sin++x xC
C.
4
4 sin++x xC
D.
4
sin−+x xC
Câu 38. Trong không gian
Oxyz
, cho hai điểm
( )
1; 3;4A −−
và
( )
3; 1;2B −
. Phương trình mặt cầu đường
kính
AB
là
A.
( ) ( ) ( )
2 22
1 2 3 24xy z+ +− ++ =
. B.
(
) (
) (
)
2 22
1 2 3 24
xy z− ++ +− =
.
C.
( ) ( ) ( )
2 22
1 2 36xy z− ++ +− =
. D.
(
) ( ) ( )
2 22
1 2 36xy z+ +− ++ =
.
Câu 39. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 3 50− + −=
Px y z
. Điểm nào dưới đây thuộc mặt
phẳng
( )
P
?
A.
( )
0;1;1P
. B.
(
)
2; 1; 3
−Q
. C.
( )
0; 1;1−M
. D.
( )
1; 2; 3
N
.
Câu 40. Họ tất cả các nguyên hàm của hàm số
( )
54
65=++
x
fx x x e
là
A.
65
+++
x
xxeC
. B.
43
30 20+ ++
x
x xeC
.
C.
1
65
1
+
++ +
+
x
e
xx C
x
. D.
65 1
+
++ +
x
xxe C
.
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hai hàm số
3
2=−+yx
và
2
22=−+yx x
Câu 2. Trong không gian
Oxyz
, cho ba điểm
( )
3; 1; 2A −
,
(
)
4;1;1B
−−
và
( )
2;0; 2C
. Viết phương trình mặt
phẳng
( )
ABC
Câu 3. Cho hàm số bậc ba
32
2
7
y f x ax bx x d 
và
đường thẳng
( )
y gx=
có đồ thị như hình vẽ bên. Biết
4 65
7
=AB
,
diện tích hình phẳng giới hạn bởi hai đồ thị
y fx
và
(
)
y gx=
bằng bao nhiêu?
Câu 4. Cho hàm số
()fx
liên tục trên
thỏa mãn
(
)
2
1
2
0
() 2 3 d13 63= −
++
∫
f xx x xf x
. Giá trị của
( )
2
0
d
∫
fx x
bằng
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ...................
1/4 - Mã đề 103
THPT SỐ 3 BẢO THẮNG
TỔ: TOÁN – TIN - CN
(Đề thi có 04 trang)
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM (8 điểm)
Câu 1. Trong không gian
Oxyz
, cho hai điểm
( 1; 0; 2)A
và
(3; 4; 6)B
. Toạ độ trung điểm
I
của đoạn
thẳng
AB
là
A.
(2; 4;8)A
.
B.
(2; 2; 2)A
. C.
( 1; 2; 4)A 
. D.
(1; 2; 4)A
.
Câu 2. Biết
(
)
2
1
d3=
∫
fx x
và
(
)
5
2
d1
= −
∫
fx x
. Khi đó
( )
5
1
d
∫
fx x
bằng
A. 2. B. 3. C.
2−
. D. 4.
Câu 3. Trong không gian
Oxyz
, cho ba điểm
( )
( )
2;0;0 , 0;3;0
−AB
và
( )
0;0; 4C
. Mặt phẳng
( )
ABC
có
phương trình là
A.
1
2 34
+ +=
−
xyz
. B.
1
23 4
++ =
−
xy z
. C.
1
234
++=
xyz
. D.
1
234
++=
−
x yz
.
Câu 4. Cho hàm số
( )
fx
có đạo hàm
( )
′
fx
liên tục trên đoạn
[ ]
2; 4
và thỏa mãn
( )
2 3,=f
( )
4 10=f
. Giá
trị của
( )
4
2
d
′
∫
fxx
bằng
A.
7−
. B.
2
C.
13
. D.
7
.
Câu 5. Mệnh đề nào dưới đây đúng?
A.
( )
54
5d
′
=−+
∫
x x xC
.B.
( )
55
d
′
= +
∫
x xx C
. C.
(
)
54
5d
′
= +
∫
x x xC
. D.
( )
55
d
′
=−+
∫
x x xC
.
Câu 6. Họ tất cả các nguyên hàm của hàm số
( )
sin 5fx x=
là:
A.
cos5xC+
. B.
cos5xC−+
. C.
1
cos5
5
xC−+
. D.
1
cos5
5
xC+
.
Câu 7. Họ tất cả các nguyên hàm của hàm số
( )
2
1
cos
fx
x
=
là
A.
cot xC−+
. B.
tan xC−+
. C.
tan
xC+
. D.
cot xC+
.
Câu 8. Biết
(
)
3
2
d6
=
∫
fx x
. Giá trị của
(
)
3
2
2d
∫
fx x
bằng
A.
8
. B.
3
. C.
36
. D.
12
.
Câu 9. Trong không gian
Oxyz
, Cho mặt phẳng
( )
:2 3 5 0xy z
α
−+ +=
. Vectơ nào dưới đây là một vectơ
pháp tuyến của
( )
α
?
A.
(
)
4
2;1; 3 .n = −

B.
( )
2
2; 1; 3 .n = −

C.
(
)
1
2;1; 3 .
n =

D.
(
)
3
2;1; 3 .
n = −

Câu 10. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
1; 2; 5A
lên trục
Ox
có tọa độ là
A.
( )
1;0;0
. B.
( )
0; 2;5
. C.
( )
0; 2;0
. D.
( )
0;0;5
.
Câu 11. Xét hàm số
()fx
liên tục trên đoạn
[ ]
;ab
. Mệnh đề nào dưới
đây đúng?
A.
( ) ( )
2 d 2d
bb
aa
fxx f xx=
∫∫
. B.
( )
( )
2 d 2d . d
b ba
a ab
fx x x fx x=
∫ ∫∫
.
C.
( ) ( )
2 d2 d
bb
aa
fx x fx x=
∫∫
. D.
( ) ( )
2 d2 d
bb
aa
fx x fxx= +
∫∫
.
Câu 12. Xét
( )
fx
là một hàm số tùy ý,
(
)
Fx
là một nguyên hàm của
( )
fx
trên đoạn
[ ]
1; 2
. Mệnh đề nào
Mã đề 103
2/4 - Mã đề 103
dưới đây đúng?
A.
( ) ( ) ( )
2
1
d 12fx x F F=−−
∫
. B.
( ) ( ) ( )
2
1
d 12fx x F F= +
∫
.
C.
( ) ( ) ( )
2
1
d 12fx x F F= −
∫
. D.
( ) ( ) ( )
2
1
d 21fx x F F= −
∫
.
Câu 13. Trong không gian
Oxyz
, cho
23
=−+OM i j k


. Tọa độ điểm
M
là
A.
( )
123−−M ;;
. B.
( )
1 23−M ;;
. C.
( )
1 23−−M ;;
D.
( )
123−−−
M
;;
.
Câu 14. Trong không gian
Oxyz
, cho hai điểm
( )
1; 1;2A −
và
( )
2;1; 4B −
. Véctơ
AB

có tọa độ là
A.
( )
1;0; 6−
. B.
( )
1; 2;6−−
. C.
( )
3;0; 2−
. D.
( )
1;2; 6−
.
Câu 15. Trong không gian
Oxyz
, cho mặt cầu
22 2
( ) : ( 1) 16Sx y z+ +− =
. Bán kính của
()S
là:
A.
4
B.
8
C.
32
D.
16
Câu 16. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
1, 0, 0, 2
=+= = =
yx y x x
. Gọi
V
là thể tích của
khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
( )
2
2
2
0
1d= +
∫
Vx x
B.
( )
2
2
0
1d
π
= +
∫
V xx
C.
( )
2
2
2
0
1d
π
= +
∫
Vx x
D.
(
)
2
2
0
1d= +
∫
Vx x
Câu 17. Biết
2
1
() 2=
∫
f x dx
và
2
1
( ) 3.=
∫
g x dx
Khi đó
(
) (
)
2
1
d

+

∫
f x gx x
bằng
A.
6
. B.
1
. C.
1−
. D.
5
.
Câu 18.
2
∫
x dx
bằng
A.
3
1
3
xC+
. B.
3
3xC+
C.
3
xC+
. D.
2xC+
.
Câu 19. Mệnh đề nào dưới đây đúng?
A.
( )
55
6 d 6d d
xx
x x x xx+=−
∫ ∫∫
B.
( )
55
6 d d 6d
xx
x x xx x
+=+
∫ ∫∫
.
C.
(
)
55
6 d d.6d
xx
x x xx x+=
∫ ∫∫
D.
( )
55
6 d d 6d
xx
x x xx x+=−
∫ ∫∫
Câu 20. Giá trị
6
0
d
∫
x
bằng
A.
6
. B.
0.
C.
7
D.
6−
.
Câu 21.
3
∫
x
dx
bằng
A.
3
ln 3
+
x
C
. B.
3 +
x
C
. C.
3 .ln 3 +
x
C
. D.
1
3
1
+
+
+
x
C
x
Câu 22. Cho hàm số
()fx
liên tục và không âm trên đoạn
[ ]
1; 2 .
Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số
()
y fx=
, trục
Ox
và
2
đường thẳng
1, 2xx= =
được tính theo công thức nào
dưới đây?
A.
( )
2
1
d.S fx x
π
=
∫
B.
( )
2
2
1
d.S fx x
π
=


∫
C.
( )
2
1
d.S fx x= −
∫
D.
( )
2
1
d.S fx x=
∫
Câu 23. Họ tất cả các nguyên hàm của hàm số
() 5
x
fx e=
là
A.
1
5.
x
eC
+
+
B.
5.
x
eC+
C.
5.
x
eC−+
D.
1
5.
x
eC
+
−+
Câu 24. Cho
(
)
2
5
34
1
1d= +
∫
Ix xx
. Đặt
4
1= +tx
, mệnh đề nào dưới đây đúng?
A.
17
5
2
d.=
∫
I tt
B.
17
5
2
4 d.=
∫
I tt
C.
17
5
2
1
d.
4
=
∫
I tt
D.
2
5
1
1
td.
4
=
∫
It
3/4 - Mã đề 103
Câu 25. Xét hàm số
()fx
liên tục trên
và
( )
( )
2
3
0
83 4d2+ =
∫
fx x x
. Khi đó
(
)
2
0
d
∫
fx x
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 26. Cho hàm số bậc ba
( )
=
y fx
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( )
, 0, 1
= = = −y fx y x
và
2=x
.
Mệnh đề nào dưới đây đúng?
A.
( ) ( )
12
11
S f x dx f x dx
−
=−+
∫∫
. B.
(
)
( )
12
11
S f x dx f x dx
−
= −
∫∫
.
C.
(
) (
)
12
11
S f x dx f x dx
−
=−−
∫∫
. D.
( ) ( )
12
11
S f x dx f x dx
−
= +
∫∫
.
Câu 27. Biết
3
1
( )d 2
fx x=
∫
và
3
2
( )d 3= −
∫
fx x
. Khi đó
2
1
( )d
∫
fx x
bằng
A.
5−
. B.
1−
. C.
1
. D.
5
.
Câu 28. Họ tất cả các nguyên hàm của hàm số
( ) 2 cos= +fx x x
là
A.
2
sin−+x xC
B.
2
2 sin
++x xC
C.
2
sin++x xC
D.
2
2 sin−+x xC
Câu 29. Trong không gian
Oxyz
, khoảng cách từ điểm
( )
1 21;;A −
đến mặt phẳng
( )
2 2 50
− + +=
:
Px y z
bằng
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 30. Họ tất cả các nguyên hàm của hàm số
( )
32
43=++
x
fx x x e
là
A.
1
43
1
+
++ +
+
x
e
xx C
x
. B.
43
+++
x
xxeC
. C.
43 1+
++ +
x
xxe C
. D.
2
12 6+ ++
x
x xe C
.
Câu 31. Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
( )
fx
trên
. Giá trị của
(
)
2
1
2dfx x+


∫
bằng
A.
3
. B.
5
. C.
7
3
. D.
13
3
.
Câu 32. Cho hàm số
(
)
y fx=
liên tục trên
và
( )
9
1
d 28=
∫
fx x
. Giá trị của
( )
2
0
4 1d+
∫
fx x
bằng
A.
57
. B.
56
. C.
7
. D.
8
.
Câu 33. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 2 3 6 0− + +=
P xyz
. Điểm nào dưới đây thuộc mặt
phẳng
( )
P
?
A.
( )
3;2;3= −−Q
. B.
(
)
3;0;0=M
. C.
( )
3;3; 2= −N
. D.
( )
2; 2;3= −P
.
Câu 34. Trong không gian
Oxyz
, cho hai điểm
( )
4;0;1
A
,
( )
2; 2;5−B
. Mặt phẳng trung trực của đoạn thẳng
AB
có phương trình là
A.
3 2 40−− −=xy z
. B.
3 2 40−− +=xy z
. C.
3 2 10 0−− − =xy z
. D.
3 2 10 0++ − =xy z
.
Câu 35. Họ tất cả các nguyên hàm của hàm số
2
() 3=
x
fx
là
A.
2
l
9
n3
⋅+
x
C
B.
2.9 ln 3+
x
C
. C.
1
9
1
+
+
+
x
C
x
. D.
9
2ln 3
+
x
C
.
4/4 - Mã đề 103
Câu 36. Trong không gian
Oxyz
, cho hai điểm
(
)
0;1; 2
A
−
và
( )
3; 1;1B −
. Điểm
( )
;;M abc
thỏa mãn
50+=
 
AM MB
. Khi đó
3++a bc
bằng
A.
4
. B.
8
. C.
1
. D.
9
2
.
Câu 37. Mệnh đề nào dưới đây đúng?
A.
(
) ( )
41d 41 4 d+ =++
∫∫
x xx
x ex x e ex
. B.
( ) ( )
41d 41 d+ =+−
∫∫
x xx
x ex x e ex
.
C.
(
) ( )
41d 41 4 d+ =+−
∫∫
x xx
x ex x e ex
. D.
(
) (
)
41d 41 d
+ =++
∫∫
x xx
x ex x e ex
.
Câu 38. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
4; 3; 7 , 2;1;3−AB
. Mặt cầu đường kính
AB
có phương
trình là
A.
( ) ( ) ( )
222
3 1 5 3.x yz− ++ +− =
B.
( ) ( ) ( )
222
3 1 5 9.x yz+ +− ++ =
C.
( )
(
) ( )
222
3 1 5 3.x yz+ +− ++ =
D.
(
) ( ) ( )
222
3 1 5 9.x yz− ++ +− =
Câu 39. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
23= +fx x
và thỏa mãn
(
)
13
=
F
. Giá trị của
( )
3F
bằng
A.
17
. B.
15
. C.
16
. D.
14
.
Câu 40. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
2
2=− −−y xx
và đường thẳng
32= −yx
bằng
A.
32
3
. B.
31
3
C.
6
. D.
17
3
.
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hai hàm số
3
41=−+ −yx x
và
2
21=−+ −yx x
Câu 2. Trong không gian
Oxyz
, cho ba điểm
( )
2; 1; 3A −
,
( )
4;0;1B
và
( )
10;5;3C −
. Viết phương trình mặt
phẳng
( )
ABC
Câu 3. Cho hàm số bậc ba
32
1
5
y f x ax bx x d

và
đường thẳng
( )
y gx=
có đồ thị như hình vẽ bên. Biết
2 34
5
=AB
, diện tích
hình phẳng giới hạn bởi hai đồ thị
y fx
và
( )
y gx=
bằng bao nhiêu?
Câu 4. Cho hàm số
()fx
liên tục trên
thỏa mãn
(
)
2
1
2
0
() 2 1 d19 35= − ++
∫
f xx x xf x
. Giá trị của
( )
2
0
∫
f x dx
bằng ------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ...................
1/4 - Mã đề 104
THPT SỐ 3 BẢO THẮNG
TỔ: TOÁN – TIN - CN
(Đề thi có 04 trang)
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM (8 điểm)
Câu 1. Cho hàm số
(
)
fx
có đạo hàm
(
)
′
fx
liên tục trên đoạn
[ ]
1; 3
và thỏa mãn
(
)
1 5,=f
( )
3 11=f
. Giá
trị của
(
)
3
1
d
′
∫
fxx
bằng
A.
6
B.
16
. C.
6−
. D.
2
.
Câu 2. Trong không gian
Oxyz
, cho
23=−+
OM i j k


. Tọa độ điểm
M
là
A.
( )
231M ;;
B.
( )
23 1M −−;;
. C.
(
)
231
M
−−;;
. D.
( )
2 31
M
−;;
.
Câu 3. Mệnh đề nào dưới đây đúng?
A.
( )
22
4 d 4d d
xx
x x x xx+=−
∫ ∫∫
B.
( )
22
4 d d 4d
xx
x x xx x
+=+
∫ ∫∫
.
C.
( )
22
4 d d 4d
xx
x x xx x
+=−
∫ ∫∫
D.
( )
22
4 d d. 4d
xx
x x xx x+=
∫ ∫∫
Câu 4. Biết
( )
6
0
d7=
∫
fx x
và
( )
10
6
d3=
∫
fx x
. Khi đó
( )
10
0
d
∫
fx x
bằng
A.
4−
. B.
21
. C.
4
. D.
10
.
Câu 5. Biết
(
)
3
1
d3
=
∫
fx x
. Giá trị của
(
)
3
1
2d
∫
fx x
bằng
A.
6
. B.
5
. C.
9
. D.
3
2
.
Câu 6.
7
∫
x
dx
bằng
A.
7 +
x
C
. B.
7
ln 7
+
x
C
. C.
7 .ln 7 +
x
C
. D.
1
7
1
+
+
+
x
C
x
Câu 7. Trong không gian
Oxyz
, cho 3 điểm
( ) ( ) ( )
2;0;0 , 0; 1;0 , 0;0;3
−AB C
. Mặt phẳng
( )
ABC
có
phương trình là
A.
1
213
++=
xyz
. B.
1
213
++=
−
x yz
. C.
1
213
++=
−−
xy z
. D.
1
2 13
+ +=
−
xyz
.
Câu 8. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 4 10xyz
α
− + −=
.Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng
( )
α
?
A.
( )
3
1; 2; 4n
→
= −
. B.
( )
4
1;2;4n
→
= −
C.
( )
2
1;2;4n
→
=
. D.
( )
1
1; 2; 4n
→
= −
.
Câu 9. Trong không gian
Oxyz
, cho mặt cầu
2 22
(S) : x (y 2) 25+− + =z
. Bán kính của
(S)
bằng
A.
25
. B.
5
. C.
50
. D.
25
.
Câu 10. Trong không gian Oxyz, cho hai điểm
( )
1; 5; 2A −
và
( )
3; 3; 2B −
. Toạ độ trung điểm
M
của đoạn
thẳng
AB
là
A.
( )
1;1; 2
. B.
( )
4; 8; 0
M
−
. C.
( )
2; 2; 4M
. D.
( )
2; 4;0M −
.
Câu 11. Cho hàm số
()fx
liên tục và không âm trên đoạn
[ ]
7;8 .
Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số
()y fx=
, trục
Ox
và
2
đường thẳng
7, 8xx= =
được tính theo công thức nào
dưới đây?
A.
( )
8
2
7
d.S fx x
π
=


∫
B.
( )
8
7
d.S fx x= −
∫
C.
( )
8
7
d.S fx x=
∫
D.
( )
8
7
d.S fx x
π
=
∫
Mã đề 104
2/4 - Mã đề 104
Câu 12. Giá trị
3
0
d
∫
x
bằng
A.
3−
. B.
3
. C.
0.
D.
4
Câu 13. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
8;1; 2A
trên trục
Ox
có tọa độ là
A.
( )
0;1;2
. B.
( )
8;0;0
. C.
(
)
0;1;0
. D.
( )
0;0;2
.
Câu 14. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
2, 0, 1, 2=+===yx y x x
. Gọi
V
là thể tích của
khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
( )
2
2
2
1
2dVx x
= +
∫
B.
(
)
2
2
1
2dVx x= +
∫
C.
(
)
2
2
2
1
2d
Vx x
π
= +
∫
D.
( )
2
2
1
2dVxx
π
= +
∫
Câu 15. Trong không gian
Oxyz
, cho hai điểm
(1; 0 ;1)A
và
(2; 1; 2)B −−
. Véctơ
AB

có tọa độ là
A.
( 1;1;3)
−
. B.
(1; 1; 1)−−
. C.
(1;1; 3)−
. D.
(1; 1; 3)−−
.
Câu 16. Mệnh đề nào dưới đây đúng?
A.
(
)
2
2d
′
= +
∫
x x xC
. B.
( )
22
d
′
= +
∫
x xx C
. C.
( )
22
d
′
=−+
∫
x x xC
. D.
( )
2
2d
′
=−+
∫
x x xC
.
Câu 17.
5
∫
x dx
bằng
A.
6
xC+
. B.
4
5xC+
. C.
6
1
6
xC+
. D.
6
6xC+
.
Câu 18. Xét hàm số
()fx
liên tục trên đoạn
[ ]
;ab
. Mệnh đề nào dưới
đây đúng?
A.
( ) ( )
5 d 5d
bb
aa
fxx f xx=
∫∫
. B.
( ) ( )
5 d5 d
bb
aa
fx x fx x=
∫∫
.
C.
( ) ( )
5 d5 d
bb
aa
fx x fxx= +
∫∫
. D.
(
) (
)
5 d 5d . d
b ba
a ab
fx x x fx x=
∫ ∫∫
.
Câu 19. Họ tất cả các nguyên hàm của hàm số
( )
2
1
sin
fx
x
=
là
A.
cot xC+
. B.
tan xC−+
. C.
cot xC−+
. D.
tan xC
+
.
Câu 20. Biết
( )
3
2
4
=
∫
f x dx
và
( )
3
2
1=
∫
g x dx
. Khi đó:
( ) ( )
3
2
−


∫
f x g x dx
bằng:
A.
3
−
. B.
5
. C.
4
. D.
3
.
Câu 21. Họ tất cả các nguyên hàm của hàm số
(
)
sin 6
fx x=
là:
A.
1
cos 6
6
xC−+
. B.
cos 6xC−+
. C.
1
cos 6
6
xC+
. D.
cos 6xC+
.
Câu 22. Họ tất cả các nguyên hàm của hàm số
() 4
x
fx e=
là
A.
1
4.
x
eC
+
−+
B.
4.
x
eC−+
C.
4.
x
eC+
D.
1
4.
x
eC
+
+
Câu 23. Xét
( )
fx
là một hàm số tùy ý,
( )
Fx
là một nguyên hàm của
( )
fx
trên đoạn
[ ]
3; 4
. Mệnh đề nào
dưới đây đúng?
A.
( ) ( ) ( )
4
3
d 34fx x F F= −
∫
. B.
( ) ( ) ( )
4
3
d 43fx x F F= −
∫
.
C.
( ) ( ) ( )
4
3
d 43fx x F F= +
∫
. D.
( ) ( ) ( )
4
3
d 34fx x F F=−−
∫
.
Câu 24. Họ tất cả các nguyên hàm của hàm số
( )
2
32= ++
x
fx x x e
là
3/4 - Mã đề 104
A.
32 1
+
++ +
x
xxe C
. B.
1
32
1
+
++ +
+
x
e
xx C
x
. C.
62++ +
x
x eC
. D.
32
+++
x
xxeC
.
Câu 25. Cho hàm số
( )
y fx=
liên tục trên
và
( )
7
1
d 15=
∫
fx x
. Giá trị của
( )
2
0
3 1d+
∫
fx x
bằng
A.
30
. B.
31
. C.
5
. D.
6
.
Câu 26. Cho hàm số bậc ba
( )
=y fx
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
(
)
, 0, 2
= = = −y fx y x
và
2=x
.
Mệnh đề nào dưới đây là đúng?
A.
( ) ( )
12
21−
=−+
∫∫
S f x dx f x dx
. B.
( ) ( )
12
21−
= −
∫∫
S f x dx f x dx
.
C.
( ) ( )
12
21
−
= +
∫∫
S f x dx f x dx
. D.
( ) ( )
12
21−
=−−
∫∫
S f x dx f x dx
.
Câu 27. Cho
(
)
Fx
là một nguyên hàm của hàm số
( )
25= +fx x
và thỏa mãn
(
)
13
= −F
. Giá trị của
( )
3F
bằng
A.
15
. B.
17
. C.
16
. D.
14
.
Câu 28. Họ tất cả các nguyên hàm của hàm số
2
() 9
=
x
fx
là
A.
2.81 ln 9 +
x
C
. B.
l
8
29
1
n
+
x
C
. C.
2
l
81
n9
⋅+
x
C
D.
1
8
1
1
+
+
+
x
C
x
.
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
2
23=−+ −yx x
và đường thẳng
3
=−−yx
bằng
A.
5
. B.
11
2
C.
7
2
. D.
9
2
.
Câu 30. Biết
3
()Fx x
=
là một nguyên hàm của hàm số
()fx
trên
. Giá trị của
3
1
(1 ( ) d)x xf+
∫
bằng
A. 28. B. 20. C. 26. D. 22.
Câu 31. Cho
( )
2
4
23
1
1d= +
∫
Ix xx
. Đặt
3
1= +tx
, mệnh đề nào dưới đây đúng?
A.
9
4
2
1
d.
3
=
∫
I tt
B.
9
4
2
3 d.
=
∫
I tt
C.
2
4
1
1
td.
3
=
∫
It
D.
9
4
2
d.=
∫
I tt
Câu 32. Mệnh đề nào dưới đây đúng?
A.
( ) ( )
21d 21 2 d+ =++
∫∫
x xx
x ex x e ex
. B.
( ) ( )
21d 21 d+ =+−
∫∫
x xx
x ex x e ex
.
C.
( ) ( )
21d 21 d+ =++
∫∫
x xx
x ex x e ex
. D.
( ) ( )
21d 21 2 d+ =+−
∫∫
x xx
x ex x e ex
.
Câu 33. Trong không gian
Ox ,yz
cho hai điểm
( ) ( )
1; 2; 0 , 3;0; 2AB−
. Phương trình mặt phẳng trung trực của
đoạn thẳng
AB
là
A.
2 20xyz−++=
. B.
2 20xyz−+−=
. C.
2 60++−=xyz
. D.
2 40−+−=xyz
.
Câu 34. Họ tất cả các nguyên hàm của hàm số
2
( ) 3 cos= +fx x x
là
4/4 - Mã đề 104
A.
3
3 sin++
x xC
B.
3
sin−+x xC
C.
3
sin++x xC
D.
3
3 sin−+x xC
Câu 35. Trong không gian
Oxyz
, cho mặt phẳng
( ) : 3 2 4 10 0−++=Pxyz
. Điểm nào dưới đây thuộc
()P
?
A.
(1; 2; 3)−N
. B.
( 2; 1;3)−Q
. C.
(2;2; 3)−P
. D.
(3; 2;4)−M
.
Câu 36. Trong không gian
Oxyz
, cho hai điểm
( )
3;1; 2−A
,
(
)
2; 3;5
−
B
. Điểm
( )
;;M abc
thỏa mãn
20+=
 
MA MB
. Khi đó
3++a bc
bằng
A.
10
. B.
10
3
. C.
5
. D.
0
.
Câu 37. Biết
3
1
( )d 5=
∫
fx x
và
2
1
( )d 2= −
∫
fx x
. Khi đó
3
2
( )d
∫
fx x
bằng
A.
7
. B.
3−
. C.
3
. D.
7
−
.
Câu 38. Trong không gian
Oxyz
, khoảng cách từ điểm
( )
1;2;1M
đến mặt phẳng
(
)
: 2 2 13 0−− − =
P xy z
bằng
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 39. Xét hàm số
()fx
liên tục trên
và
( )
( )
2
4
0
04 5d
4+
=
∫
fx x x
. Khi đó
( )
2
0
d
∫
fx x
bằng
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 40. Trong không gian
Oxyz
, cho hai điểm
( )
1;3; 2A −
,
( )
3; 1; 4B
−
. Mặt cầu đường kính
AB
có
phương trình
A.
(
)
(
) (
)
2 22
2 1 1 14
x yz+ ++ ++ =
. B.
( )
(
)
(
)
2 22
2 1 1 14x yz− +− +− =
.
C.
(
)
(
)
( )
2 22
2 1 1 14
x yz
− +− +− =
. D.
(
) (
)
( )
2 22
2 1 1 14x yz+ ++ ++ =
.
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hai hàm số
3
1= −−yx x
và
2
1
=− +−y xx
Câu 2. Trong không gian
Oxyz
, cho ba điểm
( )
1; 3; 2A −
,
( )
1; 0;1B
và
( )
2; 3; 0C
. Viết phương trình mặt
phẳng
(
)
ABC
Câu 3. Cho hàm số bậc ba
32
1
5
y f x ax bx x d 
và đường
thẳng
( )
y gx=
có đồ thị như hình vẽ bên. Biết
4 34
5
=AB
, diện tích hình
phẳng giới hạn bởi hai đồ thị
y fx
và
( )
y gx
=
bằng bao nhiêu?
Câu 4. Cho hàm số
()
fx
liên tục trên
thỏa mãn
(
)
2
1
2
0
() 2 9 1 15 d= − ++
∫
f xx x xf x
. Giá trị của
( )
2
0
∫
f x dx
bằng
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ...................
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

THPT SỐ 3 BẢO THẮNG
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022 TỔ: TOÁN – TIN - CN
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(Đề thi có 04 trang)
(không kể thời gian phát đề) Mã đề 101
PHẦN I. TRẮC NGHIỆM (8 điểm)
Câu 1. Họ tất cả các nguyên hàm của hàm số f (x) = sin3x là:
A. cos3x + C .
B. −cos3x + C .
C. 1 cos3x + C . D. 1 − cos3x + C . 3 3 Câu 2. 4d ∫ x x bằng 1 A. 3 4x + C B. 5 x + C C. 5 x + C D. 5 5x + C 5    
Câu 3. Trong không gian Oxyz , cho OM = i + j − 3k . Tọa độ điểm M là
A. M (1;1;3) . B. M ( 1 − ; 1 − ; 3 − ) C. M ( 1 − ;1; 3 − ) . D. M (1;1; 3 − ) .
Câu 4. Mệnh đề nào dưới đây đúng? A. ( 3)′ 2 d = 3 +
∫ x x x C . B. ( 3)′ 3 d = +
∫ x x x C . C. ( 3)′ 2 d = 3 − + ∫ x x x C . D. ( 3 )′ 3 d = − + ∫ x x x C .
Câu 5. Trong không gian Oxyz , cho mặt phẳng (α ) : 2x −3y + 4z −1= 0 . Vectơ nào dưới đây là một vectơ pháp tuyến của (α ) ?     A. n = 2;3; 4 − n = 2;3;4 n = 2 − ;3;4 n = 2; 3 − ;4 2 ( ). B. 1 ( ). C. 4 ( ). D. 3 ( ) . Câu 6. 5 ∫ xdxbằng x 1 + x A. 5
5x + C .
B. 5x.ln 5 + C . C. + C D. 5 + C . x +1 ln 5
Câu 7. Họ tất cả các nguyên hàm của hàm số ( ) = 2 x f x e là A. x 1
2e + + C. B. 2 x
− e + C. C. 2 x e + C. D. x 1 2e + − + C. 5 Câu 8. Giá trị d ∫ x bằng 0 A. 5 . B. 6 C. 5 − . D. 0.
Câu 9. Họ tất cả các nguyên hàm của hàm số f (x) = sin x là A. 1
cos x + C . B. 2
sin x + C .
C. −sin x + C .
D. −cos x + C . 2
Câu 10. Trong không gian Oxyz , cho mặt cầu (S ) 2 2
: x + y + (z + 2)2 = 9. Bán kính của (S) bằng A. 3 . B. 18. C. 9 . D. 6 .
Câu 11. Xét f (x) là một hàm số tùy ý, F (x) là một nguyên hàm của f (x) trên đoạn[7;8]. Mệnh đề nào dưới đây đúng? 8 6 A. f
∫ (x)dx = F (7)− F (8). B. f
∫ (x)dx = F (8)+ F (7). 7 5 8 6 C. f
∫ (x)dx = F (8)− F (7). D. f
∫ (x)dx = −F (7)− F (8). 7 5
Câu 12. Trong không gian Oxyz cho điểm A(2;1;3) và điểm B(4; 3 − ; )
1 . Toạ độ trung điểm I của đoạn thẳng AB là A. (6; 2; − 4) . B. (3; 1; − 2). C. (1; 2 − ;− ) 1 . D. (2; 4; − 2 − ) . 1/4 - Mã đề 101
Câu 13. Cho hàm số f (x) có đạo hàm f ′(x) liên tục trên đoạn [3;5] và thỏa mãn f (3) = 2, f (5) =10 . Giá 5 trị của ′
∫ f (x)dx bằng 3 A. 8 . B. 2 C. 12. D. 8 − .
Câu 14. Cho hàm số f (x) liên tục và không âm trên đoạn [5;6]. Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số y = f (x) , trục Ox và 2 đường thẳng x = 5, x = 6 được tính theo công thức nào dưới đây? 6 6 6 6
A. S = − f
∫ (x)d .x B. S = f
∫ (x)d .x
C. S = π  f
∫ (x) 2 d .x
D. S = π f ∫ (x)d .x 5 5 5 5 2 2021 2021
Câu 15. Biết ∫ f (x)dx = 4 và f (x)dx = 1 − ∫ . Khi đó f (x)dx ∫ bằng 1 2 1 A. 3 − . B. 5. C. 5 − . D. 3.
Câu 16. Trong không gian Oxyz , cho ba điểm A(3;0;0) , B(0;1;0) và C (0;0; 2
− ) . Mặt phẳng ( ABC) có phương trình là:
A. x + y + z =1.
B. x + y + z =1.
C. x + y + z =1.
D. x + y + z =1. 3 1 2 3 1 − 2 3 1 2 − 3 − 1 2
Câu 17. Mệnh đề nào dưới đây đúng? A. ∫( 3 x + ) 3 3 d = d − 3x x x x x dx ∫ ∫ B. ∫( 3 x + ) 3 3 d = d + 3x x x x x dx ∫ ∫ . C. ∫( 3 x x + ) x 3
3 dx = 3 dx − x dx ∫ ∫ D. ∫( 3 x + ) 3 3 d = d . 3x x x x x dx ∫ ∫ 2 2
Câu 18. Biết ∫ f (x)dx = 2. Giá trị của 3
∫ f (x)dx bằng 1 1 2 A. 8 . B. 6 . C. . D. 5 . 3
Câu 19. Xét hàm số f (x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây đúng? b b b b a A. 3 f
∫ (x)dx = f
∫ (3x)dx. B. 3 f
∫ (x)dx = 3d .x f ∫ ∫ (x)dx. a a a a b b b b b C. 3 f
∫ (x)dx = 3 f
∫ (x)dx. D. 3 f
∫ (x)dx = 3+ f ∫ (x)dx . a a a a 
Câu 20. Trong không gian Oxyz , cho hai điểm A(2;− 2; )
1 và B(1;−1;3) . Véctơ AB có tọa độ là A. ( 1; − 1;2) . B. ( 3; − 3;− 4). C. (3;−3;4). D. (1;−1;− 2) . 3 3 3
Câu 21. Biết ∫ f (x)dx = 3 và ∫ g(x)dx =1. Khi đó 
∫ f (x)+ g(x)d  x bằng 2 2 2 A. 2 . B. 2 − . C. 4 . D. 3 .
Câu 22. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x + 3, y = 0, x = 0, x =1. Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 1 1
A. V = π ∫(x +3)2 2 dx
B. V = π ∫( 2x +3)dx 0 0 1 1
C. V = ∫( 2x +3)dx
D. V = ∫(x +3)2 2 dx 0 0
Câu 23. Trong không gian Oxyz , hình chiếu vuông góc của điểm A(3;2; )
1 trên trục Ox có tọa độ là: A. (0;0; ) 1 . B. (0;2;0) . C. (0;2; ) 1 . D. (3;0;0). 2/4 - Mã đề 101
Câu 24. Mệnh đề nào dưới đây đúng?
A. ∫(5 +3) x d = (5 +3) x + x x e x x e e d ∫ x.
B. ∫(5 +3) x d = (5 +3) x +5 x x e x x e e d ∫ x.
C. ∫(5 +3) x d = (5 +3) x −5 x x e x x e e d ∫ x .
D. ∫(5 +3) x d = (5 +3) x − x x e x x e e d ∫ x.
Câu 25. Trong không gian Oxyz, khoảng cách từ điểm A(1;3; 2
− ) đến mặt phẳng (P): 2x + y − 2z −3 = 0 bằng A. 3 . B. 5. C. 4 . D. 2 .
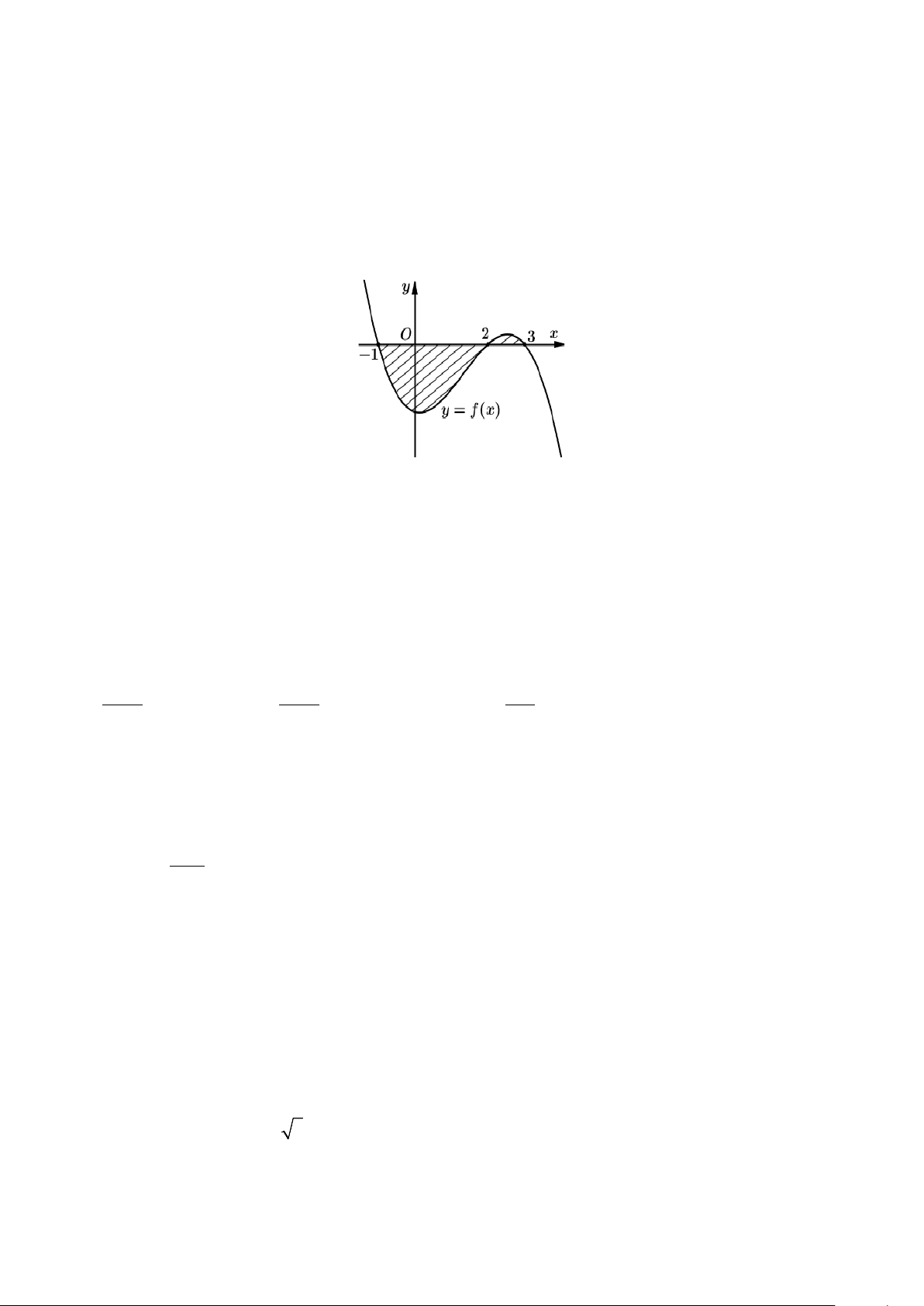
Câu 26. Cho hàm số bậc ba y = f (x) . Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f (x) , y = 0, x = 1
− và x = 3. Mệnh đề nào dưới đây là đúng? 2 3 2 3
A. S = f (x)dx + ∫
∫ f (x)dx.
B. S = f (x)dx − ∫
∫ f (x)dx. 1 − 2 1 − 2 2 3 2 3
C. S = − f (x)dx − ∫
∫ f (x)dx .
D. S = − f (x)dx + ∫
∫ f (x)dx. 1 − 2 1 − 2 11 2
Câu 27. Cho hàm số y = f (x) liên tục trên  và ∫ f (x)dx = 45. Giá trị của (5 +
∫ f x )1dx bằng 1 0 A. 9. B. 10. C. 90. D. 91.
Câu 28. Họ tất cả các nguyên hàm của hàm số 2 ( ) = 7 x f x là x x 1 x
A. 49 + C .
B. 49 + + C . C. 2 49 ⋅ + C
D. 2.49x ln 7 + C . 2ln 7 x +1 ln 7 4 4 2
Câu 29. Biết ∫ f (x)dx = 5 và f (x)dx = 1 − ∫ . Khi đó ( )d ∫ f x x bằng 0 2 0 A. 4 − . B. 6 . C. 4 . D. 6 − .
Câu 30. Họ tất cả các nguyên hàm của hàm số ( ) 4 3 = 5 + 4 + x f x x x e là x 1 + A. 5 4 + + e x x + C .B. 3 2 20 +12 + x x x e + C . C. 5 4 + + x x x
e + C . D. 5 4 x 1 +
x + x + e + C . x +1 2 2
Câu 31. Xét hàm số f (x) liên tục trên  và ∫(5 f (x)+ 2x)dx = 9 1 . Khi đó ( )d
∫ f x x bằng 0 0 A. 2 . B. 3. C. 1. D. 4 .
Câu 32. Họ tất cả các nguyên hàm của hàm số 4
f (x) = 5x + cos x là A. 5
5x − sin x + C B. 5
x − sin x + C C. 5
x + sin x + C D. 5
5x + sin x + C
Câu 33. Trong không gian Oxyz , cho hai điểm A(2; 1;
− 2); B(0;1;0). Mặt cầu đường kính AB có phương trình là A. (x − )2 2
1 + y + (z − )2 1 = 3.
B. (x + )2 + ( y − )2 + (z + )2 2 2 2 = 2 . C. (x − )2 2
1 + y + (z − )2 1 = 3 . D. (x − )2 2
1 + y + (z − )2 1 =12 .
Câu 34. Cho F (x) là một nguyên hàm của hàm số f (x) = 2x + 4 và thỏa mãn F ( )
1 = 0 . Giá trị của F (3) bằng A. 15. B. 16. C. 17 . D. 14. 3/4 - Mã đề 101 Câu 35. Biết ( ) 2
F x = x là một nguyên hàm của hàm số f (x) trên  . Giá trị của 3 1  + f ∫ 
(x)dx bằng. 1  32 26 A. . B. 8 . C. 10. D. . 3 3
Câu 36. Trong không gian Oxyz , cho hai điểm A(1;3;0) và B(5;1; 2
− ) . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là
A. 2x + y + z − 7 = 0 . B. 2x − y − z + 5 = 0 .
C. 2x − y − z −1 = 0 . D. 2x − y − z −5 = 0 .
Câu 37. Trong không gian Oxyz , cho mặt phẳng (P): x −3y + 5z − 2 = 0. Điểm nào dưới đây thuộc mặt phẳng (P) ?
A. N (1;1;7).
B. Q(4;4;2) . C. P(4; 1; − 3) . D. M (0;0;2) .
Câu 38. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 2
y = −x + 4x +1 và đường thẳng y = 2x +1 bằng A. 4 . B. 16 C. 4 . D. 20 . 3 3 3 2
Câu 39. Cho I = x (1+ ∫ x )6 4 5 dx . Đặt 5
t =1+ x , mệnh đề nào dưới đây đúng? 1 2 33 33 33 A. 1 6 I = t dt. B. 6
I = 5 t dt. C. 6
I = t dt. D. 1 6 I = t dt. 5 ∫ ∫ ∫ 5 ∫ 1 2 2 2
Câu 40. Trong không gian Oxyz cho hai điểm A(4; 2; ) 1 , B( 2
− ;−1;4) . Điểm M (a; ; b c) thỏa mãn   
AM + 3BM = 0 . Khi đó 2a + b + c bằng A. 2 . B. 3 . C. 5 . D. 6 . 2
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số 3
y = x + 3x + 3 và 2
y = x + 5x + 3
Câu 2. Trong không gian Oxyz , cho ba điểm A(0;1;2) , B(2;0;3) và C (3;4;0) . Viết phương trình mặt phẳng ( ABC)
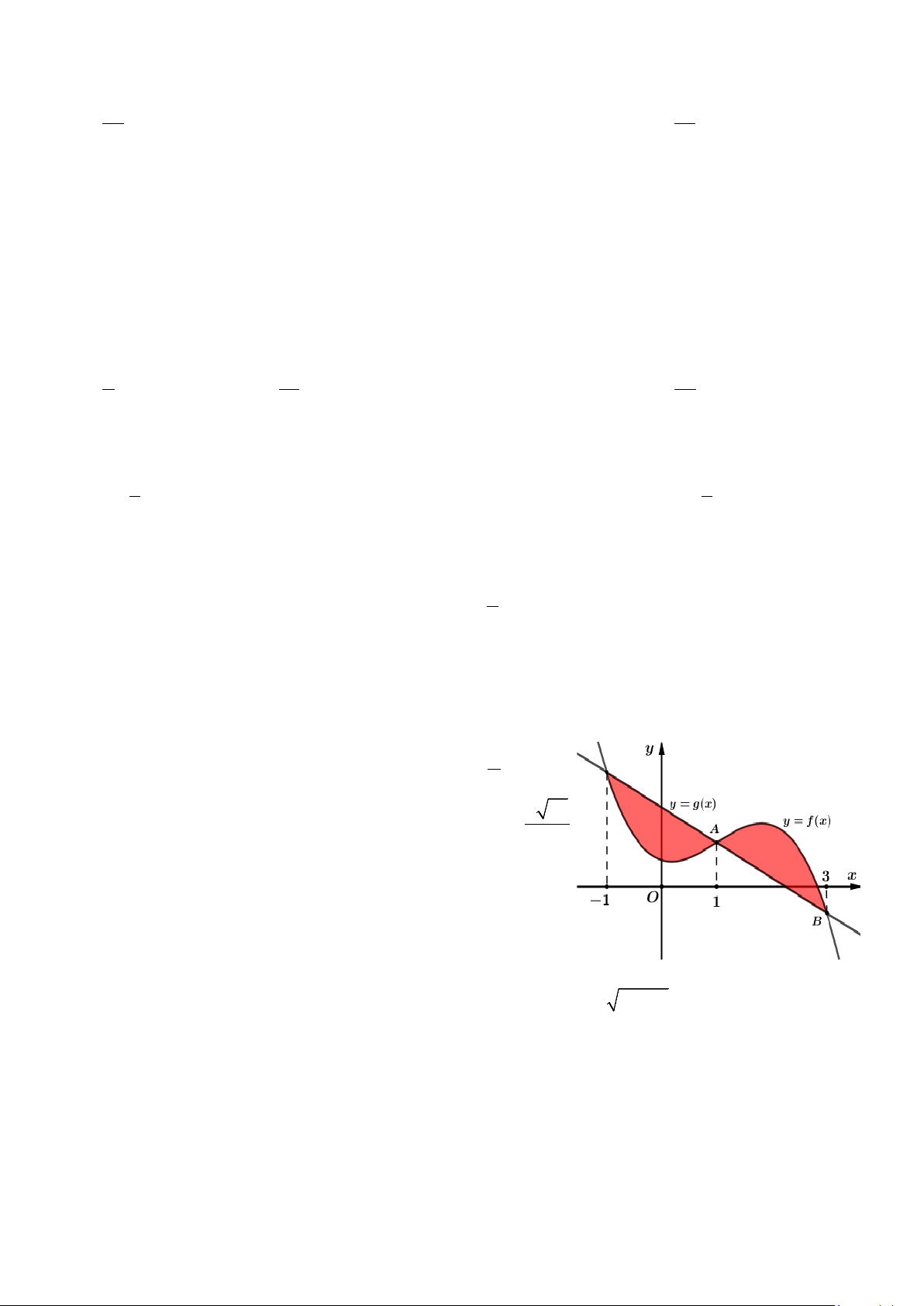
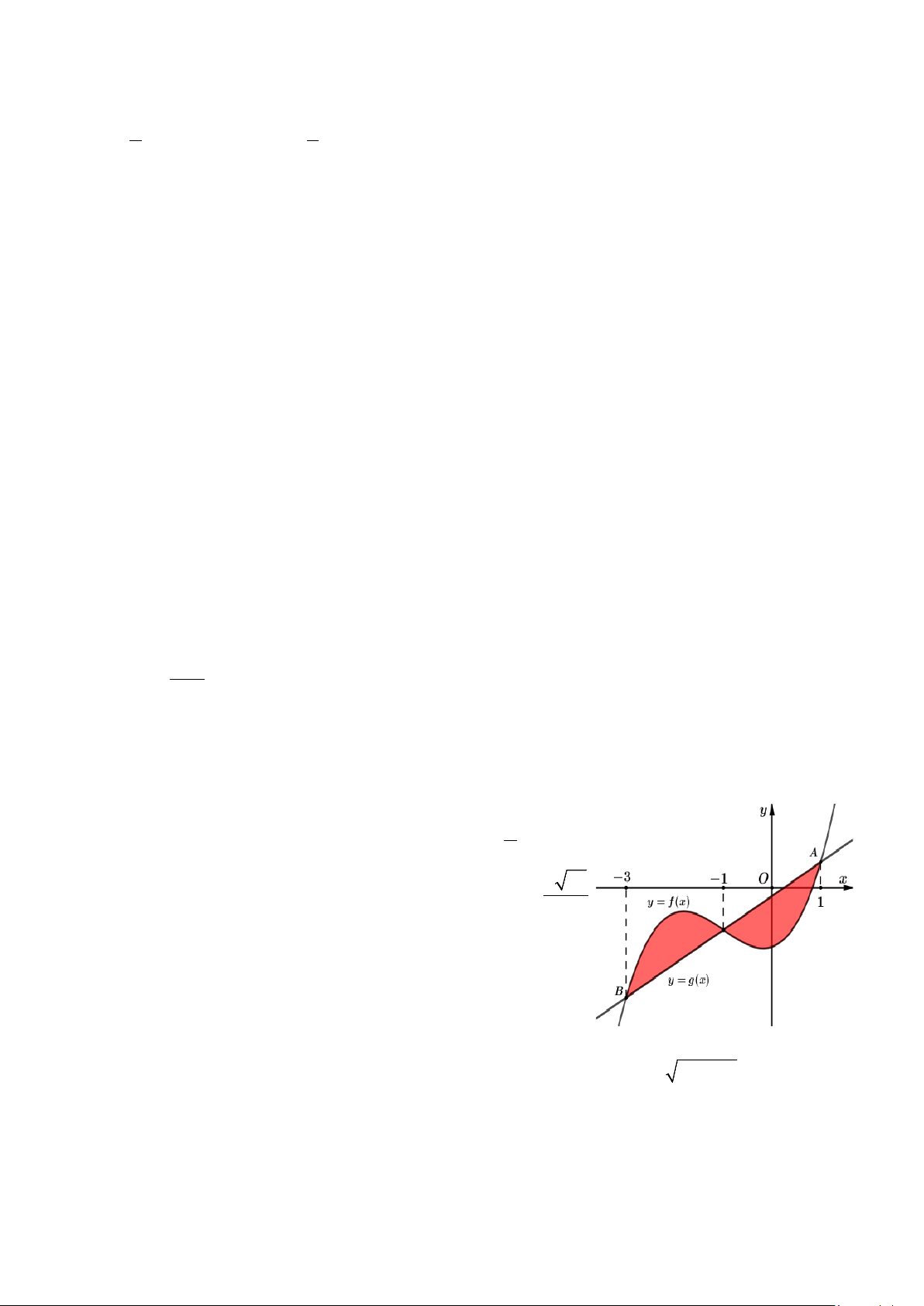
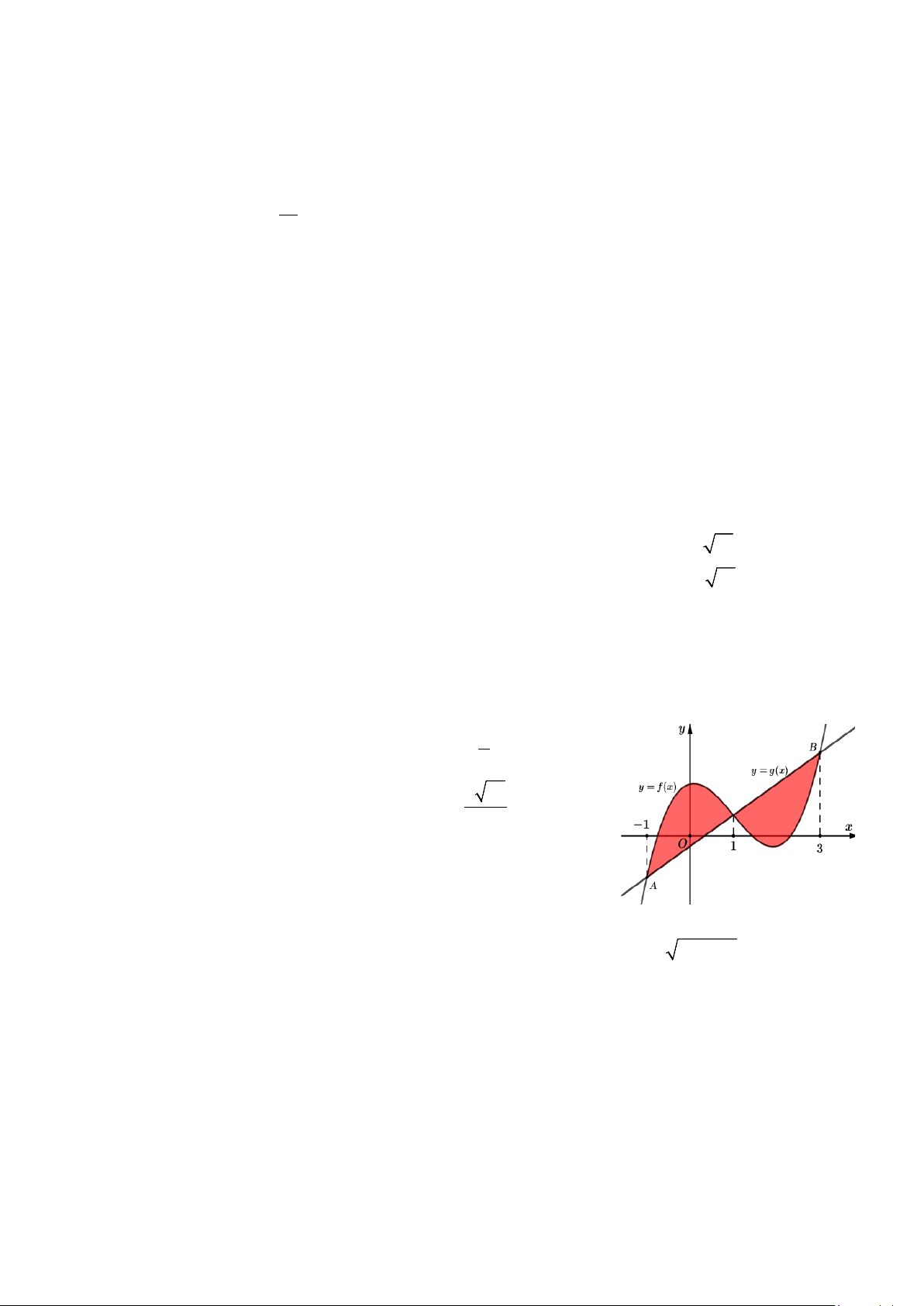
Câu 3. Cho hàm số bậc ba y f x 3 2 2
ax bx x d và 7
đường thẳng y = g (x) có đồ thị như hình vẽ bên. Biết 2 65 AB = , 7
diện tích hình phẳng giới hạn bởi hai đồ thị y f x và
y = g (x) bằng bao nhiêu? 1 2
Câu 4. Cho hàm số f (x) liên tục trên  thỏa mãn 2
f (x) = 2x − 3+ ∫ xf ( 2
1+ 3x )dx . Giá trị của ∫ f (x)dx 0 0 bằng
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ................... 4/4 - Mã đề 101
THPT SỐ 3 BẢO THẮNG
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022 TỔ: TOÁN – TIN - CN
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(Đề thi có 04 trang)
(không kể thời gian phát đề) Mã đề 102
PHẦN I. TRẮC NGHIỆM (8 điểm) 2 2 2
Câu 1. Biết ∫ f (x)dx = 3 và ∫ g(x)dx = 2. Khi đó 
∫ f (x)− g(x)d  x bằng? 1 1 1 A. 1 − . B. 1. C. 5. D. 6 . 4 Câu 2. Giá trị d ∫ x bằng 0 A. 4 . B. 0. C. 4 − . D. 5
Câu 3. Trong không gian Oxyz , hình chiếu vuông góc của điểm A(4;5;2) trên trục Ox có tọa độ là A. (0;0;2) . B. (0;5;2) . C. (4;0;0) . D. (0;5;0) .
Câu 4. Xét hàm số f (x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây đúng? b b b b A. 4 f
∫ (x)dx = 4 f
∫ (x)dx. B. 4 f
∫ (x)dx = f ∫ (4x)dx . a a a a b b a b b C. 4 f
∫ (x)dx = 4d .x f
∫ ∫ (x)dx . D. 4 f
∫ (x)dx = 4+ f ∫ (x)dx. a a b a a
Câu 5. Mệnh đề nào dưới đây đúng? A. ∫( 4 x + ) 4 5 d = d . 5x x x x x dx ∫ ∫ B. ∫( 4 x + ) 4 5 d = d + 5x x x x x dx ∫ ∫ . C. ∫( 4 x x + ) x 4
5 dx = 5 dx − x dx ∫ ∫ D. ∫( 4 x + ) 4 5 d = d − 5x x x x x dx ∫ ∫
Câu 6. Họ tất cả các nguyên hàm của hàm số ( ) = 3 x f x e là A. 3 x e + C. B. x 1 3e + − + C. C. x 1
3e + + C. D. 3 x − e + C.
Câu 7. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x + 4, y = 0, x =1, x = 3 . Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 3 3 3 3
A. V = ∫( 2x + 4)dx B. V = ∫(x + 4)2 2 dx
C. V = π ∫( 2x + 4)dx D. V =π ∫(x + 4)2 2 dx 1 1 1 1 3 5 5 Câu 8. Biết ( )d = 5 − ∫ f x x
và ∫ f (x)dx = 2 . Khi đó ( )d ∫ f x x bằng 1 3 1 A. 1. B. 3 − . C. 1 − . D. 3 .
Câu 9. Họ tất cả các nguyên hàm của hàm số f (x) = sin 4x là: A. 1
− cos 4x + C .
B. cos 4x + C .
C. −cos 4x + C .
D. 1 cos 4x + C . 4 4
Câu 10. Trong không gian Oxyz , cho mặt cầu (S ) 2 2
: x + y + (z − 2)2 = 36 . Bán kính của (S ) bằng: A. 36. B. 72 . C. 6 . D. 12.
Câu 11. Họ tất cả các nguyên hàm của hàm số f (x) = cos x là A. 1
− cos x + C . B. 2
cos x + C .
C. −sin x + C .
D. sin x + C . 2
Câu 12. Xét f (x) là một hàm số tùy ý, F (x) là một nguyên hàm của f (x) trên đoạn[5;6]. Mệnh đề nào dưới đây đúng? 1/4 - Mã đề 102 6 6 A. f
∫ (x)dx = F (5)− F (6). B. f
∫ (x)dx = F (6)+ F (5). 5 5 6 6 C. f
∫ (x)dx = −F (5)− F (6). D. f
∫ (x)dx = F (6)− F (5). 5 5
Câu 13. Trong không gian Oxyz , cho 3 điểm A( 1
− ;0;0), B(0;2;0) và C (0;0;3). Mặt phẳng ( ABC) có phương trình là
A. x + y + z =1.
B. x + y + z =1.
C. x + y + z =1.
D. x + y + z =1. 1 2 3 1 2 3 − 1 − 2 3 1 2 − 3
Câu 14. Mệnh đề nào dưới đây đúng? A. ( 4 )′ 3 d = 4 + ∫ x x x C . B. ( 4 )′ 4 d = − + ∫ x x x C . C. ( 4 )′ 4 d = + ∫ x x x C . D. ( 4 )′ 3 d = 4 − + ∫ x x x C . 
Câu 15. Trong không gian Oxyz , cho hai điểm A(3;2;0) và B(1;4;3) . Véctơ AB có tọa độ là A. (2; 2; − 3 − ). B. ( 2; − 2;3). C. (2; 2; − 3). D. (2;2;3) . Câu 16. 3 ∫ x dxbằng. A. 1 4 x C B. 2 3x C C. 4 x C D. 4 4x C 4
Câu 17. Cho hàm số f (x) có đạo hàm f ′(x) liên tục trên đoạn [5;6] và thỏa mãn f (5) =1, f (6) =11. Giá 6 trị của ′
∫ f (x)dx bằng 5 A. 10. B. 1 C. 10 − . D. 12. 5 5 Câu 18. Biết ( ) 4 =
∫ f x dx . Giá trị của 3 x
∫ f ( ) dx bằng 1 1 A. 7 . B. 12. C. 4 . D. 64 . 3
Câu 19. Cho hàm số f (x) liên tục và không âm trên đoạn [3;4]. Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số y = f (x) , trục Ox và 2 đường thẳng x = 3, x = 4 được tính theo công thức nào dưới đây? 4 4 4 4
A. S = π f
∫ (x)d .x B. S = − f
∫ (x)d .x
C. S = π  f
∫ (x) 2 d .x D. S = f ∫ (x)d .x 3 3 3 3 Câu 20. 2 ∫ xdx bằng x x 1 + A. 2 2 + C .
B. 2x + C . C. + C
D. 2x.ln 2 + C . ln 2 x +1
Câu 21. Trong không gian Oxyz , cho mặt phẳng (α ) : 2x + 4y − z + 3 = 0 . Véctơ nào dưới đây là véc tơ pháp tuyến của (α ) ?    
A. n = 2;− 4;1 . B. n = 2; − 4;1 . C. n = 2;4; 1 − . D. n = 2;4;1 . 1 ( ) 1 ( ) 3 ( ) 2 ( )
Câu 22. Trong không gian Oxyz , cho hai điểm A( 1; − 2;3) , B(3;4; 3
− ) . Toạ độ trung điểm I của đoạn thẳng AB là A. (2;1; 3 − ). B. (1;3;0). C. (2;6;0). D. ( 2 − ; 1; − 3) .    
Câu 23. Trong không gian Oxyz , cho OM = 2i − j − k . Tọa độ điểm M là A. M ( 2 − ; 1 − ; − ) 1 . B. M ( 2 − ;1; ) 1 . C. M ( 2 − ; 1 − ; ) 1 D. M (2; 1 − ; − ) 1 . 2/4 - Mã đề 102
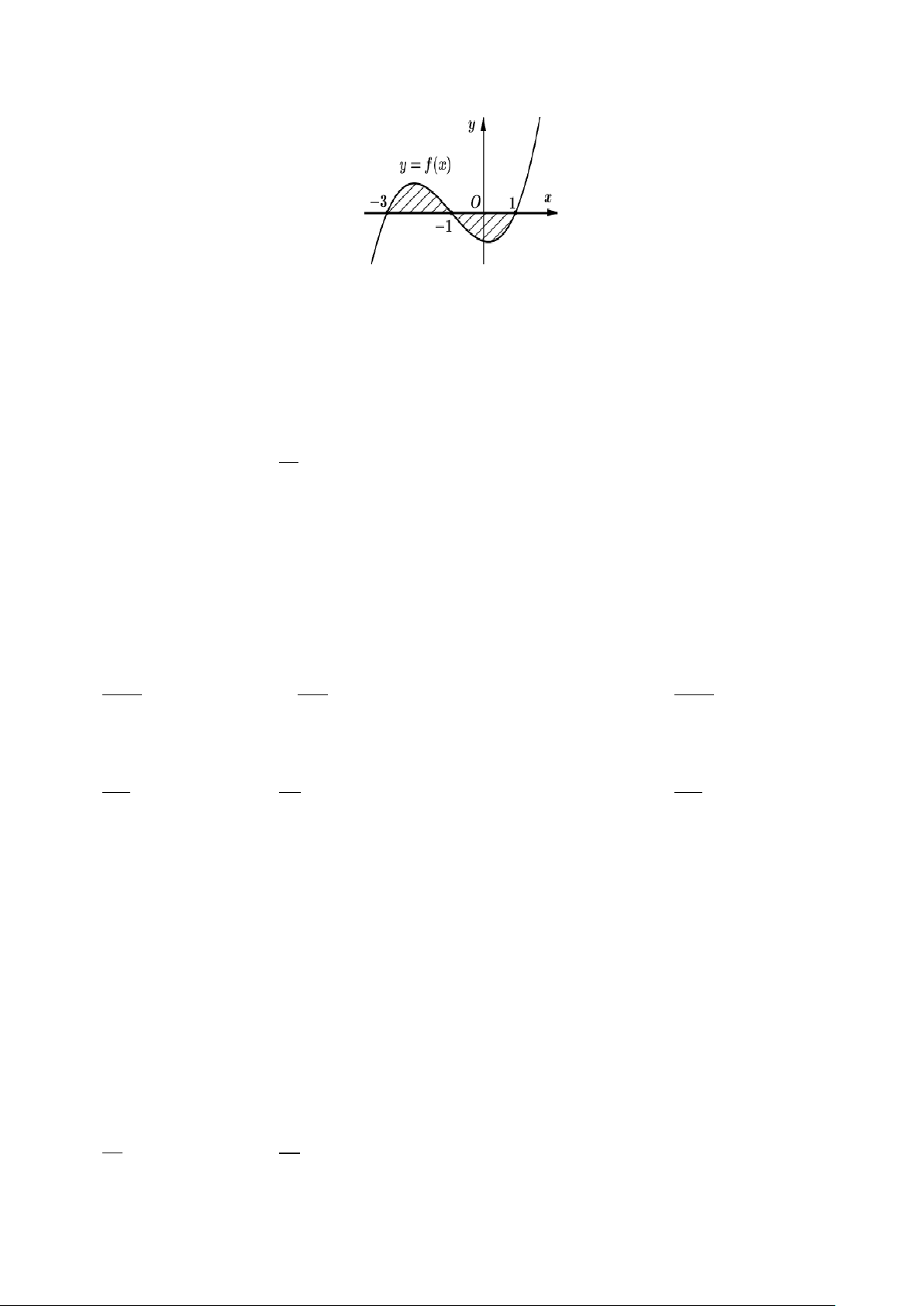
Câu 24. Cho hàm số bậc ba y = f (x) . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y = f (x), y = 0, x = 3
− và x = 1. Mệnh đề nào dưới đây là đúng? 1 − 1 1 − 1
A. S = f (x)dx + ∫
∫ f (x)dx.
B. S = f (x)dx − ∫
∫ f (x)dx . 3 − 1 − 3 − 1 − 1 − 1 1 − 1 −
C. S = − f (x)dx + ∫
∫ f (x)dx
D. S = − f (x)dx − ∫
∫ f (x)dx . 3 − 1 − 3 − 1 −
Câu 25. Trong không gian Oxyz , cho hai điểm là A(1;3;− ) 1 , B(3; 1;
− 5). Điểm M (a; ; b c) thỏa mãn   
AM + 4BM = 0. Khi đó a + 2b + c bằng A. 6 . B. 31. C. 9. D. 8 . 5
Câu 26. Trong không gian Oxyz , khoảng cách từ điểm A( 1;
− 0;2) đến mặt phẳng (P) : x + 2y − 2z +14 = 0 bằng A. 2 . B. 4 . C. 5. D. 3 . 2 3 3 Câu 27. Biết ( )d = 2 − ∫ f x x
và ∫ f (x)dx = 7. Khi đó ( )d ∫ f x x bằng 1 1 2 A. 5 − . B. 5. C. 9. D. 9 − .
Câu 28. Họ tất cả các nguyên hàm của hàm số 2 ( ) 5 x f x = là x 1 + x x
A. 25 + C . B. 2 25 ⋅ + C
C. 2.25x ln 5 + C . D. 25 + C . x +1 ln 5 2ln 5
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 2
y = −x + 2x −1 và đường thẳng y = 3 − x −1 bằng A. 135 . B. 25 C. 7 . D. 125 . 6 6 6 2 2
Câu 30. Xét hàm số f (x) liên tục trên  và ∫(2 f (x) 2 + 3x )dx =1 . 0 Khi đó ( )d
∫ f x x bằng 0 0 A. 4 . B. 2 . C. 1. D. 3.
Câu 31. Mệnh đề nào dưới đây đúng?
A. ∫(3 + 2) x d = (3 + 2) x + x x e x x e e d ∫ x .
B. ∫(3 + 2) x d = (3 + 2) x +3 x x e x x e e d ∫ x.
C. ∫(3 + 2) x d = (3 + 2) x −3 x x e x x e e d ∫ x .
D. ∫(3 + 2) x d = (3 + 2) x − x x e x x e e d ∫ x.
Câu 32. Cho F (x) là một nguyên hàm của hàm số f (x) = 2x + 6 và thỏa mãn F ( ) 1 = 6 − . Giá trị của F (3) bằng A. 15. B. 17 . C. 16. D. 14. 2 Câu 33. Biết ( ) 3
F x = x là một nguyên hàm của hàm số f (x) trên  . Giá trị của 2 + f ∫ (x) dx    bằng 1 A. 15 . B. 23 . C. 7 . D. 9. 4 4 3/4 - Mã đề 102 2
Câu 34. Cho I = x(1+ ∫ x )3 2 dx . Đặt 2
t =1+ x , mệnh đề nào dưới đây đúng? 1 5 2 5 5 A. 1 3 I = t dt. B. 1 3 I = t dt. C. 3
I = t dt. D. 3
I = 2 t dt. 2 ∫ 2 ∫ ∫ ∫ 2 1 2 2
Câu 35. Trong không gian Oxyz , cho hai điểm A(2;1;2) và B(6;5; 4
− ) . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là
A. 2x + 2y − 3z −17 = 0 .B. 2x + 2y −3z = 0.
C. 2x + 2y − 3z +17 = 0 . D. 2x + 2y + 3z −11 = 0 . 5 2
Câu 36. Cho hàm số y = f (x) liên tục trên  và ∫ f (x)dx = 6. Giá trị của (2 +
∫ f x )1dx bằng 1 0 A. 12. B. 3 . C. 4 . D. 13.
Câu 37. Họ tất cả các nguyên hàm của hàm số 3
f (x) = 4x + cos x là A. 4
4x − sin x + C B. 4
x + sin x + C C. 4
4x + sin x + C D. 4
x − sin x + C
Câu 38. Trong không gian Oxyz , cho hai điểm A( 1; − 3 − ;4) và B(3; 1;
− 2). Phương trình mặt cầu đường kính AB là
A. (x + )2 + ( y − )2 + (z + )2 1 2 3 = 24 .
B. (x − )2 + ( y + )2 + (z − )2 1 2 3 = 24 .
C. (x − )2 + ( y + )2 + (z − )2 1 2 3 = 6.
D. (x + )2 + ( y − )2 + (z + )2 1 2 3 = 6 .
Câu 39. Trong không gian Oxyz , cho mặt phẳng (P): x − 2y + 3z −5 = 0. Điểm nào dưới đây thuộc mặt phẳng (P) ? A. P(0;1 ) ;1 . B. Q(2; 1; − 3). C. M (0; 1; − ) 1 . D. N (1;2;3) .
Câu 40. Họ tất cả các nguyên hàm của hàm số ( ) 5 4 = 6 + 5 + x f x x x e là A. 6 5 + + x x
x e + C . B. 4 3 30 + 20 + x x x e + C . x 1 + C. 6 5 + + e x x + C . D. 6 5 x 1 +
x + x + e + C . x +1
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số 3
y = −x + 2 và 2
y = x − 2x + 2
Câu 2. Trong không gian Oxyz , cho ba điểm A(3; 1; − 2) , B(4; 1 − ;− )
1 và C (2;0;2). Viết phương trình mặt phẳng ( ABC)
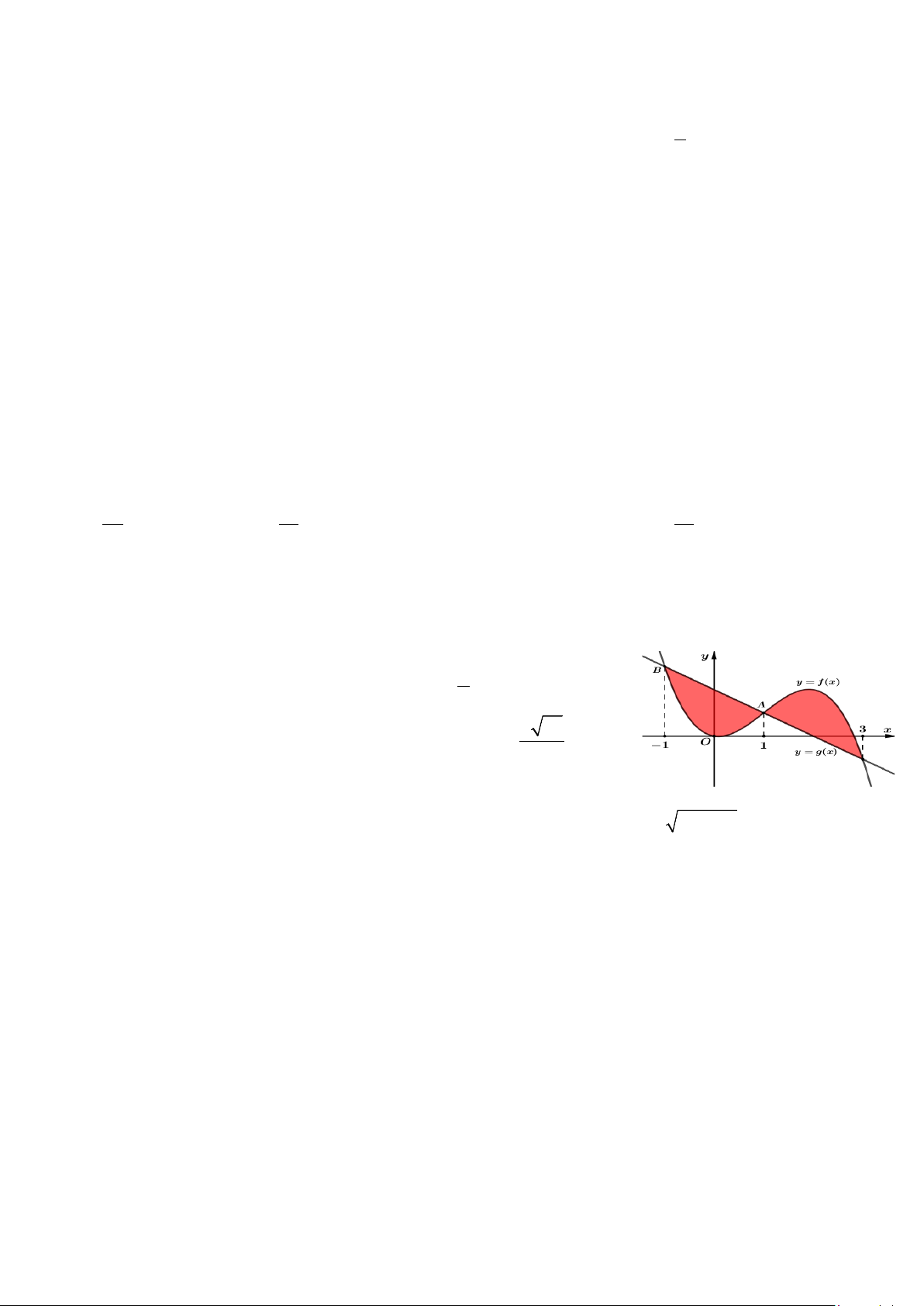
Câu 3. Cho hàm số bậc ba y f x 3 2 2
ax bx x d và 7
đường thẳng y = g (x) có đồ thị như hình vẽ bên. Biết 4 65 AB = , 7
diện tích hình phẳng giới hạn bởi hai đồ thị y f x và
y = g (x) bằng bao nhiêu? 1
Câu 4. Cho hàm số f (x) liên tục trên  thỏa mãn 2
f (x) = 2x − 33+ ∫ xf ( 2
1+ 63x )dx . Giá trị của 0 2 ( )d ∫ f x x bằng 0
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ................... 4/4 - Mã đề 102
THPT SỐ 3 BẢO THẮNG
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022 TỔ: TOÁN – TIN - CN
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(Đề thi có 04 trang)
(không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM (8 điểm) Mã đề 103
Câu 1. Trong không gian Oxyz , cho hai điểm (
A 1;0;2) và B(3;4;6) . Toạ độ trung điểm I của đoạn thẳng AB là A. ( A 2;4;8) . B. ( A 2;2;2). C. (
A 1;2;4) . D. ( A 1;2;4) . 2 5 5
Câu 2. Biết ∫ f (x)dx = 3 và ( )d = 1 − ∫ f x x . Khi đó ( )d ∫ f x x bằng 1 2 1 A. 2. B. 3. C. 2 − . D. 4.
Câu 3. Trong không gian Oxyz , cho ba điểm A( 2;
− 0;0), B(0;3;0) và C (0;0;4) . Mặt phẳng ( ABC) có phương trình là
A. x + y + z =1.
B. x + y + z =1.
C. x + y + z =1.
D. x + y + z =1. 2 3 − 4 2 3 4 − 2 3 4 2 − 3 4
Câu 4. Cho hàm số f (x) có đạo hàm f ′(x) liên tục trên đoạn [2;4] và thỏa mãn f (2) = 3, f (4) =10. Giá 4 trị của ′
∫ f (x)dx bằng 2 A. 7 − . B. 2 C. 13. D. 7 .
Câu 5. Mệnh đề nào dưới đây đúng? A. ( 5 )′ 4 d = 5 − + ∫ x x x C .B. ( 5 )′ 5 d = +
∫ x x x C . C. ( 5)′ 4 d = 5 +
∫ x x x C . D. ( 5)′ 5 d = − + ∫ x x x C .
Câu 6. Họ tất cả các nguyên hàm của hàm số f (x) = sin5x là:
A. cos5x + C .
B. −cos5x + C . C. 1
− cos5x + C .
D. 1 cos5x + C . 5 5
Câu 7. Họ tất cả các nguyên hàm của hàm số f (x) 1 = là 2 cos x
A. −cot x + C .
B. − tan x + C .
C. tan x + C .
D. cot x + C . 3 3
Câu 8. Biết ∫ f (x)dx = 6 . Giá trị của 2 ( )d ∫ f x x bằng 2 2 A. 8 . B. 3 . C. 36. D. 12.
Câu 9. Trong không gian Oxyz , Cho mặt phẳng (α ) : 2x − y + 3z + 5 = 0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của (α ) ?     A. n = 2;1; 3 − . B. n = 2; 1; − 3 .
C. n = 2;1;3 . D. n = 2 − ;1;3 . 3 ( ) 1 ( ) 2 ( ) 4 ( )
Câu 10. Trong không gian Oxyz , hình chiếu vuông góc của điểm A(1;2;5) lên trục Ox có tọa độ là A. (1;0;0) . B. (0;2;5) . C. (0;2;0) . D. (0;0;5) .
Câu 11. Xét hàm số f (x) liên tục trên đoạn [ ;
a b]. Mệnh đề nào dưới đây đúng? b b b b a A. 2 f
∫ (x)dx = f
∫ (2x)dx . B. 2 f
∫ (x)dx = 2d .x f ∫ ∫ (x)dx . a a a a b b b b b C. 2 f
∫ (x)dx = 2 f
∫ (x)dx. D. 2 f
∫ (x)dx = 2+ f ∫ (x)dx. a a a a
Câu 12. Xét f (x) là một hàm số tùy ý, F (x) là một nguyên hàm của f (x) trên đoạn[1;2]. Mệnh đề nào 1/4 - Mã đề 103 dưới đây đúng? 2 2 A. f
∫ (x)dx = −F ( )1− F (2) . B. f
∫ (x)dx = F ( )1+ F (2). 1 1 2 2 C. f
∫ (x)dx = F ( )1− F (2) . D. f
∫ (x)dx = F (2)− F ( )1 . 1 1    
Câu 13. Trong không gian Oxyz , cho OM = i − 2 j + 3k . Tọa độ điểm M là A. M (1; 2 − ; 3 − ). B. M (1; 2 − ;3) . C. M ( 1 − ; 2 − ;3) D. M ( 1 − ; 2 − ; 3 − ). 
Câu 14. Trong không gian Oxyz , cho hai điểm A(1;−1;2) và B(2;1;− 4) . Véctơ AB có tọa độ là
A. (1;0;− 6) . B. ( 1; − − 2;6).
C. (3;0;− 2) . D. (1;2;− 6).
Câu 15. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x + y + (z −1) =16 . Bán kính của (S) là: A. 4 B. 8 C. 32 D. 16
Câu 16. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x +1, y = 0, x = 0, x = 2 . Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2
A. V = (x + ∫ )2 2
1 dx B. V = π ( 2 x + ∫ )1dx
C. V = π (x + ∫ )2 2
1 dx D. V = ( 2 x + ∫ )1dx 0 0 0 0 2 2 2 Câu 17. Biết ( ) = 2
∫ f x dx và ( ) = 3. ∫ g x dx Khi đó  ∫ f (x)+  g (x) d  x bằng 1 1 1 A. 6 . B. 1. C. 1 − . D. 5. Câu 18. 2 ∫ x dx bằng A. 1 3 x + C . B. 3 3x + C C. 3 x + C .
D. 2x + C . 3
Câu 19. Mệnh đề nào dưới đây đúng? A. ∫( 5 x x + ) x 5
6 dx = 6 dx − x dx ∫ ∫ B. ∫( 5 x + ) 5 6 d = d + 6x x x x x dx ∫ ∫ . C. ∫( 5 x + ) 5 6 d = d . 6x x x x x dx ∫ ∫ D. ∫( 5 x + ) 5 6 d = d − 6x x x x x dx ∫ ∫ 6 Câu 20. Giá trị d ∫ x bằng 0 A. 6 . B. 0. C. 7 D. 6 − . Câu 21. 3 ∫ xdx bằng x x 1 3 +
A. 3 + C .
B. 3x + C .
C. 3x.ln 3+ C . D. + C ln 3 x +1
Câu 22. Cho hàm số f (x) liên tục và không âm trên đoạn [1;2]. Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số y = f (x) , trục Ox và 2 đường thẳng x =1, x = 2 được tính theo công thức nào dưới đây? 2 2 2 2
A. S = π f
∫ (x)d .x B. S =π  f
∫ (x) 2 d .x
C. S = − f
∫ (x)d .x D. S = f ∫ (x)d .x 1 1 1 1
Câu 23. Họ tất cả các nguyên hàm của hàm số ( ) = 5 x f x e là A. x 1
5e + + C. B. 5 x e + C. C. 5 x
− e + C. D. x 1 5e + − + C. 2
Câu 24. Cho I = x (1+ ∫ x )5 3 4 dx . Đặt 4
t =1+ x , mệnh đề nào dưới đây đúng? 1 17 17 17 2 A. 5 I = t dt. ∫ B. 5
I = 4 t dt. ∫ C. 1 5 I = t dt. D. 1 5 I = t dt. 4 ∫ 4 ∫ 2 2 2 1 2/4 - Mã đề 103 2 2
Câu 25. Xét hàm số f (x) liên tục trên  và ∫(3f (x) 3 + 4x )dx = 8 2 . Khi đó ( )d
∫ f x x bằng 0 0 A. 1. B. 4 . C. 2 . D. 3.
Câu 26. Cho hàm số bậc ba y = f (x) . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y = f (x), y = 0, x = 1 − và x = 2 .
Mệnh đề nào dưới đây đúng? 1 2 1 2
A. S = − f
∫ (x)dx+ f
∫ (x)dx. B. S = f
∫ (x)dx− f ∫ (x)dx. 1 − 1 1 − 1 1 2 1 2
C. S = − f
∫ (x)dx− f
∫ (x)dx . D. S = f
∫ (x)dx+ f ∫ (x)dx. 1 − 1 1 − 1 3 3 2
Câu 27. Biết f (x)dx = 2 ∫ và ( )d = 3 − ∫ f x x . Khi đó ( )d ∫ f x x bằng 1 2 1 A. 5 − . B. 1 − . C. 1. D. 5 .
Câu 28. Họ tất cả các nguyên hàm của hàm số f (x) = 2x + cos x là A. 2
x − sin x + C B. 2
2x + sin x + C C. 2
x + sin x + C D. 2
2x − sin x + C
Câu 29. Trong không gian Oxyz , khoảng cách từ điểm A(1; 2 − ; )
1 đến mặt phẳng (P) : x − 2y + 2z + 5 = 0 bằng A. 4 . B. 5. C. 3 . D. 2 .
Câu 30. Họ tất cả các nguyên hàm của hàm số ( ) 3 2 = 4 + 3 + x f x x x e là x 1 + A. 4 3 + + e x x + C . B. 4 3 + + x x
x e + C . C. 4 3 x 1 +
x + x + e + C . D. 2 12 + 6 + x x x e + C . x +1 2 Câu 31. Biết ( ) 2
F x = x là một nguyên hàm của hàm số f (x) trên  . Giá trị của 2 + f ∫ (x)dx  bằng 1 A. 3 . B. 5 . C. 7 . D. 13 . 3 3 9 2
Câu 32. Cho hàm số y = f (x) liên tục trên  và ∫ f (x)dx = 28. Giá trị của (4 +
∫ f x )1dx bằng 1 0 A. 57 . B. 56. C. 7 . D. 8 .
Câu 33. Trong không gian Oxyz , cho mặt phẳng (P): 2x− 2y+ 3z+ 6 =0. Điểm nào dưới đây thuộc mặt phẳng (P) ? A. Q = (3; 2 − ; 3 − ).
B. M = (3;0;0) . C. N = (3;3; 2 − ) . D. P = (2; 2; − 3) .
Câu 34. Trong không gian Oxyz , cho hai điểm A(4;0; ) 1 , B( 2;
− 2;5) . Mặt phẳng trung trực của đoạn thẳng
AB có phương trình là
A. 3x − y − 2z − 4 = 0 . B. 3x − y − 2z + 4 = 0 .
C. 3x − y − 2z −10 = 0. D. 3x + y + 2z −10 = 0 .
Câu 35. Họ tất cả các nguyên hàm của hàm số 2 ( ) = 3 x f x là x x 1 + x A. 2 9 ⋅ + C B. 2.9x ln 3 9 + C . C. + C . D. 9 + C . ln 3 x +1 2ln 3 3/4 - Mã đề 103
Câu 36. Trong không gian Oxyz , cho hai điểm A(0;1; 2 − ) và B(3; 1; − )
1 . Điểm M (a; ; b c) thỏa mãn   
AM + 5MB = 0 . Khi đó a + 3b + c bằng A. 4 . B. 8. C. 1. D. 9 . 2
Câu 37. Mệnh đề nào dưới đây đúng?
A. ∫(4 + )1 x d = (4 + )1 x + 4 x x e x x e e d ∫ x .
B. ∫(4 + )1 x d = (4 + )1 x − x x e x x e e d ∫ x.
C. ∫(4 + )1 x d = (4 + )1 x −4 x x e x x e e d ∫ x .
D. ∫(4 + )1 x d = (4 + )1 x + x x e x x e e d ∫ x .
Câu 38. Trong không gian Oxyz , cho hai điểm A(4; 3
− ;7), B(2;1;3) . Mặt cầu đường kính AB có phương trình là
A. (x − )2 + ( y + )2 + (z − )2 3 1 5 = 3.
B. (x + )2 + ( y − )2 + (z + )2 3 1 5 = 9.
C. (x + )2 + ( y − )2 + (z + )2 3 1 5 = 3.
D. (x − )2 + ( y + )2 + (z − )2 3 1 5 = 9.
Câu 39. Cho F (x) là một nguyên hàm của hàm số f (x) = 2x + 3 và thỏa mãn F ( )
1 = 3. Giá trị của F (3) bằng A. 17 . B. 15. C. 16. D. 14.
Câu 40. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 2
y = −x − x − 2 và đường thẳng y = 3x − 2 bằng A. 32 . B. 31 C. 6 . D. 17 . 3 3 3
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số 3
y = −x + 4x −1 và 2
y = −x + 2x −1
Câu 2. Trong không gian Oxyz , cho ba điểm A(2; 1;
− 3) , B(4;0; )1 và C( 1
− 0;5;3) . Viết phương trình mặt phẳng ( ABC)
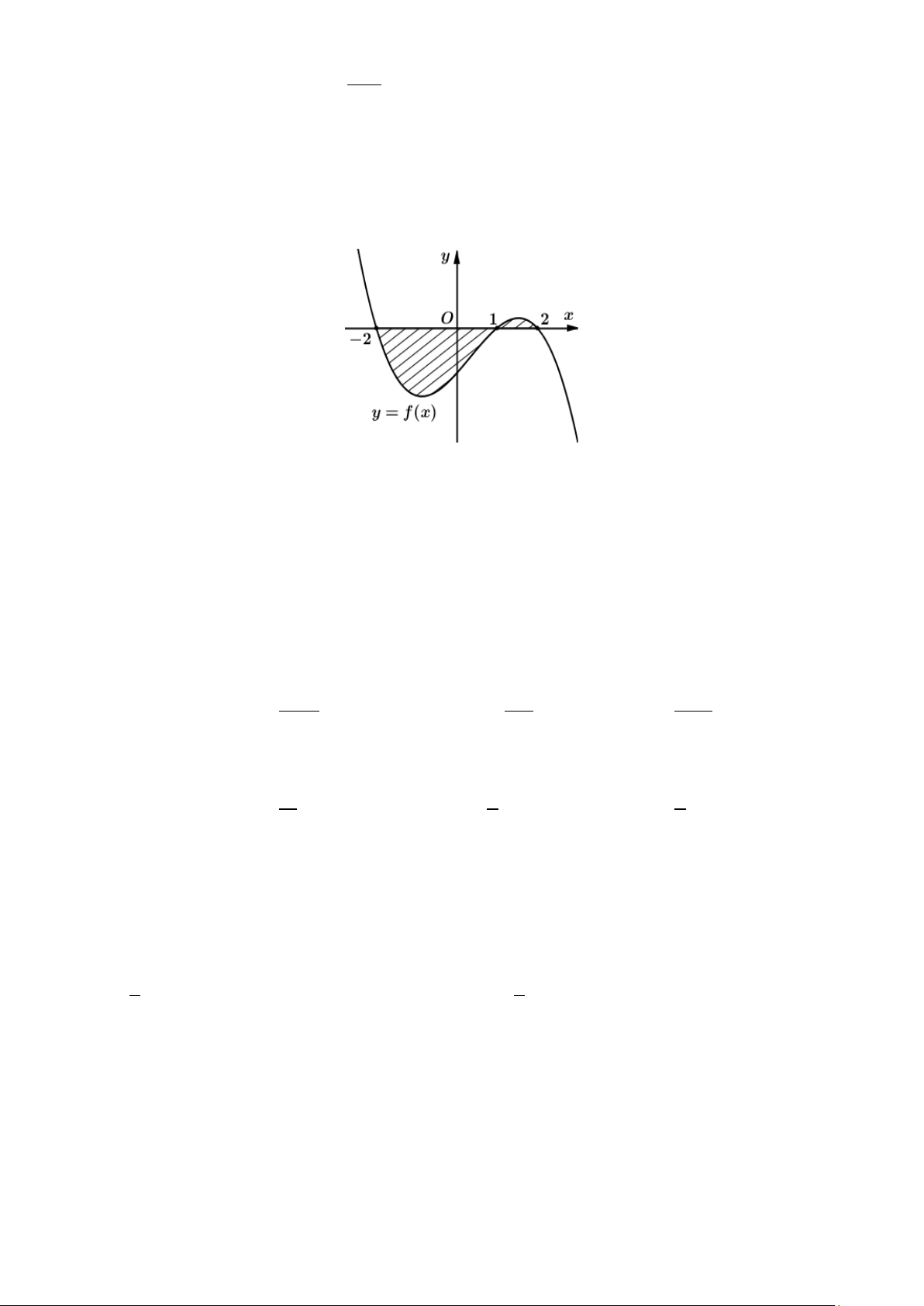
Câu 3. Cho hàm số bậc ba y f x 3 2 1
ax bx x d và 5
đường thẳng y = g (x) có đồ thị như hình vẽ bên. Biết 2 34 AB = , diện tích 5
hình phẳng giới hạn bởi hai đồ thị y f x và y = g (x) bằng bao nhiêu? 1
Câu 4. Cho hàm số f (x) liên tục trên  thỏa mãn 2
f (x) = 2x −19 + ∫ xf ( 2
1+ 35x )dx. Giá trị của 0
2∫ f (x)dx bằng ------ HẾT ------ 0
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ................... 4/4 - Mã đề 103
THPT SỐ 3 BẢO THẮNG
KIỂM TRA GIỮA KỲ 2 NĂM HỌC 2021 - 2022 TỔ: TOÁN – TIN - CN
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(Đề thi có 04 trang)
(không kể thời gian phát đề) Mã đề 104
PHẦN I. TRẮC NGHIỆM (8 điểm)
Câu 1. Cho hàm số f (x) có đạo hàm f ′(x) liên tục trên đoạn [1; ] 3 và thỏa mãn f ( ) 1 = 5, f (3) =11. Giá 3 trị của ′
∫ f (x)dx bằng 1 A. 6 B. 16. C. 6 − . D. 2 .    
Câu 2. Trong không gian Oxyz , cho OM = 2i − 3 j + k . Tọa độ điểm M là A. M (2;3; ) 1 B. M ( 2 − ;3; − ) 1 . C. M (2; 3 − ; − ) 1 . D. M (2; 3 − ; ) 1 .
Câu 3. Mệnh đề nào dưới đây đúng? A. ∫( 2 x x + ) x 2
4 dx = 4 dx − x dx ∫ ∫ B. ∫( 2 x + ) 2 4 d = d + 4x x x x x dx ∫ ∫ . C. ∫( 2 x + ) 2 4 d = d − 4x x x x x dx ∫ ∫ D. ∫( 2 x + ) 2 4 d = d . 4x x x x x dx ∫ ∫ 6 10 10
Câu 4. Biết ∫ f (x)dx = 7 và ∫ f (x)dx = 3. Khi đó ( )d ∫ f x x bằng 0 6 0 A. 4 − . B. 21. C. 4 . D. 10. 3 3
Câu 5. Biết ∫ f (x)dx = 3. Giá trị của 2 ( )d ∫ f x x bằng 1 1 A. 6 . B. 5 . C. 9 . D. 3 . 2 Câu 6. 7 ∫ xdx bằng x x 1 7 +
A. 7x + C .
B. 7 + C .
C. 7x.ln 7 + C . D. + C ln 7 x +1
Câu 7. Trong không gian Oxyz , cho 3 điểm A(2;0;0), B(0;−1;0), C (0;0;3) . Mặt phẳng ( ABC) có phương trình là
A. x + y + z =1.
B. x + y + z =1.
C. x + y + z =1.
D. x + y + z =1. 2 1 3 2 − 1 3 2 1 − 3 − 2 1 − 3
Câu 8. Trong không gian Oxyz , cho mặt phẳng (α ): x − 2y + 4z −1= 0 .Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng (α ) ? → → → → A. n = 1; 2 − ;4 . B. n = 1 − ;2;4
C. n = 1;2;4 . D. n = 1;2; 4 − . 1 ( ) 2 ( ) 4 ( ) 3 ( )
Câu 9. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x + (y− 2) + z = 25 . Bán kính của (S) bằng A. 25. B. 5 . C. 50. D. 25 .
Câu 10. Trong không gian Oxyz, cho hai điểm A( 1; − 5;2) và B(3; 3
− ;2) . Toạ độ trung điểm M của đoạn thẳng AB là A. (1;1;2) . B. M (4; 8; − 0).
C. M (2;2;4). D. M (2; 4; − 0) .
Câu 11. Cho hàm số f (x) liên tục và không âm trên đoạn [7;8]. Diện tích hình thang cong giới hạn bởi đồ
thị của hàm số y = f (x) , trục Ox và 2 đường thẳng x = 7, x = 8 được tính theo công thức nào dưới đây? 8 8 8 8
A. S = π  f
∫ (x) 2 d .x
B. S = − f
∫ (x)d .x C. S = f
∫ (x)d .x
D. S = π f ∫ (x)d .x 7 7 7 7 1/4 - Mã đề 104 3 Câu 12. Giá trị d ∫ x bằng 0 A. 3 − . B. 3 . C. 0. D. 4
Câu 13. Trong không gian Oxyz , hình chiếu vuông góc của điểm A(8;1;2) trên trục Ox có tọa độ là A. (0;1;2) . B. (8;0;0) . C. (0;1;0) . D. (0;0;2) .
Câu 14. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x + 2, y = 0, x =1, x = 2. Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2
A. V = ∫(x + 2)2 2
dx B. V = ∫( 2x + 2)dx
C. V = π ∫(x + 2)2 2
dx D. V = π ∫( 2x + 2)dx 1 1 1 1 
Câu 15. Trong không gian Oxyz , cho hai điểm (1
A ;0;1) và B(2;−1;−
2) . Véctơ AB có tọa độ là A. ( 1; − 1;3) .
B. (1;−1;−1) .
C. (1;1;− 3) . D. (1;−1;−3) .
Câu 16. Mệnh đề nào dưới đây đúng? A. ( 2 )′ d = 2 +
∫ x x x C . B. ( 2)′ 2 d = +
∫ x x x C . C. ( 2)′ 2 d = − +
∫ x x x C . D. ( 2)′ d = 2 − + ∫ x x x C . Câu 17. 5 ∫ x dx bằng A. 6 x + C . B. 4
5x + C . C. 1 6 x + C . D. 6 6x + C . 6
Câu 18. Xét hàm số f (x) liên tục trên đoạn [ ;
a b]. Mệnh đề nào dưới đây đúng? b b b b A. 5 f
∫ (x)dx = f
∫ (5x)dx . B. 5 f
∫ (x)dx = 5 f ∫ (x)dx . a a a a b b b b a C. 5 f
∫ (x)dx = 5+ f
∫ (x)dx . D. 5 f
∫ (x)dx = 5d .x f ∫ ∫ (x)dx. a a a a b
Câu 19. Họ tất cả các nguyên hàm của hàm số f (x) 1 = là 2 sin x
A. cot x + C .
B. − tan x + C .
C. −cot x + C .
D. tan x + C . 3 3 3
Câu 20. Biết ∫ f (x)dx = 4 và ∫ g(x)dx =1. Khi đó: 
∫ f (x)− g(x)  dx bằng: 2 2 2 A. 3 − . B. 5 . C. 4 . D. 3 .
Câu 21. Họ tất cả các nguyên hàm của hàm số f (x) = sin 6x là: A. 1
− cos6x + C .
B. −cos6x + C .
C. 1 cos6x + C .
D. cos6x + C . 6 6
Câu 22. Họ tất cả các nguyên hàm của hàm số ( ) = 4 x f x e là A. x 1 4e + − + C. B. 4 x
− e + C. C. 4 x e + C. D. x 1 4e + + C.
Câu 23. Xét f (x) là một hàm số tùy ý, F (x) là một nguyên hàm của f (x) trên đoạn[3;4]. Mệnh đề nào dưới đây đúng? 4 4 A. f
∫ (x)dx = F (3)− F (4). B. f
∫ (x)dx = F (4)− F (3). 3 3 4 4 C. f
∫ (x)dx = F (4)+ F (3). D. f
∫ (x)dx = −F (3)− F (4). 3 3
Câu 24. Họ tất cả các nguyên hàm của hàm số ( ) 2 = 3 + 2 + x f x x x e là 2/4 - Mã đề 104 x 1 + A. 3 2 x 1 + x e
+ x + e + C . B. 3 2 x + x + + C . C. 6 + 2 + x x e + C . D. 3 2 + + x x x e + C . x +1 7 2
Câu 25. Cho hàm số y = f (x) liên tục trên  và ∫ f (x)dx =15 . Giá trị của (3 +
∫ f x )1dx bằng 1 0 A. 30. B. 31. C. 5. D. 6 .
Câu 26. Cho hàm số bậc ba y = f (x) . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y = f (x), y = 0, x = 2 − và x = 2 .
Mệnh đề nào dưới đây là đúng? 1 2 1 2
A. S = − f (x)dx + ∫
∫ f (x)dx .
B. S = f (x)dx − ∫
∫ f (x)dx . 2 − 1 2 − 1 1 2 1 2
C. S = f (x)dx + ∫
∫ f (x)dx .
D. S = − f (x)dx − ∫
∫ f (x)dx. 2 − 1 2 − 1
Câu 27. Cho F (x) là một nguyên hàm của hàm số f (x) = 2x + 5 và thỏa mãn F ( ) 1 = 3
− . Giá trị của F (3) bằng A. 15. B. 17 . C. 16. D. 14.
Câu 28. Họ tất cả các nguyên hàm của hàm số 2 ( ) = 9 x f x là x x x 1 A. 2.81x ln 9 81 81 81 + + C . B. + C . C. 2⋅ + C D. + C . 2ln 9 ln 9 x +1
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 2
y = −x + 2x − 3 và đường thẳng y = −x − 3 bằng A. 5. B. 11 C. 7 . D. 9 . 2 2 2 3 Câu 30. Biết 3
F(x) = x là một nguyên hàm của hàm số f (x) trên  . Giá trị của (1+ f (x))dx ∫ bằng 1 A. 28. B. 20. C. 26. D. 22. 2
Câu 31. Cho I = x (1+ ∫ x )4 2 3 dx . Đặt 3
t =1+ x , mệnh đề nào dưới đây đúng? 1 9 9 2 9 A. 1 4 I = t dt. B. 4
I = 3 t dt. C. 1 4 I = t dt. D. 4
I = t dt. 3 ∫ ∫ 3 ∫ ∫ 2 2 1 2
Câu 32. Mệnh đề nào dưới đây đúng?
A. ∫(2 + )1 x d = (2 + )1 x + 2 x x e x x e e d ∫ x .
B. ∫(2 + )1 x d = (2 + )1 x − x x e x x e e d ∫ x.
C. ∫(2 + )1 x d = (2 + )1 x + x x e x x e e d ∫ x .
D. ∫(2 + )1 x d = (2 + )1 x −2 x x e x x e e d ∫ x .
Câu 33. Trong không gian Oxyz, cho hai điểm A( 1
− ;2;0), B(3;0;2) . Phương trình mặt phẳng trung trực của
đoạn thẳng AB là
A. 2x − y + z + 2 = 0 . B. 2x − y + z − 2 = 0.
C. 2x + y + z − 6 = 0. D. 2x − y + z − 4 = 0.
Câu 34. Họ tất cả các nguyên hàm của hàm số 2
f (x) = 3x + cos x là 3/4 - Mã đề 104 A. 3
3x + sin x + C B. 3
x − sin x + C C. 3
x + sin x + C D. 3
3x − sin x + C
Câu 35. Trong không gian Oxyz , cho mặt phẳng (P) :3x − 2y + 4z +10 = 0 . Điểm nào dưới đây thuộc(P) ?
A. N(1;2;− 3).
B. Q(2;−1;3) .
C. P(2;2;− 3) .
D. M (3;− 2;4) .
Câu 36. Trong không gian Oxyz , cho hai điểm A(3;1;− 2), B(2;−3;5) . Điểm M (a; ; b c) thỏa mãn   
MA + 2MB = 0. Khi đó a + 3b + c bằng A. 10. B. 10 . C. 5. D. 0 . 3 3 2 3 Câu 37. Biết ( )d = 5 ∫ f x x và ( )d = 2 − ∫ f x x . Khi đó ( )d ∫ f x x bằng 1 1 2 A. 7 . B. 3 − . C. 3 . D. 7 − .
Câu 38. Trong không gian Oxyz , khoảng cách từ điểm M (1;2; )
1 đến mặt phẳng (P): 2x − y − 2z −13 = 0 bằng A. 2 . B. 3 . C. 4 . D. 5. 2 2
Câu 39. Xét hàm số f (x) liên tục trên  và ∫(4 f (x) 4
+ 5x )dx = 40 . Khi đó ( )d
∫ f x x bằng 0 0 A. 4 . B. 2 . C. 1. D. 3.
Câu 40. Trong không gian Oxyz , cho hai điểm A(1;3;− 2), B(3;−1;4). Mặt cầu đường kính AB có phương trình
A. (x + )2 + ( y + )2 + (z + )2 2 1 1 =14 .
B. (x − )2 + ( y − )2 + (z − )2 2 1 1 = 14 .
C. (x − )2 + ( y − )2 + (z − )2 2 1 1 =14 .
D. (x + )2 + ( y + )2 + (z + )2 2 1 1 = 14 .
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số 3
y = x − x −1 và 2
y = −x + x −1
Câu 2. Trong không gian Oxyz , cho ba điểm A(1;− 3;2) , B(1;0; )
1 và C (2;3;0) . Viết phương trình mặt phẳng ( ABC)
Câu 3. Cho hàm số bậc ba y f x 3 2 1
ax bx x d 5 và đường 4 34
thẳng y = g ( x) có đồ thị như hình vẽ bên. Biết AB = , diện tích hình 5
phẳng giới hạn bởi hai đồ thị y f x và y = g ( x) bằng bao nhiêu? 1
Câu 4. Cho hàm số f (x) liên tục trên  thỏa mãn 2
f (x) = 2x − 9 + ∫ xf ( 2
1+15x )dx. Giá trị của 0
2∫ f (x)dx bằng 0
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ................... 4/4 - Mã đề 104
Document Outline

  • 02.de 101
  • 03.de 102
  • 04.de 103
  • 05.de 104