Đề giữa kỳ 2 Toán 12 năm 2022 – 2023 trường THPT Hướng Hóa – Quảng Trị

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giữa học kì 2 môn Toán 12 năm học 2022 – 2023 .Mời bạn đọc đón xem.

29 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang

- Mã đề 121

SỞ GD & ĐT QUẢNG TRỊ

TRƯỜNG THPT HƯỚNG HÓA

ĐỀ KIỂM TRA GIỮA KỲ II, NĂM HỌC 2022 - 2023

MÔN TOÁN - Khối 12

Thời gian làm bài: 90 phút

ĐỀ CHÍNH THỨC

(

Đề

trang)

Họ tên: ...........................................…….Lớp:............ Số báo danh: ...........…..

Mã đề 121

PHẦN I. TRẮC NGHIỆM (35 câu: 7,0 điểm)

Câu 1: Cho hàm số





y f x



liên tục trên



Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số





y f x



, trục hoành và hai đường thẳng

 



(như hình vẽ bên dưới).

Mệnh đề nào sau đây đúng?

   

1 2

1 1

d d

S f x x f x x



  

 

. B.

   

1 2

1 1

d d

S f x x f x x



 

 

   

1 2

1 1

d d

S f x x f x x



 

 

. D.

   

1 2

1 1

d d

S f x x f x x



  

 

Câu 2: Trong không gian

Oxyz

, mặt cầu

       

2 2 2

: 2 3 4 3

S x y z

     

có tâm và bán kính lần

lượt là





2;3; 4

 

;



. B.





2; 3;4

I 

;

R 





2; 3;4

I 

;



. D.





2;3; 4

 

;

R 

Câu 3: Họ tất cả các nguyên hàm của hàm số





cos

f x x



là

cos

x C

 

. B.

sin

x C



. C.

cos

x C



. D.

sin

x C

 

Câu 4: Gọi

là hình phẳng giới hạn bởi các đường

3 , 0, 0

y y x

  

và



. Thể tích khối tròn

xoay tạo thành khi quay

quanh trục hoành

bằng

3 d



. B.

3 d



. C.

3 d





. D.

3 d





Câu 5: Trong không gian

Oxyz

với hệ tọa độ





; , ,

O i j k



 

cho

2 3

OA j k

 

 



. Tìm tọa độ điểm





0;2; 3



. B.





2; 3;0



. C.





2; 3



. D.





2;0; 3



Câu 6: Trong không gian

Oxyz

cho mặt phẳng





: 4 3 2 1 0

x y z



   

. Mặt phẳng nào dưới đây song

song với











: 4 3 2 3 0.

R x y z

   





: 4 3 2 1 0.

Q x y z

   





: 4 3 2 2 0.

S x y z

   





: 4 3 2 2 0.

P x y z

   

Câu 7: Cho hàm số





f x

liên tục trên đoạn





3;4



. Gọi





F x

là một nguyên hàm của hàm số





f x

trên





3;4



và









4 4; 3 2

F F

  

. Tính

 

I f x dx







. B.

. C.



. D.

Trang

- Mã đề 121

Câu 8: Cho

là thể tích của vật thể





giới hạn bởi hai mặt phẳng vuông góc với trục

tại các

điểm



và



, biết thiết diện của vật thể





bị cắt bởi mặt phẳng vuông góc với trục

tại điểm

có hoành độ bằng





0 3

x x

 

là một tam giác có diện tích bằng

. Mệnh đề nào sau đây đúng?

4 .

V x dx







V x dx





4 .

V x dx





16 .

V x dx







Câu 9: Cho hàm số





f x

liên tục trên



và có

 

d 3,

f x x







 

d 8

f x x





. Tính

 

d .

I f x x







 

. B.



. C.



. D.



Câu 10: Cho hai hàm số





u u x



và





v v x



có đạo hàm liên tục trên



. Khẳng định nào sau đây

đúng?

























' '

u x v x dx u x v x u x v x dx

 

 

. B.

























' ' '

u x v x dx u x v x u x v x dx

 

 

























' ' ' '

u x v x dx u x v x u x v x dx

 

 

. D.

























' '

u x v x dx u x v x u x v x dx

 

 

Câu 11: Cho hàm số





y f x



liên tục trên khoảng

và

, ,

a b c K



. Mệnh đề nào sau đây sai?

 

d 0

f x x





. B.

   

d d

b a

a b

f x x f x x

 

 

   

d dt

b b

a a

f x x f t



 

. D.

     

d d d

b b c

a c a

f x x f x x f x x

 

  

Câu 12: Trong không gian

Oxyz

, cho mặt phẳng





: 2 5 1 0

P y z

  

. Mặt phẳng





có một vectơ

pháp tuyến là





2; 5; 1

  



. B.





2;0; 5

 



. C.





2; 5;0

n  



. D.





0;2; 5

 



Câu 13: Tìm họ nguyên hàm





F x

của hàm số





f x x



 

F x



. B.

x C



. C.

 

F x C

 

. D.





F x x C

 

Câu 14: Họ tất cả các nguyên hàm của hàm số





f x e x

 

là

2 .

e C

 

e x C

 

e x C

 

e x C

 

Câu 15: Trong không gian

Oxyz

, điểm nào sau đây thuộc mặt phẳng





: 2 3 6 0

P x y z

   





1;1; 1



. B.





1;2;1

. C.





5; 1;1

N 

. D.





1;2;3

Câu 16: Trong không gian

Oxyz

, cho hai điểm





1;2; 3

 

và





3; 2; 1

  

. Tìm tọa độ của







2;0; 2

  



. B.





2;4; 2

 



. C.





2; 4;2

AB   



. D.





1; 2;1

AB   



Câu 17: Cho hai hàm số





y f x



và





y g x



liên tục trên



. Trong các mệnh đề sau, mệnh đề nào

sai?

















. .

f x g x dx f x dx g x dx



  

















f x g x dx f x dx g x dx

   

 

  

















f x g x dx f x dx g x dx

   

 

  









kf x dx k f x dx



 

với mọi hằng số





\ 0

k 



Câu 18: Trong không gian

Oxyz

, mặt phẳng đi qua ba điểm





0;0; 3







1;0;0

và





0;5;0

có

phương trình là

1 5 3

x y z

  



. B.

1 5 3

x y z

  



. C.

3 1 5

x y z

  



. D.

1 5 3

x y z

   



Trang

- Mã đề 121

Câu 19: Trong không gian

Oxyz

, cho hai điểm





1;2;3

A 

và





3; 2;1

B  

. Tìm tọa độ trung điểm

đoạn thẳng





1; 2; 1

  

. B.





2;0;2

I 

. C.





4;0;4

I 

. D.





2; 4; 2

  

Câu 20: Cho hàm số





y f x



có





3 4







1 2

 

và hàm số





f x



liên tục trên





1;3



. Khi đó

 

f x x







bằng

. B.

. C.



. D.

Câu 21: Trong không gian

Oxyz

, cho điểm





1;2; 3



và mặt phẳng





: 2 2 10 0

P x y z

   

. Tính

khoảng cách từ điểm

đến mặt phẳng





. B.

. C.



. D.

Câu 22: Biết





F x e x

 

là một nguyên hàm của hàm số





f x

trên



. Khi đó





2 d

f x x



bằng

2 2

e x C

 

. B.

2 2

e x C

 

. C.

2 2

e x C

 

. D.

2 2

e x C

 

Câu 23: Tìm phương trình mặt cầu tâm





1;2; 3

 

và đi qua điểm





2;0;0

     

2 2 2

1 2 3 22.

x y z     

     

2 2 2

1 2 3 22.

     x y z

     

2 2 2

1 2 3 22.

     x y z

     

2 2 2

1 2 3 11.

     x y z

Câu 24: Tính diện tích

của hình phẳng giới hạn bởi





: 4 3

P y x x

  

và trục hoành.





Câu 25: Tìm họ nguyên hàm của hàm số

 

3 2

f x





 

ln 3 2

f x dx x C

  



. B.





3ln 3 2

f x dx x C

  



   

ln 3 2

f x dx x C

  



. D.





ln 3 2

f x dx x C

  



Câu 26: Trong không gian

Oxyz

, cho điểm





2; 1; 3

 

và mặt phẳng





:3 2 4 5 0

P x y z

   

. Mặt

phẳng





đi qua

và song song với mặt phẳng





có phương trình là





:3 2 4 4 0.

Q x y z

   





:3 2 4 4 0.

Q x y z

   





:3 2 4 5 0.

Q x y z

   





:3 2 4 8 0.

Q x y z

   

Câu 27: Cho hàm số





f x

liên tục trên



và

 

d 16

f x x





. Tính

 

2 d

f x x



. B.

. C.

. D.

Câu 28: Trong không gian

Oxyz

, gọi



là góc giữa hai vectơ





3;4;0

a  



và





5;0;12

b 



. Tính

cos





. B.

. C.

. D.



Câu 29: Tính tích phân

cos2 d

I x x x





bằng cách đặt

d cos 2 d

u x

v x x











. Mệnh đề nào dưới đây đúng?

2 π

sin 2 sin 2 d

I x x x x x

 



. B.

2 π

sin 2 2 sin 2 d

I x x x x x

 



Trang

- Mã đề 121

2 π

sin 2 2 sin 2 d

I x x x x x

 



. D.

2 π

sin 2 sin 2 d

I x x x x x

 



Câu 30: Trong không gian

Oxyz

, cho ba điểm





1;1;1

A 





2;1;0





1; 1;2

C 

. Mặt phẳng đi qua

và

vuông góc với đường thẳng

có phương trình là

2 2 1 0

x y z

   

. B.

2 2 1 0

x y z

   

. C.

3 2 1 0

x z

  

. D.

2 2 1 0

x y z

   

Câu 31: Cho

 

4 2 1

f x x dx

 

 

 



. Tính tích phân

 

f x dx



. B.



. C.

. D.



Câu 32: Cho hàm số





f x

thỏa mãn





3 5sin

f x x



 

và





0 10



. Mệnh đề nào dưới đây là đúng?





3 5cos 15

f x x x

  

. B.





3 5cos 2

f x x x

  





3 5cos 2

f x x x

  

. D.





3 5cos 5

f x x x

  

Câu 33: Cho

 

f x dx







và

 

g x dx







. Tính

 

2 3 ( )

I f x g x dx



 

 

 



 



18.



18.

 

Câu 34: Tính thể tích

của vật thể giới hạn bởi hai mặt phẳng

 

và



, biết rằng thiết diện của

vật thể cắt bởi mặt phẳng vuông góc với trục

tại điểm có hoành độ





1 1

x x

  

là một hình vuông

có cạnh bằng

2 1



V 











Câu 35: Cho

  

ln 2 ln 3 ln 5

1 2

a b c

x x

  

 



với

, ,

a b c

là các số hữu tỉ. Tính giá trị của biểu thức

2 3

a b c

 

. B.

. C.

. D.

PHẦN II. TỰ LUẬN (4 câu: 3,0 điểm)

Câu 1: (1,0 điểm) Tìm họ nguyên hàm của hàm số





2023

3 4

( ) 4 3f x x x 

Câu 2: (1,0 điểm) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm









1;3; 1 , 2; 1;0

A B

   

và mặt

phẳng





: 3 2 3 0.

P x y z

   

Viết phương trình mặt phẳng







đi qua hai điểm

A B

và vuông góc với

mặt phẳng





Câu 3: (0,5 điểm) Cho hàm số

( )

f x

có đạo hàm liên tục trên đoạn





0;1

thỏa mãn





1 1



 

f x x





 

 



và

 

. d

x f x x





. Tính tích phân

 

I f x x





Câu 4: (0,5 điểm) Một khuôn viên có dạng elip





có

độ dài trục lớn

AB m



, độ dài trục bé

CD m



Trên đó người thiết kế hai phần: một phần để trồng hoa

(phần tô màu) có dạng của một cánh hoa hình parabol





có đỉnh trùng với tâm

của





, trục đối xứng là

đường thẳng

và hai đầu mút

M N

của cánh hoa

nằm trên





có

// , 6

MN AB MN m



; phần còn lại của

khuôn viên (phần không tô màu) dành để trồng rau. Hỏi

cần bao nhiêu tiền để trồng rau trên khuôn viên đó biết

chi phí trồng rau là 30000 đồng

------ HẾT ------

Trang

- Mã đề 122

SỞ GD & ĐT QUẢNG TRỊ

TRƯỜNG THPT HƯỚNG HÓA

ĐỀ KIỂM TRA GIỮA KỲ II, NĂM HỌC 2022 - 2023

MÔN TOÁN - Khối 12

Thời gian làm bài: 90 phút

ĐỀ CHÍNH THỨC

(

Đề

trang)

Họ tên: ...........................................…….Lớp:............ Số báo danh: ...........…..

Mã đề 122

PHẦN I. TRẮC NGHIỆM (35 câu: 7,0 điểm)

Câu 1: Cho hàm số





f x

liên tục trên



và có

 

d 2,

f x x







 

d 6

f x x

 



. Tính

 

d .

I f x x







 

. B.



. C.

 

. D.



Câu 2: Cho





f x

là hàm số liên tục trên





;

a b

và





F x

là một nguyên hàm của





f x

. Khẳng định

nào sau đây đúng?

       

f x dx f x f b f a

  



. B.

       

f x dx F x F a F b

  



       

f x dx F x F b F a

   



. D.

       

f x dx F x F b F a

  



Câu 3: Trong không gian

Oxyz

, cho mặt phẳng





:3 2 1 0

P x z

  

. Mặt phẳng





có một vectơ pháp

tuyến là





3; 2;0

n  



. B.





3;0; 2

 



. C.





3; 2; 1

  



. D.





3; 1; 2

  



Câu 4: Cho

là thể tích của vật thể





giới hạn bởi hai mặt phẳng vuông góc với trục

tại các

điểm



và



, biết thiết diện của vật thể





bị cắt bởi mặt phẳng vuông góc với trục

tại điểm

có hoành độ bằng





0 3

x x

 

là một tam giác có diện tích bằng

. Mệnh đề nào sau đây đúng?

25 .

V x dx







5 .

V x dx





V x dx





5 .

V x dx







Câu 5: Cho hàm số





f x

liên tục trên đoạn





3;4



. Gọi





F x

là một nguyên hàm của hàm số





f x

trên





3;4



và









4 4; 3 2

F F

    

. Tính

 

I f x dx







. B.



. C.



. D.



Câu 6: Cho hai hàm số





y f x



và





y g x



liên tục trên



. Trong các mệnh đề sau, mệnh đề nào

đúng?

















f x g x dx f x dx g x dx

   

 

  









kf x dx k f x dx

 

 

với mọi hằng số





\ 0

k 



















   

 

  

f x g x dx f x dx g x dx

















. .

f x g x dx f x dx g x dx



  

Câu 7: Trong không gian

Oxyz

với hệ tọa độ





; , ,

O i j k



 

cho

3 4

OA j k

  

  

. Tìm tọa độ điểm





3;4



. B.





0; 3;4



. C.





3;0;4



. D.





3;4;0



Câu 8: Họ tất cả các nguyên hàm của hàm số





sin

f x x



là

sin

x C



. B.

cos

x C

 

. C.

cos

x C



. D.

sin

x C

 

Câu 9: Họ tất cả các nguyên hàm của hàm số





f x x e

 

là

3 x

x e C

 

. B.

x e C

 

. C.

x e C

 

. D.

3 x

x e C

 

Trang

- Mã đề 122

Câu 10: Trong không gian

Oxyz

, điểm nào sau đây thuộc mặt phẳng





: 2 3 6 0

P x y z

   





1;2;3

. B.





1;1; 1



. C.





1;2;1

. D.





3;3;1

P 

Câu 11: Tìm họ nguyên hàm





F x

của hàm số





f x x



 

F x C

 

. B.

 

F x 

. C.

x C



. D.





F x x C

 

Câu 12: Cho hai hàm số





u u x



và





v v x



có đạo hàm liên tục trên



. Khẳng định nào sau đây

đúng?

























' '

u x v x dx u x v x u x v x dx

 

 

. B.

























' ' '

u x v x dx u x v x u x v x dx

 

 

























' ' ' '

u x v x dx u x v x u x v x dx

 

 

. D.

























' '

u x v x dx u x v x u x v x dx

 

 

Câu 13: Trong không gian

Oxyz

, cho hai điểm





1;2;3

và





3; 2;1

B 

. Tìm tọa độ của







1; 2; 1

  



. B.





2;0;2

AB 



. C.





2;4;2

AB  



. D.





2; 4; 2

  



Câu 14: Gọi

là hình phẳng giới hạn bởi các đường

2 , 0, 0

y y x

  

và



. Thể tích của khối

tròn xoay tạo thành khi quay

quanh trục hoành

bằng





. B.



. C.



. D.





Câu 15: Cho hàm số





y f x



có





4 3







2 2

 

và hàm số





f x



liên tục trên





2;4



. Khi đó

 

f x x







bằng



. B.

. C.

. D.

Câu 16: Trong không gian

Oxyz

, mặt cầu

       

2 2 2

: 3 2 5 9

S x y z

     

có tâm và bán kính lần

lượt là





3;2; 5

 

;



. B.





3; 2;5

I 

;



. C.





3; 2;5

I 

;



. D.





3;2; 5

 

;



Câu 17: Trong không gian

Oxyz

cho mặt phẳng





: 3 5 2 0

x y z



   

. Mặt phẳng nào dưới đây song

song với











: 3 5 2 0.

R x y z

   





: 3 5 1 0.

Q x y z

   





: 3 5 3 0.

P x y z

   





: 3 5 2 0.

S x y z

    

Câu 18: Trong không gian

Oxyz

, mặt phẳng đi qua ba điểm





5;0;0





0;0; 3



và





0;4;0

có

phương trình là

5 3 4

x y z

  



. B.

5 4 3

x y z

  



. C.

5 4 3

x y z

   



. D.

5 4 3

x y z

  



Câu 19: Cho hàm số





y f x



liên tục trên



Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm

số





y f x



, trục hoành và hai đường thẳng

 



(như hình vẽ bên dưới).

Mệnh đề nào sau đây đúng?

Trang

- Mã đề 122

1 5

1 1

( )d ( )d

S f x x f x x



  

 

. B.

1 5

1 1

( )d ( )d

S f x x f x x



  

 

1 5

1 1

( )d ( )d

S f x x f x x



 

 

. D.

1 5

1 1

( )d ( )d

S f x x f x x



 

 

Câu 20: Trong không gian

Oxyz

, cho hai điểm





1;2;3

và





3; 2;1

B 

. Tìm tọa độ trung điểm

đoạn

thẳng





1; 2; 1

 

. B.





4;0;4

. C.





2;0;2

. D.





2; 4; 2

 

Câu 21: Biết

  

ln 2 ln 3 ln 5

1 2 1

a b c

x x

  

 



. Tính giá trị của biểu thức

a b c

 

. B.



. C.

. D.

Câu 22: Tính tích phân

sin

I x xdx







bằng cách đặt

sin

u x

dv xdx











. Mệnh đề nào sau đây đúng?

cos | cos

I x x xdx



 



. B.

sin | sin

I x x xdx



 



sin | sin

I x x xdx



  



. D.

cos | cos

I x x xdx



  



Câu 23: Tìm họ nguyên hàm của hàm số

 

4 1

f x









d 4ln 4 1

f x x x C

  



. B.

   

d ln 4 1

f x x x C

  







d ln 4 1

f x x x C

  



. D.

 

d ln 4 1

f x x x C

  



Câu 24: Tìm phương trình mặt cầu

( )

tâm





3; 3;1

I

và đi qua





5; 2;1

A

     

2 2 2

3 3 1 5.

     

x y z

     

2 2 2

3 3 1 5.

     x y z

     

2 2 2

3 3 1 5.

x y z

     

     

2 2 2

5 2 1 5.

     

x y z

Câu 25: Trong không gian

Oxyz

, cho điểm





1;3; 2



và mặt phẳng





: 2 3 4 0

P x y z

   

. Mặt phẳng





đi qua

và song song với mặt phẳng





có phương trình là

2 3 7 0

x y z

   

. B.

2 3 7 0

x y z

   

. C.

2 3 7 0

x y z

   

. D.

2 3 7 0

x y z

   

Câu 26: Tính thể tích

của vật thể giới hạn bởi hai mặt phẳng



và



, biết rằng thiết diện của

vật thể cắt bởi mặt phẳng vuông góc với trục

tại điểm có hoành độ





0 3

x x

 

là một hình chữ nhật

có hai kích thước là

và

2 9



27 .





27.



18 .





18.



Câu 27: Biết





F x e x

 

là một nguyên hàm của hàm số





f x

trên



. Khi đó





f x dx



bằng

2 2

2 .

e x C

 

2 2

4 .

e x C

 

2 2

e x C

 

2 2 .

e x C

 

Câu 28: Cho hàm số





f x

liên tục trên



và

 

d 15

f x x





. Tính

 

3 d

f x x



. B.

. C.

. D.

Câu 29: Trong không gian

Oxyz

, gọi



là góc giữa hai vectơ





3; 4;0

a  



và





5;0;12

b  



. Tính

Trang

- Mã đề 122

cos





. B.

. C.

. D.



Câu 30: Tìm nguyên hàm





F x

của hàm số





3 2

4 3 4 3

f x x x x

   

thỏa mãn





1 10







4 3 2

2 3 .

F x x x x

  







4 3 2

2 3 10.

F x x x xx

   







4 3 2

2 3 11.

F x x x xx

   







6 4.

12F x xx

 



Câu 31: Trong không gian

Oxyz

, cho điểm





1;2;0

M 

và mặt phẳng





: 2 2 1 0

P x y z

   

. Tính

khoảng cách từ điểm

đến mặt phẳng





. B.

. C.



. D.

Câu 32: Trong không gian

Oxyz

, cho ba điểm













2;1; 1 , 1;0;4 , 0; 2; 1

A B C

   

. Phương trình mặt

phẳng đi qua

và vuông góc với

là

2 5 5 0

x y z

   

. B.

2 5 5 0

x y z

   

. C.

2 5 0

x y

  

. D.

2 5 5 0

x y z

   

Câu 33: Tính diện tích S của hình phẳng giới hạn bởi các đường

y x x

 

và

y x

 

S .



S .



S .



S .



Câu 34: Cho

 

d 2

f x x

 



. Tính tích phân

 

4 3 d

f x x x

 



 



130



. B.

120



. C.

140



. D.

133



Câu 35: Cho

 

f x dx





và

 

g x dx





. Tính

 

2 3 ( )

I f x g x dx

 

 

 



 

18.



18.

 

PHẦN II. TỰ LUẬN (4 câu: 3,0 điểm)

Câu 1: (1,0 điểm) Tìm họ nguyên hàm của hàm số





2023

4 5

( ) 5 2f x x x 

Câu 2: (1,0 điểm) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm









2; 1; 3 0; 1;2

A B

  

và mặt

phẳng





:2 3 2 0.

P x y z

   

Viết phương trình mặt phẳng







đi qua hai điểm

A B

và vuông góc với

mặt phẳng





Câu 3: (0,5 điểm) Cho hàm số

( )

f x

có đạo hàm liên tục trên đoạn





0;1

thỏa mãn





1 1



 

f x x





 

 



và

 

. d

x f x x





. Tính tích phân

 

I f x x





Câu 4: (0,5 điểm) Một khuôn viên có dạng elip





có

độ dài trục lớn

AB m



, độ dài trục bé

CD m



. Trên

đó người thiết kế hai phần: một phần để trồng rau (phần

tô màu) có dạng của một cánh hoa hình parabol





có

đỉnh trùng với

, trục đối xứng là đường thẳng

và

hai đầu mút

M N

của cánh hoa nằm trên





có

// , 6

MN AB MN m



; phần còn lại của khuôn viên (phần

không tô màu) dành để trồng hoa. Hỏi cần bao nhiêu tiền

để trồng hoa trên khuôn viên đó biết chi phí trồng hoa là

50000 đồng

------ HẾT ------

SỞ GD & ĐT QUẢNG TRỊ

TRƯỜNG THPT HƯỚNG HÓA

ĐỀ CHÍNH THỨC

ĐÁP ÁN KIỂM TRA GIỮA KỲ II, NĂM HỌC 2022-2023

MÔN: TOÁN - Khối 12

PHẦN I. ĐÁP ÁN TRẮC NGHIỆM (35 câu: 7,0 điểm)

121 123 125 127 122 124 126 128

1 B A A B A D A C

2 D B A A D B A A

3 B C B D B C B B

4 C C B A B C C B

5 A C B B D C B D

6 B D C D A A B A

7 D A D A B D A A

8 C C B A B A A A

9 B A B A A B B A

10 A A D B D B A B

11 D B B A A A B B

12 D A D B D B D D

13 C D B C D A C D

14 C D B C A D B B

15 C D B D B D C B

16 C B A A B C B A

17 A C B A C D B D

18 A C B B B D D C

19 B D C D C D B B

20 B A B C C B C C

21 B A B C A B B C

22 B A B A D C C A

23 C B C D D B D D

24 B C A A A D A B

25 A B A A B A A B

26 A B D D D B A B

27 D B C D A B C C

28 A D D D B A D A

29 A B D A A D A D

30 D A B A C B C A

31 A C C B B B C A

32 D D C A D A B C

33 A C A B B B B A

34 A B A D D C B A

35 A D B B B C B A

PHẦN II. ĐÁP ÁN TỰ LUẬN (3,0 điểm)

ĐỀ LẺ (121, 123, 125, 127):

Câu Đáp án Điểm

Tìm họ nguyên hàm của hàm số





2023

3 4

( ) 4 3f x x x 

1,0

Đặt

t x

 

, ta có

d 4 d

t x x



0,25

Khi đó





 

2023

2024

d d

2024

= .

2024

f x x t t

C C







 

 



0,25

Trong không gian với hệ tọa độ

Oxyz

cho hai điểm









1;3; 1 , 2; 1;0

A B

   

và

mặt phẳng





:3 2 3 0.

P x y z

   

Viết phương trình mặt phẳng







đi qua hai

điểm

A B

và vuông góc với mặt phẳng





1,0

Ta có





1; 4;1 .

AB   



Mặt phẳng





có VTPT





3;1; 2 .

 



0,25

Mặt phẳng







đi qua hai điểm

A B

và vuông góc với mặt phẳng





nên có một

VTPT là





, 7;1;11

n AB n

 

 

 

 



 

0,25

Do đó







có phương trình













7 1 1 3 11 1 0

x y z

     

0,25

7 11 15 0.

x y z

    

0,25

Cho hàm số

( )

f x

có đạo hàm liên tục trên đoạn





0;1

thỏa mãn





1 1



 

f x x





 

 



và

 

. d

x f x x





. Tính tích phân

 

I f x x





0,5

Ta có

   

 

   

 

1 1 1

2 2 2 2

0 0 0

d d . d

x f x x x f x x f x f x x



  

  

   

1 3

1 2 d 1 2. .

5 5

f xf x x

    



Khi đó

 

1 1

2 2

2 2 2

0 0

3 d 2. .3 3 d

f x x x f x f x x x x

 

  

   

 

 

 

 

1 1 1

2 4

0 0 0

9 3

d 6 d 9 d 6. 9. 0.

5 5 5

f x x x f x x x x

 

      

  

0,25

Suy ra

 





 

2 2

3 0 3 0

f x x f x x

 

    





f x x



 





f x x C

  

Mà





1 1



nên





f x x



Vậy

 

1 1

0 0

d d

I f x x x x

  

 

0,25

Một khuôn viên có dạng elip





có độ dài

trục lớn

AB m



, độ dài trục bé

CD m



. Trên đó người thiết kế hai phần:

một phần để trồng hoa (phần tô màu) có

dạng của một cánh hoa hình parabol





có đỉnh trùng với tâm

của





, trục đối

xứng là đường thẳng

và hai đầu mút

0,5

M N

của cánh hoa nằm trên





có

// , 6

MN AB MN m



; phần còn lại của khuôn

viên (phần không tô màu) dành để trồng rau. Hỏi cần bao nhiêu tiền để trồng rau

trên khuôn viên đó biết chi phí trồng rau là 30000 đồng

Chọn hệ trục tọa độ

Oxy

như hình vẽ sao

cho

















5;0 , 5;0 , 0; 3 , 0;3

A B C D

 

Khi đó elip





có phương trình

25 9

 

. Suy ra nửa





phía trên

có phương trình

y x

 

0,25

Vì





, ;

M N E



// , 6

MN AB MN m



nên

12 12

3; , 3;

5 5

M N

   

   

   



Do parabol





đi qua các điểm

, ,

M N O

nên

 

: .

P y x



Diện tích hình phẳng giới hạn bởi





là

 

2 2

2 25 d 15 m .

S x x





  



Diện tích hình phẳng giới hạn bởi





và





(phần tô đậm) là

 

2 2 2

3 4

25 d 12,053 m .

5 15

S x x x



 

 

 

  





Diện tích phần trồng rau là

 





15 12,053 35,07 m .

S S S



   

Vậy số tiền trồng rau trên khuôn viên đó khoảng

35,07 30000 1052100

 

đồng.

0,25

ĐỀ CHẴN (122, 124, 126, 128):

Câu Đáp án Điểm

Tìm họ nguyên hàm của hàm số





2023

4 5

( ) 5 2f x x x 

1,0

Đặt

t x

 

, ta có

d 5 d

t x x



0,25

Khi đó





 

2023

2024

d d

2024

= .

2024

f x x t t

C C







 

 



0,25

Trong không gian với hệ tọa độ

Oxyz

cho hai điểm









2; 1; 3 0; 1;2

A B

  

và mặt

phẳng





: 2 3 2 0.

P x y z

   

Viết phương trình mặt phẳng







đi qua hai điểm

A B

và vuông góc với mặt phẳng





1,0

Ta có





2;0;5 .

AB  



Mặt phẳng





có VTPT





2;1; 3 .

 



0,25

Mặt phẳng







đi qua hai điểm

A B

và vuông góc với mặt phẳng





nên có một

VTPT là





, 5;4; 2

n AB n

 

 

 

   



 

0,25

Do đó







có phương trình













5 0 4 1 2 2 0

x y z

     

0,25

5 4 2 8 0.

x y z

     

0,25

Cho hàm số

( )

f x

có đạo hàm liên tục trên đoạn





0;1

thỏa mãn





1 1



0,5

 

f x x





 

 



và

 

. d

x f x x





. Tính tích phân

 

I f x x





Ta có

   

 

   

 

1 1 1

3 3 3 3

0 0 0

d d . d

x f x x x f x x f x f x x



  

  

   

1 4

1 3 d 1 3. .

7 7

f x f x x

    



Khi đó

 

1 1

2 2

3 3 3

0 0

4 d 2. .4 4 d

f x x x f x f x x x x

 

  

   

 

 

 

 

1 1 1

3 6

0 0 0

16 4

d 8 d 16 d 8. 16. 0.

7 7 7

f x x x f x x x x

 

      

  

0,25

Suy ra

 





 

3 3

4 0 4 0

f x x f x x

 

    





f x x



 





f x x C

  

Mà





1 1



nên





f x x



Vậy

 

1 1

0 0

d d

I f x x x x

  

 

0,25

Một khuôn viên có dạng elip





có độ

dài trục lớn

AB m



, độ dài trục bé

CD m



. Trên đó người thiết kế hai

phần: một phần để trồng rau (phần tô màu)

có dạng của một cánh hoa hình parabol





có đỉnh trùng với

, trục đối xứng là

đường thẳng

và hai đầu mút

M N

0,5

của cánh hoa nằm trên





có

// , 6

MN AB MN m



; phần còn lại của khuôn viên

(phần không tô màu) dành để trồng hoa. Hỏi cần bao nhiêu tiền để trồng hoa trên

khuôn viên đó biết chi phí trồng hoa là 50000 đồng

Chọn hệ trục tọa độ

Oxy

như hình vẽ sao

cho

















5;0 , 5;0 , 0; 3 , 0;3

A B C D

 

Khi đó elip





có phương trình

25 9

 

. Suy ra nửa





phía trên

có phương trình

y x

 

0,25

Vì





, ;

M N E



// , 6

MN AB MN m



nên

12 12

3; , 3;

5 5

M N

   

   

   



Do parabol





đi qua các điểm

, ,

M N C

nên

 

: 3.

P y x

 

Diện tích hình phẳng giới hạn bởi





là

 

2 2

2 25 d 15 m .

S x x





  



Diện tích hình phẳng giới hạn bởi





và





(phần tô đậm) là

 

2 2 2

3 3

25 3 d 24,053 m .

5 5

S x x x



 

 

 

   





Diện tích phần trồng hoa là

 





15 24,053 23,07 m .

S S S



   

Vậy số tiền trồng hoa trên khuôn viên đó khoảng

23,07 50000 1153500

 

đồng.

0,25

Bấm Tải xuống để xem toàn bộ.

| 1/12

| | Tải xuống

Preview text:

SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II, NĂM HỌC 2022 - 2023 TRƯỜNG THPT HƯỚNG HÓA MÔN TOÁN - Khối 12
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC (Đề có 4 trang)
Họ tên: ...........................................…….Lớp:............ Số báo danh: ...........….. Mã đề 121
PHẦN I. TRẮC NGHIỆM (35 câu: 7,0 điểm)
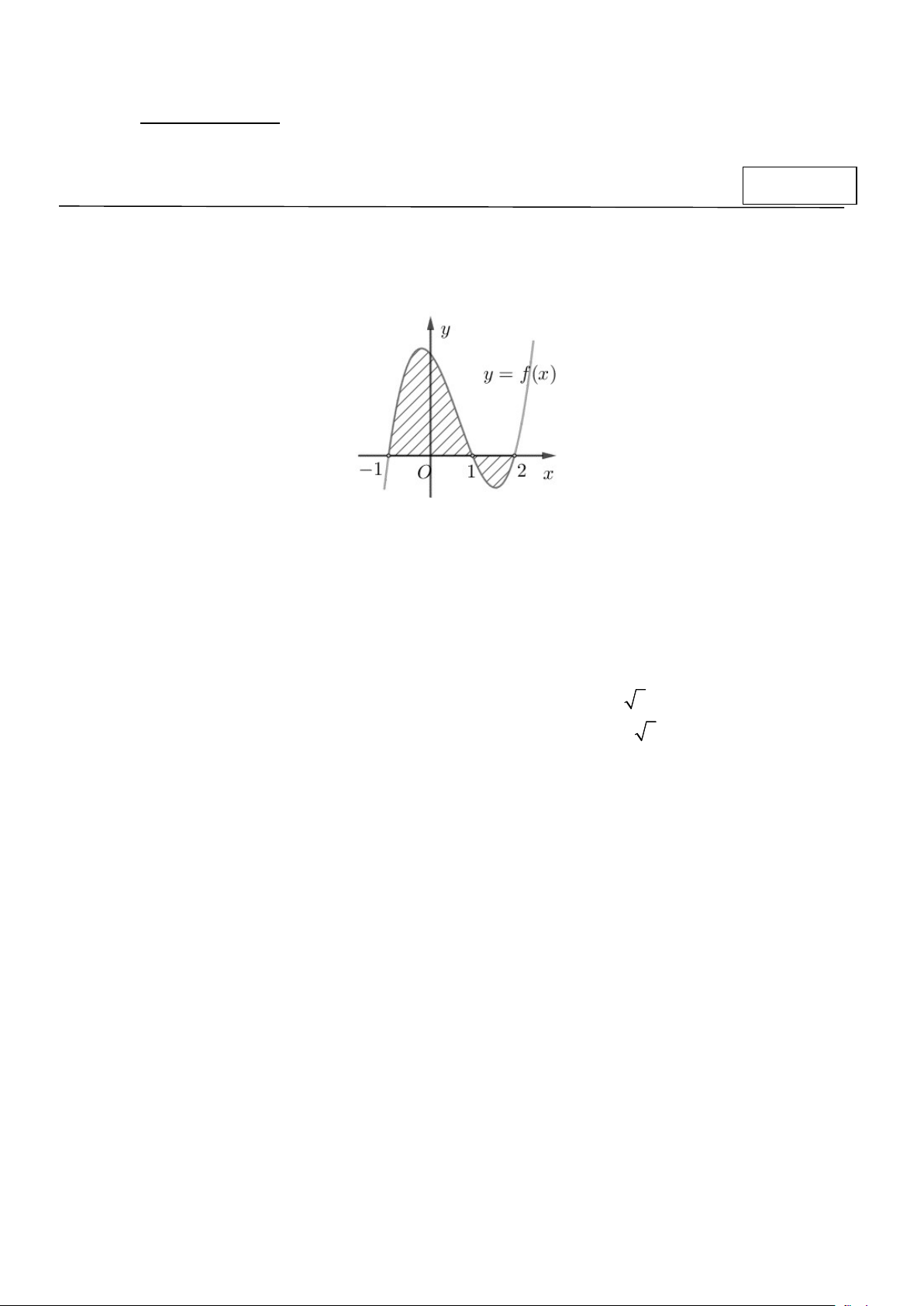
Câu 1: Cho hàm số y  f  x liên tục trên .
 Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y  f  x , trục hoành và hai đường thẳng x  1
 , x  2 (như hình vẽ bên dưới).
Mệnh đề nào sau đây đúng? 1 2 1 2 A. S   f  x dx  f  x dx . B. S  f  x dx  f  x dx . 1  1 1  1 1 2 1 2 C. S  f  x dx  f  x dx . D. S   f  x dx  f  x dx . 1  1 1  1
Câu 2: Trong không gian Oxyz , mặt cầu S   x  2   y  2   z  2 : 2 3
4  3 có tâm và bán kính lần lượt là A. I  2  ;3; 4   ; R  3. B. I 2; 3  ;4 ; R  3 . C. I 2; 3  ;4 ; R  3. D. I  2  ;3; 4   ; R  3 .
Câu 3: Họ tất cả các nguyên hàm của hàm số f  x  cos x là A. cos xC . B. sin x C . C. cos x C . D. sin x C .
Câu 4: Gọi D là hình phẳng giới hạn bởi các đường 2  3 x y
, y  0, x  0 và x  2 . Thể tích khối tròn
xoay tạo thành khi quay D quanh trục hoành Ox bằng 2 2 2 2 A. 2 3 x dx  . B. 4 3 x dx  . C. 4  3 x dx  . D. 2  3 x dx  . 0 0 0 0      
Câu 5: Trong không gian Oxyz với hệ tọa độ O;i , j,k  cho OA  2 j  3k . Tìm tọa độ điểm A . A. 0;2; 3   . B. 2; 3  ;0 . C. 2; 3  . D. 2;0; 3   .
Câu 6: Trong không gian Oxyz, cho mặt phẳng   : 4x  3y  2z 1  0 . Mặt phẳng nào dưới đây song song với  ?
A. R : 4x  3y  2z  3  0.
B. Q : 4x  3y  2z 1  0.
C. S  : 4x  3y  2z  2  0.
D. P : 4x  3y  2z  2  0.
Câu 7: Cho hàm số f  x liên tục trên đoạn 3;4 . Gọi F  x là một nguyên hàm của hàm số f  x 4
trên 3;4 và F 4  4; F 3  2 . Tính I  f  xdx . 3 A. 6 . B. 4 . C. 2  . D. 2 . Trang 1/4 - Mã đề 121
Câu 8: Cho V là thể tích của vật thể T  giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các
điểm x  0 và x  3 , biết thiết diện của vật thể T  bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm
có hoành độ bằng x 0  x  3 là một tam giác có diện tích bằng 3
4x . Mệnh đề nào sau đây đúng? 3 3 3 3 A. 3 V   4x d . x  B. 4 V  x d . x  C. 3 V  4x d . x  D. 6 V   16x d . x  0 0 0 0 2 3 3
Câu 9: Cho hàm số f  x liên tục trên  và có f  xdx  3, f
 xdx  8. Tính I  f  xd .x 1 2 1  A. I  5 . B. I  11. C. I  24 . D. I  5 .
Câu 10: Cho hai hàm số u  u  x và v  v x có đạo hàm liên tục trên  . Khẳng định nào sau đây đúng? A. u
 xv'xdx  uxvx u'  xvxdx . B. u
 xv'xdx  uxvx u'  xv'xdx . C. u
 xv'xdx  u'xv'x u'  xvxdx. D. u
 xv'xdx  u'xvx u  xvxdx .
Câu 11: Cho hàm số y  f  x liên tục trên khoảng K và a, ,
b c  K . Mệnh đề nào sau đây sai? a b a A. f  xdx  0. B. f  xdx   f  xdx. a a b b b b b c C. f  xdx  f  tdt . D. f  xdx  f  xdx  f  xdx. a a a c a
Câu 12: Trong không gian Oxyz , cho mặt phẳng P : 2y  5z 1  0 . Mặt phẳng P có một vectơ pháp tuyến là     A. n  2; 5;  1 . B. n  2;0; 5 . C. n  2; 5;0 . D. n  0;2; 5 .
Câu 13: Tìm họ nguyên hàm F  x của hàm số   4 f x  x . 5 x 5 x A. F  x  . B. 3 4x  C . C. F  x   C . D.   4 F x  x  C . 5 5
Câu 14: Họ tất cả các nguyên hàm của hàm số   x f x  e  2x là A. x e  2  C. B. x e  x  C. C. x 2 e  x  C. D. x 2 e  x  C.
Câu 15: Trong không gian Oxyz , điểm nào sau đây thuộc mặt phẳng P : x  2y  3z  6  0 ? A. Q 1;1;  1 . B. P 1;2;  1 . C. N 5;1;  1 . D. M 1;2;3 .
Câu 16: Trong không gian Oxyz , cho hai điểm A1;2; 3   và B 3  ; 2  ; 
1 . Tìm tọa độ của AB .     A. AB   2  ;0; 2  . B. AB  2;4;2 . C. AB  2;4;2 . D. AB   1  ; 2  ;  1 .
Câu 17: Cho hai hàm số y  f  x và y  g x liên tục trên  . Trong các mệnh đề sau, mệnh đề nào sai? A. f  x.gxdx  f  xd .x g  xdx. B.  f
 x gxdx  f   xdx g  xdx . C.  f
 x gxdx  f   xdx g  xdx. D. kf  xdx  k f
 xdx với mọi hằng số k  \ 0.
Câu 18: Trong không gian Oxyz , mặt phẳng đi qua ba điểm A0;0; 3
  , B1;0;0 và C 0;5;0 có phương trình là x y z x y z x y z x y z A.    1. B.    0 . C.    1. D.    1  . 1 5 3  1 5 3  3 1 5 1 5 3  Trang 2/4 - Mã đề 121
Câu 19: Trong không gian Oxyz , cho hai điểm A 1  ;2;3 và B 3  ; 2  ; 
1 . Tìm tọa độ trung điểm I đoạn thẳng AB . A. I  1  ; 2  ;  1 . B. I 2;0;2 . C. I 4;0;4 . D. I  2  ; 4  ; 2   .
Câu 20: Cho hàm số y  f  x có f 3  4 , f  
1  2 và hàm số f  x liên tục trên 1;  3 . Khi đó 3 f   xdx bằng 1  A. 8 . B. 2 . C. 2 . D. 6 .
Câu 21: Trong không gian Oxyz , cho điểm M 1;2; 3
  và mặt phẳng P :x  2y  2z 10  0 . Tính
khoảng cách từ điểm M đến mặt phẳng P . 11 11 4 A. 11. B. . C.  . D. . 3 3 3 Câu 22: Biết F  x x 2
 e  x là một nguyên hàm của hàm số f x trên  . Khi đó f 2xdx  bằng 1 1 A. 2 x 2 e  4x  C . B. 2 x 2 e  2x  C . C. x 2 2e  2x  C . D. 2 x 2 e  x  C . 2 2
Câu 23: Tìm phương trình mặt cầu tâm I 1;2;3 và đi qua điểm A2;0;0 .
A.  x  2   y  2   z  2 1 2 3  22.
B.  x  2   y  2   z  2 1 2 3  22.
C.  x  2   y  2   z  2 1 2 3  22.
D.  x  2   y  2   z  2 1 2 3  11.
Câu 24: Tính diện tích S của hình phẳng giới hạn bởi P 2
: y  x  4x  3 và trục hoành. 4 4 1 2 A. S   . B. S  . C. S  . D. S  . 3 3 3 3
Câu 25: Tìm họ nguyên hàm của hàm số f  x 1  . 3x  2 A. f  x 1 dx  ln 3x  2  C . B. f
 xdx  3ln 3x2 C . 3 1 C. f
 xdx  ln3x2C . D. f
 xdx  ln 3x  2  C . 3
Câu 26: Trong không gian Oxyz , cho điểm A2;1;3 và mặt phẳng P : 3x  2y  4z  5  0 . Mặt
phẳng Q đi qua A và song song với mặt phẳng P có phương trình là
A. Q :3x  2y  4z  4  0.
B. Q :3x  2y  4z  4  0.
C. Q :3x  2y  4z  5  0.
D. Q :3x  2y  4z  8  0. 6 3
Câu 27: Cho hàm số f x liên tục trên  và f
 xdx 16 . Tính f 2xdx  . 0 0 A. 16 . B. 4. C. 32. D. 8.  
Câu 28: Trong không gian Oxyz , gọi  là góc giữa hai vectơ a   3
 ;4;0 và b  5;0;12 . Tính cos . 3 3 5 5 A.  . B. . C. . D.  . 13 13 6 6 π 2   Câu 29: Tính tích phân 2 u x I  x cos 2 d x x  bằng cách đặt 
. Mệnh đề nào dưới đây đúng? dv  cos 2 d x x 0 π 1 π 1 A. 2 π I  x sin 2x  x sin 2 d x x 2 π
I  x sin 2x  2 x sin 2xdx 0  . B.  . 2 0 2 0 0 Trang 3/4 - Mã đề 121 π 1 π 1 C. 2 π
I  x sin 2x  2 x sin 2xdx 2 π I  x sin 2x  x sin 2xdx 0  . D.  . 2 0 2 0 0
Câu 30: Trong không gian Oxyz , cho ba điểm A1;1;  1 , B 2;1;0 C 1; 1
 ;2 . Mặt phẳng đi qua A và
vuông góc với đường thẳng BC có phương trình là
A. x  2 y  2z 1  0 . B. x  2 y  2z 1  0 . C. 3x  2z 1  0 .
D. x  2 y  2z 1  0 . 2 2 Câu 31: Cho 4 f  x2xdx 1  . Tính tích phân f  xdx  . 1 1 A. 1. B. 1  . C. 3 . D. 3  .
Câu 32: Cho hàm số f  x thỏa mãn f  x  3 5sin x và f 0 10. Mệnh đề nào dưới đây là đúng?
A. f  x  3x 5cos x 15 .
B. f  x  3x  5cos x  2.
C. f  x  3x  5cos x  2 .
D. f  x  3x  5cos x  5 . 3 1  3 Câu 33: Cho f  xdx  3 và g
 xdx  4 . Tính I  2 f   x3g(x)dx  . 1  3 1  A. I  6. B. I  6. C. I  18. D. I  18.
Câu 34: Tính thể tích V của vật thể giới hạn bởi hai mặt phẳng x  1 và x 1, biết rằng thiết diện của
vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x  1   x   1 là một hình vuông có cạnh bằng 2 2 1 x . 16 8 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 3 dx Câu 35: Cho
 a ln 2  b ln 3  c ln 5 
với a, b, c là các số hữu tỉ. Tính giá trị của biểu thức x 1 x  2 2    2 3 a  b  c . A. 6 . B. 5 . C. 4 . D. 3 .
PHẦN II. TỰ LUẬN (4 câu: 3,0 điểm)
Câu 1: (1,0 điểm) Tìm họ nguyên hàm của hàm số f x  x x  2023 3 4 ( ) 4 3 .
Câu 2: (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1  ;3;  1 , B 2  ; 1  ;0 và mặt
phẳng P: 3x  y  2z 3  0. Viết phương trình mặt phẳng   đi qua hai điểm , A B và vuông góc với mặt phẳng P .
Câu 3: (0,5 điểm) Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  1 , 1 1 1  1 f   x 2 9  dx   và . x f  xdx   . Tính tích phân I  f  xdx . 5 5 0 0 0
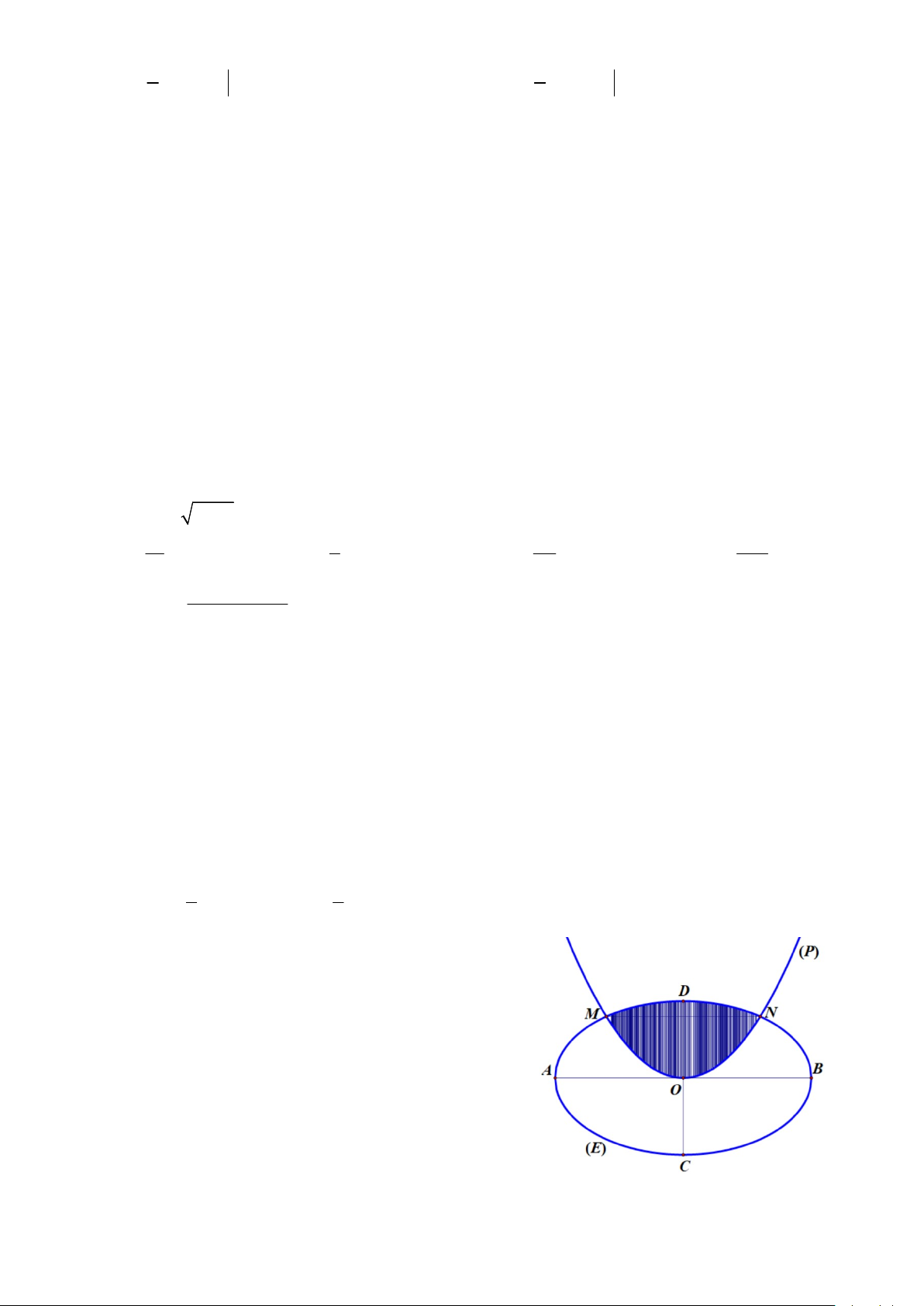
Câu 4: (0,5 điểm) Một khuôn viên có dạng elip E có
độ dài trục lớn AB  10m , độ dài trục bé CD  6m .
Trên đó người thiết kế hai phần: một phần để trồng hoa
(phần tô màu) có dạng của một cánh hoa hình parabol
P có đỉnh trùng với tâm O của E , trục đối xứng là
đường thẳng CD và hai đầu mút M , N của cánh hoa
nằm trên E có MN //AB, MN  6m ; phần còn lại của
khuôn viên (phần không tô màu) dành để trồng rau. Hỏi
cần bao nhiêu tiền để trồng rau trên khuôn viên đó biết
chi phí trồng rau là 30000 đồng 2 /m ? ------ HẾT ------ Trang 4/4 - Mã đề 121
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II, NĂM HỌC 2022 - 2023 TRƯỜNG THPT HƯỚNG HÓA MÔN TOÁN - Khối 12
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC (Đề có 4 trang)
Họ tên: ...........................................…….Lớp:............ Số báo danh: ...........….. Mã đề 122
PHẦN I. TRẮC NGHIỆM (35 câu: 7,0 điểm) 2 3 3
Câu 1: Cho hàm số f  x liên tục trên  và có f
 xdx  2, f xdx  6   . Tính I  f  xd .x 2 2 2  A. I  4 . B. I  4 . C. I  8  . D. I  8 .
Câu 2: Cho f  x là hàm số liên tục trên a;b và F x là một nguyên hàm của f  x . Khẳng định nào sau đây đúng? b b A. b f
 xdx  f xb  f b f a . B. f
 xdx  F x  F a  F b. a a a a b b C. f
 xdx  F xb  F b F a. D. f
 xdx  F xb  F b F a. a a a a
Câu 3: Trong không gian Oxyz , cho mặt phẳng P :3x  2z 1  0 . Mặt phẳng P có một vectơ pháp tuyến là    A. n  3; 2;0 . B. n  3;0; 2 . C. n  3; 2;  1 . D. n  3;1; 2 .
Câu 4: Cho V là thể tích của vật thể T  giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các
điểm x  0 và x  3 , biết thiết diện của vật thể T  bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm
có hoành độ bằng x 0  x  3 là một tam giác có diện tích bằng 4
5x . Mệnh đề nào sau đây đúng? 3 3 3 3 A. 8 V   25x d . x  B. 4 V  5x d . x  C. 5 V  x d . x  D. 4 V   5x d . x  0 0 0 0
Câu 5: Cho hàm số f  x liên tục trên đoạn 3;4 . Gọi F  x là một nguyên hàm của hàm số f  x 4
trên 3;4 và F 4  4; F 3  2  . Tính I  f  xdx . 3 A. 2 . B. 4  . C. 6  . D. 2  .
Câu 6: Cho hai hàm số y  f  x và y  g x liên tục trên  . Trong các mệnh đề sau, mệnh đề nào đúng? A.  f
 x gxdx  f   xdx g  xdx . B. kf  xdx  k  f
 xdx với mọi hằng số k  \ 0. C. 
 f x gxdx  
 f xdx gxdx . D. f  x.gxdx  f  xd .x g  xdx.      
Câu 7: Trong không gian Oxyz với hệ tọa độ O;i , j,k  cho OA  3 j  4k . Tìm tọa độ điểm A . A.  3  ;4. B. 0; 3  ;4 . C.  3  ;0;4 . D.  3  ;4;0 .
Câu 8: Họ tất cả các nguyên hàm của hàm số f  x  sin x là A. sin x C . B. cos xC . C. cos x C . D. sin x C .
Câu 9: Họ tất cả các nguyên hàm của hàm số   2  3 x f x x  e là A. 3 x x  e  C . B. 3 3 x x  e  C . C. 6 x x  e  C . D. 3 x x  e  C . Trang 1/4 - Mã đề 122
Câu 10: Trong không gian Oxyz , điểm nào sau đây thuộc mặt phẳng P : x  2y  3z  6  0 ? A. M 1;2;3 . B. N 1;1;  1 . C. Q 1;2;  1 . D. P 3;3;  1 .
Câu 11: Tìm họ nguyên hàm F  x của hàm số   3 f x  x . 4 x 4 x A. F  x   C . B. F  x  . C. 2 3x  C . D.   3 F x  x  C . 4 4
Câu 12: Cho hai hàm số u  u  x và v  v x có đạo hàm liên tục trên  . Khẳng định nào sau đây đúng? A. u
 xv'xdx  u'xvx u  xvxdx . B. u
 xv'xdx  uxvx u'  xv'xdx . C. u
 xv'xdx  u'xv'x u'  xvxdx. D. u
 xv'xdx  uxvx u'  xvxdx . 
Câu 13: Trong không gian Oxyz , cho hai điểm A1;2;3 và B 3; 2  ; 
1 . Tìm tọa độ của AB .     A. AB  1; 2  ;  1 . B. AB  2;0;2 . C. AB  2;4;2 . D. AB  2;4;2 .
Câu 14: Gọi D là hình phẳng giới hạn bởi các đường  2x y
, y  0, x  0 và x  2 . Thể tích của khối
tròn xoay tạo thành khi quay D quanh trục hoành Ox bằng 2 2 2 2 A. 2  2 x dx  . B. 2x dx  . C. 2 2 x dx  . D.  2x dx  0 0 0 0
Câu 15: Cho hàm số y  f  x có f 4  3 , f 2  2 và hàm số f  x liên tục trên 2;4 . Khi đó 4 f   xdx bằng 2  A. 1  . B. 1. C. 6 . D. 5.
Câu 16: Trong không gian Oxyz , mặt cầu S   x  2   y  2   z  2 : 3 2
5  9 có tâm và bán kính lần lượt là A. I  3  ;2; 5  ; R  9. B. I 3; 2  ;5 ; R  3 . C. I 3; 2  ;5 ; R  9. D. I  3  ;2; 5  ; R  3.
Câu 17: Trong không gian Oxyz, cho mặt phẳng   : x  3y  5z  2  0 . Mặt phẳng nào dưới đây song song với  ?
A. R : x  3y  5z  2  0.
B. Q : x  3y  5z 1  0.
C. P : x  3y  5z  3  0.
D. S  : x  3y  5z  2  0.
Câu 18: Trong không gian Oxyz , mặt phẳng đi qua ba điểm A5;0;0 , B 0;0;3 và C 0;4;0 có phương trình là x y z x y z x y z x y z A.    1. B.    1. C.    1  . D.    0 . 5 3 4 5 4 3  5 4 3  5 4 3 
Câu 19: Cho hàm số y  f  x liên tục trên .
 Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm
số y  f  x , trục hoành và hai đường thẳng x  1
 , x  5 (như hình vẽ bên dưới).
Mệnh đề nào sau đây đúng? Trang 2/4 - Mã đề 122 1 5 1 5
A. S   f (x)dx  f (x)dx   .
B. S   f (x)dx  f (x)dx   . 1  1 1  1 1 5 1 5 C. S  f (x)dx  f (x)dx   . D. S  f (x)dx  f (x)dx   . 1 1 1 1
Câu 20: Trong không gian Oxyz , cho hai điểm A1;2;3 và B 3; 2  ; 
1 . Tìm tọa độ trung điểm I đoạn thẳng AB . A. I 1; 2  ;  1 . B. I 4;0;4 . C. I 2;0;2 . D. I 2; 4  ; 2   . 2 dx Câu 21: Biết
 a ln 2  b ln 3  c ln 5 
. Tính giá trị của biểu thức a  b  c . x 1 2x 1 1    A. 0 . B. 3  . C. 1. D. 2 .  2 u   x
Câu 22: Tính tích phân I  xsin xdx  bằng cách đặt 
. Mệnh đề nào sau đây đúng? dv  sin xdx 0    2  2 A. 2 I  x cos x |  cos xdx 2 I  x sin x |  sin xdx 0  . B. 0  . 0 0    2  2 C. 2 I  x sin x |  sin xdx 2 I  x cos x |  cos xdx 0  . D. 0  . 0 0
Câu 23: Tìm họ nguyên hàm của hàm số f  x 1  . 4x 1 1 A. f
 xdx  4ln 4x1 C . B. f
 xdx  ln4x  1C . 4 C. f
 xdx  ln 4x1 C . D. f  x 1 dx  ln 4x 1  C . 4
Câu 24: Tìm phương trình mặt cầu (S) tâm I 3;3;  1 và đi qua A5; 2  ;  1 .
A.  x  2   y  2  z  2 3 3 1  5.
B.  x  2   y  2  z  2 3 3 1  5.
C.  x  2   y  2  z  2 3 3 1  5.
D.  x  2   y  2   z  2 5 2 1  5.
Câu 25: Trong không gian Oxyz , cho điểm A1;3; 2
  và mặt phẳng P : 2x  y  3z  4  0 . Mặt phẳng
Q đi qua A và song song với mặt phẳng P có phương trình là
A. 2x  y  3z  7  0 . B. 2x  y  3z  7  0 .
C. 2x  y  3z  7  0 .
D. 2x  y  3z  7  0 .
Câu 26: Tính thể tích V của vật thể giới hạn bởi hai mặt phẳng x  0 và x  3 , biết rằng thiết diện của
vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x  3 là một hình chữ nhật
có hai kích thước là x và 2 2 9  x . A. V  27. B. V  27. C. V  18. D. V 18. Câu 27: Biết F  x x 2
 e  x là một nguyên hàm của hàm số f x trên . Khi đó f 2xdx  bằng 1 1 A. 2 x 2 e  2x  C. B. 2x 2 e  4x  C. C. 2 x 2 e  x  C. D. x 2 2e  2x  C. 2 2 9 3
Câu 28: Cho hàm số f x liên tục trên  và f
 xdx 15 . Tính f 3xdx  . 0 0 5 A. . B. 5. C. 45 . D. 15 . 2  
Câu 29: Trong không gian Oxyz , gọi  là góc giữa hai vectơ a  3; 4;0 và b  5;0;12 . Tính Trang 3/4 - Mã đề 122 cos . 3 5 3 5 A.  . B. . C. . D.  . 13 6 13 6
Câu 30: Tìm nguyên hàm F x của hàm số f  x 3 2
 4x 3x  4x 3 thỏa mãn F   1  10 . A. F  x 4 3 2  x  x  2x  3 . x B. F  x 4 3 2
 x  x  2x  3x 10. C. F  x 4 3 2
 x  x  2x  3x 11. D. F  x 2 12x  6x  4.
Câu 31: Trong không gian Oxyz , cho điểm M 1;2;0 và mặt phẳng P : 2x  2y  z 1  0 . Tính
khoảng cách từ điểm M đến mặt phẳng P . 5 5 7 A. 5 . B. . C.  . D. . 3 3 3
Câu 32: Trong không gian Oxyz , cho ba điểm A2;1;  1 , B 1  ;0;4, C 0; 2  ;  1 . Phương trình mặt
phẳng đi qua A và vuông góc với BC là
A. 2x  y  5z  5  0 . B. x  2 y  5z  5  0 . C. x  2y  5  0 .
D. x  2 y  5z  5  0 .
Câu 33: Tính diện tích S của hình phẳng giới hạn bởi các đường 2
y  2x  x và y  2  x . 1 1 5 6 A. S  . B. S  . C. S  . D. S  . 2 6 2 5 5 5 Câu 34: Cho f  xdx  2   . Tính tích phân 4 f  x 2  3x  dx   . 0 0 A. 130 . B. 120 . C. 140 . D. 133 . 4 1 4 Câu 35: Cho f  xdx  3 và g
 xdx  4. Tính I  2 f  x3g(x)dx  . 1 4 1 A. I  6. B. I  18. C. I  6. D. I  18.
PHẦN II. TỰ LUẬN (4 câu: 3,0 điểm)
Câu 1: (1,0 điểm) Tìm họ nguyên hàm của hàm số f x  x x  2023 4 5 ( ) 5 2 .
Câu 2: (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2; 1  ;  3 , B0; 1  ;2 và mặt
phẳng P: 2x  y 3z  2  0. Viết phương trình mặt phẳng   đi qua hai điểm , A B và vuông góc với mặt phẳng P .
Câu 3: (0,5 điểm) Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  1 , 1 1 1  1 f   x 2 16  dx   và 2 x . f  xdx   . Tính tích phân I  f  xdx . 7 7 0 0 0
Câu 4: (0,5 điểm) Một khuôn viên có dạng elip E có
độ dài trục lớn AB  10m , độ dài trục bé CD  6m . Trên
đó người thiết kế hai phần: một phần để trồng rau (phần
tô màu) có dạng của một cánh hoa hình parabol P có
đỉnh trùng với C , trục đối xứng là đường thẳng CD và
hai đầu mút M , N của cánh hoa nằm trên E có
MN //AB, MN  6m ; phần còn lại của khuôn viên (phần
không tô màu) dành để trồng hoa. Hỏi cần bao nhiêu tiền
để trồng hoa trên khuôn viên đó biết chi phí trồng hoa là 50000 đồng 2 /m ? ------ HẾT ------ Trang 4/4 - Mã đề 122
SỞ GD & ĐT QUẢNG TRỊ
ĐÁP ÁN KIỂM TRA GIỮA KỲ II, NĂM HỌC 2022-2023 TRƯỜNG THPT HƯỚNG HÓA MÔN: TOÁN - Khối 12 ĐỀ CHÍNH THỨC
PHẦN I. ĐÁP ÁN TRẮC NGHIỆM (35 câu: 7,0 điểm) 121 123 125 127 122 124 126 128 1 B A A B A D A C 2 D B A A D B A A 3 B C B D B C B B 4 C C B A B C C B 5 A C B B D C B D 6 B D C D A A B A 7 D A D A B D A A 8 C C B A B A A A 9 B A B A A B B A 10 A A D B D B A B 11 D B B A A A B B 12 D A D B D B D D 13 C D B C D A C D 14 C D B C A D B B 15 C D B D B D C B 16 C B A A B C B A 17 A C B A C D B D 18 A C B B B D D C 19 B D C D C D B B 20 B A B C C B C C 21 B A B C A B B C 22 B A B A D C C A 23 C B C D D B D D 24 B C A A A D A B 25 A B A A B A A B 26 A B D D D B A B 27 D B C D A B C C 28 A D D D B A D A 29 A B D A A D A D 30 D A B A C B C A 31 A C C B B B C A 32 D D C A D A B C 33 A C A B B B B A 34 A B A D D C B A 35 A D B B B C B A
PHẦN II. ĐÁP ÁN TỰ LUẬN (3,0 điểm)
ĐỀ LẺ (121, 123, 125, 127): Câu Đáp án Điểm 1
Tìm họ nguyên hàm của hàm số f x  x x  2023 3 4 ( ) 4 3 . 1,0 Đặt 4 t  x  3 , ta có 3 dt  4x dx . 0,25 Khi đó f  x 2023 dx  t dt  0,25 2024 t =  C 2024 0,25 x 32024 4 =  C C  . 2024 0,25
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1  ;3;  1 , B 2  ; 1  ;0 và 2
mặt phẳng P:3x  y  2z 3  0. Viết phương trình mặt phẳng   đi qua hai 1,0 điểm ,
A B và vuông góc với mặt phẳng P .   Ta có AB   1  ;4; 
1 . Mặt phẳng P có VTPT n  3;1; 2  . 0,25 P
Mặt phẳng   đi qua hai điểm ,
A B và vuông góc với mặt phẳng P nên có một    0,25 VTPT là n   AB, n    .   7;1;11 P  
Do đó   có phương trình 7 x   1   1 y  3 11z   1  0 0,25
 7x  y 11z 15  0. 0,25
Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  1 , 3 1 1 1 0,5  1 f   x 2 9  dx   và . x f  xdx   . Tính tích phân I  f  xdx . 5 5 0 0 0 1 1 1 Ta có x f   xdx  x d
  f x  x .f x1 2 2 2  f  xd 2x 0 0 0 0 1  f    xf  x 1 3 1 2 dx  1 2.  . 5 5 0 1 1 0,25
Khi đó   f x  3x 2 dx     f x2 2  2. f  x 2 .3x   2 3x 2     dx   0 0 1 1   1 1 5 f  x2 9 3 x 2 dx  6 x f   x 4 dx  9x dx   6.  9.  0.  5 5 5 0 0 0 0 2 Suy ra  f x 2  x    f x 2 3 0 3x  0  f x 2  3x    3 f x  x C . Mà f   1 1 nên   3 f x  x . 0,25 1 1 1 Vậy I  f  x 3 dx  x dx    . 4 0 0
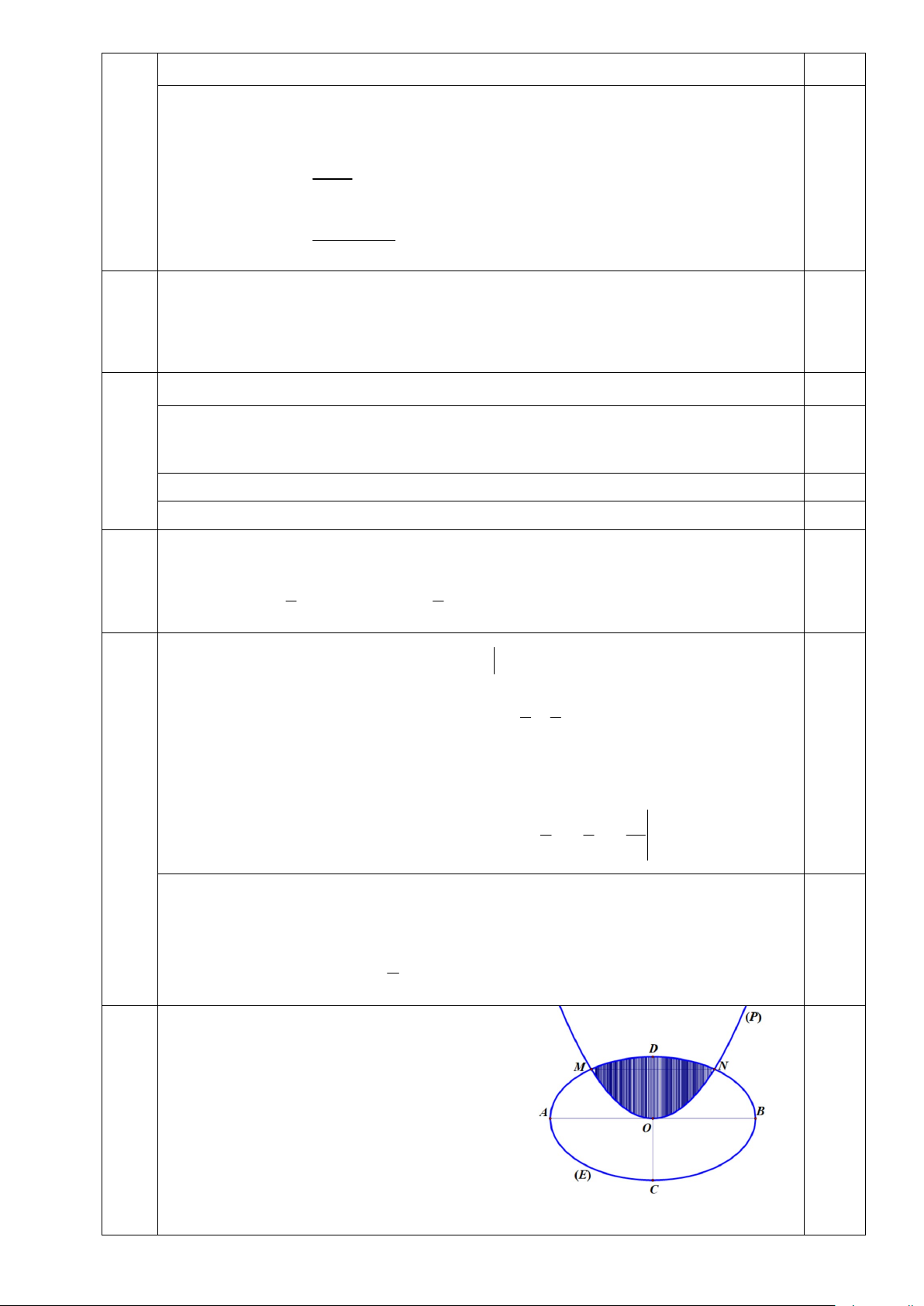
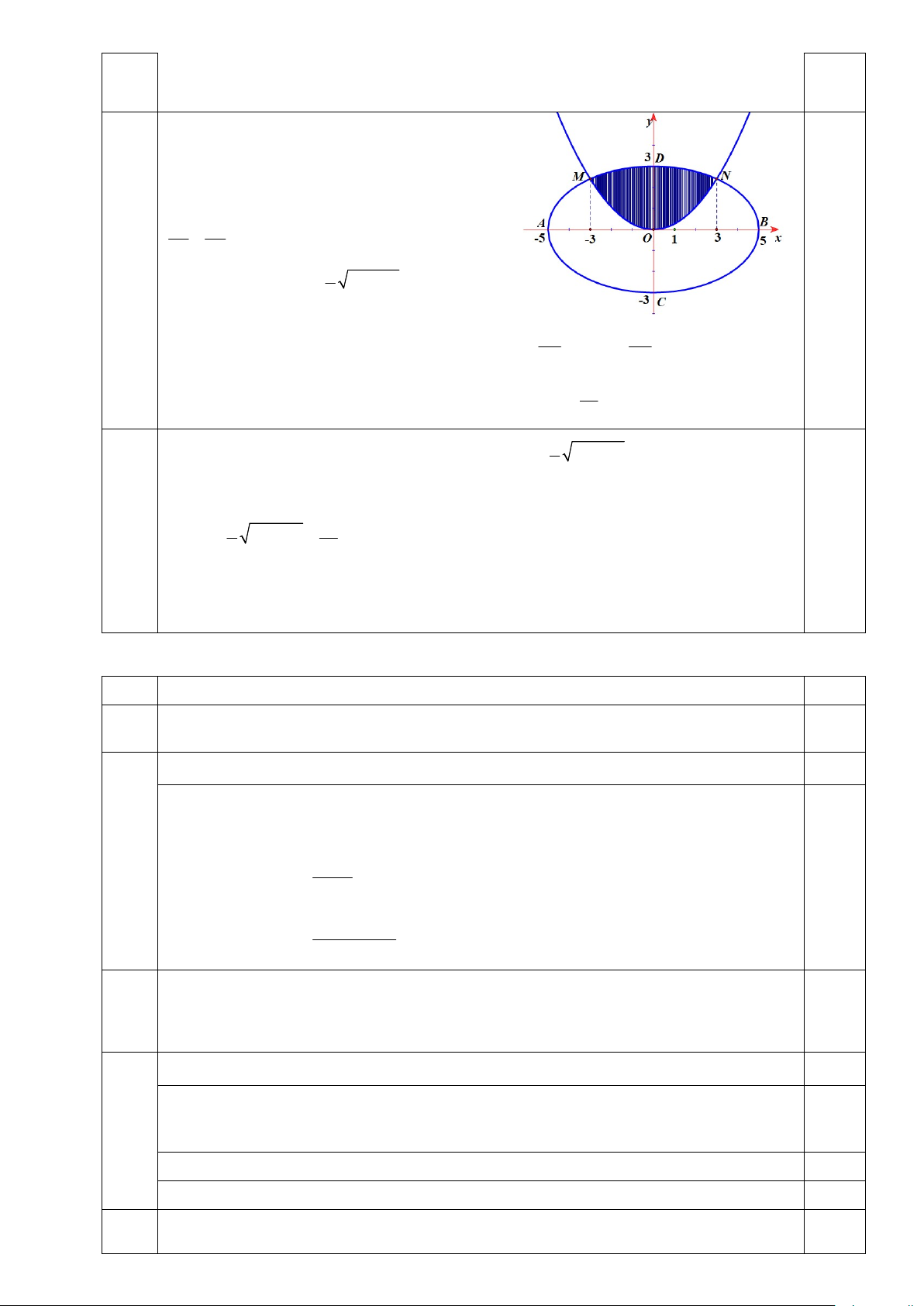
Một khuôn viên có dạng elip E có độ dài
trục lớn AB  10m , độ dài trục bé
CD  6m . Trên đó người thiết kế hai phần:
một phần để trồng hoa (phần tô màu) có 4
dạng của một cánh hoa hình parabol P 0,5
có đỉnh trùng với tâm O của E , trục đối
xứng là đường thẳng CD và hai đầu mút
M , N của cánh hoa nằm trên E có MN //AB, MN  6m ; phần còn lại của khuôn
viên (phần không tô màu) dành để trồng rau. Hỏi cần bao nhiêu tiền để trồng rau
trên khuôn viên đó biết chi phí trồng rau là 30000 đồng 2 /m ?
Chọn hệ trục tọa độ Oxy như hình vẽ sao cho A 5
 ;0, B5;0, C0; 3  , D0;  3 . Khi đó elip E có phương trình 2 2 x y 
1. Suy ra nửa E phía trên Ox 25 9 0,25 có phương trình 3 2 y  25 x . 5  12   12 
Vì M, NE; MN //AB, MN  6m nên M 3; , N 3;  . 5   5     
Do parabol P đi qua các điểm M, N, O nên P 4 2 : y  x . 15 5
Diện tích hình phẳng giới hạn bởi E là 3 2 S  2 25  x dx 15  E  2 m    . 5 5 
Diện tích hình phẳng giới hạn bởi E và
P (phần tô đậm) là 3  3 2 4 2  S   0,25   x  x  x  T 25 d 12,053  2 m .  5 15 3  
Diện tích phần trồng rau là S  S  S      2 15 12,053 35,07 m    . E T
Vậy số tiền trồng rau trên khuôn viên đó khoảng 35,0730000 1052100 đồng.
ĐỀ CHẴN (122, 124, 126, 128): Câu Đáp án Điểm 1
Tìm họ nguyên hàm của hàm số f x  x x  2023 4 5 ( ) 5 2 . 1,0 Đặt 5 t  x  2 , ta có 4 dt  5x dx . 0,25 Khi đó f  x 2023 dx  t dt  0,25 2024 t =  C 2024 0,25 x 22024 5 =  C C  . 2024 0,25
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2; 1  ;  3 , B0; 1  ;2 và mặt 2
phẳng P: 2x  y 3z  2  0. Viết phương trình mặt phẳng   đi qua hai điểm 1,0 ,
A B và vuông góc với mặt phẳng P .  
Ta có AB  2;0;5. Mặt phẳng P có VTPT n  2;1;  3 . 0,25 P
Mặt phẳng   đi qua hai điểm ,
A B và vuông góc với mặt phẳng P nên có một    0,25 VTPT là n   A , B n      .    5;4; 2 P  
Do đó   có phương trình 5
 x 0 4 y   1  2z 2  0 0,25  5
 x  4y  2z 8  0. 0,25 3
Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  1 , 0,5 1 1 1  1 f   x 2 16  dx   và 2 x . f  xdx   . Tính tích phân I  f  xdx . 7 7 0 0 0 1 1 1 Ta có x f   xdx  x d
  f x  x .f x1 3 3 3  f  xd 3x 0 0 0 0 1  f   1 4 2 1  3 x f  xdx 13.  . 7 7 0 1 1 0,25
Khi đó   f x 4x 2 dx     f x2 3  2. f  x 3 .4x   3 4x 2     dx   0 0 1 1   1 1 7 f  x2 16 4 x 3 dx  8 x f   x 6 dx  16x dx  8. 16.  0.  7 7 7 0 0 0 0 2 Suy ra  f x 3  x    f x 3 4 0  4x  0  f x 3  4x    4 f x  x C . Mà f   1 1 nên   4 f x  x . 0,25 1 1 1 Vậy I  f  x 4 dx  x dx    . 5 0 0
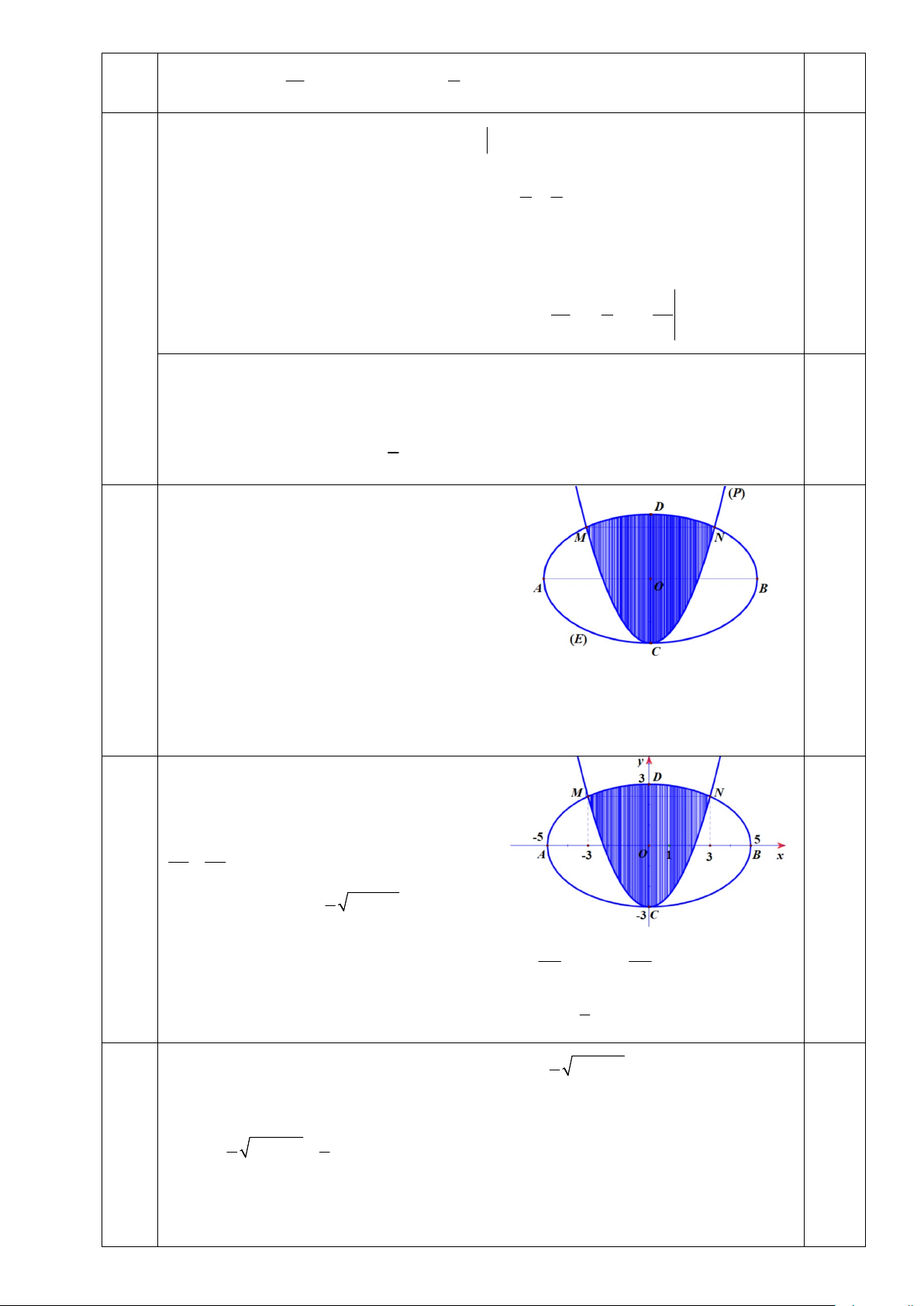
Một khuôn viên có dạng elip E có độ
dài trục lớn AB  10m , độ dài trục bé
CD  6m . Trên đó người thiết kế hai
phần: một phần để trồng rau (phần tô màu)
có dạng của một cánh hoa hình parabol 4
P có đỉnh trùng với C , trục đối xứng là 0,5
đường thẳng CD và hai đầu mút M , N
của cánh hoa nằm trên E có MN //AB, MN  6m ; phần còn lại của khuôn viên
(phần không tô màu) dành để trồng hoa. Hỏi cần bao nhiêu tiền để trồng hoa trên
khuôn viên đó biết chi phí trồng hoa là 50000 đồng 2 /m ?
Chọn hệ trục tọa độ Oxy như hình vẽ sao cho A 5
 ;0, B5;0, C0; 3  , D0;  3 . Khi đó elip E có phương trình 2 2 x y 
1. Suy ra nửa E phía trên Ox 25 9 có phương trình 3 2 y  25 x . 0,25 5  12   12 
Vì M, NE; MN //AB, MN  6m nên M 3; , N 3;  . 5   5     
Do parabol P đi qua các điểm M, N, C nên P 3 2 : y  x  3. 5 5
Diện tích hình phẳng giới hạn bởi E là 3 2 S  2 25  x dx 15  E  2 m    . 5 5 
Diện tích hình phẳng giới hạn bởi E và
P (phần tô đậm) là 3  3 2 3 2  S  0,25   x  x    x  T 25 3 d 24,053  2 m .  5 5 3  
Diện tích phần trồng hoa là S  S  S      2 15 24,053 23,07 m    . E T
Vậy số tiền trồng hoa trên khuôn viên đó khoảng 23,0750000 1153500 đồng.
Document Outline

DE_GKII12_121_d9f80
DE_GKII12_122_d3f07
DAP_AN_TOAN_12_GKII_f5aeb

Đề giữa kỳ 2 Toán 12 năm 2022 – 2023 trường THPT Hướng Hóa – Quảng Trị

Thông tin :

Tài liệu liên quan:

Đề giữa học kì 2 Toán 12 năm 2023 – 2024 trường THPT Chu Văn An – Hà Nội

Đề giữa học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Thị xã Quảng Trị

Đề giữa kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Nguyễn Tất Thành – TP HCM

Đề giữa kì 2 Toán 12 năm 2023 – 2024 trường Trung học Thực hành ĐHSP – TP HCM

Đề giữa học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Giao Thủy B – Nam Định