Đề giữa kỳ 2 Toán 12 năm 2022 – 2023 trường THPT Thị xã Quảng Trị

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giữa học kì 2 môn Toán 12 năm học 2022 – 2023 .Mời bạn đọc đón xem.

57 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/4 - Mã đề 123
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ...................
Phần I: Trắc nghiệm (7 điểm)
Câu 1: Họ nguyên hàm của hàm số
( )
1
54
=
+
fx
x
là:
A.
ln 5 4++xC
. B.
1
ln 5 4
5
++xC
. C.
1
ln 5 4
ln 5
++xC
. D.
.
Câu 2: Tích phân
d
b
a
x
∫
bằng.
A.
ab−
. B.
ab+
. C.
ba−
. D.
a.b
.
Câu 3: Nếu
( ) ( )
df u u Fu C= +
∫
và
( )
u ux=
có đạo hàm liên tục thì
A.
( )
(
)
d.f ux x Fux C= +
 
 
∫
B.
( ) ( ) (
)
d.
f ux u x x Fx C
′
= +


∫
C.
(
)
( ) (
)
d.f xu x x F ux C
′
= +


∫
D.
( ) (
) (
)
d.
f ux u x x Fux C
′
= +
 
 
∫
Câu 4: Trong không gian
Oxyz
, cho vectơ
37
u i jk=−+ +

. Tọa độ của vectơ
u
là
A.
( )
3; 7 ;1
. B.
( )
3;7;0−
. C.
( )
3;7;0
. D.
( )
3; 7 ;1−
.
Câu 5: Tích phân
1
2019
0
dIxx=
∫
bằng
A.
1
. B.
1
2019
. C.
1
2020
. D.
0
.
Câu 6: Cho hàm số
( )
fx
có đạo hàm trên
,
( )
12f −=−
và
( )
32f =
. Tính
(
)
3
1
'.I f x dx
−
=
∫
A.
0.I =
B.
3.I =
C.
4.I = −
D.
4.I =
Câu 7: Mệnh đề nào sau đây là đúng ?
A.
d
=++
∫
x xx
xe x e xe C
. B.
d = −+
∫
x xx
xe x xe e C
.
C.
2
d
2
= ++
∫
x xx
x
xe x e e C
. D.
2
d
2
= +
∫
xx
x
xe x e C
.
Câu 8: Trong không gian
Oxyz
, mặt cầu
( ) (
) (
) ( )
2 22
: 2 5 94
Sx y z− ++ +− =
có bán kính bằng
A.
16
. B.
8
. C.
2
. D.
4
.
Câu 9: Khẳng định nào sau đây đúng?
A.
1
sin2 d cos 2
2
xx x C=−+
∫
. B.
sin2 d 2cos 2
xx x C=−+
∫
.
C.
sin2 d 2cos 2xx x C= +
∫
. D.
1
sin2 d cos 2
2
xx x C= +
∫
.
Câu 10: Cho hai hàm số
( )
fx
và
( )
gx
liên tục trên
K
,
,ab K∈
. Khẳng định nào sau đây là khẳng
định sai?
A.
( )
( ) ( )
d d0
bb
aa
kfx x kfx x k= ≠
∫∫
. B.
( ) ( ) ( ) ( )
d dd
b bb
a aa
f x gx x f x x gx x+= +


∫ ∫∫
.
Mã đề 123
Trang 2/4 - Mã đề 123
C.
( ) ( ) ( )
( )
d d. d
b bb
a aa
fxgxx fxxgxx=
∫ ∫∫
. D.
( ) ( ) ( ) ( )
d dd
b bb
a aa
f x gx x f x x gx x−= −


∫ ∫∫
.
Câu 11: Cho 2 hàm số
()u ux
và
()v vx
có đạo hàm liên tục trên khoảng
K
. Khẳng định nào
sau đây đúng?
A.
()'() ()() '()()uxv xdx uxvx u xvxdx

. B.
()'() ()'() '()()uxv xdx uxv x u xvxdx

.
C.
()'() '()() '()()
uxv xdx u xvx u xvxdx

. D.
()'() ()() ()()uxv xdx uxvx uxvxdx

.
Câu 12: Cho
( )
2
1
d3fx x=
∫
và
( ) ( )
2
1
3 d 10f x gx x−=


∫
. Khi đó
( )
2
1
dgx x
∫
bằng
A.
4−
. B.
1−
. C. 1. D. 17.
Câu 13: Trong không gian
Oxyz
, cho mặt cầu
( ) ( )
2
22
:1 4Sx yz
−++=
. Tâm của
( )
S
là điểm nào
sau đây?
A.
( )
1;0;0−
B.
( )
1;1;1−
C.
( )
1;0;0
D.
(
)
1;1;1
Câu 14: Trong không gian
Oxyz
, mặt cầu
( )
S
có tâm
( )
1; 3; 0I −
và bán kính bằng
2
. Phương trình
của
( )
S
là
A.
( )
2
22
1 ( 3) 2x yz− ++ +=
. B.
( )
2
22
1 ( 3) 4x yz+ +− +=
.
C.
(
)
2
22
1 ( 3) 4x yz− ++ +=
. D.
( )
2
22
1 ( 3) 2x yz
+ +− +=
.
Câu 15: Biết
( ) ( )
f x dx F x C= +
∫
.Trong các khẳng định sau, khẳng định nào đúng?
A.
(
) ( ) ( )
b
a
f x dx F b F a= −
∫
. B.
( ) ( ) ( )
b
a
f x dx F a F b= −
∫
.
C.
( ) ( ) ( )
b
a
f x dx F b F a= +
∫
. D.
(
)
( )
( )
.
b
a
f x dx F b F a
=
∫
.
Câu 16: Tìm họ nguyên hàm của hàm số
(
)
3
e
x
fx=
.
A.
( )
3
1
d .e
3
x
fxx=
∫
. B.
( )
d ln 3fxx x C
= +
∫
. C.
( )
3
de
x
fxx C= +
∫
. D.
( )
3
1
d .e
3
x
fxx C= +
∫
.
Câu 17: Nguyên hàm của hàm số
( )
2
31fx x= +
là
A.
3
3
x
xC++
. B.
6xC+
. C.
3
x xC
++
. D.
3
xC+
.
Câu 18: Trên khoảng
( )
0; +∞
, hàm số
( )
lnFx x=
là một nguyên hàm của hàm số?
A.
(
)
1
,f x CC
x
=+∈
. B.
( )
ln ,f x x x x CC= −+ ∈
.
C.
( )
1
fx
x
=
. D.
( )
lnfx x x x= −
.
Câu 19: Giả sử
f
là hàm số liên tục trên khoảng
K
và
, ,
abc
là ba số bất kỳ trên khoảng
K
.
Khẳng định nào sau đây sai?
A.
( )
d1
a
a
fx x=
∫
. B.
( ) ( ) ( ) ( )
d d d , ;
cb b
ac a
fx x fx x fx xc ab+= ∈
∫∫∫
.
C.
( )
( )
dd
ba
ab
fx x fx x= −
∫∫
. D.
( ) ( )
d
bb
aa
f x dx f t t=
∫∫
.
Câu 20: Hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
fx
trên khoảng
( )
;ab
nếu
A.
( ) ( ) ( )
,;F x f x x ab
′
= ∀∈
. B.
( ) ( ) ( )
,;F x f x x ab
′
=− ∀∈
.
Trang 3/4 - Mã đề 123
C.
( ) ( ) (
)
,;f x F x x ab
′
=− ∀∈
. D.
( ) ( ) ( )
,;f x F x x ab
′
= ∀∈
.
Câu 21: Tính tích phân
2
1
1
d
21
Ix
x
=
−
∫
.
A.
ln 3
3
I =
. B.
ln 3 1I = +
. C.
ln 3 1
2
I
−
=
. D.
ln 3
2
I =
.
Câu 22: Nếu
( )
2
5
d2fxx=
∫
thì
( )
5
2
3dfxx
∫
bằng
A.
3
. B.
6
. C.
6−
. D.
12
.
Câu 23: Cho
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
( )
0; 4
. B.
( )
;0−∞
. C.
( )
1; 2
−
. D.
( )
3;1−
.
Câu 24: Trong không gian
Oxyz
, cho hai điểm
( )
2; 1;2A
−
và
( )
0;1;0B
. Mặt cầu đường kính
AB
có
phương trình là
A.
( ) ( )
22
2
1 13x yz− ++− =
. B.
( ) ( )
22
2
1 1 12x yz− ++− =
.
C.
( ) ( )
22
2
1 13x yz− + +− =
. D.
(
) (
) ( )
2 22
2 2 22xyz+ +− ++ =
.
Câu 25: Họ nguyên hàm của hàm số
( )
ln x
fx
x
=
là
A.
2
1
ln ln
2
x xC++
. B.
2
ln xC+
. C.
2
1
ln
2
xC+
. D.
(
)
ln ln
xC+
.
Câu 26: Cho
( )
fx
là hàm đa thức. Khi đó
( )
d
fx
x
x
′
∫
bằng:
A.
( )
fxC+
. B.
( )
2 fxC
−+
. C.
( )
2 fxC+
. D.
( )
1
2
fxC+
.
Câu 27: Trong không gian với hệ trục
Oxyz
cho ba điểm
( )
2;1;3A
,
( )
1; 2; 2B −
,
( )
; ;5Cxy
thẳng
hàng. Khi đó,
xy+
bằng
A.
10
. B.
3
. C.
12
. D.
11
.
Câu 28: Cho
( )
Fx
là nguyên hàm của
( )
1
2
fx
x
=
+
thỏa mãn
( )
24F =
. Giá trị
( )
1F −
bằng:
A.
23
. B.
3
. C.
2
. D.
1
.
Câu 29: Cho
( )
2
1
dx=3I fx
−
=
∫
. Khi đó
( )
2
1
3 4 dxJ fx
−
= −


∫
bằng:
A.
5
. B.
3−
. C.
1−
. D.
2
.
Câu 30: Biết
( )
1
0
d8fx x=
∫
và
(
)
5
1
d3fx x= −
∫
, khi đó
( )
5
0
dfx x
∫
bằng
A. 5. B. 11. C.
8
3
−
. D.
11−
.
Câu 31: Trong không gian
Oxyz
, cho hai điểm
( )
2;3; 1A −−
và
( )
4;1;9B −
. Trung điểm
I
của đoạn
thẳng
AB
có tọa độ là
A.
( )
2; 2;10−−
. B.
( )
3;2;4−
. C.
( )
6;4;8−
. D.
( )
3;2; 4−−
.
Câu 32: Họ nguyên hàm của hàm số
( )
sin 3f x x+ x=
là
Trang 4/4 - Mã đề 123
A.
2
3cos3
2
x
xC−+
. B.
2
1
cos3
23
x
xC−+
. C.
2
3cos3
2
x
xC++
. D.
2
1
cos3
23
x
xC++
.
Câu 33: Họ nguyên hàm của hàm số
2
3
()
1
x
fx
x
=
+
là
A.
3
2
1.
3
xC++
B.
3
1
.
31
C
x
+
+
C.
3
1
1.
3
xC++
D.
3
2
.
31
C
x
+
+
Câu 34: Biết
( )
Fx
là một nguyên hàm của hàm số
(
)
sin cos
= +fx x x
thỏa mãn
( )
01=F
. Hàm số
( )
Fx
là
A.
cos sin 1xx−+
. B.
cos sin 2xx−++
. C.
cos sin 1xx−++
. D.
cos sin 2xx−+−
.
Câu 35: Trong không gian
Oxyz
, cho
23OM i j k=−+

. Hình chiếu của điểm
M
trên mặt phẳng
( )
Oxy
là
A.
( )
1
2; 0; 0M
. B.
(
)
4
2; 0;1M
. C.
( )
3
2; 3; 0M −
. D.
( )
2
0; 0;1M
.
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : Biết
Fx
là một nguyên hàm của hàm số
2 sin
fx x x

và thỏa mãn
0 21F
.
Tính
2
F


.
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ
,
Oxyz
cho điểm
( )
1;1; 2A
,
( )
2 ; 3; 3B −
. Viết
phương trình mặt cầu
( )
S
có tâm
I
thuộc trục
Oy
và đi qua hai điểm
,AB
.
Câu 3 (0,5 điểm): Biết
( )
Fx
và
(
)
Gx
là hai nguyên hàm của hàm số
( )
fx
trên
và thỏa mãn
( ) ( ) (
)
3
0
30f x dx F G a=−+
∫
( )
0a >
. Gọi
( ) ( )
3
0
.S F x G x dx= −
∫
Tính giá trị của
a
khi
15.S =
Câu 4 (0,5 điểm): Cho hàm số
f
có đạo hàm liên tục trên
và luôn nhận giá trị dương, đồng thời thỏa
mãn
(
) ( ) ( )
26
.' 2
x
fxf x f x e−=
với mọi
x
. Biết
(
)
01f
=
. Hãy tính
( )
1.f
-----------------------HẾT------------------------
Trang 1/4 - Mã đề 234
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ...................
Phần I: Trắc nghiệm (7 điểm)
Câu 1: Tích phân
1
2019
0
dIxx
=
∫
bằng
A.
1
2020
. B.
1
2019
. C.
1
. D.
0
.
Câu 2: Mệnh đề nào sau đây là đúng ?
A.
2
d
2
= ++
∫
x xx
x
xe x e e C
. B.
d =++
∫
x xx
xe x e xe C
.
C.
2
d
2
= +
∫
xx
x
xe x e C
. D.
d
= −+
∫
x xx
xe x xe e C
.
Câu 3: Cho 2 hàm số
()u ux
và
()v vx
có đạo hàm liên tục trên khoảng
K
. Khẳng định nào sau
đây đúng?
A.
()'() ()() '()()uxv xdx uxvx u xvxdx


. B.
()'() ()'() '()()
uxv xdx uxv x u xvxdx

.
C.
()'() '()() '()()
uxv xdx u xvx u xvxdx

. D.
()'() ()() ()()uxv xdx uxvx uxvxdx

.
Câu 4: Cho hai hàm số
( )
fx
và
( )
gx
liên tục trên
K
,
,ab
K∈
. Khẳng định nào sau đây là khẳng
định sai?
A.
( ) ( ) ( ) ( )
d dd
b bb
a aa
f x gx x f x x gx x+= +


∫ ∫∫
. B.
( )
( ) ( )
d d0
bb
aa
kfx x kfx x k
= ≠
∫∫
.
C.
(
) ( ) ( ) ( )
d dd
b bb
a aa
f x gx x f x x gx x
−= −


∫ ∫∫
. D.
( ) ( ) ( ) ( )
d d. d
b bb
a aa
fxgxx fxxgxx=
∫ ∫∫
.
Câu 5: Cho
( )
2
1
d3fx x=
∫
và
( ) ( )
2
1
3 d 10f x gx x−=


∫
. Khi đó
( )
2
1
dgx x
∫
bằng
A. 1. B. 17. C.
1−
. D.
4−
.
Câu 6: Nếu
( )
( )
df u u Fu C= +
∫
và
( )
u ux=
có đạo hàm liên tục thì
A.
( ) ( ) ( )
d.
f xu x x F ux C
′
= +


∫
B.
(
) ( )
d.f ux x Fux C
= +
 
 
∫
C.
( )
( ) ( )
d.f ux u x x Fux C
′
= +
 
 
∫
D.
( ) ( ) ( )
d.f ux u x x Fx C
′
= +


∫
Câu 7: Hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
fx
trên khoảng
( )
;ab
nếu
A.
( ) ( ) ( )
,;
f x F x x ab
′
= ∀∈
. B.
( ) ( ) ( )
,;F x f x x ab
′
=− ∀∈
.
C.
( ) ( ) ( )
,;f x F x x ab
′
=− ∀∈
. D.
( ) ( ) ( )
,;F x f x x ab
′
= ∀∈
.
Câu 8: Tích phân
d
b
a
x
∫
bằng.
A.
ab+
. B.
ba−
. C.
a.b
. D.
ab−
.
Câu 9: Nguyên hàm của hàm số
( )
2
31
fx x= +
là
A.
3
xC+
. B.
3
3
x
xC++
. C.
6xC
+
. D.
3
x xC++
.
Mã đề 234
Trang 2/4 - Mã đề 234
Câu 10: Tìm họ nguyên hàm của hàm số
( )
3
e
x
fx
=
.
A.
( )
3
1
d .e
3
x
fxx C
= +
∫
. B.
( )
3
de
x
fxx C= +
∫
. C.
(
)
d ln 3fxx x C= +
∫
. D.
( )
3
1
d .e
3
x
fxx=
∫
.
Câu 11: Họ nguyên hàm của hàm số
( )
1
54
=
+
fx
x
là:
A.
ln 5 4++xC
. B.
( )
1
ln 5 4
5
++
xC
. C.
1
ln 5 4
ln 5
++xC
. D.
1
ln 5 4
5
++xC
.
Câu 12: Giả sử
f
là hàm số liên tục trên khoảng
K
và
, ,
abc
là ba số bất kỳ trên khoảng
K
.
Khẳng định nào sau đây sai?
A.
( )
d1
a
a
fx x=
∫
. B.
(
)
(
)
dd
ba
ab
fx x fx x
= −
∫∫
.
C.
( ) ( ) ( ) ( )
d d d , ;
cb b
ac a
fx x fx x fx xc ab+= ∈
∫∫∫
. D.
( ) ( )
d
bb
aa
f x dx f t t=
∫∫
.
Câu 13: Cho hàm số
( )
fx
có đạo hàm trên
,
( )
12f −=−
và
( )
32f =
. Tính
( )
3
1
'.I f x dx
−
=
∫
A.
0.I =
B.
4.I = −
C.
4.I
=
D.
3.I =
Câu 14: Trong không gian
Oxyz
, cho mặt cầu
( )
( )
2
22
:1 4Sx yz−++=
. Tâm của
( )
S
là điểm nào sau
đây?
A.
( )
1;1;1−
B.
( )
1;0;0−
C.
( )
1;0;0
D.
( )
1;1;1
Câu 15: Trong không gian
Oxyz
, cho vectơ
37u i jk=−+ +

. Tọa độ của vectơ
u
là
A.
( )
3; 7 ;1
. B.
( )
3; 7 ;1−
. C.
( )
3;7;0
. D.
( )
3;7;0−
.
Câu 16: Khẳng định nào sau đây đúng?
A.
sin2 d 2cos 2xx x C= +
∫
. B.
1
sin2 d cos 2
2
xx x C
= +
∫
.
C.
sin2 d 2cos2xx x C=−+
∫
. D.
1
sin2 d cos 2
2
xx x C=−+
∫
.
Câu 17: Trong không gian
Ox
yz
, mặt cầu
( )
( )
( )
(
)
2 22
: 2 5 94
Sx y z− ++ +− =
có bán kính bằng
A.
4
. B.
2
. C.
8
. D.
16
.
Câu 18: Biết
( ) ( )
f x dx F x C= +
∫
.Trong các khẳng định sau, khẳng định nào đúng?
A.
( ) ( ) ( )
b
a
f x dx F b F a= +
∫
. B.
( ) ( ) ( )
b
a
f x dx F a F b= −
∫
.
C.
( ) (
) ( )
.
b
a
f x dx F b F a=
∫
. D.
( ) ( ) ( )
b
a
f x dx F b F a= −
∫
.
Câu 19: Trong không gian
Oxyz
, mặt cầu
( )
S
có tâm
(
)
1; 3; 0I −
và bán kính bằng
2
. Phương trình
của
( )
S
là
A.
( )
2
22
1 ( 3) 4x yz− ++ +=
. B.
( )
2
22
1 ( 3) 2x yz+ +− +=
.
C.
( )
2
22
1 ( 3) 4x yz+ +− +=
. D.
( )
2
22
1 ( 3) 2
x yz− ++ +=
.
Câu 20: Trên khoảng
(
)
0;
+∞
, hàm số
( )
lnFx x=
là một nguyên hàm của hàm số?
A.
( )
ln ,f x x x x CC= −+ ∈
. B.
( )
lnfx x x x= −
.
C.
( )
1
fx
x
=
. D.
( )
1
,f x CC
x
=+∈
.
Trang 3/4 - Mã đề 234
Câu 21: Họ nguyên hàm của hàm số
( )
ln x
fx
x
=
là
A.
2
ln xC+
. B.
2
1
ln
2
xC+
. C.
2
1
ln ln
2
x xC++
. D.
( )
ln ln xC
+
.
Câu 22: Biết
( )
1
0
d8fx x=
∫
và
( )
5
1
d3fx x= −
∫
, khi đó
( )
5
0
dfx x
∫
bằng
A.
11−
. B. 5. C. 11. D.
8
3
−
.
Câu 23: Biết
( )
Fx
là một nguyên hàm của hàm số
( )
sin cos= +fx x x
thỏa mãn
( )
01
=F
. Hàm số
( )
Fx
là
A.
cos sin 2xx−+−
. B.
cos sin 1
xx
−++
. C.
cos sin 1xx−+
. D.
cos sin 2
xx
−++
.
Câu 24: Cho
( )
2
1
dx=3I fx
−
=
∫
. Khi đó
( )
2
1
3 4 dxJ fx
−
= −


∫
bằng:
A.
5
. B.
3−
. C.
1−
. D.
2
.
Câu 25: Cho
(
)
fx
là hàm đa thức. Khi đó
( )
d
fx
x
x
′
∫
bằng:
A.
( )
2
fxC−+
. B.
( )
2
fxC+
. C.
( )
fxC+
. D.
( )
1
2
fxC+
.
Câu 26: Cho
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
( )
0; 4
. B.
( )
3;1−
. C.
( )
1; 2−
. D.
( )
;0−∞
.
Câu 27: Tính tích phân
2
1
1
d
21
Ix
x
=
−
∫
.
A.
ln 3 1
2
I
−
=
. B.
ln 3 1I = +
. C.
ln 3
3
I =
. D.
ln 3
2
I =
.
Câu 28: Trong không gian
Oxyz
, cho
23OM i j k=−+

. Hình chiếu của điểm
M
trên mặt phẳng
( )
Oxy
là
A.
( )
4
2; 0;1M
. B.
( )
1
2; 0; 0M
. C.
( )
3
2; 3; 0M
−
. D.
( )
2
0; 0;1M
.
Câu 29: Trong không gian
Oxyz
, cho hai điểm
( )
2; 1;2
A
−
và
( )
0;1;0B
. Mặt cầu đường kính
AB
có
phương trình là
A.
( ) ( )
22
2
1 1 12x yz− ++− =
. B.
( ) ( )
22
2
1 13x yz− ++− =
.
C.
( ) ( )
22
2
1 13x yz− + +− =
. D.
( ) ( ) (
)
2 22
2 2 22xyz+ +− ++ =
.
Câu 30: Họ nguyên hàm của hàm số
(
)
sin 3
f x x+ x=
là
A.
2
3cos3
2
x
xC−+
. B.
2
3cos3
2
x
xC++
. C.
2
1
cos3
23
x
xC−+
. D.
2
1
cos3
23
x
xC++
.
Câu 31: Trong không gian với hệ trục
Oxyz
cho ba điểm
( )
2;1;3A
,
( )
1; 2; 2B −
,
( )
; ;5Cxy
thẳng
hàng. Khi đó,
xy+
bằng
A.
3
. B.
10
. C.
11
. D.
12
.
Trang 4/4 - Mã đề 234
Câu 32: Nếu
( )
2
5
d2fxx=
∫
thì
(
)
5
2
3dfxx
∫
bằng
A.
12
. B.
6
−
. C.
6
. D.
3
.
Câu 33: Cho
(
)
Fx
là nguyên hàm của
(
)
1
2
fx
x
=
+
thỏa mãn
( )
24F =
. Giá trị
( )
1F −
bằng:
A.
3
. B.
2
. C.
1
. D.
23
.
Câu 34: Họ nguyên hàm của hàm số
2
3
()
1
x
fx
x
=
+
là
A.
3
1
.
31
C
x
+
+
B.
3
2
1.
3
xC++
C.
3
2
.
31
C
x
+
+
D.
3
1
1.
3
xC
++
Câu 35: Trong không gian
Oxyz
, cho hai điểm
( )
2;3; 1A −−
và
( )
4;1;9B −
. Trung điểm
I
của đoạn
thẳng
AB
có tọa độ là
A.
( )
2; 2;10
−−
. B.
( )
3;2; 4−−
. C.
( )
6;4;8−
. D.
( )
3;2;4−
.
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : Biết
Fx
là một nguyên hàm của hàm số
2 cosfx x x
và thỏa mãn
0 20F
.
Tính
2
F


.
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ
,Oxyz
cho điểm
( )
1;1; 2
A
,
( )
2 ; 3; 3
B
−
. Viết
phương trình mặt cầu
( )
S
có tâm
I
thuộc trục
Ox
và đi qua hai điểm
,AB
Câu 3 (0,5 điểm): Biết
( )
Fx
và
( )
Gx
là hai nguyên hàm của hàm số
( )
fx
trên
và thỏa mãn
( ) ( ) (
)
5
0
50f x dx F G a
=−+
∫
( )
0a >
. Gọi
( ) ( )
5
0
.S F x G x dx= −
∫
Tính giá trị của
a
khi
20.S =
Câu 4 (0,5 điểm): Cho hàm số
f
có đạo hàm liên tục trên
và luôn nhận giá trị dương, đồng thời thỏa
mãn
( ) ( )
( )
26
.' 2
x
fxf x f x e
−=
với mọi
x
. Biết
( )
01f =
. Hãy tính
( )
1.f
-------------------------------HẾT-------------------------------
Trang 1/4 - Mã đề 345
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút;
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ...................
Phần I: Trắc nghiệm (7 điểm)
Câu 1: Trên khoảng
( )
0; +∞
, hàm số
(
)
lnFx x=
là một nguyên hàm của hàm số?
A.
( )
1
fx
x
=
. B.
( )
lnfx x x x= −
.
C.
( )
1
,f x CC
x
=+∈
. D.
( )
ln ,f x x x x CC= −+ ∈
.
Câu 2: Trong không gian
Oxyz
, cho mặt cầu
( )
(
)
2
22
:1 4Sx yz
−++=
. Tâm của
( )
S
là điểm nào sau
đây?
A.
( )
1;0;0
B.
( )
1;1;1−
C.
( )
1;1;1
D.
( )
1;0;0−
Câu 3: Trong không gian
Oxyz
, cho vectơ
37
u i jk=−+ +

. Tọa độ của vectơ
u
là
A.
( )
3;7;0
−
. B.
( )
3; 7 ;1−
. C.
( )
3; 7 ;1
. D.
( )
3;7;0
.
Câu 4: Nguyên hàm của hàm số
( )
2
31fx x= +
là
A.
3
xC+
. B.
3
x xC++
. C.
6xC+
. D.
3
3
x
xC++
.
Câu 5: Cho
( )
2
1
d3
fx x
=
∫
và
( ) (
)
2
1
3 d 10f x gx x
−=


∫
. Khi đó
( )
2
1
dgx x
∫
bằng
A.
1−
. B. 17. C. 1. D.
4−
.
Câu 6: Mệnh đề nào sau đây là đúng ?
A.
2
d
2
= +
∫
xx
x
xe x e C
. B.
d = −+
∫
x xx
xe x xe e C
.
C.
d =++
∫
x xx
xe x e xe C
. D.
2
d
2
= ++
∫
x xx
x
xe x e e C
.
Câu 7: Họ nguyên hàm của hàm số
( )
1
54
=
+
fx
x
là:
A.
1
ln 5 4
ln 5
++xC
. B.
ln 5 4++
xC
. C.
1
ln 5 4
5
++xC
. D.
.
Câu 8: Giả sử
f
là hàm số liên tục trên khoảng
K
và
, , abc
là ba số bất kỳ trên khoảng
K
. Khẳng
định nào sau đây sai?
A.
( )
( ) ( )
( )
d d d , ;
cb b
ac a
fx x fx x fx xc ab+= ∈
∫∫∫
. B.
( )
( )
dd
ba
ab
fx x fx x= −
∫∫
.
C.
( ) (
)
d
bb
aa
f x dx f t t=
∫∫
. D.
( )
d1
a
a
fx x=
∫
.
Câu 9: Trong không gian
Oxyz
, mặt cầu
( ) (
) ( ) ( )
2 22
: 2 5 94
Sx y z− ++ +− =
có bán kính bằng
A.
4
. B.
16
. C.
8
. D.
2
.
Câu 10: Tìm họ nguyên hàm của hàm số
( )
3
e
x
fx=
.
Mã đề 345
Trang 2/4 - Mã đề 345
A.
( )
d ln 3fxx x C= +
∫
. B.
( )
3
1
d .e
3
x
fxx
=
∫
. C.
( )
3
de
x
fxx C= +
∫
. D.
(
)
3
1
d .e
3
x
fxx C= +
∫
.
Câu 11: Nếu
( )
( )
d
f u u Fu C= +
∫
và
( )
u ux=
có đạo hàm liên tục thì
A.
( ) ( )
d.
f ux x Fux C= +
 
 
∫
B.
( ) ( ) ( )
d.f xu x x F ux C
′
= +


∫
C.
(
) (
)
( )
d.f ux u x x Fux C
′
= +
 
 
∫
D.
( ) ( ) ( )
d.f ux u x x Fx C
′
= +


∫
Câu 12: Cho 2 hàm số
()
u ux
và
()
v vx
có đạo hàm liên tục trên khoảng
K
. Khẳng định nào
sau đây đúng?
A.
()'() ()() ()()uxv xdx uxvx uxvxdx

. B.
()'() ()'() '()()uxv xdx uxv x u xvxdx

.
C.
()'() ()() '()()uxv xdx uxvx u xvxdx

. D.
()'() '()() '()()
uxv xdx u xvx u xvxdx


.
Câu 13: Khẳng định nào sau đây đúng?
A.
sin2 d 2cos 2xx x C= +
∫
. B.
1
sin2 d cos 2
2
xx x C=−+
∫
.
C.
1
sin2 d cos 2
2
xx x C= +
∫
. D.
sin2 d 2cos2xx x C=−+
∫
.
Câu 14: Biết
(
) (
)
f x dx F x C= +
∫
.Trong các khẳng định sau, khẳng định nào đúng?
A.
( ) ( ) ( )
b
a
f x dx F a F b= −
∫
. B.
( ) ( ) ( )
b
a
f x dx F b F a= −
∫
.
C.
( ) ( ) ( )
b
a
f x dx F b F a= +
∫
. D.
(
) (
)
( )
.
b
a
f x dx F b F a=
∫
.
Câu 15: Cho hai hàm số
( )
fx
và
( )
gx
liên tục trên
K
,
,ab K∈
. Khẳng định nào sau đây là khẳng
định sai?
A.
( ) (
) ( ) (
)
d d. d
b bb
a aa
fxgxx fxxgxx
=
∫ ∫∫
. B.
( ) ( ) ( ) ( )
d dd
b bb
a aa
f x gx x f x x gx x−= −


∫ ∫∫
.
C.
(
) (
) ( )
d d0
bb
aa
kfx x kfx x k
= ≠
∫∫
. D.
( ) ( ) (
) ( )
d dd
b bb
a aa
f x gx x f x x gx x+= +


∫ ∫∫
.
Câu 16: Hàm số
( )
Fx
là một nguyên hàm của hàm số
(
)
fx
trên khoảng
( )
;ab
nếu
A.
( ) ( ) (
)
,;f x F x x ab
′
= ∀∈
. B.
( ) ( )
( )
,;F x f x x ab
′
= ∀∈
.
C.
( )
( ) ( )
,;f x F x x ab
′
=− ∀∈
. D.
( ) ( ) ( )
,;F x f x x ab
′
=− ∀∈
.
Câu 17: Tích phân
d
b
a
x
∫
bằng.
A.
ab+
. B.
ab−
. C.
ba−
. D.
a.b
.
Câu 18: Tích phân
1
2019
0
dIxx=
∫
bằng
A.
0
. B.
1
2020
. C.
1
. D.
1
2019
.
Câu 19: Cho hàm số
( )
fx
có đạo hàm trên
,
(
)
12f −=−
và
( )
32f =
. Tính
( )
3
1
'.I f x dx
−
=
∫
A.
4.I = −
B.
0.I =
C.
3.I =
D.
4.I =
Câu 20: Trong không gian
Oxyz
, mặt cầu
( )
S
có tâm
( )
1; 3; 0I −
và bán kính bằng
2
. Phương trình
của
( )
S
là
Trang 3/4 - Mã đề 345
A.
(
)
2
22
1 ( 3) 4
x yz
+ +− +=
. B.
(
)
2
22
1 ( 3) 2x yz
+ +− +=
.
C.
( )
2
22
1 ( 3) 4x yz− ++ +=
. D.
( )
2
22
1 ( 3) 2x yz− ++ +=
.
Câu 21: Biết
( )
1
0
d8
fx x=
∫
và
( )
5
1
d3fx x= −
∫
, khi đó
( )
5
0
dfx x
∫
bằng
A.
8
3
−
. B. 11. C.
11−
. D. 5.
Câu 22: Biết
( )
Fx
là một nguyên hàm của hàm số
( )
sin cos= +fx x x
thỏa mãn
( )
01=F
. Hàm số
( )
Fx
là
A.
cos sin 2
xx−+−
. B.
cos sin 1xx−+
. C.
cos sin 2xx
−++
. D.
cos sin 1xx−++
.
Câu 23: Cho
( )
fx
là hàm đa thức. Khi đó
( )
d
fx
x
x
′
∫
bằng:
A.
( )
1
2
fxC+
. B.
( )
2 fxC
+
. C.
( )
fxC+
. D.
( )
2 fxC−+
.
Câu 24: Họ nguyên hàm của hàm số
( )
sin 3f x x+ x=
là
A.
. B.
2
1
cos3
23
x
xC++
. C.
2
3cos3
2
x
xC−+
. D.
2
1
cos3
23
x
xC−+
.
Câu 25: Nếu
( )
2
5
d2fxx
=
∫
thì
( )
5
2
3dfxx
∫
bằng
A.
12
. B.
6
−
. C.
3
. D.
6
.
Câu 26: Trong không gian
Oxyz
, cho hai điểm
( )
2;3; 1A −−
và
( )
4;1;9B −
. Trung điểm
I
của đoạn
thẳng
AB
có tọa độ là
A.
( )
3;2;4−
. B.
(
)
2; 2;10
−−
. C.
(
)
3;2; 4−−
. D.
( )
6;4;8−
.
Câu 27: Họ nguyên hàm của hàm số
( )
ln
x
fx
x
=
là
A.
2
1
ln ln
2
x xC++
. B.
2
ln xC+
. C.
2
1
ln
2
xC+
. D.
( )
ln ln
xC+
.
Câu 28: Cho
(
)
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
( )
3;1−
. B.
( )
0; 4
. C.
( )
1; 2−
. D.
(
)
;0−∞
.
Câu 29: Cho
(
)
Fx
là nguyên hàm của
( )
1
2
fx
x
=
+
thỏa mãn
(
)
24F =
. Giá trị
( )
1
F −
bằng:
A.
3
. B.
1
. C.
23
. D.
2
.
Câu 30: Cho
( )
2
1
dx=3I fx
−
=
∫
. Khi đó
( )
2
1
3 4 dxJ fx
−
= −


∫
bằng:
A.
2
. B.
5
. C.
3−
. D.
1−
.
Câu 31: Trong không gian
Oxyz
, cho hai điểm
( )
2; 1;2A −
và
( )
0;1;0B
. Mặt cầu đường kính
AB
có
phương trình là
A.
( ) ( )
22
2
1 1 12x yz− ++− =
. B.
( ) ( )
22
2
1 13x yz− ++− =
.
C.
( ) ( ) ( )
2 22
2 2 22xyz+ +− ++ =
. D.
( ) ( )
22
2
1 13x yz− + +− =
.
Trang 4/4 - Mã đề 345
Câu 32: Trong không gian với hệ trục
Oxyz
cho ba điểm
( )
2;1;3A
,
( )
1; 2; 2B −
,
( )
; ;5Cxy
thẳng
hàng. Khi đó,
xy+
bằng
A.
10
. B.
11
. C.
3
. D.
12
.
Câu 33: Tính tích phân
2
1
1
d
21
Ix
x
=
−
∫
.
A.
ln 3
2
I =
. B.
ln 3 1
2
I
−
=
. C.
ln 3
3
I =
. D.
ln 3 1I
= +
.
Câu 34: Họ nguyên hàm của hàm số
2
3
()
1
x
fx
x
=
+
là
A.
3
2
.
31
C
x
+
+
B.
3
1
.
31
C
x
+
+
C.
3
2
1.
3
xC
++
D.
3
1
1.
3
xC++
Câu 35: Trong không gian
Oxyz
, cho
23
OM i j k
=−+

. Hình chiếu của điểm
M
trên mặt phẳng
( )
Oxy
là
A.
( )
1
2; 0; 0
M
. B.
( )
4
2; 0;1M
. C.
( )
3
2; 3; 0
M −
. D.
( )
2
0; 0;1M
.
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : Biết
Fx
là một nguyên hàm của hàm số
2 sin
fx x x

và thỏa mãn
0 21F
.
Tính
2
F


.
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ
,
Oxyz
cho điểm
( )
1;1; 2A
,
( )
2 ; 3; 3B −
. Viết
phương trình mặt cầu
( )
S
có tâm
I
thuộc trục
Oy
và đi qua hai điểm
,AB
.
Câu 3 (0,5 điểm): Biết
( )
Fx
và
( )
Gx
là hai nguyên hàm của hàm số
(
)
fx
trên
và thỏa mãn
( ) ( ) ( )
3
0
30f x dx F G a=−+
∫
(
)
0
a
>
. Gọi
(
) ( )
3
0
.S F x G x dx= −
∫
Tính giá trị của
a
khi
15.S =
Câu 4 (0,5 điểm): Cho hàm số
f
có đạo hàm liên tục trên
và luôn nhận giá trị dương, đồng thời thỏa
mãn
(
) (
) ( )
26
.' 2
x
fxf x f x e−=
với mọi
x
. Biết
( )
01f =
. Hãy tính
( )
1.f
----------------------------HẾT---------------------------
Trang 1/4 - Mã đề 456
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút;
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ...................
Phần I: Trắc nghiệm (7 điểm)
Câu 1: Tích phân
d
b
a
x
∫
bằng.
A.
ab+
. B.
ba
−
. C.
a.b
. D.
ab−
.
Câu 2: Nếu
(
)
( )
df u u Fu C= +
∫
và
( )
u ux=
có đạo hàm liên tục thì
A.
(
) (
)
( )
d.
f xu x x F ux C
′
= +


∫
B.
( ) ( )
d.f ux x Fux C= +
 
 
∫
C.
( ) ( ) ( )
d.f ux u x x Fux C
′
= +
 
 
∫
D.
( ) ( ) ( )
d.f ux u x x Fx C
′
= +


∫
Câu 3: Trong không gian
Oxyz
, mặt cầu
( )
S
có tâm
(
)
1; 3; 0
I
−
và bán kính bằng
2
. Phương trình
của
( )
S
là
A.
( )
2
22
1 ( 3) 4x yz− ++ +=
. B.
(
)
2
22
1 ( 3) 2
x yz
− ++ +=
.
C.
( )
2
22
1 ( 3) 4x yz+ +− +=
. D.
( )
2
22
1 ( 3) 2x yz+ +− +=
.
Câu 4: Cho
(
)
2
1
d3fx x=
∫
và
( ) ( )
2
1
3 d 10f x gx x−=


∫
. Khi đó
( )
2
1
dgx x
∫
bằng
A. 17. B. 1. C.
4−
. D.
1−
.
Câu 5: Hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
fx
trên khoảng
( )
;ab
nếu
A.
( ) (
) ( )
,;F x f x x ab
′
=− ∀∈
. B.
( )
( ) (
)
,;
F x f x x ab
′
= ∀∈
.
C.
( ) ( ) ( )
,;f x F x x ab
′
=− ∀∈
. D.
( )
( ) (
)
,;f x F x x ab
′
= ∀∈
.
Câu 6: Trong không gian
Oxyz
, mặt cầu
( ) ( ) ( ) ( )
2 22
: 2 5 94Sx y z− ++ +− =
có bán kính bằng
A.
4
. B.
16
. C.
8
. D.
2
.
Câu 7: Khẳng định nào sau đây đúng?
A.
1
sin2 d cos 2
2
xx x C=−+
∫
. B.
sin2 d 2cos 2xx x C
= +
∫
.
C.
sin2 d 2cos2
xx x C=−+
∫
. D.
1
sin2 d cos 2
2
xx x C= +
∫
.
Câu 8: Cho hàm số
( )
fx
có đạo hàm trên
,
(
)
12f −=−
và
( )
32f =
. Tính
( )
3
1
'.I f x dx
−
=
∫
A.
4.I = −
B.
3.I =
C.
4.I =
D.
0.I =
Câu 9: Họ nguyên hàm của hàm số
( )
1
54
=
+
fx
x
là:
A.
1
ln 5 4
ln 5
++xC
. B.
( )
1
ln 5 4
5
++xC
. C.
ln 5 4++xC
. D.
1
ln 5 4
5
++xC
.
Câu 10: Tích phân
1
2019
0
dIxx=
∫
bằng
Mã đề 456
Trang 2/4 - Mã đề 456
A.
0
. B.
1
. C.
1
2019
. D.
1
2020
.
Câu 11: Cho hai hàm số
( )
fx
và
( )
gx
liên tục trên
K
,
,ab K∈
. Khẳng định nào sau đây là khẳng
định sai?
A.
( ) ( ) ( )
( )
d d. d
b bb
a aa
fxgxx fxxgxx
=
∫ ∫∫
. B.
( ) ( )
(
) (
)
d dd
b bb
a aa
f x gx x f x x gx x+= +


∫ ∫∫
.
C.
( ) ( ) ( )
d d0
bb
aa
kfx x kfx x k= ≠
∫∫
. D.
( ) ( ) ( ) ( )
d dd
b bb
a aa
f x gx x f x x gx x−= −


∫ ∫∫
.
Câu 12: Giả sử
f
là hàm số liên tục trên khoảng
K
và
, ,
abc
là ba số bất kỳ trên khoảng
K
.
Khẳng định nào sau đây sai?
A.
( )
d1
a
a
fx x=
∫
. B.
(
)
( )
dd
ba
ab
fx x fx x= −
∫∫
.
C.
(
) (
) ( ) ( )
d d d , ;
cb b
ac a
fx x fx x fx xc ab
+= ∈
∫∫∫
. D.
(
) (
)
d
bb
aa
f x dx f t t
=
∫∫
.
Câu 13: Cho 2 hàm số
()u ux
và
()v vx
có đạo hàm liên tục trên khoảng
K
. Khẳng định nào
sau đây đúng?
A.
()'() ()() '()()
uxv xdx uxvx u xvxdx

. B.
()'() ()() ()()uxv xdx uxvx uxvxdx

.
C.
()'() '()() '()()uxv xdx u xvx u xvxdx


. D.
()'() ()'() '()()uxv xdx uxv x u xvxdx

.
Câu 14: Nguyên hàm của hàm số
( )
2
31fx x= +
là
A.
6xC+
. B.
3
3
x
xC++
. C.
3
x xC++
. D.
3
xC
+
.
Câu 15: Trong không gian
Oxyz
, cho mặt cầu
( ) ( )
2
22
:1 4Sx yz−++=
. Tâm của
( )
S
là điểm nào sau
đây?
A.
( )
1;0;0
B.
(
)
1;0;0−
C.
( )
1;1;1−
D.
( )
1;1;1
Câu 16: Mệnh đề nào sau đây là đúng ?
A.
d =++
∫
x xx
xe x e xe C
. B.
2
d
2
= ++
∫
x xx
x
xe x e e C
.
C.
2
d
2
= +
∫
xx
x
xe x e C
. D.
d = −+
∫
x xx
xe x xe e C
.
Câu 17: Biết
( ) ( )
f x dx F x C= +
∫
.Trong các khẳng định sau, khẳng định nào đúng?
A.
( ) ( ) ( )
b
a
f x dx F b F a= −
∫
. B.
( ) ( ) ( )
b
a
f x dx F b F a= +
∫
.
C.
( ) ( )
( )
.
b
a
f x dx F b F a=
∫
. D.
(
) ( ) ( )
b
a
f x dx F a F b= −
∫
.
Câu 18: Trên khoảng
( )
0; +∞
, hàm số
( )
lnFx x=
là một nguyên hàm của hàm số?
A.
( )
lnfx x x x= −
. B.
( )
ln ,f x x x x CC= −+ ∈
.
C.
( )
1
,f x CC
x
=+∈
. D.
( )
1
fx
x
=
.
Câu 19: Tìm họ nguyên hàm của hàm số
( )
3
e
x
fx=
.
A.
( )
3
de
x
fxx C= +
∫
. B.
( )
3
1
d .e
3
x
fxx=
∫
. C.
( )
d ln 3
fxx x C= +
∫
. D.
( )
3
1
d .e
3
x
fxx C= +
∫
.
Câu 20: Trong không gian
Oxyz
, cho vectơ
37u i jk=−+ +

. Tọa độ của vectơ
u
là
Trang 3/4 - Mã đề 456
A.
( )
3; 7 ;1
. B.
(
)
3; 7 ;1
−
. C.
( )
3;7;0−
. D.
(
)
3;7;0
.
Câu 21: Trong không gian
Oxyz
, cho hai điểm
( )
2; 1;2A −
và
(
)
0;1;0B
. Mặt cầu đường kính
AB
có
phương trình là
A.
( ) ( )
22
2
1 1 12x yz
− + +− =
. B.
(
) (
)
( )
2 22
2 2 22xyz
+ +− ++ =
.
C.
(
) (
)
22
2
1 13
x yz
− ++− =
. D.
( ) (
)
22
2
1 13x yz− ++− =
.
Câu 22: Biết
( )
Fx
là một nguyên hàm của hàm số
( )
sin cos= +fx x x
thỏa mãn
(
)
01=
F
. Hàm số
( )
Fx
là
A.
cos sin 2xx−++
. B.
cos sin 2xx−+−
. C.
cos sin 1xx−++
. D.
cos sin 1
xx
−+
.
Câu 23: Họ nguyên hàm của hàm số
(
)
sin 3f x x+ x
=
là
A.
2
3cos3
2
x
xC−+
. B.
2
1
cos3
23
x
xC−+
. C.
2
1
cos3
23
x
xC++
. D.
2
3cos3
2
x
xC++
.
Câu 24: Cho
( )
2
1
dx=3
I fx
−
=
∫
. Khi đó
( )
2
1
3 4 dxJ fx
−
= −


∫
bằng:
A.
3−
. B.
1−
. C.
5
. D.
2
.
Câu 25: Nếu
( )
2
5
d2fxx=
∫
thì
( )
5
2
3dfxx
∫
bằng
A.
3
. B.
6
. C.
12
. D.
6
−
.
Câu 26: Họ nguyên hàm của hàm số
( )
ln
x
fx
x
=
là
A.
( )
ln ln xC+
. B.
2
1
ln
2
xC+
. C.
2
1
ln ln
2
x xC++
. D.
2
ln xC
+
.
Câu 27: Biết
( )
1
0
d8fx x
=
∫
và
( )
5
1
d3fx x= −
∫
, khi đó
(
)
5
0
d
fx x
∫
bằng
A. 11. B. 5. C.
11−
. D.
8
3
−
.
Câu 28: Cho
( )
Fx
là nguyên hàm của
( )
1
2
fx
x
=
+
thỏa mãn
( )
24F =
. Giá trị
( )
1
F −
bằng:
A.
2
. B.
3
. C.
1
. D.
23
.
Câu 29: Trong không gian
Oxyz
, cho
23OM i j k=−+

. Hình chiếu của điểm
M
trên mặt phẳng
(
)
Oxy
là
A.
( )
3
2; 3; 0M −
. B.
( )
1
2; 0; 0M
. C.
( )
4
2; 0;1M
. D.
( )
2
0; 0;1M
.
Câu 30: Cho
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
( )
;0−∞
. B.
( )
3;1−
. C.
( )
0; 4
. D.
( )
1; 2−
.
Câu 31: Cho
( )
fx
là hàm đa thức. Khi đó
( )
d
fx
x
x
′
∫
bằng:
A.
( )
fxC+
. B.
( )
2 fxC−+
. C.
( )
2 fxC+
. D.
( )
1
2
fxC+
.
Câu 32: Họ nguyên hàm của hàm số
2
3
()
1
x
fx
x
=
+
là
Trang 4/4 - Mã đề 456
A.
3
1
1.
3
xC++
B.
3
2
1.
3
xC++
C.
3
2
.
31
C
x
+
+
D.
3
1
.
31
C
x
+
+
Câu 33: Trong không gian với hệ trục
Oxyz
cho ba điểm
( )
2;1;3A
,
( )
1; 2; 2B −
,
( )
; ;5Cxy
thẳng
hàng. Khi đó,
xy+
bằng
A.
3
. B.
10
. C.
12
. D.
11
.
Câu 34: Trong không gian
Oxyz
, cho hai điểm
( )
2;3; 1A −−
và
( )
4;1;9B −
. Trung điểm
I
của đoạn
thẳng
AB
có tọa độ là
A.
( )
3;2;4−
. B.
( )
2; 2;10
−−
. C.
(
)
3;2; 4
−−
. D.
(
)
6;4;8−
.
Câu 35: Tính tích phân
2
1
1
d
21
Ix
x
=
−
∫
.
A.
ln 3 1
2
I
−
=
. B.
ln 3 1I = +
. C.
ln 3
3
I =
. D.
ln 3
2
I =
.
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : : Biết
Fx
là một nguyên hàm của hàm số
2 cosfx x x
và thỏa mãn
0 20F
.
Tính
2
F


.
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ
,Oxyz
cho điểm
( )
1;1; 2
A
,
( )
2 ; 3; 3
B −
. Viết
phương trình mặt cầu
( )
S
có tâm
I
thuộc trục
Ox
và đi qua hai điểm
,AB
Câu 3 (0,5 điểm): Biết
( )
Fx
và
( )
Gx
là hai nguyên hàm của hàm số
( )
fx
trên
và thỏa mãn
( )
( ) ( )
5
0
50f x dx F G a=−+
∫
( )
0a >
. Gọi
( ) ( )
5
0
.S F x G x dx= −
∫
Tính giá trị của
a
khi
20.S =
Câu 4 (0,5 điểm): Cho hàm số
f
có đạo hàm liên tục trên
và luôn nhận giá trị dương, đồng thời thỏa
mãn
( ) ( ) ( )
26
.' 2
x
fxf x f x e−=
với mọi
x
. Biết
( )
01f =
. Hãy tính
( )
1.f
------------------------------ -HẾT-------------------------------
1
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm:
123
234
345
456
1
B
A
A
B
2
C
D
A
C
3
D
A
B
A
4
D
D
B
D
5
C
C
A
B
6
D
C
B
D
7
B
D
C
A
8
C
B
D
C
9
A
D
D
D
10
C
A
D
D
11
A
D
C
A
12
B
A
C
A
13
C
C
B
A
14
C
C
B
C
15
A
B
A
A
16
D
D
B
D
17
C
B
C
A
18
C
D
B
D
19
A
A
D
D
20
A
C
C
B
21
D
B
D
D
22
C
B
C
A
23
A
D
B
B
24
C
B
D
A
25
C
B
B
D
26
C
A
A
B
27
D
D
C
B
28
C
C
B
A
29
B
B
D
A
30
A
C
C
C
31
B
C
D
C
32
B
B
B
B
33
A
B
A
D
34
B
B
C
A
35
C
D
C
D
2
Đáp án mã đề 123, 345
Câu
Nội dung
Điểm
Câu 1
2
( ) 2 sin d cosF x x x x x x C
Giả thiết
2
0 21 0 cos0 21 20F C C
Suy ra
2
2
cos 20 20.
24
F x x x F
0,5
0,5
Câu 2
Ta có
( )
0; ;0I Oy I a
. Khi đó
( )
1;1 ;2IA a−
,
( )
2;3 ; 3IB a−−
.
Do
( )
S
đi qua hai điểm
,AB
nên:
( ) ( )
22
1 5 3 13IA IB a a= − + = − +
4 16 4aa = =
( )
S
có tâm
( )
0;4;0I
, bán kính
14R IA==
.
Vậy
( ) ( )
2
22
: 4 14.S x y z+ − + =
0,25
0,25
0,25
0,25
Câu 3
Giả thiết
( ) ( )
,F x G x
đều là nguyên hàm của
( )
fx
nên ta có:
( ) ( ) ( ) ( )
00F x G x C F G C= + = +
(1).
Ta có
( ) ( ) ( ) ( ) ( ) ( )
( )
( ) ( )
3
3
0
0
d 3 0 3 0 3 0f x x F x F F F G C F G C= = − = − + = − −
.
Mà theo giả thiết
( ) ( ) ( )
3
0
d 3 0f x x F G a= − +
nên
Ca=−
.
Suy ra
( ) ( ) ( ) ( )
F x G x a F x G x a= − − = −
.
Ta có
( ) ( )
33
3
0
00
d d 3S F x G x x a x ax a= − = − = =

.
Mà
15S =
nên ta có
5a =
.
0,25
0,25
Câu 4
Với mọi
x
, ta có
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
26
2 2 2
4
4
'
22
4 4 4
22
. ' 2
2 . ' . 2 .
4
4 4 .
x
xx
x
x
x x x
xx
f x f x f x e
f x f x e e f x
e
e
f x f x
e e dx e C
ee
−=
−
=

= = = +



Suy ra
( )
2
0
1 0.
1
f
CC= + =
Do đó
( ) ( )
2 6 3
,
xx
f x e f x e x= =
.
Vậy
( )
3
1.fe=
0,25
0,25
3
Đáp án các mã 234, 456
Câu
Nội dung
Điểm
Câu 1
2
( ) 2 cos d sinF x x x x x x C
Giả thiết
2
0 20 0 sin0 20 20F C C
Suy ra
2
2
sin 20 21.
24
F x x x F
0,5
0,5 .
Câu 2
Ta có
( )
;0;0I Ox I a
. Khi đó
( )
1 ;1;2IA a−
,
( )
2 ;3; 3IB a−−
.
Do
( )
S
đi qua hai điểm
,AB
nên:
( ) ( )
22
1 5 2 18IA IB a a= − + = − +
2 16 8aa = =
( )
S
có tâm
( )
8;0;0I
, bán kính
54R IA==
.
Vậy
( ) ( )
2
22
: 8 54.S x y z− + + =
0,25
0,25
0,25
0,25
Câu 3
Giả thiết
( ) ( )
,F x G x
đều là nguyên hàm của
( )
fx
nên ta có:
( ) ( ) ( ) ( )
00F x G x C F G C= + = +
(1).
Ta có
( ) ( ) ( ) ( ) ( ) ( )
( )
( ) ( )
5
5
0
0
d 5 0 5 0 5 0f x x F x F F F G C F G C= = − = − + = − −
.
Mà theo giả thiết
( ) ( ) ( )
5
0
d 5 0f x x F G a= − +
nên
Ca=−
.
Suy ra
( ) ( ) ( ) ( )
F x G x a F x G x a= − − = −
.
Ta có
( ) ( )
55
5
0
00
d d 5S F x G x x a x ax a= − = − = =

.
Mà
20S =
nên ta có
4.a =
0,25
0,25
Câu 4
Với mọi
x
, ta có
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
26
2 2 2
4
4
'
22
4 4 4
22
. ' 2
2 . ' . 2 .
4
4 4 .
x
xx
x
x
x x x
xx
f x f x f x e
f x f x e e f x
e
e
f x f x
e e dx e C
ee
−=
−
=

= = = +



Suy ra
( )
2
0
1 0.
1
f
CC= + =
Do đó
( ) ( )
2 6 3
,
xx
f x e f x e x= =
.
Vậy
( )
3
1.fe=
0,25
0,25
4
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

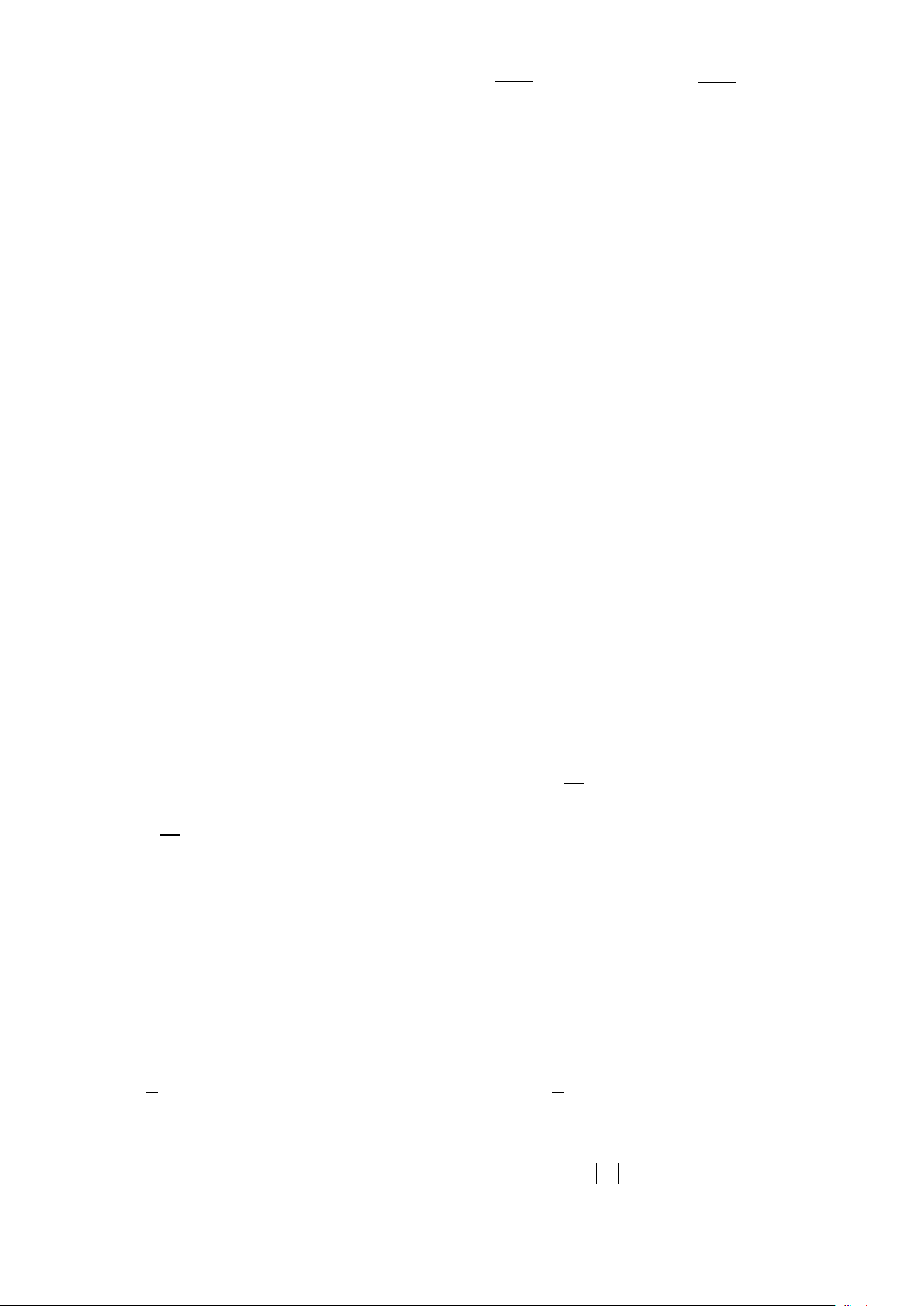
Preview text:

SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 123
Phần I: Trắc nghiệm (7 điểm)
Câu 1: Họ nguyên hàm của hàm số f (x) 1 = là: 5x + 4
A. ln 5x + 4 + C .
B. 1 ln 5x + 4 + C .
C. 1 ln 5x + 4 + C .
D. 1 ln(5x + 4) + C . 5 ln 5 5 b
Câu 2: Tích phân dx ∫ bằng. a A. a − b . B. a + b. C. b − a . D. a.b . Câu 3: Nếu f
∫ (u)du = F (u)+C và u = u(x) có đạo hàm liên tục thì
A. f u
∫  (x)dx = F u   ( x) + C.  B. f u
∫  (x)u′
 ( x)dx = F ( x) + C. C. f
∫ (x)u′(x)dx = F u(x) +C.  D. f u
∫  (x)u′
 ( x)dx = F u  ( x) + C.  
Câu 4: Trong không gian    
Oxyz , cho vectơ u = 3
− i + 7 j + k . Tọa độ của vectơ u là A. (3;7; ) 1 . B. ( 3 − ;7;0) . C. (3;7;0) . D. ( 3 − ;7; ) 1 . 1 Câu 5: Tích phân 2019 I = x dx ∫ bằng 0 A. 1 1. B. . C. 1 . D. 0 . 2019 2020 3
Câu 6: Cho hàm số f (x) có đạo hàm trên  , f (− ) 1 = 2
− và f (3) = 2 . Tính I = f ' ∫ (x) . dx 1 − A. I = 0. B. I = 3. C. I = 4. − D. I = 4.
Câu 7: Mệnh đề nào sau đây là đúng ? A. d = + + ∫ x x x xe x e xe C . B. d = − + ∫ x x x xe x xe e C . 2 2 C. d = x xe x e + e + ∫ x x x C . D. d = x xe x e + C . 2 ∫ x x 2
Câu 8: Trong không gian Oxyz , mặt cầu (S) (x − )2 + ( y + )2 + (z − )2 : 2 5 9 = 4 có bán kính bằng A. 16. B. 8. C. 2 . D. 4 .
Câu 9: Khẳng định nào sau đây đúng? A. 1 sin2 d
x x = − cos 2x + C ∫ . B. sin2 d x x = 2 − cos 2x + C 2 ∫ . C. sin2 d
x x = 2cos 2x + C ∫ . D. 1 sin2 d
x x = cos 2x + C ∫ . 2
Câu 10: Cho hai hàm số f (x) và g (x) liên tục trên K , a, b∈ K . Khẳng định nào sau đây là khẳng định sai? b b b b b A. kf
∫ (x)dx = k f
∫ (x)dx (k ≠ 0). B. f
∫ (x)+ g(x)dx = f
∫ (x)dx+ g ∫ (x)dx. a a a a a Trang 1/4 - Mã đề 123 b b b b b b C. f
∫ (x)g(x)dx = f ∫ (x)d .x g ∫ (x)dx . D. f
∫ (x)− g(x)dx = f
∫ (x)dx− g ∫ (x)dx . a a a a a a
Câu 11: Cho 2 hàm số u u(x) và v v(x) có đạo hàm liên tục trên khoảng K . Khẳng định nào sau đây đúng?
A. u(x)v'(x)dx u(x)v(x) u '(x)v(x)dx   .
B. u(x)v'(x)dx u(x)v'(x) u '(x)v(x)dx   .
C. u(x)v'(x)dx u '(x)v(x) u '(x)v(x)dx  
. D. u(x)v'(x)dx u(x)v(x) u(x)v(x)dx   . 2 2 2 Câu 12: Cho f
∫ (x)dx = 3 và 3f
∫  (x)− g(x)dx =10 
. Khi đó g (x)dx ∫ bằng 1 1 1 A. 4 − . B. 1 − . C. 1. D. 17.
Câu 13: Trong không gian Oxyz , cho mặt cầu (S) (x − )2 2 2 :
1 + y + z = 4 . Tâm của (S ) là điểm nào sau đây? A. ( 1 − ;0;0) B. ( 1; − 1; ) 1 C. (1;0;0) D. (1;1; ) 1
Câu 14: Trong không gian Oxyz , mặt cầu (S ) có tâm I (1; 3
− ;0) và bán kính bằng 2 . Phương trình của (S ) là A. (x − )2 2 2
1 + (y + 3) + z = 2 . B. (x + )2 2 2
1 + (y − 3) + z = 4 . C. (x − )2 2 2
1 + (y + 3) + z = 4 . D. (x + )2 2 2
1 + (y − 3) + z = 2 .
Câu 15: Biết f
∫ (x)dx = F (x)+C .Trong các khẳng định sau, khẳng định nào đúng? b b A. f
∫ (x)dx = F (b)− F (a) . B. f
∫ (x)dx = F (a)− F (b). a a b b C. f
∫ (x)dx = F (b)+ F (a). D. f
∫ (x)dx = F (b).F (a). a a
Câu 16: Tìm họ nguyên hàm của hàm số ( ) 3 e x f x = . A. ( ) 1 3 d .e x f x x = ∫ . B. 1
f (x)dx = ln 3x + ∫ C . C. ( ) 3 d = e x f x x + ∫ C . D. ( ) 3 d = .e x f x x + ∫ C . 3 3
Câu 17: Nguyên hàm của hàm số f (x) 2 = 3x +1 là 3
A. x + x + C .
B. 6x + C .
C. 3x + x + C .
D. 3x + C . 3
Câu 18: Trên khoảng (0;+∞), hàm số F (x) = ln x là một nguyên hàm của hàm số?
A. f (x) 1
= + C,C ∈  .
B. f (x) = xln x − x + C,C ∈ . x C. ( ) 1 f x = .
D. f (x) = xln x − x . x
Câu 19: Giả sử f là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K .
Khẳng định nào sau đây sai? a c b b A. f ∫ (x)dx =1.
B. f (x)dx + f (x)dx = f (x)dx, c∈ ∫ ∫ ∫ (a;b) . a a c a b a b b C. f
∫ (x)dx = − f ∫ (x)dx. D. f
∫ (x)dx = f ∫ (t)dt . a b a a
Câu 20: Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng ( ; a b) nếu
A. F′(x) = f (x), x ∀ ∈(a;b) .
B. F′(x) = − f (x), x ∀ ∈(a;b) . Trang 2/4 - Mã đề 123
C. f ′(x) = −F (x), x ∀ ∈(a;b) .
D. f ′(x) = F (x), x ∀ ∈(a;b) . 2
Câu 21: Tính tích phân 1 I = dx ∫ . 2x −1 1 A. ln 3 I = . B. I = ln3+1. C. ln 3 1 I − = . D. ln 3 I = . 3 2 2 2 5
Câu 22: Nếu f
∫ (x)dx = 2 thì 3f (x)dx ∫ bằng 5 2 A. 3. B. 6. C. 6 − . D. 12 . m Câu 23: Cho ∫( 2 3x − 2x + )
1 dx = 6. Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. (0;4) . B. ( ;0 −∞ ). C. ( 1; − 2) . D. ( 3 − ; ) 1 .
Câu 24: Trong không gian Oxyz , cho hai điểm A(2;−1;2) và B(0;1;0). Mặt cầu đường kính AB có phương trình là A. (x − )2 2
1 + y + (z − )2 1 = 3 . B. (x − )2 2
1 + y + ( z − )2 1 =12 . C. (x − )2 2
1 + y + (z − )2 1 = 3.
D. (x + )2 + ( y − )2 + (z + )2 2 2 2 = 2 .
Câu 25: Họ nguyên hàm của hàm số ( ) ln x f x = là x A. 1 2
ln x + ln x + C . B. 2 ln x + C . C. 1 2 ln x + C .
D. ln(ln x) + C . 2 2 f ′( x)
Câu 26: Cho f (x) là hàm đa thức. Khi đó dx ∫ bằng: x A. 1
f ( x ) + C . B. 2
− f ( x ) + C .
C. 2 f ( x)+C .
D. f ( x)+C . 2
Câu 27: Trong không gian với hệ trục Oxyz cho ba điểm A(2;1;3) , B(1;− 2;2), C (x; y;5) thẳng
hàng. Khi đó, x + y bằng A. 10. B. 3. C. 12. D. 11.
Câu 28: Cho F (x) là nguyên hàm của f (x) 1 =
thỏa mãn F (2) = 4. Giá trị F (− ) 1 bằng: x + 2 A. 2 3 . B. 3 . C. 2 . D. 1. 2 2
Câu 29: Cho I = f
∫ (x)dx=3. Khi đó J = 3f ∫  (x)−4dx  bằng: 1 − 1 − A. 5. B. 3 − . C. 1 − . D. 2 . 1 5 5
Câu 30: Biết f
∫ (x)dx = 8 và f (x)dx = 3 − ∫
, khi đó f (x)dx ∫ bằng 0 1 0 A. 5. B. 11. C. 8 − . D. 11 − . 3
Câu 31: Trong không gian Oxyz , cho hai điểm A( 2 − ;3;− ) 1 và B( 4
− ;1;9) . Trung điểm I của đoạn
thẳng AB có tọa độ là A. ( 2; − − 2;10) . B. ( 3 − ;2;4). C. ( 6; − 4;8) . D. ( 3; − 2;− 4) .
Câu 32: Họ nguyên hàm của hàm số f (x) = x+sin3x là Trang 3/4 - Mã đề 123 2 2 2 2
A. x −3cos3x + C . B. x 1 − cos3x + C .
C. x + 3cos3x + C . D. x 1 + cos3x + C . 2 2 3 2 2 3 2
Câu 33: Họ nguyên hàm của hàm số ( ) x f x = là 3 x +1 A. 2 3 x +1 + C. B. 1 + C. C. 1 3 x +1 + C. D. 2 + C. 3 3 3 x +1 3 3 3 x +1
Câu 34: Biết F (x) là một nguyên hàm của hàm số f (x) = sin x + cos x thỏa mãn F (0) =1. Hàm số F (x) là
A. cos x −sin x +1.
B. −cos x + sin x + 2 .
C. −cos x +sin x +1.
D. −cos x + sin x − 2 .    
Câu 35: Trong không gian Oxyz , cho OM = 2i −3 j + k . Hình chiếu của điểm M trên mặt phẳng (Oxy) là A. M 2;0;0 . B. M 2;0;1 . C. M 2; 3 − ;0 . D. M 0;0;1 . 2 ( ) 3 ( ) 4 ( ) 1 ( )
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : Biết F x là một nguyên hàm của hàm số f x 2xsin x và thỏa mãn F 0 21.   Tính F     .  2
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;1;2), B(2;3;−3) . Viết
phương trình mặt cầu (S ) có tâm I thuộc trục Oy và đi qua hai điểm , A B .
Câu 3 (0,5 điểm): Biết F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên  và thỏa mãn 3 3 f
∫ (x)dx = F (3)−G(0)+ a (a > 0). Gọi S = F
∫ (x)−G(x) .
dx Tính giá trị của a khi S =15. 0 0
Câu 4 (0,5 điểm): Cho hàm số f có đạo hàm liên tục trên  và luôn nhận giá trị dương, đồng thời thỏa mãn ( ) ( ) 2 − ( ) 6 . ' = 2 x f x f x f x
e với mọi x . Biết f (0) =1. Hãy tính f ( ) 1 .
-----------------------HẾT------------------------ Trang 4/4 - Mã đề 123
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 234
Phần I: Trắc nghiệm (7 điểm) 1 Câu 1: Tích phân 2019 I = x dx ∫ bằng 0 A. 1 . B. 1 . C. 1. D. 0 . 2020 2019
Câu 2: Mệnh đề nào sau đây là đúng ? 2 A. d = x xe x e + e + ∫ x x x C . B. d = + + 2 ∫ x x x xe x e xe C . 2 C. d = x xe x e + ∫ x x C . D. d = − + 2 ∫ x x x xe x xe e C .
Câu 3: Cho 2 hàm số u u(x) và v v(x) có đạo hàm liên tục trên khoảng K . Khẳng định nào sau đây đúng?
A. u(x)v'(x)dx u(x)v(x) u '(x)v(x)dx   .
B. u(x)v'(x)dx u(x)v'(x) u '(x)v(x)dx   .
C. u(x)v'(x)dx u '(x)v(x) u '(x)v(x)dx   .
D. u(x)v'(x)dx u(x)v(x) u(x)v(x)dx   .
Câu 4: Cho hai hàm số f (x) và g (x) liên tục trên K , a, b∈ K . Khẳng định nào sau đây là khẳng định sai? b b b b b A. f
∫ (x)+ g(x)dx = f
∫ (x)dx+ g ∫ (x)dx. B. kf
∫ (x)dx = k f
∫ (x)dx (k ≠ 0). a a a a a b b b b b b C. f
∫ (x)− g(x)dx = f
∫ (x)dx− g ∫ (x)dx . D. f
∫ (x)g(x)dx = f ∫ (x)d .x g ∫ (x)dx . a a a a a a 2 2 2 Câu 5: Cho f
∫ (x)dx = 3 và 3f
∫  (x)− g(x)dx =10 
. Khi đó g (x)dx ∫ bằng 1 1 1 A. 1. B. 17. C. 1 − . D. 4 − . Câu 6: Nếu f
∫ (u)du = F (u)+C và u = u(x) có đạo hàm liên tục thì A. f
∫ (x)u′(x)dx = F u(x) +C. 
B. f u
∫  (x)dx = F u   ( x) + C. 
C. f u
∫  (x)u′
 ( x)dx = F u  ( x) + C.  D. f u
∫  (x)u′
 ( x)dx = F ( x) + C.
Câu 7: Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng (a;b) nếu
A. f ′(x) = F (x), x ∀ ∈(a;b) .
B. F′(x) = − f (x), x ∀ ∈(a;b) .
C. f ′(x) = −F (x), x ∀ ∈(a;b) .
D. F′(x) = f (x), x ∀ ∈(a;b) . b
Câu 8: Tích phân dx ∫ bằng. a A. a + b. B. b − a . C. a.b . D. a − b .
Câu 9: Nguyên hàm của hàm số f (x) 2 = 3x +1 là 3 A. 3x x + C . B. + x + C .
C. 6x + C .
D. 3x + x + C . 3 Trang 1/4 - Mã đề 234
Câu 10: Tìm họ nguyên hàm của hàm số ( ) 3 e x f x = . A. ( ) 1 3 d = .e x f x x + ∫ C . B. ( ) 3 d 1 = e x f x x + ∫
C . C. f (x)dx = ln 3x + ∫ C . D. ∫ ( ) 3 d .e x f x x = . 3 3
Câu 11: Họ nguyên hàm của hàm số f (x) 1 = là: 5x + 4
A. ln 5x + 4 + C .
B. 1 ln(5x + 4) + C .
C. 1 ln 5x + 4 + C .
D. 1 ln 5x + 4 + C . 5 ln 5 5
Câu 12: Giả sử f là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K .
Khẳng định nào sau đây sai? a b a A. f ∫ (x)dx =1. B. f
∫ (x)dx = − f ∫ (x)dx. a a b c b b b b
C. f (x)dx + f (x)dx = f (x)dx, c∈ ∫ ∫ ∫ (a;b) . D. f
∫ (x)dx = f ∫ (t)dt . a c a a a 3
Câu 13: Cho hàm số f (x) có đạo hàm trên  , f (− ) 1 = 2
− và f (3) = 2 . Tính I = f ' ∫ (x) . dx 1 − A. I = 0. B. I = 4. − C. I = 4. D. I = 3.
Câu 14: Trong không gian Oxyz , cho mặt cầu (S) (x − )2 2 2 :
1 + y + z = 4 . Tâm của (S ) là điểm nào sau đây? A. ( 1; − 1; ) 1 B. ( 1 − ;0;0) C. (1;0;0) D. (1;1; ) 1 
Câu 15: Trong không gian    
Oxyz , cho vectơ u = 3
− i + 7 j + k . Tọa độ của vectơ u là A. (3;7; ) 1 . B. ( 3 − ;7; ) 1 . C. (3;7;0) . D. ( 3 − ;7;0) .
Câu 16: Khẳng định nào sau đây đúng? A. sin2 d
x x = 2cos 2x + C ∫ . B. 1 sin2 d
x x = cos 2x + C ∫ . 2 C. sin2 d x x = 2 − cos 2x + C ∫ . D. 1 sin2 d
x x = − cos 2x + C ∫ . 2
Câu 17: Trong không gian Oxyz , mặt cầu (S) (x − )2 + ( y + )2 + (z − )2 : 2 5 9 = 4 có bán kính bằng A. 4 . B. 2 . C. 8. D. 16.
Câu 18: Biết f
∫ (x)dx = F (x)+C .Trong các khẳng định sau, khẳng định nào đúng? b b A. f
∫ (x)dx = F (b)+ F (a). B. f
∫ (x)dx = F (a)− F (b). a a b b C. f
∫ (x)dx = F (b).F (a). D. f
∫ (x)dx = F (b)− F (a) . a a
Câu 19: Trong không gian Oxyz , mặt cầu (S ) có tâm I (1; 3
− ;0) và bán kính bằng 2 . Phương trình của (S ) là A. (x − )2 2 2
1 + (y + 3) + z = 4 . B. (x + )2 2 2
1 + (y − 3) + z = 2 . C. (x + )2 2 2
1 + (y − 3) + z = 4 . D. (x − )2 2 2
1 + (y + 3) + z = 2 .
Câu 20: Trên khoảng (0;+∞), hàm số F (x) = ln x là một nguyên hàm của hàm số?
A. f (x) = xln x − x + C,C ∈ .
B. f (x) = xln x − x . C. ( ) 1 f x = .
D. f (x) 1
= + C,C ∈  . x x Trang 2/4 - Mã đề 234
Câu 21: Họ nguyên hàm của hàm số ( ) ln x f x = là x A. 2 ln x + C . B. 1 2 ln x + C . C. 1 2
ln x + ln x + C .
D. ln(ln x) + C . 2 2 1 5 5
Câu 22: Biết f
∫ (x)dx = 8 và f (x)dx = 3 − ∫
, khi đó f (x)dx ∫ bằng 0 1 0 A. 11 − . B. 5. C. 11. D. 8 − . 3
Câu 23: Biết F (x) là một nguyên hàm của hàm số f (x) = sin x + cos x thỏa mãn F (0) =1. Hàm số F (x) là
A. −cos x + sin x − 2 .
B. −cos x +sin x +1.
C. cos x −sin x +1.
D. −cos x + sin x + 2 . 2 2
Câu 24: Cho I = f
∫ (x)dx=3. Khi đó J = 3f ∫  (x)−4dx  bằng: 1 − 1 − A. 5. B. 3 − . C. 1 − . D. 2 . f ′( x)
Câu 25: Cho f (x) là hàm đa thức. Khi đó dx ∫ bằng: x A. 1 2
− f ( x ) + C .
B. 2 f ( x)+C .
C. f ( x)+C .
D. f ( x)+C . 2 m Câu 26: Cho ∫( 2 3x − 2x + )
1 dx = 6. Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. (0;4) . B. ( 3 − ; ) 1 . C. ( 1; − 2) . D. ( ;0 −∞ ). 2
Câu 27: Tính tích phân 1 I = dx ∫ . 2x −1 1 A. ln 3 1 I − = . B. I = ln3+1. C. ln 3 I = . D. ln 3 I = . 2 3 2    
Câu 28: Trong không gian Oxyz , cho OM = 2i −3 j + k . Hình chiếu của điểm M trên mặt phẳng (Oxy) là A. M 2;0;1 . B. M 2;0;0 . C. M 2; 3 − ;0 . D. M 0;0;1 . 2 ( ) 3 ( ) 1 ( ) 4 ( )
Câu 29: Trong không gian Oxyz , cho hai điểm A(2;−1;2) và B(0;1;0). Mặt cầu đường kính AB có phương trình là A. (x − )2 2
1 + y + ( z − )2 1 =12 . B. (x − )2 2
1 + y + (z − )2 1 = 3. C. (x − )2 2
1 + y + (z − )2 1 = 3 .
D. (x + )2 + ( y − )2 + (z + )2 2 2 2 = 2 .
Câu 30: Họ nguyên hàm của hàm số f (x) = x+sin3x là 2 2 2 2
A. x −3cos3x + C .
B. x + 3cos3x + C . C. x 1 − cos3x + C . D. x 1 + cos3x + C . 2 2 2 3 2 3
Câu 31: Trong không gian với hệ trục Oxyz cho ba điểm A(2;1;3) , B(1;− 2;2), C (x; y;5) thẳng
hàng. Khi đó, x + y bằng A. 3. B. 10. C. 11. D. 12. Trang 3/4 - Mã đề 234 2 5
Câu 32: Nếu f
∫ (x)dx = 2 thì 3f (x)dx ∫ bằng 5 2 A. 12 . B. 6 − . C. 6. D. 3.
Câu 33: Cho F (x) là nguyên hàm của f (x) 1 =
thỏa mãn F (2) = 4. Giá trị F (− ) 1 bằng: x + 2 A. 3 . B. 2 . C. 1. D. 2 3 . 2
Câu 34: Họ nguyên hàm của hàm số ( ) x f x = là 3 x +1 A. 1 + C. B. 2 3 x +1 + C. C. 2 + C. D. 1 3 x +1 + C. 3 3 x +1 3 3 3 x +1 3
Câu 35: Trong không gian Oxyz , cho hai điểm A( 2 − ;3;− ) 1 và B( 4
− ;1;9) . Trung điểm I của đoạn
thẳng AB có tọa độ là A. ( 2; − − 2;10) . B. ( 3; − 2;− 4) . C. ( 6; − 4;8) . D. ( 3 − ;2;4).
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : Biết F x là một nguyên hàm của hàm số f x 2x cos x và thỏa mãn F 0 20 .   Tính F     .  2
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;1;2), B(2;3;−3) . Viết
phương trình mặt cầu (S ) có tâm I thuộc trục Ox và đi qua hai điểm , A B
Câu 3 (0,5 điểm): Biết F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên  và thỏa mãn 5 5 f
∫ (x)dx = F (5)−G(0)+ a (a > 0). Gọi S = F
∫ (x)−G(x) .
dx Tính giá trị của a khi S = 20. 0 0
Câu 4 (0,5 điểm): Cho hàm số f có đạo hàm liên tục trên  và luôn nhận giá trị dương, đồng thời thỏa mãn ( ) ( ) 2 − ( ) 6 . ' = 2 x f x f x f x
e với mọi x . Biết f (0) =1. Hãy tính f ( ) 1 .
-------------------------------HẾT------------------------------- Trang 4/4 - Mã đề 234
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút;
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 345
Phần I: Trắc nghiệm (7 điểm)
Câu 1: Trên khoảng (0;+∞), hàm số F (x) = ln x là một nguyên hàm của hàm số? A. ( ) 1 f x = .
B. f (x) = xln x − x . x
C. f (x) 1
= + C,C ∈  .
D. f (x) = xln x − x + C,C ∈ . x
Câu 2: Trong không gian Oxyz , cho mặt cầu (S) (x − )2 2 2 :
1 + y + z = 4 . Tâm của (S ) là điểm nào sau đây? A. (1;0;0) B. ( 1; − 1; ) 1 C. (1;1; ) 1 D. ( 1 − ;0;0) 
Câu 3: Trong không gian    
Oxyz , cho vectơ u = 3
− i + 7 j + k . Tọa độ của vectơ u là A. ( 3 − ;7;0) . B. ( 3 − ;7; ) 1 . C. (3;7; ) 1 . D. (3;7;0) .
Câu 4: Nguyên hàm của hàm số f (x) 2 = 3x +1 là 3 A. 3x x + C .
B. 3x + x + C .
C. 6x + C .
D. + x + C . 3 2 2 2 Câu 5: Cho f
∫ (x)dx = 3 và 3f
∫ (x)− g(x)dx =10 
. Khi đó g (x)dx ∫ bằng 1 1 1 A. 1 − . B. 17. C. 1. D. 4 − .
Câu 6: Mệnh đề nào sau đây là đúng ? 2 A. d = x xe x e + ∫ x x C . B. d = − + 2 ∫ x x x xe x xe e C . 2 C. d x = + + ∫ x x x xe x e xe C .
D. xe dx = e + e + ∫ x x x C . 2
Câu 7: Họ nguyên hàm của hàm số f (x) 1 = là: 5x + 4
A. 1 ln 5x + 4 + C .
B. ln 5x + 4 + C .
C. 1 ln 5x + 4 + C .
D. 1 ln(5x + 4) + C . ln 5 5 5
Câu 8: Giả sử f là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K . Khẳng
định nào sau đây sai? c b b b a
A. f (x)dx + f (x)dx = f (x)dx, c∈ ∫ ∫ ∫ (a;b) . B. f
∫ (x)dx = − f ∫ (x)dx. a c a a b b b a C. f
∫ (x)dx = f ∫ (t)dt . D. f ∫ (x)dx =1. a a a
Câu 9: Trong không gian Oxyz , mặt cầu (S) (x − )2 + ( y + )2 + (z − )2 : 2 5 9 = 4 có bán kính bằng A. 4 . B. 16. C. 8. D. 2 .
Câu 10: Tìm họ nguyên hàm của hàm số ( ) 3 e x f x = . Trang 1/4 - Mã đề 345 A. 1 1
f (x)dx = ln 3x + ∫ C . B. ( ) 3 d .e x f x x = ∫ . C. ( ) 3 d = e x f x x + ∫ C . D. ( ) 3 d = .e x f x x + ∫ C . 3 3
Câu 11: Nếu f
∫ (u)du = F (u)+C và u = u(x) có đạo hàm liên tục thì
A. f u
∫  (x)dx = F u   ( x) + C.  B. f
∫ (x)u′(x)dx = F u(x) +C. 
C. f u
∫  (x)u′
 ( x)dx = F u  ( x) + C.  D. f u
∫  (x)u′
 ( x)dx = F ( x) + C.
Câu 12: Cho 2 hàm số u u(x) và v v(x) có đạo hàm liên tục trên khoảng K . Khẳng định nào sau đây đúng?
A. u(x)v'(x)dx u(x)v(x) u(x)v(x)dx   .
B. u(x)v'(x)dx u(x)v'(x) u '(x)v(x)dx   .
C. u(x)v'(x)dx u(x)v(x) u '(x)v(x)dx   .
D. u(x)v'(x)dx u '(x)v(x) u '(x)v(x)dx   .
Câu 13: Khẳng định nào sau đây đúng? A. sin2 d
x x = 2cos 2x + C ∫ . B. 1 sin2 d
x x = − cos 2x + C ∫ . 2 C. 1 sin2 d
x x = cos 2x + C ∫ . D. sin2 d x x = 2 − cos 2x + C 2 ∫ .
Câu 14: Biết f
∫ (x)dx = F (x)+C .Trong các khẳng định sau, khẳng định nào đúng? b b A. f
∫ (x)dx = F (a)− F (b). B. f
∫ (x)dx = F (b)− F (a) . a a b b C. f
∫ (x)dx = F (b)+ F (a). D. f
∫ (x)dx = F (b).F (a). a a
Câu 15: Cho hai hàm số f (x) và g (x) liên tục trên K , a, b∈ K . Khẳng định nào sau đây là khẳng định sai? b b b b b b A. f
∫ (x)g(x)dx = f ∫ (x)d .x g ∫ (x)dx . B. f
∫ (x)− g(x)dx = f
∫ (x)dx− g ∫ (x)dx . a a a a a a b b b b b C. kf
∫ (x)dx = k f
∫ (x)dx (k ≠ 0). D. f
∫ (x)+ g(x)dx = f
∫ (x)dx+ g ∫ (x)dx. a a a a a
Câu 16: Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng ( ; a b) nếu
A. f ′(x) = F (x), x ∀ ∈(a;b) .
B. F′(x) = f (x), x ∀ ∈(a;b) .
C. f ′(x) = −F (x), x ∀ ∈(a;b) .
D. F′(x) = − f (x), x ∀ ∈(a;b) . b
Câu 17: Tích phân dx ∫ bằng. a A. a + b. B. a − b . C. b − a . D. a.b . 1 Câu 18: Tích phân 2019 I = x dx ∫ bằng 0 A. 1 0 . B. 1 . C. 1. D. . 2020 20193
Câu 19: Cho hàm số f (x) có đạo hàm trên  , f (− ) 1 = 2
− và f (3) = 2 . Tính I = f ' ∫ (x) . dx 1 − A. I = 4. − B. I = 0. C. I = 3. D. I = 4.
Câu 20: Trong không gian Oxyz , mặt cầu (S ) có tâm I (1; 3
− ;0) và bán kính bằng 2 . Phương trình của (S ) là Trang 2/4 - Mã đề 345 A. (x + )2 2 2
1 + (y − 3) + z = 4 . B. (x + )2 2 2
1 + (y − 3) + z = 2 . C. (x − )2 2 2
1 + (y + 3) + z = 4 . D. (x − )2 2 2
1 + (y + 3) + z = 2 . 1 5 5
Câu 21: Biết f
∫ (x)dx = 8 và f (x)dx = 3 − ∫
, khi đó f (x)dx ∫ bằng 0 1 0 A. 8 − . B. 11. C. 11 − . D. 5. 3
Câu 22: Biết F (x) là một nguyên hàm của hàm số f (x) = sin x + cos x thỏa mãn F (0) =1. Hàm số F (x) là
A. −cos x + sin x − 2 .
B. cos x −sin x +1.
C. −cos x + sin x + 2 .
D. −cos x +sin x +1. f ′( x)
Câu 23: Cho f (x) là hàm đa thức. Khi đó dx ∫ bằng: x
A. 1 f ( x)+C .
B. 2 f ( x)+C .
C. f ( x)+C . D. 2
− f ( x ) + C . 2
Câu 24: Họ nguyên hàm của hàm số f (x) = x+sin3x là 2 2 2 2
A. x + 3cos3x + C . B. x 1 + cos3x + C .
C. x −3cos3x + C . D. x 1 − cos3x + C . 2 2 3 2 2 3 2 5
Câu 25: Nếu f
∫ (x)dx = 2 thì 3f (x)dx ∫ bằng 5 2 A. 12 . B. 6 − . C. 3. D. 6.
Câu 26: Trong không gian Oxyz , cho hai điểm A( 2 − ;3;− ) 1 và B( 4
− ;1;9) . Trung điểm I của đoạn
thẳng AB có tọa độ là A. ( 3 − ;2;4). B. ( 2; − − 2;10) . C. ( 3; − 2;− 4) . D. ( 6; − 4;8) .
Câu 27: Họ nguyên hàm của hàm số ( ) ln x f x = là x A. 1 2
ln x + ln x + C . B. 2 ln x + C . C. 1 2 ln x + C .
D. ln(ln x) + C . 2 2 m Câu 28: Cho ∫( 2 3x − 2x + )
1 dx = 6. Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. ( 3 − ; ) 1 . B. (0;4) . C. ( 1; − 2) . D. ( ;0 −∞ ).
Câu 29: Cho F (x) là nguyên hàm của f (x) 1 =
thỏa mãn F (2) = 4. Giá trị F (− ) 1 bằng: x + 2 A. 3 . B. 1. C. 2 3 . D. 2 . 2 2
Câu 30: Cho I = f
∫ (x)dx=3. Khi đó J = 3f ∫  (x)−4dx  bằng: 1 − 1 − A. 2 . B. 5. C. 3 − . D. 1 − .
Câu 31: Trong không gian Oxyz , cho hai điểm A(2;−1;2) và B(0;1;0). Mặt cầu đường kính AB có phương trình là A. (x − )2 2
1 + y + ( z − )2 1 =12 . B. (x − )2 2
1 + y + (z − )2 1 = 3 .
C. (x + )2 + ( y − )2 + (z + )2 2 2 2 = 2 . D. (x − )2 2
1 + y + (z − )2 1 = 3. Trang 3/4 - Mã đề 345
Câu 32: Trong không gian với hệ trục Oxyz cho ba điểm A(2;1;3) , B(1;− 2;2), C (x; y;5) thẳng
hàng. Khi đó, x + y bằng A. 10. B. 11. C. 3. D. 12. 2
Câu 33: Tính tích phân 1 I = dx ∫ . 2x −1 1 A. ln 3 I = . B. ln 3 1 I − = . C. ln 3 I = . D. I = ln3+1. 2 2 3 2
Câu 34: Họ nguyên hàm của hàm số ( ) x f x = là 3 x +1 A. 2 + C. B. 1 + C. C. 2 3 x +1 + C. D. 1 3 x +1 + C. 3 3 x +1 3 3 x +1 3 3    
Câu 35: Trong không gian Oxyz , cho OM = 2i −3 j + k . Hình chiếu của điểm M trên mặt phẳng (Oxy) là A. M 2;0;0 . B. M 2;0;1 . C. M 2; 3 − ;0 . D. M 0;0;1 . 2 ( ) 3 ( ) 4 ( ) 1 ( )
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : Biết F x là một nguyên hàm của hàm số f x 2xsin x và thỏa mãn F 0 21.   Tính F     .  2
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;1;2), B(2;3;−3) . Viết
phương trình mặt cầu (S ) có tâm I thuộc trục Oy và đi qua hai điểm , A B .
Câu 3 (0,5 điểm): Biết F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên  và thỏa mãn 3 3 f
∫ (x)dx = F (3)−G(0)+ a (a > 0). Gọi S = F
∫ (x)−G(x) .
dx Tính giá trị của a khi S =15. 0 0
Câu 4 (0,5 điểm): Cho hàm số f có đạo hàm liên tục trên  và luôn nhận giá trị dương, đồng thời thỏa mãn ( ) ( ) 2 − ( ) 6 . ' = 2 x f x f x f x
e với mọi x . Biết f (0) =1. Hãy tính f ( ) 1 .
----------------------------HẾT--------------------------- Trang 4/4 - Mã đề 345
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút;
(Đề có 4 trang)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 456
Phần I: Trắc nghiệm (7 điểm) b
Câu 1: Tích phân dx ∫ bằng. a A. a + b. B. b − a . C. a.b . D. a − b . Câu 2: Nếu f
∫ (u)du = F (u)+C và u = u(x) có đạo hàm liên tục thì A. f
∫ (x)u′(x)dx = F u(x) +C. 
B. f u
∫  (x)dx = F u   ( x) + C. 
C. f u
∫  (x)u′
 ( x)dx = F u  ( x) + C.  D. f u
∫  (x)u′
 ( x)dx = F ( x) + C.
Câu 3: Trong không gian Oxyz , mặt cầu (S ) có tâm I (1; 3
− ;0) và bán kính bằng 2 . Phương trình của (S ) là A. (x − )2 2 2
1 + (y + 3) + z = 4 . B. (x − )2 2 2
1 + (y + 3) + z = 2 . C. (x + )2 2 2
1 + (y − 3) + z = 4 . D. (x + )2 2 2
1 + (y − 3) + z = 2 . 2 2 2 Câu 4: Cho f
∫ (x)dx = 3 và 3f
∫ (x)− g(x)dx =10 
. Khi đó g (x)dx ∫ bằng 1 1 1 A. 17. B. 1. C. 4 − . D. 1 − .
Câu 5: Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng ( ; a b) nếu
A. F′(x) = − f (x), x ∀ ∈(a;b) .
B. F′(x) = f (x), x ∀ ∈(a;b) .
C. f ′(x) = −F (x), x ∀ ∈(a;b) .
D. f ′(x) = F (x), x ∀ ∈(a;b) .
Câu 6: Trong không gian Oxyz , mặt cầu (S) (x − )2 + ( y + )2 + (z − )2 : 2 5 9 = 4 có bán kính bằng A. 4 . B. 16. C. 8. D. 2 .
Câu 7: Khẳng định nào sau đây đúng? A. 1 sin2 d
x x = − cos 2x + C ∫ . B. sin2 d
x x = 2cos 2x + C 2 ∫ . C. sin2 d x x = 2 − cos 2x + C ∫ . D. 1 sin2 d
x x = cos 2x + C ∫ . 2 3
Câu 8: Cho hàm số f (x) có đạo hàm trên  , f (− ) 1 = 2
− và f (3) = 2 . Tính I = f ' ∫ (x) . dx 1 − A. I = 4. − B. I = 3. C. I = 4. D. I = 0.
Câu 9: Họ nguyên hàm của hàm số f (x) 1 = là: 5x + 4
A. 1 ln 5x + 4 + C .
B. 1 ln(5x + 4) + C .
C. ln 5x + 4 + C .
D. 1 ln 5x + 4 + C . ln 5 5 5 1 Câu 10: Tích phân 2019 I = x dx ∫ bằng 0 Trang 1/4 - Mã đề 456 A. 1 0 . B. 1. C. . D. 1 . 2019 2020
Câu 11: Cho hai hàm số f (x) và g (x) liên tục trên K , a, b∈ K . Khẳng định nào sau đây là khẳng định sai? b b b b b b A. f
∫ (x)g(x)dx = f ∫ (x)d .x g ∫ (x)dx . B. f
∫ (x)+ g(x)dx = f
∫ (x)dx+ g ∫ (x)dx. a a a a a a b b b b b C. kf
∫ (x)dx = k f
∫ (x)dx (k ≠ 0). D. f
∫ (x)− g(x)dx = f
∫ (x)dx− g ∫ (x)dx . a a a a a
Câu 12: Giả sử f là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K .
Khẳng định nào sau đây sai? a b a A. f ∫ (x)dx =1. B. f
∫ (x)dx = − f ∫ (x)dx. a a b c b b b b
C. f (x)dx + f (x)dx = f (x)dx, c∈ ∫ ∫ ∫ (a;b) . D. f
∫ (x)dx = f ∫ (t)dt . a c a a a
Câu 13: Cho 2 hàm số u u(x) và v v(x) có đạo hàm liên tục trên khoảng K . Khẳng định nào sau đây đúng?
A. u(x)v'(x)dx u(x)v(x) u '(x)v(x)dx   .
B. u(x)v'(x)dx u(x)v(x) u(x)v(x)dx   .
C. u(x)v'(x)dx u '(x)v(x) u '(x)v(x)dx   .
D. u(x)v'(x)dx u(x)v'(x) u '(x)v(x)dx   .
Câu 14: Nguyên hàm của hàm số f (x) 2 = 3x +1 là 3
A. 6x + C .
B. x + x + C .
C. 3x + x + C .
D. 3x + C . 3
Câu 15: Trong không gian Oxyz , cho mặt cầu (S) (x − )2 2 2 :
1 + y + z = 4 . Tâm của (S ) là điểm nào sau đây? A. (1;0;0) B. ( 1 − ;0;0) C. ( 1; − 1; ) 1 D. (1;1; ) 1
Câu 16: Mệnh đề nào sau đây là đúng ? 2 A. d x = + + ∫ x x x xe x e xe C .
B. xe dx = e + e + ∫ x x x C . 2 2 C. d = x xe x e + ∫ x x C . D. d = − + 2 ∫ x x x xe x xe e C .
Câu 17: Biết f
∫ (x)dx = F (x)+C .Trong các khẳng định sau, khẳng định nào đúng? b b A. f
∫ (x)dx = F (b)− F (a) . B. f
∫ (x)dx = F (b)+ F (a). a a b b C. f
∫ (x)dx = F (b).F (a). D. f
∫ (x)dx = F (a)− F (b). a a
Câu 18: Trên khoảng (0;+∞), hàm số F (x) = ln x là một nguyên hàm của hàm số?
A. f (x) = xln x − x .
B. f (x) = xln x − x + C,C ∈ .
C. f (x) 1
= + C,C ∈  . D. ( ) 1 f x = . x x
Câu 19: Tìm họ nguyên hàm của hàm số ( ) 3 e x f x = . A. ( ) 3 d 1 1 = e x f x x + ∫ C . B. ( ) 3 d .e x f x x = ∫ .
C. f (x)dx = ln 3x + ∫ C . D. ( ) 3 d = .e x f x x + ∫ C . 3 3 
Câu 20: Trong không gian    
Oxyz , cho vectơ u = 3
− i + 7 j + k . Tọa độ của vectơ u là Trang 2/4 - Mã đề 456 A. (3;7; ) 1 . B. ( 3 − ;7; ) 1 . C. ( 3 − ;7;0) . D. (3;7;0) .
Câu 21: Trong không gian Oxyz , cho hai điểm A(2;−1;2) và B(0;1;0). Mặt cầu đường kính AB có phương trình là A. (x − )2 2
1 + y + ( z − )2 1 =12 .
B. (x + )2 + ( y − )2 + (z + )2 2 2 2 = 2 . C. (x − )2 2
1 + y + (z − )2 1 = 3 . D. (x − )2 2
1 + y + (z − )2 1 = 3.
Câu 22: Biết F (x) là một nguyên hàm của hàm số f (x) = sin x + cos x thỏa mãn F (0) =1. Hàm số F (x) là
A. −cos x + sin x + 2 .
B. −cos x + sin x − 2 .
C. −cos x +sin x +1.
D. cos x −sin x +1.
Câu 23: Họ nguyên hàm của hàm số f (x) = x+sin3x là 2 2 2 2
A. x −3cos3x + C . B. x 1 − cos3x + C . C. x 1 + cos3x + C .
D. x + 3cos3x + C . 2 2 3 2 3 2 2 2
Câu 24: Cho I = f
∫ (x)dx=3. Khi đó J = 3f ∫  (x)−4dx  bằng: 1 − 1 − A. 3 − . B. 1 − . C. 5. D. 2 . 2 5
Câu 25: Nếu f
∫ (x)dx = 2 thì 3f (x)dx ∫ bằng 5 2 A. 3. B. 6. C. 12 . D. 6 − .
Câu 26: Họ nguyên hàm của hàm số ( ) ln x f x = là x
A. ln(ln x) + C . B. 1 2 ln x + C . C. 1 2
ln x + ln x + C . D. 2 ln x + C . 2 2 1 5 5
Câu 27: Biết f
∫ (x)dx = 8 và f (x)dx = 3 − ∫
, khi đó f (x)dx ∫ bằng 0 1 0 A. 11. B. 5. C. 11 − . D. 8 − . 3
Câu 28: Cho F (x) là nguyên hàm của f (x) 1 =
thỏa mãn F (2) = 4. Giá trị F (− ) 1 bằng: x + 2 A. 2 . B. 3 . C. 1. D. 2 3 .    
Câu 29: Trong không gian Oxyz , cho OM = 2i −3 j + k . Hình chiếu của điểm M trên mặt phẳng (Oxy) là A. M 2; 3 − ;0 . B. M 2;0;0 . C. M 2;0;1 . D. M 0;0;1 . 2 ( ) 4 ( ) 1 ( ) 3 ( ) m Câu 30: Cho ∫( 2 3x − 2x + )
1 dx = 6. Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. ( ;0 −∞ ). B. ( 3 − ; ) 1 . C. (0;4) . D. ( 1; − 2) . f ′( x)
Câu 31: Cho f (x) là hàm đa thức. Khi đó dx ∫ bằng: x A. 1
f ( x ) + C . B. 2
− f ( x ) + C .
C. 2 f ( x)+C .
D. f ( x)+C . 2 2
Câu 32: Họ nguyên hàm của hàm số ( ) x f x = là 3 x +1 Trang 3/4 - Mã đề 456 A. 1 3 x +1 + C. B. 2 3 x +1 + C. C. 2 + C. D. 1 + C. 3 3 3 3 x +1 3 3 x +1
Câu 33: Trong không gian với hệ trục Oxyz cho ba điểm A(2;1;3) , B(1;− 2;2), C (x; y;5) thẳng
hàng. Khi đó, x + y bằng A. 3. B. 10. C. 12. D. 11.
Câu 34: Trong không gian Oxyz , cho hai điểm A( 2 − ;3;− ) 1 và B( 4
− ;1;9) . Trung điểm I của đoạn
thẳng AB có tọa độ là A. ( 3 − ;2;4). B. ( 2; − − 2;10) . C. ( 3; − 2;− 4) . D. ( 6; − 4;8) . 2
Câu 35: Tính tích phân 1 I = dx ∫ . 2x −1 1 A. ln 3 1 I − = . B. I = ln3+1. C. ln 3 I = . D. ln 3 I = . 2 3 2
Phần II: Tự luận (3 điểm)
Câu 1 (1 điểm) : : Biết F x là một nguyên hàm của hàm số f x 2x cos x và thỏa mãn F 0 20 .   Tính F     .  2
Câu 2 (1 điểm) : Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;1;2), B(2;3;−3) . Viết
phương trình mặt cầu (S ) có tâm I thuộc trục Ox và đi qua hai điểm , A B
Câu 3 (0,5 điểm): Biết F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên  và thỏa mãn 5 5 f
∫ (x)dx = F (5)−G(0)+ a (a > 0). Gọi S = F
∫ (x)−G(x) .
dx Tính giá trị của a khi S = 20. 0 0
Câu 4 (0,5 điểm): Cho hàm số f có đạo hàm liên tục trên  và luôn nhận giá trị dương, đồng thời thỏa mãn ( ) ( ) 2 − ( ) 6 . ' = 2 x f x f x f x
e với mọi x . Biết f (0) =1. Hãy tính f ( ) 1 .
-------------------------------HẾT------------------------------- Trang 4/4 - Mã đề 456
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm: 123 234 345 456 1 B A A B 2 C D A C 3 D A B A 4 D D B D 5 C C A B 6 D C B D 7 B D C A 8 C B D C 9 A D D D 10 C A D D 11 A D C A 12 B A C A 13 C C B A 14 C C B C 15 A B A A 16 D D B D 17 C B C A 18 C D B D 19 A A D D 20 A C C B 21 D B D D 22 C B C A 23 A D B B 24 C B D A 25 C B B D 26 C A A B 27 D D C B 28 C C B A 29 B B D A 30 A C C C 31 B C D C 32 B B B B 33 A B A D 34 B B C A 35 C D C D 1
Đáp án mã đề 123, 345 Câu Nội dung Điểm Câu 1 2 F (x) 2x sin x dx x cos x C 0,5 Giả thiết 2 F 0 21 0 cos 0 C 21 C 20 2 Suy ra 2 F x x cos x 20 F 20. 0,5 2 4 Câu 2
Ta có I Oy I (0;a;0) . Khi đó IA(1;1− a; 2) , IB (2;3 − a; 3 − ) . 0,25
Do (S ) đi qua hai điểm , A B nên: 0,25
IA = IB  ( − a)2 + = ( − a)2 1 5 3
+13  4a = 16  a = 4  (
S ) có tâm I (0; 4;0) , bán kính R = IA = 14 . 0,25
Vậy (S ) x + ( y − )2 2 2 : 4 + z =14. 0,25 Câu 3
Giả thiết F ( x),G ( x) đều là nguyên hàm của f ( x) nên ta có:
F ( x) = G ( x) + C F (0) = G (0) + C (1). Ta có 3 f
 (x)dx = F (x)3 = F (3)− F (0) = F (3)−(G(0)+C) = F (3)−G(0)−C . 0 0,25 0 3
Mà theo giả thiết f
 (x)dx = F (3)−G(0)+a nên C = −a. 0
Suy ra F ( x) = G ( x) − a F ( x) − G ( x) = −a . 3 3 3 Ta có S = F
 (x)−G(x) dx = −a dx = ax = 3a  . 0 0,25 0 0
Mà S = 15 nên ta có a = 5 . Câu 4 Với mọi x  , ta có
f ( x). f '( x) 2 − f (x) 6 = 2 x e
2 f ( x). f '( x) 2x 2 x 2 .e
− 2e . f (x) 4  = 4 x e 4 x e 0,25 f (x) ' 2 2  f x 4 x ( ) 4 x 4    = 4e  = 4 x e dx = e + C.  2 x 2 xee   2 f (0) Suy ra = 1+ C C = 0. 1 Do đó 2 ( ) 6 x =  ( ) 3x f x e
f x = e , x  . Vậy f ( ) 3 1 = e . 0,25 2
Đáp án các mã 234, 456 Câu Nội dung Điểm Câu 1 2 F (x) 2x cos x dx x sin x C 0,5 Giả thiết 2 F 0 20 0 sin 0 C 20 C 20 2 Suy ra 2 F x x sin x 20 F 21. 0,5 . 2 4 Câu 2
Ta có I Ox I (a;0;0) . Khi đó IA(1− a ;1; 2) , IB (2 − ; a 3; 3 − ) . 0,25
Do (S ) đi qua hai điểm , A B nên: 0,25
IA = IB  ( − a)2 + = ( − a)2 1 5 2
+18  2a = 16  a = 8  (
S ) có tâm I (8;0;0) , bán kính R = IA = 54 . 0,25
Vậy (S ) ( x − )2 2 2 : 8 + y + z = 54. 0,25 Câu 3
Giả thiết F ( x),G ( x) đều là nguyên hàm của f ( x) nên ta có:
F ( x) = G ( x) + C F (0) = G (0) + C (1). Ta có 5 f
 (x)dx = F (x)5 = F (5)− F (0) = F (5)−(G(0)+C) = F (5)−G(0)−C . 0 0,25 0 5
Mà theo giả thiết f
 (x)dx = F (5)−G(0)+a nên C = −a. 0
Suy ra F ( x) = G ( x) − a F ( x) − G ( x) = −a . 5 5 5 Ta có S = F
 (x)−G(x) dx = −a dx = ax = 5a  . 0 0 0
Mà S = 20 nên ta có a = 4. 0,25 Câu 4 Với mọi x  , ta có
f ( x). f '( x) 2 − f (x) 6 = 2 x e
2 f ( x). f '( x) 2x 2 x 2 .e
− 2e . f (x) 4  = 4 x e 4 x e f (x) ' 2 2  f x 4 x ( ) 4 x 4    = 4e  = 4 x e dx = e + C.  2 x 2 xee   0,25 2 f (0) Suy ra = 1+ C C = 0. 1 Do đó 2 ( ) 6 x =  ( ) 3x f x e
f x = e , x  . Vậy f ( ) 3 1 = e . 0,25 3 4
Document Outline

  • de 123
  • de 234
  • de 345
  • de 456
  • ĐÁP ÁN ĐỀ GIỮA KỲ 2-TOÁN 12