Đề giữa kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Nguyễn Tất Thành – TP HCM

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kỳ 2 môn Toán 12 năm học 2023 – 2024 trường THPT Nguyễn Tất Thành, thành phố Hồ Chí Minh; đề thi có đáp án trắc nghiệm mã đề 431 – 542 – 653 – 764. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

46 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

9 trang 4 tháng trước

Tác giả:

Profile M. Hậu
Trang 1/2 Mã đề 764
KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024
Môn: Toán - Lớp 12
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:...................
Câu 1.
cos .
x dx
A.
sin .x C
B.
sin . .x x C
C.
sin .x C
D.
sin . .x x C
Câu 2. Trong không gian Oxyz, mặt cầu
2 2 2
: 2 4 8 5 0
S x y z x y z
có tâm là
A.
2;4; 8 .
P
B.
1;2; 4 .
P
C.
1; 2;4 .
P
D.
4; 8;16 .
P
Câu 3. Trong không gian Oxyz, một vectơ pháp tuyến của
là
A.
1; 3;2 .
n
B.
1;3;2 .
n
C.
2; 6;4 .
n
D.
2;6;4 .
n
Câu 4. Trong không gian Oxyz, cho mặt cầu
2 2 2
: 2 2 2 0
S x y z ax by cz d
Ta có
A.
2 2 2
.a b c d
B.
2 2 2
.a b c d
C.
2 2 2
.a b c d
D.
2 2 2
.a b c d
Câu 5. Mệnh đề nào dưới đây đúng?
A.
1
.x dx x C
B.
.
x x
a dx a C
C.
' .f x dx f x C
D.
.dx C
Câu 6. Trong không gian Oxyz, cho hai điểm
3; 1;2 , 1;3; 4 .
M N
Tọa độ trung điểm của đoạn thẳng MN là
A.
2;1; 1 .
P
B.
4;2; 2 .
P
C.
2;4; 6 .
P
D.
1;2; 3 .
P
Câu 7. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O,
3; 1;2 , 1;3; 4
M N
là
A.
7 5 0.x y z
B.
2 3 0.x y z
C.
3 2 0.x y z
D.
3 4 0.x y z
Câu 8. Trong không gian Oxyz, cho ba điểm
3; 1;2 , 1;3; 4 ,
M N
5;1; 2
P
và điểm
; ;I a b c
thỏa mãn
2 3 0IM IN IP
. Tính
2 6 .a b c
A.
24.
B.
16.
C.
12.
D.
18.
Câu 9. Trong không gian Oxyz, cho
3; 1;2 , 1;3; 4 , 2;0;4 .
a b c
Tọa độ của
2 3u a b c
là
A.
11;7;4 .
B.
7;7; 12 .
C.
2;4; 6 .
D.
1;2; 3 .
Câu 10.
sin
x xdx
A.
sin cos .x x x C
B.
sin cos .x x x C
C.
cos .x x C
D.
cos sin .x x x C
Câu 11. Trong không gian Oxyz, cho bốn điểm
3; 1;2 , 1;3; 4 ,
M N
0;4; 3 , 2;0;3 .
P Q
Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A.
15.
B.
12.
C.
10.
D.
13.
Câu 12. Trong không gian Oxyz,
: 3 2 1 0mp x y z
chứa điểm nào dưới đây?
A.
2;1; 1 .
P
B.
4;1;0 .
Q
C.
2;4; 6 .
R
D.
0;2; 3 .
S
Câu 13. Trong không gian Oxyz, mặt cầu có tâm
3; 1;2
M
bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A.
3.x
B.
3.z
C.
3.y
D.
3.x y z
Câu 14. Biết
2
ln 1 .f x dx x x C
Tính
2 3 .
f
A.
7.
B.
5.
C.
3.
D.
1.
Câu 15. Cho F(x) là một nguyên hàm của
2 1f x x
trên
và
1 3
F
. Tính
2 3 .
F F
A.
8.
B.
14.
C.
18.
D.
20.
Câu 16. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm
1;0;0 , 0;1;0 , 0;0;1
I J K
là
A.
0.
B.
1.
C.
2.
D. Vô số
.
Câu 17. Trên
2 3
, 2
f x dx x C g x dx x C
. Tính
. .f x g x dx
A.
4
3 .x C
B.
5
2 .x C
C.
6
6 .x C
D.
8
9 .x C
Mã đề 764
Trang 2/2 Mã đề 764
Câu 18. Cho F(x) là một nguyên hàm của
, 3.
b
a
f x f x dx
Ta có
A.
3.
F a F b
B.
' ' 3.
f b f a
C.
3.
F b F a
D.
3.
f b f a
Câu 19. Biết
4.
b
a
xdx
Tính
2 2
.a b
A.
8.
B.
8.
C.
2.
D.
16.
Câu 20. Biết
2, 3.
b b
a a
f x dx g x dx
Tính
2 3 .
b
a
f x g x dx
A.
13.
B.
5.
C.
5.
D.
15.
Câu 21.
1
0
x
e dx
A.
.e
B.
1.e
C.
1.
D.
1.e
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên
, 1, 3.
f a f b
Tính
1 . ' .
b
a
f x f x dx
A.
8.
B.
6.
C.
10.
D.
12.
Câu 23. Biết
3
2
2
0,75
3
3 4
16
a b
x dx
. Tính
2 .a b
A.
5.
B.
11.
C.
7.
D.
9.
Câu 24.
1
0
ln 1 ln 2 .x dx a b
Tính
2
.ab
A.
4.
B.
2.
C.
2.
D.
9.
Câu 25. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm
3; 1;2
M
và giao tuyến của hai mặt
phẳng
: 3 0, : 2 4 0
P x z Q x y z
là
A.
2 4 0.x y z
B.
2 3 0.x y z
C.
2 2 0.x y z
D.
2 1 0.x y z
Câu 26. Cho F(x) là một nguyên hàm của
2
2
3
x
f x
x
trên
và
0 2 3.
F
Phương trình tiếp tuyến của
đồ thị hàm số
y F x
tại điểm
1x
là
A.
2 1.y x
B.
3 5.
y x
C.
3 4.y x
D.
3.y x
Câu 27. Cho hàm số f(x) có đạo hàm liên tục trên
, 0 1, 1 1.
f f
Tính
1
0
' . .
x
f x f x e dx
A.
1.e
B.
1.e
C.
0.
D.
2.
Câu 28. Cho hàm số
f x
có đạo hàm và
0
f x
trên
,
' 2 1 , 0 1.
f x x f x f
Tính
2 .
f
A.
1.
B.
.e
C.
2
.e
D.
4
.e
Câu 29.
4
3
8
ln5 ln 2.
1 2
x
dx a b c
x x
Tính
.a b c
A.
2.
B.
4.
C.
5.
D.
11.
Câu 30. Biết
1
ln 2 .
2
x
dx mx n x C
x
Tính
.m n
A.
0.
B.
1.
C.
2.
D.
2.
------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm.
KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024
Môn: Toán - Lớp 12
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:...................
Câu 1. Trong không gian Oxyz, một vectơ pháp tuyến của
là
A.
1; 3;2 .
n
B.
1;3;2 .
n
C.
2; 6;4 .
n
D.
2;6;4 .
n
Câu 2. Trong không gian Oxyz, cho mặt cầu
2 2 2
: 2 2 2 0
S x y z ax by cz d
Ta có
A.
2 2 2
.a b c d
B.
2 2 2
.a b c d
C.
2 2 2
.a b c d
D.
2 2 2
.a b c d
Câu 3. Trong không gian Oxyz, mặt cầu
2 2 2
: 2 4 8 5 0
S x y z x y z
có tâm là
A.
2;4; 8 .
P
B.
1;2; 4 .
P
C.
1; 2;4 .
P
D.
4; 8;16 .
P
Câu 4. Mệnh đề nào dưới đây đúng?
A.
1
.x dx x C
B.
.
x x
a dx a C
C.
' .f x dx f x C
D.
.dx C
Câu 5. Trong không gian Oxyz, cho hai điểm
3; 1;2 , 1;3; 4 .
M N
Tọa độ trung điểm của đoạn thẳng MN là
A.
2;1; 1 .
P
B.
4;2; 2 .
P
C.
2;4; 6 .
P
D.
1;2; 3 .
P
Câu 6. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O,
3; 1;2 , 1;3; 4
M N
là
A.
7 5 0.x y z
B.
2 3 0.x y z
C.
3 2 0.x y z
D.
3 4 0.x y z
Câu 7.
cos .
x dx
A.
sin .x C
B.
sin . .x x C
C.
sin .x C
D.
sin . .x x C
Câu 8. Trong không gian Oxyz, cho ba điểm
3; 1;2 , 1;3; 4 ,
M N
5;1; 2
P
và điểm
; ;I a b c
thỏa mãn
2 3 0IM IN IP
. Tính
2 6 .a b c
A.
24.
B.
16.
C.
12.
D.
18.
Câu 9. Trong không gian Oxyz,
: 3 2 1 0mp x y z
chứa điểm nào dưới đây?
A.
2;1; 1 .
P
B.
4;1;0 .
Q
C.
2;4; 6 .
R
D.
0;2; 3 .
S
Câu 10. Trong không gian Oxyz, cho
3; 1;2 , 1;3; 4 , 2;0;4 .
a b c
Tọa độ của
2 3u a b c
là
A.
11;7;4 .
B.
7;7; 12 .
C.
2;4; 6 .
D.
1;2; 3 .
Câu 11.
sin
x xdx
A.
sin cos .x x x C
B.
sin cos .x x x C
C.
cos .x x C
D.
cos sin .x x x C
Câu 12. Trong không gian Oxyz, cho bốn điểm
3; 1;2 , 1;3; 4 ,
M N
0;4; 3 , 2;0;3 .
P Q
Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A.
15.
B.
12.
C.
10.
D.
13.
Câu 13. Biết
ln 1 .f x dx x x C
Tính
2 3 .
f
A.
7.
B.
5.
C.
3.
D.
1.
Câu 14. Cho F(x) là một nguyên hàm của
2 1f x x
trên
và
1 3
F
. Tính
2 3 .
F F
A.
8.
B.
14.
C.
18.
D.
20.
Câu 15. Trên
2 3
, 2
f x dx x C g x dx x C
. Tính
. .f x g x dx
A.
4
3 .x C
B.
5
2 .x C
C.
6
6 .x C
D.
8
9 .x C
Câu 16. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm
1;0;0 , 0;1;0 , 0;0;1
I J K
là
A.
0.
B.
1.
C.
2.
D. Vô số
.
Câu 17. Trong không gian Oxyz, mặt cầu có tâm
3; 1;2
M
bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A.
3.x
B.
3.z
C.
3.y
D.
3.x y z
Mã đề 653
Trang
1
/2
Mã
đề
653
Câu 18. Biết
4.
b
a
xdx
Tính
2 2
.a b
A.
8.
B.
8.
C.
2.
D.
16.
Câu 19. Biết
2, 3.
bb
a a
f x dx g x dx
Tính
2 3 .
b
a
f x g x dx
A.
13.
B.
5.
C.
5.
D.
15.
Câu 20.
1
0
x
e dx
A.
.e
B.
1.e
C.
1.
D.
1.e
Câu 21. Cho F(x) là một nguyên hàm của
, 3.
b
a
f x f x dx
Ta có
A.
3.
F a F b
B.
' ' 3.
f b f a
C.
3.
F b F a
D.
3.
f b f a
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên
, 1, 3.
f a f b
Tính
1 . ' .
b
a
f x f x dx
A.
8.
B.
6.
C.
10.
D.
12.
Câu 23. Biết
3
2
2
0,75
3
3 4
16
a b
x dx
. Tính
2 .a b
A.
5.
B.
11.
C.
7.
D.
9.
Câu 24.
1
0
ln 1 ln 2 .x dx a b
Tính
2
.ab
A.
4.
B.
2.
C.
2.
D.
9.
Câu 25. Biết
1
.ln
2
x
Cdx mx n
x
Tính
.m n
A.
0.
B.
1.
C.
2.
D.
2.
Câu 26. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm
3; 1;2
M
và giao tuyến của hai mặt
phẳng
: 3 0, : 2 4 0
P x z Q x y z
là
A.
2 4 0.x y z
B.
2 3 0.x y z
C.
2 2 0.x y z
D.
2 1 0.x y z
Câu 27. Cho F(x) là một nguyên hàm của
2
2
3
x
f x
x
trên
và
0 2 3.
F
Phương trình tiếp tuyến của
đồ thị hàm số
y F x
tại điểm
1x
là
A.
2 1.y x
B.
3 5.
y x
C.
3 4.y x
D.
3.y x
Câu 28.
4
3
8
ln5 ln 2.
1 2
x
dx a b c
x x
Tính
.a b c
A.
2.
B.
4.
C.
5.
D.
11.
Câu 29. Cho hàm số f(x) có đạo hàm liên tục trên
, 0 1, 1 1.
f f
Tính
1
0
' . .
x
f x f x e dx
A.
1.e
B.
1.e
C.
0.
D.
2.
Câu 30. Cho hàm số
f x
có đạo hàm và
0
f x
trên
,
' 2 1 , 0 1.
f x x f x f
Tính
2 .
f
A.
1.
B.
.e
C.
2
.e
D.
4
.e
------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm.
Trang
2
/2
Mã
đề
653
Trang 5/2 Mã đề 764
KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024
Môn: Toán - Lớp 12
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:...................
Câu 1. Trong không gian Oxyz, cho mặt cầu
2 2 2
: 2 2 2 0
S x y z ax by cz d
Ta có
A.
2 2 2
.a b c d
B.
2 2 2
.a b c d
C.
2 2 2
.a b c d
D.
2 2 2
.a b c d
Câu 2. Mệnh đề nào dưới đây đúng?
A.
1
.x dx x C
B.
.
x x
a dx a C
C.
' .f x dx f x C
D.
.dx C
Câu 3. Trong không gian Oxyz, cho hai điểm
3; 1;2 , 1;3; 4 .
M N
Tọa độ trung điểm của đoạn thẳng MN là
A.
2;1; 1 .
P
B.
4;2; 2 .
P
C.
2;4; 6 .
P
D.
1;2; 3 .
P
Câu 4. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O,
3; 1;2 , 1;3; 4
M N
là
A.
7 5 0.x y z
B.
2 3 0.x y z
C.
3 2 0.x y z
D.
3 4 0.x y z
Câu 5.
cos .
x dx
A.
sin .x C
B.
sin . .x x C
C.
sin .x C
D.
sin . .x x C
Câu 6. Trong không gian Oxyz, cho ba điểm
3; 1;2 , 1;3; 4 ,
M N
5;1; 2
P
và điểm
; ;I a b c
thỏa mãn
2 3 0IM IN IP
. Tính
2 6 .a b c
A.
24.
B.
16.
C.
12.
D.
18.
Câu 7. Trong không gian Oxyz, một vectơ pháp tuyến của
là
A.
1; 3;2 .
n
B.
1;3;2 .
n
C.
2; 6;4 .
n
D.
2;6;4 .
n
Câu 8. Trong không gian Oxyz,
: 3 2 1 0mp x y z
chứa điểm nào dưới đây?
A.
2;1; 1 .
P
B.
4;1;0 .
Q
C.
2;4; 6 .
R
D.
0;2; 3 .
S
Câu 9. Trong không gian Oxyz, mặt cầu
2 2 2
: 2 4 8 5 0
S x y z x y z
có tâm là
A.
2;4; 8 .
P
B.
1;2; 4 .
P
C.
1; 2;4 .
P
D.
4; 8;16 .
P
Câu 10. Trong không gian Oxyz, cho
3; 1;2 , 1;3; 4 , 2;0;4 .
a b c
Tọa độ của
2 3u a b c
là
A.
11;7;4 .
B.
7;7; 12 .
C.
2;4; 6 .
D.
1;2; 3 .
Câu 11.
sin
x xdx
A.
sin cos .x x x C
B.
sin cos .x x x C
C.
cos .x x C
D.
cos sin .x x x C
Câu 12. Trong không gian Oxyz, mặt cầu có tâm
3; 1;2
M
bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A.
3.x
B.
3.z
C.
3.y
D.
3.x y z
Câu 13. Cho F(x) là một nguyên hàm của
2 1f x x
trên
và
1 3
F
. Tính
2 3 .
F F
A.
8.
B.
14.
C.
18.
D.
20.
Câu 14. Trên
2 3
, 2
f x dx x C g x dx x C
. Tính
. .f x g x dx
A.
4
3 .x C
B.
5
2 .x C
C.
6
6 .x C
D.
8
9 .x C
Câu 15. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm
1;0;0 , 0;1;0 , 0;0;1
I J K
là
A.
0.
B.
1.
C.
2.
D. Vô số
.
Câu 16. Trong không gian Oxyz, cho bốn điểm
3; 1;2 , 1;3; 4 ,
M N
0;4; 3 , 2;0;3 .
P Q
Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A.
15.
B.
12.
C.
10.
D.
13.
Câu 17. Biết
2
ln 1 .f x dx x x C
Tính
2 3 .
f
A.
7.
B.
5.
C.
3.
D.
1.
Mã đề 542
Câu 18.
1
0
x
e dx
A.
.e
B.
1.e
C.
1.
D.
1.e
Câu 19. Biết
4.
b
a
xdx
Tính
2 2
.a b
A.
8.
B.
8.
C.
2.
D.
16.
Câu 20. Biết
2, 3.
bb
a a
f x dx g x dx
Tính
2 3 .
b
a
f x g x dx
A.
13.
B.
5.
C.
5.
D.
15.
Câu 21. Cho F(x) là một nguyên hàm của
, 3.
b
a
f x f x dx
Ta có
A.
3.
F a F b
B.
' ' 3.
f b f a
C.
3.
F b F a
D.
3.
f b f a
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên
, 1, 3.
f a f b
Tính
1 . ' .
b
a
f x f x dx
A.
8.
B.
6.
C.
10.
D.
12.
Câu 23.
1
0
ln 1 ln 2 .x dx a b
Tính
2
.ab
A.
4.
B.
2.
C.
2.
D.
9.
Câu 24. Biết
1
.ln
2
x
Cdx mx n
x
Tính
.m n
A.
0.
B.
1.
C.
2.
D.
2.
Câu 25. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm
3; 1;2
M
và giao tuyến của hai mặt
phẳng
: 3 0, : 2 4 0
P x z Q x y z
là
A.
2 4 0.x y z
B.
2 3 0.x y z
C.
2 2 0.x y z
D.
2 1 0.x y z
Câu 26. Biết
3
2
2
0,75
3
3 4
16
a b
x dx
. Tính
2 .a b
A.
5.
B.
11.
C.
7.
D.
9.
Câu 27.
4
3
8
ln5 ln 2.
1 2
x
dx a b c
x x
Tính
.a b c
A.
2.
B.
4.
C.
5.
D.
11.
Câu 28. Cho hàm số
f x
có đạo hàm và
0
f x
trên
,
' 2 1 , 0 1.
f x x f x f
Tính
2 .
f
A.
1.
B.
.e
C.
2
.e
D.
4
.e
Câu 29. Cho hàm số f(x) có đạo hàm liên tục trên
, 0 1, 1 1.
f f
Tính
1
0
' . .
x
f x f x e dx
A.
1.e
B.
1.e
C.
0.
D.
2.
Câu 30. Cho F(x) là một nguyên hàm của
2
2
3
x
f x
x
trên
và
0 2 3.
F
Phương trình tiếp tuyến của
đồ thị hàm số
y F x
tại điểm
1x
là
A.
2 1.y x
B.
3 5.
y x
C.
3 4.y x
D.
3.y x
------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm.
Trang
2
/2
Mã
đề
542
KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024
Môn: Toán - Lớp 12
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:...................
Câu 1. Mệnh đề nào dưới đây đúng?
A.
1
.x dx x C
B.
.
x x
a dx a C
C.
' .f x dx f x C
D.
.dx C
Câu 2. Trong không gian Oxyz, cho hai điểm
3; 1;2 , 1;3; 4 .
M N
Tọa độ trung điểm của đoạn thẳng MN là
A.
2;1; 1 .
P
B.
4;2; 2 .
P
C.
2;4; 6 .
P
D.
1;2; 3 .
P
Câu 3. Trong không gian Oxyz, cho
3; 1;2 , 1;3; 4 , 2;0;4 .
a b c
Tọa độ của
2 3u a b c
là
A.
11;7;4 .
B.
7;7; 12 .
C.
2;4; 6 .
D.
1;2; 3 .
Câu 4.
cos .
x dx
A.
sin .x C
B.
sin . .x x C
C.
sin .x C
D.
sin . .x x C
Câu 5. Trong không gian Oxyz, cho ba điểm
3; 1;2 , 1;3; 4 ,
M N
5;1; 2
P
và điểm
; ;I a b c
thỏa mãn
2 3 0IM IN IP
. Tính
2 6 .a b c
A.
24.
B.
16.
C.
12.
D.
18.
Câu 6. Trong không gian Oxyz, một vectơ pháp tuyến của
là
A.
1; 3;2 .
n
B.
1;3;2 .
n
C.
2; 6;4 .
n
D.
2;6;4 .
n
Câu 7. Trong không gian Oxyz,
: 3 2 1 0mp x y z
chứa điểm nào dưới đây?
A.
2;1; 1 .
P
B.
4;1;0 .
Q
C.
2;4; 6 .
R
D.
0;2; 3 .
S
Câu 8. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O,
3; 1;2 , 1;3; 4
M N
là
A.
7 5 0.x y z
B.
2 3 0.x y z
C.
3 2 0.x y z
D.
3 4 0.x y z
Câu 9. Trong không gian Oxyz, mặt cầu
2 2 2
: 2 4 8 5 0
S x y z x y z
có tâm là
A.
2;4; 8 .
P
B.
1;2; 4 .
P
C.
1; 2;4 .
P
D.
4; 8;16 .
P
Câu 10. Trong không gian Oxyz, cho mặt cầu
2 2 2
: 2 2 2 0
S x y z ax by cz d
Ta có
A.
2 2 2
.a b c d
B.
2 2 2
.a b c d
C.
2 2 2
.a b c d
D.
2 2 2
.a b c d
Câu 11. Trong không gian Oxyz, mặt cầu có tâm
3; 1;2
M
bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A.
3.x
B.
3.z
C.
3.y
D.
3.x y z
Câu 12.
sin
x xdx
A.
sin cos .x x x C
B.
sin cos .x x x C
C.
cos .x x C
D.
cos sin .x x x C
Câu 13. Cho F(x) là một nguyên hàm của
2 1f x x
trên
và
1 3
F
. Tính
2 3 .
F F
A.
8.
B.
14.
C.
18.
D.
20.
Câu 14. Trên
2 3
, 2
f x dx x C g x dx x C
. Tính
. .f x g x dx
A.
4
3 .x C
B.
5
2 .x C
C.
6
6 .x C
D.
8
9 .x C
Câu 15. Trong không gian Oxyz, cho bốn điểm
3; 1;2 , 1;3; 4 ,
M N
0;4; 3 , 2;0;3 .
P Q
Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A.
15.
B.
12.
C.
10.
D.
13.
Câu 16. Biết
ln 1 .f x dx x x C
Tính
2 3 .
f
A.
7.
B.
5.
C.
3.
D.
1.
Câu 17. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm
1;0;0 , 0;1;0 , 0;0;1
I J K
là
A.
0.
B.
1.
C.
2.
D. Vô số
.
Mã đề 431
Trang
1
/2
Mã
đề
431
Câu 18. Biết
2, 3.
bb
a a
f x dx g x dx
Tính
2 3 .
b
a
f x g x dx
A.
13.
B.
5.
C.
5.
D.
15.
Câu 19. Cho F(x) là một nguyên hàm của
, 3.
b
a
f x f x dx
Ta có
A.
3.
F a F b
B.
' ' 3.
f b f a
C.
3.
F b F a
D.
3.
f b f a
Câu 20.
1
0
x
e dx
A.
.e
B.
1.e
C.
1.
D.
1.e
Câu 21. Biết
4.
b
a
xdx
Tính
2 2
.a b
A.
8.
B.
8.
C.
2.
D.
16.
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên
, 1, 3.
f a f b
Tính
1 . ' .
b
a
f x f x dx
A.
8.
B.
6.
C.
10.
D.
12.
Câu 23. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm
3; 1;2
M
và giao tuyến của hai mặt
phẳng
: 3 0, : 2 4 0
P x z Q x y z
là
A.
2 4 0.x y z
B.
2 3 0.x y z
C.
2 2 0.x y z
D.
2 1 0.x y z
Câu 24.
1
0
ln 1 ln 2 .x dx a b
Tính
2
.ab
A.
4.
B.
2.
C.
2.
D.
9.
Câu 25. Cho F(x) là một nguyên hàm của
2
2
3
x
f x
x
trên
và
0 2 3.
F
Phương trình tiếp tuyến của
đồ thị hàm số
y F x
tại điểm
1x
là
A.
2 1.y x
B.
3 5.
y x
C.
3 4.y x
D.
3.y x
Câu 26. Biết
1
.ln
2
x
Cdx mx n
x
Tính
.m n
A.
0.
B.
1.
C.
2.
D.
2.
Câu 27.
4
3
8
ln5 ln 2.
1 2
x
dx a b c
x x
Tính
.a b c
A.
2.
B.
4.
C.
5.
D.
11.
Câu 28. Cho hàm số
f x
có đạo hàm và
0
f x
trên
,
' 2 1 , 0 1.
f x x f x f
Tính
2 .
f
A.
1.
B.
.e
C.
2
.e
D.
4
.e
Câu 29. Cho hàm số f(x) có đạo hàm liên tục trên
, 0 1, 1 1.
f f
Tính
1
0
' . .
x
f x f x e dx
A.
1.e
B.
1.e
C.
0.
D.
2.
Câu 30. Biết
3
2
2
0,75
3
3 4
16
a b
x dx
. Tính
2 .a b
A.
5.
B.
11.
C.
7.
D.
9.
------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm.
Trang
2
/2
Mã
đề
431
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT NGUYỄN TẤT THÀNH
ĐÁP ÁN KIỂM TRA GIỮA KỲ 2
NĂM HỌC 2023 - 2024
MÔN TOÁN - KHỐI 12
| 1/9
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024 Môn: Toán - Lớp 12 Mã đề 764
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:................... Câu 1.  cos . x dx  
A.  sin x C. B.  sin .
x x C. C. sin x C. D. sin . x x C.
Câu 2. Trong không gian Oxyz, mặt cầu  S  2 2 2
: x y z  2x  4 y  8z  5  0 có tâm là A. P  2  ;4; 8
 . B. P 1  ; 2; 4
 . C. P1; 2
 ; 4. D. P4; 8  ;16.
Câu 3. Trong không gian Oxyz, một vectơ pháp tuyến của mp : x  3y  2z 1  0 là    
A. n  1;3;2. B. n  1;3;2. C. n  2; 6
 ; 4. D. n  2;6;4.
Câu 4. Trong không gian Oxyz, cho mặt cầu S  2 2 2
: x y z  2ax  2by  2cz d  0 Ta có A. 2 2 2
a b c d. B. 2 2 2
a b c d. C. 2 2 2
a b c d. D. 2 2 2
a b c d.
Câu 5. Mệnh đề nào dưới đây đúng? A.   1 x dxx    C.  B. x x
a dx a C.  C.
f ' xdx f x  C. 
D. dx C. 
Câu 6. Trong không gian Oxyz, cho hai điểm M 3; 1  ; 2, N 1;3; 4
 . Tọa độ trung điểm của đoạn thẳng MN là
A. P 2;1; 
1 . B. P 4;2; 2
 . C. P 2  ;4; 6
 . D. P 1  ; 2; 3  .
Câu 7. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O, M 3; 1  ;2, N 1;3; 4   là
A. x  7 y  5z  0. B. x  2 y  3z  0. C. 3x y  2z  0. D. x  3y  4z  0.
Câu 8. Trong không gian Oxyz, cho ba điểm M 3; 1  ;2, N 1;3; 4  , P5;1; 2
  và điểm I  ; a ; b c thỏa mãn    
IM  2IN  3IP  0 . Tính 2a  6b  . c
A. 24. B. 16. C. 12. D. 18.       
Câu 9. Trong không gian Oxyz, cho a  3;1;2, b  1;3; 4
 , c  2;0;4. Tọa độ của u  2a  3b c là
A. 11;7;4. B. 7;7; 1  2. C.  2  ; 4; 6  . D.  1  ;2;  3 .
Câu 10. x sin xdx  
A. sin x x cos x C. B. sin x x cos x C. C. x cos x  .
C D. x cos x  sin x C.
Câu 11. Trong không gian Oxyz, cho bốn điểm M 3; 1  ; 2, N 1;3; 4  , P0;4; 3  , Q2;0;  3 . Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A. 15. B. 12. C. 10. D. 13.
Câu 12. Trong không gian Oxyz, mp : x  3y  2z 1  0 chứa điểm nào dưới đây?
A. P 2;1;  1 . B. Q 4
 ;1;0. C. R 2  ;4; 6
 . D. S 0;2; 3  .
Câu 13. Trong không gian Oxyz, mặt cầu có tâm M 3; 1
 ; 2 bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A. x  3. B. z  3. C. y  3. D. x y z  3. Câu 14. Biết
f xdx    2
ln x x 1  C. Tính 2 f  3.
A. 7. B. 5. C. 3. D. 1.
Câu 15. Cho F(x) là một nguyên hàm của f x  2x 1 trên  và F  
1  3 . Tính F 2  F 3.
A. 8. B. 14. C. 18. D. 20.
Câu 16. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm I 1;0;0, J 0;1;0, K 0;0;  1 là
A. 0. B. 1. C. 2. D. Vô số. Câu 17. Trên  f x 2
dx x C g x 3 ,
dx  2x C   . Tính
f x.g x . dx A. 4
3x C. B. 5 2x  . C C. 6 6x  . C D. 8 9x  . C Trang 1/2 Mã đề 764 b
Câu 18. Cho F(x) là một nguyên hàm của f x, f xdx  3.  Ta có a
A. F a  F b  3. B. f 'b  f 'a  3. C. F b  F a  3. D. f b  f a  3. b
Câu 19. Biết xdx  4.  Tính 2 2 a b . a A. 8. B. 8  . C. 2. D. 1  6. b b b Câu 20. Biết
f xdx  2, g xdx  3  .  
Tính 2 f x  3g x . dx    a a a A. 13. B. 5
 . C. 5. D. 15. 1 Câu 21. x e dx   0 A. .
e B. e 1. C. 1. D. e 1. b
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên , f a  1, f b  3. Tính  f x 1. f ' x . dx    a
A. 8. B. 6. C. 10. D. 12. 3 2 a  b 3 Câu 23. Biết 2 3  4x dx   . Tính 2a  . b 16 0,75
A. 5. B. 11. C. 7. D. 9. 1
Câu 24. ln  x  
1 dx a ln 2  . b  Tính 2 ab . 0 A. 4. B. 2
 . C. 2. D. 9.
Câu 25. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm M 3; 1
 ; 2 và giao tuyến của hai mặt
phẳng  P : x z  3  0,Q : 2x y z  4  0 là
A. x  2 y z  4  0. B. x  2 y z  3  0. C. x  2 y z  2  0. D. x  2 y z  1  0. 2x
Câu 26. Cho F(x) là một nguyên hàm của f x 
trên  và F 0  2 3. Phương trình tiếp tuyến của 2 x  3
đồ thị hàm số y F x tại điểm x 1 là
A. y  2 x  1. B. y
3x  5. C. y  3x  4. D. y x  3. 1
Câu 27. Cho hàm số f(x) có đạo hàm liên tục trên , f 0  1, f  
1  1. Tính     ' . x f x f x e . dx    0
A. e 1. B. e 1. C. 0. D. 2.
Câu 28. Cho hàm số f x có đạo hàm và f x  0 trên  , f ' x  2x  
1 f x, f 0  1. Tính f 2. A. 1. B. . e C. 2 e . D. 4 e . 4 x  8 Câu 29.
dx a b ln 5  c ln 2. 
Tính a b  . c x 1 x  2 3    A. 2. B. 4  . C. 5  . D. 11. x 1 Câu 30. Biết
dx mx n ln x  2  C.  Tính m  . n x  2 A. 0. B. 1  . C. 2  . D. 2. ------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm. Trang 2/2 Mã đề 764
KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024 Môn: Toán - Lớp 12 Mã đề 653
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:...................
Câu 1. Trong không gian Oxyz, một vectơ pháp tuyến của mp : x  3y  2z 1  0 là    
A. n  1;3;2. B. n  1;3;2. C. n  2; 6
 ; 4. D. n  2;6;4.
Câu 2. Trong không gian Oxyz, cho mặt cầu S  2 2 2
: x y z  2ax  2by  2cz d  0 Ta có A. 2 2 2
a b c d. B. 2 2 2
a b c d. C. 2 2 2
a b c d. D. 2 2 2
a b c d.
Câu 3. Trong không gian Oxyz, mặt cầu  S  2 2 2
: x y z  2x  4 y  8z  5  0 có tâm là A. P  2  ;4; 8
 . B. P 1  ; 2; 4
 . C. P1; 2
 ; 4. D. P4; 8  ;16.
Câu 4. Mệnh đề nào dưới đây đúng? A.   1 x dxx    C.  B. x x
a dx a C.  C.
f ' xdx f x  C. 
D. dx C. 
Câu 5. Trong không gian Oxyz, cho hai điểm M 3; 1  ; 2, N 1;3; 4
 . Tọa độ trung điểm của đoạn thẳng MN là
A. P 2;1; 
1 . B. P 4;2; 2
 . C. P 2  ;4; 6
 . D. P 1  ; 2; 3  .
Câu 6. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O, M 3; 1  ;2, N 1;3; 4   là
A. x  7 y  5z  0. B. x  2 y  3z  0. C. 3x y  2z  0. D. x  3y  4z  0. Câu 7.  cos . x dx  
A.  sin x C. B.  sin .
x x C. C. sin x C. D. sin . x x C.
Câu 8. Trong không gian Oxyz, cho ba điểm M 3; 1  ;2, N 1;3; 4  , P5;1; 2
  và điểm I  ; a ; b c thỏa mãn    
IM  2IN  3IP  0 . Tính 2a  6b  . c
A. 24. B. 16. C. 12. D. 18.
Câu 9. Trong không gian Oxyz, mp : x  3y  2z 1  0 chứa điểm nào dưới đây?
A. P 2;1;  1 . B. Q 4
 ;1;0. C. R 2  ;4; 6
 . D. S 0;2; 3  .       
Câu 10. Trong không gian Oxyz, cho a  3;1;2, b  1;3; 4
 , c  2;0;4. Tọa độ của u  2a  3b c là
A. 11;7;4. B. 7;7; 1  2. C.  2  ; 4; 6  . D.  1  ;2;  3 .
Câu 11. x sin xdx  
A. sin x x cos x C. B. sin x x cos x C. C. x cos x  .
C D. x cos x  sin x C.
Câu 12. Trong không gian Oxyz, cho bốn điểm M 3; 1  ; 2, N 1;3; 4  , P0;4; 3  , Q2;0;  3 . Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A. 15. B. 12. C. 10. D. 13. Câu 13. Biết
f xdx ln 
x x 1 C. Tính 2 f  3.
A. 7. B. 5. C. 3. D. 1.
Câu 14. Cho F(x) là một nguyên hàm của f x  2x 1 trên  và F  
1  3 . Tính F 2  F 3.
A. 8. B. 14. C. 18. D. 20. Câu 15. Trên  f x 2
dx x C g x 3 ,
dx  2x C   . Tính
f x.g x . dx A. 4
3x C. B. 5 2x  . C C. 6 6x  . C D. 8 9x  . C
Câu 16. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm I 1;0;0, J 0;1;0, K 0;0;  1 là
A. 0. B. 1. C. 2. D. Vô số.
Câu 17. Trong không gian Oxyz, mặt cầu có tâm M 3; 1
 ; 2 bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A. x  3. B. z  3. C. y  3. D. x y z  3. Trang 1 /2 Mã đ ề 653 b
Câu 18. Biết xdx  4.  Tính 2 2 a b . a A. 8. B. 8  . C. 2. D. 1  6. b b b Câu 19. Biết
f xdx  2, g xdx  3  .  
Tính 2 f x  3g x . dx    a a a A. 13. B. 5
 . C. 5. D. 15. 1 Câu 20. x e dx   0 A. .
e B. e 1. C. 1. D. e 1. b
Câu 21. Cho F(x) là một nguyên hàm của f x, f xdx  3.  Ta có a
A. F a  F b  3. B. f 'b  f 'a  3. C. F b  F a  3. D. f b  f a  3. b
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên , f a  1, f b  3. Tính  f x 1. f ' x . dx    a
A. 8. B. 6. C. 10. D. 12. 3 2 a  b 3 Câu 23. Biết 2 3  4x dx   . Tính 2a  . b 16 0,75
A. 5. B. 11. C. 7. D. 9. 1
Câu 24. ln  x  
1 dx a ln 2  . b  Tính 2 ab . 0 A. 4. B. 2
 . C. 2. D. 9. x 1 Câu 25. Biết
dx mx n ln  C.  Tính m  . n x  2 A. 0. B. 1  . C. 2  . D. 2.
Câu 26. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm M 3; 1
 ; 2 và giao tuyến của hai mặt
phẳng  P : x z  3  0,Q : 2x y z  4  0 là
A. x  2 y z  4  0. B. x  2 y z  3  0. C. x  2 y z  2  0. D. x  2 y z  1  0. 2x
Câu 27. Cho F(x) là một nguyên hàm của f x 
trên  và F 0  2 3. Phương trình tiếp tuyến của 2 x  3
đồ thị hàm số y F x tại điểm x 1 là
A. y  2 x  1. B. y
3x  5. C. y  3x  4. D. y x  3. 4 x  8 Câu 28.
dx a b ln 5  c ln 2. 
Tính a b  . c x 1 x  2 3    A. 2. B. 4  . C. 5  . D. 11. 1
Câu 29. Cho hàm số f(x) có đạo hàm liên tục trên , f 0  1  , f  
1  1. Tính     ' . x f x f x e . dx    0
A. e 1. B. e 1. C. 0. D. 2.
Câu 30. Cho hàm số f x có đạo hàm và f x  0 trên  , f ' x  2x  
1 f x, f 0  1. Tính f 2. A. 1. B. . e C. 2 e . D. 4 e . ------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm. Trang 2 /2 Mã đ ề 653
KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024 Môn: Toán - Lớp 12 Mã đề 542
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:...................
Câu 1. Trong không gian Oxyz, cho mặt cầu S  2 2 2
: x y z  2ax  2by  2cz d  0 Ta có A. 2 2 2
a b c d. B. 2 2 2
a b c d. C. 2 2 2
a b c d. D. 2 2 2
a b c d.
Câu 2. Mệnh đề nào dưới đây đúng? A.   1 x dxx    C.  B. x x
a dx a C.  C.
f ' xdx f x  C. 
D. dx C. 
Câu 3. Trong không gian Oxyz, cho hai điểm M 3; 1  ; 2, N 1;3; 4
 . Tọa độ trung điểm của đoạn thẳng MN là
A. P 2;1; 
1 . B. P 4;2; 2
 . C. P 2  ;4; 6
 . D. P 1  ; 2; 3  .
Câu 4. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O, M 3; 1  ;2, N 1;3; 4   là
A. x  7 y  5z  0. B. x  2 y  3z  0. C. 3x y  2z  0. D. x  3y  4z  0. Câu 5.  cos . x dx  
A.  sin x C. B.  sin .
x x C. C. sin x C. D. sin . x x C.
Câu 6. Trong không gian Oxyz, cho ba điểm M 3; 1  ;2, N 1;3; 4  , P5;1; 2
  và điểm I  ; a ; b c thỏa mãn    
IM  2IN  3IP  0 . Tính 2a  6b  . c
A. 24. B. 16. C. 12. D. 18.
Câu 7. Trong không gian Oxyz, một vectơ pháp tuyến của mp : x  3y  2z 1  0 là    
A. n  1;3;2. B. n  1;3;2. C. n  2; 6
 ; 4. D. n  2;6;4.
Câu 8. Trong không gian Oxyz, mp : x  3y  2z 1  0 chứa điểm nào dưới đây?
A. P 2;1;  1 . B. Q 4
 ;1;0. C. R 2  ;4; 6
 . D. S 0;2; 3  .
Câu 9. Trong không gian Oxyz, mặt cầu  S  2 2 2
: x y z  2x  4 y  8z  5  0 có tâm là A. P  2  ;4; 8
 . B. P 1  ; 2; 4
 . C. P1; 2
 ; 4. D. P4; 8  ;16.       
Câu 10. Trong không gian Oxyz, cho a  3;1;2, b  1;3; 4
 , c  2;0;4. Tọa độ của u  2a  3b c là
A. 11;7;4. B. 7;7; 1  2. C.  2  ; 4; 6  . D.  1  ;2;  3 .
Câu 11. x sin xdx  
A. sin x x cos x C. B. sin x x cos x C. C. x cos x  .
C D. x cos x  sin x C.
Câu 12. Trong không gian Oxyz, mặt cầu có tâm M 3; 1
 ; 2 bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A. x  3. B. z  3. C. y  3. D. x y z  3.
Câu 13. Cho F(x) là một nguyên hàm của f x  2x 1 trên  và F  
1  3 . Tính F 2  F 3.
A. 8. B. 14. C. 18. D. 20. Câu 14. Trên  f x 2
dx x C g x 3 ,
dx  2x C   . Tính
f x.g x . dx A. 4
3x C. B. 5 2x  . C C. 6 6x  . C D. 8 9x  . C
Câu 15. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm I 1;0;0, J 0;1;0, K 0;0;  1 là
A. 0. B. 1. C. 2. D. Vô số.
Câu 16. Trong không gian Oxyz, cho bốn điểm M 3; 1  ; 2, N 1;3; 4  , P0;4; 3  , Q2;0;  3 . Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A. 15. B. 12. C. 10. D. 13. Câu 17. Biết
f xdx    2
ln x x 1  C. Tính 2 f  3.
A. 7. B. 5. C. 3. D. 1. Trang 5/2 Mã đề 764 1 Câu 18. x e dx   0 A. .
e B. e 1. C. 1. D. e 1. b
Câu 19. Biết xdx  4.  Tính 2 2 a b . a A. 8. B. 8  . C. 2. D. 1  6. b b b Câu 20. Biết
f xdx  2, g xdx  3  .  
Tính 2 f x  3g x . dx    a a a A. 13. B. 5
 . C. 5. D. 15. b
Câu 21. Cho F(x) là một nguyên hàm của f x, f xdx  3.  Ta có a
A. F a  F b  3. B. f 'b  f 'a  3. C. F b  F a  3. D. f b  f a  3. b
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên , f a  1, f b  3. Tính  f x 1. f ' x . dx    a
A. 8. B. 6. C. 10. D. 12. 1
Câu 23. ln  x  
1 dx a ln 2  . b  Tính 2 ab . 0 A. 4. B. 2
 . C. 2. D. 9. x 1 Câu 24. Biết
dx mx n ln  C.  Tính m  . n x  2 A. 0. B. 1  . C. 2  . D. 2.
Câu 25. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm M 3; 1
 ; 2 và giao tuyến của hai mặt
phẳng  P : x z  3  0,Q : 2x y z  4  0 là
A. x  2 y z  4  0. B. x  2 y z  3  0. C. x  2 y z  2  0. D. x  2 y z  1  0. 3 2 a  b 3 Câu 26. Biết 2 3  4x dx   . Tính 2a  . b 16 0,75
A. 5. B. 11. C. 7. D. 9. 4 x  8 Câu 27.
dx a b ln 5  c ln 2. 
Tính a b  . c x 1 x  2 3    A. 2. B. 4  . C. 5  . D. 11.
Câu 28. Cho hàm số f x có đạo hàm và f x  0 trên  , f ' x  2x  
1 f x, f 0  1. Tính f 2. A. 1. B. . e C. 2 e . D. 4 e . 1
Câu 29. Cho hàm số f(x) có đạo hàm liên tục trên , f 0  1, f  
1  1. Tính     ' . x f x f x e . dx    0
A. e 1. B. e 1. C. 0. D. 2. 2x
Câu 30. Cho F(x) là một nguyên hàm của f x 
trên  và F 0  2 3. Phương trình tiếp tuyến của 2 x  3
đồ thị hàm số y F x tại điểm x 1 là
A. y  2 x  1. B. y
3x  5. C. y  3x  4. D. y x  3. ------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm. Trang 2 /2 Mã đ ề 542
KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023 - 2024 Môn: Toán - Lớp 12 Mã đề 431
Thời gian làm bài: 60 phút (không kể thời gian giao đề)
Họ và tên thí sinh:..................................................... Số báo danh:...................
Câu 1. Mệnh đề nào dưới đây đúng? A.   1 x dxx    C.  B. x x
a dx a C.  C.
f ' xdx f x  C. 
D. dx C. 
Câu 2. Trong không gian Oxyz, cho hai điểm M 3; 1  ; 2, N 1;3; 4
 . Tọa độ trung điểm của đoạn thẳng MN là
A. P 2;1; 
1 . B. P 4;2; 2
 . C. P 2  ;4; 6
 . D. P 1  ; 2; 3  .       
Câu 3. Trong không gian Oxyz, cho a  3;1;2, b  1;3; 4
 , c  2;0;4. Tọa độ của u  2a  3b c là
A. 11;7;4. B. 7;7; 1  2. C.  2  ; 4; 6  . D.  1  ;2;  3 . Câu 4.  cos . x dx  
A.  sin x C. B.  sin .
x x C. C. sin x C. D. sin . x x C.
Câu 5. Trong không gian Oxyz, cho ba điểm M 3; 1  ;2, N 1;3; 4  , P5;1; 2
  và điểm I  ; a ; b c thỏa mãn    
IM  2IN  3IP  0 . Tính 2a  6b  . c
A. 24. B. 16. C. 12. D. 18.
Câu 6. Trong không gian Oxyz, một vectơ pháp tuyến của mp : x  3y  2z 1  0 là    
A. n  1;3;2. B. n  1;3;2. C. n  2; 6
 ; 4. D. n  2;6;4.
Câu 7. Trong không gian Oxyz, mp : x  3y  2z 1  0 chứa điểm nào dưới đây?
A. P 2;1;  1 . B. Q 4
 ;1;0. C. R 2  ;4; 6
 . D. S 0;2; 3  .
Câu 8. Trong không gian Oxyz, phương trình mặt phẳng chứa cả ba điểm O, M 3; 1  ;2, N 1;3; 4   là
A. x  7 y  5z  0. B. x  2 y  3z  0. C. 3x y  2z  0. D. x  3y  4z  0.
Câu 9. Trong không gian Oxyz, mặt cầu  S  2 2 2
: x y z  2x  4 y  8z  5  0 có tâm là A. P  2  ;4; 8
 . B. P 1  ; 2; 4
 . C. P1; 2
 ; 4. D. P4; 8  ;16.
Câu 10. Trong không gian Oxyz, cho mặt cầu S  2 2 2
: x y z  2ax  2by  2cz d  0 Ta có A. 2 2 2
a b c d. B. 2 2 2
a b c d. C. 2 2 2
a b c d. D. 2 2 2
a b c d.
Câu 11. Trong không gian Oxyz, mặt cầu có tâm M 3; 1
 ; 2 bán kính bằng 1 tiếp xúc mặt phẳng nào dưới đây?
A. x  3. B. z  3. C. y  3. D. x y z  3.
Câu 12. x sin xdx  
A. sin x x cos x C. B. sin x x cos x C. C. x cos x  .
C D. x cos x  sin x C.
Câu 13. Cho F(x) là một nguyên hàm của f x  2x 1 trên  và F  
1  3 . Tính F 2  F 3.
A. 8. B. 14. C. 18. D. 20. Câu 14. Trên  f x 2
dx x C g x 3 ,
dx  2x C   . Tính
f x.g x . dx A. 4
3x C. B. 5 2x  . C C. 6 6x  . C D. 8 9x  . C
Câu 15. Trong không gian Oxyz, cho bốn điểm M 3; 1  ; 2, N 1;3; 4  , P0;4; 3  , Q2;0;  3 . Tính diện tích
tứ giác MNPQ (kết quả chính xác đến hàng đơn vị).
A. 15. B. 12. C. 10. D. 13. Câu 16. Biết
f xdx ln 
x x 1 C. Tính 2 f  3.
A. 7. B. 5. C. 3. D. 1.
Câu 17. Trong không gian Oxyz, số mặt cầu có bán kính bằng 5 chứa cả ba điểm I 1;0;0, J 0;1;0, K 0;0;  1 là
A. 0. B. 1. C. 2. D. Vô số. Trang 1 /2 Mã đ ề 431 b b b Câu 18. Biết
f xdx  2, g xdx  3  .  
Tính 2 f x  3g x . dx    a a a A. 13. B. 5
 . C. 5. D. 15. b
Câu 19. Cho F(x) là một nguyên hàm của f x, f xdx  3.  Ta có a
A. F a  F b  3. B. f 'b  f 'a  3. C. F b  F a  3. D. f b  f a  3. 1 Câu 20. x e dx   0 A. .
e B. e 1. C. 1. D. e 1. b
Câu 21. Biết xdx  4.  Tính 2 2 a b . a A. 8. B. 8  . C. 2. D. 1  6. b
Câu 22. Cho hàm số f(x) có đạo hàm liên tục trên , f a  1, f b  3. Tính  f x 1. f ' x . dx    a
A. 8. B. 6. C. 10. D. 12.
Câu 23. Trong không gian Oxyz, phương trình mặt phẳng chứa điểm M 3; 1
 ; 2 và giao tuyến của hai mặt
phẳng  P : x z  3  0,Q : 2x y z  4  0 là
A. x  2 y z  4  0. B. x  2 y z  3  0. C. x  2 y z  2  0. D. x  2 y z  1  0. 1
Câu 24. ln  x  
1 dx a ln 2  . b  Tính 2 ab . 0 A. 4. B. 2
 . C. 2. D. 9. 2x
Câu 25. Cho F(x) là một nguyên hàm của f x 
trên  và F 0  2 3. Phương trình tiếp tuyến của 2 x  3
đồ thị hàm số y F x tại điểm x 1 là
A. y  2 x  1. B. y
3x  5. C. y  3x  4. D. y x  3. x 1 Câu 26. Biết
dx mx n ln  C.  Tính m  . n x  2 A. 0. B. 1  . C. 2  . D. 2. 4 x  8 Câu 27.
dx a b ln 5  c ln 2. 
Tính a b  . c x 1 x  2 3    A. 2. B. 4  . C. 5  . D. 11.
Câu 28. Cho hàm số f x có đạo hàm và f x  0 trên  , f ' x  2x  
1 f x, f 0  1. Tính f 2. A. 1. B. . e C. 2 e . D. 4 e . 1
Câu 29. Cho hàm số f(x) có đạo hàm liên tục trên , f 0  1, f  
1  1. Tính     ' . x f x f x e . dx    0
A. e 1. B. e 1. C. 0. D. 2. 3 2 a  b 3 Câu 30. Biết 2 3  4x dx   . Tính 2a  . b 16 0,75
A. 5. B. 11. C. 7. D. 9. ------ HẾT ------
Học sinh không được dùng tài liệu; giám thị không giải thích gì thêm. Trang 2 /2 Mã đ ề 431
SỞ GIÁO DỤC VÀ ĐÀO TẠO
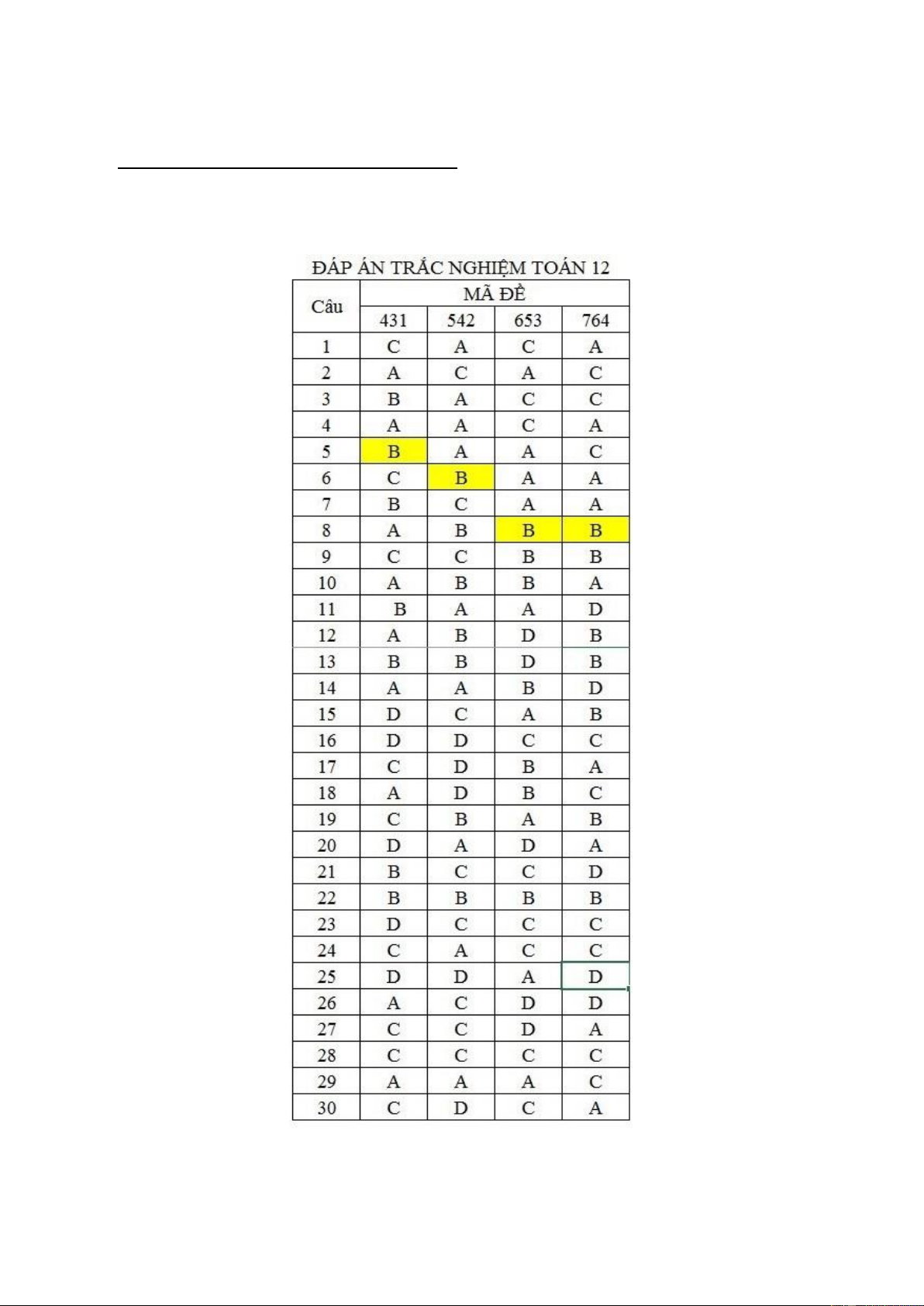
ĐÁP ÁN KIỂM TRA GIỮA KỲ 2
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2023 - 2024
TRƯỜNG THPT NGUYỄN TẤT THÀNH MÔN TOÁN - KHỐI 12
Document Outline

  • kt-giua-ky-2-23-24-12_6320249
  • SỞ GIÁO DỤC VÀ ĐÀO TẠO