Đề học kì 1 Toán 9 năm 2022 – 2023 phòng GD&ĐT Nam Từ Liêm – Hà Nội

UBND QUẬN NAM TỪ LIÊM
ĐỀ KIỂM TRA HỌC KÌ I LỚP 9
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022 - 2023 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (Không kể thời gian phát đề)
Ngày kiểm tra: 28/12/2022
(Đề thi có 01 trang)
Bài I (2,0 điểm).
1) Rút gọn các biểu thức sau: 1 2 a) 12  75  2 48 b) 10  5 5  2
2) Giải các phương trình: a) 2
x  2x 1  4
b) x  5 x  36  0 2 x 2 x 3x  4
Bài II (2,0 điểm). Cho biểu thức: A  và B   
với x  0; x  4 x  6 x  2 x  2 x  4
1) Tính giá trị của biểu thức A khi x  9 2 2) Chứng minh: B  x  2 A 2
3) Tìm số nguyên tố x lớn nhất thỏa mãn  B 3
Bài III (2,0 điểm). Cho hàm số bậc nhất y  mx  4 (với m  0 ) có đồ thị là đường thẳng d 
1) Tìm m để đường thẳng d  đi qua điểm M  1
 ;3. Vẽ đồ thị hàm số ứng với m vừa tìm được.
2) Tìm m để đường thẳng d  song song với đường thẳng y  5  2x
3) Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng d  bằng 8
Bài IV (3,5 điểm).
1.(0,5 điểm). Một cột đèn có bóng chiếu trên mặt đất dài 4,5m. Các tia sáng mặt trời chiếu
qua đỉnh cột đèn tạo với mặt đất một góc xấp xỉ bằng 0
57 . Tính chiều cao của cột đèn (làm tròn
kết quả đến chữ số thập phân thứ nhất).
2. (3,0 điểm). Cho A
 BC vuông tại A (AB < AC), đường cao AH. Vẽ đường tròn đường
tâm A, bán kính AH. Từ điểm C kẻ tiếp tuyến CM với đường tròn (A, AH) (M là tiếp điểm, M
không nằm trên đường thẳng BC).
a) Chứng minh bốn điểm A, M, C và H cùng thuộc cùng một đường tròn.
b) Gọi I là giao điểm của AC và MH. Kẻ đường kính MD của đường tròn (A). Chứng minh
BD là tiếp tuyến của đường tròn (A) và BH.HC  AI.AC
c) Vẽ đường tròn tâm O, đường kính BC cắt đường tròn (A) tại P và Q. Chứng minh PQ//DM.
Bài V (0,5 điểm). Cho các số dương a, b, c thỏa mãn: a + b + c = 1. Chứng minh rằng: 𝑎 𝑏 𝑐 1 1 1 1 + + ≤ ( + + ) 𝑎 + 𝑏2 𝑏 + 𝑐2 𝑐 + 𝑎2 4 𝑎 𝑏 𝑐
................................ Hết ...................................
Họ và tên thí sinh…………………………………….Số báo danh…………………………… UBND QUẬN NAM TỪ LIÊM
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HKI LỚP 9
NĂM HỌC 2022-2023 - MÔN: TOÁN A. Hướng dẫn chung
- Nếu học sinh giải theo cách khác mà đúng và đủ các bước thì giám khảo vẫn cho điểm tối đa.
- Trong mỗi bài, nếu ở một bước nào đó bị sai thì các bước sau có liên quan không được điểm.
- Bài hình học bắt buộc phải vẽ đúng hình thì mới chấm điểm, nếu không có hình vẽ đúng ở phần nào
thì giám khảo không cho điểm phần lời giải liên quan đến hình của phần đó.
- Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn.
B. Đáp án và thang điểm Bài ý Đáp án Điểm Bài I 1 12  75  2 48 = 2 2 2
2 .3  5 .3  2 4 .3 = 2 3  5 3  2.4 3 0,25đ (2,0 điể      m) (1 đ) 2 3 5 3 8 3 3 0,25đ . 2 5  2 1 2 10  = 2 5   2 5  2 5  2 0,25đ 5 5  2  52 52  2 5  2 5  4  4  0,25đ 2 x  x   2  x    x 1  4 (1 đ) a) 2 2 1 4 ( 1) 4 0,25đ TH1: x + 1 = 4 => x = 3 TH2 : x + 1 = -4 => x = -5 0,25đ
Vậy phương trình có tập nghiệm S  3;  5
b) x  5 x  36  0 . ĐK: x  0  0,25đ
x  9 x 4  0  x  9  0  x  9  loai    
 x  16t / m  x  4  0  x  4 0,25đ
Vậy tập nghiệm của phương trình là: S    16 Bài II 1 2 0,25đ A  x  x  (2,0 (0,5đ) với 0; 4 x  6 điểm) . 2 2
Thay x  9 (thỏa mãn ĐK) vào A ta có A   9  6 9 2 0,25đ
Vậy x  9 thì A  9 2 x 2 x 3x  4 B   
với x  0; x  4 x  2 x  2 x  4 (1đ) 0,25đ x  x 2
2 x  x 2 3x  4 B    
x  2 x 2  x 2 x 2  x 2 x 2
x  2 x  2x  4 x  3x  4 0,25đ B  
x  2 x 2 2 x  4 0,25đ B  
x  2 x 2 2 x 2 0,25đ 2 B   
x  2 x 2 x  2 3 A 2 x  2 2 x  6 0,25đ (0,5đ) Ta có      0 x  x  B 3 với 0; 4 x  6 3 3 x 6
Vì x  0; x  4 nên 3 x  6  0  x  6  x  36
Kết hợp với điều kiện x  0; x  4 và x là số nguyên tố lớn nhất ta được 0,25đ
x  31. Vậy x  31 Bài III 1
1) đường thẳng d  đi qua điểm M  1  ;3. Thay x  1
 ; y  3 vào công 0,25đ (2,0 (1đ) điểm)
thức y  mx  4 ta có 3  . m  
1  4  m 1 (t/m) .
Với m = 1 ta có hàm số y  x  4 0,25đ
Lập bảng và chỉ ra đồ thị của hàm số y  x  4 là đường thẳng đi qua hai 0,25đ điểm (0;4) và (-4; 0) y y=x+4 4 -4 O 1 x 0,25đ
Vẽ chính xác đồ thị được 0,25đ 2
2) Tìm m để đường thẳng d  song song với đường thẳng y  5  2x . (0,5đ)
Để đường thẳng đường thẳng d  song song với đường thẳng y  5 2x 0,25đ a  a' m  2     b b'   4  5  m  2  t / m 0,25đ Vậy m = -2 3  4   (0,5đ) d A ;0
3) Tìm được giao điểm của đường thẳng   với trục Ox là  m  với   0,25đ 4
trục Oy là B 0;4  OA  ;OB  4 m
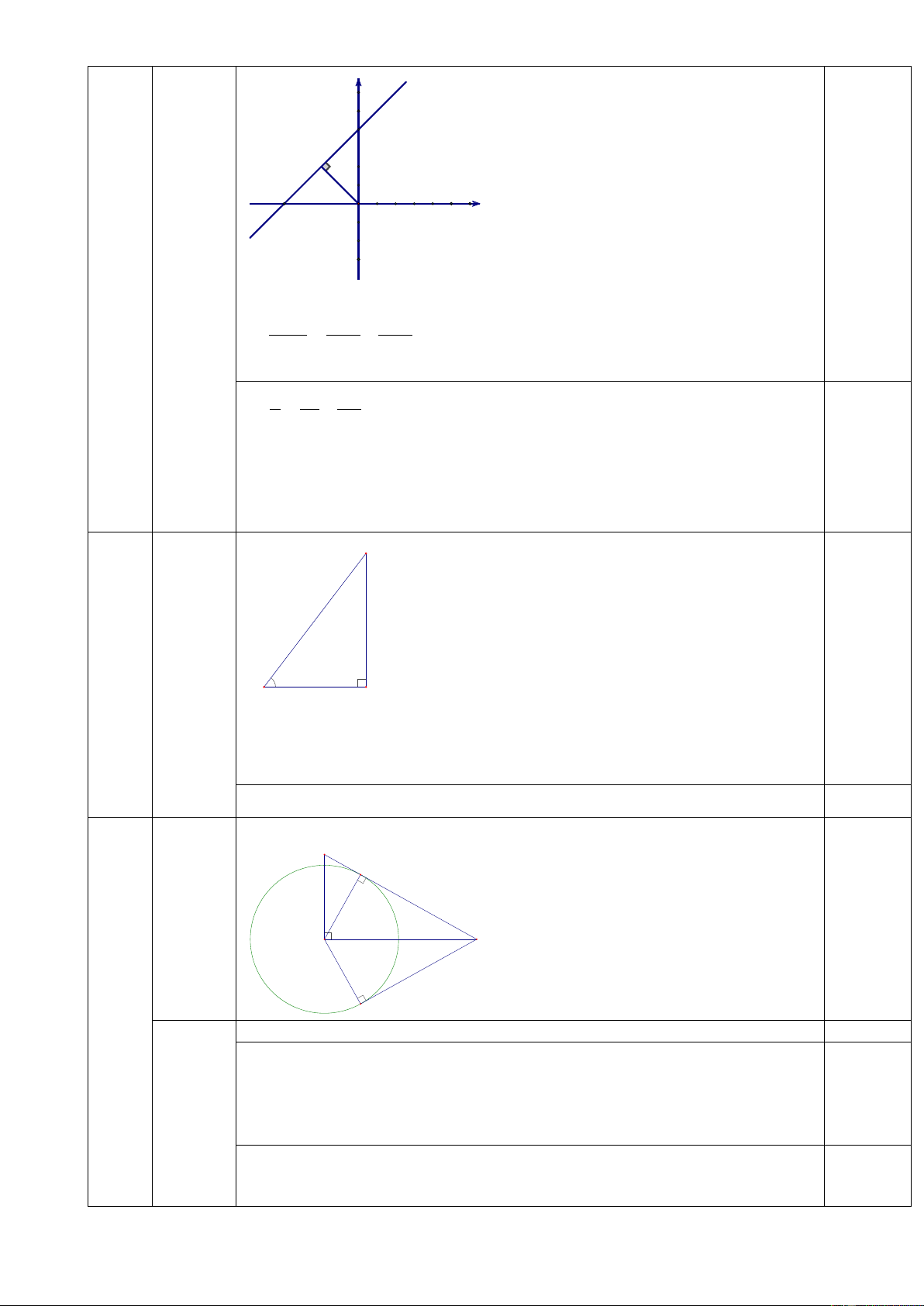
Kẻ OH  AB H  AB  OH  8 y (d) 4 B H A O 1 x Xét O
 AB vuông tại O có đường cao OH 1 1 1 =>  
(Hệ thức lượng trong tam giác vuông) 2 2 2 OH OA OB 2 1 1 m 0,25đ 2     m  1 8 16 16
m 1 t / m   m  1  (t / m Vậy m  1  ;  1 Bài 1. C IV (0,5 (3,5 điểm). điểm) . 570 A 4,5m B 0,25đ
Gọi chiều cao của cột đèn là BC, bóng của cột đèn trên mặt đất là AB
Xét ∆ABC vuông tại B có BC  A . B tan CAB
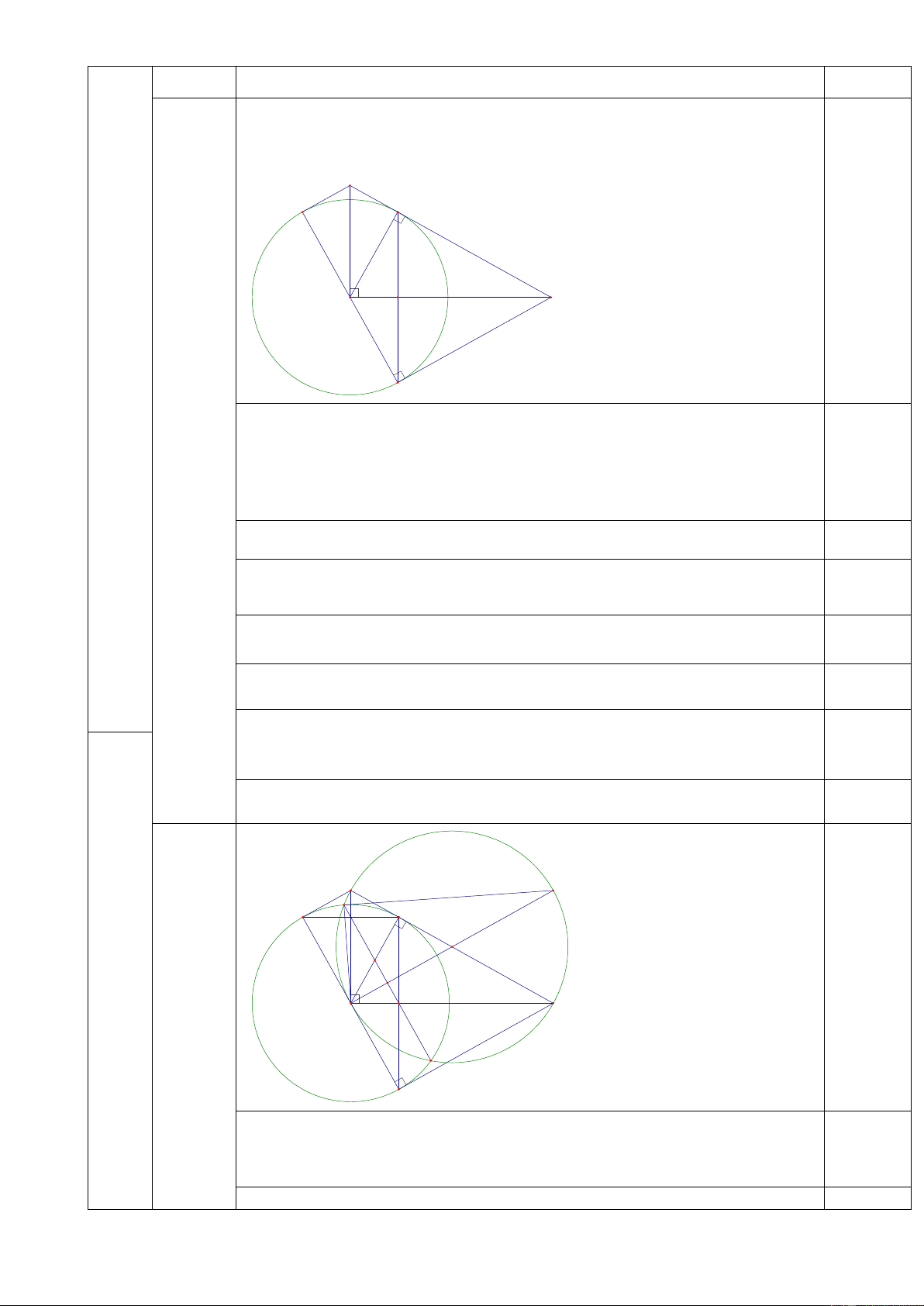
=> BC  4,5.tan 57  6,9m .Vậy chiều cao của cột đèn khoảng 6,9m 0,25đ 2. Hình vẽ: (3,0 B điểm). H 0,25đ A C M a.
a) Chứng minh: 4 điểm A, M, C, H cùng thuộc cùng một đường tròn. (0,75)
Xét đường tròn (A) có CM là tiếp tuyến của A  0,25đ
=> CM  AM  A
 MC vuông tại M  ,
A M,C cùng thuộc đường tròn đường kính AC
AH  BC (gt)  A
 HC vuông tại H 0,25đ  ,
A H,C cùng thuộc đường tròn đường kính AC .
Vậy bốn điểm A ,M ,C ,H cùng nằm trên đường tròn đường kính AC . 0,25đ b
b) Gọi I là giao điểm của AC và MH. Kẻ đường kính MD của đường (1,5đ)
tròn (A). Chứng minh BD là tiếp tuyến của đường tròn (A) và
BH.HC  AI.AC B D H C A I M Ta có 0 BAC  90 do A  BC vuông tại A 0,25đ => 0
HAB  HAC  90 0 0
MAD 180  DAB  MAC  90
Mà HAC  MAC (tính chất hai tiếp tuyến cắt nhau)  DAB  HAB 0.25đ Chứng minh A  DB  A  HB .c .
g c  ADB  AHB => 0 ADB  90
 BD  AD và D thuộc đường tròn  A 0,25đ
=> BD là tiếp tuyến của đường tròn (A) Xét A
 BC vuông tại A có AH là đường cao 0.25đ 2
=> AH  BH.HC (hệ thức lượng trong tam giác vuông) C/m HM AC tại I 0.25đ Xét A
 HC vuông tại H có HI là đường cao => 2
AH  AI.AC (hệ thức lượng trong tam giác vuông)
=> BH.HC  AI.AC 0,25đ
c) Đường tròn tâm O đường kính BC cắt đường tròn (A) tại P và Q. (0,5đ) Chứng minh DM//PQ c B E D P H O G N I A C Q M
Vì đường tròn (A) và (O) cắt nhau tại P và Q nên AO  PQ tại N (tính chất 0,25đ đường nối tâm) (1)
DBCM là hình thang vuông có 0,25đ
DA = DM; OB = OC => OA là đườ
ng trung bình của hình thang DBCM =>OA //BD//CM Mà BD DM =>OA  DM (2) Từ (1) và (2) =>DM//PQ Bài V
Bài 5. Cho các số dương a, b, c thỏa mãn: a + b + c = 1. Chứng (0,5 điểm) minh rằng: 𝑎 𝑏 𝑐 1 1 1 1 + + ≤ ( + + ) 𝑎 + 𝑏2 𝑏 + 𝑐2 𝑐 + 𝑎2 4 𝑎 𝑏 𝑐
Theo bất đẳng thức Cô – si ta có 𝑎 + 𝑏2 = 𝑎(𝑎 + 𝑏 + 𝑐) + 𝑏2 ≥ 0,25đ 3𝑎𝑏 + 𝑎𝑐 1 Áp dụng bất thức ≤ 1 (1 + 1) ta có: 𝑥+𝑦 4 𝑥 𝑦 𝑎 ≤ 𝑎 = 1
≤ 1 ( 1 + 1 ) ≤ 1 + 1 (1 + 1) = 𝑎+𝑏2 3𝑎𝑏+𝑎𝑐 2𝑏+𝑏+𝑐 4 2𝑏 𝑏+𝑐 8𝑏 16 𝑏 𝑐 1 (3 + 1) 16 𝑏 𝑐
Chứng minh tương tự, ta có 𝑏 1 3 1 𝑐 1 3 1 ≤ ( + ) ; ≤ ( + ) 𝑏 + 𝑐2 16 𝑐 𝑎 𝑐 + 𝑎2 16 𝑎 𝑏
Cộng ba bất đẳng thức cùng chiều, ta được điều phải chứng minh. 0,25đ
Dấu bằng xảy ra khi a = b = c