

Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN, BIỂU ĐIỂM CHẤM THẠCH THẤT
BÀI KIỂM TRA HỌC KÌ I
Năm học: 2022 - 2023
(Hướng dẫn chấm gồm 03 trang) MÔN: TOÁN LỚP 9 BÀI Ý HƯỚNG DẪN ĐIỂM 1)
3x − 6 có nghĩa khi 3x − 6 0 x 2 0,5đ 1 1 1 a) 12 − 27 +
48 = 2 3 − 3 3 + .4 3 = (2 − 3 + 2) 3 = 3 2 2 0,5đ (1,5 2) − + + điểm 2 2 2 5 4 2 5 4 ) b) + =..= = 4 5 2 0,5đ 5 + 2 5 − 2 ( 5) 2 − 2 a
y = (m + 1)x – 2 là hàm số trên nghịch biến khi m + 1 < 0 m < -1 0,5đ 2
Với m = 1 thì hàm số có dạng: y = 2x – (1,5 2 1 đ điểm b )
HS trình bày đầy đủ các bước và vẽ đúng Tính A khi x = 16
Với x = 16 (Thỏa mãn ĐKXĐ). Khi đó A = 16 0,25đ a 16 + 2 4 4 2 A = = = 0,5đ 3 4 + 2 6 3 (2,5
Rút gọn biểu thức B ( với x 0; x 4) điểm ) x 1 1 0,5đ B = + +
( x − 2)( x + 2) x − 2 x + 2
x + x + 2 + x − 2 B = 0,25đ b ( x − 2)( x + 2) x + 2 x B = 0,25đ ( x − 2)( x + 2) x( x + 2) x B = = 0,25đ
( x − 2)( x + 2) x − 2
Tìm các giá trị nguyên của x để biểu thức Q = A.B có giá trị là số nguyên.
với ĐKXĐ x 0 và x 4 ta có: x x x x − 4 + 4 4 Q = A.B = . = = 1+ 0,25đ + − = x − 4 x − 4 x − 4 c x 2 x 2
Vì x là số nguyên, nên x – 4 là số nguyên Do đó: Q Z 4 Z x- 4 Ư x − 4 (4) = {-1; -2; - 4; 1; 2; 4}
Tìm được x {0; 2; 3; 5; 6; 8} 0,25đ
Kết hợp với đk và kết luận ………. 1
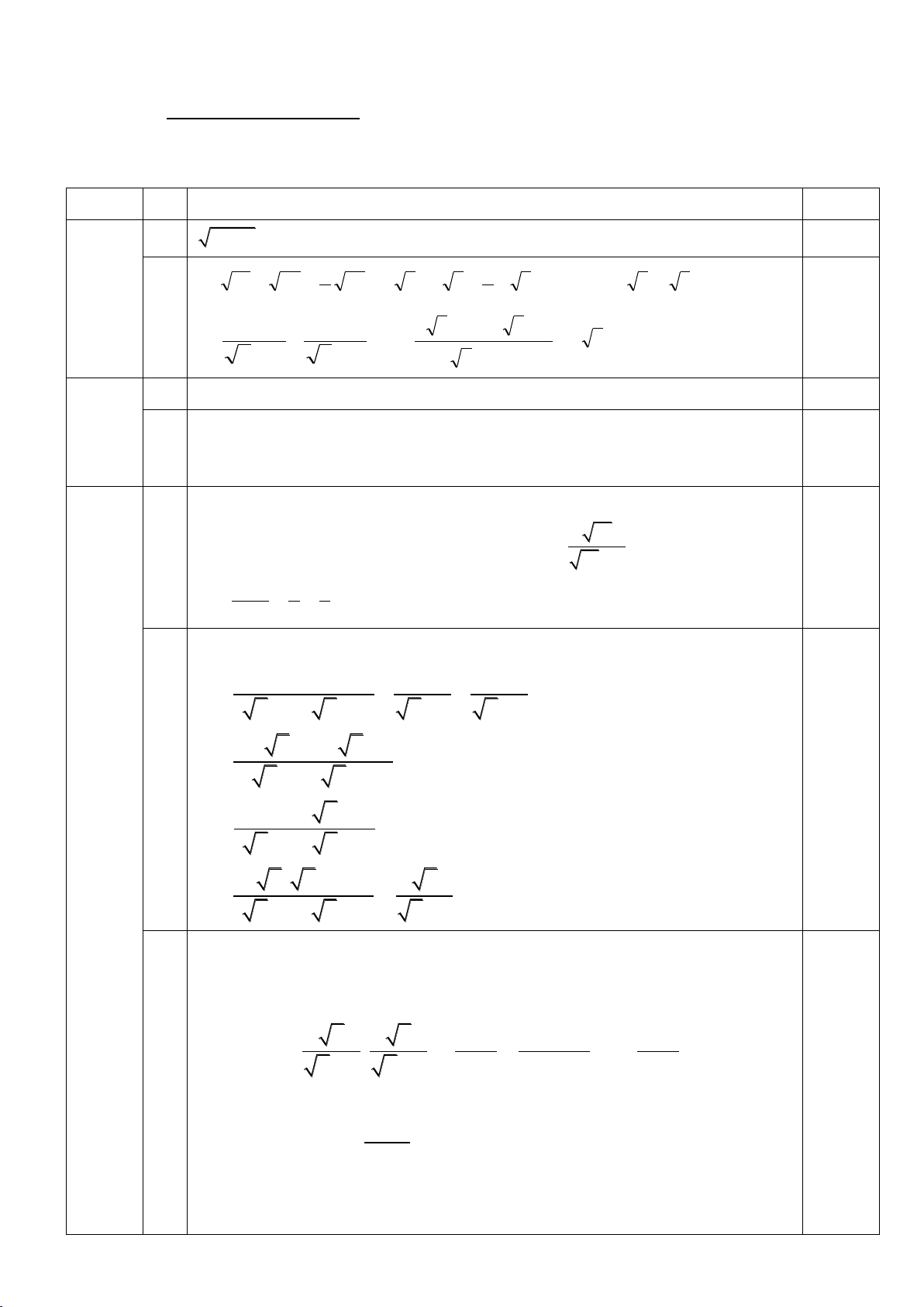
Gọi chiều cao của cột cờ là AB B Bóng của cột cờ là AC
Do ABC vuông tại A nên ta có: 1) AB = AC.tanC 1,0đ = 12.tan350 12m 350 8,402 (m) A C
(Không có hình vẽ thì phải dẫn giải)
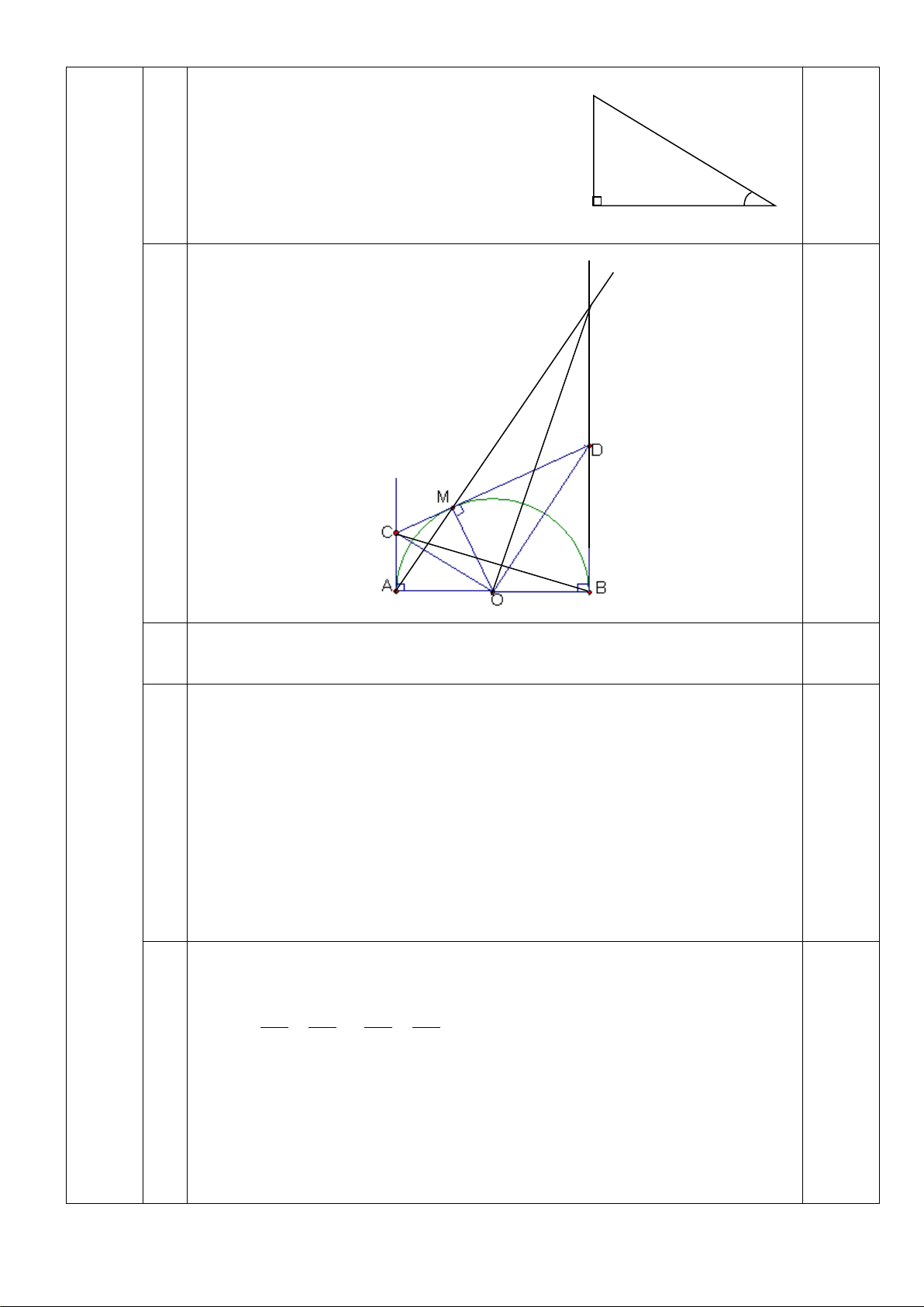
Vẽ hình đúng đến câu a. y K 0,5đ x H 4 (4,0 0,5đ điểm) a
Ta có AC = CM; BD = MD (T/c hai tiếp tuyến cắt nhau) CD = CM + MD = AC + BD. 0,25đ
* Theo tính chất 2 tiếp tuyến cắt nhau, ta có:
OC là tia phân giác của AOM 0,25đ OD là tia phân giác của BOM
Mà AOM và BOM là hai góc kề bù nên 0,25đ b OC ⊥ OD tại O
Hay COD = 900 . Trong tam giác vuông COD có OM là đường cao.
CM. MD = OM2 (hệ thức lượng trong tam giác vuông). 0,5đ mà CM = AC, MD = BD, OM = R. AC. BD = R2. 0,25đ
* Chứng minh: ACO đồng dạng BAK (CAO = ABK = 900;
AOC = BKA vì cùng phụ với KAB ) 0,25đ AC AO AC BO Suy ra = =
tanCBA = tanOKB CBA = OKB AB BK AB BK
Gọi H là giao điểm của OK và BC c
Ta có CBA = OKB HBO = OKB
Mà OKB + KOB = 900 (OBK vuông tại B)
HBO+ KOB = 900 0,25đ
Hay HBO + HOB = 900 OHB = 900 OK ⊥ BC tại H 2 ĐKXĐ: với mọi x 2
x + 4x + 7 = (x + ) 4 2 x + 7 (1) 2
x + 4x + 7 − (x + ) 4 2 x + 7 = 0 5 2 2 2
x + − x x + + x − x + = (0,5 điểm) 7 7 4 4 7 0 0,5đ ( 2 x + 7 − )( 2 x x + 7 − ) 4 = 0 ( 2
x + 7 − x) = 0 hoặc ( 2 x + 7 − ) 4 = 0
Vậy phương trình (1) có 2 nghiệm x = − ; 3 x = 3 1 2
Chú ý: - Học sinh làm cách khác đúng vẫn cho điểm tối đa;
- Điểm toàn bài làm tròn đến 0,5 điểm./. 3
Document Outline
- Doc1
- HD CHẤM Bài kiểm tra HK I (22-23)TOÁN 9




