Đề học kì 1 Toán 9 năm 2023 – 2024 sở GD&ĐT Thái Bình

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KÌ I NĂM HỌC 2023 - 2024 THÁI BÌNH Môn: TOÁN 9
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1. (2,0 điểm)
1) Rút gọn các biểu thức:
a) A  8  2 18  3 32 b) B     2 4 10 5 1  5 1 5
2) Giải phương trình: 16x 16  4x  4  x 1  2
Bài 2. (1,5 điểm)  x  2 x x  1 Cho biểu thức A    .
(với x  0; x  4 )   x 1 x 2 x x 2     
1) Rút gọn biểu thức A.
2) Tìm x để A < 0.
Bài 3. (2,0 điểm)
Cho hàm số y = (m – 2)x + 2m – 1 có đồ thị là đường thẳng (d)
1) Với m = 1 hàm số trên đồng biến hay nghịch biến? Vì sao?
2) Tìm m để (d) song song với đường thẳng (d’): y = – 2x + 3.
3) Tìm m để (d) cắt đường thẳng (d1): y = x – 2 tại một điểm thuộc trục hoành.
Bài 4. (4,0 điểm)
1) Một tòa nhà cao tầng vuông góc với mặt đất. Tại thời điểm tia nắng tạo với mặt
đất một góc bằng 50o thì bóng của tòa nhà trên mặt đất dài 63m. Tính chiều cao
của tòa nhà (kết quả làm tròn đến chữ số hàng đơn vị).
2) Từ điểm A ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến AB, AC (với B và C là hai
tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn;
b) Chứng minh OA  BC và tính tích OH.OA theo R;
c) Tia AO cắt đường tròn (O; R) tại M, N (M nằm giữa A và N). Chứng minh: AM.AN = AH.AO;
d) Kẻ đường kính BD của đường tròn (O; R). Gọi E là hình chiếu của C trên BD,
K là giao điểm của AD và CE. Chứng minh K là trung điểm CE.
Bài 5. (0,5 điểm) 9
Cho x, y, z là các số thực dương thỏa mãn xy  yz  xz 
. Tìm giá trị nhỏ nhất của 4 biểu thức 2 2 2
A  x 14 y 10z  4 2 y . --- HẾT ---
Họ và tên:................................................................. Số báo danh:................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I NĂM HỌC 2023-2024 THÁI BÌNH
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN 9 (Gồm 05 trang)
Bài 1. (2,0 điểm)
1) Rút gọn các biểu thức: a) A  8  2 18  3 32 b) B     2 4 10 5 1  5 1 5
2) Giải phương trình: 16x 16  4x  4  x 1  2 Ý Đáp án Điểm 1)
a) A  8  2 18  3 32 1,0 đ  4.2  2 9.2  3 16.2 0,25  2 2  2.3 2  3.4 2  2 2  6 2 12 2 = 2  6 12 2  4  2 0,25 b) B     2 4 10 5 1  5 1 5 4 5   1 10 5   5 1  0,25  5  1 5  1 5 4( 5 1)   5 1 2 5 5 1  5 1 5 1 2 5 0,25 = 0 2)
2. Giải phương trình: 16x 16  4x  4  x 1  2 (1) 0,25 1,0 đ
Đkxđ: x 1  0  x  1
PT (1)  16(x 1)  4(x 1)  x 1  2 0,25
 4 x 1  2 x 1  x 1  2  x 1  2  x 1  4 0,25  x  5 (nhận)
Vậy tập nghiệm của phương trình là S    5 . 0,25 1
Bài 2. (1,5 điểm)  x  2 x x  1 Cho biểu thức A    .
(với x  0; x  4 )   x 1 x 2 x x 2     
1) Rút gọn biểu thức A.
2) Tìm x để A < 0. Ý Đáp án Điểm
Với x  0; x  4 , ta có:  x ( x  2) x  1 0,25 A    .  x ( x 2) x 2    x 1    x  2 x  1 x  2  x 1 1)    .  . 0,25  x 2 x 2    x 1 x  2 x 1 1,0đ   2 x  2 1 2( x 1) 1 2  .  .  0,25 x  2 x 1 x  2 x 1 x  2 2 Vậy A 
với x  0; x  4 . 0,25 x  2
Với x  0; x  4 , để A < 0 thì: 2 2)  0  x  2  0 
x  2  x  4 0,25 x  2 0,5đ
Kết hợp với điều kiện x  0; x  4 suy ra: 0  x  4
Vậy với 0  x  4 thì A  0 . 0,25
Bài 3. (2,0 điểm)
Cho hàm số y = (m – 2)x + 2m – 1 có đồ thị là đường thẳng (d)
1) Với m = 1 hàm số trên đồng biến hay nghịch biến? Vì sao?
2) Tìm m để (d) song song với đường thẳng (d’): y = – 2x + 3
3) Tìm m để (d) cắt đường thẳng (d1): y = x – 2 tại một điểm thuộc trục hoành. Ý Đáp án Điểm 1) y = (m – 2)x + 2m – 1 0,25
0,5 đ Thay m = 1 vào hàm số ta có y = – x +1
Khi đó hệ số a = –1 < 0 nên hàm số trên nghịch biến. 0,25
Vậy với m = 1 thì hàm số đã cho nghịch biến 2) m  2  2 0,25
Để (d) song song với (d’): y = – 2x + 3 thì  0,75 đ 2m 1  3  m  0 0,25    m = 0 m  2 
Vậy m = 0 thì (d) // (d’) 0,25 2 3)
Đường thẳng (d) cắt đường thẳng (d1): y = x – 2 khi :
0,75 đ m – 2 ≠ 1  m ≠ 3. 0,25 Giao điểm của (d) và (d
1) nằm trên trục hoành nên giao điểm có tung độ là y = 0
Thay y = 0 vào (d1)  0 = x – 2  x = 2 Thay x = 2; y = 0 vào (d) 0,25
Ta có: 0 = (m – 2). 2 + 2m – 1  2m – 4 + 2m – 1 = 0 5  4m = 5 m = (thoả mãn điều kiện) 4 5 0,25 Vậy m =
thì (d) cắt (d’) tại một điểm nằm trên trục hoành. 4
Bài 4. (4,0 điểm)
1) Một tòa nhà cao tầng vuông góc với mặt đất. Tại thời điểm tia nắng tạo với mặt đất
một góc bằng 50o thì bóng của tòa nhà trên mặt đất dài 63m. Tính chiều cao của tòa
nhà (kết quả làm tròn đến chữ số hàng đơn vị).
2) Từ điểm A ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến AB, AC (với B và C là hai
tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn;
b) Chứng minh OA  BC và tính tích OH. OA theo R;
c) Tia AO cắt đường tròn (O; R) tại M, N (M nằm giữa A và N) .
Chứng minh: AM. AN = AH. AO;
d) Kẻ đường kính BD của đường tròn (O; R). Gọi E là hình chiếu của C trên BD,
K là giao điểm của AD và CE. Chứng minh K là trung điểm CE. Ý Đáp án Điểm B 1
Gọi chiều cao tòa nhà là AB, bóng của tòa nhà trên mặt đất là AC
0,5 đ Xét ABC vuông tại A, ta có AB = AC.tan C 0,25  AB = 63. tan 50o  AB  75 (m) C A
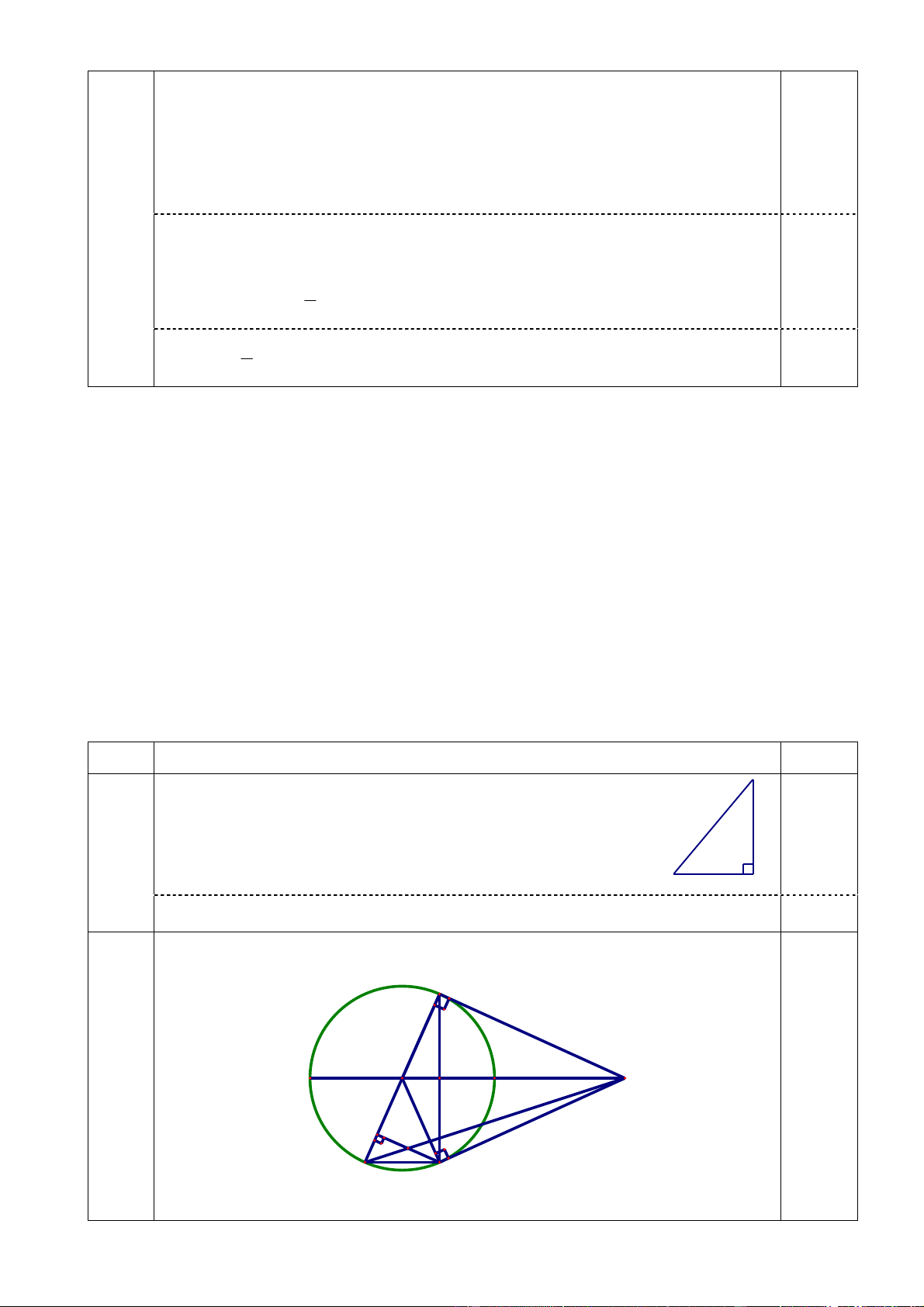
Vậy tòa nhà cao khoảng 75 m 0,25 B 2 O N A 3,5 đ H M E K D C 3 a)
- Đường tròn (O; R) có AB là tiếp tuyến, B là tiếp điểm suy ra ABOB 0,25
tại B OAB vuông tại B  3 điểm A, B, O cùng thuộc đường tròn đường kính AO (1)
- Chứng minh tương tự có 3 điểm A, C, O cùng thuộc đường tròn đường 0,25 kính AO (2)
Từ (1) và (2) suy ra 4 điểm A, B, O, C cùng thuộc đường tròn đường 0,25 kính AO b)
- Đường tròn (O; R) có AB, AC là 2 tiếp tuyến cắt nhau tại A 0, 5
 AB = AC (tính chất)  A thuộc trung trực của BC (3)
Mặt khác OB = OC = R  O thuộc trung trực của BC (4)
Từ (3) và (4) suy ra OA là đường trung trực của đoạn thẳng BC Suy ra OA  BC tại H 0,25
- Xét OAB vuông tại B, đường cao BH
Suy ra: OH.OA= OB2 (hệ thức về cạnh và đường cao trong tam giác 0,25 vuông) Mà OB= R suy ra OH. OA= R2 0,25 c)
- Xét OAB vuông tại B, đường cao BH có
AH. AO = AB2 (hệ thức về cạnh và đường cao trong tam giác vuông) (5) 0,25
AB2 = AO2 – R2 (định lí Py-ta-go) (6) 0,25
- Có AM. AN = (AO – OM)(AO + ON) = AO2 – R2 (7) 0,25
Từ (5), (6), (7) suy ra AM. AN = AH. AO. 0,25 d)
Có CE // AB ( cùng vuông góc với BD ) EK DE Suy ra 
(hệ quả định lí Ta-let )  EK. BD = DE. AB (8) AB DB 0,25
Chứng minh được: ABO CED (g-g) DE CE Suy ra: 
(tính chất ) CE. BO = DE. AB (9) BO AB
Từ (8) và (9) suy ra: CE. BO = EK. BD
Mà BD = 2BO, suy ra CE. BO = EK. 2BO  CE = 2EK 0,25
Suy ra K là trung điểm của CE 4
Bài 5. (0,5 điểm) 9
Cho x, y, z là các số thực dương thỏa mãn xy  yz  xz 
. Tìm giá trị nhỏ nhất của 4 biểu thức 2 2 2
A  x 14 y 10z  4 2 y Ý Đáp án Điểm 0,5đ 2 2  x   x  2 2 A = + 8y + + 8z + 2      2 2 y + z  2 + 4y  4 2y 2 2     2 2  x   x  = + 8y + + 8z + 2     y + z  + 2y - 2 2 2 2 2 1 + 4y - 4 2y -1 2 2     2 2  x   x  = + 8y + + 8z + 2     y + z  2 + 2y - 2 2 2 2 2 1 + 2  2y -  1 - 3 0,25 2 2     2 2 x x Vì 2 2  8 y  4xy;  8z  4xz; 2 2 2 2 2 2
2( y  z )  4 yz; (2 y 1)  0; 2( 2 y 1)  0 Suy ra
A ≥ 4xy + 4xz + 4yz - 3  A ≥ 4(xy + xz + yz) – 3 9  A  4.  3  A  6 4 2 2  x x 2 2  8 y ;  8z  2 2   2 2 2 2
Dấu bằng xảy ra khi 2( y  z )  0; (2 y 1)  0; 2( 2 y 1)  0  9
xy  yz  zx   4  x  2    1 y  z    2 x  2  Vậy MinA = 6 khi  1 0,25 y  z    2 Ghi chú:
- Nếu học sinh làm cách khác đúng vẫn cho điểm tối đa
- Bài 4 ý 2 không vẽ hình hoặc vẽ sai hình thì không chấm điểm. ______________________ 5
Document Outline

• De_TOAN9__I_23-24
• DapAn_TOAN9__I_23-24