


Preview text:
UBND QUẬN TÂY HỒ
ĐỀ KIỂM TRA HỌC KÌ II
TRƯỜNG THCS CHU VĂN AN
MÔN: TOÁN – LỚP 9
Năm học 2022 – 2023 (Đề có 01 trang)
Thời gian làm bài: 90 phút
Bài 1 (2,0 điểm) Cho hai biểu thức: x − + M = và x x x x N = 1+ 1+ với x ≥ 0; x ≠ 1 x +1 1 x 1 x − +
1) Tính giá trị của biểu thức M tại x = 36 2) Chứng tỏ N = 1 − x.
3) Tìm giá trị của x thỏa mãn M.N = − x − 3.
Bài II (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một lâm trường dự định trồng 75 ha rừng trong một số tuần. Khi thực hiện, do cải tiến kĩ
thuật nên mỗi tuần họ trồng vượt mức 5 ha so với kế hoạch. Vì vậy lâm trường đã trồng được
80 ha và hoàn thành sớm hơn dự định 1 tuần. Hỏi mỗi tuần lâm trường dự định trồng bao nhiêu ha rừng?
2) Một chiếc nón lá có đường sinh bằng 30cm, đường kính đáy bằng 40cm. Người ta dùng
hai lớp lá để phủ lên bề mặt xung quanh của nón. Tính diện tích lá cần dùng cho một chiếc nón đó.
Bài III (2,0 điểm) 2 3 7 + =
1) Giải hệ phương trình sau: x −1 y −1 2 3 2 − = 2
x −1 y −1
2) Trong mặt phẳng tọa độ Oxy, cho parabol (P): 2 y = x và đường thẳng (d) : y = mx + m + 1
a) Khi m = 2, không vẽ đồ thị, hãy tìm tọa độ giao điểm của (P) và (d).
b) Tìm các giá trị của m để (d) cắt (P) tại 2 điểm phân biệt nằm về bên phải của trục tung.
Bài IV (3,0 điểm)
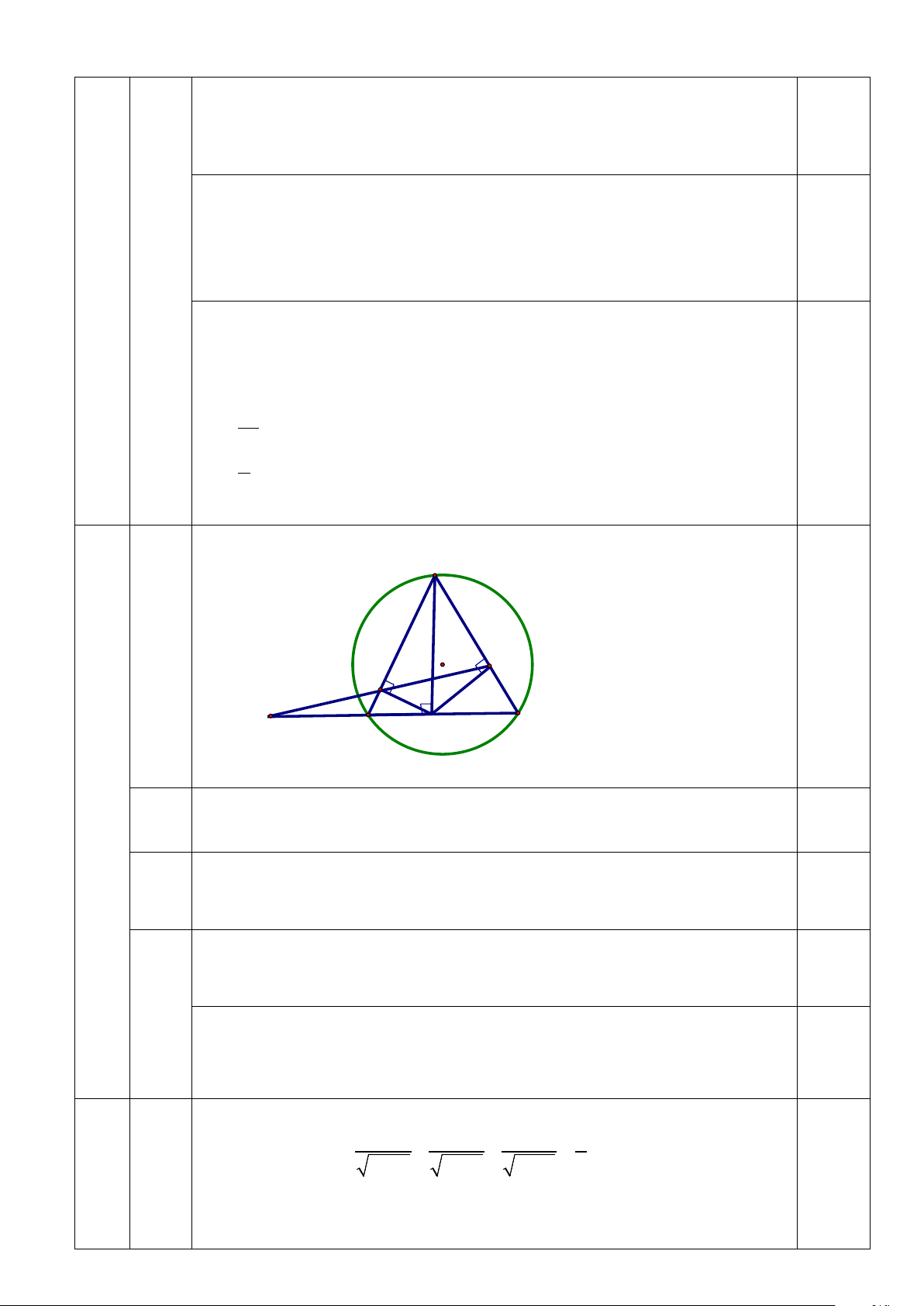
Cho ΔABC nhọn (AB < AC) nội tiếp đường tròn (O) , đường cao AH. Gọi M và N lần
lượt là hình chiếu của H trên cạnh AB và AC.
1) Chứng minh: Bốn điểm A, M, H, N cùng nằm trên một đường tròn.
2) Chứng minh: tam giác AMN và tam giác ACB đồng dạng.
3) Đường thẳng NM cắt đường thẳng BC tại P. Chứng minh: 2 PH = PB.PC.
Bài V (0,5 điểm) Cho a,b,c là các số dương thỏa mãn điều kiện ab + bc +ca =1. Chứng minh rằng: a b c 3 + + ≤ 2 2 2 1+ a 1+ b 1+ c 2
-------------------Hết-------------------
Giáo viên coi kiểm tra không giải thích gì thêm.
Họ và tên học sinh: …………………………………………… SBD: …………… UBND QUẬN TÂY HỒ HƯỚNG DẪN CHẤM
TRƯỜNG THCS CHU VĂN AN
MÔN: TOÁN – LỚP 9 HK II
Năm học 2022 – 2023 BÀI CÂU NỘI DUNG ĐIỂM Thay x = 36 (tmđk) vào M a 0,25 6 0,5 ⇒ x = 36 = 6; M = 7 0,25 1 b
2,0 1,0 Rút gọn được N =1− x (đpcm) 1,0 c) M.N
= − x − 3 ⇔ x (1− x) = − x − 3 c
0,5 ⇔ ( x − 3)( x + ) 1 = 0 0,25 ⇔ x = 9(tmdk) 0,25
Gọi số ha rừng lâm trường dự định trồng trong mỗi tuần là x (ha; x > 0) 0,25
Thời gian trồng rừng theo theo kế hoạch là: 75 (tuần) 0,25 x
Thực tế mỗi tuần lâm trường trồng được x + 5 (ha) 0,25
1) Thời gian trồng rừng trên thực tế là: 80 (tuần) 0,25 2,0 x + 5
Vì thực tế hoàn thành sớm hơn dự định 1 tuần nên ta có phương trình 0,25 75 80 − = 1 x x + 5 2 2
⇔ x +10x − 375 = 0 2,5
Giải được x = 15 (TMĐK) hoặc x = -25 (L) 0,5
Vậy số ha rừng lâm trường dự định trồng trong một tuần là 15 ha 0,25
Bán kính đáy của hình nón là r = 40 : 2 = 20cm
Diện tích xung quanh của hình nón là 0,25 2) 2
S = π rl = π.20.30 = 600π (cm )
0,5 Người ta dùng hai lớp lá để phủ lên bề mặt xung quanh của nón nên diện 0,25
tích lá cần dùng cho một chiếc nón đó là: 2 600π.2 =1200π (cm ) 2 3 7 + =
x −1 y −1 2
(x ≠ 1; y ≠ 1) 3 2 0,25 − = 2 3
x −1 y −1 2,0 1 = 1 1 x −1 Tìm được 1,0 1 1 0,5 = y −1 2 1 ...Tìm được x = 2 (t/m) y = 3 (t/m) 0,25
Vậy nghiệm của hệ là (x;y) = (2;3)
2a) Thay m = 2 vào y = 2x + m + 1 ⇒ y = 2x + 3 0, 25
ta được phương trình hoành độ giao điểm của (P) và (d) là: 2
x − 2x − 3 = 0 (1)
Giải phương trình (1) và tìm được tọa độ giao điểm là A( 1 − ;1) và B 3 ( ;9) 0, 25 2
1,0 2b) (d) cắt (P) tại 2 điểm phân biệt nằm về bên phải của trục tung khi
phương trình hoành độ giao điểm có hai nghiệm dương phân biệt ∆ > 0 0,25 − b m > 0 ⇔ > 0 ⇒ ... ⇒ ⇒ m ∈ ∅ a m < 1 − c > 0 0,25 a
Vậy không có giá trị của m thỏa mãn điều kiện đề bài A o N M P H C B
Vẽ hình đến hết câu a 0,25
a) Chứng minh được A, M, H, N cùng thuộc một đường tròn a 1,25 1,25 0,75 b
b) Chứng minh được
AMN = AHN = ACB 4 1,0 ⇒ A ∆ MN ∽ A ∆ CB (g.g) 3,0 0,25
c) Chứng minh được
MHB = MNH (= MAH ). 0,25 ⇒ ∆ c PMH ∽ PH ∆ N (g.g) 2
⇒ PM.PN = PH
0,5 Chứng minh được
PMB = AMN = ACB. 0,25 ⇒ PM ∆ B ∽ PC ∆
N (g.g) ⇒ PM.PN = PB.PC 2
⇒ PH = PB.PC
Cho a,b,c là các số dương thỏa mãn điều kiện ab + bc +ca =1. a b c 3 Chứng minh rằng: + + ≤ 2 2 2 1+ a 1+ b 1+ c 2 0, 5 2 2
1 + a = ab + bc + ca + a = (a + b)(a + c) 5 tương tự 2
1 + b = (b + a)(b + c) 2 0,5 2
1 + c = (c + a)(c + b)
Áp dụng bất đẳng thức Cauchy cho các số dương 1 1 1 ; ;
a + b b + c c + a 1 1 2 b b 2b + ≥ ⇒ + ≥
a + b b + c
(a +b)(b + c) 2
a + b b + c 1+ b Ta có: 1 1 2 c c 2c + ≥ ⇒ + ≥
b + c c + a
(b + c)(c + a) 2
b + c c + a 1+ c 1 1 2 a a 2a + ≥ ⇒ + ≥
c + a a + b
(c + a)(a +b) 2
c + a a + b 1+ a
Cộng từng vế của các bất đẳng thức ta có:
a + b b + c c + a + + ≥ 2 a b c + + 2 2 2
a + b b + c c + a 1+ a 1+ b 1+ c 3 a b c ⇒ ≥ + + ( Điều phải c/m) 2 2 2 2 1+ a 1+ b 1+ c
*) Lưu ý: Nếu học sinh giải theo cách khác đúng, cho điểm tương đương. 3




