Đề học kỳ 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Hà Trung – Thanh Hóa
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề khảo sát chất lượng cuối học kỳ 1 môn Toán 9 năm học 2023 – 2024 phòng Giáo dục và Đào tạo UBND huyện Hà Trung, tỉnh Thanh Hóa; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem.
Preview text:
UBND HUYỆN HÀ TRUNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023-2024 Môn: Toán 9
Thời gian: 90 phút (Không
kể thời gian giao đề)
Bài 1: (2 điểm)
1) Trục căn thức ở mẫu của biểu thức: 5 A = 7 − 2
2) Cho biểu thức: B = 1 1 x +1 + :
(với x >0; x≠1 ) x − x
x −1 x − 2 x +1 a) Rút gọn B b) Tìm x để B = -1
Bài 2: ( 2 điểm)
Cho hàm số y = (m +2)x - 2 (với m ≠-2) có đồ thị là đường thẳng (d)
1) Tìm m biết đồ thị hàm số đi qua điểm I(2; 4).
2) Vẽ đồ thị hàm số đã cho với m vừa tìm được ở ý 1.
3) Gọi A, B lần lượt là giao điểm của (d) với hai trục Ox và Oy. Tìm m, để tỉ
số độ dài của hai đoạn thẳng OB và OA bằng 3.
Bài 3: (2 điểm)
1) Giải phương trình: 2x + 5y =1 x − 2y = 2
2) Giải hệ phương trình: 2x − 6y = 5
Bài 4: (3,5 điểm)
Cho nửa đường tròn (O , R) có đường kính AB. Lấy điểm C tùy ý trên nửa đường
tròn (C khác A và B). Gọi H là trung điểm của AC.
1) Tính số đo góc ACB và chứng minh: OH / BC.
2) Tiếp tuyến tại C của (O) cắt OH ở M. Chứng minh AM là tiếp tuyến của (O).
3) Đường thẳng MB cắt (O) tại K. Chứng minh rằng : 2
MO − MK.MB có giá trị không đổi.
Bài 5: (0,5 điểm) 2 2
Cho x > y và x.y = 1.Tìm giá trị nhỏ nhất của biểu thức M = x + y x − y
------------------HẾT-----------------
Cán bộ coi thi không giải thích gì thêm. UBND HUYỆN HÀ TRUNG
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
CHẤT LƯỢNG HỌC KỲ I, NĂM HỌC 2023-2024
MÔN: T oán 9 BÀI NỘI DUNG ĐIỂM Bài 1 (2 điểm)
1) Trục căn thức ở mẫu của biẻu thức: 5 A = 7 − 2
2) Cho biểu thức: B = 1 1 x +1 + :
(với x >0; x≠1 ) x − x
x −1 x − 2 x +1
a) Rút gọn B
b) Tìm x để B = -1 1) 5( 7 + 2 5 ) A = = 0,25 7 − 2 7 − 2 5( 7 + 2) = = 7 + 2 0,25 5 2) a) Rút gọn : 1 1 x +1 1 x x +1 B : = + = + 0,5 x − x x − x − x +
x ( x − ) x ( x − ) : 1 2 1 1 1 ( x − )2 1 ( x x − + )2 1 1 x −1 0,5 = = x ( x − ). 1 x +1 x
b) Với x >0; x≠1 x −1 B = 1 − ⇒ = 1
− ⇔ x −1 = − x ⇔ 2 x =1 x 0,25 1 1
⇔ x = ⇔ x = (TM ) 2 4 0,25
Bài 2:( 2 điểm)
Cho hàm số y = (m +2)x - 2 (với m ≠-2) có đồ thị là đường thẳng (d)
1)Tìm m biết đồ thị hàm số đi qua I(2; 4).
2) Vẽ đồ thị hàm số đã cho với m vừa tìm được ở ý 1.
3) Gọi A, B lần lượt là giao điểm của (d) với hai trục Ox và Oy. Tìm m,
biết tỉ số độ dài của hai đoạn thẳng OB và OA bằng 3.
1) Vì (d) di qua I(2;4) nên thay x= 2; y= 4 vào hàm số ta được: 0,25
4 = (m +2).2 - 2 4 = (m + 2)2 − 2 ⇔ 2m = 2 ⇔ m =1 0,25 2)
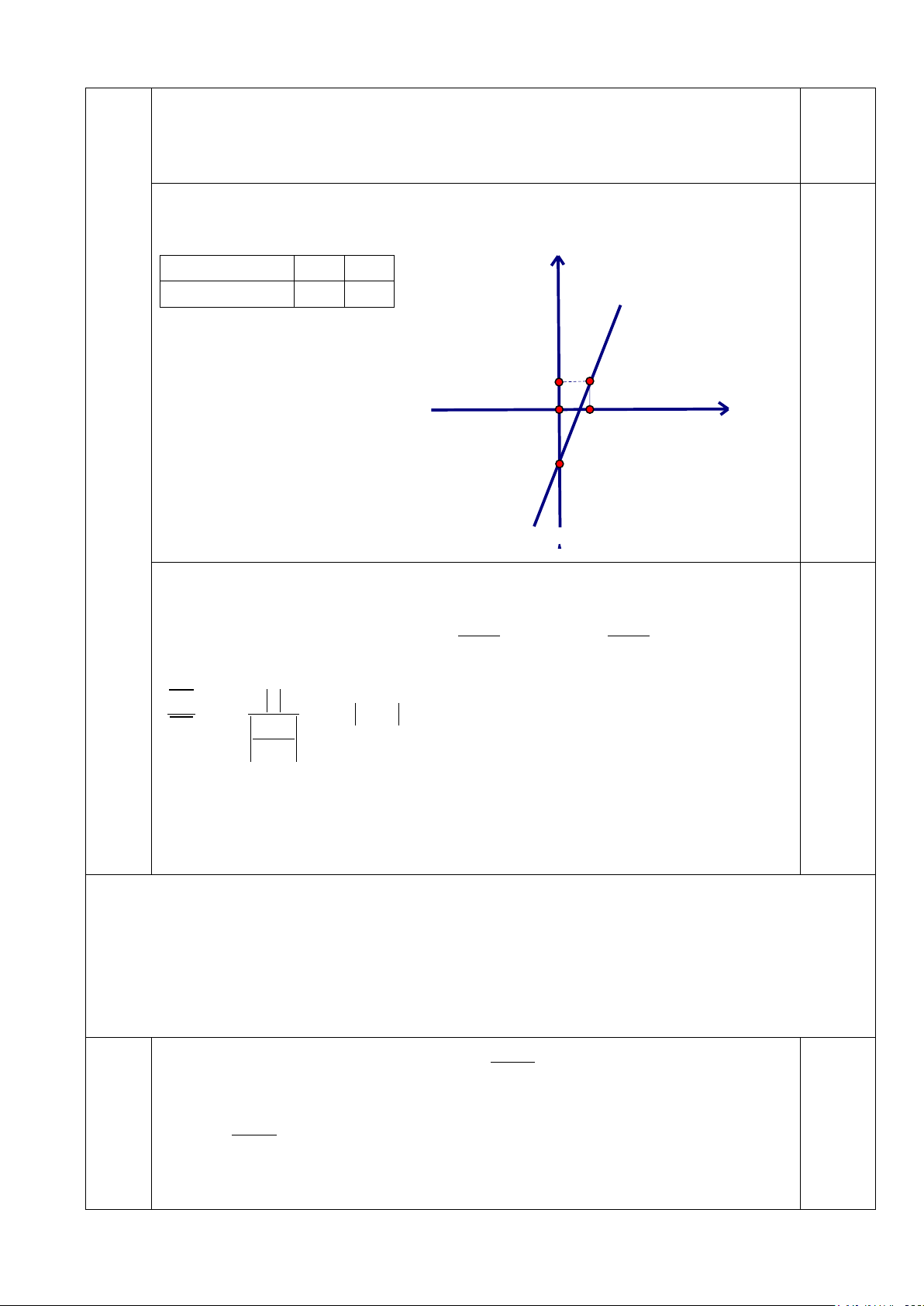
*Thay m= 1 ta được hàm số: y = 3x - 2 0,25 *Bảng giá trị: x 0 1 y 0,25 y = 2x + 5 -2 1 *Đồ thị: y=3x-2 1 O 1 x 0,25 -2
3) Gọi giao điểm của đồ thị hàm số với trục Ox, Oy lần lượt là A và B.
Cho x = 0 thay vào hàm số được y = -2. Suy ra : B(0 ; -2)
Cho y = 0 thay vào hàm số được 2 x = . Suy ra : 2 A ;0 m + 2 m 2 + 0,25 Khi đó : OB 2 = 3 ⇒ = 3 ⇔ m + 2 = 3 OA 2 m + 2 0,25 m + 2 = 3 m =1(TM ) ⇔ ⇔ m 2 3 + = − m = 5( − TM )
Vậy với m = 1 hoặc m = -5 thì tỉ số độ dài của hai đoạn thẳng OB và OA 0,25 bằng 3.
Bài 3:(2 điểm)
1) Giải phương trình: 2x +5y =1 x − 2y = 2
2) Giải hệ phương trình: 2x − 6y = 5 1) Giải phương trình: 1 5 2 5 1 y x y x − + = ⇔ = 2 0,5
Vậy phương trình đã cho có vô số nghiệm. Nghiệm TQ là: ( ) 1−5 ; y x y ; y R = ∈ 2 0,5
2)Giải hệ phương trình: x − 2y = 2 x = 2y + 2 x = 2y + 2 0,25 ⇔ ⇔ 2x − 6y = 5 2 (2y 2) 6y 5 + − = 2 − y =1 x = 2y + 2 x =1 0,5 ⇔ 1 − ⇔ 1 y y − = = 2 2 0,25
Vậy hệ phương trình có 1 nghiệm là : (x y) 1 ; 1; − = 2
Bài 4 : (3,5 điểm)
Cho nửa đường tròn (O , R) có đường kính AB. Lấy điểm C tùy ý trên nửa đường tròn
(C khác A và B). Gọi H là trung điểm của AC.
1)Tính số đo góc ACB và chứng minh: OH // BC.
2)Tiếp tuyến tại C của (O) cắt OH ở M. Chứng minh AM là tiếp tuyến của (O).
4) Đường thẳng MB cắt (O) tại K. Chứng minh rằng : 2
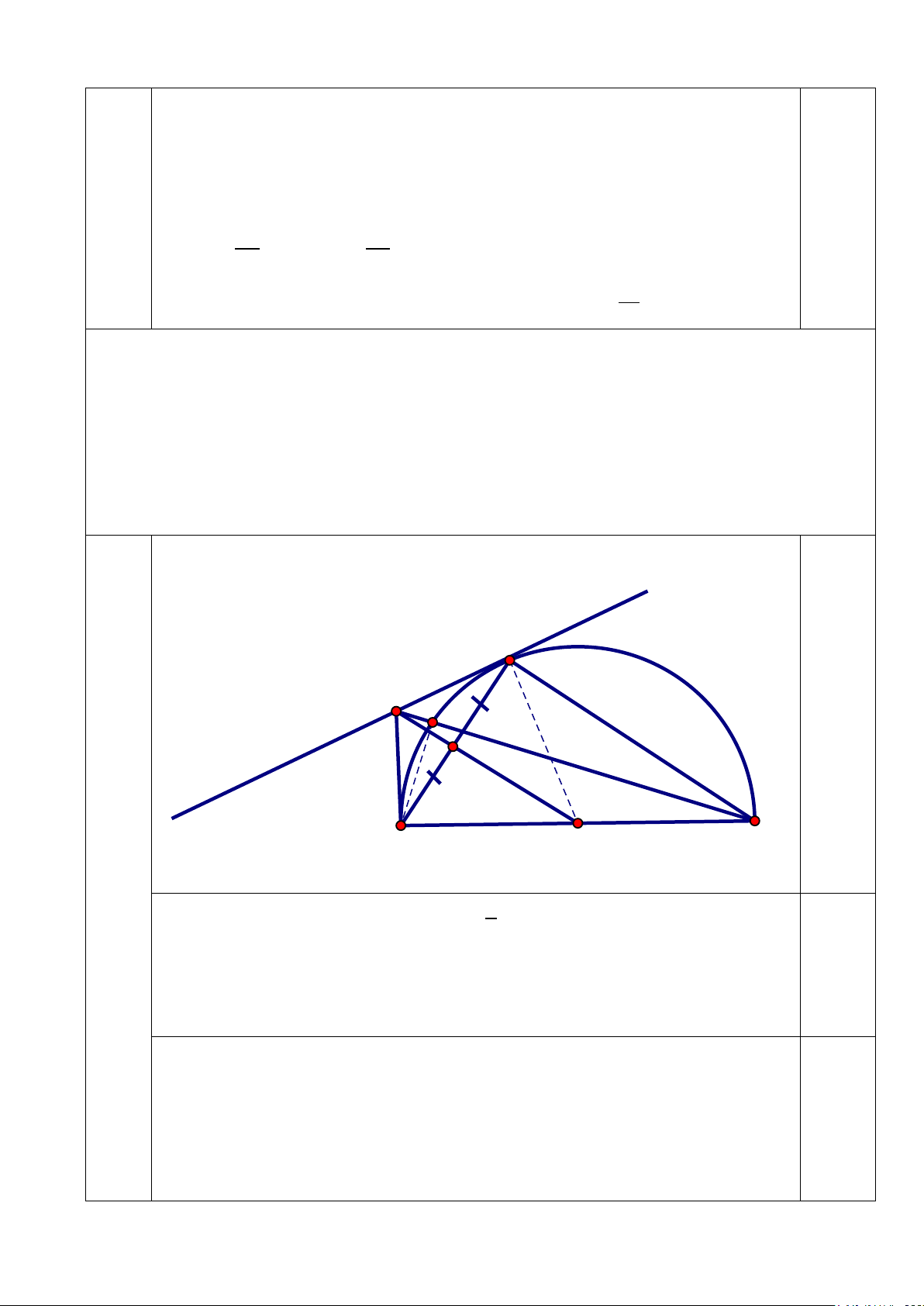
MO − MK.MB có giá trị không đổi. Hình vẽ: C M KH A O B
1)Tam giác CAB có trung tuyến 1
CO = AB => ∆ CAB vuông tại C =>góc 2 0,5 ACB = 900
Vì H là trung điểm của AC => OH ⊥ AC ( Quan hệ đường kính và dây
cung). Do đó OH // BC ( vì cùng vuông góc với AC) 0,5
2) OC = AO = R => ∆ ACO cân tại O
mà AH là đường trung tuyến nên AH cũng là đường phân giác của góc AOC 0,25 =>.Góc AOM = góc COM
Xét hai tam giác AMO và CMO có: MO cạnh chung. 0,5
Góc AOM = góc COM (CM trên) OA = OC = R
Do đó: ∆AMO = ∆CMO (c.g.c) =>.Góc OCM = Góc OAM , mà góc OCM = 0,5
900( t/c tiếp tuyến) nên góc OAM= 900 =>AM ⊥ AO tại A thuộc (O), do đó
AM là tiếp tuyến của (O). 0,25
3) Tam giác AKB vuông tại K (CM tương tự ý 1).=>AK ⊥ MB
Áp dụng hệ thức giữa cạnh và đường cao trong ∆ AMB có: 0,5 MK.MB = MA2. Do đó: 2
MO − MK.MB= 2 2 2 2
MO − MA = AO = R ( không đổi). 0,5
Bài 5: (0,5điểm) 2 2
Cho x > y và x.y = 1.Tìm giá trị nhỏ nhất của biểu thức M = x + y x − y 2 2 2
M = x + y = (x − y) + 2 = (x-y) + 2 ≥ 2 2 x − y x − y x − y 0,25 Dấu= xảy ra khi : 2 x − y =
⇔ (x − y)2 = 2 ⇔ x − y = 2 ⇔ x = 2 + y ( vì x − y x>y)
Lại có: xy = ⇒ y( y + ) 2 1 3 1 2 =1 ⇔ y + = 2 2 1 3 1 3 2 3 y y − ± ⇔ + = ± ⇔ = − ± = 2 2 2 2 2 3− 2 3+ 2 3 − − 2 3 − + 2 y = ⇒ x = ; y = ⇒ x = 0,25 2 2 2 2 + − Vậy GTNN của M bằng 2 2 khi (x y) 3 2 3 2 ; = ; 2 2 ( − + − − x y) 3 2 3 2 ; = ; Hoặc 2 2 Lưu ý:
- Bài hình nếu vẽ hình sai hoặc vẽ không chính xác thì không chấm điểm bài hình.
- Học sinh giải cách giải khác mà đúng thì vẫn cho điểm tối đa.