Đề học kỳ 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Thạch Thất – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra cuối học kỳ 1 môn Toán 9 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Thạch Thất, thành phố Hà Nội; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem.
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO
BÀI KIỂM TRA HỌC KÌ I TẠO THẠCH THẤT
Năm học: 2023 – 2024 MÔN: TOÁN LỚP 9
(Thời gian: 90 phút không kể thời gian giao đề) Bài 1. (1,5 điểm)
1) Tìm điều kiện của x để biểu thức sau có nghĩa: 4x +8 2) Thực hiện phép tính: a) 12 + 2 27 − 3 b) 2 ( 5 − 2) + 2 − 3 5
Bài 2. (2,0 điểm) Cho hai biểu thức: − 2 = x A 2 x x 2x và B = + − (với x > 0; x x + 3 x − 3 x − 9 x ≠ 9)
1) Tính giá trị của biểu thức A tại x = 16. 2) Chứng minh = x B . x + 3 3) Đặt P = .
A B . Tìm các giá trị nguyên của x để P < 0.
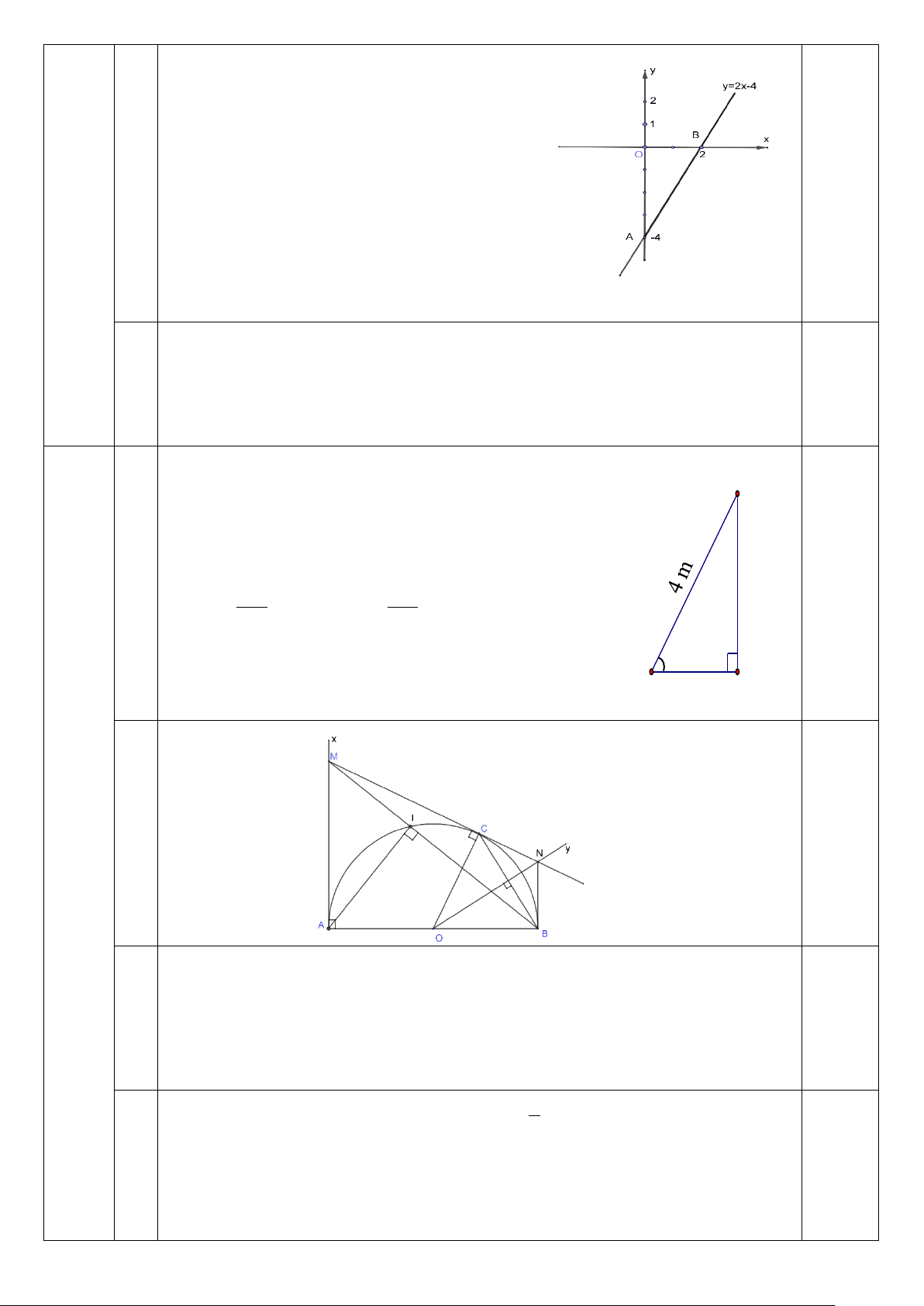
Bài 3. (2,0 điểm): Cho hàm số: y = (m + 1)x - 4 (d) (m là tham số, m ≠ -1)
a) Xác định m để hàm số trên là hàm số đồng biến ?
b) Vẽ đồ thị hàm số trên khi m = 1
c) Tìm m để (d) song song với đường thẳng (d1): y = 2x + 3. Bài 4. (4 điểm):
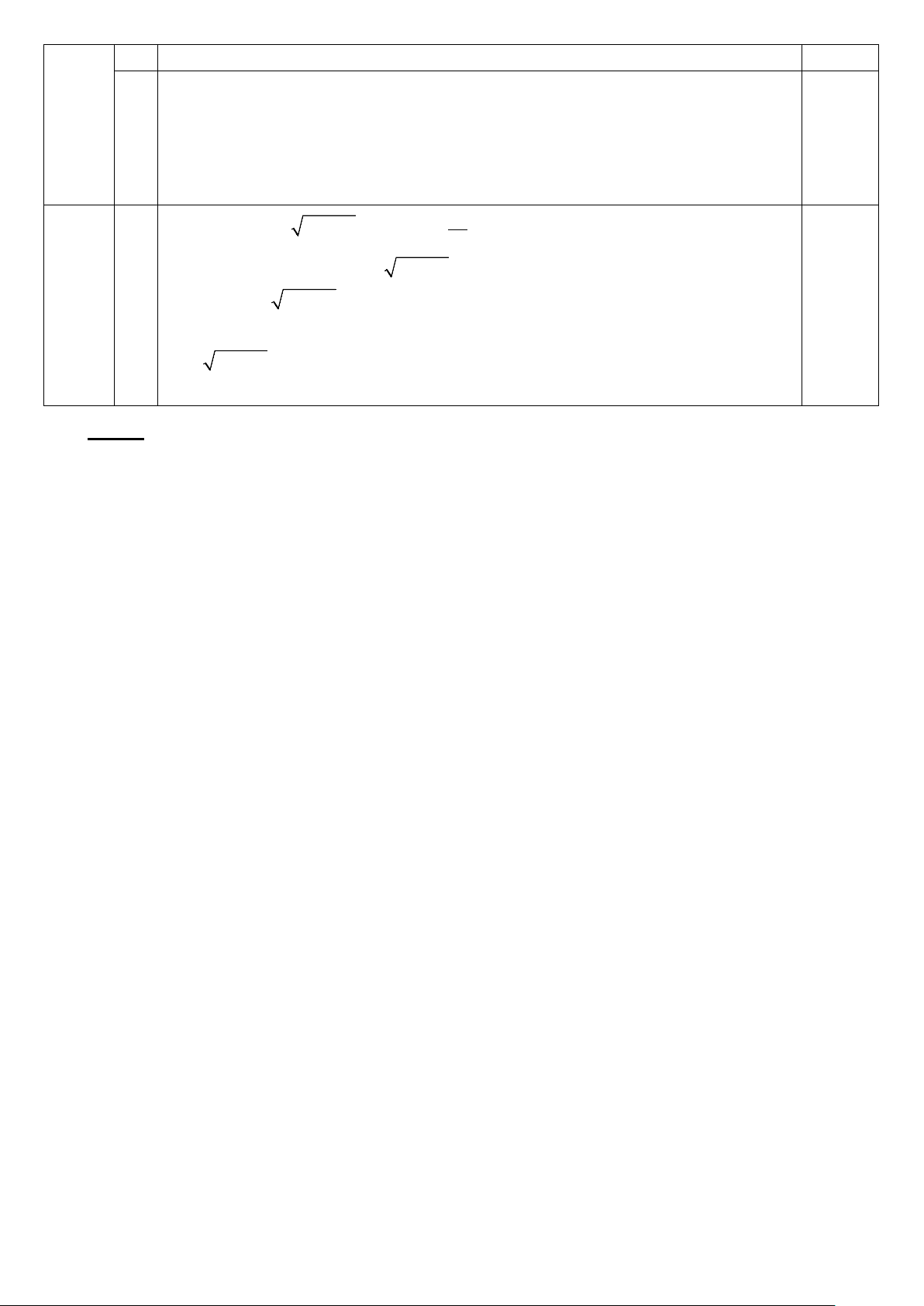
1) Nhà bạn Minh có một chiếc thang dài 4m. Cần
đặt chân thang cách chân tường một khoảng cách
bằng bao nhiêu để nó tạo được với mặt đất một
góc “an toàn” là 65° (tức là đảm bảo thang không
bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
2) Cho nửa đường tròn (O;R), đường kính AB. Kẻ tiếp tuyến Ax với nửa đường tròn.
Gọi C là một điểm thuộc nửa đường tròn (C khác A và B). Tiếp tuyến tại C của nửa
đường tròn cắt Ax tại M. Điểm I là giao điểm của MB với đường tròn (O).
a) Chứng minh 4 điểm C, M, A, O cùng thuộc 1 đường tròn.
b) Chứng minh tam giác AIB vuông và 2
MI.MB = CM .
c) Từ O kẻ tia Oy vuông góc CB, cắt tia MC tại N. Chứng minh NB là tiếp tuyến của đường tròn tâm O.
Bài 5. (0,5 điểm) Giải phương trình: x2 + 9x + 20 = 2. 3x +10
-------------------- HẾT --------------------
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN, BIỂU ĐIỂM CHẤM THẠCH THẤT
BÀI KIỂM TRA HỌC KÌ I
Năm học: 2023 - 2024
(Hướng dẫn chấm gồm 03 trang) MÔN: TOÁN - LỚP 9 BÀI Ý HƯỚNG DẪN ĐIỂM 1
4x +8 có nghĩa khi 4x +8 ≥ 0 ⇒ 4x ≥ 8 − ⇒ x ≥ 2 − 0,5 1 Thực hiện phép tính:
(1,5đ) 1 a) 12 + 2 27 − 3 = 2 3 + 6 3 − 3 = 7 3 0,5 b) 2
( 5 − 2) + 2 − 3 5 = 5 − 2 + 2 − 3 5 = 2 − 5 0.5 Cho hai biểu thức: − 2 x x x = x A và 2 2 B = + − (với x > 0; x ≠ 9) x x + 3 x − 3 x − 9
Thay x = 16 (t/m ĐKXĐ) vào A 1 16 2 1 A − = = 0,5 16 2 Chứng minh x B = ; x − 3 2 x x 2x 2 x x 2x B = + − = + − 0,25 x + 3 x − 3 x − 9 x + 3
x − 3 ( x +3)( x −3) 2 x ( x −3) x ( x +3) 2x 2 = ( + − 0,25
x + 3)( x −3) ( x +3)( x −3) ( x +3)( x −3) 2
2x − 6 x + x + 3 x − 2x x − 3 x (2đ) = ( = x + 3)( x −3) ( x +3)( x −3) 0,25 x ( x −3) x = ( = (đpcm) x + 3)( x −3) x + 3 0,25 x − 2 x x − 2
P = A⋅ B = ⋅ = x x + 3 x + 3 Để x − 2 P < 0 ⇔ < 0 0,25 3 x + 3 Mà x +3 > 0
⇒ x − 2 < 0 ⇔ x < 4
Kết hợp với ĐKXĐ: x > 0; x ≠ 9⇒0 < x < 4
Mà x∈ Z . Vậy x∈{1;2; } 3 0,25
1 Hàm số y = (m + 1)x – 4 là hàm số đồng biến khi m + 1 > 0 ⇔ m > -1 0,5
Khi m =1thì hàm số có dạng: y = 2x − 4 0,25
HS trình bày đầy đủ các bước và vẽ đúng cắt Oy tại ( A 0; 4
− ) và cắt Ox tại B(2;0) 0,25 2 3 0,5 (2đ)
Tìm m để (d) song song với đường thẳng (d ): y = 2x +3 1 2 0,25 Để m +1 = 2
(d)// (d ) ⇔ ⇔ m =1 (tmđk) 1 4 − ≠ 3 Vậy với m = 1 thì (d)//(d 0,25 1)
+ AB là chiều dài chiếc thang + Â = 650 là góc an toàn B 0,25
+ AH là khoảng cách từ chân thang đến chân tường ABH, vuông tại H: 0,25 1
cosA = AH ⇒ cos650 = AH AB 4 0,25 650
Suy ra: AH = 4. Cos650 » 1,69 (m) A 0,25
Vậy cần đặt chân thang cách chân tường khoảng 1,69 mét H 2 0,5
Xét tam giác AOM vuông tại A (AM là tiếp tuyến) 4
Suy ra A, O, M cùng thuộc đường tròn, đường kính MO (1) 0,25
(4đ) a Xét tam giác COM vuông tại C (CM là tiếp tuyến)
Suy ra C, O, M cùng thuộc đường tròn, đường kính MO (2) 0,25
Từ (1) (2) suy ra A, O, C, M cùng thuộc đường tròn, đường kính MO 0,25
* Xét tam giác AIB có OA = OB = OI = 1 AB 0,25 2
b Suy ra tam giác AIB vuông tại I. 0,25
* Xét tam giác AMB vuông tại A có AI là đường cao 2
⇒ MA = MI.MB (3) 0,25
Mà MA = CM (theo tính chất 2 tiếp tuyến cắt nhau) (4) Từ (3) và (4) 2
⇒ CM = MI.MB (đpcm) 0,25
ON là trung trực của BC ⇒ NC = NB 0,25 Xét OC ∆ N và OB ∆
N có OC = OB; NC = NB; ON chung c ⇒ OC ∆ N = OB ∆ N (c.c.c) = 0 OCN OBM = 90 0,25
⇒ OB ⊥ NB . Vậy NB là tiếp tuyến của đường tròn (O). 0,25
2x +9x + 20 = 2 3x +10 (đk 10 x ≥ − ) 3 2
⇔ (x + 6x + 9) + (3x +10 − 2 3x +10 +1) = 0 5 2 2
⇔ (x + 3) + ( 3x +10 −1) = 0 (0,5đ) 0,25 x + 3 = 0 x = 3 − ⇔ ⇔ ⇔ x = 3( − tm) 3x +10 −1 = 0 3 x +10 = 1
Vậy phương trình có nghiệm x = 3 − 0,25
Chú ý: - Học sinh làm cách khác đúng vẫn cho điểm tối đa;
- Điểm toàn bài làm tròn đến 0,5 điểm./.
--------------------- Hết -----------------------