Đề học sinh giỏi cấp tỉnh Toán 12 năm 2023 – 2024 sở GD&ĐT Bình Phước

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI BÌNH PHƯỚC
CẤP TỈNH LỚP 12 THPT NĂM HỌC 2023 – 2024 ĐỀ CHÍNH THỨC Môn: Toán
(Đề thi gồm 01 trang)
Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 04/11/2023 Câu 1. (4,0 điểm) 1
a) Tìm tất cả các giá trị của tham số m để hàm số 3 2 y =
x − mx + (2m + 3)x + 2023 đồng biến 3 trên .
b) Cho hàm số y = f (x) có đạo hàm 2
f '(x) = x(x − 4) . Tìm các điểm cực trị của hàm số 2
g(x) = f (x − x) + 2024.
Câu 2. (2,0 điểm) Cho các số thực dương x, y thoả mãn: 2 2 log
(16x + 9y + 7) + log (8xy + 2023) = 2. 8xy+2023 24xy+7
Tính giá trị của biểu thức 2 2
P = 2x + y .
Câu 3. (2,0 điểm) Cho các số thực dương ,
x y, z thoả mãn điều kiện 2 2 2
x + y + z = 1. Tìm giá trị nhỏ nhất của biểu thức 1 1 2 P = + + . 2 2 + + 1+ z x xy y xy 2 2
y − x + 2(y − 2x) = 3+5  ( x+3− y+2)
Câu 4. (2,0 điểm) Giải hệ phương trình 
 x − 2 + 4 y = 8 − x + y + 29.  u  = 3
Câu 5. (2,0 điểm) Cho dãy số (u ) xác định bởi 1 
. Chứng minh rằng dãy số n u = 2u − 2, n  1  n 1+ n (v ) với * v = 2u − 4, n  
là một cấp số nhân và tìm công bội của cấp số nhân đó. n n n
Câu 6. (2,0 điểm) Gọi S là tập hợp các số tự nhiên có 5 chữ số đôi một khác nhau và các chữ số
này được lấy từ các chữ số 1, 2,3, 4,5,6,7,8,9. Chọn ngẫu nhiên một số từ tập S, tính xác suất để số
được chọn là số chẵn trong đó có đúng hai chữ số lẻ và hai chữ số lẻ này không đứng cạnh nhau.
Câu 7. (4,0 điểm) Cho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. Biết
SO = a 2, góc giữa đường thẳng SA và mặt phẳng (ABC ) D bằng 0 45 .
a) Tính thể tích khối chóp S.ABCD theo . a +
b) Gọi K là điểm di động trong mặt phẳng (ABC )
D . Tìm SAK để biểu thức SA AK T = đạt SK giá trị lớn nhất.
Câu 8. (2,0 điểm) Cho hình trụ có đường kính đáy bằng 4 5. Một mặt phẳng không vuông góc
với đáy và cắt hai đáy theo hai dây cung song song MN, M ' N ' thoả mãn MN = 8, M ' N ' = 4. Biết
rằng tứ giác MNN 'M ' có diện tích bằng 54. Tính thể tích khối trụ đã cho. ......HẾT......
- Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
- Giám thị coi thi không giải thích gì thêm.
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 THPT NĂM 2023 - 2024 MÔN THI: TOÁN Câu Nội dung Điểm
Câu 1a Tìm tất cả các giá trị của tham số m để hàm số 1 3 2 y =
x − mx + (2m + 3)x + 2023 đồng biến trên . 3 2.0
Hàm số đồng biến trên khi và chỉ khi 2
y ' = x − 2mx + 2m + 3  0, x   2
y ' = x − 2mx + 2m + 3  0, x   2
  ' = m − 2m − 3  0  1 −  m  3. Vậy 1 −  m  3 .
Câu 1b Cho hàm số y = f (x) có đạo hàm 2
f '(x) = x(x − 4) . Tìm các điểm cực 2.0 trị của hàm số 2
g(x) = f (x − x) + 2024. Ta có
f '(x) = x(x − 2)(x + 2) 2
g '(x) = (2x −1) f '(x − x) 2 2 2
 g '(x) = (2x −1)(x − x)(x − x − 2)(x − x + 2) 2
= (2x −1)x(x −1)(x +1)(x − 2)(x − x + 2)  1 x =  2  x = 0 
g '(x) = 0   x = 1 −   x =1   x = 2. Bảng xét dấu x − 1 −1 0 1 2 + 2
g '(x) − 0 + 0 − 0 + 0 − 0 +
Kết luận: Hàm số g(x) có 5 điểm cực trị là 1
x = −1, x = 0, x = , x = 1, x = 2. 2 Câu 2
Cho các số thực dương x, y thoả mãn 2.0 2 2 log
(16x + 9y + 7) + log (8xy + 2023) = 2. 8xy+2023 24xy+7
Tính giá trị của biểu thức 2 2
P = 2x + y . 2 2 16
 x + 9y + 7  7  Nhận xét: Với  , x y  0 ta có 8  xy + 2023  2023 24xy + 7  7. 
Theo bất đẳng thức Cauchy ta có 2 2 2 2
16x + 9y + 7  2 16x .9y + 7 = 24xy + 7 2 2  log
(16x + 9y + 7)  log (24xy + 7) 8xy+2023 8xy+2023 2 2  log
(16x + 9 y + 7) + log (8xy + 2023) 8 xy+2023 24 xy+7  log (24xy + 7) + log (8xy + 2023) 8 xy+2023 24 xy+7
Theo bất đẳng thức Cauchy ta có log (24xy + 7) + log (8xy + 2023) 8 xy+2023 24 xy+7  2 log (24xy + 7)  log (8xy + 2023) = 2. 8 xy+2023 24 xy+7
Dấu “=” xảy ra khi và chỉ khi 2 2 1  6x = 9y  log (24xy + 7) = log (8xy + 2023) = 1  8 xy+2023 24 xy+7  189 2 2 2 2 2 1  6x = 9y 1  6x = 9y x =       2
24xy + 7 = 8xy + 2023 xy =126 2 y =168. Vậy 2 2
P = 2x + y = 357. Câu 3 Cho các số thực dương ,
x y, z thoả mãn điều kiện 2 2 2
x + y + z = 1. 2.0
Tìm giá trị nhỏ nhất của biểu thức 1 1 2 P = + + . 2 2 + + 1+ z x xy y xy
Theo bất đẳng thức Cauchy ta có 1 1 2 +  2 2 x + xy y + xy ( 2x + xy)( 2 4 y + xy ) 2  2 2
x + xy + y + xy 2 2 = x+ y 2
Theo bất đẳng thức Bunhiacopski, ta có 2 2 2  = + 2 2 2 x y x + y 1− z 2 Khi đó 2 2 P  + . 2 − 1 1 + z z Xét hàm số 2 2 f (z) = + , z  (0;1) 2 − 1 1 + z z 2z 2 f '(z) = − 2 2 2 − − (1+ z) (1 z ) 1 z
2 z +1( 2z z +1 − (1− z) 1− z ) = 2 2 (1− z)(1+ z) 1− z 3 2
2(3z − z + 3z −1) f '(z) = 2 2 (1− z)(1+ z)
1− z ( 2z z +1 + (1− z) 1− z ) 2 2(3z −1)(z +1) = 2 2 (1− z)(1+ z)
1− z ( 2z z +1 + (1− z) 1− z ) 1
f '(z) = 0  z = . 3 Ta có bảng biến thiên  1  9 2
Suy ra P  f (z)  f = .    3  4
Các dấu bằng xảy ra khi và chỉ khi  1 z =   2 3 x = y =   3 x = y   1   2 2 2 + + = z = . x y z 1   3   2 x = y = 
Vậy giá trị nhỏ nhất của 9 2 3 P là khi  4 1 z = .  3 Câu 4 2 2
y − x + 2(y − 2x) = 3+5 
( x+3− y+2), (1)
Giải hệ phương trình  2.0
 x − 2 + 4 y = 8 − x + y + 29, (2)  x 2 Điều kiện: y 0. ( ) 2 2
1  ( y +1) + 5 ( y +1) +1 = (x + 2) + 5 (x + 2) +1 Xét hàm số 2
f (t) = t + 5 t +1 với t  0 . 5
Ta có f '(t) = 2t +  0, t   0. 2 t +1
Do đó hàm số f (t) đồng biến trên khoảng (0; ) + .
Mà f (y +1) = f (x + 2)  y +1= x + 2  y = x +1.
Thế y = x +1 vào (2) ta được:
x − 2 + 4 x +1 = 7 − x + 30  ( x − 2 − )
1 + 4( x +1 − 2) + 7(x − 3) = 0 x − 3 x − 3  + 4. + 7(x − 3) = 0 x − 2 +1 x +1 + 2  1 4   (x − 3) + + 7 = 0    x − 2 +1 x +1 + 2 
 x=3 y =4. 1 4 Vì + + 7  0, x   2. x − 2 +1 x +1 + 2
Vậy hệ phương trình có nghiệm ( ; x y) là (3;4). Câu 5 u  = 3
Cho dãy số (u ) xác định bởi 1  . Chứng minh rằng n u = 2u − 2, n  1  2.0 n 1 + n dãy số (v ) với * v = 2u − 4, n  
là một cấp số nhân và tìm công bội n n n của cấp số nhân đó. Ta có v
= 2u − 4 = 2(2u − 2) − 4 = 4u −8. n 1 + n 1 + n n Khi đó v 4u − 8 n 1 + n = v 2u − 4 n n 2(2u − 4) n = 2u − 4 n * = 2, n   .
Suy ra (v ) là cấp số nhân với công bội q = 2. n Câu 6
Gọi S là tập hợp các số tự nhiên có 5 chữ số đôi một khác nhau và các 2.0
chữ số này được lấy từ các chữ số 1,2,3,4,5,6,7,8,9. Chọn ngẫu nhiên
một số từ tập S, tính xác suất để số được chọn là số chẵn trong đó có
đúng hai chữ số lẻ và hai chữ số lẻ này không đứng cạnh nhau. Không gian mẫu 5 n() = A . 9
Biến cố A : “Số được chọn từ tập S là số chẵn trong đó có đúng hai
chữ số lẻ và hai chữ số lẻ này không đứng cạnh nhau”
Xét ba trường hợp (kí hiệu l là chữ số lẻ, c là chữ số chẵn)
- TH1: Số có dạng lcclc , có 2 3 A A (cách). 5 4
- TH2: Số có dạng lclcc , có 2 3 A A (cách). 5 4
- TH3: Số có dạng clclc , có 2 3 A A (cách). 5 4 Suy ra 2 3 n( )
A = 3 A A (cách). 5 4
Xác suất của biến cố A là 2 3 n( ) A 3 A A 2 5 4 P( ) A = = = . 5 n() A 21 9
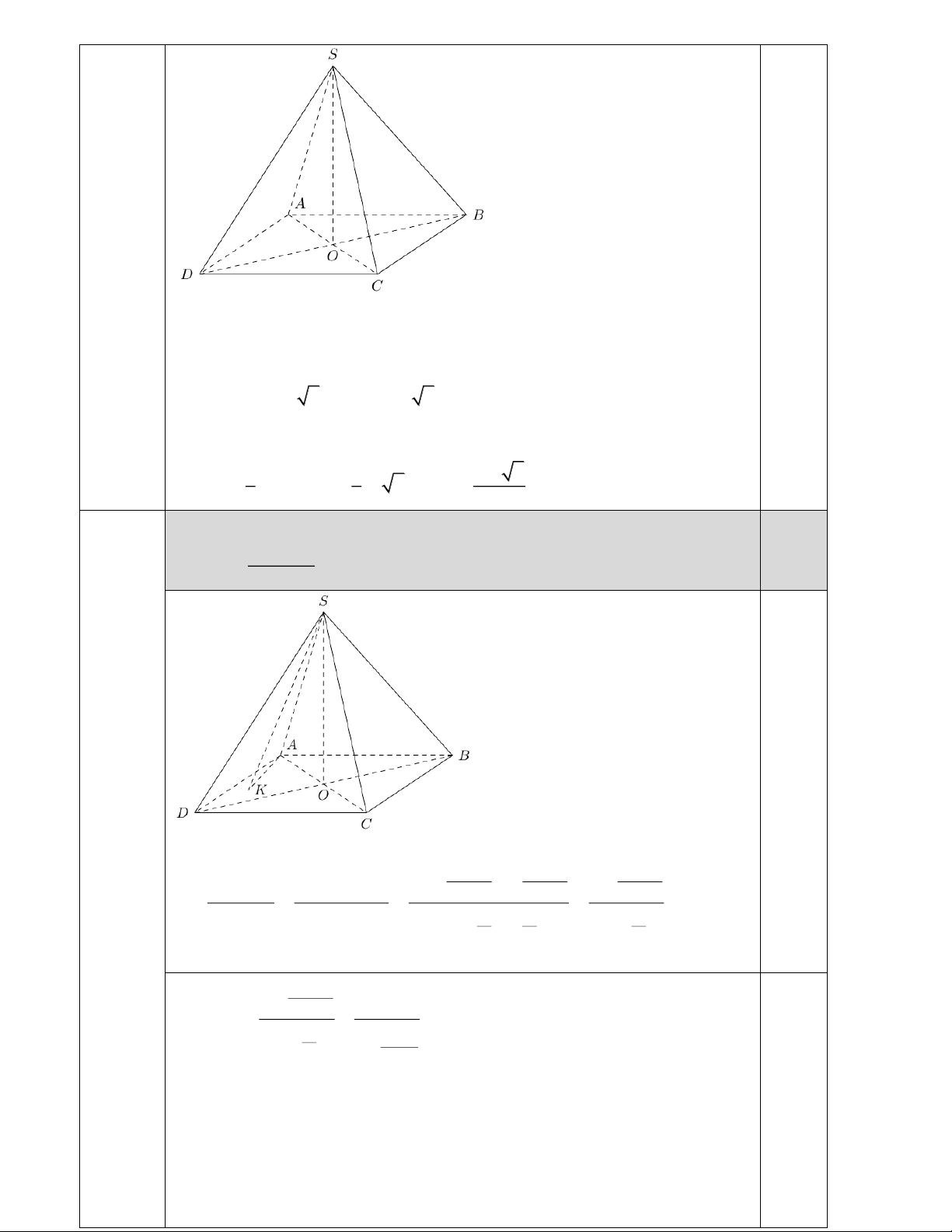
Câu 7a Cho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. 2.0
Biết SO = a 2, góc giữa đường thẳng SA và mặt phẳng (ABC ) D bằng 0 45 .
a) Tính thể tích khối chóp S.ABCD theo . a
Ta có SO ⊥ (ABC ) D  (SA ABCD ) 0 , ( ) = SAO = 45
 Tam giác SAO vuông cân tại O
 AO = SO = a 2  AC = 2a 2 Ta có 2 2 2 2 2
AD + DC = AC  2AD = 8a  AD = 2a
Suy ra thể tích khối chóp S.ABCD là 3 1 1 4a 2 2 V = SO S
= a 2 (2a) = (đvtt) S .ABCD 3 ABCD 3 3
Câu 7b b) Gọi K là điểm di động trong mặt phẳng (ABC )
D . Tìm SAK để biểu 2.0 + thức SA AK T =
đạt giá trị lớn nhất. SK
Áp dụng định lí hàm số sin vào tam giác SAK , ta có: K + S K − S K − S 2sin cos cos SA + AK sin K + sin S 2 2 2 T = = = = SK sin A A A A 2sin cos sin 2 2 2 K − S cos 1 Ta có: 2 T =  . A sin SAK sin 2 2
Dấu bằng xảy ra khi S = K , hay tam giác SAK cân tại A . Ta có (SA ABCD ) 0 , ( ) = SAO = 45 SAO SAK và 0 0 0 0
0  SAO  SAK  180  0    90 . 2 2 SAK  0  sin ( 1 1 0 22, 5 )  sin   2 SAK sin ( 0 22, 5 ) sin 2
Dấu “=” xảy ra khi SAO = SAK Do đó: 1 1 T   . SAK sin ( 0 22,5 ) sin 2 1 Vậy T =
khi K nằm trên đường thẳng AO sao cho AK = S . A max sin ( 0 22,5 ) Lúc này 0 SAK = 45 . Câu 8
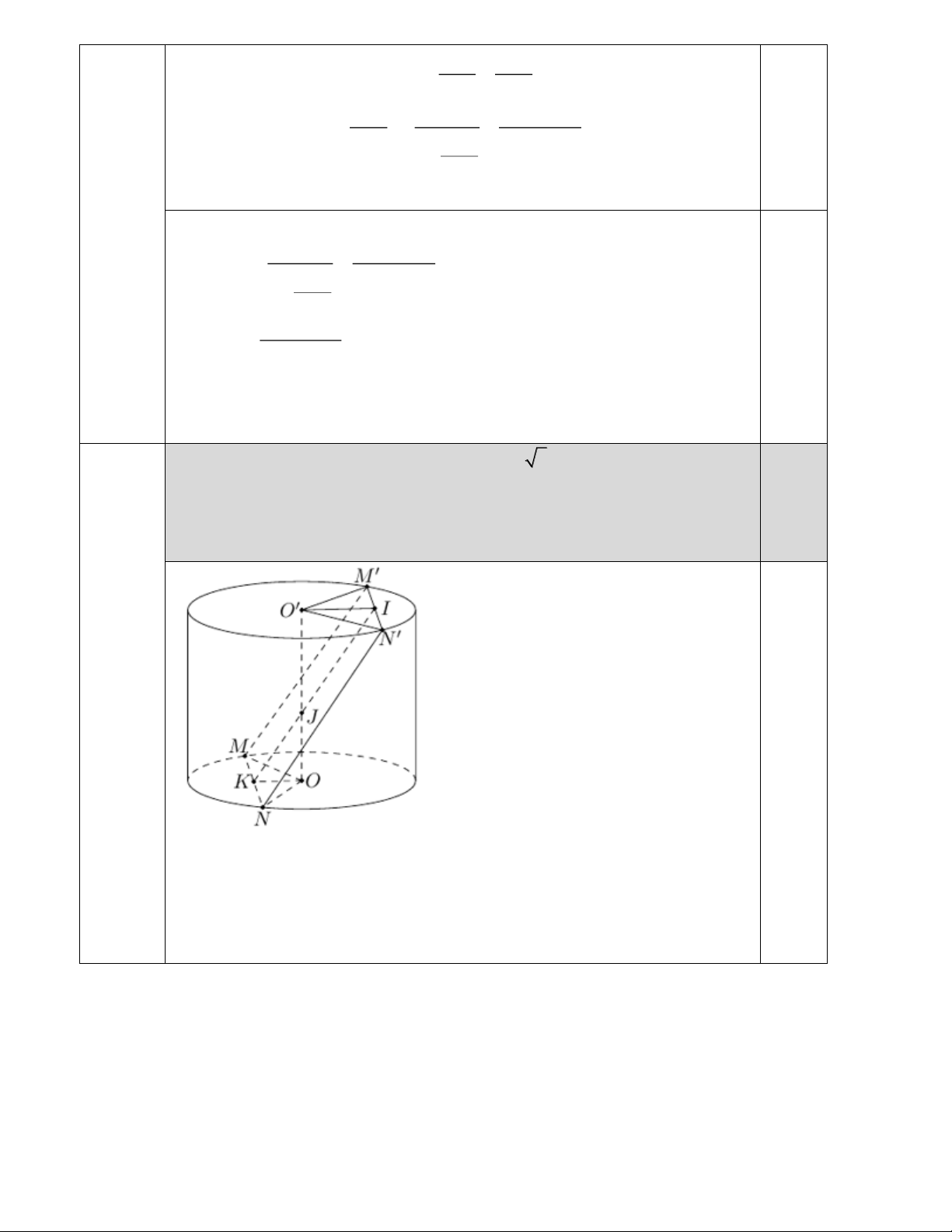
Cho hình trụ có đường kính đáy bằng 4 5. Một mặt phẳng không 2.0
vuông góc với đáy và cắt hai đáy theo hai dây cung song song
MN, M ' N ' thoả mãn MN = 8, M ' N ' = 4. Biết rằng tứ giác MNN ' M ' có
diện tích bằng 54. Tính thể tích khối trụ đã cho.
Gọi I, K lần lượt là trung điểm của M ' N ' và MN . Ta có: 4 điểm O', ,
O I, K đồng phẳng.
Gọi J là giao điểm của OO ' và IK . Khi đó IK là đường cao của hình
thang MNN ' M ' .
Khi đó diện tích hình thang MNN 'M ' là
(MN + M ' N ')  IK (8 + 4)  IK S =  54 =  IK = 9 MNN ' M ' 2 2 Mặt khác
O I = O M − M I = ( )2 2 2 2 ' ' ' ' 2 5 − 2 = 4
OK = OM − MK = ( )2 2 2 2 2 5 − 4 = 2 OK JO JK 1
Ta có O ' I OK  = = = O ' I JO ' JI 2 Khi đó 1 JK = IK = 3 3 2 2
 OJ = JK − OK = 5  OO' = 3OJ = 3 5
Vậy thể tích khối trụ là V =  ( )2 3 5 2 5 = 60 5 (đvtt).