Đề học sinh giỏi huyện Toán 9 năm 2014 – 2015 phòng GD&ĐT Nho Quan – Ninh Bình

UBND HUYỆN NHO QUAN
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 9
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2014 - 2015 Môn thi: TOÁN
Thời gian làm bài: 150 phút ĐỀ CHÍNH THỨC
(Đề thi gồm 5 câu trong 01 trang) Câu I (5,0 điểm).
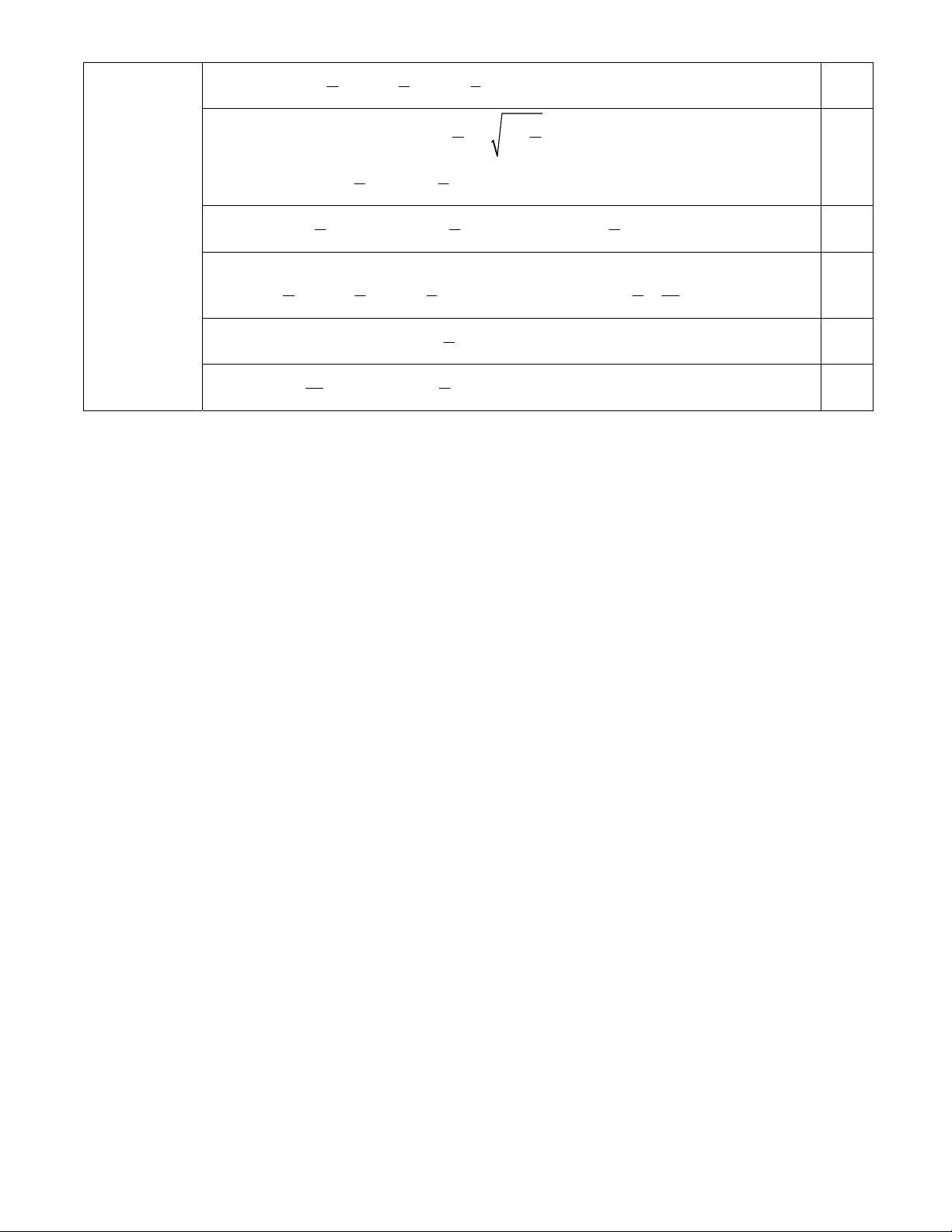
1. Rút gọn các biểu thức sau: 10  3 11
a) M  4  2 3  4  2 3 b) N  2 2 2x2  4 1 1
2. Cho biểu thức A   
với x  0, x  1. 1  x3 1  x 1  x
a) Rút gọn biểu thức A .
b) Tìm giá trị lớn nhất của biểu thức A .
Câu II ( 4,0 điểm).
1. Cho hàm số bậc nhất     2 y
1 3m x  5m  2 (1) và đường thẳng d: y  2x  3 .
a) Tìm giá trị của tham số m để hàm số (1) là hàm số đồng biến trên  .
b) Tìm giá trị của tham số m để đồ thị hàm số     2 y
1 3m x  5m  2 và đường thẳng d cắt
nhau tại một điểm trên trục tung.
c) Tìm trên đường thẳng d những điểm có tọa độ thoả mãn đẳng thức 2 2
x  y  2xy  4  0 .
2. Giải phương trình x  2x  5  2  x  3 2x  5  2  2 2 .
Câu III (4,0 điểm).
1. Cho m là một số nguyên. Chứng minh rằng: a) 5
m  m chia hết cho 30. 5 3 2 m m m 7m b) Biểu thức P     là một số nguyên. 30 6 2 10
2. Tìm nghiệm nguyên của phương trình 2 2
x y  xy  2x  3x  4  0 . Câu IV (5,5 điểm).
Cho tam giác ABC cân tại A và nội tiếp đường tròn (O) , các đường cao AE, BF,CG cắt
nhau tại H (E  BC, F  AC,G  AB) . 1. Chứng minh rằng: a) Bốn điểm ,
A F, H ,G cùng thuộc một đường tròn. Xác định tâm I của đường tròn đi qua 4 bốn điểm ,
A F, H ,G . b) A .
G AC  AH.AE .
c) EF là tiếp tuyến của đường tròn tâm I . 2. Đặt  
EIF  , IEF   . Tính 6 6 2 2 T  os c   o
c s   3sin  sin  . Câu V (1,5 điểm). 3
Cho a,b,c là ba số thực dương thỏa mãn điều kiện a  b  c  . Tìm giá trị nhỏ nhất của biểu 2 1 1 1
thức Q  a  b  c    . a b c
……………….Hết……………….
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm. UBND HUYỆN NHO QUAN
HD VÀ BIỂU ĐIỂM CHẤM MÔN TOÁN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI NĂM HỌC 2014 - 2015 ĐỀ CH ÍNH THỨC
Hướng dẫn chấm gồm : 04 trang
I) HƯỚNG DẪN CHUNG.
- Thí sinh làm bài theo cách khác đáp án, nếu đúng thì cho điểm tương đương.
- Việc chi tiết điểm số (nếu có) so với biểu điểm phải được thống nhất trong Hội đồng chấm.
Bài hình nếu hình vẽ không khớp với CM, hoặc không vẽ hình thì không chấm.
- Sau khi cộng điểm toàn bài, điểm lẻ đến 0,25 điểm.
II) ĐÁP ÁN VÀ BIỂU ĐIỂM CHẤM. Câu Nội dung Điểm Câu I (5,0đ)
M  4  2 3  4  2 3 = 2 2
( 3 1)  ( 3 1) 0,25 1a = 3 1  3 1 0,25 (1,0 điểm) 3 1 3 1 ( ì v 3  1) 0,25  2 3 0,25 10  3 11 1 10  3 11  N   1 20 6 11  0,5 2 2 2 2 2 4 1b (1,0 điểm)   2 3 11 3  11 1 1 3  11    0,5 2 4 2 2 4 2x2  4 1 1 2
2x  4 1 x 1 x  a) A        0,5 1  x3 1  x 1  x 3 1 x  1 x      2x2  4 2 2 2x  4  2 2 1 x  x  =   0,5 1  x3 1  x 1 x 2 1 x  x  2 21 x 2 ( 3,0 điểm)   = . 1 x 2 1 x  x  2 1 x  x 0,5 x  0 2 b) Với  thì A = 2 1 x  x  1 A   2 . x  1 2 1 x  x 0,5 A  2 khi x  0 . 0,25
Vậy giá trị lớn nhất của biểu thức A bằng 2 khi x  0 . 0,25 Câu II (4,0đ)
a) Hàm số bậc nhất     2 y
1 3m x  5m  2 đồng biến trên   1 3m  0 0,25 1 
3m  1  m  . 3 0,25
b) Đường thẳng y  2x  3 cắt trục tung tại điểm có tung độ bằng 3  x  0 ta được 0,25 1  (2,5đ) (0;3) Oy
Để đồ thị hàm số (1) và đường thẳng d cắt nhau tại 1 điểm trên trục tung thì tọa độ
(0;3) thỏa mãn (1), ta có    2 2
1 3m .0  5m  2  3  5m  5 2  m 1 0,5  m  1  . Vậy m  1
 thỏa mãn yêu cầu bài toán. 0,25
c) Thay y = 2x + 3 vào đẳng thức ta được: x2 + (2x + 3)2 – 2x(2x + 3) – 4 = 0 0,25
 x2 + 6x + 5 = 0  (x + 1)(x + 5) = 0  x = –1 ( y = 1), x = –5 (  y = –7). 0,5
Những điểm có toạ độ thoả mãn đẳng thức 2 2
x  y  2xy  4  0 là (–1; 1) và ( –5; –7). 0,25 5 ĐK: x  2 0,25
PT  2x  2 2x  5  4  2x  6 2x  5  4  4 0,25 2 2
 ( 2x  5 1)  ( 2x  5  3)  4
 2x  5 1 2x  5  3  4 0,25 2 (1,5đ)
 2x  5  3  3 2x  5 0,25
 3 2x  5  0  2x  5  3 0,25
 2x  5  9  2x  14  x  7 0,25 5
Kết hợp với điều kiện ta được nghiệm phương trình là  x  7 2 0,25 Câu III (4,0đ) C = 5 m  m = 4 2 2 2 2
m(m 1)  m(m 1)(m 1)  m(m 1) (m  4)  5)   0,25
= (m - 2)(m - 1)m(m+1)(m + 2)+ 5(m - 1)m(m+1) 0,25
Ta có A  (m  2)(m 1)m(m  1)(m  2) là tích của năm số nguyên liên tiếp nên 0,5 1a
A2, A3, A5 . Vì 2, 3, 5 là các số đôi một nguyên tố cùng nhau nên A30 (1) (2,0 điểm)
B  5(m 1)m(m 1) là tích của 3 số nguyên liên tiếp nên B2, B3, ì
v (2,3) 1 B6 . 0,5
Mặt khác B5 , vì (5;6)  1  B30 (2) 0,25
Từ (1) và (2)  C30 0,25 5 3 2 m m m 7m 5 3 2
m  m m  m m  m P     =   0,5 30 6 2 10 30 6 2      Theo chứng minh trên 5 3 2 m m 30 ; m m 6; m m2 075 5 3 2
m  m m  m m  m 1b  , , là các số nguyên. 0,5 30 6 2 (2,0 điểm) 5 3 2 m m m 7m Biểu thức P     là một số nguyên. 30 6 2 10 0,25 2 2
x y  xy  2x  3x  4  0 (1)
(1)  x(x 1)( y  2)  x  4 (2) 0,25 *) x  1
 không là nghiệm của (2) nên  x  1. Từ (2) ta có x  4 5 x( y  2)  1 . 0,25 x 1 x 1 2
Do x, y  x( y  2)  nên PT có nghiệm nguyên khi ( 2,0 điểm) x 1 0,25
là ước của 5  x 1 5  ;1; 1  ;5  x  6;   2;0;  4 (3)
*) Mặt khác x  0 không là nghiệm của (2)  x  0 Từ (2) ta có x  4 4
(x 1)( y  2)  1 0,25 x x
Do x, y  (x 1)( y  2)  nên PT có nghiệm nguyên khi 0,25
x là ước của 4  x  4;   2;1;1;2;  4 (4)
Từ (3) và (4) ta có x  2;   4 0,25 x  2   y  1
 , x  4  y 2 thoả mãn (1) 0,25
Vậy PT có nghiệm nguyên là ( 2  ; 1  ),(4;2) 0,25 Câu IV (5,5đ) A I (0,25 điểm) O 0,25 G F H B C E
a) BF  AC (gt)  0
 AFH  90  F  đường tròn đường kính AH (1) 0,25
CG  AB (gt)  0
 AGH  90  G  đường tròn đường kính AH (2) 0,25 a
(1,25 điểm) Từ (1) và (2)  F à
v G cùng thuộc đường tròn đường kính AH 0,25 Vậy bốn điểm ,
A F, H ,G cùng thuộc đường tròn đường kính AH 0,25
Tâm I của đường tròn đi qua bốn điểm ,
A F, H ,G là trung điểm của AH 0,25 b) Xét A  GH à v AEB  có  BAE chung,   0
AGH  AEB  90 (gt)  0,5 A
 GH AEB (g.g) b (1,5 điểm) AG AH    A .
B AG  AH.AE AE AB 0,5
Lại có AB  AC (gt)  A .
G AC  AH.AE 0,5 c) Xét IAF 
có IA  IF  IAF  cân tại  
I  IAF  IFA (3) 0,5
Ta có BE  BC (do AE là đường cao của tam giác cân ABC ) nên FE là trung c
tuyến thuộc cạnh huyền BC của  vuông BFC  EF  EB  B  EF cân 0,5 (1,5 điểm) tại E  
 EBF  EFB (4) Mặt khác   0   0
IAF  C  90 ; EBF  C  90    
 IAF  IFA  EBF  EFB (5) 0,5 Mà   0
IFA  IFH  90 (5) 0,25 Từ (3), (4), (5)   0
 IFH  HFE  90  EF  IF  EF là tiếp tuyến của (I) . 0,25
d) Theo chứng minh trên ta có EF  IF nên IFE  vuông tại F nên 0     90             0,25 os c  sin , os c  sin . Do đó 6 6 2 2 T os c os c 3sin sin d = 6 6 2 2 os c
  sin   3sin  cos  (1,0 điểm) 2 3 2 3 2 2
 (cos )  (sin )  (3cos  sin  ).1 0,25 2 3 2 3 2 2 2 2
 (cos )  (sin )  3cos  sin .(sin   cos ) 0,25 2 3 2 3 2 4 4 2
 (cos )  (sin )  3cos  sin   3cos  sin  2 2 3 3
 (sin   cos ) 1 1 0,25 1 1 1
Ta có Q  (4a  )  (4b  )  (4c  )  3(a  b  c) a b c 0,25 1 1
Áp dụng BĐT Cauchy ta có: 4a   2 4a   4 . a a 0,25 1 1
Tương tự ta có 4b   4 , 4c   4 b c 3 9 Câu V
Mà a  b  c  9
 3(a  b  c)   3(
 a  b  c)   0,25 (1,5đ) 2 2 2
Kết hợp các đánh giá trên ta có 1 1 1 9 15 0,25
Q  (4a  )  (4b  )  (4c  )  3(a  b  c)  4  4  4   a b c 2 2 1
Đẳng thức xảy ra khi a  b  c  2 0,25 15 1 Vậy MinQ 
khi a  b  c  2 2 0,25