Đề học sinh giỏi MTCT Toán THPT năm 2022 – 2023 sở GD&ĐT Vĩnh Long

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi chọn học sinh giỏi cấp tỉnh giải toán bằng máy tính cầm tay môn Toán THPT năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Vĩnh Long; kỳ thi được diễn ra vào ngày 09 tháng 04 năm 2023; đề thi có đáp án và hướng dẫn giải.

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
1
UBND TỈNH VĨNH LONG
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIẢI TOÁN BẰNG MÁY TÍNH CẦM TAY
Môn: Toán THPT
Khóa ngày: 09/4/2023 - Năm học: 2022-2023
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Điểm
(B
ằ
ng s
ố
)
Điểm
(B
ằ
ng ch
ữ
)
Chữ ký
ả
o 1
Chữ ký
ả
o 2
Số mật mã
Do ch
ủ
kh
ả
o ghi
Chú ý:
- Đề thi gồm 02 trang, thí sinh ghi đáp số vào ô kết quả.
- Các kết quả tính toán gần đúng; nếu không có chỉ định cụ thể, thì được ngầm hiểu là chính xác tới
6 (sáu) chữ số thập phân.
Bài 1: (10 điểm)
Tìm gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( ) 3 2
f x x x x
(làm tròn đến 9 chữ số thâp phân).
Kết quả:
Bài 2: (10 điểm)
Cho hàm số
2 2
( ) 3 2 5 4 3
y f x x x x x
a) Tính giá trị của hàm số khi
2 3
x
(làm tròn đến 5 chữ số thâp
phân).
b) Tính gần đúng a, b biết đường thẳng y = ax + b là tiếp tuyến của đồ thị
(C) tại điểm có hoành độ
2 3
x
(làm tròn đến 5 chữ số thâp
phân).
Kết quả:
Bài 3 : (10 điểm)
Cho dãy số với .
Tính gần đúng và .
Kết quả:
Bài 4: (10 điểm)
Tính gần đúng giá trị của m để hàm số
đạt cực đại tại .
Kết quả:
Bài 5: (10 điểm)
Trong mặt phẳng
Oxy
cho đường thẳng và elip
.
a) Tìm gần đúng tọa độ giao điểm của và .
b) Tìm gần đúng tọa độ điểm M nằm trên sao cho khoảng cách từ điểm
M đến tiêu điểm (có hoành độ dương) của bằng tiêu cự của .
Kết quả:
( )
n
u
*
3 3
1 2 1 2
1; 2; , , 3
n n n
u u u u u n N n
50
u
50
S
3 4 2
( ) 3 3 1
y f x x m x mx
1
2
x
: 2 7 0
x y
2 2
( ) : 1
25 16
x y
E
( )
E
( )
E
( )
E
Đ
Ề
THI CHÍNH TH
Ứ
C
2
Bài 6: (10 điểm)
Tìm cặp số nguyên dương
( ; )
x y
thỏa mãn phương trình
3 2
4 17(2 ) 161312
x x y .
Kết quả:
Bài 7: (10 điểm)
Xác định các khoảng gần đúng của
a
để phương trình sau đây có
3
nghiệm thực phân biệt:
3 2
2 0
x x ax a
(làm tròn đến 5 chữ số
thâp phân).
Kết quả:
Bài 8: (10 điểm)
Một người gửi triệu đồng vào ngân hàng với kì hạn tháng ( quý),
lãi suất một quý theo hình thức lãi kép. Sau đúng tháng, người đó
lại gửi thêm triệu đồng với hình thức và lãi suất như trên. Hỏi sau
năm tính từ lần gửi đầu tiên người đó nhận được số tiền gần với kết quả
nào nhất? (làm tròn đến 1 chữ số thâp phân)
Kết quả:
Bài 9: (10 điểm)
Cho 2023 đường tròn đồng tâm nội tiếp trong
2023 hình vuông (dạng như hình vẽ). Tính gần
đúng diện tích phần tô đậm, biết hình vuông lớn
nhất có cạnh bằng 1 cm (làm tròn đến 5 chữ số
thâp phân).
Kết quả:
Bài 10: (10 điểm)
Cho tam giác
ABC
có
3,5
AB
;
5,3
BC
;
4,8
CA
. Gọi
M
là trung
điểm của
AC
;
N
là điểm trên cạnh
BC
sao cho
3
BC BN
và
BM
cắt
AN
tại
I
. Trên đường thẳng vuông góc với mặt phẳng
( )
ABC
tại
I
, lấy
điểm
S
sao cho
7
SI
. Tính gần đúng
a) Độ dài các cạnh
SA
,
SB
,
SC
của tứ diện
SABC
(làm tròn đến 9
chữ số thâp phân).
b) Chiều cao
BK
của tứ diện
SABC
(làm tròn đến 9 chữ số thâp phân).
c) Bán kính
R
của mặt cầu ngoại tiếp tứ diện
SABC
(làm tròn đến 9
chữ số thâp phân).
Kết quả:
HẾT.
100
3
1
6%
6
100
1
3
UBND TỈNH VĨNH LONG
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIẢI TOÁN BẰNG MÁY TÍNH CẦM TAY
Môn: Toán THPT
Khóa ngày: 09/4/2023 - Năm học: 2022-2023
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
ĐÁP ÁN
Bài 1: (10 điểm)
Tìm gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( ) 3 2
f x x x x
.
Kết quả:
GTLN
( ) 3,828427125
f x
;
GTNN
( ) 1
f x
.
Bài 2: (10 điểm)
Cho hàm số
2 2
( ) 3 2 5 4 3
y f x x x x x
a) Tính giá trị của hàm số khi
2 3
x
.
b) Tính gần đúng a, b biết đường thẳng y = ax + b là tiếp tuyến của đồ thị
(C) tại điểm có hoành độ
2 3
x
.
Kết quả:
a) f
2 3
2,17298
b) a = f
’
(x
0
)
- 4,40166
b
4,45144.
Bài 3 : (10 điểm)
Cho dãy số với .
Tính gần đúng và .
Kết quả:
50 50
1,474705, 2,737353
u S
Bài 4: (10 điểm)
Tính gần đúng giá trị của m để hàm số
đạt cực đại tại .
Kết quả:
1,072350
m
Bài 5: (10 điểm)
Trong mặt phẳng Oxy cho đường thẳng và elip
.
a) Tìm gần đúng tọa độ giao điểm của và .
b) Tìm gần đúng tọa độ điểm M nằm trên sao cho khoảng cách từ điểm
M đến tiêu điểm (có hoành độ dương) của bằng tiêu cự của .
Kết quả:
(4,577709;5,788854)
M
( 2,577709;2,211146)
M
Bài 6: (10 điểm)
Tìm cặp số nguyên dương
( ; )
x y
thỏa mãn phương trình
3 2
4 17(2 ) 161312
x x y .
Kết quả:
30
116.
x
y
;
30
4
x
y
Bài 7: (10 điểm)
Xác định các khoảng gần đúng của
a
để phương trình sau đây có
3
nghiệm thực phân biệt:
3 2
2 0
x x ax a
(làm tròn đến 5 chữ số
thâp phân)
Kết quả:
- 0,52377 < a < 0;
a > 15,27377.
( )
n
u
*
3 3
1 2 1 2
1; 2; , , 3
n n n
u u u u u n N n
50
u
50
S
3 4 2
( ) 3 3 1
y f x x m x mx
1
2
x
: 2 7 0
x y
2 2
( ): 1
25 16
x y
E
( )
E
( )
E
( )
E
Đ
Ề
THI CHÍNH TH
Ứ
C
4
Bài 8: (10 điểm)
Một người gửi triệu đồng vào ngân hàng với kì hạn tháng ( quý),
lãi suất một quý theo hình thức lãi kép. Sau đúng tháng, người đó
lại gửi thêm triệu đồng với hình thức và lãi suất như trên. Hỏi sau
năm tính từ lần gửi đầu tiên người đó nhận được số tiền gần với kết quả
nào nhất? (làm tròn đến 1 chữ số thâp phân)
Kết quả:
238 6, triệu đồng
Bài 9: (10 điểm)
Cho 2023 đường tròn đồng tâm nội tiếp trong
2023 hình vuông (dạng như hình vẽ). Tính gần
đúng diện tích phần tô đậm, biết hình vuông lớn
nhất có cạnh bằng 1 cm.
Kết quả:
2
0,42920 cmS
Bài 10: (10 điểm)
Cho tam giác
ABC
có
3,5AB
;
5,3BC
;
4,8CA
. Gọi
M
là trung
điểm của
AC
;
N
là điểm trên cạnh
BC
sao cho
3BC BN
và
BM
cắt
AN
tại
I
. Trên đường thẳng vuông góc với mặt phẳng
( )ABC
tại
I
, lấy
điểm
S
sao cho
7SI
. Tính gần đúng
a) Độ dài các cạnh
SA
,
SB
,
SC
của tứ diện
SABC
.
b) Chiều cao
BK
của tứ diện
SABC
.
c) Bán kính
R
của mặt cầu ngoại tiếp tứ diện
SABC
.
Kết quả:
a)
7,375805041SA
;
7,252758096SB
;
7,894460083SC
b) 3,32111312BK
c)
4,072300745R
HẾT.
100
3
1
6%
6
100
1
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

UBND TỈNH VĨNH LONG
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIẢI TOÁN BẰNG MÁY TÍNH CẦM TAY Môn: Toán THPT
Khóa ngày: 09/4/2023 - Năm học: 2022-2023
Thời gian làm bài: 120 phút (không kể thời gian phát đề) ĐỀ THI CHÍNH THỨC Điểm Điểm Chữ ký Chữ ký Số mật mã (Bằng số) (Bằng chữ) Giám khảo 1 Giám khảo 2 Do chủ khảo ghi Chú ý:
- Đề thi gồm 02 trang, thí sinh ghi đáp số vào ô kết quả.
- Các kết quả tính toán gần đúng; nếu không có chỉ định cụ thể, thì được ngầm hiểu là chính xác tới
6 (sáu) chữ số thập phân.
Bài 1: (10 điểm)
Tìm gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số Kết quả: 2
f (x)  x  3  2x x (làm tròn đến 9 chữ số thâp phân).
Bài 2: (10 điểm) Cho hàm số 2 2
y f (x)  x  3x  2  5  4x  3x Kết quả:
a) Tính giá trị của hàm số khi x
2  3 (làm tròn đến 5 chữ số thâp phân).
b) Tính gần đúng a, b biết đường thẳng y = ax + b là tiếp tuyến của đồ thị
(C) tại điểm có hoành độ x
2  3 (làm tròn đến 5 chữ số thâp phân).
Bài 3 : (10 điểm)
Cho dãy số (u ) với * 3 3
u  1;u  2;u uu , n
  N , n  3 . Kết quả: n 1 2 n n 1  n2
Tính gần đúng u và S . 50 50
Bài 4: (10 điểm)
Tính gần đúng giá trị của m để hàm số 3 4 2
y f (x)  x  3m x  3mx  1 Kết quả: 1
đạt cực đại tại x  . 2
Bài 5: (10 điểm)
Trong mặt phẳng Oxy cho đường thẳng  : x  2 y  7  0 và elip Kết quả: 2 2 x y (E) :   1. 25 16
a) Tìm gần đúng tọa độ giao điểm của  và (E) .
b) Tìm gần đúng tọa độ điểm M nằm trên  sao cho khoảng cách từ điểm
M đến tiêu điểm (có hoành độ dương) của (E) bằng tiêu cự của (E) . 1
Bài 6: (10 điểm)
Tìm cặp số nguyên dương ( ;
x y) thỏa mãn phương trình Kết quả: 3 2
4x 17(2x y)  161312 .
Bài 7: (10 điểm)
Xác định các khoảng gần đúng của a để phương trình sau đây có 3 Kết quả:
nghiệm thực phân biệt: 3 2
x  2x ax a  0 (làm tròn đến 5 chữ số thâp phân).
Bài 8: (10 điểm)
Một người gửi 100 triệu đồng vào ngân hàng với kì hạn 3 tháng (1 quý), Kết quả:
lãi suất 6% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó
lại gửi thêm 100 triệu đồng với hình thức và lãi suất như trên. Hỏi sau 1
năm tính từ lần gửi đầu tiên người đó nhận được số tiền gần với kết quả
nào nhất? (làm tròn đến 1 chữ số thâp phân)
Bài 9: (10 điểm)
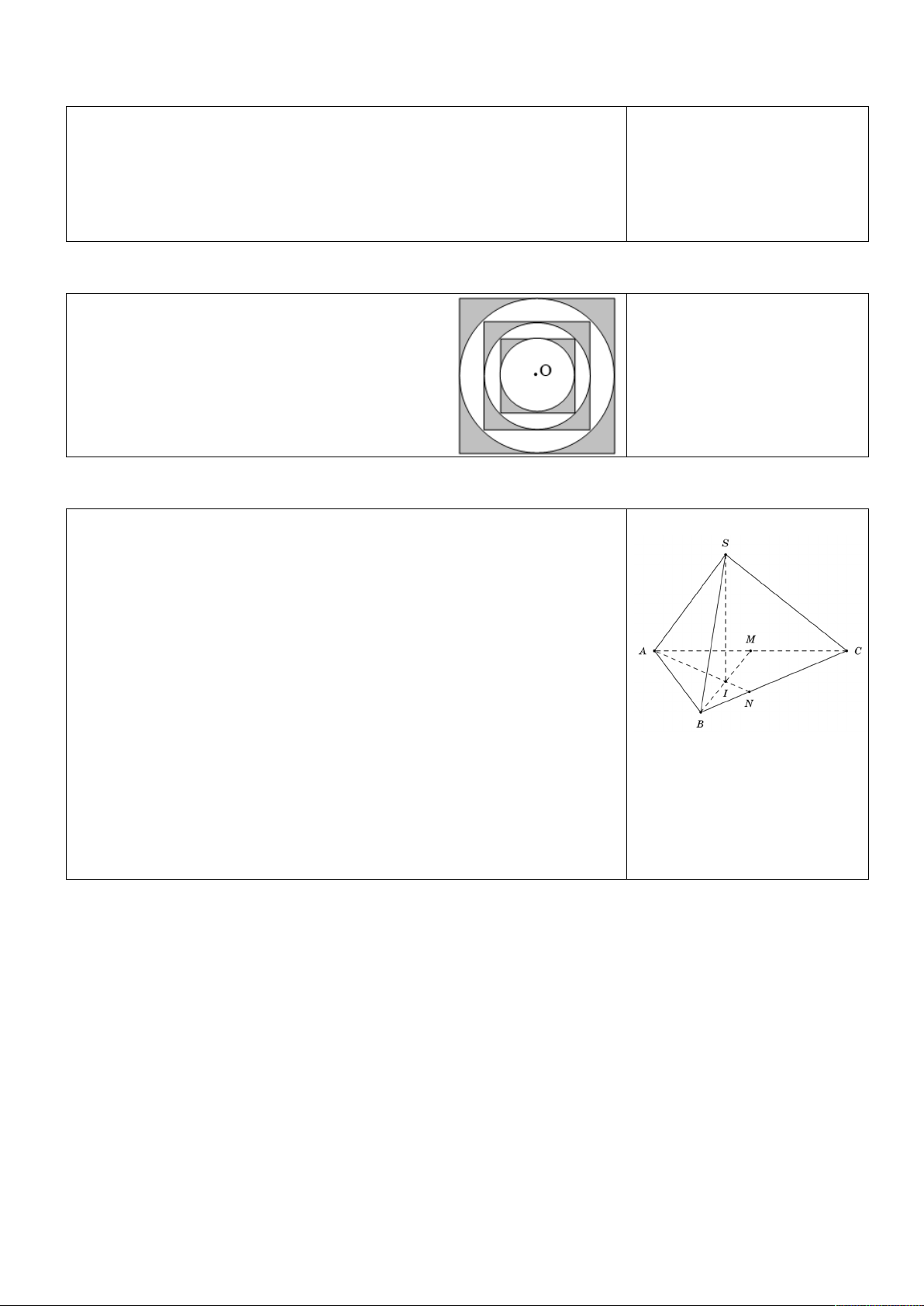
Cho 2023 đường tròn đồng tâm nội tiếp trong Kết quả:
2023 hình vuông (dạng như hình vẽ). Tính gần
đúng diện tích phần tô đậm, biết hình vuông lớn
nhất có cạnh bằng 1 cm (
làm tròn đến 5 chữ số
thâp phân).
Bài 10: (10 điểm)
Cho tam giác ABC có AB  3, 5 ; BC  5,3 ; CA  4,8 . Gọi M là trung Kết quả:
điểm của AC ; N là điểm trên cạnh BC sao cho BC  3BN và BM cắt
AN tại I . Trên đường thẳng vuông góc với mặt phẳng ( ABC) tại I , lấy
điểm S sao cho SI  7 . Tính gần đúng
a) Độ dài các cạnh SA , SB , SC của tứ diện SABC (làm tròn đến 9
chữ số thâp phân).
b) Chiều cao BK của tứ diện SABC (làm tròn đến 9 chữ số thâp phân).
c) Bán kính R của mặt cầu ngoại tiếp tứ diện SABC (làm tròn đến 9
chữ số thâp phân). HẾT. 2
UBND TỈNH VĨNH LONG KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIẢI TOÁN BẰNG MÁY TÍNH CẦM TAY Môn: Toán THPT
Khóa ngày: 09/4/2023 - Năm học: 2022-2023
Thời gian làm bài: 120 phút (không kể thời gian phát đề) ĐỀ THI CHÍNH THỨC ĐÁP ÁN
Bài 1: (10 điểm)
Tìm gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số Kết quả: 2
f (x)  x  3  2x x .
GTLN f (x)  3,828427125 ; GTNN f (x)  1  .
Bài 2: (10 điểm) 2 2 Kết quả:
Cho hàm số y f (x)  x  3x  2  5  4x  3x
a) Tính giá trị của hàm số khi x  2  3 .
a) f  2  3   2,17298
b) Tính gần đúng a, b biết đường thẳng y = ax + b là tiếp tuyến của đồ thị
b) a = f ’(x0)  - 4,40166
(C) tại điểm có hoành độ x  2  3 . b  4,45144.
Bài 3 : (10 điểm)
Cho dãy số (u ) với * 3 3
u  1;u  2;u uu , n
  N , n  3 . Kết quả: n 1 2 n n 1  n2
u  1, 474705, S  2, 737353
Tính gần đúng u và S . 50 50 50 50
Bài 4: (10 điểm)
Tính gần đúng giá trị của m để hàm số 3 4 2
y f (x)  x  3m x  3mx  1 Kết quả: 1
đạt cực đại tại x  . m  1, 072350 2
Bài 5: (10 điểm)
Trong mặt phẳng Oxy cho đường thẳng  : x  2 y  7  0 và elip Kết quả: 2 2 x y (E) :   1. M (4,577709;5, 788854) 25 16
a) Tìm gần đúng tọa độ giao điểm của  và (E) . M ( 2  , 577709; 2, 211146)
b) Tìm gần đúng tọa độ điểm M nằm trên  sao cho khoảng cách từ điểm
M đến tiêu điểm (có hoành độ dương) của (E) bằng tiêu cự của (E) .
Bài 6: (10 điểm)
Tìm cặp số nguyên dương ( ;
x y) thỏa mãn phương trình Kết quả: 3 2
4x 17(2x y)  161312 . x  30 x  30  ;  y  116.  y  4 
Bài 7: (10 điểm)
Xác định các khoảng gần đúng của a để phương trình sau đây có 3 Kết quả:
nghiệm thực phân biệt: 3 2
x  2x ax a  0 (làm tròn đến 5 chữ số
- 0,52377 < a < 0; thâp phân) a > 15,27377. 3
Bài 8: (10 điểm)
Một người gửi 100 triệu đồng vào ngân hàng với kì hạn 3 tháng (1 quý), Kết quả:
lãi suất 6% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó
lại gửi thêm 100 triệu đồng với hình thức và lãi suất như trên. Hỏi sau 1 238,6 triệu đồng
năm tính từ lần gửi đầu tiên người đó nhận được số tiền gần với kết quả
nào nhất? (làm tròn đến 1 chữ số thâp phân)
Bài 9: (10 điểm)
Cho 2023 đường tròn đồng tâm nội tiếp trong Kết quả:
2023 hình vuông (dạng như hình vẽ). Tính gần 2 S  0,42920 cm
đúng diện tích phần tô đậm, biết hình vuông lớn
nhất có cạnh bằng 1 cm.
Bài 10: (10 điểm)
Cho tam giác ABC có AB  3, 5 ; BC  5,3 ; CA  4,8 . Gọi M là trung Kết quả:
điểm của AC ; N là điểm trên cạnh BC sao cho BC  3BN và BM cắt
AN tại I . Trên đường thẳng vuông góc với mặt phẳng ( ABC) tại I , lấy
điểm S sao cho SI  7 . Tính gần đúng
a) Độ dài các cạnh SA , SB , SC của tứ diện SABC .
b) Chiều cao BK của tứ diện SABC .
c) Bán kính R của mặt cầu ngoại tiếp tứ diện SABC .
a) SA  7, 375805041; SB  7, 252758096 ; SC  7,894460083 b) BK  3,32111312 c) R  4, 072300745 HẾT. 4